螺旋千斤顶课程设计计算书

合集下载

清华大学机械设计课程大作业-螺旋起重器设计计算书

H 53 17.6mm 。 3 3
m m，高 H r1 9 m m，手柄套高 H r 2 36mm ，直径轴颈直径 Dr1 1 7 . 8 Dr 2 44mm 。凸台高度 H r 3 12mm ，凸台直径 Dr 3 22mm 。
Step10：托杯尺寸设计
m
FP 30000 6 0.239 。 N 2 L 200 2 600
怎样设计可以省力？减小螺距（但工作时旋转手柄的圈数会增加，容易使人疲劳）；增长手柄或两侧都设计成有手柄。怎样设计可以节省操作空间？手柄上套有加长套筒，不用时可以拆卸；加装齿轮减速装置。注：以上尺寸设计中用到的、未列出的经验公式参见：《机械设计习题与解析》，修世超主编。北京：科学出版社，2008。
MPa ，许用挤压应力螺母螺纹牙，由表 2-40 ，许用弯曲应力 [ b ] 50
[ p ] 75MPa ，许用剪应力 [ ] 30MPa 。螺纹牙根部厚度 b 0.5P 3mm ，螺纹
2
2
2
2
高度 h 0.5P 3mm ，校核其强度 3Fh 3 30000 3 b 45MPa [ b ] 2 Z db 8.83 24 32 F 30000 15MPa [ ] 。 Z db 8.83 24 3 螺纹形状如图：
Step12：手柄尺寸设计
手柄材料为 HT250。外形如图：
由工作时载荷平衡
NL F d2 1 D 3 Dc 23 tan v fF c12 2 3 Dc1 Dc 2 2
得手柄长度
403 163 21 1 L 30000 tan 5.20 5.71 0.10 30000 2 200 526mm 2 2 3 40 16

螺旋千斤顶设计说明书

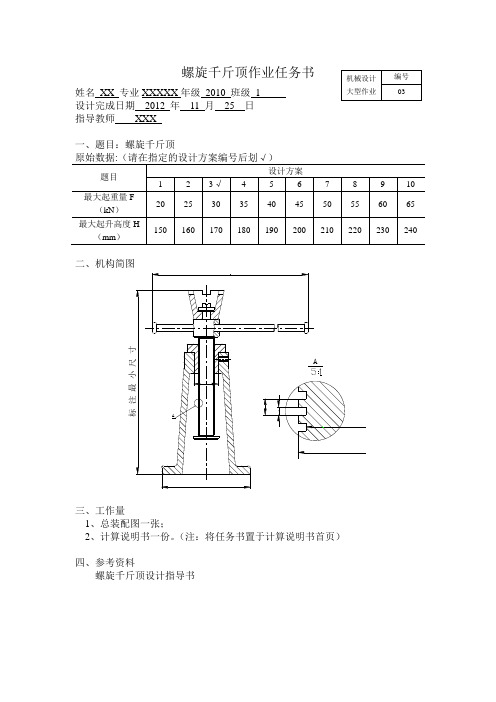
螺旋千斤顶作业任务书姓名 XX 专业XXXXX 年级 2010 班级 1设计完成日期 2012 年 11 月 25 日指导教师 XXX一、题目：螺旋千斤顶原始数据:（请在指定的设计方案编号后划√）题目设计方案1 2 3√ 4 5 6 7 8 9 10 最大起重量F （kN ） 20 25 30 35 40 45 50 55 60 65 最大起升高度H（mm ）150160170180190200210220230240二、机构简图标注最小尺寸AA三、工作量1、总装配图一张；2、计算说明书一份。

（注：将任务书置于计算说明书首页）四、参考资料螺旋千斤顶设计指导书机械设计大型作业编号03目录一、设计题目 (4)二、螺杆的设计与计算2.1 螺纹的牙型 (3)2.2螺杆的材料 (3)2.3螺纹直径 (3)2.4自锁验算 (4)2.5其他结构设计 (5)2.6螺杆的强度校核 (5)三、螺母的设计与计算3.1材料 (6)3.2螺纹圈数Z与高度H (6)3.3螺母其他尺寸 (6)3.4螺母与底座的配合 (7)四、螺杆稳定性验算 (7)五、托杯的设计与计算 (8)六、手柄设计与计算 (8)6.1材料 (9)6.2手柄长度 (9)6.3手柄直径 (9)6.4其他结构 (10)七、底座设计11八、千斤顶的效率12计算及说明结果一、设计题目螺旋千斤顶主要零件：螺杆、螺母、托杯、手柄和底座。

扳动手柄可使螺杆在固定螺母中旋转，从而将托杯上的重物举起或放落。

设计的原始数据：最大起重F=30KN 、最大升起高度H=170mm 。

二、螺杆的设计与计算：2.1 螺纹的牙型选用矩形螺纹，采用内径对中，配合选H8/h8，由于螺纹的径向间隙很小，在强度计算时不予考虑。

2.2螺杆的材料查资料]1[可知，螺杆可选用45钢，弹性模量MPa E 196=2.3螺纹直径螺杆工作时，同时受压力与扭矩的作用，因此它的计算可近似按紧螺栓联接的计算公式估算出螺纹内径，即：F=30KN H=170mmH8/h8螺杆45钢弹性模量MPa E 196=[]σπFd 3.1x 41≥（1）参考资料]2[得知，螺杆的屈服极限MPa s 345=σ，取安全因数3=S ，得许用应力[]MPa Ss115==σσ （2）将数据带入式（1）得螺纹内径估算值为mm d 78.201011510303.14631=⨯⨯⨯⨯⨯≥π （3）根据经验公式4P 1d =，得mm P 20.5=。

机械设计教程大作业螺旋千斤顶设计方案

机械设计教程大作业——螺旋千斤顶设计一、要求条件根据最大起升重量选择材料和螺纹尺寸，要求满足耐磨性条件、强度条件、稳定性条件和自锁条件。

确定全部结构形式和尺寸，绘制装配图和螺母零件图。

设计计算部分包括螺旋传动的材料选择，螺纹牙型的选择，工作能力计算和自锁性计算，其它结构的工作能力计算（螺母许用挤压应力[σp ]≈1.5 [σb ]）；地面承压能力计算，确定下支承面尺寸(木材许用挤压应力[σp ]=3MPa)；人手的操作能力计算，确定手柄的直径和长度（人手最大操作力≈200N ）。

根据学号尾数为3，对应的最大起升重量为F max =50kN ，最大升距为h max =300mm 。

二、设计及计算1、螺杆的设计及计算1.1、螺杆螺纹类型选择螺纹根据牙形，分为普通螺纹、矩形螺纹、梯形螺纹、锯齿形螺纹。

其中，本题选择梯形螺纹，右旋单线，截面为等腰梯形，牙型角α=30º，内外螺纹以锥面贴紧不易松动，基本牙型按照GB/T5796.2-2005规定。

1.2、选材由于螺旋千斤顶受力较大，转速较低且为传力螺旋，由教材P98表2-38，选择45或50钢正火。

本设计采用45钢。

1.3、确定螺杆直径由耐磨性及设计公式 d 2≥[]p h F πφP依国家规定，∅=1.2~2.5，考虑到螺母为整体结构，取∅=1.2。

又由于梯形螺纹，h =0.5P 。

由于为重载低速场合，螺母取ZCuAl10Fe3材料，则螺杆螺母为钢-青铜材料，[p]=18~25Mpa 。

由于∅<2.5，提高20%，故[p ]=21.6~30Mpa ，则取[p]=28Mpa ，取f=0.09。

代入数据，如下计算得到d 2≥[]p h F πφP = 0.8][p F φ=0.8√500001.2×22×106=34.82mm 。

查询GB/T5796.2-2005，取d 2=36.5mm ，d=40mm ，P=7mm ，D 4=41mm ，d 3=32mm （即以下计算中的d1），D1=33mm。

毕业设计(论文)-电动螺旋千斤顶的结构设计

摘要本设计主要是对电动螺旋千斤顶的结构设计，在原有手动螺旋千斤顶的基础上，通过对螺旋千斤顶了解和学习，选择对其进行改进，设计出一套蜗轮蜗杆机构，利用电机带动蜗杆，蜗杆蜗轮传动带动丝杠运转，由丝杠螺母形成的滑动螺旋副运动将重物顶起，既发挥了螺旋副的自锁性的优点又可改善劳动条件。

同时提高了市场的竞争能力。

本设计根据承受载荷，设计出丝杠传动机构，根据丝杠传动的工作速度与螺杆所承受的扭矩，来设计蜗杆和蜗轮传动机构，得出蜗杆传动扭矩来进行电机的选型，并使用Pro/ENGINEER 5.0和AutoCAD三维建模软件，设计零件并进行装配。

用SolidWorks进行仿真制作。

并对蜗杆模型通过ANSYS软件进行简单的有限元分析来完成整个设计。

关键字：蜗轮蜗杆；有限元分析；丝杠传动；仿真；三维建模AbstractThe design is mainly for the structural design of screw jacks, screw jacks in the original on the jackscrew through understanding and learning, choose to improve it, to design a worm gear mechanism, the use of motor driven worm and worm gear drive screw operation, the heavy top, both played a spiral lock of the advantages of self but also improve people's deputy of the working conditions. Improve the competitiveness of the market.The design of the load bearing design of the screw drive mechanism according to the operating speed of the screw drive torque of the screw is exposed to the worm and the worm gear is enough design, draw worm drive torque of the motor to the selection and use Autocad Proe 5.0 and three-dimensional modeling software, design and assembly of parts. With solidworks simulation production. And a simple worm model by ANSYS finite element analysis software to complete the entire design.Keywords：Worm; Finite Element; Analysis Screw drive; Simulation;Three-dimensional modeling目录第1章绪论 01.1 起重机械 01.2 千斤顶 01.3 国内外千斤顶发展情况 01.4 研究目的 01.5 设计规格 (1)1.6 设计原理 (1)1.7 使用方法 (1)第2章丝杠传动的设计和计算 (2)2.1 丝杠传动 (2)2.2 丝杠传动的结构及材料 (3)2.2.1 丝杠传动的结构 (3)2.2.2 丝杠传动中常用材料 (3)2.3 丝杠传动的设计计算 (5)2.3.1 耐磨性与自锁性计算 (5)2.3.2 螺杆的强度计算 (8)2.3.3 螺母螺纹牙的强度计算 (8)2.3.4 螺杆的稳定性计算 (9)第3章蜗轮蜗杆传动的设计和计算 (11)3.1 蜗轮蜗杆传动的特点 (11)3.2 蜗杆传动的类型 (11)3.2.1 普通圆柱蜗杆传动 (11)3.2.2 圆弧圆柱蜗杆传动 (11)3.3 蜗轮蜗杆传动的设计参数选择 (11)3.3.1 蜗杆传动选型 (11)3.3.2 选择蜗轮蜗杆材料 (11)3.3.3 蜗杆传动设计 (12)3.3.4 蜗杆与蜗轮的参数计算 (13)3.3.5 齿根弯曲疲劳强度校核 (13)3.3.6 实际传动效率 (14)3.3.7 精度等级 (14)第4章螺旋千斤顶电机的选择 (16)4.1 电机类型选择 (16)4.2 蜗杆力矩计算 (16)4.3 电动机功率计算 (16)4.4 电动机选择 (17)第5章蜗杆的有限元分析 (18)5.1 有限元分析 (18)5.2 文件的导入 (18)5.3 设置材料常数 (18)5.4 划分网格 (18)5.6 求解计算 (20)5.7 结论 (20)第6章螺旋千斤顶的三维建模 (22)6.1 蜗杆的三维建模 (22)6.2 蜗轮的三维建模 (23)6.3 螺杆的三维建模 (24)6.4 螺母的三维建模 (25)6.5 千斤顶的装配 (26)6.6 千斤顶的仿真 (26)设计总结 (28)参考文献 (29)致谢 (30)第1章绪论1.1 起重机械起重机械是一种通过重复循环运动对物料进行起升的机械，其运动形式主要有起动、制动、正向和反向运动。

机械设计-螺旋千斤顶

螺旋千斤顶大作业院系机械工程专业年级车辆工程141设计者周六圆指导教师陈丰2016 年10 月 6 日..要求1、总体设计结构合理，操作方便（可自己设计结构如用侧面手柄上下往复式或脚踏式等）；2、设计要求：绘制千斤顶装配图，主要零件图两张（计算机绘图，二维图必须，三维图随便），完整的设计说明书；3、网上有类似内容（哈工大机械设计大作业），不得抄袭；4、大胆创新，发动脑筋，奇思妙想，功能和结构上创新；5、螺杆和螺母材料自定，原始数据不同，具体分配如下：根据学号1608140134尾数可得：起重量为35KN起重高度为200mm第一部分千斤顶的概述千斤顶又叫举重器、顶重机、顶升机等，是一种用比较小的力就能把重物顶升、下降或移位的简单起重机具，也可用来校正设备安装的偏差和构件的变形等。

千斤顶主要用于厂矿、交通运输等部门作为车辆修理及其它起重、支撑等工作。

其结构轻巧坚固、灵活可靠，一人即可携带和操作。

千斤顶是用刚性顶举件作为工作装置，通过顶部托座或底部托爪在小行程内顶升重物的轻小起重设备，千斤顶的顶升高度一般为400mm，顶升速度一般为10-35mm/min，起重能力最大可达500t。

第二部分螺旋传动的设计与计算2.1螺旋传动的应用和类型螺旋传动是利用螺杆（丝杠）和螺母组成的螺旋副来实现传动要求的。

它主要用于将回转运动转变为直线运动，同时传递运动和动力。

它具有结构紧凑、转动均匀、准确、平稳、易于自锁等优点，在工业中获得了广泛应用。

（1）按螺杆与螺母的相对运动方式，螺旋传动可以有以下四种运动方式：①螺母固定不动，如图(a)螺杆转动并往复移动，这种结构以固定螺母为主要支承，结构简单，但占据空间大。

常用于螺旋压力机、螺旋千斤顶等。

②螺母转动，如图(b)螺杆做直线移动，螺杆应设防转机构，螺母转动要设置轴承均使结构复杂，且螺杆行程占据尺寸故应用较少。

③螺母旋转并沿直线移动，如图(c)由于螺杆固定不动，因而二端支承结构较简单，但精度不高。

螺旋千斤顶课程设计

螺旋千斤顶课程设计一、课程目标知识目标：1. 学生能理解螺旋千斤顶的基本结构、工作原理及其在工程中的应用。

2. 学生能掌握螺旋千斤顶的力学计算方法，并运用相关公式进行简单问题的求解。

3. 学生了解螺旋千斤顶的设计要点，能分析其优缺点。

技能目标：1. 学生能够运用所学的螺旋千斤顶知识，解决实际生活中的简单问题。

2. 学生通过小组合作，设计并制作一个简易的螺旋千斤顶模型，提高动手实践能力。

情感态度价值观目标：1. 培养学生对机械原理的兴趣，激发他们探索科学技术的热情。

2. 培养学生的团队合作意识，让他们在合作中学会互相尊重、沟通与协作。

3. 增强学生的创新意识，鼓励他们在设计过程中勇于尝试、不断改进。

课程性质：本课程为初中物理学科的一节实践性课程，结合学生特点，注重理论联系实际。

学生特点：初中学生具有一定的物理知识基础，对新鲜事物充满好奇心，动手能力强，但可能缺乏团队协作经验。

教学要求：教师需引导学生运用所学知识，通过小组合作完成螺旋千斤顶的设计与制作，注重培养学生的实践能力和创新精神。

在教学过程中，关注学生的个体差异，给予个性化指导，确保课程目标的实现。

二、教学内容1. 引入新课：通过展示不同类型的螺旋千斤顶图片，激发学生对本节课的兴趣，为新课的学习做好铺垫。

2. 理论知识学习：a. 螺旋千斤顶的结构与工作原理。

b. 螺旋千斤顶在工程中的应用。

c. 螺旋千斤顶的力学计算方法及相关公式。

3. 动手实践：a. 学生分组讨论，分析螺旋千斤顶的设计要点。

b. 学生根据所学知识，设计并制作一个简易的螺旋千斤顶模型。

4. 教学内容安排与进度：a. 新课引入和理论知识学习（1课时）。

b. 动手实践：螺旋千斤顶设计及制作（2课时）。

5. 教材章节及内容：a. 教材第十一章：简单机械及其应用。

- 第三节：螺旋千斤顶的结构、工作原理及计算方法。

b. 教材第十二章：实践与创新。

- 第三节：简单机械的设计与制作。

教学内容注重科学性和系统性，结合课程目标，确保学生在学习过程中掌握螺旋千斤顶的相关知识，提高实践能力。

螺旋千斤顶设计说明

螺旋千斤顶设计计算说明书院系专业年级设计者指导教师成绩2016年11月目录1设计任务书 (3)1。

1 设计题目:设计螺旋千斤顶（参考下图a） (3)1.2 原始数据 (3)1.3 设计工作量 (3)1.3.1 绘制出总装配图一张 (3)1。

3.2 编写设计计算说明书一份 (3)2计算内容和设计步骤......................................... 错误!未定义书签。

2.1螺杆的设计与计算 (4)2.1。

1 螺杆螺纹类型的选择 (4)2.1.2选取螺杆材料 (4)2.1.3确定螺杆直径 (4)2。

1.4自锁验算 (4)2。

1.5结构设计 (5)2.1。

6螺杆强度计算 (7)2.1。

7稳定性计算 (8)2。

2螺母设计计算 (9)2.2.1选取螺母材料 (9)2.2。

2确定螺母高度及工作圈数 (9)2.2。

3校核螺纹牙强度 (9)2.2。

4螺母与底座孔配合 (7)2.3托环的设计与计算 (7)2。

3。

1托杯材料的选择 (7)2。

3.2结构设计 (11)2.3.3接触面强度校核 (8)2.4手柄的设计计算 (8)2。

4。

1手柄材料的选择 (8)2。

4。

2计算手柄长度 (8)2.4。

3手柄直径的确定 (9)2。

4。

4结构 (9)2。

5底座设计............................................ 错误!未定义书签。

2.5.1选择底座材料 (9)2.5.2结构设计 (9)2。

5.3底座设计计算 (9)3.关于螺旋千斤顶结构设计等的补充说明 (17)参考文献: (17)2.1螺杆的设计与计算2。

1.1 螺杆螺纹类型的选择选择梯形螺纹，牙型角α=30˚，梯形螺纹的内外螺纹以锥面贴紧不易松动；它的基本牙型按GB/T5796。

1—2005的规定.2。

1。

2选取螺杆材料螺杆材料的选择螺杆材料常用的有Q235、Q275、40、45、55钢，由于是承受轻载荷，选择45钢，查手册表2-7得;查表5-13取安全系数S=4，则；螺母材料选用ZCuA19Mn2，查表确定需用压强[P］=15MPa。

机械设计_螺旋千斤顶设计说明书_天津大学

螺旋千斤顶作业任务书姓名专业机械设计制造年级班级设计完成日期 2012 年 11 月 25 日指导教师一、题目：螺旋千斤顶二、机构简图图1三、工作量1、总装配图一张；2、计算说明书一份。

四、参考资料螺旋千斤顶设计指导书目录1、选题及设计方案-----------------------------------------------------------------32、设计目的-----------------------------------------------------------------------------33、螺旋千斤顶计算说明书-----------------------------------------------------43.1螺杆的设计与计算----------------------------------------------------------43.2螺母的设计与计算----------------------------------------------------------63.3螺杆稳定性验算--------------------------------------------------------------83.4托杯的设计与计算----------------------------------------------------------83.5手柄设计与计算--------------------------------------------------------------93.6底座设计与计算-------------------------------------------------------------113.7千斤顶的效率----------------------------------------------------------------124、参考资料-----------------------------------------------------------------------------12选题及设计方案设计目的1、熟悉螺旋千斤顶的的工作原理与设计计算方法；2、运用所学的知识解决设计中所遇到的具体实际问题，培养学生独立工作能力，以及初步学会综合运用所学知识解决材料的选择、强度和刚度计算、制造与装配工艺等方面的问题；3、熟悉有关设计资料，学会查阅手册和运用国家标准；螺旋千斤顶计算说明书根据手柄直径p d 确定， ≈p k d d 柄的设计与计算）。

机械设计作业螺旋起重器

机械设计作业螺旋起重器[键入文档标题] [键入文档副标题]题目：螺旋起重器学院：班号：学号：姓名：日期：机械设计基础设计实践任务书题目：螺旋起重器设计原始数据及要求：螺旋起重器（千斤顶）F=40KN，最大起重高度H=200mm。

已知条件：起重量Q目录一．强度校核1.耐磨性计算2.螺杆的强度校核3.螺旋牙的强度校核4.自锁条件校核5.螺杆的稳定性校核6.手柄设计7.底座校核二．主要部件尺寸三．参考文献一．强度计算1. 耐磨性计算螺杆选用45号钢淬火，螺母选用铸造铝青铜，选用梯形螺纹，0.5h p =225.3d mm≥= 取226d mm =式中2d ——梯形螺纹的中径（mm ） Q F ——起重载荷（N ）ψ——系数，整体式螺母，取2ψ=[]p ——螺旋副的许用压强（MPa ），钢-青铜，低速，查表取[]20p MPa =查GB/T5796.4—1986取外螺纹公称直径226d mm =,螺距p 6mm =，小径123d mm =，中径2227d D mm ==，内螺纹大径331D mm =，中径227D mm =，小径124D mm =，且有222754H d mm mm ψ==⨯=。

2. 螺杆强度校核[]e σσ=≤Q F ——螺杆收到的轴向载荷（N ）； 1T ——螺杆收到的摩擦力矩（N mm ）;1d ——螺纹小径（mm ）;[]σ——螺杆材料的需用拉应力（Mpa ），查表，取400[]133.3333sMpa Mpa σσ=== 其中21tan()2Q V d T F ϕρ=+V ρ为当量摩擦角，arctancos V fρβ= 取0.1f =, β为牙侧角，152αβ==︒，算得V ρ 5.91=︒ϕ为螺纹升角，222arctan arctan arctan 4.05s np p d d d ϕπππ====︒ 算得1T =94828N mm ⋅进而得到118.08[]e σσ=≤3. 螺旋牙强度校核3Q F Z D bτπ=[]τ≤3D ——螺母螺纹大径，由上可得331D mm =Z ——螺纹旋合圈数，29d Z pψ== b ——螺纹牙的根部厚度（mm ），对于梯形螺纹，0.65 3.9b p mm ==[]τ——螺母材料的许用剪应力（Mpa ），查表[]0.6[]80Mpa τσ== 算得τ=11.7[]Mpa τ≤满足剪切强度条件。

螺旋千斤顶2

机械设计课程《螺旋千斤顶》设计说明书学生姓名学院名称专业学号2012年11 月日螺旋千斤顶作业任务书姓名专业年级2010级班级 1设计完成日期2012 年11 月日指导教师王喆一、题目：螺旋千斤顶原始数据:二、机构简图«Skip Record If...»三、工作量一、总装配图一张；二、计算说明书一份。

四、参考资料螺旋千斤顶设计指导书目录一、目的 (1)二、题目与设计方案 (1)三、装配简图 (1)四、计算及说明 (1)五、参考文献 (11)一、目的1. 熟悉螺旋千斤顶的工作原理与设计计算方式；2. 学会运用所学过的知识，解决实际设计中碰到的问题，培育独立工作能力，初步学会综运用所学知识解决材料选择、强度和刚度计算、制造与装配工艺等问题；3. 熟悉有关设计资料，学会查阅手册何用国家标准。

二、题目与设计方案题目：螺旋千斤顶方案编号 8 最大起重量F （kN ） 55 最大起升高度H （mm ）220三、装配简图四、计算及说明计算及说明结果1、螺杆的设计与计算 1)螺纹牙型螺纹牙型有矩形、梯形、锯齿形和三角形，千斤顶常用矩形矩形螺纹配合H9/h9图1托杯手柄螺母螺杆底座图2手柄孔径«Skip Record If...»根据手柄直径«Skip Record If...»确定，«Skip Record If...»。

为了便于切制螺纹，螺杆上应有退刀槽，退刀槽的直径应比«Skip Record If...»小约~0.5mm，取退刀槽直径«Skip Record If...»。

退刀槽的宽度取为«Skip Record If...»。

为了便于螺杆旋入螺母，螺杆端部应有倒角或制出稍小于«Skip Record If...»的圆柱形凸台。

螺旋千斤顶设计

一、设计原始参数螺旋千斤顶的最大起重重量F=60KN，最大起重高度H=230mm。

二、设计计算书4、稳定性校核细长的螺杆工作时受到较大的轴向压力，螺杆可能失稳，为此按下式验算螺杆的稳定性。

/ 2.5~4.0er F F ≥式中，er F 为螺杆的临界压力。

22()er EIF L πβ=。

查【2】P4，E=206GPa ，42441*368.24*106464d I mm ππ===。

52305*765330L H P l mm '=++=++=。

由002//125/40.5 3.083l d H d ''===>，为固定支承见【1】P121，2β=（一端固定，一端自由）。

25442*2.0*10*8.24*1038.46*10N (2*330)er F π==/38.46/6 6.44er F F ==>，压杆可以稳定工作。

图2 螺杆简图（二）螺母的设计计算螺母常用铸铁或青铜制造，在这里选用HT300 1、确定螺纹旋合圈数Z依【1】P120式（6-19），根据耐磨性计算螺纹旋合圈数Z ，E=206GPa448.24*10I mm =L=330mm2β=438.46*10N er F =/ 6.4er F F =查【1】P121表6.6 []45~55b MPa σ=323*60*10*3.523.79[]*45*4.44*9.5b b σσπ==≤，故满足要求。

3、螺母其他结构尺寸螺母外径(1.6~1.8)(1.6~1.8)*4572~81D D mm '===取72D mm '=(1.3~1.4)(1.3~1.4)*7293.6~100.8D D mm '''===取95D mm ''= 螺母凸缘厚度/365/325.6a H mm '===取26a mm =，结果见图图3 螺母简图4、螺母外径和凸缘强度的计算及螺母悬置部分拉——扭组合校核（注：螺母旋合长度77H mm '=，螺母实际长度125H mm ''=，1257748H H mm '''-=-=。

机械设计设计螺旋千斤顶所需参数及其公式

螺杆 FP= d= d1= H= f=( 2 tan 2 d FTV⋅+=ϕψ2 124 31⎪⎪⎭⎫⎝⎛+=d T F Acaσ2dnP π=ψψ≥=βϕcos f Vl=i=E=螺母b=0.65*PD=d+0.56441d I π=2l EI F cr μπ=D 10=(2.4~2.5d D 11=(0.6~0.7d D 13=(1.7~1.9d D 12= D13-(2~4 h=(1.5~1.8D手柄底座2 7 84D FDp+ =σπ梯形螺纹材料起重力螺纹升角螺杆中径许用压力螺距公称直径小径螺母高度摩擦系数中径处升角当量摩擦角螺钉公称直径螺钉型号螺杆所受扭矩计算应力许用应力长度系数高度螺杆危险界面惯性半径柔度惯性矩拉压弹性模量临界载荷材料螺纹工作圈数实际螺母高度螺纹牙危险截面的剪切强度条件螺纹牙危险界面的弯曲强度条件螺纹牙跟处厚度内螺纹大径弯曲力臂螺母外径螺母大外径压力强度材料工人的臂力手柄长度托杯与轴端支撑面的摩擦力矩实际手柄长度手柄直径手柄材料需用弯曲应力螺旋千斤顶高度不加套管长度材料斜度壁厚底座上直径底座下直径底座接地直径底座下枕垫物的许用挤压应力α=30度 4525KN 4.25度 21.5mm 18MPa 5mm 24mm 18.5mm 53.75mm 0.094.25度5.34度 2.56mmM6*12 45407N.mm 83.32MPa 333.28 2218.6~223.4mm219mm 4.625mm 189.4》40 5746.94200~220GPa52.89*1000>2.5青铜10.75取10 50mm9.999MPa<30~40MPa27.69MPa<40~60MPa3.25mm24.5mm1.5mm39.2~44.1mm取40mm 52~56mm取54mm57.6~60 14.4~16.8 40.8~45.6 41~43 36~43.2 19.6MPa<20MPa Q235 150~250N 520.22mm 45407.41N.mm 32625N.mm 592.71~692.71mm 32.92mm 120MPa272.75mm 240mm 取60mm 取15mm 取45mm 取43mm 取40mm 150N 取600mmHT200 1:10 大于8~12mm 174~188mm 45~50mm 86mm 146.86mm 2.5MPa 8mm 180mm 50mm。

机械设计课程设计---螺旋千斤顶计算说明书

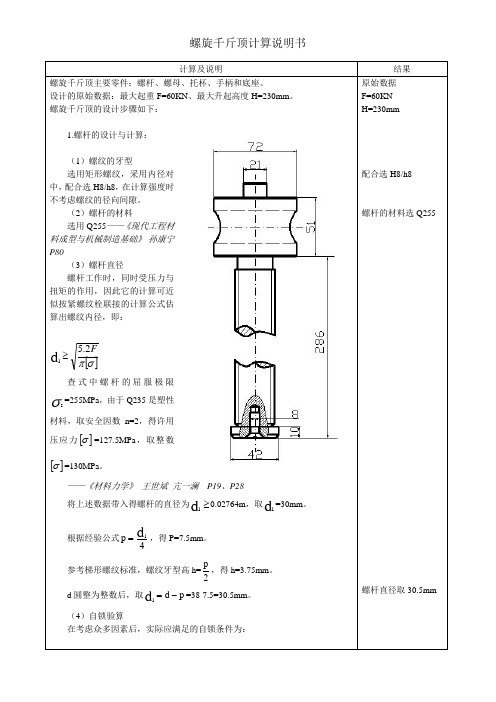
计算及说明结果螺旋千斤顶主要零件：螺杆、螺母、托杯、手柄和底座。

设计的原始数据：最大起重F=60KN 、最大升起高度H=230mm 。

螺旋千斤顶的设计步骤如下：1.螺杆的设计与计算：（1）螺纹的牙型选用矩形螺纹，采用内径对中，配合选H8/h8，在计算强度时不考虑螺纹的径向间隙。

（2）螺杆的材料选用Q255——《现代工程材料成型与机械制造基础》孙康宁 P80（3）螺杆直径螺杆工作时，同时受压力与扭矩的作用，因此它的计算可近似按紧螺纹栓联接的计算公式估算出螺纹内径，即：[]σπF2.5d 1≥查式中螺杆的屈服极限σs=255MPa ，由于Q235是塑性材料，取安全因数n=2，得许用压应力[]σ=127.5MPa ，取整数[]σ=130MPa 。

——《材料力学》王世斌亢一澜 P19、P28将上述数据带入得螺杆的直径为d1≥0.02764m ，取d 1=30mm 。

根据经验公式4p d1=，得P=7.5mm 。

参考梯形螺纹标准，螺纹牙型高h=2p，得h=3.75mm 。

d 圆整为整数后，取p d d1-==38-7.5=30.5mm 。

（4）自锁验算在考虑众多因素后，实际应满足的自锁条件为：原始数据 F=60KN H=230mm配合选H8/h8螺杆的材料选Q255螺杆直径取30.5mm1-'≤ρψ由)(/np tan d 2πψ= n=1，p=7.5mm ，d 2=2h2d 1+⨯=32.375mm得tan ψ=0.07373——《机械原理与机械设计》张策 P38 当量摩擦角ρ'=arctanμ，在有润滑油情况下μ=0.1，得1-'ρ=4.574验证结束，左边小于右边，达到自锁条件。

——《机械原理与机械设计》张策 P71 （5）结构手柄孔径dK根据手柄直径p d 决定，mm 5.0d d p k +≈。

根据后面手柄部分的计算得到p d =26mm ，所以k d =26.5mm 。

螺旋千斤顶大作业任务书和指导书.doc

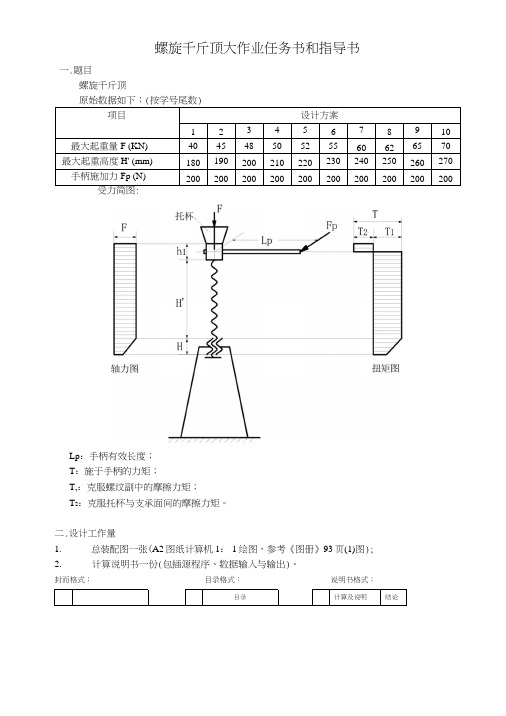
螺旋千斤顶大作业任务书和指导书一.题目螺旋千斤顶原始数据如下：(按学号尾数)项目设计方案1 2 3 4 5 6 7 8 9 10最大起重量F (KN) 40 45 48 50 52 55 60 62 65 70 最大起重高度H' (mm) 180 190 200 210 220 230 240 250 260 270 手柄施加力Fp (N) 200 200 200 200 200 200 200 200 200 200 受力简图:Lp：手柄有效长度；T：施于手柄的力矩；T,：克服螺纹副中的摩擦力矩；T2：克服托杯与支承面间的摩擦力矩。

二.设计工作量1.总装配图一张(A2图纸计算机1： 1绘图，参考《图册》93页(1)图);2.计算说明书一份(包插源程序、数据输入与输出)。

封而格式：目录格式：说明书格式：目录计算及说明结论三•计算内容1. 选择螺杆和螺母的材料2. 螺杆的设计计算(1) 选择螺杆的牙型(梯形)(2) 按强度计算螺杆的小径山(d&1.25」邑) \[O]梯形螺纹参数数组A (I, J)(mm)(3) 定螺距P,查出标准螺距P 及螺杆螺纹小径山、中径(12、大径d 、螺母螺纹大径D (4) 验算自锁性：屮冬①v7T 2EI(5) 验算螺杆的稳定性：Fc 「/F$3.5〜5 (临界载荷珂尸丝送;,其中螺杆的工作长度(山)「1 二h]+H'+H/2,长度系数 U=2)3. 螺母的设计计算FP(1) 根据耐磨性定出螺母的高度H (H3 ----------------- ，収整)，求旋合圈数u(uW10,不必収Kd 2h[p]整)，校核 e=H/d2二 1.2〜2.5F(2) 校核螺纹牙的剪切强度(工二 ----- D 为螺母螺纹大径,b=0.634 P )和弯曲兀Dbu 强度(O b= ■ c o bl, h=o.5 P)错误!未指定书签。

错误!未指定书签。

兀 Db 「u 4. 手柄的设计计算(1)选择材料(一般用Q235,35)装订位買⑵计算手柄的总长度L(L二Lp+D/2,取整。

千斤顶校定反力计算书

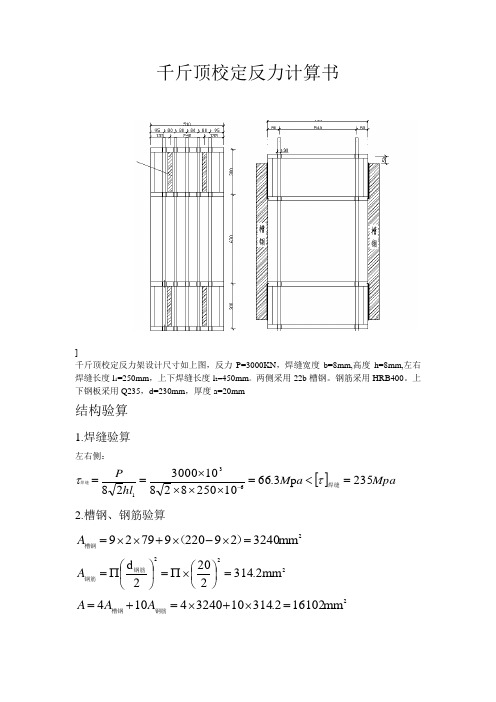
千斤顶校定反力计算书]千斤顶校定反力架设计尺寸如上图，反力P=3000KN ，焊缝宽度b=8mm,高度h=8mm,左右焊缝长度l 1=250mm ，上下焊缝长度l 2=450mm 。

两侧采用22b 槽钢。

钢筋采用HRB400。

上下钢板采用Q235，d=230mm ，厚度a=20mm结构验算1.焊缝验算左右侧：[]Mpa a M hl P 235p 3.661025082810300028631=<=⨯⨯⨯⨯==-焊缝焊缝ττ 2.槽钢、钢筋验算2mm 32402922097929=⨯-⨯+⨯⨯=）（槽钢A 222mm 2.3142202d =⎪⎭⎫ ⎝⎛⨯∏=⎪⎭⎫ ⎝⎛∏=钢筋钢筋A 2mm 161022.3141032404104=⨯+⨯=+=钢筋槽钢A A Apa 3.186101610210300063M A P =⨯⨯===-钢筋槽钢σσ 则[]pa 235M =<槽钢槽钢σσ []pa 400M =<钢筋钢筋σσ3.钢板验算[]pa 235pa 6.2071020230103000da 63M M P =<=⨯⨯⨯∏⨯=∏=-钢板钢板ττ []pa 235pa 2.721022301030002d 6232M M P =<=⨯⎪⎭⎫ ⎝⎛⨯∏⨯=⎪⎭⎫ ⎝⎛∏=-钢板钢板钢板σσ 4.钢板受弯截面正应力m 1005.410270101500533∙⨯=⨯⨯⨯=-N M 3622m m 101.863005406h b ⨯=⨯==钢板钢板钢板W []Mpa M W M 235pa 5010101.81005.49-65=<=⨯⨯⨯==钢板钢板钢板σσ 5.钢板的挠度4933m m 10215.11230054012h ⨯=⨯==钢板钢板b J m 1005.41010215.110200481054010300048l y 5-12-999333⨯=⨯⨯⨯⨯⨯⨯⨯⨯==-EJ P 6.结论通过以上计算可知，本支撑体系受力满足要求。

千斤顶机械设计计算说明书

.千斤顶设计计算说明书班级：09车辆2班姓名：**20091225王洪涛20091226指导老师：***2012年6月目录千斤顶设计第1章问题的提出1.1项目背景 (3)第2章机构选型设计2.1自锁装置的选择 (3)2.1.1螺旋副自锁机构 (3)2.1.2斜面自锁机构 (6)2.2力放大机构的选择 (8)2.2.1方案一 (8)2.2.2方案二 (9)第3章机构尺度综合3.1力放大机构齿轮尺寸 (10)3.2斜面自锁机构斜面倾角尺寸 (15)第4章力放大机构各齿轮强度校核 (16)第5章机构运动分析机构运动分析 (26)力放大机构各齿轮运动分析................................. (26)第6章机构动力分析………………………………………………. ..286.1自锁机构动力分析……………………………………..... ..286.1.1螺旋副自锁机构动力分析 (28)6.1.2斜面自锁机构动力分析 (30)6.2力放大机构动力分析 (32)第7章收获与体会 (36)第8章致谢 (37)参考文献 (37)附录1 (38)附录2 (45)附录3 (46)第1章.问题的提出1.1项目背景千斤顶是一种垂直起重高度小于一米的最简单的起重设备，千斤顶一般用于厂矿、交通运输等部门完成起重、支撑等工作。

其结构轻巧坚固、灵活可靠，一人即可携带和操作。

千斤顶以它可实现力矩放大和受力自锁这两个主要特性，为现在的实际生产生活带来了巨大的便捷。

因此在做这次机械设计课程设计的时候，我们把目光投向了千斤顶，据我们所知，常用的千斤顶可分为三类：齿条千斤顶，螺旋千斤顶，液压千斤顶和气囊式气动千斤顶。

它们又分别具有以下特点：一齿条千斤顶：由人力通过杠杆和齿轮带动齿条顶举重物。

起重量一般不超过20吨，可长期支持重物，主要用在作业条件不方便的地方或需要利用下部的托爪提升重物的场合，如铁路起轨作业。

二螺旋千斤顶：由人力通过螺旋副传动，螺杆或螺母套筒作为顶举件。

螺旋千斤顶设计任务书

螺旋千斤顶设计任务书目录一、机构简图...............................................................................................................................- 4 -二、设计计算说明书...................................................................................................................- 5 -1、螺杆的设计与计算.........................................................................................................- 5 -（1）螺纹的牙型.........................................................................................................- 5 -（2）螺杆的材料.........................................................................................................- 5 -（3）螺杆的直径.........................................................................................................- 5 -（4）螺纹副自锁条件校核.........................................................................................- 6 -（5）螺杆结构的计算.................................................................................................- 6 -（6）螺杆强度计算.....................................................................................................- 7 -（7）稳定性计算.........................................................................................................- 8 -2、螺母设计与计算.............................................................................................................- 9 -（1）螺母的材料.........................................................................................................- 9 -（2）螺母的直径.........................................................................................................- 9 -（3）螺母的其它参数.................................................................................................- 9 -（4）螺母螺纹牙强度计算.........................................................................................- 9 -（5）螺母与底座孔的配合...................................................................................... - 11 -3、托杯的设计与计算...................................................................................................... - 11 -4、手柄设计与计算.......................................................................................................... - 12 -（1）手柄材料.......................................................................................................... - 12 -（2）手柄长度.......................................................................................................... - 12 -（3）手柄直径.......................................................................................................... - 12 -（4）手柄结构.......................................................................................................... - 13 -5、底座设计...................................................................................................................... - 13 -6、参考文献...................................................................................................................... - 14 -三、总结.................................................................................................................................... - 14 -一、机构简图二、设计计算说明书1、螺杆的设计与计算（1）螺纹的牙型因为梯形螺纹易于制造，牙根强度高所以选用梯形螺纹，牙型角α=30º（2）螺杆的材料45钢（3）螺杆的直径P s=FA=Fpπd2hH≤[P]引入系数ψ=Hd2，且对于梯形螺纹h=0.5p，则d2≥0.8√Fψ[P]因为千斤顶的螺杆与螺母的相互运动是低速滑动，所以两者的材料均选为钢，根据书P78表5.8，取[P]=10MPa因为磨损后间隙不能调整，所以取ψ=2.5因此d2≥0.8√Fψ[P]=0.8√6×1042.5×10≈39.2mm根据机械设计手册P41表3-7和表3-8取，螺纹公称直d=48mm、螺距p=12mm、螺纹小径d1=d−13=35mm,螺纹中d2=d−6=42mm≥39.2mm（4）螺纹副自锁条件校核自锁条件为：φ≤ρ＇、ρ＇=arctanf＇因为螺纹副材料均为钢制，按照书P80表5.10取f＇=0.17所以ρ＇=arctanf＇=arctan0.17≈9.65°φ=arctan npπd2=arctan1×123.14×42≈5.20°≤9.65°因此符合自锁条件（5）螺杆结构的计算为了便于切制螺纹，螺纹上端应设有退刀槽。