高中阶段三角函数公式大全
高中数学-三角函数公式汇总

高中数学-三角函数公式汇总以下是高中数学三角函数公式的汇总:一、任意角的三角函数:在角α的终边上任取一点P(x,y),记:r=x²+y²正弦:sinα=y/r余弦:cosα=x/r正切:tanα=y/x余切:cotα=x/y正割:secα=r/x余割:cscα=r/y注:我们还可以用单位圆中的有向线段表示任意角的三角函数,如图,与单位圆有关的有向线段MP、OM、AT分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式:倒数关系:sinα·cscα=1,cosα·secα=1,tanα·cotα=1.商数关系:tanα=sinα/cosα,cotα=cosα/sinα。
平方关系:sin²α+cos²α=1,1+tan²α=sec²α,1+cot²α=csc²α。
三、诱导公式:⑴ α+2kπ(k∈Z)、-α、π+α、π-α、2π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号。
(口诀:函数名不变,符号看象限)⑵π/3+α、π/3-α、π-α、π+α的三角函数值,等于α的异名函数值,前面加上一个把α看成锐角时原函数值的符号。
(口诀:函数名改变,符号看象限)四、和角公式和差角公式:sin(α+β)=sinα·cosβ+cosα·sinβsin(α-β)=sinα·cosβ-cosα·sinβcos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)五、二倍角公式:sin2α=2sinα·cosαcos2α=cos²α-sin²α=2cos²α-1=1-2sin²α…(∗)tan2α=2tanα/(1-tan²α)二倍角的余弦公式(∗)有以下常用变形:(规律:降幂扩角,升幂缩角)1+cos2α=2cos²α1-cos2α=2sin²α1+sin2α=(sinα+cosα)²1-sin2α=(sinα-cosα)²cos2α=(1+cos2α)/(1-cos2α)sin2α=(1-cos2α)/(1+cos2α)tanα=sin2α/(1+cos2α)1.根据公式,cos2α=sin2α=tan2α=1/(1+tan2α),tanα可以用半角的正切表示。
三角函数高中所有公式

三角函数高中所有公式三角函数是高中数学中的重要内容,以下是其所有公式及详细介绍:基础三角函数公式:正弦函数:sin(x) = y/r余弦函数:cos(x) = x/r正切函数:tan(x) = y/x余切函数:cot(x) = x/y正割函数:sec(x) = r/x余割函数:csc(x) = r/y诱导公式:sin(x) = cos(x - π/2)cos(x) = sin(x + π/2)tan(x) = cot(x) = 1/tan(x)sec(x) = 1/cos(x)csc(x) = 1/sin(x)和差公式:sin(x + y) = sinxcosy + cosxsinysin(x - y) = sinxcosy - cosxsinycos(x + y) = cosxcosy - sinxsinycos(x - y) = cosxcosy + sinxsiny倍角公式:sin2x = 2sinxcosxcos2x = cos²x - sin²xtan2x = 2tanx / (1 - tan²x)sin(x/2) = ±√[(1 - cosx)/2]cos(x/2) = ±√[(1 + cosx)/2]tan(x/2) = ±√[(1 - cosx)/(1 + cosx)]和差化积公式:sinxcosy = 1/2 * (sin(x + y) + sin(x - y)) cosxcosy = 1/2 * (cos(x + y) + cos(x - y)) sinxsiny = 1/2 * (cos(x - y) - cos(x + y))积化和差公式:sinxcosy = 1/2 * (sin(x + y) + sin(x - y)) cosxcosy = 1/2 * (cos(x + y) - cos(x - y)) sinxsiny = 1/2 * (cos(x + y) - cos(x - y))双角公式:sin2α = 2sinαcosαcos2α = cos²α - sin²αtan2α = 2tanα / (1 - tan²α)辅助角公式:sinx = 2tan(x/2) / [1 + tan²(x/2)]cosx = [1 - tan²(x/2)] / [1 + tan²(x/2)]tanx = 2tan(x/2) / [1 - tan²(x/2)]倍角辅助角公式:sin30° = 1/2,cos30° = √3/2,tan30° = √3/3 sin45° = √2/2,cos45° = √2/2,tan45° = 1 sin60° = √3/2,cos60° = 1/2,tan60° = √3sin3α = 3sinα - 4sin³αcos3α = 4cos³α - 3cosα四倍角公式:sin4α = 8sin²α - 8sin⁴α + 1cos4α = 8cos⁴α - 8cos²α + 1五倍角公式:sin5α = (30sin³α - 10sinα + 2sin(-α)) / 16 cos5α = (30cos³α + 10cosα + 8cos(-α)) / 16。
高中数学《三角函数》公式大全

高中数学《三角函数》公式大全三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
而掌握三角函数的内部规律及本质也是学好三角函数的关键所在,下面是为大家整理的三角函数公式大全:锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边 / ∠α的邻边cot α=∠α的邻边 / ∠α的对边倍角公式Sin2A=2SinA?CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注:SinA^2 是sinA的平方 sin2(A) )三倍角公式sin3α=4sinα²sin(π/3+α)sin(π/3-α)cos3α=4cosα²cos(π/3+α)cos(π/3-α)tan3a = tan a ² tan(π/3+a)² tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t),其中第1页(共16页)sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t),tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)第2页(共16页)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))三角和sin(α+β+γ)=sinα²cosβ²cosγ+cosα²sinβ²cosγ+cosα²cosβ²sinγ-sin α²sinβ²sinγcos(α+β+γ)=cosα²cosβ²cosγ-cosα²sinβ²sinγ-sinα²cosβ²sinγ-sin α²sinβ²cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα²tanβ²tanγ)/(1-tanα²tanβ-tanβ²t anγ-tanγ²tanα)第3页(共16页)两角和差cos(α+β)=cosα²cosβ-sinα²sinβcos(α-β)=cosα²cosβ+sinα²sinβsin(α±β)=sinα²cosβ±cosα²sinβtan(α+β)=(tanα+tanβ)/(1-tanα²tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα²tanβ)和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2] sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2诱导公式sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinα第4页(共16页)sin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得第5页(共16页)tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1) /n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n] =0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0第6页(共16页)。
高中三角函数公式大全

高中三角函数公式大全以下为改写后的文章:高中三角函数公式大全三角函数公式:1.两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-XXX)tan(A-B) = (tanA-tanB)/(1+XXX)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)2.倍角公式tan2A = (2tanA)/(1-tanA)sin2A = 2sinAcosAcos2A = cos²A-sin²A = 2cos²A-1 = 1-2sin²A 3.三倍角公式sin3A = 3sinA-4sin³Acos3A = 4cos³A-3cosAtan3A = tana·tan(A+π)·XXX(A-π) 4.半角公式sin(A/2) = ±√((1-cosA)/2)cos(A/2) = ±√((1+cosA)/2)tan(A/2) = ±√((1-cosA)/(1+cosA)) cot(A/2) = ±√((1+cosA)/(1-cosA)) 5.和差化积sin(a+b) = 2sin((a+b)/2)cos((a-b)/2) cos(a+b) = 2cos((a+b)/2)cos((a-b)/2) sin(a-b) = 2sin((a-b)/2)cos((a+b)/2)tan(a+b) = (tanA+tanB)/(1-XXX)6.积化和差sinA·sinB = (1/2)(cos(A-B)-cos(A+B)) cosA·cosB = (1/2)(cos(A-B)+cos(A+B)) sinA·cosB = (1/2)(sin(A+B)+sin(A-B)) cosA·sinB = (1/2)(sin(A+B)-sin(A-B)) 7.诱导公式sin(-A) = -sinAcos(-A) = cosAsin(π-A) = sinAcos(π-A) = -cosAsin(π+A) = -sinAcos(π+A) = -cosACos(π-a)=-cos aSin(π+a)=-sin aCos(π+a)=-cos aSin a万能公式:a^2 tan^2 a=a^2/(1+tan^2 a)a^2/(1-tan^2 a)=cos^2 a其他公式:2a sina+b cosa=(a^2+b^2)sin(a+c),其中tanc=a sin(a)-b cos(a)=b/(a+cos a)1+sin a=(sin a+cos a)^2/2其他非重点三角函数:csc a=1/sin asec a=1/cos a双曲函数:sinh a=(e^a-e^-a)/2cosh a=(e^a+e^-a)/2XXX a公式一:对于任意角α,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα,cos(2kπ+α)=cosα,tan(2kπ+α)=tanα,cot(2kπ+α)=cotα公式二:对于任意角α,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinα,cos(π+α)=-cosα,tan(π+α)=tanα,cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)=-sinα,cos(-α)=cosα,tan(-α)=-tanα,cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinα,cos(π-α)=-cosα,tan(π-α)=-tanα,cot(π-α)=-cotα公式五:利用公式二和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinα,cos(2π-α)=cosα,tan(2π-α)=-tanα,cot(2π-α)=-cotα公式六:对于±α及±α,与α的三角函数值之间的关系为:sin(+α)=cosα,cos(+α)=-sinα以下是一些常用的三角函数公式:tan(+α)= -cotα,cot(+α)= -tanα这两个公式表示正弦和余弦的相反数的比值等于余切和正切的相反数。
高中三角函数公式大全

高中三角函数公式大全三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=AA cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a -sina-sinb=2cos2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1公式一:设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= co sαtan (-α)= -tanαcot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= c osαcos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)。
高中三角函数公式汇总

高中三角函数公式汇总两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =A tan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A+ tan(2A )=AAcos 1cos 1+- cot(2A )=A Acos 1cos 1-+ tan(2A )=AA sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a -cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=b a b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式sin(-a) = -sinacos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan2a a+ cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a)2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数csc(a) =asin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -a a cosh(a)=2e e -a a tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanαsin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h 斜棱柱体积V=S'L 注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差: 相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差: 相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住不,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)tanA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1) tan(α+β)=(1+m)/(1-m)tanβ。
高中数学_三角函数公式大全

高中数学_三角函数公式大全一、基本公式1.正弦函数的基本公式:sin(A±B) = sinAcosB ± cosAsinBsin2A = 2sinAcosAsin(A+B) + sin(A-B) = 2sinAcosB2.余弦函数的基本公式:cos(A±B) = cosAcosB ∓ sinAsinBcos2A = cos^2(A) - sin^2(A)cos(A+B) + cos(A-B) = 2cosAcosB3.正切函数的基本公式:tan(A±B) = (tanA ± tanB) / (1 ∓ tanAtanB)tan2A = (2tanA) / (1 - tan^2(A))tan(A+B) = (tanA + tanB) / (1 - tanAtanB)tan(A-B) = (tanA - tanB) / (1 + tanAtanB)二、和差化积公式1.正弦函数的和差化积公式:sin(A+B) = sinAcosB + cosAsinBsin(A-B) = sinAcosB - cosAsinB2.余弦函数的和差化积公式:cos(A+B) = cosAcosB - sinAsinBcos(A-B) = cosAcosB + sinAsinB三、倍角公式1.正弦函数的倍角公式:sin2A = 2sinAcosA2.余弦函数的倍角公式:cos2A = cos^2(A) - sin^2(A)3.正切函数的倍角公式:tan2A = (2tanA) / (1 - tan^2(A))四、半角公式1.正弦函数的半角公式:sin(A/2) = ±√[(1 - cosA) / 2]2.余弦函数的半角公式:cos(A/2) = ±√[(1 + cosA) / 2]3.正切函数的半角公式:tan(A/2) = ±√[(1 - cosA) / (1 + cosA)]五、和差化积公式1.正弦函数的和差化积公式:sin(A±B) = sinAcosB ± cosAsinB2.余弦函数的和差化积公式:cos(A±B) = cosAcosB ∓ sinAsinB六、和差化积公式的应用1. sinA + sinB = 2sin((A+B)/2)cos((A-B)/2)sinA - sinB = 2sin((A-B)/2)cos((A+B)/2)2. cosA + cosB = 2cos((A+B)/2)cos((A-B)/2)cosA - cosB = -2sin((A+B)/2)sin((A-B)/2)3. tanA + tanB = sin(A+B) / cosAcosBtanA - tanB = sin(A-B) / cosAcosB以上是一些常用的三角函数公式,其中涉及到的角度均为弧度制。
高中三角函数公式大全

高中三角函数公式大全sin(a+b)=sinacosb+cosasinbsin(a-b)=sinacosb-cosasinbcos(a+b)=cosacosb-sinasinbcos(a-b)=cosacosb+sinasinbtan(a+b)=(tana+tanb)/(1-tanatanb)tan(a-b)=(tana-tanb)/(1+tanatanb)cot(a+b)=(cotacotb-1)/(cotb+cota)cot(a-b)=(cotacotb+1)/(cotb-cota)倍角公式tan2a=2tana/(1-tan^2a)sin2a=2sina•cosacos2a=cos^2asin^2a=2cos^2a—1=1—2sin^2a三倍角公式sin3a=3sina-4(sina)^3;cos3a=4(cosa)^3-3cosatan3a=tana•tan(π/3+a)•tan(π/3-a)半角公式sin(a/2)=√{(1cosa)/2}cos(a/2)=√{(1+cosa)/2}tan(a/2)=√{(1c osa)/(1+cosa)}cot(a/2)=√{(1+cosa)/(1-cosa)}tan(a/2)=(1cosa)/sina=sina/(1+cosa)和差化积sin(a)+sin(b)=2sin[(a+b)/2]cos[(a-b)/2]sin(a)-sin(b)=2cos[(a+b)/2]sin[(a-b)/2]cos(a)+cos(b)=2cos[(a+b)/2]cos[(a-b)/2]cos(a)-cos(b)=-2sin[(a+b)/2]sin[(a-b)/2]tana+tanb=sin(a+b)/cosacosb积化和差sin(a)sin(b)=-1/2*[cos(a+b)-cos(a-b)]cos(a)cos(b)=1/2*[cos(a+b)+cos(a-b)]sin(a)cos(b)=1/2*[sin(a+b)+sin(a-b)]cos(a)sin(b)=1/2*[sin(a+b)-sin(a-b)]诱导公式sin(-a)=-sin(a)cos(-a)=cos(a)sin(π/2-a)=cos(a)cos(π/2-a)=sin(a)sin(π/2+a)=cos(a)cos(π/2+a)=-sin(a)sin(π-a)=sin(a)cos(π-a)=-cos(a)sin(π+a)=-sin(a)cos(π+a)=-cos(a)tga=tana=sina/cosa万能公式sin(a)=[2tan(a/2)]/{1+[tan(a/2)]^2}cos(a)={1-[tan(a/2)]^2}/{1+[tan(a/2)]^2}tan(a)=[2tan(a/2)]/{1-[tan(a/2)]^2} 其它公式a•sin(a)+b•cos(a)=[√(a^2+b^2)]*sin(a+c)[其中,tan(c)=b/a]a•sin(a)-b•cos(a)=[√(a^2+b^2)]*cos(a-c)[其中,tan(c)=a/b]1+sin(a)=[sin(a/2)+cos(a/2)]^2;1-sin(a)=[sin(a/2)-cos(a/2)]^2;;其他非重点三角函数csc(a)=1/sin(a)sec(a)=1/cos(a)双曲函数sinh(a)=[e^a-e^(-a)]/2cosh(a)=[e^a+e^(-a)]/2tgh(a)=sinh(a)/cosh(a)sin30°=1/2sin37°=0。
【精品推荐】高中三角函数公式大全

【精品推荐】高中三角函数公式大全一、诱导公式sin(α+2kπ)=sinαcos(α+2kπ)=cosαtan(α+2kπ)=tanαsin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα这里仅作示范,诱导公式只要通过奇变偶不变,符号看象限的口诀就可以了二、两角和与差正余弦公式余弦cos(α-β)=cosαcosβ+sinαsinβcos(α+β)=cosαcosβ-sinαsinβ正弦sin(α-β)=sinαcosβ-cosαsinβsin(α+β)=sinαcosβ+cosαsinβ正切tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)正余弦记忆法(个人向):①磕磕死死,死磕磕死(分别对应余正弦)②余弦正负号变,正弦不变正弦记忆法:①分子加减与原来相同②上加下减,上减下加三、倍角公式二倍角sin2α=2sinαcosαcos2α=cos²α-sin(2cos²α-1→1+cos2α=2cos²α)(1-2sin²α→1-sin2α=2sin²α)tan2α=2tanα/(1-tan²α)sin2α=2tanα/(1+tan²α)cos2α=(1-tan²α)/(1+tan²α)2.三倍角sin3α=3sinα-4sin³αcos3α=4cos³α-3cosα四、半角公式sin(α/2)=±√(1-cosα/2)cos(α/2)=±√(1+cosα/2)tan(α/2)=(1-cosα)/sinαtan(α/2)=sinα/(1+cosα)tan(α/2)=(1-cosα+sinα)/(1+cosα+sinα)五、万能公式积化和差公式sinαcosβ=½[sin(α+β)+sin(α-β)]cosαsinβ=½[sin(α+β)-sin(α-β)]cosαcosβ=½[cos(α+β)+cos(α-β)]sinαsinβ=-½[cos(α+β)-cos(α-β)]记忆法:①除两个sin是-1/2外都以1/2开头②式子左边sin结尾,后面为减号;式子左边cos结尾,右边为加号③式子左边函数名相同则后面是两个cos;不同则后面是两个sin2.和差化积公式sinα+sinβ=2sin½(α+β)cos½(α-β)sinα-sinβ=2cos½(α+β)sin½(α-β)cosα+cosβ=2cos½(α+β)cos½(α-β)cosα-cosβ=-2sin½(α+β)sin½(α-β)记忆法:①除cos-cos是-2外都以2开头②式子右边sin结尾,前面为减号;式子右边cos结尾,前面为加号③式子左边函数名都是sin则右边函数名不同;都是cos则后面函数名相同六、辅助角公式Asinα+Bcosα=√(A²+B²)·[sinφsinα+cosφcosα]=√(A²+B²)sin(α+φ)φ为A²/√(A²+B²)对应的正弦值φ为B²/√(A²+B²)对应的余弦值七、自己整理的公式cos²α+sinβ+sin(α-β)sin(α+β)=1sin²α+cos²(α+30°)+sinαcos(α+30°)=3/41+sin2α=(sinα+cosα)²常见变换——二倍角cosωα-sinωα=-√2sin(ωα+4/π)常见变换——辅助角公式已知tan(α+¼π)=n,可知tanα=(n-1)/(n+1)常见变换——展开式sinα+cosα=±√[(tan²α+tanα+1)/tan²+1]常见变换——弦化切。
高中三角函数公式大全

高中三角函数公式大全两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB-1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotAcotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=AA cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2b a -sina-sinb=2cos2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式sin(-a) = -sinacos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sinacos(π-a) = -cosasin (π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan 2a a + cosa=22)2(tan 1)2(tan 1a a +-tana=2)2(tan 12tan2a a- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos (a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =asin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -t anαcot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosαcos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式 |a+b|≤|a|+|b| |a -b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住不,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)tanA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
高中阶段三角函数公式大全

高中阶段三角函数公式大全三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB cos(A+B) = cosAcosB-sinAsinB sin(A-B) = sinAcosB-cosAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + cot(A+B) =cotAcotB 1-cotAcotB + tan(A-B) =tanAtanB 1tanB tanA +- cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - tan(2A )=A A cos 1cos 1+- cos(2A )=2cos 1A + cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin2b a +cos 2b a - cosa+cosb = 2cos 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+ 积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin万能公式 sina=2)2(tan 12tan2a a + tana=2)2(tan 12tan 2a a - cosa=22)2(tan 1)2(tan 1a a +- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b •cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinα tan (2kπ+α)= tanα cos (2kπ+α)= cosα cot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinα tan (π+α)= tanα cos (π+α)= -cosα cot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinα tan (-α)= -tanα cos (-α)= cos α cot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα tan (π-α)= -tanα cos (π-α)= -cosα cot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα tan (2π-α)= -tanα cos (2π-α)= cosα cot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα tan (2π+α)= -cotα cos (2π+α)= -sinα cot (2π+α)= -tanαsin (2π-α)= cosα tan (2π-α)= cotα cos (2π-α)= sinα cot (2π-α)= tanαsin (23π+α)= -cosα tan (23π+α)= -cotα cos (23π+α)= sinα cot (23π+α)= -tanαsin (23π-α)= -cosα tan (23π-α)= cotα cos (23π-α)= -sinα cot (23π-α)= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2)a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b||a|≤b<=>-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b2-4ac)/2a -b-√(b2-4ac)/2a根与系数的关系 X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式 b2-4ac=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式 tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+co sA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程 (x-a)2+(y-b)2=r2注:(a,b)是圆心坐标圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)t anA+tanB+tanC=tanA·tanB·tanC(2)sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
高中必背三角函数公式表

高中必背三角函数公式表高中必背三角函数公式表作为高中数学的重要部分,三角函数是很多学生所苦恼的部分,需要反复理解和重复记忆才能掌握好。
今天,我们就来看一下高中必背的三角函数公式表,相信对你的学习有所帮助。
I. 基本三角函数公式1. 正弦函数(sin)sinA = 对边 / 斜边sin A = a/c2. 余弦函数(cos)cos A = 邻边 / 斜边cos A = b/c3. 正切函数(tan)tan A = 对边 / 邻边tan A = a/b4. 正割函数(sec)sec A = 斜边 / 邻边sec A = c/b5. 余割函数(csc)csc A = 斜边 / 对边csc A = c/a6. 割正切函数(cot)cot A = 邻边 / 对边cot A = b/aII. 商数与余数公式1. 正弦函数的商数与余数公式sin (A ± B) = sin A cos B ± cos A sin Bsin 2A = 2sin A cos Asin (π/2 - A) = cos Asin (π + A) = -sin Asin (π - A) = sin Asin (2π - A) = -sin A2. 余弦函数的商数与余数公式cos (A ± B) = cos A cos B ∓ sin A sin B cos 2A = cos² A - sin² Acos (π/2 - A) = sin Acos (π + A) = -cos Acos (π - A) = -cos Acos (2π - A) = cos A3. 正切函数的商数与余数公式tan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B) tan² A + 1 = sec² AIII. 其他常用公式1. 三角函数同角变换公式sin (-A) = -sin Acos (-A) = cos Atan (-A) = -tan A2. 三角函数的平方和差公式sin² (A ± B) = sin² A ± 2sin A sin B + sin² B cos² (A ± B) = cos² A ∓ 2cos A cos B + cos² B 3. 三角函数的倍角公式sin 2A = 2sin A cos Acos 2A = cos² A - sin² Atan 2A = (2tan A) / (1 - tan² A)4. 半角公式sin (A/2) = ± √[(1 - cos A) / 2]cos (A/2) = ± √[(1 + cos A) / 2]tan (A/2) = ± √[(1 - cos A) / (1 + cos A)]总结高中数学中,三角函数是考试不可避免的一部分,而掌握好三角函数公式,则是解题的必要条件。
高中三角函数公式大全

高中三角函数公式大全1. 正弦函数(sine function):正弦函数用sin表示,定义域为实数集,值域为[-1,1]。
基本关系式:sinθ=opposite/hypotenuse基本恒等式:- 余角关系式:sin(π/2 - θ) = cosθ ;sin(π/2 + θ) = cosθ- 符号关系式:sin(-θ) = - sinθ ;sin(θ + 2πn) = sinθ (n 为任意整数)三角和差化简公式:- 和差化简:sin(α ± β) = sinα * cosβ ± cosα * sinβ- 差和化简:sinα + sinβ = 2 * sin((α + β) / 2) *cos((α - β) / 2)- 和差化简:sinα - sinβ = 2 * cos((α + β) / 2) *sin((α - β) / 2)2. 余弦函数(cosine function):余弦函数用cos表示,定义域为实数集,值域为[-1,1]。
基本关系式:cosθ = adjacent/hypotenuse基本恒等式:- 余角关系式:cos(π/2 - θ) = sinθ ;cos(π/2 + θ) = -sinθ- 符号关系式:cos(-θ) = cosθ ;cos(θ + 2πn) = cosθ (n 为任意整数)三角和差化简公式:- 和差化简:cos(α ± β) = cosα * cosβ ∓ sinα * sinβ- 差和化简:cosα + cosβ = 2 * cos((α + β) / 2) * cos((α - β) / 2)- 和差化简:cosα - cosβ = -2 * sin((α + β) / 2) *sin((α - β) / 2)3. 正切函数(tangent function):正切函数用tan表示,定义域为实数集,值域为整个实数集。
基本关系式:tanθ = opposite/adjacent基本恒等式:- 余角关系式:tan(π/2 - θ) = 1/tanθ ;tan(π/2 + θ) = -1/tanθ三角和差化简公式:- 和差化简:tan(α ± β) = (tanα ± tanβ) / (1 ∓ tanα * tanβ)- 和差化简:tanα + tanβ = sin(α + β) / cosα * cosβ- 和差化简:tanα - tanβ = sin(α - β) / cosα * cosβ4. 正割函数(secant function):正割函数用sec表示,定义域为除了θ = π/2 + πn (n为任意整数)的实数集,值域为实数集的负数和正数。
高中阶段三角函数公式大全

高中阶段三角函数公式大全三角函数公式两角与公式sin(A+B) = sinAcosB+cosAsinBcos(A+B) = cosAcosB-sinAsinBsin(A—B) =sinAcosB-cosAsinB cos(A—B)= cosAcosB+si nAsinBtan(A+B) =cot(A+B) =tan(A—B)=cot(A-B) =倍角公式tan2A = Sin2A=2SinA•CosACos2A = Cos2A—Sin2A=2Cos2A—1=1-2sin2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A=4(cosA)3-3cosAtan3a=tana·tan(+a)·tan(—a)半角公式sin()=tan()=cos()=cot()=tan()==与差化积sina+sinb=2sincos cosa+cosb= 2coscossina—sinb=2cossincosa-cosb=—2sinsintana+tanb=积化与差sinasinb=—[cos(a+b)-cos(a—b)]cosacosb =[cos(a+b)+cos(a—b)]sinacosb=[sin(a+b)+sin(a—b)]cosasinb = [sin(a+b)-sin(a-b)]诱导公式sin(—a) = —sina cos(-a) = cosasin(-a) =cosa cos(—a) =sin asin(+a) = cosacos(+a) = —sinasin(π—a) =sina cos(π-a) = —cosasin(π+a) = -sina cos(π+a) = —cosatgA=tanA =万能公式sina=tana=cosa=其它公式a•sina+b•cosa=×sin(a+c) [其中tanc=]a•sin(a)-b•cos(a) = ×cos(a—c) [其中tan(c)=]1+sin(a)=(sin+cos)21-sin(a) = (sin-cos)2其她非重点三角函数csc(a) =sec(a) =双曲函数sinh(a)=cosh(a)=tg h(a)=公式一:设α为任意角,终边相同得角得同一三角函数得值相等:sin(2kπ+α)=sinα tan(2kπ+α)= tanαcos(2kπ+α)= cosα cot(2kπ+α)=cotα公式二:设α为任意角,π+α得三角函数值与α得三角函数值之间得关系:sin(π+α)=—sinα tan(π+α)=tanαcos(π+α)= —cosα cot(π+α)= cotα公式三:任意角α与—α得三角函数值之间得关系:sin(-α)=—sinα tan(-α)= -tanαcos(-α)=cosα cot(-α)= -cotα公式四:利用公式二与公式三可以得到π-α与α得三角函数值之间得关系:sin(π—α)=sinα tan(π—α)=—tanαcos(π—α)=-cosα cot(π—α)= -cotα公式五:利用公式-与公式三可以得到2π-α与α得三角函数值之间得关系:sin(2π-α)= —sinα tan(2π-α)= -tanαcos(2π-α)= cosα cot(2π—α)=-cotα公式六:±α及±α与α得三角函数值之间得关系:sin(+α)=cosα tan(+α)= -cotαcos(+α)=-sinα cot(+α)= —tanαsin(—α)= cosαtan(-α)=cotαcos(-α)=sinα cot(-α)=tanαsin(+α)= -cosαtan(+α)=-cotαcos(+α)= sinαcot(+α)= -tanαsin(-α)=-cosαtan(—α)= cotαcos(-α)= —sinαcot(-α)= tanα(以上k∈Z)这个物理常用公式我费了半天得劲才输进来,希望对大家有用A•sin(ωt+θ)+B•sin(ωt+φ) =×sin三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a—b) a3+b3=(a+b)(a2—ab+b2) a3—b3=(a—b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=〉-b≤a≤b|a-b|≥|a|—|b| -|a|≤a≤|a|一元二次方程得解—b+√(b2—4ac)/2a —b—√(b2—4ac)/2a根与系数得关系X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式b2-4ac=0 注:方程有相等得两实根b2-4ac〉0注:方程有一个实根b2—4ac<0 注:方程有共轭复数根三角函数公式两角与公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+s inAsinBtan(A+B)=(tanA+tanB)/(1—tanAtanB) tan(A—B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A—B)=(ctgActgB+1)/(ctgB—ctgA)倍角公式tan2A=2tanA/(1—tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a—1=1-2sin2a半角公式sin(A/2)=√((1—cosA)/2) sin(A/2)=-√((1—cosA)/2)cos(A/2)=√((1+cosA)/2)cos(A/2)=—√((1+co sA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=—√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1—cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))与差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)—cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A—B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A—B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/si nAsinB某些数列前n项与1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n—1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形得外接圆半径余弦定理b2=a2+c2—2accosB注:角B就是边a与边c得夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆得标准方程(x-a)2+(y-b)2=r2注:(a,b)就是圆心坐标圆得一般方程x2+y2+Dx+Ey+F=0 注:D2+E2—4F〉0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h’ 正棱台侧面积S=1/2(c+c’)h'圆台侧面积S=1/2(c+c’)l=pi(R+r)l球得表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra就是圆心角得弧度数r 〉0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注:其中,S'就是直截面面积,L就是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h—-—----—-----———--—-—--三角函数积化与差与差化积公式记不住就自己推,用两角与差得正余弦:cos(A+B)=cosAcosB—sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化与差:相加:cosAcosB=[cos(A+B)+cos(A—B)]/2相减:sinAsinB=—[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A—B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化与差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A—B)]/2这样一共4组积化与差,然后倒过来就就是与差化积了不知道这样您可以记住伐,实在记不住考试得时候也可以临时推导一下正加正正在前正减正余在前余加余都就是余余减余没有余还负正余正加余正正减余余余加正正余减还负3、三角形中得一些结论:(不要求记忆)(1)tanA+tanB+tanC=tanA·tanB·tanC(2)sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1 (4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC—1 、、。
高中三角函数的所有公式

高中三角函数的所有公式高中三角函数的所有公式大全两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)倍角公式tan2A = 2tanA/(1-tan^2 A)Sin2A=2SinA?CosACos2A = Cos^2 A--Sin^2 A=2Cos^2 A—1=1—2sin^2 A三倍角公式sin3A = 3sinA-4(sinA)^3;cos3A = 4(cosA)^3 -3cosAtan3a = tan a ? tan(π/3+a)? tan(π/3-a) 半角公式sin(A/2) = √{(1--cosA)/2}cos(A/2) = √{(1+cosA)/2}tan(A/2) = √{(1--cosA)/(1+cosA)}cot(A/2) = √{(1+cosA)/(1-cosA)} ?tan(A/2) = (1--cosA)/sinA=sinA/(1+cosA)和差化积sin(a)+sin(b) = 2sin[(a+b)/2]cos[(a-b)/2] sin(a)-sin(b) = 2cos[(a+b)/2]sin[(a-b)/2] cos(a)+cos(b) = 2cos[(a+b)/2]cos[(a-b)/2] cos(a)-cos(b) = -2sin[(a+b)/2]sin[(a-b)/2] tanA+tanB=sin(A+B)/cosAcosB积化和差sin(a)sin(b) = -1/2__[cos(a+b)-cos(a-b)] cos(a)cos(b) = 1/2__[cos(a+b)+cos(a-b)] sin(a)cos(b) = 1/2__[sin(a+b)+sin(a-b)]cos(a)sin(b) = 1/2__[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sin(a)cos(-a) = cos(a)sin(π/2-a) = cos(a)cos(π/2-a) = sin(a)sin(π/2+a) = cos(a)cos(π/2+a) = -sin(a)sin(π-a) = sin(a)cos(π-a) = -cos(a)sin(π+a) = -sin(a)cos(π+a) = -cos(a)tgA=tanA = sinA/cosA万能公式sin(a) = [2tan(a/2)] / {1+[tan(a/2)]^2}cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]^2}tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}其它公式a?sin(a)+b?cos(a) = [√(a^2+b^2)]__sin(a+c) [其中,tan(c)=b/a]a?sin(a)-b?cos(a) = [√(a^2+b^2)]__cos(a-c) [其中,tan(c)=a/b] 1+sin(a) = [sin(a/2)+cos(a/2)]^2;1-sin(a) = [sin(a/2)-cos(a/2)]^2;;其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)三角函数的基本公式一、倍角公式1、Sin2A=2SinA__CosA2、Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-13、tan2A=(2tanA)/(1-tanA^2)(注:SinA^2是sinA的平方sin2(A))二、降幂公式1、sin^2(α)=(1-cos(2α))/2=versin(2α)/22、2cos^2(α)=(1+cos(2α))/2=covers(2α)/23、tan^2(α)=(1-cos(2α))/(1+cos(2α))三、推导公式1、1tanα+cotα=2/sin2α2、tanα-cotα=-2cot2α3、1+cos2α=2cos^2α4、4-cos2α=2sin^2α5、1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina四、两角和差1、1cos(α+β)=cosα·cosβ-sinα·sinβ2、cos(α-β)=cosα·cosβ+sinα·sinβ3、sin(α±β)=sinα·cosβ±cosα·sinβ4、4tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)5、tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)三角函数的8个诱导公式是什么1. 正弦函数的诱导公式sin(-x) = -sin(x)这个公式表明,正弦函数的值在x轴上是关于原点对称的。
高中阶段三角函数公式大全

高中阶段三角函数公式大全三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB cos(A+B) = cosAcosB-sinAsinBsin(A-B) = sinAcosB-cosAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + cot(A+B) =cotAcotB 1-cotAcotB + tan(A-B) =tanAtanB 1tanB tanA +- cot(A-B) =cotAcotB 1cotAcotB -+倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - tan(2A )=A A cos 1cos 1+- cos(2A )=2cos 1A + cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积 sina+sinb=2sin2b a +cos 2b a - cosa+cosb = 2cos 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin万能公式 sina=2)2(tan 12tan 2a a + tana=2)2(tan 12tan 2a a - cosa=22)2(tan 1)2(tan 1a a +- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b •cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinα tan (2kπ+α)= tanαcos (2kπ+α)= cosα cot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)= -sinα tan (π+α)= tanαcos (π+α)= -cosα cot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinα tan (-α)= -tanαcos (-α)= cos α cot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sinα tan (π-α)= -tanαcos (π-α)= -cosα cot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinα tan (2π-α)= -tanαcos (2π-α)= cosα cot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα tan (2π+α)= -cotα cos (2π+α)= -sinα cot (2π+α)= -tanαsin (2π-α)= cosα tan (2π-α)= cotα cos (2π-α)= sinα cot (2π-α)= tanαsin (23π+α)= -cosα tan (23π+α)= -cotαcos (23π+α)= sinα cot (23π+α)= -tanα sin (23π-α)= -cosα tan (23π-α)= cotα cos (23π-α)= -sinα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解 a 2-b 2=(a+b)(a-b) a 3+b 3=(a+b)(a 2-ab+b 2) a 3-b 3=(a-b)(a 2+ab+b 2) 三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b 2-4ac)/2a -b-√(b 2-4ac)/2a根与系数的关系 X 1+X 2=-b/a X 1*X 2=c/a 注:韦达定理判别式 b 2-4ac=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+co sA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L 注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h 圆柱体V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)tanA+tanB+tanC=tanA·tanB·tanC(2)sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
(完整版)高中数学三角函数公式大全全解
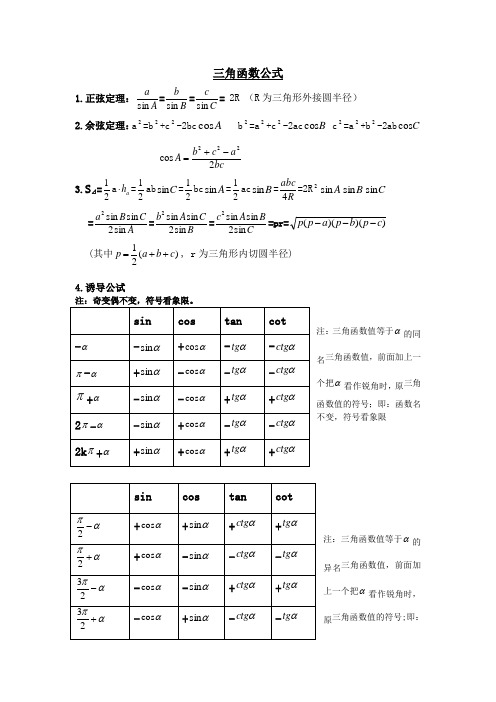
三角函数公式1.正弦定理:A a sin =B b sin =Cc sin = 2R (R 为三角形外接圆半径) 2.余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=3.S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin =AC B a sin 2sin sin 2=B C A b sin 2sin sin 2=C B A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)4.诱导公试注:奇变偶不变,符号看象限。
注:三角函数值等于α的同名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看象限注:三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名改变,符号看象限5.和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±6.二倍角公式:(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=7.半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sinθθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg8.积化和差公式:[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(21sin sin9.和差化积公式:①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=- 锐角三角形函数公式总结大全1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
高中所有三角函数公式整理

高中所有三角函数公式整理一、基本关系公式。
1. 平方关系。
- sin^2α+cos^2α = 1- 1+tan^2α=sec^2α(secα=(1)/(cosα))- 1+cot^2α=csc^2α(cscα=(1)/(sinα))2. 商数关系。
- tanα=(sinα)/(cosα)- cotα=(cosα)/(sinα)二、诱导公式。
1. 终边相同的角的三角函数值关系(k∈ Z)- sin(α + 2kπ)=sinα- cos(α+2kπ)=cosα- tan(α + 2kπ)=tanα2. 关于x轴对称的角的三角函数值关系。
- sin(-α)=-sinα- cos(-α)=cosα- tan(-α)=-tanα3. 关于y轴对称的角的三角函数值关系。
- sin(π-α)=sinα- cos(π - α)=-cosα- tan(π-α)=-tanα4. 关于原点对称的角的三角函数值关系。
- sin(π+α)=-sinα- cos(π+α)=-cosα- tan(π+α)=tanα5. 关于直线y = x对称的角的三角函数值关系。
- sin((π)/(2)-α)=cosα- cos((π)/(2)-α)=sinα- tan((π)/(2)-α)=cotα- sin((π)/(2)+α)=cosα- cos((π)/(2)+α)=-sinα- tan((π)/(2)+α)=-cotα三、两角和与差的三角函数公式。
1. 两角和公式。
- sin(α+β)=sinαcosβ+cosαsinβ- c os(α+β)=cosαcosβ-sinαsinβ- tan(α+β)=(tanα+tanβ)/(1 - tanαtanβ)2. 两角差公式。
- sin(α-β)=sinαcosβ-cosαsinβ- cos(α-β)=cosαcosβ+sinαsinβ- tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)四、二倍角公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中阶段三角函数公式大全三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB cos(A+B) = cosAcosB-sinAsinB sin(A-B) = sinAcosB-cosAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + cot(A+B) =cotAcotB 1-cotAcotB + tan(A-B) =tanAtanB 1tanB tanA +- cot(A-B) =cotAcotB 1cotAcotB -+倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - tan(2A )=A A cos 1cos 1+- cos(2A )=2cos 1A + cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积 sina+sinb=2sin2b a +cos 2b a - cosa+cosb = 2cos 2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tana+tanb=ba b a cos cos )sin(+积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin万能公式 sina=2)2(tan 12tan 2a a + tana=2)2(tan 12tan 2a a - cosa=22)2(tan 1)2(tan 1a a +- 其它公式 a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b •cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a 公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinα tan (2kπ+α)= tanα cos (2kπ+α)= cosα cot (2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinα tan (π+α)= tanα cos (π+α)= -cosα cot (π+α)= cotα公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinα tan (-α)= -tanα cos (-α)= cos α cot (-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinα tan (π-α)= -tanα cos (π-α)= -cosα cot (π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)= -sinα tan (2π-α)= -tanα cos (2π-α)= cosα cot (2π-α)= -cotα公式六:2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα tan (2π+α)= -cotα cos (2π+α)= -sinα cot (2π+α)= -tanαsin (2π-α)= cosα tan (2π-α)= cotα cos (2π-α)= sinα cot (2π-α)= tanαsin (23π+α)= -cosα tan (23π+α)= -cotαcos (23π+α)= sinα cot (23π+α)= -tanα sin (23π-α)= -cosα tan (23π-α)= cotα cos (23π-α)= -sinα cot (23π-α)= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解 a 2-b 2=(a+b)(a-b) a 3+b 3=(a+b)(a 2-ab+b 2)a 3-b 3=(a-b)(a 2+ab+b 2)三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|一元二次方程的解 -b+√(b 2-4ac)/2a -b-√(b 2-4ac)/2a根与系数的关系 X 1+X 2=-b/a X 1*X 2=c/a 注:韦达定理判别式 b 2-4ac=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式 tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+co sA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理 a/sinA=b/sinB=c/sinC=2R 注:其中 R 表示三角形的外接圆半径余弦定理 b2=a2+c2-2accosB 注:角B是边a和边c的夹角正切定理:[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程 (x-a)2+(y-b)2=r2注:(a,b)是圆心坐标圆的一般方程 x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h斜棱柱体积 V=S'L 注:其中,S'是直截面面积, L是侧棱长柱体体积公式 V=s*h 圆柱体 V=pi*r2h-----------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负3.三角形中的一些结论:(不要求记忆)(1)t anA+tanB+tanC=tanA·tanB·tanC(2)sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1) tan(α+β)=(1+m)/(1-m)tanβ。
