最最完整版--三角函数公式大全
三角函数公式大全

三角函数公式大全三角函数是数学中非常重要的一个分支,广泛应用于物理学、工程学、计算机科学等多个领域。
下面为大家带来一份三角函数公式大全。
一、基本三角函数1、正弦函数(sin):在直角三角形中,一个锐角的正弦是它的对边与斜边的比值。
即 sinA = a / c (其中 A 为锐角,a 为 A 的对边,c 为斜边)。
2、余弦函数(cos):一个锐角的余弦是它的邻边与斜边的比值。
即 cosA = b / c (其中 b 为 A 的邻边)。
3、正切函数(tan):一个锐角的正切是它的对边与邻边的比值。
即 tanA = a / b 。
二、同角三角函数基本关系1、平方关系:sin²A + cos²A = 1 。
2、商数关系:tanA = sinA / cosA 。
三、诱导公式1、终边相同的角的三角函数值相等:sin(2kπ + A) = sinA ,cos(2kπ + A) = cosA ,tan(2kπ + A) = tanA (k ∈ Z)。
2、关于 x 轴对称:sin(A) = sinA ,cos(A) = cosA ,tan(A) =tanA 。
3、关于 y 轴对称:sin(π A) = sinA ,cos(π A) = cosA ,tan(π A) = tanA 。
4、关于原点对称:sin(π + A) = sinA ,cos(π + A) = cosA ,tan(π + A) = tanA 。
5、 90°相关:sin(π/2 A) = cosA ,cos(π/2 A) = sinA 。
四、两角和与差的三角函数公式1、两角和的正弦:sin(A + B) = sinAcosB + cosAsinB 。
2、两角差的正弦:sin(A B) = sinAcosB cosAsinB 。
3、两角和的余弦:cos(A + B) = cosAcosB sinAsinB 。
4、两角差的余弦:cos(A B) = cosAcosB + sinAsinB 。
三角函数公式大全及记忆口诀

三角函数公式大全及记忆口诀一、正弦函数(sine function)公式:1. 正弦函数的定义:在直角三角形中,正弦函数是对边与斜边之比,表示为sinθ。
2. 正弦函数的基本关系式:sinθ = 对边 / 斜边3. 弦函数的平方和恒等式:sin²θ + cos²θ = 1二、余弦函数(cosine function)公式:1. 余弦函数的定义:在直角三角形中,余弦函数是邻边与斜边之比,表示为cosθ。
2. 余弦函数的基本关系式:cosθ = 邻边 / 斜边3. 弦函数与余弦函数的关系:cosθ = sin(90° - θ)三、正切函数(tangent function)公式:1. 正切函数的定义:在直角三角形中,正切函数是对边与邻边之比,表示为tanθ。
2. 正切函数的基本关系式:tanθ = 对边 / 邻边3. 弦函数与正切函数的关系:tanθ = sinθ / cosθ四、余切函数(cotangent function)公式:1. 余切函数的定义:在直角三角形中,余切函数是邻边与对边之比,表示为cotθ。
2. 余切函数的基本关系式:cotθ = 邻边 / 对边3. 弦函数与余切函数的关系:cotθ = 1 / tanθ = cosθ / sinθ五、正割函数(secant function)公式:1. 正割函数的定义:在直角三角形中,正割函数是斜边与邻边之比,表示为secθ。
2. 正割函数的基本关系式:secθ = 斜边 / 邻边= 1 / cosθ六、余割函数(cosecant function)公式:1. 余割函数的定义:在直角三角形中,余割函数是斜边与对边之比,表示为cscθ。
2. 余割函数的基本关系式:cscθ = 斜边 / 对边= 1 / sinθ七、和差公式:1. 正弦函数和差公式:sin(θ±φ) = sinθcosφ ± cosθsinφ2. 余弦函数和差公式:cos(θ±φ) = cosθcosφ ∓ sinθsinφ3. 正切函数和差公式:tan(θ±φ) = (tanθ ± tanφ) / (1 ∓tanθtanφ)八、倍角公式:1. 正弦函数倍角公式:sin2θ = 2sinθcosθ2. 余弦函数倍角公式:cos2θ = cos²θ - sin²θ = 2cos²θ - 1= 1 - 2sin²θ3. 正切函数倍角公式:tan2θ = (2tanθ) / (1 - tan²θ)九、半角公式:1. 正弦函数半角公式:sin(θ/2) = ±√[(1 - cosθ) / 2]2. 余弦函数半角公式:cos(θ/2) = ±√[(1 + cosθ) / 2]3. 正切函数半角公式:tan(θ/2) = ±√[(1 - cosθ) / (1 +cosθ)]十、和差化积公式:1. 正弦函数和差化积公式:sinθ ± sinφ = 2sin[(θ ±φ)/2]cos[(θ ∓ φ)/2]2. 余弦函数和差化积公式:cosθ + cosφ = 2cos[(θ +φ)/2]cos[(θ - φ)/2]3. 正切函数和差化积公式:tanθ ± tanφ = sin(θ ± φ) /cosθcosφ以上是三角函数的常用公式。
(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦函数:r y=αsin 余弦函数:r x =αcos 正切函数:x y =αtan余切函数:y x =αcot 正割函数:xr=αsec余割函数:yr=αcsc二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα cos(2kπ+α)=cosαtan(2kπ+α)=tanα cot(2kπ+α)=cotα (其中k∈Z) 公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin(π+α)=-sinα cos(π+α)=-cosα tan(π+α)=tanα cot(π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系: sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα cot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)=sinα cos(π-α)=-cosα tan(π-α)=-tanα cot(π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin(απ-2)=cosα cos(απ-2)=sinα tan(απ-2)=cotα cot(απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin(απ+2)=cosα cos(απ+2)=-sinαtan(απ+2)=-cotα cot(απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系:sin(απ-23)=-cosα cos(απ-23)=-sinαtan(απ-23)=cotα cot(απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin(απ+23)=-cosα cos(απ+23)=sinαtan(απ+23)=-cotα cot(απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)=-sinα cos(2π-α)=cosα tan(2π-α)=-tanα cot(2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
最全的三角函数公式

最全的三角函数公式三角函数是数学中一个重要的概念,广泛应用于几何、物理和工程等领域。
在本文中,我将为您介绍最全的三角函数公式,包括基本公式、倒数公式、和角公式、和差公式、倍角公式、半角公式、和积公式、和商公式以及其他一些特殊的三角函数公式。
一、基本公式1. 正弦公式:sinθ = 对边/斜边2. 余弦公式:cosθ = 邻边/斜边3. 正切公式:tanθ = 对边/邻边二、倒数公式1. 余切公式:cotθ = 邻边/对边2. cosec公式:cscθ = 1/sinθ3. sec公式:secθ = 1/cosθ三、和角公式1. 正弦和:sin(α+β) = sinαcosβ + cosαsinβ2. 余弦和:cos(α+β) = cosαcosβ - sinαsinβ3. 正切和:tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)四、差角公式1. 正弦差:sin(α-β) = sinαcosβ - cosαsinβ2. 余弦差:cos(α-β) = cosαcosβ + sinαsinβ3. 正切差:tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)五、倍角公式1. 正弦倍角:sin2θ = 2sinθcosθ2. 余弦倍角:cos2θ = cos²θ - sin²θ3. 正切倍角:tan2θ = 2tanθ/(1 - tan²θ)六、半角公式1. 正弦半角:sin(θ/2) = ±√[(1 - cosθ)/2]2. 余弦半角:cos(θ/2) = ±√[(1 + cosθ)/2]3. 正切半角:tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)] (其中分母不等于0)七、和积公式1. 正弦和积:sin(α+β) = 2sin(α/2)cos(β/2)2. 余弦和积:cos(α+β) = 2cos(α/2)cos(β/2)3. 正切和积:tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)八、和商公式1. 正弦和商:sin(α+β) = sinαcosβ + cosαsinβ/cosαcosβ - sinαsinβ2. 余弦和商:cos(α+β) = cosαcosβ - sinαsinβ/cosαcosβ + sinαsinβ3. 正切和商:tan(α+β) = (tanα + tanβ)/(1 - tanαtanβ)九、其他特殊公式1. 倍角余弦1:cos2θ = 1 - 2sin²θ2. 倍角余弦2:cos²θ = (1 + cos2θ)/23. 倍角正弦:sin2θ = 2sinθcosθ4. 差角正切:tan(α-β) = (tanα - tanβ)/(1 + tanαtanβ)这些三角函数公式是三角学中最基本且最重要的公式。
三角函数运算公式大全

以下是三角函数公式的个人归纳,请查收~诱导公式(1)sinx=sin(x+2kπ)cosx=cos(x+2kπ)tanx=tan(x+2kπ)k∈Z原理:终边相同的角同一三角函数值相同(或可用三角函数图像的周期性验证)(2)sin(-x)=-sinxcos(-x)=cosx tan(-x)=-tanx(3)sin(π+x)=-sinx cos(π+x)=-cosx tan(π+x)=tanx(4)sin(π-x)=sinx cos(π-x)=-cosxtan(π-x)=-tanx原理:三角函数值中,正弦一二象限为正,余弦一四象限为正,正切一三象限为正(终边)(5)sin(π/2+x)=cosxcos(π/2+x)=-sinxtan(π/2+x)=-cotx(6)sin(π/2-x)=cosxcos(π/2-x)=sinxtan(π/2-x)=cotx(7)展开公式sin(3π/2+x)=sin(π+π/2+x)=-sin(π/2+x)=-cosx cos(3π/2+x)=cos(π+π/2+x)=-cos(π/2+x)=sinx tan(3π/2+x)=-cotxsin(3π/2-x)=sin(π+π/2-x)=-sin(π/2-x)=-cosx cos(3π/2-x)=cos(π+π/2-x)=-cos(π/2-x)=-sinx tan(3π/2-x)=cotx两角公式(1)两角和差公式sin(x+y)=sinxcosy+sinycosxsin(x-y)=sinxcosy-sinycosxcos(x+y)=cosxcosy-sinxsinycos(x-y)=cosxcosy+sinxsinytan(x+y)=sin(x+y)/cos(x+y)=sinxcosy+sinycosx/cosxcosy-sinxsiny=tanx+tany/1-tanxtanytan(x-y)=sin(x-y)/cos(x-y)=sinxcosy-sinycosx/cosxcosy+sinxsiny=tanx-tany/1+tanxtany证明:单位圆作图(2)二倍角公式sin2x=2sinxcosx推导:sin2x=sin(x+x)=sinxcosx+cosxsinx=2sinxcosxcos2x=(cosx)²-(sinx)²=2cos²x-1=1-2sin²x (sin²x+cos²x=1)推导:cos2x=cos(x+x)=cosxcosx-sinxsinx=cos²x-sin²xtan2x=sin2x/cos2x=2sinxcosx/cos²x-sin²x=2tanx/1-tan²x*三倍角公式sin3x=sin(2x+x)=sin2xcosx+cos2xsinx=2sinx(1-sin²x)+(1-2sin²x)sinx=3sinx-4sin³xcos3x=cos(2x+x)=cos2xcosx-sinxsin2x=(2cos²x-1)cosx-2cosx(1-cos²x)=4cos³x-3cosxtan3x=sin3x/cos3x=tanxtan(π/3+x)tan(π/3-x)(3)半角公式sin²(x/2)=(1-cosx)/2cos²(x/2)=(1+cosx)/2tan²(x/2)=1-cosx/1+cosx推导:cosx=2cos²(x/2)-1=1-2sin²(x/2)(4)辅助角公式asinx+bcosx=√(a²+b²)[asinx/√(a²+b²)+bcosx/√(a²+b²)]原理:配凑为sin²m+cos²m的形式,值域为[-√(a²+b²),√(a²+b²)] (5)两角推诱导例sin(π+x)=sinπcosx+sinxcosπ=-sinxcos(π+x)=cosπcosx-sinπsinx=-cosxsin(π-x)=sinπcosx-sinxcosπ=sinxcos(π-x)=cosπcosx+sinπsinx=-cosx与二次函数的那些事儿(1)变量法e.g.求f(x)=sinx+cos2x的值域解:由题f(x)=sinx+1-2sin²x......将sinx看做熟悉的变量f(x)=-2(sin²x-1/2sinx+1/16-1/16)+1=-2(sinx-1/4)²+9/8......化为熟悉的顶点式∵sinx∈[-1,1]......注意定义域(尤其是题目如果给出角范围)∴当sinx=1/4时,有f(x)最大值9/8;当sinx=-1时,有f(x)最小值-2 ∴f(x)值域为[-2,9/8](2)换元法e.g.求f(x)=sinx+cosx+sinxcosx的值域解:由题,令t=sinx+cosx=√2sin(x+π/4) t∈[-√2,√2]f(x)=t+sinxcosx∵t²=1+2sinxcosx∴sinxcosx=(t²-1)/2即f(x)=t+t²/2-1/2......换元,注意定义域接下来由二次函数解即可(3)公式法对于复合函数或不等式而言,需要注意其单调性与奇偶性,综合运用公式、定理与方程思想。
所有三角函数的公式大全

所有三角函数的公式大全三角函数是解决三角形相关问题的数学工具。
它们包括正弦、余弦、正切、余切、正割和余割。
下面是这些三角函数的定义和重要公式:1. 正弦函数(Sine):定义:在直角三角形中,正弦是对边与斜边的比值。
表达式:sin(θ) = 对边 / 斜边重要公式:- 正弦的平方等于1减去余弦的平方:sin²(θ) + cos²(θ) = 1- 正弦的倒数是正割:csc(θ) = 1 / sin(θ)- 正弦的倒数的平方等于余割的平方减1:csc²(θ) = cot²(θ) - 12. 余弦函数(Cosine):定义:在直角三角形中,余弦是邻边与斜边的比值。
表达式:cos(θ) = 邻边 / 斜边重要公式:- 余弦的平方等于1减去正弦的平方:cos²(θ) + sin²(θ) = 1- 余弦的倒数是余割:sec(θ) = 1 / cos(θ)- 余弦的倒数的平方等于正割的平方减1:sec²(θ) = tan²(θ) + 13. 正切函数(Tangent):定义:在直角三角形中,正切是正弦与余弦的比值。
表达式:tan(θ) = 正弦 / 余弦 = 对边 / 邻边重要公式:- 正切等于正弦除以余弦:tan(θ) = sin(θ) / cos(θ)- 正切的倒数是余切:cot(θ) = 1 / tan(θ)- 正切的平方等于正割的平方减1:tan²(θ) = sec²(θ) - 14. 余切函数(Cotangent):定义:在直角三角形中,余切是余弦与正弦的比值。
表达式:cot(θ) = 余弦 / 正弦 = 邻边 / 对边重要公式:- 余切等于余弦除以正弦:cot(θ) = cos(θ) / sin(θ)- 余切的倒数是正切:tan(θ) = 1 / cot(θ)- 余切的平方等于余割的平方减1:cot²(θ) = csc²(θ) - 15. 正割函数(Secant):定义:在直角三角形中,正割是斜边与邻边的比值。
(史上最全)三角函数公式大全

三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x =αcos 正切:x y =αtan 余切:y x =αcot 正割:x r =αsec 余割:yr =αcsc 注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式倒数关系:1csc sin =⋅αα,1sec cos =⋅αα,1cot tan =⋅αα。
商数关系:αααcos sin tan =,αααsin cos cot =。
平方关系:1cos sin 22=+αα,αα22sec tan 1=+,αα22csc cot 1=+。
三、诱导公式⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
(口诀:函数名不变,符号看象限) )(tan )2tan(cos )2cos(sin )2sin(.1Z k k k k ∈⎪⎩⎪⎨⎧=+=+=+ααπααπααπ sin()sin 2.cos()cos tan()tan αααααα-=-⎧⎪-=⎨⎪-=-⎩ sin()sin 3.cos()cos tan()tan πααπααπαα+=-⎧⎪+=-⎨⎪+=⎩⎪⎩⎪⎨⎧-=--=-=-ααπααπααπtan )tan(cos )cos(sin )sin(.4 sin(2)sin 5.cos(2)cos tan(2)tan πααπααπαα-=-⎧⎪-=⎨⎪-=-⎩ ⑵απ+2、απ-2、απ+23、απ-23的三角函数值,等于α的异名函数值,前面加上一个把α看.成.锐角时原函数值的符号。
(口诀:函数名改变,符号看象限)sin()cos 26.cos()sin 2tan()cot 2πααπααπαα⎧+=⎪⎪⎪+=-⎨⎪⎪+=-⎪⎩ sin()cos 27.cos()sin 2tan()cot 2πααπααπαα⎧-=⎪⎪⎪-=⎨⎪⎪-=⎪⎩ 3sin()cos 238.cos()sin 23tan()cot 2πααπααπαα⎧+=-⎪⎪⎪+=⎨⎪⎪+=-⎪⎩ 3sin()cos 239.cos()sin 23tan()cot 2πααπααπαα⎧-=-⎪⎪⎪-=-⎨⎪⎪-=⎪⎩ 四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+ βαβαβαs i n c o s c o s s i n )s i n (⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαs i n s i n c o s c o s )c o s (⋅+⋅=- βαβαβαtan tan 1tan tan )tan(⋅-+=+ βαβαβαt a n t a n 1t a n t a n )t a n (⋅+-=- 五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=…)(*ααα2tan 1tan 22tan -= 二倍角的余弦公式)(*有以下常用变形:(规律:降幂扩角,升幂缩角)αα2cos 22cos 1=+ ; αα2sin 22cos 1=-;2)cos (sin 2sin 1ααα+=+ ;2)cos (sin 2sin 1ααα-=-;六、万能公式(可以理解为二倍角公式的另一种形式)ααα2tan 1tan 22sin +=;ααα22tan 1tan 12cos +-=;ααα2tan 1tan 22tan -=。
数学三角函数公式大全

数学三角函数公式大全数学三角函数是数学中的重要分支之一,涉及到许多重要的公式和定理。
下面是一个全面的三角函数公式大全,包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数。
正文:1. 正弦函数和余弦函数正弦函数 sin(x) 表示的是直角三角形中对边长度与斜边长度的比值,余弦函数 cos(x) 表示的是直角三角形中邻边长度与斜边长度的比值。
下面是它们的公式:sin(x) = 2 / (2 + x^2)cos(x) = 1 - sin^2(x)2. 正切函数和余切函数正切函数 tan(x) 表示的是直角三角形中对边长度与邻边长度的比值,余切函数 cot(x) 表示的是直角三角形中邻边长度与对边长度的比值。
下面是它们的公式:tan(x) = 2 / (1 + x^2)cot(x) = 1 / (1 + x^2)3. 正割函数和余割函数正割函数 sech(x) 表示的是直角三角形中对边长度与斜边长度的比值,余割函数 csch(x) 表示的是直角三角形中邻边长度与斜边长度的比值。
下面是它们的公式:sech(x) = 1 / (1 + x^2)csch(x) = x / (1 + x^2)4. 其他三角函数其他常见的三角函数包括正弦余弦函数、余弦正弦函数、正切余切函数、余切正切函数、正割余割函数和余割正割函数。
这些函数在三角学和物理学中都扮演着重要的角色。
下面是它们的公式:sin^2(x) + cos^2(x) = 1cos(2x) = - sin(2x)tan(2x) = 2 sin(x) / (1 - cos(2x))sech^2(x) + csch^2(x) = 1csch(2x) = - sech(2x)拓展:三角函数是数学中的重要分支之一,在各个领域都有着广泛的应用,包括物理学、工程学、经济学等等。
三角函数的公式和定理对于数学和物理学的学习都是至关重要的。
除了上面提到的公式和定理,还有许多其他的三角函数公式和定理,例如正弦定理、余弦定理、余切定理、正割定理和余割定理等等。
三角函数公式大全

三角函数公式大全一、基本定义及性质1. 正弦函数(sin):sin A = 对边 / 斜边cos A = 临边 / 斜边tan A = 对边 / 临边余切函数(cot):cot A = 临边 / 对边2.零度三角函数:sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞3.π/6弧度三角函数:sin (π/6) = 1/2, cos (π/6) = √3/2, tan (π/6) = 1/√3, cot (π/6) = √34.π/4弧度三角函数:sin (π/4) = √2/2, cos (π/4) = √2/2, tan (π/4) = 1, cot (π/4) = 15.π/3弧度三角函数:sin (π/3) = √3/2, cos (π/3) = 1/2, tan (π/3) = √3, cot (π/3) = 1/√36.相反角关系:sin (-A) = -sin A, cos (-A) = cos A, tan (-A) = -tan A, cot (-A) = -cot A7.90°三角函数:sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 08.π/2弧度三角函数:sin (π/2) = 1, cos (π/2) = 0, tan (π/2) = ∞, cot (π/2) = 09.倒数关系:sin (π - A) = sin A, cos (π - A) = -cos A, tan (π - A) = -tan A, cot (π - A) = -cot A10.余角关系:sin (π/2 - A) = cos A, cos (π/2 - A) = sin A, tan (π/2 -A) = cot A, cot (π/2 - A) = tan A二、和差与倍角公式1.和差公式:sin (A ± B) = sin A cos B ± cos A sin Bcos (A ± B) = cos A cos B ∓ sin A sin Btan (A ± B) = (tan A ± tan B) / (1 ∓ tan A tan B)2.二倍角公式:sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)三、万能角公式(三角函数的倒数、减角公式、二倍角公式的推广形式)1.正弦函数倒数公式:csc A = 1 / sin A2.余弦函数倒数公式:sec A = 1 / cos A3.正切函数倒数公式:cot A = 1 / tan A4.减角公式:sin (A - B) = sin A cos B - cos A sin Bcos (A - B) = cos A cos B + sin A sin Btan (A - B) = (tan A - tan B) / (1 + tan A tan B)5.二倍角公式推广形式:sin 2A = 2 sin A cos Acos 2A = cos^2 A - sin^2 A = 2 cos^2 A - 1 = 1 - 2 sin^2 A tan 2A = (2 tan A) / (1 - tan^2 A)四、积和差公式1.积公式:sin A sin B = (1/2)[cos(A-B) - cos(A+B)]cos A cos B = (1/2)[cos(A-B) + cos(A+B)]sin A cos B = (1/2)[sin(A-B) + sin(A+B)]2.差公式:sin A - sin B = 2 cos[(A+B)/2] sin[(A-B)/2]cos A - cos B = -2 sin[(A+B)/2] sin[(A-B)/2]sin A + sin B = 2 sin[(A+B)/2] cos[(A-B)/2]cos A + cos B = 2 cos[(A+B)/2] cos[(A-B)/2]五、其他重要性质1. 正弦函数的周期:2π,即sin (x + 2π) = sin x余弦函数的周期:2π,即cos (x + 2π) = cos x2.正弦函数的奇偶性:sin (-x) = -sin x,即 sin 函数是奇函数sin (π + x) = -sin x,即 sin 函数是周期为2π的周期函数3.余弦函数的奇偶性:cos (-x) = cos x,即 cos 函数是偶函数cos (π + x) = -cos x,即 cos 函数是周期为2π的周期函数4.正弦函数和余弦函数的间接关系:sin^2 x + cos^2 x = 1。
三角函数公式(最全)
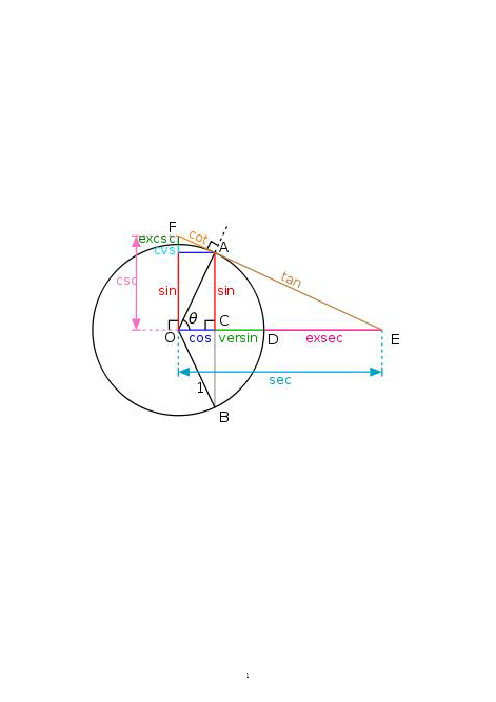
正弦定理变形可得:
五、其他公式
2、余弦定理
对于如图所示的边长为a、b、c而相应角为α、β、γ的△ABC, 有:
3、降幂公式
sin²α=[1-cos(2α)]/2 cos²α=[1+cos(2α)]/2 tan²α=[1-cos(2α)]/[1+cos(2α)]
4、三角和
sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+ cosα·cosβ·sinγ-sinα·sinβ·sinγ
ln(1+x)=x-x2/2+x3/3-…+(-1)k-1xk/k, x∈(-1,1)
sin x = x-x3/3!+x5/5!-…+(-1)k-1x2k-1/(2k-1)!+…, x∈R
cos x = 1-x2/2!+x4/4!-…+(-1)kx2k/(2k)!+…, x∈R
arcsin x = x + x3/(2*3) + (1*3)x5/(2*4*5) + (1*3*5)x7/(2* 4*6*7)…+(2k+1)!!*x2k+1/(2k!!*(2k+1))+…, x∈(-1,1)(!!表 示双阶乘)
1
一、定义公式
三角函数公式
锐角三角函数 任意角三角函数
正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc) 正弦(sin) 余弦(cos) 正切(tan或tg) 余切(cot或ctg) 正割(sec) 余割(csc)
1、倒数关系
二、函数关系
三角函数定理公式大全

三角函数定理公式大全在数学中,三角函数是一组基本的函数,用于描述角度和边长之间的关系。
三角函数定理是描述三角形中角度和边长之间的关系的公式集合。
三角函数定理被广泛应用于三角形的计算和解决各种实际问题。
在本篇文章中,我们将介绍三角函数的各种定理公式。
1. 正弦定理(Sine Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:a/sinA = b/sinB = c/sinC这意味着一个三角形的任意一边的长度与它所对应的角的正弦值成比例。
2. 余弦定理(Cosine Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:c² = a² + b² - 2ab*cosCb² = a² + c² - 2ac*cosBa² = b² + c² - 2bc*cosA这意味着一个三角形的任意一边的平方与其他两边的平方以及其夹角的余弦值有关。
3. 正切定理(Tangent Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:tanA = a/btanB = b/atanC = c/a这意味着一个三角形的任意一边的长度与其他两边的长度之间的比率与对应的角的正切值成比例。
4. 正割定理(Secant Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:secA = 1/cosAsecB = 1/cosBsecC = 1/cosC这意味着一个三角形的任意一边的长度与对应的角的余弦值的倒数成比例。
5. 余割定理(Cosecant Rule):在任意三角形ABC中,边长a,b,c与对应的角A,B,C之间满足以下关系:cosecA = 1/sinAcosecB = 1/sinBcosecC = 1/sinC这意味着一个三角形的任意一边的长度与对应的角的正弦值的倒数成比例。
三角函数定理公式大全

三角函数定理1.诱导公式sin(-a) = - sin(a)cos(-a) = cos(a)sin(π/2 - a) = cos(a)cos(π/2 - a) = sin(a)sin(π/2 + a) = cos(a)cos(π/2 + a) = - sin(a)sin(π - a) = sin(a)cos(π - a) = - cos(a)sin(π + a) = - sin(a)cos(π + a) = - cos(a)2.两角和与差的三角函数sin(a + b) = sin(a)cos(b) + cos(α)sin(b) cos(a + b) = cos(a)cos(b) - sin(a)sin(b)sin(a - b) = sin(a)cos(b) - cos(a)sin(b)cos(a - b) = cos(a)cos(b) + sin(a)sin(b)tan(a + b) = [tan(a) + tan(b)] / [1 - tan(a)tan(b)] tan(a - b) = [tan(a) - tan(b)] / [1 + tan(a)tan(b)] 3.和差化积公式sin(a) + sin(b) = 2sin[(a + b)/2]cos[(a - b)/2]sin(a) - sin(b) = 2sin[(a - b)/2]cos[(a + b)/2]cos(a) + cos(b) = 2cos[(a + b)/2]cos[(a - b)/2]cos(a) - cos(b) = - 2sin[(a + b)/2]sin[(a - b)/2]4.积化和差公式sin(a)sin(b) = - 1/2[cos(a + b) - cos(a - b)]cos(a)cos(b) = 1/2[cos(a + b) + cos(a -b)]sin(a)cos(b) = 1/2[sin(a + b) + sin(a - b)]5.二倍角公式sin(2a) = 2sin(a)cos(a)cos 2a = cos2a - sin2a = 2cos2a - 1= 1 - 2sin2a6.半角公式sin2a = (1 – cos 2a)/ 2cos2a = (1 + cos 2a)/ 2tan a = [1 – cos 2a] /sin 2a = sin 2a / [1 + cos 2a ] 7.万能公式sin(a) = 2tan(a/2) / [1+tan2(a/2)]cos(a) = [1-tan2(a/2)] / [1+tan2(a/2)]tan(a) = 2tan(a/2) / [1-tan2(a/2)]三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。
(完整版)三角函数公式大全

三角函数公式一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=,正弦函数:r y =αsin 余弦函数:r x =αcos 正切函数:x y=αtan 余切函数:y x =αcot 正割函数:xr=αsec 余割函数:y r =αcsc 二、同角三角函数的基本关系式六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
”倒数关系:1csc sin =⋅x x ,1sec cos =⋅x x ,1cot tan =⋅x x 。
商数关系:x x x cos sin tan =,xxx sin cos cot =。
平方关系:1cos sin 22=+x x ,x x 22sec tan 1=+,x x 22csc cot 1=+。
积的关系:sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)=sinα cos (2kπ+α)=cosαtan (2kπ+α)=tanα cot (2kπ+α)=cotα (其中k ∈Z)公式二:设α为任意角,π+α的三角函数的值与α的三角函数值之间的关系: sin (π+α)=-sinα cos (π+α)=-cosα tan (π+α)=tanα cot (π+α)=cotα公式三:任意角α与-α的三角函数值之间的关系:sin (-α)=-sinα cos (-α)=cosα tan (-α)=-tanα cot (-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)=sinα cos (π-α)=-cosα tan (π-α)=-tanα cot (π-α)=-cotα 公式五:απ-2与α的三角函数值之间的关系:sin (απ-2)=cosα cos (απ-2)=sinα tan (απ-2)=cotα cot (απ-2)=tanα公式六:απ+2与α的三角函数值之间的关系:sin (απ+2)=cosα cos (απ+2)=-sinα tan (απ+2)=-cotα cot (απ+2)=-tanα公式七:απ-23与α的三角函数值之间的关系: sin (απ-23)=-cosα cos (απ-23)=-sinαtan (απ-23)=cotα cot (απ-23)=tanα公式八:απ+23与α的三角函数值之间的关系:sin (απ+23)=-cosα cos (απ+23)=sinαtan (απ+23)=-cotα cot (απ+23)=-tanα公式九:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系: sin (2π-α)=-sinα cos (2π-α)=cosα tan (2π-α)=-tanα cot (2π-α)=-cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值,前面加上一个把α看成..锐角时原函数值的符号。
所有三角函数的公式大全

所有三角函数的公式大全在学习三角函数的过程中,公式是很重要的基础之一。
掌握了三角函数的公式,我们就能够更好地理解三角函数的性质,从而更好地解题。
以下是所有三角函数的公式大全。
一、正弦函数(sin)1. 定义:在一个直角三角形中,正弦函数的值等于其对边的长度与斜边的长度的比值。
2. 周期性:sin(x + 2π) = sin(x),其中π为圆周率。
3. 奇偶性:sin(-x) = -sin(x),即sin函数是奇函数。
4. 余角公式:sin(π - x) = sin(x)sin(π + x) = -sin(x)sin(2π - x) = -sin(x)5. 和差公式:sin(x ± y) = sin(x) cos(y) ± cos(x) sin(y)6. 二倍角公式:sin(2x) = 2sin(x) cos(x)sin²(x) = (1 - cos(2x)) / 27. 三倍角公式:sin(3x) = 3sin(x) - 4sin³(x)8. 多倍角公式:sin(nx) = 2^(n-1) sin(x) cos(x) cos(2x) ...cos((n-1)x)9. 单位圆上的正弦函数:sin(x) = y,其中x为角度,称为弧度制下的角度。
在单位圆上,角度为x对应的点的y坐标即为sin(x)的值。
二、余弦函数(cos)1. 定义:在一个直角三角形中,余弦函数的值等于其邻边的长度与斜边的长度的比值。
2. 周期性:cos(x + 2π) = cos(x),其中π为圆周率。
3. 奇偶性:cos(-x) = cos(x),即cos函数是偶函数。
4. 余角公式:cos(π - x) = -cos(x)cos(π + x) = -cos(x)cos(2π - x) = cos(x)5. 和差公式:cos(x ± y) = cos(x) cos(y) ∓ sin(x) sin(y)6. 二倍角公式:cos(2x) = cos²(x) - sin²(x) = 2cos²(x) - 1 = 1 - 2sin²(x)7. 三倍角公式:cos(3x) = 4cos³(x) - 3cos(x)8. 多倍角公式:cos(nx) = 2^(n-2) cos²(x) - 2^(n-4) cos⁴(x) ...(-1)^(n-1) cos((n-1)x)9. 单位圆上的余弦函数:cos(x) = x,其中x为角度,称为弧度制下的角度。
三角函数公式大全

三角函数公式大全本文主要介绍三角函数公式的大全,包括正弦、余弦、正切、余切、正割、余割、弧度制、角度制等,共计52个公式。
三角函数是初等数学中重要的一部分,以它为基础可以推导出很多数学公式,也是物理、化学等自然科学中常用的数学工具。
1、正弦(sin)与余弦(cos)的关系公式sin θ = cos(90° - θ)cos θ = sin(90° - θ)2、正弦(sin)与余切(ctg)的关系公式sin θ = 1 / ctg θctg θ = 1 / sin θ3、正弦(sin)与正割(sec)的关系公式sin θ = 1 / sec(90° - θ)sec θ = 1 / sin(90° - θ)4、余弦(cos)与正切(tan)的关系公式cos θ = 1 / tan(90° - θ)tan θ = 1 / cos(90° - θ)5、余弦(cos)与余切(cot)的关系公式cos θ = 1 / cot(90° - θ)cot θ = 1 / cos(90° - θ)6、余弦(cos)与余割(cosec)的关系公式c os θ = 1 / cosec(90° - θ)cosec θ = 1 / cos(90° - θ)7、正切(tan)与余切(cot)的关系公式tan θ = 1 / cot θcot θ = 1 / tan θ8、正切(tan)与正割(sec)的关系公式tan θ = 1 / sec(90° - θ)sec θ = 1 / cot(90° - θ)9、正切(tan)与余割(cosec)的关系公式tan θ = 1 / cosec(90° - θ)cosec θ = 1 / cot(90° - θ)10、余切(cot)与正割(sec)的关系公式cot θ = 1 / sec θsec θ = 1 / cot θ11、余切(cot)与余割(cosec)的关系公式cot θ = 1 / cosec(90° - θ)cosec θ = 1 / tan(90° - θ)12、正割(sec)与余割(cosec)的关系公式sec θ = 1 / cosec(90° - θ)cosec θ = 1 / sec(90° - θ)13、正弦(sin)的倒数公式sin(-θ) = -sin θsin(θ ± 360°) = sin θ14、余弦(cos)的倒数公式cos(-θ) = cos θcos(θ ± 360°) = cos θ15、正切(tan)的倒数公式tan(-θ) = -tan θtan(θ ± 180°) = tan θ16、余切(cot)的倒数公式cot(-θ) = -cot θcot(θ ± 180°) = cot θ17、正割(sec)的倒数公式sec(-θ) = sec θsec(θ ± 360°) = sec θ18、余割(cosec)的倒数公式cosec(-θ) = -cosec θcosec(θ ± 360°) = cosec θ19、正弦(sin)的平方公式sin² θ + cos² θ = 11 - sin² θ = cos² θsin² θ = 1 - cos² θ20、余弦(cos)的平方公式sin² θ + cos² θ = 11 - cos² θ = sin² θcos² θ = 1 - sin² θ21、正切(tan)的平方公式tan² θ + 1 = sec² θ1 + cot² θ = cosec² θtan² θ = sec² θ - 122、余切(cot)的平方公式cot² θ + 1 = cosec² θ1 + tan² θ = sec² θcot² θ = cosec² θ - 123、正弦(sin)的角和公式sin(A + B) = sin A cos B + cos A sin Bsin(A - B) = sin A cos B - cos A sin B 24、余弦(cos)的角和公式cos(A + B) = cos A cos B - sin A sin B cos(A - B) = cos A cos B + sin A sin B 25、正弦(sin)的二倍角公式sin 2A = 2 sin A cos A26、余弦(cos)的二倍角公式cos 2A = cos² A - sin² A27、正切(tan)的二倍角公式tan 2A = 2 tan A / (1 - tan² A)28、余切(cot)的二倍角公式cot 2A = (cot² A - 1) / 2 cot A29、正割(sec)的二倍角公式sec 2A = (sec² A + 1) / (2 sec A)30、余割(cosec)的二倍角公式cosec 2A = (cosec² A + 1) / (2 cosec A) 31、正弦(sin)的三倍角公式sin 3A = 3 sin A - 4 sin³ A32、余弦(cos)的三倍角公式cos 3A = 4 cos³ A - 3 cos A33、正切(tan)的三倍角公式tan 3A = (3 tan A - tan³ A) / (1 - 3 tan² A) 34、余切(cot)的三倍角公式cot 3A = (3 cot A - cot³ A) / (3 cot² A - 1) 35、正弦(sin)的四倍角公式sin 4A = 4 sin A cos A (2 cos² A - 1) 36、余弦(cos)的四倍角公式cos 4A = cos² 2A - sin² 2A37、正切(tan)的四倍角公式tan 4A = (4 tan A - 4 tan³ A) / (1 - 6 tan² A + tan⁴ A) 38、余切(cot)的四倍角公式cot 4A = (cot² 2A - 1) / 2 cot 2A39、正弦(sin)的半角公式sin (A/2) = ±√[(1 - cos A) / 2]40、余弦(cos)的半角公式cos (A/2) = ±√[(1 + cos A) / 2]41、正切(tan)的半角公式tan (A/2) = ±√[(1 - cos A) / (1 + cos A)]42、余切(cot)的半角公式cot (A/2) = ±√[(1 + cos A) / (1 - cos A)]43、正割(sec)的半角公式sec (A/2) = ±√[(1 + cos A) / (1 - cos A)]44、余割(cosec)的半角公式cosec (A/2) = ±√[(1 - cos A) / (1 + cos A)]45、正弦(sin)的万能公式a sin x +b cos x = √(a² + b²) sin(x + atan(b/a))46、余弦(cos)的万能公式a cos x -b sin x = √(a² + b²) cos(x + atan(b/a))47、正切(tan)的万能公式a tan x -b cot x = atan[(a sin x - b cos x)/(a cos x + b sin x)]48、余切(cot)的万能公式a cot x -b tan x = atan[(b sin x - a cos x)/(a sin x + b cos x)]49、正割(sec)的万能公式a sec x +b cosec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) + sin(2x - atan(b/a))]50、余割(cosec)的万能公式a cosec x +b sec x = 2 √(a² + b²) / [sin(2x + atan(b/a)) - sin(2x - atan(b/a))]51、弧度制与角度制的转换公式弧度制 = 角度制× π / 180角度制 = 弧度制× 180 / π52、三角函数的图像正弦(sin)的图像:余弦(cos)的图像:正切(tan)的图像:余切(cot)的图像:正割(sec)的图像:余割(cosec)的图像:以上是三角函数公式的大全,通过掌握这些公式可以更深入地了解三角函数的性质和应用,有助于提高数学水平。
三角函数 定律公式大全

三角函数定律公式大全以下是常见的三角函数的定律和公式:1.正弦定律(Sine Law): a/sin A = b/sin B = c/sin C其中,a、b、c为三角形的边长,A、B、C为对应的角度。
2.余弦定律(Cosine Law): c^2 = a^2 + b^2 - 2ab cos C其中,c为三角形的边长,a、b为其他两条边的长度,C为夹角。
3.正切函数(Tangent): tan A = sin A / cos A其中,A为角度。
4.余切函数(Cotangent): cot A = 1 / tan A = cos A / sin A其中,A为角度。
5.正割函数(Secant): sec A = 1 / cos A其中,A为角度。
6.余割函数(Cosecant): csc A = 1 / sin A其中,A为角度。
7.和差公式: sin(A ± B) = sin A * cos B ± cos A * sin B cos(A ± B)= cos A * cos B ∓ sin A * sin B tan(A ± B) = (tan A ± tan B) / (1 ∓tan A * tan B)8.和角公式: sin(A + B) = sin A * cos B + cos A * sin B sin(A - B)= sin A * cos B - cos A * sin B cos(A + B) = cos A * cos B - sin A * sin B cos(A - B) = cos A * cos B + sin A * sin B tan(A + B) = (tan A + tan B) / (1 - tan A * tan B) tan(A - B) = (tan A - tan B) /(1 + tan A * tan B)这些三角函数的定律和公式在解决三角形问题、三角函数的计算、物理学和工程学等领域中非常有用。
(完整版)高中数学三角函数公式大全全解
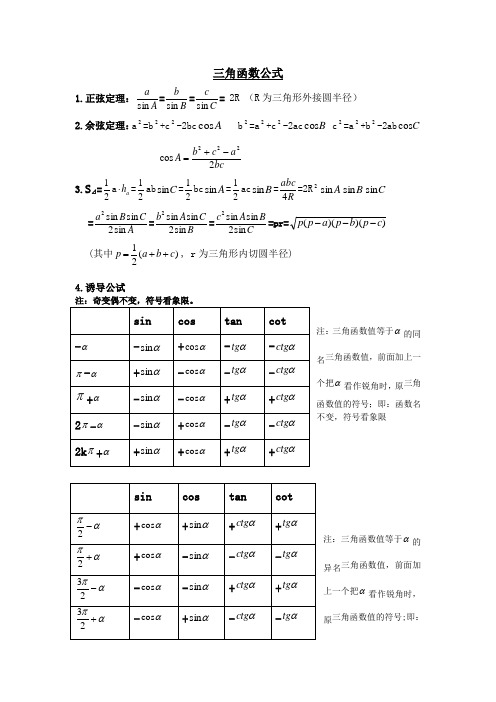
三角函数公式1.正弦定理:A a sin =B b sin =Cc sin = 2R (R 为三角形外接圆半径) 2.余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=3.S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin =AC B a sin 2sin sin 2=B C A b sin 2sin sin 2=C B A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)4.诱导公试注:奇变偶不变,符号看象限。
注:三角函数值等于α的同名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看象限注:三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名改变,符号看象限5.和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±6.二倍角公式:(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=7.半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sinθθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg8.积化和差公式:[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(21sin sin9.和差化积公式:①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=- 锐角三角形函数公式总结大全1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
完整版)完整三角函数公式表

完整版)完整三角函数公式表三角函数公式表同角三角函数的基本关系式三角函数是数学中的重要概念,它们在数学和物理学中都有广泛的应用。
同角三角函数的基本关系式包括倒数关系、商的关系和平方关系。
其中,倒数关系式如下:tan\alpha\cdot\cot\alpha=1$$sin\alpha\cdot\csc\alpha=1$$cos\alpha\cdot\sec\alpha=1$$商的关系式如下:frac{\sin\alpha}{\cos\alpha}=\tan\alpha=\frac{\sec\alpha}{\csc\alpha}$$frac{\cos\alpha}{\sin\alpha}=\cot\alpha=\frac{\csc\alpha}{\sec\alpha}$$平方关系式如下:sin^2\alpha+\cos^2\alpha=1$$2^2+ \tan^2\alpha=\sec^2\alpha$$1+\cot^2\alpha=\csc^2\alpha$$这些关系式可以用六边形记忆法和记忆方法来记忆。
其中,六边形记忆法是指图形结构“上弦中切下割,左正右余中间1”,而记忆方法是指对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
诱导公式诱导公式是指通过已知的三角函数值来推导其他角度的三角函数值的公式。
它们可以用口诀“奇变偶不变,符号看象限”来记忆。
具体来说,诱导公式包括三角函数的奇偶性和象限问题。
奇偶性公式如下:sin(-\alpha)=-\sin\alpha$$cos(-\alpha)=\cos\alpha$$tan(-\alpha)=-\tan\alpha$$cot(-\alpha)=-\cot\alpha$$象限问题公式如下:sin\left(\frac{3\pi}{2}-\alpha\right)=-\cos\alpha$$ cos\left(\frac{3\pi}{2}-\alpha\right)=-\sin\alpha$$ sin(2\pi-\alpha)=-\sin\alpha$$cos(2\pi-\alpha)=\cos\alpha$$tan\left(\frac{3\pi}{2}-\alpha\right)=\cot\alpha$$ tan(2\pi-\alpha)=-\tan\alpha$$cot\left(\frac{3\pi}{2}-\alpha\right)=\tan\alpha$$ cot(2\pi-\alpha)=-\cot\alpha$$另外,还有两个特殊的角度:sin\left(\frac{\pi}{2}-\alpha\right)=\cos\alpha$$cos\left(\frac{\pi}{2}-\alpha\right)=\sin\alpha$$ tan\left(\frac{\pi}{2}-\alpha\right)=\cot\alpha$$ cot\left(\frac{\pi}{2}-\alpha\right)=\tan\alpha$$ sin\left(\frac{\pi}{2}+\alpha\right)=\cos\alpha$$ cos\left(\frac{\pi}{2}+\alpha\right)=-\sin\alpha$$ tan\left(\frac{\pi}{2}+\alpha\right)=-\cot\alpha$$ cot\left(\frac{\pi}{2}+\alpha\right)=-\tan\alpha$$ sin(\pi-\alpha)=\sin\alpha$$cos(\pi-\alpha)=-\cos\alpha$$tan(\pi-\alpha)=-\tan\alpha$$cot(\pi-\alpha)=-\cot\alpha$$sin(\pi+\alpha)=-\sin\alpha$$cos(\pi+\alpha)=-\cos\alpha$$tan(\pi+\alpha)=\tan\alpha$$cot(\pi+\alpha)=\cot\alpha$$两角和与差的三角函数公式最后,还有两角和与差的三角函数公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数与反三角函数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβ tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)·半角公式:sin(α/2)=±√((1-cosα)/2) cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinαcot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1)) csc(α/2)=±√((2secα/(secα-1))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))·辅助角公式:Asinα+Bcosα=√(A^2+B^2)sin(α+φ)(tanφ=B/A)Asinα+Bcosα=√(A^2+B^2)cos(α-φ)(tanφ=A/B)·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2 cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数:sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sin β·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sin β·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2] tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB·积化和差公式:sin α·cos β=(1/2)[sin(α+β)+sin(α-β)] cos α·sin β=(1/2)[sin(α+β)-sin(α-β)] cos α·cos β=(1/2)[cos(α+β)+cos(α-β)] sin α·sin β=-(1/2)[cos(α+β)-cos(α-β)] ·倍角公式:sin(2α)=2sin α·cos α=2/(tan α+cot α)cos(2α)=(cos α)^2-(sin α)^2=2(cos α)^2-1=1-2(sin α)^2tan(2α)=2tan α/(1-tan^2α) cot(2α)=(cot^2α-1)/(2cot α) sec(2α)=sec^2α/(1-tan^2α) csc(2α)=1/2*sec α·csc α ·三倍角公式:sin(3α) = 3sin α-4sin^3α = 4sin α·sin(60°+α)sin(60°-α) cos(3α) = 4cos^3α-3cos α = 4cos α·cos(60°+α)cos(60°-α)tan(3α) = (3tan α-tan^3α)/(1-3tan^2α) = tan αtan(π/3+α)tan(π/3-α) cot(3α)=(cot^3α-3cot α)/(3cot^2α-1) ·n 倍角公式:sin(n α)=ncos^(n-1)α·sin α-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-… cos(n α)=cos^n α-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·三角和的三角函数:sin(α+β+γ)=sin α·cos β·cos γ+cos α·sin β·cos γ+cos α·cos β·sin γ-sin α·sin β·sin γcos(α+β+γ)=cos α·cos β·cos γ-cos α·sin β·sin γ-sin α·cos β·sin γ-sin α·sin β·cos γtan(α+β+γ)=(tan α+tan β+tan γ-tan α·tan β·tan γ)/(1-tan α·tan β-tan β·tan γ-tan γ·tan α) ·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^ csc(a)=1/sin(a) sec(a)=1/cos(a) ·推导公式tan α+cot α=2/sin2α tan α-cot α=-2cot2α 1+cos2α=2cos^2α 1-cos2α=2sin^2α1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2 csc(a)=1/sin(a) sec(a)=1/cos(a) 。
诱导公式sin(-a) = -sina cos(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1双曲函数sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin (2k π+α)= sin α cos (2k π+α)= cos α tan (2k π+α)= tan α cot (2k π+α)= cot α 公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin (π+α)= -sin α cos (π+α)= -cos α tan (π+α)= tan α cot (π+α)= cot α 公式三:任意角α与 -α的三角函数值之间的关系:sin (-α)= -sin α cos (-α)= cos α tan (-α)= -tan α cot (-α)= -cot α 公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin (π-α)= sin α cos (π-α)= -cos α tan (π-α)= -tan α cot (π-α)= -cot α 公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sin α cos (2π-α)= cos α tan (2π-α)= -tan α cot (2π-α)= -cot α 公式六:2π±α及23π±α与α的三角函数值之间的关系:sin (2π+α)= cos α cos (2π+α)= -sin α tan (2π+α)= -cot α cot (2π+α)= -tan αsin (2π-α)= cos α cos (2π-α)= sin α tan (2π-α)= cot α cot (2π-α)= tan α sin (23π+α)= -cos α cos (23π+α)= sin α tan (23π+α)= -cot αcot (23π+α)= -tan α sin (23π-α)= -cos α cos (23π-α)= -sin αtan (23π-α)= cot α cot (23π-α)= tan α (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A •sin(ωt+θ)+ B •sin(ωt+φ) =)cos(222ϕθ⋅++AB B A sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A同角关系sec^2α=1/cos^2α=tan^2α+1 csc^2α=1/sin^2α=cot^2α+1 tanαcotα=1 sinαcscα=1 cosαsecα=1 三角形中的一些结论:(不要求记忆) (1)tanA+tanB+tanC=tanA ·tanB ·tanC(2)sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1 (4)sin2A+sin2B+sin2C=4sinA ·sinB ·sinC (5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1三角形中三角函数基本定理【正弦定理】式中R 为ABC 的外接圆半径【余弦定理】【勾股定理】在直角三角形(C为直角)中,勾方加股方等于弦方(图1.4),即勾股定理也称商高定理,外国书刊中称毕达哥拉斯定理.【正切定理】或【半角与边长的关系公式】式中,r为ABC的内切圆半径,且式中S为ABC的面积. 三角函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα函数y=sinx y=cosx y=tanx y=cotx定义域R R {x|x∈R且x≠kπ+2π,k∈Z}{x|x∈R且x≠kπ,k∈Z}值域[-1,1]x=2kπ+2π时y max=1x=2kπ-2π时y min=-1[-1,1]x=2kπ时y max=1x=2kπ+π时y min=-1R无最大值无最小值R无最大值无最小值周期性周期为2π周期为2π周期为π周期为π奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)反三角函数图像与反三角函数特征反正弦曲线反余弦曲线拐点(同曲线对称中心):,该点切线斜率为1 拐点反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1 拐点(同曲线对称中心):,该点切线斜率为-1反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为1 拐点:,该点切线斜率为-1渐近线:渐近线:名称反正割曲线反余割曲线方程图像顶点渐近线性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosxarctan(-x)=-arctanxarccot(-x)=π-arccotx周期性都不是同期函数恒等式sin(arcsinx)=x(x∈[-1,1])arcsin(sinx)=x(x∈[-2π,2π])cos(arccosx)=x(x∈[-1,1])arccos(cosx)=x(x∈[0,π])tan(arctanx)=x(x∈R)arctan(tanx)=x(x∈(-2π,2π))cot(arccotx)=x(x∈R)arccot(cotx)=x(x∈(0,π))互余恒等式arcsinx+arccosx=2π(x∈[-1,1]) arctanx+arccotx=2π(X∈R)arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =。
