算术编码过程实例
三年级数学编码例子

三年级数学编码例子
在三年级数学学习中,编码也是一个重要的知识点。
下面给大家举几个三年级数学编码的例子。
1. 数字编码:将数字转换成对应的编码,比如数字1可以编码为'a',数字2可以编码为'b',以此类推。
2. 字母编码:将字母转换成对应的编码,比如字母'a'可以编码为'1',字母'b'可以编码为'2',以此类推。
3. 符号编码:将符号转换成对应的编码,比如加号'+'可以编码为'#',减号'-'可以编码为'@',以此类推。
通过这些编码例子,三年级的孩子们可以更加深入地理解编码的概念,也能够提高他们的逻辑思维能力和数学运算能力。
- 1 -。
4.4 算术编码

4.3.2 自适应模型算术编码 4.3.3 二进制算术编码 4.3.4 二进制算术解码 4.3.5 算术编码评价
6
4.3 算术编码(Arithmetic Coding )
二、算术编码定义
它是一种非分组编码算法。它是从全序列出发,采用递推形 式的连续编码。它不是将单个的信源符号映射成一个码字, 而是将整个输入序列的符号依据它们的概率映射为实数轴上 区间[0 1)内的一个小区间,再在该小区间内选择一个代表性 的二进制小数,作为实际的编码输出。
例题1:设某信源取自符号集S={a,b,c,d,e,!},!表示编码 结束,各符号概率和初始子区间如下,设待编码的为 “dead!”,编码器和解码器的初值区间[0,1)
表1
10
4.3.1多元符号算术编码
编码第一个字符d时
P(d ) p(a) p(b) p(c) 0.2 0.1 0.1 0.4
解:根据这些概率可把间隔[0, 1)分成4个子间 隔:[0, 0.1), [0.1, 0.5), [0.5, 0.7), [0.7, 1) 。 信息可综合在表中。
符号
a
b
c
d
概率
0.1
0.4
0.2
0.3
初始编码间 [0, 0.1) [0.1, 0.5) [0.5, 0.7) [0.7, 1)
隔
17
4.3.1多元符号算术编码
[C(),C() A()) [0,1)
当处理ai时,区间A(s)宽度根据ai出现概率p(ai)而变 窄,符号序列越长,相应的子区间越窄,编码的位 数越多。符号串每一步新扩展的码字C(sai)都是由原 符号串的码字C(s)与新区间宽度A(sai)的算术相加, “算术码”由此得名。
算术编码

range=high一low=0.7一0.6=0.1 S将区间[0,1) [0.6,0.7) 注意:字符“”表示“分割为”字符。
1 编码过程
•
(3)对第2个字符t编码,使用的新生成范围 为[0.6,0.7),因为t的range low=0.70, range high=1.00,因此下一个low,high分别 为:
1 编码过程
•
将编码后的区间范围综合如图3-9 所示:
我们用0.6753031606代表字符串“state tree”,从而达到高 效编码的目的,这就是算术编码的基本思想。
1 编码过程
• 上述算术编码区间分割过程可用图3-10 表示。
2 解码过程
• 通过编码,最后一个子区间的的下界值 0.6753031606就是字符串“state tree”的惟一 编码。然后在解码时,通过判断哪一个字符能 拥有我们已编码的消息落在的空间来找出消息 中的第一个字符。由于0.6753031606落在[0.6, 0.7]之问,因此马上就可解得第1个符号是S。
•
按对‘state stree”’的算术编码过程为: (1)初始化时,被分割的范围 range=high -low=[0,1) = 1 - 0 = 1,下一个范围 的低、高端分别由下式计算: low=low+range×range low high=low+range×range high 其中等号右边的low为上一个被编码字符的 范围低值;range low和range high分别为本次 被编符号已给定出现的概率范围的low和high。
算术编码
• 用算术编码方法是将被编码的一个消息或一个 符号串(序列)表示成0和1之间的一个间隔, 即对一串符号直接编码成[0,1)区间上的一个 浮点小数,在传输任何符号串(消息)之前, 设符号串的完整范围为[0,1)。当一个符号被 处理时,这一范围就依据分配给这一符号的那 一范围变窄,间隔变小,当符号串序列越长, 则编码表示它的间隔越小,同时表示这一间隔 所需的位数就越多,直到完成对所有符号串的 编码。算术编码的过程,实际上就是依据信息 源符号串的发生概率对码区间分割的过程。
多媒体实验——算术编码(2)

实验四算术编码算法的实现一、实验目的1、学习Matlab软件的使用和编程;2、进一步深入理解算术编码算法的原理;二、实验内容1、用Matlab软件对文本文件“seq1.txt”实现整数型的算术编码。
三、实验原理1、编码器在开始时将“当前间隔”[L,H)设置为[0,1)。
2、对每一事件,编码器按步骤(a)和(b)进行处理。
a、编码器将“当前间隔”分为子间隔,每一个事件一个。
b、编码器选择子间隔应与下一个确切发生的事件相对应,并使它成为新的“当前间隔”。
3、最后输出的“当前间隔”的下边界就是该给定事件序列的算术编码。
四、算术编码的Matlab源程序及运行结果function arithscale()clc;fid=fopen('seq1.txt','r');seq=fread(fid,'*char');fclose(fid);seq=reshape(seq,1,length(seq));[alpha prob]=probmodel(seq);if~isempty(alpha)[tag mnm]=arithscalecod(alpha,prob,seq);disp(strcat('Tag=',tag));seq=arithscaledecod(tag,alpha,prob,length(seq),mnm);disp('Sequence=');disp(seq);elsedisplay('Empty Sequence....');endendfunction[alpha prob]=probmodel(seq)if~isempty(seq)alpha(1)=seq(1);prob(1)=1;l=length(seq);k=2;for i=2:lidx=find(seq(i)==alpha);if isempty(idx)alpha(k)=seq(i);prob(k)=1;k=k+1;elseprob(idx)=prob(idx)+1;endendprob=prob./l;elsealpha=[];prob=[];endendfunction[tag mnm]=arithscalecod(alpha,prob,seq)ls=length(seq);l=0;u=1;Fx(1)=0;for i=1:length(prob)Fx(i+1)=Fx(i)+prob(i);endtag=[];dif=[];while~isempty(seq)dif(end+1)=u-l;if l>=0&u<0.5tag=strcat(tag,'0');l=2*l;u=2*u;elseif l>=0.5&u<1tag=strcat(tag,'1');l=2*(l-0.5);u=2*(u-0.5);elsep=find(seq(1)==alpha);l1=l+(u-l)*Fx(p);u=l+(u-l)*Fx(p+1);l=l1;seq(1)='';endendwl=8;b=numb2bin(u,wl);tag=strcat(tag,b);mnm=min(dif);endfunction b=numb2bin(l,wl)b=[];for i=1:wlv=l*2;f=floor(v);b=strcat(b,num2str(f));l=v-f;endendarithscaledecod函数function seq=arithscaledecod(tag,alpha,prob,lgt,mnm) l=0;u=1;Fx(1)=0;for i=1:length(prob)Fx(i+1)=Fx(i)+prob(i);endseq='';k=ceil(log2(1/mnm));k=2*k;ln=length(tag);if k>lnk=ln;endwhile lgt>0if l>=0&u<0.5tag(1)='';tag(end+1)='0';l=2*l;u=2*u;elseif l>=0.5&u<1tag(1)='';tag(end+1)='0';l=2*(l-0.5);u=2*(u-0.5);elseb=tag(1:k);tg=bin2numb(b);t=(tg-l)/(u-l);for j=1:length(prob)if t>=Fx(j)&t<Fx(j+1)breakendendseq=[seq alpha(j)];l1=l+(u-l)*Fx(j);u=l+(u-l)*Fx(j+1);l=l1;lgt=lgt-1;endendendfunction d=bin2numb(b)d=0;for i=1:length(b)bt=str2num(b(i));d=d+bt*2^(-i);endend五、运行结果:Tag=1010011110000000001000001000110001000110010110Sequence= ABCAAAACCCCAAAAACCCCAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA。
算术编码2

算术编码算术编码是一种无损数据压缩方法,也是一种熵编码的方法和其它熵编码方法不同的地方在于,其他的熵编码方法通常是把输入的消息分割为符号,然后对每个符号进行编码,而算术编码是直接把整个输入的消息编码为一个数,一个满足(0.0 ≤ n < 1.0)的小数n。
编码原理在给定符号集和符号概率的情况下,算术编码可以给出接近最优的编码结果。
使用算术编码的压缩算法通常先要对输入符号的概率进行估计,然后再编码。
这个估计越准,编码结果就越接近最优的结果。
根据信源可能发现的不同符号序列的概率,把[0,1]区间划分为互不重叠的子区间,子区间的宽度恰好是各符号序列的概率。
这样信源发出的不同符号序列将与各子区间一一对应,因此每个子区间内的任意一个实数都可以用来表示对应的符号序列,这个数就是该符号序列所对应的码字。
显然,一串符号序列发生的概率越大,对应的子区间就越宽,要表达它所用的比特数就减少,因而相应的码字就越短。
编码过程算术编码是用符号的概率和它的编码间隔两俩个基本参数来描述的。
算术编码可以是静态的或是自适应的。
在静态算术编码中,信源符号的概率是固定的。
在自适应算术编码中,信源符号的概率根据编码时符号出现的频繁程度动态地进行修改。
在编码期间估算信源符号概率的过程叫建模。
需要开发动态算术编码的原因,是因为事先知道精确的信源符号概率是很难的,而且是不切实际的。
动态建模是确定编码器压缩效率的关键。
算术编码应用例子例: 对一个简单的信号源进行观察,得到的统计模型如下:60% 的机会出现符号中性20% 的机会出现符号阳性10% 的机会出现符号阴性10% 的机会出现符号数据结束符. (出现这个符号的意思是该信号源'内部中止',在进行数据压缩时这样的情况是很常见的。
当第一次也是唯一的一次看到这个符号时,解码器就知道整个信号流都被解码完成了。
)算术编码可以处理的例子不止是这种只有四种符号的情况,更复杂的情况也可以处理,包括高阶的情况。
第四章:算术编码

A = {a, b, c}, P(a) = 0.95, P(b) = 0.02, P(c) = 0.03
H = 0.335 bits/symbol l1 = 1.05, l2 = 0.611, … 当n = 8时编码性能才变得可接受 但此时|alphabet| = 38 = 6561 !!!
(1)
u
l (1)
F
X (3) 0.8
1321
l (4) = l (1) + (u (3) - l (3) ) FX (0) = 0.7712 u (4) = l (3) + (u (3) - l (3) ) FX (1) = 0.773504
u (4) l (4) TX 1321 0.772352 2
2. 3. 4.
Find the xk: FX(xk-1) t* FX(xk). Update u(k), l(k) If done--exit, otherwise goto 1.
2 2
对公平掷骰子的例子:{1, 2, 3, 4, 5, 6}
1 P X k 6
for k 1..6
1 TX 2 P X 1 P X 2 0.25 2 1 4 TX 5 k 1 P X k P X 5 0.75 2
基本思想
上述骰子的例子:
(2) FX 32 P(x 11) ... P(x 16) P(x 21) ... P(x 26) P(x 31) P(x 32)
区间构造
(2) FX 32 P(x 11) ... P(x 16) P(x 21) ... P(x 26) P(x 31) P(x 32)
算术编码(Arithmeticcoding)的实现
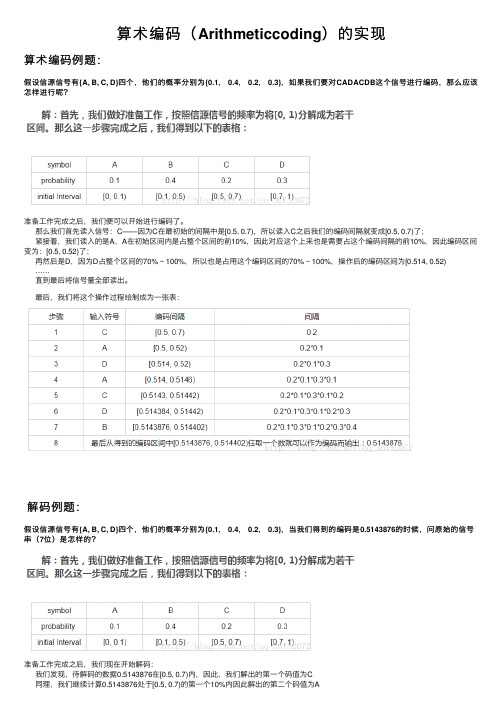
算术编码(Arithmeticcoding)的实现算术编码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},如果我们要对CADACDB这个信号进⾏编码,那么应该怎样进⾏呢?准备⼯作完成之后,我们便可以开始进⾏编码了。
那么我们⾸先读⼊信号:C——因为C在最初始的间隔中是[0.5, 0.7),所以读⼊C之后我们的编码间隔就变成[0.5, 0.7)了; 紧接着,我们读⼊的是A,A在初始区间内是占整个区间的前10%,因此对应这个上来也是需要占这个编码间隔的前10%,因此编码区间变为:[0.5, 0.52)了; 再然后是D,因为D占整个区间的70% ~ 100%,所以也是占⽤这个编码区间的70% ~ 100%,操作后的编码区间为[0.514, 0.52) …… 直到最后将信号量全部读出。
最后,我们将这个操作过程绘制成为⼀张表:解码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},当我们得到的编码是0.5143876的时候,问原始的信号串(7位)是怎样的?准备⼯作完成之后,我们现在开始解码: 我们发现,待解码的数据0.5143876在[0.5, 0.7)内,因此,我们解出的第⼀个码值为C 同理,我们继续计算0.5143876处于[0.5, 0.7)的第⼀个10%内因此解出的第⼆个码值为A …… 这个过程持续直到执⾏七次全部执⾏完为⽌。
那么以上的过程我们同样可以列表表⽰:作业:对任⼀概率序列,实现算术编码,码长不少于16位,不能固定概率,语⾔⾃选。
基于Python实现:from collections import Counter #统计列表出现次数最多的元素import numpy as npprint("Enter a Sequence\n")inputstr = input()print (inputstr + "\n")res = Counter(inputstr) #统计输⼊的每个字符的个数,res是⼀个字典类型print (str(res))# print(res)#sortlist = sorted(res.iteritems(), lambda x, y : cmp(x[1], y[1]), reverse = True)#print sortlistM = len(res)#print (M)N = 5A = np.zeros((M,5),dtype=object) #⽣成M⾏5列全0矩阵#A = [[0 for i in range(N)] for j in range(M)]reskeys = list(res.keys()) #取字典res的键,按输⼊符号的先后顺序排列# print(reskeys)resvalue = list(res.values()) #取字典res的值totalsum = sum(resvalue) #输⼊⼀共有⼏个字符# Creating TableA[M-1][3] = 0for i in range(M):A[i][0] = reskeys[i] #第⼀列是res的键A[i][1] = resvalue[i] #第⼆列是res的值A[i][2] = ((resvalue[i]*1.0)/totalsum) #第三列是每个字符出现的概率i=0A[M-1][4] = A[M-1][2]while i < M-1: #倒数两列是每个符号的区间范围,与输⼊符号的顺序相反A[M-i-2][4] = A[M-i-1][4] + A[M-i-2][2]A[M-i-2][3] = A[M-i-1][4]i+=1print (A)# Encodingprint("\n------- ENCODING -------\n" )strlist = list(inputstr)LEnco = []UEnco = []LEnco.append(0)UEnco.append(1)for i in range(len(strlist)):result = np.where(A == reskeys[reskeys.index(strlist[i])]) #满⾜条件返回数组下标(0,0),(1,0) addtollist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],3]))addtoulist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],4]))LEnco.append(addtollist)UEnco.append(addtoulist)tag = (LEnco[-1] + UEnco[-1])/2.0 #最后取区间的中点输出LEnco.insert(0, " Lower Range")UEnco.insert(0, "Upper Range")print(np.transpose(np.array(([LEnco],[UEnco]),dtype=object))) #np.transpose()矩阵转置print("\nThe Tag is \n ")print(tag)# Decodingprint("\n------- DECODING -------\n" )ltag = 0utag = 1decodedSeq = []for i in range(len(inputstr)):numDeco = ((tag - ltag)*1.0)/(utag - ltag) #计算tag所占整个区间的⽐例for i in range(M):if (float(A[i,3]) < numDeco < float(A[i,4])): #判断是否在某个符号区间范围内decodedSeq.append(str(A[i,0]))ltag = float(A[i,3])utag = float(A[i,4])tag = numDecoprint("The decoded Sequence is \n ")print("".join(decodedSeq))Arithmetic coding Code参考:。
第二章算术编码

算术码之例(5)
用数轴来说明算术编码更直观 |————|————|————————| 0 0 1/4 1/2 1 1 1/4 10 7/16 1/2 11 1 7/16 110 17/32 111 3/4 1 …………………………………………… [0,1)分割成为2n区间,代表2n个序列。
12
17
算术码之例(11)
* 1.10 10.00 0.101 …………………………………… 0 0.01 101.01 ** 1.00 10101.00 0.00 0 0.01 10101.00 ** 1.00 1010100.00 移位次数=7, C=0.1010100
18
算术码之例(12)
0---2比特 1---与游程长度有关, L=2N+1或2N+2 N+1比特 p’(L)=p(1-p), l=2p+(1-p) [(N+1)p’(2N+1)/(2N+1) +p’(2N+2)/2]=0.997 =0.811/0.997=81.4% (92.7%) 编码效率有所下降。若保留4位可提高。
24
一般马氏链的算术编码(6)
3.进位引入差错的防止 [P(Aar)+p(Aar)]2-L(Aar) =[P(A)+p(A)∑P(ar|S)]W2-L(A) +[p(A)P(ar|S)]2-L(A)≦[P(A)+p(A)]2-L(A), 递推至加一序列B, [P(AB)+p(AB)]2-L(AB)≦[P(A)+p(A)]2-L(A), 若加B过程内未移位,则P(AB)-P(A)<1
21
一般马氏链的算术编码(3)
译码公式
算术编码ArithmeticCoding-高质量代码实现详解

算术编码ArithmeticCoding-⾼质量代码实现详解关于算术编码的具体讲解我不多细说,本⽂按照下述三个部分构成。
两个例⼦分别说明怎么⽤算数编码进⾏编码以及解码(来源:ARITHMETIC CODING FOR DATA COIUPRESSION);接下来我会给出算术编码的压缩效果接近熵编码的证明⽅法(这⼀部分参考惠普公司的论⽂:Introduction to Arithmetic Coding - Theory and Practice);最后我会详细说明⼀下算数编码的实现代码(代码来源:ACM87 ARITHMETIC CODING FOR DATA COIUPRESSION);⼀, 直观上去认识算术编码编码过程:将字符映射到 [0,1) 的区间的⼀个数稍微说明⼀下,⼀开始将区间分为好⼏段,每⼀段表⽰⼀个字符。
编码字符e的时候,就把原先区间表⽰e的那⼀段放⼤,对这个区间进⾏划分获得⼦区间,每个⼦区间也是代表⼀个字符。
依次进⾏下去。
编码结束的时候获得的那个区间就是我们要的,我们可以在这中间取个数就好了。
伪代码是这样的:解码过程:将编码得到的数还原成字符串。
⼤概思路是这样的,就是每次看那个数处落在哪个⼦区间段,然后输出这个区间段所表⽰的字符。
之后,调整区间以及这个数,递归知道输出所有编码字符为⽌。
⼆,证明算术编码的压缩效率⾸先我们得确切知道我们到底编码出来的是什么,然后我们才能去进⼀步去证明。
经过上⼀步的直观认识,我们应该知道编码结束的时候我们获得⼀个最终的区间,然后取这个区间中的⼀个值来表⽰最终的编码。
在实践中,我们是输出⼦区间上下界中的共同位。
⽐如我们最终得到的区间是[0.1010011,0.1010000)那么共同位就是0.10100,当然喽,⽅便起见,我们就只保存10100就好了,⽽把⼩数点什么的去掉。
接下来就是证明了。
三,实现代码详解着重讲⼀下编码过程中字符编码的实现,先看⼀下代码。
算术编码

《多媒体计算机技术》上机实验报告实验题目:班级:学号:姓名:指导教师:完成日期:一、算术编码原理算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔(Interval),消息越长,编码表示它的间隔就越小,表示这一间隔所需的二进制位就越多。
算术编码用到两个基本的参数:符号的概率和它的编码间隔。
信源符号的概率决定压缩编码的效率,也决定编码过程中信源符号的间隔,而这些间隔包含在0到1之间。
编码过程中的间隔决定了符号压缩后的输出。
二、算术编码步骤(1)编码器在开始时将“当前间隔”[ L,H) 设置为[0,1)。
(2)对每一事件,编码器按步骤(a)和(b)进行处理(a)编码器将“当前间隔”分为子间隔,每一个事件一个。
(b)一个子间隔的大小与下一个将出现的事件的概率成比例,编码器选择子间隔对应于下一个确切发生的事件相对应,并使它成为新的“当前间隔”。
(3)最后输出的“当前间隔”的下边界就是该给定事件序列的算术编码。
设Low和High分别表示“当前间隔”的下边界和上边界,CodeRange为编码间隔的长度,LowRange(symbol)和HighRange(symbol)分别代表为了事件symbol分配的初始间隔下边界和上边界。
上述过程的实现可用伪代码描述如下:set Low to 0set High to 1while there are input symbols dotake a symbolCodeRange = High – LowHigh = Low + CodeRange *HighRange(symbol)Low = Low + CodeRange * LowRange(symbol)end of whileoutput Low算术码解码过程用伪代码描述如下:get encoded numberdofind symbol whose range straddles the encoded numberoutput the symbolrange = symbo.LowValue – symbol.HighValuesubstractisymbol.LowValue from encoded numberdivide encoded number by rangeuntil no more symbols算术编码器的编码解码过程可用例子演示和解释。
算术编码

算术编码算术编码在图像数据压缩标准(如JPEG,JBIG)中扮演了重要的角色。
在算术编码中,消息用0到1之间的实数进行编码,算术编码用到两个基本的参数:符号的概率和它的编码间隔。
信源符号的概率决定压缩编码的效率,也决定编码过程中信源符号的间隔,而这些间隔包含在0到1之间。
编码过程中的间隔决定了符号压缩后的输出。
算术编码器的编码过程可用下面的例子加以解释。
[例4.2]假设信源符号为{00,01,10,11},这些符号的概率分别为{0.1,0.4,0.2, 0.3},根据这些概率可把间隔[0,1)分成4个子间隔:[0,0.1),[0.1,0.5),[0.5,0.7),[0.7,1),其中表示半开放间隔,即包含不包含。
上面的信息可综合在表4-04中。
表4-04信源符号,概率和初始编码间隔符号00011011概率0.10.40.20.3初始编码间[0,0.1)[0.1,0.5)[0.5,0.7)[0.7,1)隔如果二进制消息序列的输入为:10001100101101。
编码时首先输入的符号是10,找到它的编码范围是[0.5,0.7)。
由于消息中第二个符号00的编码范围是[0,0.1),因此它的间隔就取[0.5,0.7)的第一个十分之一作为新间隔[0.5,0.52)。
依此类推,编码第3个符号11时取新间隔为[0.514,0.52),编码第4个符号00时,取新间隔为[0.514,0.5146),…。
消息的编码输出可以是最后一个间隔中的任意数。
整个编码过程如图4-03所示。
图4-03算术编码过程举例这个例子的编码和译码的全过程分别表示在表4-05和表4-06中。
根据上面所举的例子,可把计算过程总结如下。
考虑一个有M个符号的字符表集,假设概率,而。
输入符号用表示,第个子间隔的范围用表示。
其中,和,表示间隔左边界的值,表示间隔右边界的值,表示间隔长度。
编码步骤如下:步骤1:首先在1和0之间给每个符号分配一个初始子间隔,子间隔的长度等于它的概率,初始子间隔的范围用[,)表示。
信息论哈夫曼编码算术编码lz编码

信息论实验报告实验人:邓放学号:20123022572014年11月21日一、实验目的1、掌握哈夫曼编码算法的基本原理;要求对图片进行哈夫曼编码。
2、掌握算术编码算法的基本原理;要求对图片进行算术编码。
3、掌握LZ算法的基本原理;要求对图片进行LZ编码。
二、实验原理1、哈夫曼编码l)将信号源的符号按照出现概率递减的顺序排列。
(注意,一定要递减)2)将最下面的两个最小出现概率进行合并相加,得到的结果作为新符号的出现的概率。
3)重复进行步骤1和2直到概率相加的结果等于1为止。
4)在合并运算时,概率大的符号用编码0表示,概率小的符号用编码1表示。
5)记录下概率为1处到当前信号源符号之间的0,l序列,从而得到每个符号的编码。
下面我举个简单例子:一串信号源S={s1,s2,s3,s4,s5}对应概率为p={40,30,15,10,5},(百分率)按照递减的格式排列概率后,根据第二步,会得到一个新的概率列表,依然按照递减排列,注意:如果遇到相同概率,合并后的概率放在下面!最后概率最大的编码为0,最小的编码为1。
如图所示:所以,编码结果为s1=1s2=00s3=010s4=0110s5=0111霍夫曼编码具有如下特点:1)编出来的码都是异字头码,保证了码的唯一可译性。
2)由于编码长度可变。
因此译码时间较长,使得霍夫曼编码的压缩与还原相当费时。
3)编码长度不统一,硬件实现有难度。
4)对不同信号源的编码效率不同,当信号源的符号概率为2的负幂次方时,达到100%的编码效率;若信号源符号的概率相等,则编码效率最低。
5)由于0与1的指定是任意的,故由上述过程编出的最佳码不是唯一的,但其平均码长是一样的,故不影响编码效率与数据压缩性能。
2、算术编码根据信源可能发现的不同符号序列的概率,把[0,1]区间划分为互不重叠的子区间,子区间的宽度恰好是各符号序列的概率。
这样信源发出的不同符号序列将与各子区间一一对应,因此每个子区间内的任意一个实数都可以用来表示对应的符号序列,这个数就是该符号序列所对应的码字。
算术编码

算术编码原理在给定符号集和符号概率的情况下,算术编码可以给出接近最优的编码结果。
使用算术编码的压缩算法通常先要对输入符号的概率进行估计,然后再编码。
这个估计越准,编码结果就越接近最优的结果。
例: 对一个简单的信号源进行观察,得到的统计模型如下:▪60% 的机会出现符号中性▪20% 的机会出现符号阳性▪10% 的机会出现符号阴性▪10% 的机会出现符号数据结束符. (出现这个符号的意思是该信号源'内部中止',在进行数据压缩时这样的情况是很常见的。
当第一次也是唯一的一次看到这个符号时,解码器就知道整个信号流都被解码完成了。
)算术编码可以处理的例子不止是这种只有四种符号的情况,更复杂的情况也可以处理,包括高阶的情况。
所谓高阶的情况是指当前符号出现的概率受之前出现符号的影响,这时候之前出现的符号,也被称为上下文。
比如在英文文档编码的时候,例如,在字母Q或者q出现之后,字母u出现的概率就大大提高了。
这种模型还可以进行自适应的变化,即在某种上下文下出现的概率分布的估计随着每次这种上下文出现时的符号而自适应更新,从而更加符合实际的概率分布。
不管编码器使用怎样的模型,解码器也必须使用同样的模型。
一个简单的例子以下用一个符号串行怎样被编码来作一个例子:假如有一个以A、B、C三个出现机会均等的符号组成的串行。
若以简单的分组编码会十分浪费地用2 bits来表示一个符号:其中一个符号是可以不用传的(下面可以见到符号B正是如此)。
为此,这个串行可以三进制的0和2之间的有理数表示,而且每位数表示一个符号。
例如,―ABBCAB‖ 这个串行可以变成0.011201(base3)(即0为A, 1为B, 2为C)。
用一个定点二进制数字去对这个数编码使之在恢复符号表示时有足够的精度,譬如0.001011001(base2) –只用了9个bit,比起简单的分组编码少(1 –9/12)x100% = 25%。
这对于长串行是可行的因为有高效的、适当的算法去精确地转换任意进制的数字。
算术编码(1).

算术编码特点
非分组码,它是从全序列出发,考虑符号之间的依赖关系。 经香农-费诺-埃利斯编码推广而来的,直接对信源符号序列
进行编码输出。 即时码,信源符号序列对应的累积概率区间是不重叠的。
肯定也可以唯一译码。 不必预先定义概率模型,自适应模式具有独特的优点;
信源符号概率接近时,建议使用算术编码,这种情况下其效率 高于Huffman编码(约5%)。JPEG扩展系统采用。
在区间[0.06752,0.0688)内的任何数字都可以表示消息 a1a2a3a3a4,例0.06752
15 15
算术编码—编码过程
步骤 1 2 3 4 5 6
输入 a1
编码间隔 [0,0.2)
a2
[0.04,0.08)
a3
[0.056,0.072)
a3
[0.0624,0.0688)
a4
[0.06752,0.0688)
2 2
算术编码特点
算术编码并不是将单个信源符号映射成一个码字,而是把 整个信源表示为实数线上0到1之间的一个区间,其长度等于 该序列的概率。
在该区间内选择一个代表性的小数,转换为二进制作为实 际的编码输出
消息序列中的每个元素都要用来压缩这个区间 消息序列中元素越多,所得到的区间就越小,当区间变小
时,就需要更多的位数来表示这个区间
3 3
算术编码的编码过程
从信源符号全序列出发,将各信源序列依累积概率分 布函数的大小映射到[0,1]区间,将[0,1]区间分成许 多互不重叠的小区间。
此时每个符号序列均有一个小区间与之对应,因而可在 小区间内取点来代表该符号序列。
4 4
算术编码应用(1)
算术编码

实验六算术编码一、实验目的1.图像编码:利用matlab编程实现算术编码2. 熟悉MATLAB环境;3. 学习用MATLAB 编程或直接调用函数对数字图像实现处理。
;二、实验内容及要求利用matlab命令实现算术编码三、实验原理算术编码是将被编码的一则消息或符号串(序列)直接编码成[o,1)区间上的一个浮点小数。
算术编码的基本思想:从全序列出发,采用递推形式的一种连续编码。
(1)初始化:对要编码字符按照其概率密度在[0,1]区间进行初始划分,被分割区间[low,high]=[0,1];(2) for i=1:Nrange=high-low;第i次分割区间计算low=low+range* range_low;high=low+range* range_high;[range_low, range_high]为第i个编码字符的初始划分区间;End(3)被编码的字符串的码值=low2,state tree的算术编码对第1字符s编码range=1;range_low=0.6;range_high=0.7;low=low+range*range_low=0+1*0.6=0.6;high= low+range*range_high= 0+1*0.7=0.7;s将区间[0,1]分割为[ 0.6,0.7];对第2字符t编码range= 0.7- 0.6 =0.1;range_low=0.7;range_high=1;low=low+range*range_low= 0.6 + 0.1*0.7=0.67;high= low+range*range_high= 0.6 + 0.1 *1=0.7;t将区间[ 0.6,0.7] 分割为[0.67, 0.7];对第3字符a编码range= 0.7- 0.67 =0.03;range_low=0.1;range_high=0.2;low=low+range*range_low= 0.67 + 0.03 *0.1=0.673;high= low+range*range_high= 0.67 + 0.03 *0.2 = 0.676;t将区间[0.67, 0.7]分割为[0.673, 0.676];四.实验程序及结果clear alllow=0.00;high=1.00;range_low=[0.60 0.70 0.10 0.70 0.20 0.00 0.70 0.50 0.20 0.20]; range_high=[0.70 1.00 0.20 1.00 0.50 0.10 1.00 0.60 0.50 0.50]; format long efor i=1:10range=high-low;high=low+range*range_high(i);low=low+range*range_low(i);endlowHighlow =6.753031605999998e-001high =6.753032334999998e-001五.实验分析从全序列出发,采用递推形式完成了连续编码。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d=r-l;
end
运行过程如下:
'本实例说明:'
'字符串不能太长,程序不加判断,请注意溢出;'
'本实例只限定少数字符串a b c d e;'
'实例只是说明一下算术编码过程。'
请输入编码的字符串(本程序仅仅是一个实例,请仅输入a b c d e):'aaabded'
a b c d e
0.2 0.3 0.1 0.15 0.25
输入第1符号的间隔左右边界:
0
0.
输入第2符号的间隔左右边界:
0
00
输入第3符号的间隔左右边界:
0
0.0000000
输入第4符号的间隔左右边界:
0.0000000
0.0000000
输入第5符号的间隔左右边界:
0.0000000
0.0000000
end
%判断字符
pl=0;pr=0;
for j=1:m-1
pl=pl+p(j);
end
for j=1:m
pr=pr+p(j);
end
%概率统计
l=l+d*pl;
r=l+d*(pr-pl);
strl=strcat('输入第',int2str(i),'符号的间隔左右边界:');
disp(strl);
format long
目前为止还没有使用算术编码作为默认压缩算法的Windows应用程序,WinRAR和WinIMP能够支持bzip2的解压。除此之外,在最新的JPEG标准中也用到了经过修改的算术编码压缩算法,但JPEG所用的那种算法受专利保护,因此使用时必须获得授权。
在之后的文章会很好的研究这个算法的实现:
现在给出一个简单的实例:
算术编码过程实例
正确实现的算术编码算法压缩能力Shannond定理描述的理论极限,是目前已知的压缩能力最强的无损压缩算法。
不过,由于算术编码算法的实现比较复杂,使用它作为默认压缩算法的应用程序还相当少。在Unix平台上非常流行的bzip2(这个工具有命令行模式的Windows版本)使用的就是经过修改的算术编码算法。
输入第6符号的间隔左右边界:
0.0033
0.0000000
输入第7符号的间隔左右边界:
0.0000000
0.0000000
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%算术编码过程实例ssbm.m
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
about={...
'本实例说明:'
'字符串不能太长,程序不加判断,请注意溢出;'
'本实例只限定少数字符串a b c d e;'
'实例只是说明一下算术编码过程。'};
disp(about);
str=input('请输入编码的字符串(本程序仅仅是一个实例,请仅输入a b c d e):');
l=0;r=1;d=1;
%初始间隔
%程序限定字符为:a、b、c、d、e
p=[0.2 0.3 0.1 0.15 0.25];
%字符的概率分布,sum(p)=1
n=length(str);
disp('a b c d e')
disp(num2str(p))
for i=1:n
switch str(i)
case 'a'
m=1;
case 'b'
m=2;
case 'c'
m=3;
case 'd'
m=4;
case 'e'
m=5;
otherwise
error('请不要输入其它字符!');
