图论习题

图论习题答案

习题一1. 一个工厂为一结点；若两个工厂之间有业务联系，则此两点之间用边相联；这样就得到一个无向图。

若每点的度数为3，则总度数为27，与图的总度数总是偶数的性质矛盾。

若仅有四个点的度数为偶数，则其余五个点度数均为奇数，从而总度数为奇数，仍与图的总度数总是偶数的性质矛盾。

2. 若存在孤立点，则m 不超过K n-1的边数, 故 m <= (n-1)(n-2)/2, 与题设矛盾。

3.4. 用向量(a 1,a 2,a 3)表示三个量杯中水的量, 其中a i 为第i 杯中水的量, i = 1,2,3.以满足a 1+a 2+a 3 = 8 (a 1,a 2,a 3为非负整数)的所有向量作为各结点, 如果(a 1,a 2,a 3)中某杯的水倒满另一杯得到 ( a ’1, a ’2, a ’3 ) , 则由结点到结点画一条有向边。

这样可得一个有向图。

本题即为在此图中找一条由( 8, 0, 0 )到( 4, 4, 0 )的一条有向路，以下即是这样的一条：5. 可以。

7. 同构。

同构的双射如下：8. 记e 1= (v 1,v 2), e 2= ( v 1,v 4), e 3= (v 3,v 1), e 4= (v 2,v 5), e 5= (v 6,v 3), e 6= (v 6,v 4), e 7= (v 5,v 3), e 8= (v 3,v 4), e 9 = (v 6,v 1), 则邻接矩阵为：关联矩阵为：∑∑∑∑∑∑∑==+====-=++=-==---=--=ni i n i i n i n i n i ni i i n i i n i i i i a a n n a a a n n n a n a v v 1111121212/)1()1(2)1(])1[(。

，　所以因为，＋的负度数，则为结点的正度数，为结点记－－－－－22 222 i i C a a ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡---------100110000001001000010100010011010100000001001100000111, 001101000100000000001001010000001010⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡( 8, 0, 0 ) ( 5, 3, 0 ) ( 5, 0, 3 ) ( 2, 3, 3 ) ( 2, 5, 1 )(7, 0, 1 ) ( 7, 1, 0 ) ( 4, 4, 0 )( 4, 1, 3 )边列表为：A= (1,1,3,2,6,6,5,3,6), B= (2,4,1,5,3,4,3,4,1). 正向表为：A= (1,3,4,6,6,7,10), B= (2,4,5,1,4,3,3,4,1).习题二1. 用数学归纳法。

离散数学图论部分经典试题及答案

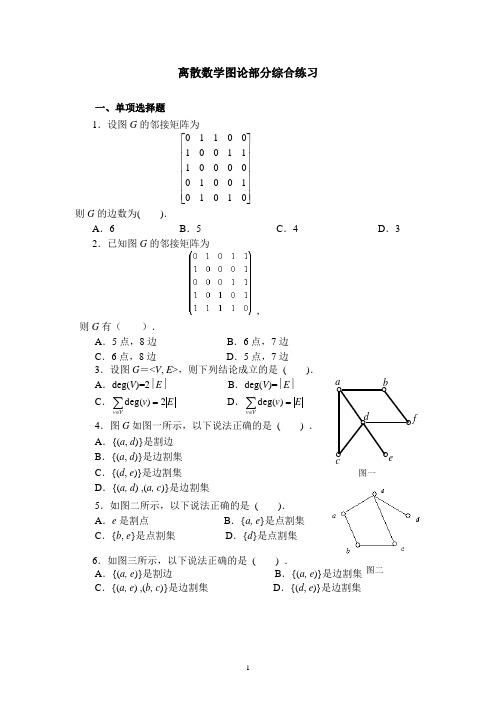
离散数学图论部分综合练习一、单项选择题1．设图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010*******11100100110则G 的边数为( )．A ．6B ．5C ．4D ．32．已知图G 的邻接矩阵为，则G 有（）．A ．5点，8边B ．6点，7边C ．6点，8边D ．5点，7边3．设图G ＝<V , E >，则下列结论成立的是 ( )．A ．deg(V )=2∣E ∣B ．deg(V )=∣E ∣C ．E v Vv 2)deg(=∑∈ D ．E v Vv =∑∈)deg(4．图G 如图一所示，以下说法正确的是 ( ) ． A ．{(a , d )}是割边 B ．{(a , d )}是边割集 C ．{(d , e )}是边割集 D ．{(a, d ) ,(a, c )}是边割集5．如图二所示，以下说法正确的是 ( )． A ．e 是割点 B ．{a, e }是点割集 C ．{b , e }是点割集 D ．{d }是点割集6．如图三所示，以下说法正确的是 ( ) ．A ．{(a, e )}是割边B ．{(a, e )}是边割集C ．{(a, e ) ,(b, c )}是边割集D ．{(d , e )}是边割集οο ο ο οca b edο f图一图二图三7．设有向图（a ）、（b ）、（c ）与（d ）如图四所示，则下列结论成立的是 ( )．图四A ．（a ）是强连通的B ．（b ）是强连通的C ．（c ）是强连通的D ．（d ）是强连通的应该填写：D8．设完全图K n 有n 个结点(n ≥2)，m 条边，当（）时，K n 中存在欧拉回路．A ．m 为奇数B ．n 为偶数C ．n 为奇数D ．m 为偶数 9．设G 是连通平面图，有v 个结点，e 条边，r 个面，则r = ( )．A ．e －v ＋2B ．v ＋e －2C ．e －v －2D ．e ＋v ＋2 10．无向图G 存在欧拉通路，当且仅当( )． A ．G 中所有结点的度数全为偶数 B ．G 中至多有两个奇数度结点 C ．G 连通且所有结点的度数全为偶数 D ．G 连通且至多有两个奇数度结点11．设G 是有n 个结点，m 条边的连通图，必须删去G 的( )条边，才能确定G 的一棵生成树．A ．1m n -+B ．m n -C ．1m n ++D ．1n m -+ 12．无向简单图G 是棵树，当且仅当( )．A ．G 连通且边数比结点数少1B ．G 连通且结点数比边数少1C ．G 的边数比结点数少1D ．G 中没有回路．二、填空题1．已知图G 中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G 的边数是． 2．设给定图G (如图四所示)，则图G 的点割ο οο οc a b f集是．3．若图G=<V , E>中具有一条汉密尔顿回路，则对于结点集V 的每个非空子集S ，在G 中删除S 中的所有结点得到的连通分支数为W ，则S 中结点数|S|与W 满足的关系式为．4．无向图G 存在欧拉回路，当且仅当G 连通且．5．设有向图D 为欧拉图，则图D 中每个结点的入度．应该填写：等于出度6．设完全图K n 有n 个结点(n 2)，m 条边，当时，K n 中存在欧拉回路．7．设G 是连通平面图，v , e , r 分别表示G 的结点数，边数和面数，则v ，e 和r 满足的关系式．8．设连通平面图G 的结点数为5，边数为6，则面数为． 9．结点数v 与边数e 满足关系的无向连通图就是树．10．设图G 是有6个结点的连通图，结点的总度数为18，则可从G 中删去条边后使之变成树．11．已知一棵无向树T 中有8个结点，4度，3度，2度的分支点各一个，T 的树叶数为．12．设G ＝<V , E >是有6个结点，8条边的连通图，则从G 中删去条边，可以确定图G 的一棵生成树．13．给定一个序列集合{000，001，01，10，0}，若去掉其中的元素，则该序列集合构成前缀码．三、判断说明题1．如图六所示的图G 存在一条欧拉回路．2．给定两个图G 1，G 2（如图七所示）：（1）试判断它们是否为欧拉图、汉密尔顿图？并说明理由．（2）若是欧拉图，请写出一条欧拉回路．v 123图六图七3．判别图G (如图八所示)是不是平面图，并说明理由．4．设G 是一个有6个结点14条边的连通图，则G 为平面图．四、计算题1．设图G =<V ，E >，其中V ={a 1, a 2, a 3, a 4, a 5},E ={<a 1, a 2>，<a 2, a 4>，<a 3, a 1>，<a 4, a 5>，<a 5, a 2>}（1）试给出G 的图形表示；（2）求G 的邻接矩阵；（3）判断图G 是强连通图、单侧连通图还是弱连通图？2．设图G =<V ，E >，V ={ v 1，v 2，v 3，v 4，v 5}，E ={ (v 1, v 2)，(v 1, v 3)，(v 2, v 3)，(v 2, v 4)，(v 3, v 4)，(v 3, v 5)，(v 4, v 5) }，试（1）画出G 的图形表示；（2）写出其邻接矩阵；（2）求出每个结点的度数；（4）画出图G 的补图的图形． 3．设G =<V ，E >，V ={ v 1，v 2，v 3，v 4，v 5}，E ={ (v 1,v 3)，(v 2,v 3)，(v 2,v 4)，(v 3,v 4)，(v 3,v 5)，(v 4,v 5) }，试（1）给出G 的图形表示；（2）写出其邻接矩阵；（3）求出每个结点的度数；（4）画出其补图的图形． 4．图G =<V , E >，其中V ={ a , b , c , d , e }，E ={ (a , b ), (a , c ), (a , e ), (b , d ), (b , e ), (c , e ), (c , d ), (d , e ) }，对应边的权值依次为2、1、2、3、6、1、4及5，试（1）画出G 的图形；（2）写出G 的邻接矩阵；（3）求出G 权最小的生成树及其权值．5.用Dijkstra 算法求右图中A 点到其它各点的最短路径。

称为向量组的秩，记作{1, 2, …., s }=r。
9. 若图G=(V, E)是连通图，且eE，证明：
(1)e属于每一棵生成树的充要条件是{e} 为G的割集；
(2)e不属于G的任何一棵生成树的充要条件是e为G中的环。
提示：反证
分析： (1) e属于每一棵生成树, 要证G删去e后
0
P(G2) ......
0

...... ...... ...... 0

0
0 ...... P(Gr )
因为Gi是连通图，Gi的秩是连通分支Gi的结点个数-1，所以 rank(G)=rank(Gi)=n-r。
本题背景：
1 线性相关/线性无关

如果对m个向量1, 2, …., mFm，
（3）1，2，3，4，5，5
（4）2，2，2，3，3，4
（西南交大1995考研）
(1) V1={a, c, e}, V2={b, d, f}. (2) 不可能画出图。(顶点度数之和为偶数)
(3) 不可能画出图和二分图。由于有两个结点的度数为5，则该两个结点的度数必与其余5个结点有边相连（因为是简单图），所以其余4 个结点度数至少为2，但有一个结点的度数为1。
1. n个结点的简单图G，n>2且n奇数，G 和G补图中度数为奇数的结点个数是否相等？请证明或给出反例。
（西南交大2001考研）
解：一定相等。
因为n>2且n奇数，则对于奇数个结点的完全图，每个结点的度数必为偶数。若G 中度数为奇数的结点个数是m，则G的补图中m个结点的度数为（偶数-奇数）=奇数。 G中度数为偶数的结点，在G的补图中这些结点的度数仍为（偶数-偶数）=偶数。

图论复习题

图论复习题（二）图论复习题一、选择题1．设图G ＝<V , E >，v ∈V ，则下列结论成立的是 ( C ) ． A ．deg(v )=2∣E ∣ B ． deg(v )=∣E ∣ C ．E v Vv 2)deg(=∑∈ [PPT 23] D ．Ev Vv =∑∈)deg(定理1 图G=（V ，E ）中，所有点的次之和为边数的两倍 2．设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100100110则G 的边数为( B )．A ．6B ．5C ．4D ．33、设完全图K n 有n 个结点(n ≥2)，m 条边，当（ C ）时，K n 中存在欧拉回路．A ．m 为奇数B ．n 为偶数C ．n 为奇数D ．m 为偶数解释：K n 每个结点的度都为n －1，所以若存在欧拉回路则n －1必为偶数。

n 必为奇数。

4．欧拉回路是（ B ）A. 路径B. 简单回路[PPT 40]C. 既是基本回路也是简单回路D.既非基本回路也非简单回路5．哈密尔顿回路是（ C ）A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路[PPT 40]：哈密尔顿回路要求走遍所有的点，即是基本回路的点不重复，也可以是简单回路的边不重复。

6．设G 是简单有向图，可达矩阵P(G)刻划下列关系中的是（ C ） A 、点与边 B 、边与点 C 、点与点 D 、边与边7．下列哪一种图不一定是树（C ）。

A.无简单回路的连通图B. 有n 个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图8．在有n 个结点的连通图中，其边数（B ）A.最多有n-1条B.至少有n-1条C.最多有n 条D.至少有n 条9．下列图为树的是（C ）。

A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a GB 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a GC 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a GD 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 10、下面的图7-22是（C ）。

图论习题

课前练习一、填空题1、图G 是简单图当且仅当。

2、简单图G 是二部图当且仅当。

3、若简单图G 满足(G)δ≥3，则G 中存在长度至少为的圈。

4、连通图G 具有欧拉通路，而无欧拉回路的充要条件为。

5、一颗树有两个2度分支点，一个3度分支点，三个4度分支点，则该树有片树叶。

6、设T 为高为k 的二叉树，则T 最多有个顶点。

7、设图G 是具有6条边、4个顶点的平面图,则图G 的面数为。

8、一个图为非平面图当且仅当。

9、S V ⊂，S 是图G 的极大独立集，则()V G S -是图G 的。

10、带权为1，3，5，7，8，11，13的最优二叉树T 的权W(T)= 。

二、解答题1、求下图G 1的色多项式，并指出其色数、点连通度和边连通度。

图G 12、（1）证明自补图的阶数n 4k =或者n 4k 1=+，k 为某个自然数。

（2）找出所有4阶的自补图。

3、（1）证明：设G 是有v 个顶点ε条边，且G 是自对偶平面图，则2v 2ε=-。

（2）已知一颗无向树T 有三个3度结点，一个二度结点，其余都是1度结点。

①T 有几个1度结点？②试画出两棵满足上述度数要求的非同构的无向树。

4、通过布尔变量的运算，求下图3的全部极小支配集。

V 16 图3图G 25、用破圈法求下图G 3中的一颗最小生成树,写出具体过程，并计算生成树的权。

图G 36、设简单图,, |V|=n, |E|=m,G V E =<> 若有212n m C -≥+，则G 是哈密尔顿图。

7、证明：5K 不是平面图.8、证明：若,(,1)m n K m n ≥是哈密顿图，则必有.m n = 9、若,m n K 是树，求,m n 应满足的条件.132411253e 6e 1e 2e 3e 4e 5e 7e 8e 9。

图论习题参考答案

二、应用题题0：（1996年全国数学联赛）有n（n≥6）个人聚会，已知每个人至少认识其中的[n/2]个人，而对任意的[n/2]个人，或者其中有两个人相互认识，或者余下的n-[n/2]个人中有两个人相互认识。

证明这n个人中必有3个人互相认识。

注：[n/2]表示不超过n/2的最大整数。

证明将n个人用n个顶点表示，如其中的两个人互相认识，就在相应的两个顶点之间连一条边，得图G。

由条件可知，G是具有n个顶点的简单图，并且有（1）对每个顶点x，)(xN G≥[n/2]；（2）对V的任一个子集S，只要S＝[n/2]，S中有两个顶点相邻或V-S中有两个顶点相邻。

需要证明G中有三个顶点两两相邻。

反证，若G中不存在三个两两相邻的顶点。

在G中取两个相邻的顶点x1和y1,记N G(x1)＝{y1,y2,……,y t}和N G(y1)={x1,x2,……,x k},则N G(x1)和N G(y1)不相交，并且N G(x1)（N G(y1)）中没有相邻的顶点对。

情况一；n=2r：此时[n/2]＝r，由（1）和上述假设，t=k=r且N G(y1)＝V-N G(x1)，但N G(x1)中没有相邻的顶点对，由（2），N G(y1)中有相邻的顶点对，矛盾。

情况二；n=2r+1: 此时[n /2]＝r ，由于N G (x 1)和N G (y 1)不相交，t ≥r,k ≥r,所以r+1≥t,r+1≥k 。

若t=r+1,则k=r ，即N G (y 1)=r ，N G (x 1)＝V-N G (y 1)，由（2），N G (x 1)或N G (y 1)中有相邻的顶点对，矛盾。

故k ≠r+1，同理t ≠r+1。

所以t=r,k=r 。

记w ∈V- N G (x 1) ∪N G (y 1),由（2），w 分别与N G (x 1)和N G (y 1)中一个顶点相邻，设wx i0∈E, wy j0∈E 。

若x i0y j0∈E ，则w ，x i0, y j0两两相邻，矛盾。

图论测试题及答案

图论测试题及答案一、选择题1. 在图论中，如果一个图的每个顶点的度数都是偶数，那么这个图一定存在欧拉路径吗？A. 是的B. 不一定C. 没有欧拉路径D. 无法确定答案：B2. 图论中的哈密顿路径是指什么？A. 经过图中所有顶点的路径B. 经过图中所有顶点的回路C. 经过图中某些顶点的路径D. 经过图中某些顶点的回路答案：A3. 如果一个图是完全图，那么它的边数是多少？A. 顶点数的一半B. 顶点数的平方C. 顶点数的两倍D. 顶点数减一答案：B二、填空题4. 在无向图中，如果存在一条路径，使得每个顶点只被经过一次，并且起点和终点相同，这样的路径被称为________。

答案：欧拉回路5. 图论中的二分图是指图中的顶点可以被分成两个不相交的集合，使得同一个集合内的顶点之间没有边，而不同集合之间的顶点之间有边，这种图也被称为________。

答案：二部图三、简答题6. 请简述图论中的最短路径问题，并给出解决该问题的一种算法。

答案：最短路径问题是在图中找到两个顶点之间的最短路径的问题。

解决该问题的一种算法是迪杰斯特拉算法（Dijkstra's algorithm），该算法通过维护一个顶点集合来记录已经找到最短路径的顶点，并迭代更新距离，直到找到从起点到所有顶点的最短路径。

7. 描述图论中的图着色问题，并说明其在实际生活中的应用。

答案：图着色问题是将图的顶点着色，使得任何两个相邻的顶点颜色不同。

在实际生活中，图着色问题可以应用于时间表的安排、频率分配、电路设计等领域，其中每个顶点代表一个任务或频道，而颜色则代表不同的时间段或频率。

结束语：以上是图论测试题及答案，希望能够帮助大家更好地理解和掌握图论的基本概念和算法。

图论复习题

图论及网络总复习题一、选择题1、设G是由5个顶点构成的完全图，则从G中删去（）边可以得到树。

A．6 B．5 C．8 D．42、下面哪几种图不一定是树（）。

A．无回路的连通图B．有n个结点，n-1条边的连通图C．对每对结点间都有通路的图D．连通但删去任意一条边则不连通的图。

3、5阶无向完全图的边数为（）。

A．5 B．10 C．15 D．204、把平面分成x个区域，每两个区域都相邻，问x最大为（）A．6 B．4 C．5 D．35、设图G有n个结点，m条边，且G中每个结点的度数不是k，就是k+1，则G中度数为k的节点数是（）A．n/2 B．n(n+1) C．nk-2m D．n(k+1)-2m 6、图G1和G2的结点和边分别存在一一对应关系是G1和G2同构的（）。

A．充分条件B．必要条件C．充分必要条件D．既不充分也不必要条件7、设G=<V，E>为有向图，V={a,b,c,d,e,f}，E={<a,b>,<b,c>,<a,d>,<d,e>,<f,e>}是（）。

A．强连通图B．单向连通图C．弱连通图D．不连通图8、无向图G中的边e是G的割边（桥）的充分必要条件是（）。

A．e是重边B．e不是重边C．e不包含在G的任一简单回路中D．e不包含在G的某一简单回路中9、在有n个结点的连通图中，其边数（）A．最多有n-1条B．至少有n-1条C．最多有n条D．至少有n条10．设无向简单图的顶点个数为n，则该图最多有（）条边。

A．n-1 B．n(n-1)/2 C． n(n+1)/2 D．n211．n个结点的完全有向图含有边的数目（）。

A．n*n Ｂ．n（n＋１） C．n／2 D．n*（n－l）12．在一个无向图中，所有顶点的度数之和等于所有边数（）倍。

A．1/2 B．2 C．1 D．413．连通图G是一棵树，当且仅当G中（）A．有些边不是割边B．所有边都是割边C．无割边集D．每条边都不是割边14．4个顶点的完全图G，其生成树个数是（）。

图论试题及答案解析图片

图论试题及答案解析图片一、选择题1. 图论中，图的基本元素是什么？A. 点和线B. 点和面C. 线和面D. 点和边答案：A2. 在无向图中，如果两个顶点之间存在一条边，则称这两个顶点是：A. 相邻的B. 相连的C. 相等的D. 相异的答案：A3. 在有向图中，如果从顶点A到顶点B有一条有向边，则称顶点A是顶点B的：A. 父顶点B. 子顶点C. 邻接顶点D. 非邻接顶点答案：B4. 一个图的度是指：A. 图中顶点的总数B. 图中边的总数C. 一个顶点的边数D. 图的连通性答案：C5. 一个图是连通的，当且仅当：A. 图中任意两个顶点都是相邻的B. 图中任意两个顶点都可以通过边相连C. 图中任意两个顶点都可以通过路径相连D. 图中任意两个顶点都可以通过子顶点相连答案：C二、填空题1. 在图论中，一个顶点的度数是该顶点的________。

答案：边数2. 如果一个图的任意两个顶点都可以通过边相连，则称该图为________。

答案：完全图3. 一个图中，如果存在一个顶点到其他所有顶点都有边相连，则称该顶点为________。

答案：中心顶点4. 图论中，最短路径问题是指在图中找到两个顶点之间的________。

答案：最短路径5. 如果一个图的任意两个顶点都可以通过有向路径相连，则称该图为________。

答案：强连通图三、简答题1. 请简述图论中的欧拉路径和哈密顿路径的定义。

答案：欧拉路径是指在图中经过每条边恰好一次的路径，而哈密顿路径是指在图中经过每个顶点恰好一次的路径。

2. 什么是图的着色问题？答案：图的着色问题是指将图中的顶点用不同的颜色进行标记，使得相邻的两个顶点颜色不同。

四、计算题1. 给定一个无向图G，顶点集为{A, B, C, D, E}，边集为{AB, BC, CD, DE, EA}，请画出该图，并计算其最小生成树的权重。

答案：首先画出图G的示意图，然后使用克鲁斯卡尔算法或普里姆算法计算最小生成树的权重。

图论期末复习题

17．任何简单平面图，均有． G 3
二、解答题
1.同构的判定及理由
3.左图称作什么图？两图是否同构？为什么？
x
y
z
x
c
a
a
b
c
z
y b
2、给定图：
(1)给出图的一个生成树。 (2)给出图的顶点的最大度数。
(3)给出图的最长链。 (4)给出图的一个边数最多的割集。
d
f
a
e1 b
在或不存在〕完美匹配．
35.在计算平面图面的次数之和时，每条边边计算了______ 次．
36．一个图是平面图当且仅当它既没有收缩到K5的子图，也没有收缩到的子图．
37．如果一个平面图有一个面的次数为4，那么该图______ 〔填是或不是〕极大平面图．
三、判断题
1．假设途径中的所有点互不相同，那么称此途径为一条链．
31．设M1和M2是图G的两个不同匹配, 由M1 M2导出的G的边导出子图记作H, 那么H的任意连通分支是以下情况之一： (1)边在M1和M2中交错出现的偶圈;(2)边在M1和M2中交错出现的．
32．二部图G中假设满足V1= V2，那么G必有完美匹配． 33． (G)=2 G是． 34.假设最大匹配的边数为p(G)/2，那么说明该图___〔填存
点连通度、边连通度与最小顶点的度数。
四、应用题
1. (蚂蚁比赛问题)甲、乙两只蚂蚁分别位于如以下图中的顶点A，B处，并设图中的边长度是相等的。甲、乙进行比赛：从它们所在的顶点出发，走过图中的所有边最后到达顶点C处。如果它们的速度相同，问谁先到达目的地？
甲A
乙
C
B
2．某地要兴建5个工厂，拟修筑道路连接这5 处。经勘测其道路可依如以下图无向边铺设。为使这5处都有道路相通，问至少要铺几条路？

图论习题+答案

1 设图G有12条边，G中有1度结点2个，2度结点2个，4度结点3个，其余结点度数不超过3．求G中至少有多少个结点？2 设有向简单图G的度数序列为(2,2,3,3）, 入度序列为(0,0,2,3),求G得出度序列 .3 设D是n阶有向简单完全图,则图D的边数为 .4设G是n阶无向简单完全图K n，则图G的边数为 .5 仅有一个孤立结点组成的图称为( )(A)零图(B)平凡图(C)补图(D)子图6设n阶图G中有m条边，每个结点的度数不是k的是k+1，若G中有N k个k度顶点，N k+1个k+1度顶点，则N k = .7设图G如右图.已知路径(1) P1=(v1e5 v5e7 v2e2 v3 )(2) P2=(v5e6 v2e2 v3e3 v4e8 v2e7 v5)(3) P3=(v2e7 v5e6 v2)(4) P4=(v1e1 v2e2 v3e3 v4e8 v2e6 v5)判断路径类型，并求其长度.81）判断下图G1中的路径类型, 并求其长度. P1=(v3e5v4e7v1e4v3e3v2e1v1e4v3)P2=(v3e3v2e2v2e1v1e4v3)P3=(v3e3v2e1v1e4v3).2）判断下图G2中的路径类型, 并求其长度. P1=(v1e1v2e6v5e7v3e2v2e6v5e8v4)P2=(v1e5v5e7v3e2v2e6v5e8v4)P3=(v1e1v2e6v5e7v3e3v4).v1e1e5v2e65e7e4 e2e8v3 4e3v e v1 设图G 有12条边，G 中有1度结点2个，2度结点2个，4度结点3个，其余结点度数不超过3．求G 中至少有多少个结点？至少9个2 设有向简单图G 的度数序列为(2,2,3,3）, 入度序列为(0,0,2,3),求G 得出度序列（2,2,5,6） .3 设D 是n 阶有向简单完全图,则图D 的边数为 )1(−n n .4 设G 是n 阶无向简单完全图K n ，则图G 的边数为 m =n (n -1)/2 .5 仅有一个孤立结点组成的图称为( B ) (A) 零图 (B)平凡图 (C)补图 (D)子图6设n 阶图G 中有m 条边，每个结点的度数不是k 的是k+1，若G 中有N k 个k 度顶点，N k+1个k+1度顶点，则N k = N k =(k+1)n-2m . 7设图G 如右图.已知路径 (1) P 1=(v 1e 5 v 5e 7 v 2e 2 v 3 ) (2) P 2=(v 5e 6 v 2e 2 v 3e 3 v 4e 8 v 2e 7 v 5) (3) P 3=(v 2e 7 v 5e 6 v 2)(4) P 4=(v 1e 1 v 2e 2 v 3e 3 v 4e 8 v 2e 6 v 5)判断路径类型，并求其长度. (1) 初级通路；3 (2) 简单回路；5 (3) 初级回路；2 (4) 简单通路. 5 81）判断下图G1中的路径类型, 并求其长度. P 1=(v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3) P 2=(v 3e 3v 2e 2v 2e 1v 1e 4v 3) P 3=(v 3e 3v 2e 1v 1e 4v 3).2）判断下图G2中的路径类型, 并求其长度. P 1=(v 1e 1v 2e 6v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 2=(v 1e 5v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 3=(v 1e 1v 2e 6v 5e 7v 3e 3v 4).解：在图G 1中，v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3是一条长度为6的回路，但既不是简单回路，也不是初级回路； v 3e 3v 2e 2v 2e 1v 1e 4v 3是一条长度为4的简单回路，但不是初级回路； v 3e 3v 2e 1v 1e 4v 3是一条长度为3的初级回路。

图论习题

4 n
2 2 1 4 A 4 1 1 2 3 9 B 8
）
6
2
．已知在传输中，a、b、c、d、e、f 、g、h 出现的频率分别为 25%、15%、15%、10%、10%、9%、6%、10%，编一个传输它们的最佳前缀码。
3
．有向图 D 如下图所示，用邻接矩阵法求 D 中长度为 3 的通路数和长度为 3 的回路数。
5. D=<V,E>
1 2 3 4 + 1 4 2 4 n n,m n
设图
三．判断题 1. 任一图 G 的△(G)必小于其结点数。（） 2. 在 n 个结点的简单图 G 中，若 n 为奇数，则 G 与 G 的度为奇数的结点数相同。（） 3. K 有 10 个生成子图。（） 4. 图 G 和 G’同构当且仅当 G 和 G’的结点和边分别存在一一对应关系。（） 5. 具有 3 个结点的有向完全图，含 4 条边的不同构的子图有 4 个。（） 6. 3 个(4,2)无向简单图中，至少有 2 个同构。（） 7. 若无向图中恰有 2 个度为奇数的结点，则这两个结点必连通。（） 8. 在有向图中，结点间的可达关系是等价的。（）（） 9. 若图 G 不连通，则 G 必连通。 10. 若图 G 的边 e 不包含在图 G 的某简单回路中，则 e 是 G 的割边。（） 11. 若无向连通图中无回路，则其每条边均为割边。（） 12. 若有向图 D 强连通，则 D 必为欧拉图。（） 13. 若有向图 D 是欧拉图，则 D 必为强连通图。（） 14. K 是哈密尔顿图。（） 15. 任一(n,m)平面图，若 n≥3，则 m≤3n-6。（） 16. 设 G=<V,E>，|V|≥11，则 G 或 G 是非平面图。（） 17. 极大平面图必连通。（） 18. 设 G=<V,E>为连通的简单平面图，若|V|≥3，则所有结点 v，有 deg(v) ≤5。（） 19. 任何树都至少有两片树叶。（） 20. 任何图 G=<V,E>都至少有一颗生成树。（） 21. 图 G 是（m，n）连通图，要求 G 的一颗生成树，则要删去 G 中的 m-n 条边。（） 22. 一个有向图 G 若仅有一个节点入度为 0，其余节点的入度全为 1，则 G 一定是有向树。（ 23.{000,001,01,10,11}是一个前缀码。（）（） 24.T 为完全 m 元树，有 t 片树叶，i 个分支点，则有关系式(m-1)i=t-1。四．综合题 1. 求下面带权图中从 A 到 B 的最短路径，要求用图示给出求解过程，并计算它们的权值。

图论复习题

图论复习题（二）图论复习题一、选择题1．设图G ＝<V , E >，v ∈V ，则下列结论成立的是 ( C ) ． A ．deg(v )=2∣E ∣ B ． deg(v )=∣E ∣ C ．E v Vv 2)deg(=∑∈ [PPT 23] D ．E v Vv =∑∈)deg(定理1 图G=（V ，E ）中，所有点的次之和为边数的两倍 2．设无向图G 的邻接矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0101010010000011100100110则G 的边数为( B )．A ．6B ．5C ．4D ．33、设完全图K n 有n 个结点(n ≥2)，m 条边，当（ C ）时，K n 中存在欧拉回路．A ．m 为奇数B ．n 为偶数C ．n 为奇数D ．m 为偶数解释：K n 每个结点的度都为n －1，所以若存在欧拉回路则n －1必为偶数。

n 必为奇数。

4．欧拉回路是（ B ）A. 路径B. 简单回路[PPT 40]C. 既是基本回路也是简单回路D.既非基本回路也非简单回路5．哈密尔顿回路是（ C ）A. 路径B. 简单回路C. 既是基本回路也是简单回路D.既非基本回路也非简单回路[PPT 40]：哈密尔顿回路要求走遍所有的点，即是基本回路的点不重复，也可以是简单回路的边不重复。

6．设G 是简单有向图，可达矩阵P(G)刻划下列关系中的是（ C ） A 、点与边 B 、边与点 C 、点与点 D 、边与边7．下列哪一种图不一定是树（C ）。

A.无简单回路的连通图B. 有n 个顶点n-1条边的连通图C. 每对顶点间都有通路的图D. 连通但删去一条边便不连通的图8．在有n 个结点的连通图中，其边数（B ）A.最多有n-1条B.至少有n-1条C.最多有n 条D.至少有n 条9．下列图为树的是（C ）。

A 、>><><><=<},,,,,{},,,,{1d c b a a a d c b a GB 、>><><><=<},,,,,{},,,,{2d c d b b a d c b a GC 、>><><><=<},,,,,{},,,,{3a c d a b a d c b a GD 、>><><><=<},,,,,{},,,,{4d d c a b a d c b a G 10、下面的图7-22是（C ）。

图论练习题

图论练习题一、基本题1、设G是由5个顶点构成的完全图，则从G中删去（A）边可以得到树。

A．6 B．5 C．8 D．42、下面哪几种图不一定是树（A）。

A．无回路的连通图B．有n个结点，n-1条边的连通图C．对每对结点间都有通路的图D．连通但删去任意一条边则不连通的图3、5阶无向完全图的边数为（B）。

A．5 B．10 C．15 D．204、设图G有n个结点，m条边，且G中每个结点的度数不是k，就是k+1，则G中度数为k的节点数是（）A．n/2 B．n(n+1) C．nk-2m D．n(k+1)-2m5、设G=<V，E>为有向图，V={a,b,c,d,e,f}，E={<a,b>,<b,c>,<a,d>,<d,e>,<f,e>}是（B）。

A．强连通图B．单向连通图C．弱连通图D．不连通图6、在有n个结点的连通图中，其边数（B）A．最多有n-1条B．至少有n-1条C．最多有n条D．至少有n条7、设无向简单图的顶点个数为n，则该图最多有（C）条边。

A．n-1 B．n(n-1)/2 C． n(n+1)/2 D．n28、要连通具有n个顶点的有向图，至少需要（A ）条边。

A．n-l B．n C．n+l D．2n9、n个结点的完全有向图含有边的数目（B）。

A．n*n Ｂ．n（n＋１） C．n／2 D．n*（n－l）10、在一个无向图中，所有顶点的度数之和等于所有边数（B）倍。

A．1/2 B．2 C．1 D．411、在一个有向图中，所有顶点的入度之和等于所有顶点出度之和的（C）倍。

A．1/2 B．2 C．1 D．412、连通图G是一棵树，当且仅当G中（B）A．有些边不是割边B．所有边都是割边C．无割边集D．每条边都不是割边13、4个顶点的完全图G，其生成树个数是（）。

A．4 B．8 C．16 D．64二、应用题题1、判断下图是否能一笔画出，并说明理由。

图论部分复习题

Q
S f d e b a
L
Z
c
Байду номын сангаас
试写出模6加法群<Z 13. 试写出模6加法群<Z6，+6>的每个子群及其相应的左陪集 14. 写出代数系统、半群、独异点、群、环、域的概念。写出代数系统、半群、独异点、域的概念。
8. 写出右图的一个生成子图。 ={m,s,z,b}的导出子图的导出子图G[V 求V1={m,s,z,b}的导出子图G[V1]。 9. 10. 11. 12. 一个图和它的补图有什么联系？一个图和它的补图有什么联系？完全图的定义是什么？完全图的定义是什么？求右图割点和割边 Z 判断是否构成格，判断是否构成格，并说明原因 a b c e d M B C
已知无向图G 12条边条边，度顶点， 1. 已知无向图G有12条边，6个3度顶点，其余顶点的度数均小于3 至少有几个顶点？小于3，问G至少有几个顶点？并画出满足条件的一个图形. 阶无向图中，度顶点的个数分别是1 2. 7阶无向图中，2度，3度，4度，5度顶点的个数分别是1、 1.求图的边数.试画出满足条件的一个图形. 求图G 3、2、1.求图G的边数.试画出满足条件的一个图形. 是否存在7 无向简单图G 其度序列为1 3. 是否存在7阶无向简单图G，其度序列为1、3、3、4、6、 7.给出相应证明给出相应证明. 6、7.给出相应证明. 个互不相同的正整数. 4. 设d1、d2、…、dn为n个互不相同的正整数. 、证明：不存在以d 证明：不存在以d1、d2、…、dn为度序列的无向简单图. 、为度序列的无向简单图. a 求右图的补图. 5. 求右图的补图. e d 6. 试画出一个自补图图和其补图同构). (图和其补图同构). 给定整数序列是否构成无向图的度序列并说明原因。 7. 给定整数序列是否构成无向图的度序列并说明原因。 c b 2 2 2 8 6 4 2 2 2 8 7 5 1 3 3 4 2 8

图论期末考试题库及答案

图论期末考试题库及答案一、单项选择题1. 图论的创始人是（）。

A. 欧拉B. 莱布尼茨C. 牛顿D. 高斯答案：A2. 在图论中，一个图的顶点集合为空，但边集合不为空的图称为（）。

A. 空图B. 完全图C. 树D. 多重图答案：A3. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。

A. 连通图B. 强连通图C. 弱连通图D. 无环图答案：A4. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。

A. 欧拉图B. 哈密顿图C. 树答案：C5. 图论中，一个图的边的集合可以划分为若干个不相交的回路，使得图中的每个顶点恰好属于其中一条回路，这样的图称为（）。

A. 欧拉图B. 哈密顿图C. 树D. 环答案：A二、多项选择题1. 下列哪些是图论中的基本术语（）。

A. 顶点B. 边D. 权重答案：ABCD2. 在图论中，以下哪些图是无向图（）。

A. 完全图B. 树C. 多重图D. 有向图答案：ABC3. 图论中，以下哪些图是连通图（）。

A. 完全图B. 树C. 多重图D. 空图答案：ABC三、填空题1. 图论中，一个图的顶点集合为V，边集合为E，那么图可以表示为G=（）。

答案：(V, E)2. 如果一个图的任意两个顶点之间都存在一条路径，则称该图为（）。

答案：连通图3. 在图论中，一个图的边的集合可以划分为若干个不相交的路径，使得图中的每个顶点恰好属于其中一条路径，这样的图称为（）。

答案：树四、简答题1. 请解释什么是图论中的“完全图”？答案：完全图是指图中每一对不同的顶点之间都恰好有一条边相连的图。

在完全图Kn中，n个顶点两两相连，共有n(n-1)/2条边。

2. 请解释什么是图论中的“欧拉路径”和“欧拉回路”？答案：欧拉路径是指图中存在一条路径，该路径恰好经过每条边一次。

欧拉回路是指图中存在一条回路，该回路恰好经过每条边一次。

五、计算题1. 给定一个图G=(V, E)，其中V={A, B, C, D, E}，E={(A, B), (B, C), (C, D), (D, E), (E, A), (A, C)}，请判断该图是否为连通图，并说明理由。

图论习题

习题 11. 证明在n 阶连通图中（1）至少有n -1条边。

（2）如果边数大于n -1，则至少有一条闭通道。

（3）如恰有n -1条边，则至少有一个奇度点。

证明(1) 若对∀v ∈V(G),有d(v)≥2,则：2m=∑d(v)≥2n ⇒ m ≥n >n-1,矛盾！若G 中有1度顶点，对顶点数n 作数学归纳。

当n=2时，G 显然至少有一条边，结论成立。

设当n=k 时，结论成立，当n=k+1时，设d(v)=1，则G-v 是k 阶连通图，因此至少有k-1条边，所以G 至少有k 条边。

(2) 考虑v 1→v 2→⋯→v n 的途径，若该途径是一条路，则长为n-1,但图G 的边数大于n-1,因此存在v i ,v j ,使得v i adgv j ,这样，v i →v i+1→⋯→v j 并上v i v j 构成一条闭通道；若该途径是一条非路，易知，图G 有闭通道。

(3) 若不然，对∀v ∈V(G),有d(v)≥2,则：2m=∑d(v)≥2n ⇒ m ≥n >n-1,与已知矛盾！ 2. 设G 是n 阶完全图，试问（1）有多少条闭通道？（2）包含G 中某边e 的闭通道有多少？（3）任意两点间有多少条路？答 (1) (n-2)! (2) (n-1)!/2 (3) 1+(n-2)+(n-2)(n-3)+(n-2)(n-3)(n-4)+…+(n -2)…1.3. 证明图1-27中的两图不同构：证明容易观察出两图中的点与边的邻接关系各不相同，因此，两图不同构。

4. 证明图1-28中的两图是同构的证明将图1-28的两图顶点标号为如下的(a)与(b)图图1-27 图1-28作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-27的两个图是同构的。

图论习题及答案

作业解答练习题2 利用matlab编程FFD算法完成下题：设有6种物品，它们的体积分别为：60、45、35、20、20和20单位体积，箱子的容积为100个单位体积。

解答一：function [num,s] = BinPackingFFD(w,capacity)%一维装箱问题的FFD（降序首次适应）算法求解:先将物体按长度从大到小排序,%然后按FF算法对物体装箱%输入参数w为物品体积，capacity为箱子容量%输出参数num为所用箱子个数，s为元胞数组，表示装箱方案，s{i}为第i个箱子所装%物品体积数组%例w = [60,45,35,20,20,20]; capacity = 100;% num=3,s={[1,3],[2,4,5],6};w = sort(w,'descend');n = length(w);s = cell(1,n);bin = capacity * ones(1,n);num = 1;for i = 1:nfor j = 1:num + 1if w(i) < bin(j)bin(j) = bin(j) - w(i);s{j} = [s{j},i];if j == num + 1num = num + 1;endbreak;endendends = s(1:num);解答二：clear;clc;V=100;v=[60 45 35 20 20 20];n=length(v);v=fliplr(sort(v));box_count=1;x=zeros(n,n);V_Left=100;for i=1:nif v(i)>=max(V_Left)box_count=box_count+1;x(i,box_count)=1;V_Left=[V_Left V-v(i)];elsej=1;while(v(i)>V_Left(j))j=j+1;endx(i,j)=1;V_Left(j)=V_Left(j)-v(i);endtemp=find(x(i,:)==1);fprintf('第%d个物品放在第%d个容器\n',i,temp) endoutput:第1个物品放在第1个容器第2个物品放在第2个容器第3个物品放在第1个容器第4个物品放在第2个容器第5个物品放在第2个容器第6个物品放在第3个容器解答三：function box_count=FFD(x)%降序首次适应算法v=100;x=fliplr(sort(x));%v=input('请输入箱子的容积:');n=length(x);I=ones(n);E=zeros(1,n);box=v*I;box_count=0;for i=1:nj=1;while(j<=box_count)if x(i)>box(j)j=j+1;continue;elsebox(j)=box(j)-x(i);E(i)=j;break;endendif j>box_countbox_count=box_count+1;box(box_count)=box(box_count)-x(i);E(i)=j;endenddisp(E);在命令窗口输入：>> x=[60,45,35,20,20,20];>> FFD(x)1 2 1 2 2 3ans =3练习题5 “超市大赢家”提供了50种商品作为奖品供中奖顾客选择,车的容量为1000dm3, 奖品i占用的空间为w i dm3,价值为v i元, 具体的数据如下:v i= { 220, 208, 198, 192, 180, 180, 165, 162, 160, 158,155, 130, 125, 122, 120, 118, 115, 110, 105, 101, 100, 100, 98,96, 95, 90, 88, 82, 80, 77, 75, 73, 72, 70, 69, 66, 65, 63, 60, 58,56, 50, 30, 20, 15, 10, 8, 5, 3, 1}w i = {80, 82, 85, 70, 72, 70, 66, 50, 55, 25, 50, 55, 40, 48,50, 32, 22, 60, 30, 32, 40, 38, 35, 32, 25, 28, 30, 22, 50, 30, 45,30, 60, 50, 20, 65, 20, 25, 30, 10, 20, 25, 15, 10, 10, 10, 4, 4, 2,1}。

数学竞赛图论试题及答案

数学竞赛图论试题及答案一、选择题（每题5分，共20分）1. 在一个无向图中，如果有5个顶点，每个顶点至少与另外两个顶点相连，那么这个图至少有多少条边？A. 5B. 6C. 7D. 82. 一个图是二分图当且仅当它没有奇环。

这个说法是正确的吗？A. 是B. 否3. 给定一个有n个顶点的完全图，求出该图的边数。

A. n(n-1)/2B. n(n+1)/2C. n^2D. 2n4. 在一个图中，如果存在一条从顶点u到顶点v的简单路径，则称u 可达v。

如果图中任意两个顶点都是相互可达的，那么这个图是：A. 连通图B. 强连通图C. 有向无环图D. 欧拉图二、填空题（每空5分，共30分）5. 一个图的度序列是指图中所有顶点的度按照______排列的序列。

6. 如果一个图的边数等于顶点数的两倍，那么这个图一定是______。

7. 在图论中，一个图的最小生成树是指连接所有顶点的______的树。

8. 一个图的着色数是指对图中的顶点进行着色，使得任何两个相邻的顶点颜色都不同，使用的最小颜色数。

三、简答题（每题25分，共50分）9. 描述什么是图的平面性，并给出判断一个图是否为平面图的方法。

10. 解释什么是图的哈密顿回路，并给出一个例子。

答案一、选择题1. C（根据边数的最小值公式，边数至少为顶点数减一的两倍）2. B（二分图没有奇环，但不是所有没有奇环的图都是二分图）3. A（完全图的边数公式）4. A（连通图的定义）二、填空题5. 非增6. 完全二部图7. 边数最少8. 最小三、简答题9. 图的平面性指的是图可以画在平面上，使得图中的边除了端点外不相交。

判断一个图是否为平面图的方法有库拉托夫斯基定理，即如果一个图包含一个子图同构于K5（完全五顶点图）或K3,3（完全二部图），则该图是非平面的。

10. 哈密顿回路是一条通过图中每个顶点恰好一次的闭合回路。

例如，一个正方形的四个顶点可以形成一个哈密顿回路，因为可以按照顺时针或逆时针方向依次访问每个顶点一次。