实验5 蒙特卡罗法求PI及排序算法
数学建模蒙特卡洛模拟方法详细案例

数学建模蒙特卡洛模拟方法详细案例
数学建模中的蒙特卡洛模拟方法是一种基于随机数生成和概率统计的方法,可以用于求解各种复杂的问题。
下面是一个详细的案例,以帮助你更好地理解蒙特卡洛模拟方法的应用。
案例:估计圆周率
假设我们要求解圆周率(π)的值。
我们可以使用蒙特卡洛模拟方法来估计π的值。
1. 定义问题的概率模型:在这个案例中,我们使用一个简单的概率模型,即在一个边长为1的正方形内随机生成点,并计算这些点到正方形中心的距离。
2. 生成随机数:使用随机数生成器生成一系列的随机数,这些随机数代表点在正方形内的坐标。
3. 计算点到中心的距离:对于每个生成的点,计算它到正方形中心的距离。
4. 计算落在圆内的点的比例:将落在半径为1的圆内的点的数量除以总的点数。
这个比例近似于圆的面积与正方形的面积之比,也就是π/4。
5. 通过比例求解π:将步骤4中的比例乘以4,即可得到π的近似值。
通过多次重复上述步骤并取平均值,可以进一步提高估计的准确性。
需要注意的是,蒙特卡洛模拟方法是一种基于随机数生成和概率统计的方法,其结果具有一定的随机性和误差。
因此,在应用蒙特卡洛模拟方法时,需要选择合适的随机数生成器和概率模型,以确保结果的准确性和可靠性。
21——matlab——用蒙特卡罗方法计算pi的值

用蒙特卡罗( Monte Carlo ) 投点法计算 的值程序:n=10000;m=0; a=2;for i=1:nx=rand(1)*a/2;y=rand(1)*a/2;if x^2+y^2<=(a/2)^2m=m+1;endendfprintf('蒙特卡罗投点法计算的pi为:%f\n',4*m/n)结果:蒙特卡罗投点法计算的pi为:3.117200蒙特卡罗投点法计算的pi为:3.132400蒙特卡罗投点法计算的pi为:3.165600蒙特卡罗投点法计算的pi为:3.135200蒙特卡罗投点法计算的pi为:3.146800蒙特卡罗投点法计算的pi为:3.140400蒙特卡罗投点法计算的pi为:3.114800蒙特卡罗投点法计算的pi为:3.117200 蒙特卡罗投点法计算的pi为:3.154800 蒙特卡罗投点法计算的pi为:3.140400 蒙特卡罗投点法计算的pi为:3.121200 蒙特卡罗投点法计算的pi为:3.134400 蒙特卡罗投点法计算的pi为:3.122800 蒙特卡罗投点法计算的pi为:3.127600 蒙特卡罗投点法计算的pi为:3.147200 蒙特卡罗投点法计算的pi为:3.145200 蒙特卡罗投点法计算的pi为:3.158400 蒙特卡罗投点法计算的pi为:3.147600 蒙特卡罗投点法计算的pi为:3.147600 蒙特卡罗投点法计算的pi为:3.146400 蒙特卡罗投点法计算的pi为:3.112000 蒙特卡罗投点法计算的pi为:3.180000 蒙特卡罗投点法计算的pi为:3.120000 蒙特卡罗投点法计算的pi为:3.153600 蒙特卡罗投点法计算的pi为:3.144000 蒙特卡罗投点法计算的pi为:3.148000 >>。
用蒙特卡罗方法计算π值实验报告

本科生实验报告实验课程蒙特卡罗模拟学院名称核技术与自动化工程学院专业名称核技术及应用学生姓名王明学生学号**********指导教师邮箱****************实验成绩二〇一七年九月二〇一八年一月实验一、选择一种编程语言模拟出π的值一、实验目的1、理解并掌握蒙特卡罗模拟的基本原理;2、运用蒙特卡洛思想解决实际问题;3、分析总结蒙特卡洛解决问题的优缺点。
二、实验原理用蒙特卡洛思想计算π的值分为如下几部:第一步构建几何原理:构建单位圆外切正方形的几何图形。
单位圆的面积为S0=π,正方形的面积S1=4;第二步产生随机数进行打把:这里用MATLAB产生均匀随机数。
分别生产均匀随机数(x,y)二维坐标。
X,y的范围为-1到1.总共生成N个坐标(x,y).统计随机生成的坐标(x,y)在单位圆内的个数M。
第三步打把结构处理:根据S0/S1=M/N计算出π的值。
因此π=4*M/N。
第四步改变N的值分析π的收敛性:总数1000开始打把,依次增长10倍到1百万个计数。
三、实验内容1、用matlab编写的实验代码,总计数率为1000。
zfx_x=[1,-1,-1,1,1];zfx_y=[1,1,-1,-1,1];plot(zfx_x,zfx_y)axis([-3 3 -3 3]);hold on;r=1; theta=0:pi/100:2*pi;x=r*cos(theta); y=r*sin(theta);rho=r*sin(theta);figure(1)plot(x,y,'-')N=1000;mcnp_x=zeros(1,N);mcnp_y=zeros(1,N);M=0;for i=1:Nx=2*(rand(1,1)-0.5);y=2*(rand(1,1)-0.5);if((x^2+y^2)<1)M=M+1;mcnp_x(i)=x;mcnp_y(i)=y;endendplot(mcnp_x,mcnp_y,'.')PI1=4*M/N;2、用matlab绘制的图形四、实验结果1.当模拟总计数为1000时,某次计算结果: PI=3.128。
蒙特卡洛(Monte—Carlo)方法求圆周率π

蒙特卡洛(Monte —Carlo )方法求圆周率π蒙特卡罗(Monte Carlo )方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。
设X 表示针的中点到最近的一条平行线的距离,Y 表示针与平行线的夹角(如图1所示),如果sin 2X l Y <,或sin 2l X Y <时,针与一条直线相交。
图1蒙特卡洛法求π示意图由于向桌面投针是随机的,所以用来确定针在桌面上位置的(,)X Y 是二维随机向量。
并且X 在0,2a ⎛⎫ ⎪⎝⎭上服从均匀分布,Y 在0,2π⎛⎫ ⎪⎝⎭上服从均匀分布, X 与Y 相互独立。
由此可以写出(,)X Y 的联合概率密度函数:40,02,2()0a x f x y y a ππ⎧<<<=<⎪⎨⎪⎩,,其它于是,所求概率为:sin 2200sin 242sin (,)2l y l x y l l P X Y f x y dxdy dxdy a a πππ<⎧⎫<===⎨⎬⎩⎭⎰⎰⎰⎰ 由于最后的结果与π有关,因此有些人想利用它来计算π的值。
其方法是向桌面投针n 次,若针与直线相交k 次,则针与直线相交的频率为k n ,以频率代替概率,则有2k l n a π=,所以2nl akπ=。
namespace 是指标识符的各种可见范围srand 函数是随机数发生器的初始化函数。
原型:void srand(unsigned seed);用法:它需要提供一个种子,这个种子会对应一个随机数,如果使用相同的种子后面的rand()函数会出现一样的随机数。
如: srand(1); 直接使用1来初始化种子。
不过为了防止随机数每次重复常常使用系统时间来初始化,即使用 time 函数来获得系统时间,它的返回值为从 00:00:00 GMT, January 1, 1970 到现在所持续的秒数,然后将time_t 型数据转化为(unsigned)型再传给srand 函数,即: srand((unsigned) time(&t)); 还有一个经常用法,不需要定义time_t 型t 变量,即: srand((unsigned) time(NULL)); 直接传入一个空指针,因为你的程序中往往并不需要经过参数获得的t 数据。
matlab蒙特卡罗方案积分计算pi值

matlab蒙特卡罗方案积分计算pi值
使用蒙特卡罗方法来计算圆周率$pi$的值,可以按照以下步骤: 1. 在一个正方形内随机生成一组点。
该正方形边长为2,中心坐标为(0,0)。
2. 统计这些点中落在以(0,0)为圆心,半径为1的圆内的点数N。
3. 计算$pi$的估计值:$piapprox4N/M$,其中M为生成的点数。
下面是MATLAB代码实现:
```MATLAB
% 生成M个点
M = 100000;
x = -1 + 2.*rand(M,1);
y = -1 + 2.*rand(M,1);
% 统计落在圆内的点数
N = sum(x.^2 + y.^2 <= 1);
% 计算估计值
pi_estimate = 4*N/M;
% 显示结果
disp(["PI的估计值为 ", num2str(pi_estimate)]);
```
请注意,由于蒙特卡罗方法是一种随机方法,因此计算结果可能会有一定的误差。
如果想要提高精度,需要增加生成的点数M。
实验五 MATLAB蒙特卡罗方法

实验任务一:记录L次实验的实验数据及误差 序号 数据 误差 1 2 3 4 5 6 7
实验任务二:修改实验程序MonteC计算L次实验数 据均值及均值误差( mean 计算平均值 ) L 8 16 32 64 128 256
均值
误差
7/10
冰淇淋锥图形绘制程序
function icecream(m,n) if nargin==0,m=20;n=100;end t=linspace(0,2*pi,n); r=linspace(0,1,m); x=r'*cos(t);y=r'*sin(t); z1=sqrt(x.^2+y.^2); z2=1+sqrt(1+eps-x.^2-y.^2); X=[x;x];Y=[y;y]; Z=[z1;z2]; mesh(X,Y,Z) view(0,-18) colormap([0 0 1]),axis off
xy 2 dxdy 其中D为y= x – 2与y2 = x 所围
D的边界曲线交点为:(–1,1),(4,2),被积函数在求 积区域内的最大值为16。积分值是三维体积,该三维 图形位于立方体区域 0≤ x ≤4,–1≤ y ≤2,0 ≤ z ≤16 内,立方体区域的体积为192。 data=rand(10000,3); x=4*data(:,1); y=-1+3*data(:,2); z=16*data(:,3); II=find(x>=y.^2&x<=y+2&z<=x.*(y.^2)); M=length(II); V=192*M/10000
N个点均匀分布于六面体中,锥体中占有m 个,则锥体与六面体体积之比近似为 m : N
2
用蒙特卡罗方法计算π值实验报告

用蒙特卡罗方法计算π值实验报告蒙特卡罗方法是一种通过随机过程来解决数学、物理和工程问题的数值方法。
在本实验中,我们将利用蒙特卡罗方法计算圆周率π的的值。
以下是实验报告。
1.实验目的本实验的主要目的是利用蒙特卡罗方法计算圆周率π的值,并分析蒙特卡罗方法的可靠性和准确性。
2.实验原理蒙特卡罗方法的基本原理是通过随机采样来估计未知参数的值。
对于圆周率π的计算,我们可以利用正方形和内切圆的关系来实现。
具体步骤如下:(1)在一个给定的单位正方形中,以原点为中心,半径为1的圆。
(2)在正方形中随机生成大量的点,然后计算这些点在圆内的个数。
(3)根据圆的面积与正方形的面积的关系,可以利用这个比例来估计圆周率π的值。
3.实验过程(1)创建一个给定边长的正方形,圆的半径为正方形边长的一半。
(2)随机生成大量坐标点,并计算这些点距离原点的距离。
(3)统计在圆内的点的个数。
(4)根据统计结果计算圆周率π的估计值。
4.实验结果我们进行了多次实验,每次实验生成了100万个点。
然后我们计算每次实验中在圆内的点的个数,并利用这些数据计算圆周率π的估计值。
实验结果如下:实验次数点个数估计π值通过这些实验数据,我们可以计算出平均圆周率π的估计值为3.14085.实验分析通过对多次实验数据的统计分析,我们可以看到蒙特卡罗方法在估计圆周率π的值上具有较高的准确性和可靠性。
实验结果的稳定性较好,不同实验的结果都接近真实值π,而且相对误差较小。
然而,虽然得到的结果接近真实值,但是实验结果的准确性仍然受到概率分布的随机性的限制。
如果我们增加实验次数,可以提高结果的准确性,但是计算的时间也会相应增加。
此外,在计算π的过程中,我们使用了随机生成的数据,因此需要进行大量的计算。
若在实际应用中需要计算更复杂的问题,计算资源和时间消耗将会更大。
6.实验总结本实验使用蒙特卡罗方法计算了圆周率π的估计值。
通过多次实验的数据统计和分析,我们可以得出蒙特卡罗方法在计算π值上的准确性和可靠性较高。
蒙特卡洛方法计算圆周率(C语言实现)

#include <stdio.h> #include <stdlib.h> #include <time.h> #include <math.h> int main() { srand(time(0)); double eps = 1e-6, delta; int r = 0, c = 0; int n = 0; double x, y, p1, p2; while (n++ < 100) { x = -1.0 + 2.0 * rand() / RAND_MAX; y = -1.0 + 2.0 * rand() / RAND_MAX; if (x * x + y * y < 1.0) { ++c; 6
20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
} else { ++r; } } p1 = 4.0 * c / (c + r); do { x = -1.0 + 2.0 * rand() / RAND_MAX; y = -1.0 + 2.0 * rand() / RAND_MAX; if (x * x + y * y < 1.0) { ++c; } else { ++r; } p2 = 4.0 * c / (c + r); ++n; delta = fabs(p2 - p1); p1 = p2; } while (delta > eps); printf("iterations: %d\n", n - 1); printf("delta: %.7lf\n", delta); printf("value of pi: %lf\n", p2); return 0; } 上述代码首先需要解释的是第 15 行至第 17 行代码,主要作用是先随机生成 100 个点,并以此计算 的圆周率近似值为迭代的初始值,否则将会出现最开始的两次圆周率近似值之差为 0 的情况,导致得不 到正确的计算结果。 第 27 行至第 41 行的循环代码作用在于随着随机点数的逐渐增加,迭代计算连续的两次圆周率近似 值之差,并与阈值进行比较,如果小于该阈值,则退出循环,将最后计算的一次圆周率近似值作为最终 结果。 编译并运行上述程序,得到如下结果: iterations: 859661 delta: 0.0000010 value of pi: 3.140340
实验5 蒙特卡罗法求PI及排序算法

浙江大学城市学院实验报告课程名称多核与并行程序设计实验项目名称实验五蒙特卡罗法求PI及排序算法学生姓名专业班级学号实验成绩指导老师(签名)日期【实验环境】硬件平台:联想4核,4GZ内存编译器:Microsoft Visual Studio C++ 6.0操作系统:Windows 2003 server sp2测试数据集合:由随机数函数产生的数据集合【实验1】一、问题描述蒙特卡洛算法可理解为通过大量实验,模拟实际行为,来收集统计数据。
本例中,算法随机产生一系列点,模拟这些点落在如下图所示的正方形区域内的情况。
其几何解释如下11图1如图1所示,正方形边长为1,左下顶点与原点重合,两边分别与x,y轴重合。
曲线为1/4圆弧,圆心位于原点,与正方形左下定点重合,半径为1。
正方形面积S1=1,圆弧内面积S2=ππ41412=r。
算法模拟大量点随机落在此正方形区域内,落在圆弧内的点的数量(n2)与点的总数(n1)的比例与面积成正比关系。
即π42121==S S n n (1) 由此可得124n n =π (2)因此,只要计算出落在圆弧内的点的数量在点总数中所占的比例,就能求出π的值。
由图1可知,所有点均落在正方形范围内,因此点的x 坐标满足10≤≤x 。
又,当点落在圆弧范围内,则点的二维坐标关系满足122≤+y x 。
检验每一个点是否满足此关系即可判定改点是否落在圆弧内。
二、串行算法描述本项目中使用了标准C 语言库中的产生随机数函数。
该函数原型为:int rand( void );此函数产生随机数列,每次调用时均返回0到RAND_MAX 之间的一个整数。
void srand( unsigned int seed );此函数为rand ()函数所生成的伪随机数序列设置起始点,使之产生不同的伪随机数。
算法:产生2n 个随机数据,范围[0,1],对每个数据点计算其坐标是否满足122≤+y x ,统计满足此关系的点的数量count ,则 n count4=π三、并行算法3.1 并行算法描述算法步骤:1、确定需要产生的点的个数n ,参与运行的处理器数m ;2、对每一个处理器,生成两个随机数x ,y ,范围[0,1];3、判断两个随机数x ,y 是否满足122≤+y x ;4、若满足,则变量COUNT i++;5、重复步骤2-4,直至每个处理器均生成n/m个随机点;6、收集COUNT i的值,并累加至变量COUNT中,此即为随机点落在圆弧内的数量;7、通过(2)式计算 的值。
python 蒙特卡洛方法求解π的方法

python 蒙特卡洛方法求解π的方法【实用版4篇】篇1 目录1.蒙特卡洛方法简介2.Python 实现蒙特卡洛方法的基本步骤3.用 Python 实现蒙特卡洛方法求解π的代码示例4.结论篇1正文1.蒙特卡洛方法简介蒙特卡洛方法是一种基于随机抽样的数值计算方法,通过大量模拟实验来近似求解问题。
它的基本思想是在一定范围内随机生成大量样本点,根据样本点满足某种特定条件的比例来估计问题的解。
蒙特卡洛方法在许多领域都有广泛应用,如数学、物理、化学、金融等。
2.Python 实现蒙特卡洛方法的基本步骤使用 Python 实现蒙特卡洛方法的基本步骤如下:(1) 设定问题范围和参数(2) 编写随机抽样函数(3) 编写问题特定条件判断函数(4) 生成大量样本点(5) 统计满足特定条件的样本点比例(6) 根据比例估计问题的解3.用 Python 实现蒙特卡洛方法求解π的代码示例下面是一个用 Python 实现蒙特卡洛方法求解π的简单示例:```pythonimport randomimport mathdef monte_carlo_pi(n):inside_circle = 0for _ in range(n):x = random.uniform(-1, 1)y = random.uniform(-1, 1)distance = math.sqrt(x ** 2 + y ** 2)if distance <= 1:inside_circle += 1return 4 * (inside_circle / n)= 10000pi_estimate = monte_carlo_pi(n)print("π的估计值为:", pi_estimate)```在这个示例中,我们用蒙特卡洛方法模拟了在单位圆内的点,然后计算了这些点在总点数中的比例。
最后,我们将这个比例乘以 4 得到π的近似值。
随着模拟次数的增加,得到的π估计值会越来越接近真实的π值。
MonteCarlo(蒙特卡洛算法)算法

用Monte Carlo 计算定积分
考虑积分
I
x 1exdx,
0
0.
假定随机变量具有密度函数
fX (x) ex,
则
I E( X 1).
用Monte Carlo 计算定积分-
2
2
T
T
Monte Carlo 模拟连续过程的欧式 期权定价-
均匀分布
R=unidrnd(N),-产生1到N间的均匀分布随 机数
R=unidrnd(N,n,m),产生1到N间的均匀分布 随机数矩阵
连续均匀分布
R=unifrnd(A,B) -产生(A,B)间的均匀分布随 机数
R=unifrnd(A,B,m,n)产生(A,B)间的均匀分布 随机数矩阵
Matlab 的随机数函数-
正态分布随机数
R=normrnd(mu,sigma) R=normrnd(mu,sigma,m) R=normrnd(mu,sigma,m,n)
特定分布随机数发生器 R=random(‘name’,A1,A2,A3,m,n)
例
a=random(‘Normal’,0,1,3,2) a=
基本思想和原理
基本思想:当所要求解的问题是某种事件出现 的概率,或者是某个随机变量的期望值时,它 们可以通过某种“试验”的方法,得到这种事 件出现的频率,或者这个随机变数的平均值, 并用它们作为问题的解。
原理:抓住事物运动的几何数量和几何特征, 利用数学方法来加以模拟,即进行一种数字模 拟实验。
实现从已知概率分布抽样
构造了概率模型以后, 按照这个概率分 布抽取随机变量 (或随机向量),这一 般可以直接由软件包调用,或抽取均匀 分布的随机数构造。这样,就成为实现 蒙特卡罗方法模拟实验的基本手段,这 也是蒙特卡罗方法被称为随机抽样的原 因。
python蒙特卡罗方法求解π的方法

python蒙特卡罗方法求解π的方法Python蒙特卡罗方法求解π的方法引言蒙特卡罗方法是一种基于随机采样的数值计算方法,可以用来估计无法通过解析方法求解的问题。
其中,利用蒙特卡罗方法求解圆周率π的方法是常见且经典的例子。
本文将详细介绍多种使用Python 实现的求解π的方法。
方法一:随机投点法1.设置一个正方形,内切一个半径为1的圆。
2.在正方形内随机生成大量的点。
3.统计落入圆内点的数量和总点数。
4.利用统计数据,计算得到π的近似值。
方法二:蒙特卡罗法1.思路与方法一相同,区别在于生成的点落在一个区间内。
2.垂直投影的线段长度为1,将其看作区间长度。
3.将模拟投点法应用于这个区间,得到的结果进行比例缩放。
4.根据缩放比例得到π的近似值。
方法三:生成一个单位半径的圆1.利用matplotlib库生成一个单位半径的圆。
2.通过生成的圆,计算圆的面积。
3.利用面积公式计算得到π的近似值。
方法四:改进的投点法1.类似于方法三,使用matplotlib库生成一个圆。
2.通过生成的圆,计算圆的面积。
3.利用统计学的SRSWOR(Simple Random Sampling WithoutReplacement)方法,生成均匀分布的点。
4.统计落入圆内点的数量和总点数。
5.根据统计数据,计算得到π的近似值。
总结蒙特卡罗方法作为一种随机采样的数值计算方法,非常适合用于求解π的问题。
本文介绍了四种方法,分别是随机投点法、蒙特卡罗法、生成单位半径的圆和改进的投点法。
通过这些方法,我们可以得到π的近似值,并且精度可以通过增加采样点的数量来提高。
以上就是使用Python蒙特卡罗方法求解π的方法的详细介绍。
希望本文能对你理解蒙特卡罗方法及其在求解π问题中的应用有所帮助。
引言蒙特卡罗方法是一种基于随机采样的数值计算方法,可以用来估计无法通过解析方法求解的问题。
其中,利用蒙特卡罗方法求解圆周率π的方法是常见且经典的例子。
(MonteCarlo)方法求圆周率π

蒙特卡洛(Monte —Carlo )方法求圆周率π蒙特卡罗(Monte Carlo )方法,或称计算机随机模拟方法,是一种基于“随机数”的计算方法。
设X 表示针的中点到最近的一条平行线的距离,Y 表示针与平行线的夹角(如图1所示),如果sin 2X l Y <,或sin 2l X Y <时,针与一条直线相交。
图1蒙特卡洛法求π示意图由于向桌面投针是随机的,所以用来确定针在桌面上位置的(,)X Y 是二维随机向量。
并且X 在0,2a ⎛⎫ ⎪⎝⎭上服从均匀分布,Y 在0,2π⎛⎫ ⎪⎝⎭上服从均匀分布, X 与Y 相互独立。
由此可以写出(,)X Y 的联合概率密度函数:40,02,2()0a x f x y y a ππ⎧<<<=<⎪⎨⎪⎩,,其它于是,所求概率为:sin 2200sin 242sin (,)2l y l x y l l P X Y f x y dxdy dxdy a a πππ<⎧⎫<===⎨⎬⎩⎭⎰⎰⎰⎰ 由于最后的结果与π有关,因此有些人想利用它来计算π的值。
其方法是向桌面投针n 次,若针与直线相交k 次,则针与直线相交的频率为k n ,以频率代替概率,则有2k l n a π=,所以2nl akπ=。
namespace 是指标识符的各种可见范围srand 函数是随机数发生器的初始化函数。
原型:void srand(unsigned seed);用法:它需要提供一个种子,这个种子会对应一个随机数,如果使用相同的种子后面的rand()函数会出现一样的随机数。
如: srand(1); 直接使用1来初始化种子。
不过为了防止随机数每次重复常常使用系统时间来初始化,即使用 time 函数来获得系统时间,它的返回值为从 00:00:00 GMT, January 1, 1970 到现在所持续的秒数,然后将time_t 型数据转化为(unsigned)型再传给srand 函数,即: srand((unsigned) time(&t)); 还有一个经常用法,不需要定义time_t 型t 变量,即: srand((unsigned) time(NULL)); 直接传入一个空指针,因为你的程序中往往并不需要经过参数获得的t 数据。
蒙特卡罗(Monte Carlo算法)算法

随机数的取得
• 如果你对随机数有更高的要求,需要自己 编辑“随机数生成器”
• 最简单、最基本、最重要的一个概率分布 是(0,1)上的均匀分布(或称矩形分布)
• 例如在Matlab中,命令“rand()”将产生 一个(0,1)中均匀分布的随机数
• 你可以根据需要给随机数一个“种子”, 以求不同的数
Matlab 的随机数函数
• 大大改善了结果!
随机数的产生
• 随机数是我们实现蒙特卡罗模拟的基本工具。 • 随机数的产生就是抽样问题。可以用物理方法
产生随机数,但价格昂贵,不能重复,使用不 便。另一种方法是用数学递推公式产生。这样 产生的序列,与真正的随机数序列不同,所以 称为伪随机数,或伪随机数序列。不过,经过 多种统计检验表明,它与真正的随机数,或随 机数序列具有相近的性质,因此可把它作为真 正的随机数来使用。
用Monte Carlo 计算定积分
• 考虑积分 • 假定随机变量具有密度函数 •则
用Monte Carlo 计算定积分-
• 抽取密度为e^{-x}的随机数X_1,…X_n • 构造统计数
•则
用Monte Carlo 计算定积分--
•且
•即
用Monte Carlo 计算定积分---
• 例如 α=1.9
Monte Carlo Simulation 简介
概述
• 蒙特卡罗(Monte Carlo)方法,或称计算 机随机模拟方法或随机抽样方法或统计 试验方法 ,属于计算数学的一个分支。 是一种基于“随机数”的rlo方法的基本思想很 以前就 被人们所发现和利用。 在17世纪,人 们就知道用事件发生的“频率”来决定 事件的“概率”。19世纪人们用投针试
• 它是以一个概率模型为基础,按照这个模型所 描绘的过程,通过模拟实验的结果,作为问题 的近似解。。
Monte Carlo方法计算Pi

实验Monte Carlo方法计算Pi实验要求:以OpenMP实现Monte Carlo计算Pi的并行程序实验分析:通过蒙特卡罗算法计算圆周率的主导思想是:统计学(概率)一个正方形有一个内切圆,向这个正方形内随机的画点,则点落在圆内的概论为P=圆面积/正方形面积。
1. 在一个平面直角坐标系下,在点(1,1)处画一个半径为R=1的圆,以这个圆画一个外接正方形,其边长为R=1(R=1时,圆面积即Pi)。
2. 随机取一点(X,Y)使得0<=X<=2R并且0<=Y<=2R,即随机点在正方形内。
3. 判断点是否在圆内,通过公式(X-R)(X-R)+(Y-R)(Y-R)<R*R计算。
4. 设所有点的个数为N,落在圆内的点的个数为M,则P=M/N=4*R*R/Pi*R*R=4/PiPi=4*N/M当实验次数越多(N越大),所计算出的Pi也越准确。
但计算机上的随机数毕竟是伪随机数,当取值超过一定值,也会出现不随机现象,因为伪随机数是周期函数。
如果想提高精度,最好能用真正的随机数生成器(需要更深的知识)。
运行结果采用并行采用串行代码:#include"stdafx.h"#include<stdio.h>#include<omp.h>#include<stdlib.h>#include<time.h>#define NUM_THREADS 4int main(){long long max=10000000;long long i,count=0;double x,y,bulk,starttime,endtime;time_t t;starttime=clock();// 产生以当前时间开始的随机种子srand((unsigned) time(&t));omp_set_num_threads(NUM_THREADS);#pragma omp parallel for reduction(+:count) private(x,y)for(i=0;i<max;i++){x=rand(); x=x/32767;y=rand(); y=y/32767;if((x*x+y*y)<=1)count++;}bulk=4*(double(count)/max);endtime= clock();printf("pi is %f \n", bulk);printf("Running time is %f \n", endtime-starttime);return 0;}加红色代码之前为串行代码,加上红色代码之后为并行代码。
python蒙特卡洛方法计算圆周率

python蒙特卡洛方法计算圆周率Python蒙特卡洛方法是一种常用的求解圆周率的方法。
其基本思路是在平面直角坐标系中随机生成一定数量的点,然后统计落在圆内的点的数量,最终得到圆的面积,从而计算出圆周率。
具体实现过程如下:1. 定义一个函数,用于判断一个点是否在圆内。
这里需要用到勾股定理判断点到圆心的距离是否小于半径,代码如下:```def is_in_circle(x, y):distance = (x ** 2 + y ** 2) ** 0.5return distance <= 1```2. 随机生成一定数量的点,这里可以使用Python自带的random 模块,代码如下:```import randomnum_points = 1000000points_inside = 0for i in range(num_points):x = random.uniform(-1, 1)y = random.uniform(-1, 1)if is_in_circle(x, y):points_inside += 1```3. 计算圆的面积和圆周率。
由于圆的面积为πr^2,而半径r=1,因此圆的面积就等于π。
而落在圆内的点占所有点的比例就是圆的面积与正方形面积的比值,因此可以用这个比例来计算圆周率,代码如下:```pi = 4 * points_inside / num_pointsprint(pi)```通过多次实验,可以发现随机生成点的数量越多,计算出的圆周率越接近真实值π。
同时还可以将计算过程可视化,将生成的点分为两类,一类落在圆内,用红色表示,另一类落在圆外,用蓝色表示,代码如下:```import matplotlib.pyplot as pltx_inside = []y_inside = []x_outside = []y_outside = []for i in range(num_points):x = random.uniform(-1, 1)y = random.uniform(-1, 1)if is_in_circle(x, y):x_inside.append(x)y_inside.append(y)else:x_outside.append(x)y_outside.append(y)fig, ax = plt.subplots()ax.scatter(x_inside, y_inside, c='r', marker='.')ax.scatter(x_outside, y_outside, c='b', marker='.')ax.set_aspect('equal', adjustable='box')plt.show()```这样就可以看到随机生成的点在平面直角坐标系中的分布情况,从而更加直观地理解蒙特卡洛方法求解圆周率的过程。
蒙特卡洛方法求圆周率

蒙特卡洛方法求圆周率嘿,朋友们!今天咱来聊聊蒙特卡洛方法求圆周率这事儿。
你说圆周率,那可是数学里的大明星啊!从咱老祖宗那时候起,就一直有人在琢磨怎么更精确地算出它来。
那蒙特卡洛方法呢,就像是个神奇的魔法棒。
想象一下哈,有个大大的正方形,里面画个内切圆。
然后呢,我们就像撒豆子一样,在这个正方形里随便乱扔好多好多的小点。
这些小点有的落在圆里,有的落在正方形其他地方。
这时候,咱就来看看落在圆里的点和总的点数的比例。
嘿嘿,神奇的事情就发生啦!这个比例和圆的面积与正方形面积的比例是差不多的呀!圆的面积咱知道,是πr²,正方形面积也好算,边长的平方呗。
这不就和圆周率挂上钩了嘛!通过统计这些点的位置,就能大概算出圆周率的数值啦。
这是不是很有意思?就像在玩一个游戏,却能得出这么重要的结果。
你说这蒙特卡洛方法是不是很巧妙?它就像是在混沌中找到了一条通往答案的小路。
虽然可能不是最精确的方法,但绝对是很有创意的一种。
咱再想想,生活中是不是也有很多这样看似不经意的方法,却能解决大问题呢?就像有时候我们随手一试,说不定就找到了一个绝妙的办法。
用蒙特卡洛方法求圆周率,让我想起了我们在生活中面对困难的时候。
有时候,常规的方法走不通,那咱就得开动脑筋,想点不一样的招儿。
说不定就像找到了蒙特卡洛方法一样,能给我们带来惊喜呢!而且啊,这也让我们看到了数学的魅力。
数学可不只是那些枯燥的公式和计算,它也能变得这么有趣,这么生动。
大家不妨也自己动手试试,用蒙特卡洛方法来求一下圆周率,感受一下这个神奇的过程。
说不定你会对数学有新的认识,对圆周率也会有更深的感情呢!总之,蒙特卡洛方法求圆周率,真的是个值得我们好好琢磨的有趣事儿啊!。
计算圆周率的算法python

计算圆周率的算法python计算圆周率的算法有许多,其中一个常见的算法是蒙特卡洛方法。
蒙特卡洛方法利用随机性来估计圆周率的值。
该方法的基本思路是:假设有一个单位正方形和一个内切圆,我们通过在正方形内随机生成大量的点,并计算这些点中落在圆内的比例来估计圆周率。
具体的算法步骤如下:1. 初始化两个变量:total_points表示总的点数,circle_points表示落在圆内的点数,初值均为0。
2. 生成随机数对(x, y),其中x和y的取值范围均为[0, 1]。
3. 计算点(x, y)到圆心的距离distance,可以使用欧几里得距离公式。
若distance小于等于1,则点在圆内,将circle_points加1;否则,点在圆外。
4. 将total_points加1。
5. 重复步骤2到4,直到完成所需的随机点的生成与判断。
这个过程可以通过使用循环进行实现。
6. 计算圆周率的估计值pi,使用公式:pi = 4 * (circle_points / total_points)。
下面是用Python语言实现的估计圆周率的简单代码示例:```pythonimport randomdef estimate_pi(n):total_points = 0circle_points = 0for _ in range(n):x = random.uniform(0, 1)y = random.uniform(0, 1)distance = x**2 + y**2if distance <= 1:circle_points += 1total_points += 1pi = 4 * (circle_points / total_points)return pi# 估计圆周率的示例调用n = 1000000 # 随机点的总数pi_estimate = estimate_pi(n)print("估计的圆周率为:", pi_estimate)```这段代码生成了1000000个随机点,并利用蒙特卡洛方法估计圆周率的值。
[资料]蒙特卡罗算法计算pi
![[资料]蒙特卡罗算法计算pi](https://img.taocdn.com/s3/m/bffe261977c66137ee06eff9aef8941ea76e4b72.png)
呵呵,刚好大二下学期学的,给你讲讲吧。
根据我的理解简单的说就是以部分估计整体,利用随机数来解决问题的方法称为蒙特卡罗算法,记得课本上讲了个例题:在数值积分法中,我们利用求单位圆的1/4的面积来求得Pi/4从而得到Pi。
单位圆的1/4面积是一个扇形,它是边长为1单位正方形的一部分(若能画图就好了!)只要能求出扇行面积S1在正方形面积S中占的比例K=S1/S就立即能得到S1,从而得到Pi的值.怎样求出扇形面积在正方形面积中占的比例K呢?一个办法是在正方形中随机投入很多点,使所投的点落在正方形中每一个位置的机会相等看其中有多少个点落在扇形内。
将落在扇形内的点数m与所投点的总数n的比m/n作为k的近似值。
怎样实现这样的随机投点呢?任何一款计算机语言都有这种功能,能够产生在区间[0,1]内均匀分布的随机数,在mathematica中,产生区间[0,1]内均匀分布随机数的语句是Random[ ]产生两个这样的随机数x,y,则以(x,y)为坐标的点就是单位正方形内的一点P,它落在正方形内每个位置的机会均等,P落在扇形内的充要条件是x^2+y^2<=1.蒙特卡罗算法计算Pin=10000;p=();Do[m=0;Do[x=Random[];y=Random[];If[x^2+y^2<=1,m++],{k,1,n}];AppendTo[p,N[4m/n]],{t,1,10}];Print[p];Sum[p[[t]],{t,1,10}]/10注:以上语句的功能是:n=10000,每次投10000个点得出Pi的近似值存放到数组p中;一共做10次得到10个近似值,通过语句Print[p]将这10个近似值全部显示出来观察。
最后再求这10个近似值的平均值,相当于随机投点100000次得到的近似值。
以上是用Mathenatica编写的程序,方法就是这样,具体只能你自己体会了。
蒙特卡罗算法以概率和统计理论方法为基础的一种计算方法。
蒙特卡罗模拟和π值模拟计算
PART2 关于蒙特卡罗模拟和π值模拟计算很多书都讲了,本书的讲解方式却很独特!?9.2.3.1 蒙特卡罗模拟基本理论蒙特卡罗方法(Monte Carlo,MC)源于美国在第二次世界大战中进行的研制原子弹的“曼哈顿计划”。
该计划的主持人之一、数学家冯·诺伊曼用驰名世界的赌城——摩纳哥的Monte Carlo——来命名这种方法。
MC方法是一种基于“随机数”的计算方法,能够比较逼真地描述事物的特点及物理实验过程,解决一些解析方法难以解决的问题,是对许多复杂的随机系统建模的仅有方法。
MC 方法的雏型可以追溯到十九世纪后期的蒲丰(Buffon)随机投针试验,即著名的蒲丰问题,这是古典概率中一个重要问题,该问题是通过将针投到地面计算其频率并结合已知的准确关系式从而确定圆周率π的值。
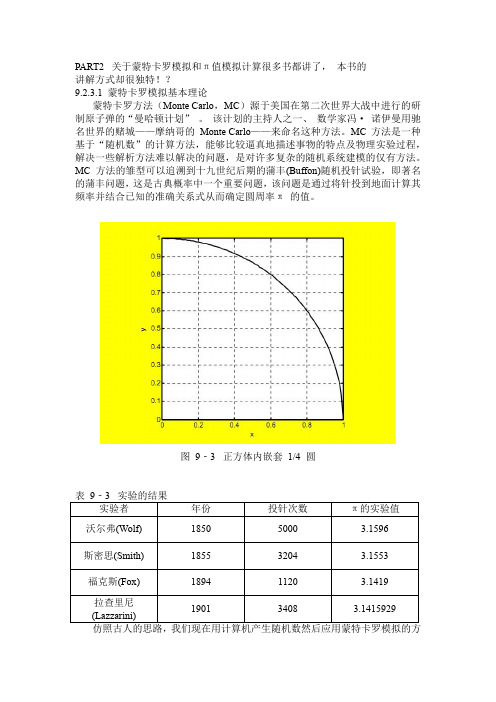
图9‐3 正方体内嵌套1/4 圆法再现π值,程序如P9‐3。
首先在一个长宽各为1 的正方体内画一个以坐标原点为圆心、半径为1 的1/4圆[5]。
如图9‐3 所示。
程序编号:P9‐3文件名称:Main903.m说明:正方体内嵌套1/4 圆绘图%本程序画出在正方体内嵌套1/4圆的组合图形%程序虽小,但是蕴含着用结构体设置图形属性和图形对象及坐标轴属性底层设置。
clc;x=0:0.01:1;y=sqrt(1-x.^2);figure;h=plot(x,y);active.linestyle='-';active.linewidth=3;active.color='k';set(h,active);set(gcf,'color','y');set(gca,'color','b');xlabel('x');ylabel('y');grid on;axis square;显然,图9‐3正方形A面积等于1,1/4 圆和坐标轴合围区域B 的面积等于 4 / π,这两个区域面积之比等于4 / π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江大学城市学院实验报告课程名称多核与并行程序设计实验项目名称实验五蒙特卡罗法求PI及排序算法学生姓名专业班级学号实验成绩指导老师(签名)日期【实验环境】硬件平台:联想4核,4GZ内存编译器:Microsoft Visual Studio C++ 6.0操作系统:Windows 2003 server sp2测试数据集合:由随机数函数产生的数据集合【实验1】一、问题描述蒙特卡洛算法可理解为通过大量实验,模拟实际行为,来收集统计数据。
本例中,算法随机产生一系列点,模拟这些点落在如下图所示的正方形区域内的情况。
其几何解释如下11图1如图1所示,正方形边长为1,左下顶点与原点重合,两边分别与x,y轴重合。
曲线为1/4圆弧,圆心位于原点,与正方形左下定点重合,半径为1。
正方形面积S1=1,圆弧内面积S2=ππ41412=r。
算法模拟大量点随机落在此正方形区域内,落在圆弧内的点的数量(n2)与点的总数(n1)的比例与面积成正比关系。
即π42121==S S n n (1) 由此可得124n n =π (2)因此,只要计算出落在圆弧内的点的数量在点总数中所占的比例,就能求出π的值。
由图1可知,所有点均落在正方形范围内,因此点的x 坐标满足10≤≤x 。
又,当点落在圆弧范围内,则点的二维坐标关系满足122≤+y x 。
检验每一个点是否满足此关系即可判定改点是否落在圆弧内。
二、串行算法描述本项目中使用了标准C 语言库中的产生随机数函数。
该函数原型为:int rand( void );此函数产生随机数列,每次调用时均返回0到RAND_MAX 之间的一个整数。
void srand( unsigned int seed );此函数为rand ()函数所生成的伪随机数序列设置起始点,使之产生不同的伪随机数。
算法:产生2n 个随机数据,范围[0,1],对每个数据点计算其坐标是否满足122≤+y x ,统计满足此关系的点的数量count ,则 n count4=π三、并行算法3.1 并行算法描述算法步骤:1、确定需要产生的点的个数n ,参与运行的处理器数m ;2、对每一个处理器,生成两个随机数x ,y ,范围[0,1];3、判断两个随机数x ,y 是否满足122≤+y x ;4、若满足,则变量COUNT i++;5、重复步骤2-4,直至每个处理器均生成n/m个随机点;6、收集COUNT i的值,并累加至变量COUNT中,此即为随机点落在圆弧内的数量;7、通过(2)式计算 的值。
3.2 并行算法在Windows下的一个例子#include<stdio.h>#include<windows.h>#include<time.h>//#include <process.h>#include<iostream>#include<fstream>#include<stdlib.h>using namespace std;HANDLE evFinish;long cs=0; //总循环次数long count=0; //主线程有效次数long count_thread=0; //thread线程有效次数time_t start, finish; //定义开始结束时间//thread线程计算量为总数的一半DWORD WINAPI thread(LPVOID param) //这个函数在PDF里WaitForSingleObject(evFinish,INFINITE);//两线程同步count+=count_thread;finish=time(NULL); //记录结束时间printf("并行情况:\n\n");printf("用时=%f 秒\n",difftime(finish,start)); //计算时间差printf("总共的循环次数=%d次\n",cs);printf(" 线程有效次数=%d次\n",count);printf("pi= %f \n",4*(double)count/(double)cs);printf("串行行情况:\n");count=0;start=time(NULL); //记录开始时间for(i=0;i<cs;i++){x=(long double)rand()/(long double)RAND_MAX;y=(long double)rand()/(long double)RAND_MAX;if((x*x+y*y)<=1)count++;// printf("主%d",i);//printf("count%d",count);}finish=time(NULL); //记录结束时间printf("用时=%f 秒\n",difftime(finish,start));printf("总共的循环次数=%d次\n",cs);printf(" 线程有效次数=%d次\n",count);printf("pi= %f \n",4*(double)count/(double)cs);return(0);}四、实验结果1、实验运行结果是多少2、本例中加速比(串行时间/并行时间):S=【实验2】一、问题描述在单核计算环境中,排序算法关注的核心问题是怎样减少要排序数据之间的比较次数或算法所需要的内存空间。
在多核计算环境中,每个核以线程为执行单元,排序程序可以通过生成相互协作的线程来完成排序。
与单核计算环境不同的是,在多核计算环境中更关注数据集的合理划分,更致力于识别可并行执行的任务。
一旦完成这些工作,程序设计上就可以生成对应的线程去执行任务。
理论上,基于相同的串行算法和相同的cache命中率,多核计算速度可以无限接近单核计算速度的P倍,其中P为核的数目。
多核上的并行排序算法所面临的问题在于:1. 未排序的数据集合理划分到每个线程后,最后怎么汇合,形成完整的排好序的数据集呢?2. 怎么保证可并行执行的线程的数目和核的数目相等或稍微多于核的数目,同时也保证这些线程之间的工作量也尽可能的相同呢?在这个实验中,串行的算法采用标准C语言库中的快速排序函数。
并行算法中,先将要处理的数据集均等的分到每个线程中,并使用C语言库中的快速排序函数各自排序。
然后所有线程开始根据相同的数对自己的数据集进行划分,这个数是依据一定的方法选出来的(详见并行算法描述)。
每个线程的数据集都会被分成K份,(其中P<= K < P2 ,P为核的数目),每份将被称为一桶。
很显然这个过程选出了K个数,这些数将被成为bound_value, 记为X1, X2, X3…… X K。
最后每个线程中小于或等于X1的数会被一个独立的线程去归并排序,同样小于或等于X2的数也会被另外一个独立的线程去归并排序,依次类推,直到排好序。
需要指出的是:这个并行版本最消耗时间的部分是一开始每个线程各自的排序,时间为:n n);不过其数据划分和线程生成也相对简单。
最后的归并排序所需时间是线性增O(log长的,即:O(n),因此即使在最后归并部分线程执行的任务已经是不均衡的,也不会对整个程序的性能产生很大的影响。
二、串行算法描述本项目中使用了标准C语言库中的快速排序函数。
该函数原型为:void(void*base,size_t num,size_t width,int(__cdecl*compare)(const void*elem1,const void*elem2));其中base: 待排序数据的数组基址;num: 待排序数据的数目;width: 待排序数据元组的大小;compare: 排序比较函数,当elem1<elem2时返回值小于0,当elem1=elem2时返回值等于0,当elem1>elem2时返回值大于0;三、并行算法3.1 并行算法描述算法:1、将原始待排序的数据分成P等份,每个处理器上对N0个数据进行排序,称每个被排序后的子集为B0,…,Bp-12、Remain_data=N,设定第0组归并起始位置全部为0, i=0,设置第0组在目标数组中的起始位置为03、循环直至remian_data<L( L=N0/P )3.1 选取所有子集中起始位置后续L个元素的最小值bound_value,并获得bound_value的桶号bucket3.2 在所有子集中从起始位置到后续L个元素中选取边界位置,使得边界位置的最后一个元素小于或等于bound_value,而边界位置后的第一元素大于bound_value。
3.3 记录所有的边界位置,并设置所有第i+1组的起始位置为第i组的起始位置加上边界位置3.4 累积所有边界值,得到该归并组的大小3.5 根据归并组大小和本组起始位置计算第i+1组在目标数组中的起始位置。
4、设置最后一个归并组的边界为N05、对所有归并组进行并行P路归并排序。
说明:A.P和多核处理器的数目相同。
比如是双核的,那么P =2;B.Remain_data是每个线程处理的数据集中还没有被X1, X2, X3……划分过的数据集的总数目。
比如,根据X1 每个线程划分出来的数据集为x,y,z……,那么Remain_data=n – x –y –z…..3.2 并行算法在Windows下的一个例子#include <stdlib.h>#include <stdio.h>#include <time.h>#include <search.h>#include<windows.h>#include<process.h>#ifndef _BASIC_SORT_H#define _BASIC_SORT_H#ifndef _SORT_P#define _SORT_Pvoid* sort(void* parameter);void generate_data(int *a,int n);void sort_s(int *a, int n);void view_data(int *a, int n);int check_data_sort(int *a,int n);int compare( const void *arg1, const void *arg2 ); #define MILLION 1000000L#define P 2#define N0 4332539//#define N0 1000000#define N N0*P#define L N0/Pvoid sort_p(int**d, int * b);time_t start, finish; //定义开始结束时间struct merge{ //归并结构int begin[P]; //数组beginint count[P]; //数组countint merge_size; //归并大小int global_pos; //全局位置int merged; //归并是否完成};struct arg_merge_data{ //归并数据结构int **d; //数组的指针struct merge* mp; //归并结构int *b; //整数bint k;//////////////////////////////////////////////// };struct arg_merge_data *tmp2;struct forsort{int *d;int k;};struct forsort forsorta[P];int find_bound_value(int **d,struct merge *mp,int *bucket);int find_min(int **d,struct merge *mp,int *bucket);void find_bound(int **d,struct merge *mp,int bucket,int bound_value);void do_last_merge_block(struct merge *mp);void merge_data(void* arg);void view_merge(int **d,struct merge *mp,int last_merge_block);int start_time();int diff_time();#endif#endifint k; //////////////HANDLE Swait[P];HANDLE Pwait[P];HANDLE pthread[P];HANDLE qthread[P];///////extern int *d[P];///////////////////////////////////////////////////////////////////void generate_data(int *a, int n){ //产生数据int i;for(i=0;i<n;i++){a[i]=rand()%10000; //产生数组a 有n个元素}for(i=0;i<P;i++){d[i]=&(a[i*N0]); //产生数组d 对应a[i]中每个n0块的第i个元素}}////////////////////////////////////////////////////////////////////void sort_s(int *a, int n){ //快排a[i]qsort((void *)a,n,sizeof(int),compare);}////////////////////////////////////////////////////////////////////void* sort( void *parameter){ //快排参数(数组)的前N0个元素struct forsort *forsortb = (struct forsort *)parameter;// printf("\nSetEvent(Swait[%d]) ",forsortb->k);/////////////////===================== int kk=forsortb->k;qsort(/*(void*)*/forsortb->d, N0, sizeof(int), compare);SetEvent(Swait[kk]);//printf("\n%d",kk);return (void*)0;}///////////////////////////////////////////////////////////////////void view_data(int *a, int n){int i=n,j;int index=0;while(i>N0){for(j=0;j<N0;j++){printf("%d\t",a[index++]); //输出a[i]中前N0个数}printf("\n");i-=N0;}for(;i>0;i--){ //输出a[i]中N0后面的个数printf("%d\t",a[index++]);}printf("\n");}//////////////////////////////////////////////////////////////////////int check_data_sort(int *a,int n){ //找出不服和大小顺序的位置int i;for(i=0;i<n-1;i++){if(a[i]>a[i+1]) break;}return i;}//////////////////////////////////////////////////////////////////////int compare( const void *arg1, const void *arg2 ){ //返回arg1与arg2的差int a=*(int *)arg1,b=*(int *)arg2;return a-b;}////////////////////////////////////////////////////////////////////int a[N];//data for parallel sortint b[N];// the result of parallel sortint *d[P];// for parallel sortint s[N];//data for serial sortstruct merge m_list[P*P];//record of partitionint merge_block; // the number of partitionDWORD thr_id[P*P];long timedif;// for estimate the exection time//struct timeval end; // ...//struct timeval start;// ...void inite(){int i;//forsorta=(struct forsort *) calloc(P, sizeof (struct forsort));for(i=0;i<P;i++){Swait[i]=CreateEvent(NULL,FALSE,FALSE,NULL);Pwait[i]=CreateEvent(NULL,FALSE,FALSE,NULL);/* for(int j=0;j<P;j++){forsorta[i].d[j]=d[j];// printf("forsorta[%d].d[%d]=%d\n",i,j,forsorta[i].d[j]);}*/}}void main() //在PDF里调用/////////////////////////////////////////////////////////////////////////////////四、实验结果1、测试数据集合:由随机数函数产生的数据集合总共有个数2、实验结果是:3、本例中加速比(串行时间/并行时间):S=。
