巧数三角形的个数
巧数图形

巧数图形巧数图形数图形包括:数线段、数角、数长方形、数正方形、数三角形等,这看似简单,其实其中学问可大了.为了能准确地数出结果,我们必须有次序、有条理地数,既不能遗漏,也不能重复.只要我们掌握了数的方法,就能数得又对又快.例1.下图中有多少条线段?(1)思路分析:每条线段均有两个端点,可以根据左端点进行分类.以A为左端点的线段为AB、AC,共有2条;以B点为左端点的线段为BC,只有1条;以C点为左端点的线段不存在.因此共有2+1=3(条).答:图中共有3条线段.(2)这题中左端点是A的线段有:AB、AC、AD、AE,共有4条;左端点是B的线段有BC、BD、BE,共有3条;左端点是C的线段有C D、CE,共有2条;左端点是D的线段有DE;左端点是E的线段不存在.所以共有4+3+2+1=10(条).答:图中共有10条线段.例2.数出下面图中共有多少条线段?思路分析:线段有一个重要特征:线段都是笔直的.所以我们在数的时候,必须将这幅图分成四个部分,每一部分分别采用以线段左端点分类数的方法,然后把四部分算得结果加起来.例题解答:第一部分从A到E共有4+3+2+1=10条线段.第二部分从G到J共有4+3+2+1=10条线段.第三部分是FG一条线段.第四部分是JK一条线段.10+10+1+1=22(条)答:这幅图共有22条线段.方法指导:数线段可以根据左端点将线段分类,数出每一类有多少条线段,然后再相加得出线段的总的条数.例3.一条线段上共有10个点,以这10个点为端点的不同线段共有多少条?思路分析:将这条线段上的10个点从左到右依次标为、、…、、以为左端点的线段为、、、、、、、、共有9条;为左端点的线段为、、、…、,共有8条;…;以为左端点的线段为,只有1条;以为左端点的线段不存在.因此,共有线段:9+8+…+3+2+1=(9+1)×9÷2=45(条)答:一共有45条线段.方法指导:一般地,如果线段上有几个点(其中n是大于或等于2的自然数),那么以这n个点为端点的线段共有:(n-1)+(n-2)+…+3+2+1=n×(n-1)÷2例4.下面图形中有几个角?思路分析:数角的个数为了不遗漏、不重复,也需要按一定的顺序去数,可以采用与数线段相同的方法.以OA为一边的角有:∠AOB、∠AOC、∠AOD,共3个;以OB为一边的角有:∠BOC、∠BOD,共2个.以OC为一边的角有:∠COD,只有1个.3+2+1=6(个)答:图中共有6个角.例5.数出下面图中共有多少个三角形?思路分析:数三角形个数的方法与数线段的方法差不多.以AB为边的三角形有:△ABD、△ABE、△ABC,共有3个.以AD为边的三角形有:△ADE、△ADC,共有2个.以AE为边的三角形有:△AEC,只有1个.所以,图中一共有三角形:3+2+1=6(个).我们还可以发现,可以抓住底边BC来考虑,底边BC中所包含的每一条线段都恰好对应一个三角形.底边左端点是B的三角形共有△BDA、△BEA、△BCA三个.底边左端点是D的三角形共有△DEA、△DCA两个.底边左端点是E的三角形只有△ECA一个.所以一共有三角形:3+2+1=6(个).方法指导:数角的个数和三角形个数这些基本图形时,所采用的方法与数线段的方法相同.即角的个数=射线数×(射线数-1)÷2.即三角形个数就是底边上的线段数.例6.数一数图中共有多少个三角形?思路分析:我们可以将这幅图分成三个部分来数,即下面三幅图.在△ABC中,一共有5+4+3+2+1=15(个)三角形,在△ABD中,一共有5+4+3+2+1=15(个)三角形;在△BDC中,一共有5个三角形.15+15+5=35(个)答:图中共有35个三角形.例7.图中共有多少个不同的三角形?思路分析:将本题分成(1)、(2)两部分来数:第(1)部分中共有三角形:3+2+1=6(个);第(2)部分中共有3+2+1=6(个)三角形.所以,共有三角形6+6=12(个).例8.数出下图中共有多少个三角形?思路分析:这题我们可以采用按基本图形组合的方法来数.把图中最小的一个三角形看作基本图形.由一个基本三角形构成的三角形共有8个;由两个基本三角形构成的三角形共有4个;由四个基本三角形构成的三角形共有4个.因此:8+4+4=16(个),所以,图中共有16个三角形.例9.数出下面图形中共有多少个三角形?思路分析:这题采用把其中最小的三角形作为一个基本图形,然后分类相加的方法.由一个基本三角形构成的三角形共有9个;由四个基本三角形构成的三角形共有3个;由九个基本三角形构成的三角形只有1个.因此9+3+1=13(个),所以,图形中共有13个三角形.例10.下面两幅图中各有多少个长方形?思路分析:(1)中长方形都是竖向的,可以利用对应的方法来数.因为每个长方形都和底边上的一条线段对应,因此用数长边上的线段条数来数长方形的个数.所以,图中长方形共有4+3+2+1=10(个).(2)我们可用按基本图形组合的方法来数.由一个基本长方形构成的长方形共有6个;由两个基本长方形构成的长方形共有7个;由三个基本长方形构成的长方形共有2个;由四个基本长方形构成的长方形共有2个;由六个基本长方形构成的长方形有1个;所以,图中共有长方形6+7+2+2+1=18(个).本题还可以结合数线段的方法,这题中长方形的长被分成了3段,线段总数为3+2+1=6条,宽被分成了2段,线段总数为2+1=3 (条).由此可见,长方形的个数=6×3=18(个).于是,可以整理出数长方形个数的方法:长方形的个数等于原长方形长上的线段数乘以宽上的线段数.例11.数出各图中正方形的个数.思路分析:(1)中最基本的正方形有9个,即边长为1的正方形有9个(9=3×3);由4个基本正方形组成的正方形,即边长为2的正方形有4个(4=2×2);由9个基本正方形组成的正方形,即边长为3的正方形有1个(1=1×1)所以共有正方形9+4+1=14(个).(2)中边长为1的正方形有16个,即16=4×4;边长为2的正方形有9个,即9=3×3;边长为3的正方形有4个,即4=2×2;边长为4的正方形有1个,即1=1×1.所以共有正方形有16+9+4+1=30(个).因此,如果一个正方形的各边被分成几个等份,那么正方形的个数便是1×1+2×2+3×3+…+n×n.方法指导:正确数出图形的个数,首先要弄清图形中包含的基本图形是什么,有多少个.然后再从各图形中所包含基本图形的个数多少出发,依次数出它们的个数,并求出它们的和是多少.有些图形被分成了几个部分,可以先从各部分的基本图形出发,数出所含图形的个数,再求各部分的总和.例12.图中共有多少个正方形?思路分析:将正方形分类,将每一类的总数相加,就可得到所有正方形的个数.由两块小三角形构成的正方形有4个;由四块小三角形构成的正方形有4个;由八块小三角形构成的正方形有1个;由十六块小三角形构成的正方形有1个.由一、三、五、七、六、九、十、十一、十二、十三、十四、十五块小三角形不能构成正方形.所以,图中共有4+4+1+1=10(个)正方形.例13.数出图中共有多少个正方形?思路分析:根据正方形边长的大小,我们将它们分成四类:第1类:边长为1的正方形有24个;第2类:边长为2的正方形有13个;第3类:边长为3的正方形有4个;第4类:边长为4的正方形有1个.所以图中共有24+13+4+1=42(个)正方形.这题如果把四条边长多出的8个小正方形去掉,很容易得出共有1×1+2×2+3×3+4×4=30(个)正方形,添上了去掉的小正方形后,这8个小正方形还能再和其他图形组成4个新的正方形.所以,图中共有30+8+4=42(个)正方形.例14.下图中共有多少个长方形?思路分析:我们可以先将大长方形中的5小块编上号:这5块都是符合要求的长方形.然后数由两小块拼成的长方形,共有4个,即①+②,②+③,③+④,④+⑤;再数由三小块拼成的长方形,共有2个,即①+③+④,③+④+⑤;没有由四小块拼成的长方形;最后数由5小块拼成的长方形只有最大的一个.所以,图中共有5+4+2+1=12(个)长方形.例15.数出下图中共有多少个三角形?思路分析:首先将大三角形中六小块分别编上号.通过观察,我们可以发现这6小块中,④和⑤不是三角形,因此,由一块形成的三角形有4个;由两块拼成的三角形有5个,即分别是①+②,①+③,③+④,②+④,⑤+⑥;由三块拼成的三角形有两个,分别为①+③+⑤,②+④+⑥;由四块拼成的三角形有1个,即是①+②+③+④;没有由五块拼成的三角形;由六块拼成的三角形有1个,即最大的三角形.所以,图中三角形一共有4+5+2+1+1=13(个).方法指导:数长方形、正方形、三角形以及一些不规则的图形都可以采用编号数图形的方法,就是将原来图中的每一小块都编上号,先看每一小块是否符合要求的图形,接着数由两个小块相拼成的图形中有几个是符合要求的图形,再依次数由三小块、四小块……拼成的图形中各有几个是符合要求的图形,最后将每一步数得的结果加起来.。
第1讲:巧数角和三角形(讲义)

练习1 下图中有多少个角?
o
用算式表达出来!
5+4+3+2+1=15(个)
例2:数一数,有多少个三角形
A
数三角形和数角 方法是否一样?
BE D 先确定基本三角形!
C
用算式表达!
基本三角形有( 3)个
3+2+1=6(个)
2个基本三角形组成的有( 2)个
3个基本三角形组成的有(1 )个
一共有( 6)个三角形
练习2:一共有几个三角形?
B
D
A 用算式表达出来!
2+1=3(个) C
例3:一共有几个三角形?
A
D
E
用算式表达出来!
B
C
3+2+1= 6(个) 6 +6 = 12(个)
3+2+1= 6(个)
答:一共有12个三角形。
第一讲:数角和三角形
琦锐少儿:窦老师
认识角
什么是角?
边
顶点
边
角有一个顶点, 两条边。
课前热身
请你找出下图的角。
(1) (4)
(2)
(3)
(5)
例1.1
数一数,下图有多少个角?
O
什么是基本角?
一共包含几个角?
基本角有( 2 )个
用算式表达!
包含两个基本角有(1)个 2+1=3(个)
例1.2
数一数,下图中有多少个角?
三角形总数合计: 10+10+4=24(个)
谢谢, 下次再见!
小总结
多层三角形:
先分层,再数基本角, 倒加到一,再相加。
(完整版)一年级下册巧数形状

(完整版)一年级下册巧数形状一年级下册巧数形状
引言
本文档介绍了一年级下册的巧数形状内容,旨在帮助学生更好地理解和应用该知识。
1. 巧数
巧数是指除以2有余数的自然数。
在研究巧数形状之前,学生需要掌握巧数的概念和特点。
巧数包括:3、5、7、9等。
2. 巧数形状
巧数形状是指可以由巧数个单位平方组成的图形。
以下是一些常见的巧数形状:
2.1 三角形
三角形是由3个单位平方组成的形状,其中一个单位平方作为底部,其他两个单位平方作为两个侧边。
学生可以根据巧数的概念和特点来找出三角形的巧数个单位平方。
2.2 五边形
五边形是由5个单位平方组成的形状,其中一个单位平方作为底部,其他四个单位平方组成四个侧边。
学生可以根据巧数的概念和特点来找出五边形的巧数个单位平方。
2.3 七边形
七边形是由7个单位平方组成的形状,其中一个单位平方作为底部,其他六个单位平方组成六个侧边。
学生可以根据巧数的概念和特点来找出七边形的巧数个单位平方。
2.4 等等
除了三角形、五边形和七边形,还存在其他的巧数形状,学生可以自行探索和发现。
结论
通过本文档的介绍,学生可以了解巧数形状的概念和特点,并能够找出巧数个单位平方构成的形状。
希望本文档能够帮助学生更好地学习和理解一年级下册的巧数形状知识。
三年级奥数巧数图形

第2讲 巧数图形知识要点同学们,我们经常会遇到数图形的问题,对于较复杂的图形,经常会出现数重复或数漏掉的错误。
怎样才能不重复也不遗漏地数出图形的个数呢?这节课,我们将一起来寻找好的方法。
要正确数出图形的个数,关键是要从基本图形入手。
首先要弄清图形中包含的基本图形是什么,有多少个,然后再数出由基本图形组成的新的图形,并求出它们的和。
精典例题例1:数出下图中有多少条线段?模仿练习数一数,每种图形有多少个?有( )条线段 有( )个三角形有( )个角 有( )个长方形 有( )个正方形例2:数出图中共有多少个三角形?从短的线段入手,再两条两条拼接起来数,你发现规律了吗?EABCDODC B A FEDC B A模仿练习数一数,每幅图里有多少个三角形? (1) (2)有( )个三角形有( )个三角形例3:下面的图形中有多少个三角形?(第九届中国青少年数学论坛趣味数学解题技能展示大赛试题)模仿练习数一数,图中共有几个正方形?(2010武汉明心数学资优生水平测试题)精典例题例4:数出下图中有多少个长方形?多少个正方形?还能用刚才的方法来数吗?三角形很多,可以尝试按三角形的方向和大小尝试分类数。
KG I H G FEDC B A模仿练习1.数一数,图中有多少个长方形?2.数一数图中有多少个正方形?家庭作业1.数一数每幅图里面图形的个数(能计算的写出算式)。
(1) (2)前面学习的数长方形的方法还有用吗?怎么能用上呢?DCBA D CBA有( )条线段 有( )个角2.右图中有多少个三角形?3.图中有多少个长方形?(把你的想法分享给你的爸爸妈妈听,你能教会他们吗?分享后让爸爸妈妈给你打星,最多5颗星)4.数一数,右图中有多少个正方形?5.(20XX 年“陈省身杯”国际青少年数学邀请赛试题)。
巧数图形的个数

第六讲角(巧数图形的个数)例题精讲
例1. 数一数右图中有多少条线段。
例2. 数一数右图中有几个角。
O 例3.数一数右图中共有多少个三角形。
例4. 数一数右图中有多少个三角形。
同步练习
2. 下图中,一共有()个角。
3. 下图中,大大小小的长方形一共有()个。
4. 数一数下图共有几条线段。
5. 下图中有()个三角形。
()条()条()条
()条
()条
b c
6. 下图中有多少个不同的正方形?
7. 在下面点子图上,以这些点为顶点的正方形可画几个?
···
···
···
8. 再添一条线段,使下图中三角形的个数为12,想一想,应该怎样添呢?
9. 数一数包含涂色的正方形有多少个?
10. 数一数图中三角形的个数。
拓展提高
1. 在一线段上任取21个点(包括两端点),则一共有( )条线段。
2. 下图一共有( )条线段。
3. 数一数,下列图中一共有( )个角。
4. 一条直线上共有50个点,可以数出( )条线段。
5. 从一点引出10条射线,可以数出(
)个小于180º的角。
6. 平面上有10个点,没有三点在一条直线上的情况。
这些点可以连成( )条线段。
7. 下图中有几个三角形?
8. 数一数图中长方形的个数。
利用三角数列,巧数 三角形

利用三角数列,巧数三角形作者:匡家应来源:《学校教育研究》2017年第06期数图形是小学生数学学习的基本技能,也是学生发展逻辑思维、空间想象能力的重要途径,在人们的生产生活、建筑设计中也有着广泛应用。
然而,数准图形又是数学教学中的难点,如下图所示,无论是学生还是老师,都很难在短时间内数出三角形的数量。
本人通过多年的教学实践,经过反复论证,借助三角数列轻松地解决了这一难题:我们从“金字塔”的塔尖往下数:第一层:1个三角形(①级);第二层:左边的3表示了3个①级小三角形,右边的1表示1个较大(由4个小三角形组成)的三角形(②级),共增加了4个三角形;第三层:左边的5表示增加了5个①级小三角形,中间的2表示增加了2个②级的三角形,右边的1表示了1个(由9个小三角形组成)的三角形(③级),共增加了8个三角形;第四层:左边的7表示增加了7个①级小三角形,中间的4表示增加了4个②级的三角形,2表示增加了2个③级的三角形,右边的1表示(由16个小三角形组成)的三角形(④级),共增加14了个三角形;第五层:左边的9表示增加了9个①级小三角形,中间的6表示增加了6个②级的三角形,3表示增加了3个③级的三角形,2表示增加了2个(④级的三角形,右边的1表示(由25个小三角形组成)的三角形(⑤级),共增加21了个三角形;第六层:左边的11表示增加了11个①级小三角形,中间的8表示增加了8个②级的三角形,5表示增加了5个③级的三角形,3表示增加了3个④级的三角形,2表示增加了2个⑤级的三角形,右边的1表示(由36个小三角形组成)的三角形(⑥级),共增加30了个三角形;第七层:左边的13表示增加了13个①级小三角形,中间的10表示增加了10个②级的三角形,7表示增加了7个③级的三角形,4表示增加了4个④级的三角形,3表示增加了3个⑤级的三角形,2表示增加了2个⑥级的三角形,右边的1表示(由49个小三角形组成)的三角形(⑦级),共增加40了个三角形;第八层:左边的15表示增加了15个①级小三角形,中间的12表示增加了12个②级的三角形,9表示增加了9个③级的三角形,6表示增加了6个④级的三角形,4表示增加了4个⑤级的三角形,3表示增加了3个⑥级的三角形,2表示增加了2个⑦级的三角形,右边的1表示(由64个小三角形组成)的三角形(⑧级),共增加52了个三角形;第九层:左边的17表示增加了17个①级小三角形,中间的14表示增加了14个②级的三角形,11表示增加了11个③级的三角形,8表示增加了8个④级的三角形,5表示增加了5个⑤级的三角形,4表示增加了4个⑥级的三角形, 3表示增加了3个⑦级的三角形, 2表示增加了2个⑧级的三角形,右边的1表示(由81个小三角形组成)的三角形(⑨级),共增加65 了个三角形;第十层:左边的19 表示增加了19个①级小三角形,中间的16表示增加了16个②级的三角形,13表示增加了13个③级的三角形,10表示增加了10个④级的三角形,7表示增加了7个⑤级的三角形,5表示增加了5 个⑥级的三角形,4 表示增加了4 个⑦级的三角形,3表示增加了3个⑧级的三角形,2表示增加了2个⑨级的三角形,右边的1表示(由100个小三角形组成)的三角形(⑩级),共增加80 了个三角形;往后以此类推,故此图共有:1 + 4 +8 +14 + 21 + 30 + 40 + 52 + 65 + 80 = 315(个)三角形。
第一讲----巧数图形

第一讲巧数图形小朋友们,我们数学课上学习了四边形,你还记得他们的特点吗你们是不是做过下面的这种题:图中共有()个平行四边形这属于我们奥数里边的一个专题:巧数图形,你能快速的数出来吗有没有什么巧妙的办法呢现在让我们一起看一下吧。
一、数线段例1数出右图中共有多少条线段。
方法一:找规律数线段。
共有3+2+1=6(条)。
方法二:分类数线段。
共有3+2+1=6(条)。
例2.数出右面图中共有多少条线段解析:线段有一个重要特征:线段都是笔直的.所以我们在数的时候,必须将这幅图分成四个部分,每一部分分别采用以线段左端点分类数的方法,然后把四部分算得结果加起来.第一部分从A到E共有4+3+2+1=10条线段.第二部分从G到J共有4+3+2+1=10条线段.第三部分是FG一条线段.第四部分是JK一条线段. 10+10+1+1=22(条)例3.一条线段上共有10个点,以这10个点为端点的不同线段共有多少条分析:一条线段上有10个点,那么我们先把线段画出来因此,共有线段:9+8+…+3+2+1=(9+1)×9÷2=45(条)总结:1、找规律数线段:一般地,如果线段上有几个点(其中n是大于或等于2的自然数),那么以这n个点为端点的线段共有:(n-1)+(n-2)+…+3+2+1=n×(n-1)÷2;2、分类数线段练习:下列图形中各有多少条线段(3)二、数角例4.右面图形中有几个角分析方法和数线段相同练习()个角()个角三、数三角形例5.数出下面图中共有多少个三角形方法一数三角形个数的方法与数线段的方法差不多.方法二我们可以发现,可以抓住底边BC来考虑,底边BC中所包含的每一条线段都恰好对应一个三角形.底边左端点是B的三角形共有△BDA、△BEA、△BCA三个.底边左端点是D的三角形共有△DEA、△DCA两个.底边左端点是E的三角形只有△ECA一个.所以一共有三角形:3+2+1=6(个).方法三我们把图中△ABC、△ACD、△ADE看作基本三角形:由1个基本三角形构成的三角形有△ABC、△ACD、△ADE;由2个基本三角形构成的三角形有△ABD、△ACE;由3个基本三角形构成的三角形有△ABE。
(完整版)如何巧数图形
如何巧数图形
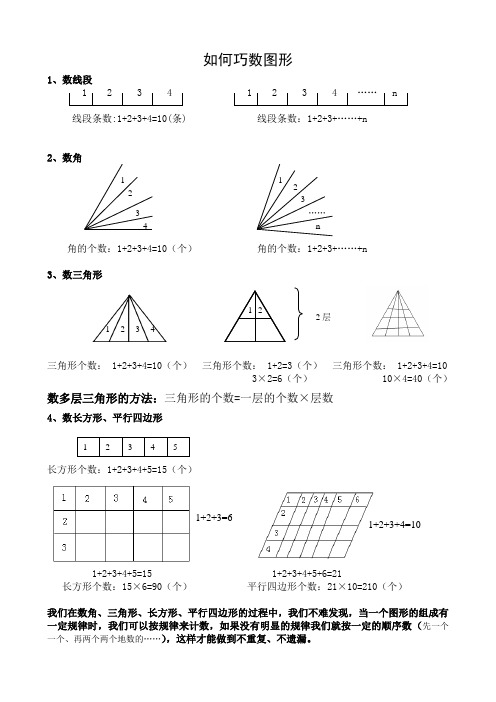
1、数线段 1 2 3 4 1 2 3 4 …… n
线段条数:1+2+3+4=10(条) 线段条数:1+2+3+……+n
2、数角
角的个数:1+2+3+4=10(个) 角的个数:1+2+3+……+n
3、数三角形
三角形个数: 1+2+3+4=10(个) 三角形个数: 1+2=3(个) 三角形个数: 1+2+3+4=10 3×2=6(个) 10×4=40(个) 数多层三角形的方法:三角形的个数=一层的个数×层数
4、数长方形、平行四边形
长方形个数:1+2+3+4+5=15(个)
1+2+3+4+5=15 1+2+3+4+5+6=21
长方形个数:15×6=90(个) 平行四边形个数:21×10=210(个)
我们在数角、三角形、长方形、平行四边形的过程中,我们不难发现,当一个图形的组成有一定规律时,我们可以按规律来计数,如果没有明显的规律我们就按一定的顺序数(先一个一个、再两个两个地数的……),这样才能做到不重复、不遗漏。
1 2 3 4 1 2 3 ……
n 1 2 3 4
1 2
2层 1 2 3 4 5 1+2+3=6 1+2+3+4=10
5、数不规则图形。
(1+2+3+4+5+6)×(1+2+3)+(1+2+3)×(1+2+3+4)-(1+2+3)×(1+2+3)=150。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
化静为动巧妙统计三角形的个数
汪金明
一、题目
如图(图Ⅰ),数出下面图形中三角形的个数。
A
F G
B C
H K
M
D E
图Ⅰ
这是2013-2014学年度初中一年级下学期数学教材上的一道题目,教学参考书上有答案——也仅仅有个答案而已。
答案是:35个。
A
F G
B C
H K
M
D E
图Ⅱ
二、困惑
就是这么一道简单的题目,可是要真正数出三角形的个数并非易事,学生或老师数的时候很容易漏掉,如果不给学生的答案,学生很难数出图中有35个三角形;如果告诉学生图中有35个三角形的话,学生常常会重复数而凑成35个。
况且,一个一个地数,繁琐、无聊、耗时、费脑力,这会使学生对学数学产生畏难厌烦情绪的,影响学生学习数学的兴趣。
我曾查找过一些资料,也上网搜索过这道题数三角形个数的方法,主要是分类来数,分类数的方法很有条理,跟盲目地数比不容易遗漏,但缺点是分类本身有一定的难度,分类和数的时候有点纷乱,常常让人眼花缭乱,仍然容易出错。
总的来说,真正地静态地数我都很不满意。
于是,我化静为动,探究动态数的方法。
三、探究
(一)把图Ⅰ简化成图Ⅱ,先数图Ⅱ里的三角形个数。
图Ⅱ中
三角形只有两类,很容易数出三角形的个数——10个。
(二)把图Ⅱ中点D、E连起来变成图Ⅲ,则图Ⅲ比图Ⅱ的三角
A
F G
B C
H K
M
D E
图Ⅲ
形的个数增加了4个,分别为△DEA,△DEH,△DEK,△DEM,图Ⅲ共有14个三角形。
(三)按顺时针方向连接图Ⅲ中的BD,得到图Ⅳ。
显然,图Ⅳ比图Ⅲ增加了5个三角形。
图Ⅳ共有19个三角形。
A
F G
B C
H K
M
D E
图Ⅳ
(四)以此类推,再依次连接AB、AC、CE,那么图Ⅳ就变回图Ⅰ。
这时,我们很容易看出:变回成图Ⅰ后,图Ⅰ中的三角形个数比图Ⅳ分别增加5个、5个、6个,共增加16个。
变回的图Ⅰ中,共有三角形35个。
其实,很容易发现规律,对图Ⅱ来说,最外面的五个点,每
相邻的两点连接起来——从总体来看,则每连一条线段就平均增加5个三角形。
所以,三角形总数为:10+5×5=35.
四、感悟
(一)一个个数或分类数方法简单,数学价值低,显得有点笨,繁琐易错,没能显示出题目本身的数学价值和教学价值,不利于学生学习兴趣培养。
(二)动态统计,把问题分成两大步来解答,第一步数里面的,第二步数外面连线增加的,过程简明扼要。
(三)数外面连线增加的三角形数,依次而行,举一反三,学生学起来轻松易懂,生动活泼有趣。
这充分展示出这道题目的数学教学价值,给学生深刻的启示。
(四)动态统计,思维活泼丰富,富有智趣,能培养学生爱动脑,启发学生勤动脑,从而更好地培养提高学生的思维能力。
(五)化静为动的思维方法值得学习和欣赏。
2019年1月22日星期二。
