人教版高中数学必修1知识点归纳总结

合集下载

高中数学人教A版必修第一册知识点总结

高中数学人教A版必修第一册知识点总结本册教材是高中数学人教版A版(2024)的必修第一册，总共包括了四个单元：集合与常用逻辑、函数与方程、数列与数学归纳法、几何与向量。

接下来将对这四个单元的知识点进行总结。

一.集合与常用逻辑1.集合与元素-集合的表示方法：列举法、描述法、条件法-集合之间的关系：相等、含于、相交、并集、交集、互补集2.集合的运算-并集、交集、差集、补集-嵌套集合的化简-运算律：交换律、结合律、分配律3.常用逻辑关系-全称量词、存在量词-逻辑运算：与、或、非-条件命题、充分条件、必要条件4.命题及命题的逻辑运算-命题的分类：命题主体、命题联结词、命题陈述、命题基础-命题的逻辑运算：否定、合取、析取、蕴含、等价二.函数与方程1.函数的概念-自变量、因变量、函数值-射影函数、指示函数2.函数的表示方法-函数的解析式-函数的图像3.函数的性质-定义域、值域、对应法则、单调性、奇偶性、周期性-奇函数、偶函数-反函数4.一次函数-一次函数的解析式及图像-平移变换、伸缩变换5.二次函数-二次函数的解析式及图像-平移变换、伸缩变换-最值、对称轴、零点及判别式三.数列与数学归纳法1.数列的概念-有限数列、无限数列、数列的一般表示2.等差数列-等差数列的概念及公式-等差数列前n项和公式-通项公式的推导3.等比数列-等比数列的概念及公比-等比数列前n项和公式-通项公式及其推导4.递推数列-递推数列的概念及表示-递推公式5.数学归纳法-数学归纳法三个步骤：证明基础、证明步骤、加强归纳前提四.几何与向量1.向量的概念-向量的定义、表示方法、相等与运算-向量的数量表示-零向量、单位向量2.向量的线性运算-加法、减法、数乘-加减法运算律、数乘运算律3.向量的坐标表示-坐标运算、线性变换4.向量的数量积-向量的点乘、模长及其性质-向量的夹角及性质5.平面向量的应用-共线向量、垂直向量、平行向量-向量在直角坐标系中的投影-多边形面积与向量运算-向量与几何问题的应用以上是《高中数学人教A版(2024)必修第一册》的知识点总结。

人教版高中数学必修一知识点总结(完整版)

第一章集合与函数概念课时一：集合有关概念1.集合的含义：集合为一些确定的、不同的东西的全体，人们能意识到这些东西，并且能判断一个给定的东西是否属于这个整体。

2.一般的研究对象统称为元素，一些元素组成的总体叫集合，简称为集。

3.集合的中元素的三个特性：（1）元素的确定性：集合确定，则一元素是否属于这个集合是确定的：属于或不属于。

例：世界上最高的山、中国古代四大美女、教室里面所有的人……（2）元素的互异性：一个给定集合中的元素是唯一的，不可重复的。

例：由HAPPY的字母组成的集合{H,A,P,Y}（3）元素的无序性:集合中元素的位置是可以改变的，并且改变位置不影响集合例：{a,b,c}和{a,c,b}是表示同一个集合3.集合的表示：{…} 如：{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}（1）用大写字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}（2）集合的表示方法：列举法与描述法。

1）列举法：将集合中的元素一一列举出来 {a,b,c……}2）描述法：将集合中元素的公共属性描述出来，写在大括号内表示集合。

{x∈R| x-3>2} ,{x| x-3>2}①语言描述法：例：{不是直角三角形的三角形}②Venn图:画出一条封闭的曲线，曲线里面表示集合。

4、集合的分类：（1）有限集：含有有限个元素的集合（2）无限集：含有无限个元素的集合（3）空集：不含任何元素的集合例：{x|x2=－5｝5、元素与集合的关系：（1）元素在集合里，则元素属于集合，即：a∈A（2）元素不在集合里，则元素不属于集合，即：a A注意：常用数集及其记法：非负整数集（即自然数集）记作：N正整数集 N*或 N+整数集Z有理数集Q实数集R课时二、集合间的基本关系1.“包含”关系—子集（1）定义：如果集合A 的任何一个元素都是集合B 的元素，我们说这两个集合有包含关系，称集合A 是集合B 的子集。

记作：B A ⊆（或B ⊇Ａ）注意：B A ⊆有两种可能（1）A 是B 的一部分，；（2）A 与B 是同一集合。

高中数学人教版必修一知识点总结

高中数学人教版必修一知识点总结Chapter 1: Concepts of Sets and nsXXX Sets1.Meaning of Sets: A set is the n of XXX to this whole。

The objects under study are called elements。

and the n of some elements is called a set。

abbreviated as a set.2.Three characteristics of the XXX:1) n of elements: If a set is determined。

then it is certain whether an element belongs to this set or not.2) Distinctiveness of elements: XXX elements in a given set are unique and cannot be repeated.3) Unorderedness of elements: The n of elements in a set can be changed。

and changing their n does not affect the set.3.n of Sets: {。

}1) XXX: A = {members of our school's basketball team}。

B = {1,2,3,4,5}.2) Methods of representing sets: listing method and n method.a。

Listing method: List all the elements in the set one by one {a。

b。

c。

}.b。

n method:① Interval method: Describe the common properties of the elements in the set and write them in curly braces to represent the set.x∈R|x-3>2}。

必修1高一数学人教版最全知识点(必须珍藏)

高中数学必修1知识点总结目录高中数学必修1知识点总结............................. 错误!未定义书签。

第一章集合与函数概念............................... 错误!未定义书签。

〖〗集合 ............................................ 错误!未定义书签。

【】集合的含义与表示................................. 错误!未定义书签。

【】集合间的基本关系................................. 错误!未定义书签。

【】集合的基本运算................................... 错误!未定义书签。

〖〗函数及其表示 .................................... 错误!未定义书签。

【】函数的概念 ...................................... 错误!未定义书签。

【】函数的表示法 .................................... 错误!未定义书签。

〖〗函数的基本性质................................... 错误!未定义书签。

【】单调性与最大（小）值............................. 错误!未定义书签。

【】奇偶性 .......................................... 错误!未定义书签。

【】函数周期性和对称性............................... 错误!未定义书签。

〖补充知识〗函数的图象............................... 错误!未定义书签。

第二章基本初等函数(Ⅰ) ............................. 错误!未定义书签。

人教版高中数学必修一第一章知识点

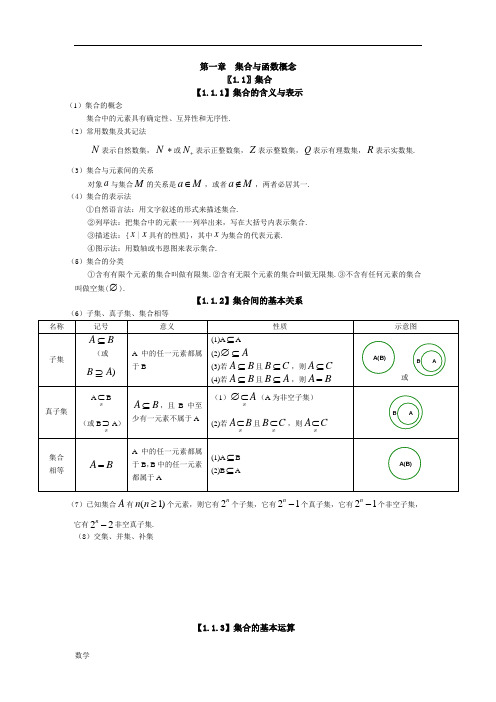
第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集，N *或N +表示正整数集，Z 表示整数集，Q 表示有理数集，R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈，或者a M ∉，两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合. ③描述法：{x |x 具有的性质}，其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（6）子集、真子集、集合相等（7）已知集合A 有(1)n n ≥个元素，则它有2n 个子集，它有21n -个真子集，它有21n -个非空子集，它有22n-非空真子集.（8）交集、并集、补集【1.1.3】集合的基本运算名称记号意义性质示意图交集A B{|,x x A∈且}x B∈（1）A A A=（2）A∅=∅（3）A B A⊆A B B⊆BA并集A B{|,x x A∈或}x B∈（1）A A A=（2）A A∅=（3）A B A⊇A B B⊇BA补集U A{|,}x x U x A∈∉且1()UA A=∅2()UA A U=【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法不等式解集||(0)x a a<>{|}x a x a-<<||(0)x a a>>|x x a<-或}x a>||,||(0)ax b c ax b c c+<+>>把ax b+看成一个整体，化成||x a<，||(0)x a a>>型不等式来求解（2）一元二次不等式的解法判别式24b ac∆=-∆>0∆=0∆<二次函数2(0)y ax bx c a=++>的图象O 一元二次方程20(0)ax bx c a++=>的根21,242b b acxa-±-=（其中12)x x<122bx xa==-无实根20(0)ax bx c a++>>的解集1{|x x x<或2}x x>{|x}2bxa≠-R()()()U U UA B A B=()()()U U UA B A B=〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f，对于集合A 中任何一个数x ，在集合B中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a xb <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <．（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1． ⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零． ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值． ③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象．yxo〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法函数的性质定义图象判定方法函数的单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x ．1．< x ．．2．时，都有f(x ．．．1．)<f(x ．．．．．2．)．，那么就说f(x)在这个区间上是增函数．．．． x 1x 2y=f(X)xy f(x )1f(x )2o（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象上升为增）（4）利用复合函数如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2，当x ．1．< x ．．2．时，都有f(x ．．．1．)>f(x ．．．．．2．)．，那么就说f(x)在这个区间上是减函数．．．． y=f(X)yxox x 2f(x )f(x )211（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象下降为减）（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数． ③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()ug x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减．（2）打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,]a -∞-、,)a +∞上为增函数，分别在[,0)a 、]a 上为减函数．（3）最大（小）值定义 ①一般地，设函数()y f x =的定义域为I，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M≤；（2）存在0x I ∈，使得0()f x M=．那么，我们称M 是函数()f x 的最大值，记作max ()f x M=．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的性质定义图象判定方法函数的奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x)．．．．,那么函数f(x)叫做奇函．．数．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于原点对称）如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于y 轴对称） ②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域； ②化解函数解析式； ③讨论函数的性质（奇偶性、单调性）； ④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象． ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象，并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．。

人教版高中数学必修1-第一章知识点知识点归纳[最新版]

知识点总结归纳【最新版】适用于老师、学生、家长一、集合有关概念1、集合的含义：某些指定的对象集在一起就成为一个集合，其中每一个对象叫元素。

2、集合中元素的三个特性：1.元素的确定性；2.元素的互异性；3.元素的无序性3、集合的表示：{ …} 如{我校的篮球队员}，{太平洋,大西洋,印度洋,北冰洋}1. 用拉丁字母表示集合：A={我校的篮球队员},B={1,2,3,4,5}2．集合的表示方法：列举法与描述法。

非负整数集（即自然数集）记作：N正整数集N*或N+ 整数集Z 有理数集Q 实数集R3.关于“属于”的概念集合的元素通常用小写的拉丁字母表示，如：a是集合A的元素，就说a属于集合A 记作a∈A ，相反，a不属于集合A 记作a∉A•列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

•描述法：将集合中的元素的公共属性描述出来，写在大括号内表示集合的方法。

用确定的条件表示某些对象是否属于这个集合的方法。

①语言描述法：例：{不是直角三角形的三角形}②数学式子描述法：例：不等式x-3>2的解集是{x∈R| x-3>2}或{x| x-3>2}•4、集合的分类：（1）有限集含有有限个元素的集合（2）无限集含有无限个元素的集合（3）空集不含任何元素的集合例：二、集合间的基本关系• 1.“包含”关系—子集注意：有两种可能（1）A是B的一部分；（2）A与B是同一集合。

反之: 集合A不包含于集合B,或集合B不包含集合A,记作A ⊆B或B ⊇A•2．“相等”关系(5≥5，且5≤5，则5=5)实例：设A= B={-1,1} “元素相同”结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，即：A=B①子集：任何一个集合是它本身的子集。

A⊆A②真子集:如果A⊆B,且B⊄A那就说集合A是集合B的真子集，记作A⊈B(或B⊉A)③如果A⊆B, B⊆C ,那么A⊆C④如果A⊆B 同时B⊆A 那么A=B3. 不含任何元素的集合叫做空集，记为Φ规定: 空集是任何集合的子集，空集是任何非空集合的真子集。

高中数学(新人教版)必修一知识点归纳

高中数学(新人教版)必修一知识点归纳
本文将归纳高中数学(新人教版)必修一的主要知识点。

以下是
各个主题的简要概述：
1. 数与式
- 数的分类：自然数、整数、有理数、实数等。

- 代数式：基本概念、多项式、公式等。

- 幂与乘方：指数、乘方、幂等运算。

- 整式的加减法：同类项、整式的加减法规则。

- 分式：基本概念、分式的性质与化简等。

2. 一元一次方程与不等式
- 一元一次方程：基本概念、解方程的方法、应用问题等。

- 一元一次不等式：基本概念、解不等式的方法、应用问题等。

3. 函数及其图像
- 函数与自变量、函数与因变量的关系。

- 函数的表示与性质：映射、函数图像、奇偶性等。

- 一次函数：定义、性质、图像、方程等。

- 反函数与复合函数：定义、性质、求反函数、求复合函数等。

4. 等差数列
- 等差数列的定义与性质。

- 等差数列的前n项和与通项公式。

- 应用问题：等差数列应用于数学与生活中的实际问题。

5. 平面向量
- 向量的基本概念与表示法。

- 向量的运算：加法、数乘等。

- 向量共线与共面的判定。

- 向量的数量积与模的概念与性质。

6. 不等式与线性规划
- 不等式的基本性质与解法。

- 一元一次不等式组：基本概念、解法、应用问题等。

- 线性规划的基本概念与常见问题。

以上是高中数学(新人教版)必修一的主要知识点的简要归纳。

详细内容可以参考相关教材或课堂讲义。

希望这份归纳对你有帮助！。

高中数学人教A版必修第一册知识点总结

高中数学新教材必修第一册知识点总结第一章集合与常用逻辑用语1.1集合的概念1.集合的描述：一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合，简称为集.2.集合的三个特性：（1）描述性：“集合”是一个原始的不加定义的概念，它同平面几何中的“点”、“线”、“面”等概念一样，都只是描述性地说明.（2）整体性：集合是一个整体，暗含“所有”、“全部”、“全体”的含义，因此一些对象一旦组成了集合，这个集合就是这些对象的总体.（3）广泛性：组成集合的对象可以是数、点、图形、多项式、方程，也可以是人或物等. 3.集合中元素的三个特性：（1）确定性：对于给定的集合，它的元素必须是确定的.即按照明确的判断标准（不能是模棱两可的）判断给定的元素，或者在这个集合里，或者不在这个集合里，二者必居其一. （2）互异性：一个给定的集合中的元素是互不相同的.也就是说集合中的元素是不能重复出现的.（3）无序性：集合中的元素排列无先后顺序，任意调换集合中的元素位置，集合不变. 4.集合的符号表示通常用大写的字母A，B，C，…表示集合，用小写的字母a，b，c表示集合中的元素.5.集合的相等当两个集合的元素是一样时，就说这两个集合相等.集合A与集合B相等记作A B=.6.元素与集合之间的关系（1）属于：如果a是集合A中的元素，就说a属于集合A，记作a A∈，读作a属于A. （2）不属于:如果a不是集合A中的元素，就说a不属于集合A，记作a A∉，读作a不属于A.7.集合的分类（1）有限集：含有有限个元素的集合叫做有限集.如方程21x=的实数根组成的集合.（2）无限集：含有无限个元素的集合叫做无限集.如不等式10x->的解组成的集合.8.常用数集及其记法.（1）正整数集：全体正整数组成的集合叫做正整数集，记作*N或N+（2）自然数集：全体非负整数组成的集合叫做自然数集，记作N.（3）整数集：全体整数组成的集合叫做整数集，记作Z.（4）有理数集：全体有理数组成的集合叫做有理数集，记作Q.（5）实数集：全体实数组成的集合叫做实数集，记作R.9.集合表示的方法（1）自然语言：用文字叙述的形式描述集合的方法.如所有正方形组成的集合，所有实数组成的集合.例如，三角形的集合.（2）列举法：把集合的元素一一列举出来表示集合的方法叫做列举法.其格式是把集合的元素一一列举出来并用逗号隔开，然后用花括号括起来.例如，我们可以吧“地球上的四大洋”组成的集合表示为{太平洋，大西洋，印度洋，北冰洋}，把“方程(1)(2)0x x -+=的所有实数根”组成的集合表示为{1,2}-.（3）描述法：通过描述集合所含元素的共同特征表示集合的方法叫做描述法.一般格式为{()}x p x ，其中x 是集合中的元素代表，()p x 则表示集合中的元素所具有的共同特征.例如，不等式73x -<的解集可以表示为{73}{10}x R x x R x ∈-<=∈<.1.2集合间的基本关系1. 子集一般地，对于两个集合A ,B ,如果集合A 中任意一个元素都是集合B 中的元素，我们就说这两个集合有包含关系，称集合A 为集合B 的子集，记为A B ⊆或（B A ⊇）读作集合A 包含于集合B （或集合B 包含集合A ）. 集合A 是集合B 的子集可用V e n n 图表示如下：或关于子集有下面的两个性质：（1）自反性：A A ⊆；（2）传递性：如果A B ⊆，且B C ⊆，那么A C ⊆. 2.真子集如果集合A B ⊆，但存在元素x B ∈，且x A ∉，我们称集合A是集合B 的真子集，记为A B ⊂≠（或B A ⊃≠），读作集合A 真包含于集合B （或集合B 真包含集合A ）. 集合A 是集合B 的真子集可用V e n n 图表示如右.3.集合的相等如果集合A B ⊆，且B A ⊆，此时集合A 与集合B 的元素是一样的，我们就称集合A 与集合B 相等，记为 A B =.集合A 与集合B 相等可用V e n n 图表示如右. 4.空集我们把不含任何元素的集合叫做空集，记为∅.我们规定空集是任何一个集合的子集，空集是任何一个非空集合的真子集，即（1）A ∅⊆（A 是任意一个集合）；（2）A ⊂∅≠（A ≠∅）.1.3集合的运算1.并集自然语言：一般地，由所有属于集合A 或属于集合B 的元素组成的集合，称为集合A 与B 的并集，记作A B ⋃（读作“A 并B ”）.符号语言： {,}A B x x A x B ⋃=∈∈或. 图形语言：(5) A =BA (4)B B（3）A (2)A 与B 没有有公共元素(1)A 与B 有公共元素，相互不包含理解：x A ∈或x B ∈包括三种情况：x A ∈且x B ∉；x B ∈且x A ∉；x A ∈且x B ∈. 并集的性质：（1）A B B A ⋃=⋃；（2）A A A ⋃=；（3）A A ⋃∅=；（4）()()A B C A B C ⋃⋃=⋃⋃；（5）A A B ⊆⋃，B A B ⊆⋃；（6）A B B A B ⋃=⇔⊆. 2.交集自然语言：一般地，由属于集合A 且属于集合B 的所有元素组成的集合，称为A 与B 的交集，记作A B ⋂（读作“A 交B ”）. 符号语言： {,}A B x x A x B ⋂=∈∈且. 图形语言：BA(5)A=B,A B=A=B(4)B A,A B=B(3)A B,A B=AA B（2）A 与B 没有公共元素,A B=（1）A 与B 有公共元素，且互不包含理解：当A 与B 没有公共元素时，不能说A 与B 没有交集，只能说A 与B 的交集是∅. 交集的性质：（1）A B B A ⋂=⋂；（2）A A A ⋂=；（3）A ⋂∅=∅；（4）()()A B C A B C ⋂⋂=⋂⋂；（5）A B A ⋂⊆，A B B ⋂⊆；（6）A B A A B ⋂=⇔⊆.3.补集（1）全集的概念：一般地，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集，通常记作U . （2）补集的概念自然语言：对于一个集合A ，由属于全集U 且不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，记为UA .符号语言： {,}UA x x U x A =∈∉且图形语言：补集的性质（1）()UA A ⋂=∅；（2）()UA A U ⋃=；（3）()()()UU UA B A B ⋃=⋂；（4）()()()U U UA B A B ⋂=⋃.1.4充分条件与必要条件1.充分条件与必要条件一般地，“若p ，则q ”为真命题，是指由p 通过推理可以得出q .这时，我们就说，由p 可推出q ，记作p q ⇒，并且说p 是q 的充分条件，q 是p 的必要条件. 在生活中， q 是p 成立的必要条件也可以说成是: q ⌝⇒p ⌝（q ⌝表示q 不成立），其实，这与p q ⇒是等价的.但是，在数学中，我们宁愿采用第一种说法. 如果“若p ，则q ”为假命题，那么由p 推不出q ，记作/p q ⇒.此时，我们就说p 不是q 的充分条件，q 不是p 的必要条件.2.充要条件如果“若p ，则q ”和它的逆命题“若q 则p ”均是真命题，即既有p q ⇒，又有q p ⇒就记作p q ⇔.此时，我们就说p 是q 的充分必要条件，简称为充要条件.显然，如果p 是q 的充要条件，那么q 也是p 的充要条件.概括地说，如果p q ⇔，那么p 与q 互为充要条件. “p 是q 的充要条件”,也说成“p 等价于q ”或“q 当且仅当p ”等.1.5全称量词与存在量词1.全称量词与存在量词（1）全称量词短语“所有的”，“任意一个”在逻辑中通常叫做全称量词，并用符号“"”表示.常见的全称量词还有“一切”，“每一个”，“任给”，“所有的”等.含有全称量词的命题，叫做全称量词命题.全称量词命题“对M 中的任意一个x ，有()p x 成立”可用符号简记为x M ∀∈，()p x ，读作“对任意x 属于M ，有()p x 成立”.（2）存在量词短语“存在一个”，“至少有一个”在逻辑中通常叫做存在量词，并用符号“$”表示.常见的存在量词还有“有些”，“有一个”，“对某个”，“有的”等. 含有存在量词的命题，叫做存在量词命题.存在量词命题“存在M 中的元素x ，使()p x 成立”可用符号简记为x M∃∈，()p x ，读作“存在M 中的元素x ，使()p x 成立”. 2.全称量词命题和存在量词命题的否定（1）全称量词命题的否定全称量词命题：x M ∀∈，()p x ，它的否定：x M∃∈，()p x ⌝.全称量词命题的否定是存在量词命题. （2）存在量词命题的否定存在量词命题：x M∃∈，()p x ，它的否定：x M ∀∈，()p x ⌝.存在量词命题的否定是全称量词命题.第二章一元二次函数、方程和不等式2.1等式性质与不等式性质1.比较原理a b a b >⇔->；0a b a b =⇔-=； 0a b a b <⇔-<.2.等式的基本性质性质1 如果a b =，那么b a =；性质2 如果a b =，b c =，那么a c =；性质3 如果a b =，那么a c b c ±=±；性质4 如果a b=，那么a c b c =；性质5 如果a b =，0c ≠，那么a b c c=.3.不等式的基本性质性质1 如果a b >，那么b a <；如果b a <，那么a b >.即a b b a >⇔<性质2 如果a b >，b c >，那么a c >.即a b >，b c >a c ⇒>.性质3 如果a b >，那么a c b c +=+.由性质3可得，()()a b c a b b c b a c b +>⇒++->+-⇒>-.这表明，不等式中任何一项可以改变符号后移到不等号的另一边.性质4 如果a b >，0c >，那么a c b c >；如果a b >，0c <，那么a c b c <. 性质5 如果a b >，c d >，那么a c b d +>+. 性质6 如果0a b >>，0c d >>，那么a c b d >. 性质7 如果0a b >>，那么nna b >（n N ∈，2n ≥）.2.2 基本不等式1.重要不等式,a b R ∀∈，有222a ba b +≥，当且仅当a b =时，等号成立. 2.基本不等式如果0a >，0b >，则2a b +≤，当且仅当a b =时，等号成立.2a b +叫做正数a ，b 的算术平均数叫做正数a ，b 的几何平均数.基本不等式表明：两个正数的算术平均数不小于它们的几何平均数. 3.与基本不等式相关的不等式（1）当,a b R ∈时，有22a b a b +⎛⎫≤ ⎪⎝⎭，当且仅当a b =时，等号成立.（2）当0a >，0b >时，有211a b≤+当且仅当a b =时，等号成立. （3）当,a b R ∈时，有22222a b a b ++⎛⎫≤ ⎪⎝⎭，当且仅当a b =时，等号成立.4.利用基本不等式求最值已知0x >，0y >，那么（1）如果积x y 等于定值P ，那么当x y =时，和x y +有最小值；（2）如果和x y +等于定值S ，那么当x y =时，积x y 有最大值214S .2.3 二次函数与一元二次方程、不等式1.一元二次不等式只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式.第三章函数的概念与性质3.1 函数的概念及其表示1.函数的概念设A ,B 是非空的实数集，如果对于集合A 中的任意一个数x ，按照某种确定的对应关系f ，在集合B 中都有唯一确定的的数y 和它对应，那么就称:f A B →为从集合A 到集合B 的一个函数，记作()y f x =,x A ∈.其中，x 叫做自变量，x 的取值范围A 叫做函数的定义域，与x 的值相对应的y 值叫做函数值，函数值的集合{|(})f x x A ∈叫做函数的值域，显然，值域是集合B 的子集. 2.区间：设a ,b 是两个实数，而且a b <，我们规定：（1）满足不等式a x b ≤≤的实数x 的集合叫做闭区间，表示为[,]a b ；（2）满足不等式a x b <<的实数x 的集合叫做开区间，表示为(,)a b ；（3）满足不等式a x b ≤<或a x b <≤的实数x 的集合叫做半开半闭区间，分别表示为：[,)a b , (,]a b .这里的实数a ，b 都叫做相应区间的端点.（4）实数集R 可以表示为(,)-∞+∞,“∞”读作“无穷大”，“-∞”读作“负无穷大”，“+∞” 读作“正无穷大”.满足x a ≥，x a >，x b ≤，x b <的实数x 的集合，用区间分别表示为[,)a +∞ ，(,)a +∞(,]b -∞，(,)b -∞.这些区间的几何表示如下表所示.注意：（1）“∞”是一个趋向符号，表示无限接近，却永远达不到，不是一个数. （2）以“-∞”或“+∞”为区间的一端时，这一端点必须用小括号. 3.函数的三要素（1）定义域；（2）对应关系；（3）值域.值域随定义域和对应关系的确定而确定. 4.函数的相等如果两个函数的定义域和对应关系分别相同，那么就说这两个函数是同一个函数. 5.函数的表示方法（1）解析法用数学表达式表示两个变量之间的对应关系的方法叫做解析法.解析法是表示函数的一种重要的方法，这种表示法从“数”的方面简明、全面地概括了变量之间的数量关系. （2）图象法用图象表示两个变量之间的对应关系的方法叫做图象法.图象法直观地表示了函数值随自变量值改变的变化趋势，从“形”的方面刻画了变量之间的数量关系.说明：将自变量的一个值0x 作为横坐标，相应的函数值0()f x 作为纵坐标，就得到坐标平面上的一个点00(,())x f x .当自变量取遍函数的定义域A 中的每一个值时，就得到一系列这样的点，所有这些点组成的图形就是函数()y f x =的图象.函数()y f x =的图象在x 轴上的射影构成的集合就是函数的定义域，在y 轴上的射影构成的集合就是函数的值域. 函数的图象既可以是连续的曲线，也可以是直线、折线、离散的点，等等. （3）列表法通过列表来表示两个变量之间的对应关系的方法叫做列表法.例如，初中学习过的平方表、立方表都是表示函数关系的. 6.分段函数（1）分段函数的概念有些函数在其定义域内，对于自变量x 的不同取值区间，有着不同的对应关系，这样的函数称为分段函数.如（1）,0,(),0x x f x x x x -<⎧==⎨≥⎩ ，（2）22,0,(),0x x f x x x ⎧≤⎪=⎨->⎪⎩. 说明：①分段函数是一个函数，而不是几个函数.处理分段函数问题时，要先确定自变量的取值在哪个区间，从而选取相应的对应关系.②分段函数在书写时用大括号把各段函数合并写成一个函数的形式.并且必须指明各段函数自变量的取值范围.③分段函数的定义域是自变量所有取值区间的并集，分段函数的定义域只能写成一个集合的形式，不能分开写成几个集合的形式.④分段函数的值域是各段函数在对应自变量的取值范围内值域的并集. （2）分段函数的图象分段函数有几段，它的图象就由几条曲线组成.在同一坐标系中，根据每段的定义区间和表达式依次画出图象，要注意每段图象的端点是空心点还是实心点，组合到一起就得到整个分段函数的图象.3.2 函数的基本性质函数的性质是指在函数变化过程中的不变性和规律性. 1.单调性与最大（小）值（1）增函数设函数()f x 的定义域为I ,区间D ⊆I .如果∀1x ，2x D ∈，当12x x <时，都有12()()f x f x <,那么就称函数()f x 在区间D 上单调递增.特别地，当函数()f x 在它的定义域上单调递增时，我们就称它是增函数.（2）减函数设函数()f x 的定义域为I ，区间D ⊆I.如果∀1x ，2x D ∈，当12x x <时，都有12()()f x f x >,那么就称函数()f x 在区间D 上单调递增.特别地，当函数()f x 在它的定义域上单调递减时，我们就称它是减函数. （3）单调性、单调区间、单调函数如果函数()y f x =在区间D 上单调递增或单调递减，那么就说函数()y f x =在区间D 上具有（严格的）单调性，区间D 叫做()y f x =的单调区间.如果函数在某个区间上具有单调性，那么就称此函数在这个区间上是单调函数. （4）证明函数()f x 在区间D 上单调递增或单调递减，基本步骤如下： ①设值：设12,x x D ∈，且 12x x <；②作差：12()()f x f x - ；③变形：对12()()f x f x -变形，一般是通分，分解因式，配方等.这一步是核心，要注意变形到底；④判断符号，得出函数的单调性. （5）函数的最大值与最小值①最大值：设函数()y f x =的定义域为I ，如果存在实数M 满足: （1）对于任意的x I ∈，都有()f x M ≤；（2）存在0x I ∈，使得0()f x M =. 那么我们称M 是函数()y f x =的最大值.②最小值：设函数()y f x =的定义域为I ，如果存在实数m 满足:（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =. 那么我们称m 是函数()y f x =的最小值. 2.奇偶性（1）偶函数设函数()f x 的定义域为I ，如果x I ∀∈，都有x I -∈，且()()f x f x -=，那么函数()f x 就叫做偶函数.关于偶函数有下面的结论：①偶函数的定义域一定关于原点对称.也就是说定义域关于原点对称是函数为偶函数的一个必要条件；②偶函数的图象关于y 轴对称.反之也成立； ③偶函数在关于原点对称的两个区间上的增减性相反. （2）奇函数设函数()f x 的定义域为I ，如果x I ∀∈，都有x I -∈，且()()f x f x -=-，那么函数()f x 就叫做奇函数.关于奇函数有下面的结论：①奇函数的定义域一定关于原点对称.也就是说定义域关于原点对称是函数为奇函数的一个必要条件；②奇函数的图象关于坐标原点对称.反之也成立；③如果奇函数当0x =时有意义，那么(0)0f =.即当0x =有意义时，奇函数的图象过坐标原点；④奇函数在关于原点对称的两个区间上的增减性相同.3.3幂函数1.幂函数的概念一般地，形如yxα=（R α∈，α为常数）的函数称为幂函数.对于幂函数，我们只研究1α=，2，3，12，1-时的图象与性质.2.五个幂函数的图象和性质3.4函数的应用（一）略.第四章指数函数与对数函数4.1 指数1.n 次方根与分数指数幂（1）方根如果nx a =，那么x 叫做a 的n 次方根，其中1n >，且*n N ∈.①当n 是奇数时，正数的n 次方根是正数，负数的n 方根是负数.这时，a 的n 表示.②当n 是偶数时，正数的n 次方根有两个，这两个数互为相反数.这时，正数a 的正的n 次负的n 次方根用符号. 正的n 次方根与负的n 次方根可以合x 12xx -1并写成0a>）. 负数没有偶次方根.0的任何次方根都是0，记作0=.根式，这里n叫做根指数，a叫做被开方数. 关于根式有下面两个等式：n a=；,,a na n⎧⎪=⎨⎪⎩为奇数为偶数..2.分数指数幂（1）正分数指数幂mna=0a>，m，*n N∈，1n>）.0的正分数指数幂等于0.（2）负分数指数幂11=mnmnaa-=0a>，m，*n N∈，1n>）.0的负分数指数幂没有意义.（3）有理数指数幂的运算性质①r s r sa a a+=（0a>，r，s Q∈）；②()r s rsa a=（0a>，r，s Q∈）；③()r r ra b a b=（0a>，0b>，r Q∈）.3. 无理数指数幂及其运算性质（1）无理数指数幂的概念当x是无理数时，x a是无理数指数幂.我们可以通过有理数指数幂来认识无理数指数幂.当x 的不足近似值m和过剩近似值n逐渐逼近x时，m a和n a都趋向于同一个数，这个数就是x a.所以无理数指数幂x a（0a>，x是无理数）是一个确定的数.（2）实数指数幂的运算性质整数指数幂的运算性质也适用于实数指数幂，即对于任意实数r，s，均有下面的运算性质.①r s r sa a a+=（0a>，r，s R∈）；②()r s rsa a=（0a>，r，s R∈）；③()r r ra b a b=（0a>，0b>，r R∈）.4.2 指数函数1.指数函数的概念函数xy a=（0a>，且1a≠）叫做指数函数，其中指数x是自变量，定义域是R.2.指数函数的图象和性质一般地，指数函数xy a=（0a>，且1a≠）的图象和性质如下表所示：4.3 对数1.对数的概念一般地，如果xa N =(0,1)a a >≠，那么数x 叫做以a 为底N 的对数，记作N x alog=.其中a 叫做对数的底数，N 叫做真数. 当0a >，且1a ≠时，lo g N xa a N x =⇔=. 2. 两个重要的对数（1）常用对数：以10为底的对数叫做常用对数，并把10lo g N 记为lg N .（2）自然对数：以e （e 是无理数， 2.71828e =…）为底的对数叫做自然对数，并把lo g e N 记作ln N .3. 关于对数的几个结论（1）负数和0没有对数；（2）lo g 10a =；（3）lo g 1a a =.4. 对数的运算如果0a >，且1a ≠，0M >，0N >，那么（1）lo g ()lo g lo g a a a M N M N =+；（2）lo g lo g lo g a a a M M N N=-；（3）lo g lo g na a Mn M =（n R ∈）.5. 换底公式lo g lo g lo g c a c bb a=（0a >，且1a ≠，0b >，0c >，1c ≠）. 4.4 对数函数1. 对数函数的概念一般地，函数lo g a y x =（0a >，且1a ≠）叫做对数函数，其中x 是自变量，定义域是(0,)+∞.2.对数函数的图象和性质3. 反函数指数函数x y a =（0a >，且1a ≠）与对数函数lo g a y x =（0a >，且1a ≠）互为反函数，它们的定义域与值域正好互换.互为反函数的两个函数的图象关于直线y x =对称. 4. 不同函数增长的差异对于对数函数lo g a y x =（1a >）、一次函数y k x =（0k >）、指数函数xy b =（1b >）来说，尽管它们在(0,)+∞上都是增函数，但是随着x 的增大，它们增长的速度是不相同的.其中对数函数lo g a y x =（1a >）的增长速度越来越慢；一次函数y k x =（0k >）增长的速度始终不变；指数函数x y b =（1b >）增长的速度越来越快.总之来说，不管a （1a >），k （0k >），b （1b >）的大小关系如何，xy b =（1b >）的增长速度最终都会大大超过y k x =（0k >）的增长速度；y k x =（0k >）的增长速度最终都会大大超过lo g a y x=（1a >）的增长速度.因此，总会存在一个0x ，当0x x >时，恒有lo g xa bk x x >>.4.5 函数的应用（二）1. 函数的零点与方程的解（1）函数零点的概念对于函数()y f x =，我们把使()0f x =的实数x 叫做函数()y f x =的零点.函数()y f x =的零点就是方程()0f x =的实数解，也是函数()y f x =的图象与x 轴的公共点的横坐标.所以方程()0f x =有实数解⇔函数()y f x =有零点⇔函数()y f x =的图象与x 轴有公共点.（2）函数零点存在定理如果函数()y f x =在区间[,]a b 上的图象是一条连续不断的曲线，且有()()0f a f b <，那么，函数()y f x =在区间(,)a b 内至少有一个零点，即存在(,)c a b ∈，使得()0f c =，这个c 也就是方程()0f x =的解. 2. 用二分法求方程的近似解对于在区间[,]a b 上图象连续不断且()()0f a f b <的函数()y f x =，通过不断地把它的零点所在区间一分为二，使所得区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫做二分法.给定精确度ε，用二分法求函数()y f x =零点0x 的近似值的一般步骤如下：（1）确定零点0x 的初始区间[,]a b ，验证()()0f a f b <. （2）求区间(,)a b 的中点c .（3）计算()f c ，并进一步确定零点所在的区间：①若()0f c =（此时0x c =），则c 就是函数的零点； ②若()()0f a f c <（此时0(,)x a c ∈），则令b c =； ③若()()0f c f b <（此时0(,)x c b ∈），则令a c =.（4）判断是否达到精确度ε：若a b ε-<，则得到零点的近似值a （或b ）；否则重复步骤（2）~（4）.由函数零点与相应方程解的关系，我们可以用二分法来求方程的近似解. 3. 函数模型的应用用函数建立数学模型解决实际问题的基本过程如下：这一过程包括分析和理解实际问题的增长情况（是“对数增长”“直线上升”还是“指数爆炸”）；根据增长情况选择函数类型构建数学模型，将实际问题化归为数学问题；通过运算、推理、求解函数模型；用得到的函数模型描述实际问题的变化规律，解决有关问题.在这一过程中，往往需要利用信息技术帮助画图、运算等.。

2019新人教版高中数学必修第一册第1章集合与常用逻辑用语知识点总结

2019新人教版高中数学必修第一册第1章集合与常用逻辑用语知识点总结的表示法是将a放在大括号中，表示一个只含有a这一个元素的集合。

2）描述法中，要注意符号的使用和表达的准确性。

3）在交集与并集的性质中，要注意交集和并集的交换律和结合律。

4）在全集和补集的性质中，要注意补集的定义和符号的使用。

第一章集合和常用逻辑用语1.1 集合的含义和表示集合是由一些元素组成的总体。

元素具有确定性、互异性和无序性。

我们通常用大写的拉丁字母A、B、C等表示集合，用小写拉丁字母a、b、c等表示元素。

如果元素x在集合A中，我们称x属于A，记为x∈A，否则称x不属于A，记作x∉A。

常用的数集有非负整数集（即自然数集）记作N，正整数集记作N*或N+，整数集记作Z，有理数集记作Q，实数集记作R。

集合的表示法有列举法、描述法和图示法。

列举法是把集合中的元素一一列举出来，然后用一个大括号括上。

描述法是用集合所含元素的公共特征表示集合的方法，可以用语言描述法和数学式子描述法。

图示法是用Venn图表示集合和元素之间的关系。

1.2 集合间的基本关系集合间有“包含”关系和“相等”关系。

如果集合A中的任何一个元素都是集合B中的元素，则A叫做B的子集，记为A⊆B，例如N⊆Z。

子集的个数为2的n次方（n为集合中元素个数）。

如果A是B的子集，而且B中存在元素不属于A，则A叫B的真子集。

真子集的个数为2的n次方减1（n为集合中元素个数）。

如果A是B的子集，B也是A的子集，则称A与B相等。

空集是不含任何元素的集合，用∅来表示。

空集∅是任何集合的子集，是任何非空集合的真子集。

1.3 集合的基本运算集合有交集和并集两种基本运算。

交集是指集合A和集合B中共同拥有的元素组成的集合，记为A∩B。

并集是指集合A和集合B中所有元素组成的集合，记为A∪B。

交集和并集有交换律和结合律。

全集是指包含所有元素的集合，通常用U来表示。

补集是指集合A中不属于集合B的元素组成的集合，记为CBA。

高一数学必修一知识点总结人教(3篇)

高一数学必修一知识点总结人教1.知识网络图复数知识点网络图2.复数中的难点（1）复数的向量表示法的运算.对于复数的向量表示有些学生掌握得不好，对向量的运算的几何意义的灵活掌握有一定的困难.对此应认真体会复数向量运算的几何意义，对其灵活地加以证明.（2）复数三角形式的乘方和开方.有部分学生对运算法则知道，但对其灵活地运用有一定的困难，特别是开方运算，应对此认真地加以训练.（3）复数的辐角主值的求法.（4）利用复数的几何意义灵活地解决问题.复数可以用向量表示，同时复数的模和辐角都具有几何意义，对他们的理解和应用有一定难度，应认真加以体会.3.复数中的重点（1）理解好复数的概念，弄清实数、虚数、纯虚数的不同点.（2）熟练掌握复数三种表示法，以及它们间的互化，并能准确地求出复数的模和辐角.复数有代数，向量和三角三种表示法.特别是代数形式和三角形式的互化，以及求复数的模和辐角在解决具体问题时经常用到，是一个重点内容.（3）复数的三种表示法的各种运算，在运算中重视共轭复数以及模的有关性质.复数的运算是复数中的主要内容，掌握复数各种形式的运算，特别是复数运算的几何意义更是重点内容.（4）复数集中一元二次方程和二项方程的解法.数学教学心得如果以上的表述并不具有数学学科的特点的话，那么加上一个定语——让学生用数学的眼光进行数学思考。

比如，百货店的促销信息，人们不仅会关注哪个折扣低，还会关注标价的高低。

美国统计学家戴维穆尔的《统计学的世界》一书中有幅漫画，画的是一个人误以为平均水深就是每一个地方都是这样的水深而溺水死亡，从侧面反映了数学常识在现实生活中的作用。

数学地思考，是数学学习的更高目标。

数学学习过程中所倡导的思考方式是具有学科特点的。

看到一幅图画时，别的学科可能关注的是这幅图是多么的美观，但是对于数学学习来说，教师需要引导学生关注这个图形的组成与分解，引导学生思考的是多边形线的条数等。

这种量化、精确化的思考方式是数学教学最根本的目标价值所在。

人教版高中数学必修1知识点汇总总结

高中数学必修1知识点第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集，N *或N +表示正整数集，Z 表示整数集，Q 表示有理数集，R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈，或者a M ∉，两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合. ③描述法：{x |x 具有的性质}，其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（7）已知集合A 有(1)n n ≥个元素，则它有2n个子集，它有21n -个真子集，它有21n-个非空子集，它有22n-非空真子集.【1.1.3】集合的基本运算（8）交集、并集、补集∅=∅ B A ⊆ B B ⊆ B{x A A = A ∅= B A ⊇ B B ⊇UA {|x x )A =∅【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法{0)()()U A B A =()()()UU U A B A B =〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f ，对于集合A 中任何一个数x ，在集合B 中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设,a b 是两个数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a x b <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <．（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零．⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法： ①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题． ⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f ，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象．〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值。

【知识点总结】高中数学人教A版必修第一册知识点总结

高中数学新教材人教A版必修第一册知识点总结专题01 集合与常用的逻辑用语 (3)知识点一集合的概念 (3)知识点二集合间的关系 (4)知识点三集合的基本运算 (5)知识点四充分条件与必要条件 (5)知识点五全称量词与存在量词 (6)专题02 一元二次方程、函数与不等式 (7)知识点一不等式的性质 (7)知识点二基本不等式 (7)知识点三二次函数与一元二次方程、不等式 (8)专题03 函数的概念与性质 (9)知识点一函数的概念与分段函数 (9)知识点二函数的三要素 (10)知识点三函数的单调性 (12)知识点四函数的奇偶性 (14)知识点六幂函数 (16)专题04指数函数与对数函数的概念、简单性质 (17)知识点一指数运算、对数运算与幂运算 (17)知识点二指数函数与对数函数的概念及图像 (18)知识点三比较大小（常与0、1、-1作比较） (18)知识点四函数的零点 (19)专题05 指数型与对数型复合函数的性质 (20)知识点一复合函数简单的单调性与奇偶性问题 (20)知识点二复合函数的单调性 (20)知识点三复合函数的最大值与最小值 (21)知识点四最值问题（含有参数） (22)知识点五恒成立问题 (22)专题06 三角函数的图像与性质 (23)知识点一任意角和弧度制 (23)知识点二常用的角的集合表示方法 (23)知识点三弧度与弧度制 (24)知识点四三角函数定义 (25)知识点五三角函数在各象限的符号 (26)知识点六特殊角的三角函数值： (26)知识点七同角三角函数的关系与诱导公式 (26)知识点八两角和与差公式的基本应用 (27)知识点九辅助角公式 (27)知识点十二倍角公式 (27)知识点十一降幂公式 (27)知识点十二基本三角函数的图像与性质（正弦、余弦与正切） (28)知识点十三函数y＝Asin(ωx＋φ)的图像 (29)知识点十四三角函数的实际应用 (30)专题07 三角函数的综合运用 (30)专题01 集合与常用的逻辑用语知识点一集合的概念1．集合的有关概念(1)集合的描述：我们把研究对象称为元素，把一些元素组成的总体叫做集合.元素通常用小写字母a,b,c,⋯表示，集合通常用大写字母A,B,C,⋯表示.(2)集合元素的特性：确定性：集合中的元素是确定的，即给定一个元素可以判断该元素在或者不在该集合中。

人教版高中数学必修一第一章知识点

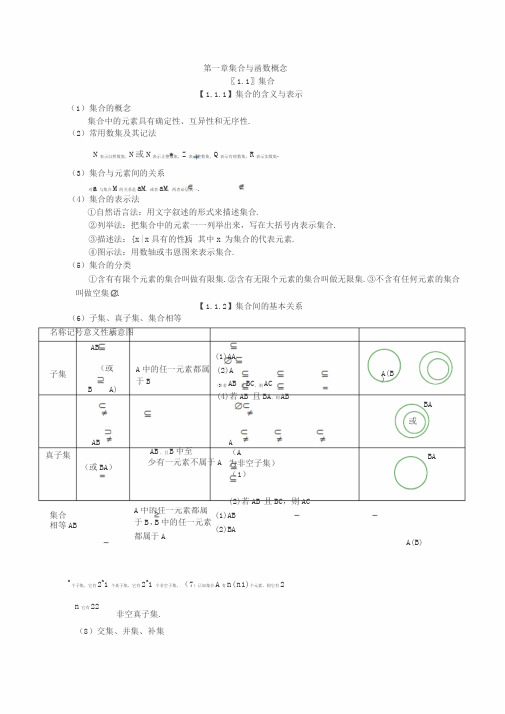
第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性.（2）常用数集及其记法N表示自然数集，N或N表示正整数集，Z表示整数集，Q表示有理数集，R表示实数集.（3）集合与元素间的关系对象a与集合M的关系是aM，或者aM，两者必居其一.（4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合.③描述法：{x|x具有的性质}，其中x为集合的代表元素.④图示法：用数轴或韦恩图来表示集合.（5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().【1.1.2】集合间的基本关系（6）子集、真子集、集合相等名称记号意义性质示意图AB(1)AA子集B （或A)A中的任一元素都属于B(2)A(3)若AB且BC，则AC(4)若AB且BA，则ABA(B)BA或真子集AB（或BA）AB，且B中至少有一元素不属于AA（A为非空子集）（1）(2)若AB且BC，则ACBA集合相等AB A中的任一元素都属于B，B中的任一元素都属于A(1)AB(2)BAA(B)n个子集，它有2n1个真子集，它有2n1个非空子集，（7）已知集合A有n(n1)个元素，则它有2n它有22非空真子集. （8）交集、并集、补集1【1.1.3】集合的基本运算名称记号意义性质示意图AB 交集{x|x A,且（1）AAA（2）AAB（3）ABAxB}ABBAB 并集{x|x A,或（1）AAA（2）AAAB（3）ABAxB}ABB1A(e U A)2()AeAUU补集e U A{x|xU,且xA} 痧U(A B)(U A)(?U B)痧U(AB)(U A)(?U B)【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法不等式解集|x|a(a0){x|axa}|x|a(a0)x|xa或xa}把axb看成一个整体，化成|x|a，|axb|c,|axb|c(c0)|x|a(a0)型不等式来求解（2）一元二次不等式的解法判别式24bac000二次函数2(0)yaxbxcaO的图象一元二次方程20(0)axbxcax1,22bb4ac2abxx122a无实根（其中x1x2)的根20(0) axbxca的解集b{x|xx或xx2}{x|x}12aR 220(0)axbxca的解集{x|xxx}12〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A、B是两个非空的数集，如果按照某种对应法则f，对于集合A中任何一个数x，在集合B中都有唯一确定的数f(x)和它对应，那么这样的对应（包括集合A，B以及A到B的对应法则f）叫做集合A到B的一个函数，记作f:AB．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设a,b是两个实数，且ab，满足a xb的实数x的集合叫做闭区间，记做[a,b]；满足axb的实数x的集合叫做开区间，记做(a,b)；满足a xb，或axb的实数x的集合叫做半开半闭区间，分别记做[a,b)，(a,b]；满足x a,xa,xb,xb的实数x的集合分别记做[a,),(a,),(,b],(,b)．注意：对于集合{x|axb}与区间(a,b)，前者a可以大于或等于b，而后者必须ab．（3）求函数的定义域时，一般遵循以下原则：①f(x)是整式时，定义域是全体实数．②f(x)是分式函数时，定义域是使分母不为零的一切实数．③f(x)是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤ytanx中，()xkkZ．2⑥零（负）指数幂的底数不能为零．⑦若f(x)是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知f(x)的定义域为[a,b]，其复合函数f[g(x)]的定义域应由不等式ag(x)b解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论．⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数yf(x)可以化成一个系数含有y的关于x的二次方程2a(y)xb(y)xc(y)0，则在a(y)0时，由于x,y为实数，故必须有byaycy，从而确定函数的值域或最值．2()4()()0④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值．⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值．⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A、B是两个集合，如果按照某种对应法则f，对于集合A中任何一个元素，在集合B中都有唯一的元素和它对应，那么这样的对应（包括集合A，B以及A到B的对应法则f）叫做集合A到B的映射，记作f:AB．②给定一个集合A到集合B的映射，且aA,bB．如果元素a和元素b对应，那么我们把元素b叫做元素a的象，元素a叫做元素b的原象．〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法函数的定义图象判定方法性质如果对于属于定义域I 内某（1）利用定义个区间上的任意两个自变量的值x2,当x ． 1、x 1．<．x ．2．时，都y y=f(X) f(x)2（2）利用已知函数的单调性有f ．(x ．．．)．<．f(．x ．．．)．，那么就说 12 f(x)在这个区间上是增函数．．．．f(x)1（3）利用函数图象（在某个区间图o x 1x 2x 象上升为增）函数的（4）利用复合函数单调性（1）利用定义如果对于属于定义域I 内某yy=f(X)（2）利用已知函数的个区间上的任意两个自变量 11、x ．<．x ．的值x2，当x ．2．时，都有f ．(x ．．12．)．，那么就说f(x) 1f(x) 2单调性（3）利用函数图象（在某个区间图f(x)在这个区间上是减函数．．．．o xx 12x象下降为减）（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数yf[g(x)]，令ug(x)，若yf(u)为增，ug(x)为增，则yf[g(x)]为增；若yf(u)为减，ug(x)为减，则y f[g(x)]为增；若yf(u)为增，ug(x)为减，则y f[g(x)]为减；若yf(u)为减，ug(x)为增，则yyf[g(x)]为减．a（2）打“√”函数()(0)fxxax的图象与性质 f(x)分别在(,a ]、[a ,)上为增函数，分别在ox[a,0)、(0,a]上为减函数．（3）最大（小）值定义①一般地，设函数yf(x)的定义域为I，如果存在实数M满足：（1）对于任意的xI，都有f(x)M；（2）存在x I，使得f(x0)M．那么，我们称M是函数f(x)的最大值，记作0f max(x)M．5②一般地，设函数yf(x)的定义域为I，如果存在实数m满足：（1）对于任意的xI，都有f(x)m；（2）存在x0I，使得f(x0)m．那么，我们称m是函数f(x)的最小值，记作f max(x)m．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内（1）利用定义（要先任意一个x，都有．f(．－．x．．)=．－．判断定义域是否关于f(x)．．．．,那么函数f(x)叫做奇．函．原点对称）数．．（2）利用图象（图象关于原点对称）函数的奇偶性如果对于函数f(x)定义域内（1）利用定义（要先任意一个x，都有f(－．x．．)=．f．(x．)．．,．．判断定义域是否关于那么函数f(x)叫做偶．函．数．．原点对称）（2）利用图象（图象关于y轴对称）②若函数f(x)为奇函数，且在x0处有定义，则f(0)0．③奇函数在y轴两侧相对称的区间增减性相同，偶函数在y轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域；②化解函数解析式；③讨论函数的性质（奇偶性、单调性）；④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换yfxyfxh()h0,h()左移个单位右移|个单位h0,h|yfxyfxk()kk()0,上移个单位下移|个单位k0,k|变换②伸缩01,伸yf(x)yf(x)1,缩6yfxyAfx()0A1,缩()A1,伸③对称变换x轴yf(x)y轴yf(x)yf(x)yf(x)原点直线1yxyf(x)yf(x)yf(x)yf(x)去掉轴左边图象yyf(x)yf(|x|)保留y轴右边图象，并作其关于y轴对称图象保留轴上方图象yfxyfx()x|()|将轴下方图象翻折上去x（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．7。

人教A版高中数学必修1知识点总结

人教A版高中数学必修1知识点总结
高中数学必修1主要涵盖了数与式、函数与方程、平面几何等内容。

下面我将对这些知识点进行总结：
一、数与式
1.整式与分式：整式包括常数项、一次项、二次项等；分式包括真分式、假分式等。

2.代数式的运算：包括加法、减法、乘法、除法的运算法则；指数与
乘方的运算法则。

3.类指数：零次指数、分数指数、负整数指数的运算规则；类指数函
数图象。

4.分式的运算：分式的加减乘除法运算法则；负指数律。

二、函数与方程
1.函数：函数的概念与性质；函数的图象、定义域与值域。

2.函数的表示法：函数的自变量与因变量；函数的映射关系与解析式。

3.线性函数：线性函数的性质与图象；线性函数的应用。

4.幂函数：幂函数的概念与性质；幂函数的图象。

5.函数的运算：函数的和、差、积、商的性质；复合函数的性质与解法。

6.一元一次方程：一元一次方程的定义与定解；一元一次方程的解法。

7.一元二次方程：一元二次方程的定义与定解；一元二次方程的解法。

8.二元一次方程：二元一次方程的解法；二元一次方程表示的直线。

三、平面几何
1.平面几何基础：点、直线、线段、角、面的定义；一次、二次、三次等距变换的性质。

2.平面图形：多边形的种类与性质；正多边形的性质；圆的性质与常见公式。

3.相似三角形：相似三角形的判定与性质；相似三角形的性质。

4.三角形：三角形的内角和定理与外角和定理；直角三角形的勾股定理与勾股数。

5.圆与圆的位置关系：切线的概念与性质；公切线与内切圆、外切圆的关系。

(完整版)人教版高中数学必修一第一章知识点

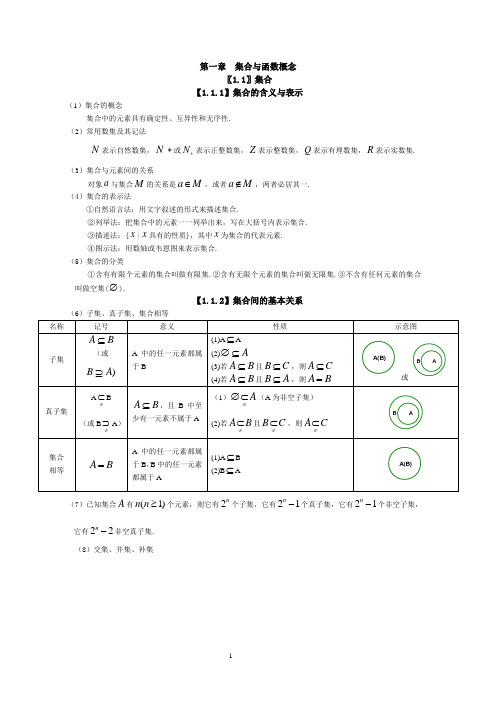
第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集，N *或N +表示正整数集，Z 表示整数集，Q 表示有理数集，R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈，或者a M ∉，两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合. ③描述法：{x |x 具有的性质}，其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（6）子集、真子集、集合相等（7）已知集合A 有(1)n n ≥个元素，则它有2n 个子集，它有21n -个真子集，它有21n -个非空子集，它有22n-非空真子集.（8）交集、并集、补集【1.1.3】集合的基本运算名称记号意义性质示意图交集A B{|,x x A∈且}x B∈（1）A A A=（2）A∅=∅（3）A B A⊆A B B⊆BA并集A B{|,x x A∈或}x B∈（1）A A A=（2）A A∅=（3）A B A⊇A B B⊇BA补集U A {|,}x x U x A∈∉且1()UA A=∅2()UA A U=【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法不等式解集||(0)x a a<>{|}x a x a-<<||(0)x a a>>|x x a<-或}x a>||,||(0) ax b c ax b c c+<+>>把ax b+看成一个整体，化成||x a<，||(0)x a a>>型不等式来求解（2）一元二次不等式的解法判别式24b ac ∆=-∆>0∆=0∆<二次函数2(0)y ax bx c a=++>的图象O一元二次方程20(0) ax bx c a++=>的根21,242b b acxa-±-=（其中12)x x<122bx xa==-无实根20(0) ax bx c a++>>的解集1{|x x x<或2}x x>{|x}2bxa≠-R ()()()U U UA B A B=()()()U U UA B A B=〖1.2〗函数及其表示【1.2.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f，对于集合A 中任何一个数x ，在集合B中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数．（2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a xb <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <．（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1． ⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零． ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义．（4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值． ③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系．（6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象．yxo〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法函数的性质定义图象判定方法函数的单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x ．1．< x ．．2．时，都有f(x ．．．1．)<f(x ．．．．．2．)．，那么就说f(x)在这个区间上是增函数．．．． x 1x 2y=f(X)xy f(x )1f(x )2o（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象上升为增）（4）利用复合函数如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2，当x ．1．< x ．．2．时，都有f(x ．．．1．)>f(x ．．．．．2．)．，那么就说f(x)在这个区间上是减函数．．．． y=f(X)yxox x 2f(x )f(x )211（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象下降为减）（4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数． ③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()ug x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减．（2）打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,]a -∞-、,)a +∞上为增函数，分别在[,0)a 、]a 上为减函数．（3）最大（小）值定义 ①一般地，设函数()y f x =的定义域为I，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M≤；（2）存在0x I ∈，使得0()f x M=．那么，我们称M 是函数()f x 的最大值，记作max ()f x M=．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的性质定义图象判定方法函数的奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x)．．．．,那么函数f(x)叫做奇函．．数．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于原点对称）如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于y 轴对称） ②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域； ②化解函数解析式； ③讨论函数的性质（奇偶性、单调性）； ④画出函数的图象．利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象． ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象，并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系．（3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．。

高中数学人教A版必修一第一章知识点总结及题型

高中数学人教A版必修一第一章知识点总结及题型高中数学必修一第一章知识点及题型一、第一章第一单元集合---知识点总结知识点一：集合的概念集合是研究对象的统称，用小写拉丁字母a，b，c等表示元素，一些元素的集合称为集合或集，用大写拉丁字母A，B，C等表示，不含任何元素的集合称为空集，记为∅。

知识点二：集合与元素的关系如果a是集合A的元素，就称a属于集合A，记作a∈A；如果a不是集合A中的元素，就称a不属于集合A，记作a∉A。

知识点三：集合的特性及分类集合元素具有唯一性、无序性和互异性。

集合可分为有限集和无限集，有限集含有有限个元素，无限集含有无限个元素。

知识点四：集合的表示方法集合的表示方法有列举法和描述法。

列举法是把集合的元素一一列举出来，并用花括号“{}”括起来表示集合的方法；描述法是用集合所含元素的特征表示集合的方法。

知识点五：集合与集合的关系集合A中的所有元素都是集合B中的元素时，称集合A是集合B的子集，记作A⊆B；如果A是B的子集，但存在元素不属于B，则称A是B的真子集，记作A⊂B。

子集的性质包括空集是任意集合的子集、任何集合都是它本身的子集、如果A是B的子集，B是C的子集，则A是C的子集。

知识点六：集合的运算集合的运算包括交集和并集。

集合A与B的并集是由A 和B中所有元素组成的集合，记作A∪B；集合A与B的交集是A和B中共有的元素组成的集合，记作A∩B。

3.交集与并集的性质交集的运算性质：A∩B = B∩A （交换律）A∩A = A （恒等律）A∩∅ = ∅（零律）A⊆B ⇔ A∩B = A （吸收律）并集的运算性质：A∪B = B∪A （交换律）A∪A = A （恒等律）A∪∅ = A （零律）A⊆B ⇔ A∪B = B （吸收律）A∪B = B∪A = {x | x∈A或x∈B} （定义）符号语言、图形语言和自然语言都可以用来表示集合的交集和并集。

4.全集在研究集合与集合之间的关系时，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集，通常记作U。

人教版高中数学必修一知识点和重难点

人教版高中数学必修一------- 各章节知识点与重难点第一章集合与函数概念1.1集合1.1.1集合的含义与表示【知识要点】1、集合的含义一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合。

2、集合的中元素的三个特性（1）元素的确定性；（2）元素的互异性；（3）元素的无序性2、“届丁”的概念我们通常用大写的拉丁字母A,B,C, ......... 表示集合，用小写拉丁字母a,b,c, ......... 表示元素如：如果a是集合A的元素，就说a届丁集合A记作a€ A,如果a不届丁集合A记作a A3、常用数集及其记法非负整数集（即自然数集）记作：N ;正整数集记作：N*或N+ ;整数集记作：Z;有理数集记作：Q;实数集记作：R4、集合的表示法（1）列举法：把集合中的元素一一列举出来，然后用一个大括号括上。

（2）描述法：用集合所含元素的公共特征表示集合的方法称为描述法。

①语言描述法：例：｛不是直角三角形的三角形｝②数学式子描述法：例：不等式x-3>2的解集是｛x£ R| x-3>2｝或｛x| x-3>2｝（3）图示法（Venn图）1.1.2集合问的基本关系【知识要点】1、“包含”关系一一子集一般地，对丁两个集合A与B,如果集合A的任何一个元素都是集合B的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集，记作A B2、“相等”关系如果集合A的任何一个元素都是集合B的元素，同时，集合B的任何一个元素都是集合A的元素，我们就说集合A等丁集合B,即：A=B A B且B A3、真子集如果A B,且A B那就说集合A是集合B的真子集，记作A B（或B A）4、空集不含任何元素的集合叫做空集，记为①规定：空集是任何集合的子集，空集是任何非空集合的真子集.1.1.3集合的基本运算【知识要点】1、交集的定义一般地，由所有届丁A且届丁B的元素所组成的集合，叫做A,B的交集.记作A A B（读作A 交B”），即An B=｛x| x€ A,且x€ B｝.2、并集的定义一般地，由所有届丁集合A或届丁集合B的元素所组成的集合，叫做A,B的并集。

新教材人教版高中数学必修第一册第三章知识点总结

必修第一册第三章函数的概念与性质3.1 函数的概念及其表示1．函数的概念：一般地，设A、B是非空的数集，如果对于集合A中的任意一个数x，按照某种确定的对应关系f，在集合B中都有唯一确定的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数。

记作：y=f(x)，x∈A。

其中，x叫做自变量，x的取值范围A叫做函数的定义域；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域。

2．构成函数的三要素：定义域、对应关系和值域（1）函数的定义域的求法：①自然型：解析式自身有意义，如分式函数的分母不为零，偶次根式函数的被开方数为非负数，对数函数的真数为正数；②实际型：解决函数的综合问题与应用问题时，应认真考察自变量x的实际意义。

（2）求函数的值域的方法：①配方法（将函数转化为二次函数）；②不等式法（运用不等式的各种性质）；③函数法（运用函数的单调性、函数图象等）。

（3）两个函数的相等：当且仅当两个函数的定义域和对应法则都分别相同时，这两个函数才是同一个函数。

3．常用的函数表示法（1）解析法：就是把两个变量的函数关系，用一个等式来表示，这个等式叫做函数的解析表达式，简称解析式；（2）列表法：就是列出表格来表示两个变量的函数关系；（3）图象法：就是用函数图象表示两个变量之间的关系。

4．分段函数：若一个函数的定义域分成了若干个子区间，而每个子区间的解析式不同，这种函数又称分段函数；5.区间的概念：设a,b是两个实数，且a<b,我们规定：（1）满足不等式a≤x≤b的实数x的集合叫做闭区间，表示[a,b];（2）满足不等式a<x<b的实数x的集合叫做开区间，表示(a,b);（3）满足不等式a≤x<b或a<x≤b的实数x的集合叫做半开半闭区间，表示[a,b)或(a,b];a,b都叫做区间的端点。

（4）代数与几何表示对照表（数轴上用实心点表示包括在区间内的端点，用空心点表示不包括在区间内的端点）（5）3.2 函数的基本性质⊆: 1．单调性：（1）定义：一般地，设函数y=f(x)的定义域为I，区间D I①∀ x1，x2∈D，当x1<x2时，都有f(x1)<f(x2)，那么就说f(x)在区间D上是增函数；特别地，当函数f(x)在它的定义域上单调递增时，我们成它是增函数。

人教版高中数学必修1知识点归纳总结

高中数学人教A版必修第一册知识点总结

人教版高中数学必修一知识点总结(完整版)

高中数学人教版必修一知识点总结

必修1高一数学人教版最全知识点(必须珍藏)

人教版高中数学必修一第一章知识点

人教版高中数学必修1-第一章知识点知识点归纳[最新版]

高中数学(新人教版)必修一知识点归纳

高中数学人教A版必修第一册知识点总结

2019新人教版高中数学必修第一册第1章集合与常用逻辑用语知识点总结

高一数学必修一知识点总结人教(3篇)

人教版高中数学必修1知识点汇总总结

【知识点总结】高中数学人教A版必修第一册知识点总结

人教版高中数学必修一第一章知识点

人教A版高中数学必修1知识点总结

(完整版)人教版高中数学必修一第一章知识点

高中数学人教A版必修一第一章知识点总结及题型

人教版高中数学必修一知识点和重难点

新教材人教版高中数学必修第一册 第三章 知识点总结

新教材人教版高中数学必修第一册第三章知识点总结