北京工业大学812材料力学I2020考研真题
北京工业大学机械工程(专业学位)专业-812材料力学I考研复习全书-真题-大纲-华文考研

北京工业大学机械工程(专业学位)专业-812材料力学I考研复习全书-真题-大纲-华文考研报考北京工业大学机械工程(专业学位)专业考研专业课资料的重要性根据考研网的统计,87.3%以上报考北京工业大学机械工程(专业学位)专业考研成功的考生,尤其是那些跨学校的考研人,他们大多都在第一时间获取了北京工业大学机械工程(专业学位)专业考研专业课指定的教材和非指定的北京工业大学机械工程(专业学位)专业内部权威复习资料,精准确定专业课考核范围和考点重点,才确保了自己的专业课高分,进而才才最后考研成功的。
如果咱们仔细的研究下问题的本质,不难发现因为非统考专业课的真题均是由北京工业大学机械工程(专业学位)专业自主命题和阅卷,对于跨校考研同学而言,初试和复试命题的重点、考点、范围、趋势、规律和阅卷的方式等关键信息都是很难获取的。
所以第一时间获取了北京工业大学机械工程(专业学位)专业考研专业课指定的教材和非指定的北京工业大学机械工程(专业学位)专业内部权威复习资料的考生,就占得了专业课复习的先机。
专业课得高分便不难理解。
那么怎么样才能顺利的考入北京工业大学机械工程(专业学位)专业呢?为了有把握的的取得专业课的高分,确保考研专业课真正意义上的成功,考研专业课复习的首要工作便是全面搜集北京工业大学机械工程(专业学位)专业的内部权威专业课资料和考研信息,建议大家做到以下两点:1、快速消除跨学校考研的信息方面的劣势。
这要求大家查询好考研的招生信息,给大家推/shop/2、确定最合适的考研专业课复习资料,明确专业课的复习方法策略,并且制定详细的复习计划,并且将复习计划较好的贯彻执行。
北京工业大学812材料力学I从基础到强化考研复习全书包括两部分。
第一部分:北京工业大学812材料力学I考研复习重点讲义。
由考研网请北京工业大学机械工程(专业学位)专业的多名研究生参与编写(均为考研网的考研高分学员),重点参考了北京工业大学机械工程(专业学位)专业812材料力学I历年真题,并找北京工业大学机械工程(专业学位)专业最权威的导师咨询考点范围。
材料力学考研真题十一套

材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2;10分二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ=;试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图;10分三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度;8分四、钢制平面直角曲拐ABC,受力如图;q=πKN/m,AB段为圆截面,σ=160MPa,设L=10d,P x=qL,试设计AB段的直径d;15分五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角不计轴力及剪力对变形的影响;12分六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动;已知板的许用弯曲正应力为σ=10Mpa,许用剪应力τ=1Mpa,胶合面上的许用剪应力τ胶=,a=1m,b=10cm,h=5cm,试求许可荷载P;10分七、图示一转臂起重机架ABC,其中AB为空心圆截面杆D=76mm,d=68mm,BC为实心圆截面杆D1=20mm,两杆材料相同,σp=200Mpa,σs=235Mpa,E=206Gpa;取强度安全系数n=,稳定安全系数n st=4;最大起重量G=20KN,临界应力经验公式为σcr=λMpa;试校核此结构;15分八、水平曲拐ABC为圆截面杆,在C段上方有一铅垂杆DK,制造时DK杆短了△;曲拐AB和BC段的抗扭刚度和抗弯刚度皆为GI P和EI;且GI P=45EI;杆DK抗拉刚度为EA,且EA=225EIa;试求:1在AB段杆的B端加多大扭矩,才可使C点刚好与D 点相接触2若C、D两点相接触后,用铰链将C、D两点连在一起,在逐渐撤除所加扭矩,求DK杆内的轴力和固定端处A截面上的内力;15分九、火车车轴受力如图,已知a、L、d、P;求轴中段截面边缘上任意一点的循环特征r,平均应力σm和应力幅σa;5分2一、作梁的内力图;10分二、直径d=100mm的圆轴,受轴向拉力P和力偶矩m的作用,材料的弹性模量E=200Gpa,泊松比μ=,现测得圆轴表面轴向线应变ε0=500×10-6,45方向线应变ε45=400×10-6;试求P和m;10分三、已知直径为d的钢制圆轴受力如图;1试确定可能危险点的位置,并用单元体表示其应力状态;2若此圆轴单向拉伸时的许用应力为σ,试列出校核此轴强度的强度条件;10分四、已知图示结构中各杆的直径均为d,以及E、G、m、a试求:1A端在y-z平面内的转角θA;2若在A端沿z方向再加上一集中力P,问θA的变化值是多少10分五、已知钢架受力如图,试求: A处的约束反力;12分六、结构如图所示,横梁AC为T型截面铸铁梁;已知其许用拉应力σt=40Mpa,许用压应力σc=160Mpa,I Z=800cm4,y1=5cm,y2=9cm,BD杆用A3钢制成,直径d=24cm,E=200Gpa,λp=100,λs=60,经验公式为σcr=λMpa,稳定安全系数n st=;试校核该结构是否安全12分七、已知: a、b两种材料的σ-ε曲线,若取安全系数n=2,是分别求出其许用应力σ;并说明何谓冷作硬化现象6分八、已知如图,1、试列出求解AB梁弯曲变形所需的挠曲线近似微分方程;不必积分2、列出确定积分常数所需的全部条件;6分九、试指出下面各截面梁在P的作用下,将产生什么变形6分十、求下列结构的弹性变形能;E、G均为已知6分十一、已知某材料的σ-1=300Mpa,σb=700Mpa,σ0=450Mpa,用此材料制成的构件的有效应力集中系数Kσ=,尺寸系数εσ=,表面质量系数β=;试作出此构件的持久极限简化折线;6分十二、已知如图,一重量为Q的冲击物,以速度v水平冲击杆AB,试根据能量守恒定律,推导水平冲击时的动荷系数;6分3一、已知:q、a,试作梁的内力图;10分二、图示矩形截面杆,上、下表面的轴向线应变分别为:εa=1×10-3,εb=×10-3,E=210Gpa1试求拉力P和偏心距e;2并画出横截面上的正应力分布图;10分三、铸铁梁上作用有可移动的荷载P,已知:y1=52mm,y2=88mm,I z=763cm4,铸铁拉伸时的σb=120Mpa,压缩时的σb=640Mpa,安全系数n=4;试确定铸铁梁的许可荷载P;并求τmax10分四、某低碳钢构件内危险点的应力状态如图,已知:σs=220Mpa,σb=400Mpa,安全系数n=2,E=200Gpa,µ=1试求该点的最大线应变;2画出该点的应力圆草图;3并对该点进行强度校核;10分五、直径为d的钢制圆轴受力如图;已知:P1=20KN,P2=10KN,m=20KN·m,q=5KN/m,σ=160Mpa,试设计AB轴的直径;10分六、已知:q、l、EI试求:等直梁间铰B左右两侧截面的相对转角;10分七、圆截面杆AB、BC的直径、材料均相同,已知:p、a,E=2.5G,且CD杆的EA=2EI/5a2,试求:CD杆的内力;12分八、已知某合金钢材料的持久极限曲线;试求:1A、B、C、D各点的循环特征r;2σ-1和σb;3G点的σmax和σmin;8分九、图示等截面钢架,受到重量为G=300N的物体冲击,已知:E=200Gpa,试求:钢架内的最大应力;10分十、图示正方形桁架,五根杆均为直径d=5cm的圆截面杆,材料为A3钢,E=200Gpa,σp=200Mpa,σs=240Mpa,a=304Mpa,b=,若取强度安全系数n=2,稳定安全系数n st=3,试确定结构的许可荷载P;10分4一、做图示结构中AD段的内力图;15分二、圆轴受弯扭组合变形,m1=m2=150N·m,d=50mm,E=200Gpa,µ=;试画出危险点的应力状态,并求其主应力、最大剪应力、最大线应变值;三、钢制实心圆截面轴AC,σ=140Mpa,L=100cm,a=15cm,皮带轮直径D=80cm,重Q=2KN,皮带水平拉力F1=8KN,F2=2KN,试设计AC轴的直径d;15分四、矩形截面组合梁,已知材料的弹性模量E、a、b、h,在突加重物Q的作用下,测得中间铰B左、右的相对转角=2,求Q值及梁内横截面上的最大正应力;15分五、圆截面平面曲拐OAB与直杆CD直径、材料均相同;已知P、L,且GI p=,EA=L2,求O端的约束反力;20分六、矩形截面悬臂梁,已知材料的弹性模量E、L、b、h,在上顶面作用着均布切向荷载q,求轴线上B点的水平位移U B、垂直位移V B、杆件的弹性变形能U;20分七、AB为T形截面铸铁梁,已知I Z=4×107mm4,y1=140mm,y2=60mm,许用拉应力σt=35Mpa,许用压应力σc=140Mpa;CD为圆截面钢杆,直径d=32mm,E=200Gpa,σp=200Mpa,σs=240Mpa,σ=120Mpa,n st=3,l=1m,直线经验公式为:σc r=λMpa;当载荷在AB范围内移动时,求此结构的许可荷载p;20分注:n st为规定的稳定安全系数;八、列出求解AB梁弯曲变形所需的挠曲线近似微分方程不必积分;写出确定积分常数所需的全部条件;画出挠曲线的大致形状;已知:q、a、弹簧刚度K,EI 为常数;10分九、分别画出低碳钢、铸铁试件在扭转实验中的受力图;将要破坏时横截面上的应力分布图;破环件的断口形式,分析破坏原因;若测得低碳钢破坏时的扭矩为m1,铸铁破坏时的扭矩为m2,写出计算剪切强度极限的表达式试件直径均为d;10分十、圆轴AB以等角速度ω回转,已知:P、L、d、ω,求危险点的循环特征r;平均应力σm;应力幅σa,画出该点的σ~t曲线;10分5一、画图示梁的剪力图和弯矩图;15分二、直径为d的钢制圆轴受力如图所示,已知材料的许用应力为σ,m=qL2,P=qL,试用第三强度理论设计该圆周的直径d;15分三、已知平面曲拐ABC和DF梁的抗弯刚度为EI、抗扭刚度为GI p和CD杆的抗拉刚度为EA,设EI=4GI P=2EAL2;试求CD杆的内力;20分四、结构受力如图所示,横梁AB为T字形截面铸铁梁,已知其许用拉应力为σ=40Mpa,许用拉应力为σc=160Mpa,I z=800cm4,y1=50mm,y2=90mm;CD t杆用A3钢制成,截面为圆形,d=30mm,E=200Gpa,λp=100,λs=60,经验公式为:σcr=λMpa,稳定安全系数n st=3;试校核该结构是否安全;载荷P可在AB 梁上移动;20分五、结构受力如图所示,设弹簧刚度为K=5EI/L3,试求C截面的挠度f c;15分六、某一钢结构危险点处的应力状态如图所示,已知E=200GPa,μ=,σ=200MPa,σb=400MPa,安全系数n=2;试求:1图示单元体的主应力;2最s大剪应力;3最大线应变;4画出相应的三向应力圆草图;5对该点进行强度校核;15分七、已知某材料的持久极限曲线如图所示,试求1A、B、C、D各点的循环特性r;2σ-1和σb;3G点的σmaz和σmin;4画出相应的持久极限曲线的简化折线;7分八、结构如图所示,试求结构在静荷载q和动荷载G=qL冲击下D点的挠度f D,设qL4=4hEI,EI为梁的抗弯刚度;15分九、圆轴受力如图所示,已知:E=200GPa,μ=,d=100mm,现测得圆轴表面A 点沿轴线方向的线应变为ε0°=5×10-4,沿45°方向的线应变为ε45°=4×10-4,试求外荷载P和M;15分十、结构受力如图所示,其中U为结构的弹性变形能,试问的力学意义是什么十一、一弹性体在广义力P1和P2共同作用下,1、2两点产生的广义位移分别为Δ1和Δ2;设P1单独作用1点时,在1、2两点产生的位移分别为Δ11和Δ21;设P2单独作用2点时,在1、2两点产生的位移分别为Δ12和Δ22;试证明:P1×Δ12= P2×Δ21;8分6一、画出图示梁的剪力图和弯矩图;15分二、结构受力如图所示,已知平面钢架ABCD的抗弯刚度为EI,EF杆的抗拉刚度为EA,设3EI=EAL2;试求E、F两点的相对位移;20分三、直径为D的钢制圆轴受力如图所示,材料的许用应力为Σ,已知L、P、M=4PL,试用第三强度理论设计该轴的直径D;15分四、已知某钢结构危险点处的应力状态如图所示,E=200GP A,Μ=;试求:1图示单元体的主应力;2最大剪应力;3最大线应变;4画出相应的三向应力圆草图;15分五、图示为平面直角钢架ABC,受一重物G自高度为H处自由降落在A点处,;15分设EI为钢架的抗弯刚度,试求直角钢架ABC内最大动弯矩MMAX,D六、已知结构某点的交变应力随时间的变化曲线如图所示,试求:1循环特性R ;2平均应力ΣM ;3应力幅度ΣA ;4在ΣM —ΣA 坐标系中,标出该应力循环对应点,并求出自原点出发且通过该点的射线与水平轴ΣM 的夹角Α;10分七、一等直杆受轴向拉伸,当应力达到Σ=250MP A 时,其应变Ε=2×10-3,已知E=200GP A ,L=300MM ,试求此杆的塑性应变;7分八、图示为一等直杆受偏心拉伸,试确定其任意X 截面上的中性轴方程;若设Y P =H /6,Z P =B /6,求其中性轴在Y 轴和Z 轴上的截距A Y =、 A Z =各为多少8分7一、画图示梁的剪力图和弯矩图;15分二、1、什么是材料的力学性质2、为什么要研究材料的力学性质3、今有一新研制的金属塑性材料,请写出应测定该材料的力学性质的名称和符号10个或10个以上;15分三、有一长L=10M,直径D=40CM的原木,Σ=6MP A,欲加工成矩形截面梁,且梁上作用有可移动荷载F,试问:1、当H、B和X为何值时,梁的承载能力最大2、求相应的许用荷载F;15分四、钢制圆轴受力如图所示,已知E=200GP A,Μ=,F1=ΠKN,F2=60ΠKN,M E=4ΠKN·M,L=0.5M,D=10CM,ΣS=360MP A,ΣB=600MP A,安全系数N=3;1试用单元体表示出危险点的应力状态;2试求危险点的主应力和最大线应变;3对该轴进行强度校核;15分五、钢制圆轴受力如图所示,已知材料的许用应力为Σ=100MP A,直径D=5CM,E=200GP A,Μ=,今测得圆轴上表面A点处的周向线应变Ε0=240×10-6,-45°方向线应变Ε-45°=-160×10-6;试求M1和M2,并对该轴进行强度校核;15分六、直径为D的钢制平面曲拐圆轴受力如图所示,已知材料的许用应力为Σ=160MP A,Q=20KN/M,F1=10KN,F2=20KN,L=1M,试设计AB轴的直径D;七、结构受力如图所示,已知M E、A,钢架各杆EI为常数,试求B截面的转角不计剪力和轴力的影响,并画出挠曲线的大致形状;10分八、已知平面钢架EI为常数,试问:若在C处下端增加一刚度为K=3EI/A3单位:N/M的弹性支座后,该钢架的承载能力强度将提高多少倍20分=5×九、已知矩形截面铝合金杆A点处的纵向线应变ΕX10-4,E=70GP A,H=18CM,B=12CM,试求荷载F;10分十、已知槽形截面铸铁梁AB,其许用拉应力为Σ=30MP A,许用压应力为ΣT=120MP A,I Z=18800CM4,Y1=96MM,Y2=164MM,CD杆材料为Q235,直径CD=50MM,L=1M,E=200GP A,ΣP=200MP A,ΣS=240MP A,稳定安全系数N ST=3,经验公式为:Σ=ΛMP A;今有一重为G=200N从高度为H=10CM自由落到AB CR梁B点,试校核AB梁的强度和CD杆的稳定性;20分8一、画图示梁的内力图;15分二、某构件危险点的因力状态如图,材料的E=200GPa,u=,s δ=240MPa,b δ =400 MPa;试求:1. 主因力;2. 最大切因力;3. 最大线因变;4. 画出因力图草图;5. 设n=,校核其强度;15分三、钢制平面直角曲拐OBC,受力如图,3/q kN m π=,OB 段为圆截面,L=10D,[]160MPa σ=;1. 用单元体表示出危险点的因力状态;2. 设计OB 段的直径D;15分四、已知具有中间铰的组合梁EI为常数;重量为G的物体从H高处自由下落,冲击到B截面;1.求A的截面转角;2.画出挠曲线的大致形状;15分五、已知梁EI为常数;今欲使梁的挠曲线在/3处出现一拐点,求12x L/M M的e e比值,并求此时该点的挠度;15分六、分别画出铸铁试件在拉伸、压缩、扭转实验中试件的受力简图;破坏件的草图;危险点的因力状态;在单元体上标出破坏件的草图;危险点的因力状态;在单元体上标出破坏面的方位;在因力图上标出对应的破坏点;分析引起破坏的原因;根据破坏的现象对铸铁抗压、抗拉、抗扭的能力给出结论;15分七、求BC杆的内力,设2/=;20分EA EI a八、 1.何谓材料的持久极限影响构件的持久极限的主要因素又那些写出脉动循环下,构件持久极限与材料持久极限的关系式;2.图示EBD为构件的持久极限简化折线;P为次构件的工作因力点;试σ;该构件的安全系数;循环特征;10分求:P点的,m p九BH 梁和CK 杆横截面均为矩形截面H=60MM ,B=40MM ,L=2.4M ,材料均为Q235,[]200,200,240,120,3p s st E GPa GPa GPa GPa n σσσ=====,经验公式(304 1.12)cr MPa σλ=-;1. 当载荷在BH 梁上无冲击地移动时,求许可载荷[]F ;2. 为提高结构的承载能力,可采取哪些改进措施;定性讨论,可图示20分十、根据强度理论,建立纯剪切因力状态的强度条件;对朔性材料,证明:材料的许用切因力[]τ与许用拉因力[]σ的关系是[][](0.5~0.6)τσ=;10分9一、已知:q 、a,试作梁的内力图;10分二、图示矩形截面杆,上、下表面的轴向线应变分别为:εa=1×10-3,εb=×10-3,E=210Gpa1试求拉力P和偏心距e;2并画出横截面上的正应力分布图;10分三、铸铁梁上作用有可移动的荷载P,已知:y1=52mm,y2=88mm,I z=763cm4,铸铁拉伸时的σb=120Mpa,压缩时的σb=640Mpa,安全系数n=4;试确定铸铁梁的许可荷载P;并求τmax10分四、某低碳钢构件内危险点的应力状态如图,已知:σs=220Mpa,σb=400Mpa,安全系数n=2,E=200Gpa,µ=1试求该点的最大线应变;2画出该点的应力圆草图;3并对该点进行强度校核;10分五、直径为d的钢制圆轴受力如图;已知:P1=20KN,P2=10KN,m=20KN·m,q=5KN/m,σ=160Mpa,试设计AB轴的直径;10分六、已知:q、l、EI试求:等直梁间铰B左右两侧截面的相对转角;10分七、圆截面杆AB、BC的直径、材料均相同,已知:p 、a,E=2.5G,且CD杆的EA=2EI/5a2,试求:CD杆的内力;12分八、已知某合金钢材料的持久极限曲线;试求:1A、B、C、D各点的循环特征r;2σ-1和σb;3G点的σmax和σmin;8分九、图示等截面钢架,受到重量为G=300N的物体冲击,已知:E=200Gpa,试求:钢架内的最大应力;10分十、图示正方形桁架,五根杆均为直径d=5cm的圆截面杆,材料为A3钢,E=200Gpa,σp=200Mpa,σs=240Mpa,a=304Mpa,b=,若取强度安全系数n=2,稳定安全系数n st=3,试确定结构的许可荷载P;10分10一、选择题每题5分,共20分1.图示等直杆,杆长为3a ,材料的抗拉刚度为EA ,受力如图;杆中点横截面的铅垂位移有四种答案:A0; B )/(EA Fa ; C )/(2EA Fa ; D )/(3EA Fa ;正确答案是 ①2.图示圆轴受扭,则A 、B 、C 三个横截面相对于D 截面的扭转角有四种答案: A DA DB DC φφφ==; B 0,DA DBDC φφφ==;C 2DA DB DC φφφ==;D ,0DA DC DB φφφ==;正确答案是 ②3. 材料相同的悬壁梁I 、II,所受载荷及截面尺寸如图所示,关于它们的最大挠度有下列结论:AI 梁最大挠度是II 梁的1/4倍; BI 梁最大挠度是II 梁的1/2倍; CI 梁最大挠度是II 梁的2倍; DI 、II 梁的最大挠度相等;确答案是 ③4.关于图于单元体属于哪种应力状态,有下列四种答案:A 单向应力状态;B 二向应力状态;C 三向应力状态;D 纯剪应力状态;正确答案是 ④ ;二、填空题每题5分,共20分1.矩形截面木拉杆连接如图示,这时接头处的切应力τ= ① ;挤压应力bs σ= ② ;2.已知图a 梁B 端挠度为4/(8)ql EI ,转角为3/(6)ql EI ,则图b 梁C 截面的转角为_________③___________3. a 、b 、c 、三种材料的应力应变曲线如图所示;其中强度最高的材料是 ④ ,弹性模量最小的材料是 ⑤ ,塑性最好的材料是 ⑥ ;4.用积分法求图示变形时, 边界条件为 ⑦ ;连续条件为 ⑧ ;三.计算题 15分作梁的F S 图、 M 图四 计算题15分如图所示的结构,横梁AB 、立柱CB 的材料均为低碳钢,许用应力MPa 160][=σ,AB 梁横截面为正方形,边长b =120mm ,梁AB 长l =3m ,CB 柱为圆形截面,其直径d =30mm ,CB 柱长1l =1m ,,试确定此结构的可载荷[]q ;n st =,E =200GPa,1011=λ;五.计算题20分截面为27525b h mm ⨯=⨯的矩形铝合金简支梁,跨中增加一弹簧刚度18/K KN m =的弹簧;重量Q =250N 的重物从高H =50mm 处自由落下,如图所示;若铝合金的弹性模量E =70GPa ;求冲击时,梁内的最大正应力;六计算题20分两个单元体的应力状态分别如图a、b所示,σ和τ数值相等;试根据第三强度理论比较两者的危险程度;七.计算题20分如图所示矩形梁中性层上C点处,测得与轴线成45︒方向的线应变为ε;矩形截面梁高为h,宽为b,弹性模量为E,泊松比为v,求载荷F;八.计算题20分已知刚架两杆抗弯刚度均为EI,不计剪力和轴力对刚架变形的影响,用力法正则方程求支座A、B的反力;11一.已知AC、BC杆布置及长度如图所示,求C点的水平和竖直位移;二.两实心圆筒连接方式如图所示,数值已在图中标出,单位mm,且M1=m, M2=m; 求:最大剪应力及其产生最大剪应力的位置;最大相对转角;三.T型梁荷载及尺寸大小如图所示,σ拉=40MPa, σ压=100Mpa;验证该梁是否安全;四.圆直杆两端铰接,长度L=,直径D=50mm,材料为A3钢,E=200Gpa .求此圆直杆的临界承载力;五.已知q、a、I.各杆材料相同,求BC杆的轴力,并画出AB、CD杆的弯矩图;六.圆筒截面如图所示,受外力作用而转动,转速n=120rad/min,圆筒表面45°方向є=,E=200Gpa,泊松比u=求圆筒轴承转动所传递的功率;七.由一直杆相连的两轮可在同一平面内转动,杆的截面如图所示,轮轴转速n=120rad/min, r=150mm,杆的比重γ=cm3,L=2m, b=25cm, h=50cm ,求杆的最大正应力;。
北京工业大学考研材料力学真题09-13
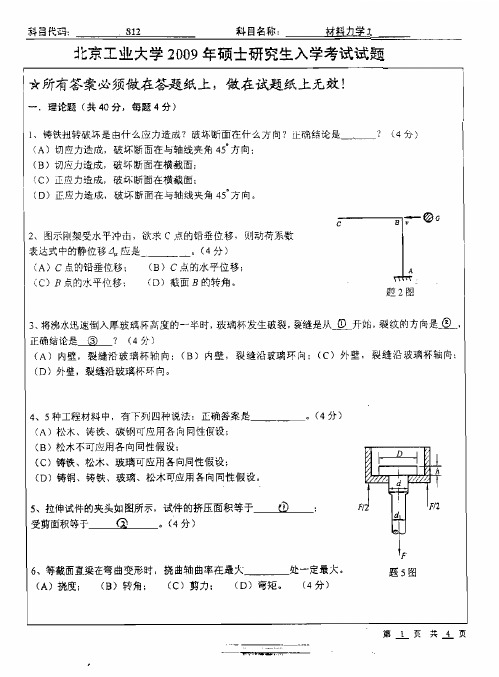
北京工业大学2012年硕士研究生入学考试试题A B C注:所有答案必须做在答题纸上,做在试题纸上无效!第页(共6 页)注:所有答案必须做在答题纸上,做在试题纸上无效!第页(共6 页)注:所有答案必须做在答题纸上,做在试题纸上无效!第页(共6 页)注:所有答案必须做在答题纸上,做在试题纸上无效!第页(共6 页)注:所有答案必须做在答题纸上,做在试题纸上无效!第页(共6 页)e23PlPl已知:2-7. 一刚性杆AB ,A 端铰支,B 端作用一集中力P ,C 、D 处与两根抗弯刚度均为EI 的细长杆铰接,4l AC CD ==,2l DB =,CE H DF ==,如图所示。
试求当结构由细长杆的失稳而毁坏时,载荷P 的临界值。
(10分)题2-7图注:所有答案必须做在答题纸上,做在试题纸上无效!第 页 (共6 页)1-5. ~OO7gIMllt%I¥J3f1J (o~O) fof:flIJ7lJ~;ff1lfl¥Jm.OO~OOOFJT7j\, iXW3ffJtff;f§[r'1JI¥J~~*~~~~, ~-~ (~ (, 4*)A.m 1fl: 5lliN;ffi , m m 5lli!t /F [r'1J ;B. m1.iL5lliNT-RJ, mm5lli!t;ffi ~;c. m1fl, mffi5lli!ttl3if§ RJ; T I50 1500i40i .oili . Ii y50 lorD ~.....--'! 30 Ij 30 4!{}I MPa A BC DR911-6 002-6. B~Q: ff~7}/{f5t\(;1iIf q(x), ;1t-g-j; Jg R, fFffl x ,r2, 0 nn ~iIDJ:.~U1~ aBC TIl]) DY.5t~: &a=O.6xlO·3 , b ,r2, C4''tiFzD DY.1f.Jg &b=1.2xlO·4 , tjf45i1!'lim. E=200GPa, rst~b~ ,lFO.3, l,J.\:sjt: 1) 7}/{f5j;-g-j; R *+, 2) 7}~j;1Ij; R fFfflOO1ft~ x? CI5?t)R60aI_---'-'-'--"-"'--_~:n2-7. ri~mJgJ:[2'j] , P3~£:7v.o, ~Jf-:7vt, (t < ~), tj*4!¥J5E!i'l1fliiJg E, ~t~b~Jg,Lt,)~WJ~*~~rPJtfct) F ~Q7'~j;1~~E Tf'Fffl (:!lQ 00), 1Jt*: ~t~~~Jf-!¥J[;Jl:1t:i: M ~QH t~I¥J [;Jl:1ti: £ill 0 CI5 *F。
材料力学考研真题十一套
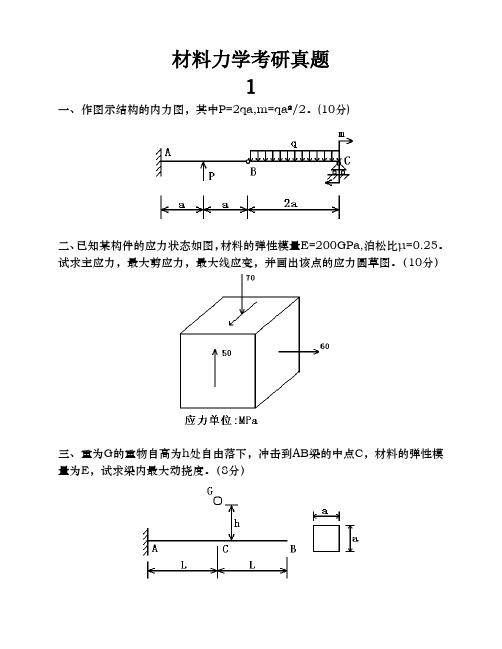
材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2。
(10分)二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ=0.25。
试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图。
(10分)三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度。
(8分)四、钢制平面直角曲拐ABC,受力如图。
q=2.5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P=qL,试设计AB段的直径d。
(15分)x五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角(不计轴力及剪力对变形的影响)。
(12分)六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa,许用剪应力[τ]=1Mpa,胶合面上的许用剪=0.34Mpa,a=1m,b=10cm,h=5cm,试求许可荷载[P]。
(10分)应力[τ]胶七、图示一转臂起重机架ABC ,其中AB 为空心圆截面杆D=76mm ,d=68mm ,BC 为实心圆截面杆D 1=20mm ,两杆材料相同,σp =200Mpa ,σs =235Mpa ,E=206Gpa 。
取强度安全系数n=1.5,稳定安全系数n st =4。
最大起重量G=20KN ,临界应力经验公式为σcr =304-1.12λ(Mpa )。
试校核此结构。
(15分)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,制造时DK 杆短了△。
曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK 抗拉刚度为EA ,且EA=225EI a。
试求: (1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触?(2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。
北京工业大学-材料力学10年考研-试题(答案-正式)说课材料

北京工业大学2010年硕士研究生入学考试试题答案
5. 图示交变应力的循环特征r = ⑽ 0 ;
应力幅度a σ= ⑾ 50 ;平均应力m σ= ⑿ 50 。
6.截面为圆环形的开口和闭口薄壁杆件的横截面如图a 、b 所示,设两杆具有相同的平均半径和壁厚,则二者 ⒀ A 。
A .抗拉强度相同;抗扭强度不同;
B .抗拉强度不同,抗扭强度相同;
C .抗拉、抗扭强度都相同;
D .抗拉、抗扭强度都不同。
7. 正三角形截面压杆,两端球铰约束,加载方向通过压杆轴线。
当载荷超过临界值时,试问压杆将绕着截面上哪一根轴发生屈曲,正确答案是 ⒁ B 。
A .绕y 轴; B.绕过形心C 的任意轴; C .绕z 轴; D.绕y 轴或z 轴。
8.简支梁受力如图所示。
正确的挠曲线形式为 ⒂ C 。
9.插销穿过水平放置的平板上的圆孔,在其下端受有一拉力P 。
该插销的剪切面面积和挤压面积分别等于 ⒃ D 。
A .,Dh π
241D π; B.,h d π 24
1
D π C. ,Dh π)(4122d D -π; D. ,h d π)(4
1
22d D -π
10. 圆轴受扭矩T 的作用,在轴表面贴一应变片,则应变片测出的是 ⒄ A 。
A. 线应变; B. 扭矩; C. 切应变; D. 切应力。
(a)
(b)
D
P d
h
P
A
B
C D 100
σ 0 t (MPa)。
材料力学考研真题与答案

材料力学考研真题与答案材料力学(又称为固体力学)是研究材料在外界力作用下的变形和破坏行为的学科。
对于考研学子来说,掌握材料力学的原理和方法是非常重要的。
为了帮助大家更好地备考材料力学,本文将介绍一些真题及其答案,希望能够对大家有所帮助。
一、选择题1. 对于弹性体的判断,下面哪个说法是正确的?A. 弹性体在外力作用下会产生永久形变。
B. 弹性体在外力作用下会产生破坏。
C. 弹性体在外力作用下会产生可逆形变。
D. 弹性体在外力作用下会产生塑性变形。
答案:C2. 材料的应力-应变关系可以通过以下哪个曲线来描述?A. S曲线B. 对数曲线C. 线性曲线D. 结合曲线答案:C3. 工程上常用的一种化学方法,可以增加材料的强度是?A. 钝化处理B. 热处理C. 激光处理D. 化学处理答案:D二、填空题1. 无固定形状的变形体,称为______。
答案:流体2. 在材料的拉伸过程中,应力与应变之间的关系一般可用______来近似描述。
答案:胡克定律3. 应力的单位为______,应变的单位为______。
答案:帕斯卡,无量纲三、计算题1. 一个弹性材料,在外力作用下产生的应变为0.02,应力为200 MPa。
该材料的弹性模量为多少?答案:弹性模量=E=应力/应变=200 MPa/0.02=10000 MPa2. 一块材料在拉伸试验中,其截面积为5 mm^2,应力-应变曲线如下图所示。
求材料的屈服强度。
(插入应力-应变曲线图)答案:屈服强度即取应力-应变曲线的弹性阶段斜率的最大值,由图可知在0.002处,该斜率最大。
因此,屈服强度为σ=应力/截面积=1000 MPa/5 mm^2=200 MPa。
四、解答题1. 请简述弹性模量的定义和计算公式。
答:弹性模量是衡量材料抵抗应力的能力的物理量,定义为单位应力下的单位应变。
计算公式为E=σ/ε,其中E为弹性模量,σ为应力,ε为应变。
2. 请解释拉压杆的稳定性条件。
答:拉压杆的稳定性条件是指当拉压杆受到压力或拉力作用时,杆件发生屈曲或失稳的条件。
北工大材料科学基础2002-2012真题及部分答案

五、下面题目偏重考察金属材料方面的基础知识:
6、渗碳是将零件置于渗碳介质中试碳原子进出工件表面,然后以下坡扩散的方式使碳原子 从表面相内部扩散的热处理方法。分析说明: (1)钢中空位密度、位错密度和晶粒大小对渗碳速度有何影响? (2)温度对于扩散速度有何影响?将碳在 γ-Fe 中的扩散温度由 927oC 提高到 1027oC,扩 散系数将增加几倍(已知碳在 γ-Fe 中的扩散常数 D0=2.0*10-5m2/s,扩散激活能 Q=140*103J/mol)(10 分)
北工大材料科学基础 2002-2012 真题及部分答案
50 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
51 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
52 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
25 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
26 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
27 北工大专业课课本和真题双重重点
北工大材料科学基础 2002-2012 真题及部分答案
28 北工大专业课课本和真题双重重点
力。( ) 5、一个位错环上必定同时存在刃位错和螺型位错。( ) 6、由一个固相同时析出成分和晶体结构均不相同的两个新固相的过程称为共析转变。( ) 7、非平衡凝固的终结温度高于平衡凝固的终结温度。( ) 8、相图表示的是体系的热力学平衡状态。( ) 9、固溶体合金结晶时,只要液相中存在足够的能量起伏和结构起伏,就可以形核。( ) 10、玻璃在常温下能长期稳定存在,因而它是热力学稳定态。( ) 四、论述及计算题(1-5 题必做,偏金属方向选做 6-9 题,偏无机材料方向选做 10-13 题) (共 100 分)。
材料力学考研真题十一套

材料力学考研真题1一、作图示结构的内力图,其中P=2qa,m=qa²/2。
(10分)二、已知某构件的应力状态如图,材料的弹性模量E=200GPa,泊松比µ=0.25。
试求主应力,最大剪应力,最大线应变,并画出该点的应力圆草图。
(10分)三、重为G的重物自高为h处自由落下,冲击到AB梁的中点C,材料的弹性模量为E,试求梁内最大动挠度。
(8分)四、钢制平面直角曲拐ABC,受力如图。
q=2.5πKN/m,AB段为圆截面,[σ]=160MPa,设L=10d,P=qL,试设计AB段的直径d。
(15分)x五、图示钢架,EI为常数,试求铰链C左右两截面的相对转角(不计轴力及剪力对变形的影响)。
(12分)六、图示梁由三块等厚木板胶合而成,载荷P可以在ABC梁上移动。
已知板的许用弯曲正应力为[σ]=10Mpa,许用剪应力[τ]=1Mpa,胶合面上的许用剪=0.34Mpa,a=1m,b=10cm,h=5cm,试求许可荷载[P]。
(10分)应力[τ]胶七、图示一转臂起重机架ABC ,其中AB 为空心圆截面杆D=76mm ,d=68mm ,BC 为实心圆截面杆D 1=20mm ,两杆材料相同,σp =200Mpa ,σs =235Mpa ,E=206Gpa 。
取强度安全系数n=1.5,稳定安全系数n st =4。
最大起重量G=20KN ,临界应力经验公式为σcr =304-1.12λ(Mpa )。
试校核此结构。
(15分)八、水平曲拐ABC 为圆截面杆,在C 段上方有一铅垂杆DK ,制造时DK 杆短了△。
曲拐AB 和BC 段的抗扭刚度和抗弯刚度皆为GI P 和EI 。
且GI P =45EI 。
杆DK 抗拉刚度为EA ,且EA=225EI a。
试求: (1)在AB 段杆的B 端加多大扭矩,才可使C 点刚好与D 点相接触?(2)若C 、D 两点相接触后,用铰链将C 、D 两点连在一起,在逐渐撤除所加扭矩,求DK 杆内的轴力和固定端处A 截面上的内力。
《材料力学 》(2020年8月整理).pdf

A.错误
B.正确
满分:2 分 3.
两根材料、杆件长度、截面面积和约束条件都相同的压杆,则其临界力也必 定相同。
A.错误
B.正确 满分:2 分 4.
圆杆两面弯曲时,各截面的合弯矩矢量不一定在同一平面内。
6
A.错误
学海无涯
B.正确 满分:2 分 5.
不能通过实验来建立复杂应力状态下的强度条件。
工作应力减小,持久极限降低。 满分:2 分 7.
脆性材料的破坏应力是()
A.
比例极限
B.
弹性极限
C.
屈服极限
D.
强度极限
满分:2 分 8.
圆截面杆受扭转作用,横截面任意一点(除圆心)的切应力方向()
A.
平行于该点与圆心连线
B.
垂直于该点与圆心连线
C.
4
学海无涯 不平行于该点与圆心连线
D.
不垂直于该点与圆心连线
A.错误
B.正确 满分:2 分 24.
强度理论只能用于复杂应力状态。
A.错误
B.正确 满分:2 分 25.
对于各种超静定问题,力法正则方程总可以写为 11X1+Δ1F=0。
A.错误
B.正确 满分:2 分 26.
11
学海无涯 动载荷作用下,构件内的动应力与构件的材料的弹性模量有关。
A.错误
B.正确 满分:2 分 27.
9
A.错误
学海无涯
B.正确 满分:2 分 18.
拉伸(压缩)和弯曲组合变形时中性轴一定不过截面的形心。
A.错误
B.正确 满分:2 分 19.
超静定结构的相当系统和补充方程不是唯一的,但其计算结果都是唯一的。
2020年北京工业大学841结构力学真题

北京工业大学2020年硕士研究生招生考试试题
科目名称:
841 科目代码z 食所有答案必须做在答题纸上,做在试题纸上无效
1.计算图示体系(各杆件均锻接〉的自由度,并对图示体系作几何组成分析。
(10分〉d
M 1j it--}it-
m /N L民,、J →
2.作图示结构的弯矩图。
己知d = 2m. 05分)
D
G
题2图
题l图3.用力法计算图示将架支座B的反力。
各杆EA 相同。
(20分)
UNHM川川wu
,
4.用位移法作图示结构的弯矩图。
EI =常数。
(20分)
B
rr i-!-/1/ / /
扣p 题4图
题3图N
F
-KA
t--··J
nu qJ
5.用力矩分配法作图示结构的弯矩图。
El =常数。
(15分)
l SkN/m l 5kN/m 口TITTlll 盯rrm口,hs 忌,c 』7D Jf 4m 8m 8m 8m 4m 1--→十←一一---+-一-一-→问一-一→+-…-I N
3-Jη 题5图第1页共2页。
北京工业大学841结构力学考研真题(2002-2020年)

北工大841结构力学考研真题(02-20年)(2021届考研)学校:姓名:目录一、北工大结构力学147分学长备考经验 (1)二、北工大841结构力学考研真题(2002-2020年) (3)北京工业大学2002年硕士研究生入学考试试题 (3)北京工业大学2003年硕士研究生入学考试试题 (5)北京工业大学2004年硕士研究生入学考试试题 (7)北京工业大学2005年硕士研究生入学考试试题 (9)北京工业大学2006年硕士研究生入学考试试题 (11)北京工业大学2007年硕士研究生入学考试试题 (14)北京工业大学2009年硕士研究生入学考试试题 (20)北京工业大学2010年学术型硕士研究生入学考试试题 (22)北京工业大学2011年硕士研究生入学考试试题 (24)北京工业大学2012年硕士研究生入学考试试题 (26)北京工业大学2013年硕士研究生入学考试试题 (28)北京工业大学2014年硕士研究生入学考试试题 (30)北京工业大学2015年硕士研究生入学考试试题 (32)北京工业大学2016年硕士研究生入学考试试题 (34)北京工业大学2017年硕士研究生招生考试试题 (36)北京工业大学2018年硕士研究生招生考试试题 (38)北京工业大学2019年硕士研究生招生考试试题 (40)北京工业大学2020年硕士研究生招生考试试题................ 待学校公布后免费领取一、北工大结构力学147分学长备考经验结构力学是两门最重要的业务课之一,复习质量的好坏直接关乎最后能否成功上岸,结构力学近些年基本全是计算大题,复习的好可以轻松拿到140+,弥补自己其他科目的不足,但太多人因为没复习好结构力学,落后其他人几十分,最后遗憾落榜。
故希望学弟学妹们重视对结构力学的学习,本贴主要分享我自己的结构力学复习过程和总结的经验建议供学弟学妹们参考。
1、复习资料结构力学课本(龙驭球版);于玲玲结构力学(第二版);李其林小黄书及视频讲解;北工大历年真题。
北京工业大学考研专业课真题_材料力学2013

(1ji:iZt, 4 %)
A
B
DA
c
D
J!
1-3
00
(4)
p
1-4. OO~*f:i*, 7.K Sf;ff ~ffi!t¥fPX:a A, bh ; B, bhtga;
C, bh/cosa;
D, bh/(cosa -sina)
0
$B$!E~f&~OO:itI~1f-li~Uti~I¥J.*JEfJ
,JEfJ $jmaa=
(4~)
/Hi 1-900
1-10. !E~OOmffiJt1ttM!liffi5tjr j]1~~E T 1'F ffl, ~J§Jf RI ~D R2 0-J3iJ.IfQTT R3 ~Q ~, ~o 00
~it1tt:tEm~1'Ffflr, R J I¥JJE~m7'1 CI' JiliJJltS1JE~1Xi-*~ Cds=
(13)
0 (
0
, 4 ~)
/Hi 1-1000
dt*I~*~ 2013 ~i9i±-fi1f~~A~;lflttutH
~Eli-\:~:
812
~§~~:
tt*~1J~I
*M*4.~
~HH~;iiij;
812
~ EI~fijt:
~*~t.J~I
"* fJf~$~&"~1l;f£$J!~J:.,
(~~,
~;f£ii.J!~J:.x~
(8)
o
1-8.-1f%~~rnHHl*lliH, ;a::tEJ:Ctt6-~~/J\fL(~D~]), !i1IJ~H!=ij ~**§ ~t
北京工业大学《812材料力学》I历年考研真题汇编

材料力学考研真题答案

材料力学考研真题答案一、选择题1. 材料力学中,描述材料弹性特性的物理量是( A )。
A. 杨氏模量B. 泊松比C. 剪切模量D. 屈服强度2. 在材料力学中,当材料受到拉伸时,其内部的应力与应变之间的关系是( B )。
A. 线性关系B. 非线性关系C. 没有关系D. 反比关系二、简答题1. 请简述材料的弹性模量和剪切模量的区别。
弹性模量是指材料在单轴拉伸或压缩时,应力与应变的比值,它反映了材料抵抗形变的能力。
剪切模量则是指材料在剪切状态下,剪切应力与剪切应变的比值,它反映了材料抵抗剪切形变的能力。
两者都是描述材料刚度的物理量,但应用的力学状态不同。
2. 解释什么是材料的屈服现象,并说明其在工程应用中的重要性。
屈服现象是指材料在受到一定的应力后,即使应力不再增加,材料也会发生明显的塑性变形。
屈服点是材料从弹性阶段过渡到塑性阶段的临界点。
在工程应用中,了解材料的屈服点对于设计结构的安全性和可靠性至关重要,可以避免结构在实际使用中发生不可逆的变形或破坏。
三、计算题1. 某材料的杨氏模量为200 GPa,泊松比为0.3。
若该材料的一根杆件受到100 MPa的拉伸应力,请计算其纵向应变。
根据胡克定律,\( \varepsilon = \frac{\sigma}{E} \),其中\( \varepsilon \) 为应变,\( \sigma \) 为应力,\( E \) 为杨氏模量。
代入数据得:\( \varepsilon = \frac{100 \times 10^6 \text{Pa}}{200\times 10^9 \text{Pa}} = 5 \times 10^{-4} \)。
2. 一根直径为20 mm的圆杆,在受到轴向拉伸力作用下,其横截面面积减小了1%。
如果材料的屈服强度为300 MPa,计算该圆杆是否处于屈服状态。
首先计算圆杆的横截面面积变化量:\( A_0 = \frac{\pi}{4}\times (20 \times 10^{-3})^2 \),\( A = A_0 \times (1 - 0.01) \)。
