运筹学基础及应用第四版胡运权主编课后练习答案
清华大学运筹学教程胡运权主编课后习题答案
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
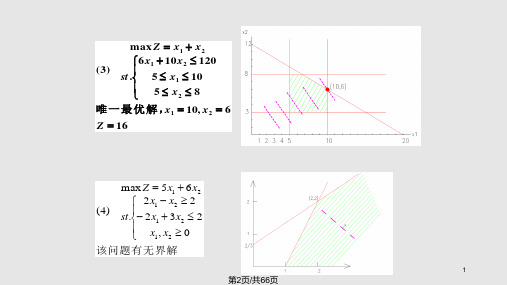
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
运筹学(胡运权第四版及答案)

主讲:谢先达
2014.09
联系方式 办公室:QL643 87313663 手机: 13600512360 邮箱: xxdhz@
绪
论
绪论
什么是运筹学?
运筹学发展历史 运筹学主要内容 运筹学的基本特征与基本方法
绪论
什么是运筹学?
定义:为决策机构在对其控制下业务活动进行决策 时,提供以数量化为基础的科学方法。
概念:可行解、最优解、最优值
第一章:线性规划及单纯形法
练习:靠近某河流有两个化工厂,流经第一化工厂的河流流量为每天 500万m3,在两个工厂之间有一条流量为每天200万m3支流,第一化工厂每 天排放含有某种有害物质的工业污水2万m3 ,第二化工厂每天排放这种 工业污水1.4万m3 。从第一化工厂排出的工业污水流到第二化工厂以前, 有20%可自净化。根据环保要求,河流中工业污水的含量应不大于0.2%, 这两个工厂都需各自处理一部分工业污水,第一化工厂处理工业污水的 成本是1000元/万m3 。第二化工厂处理污水的的成本是800元/万m3 。现 问在满足环保要求的条件下,每厂各应处理多少工业污水,使这两个工 厂总的处理工业污水费用最小。
-x1+x2+x3 = 4
-2x1+x2-x3 ≤ 6 x1 ≤ 0,x2 ≥ 0, x3取值无约束
第一章:线性规划及单纯形法
线性规划问题及其数学模型 线性规划图解法
单纯形法原理
单纯形法计算步骤
单纯形法的进一步讨论
第一章:线性规划及单纯形法
x2
目标函数: 约束条件: maxz=50x1+100x2 x1+x2≤300 2x1+x2≤400 x2≤250 x1≥0 ,x2≥0
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答z 3。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
(a)约束方程组的系数矩阵12 3 6 3 0A 8 1 4 0 23 0 0 0 0基基解是否基可行解目标函数值X1 X2 X3 X4 X5 X6P1 P2 P3163 7-60 0 0否P1 P2 P4 0 10 0 7 0 0 是10P1 P2 P50 3 0 0 72是 3习题一P46x i1-的所有X i,X2,此时目标函数值o(b)约束方程组的系数矩阵A 12 3 4A2 2 12⑻(1)图解法基 基解 是否基可行解 目标函数值X 1X 2X 3X 4P 1P 24 11否"2P 1P 3 2 0 110 是435 ~5~5P 1P 4111否—36P 2P 312是52P 2P 41否22P 3P 40 0 1 1是5最优解xT2 11 5吋omax z 10x 1 5x 2 0x 3 0x 4 3x i 4X 2 X 3st. 5x 1 2x 2 x 48 9 8 12。
min—,— — 5 3 5C j 105 0 0 C B基b X 1X 2X 3X 421143 0 X 3— 1—"5"5582110X 11C j 105 0 0 C B 基bX 1 X 2 X 3 X 4 0 X 3 9 341 0 0X 48[5] 20 1 C j Z j105令 X iX 20,0,9,8,由此列出初始单纯形表最优解即为3x1 4x2 9的解x5x 1 2x 2 81,-,最大值z 竺 2 2(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式则P 3,P 4组成一个基。
得基可行解xC j Z j0 1221 8320,min14 22新的单纯形表为C j 105 0 0 C B基b X 1X 2X 3X 435 3 5X 2— 01— —2141410X 11121—7525c jZ j14 143*35x i 1, x 2 - , X 3 0, X 4 0。
运筹学基础及指导应用第四版胡运权主编课后练习问题详解
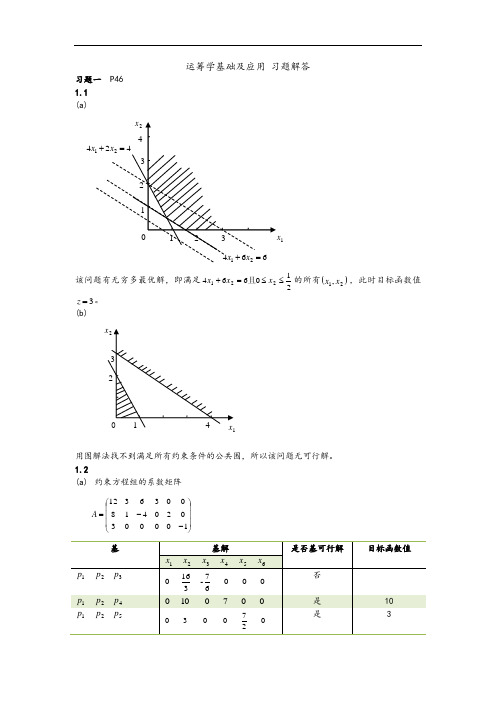
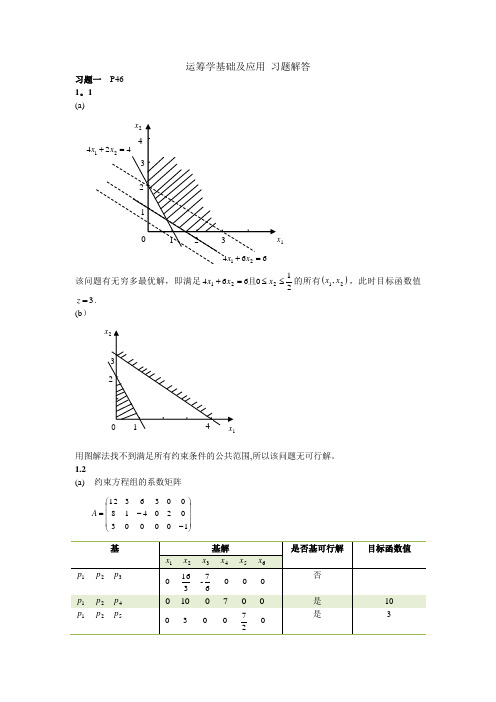
运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z 。
(b)用图解法找不到满足所有约束条件的公共围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫ ⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 231,4321====x x x x 。
最大值 235*=z (b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
运筹学基础及应用课后习题答案(第一二章习题解答)

运筹学基础及应用课后习题答案(第一二章习题解答)第一章:线性规划一、选择题1. 线性规划问题中,目标函数可以是()A. 最大化B. 最小化C. A和B都对D. A和B都不对答案:C解析:线性规划问题中,目标函数可以是最大化也可以是最小化,关键在于问题的实际背景。
2. 在线性规划问题中,约束条件通常表示为()A. 等式B. 不等式C. A和B都对D. A和B都不对答案:C解析:线性规划问题中的约束条件通常包括等式和不等式两种形式。
二、填空题1. 线性规划问题的基本假设是______。
答案:线性性2. 线性规划问题中,若决策变量个数和约束条件个数相等,则该问题称为______。
答案:标准型线性规划问题三、计算题1. 求解以下线性规划问题:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 83x + 4y ≤ 12x, y ≥ 0答案:最优解为 x = 4, y = 2,最大值为 Z = 14。
解析:画出约束条件的图形,找到可行域,再求目标函数的最大值。
具体步骤如下:1) 将约束条件化为等式,画出直线;2) 找到可行域的顶点;3) 将顶点代入目标函数,求解最大值。
第二章:非线性规划一、选择题1. 以下哪个方法适用于求解非线性规划问题()A. 单纯形法B. 拉格朗日乘数法C. 柯西-拉格朗日乘数法D. A和B都对答案:B解析:非线性规划问题通常采用拉格朗日乘数法求解,单纯形法适用于线性规划问题。
2. 非线性规划问题中,以下哪个条件不是K-T条件的必要条件()A. 梯度条件B. 正则性条件C. 互补松弛条件D. 目标函数为凸函数答案:D解析:K-T条件包括梯度条件、正则性条件和互补松弛条件,与目标函数是否为凸函数无关。
二、填空题1. 非线性规划问题中,若目标函数和约束条件都是凸函数,则该问题称为______。
答案:凸非线性规划问题2. 非线性规划问题中,K-T条件是求解______的必要条件。
运筹学 胡运权 课后答案课件

m
a ij y i c j
i1
yi 0
y
无
i
约
束
( j 1,..., n1 )
( j n1 1,..., n ) (i 1,...m 1 ) (i m 1 1,...m )
运筹学 胡运权 课后答案
2.4
运筹学 胡运权 课后答案
运筹学 胡运权 课后答案
2.9
运筹学 胡运权 课后答案
(d)
对偶问题:
max w 2y1 3 y2 5 y3
y1 2y2 y3 2
3 y1
y2 4 y3 2
4 y1 3 y2 3 y3 4
y1 0, y2 0, y3取 值 无 约 束
对偶问题:
m
m i n w b i y i i1
m
a ij y i c j
i1
(1,2章)
运筹学 胡运权 课后答案
图解法:
当 x2 2 x 11 5z经 过 运筹点 学 胡( 运1 权, 课3 2 后) 答案时 , z最 大 。
单纯形法:添加松弛变量化为标准形式,
max z 10x1 5x2 0x3 0x4
3x1 5 x1
4x2 2x2
x3
x4
9 8
x
j
0
( j 1, 2, 3, 4)
运筹学 胡运权 课后答案
1.6(a)
运筹学 胡运权 课后答案
运筹学 胡运权 课后答案
1.7
运筹学 胡运权 课后答案
1.8
(P36公式)表1-24中,x1,x5为基变量,g=1, h=0,l=0。
运筹学 胡运权 课后答案
1.11
运筹学 胡运权 课后答案
最新《运筹学》第四版课后习题答案
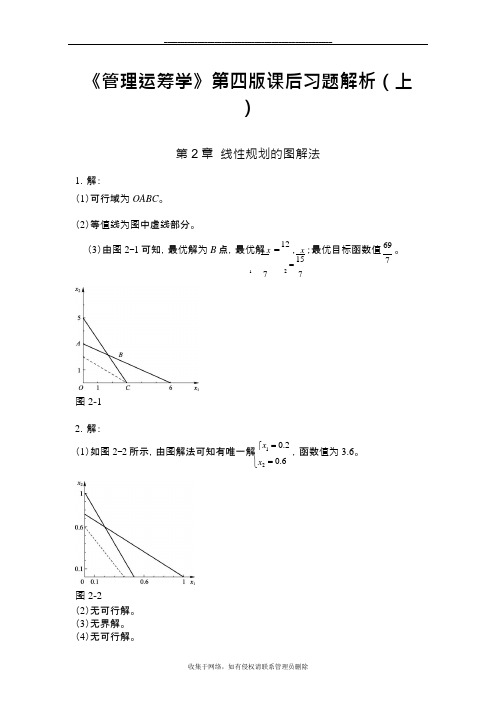
作出可行域.
x2y20
2xy16
得Q(4,8)
z最大200424082720
答:该公司安排甲、乙两种柜的日产量分别为4台和8台,可获最大利润2720元.
8.解:
设需截第一种钢板x张,第二种钢板y张,所用钢板面积zm2. 目标函数z=x+2y,线性约束条件:
xy12
2xy15
x3y27
x0
y0
x3y27
(4)x16。
x24。
(5)最优解为x1=8,x2=0。
(6)不变化。因为当斜率1≤c1
c2
1,最优解不变,变化后斜率为1,所以最优解3
不变。
7.解:
设x,y分别为甲、乙两种柜的日产量, 目标函数z=200x+240y,线性约束条件:
6x12y120
8x4y64
即
x0
y0
x2y20
2xy16
x0
y0
x350
得ቤተ መጻሕፍቲ ባይዱ
y100
即C(350,100).当直线6x+10y=0即3x+5y=0平移到
经过点C(350,100)时,z=6x+10y最大
12.解:
模型maxz500x1400x2
2x1≤300
3x2≤540
2x12x1≤440
1.2x11.5x2≤300
x1,x2≥0
(1)x1150,x270,即目标函数最优值是103000。
《管理运筹学》第四版课后习题解析(上
)
第
1.解:
(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解x=12,x15
最新《运筹学》第四版课后习题答案
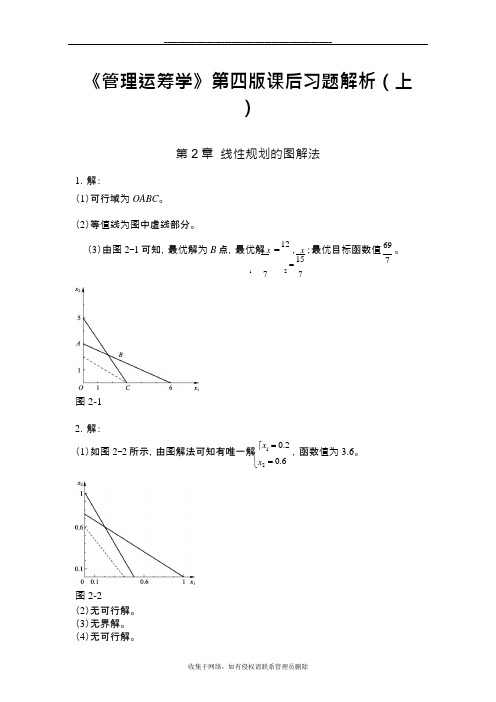
收集于网络,如有侵权请联系管理员删除⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12, x = 15 1727图2-1;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 ⎧x 1 = 0.2,函数值为3.6。
⎩x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
⎨ (5)无穷多解。
⎧x = (6)有唯一解 ⎪ 1⎪ 203 ,函数值为 92 。
8 3 x = ⎪⎩ 2 33.解: (1)标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4.解: 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
运筹学基础及应用第四版胡运权主编课后练习答案
运筹学基础及应用 习题解答习题一 P46 1。
1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z . (b )用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫ ⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1。
3(a )(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 23 1,4321====x x x x 。
最大值 235*=z(b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
运筹学基础及应用第四版胡运权主编课后练习答案【精】

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z 。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫ ⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 231,4321====x x x x 。
最大值 235*=z (b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
清华大学胡运权运筹学
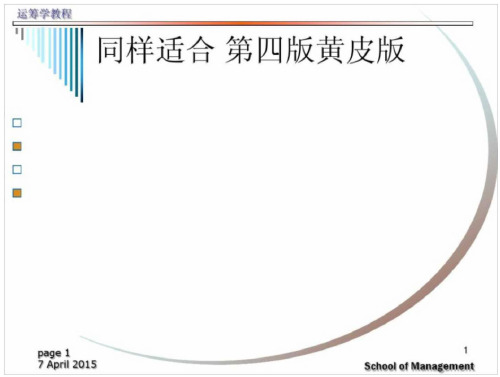
cx°-cx* >0;
V是maxZ = C*X的S优解, 故 /
C*X*-C'X°>0;
Jr
(C*-C)(X*-X°)
= C(X°-X*) + C*(X*-X°)>0
page 25 7 April 2015
25
School of Management
第一章习题解答
1.11考虑线性规划问题
□
minZ =叫 +2JC2 + — 4X4
□
行域的每个顶点依次使目标函数达到最优。 鲤. 锒剎曷錄里姉取妾加下.
c广
cd
0
0
基b Xi x2
x3
d
x2 3/ 0 1
5/14
2
X4 j
-3/4
c
page 14
7 April 2 ns
Xi 1 1 0
Qi—'0
0
-2/14 ^W35
-
3/14d- i
第一章习题解答
□ □
当c/d在3/10到5/2之间时最优解为图中 的A 点;当c/d大于5/2且c大于等于0时最优解 为图中 的B点;当c/d小于3/10且d大于0时最优 解为图中
Bi. ■
规划问题的 maxZ = C1 X (AX =b
□
最优解, 证明[在x >0这两点连线
■
上的所有点也是 对于任何0 < a < 1, 两点连线」:的点¥满足:
X =aX⑴+(l-a)JT2)也是可行解, 且
CTX = CTaXG) +Cf\l-a)X(2y
=CTaXay -aCrX(2} +CrX
School of Management
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用第四版胡运权主编课后练习答案一、线性规划1. 求解下列线性规划问题:max z = 3x1 + 2x2s.t.2x1 + x2 ≤ 8x1 + 2x2 ≤ 6x1, x2 ≥ 0答案:首先将约束条件化为标准形式,得到:max z = 3x1 + 2x2 + 0s1 + 0s2s.t.2x1 + x2 + s1 = 8x1 + 2x2 + s2 = 6x1, x2, s1, s2 ≥ 0通过单纯形法求解,得到最优解为:x1 = 2, x2 = 2,最优值为8。
2. 求解下列线性规划问题的对偶问题:min z = 2x1 + 3x2s.t.x1 + 2x2 ≥ 42x1 + x2 ≥ 6x1, x2 ≥ 0答案:原问题的对偶问题为:max z' = 4y1 + 6y2s.t.y1 + 2y2 ≤ 22y1 + y2 ≤ 3y1, y2 ≥ 0通过单纯形法求解,得到最优解为:y1 = 1, y2 = 1,最优值为10。
二、非线性规划1. 求解下列非线性规划问题:min f(x) = x^2 + 2x + 3s.t.x ∈ [0, 4]答案:首先求导数,得到f'(x) = 2x + 2。
令导数等于0,得到x = -1。
由于x ∈ [0, 4],所以只需考虑x = 0和x = 4。
计算f(0) = 3,f(4) = 31。
因此,最小值为3,对应的x = 0。
2. 求解下列非线性规划问题:max f(x) = x^3 - 3x^2 + 4s.t.x ∈ [0, 3]答案:首先求导数,得到f'(x) = 3x^2 - 6x。
令导数等于0,得到x = 0或x = 2。
计算f(0) = 4,f(2) = 2,f(3) = 2。
因此,最大值为4,对应的x = 0。
三、整数规划1. 求解下列整数规划问题:max z = 3x1 + 2x2s.t.x1 + 2x2 ≤ 8x1, x2 ∈ Z答案:通过分支定界法求解,得到最优解为:x1 = 2, x2 = 3,最优值为10。
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z 。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫ ⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 23 1,4321====x x x x 。
最大值 235*=z(b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题:
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0
清华大学《运筹学教程》胡运权主编课后习题答案

0
0
0 -1/5 2/5 0
1
0 3/5 -1/5 0
0
x3
1
0
0
1
1
1 -1
cj zj
0
0
0 -1/5 -M+7/5 -M
由于上表中所有检验数都小于等于零(且非基变量检验数都 小于0),因此已经得到唯一最优解,最优解为:
X * 25 ,9 /5 ,1 ,0 ,0 ,0 T
方法二:两阶段法
第一阶段:
4x1 x2 2x3 x4 2
(1)
stx12x1x23xx23
2x4 14 x3 x4
. 2
x1, x2, x3 0, x4无约束
minZ 2x1 2x2 3x3
(2)
st
x1 x2 x3 4 2x1 x2 x3 6
x1 0, x2 0, x3无约束
minZ 3x1 4x2 2x3 5x4
7
4 -1
1
1/3 0
0 [5/3] -1
0
5/3 0
0
5/3
-1
0 -1 -1
i
x4
x5
x6
0
10
1
0
0 1 3/2
1
00
4
0
00
0 1/3 0 3
0 -4/3 1 6/5 1 -1/3 0 9/5 0 -7/3 0
cj
0
CB
xB
b
x1
0
x1 3/5
1
0
x 2 6/5
0
0
x4
1
0
cj zj
0
4x1 x2 2x3 x41 x42 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学基础及应用 习题解答习题一 P461.1 (a)x244x 1 2x 243 2 1123 x 14x 1 6x 26该问题有无穷多最优解,即满足14x 1x 2 6且0 x 2的所有 x 1,x 2 ,此时目标函数值62z 3。
(b)x23 20 1 4x1用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵12 3 6 3 0 0 A8 1 4 0 2 03 0 00 01基基解是否基可行解目标函数值x 1xxxxx23456p 1pp2 30 16 3 - 760 0 0 否p10 0 7 0是101 pp24p 1p p250 3 0 07 2是3p1 p p2 6 7 21否4 0 0 04 4p1 p p3 4 0 0 528 0 0否p1 p p3 5 0 0 320 8 0是 3p1 p p3 6 1 0 120 0 3否p1 p p 0 0 0 3 5 0 是04 5p1 p p4 65 否150 0 2 04 4T最优解x 0,10,0, 7,0,0。
(b) 约束方程组的系数矩阵A 12223142基基解是否基可行解目标函数值x1 x x x2 3 4p1 p2 4 1120 0否p1 p3 2 11是0 05 5435p1 p4 1 11否0 03 6p2 p3 0 122 0是 5p2 p 40 120 2否p3 p 0 0 1 1 是 5 42 11 x ,0, ,05 5 T最优解。
1.3(a)(1) 图解法x243210 1 2 3 x1最优解即为3x15x14x22 x298的解3x 1,,最大值2z352(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z 10x1 5x20 x30x4s.t.3x15x14x22x2x3x498则P3 , P4 组成一个基。
令x1 x2 0得基可行解x 0,0,9,8 ,由此列出初始单纯形表c 10 5 0 0jc 基 b x1 x2 x3 x4B0 x3 3 4 1 090 x4 [5] 2 0 18c j zj10 5 0 01 。
2 min85,9385c 10 5 0 0 jc 基 b x1 x2 x3 x4 B0 x321514513510 x18512515c j z 0 1 0 2j0 2 ,min2114,8232新的单纯形表为c 10 5 0 0jc 基 b x1 x2 x3 x4 B5 x 2320 151431410 x1 11 0 1727c j zj 0 0514251431, 2 0,表明已找到问题最优解x1 1, x2 , x3 0,x4 0 。
最大值2*z352(b)(1) 图解法6x1 x22 24x2129x1 x25630 3 6 9 x1最优解即为6x1x12x2x2245的解7 3x , ,最大值2 2z172(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z 2x x 0x 0x 0x1 2 3 4 55x x 152 3s.t .6x 2x x 241 2 4x x x1 2 55则P,P4 ,P5 组成一个基。
令x1 x2 0 3得基可行解x 0,0,15,24,5 ,由此列出初始单纯形表c 2 1 0 0 0jc 基 b x1 x2 x3 x4 x5 B0 x3 15 0 5 1 0 0 0 x4 24 [6] 2 0 1 00 x5 5 1 1 0 0 1c 2 1 0 0 0 j zj1 。
224 5 min , , 46 1c 2 1 0 0 0jc 基 b x1 x2 x3 x4 x5 B0 x3 15 0 5 1 0 02 x4 4 113160 x5 10 23161c 0 j zj 13 013 00 2 ,15 3 3 min , 24,5 2 2新的单纯形表为c 2 1 0 0 0jc 基 b x1 x2 x3 x4 x5 B0 x31520 0 1541522 x4721 0 014120 x5320 1 01432c j zj 0 0 014127 151 ,表明已找到问题最优解x1 1 ,x2 ,x3 ,x4 0,x5 0 。
最大, 2 02 2值* 17z21.6' '' ''(a) 在约束条件中添加松弛变量或剩余变量,且令x2 x x x 0, x 02 2 2 2,'x x3, z'3z该问题转化为max z' 3x1'x2''x22x ' 3 0 x40 x52x 1 '3x2 3x '' 2 '4x3x412s.t .4 '''x2''x2'x ,3x13x1x ,1x2x'x2' '', x ,2 22x'xx35'3x3,x4568其约束系数矩阵为2 3 3 4 1 0A 4 1 1 2 0 13 1 1 3 0 0在A 中人为地添加两列单位向量P7 ,P82 3 3 4 1 0 0 04 1 1 2 0 1 1 03 1 1 3 0 0 0 1' '' '令 4 5 6 7 max z'3x1 x x 2x 0x 0x Mx Mx2 2 3得初始单纯形表c 3 1 1 2 0 0 M Mj' '' 'c 基 b 1 x x x x4 x5 x6 x7xB 2 2 30 x4 2 3 3 4 1 0 0 012M x6 4 1 1 - 2 0 -1 1 08M x7 6 3 1 1 -30 0 0 1c j z 3 7M 1 1 2 5M 0 M 0 0j(b) 在约束条件中添加松弛变量或剩余变量,且令' '' ' ''x x x x x3 3 3 3 0, 3 0 ,z' z该问题转化为' ''max z'3x 5x x x 0x0x1 2 3 3 4 5' ''x 2x x x x 61 2 3 3 4s.t.' ''2x x 3x 3x x 161 2 3 3 5' ''x x 5x 5x 101 2 3 3' ''x , x , x , x , x , x 01 2 3 3 4 5其约束系数矩阵为1 2 1 1 1 0A 2 1 3 3 0 11 1 5 5 0 0在A 中人为地添加两列单位向量P7 ,P81 2 1 1 1 0 1 02 13 3 0 1 0 01 1 5 5 0 0 0 1令' ''max z'3x 5x x x 0x 0x Mx Mx1 2 3 3 4 5 6 7得初始单纯形表c 3 -5 1 -1 0 0 -M Mjc 基 b x1 x2 x3 x3 x4 x5 x6 x7BM x6 61 2 1 -1 -1 0 1 00 x 1652 13 -3 0 1 0 0M x7 101 1 5 -5 0 0 0 1c j z 3 2M 5 3M 1+6 M-1-6 M-M 0 0 0j1.7(a)解1:大M 法在上述线性规划问题中分别减去剩余变量x4, x6 ,x8, 再加上人工变量x5, x7 ,x9 ,得max z 2x x 2x 0x Mx 0x Mx 0x Mx1 2 3 4 5 6 7 8 9x x x x x123456s,t,2x x x x213672x x x x02389 x,x,x,x,x,x,x,x,x0 123456789其中M是一个任意大的正数。
据此可列出单纯形表c2120M0M0Mji c基b x1x2x3x4x5x6x7x8x9bM x561111100006M x72201001100M x900[2]10000110c z2M3M12M M0M0M0j jM x56103/211001/21/24M x7220[1]0011002 1x02011/200001/21/2c z205300113M M M j jM M M222222M x53[4]00113/23/21/21/23/42x232010011001x12110001/21/21/21/2c z450003353113M M M M j jM M22222x3/411001/41/43/83/81/81/82x7/230011/21/21/41/41/41/41x7/420101/41/41/81/83/83/8c z0005/453/8399M M M j j4888由单纯形表计算结果可以看出,40且a i40(i1,2,3),所以该线性规划问题有无界解解2:两阶段法。
现在上述线性规划问题的约束条件中分别减去剩余变量x4,x6,x8,再加上人工变量x5,x7,x9,得第一阶段的数学模型据此可列出单纯形表c000010101 ji c基b x1x2x3x4x5x6x7x8x9b1x651111100006 1x272010011001x090[2]10000110c z131101010j j1x65103/211001/21/24 1x2720[1]0011002 0x02011/200001/21/2c z105/2101013j j221x35[4]00113/23/21/21/23/4 0x232010011000x12110001/21/21/21/2c z000010101j j2x3/411001/41/43/83/81/81/82x7/230011/21/21/41/41/41/4 1x7/420101/41/41/81/83/83/8c z000010101j j第一阶段求得的最优解*377TX(,,,0,0,0,0,0,0)442,目标函数的最优值*0。
因人工变量x5x7x90,所以*377TX(,,,0,0,0,0,0,0)是原线性规划问题的基可442行解。
于是可以进行第二阶段运算。
将第一阶段的最终表中的人工变量取消,并填入原问题的目标函数的系数,进行第二阶段的运算,见下表。
c z2120000ij jc基b x1x2x3x4x6x8b2x3/411001/43/81/82x7/20011/21/41/4 31x7/40101/41/83/8 2c z0005/43/89/8j j由表中计算结果可以看出,40且a i40(i1,2,3),所以原线性规划问题有无界解。
