第六节_无约束优化方法鲍威尔
无约束优化方法程序

无约束优化方法---鲍威尔方法本实验用鲍威尔方法求函数f(x)=(x1-5)2+(x2-6)2 的最优解。
一、简述鲍威尔法的基本原理从任选的初始点x⑴o出发,先按坐标轮换法的搜索方向依次沿e1.e2.e3进行一维搜索,得各自方向的一维极小点x⑴ x⑵ x⑶.连接初始点xo⑴和最末一个一维极小点x3⑴,产生一个新的矢量 S1=x3⑴-xo⑴再沿此方向作一维搜索,得该方向上的一维极小点x⑴.从xo⑴出发知道获得x⑴点的搜索过程称为一环。
S1是该环中产生的一个新方向,称为新生方向。
接着,以第一环迭代的终点x⑴作为第二环迭代的起点xo⑵,即 Xo⑵←x⑴弃去第一环方向组中的第一个方向e1,将第一环新生方向S1补在最后,构成第二环的基本搜索方向组e2,e3,S1,依次沿这些方向求得一维极小点x1⑵,x2⑵,x3⑵.连接Xo⑵与x3⑵,又得第二环的新生方向S2=x3⑵-xo⑵沿S2作一维搜索所得的极小点x⑵即为第二环的最终迭代点二、鲍威尔法的程序#include "stdafx.h" /* 文件包含*/#include <math.h>#include <stdio.h>#include <stdlib.h>#define MAXN 10#define sqr(x) ((x)*(x))double xkk[MAXN],xk[MAXN],sk[MAXN];int N,type,nt,et; //N--变量个数,type=0,1,2,3 nt,et--不等式、等式约束个数double rk;double funt(double *x,double *g,double *h){g[0]=x[0]; g[1]=x[1]-1; g[2]=11-x[0]-x[1];return sqr(x[0]-8)+sqr(x[1]-8);}double F(double *x){double f1,f2,ff,fx,g[MAXN],h[MAXN];int i;fx=funt(x,g,h);f1=f2=0.0;if(type==0 || type==2)for(i=0; i<nt; i++) f1+=(fabs(g[i])>1.0e-15)?1.0/g[i]:1.0e15;else for(i=0; i<nt; i++) f1+=(g[i]>0)?0:g[i]*g[i];for(i=0; i<et; i++) f2+=h[i]*h[i];if(type==0 || type==2)ff=fx+rk*f1+f2/sqrt(rk);else ff=fx+rk*(f1+f2);return ff;}double f(double x){int i;for (i=0; i<N; i++) xkk[i]=xk[i]+x*sk[i];return F(xkk);}void find_ab(double x0,double h0,double *a,double *b) {double h,x1,y1,x2,y2,x3,y3;h=h0;x1=x0; y1=f(x1); x2=x1+h; y2=f(x2);if (y2>=y1) {h=-h0; x3=x1; y3=y1;x1=x2; y1=y2; x2=x3; y2=y3;}for (;;) {h*=2.0; x3=x2+h; y3=f(x3);if (y2<y3) break;x1=x2; y1=y2; x2=x3; y2=y3;}if (h>0) {*a=x1; *b=x3;}else {*a=x3; *b=x1;}}void search_gold(double a,double b,double e,double *x,double *y) {double x1,x2,y1,y2;x1=a+0.382*(b-a); y1=f(x1);x2=a+0.618*(b-a); y2=f(x2);do {if (y1<y2) {b=x2; x2=x1; y2=y1;x1=a+0.382*(b-a); y1=f(x1);} else {a=x1; x1=x2; y1=y2;x2=a+0.618*(b-a); y2=f(x2);}} while ((b-a)>e);*x=0.5*(a+b); *y=f(*x);}double nc_powell(double *x0,double e1,double e2){int i,j,k=1,m;double a,b,ax,ay,d;doubless[MAXN][MAXN],s1[MAXN],ff[MAXN],x[MAXN],xn[MAXN],xn 1[MAXN],f0,f1,f2,f3;for (i=0; i<N; i++) for (j=0; j<N; j++) if (j==i) ss[i][j]=1; else ss[i][j]=0;for (;;) {for (j=0; j<N; j++) xk[j]=x0[j];for (i=0; i<N; i++) {for (j=0; j<N; j++) sk[j]=ss[i][j];find_ab(0,1,&a,&b);search_gold(a,b,e2,&ax,&ay);for (j=0; j<N; j++) xk[j]=xkk[j];ff[i]=F(xk);}for (j=0; j<N; j++) xn[j] = xkk[j];for (j=0; j<N; j++) { sk[j]=xkk[j]-x0[j]; s1[j]=sk[j];}find_ab(0,1,&a,&b);search_gold(a,b,e2,&ax,&ay);for (j=0; j<N; j++) x[j]=xkk[j];d=0;for (j=0; j<N; j++) d+=(x[j]-x0[j])*(x[j]-x0[j]);d=sqrt(d);printf("k=%d;",k);for (j=0; j<N; j++) printf("x[%d]=%lf;",j+1,x0[j]);printf("d=%lf\n",d);if (d<=e1) {for (j=0; j<N; j++) x0[j]=x[j];break;}f0=F(x0);d=f0-ff[0]; m=0;for (j=1; j<N; j++) if (d<ff[j-1]-ff[j]) {m=j; d=ff[j-1]-ff[j];} for (j=0; j<N; j++) xn1[j]=2*xn[j]-x0[j];f1=F(x0); f2=F(xn); f3=F(xn1);if (0.5*(f1-2*f2+f3)>=d) {if (f2<f3) for (j=0; j<N; j++) x0[j]=xn[j];else for (j=0; j<N; j++) x0[j]=xn1[j];} else {for (i=m+1; i<N; i++) for (j=0; j<N; j++) ss[i-1][j]=ss[i][j];for (j=0; j<N; j++) ss[N-1][j]=s1[j];for (j=0; j<N; j++) x0[j]=x[j];}k++;}for (j=0; j<N; j++) x0[j]=xkk[j];return F(xkk);}main(){double fk,fkk,ck,d1,d2,e1,e2;double g[MAXN],h[MAXN],x1[MAXN],x0[MAXN];int i;N=2;nt=3;et=0;type=1;e1=0.0001;e2=0.0001;rk=0.001; ck=2;x0[0]=8; x0[1]=8;printf("=========\n");fk = nc_powell(x0,0.01,0.001);for(i=0; i<N; i++) x1[i]=x0[i];printf("rk=%lf\n",rk);for (i=0; i<N; i++) printf("x[%d]=%lf;",i+1,x0[i]);printf("%lf\n",fk);for(;;) {rk*=ck;fkk = nc_powell(x0,0.01,0.005);printf("rk=%lf\n",rk);for (i=0; i<N; i++) printf("x[%d]=%lf;",i+1,x0[i]); printf("%lf\n",fkk);d1=0; for(i=0; i<N; i++) d1+=(x1[i]-x0[i])*(x1[i]-x0[i]); d1=sqrt(d1);d2=fabs((fkk-fk)/fk);printf("d1=%lf d2=%lf\n",d1,d2);if(d1<=e1 || d2<=e2) break;for(i=0; i<N; i++) x1[i]=x0[i];fk=fkk;}fk=funt(x0,g,h);printf("**********************\n");for (i=0; i<N; i++) printf("x[%d]=%lf;",i+1,x0[i]);printf("F* = %lf\n",fk);for (i=0; i<nt; i++) printf("g[%d]=%lf;",i+1,g [i]); return 1;}。
无约束优化方法

三. 内容:
一维搜索: 求最优步长因子α(k)
多维(变量)优化:确定搜索方向 S (k)
黄金分割 切线法 平分法 插值法 格点法
坐标轮换法 最速下降法 共轭方向法 鲍威尔法 梯度法 共轭梯度法 牛顿法 单形替换法 变尺度法
比较两试点函数值,由于 作前进搜索
此时,三个试点 函数值已经出现“高-低-高”特征, 得搜索区间为
3.2 一维搜索方法
α3(2)
黄金分割法 (0.618) :
序列消去原理:
f (α)
α
α3(1)
α12
α*
α1(1)
0
α11
α21 α22
α1(2)
α1(3)
α3(3)
1.解析法:
定义:
在第K次迭代时,从已知点 X(k)出发,沿给定方向求最优步长因子α(k),使 f (X(k) + α S(k) )达到最小值的过程,称为一维搜索。
பைடு நூலகம்
对α求导,令其为零。
01
直接法——应用序列消去原理:
02
分数法、黄金分割法
03
近似法——利用多项式函数逼近(曲线拟合)原理:
总结:将优化问题转化为一系列的一维搜索问题
沿方向S的一维搜索
3.2 一维搜索方法
单峰区间解析概念:
在区间 [α1,α3 ]内,函数只有一个峰值,则此区间为单峰区间。单峰区间内,一定存在一点α*,当任意一点α2>α*时,f(α2)>f(α*),
说明: 单峰区间内,函数可以有不可微点,也可以是不连续函数;
3.1 引言
无约束优化方法计算步骤:
若已经取得某设计点x(k),并且该点不是近似极小点,则在x(k)点根据函数f(x)的性质,选择一个方向S(k),并且沿此方向搜索函数值是下降的,称下降方向。 当搜索方向S(k)确定后,由x(k)点出发,沿S(k)方向进行搜索, 定出步长因子 (k),得到新的设计点:
机械优化设计之无约束优化方法(ppt 62页)

机械优化设计
一、概述
1、无约束优化问题
求n 维设计变量 Xx1,x使2,目x标nT函数
f Xmin ,而对 X 没有任何限制条件。
2、求解方法 (1)利用极值条件来确定极值点的位置。 (2)数值计算方法——搜索方法 基本思想:从给定的初始点 x 0 出发,沿某一搜索方向
y1,y2y12y221 2y1 y2 0 20 2 y y1 2
可以看出二者的对角形矩阵不同,前者的 等值线为一族椭圆,后者的等值线为一族同 心圆,这说明对角形矩阵是表示度量的矩阵 或者是表示尺度的矩阵,最速下降法的收敛 速度和变量的尺度有很大关系。
称其为牛顿方向,则阻尼牛顿法的迭代公式为:
X k 1 X k k d k X k k 2 fX k 1 fX k ( k 0 , 1 , 2 )
k ——阻尼因子,即沿牛顿方向进行一维搜索的最佳步长,
可通过如下极小化过程求得:
机械优化设计
章 无约束优化方法
一、概述 二、最速下降法(梯度法) 三、牛顿型方法(牛顿法和阻尼牛顿法) 四、共轭方向和共轭方向法 五、共轭梯度法 六、变尺度法 七、坐标轮换法
机械优化设计
实际中的工程问题大都是在一定限制条件下追 求某一指标为最小,属于约束优化问题。
为什么要研究无约束优化问题?
1)有些实际问题,其数学模型本身就是一个无约束问题; 2)通过熟悉它的解法可以为研究约束优化问题打下良好的 基础; 3)约束优化问题的求解可用通过一系列无约束优化方法来 达到。
f xk1 Tf xk 0 或 dk1 T dk 0
无约束优化方法

为了使目旳函数值沿搜索方向 f (xk ) 能够取得最大旳
下降值,其步长因子
应取一维搜索旳最佳步长。即有
k
f
( xk1)
f [xk
akf
( xk )]
min a
f [xk
af
( xk )]
min, ( ) a
根据一元函数极值旳必要条件和多元复合函数求导公式,得
'( ) f [ xk kf ( xk )] T f ( xk ) 0
第四章 无约束优化措施
第一节 概 述
数值解法:是从给定旳初始点x0出发,沿某一搜索方向d0
进行搜索。拟定最佳步长α,使函数值沿d0方向下降最大。 依此方式按下述公式不断进行,形成迭代旳下降算法。
x,k1 xk k d k (k 0,1, )
1)选择迭代方向即探索方向; 2)在拟定旳方向上选择合适步长迈步进行探索。 多种无约束优化措施旳区别就在于拟定其搜索方向dk旳措 施不同。所以搜索方向旳构成问题是无约束优化措施旳关键。
4)若 | xk1 xk | ,则停止迭代,
得最优解x* xk1;
否则,k k 1,转到第二步。
第四章 无约束优化措施
第二节 最速下降法
例:用最速下降法求目标函数 ,
f (x) x12 25x22
的极小点。
xk1 xk kf (xk )(k 0,1, )
第四章 无约束优化措施
解 取初始点 x0 [2,2]T f ( x0 ) 104
第四章 无约束优化措施
第四节 共轭方向及共轭方向法 •共轭方向旳形成
•格拉姆-斯密特向量系共轭化旳措施
i
d i1
vi1
,
dr i 1, r
机械优化设计鲍威尔法编程

机械优化设计鲍威尔法编程鲍威尔法(Powell's method)是一种常用于机械优化设计的迭代算法,它基于步长的方向进行,进而找到局部或全局最优解。
该算法主要用于解决无约束优化问题,即不涉及约束条件的优化设计。
下面将详细介绍鲍威尔法的编程实现。
鲍威尔法的基本思路是在迭代过程中通过多次步长方向,找到全局最优解。
具体步骤如下:1.初始化:设置初始点x0和迭代次数k=0。
2.计算方向:选择一个初始的方向d0和步长α,并将d0归一化为单位向量。
3. 求解新的迭代点:通过计算当前点xk加上步长α乘以方向dk,得到新的迭代点xk+14. 更新方向:计算新的方向dk+15. 判断是否达到终止条件:如果达到了终止条件,则输出当前点xk+1为最优解;否则,令k=k+1,返回第3步继续进行迭代。
下面给出一个使用Python编程实现鲍威尔法的示例代码:```pythonimport numpy as npdef powell_method(f, x0, alpha, eps, max_iter):#初始化x=x0d = np.eye(len(x0))k=0while k < max_iter:#计算方向和步长g=f(x)d_norm = np.linalg.norm(d, axis=0) d = d / d_normalpha = alpha / d_norm#求解新的迭代点x_new = x + alpha * d#更新方向g_new = f(x_new)delta = g_new - gd = np.roll(d, -1, axis=0)d[-1] = (x_new - x) / alpha#判断终止条件if np.linalg.norm(delta) < eps: return x_new#更新迭代点x = x_newk+=1return x#示例函数,目标是求解f(x)=(x[0]-1)^2+(x[1]-2)^2 def f(x):return (x[0] - 1) ** 2 + (x[1] - 2) ** 2#设置初始点、步长、终止条件和最大迭代次数x0 = np.array([0.0, 0.0])alpha = 0.1eps = 1e-6max_iter = 100#调用鲍威尔法进行优化设计x_opt = powell_method(f, x0, alpha, eps, max_iter) #输出最优解print("Optimal solution: ", x_opt)print("Optimal value: ", f(x_opt))```在上述代码中,目标函数f(x)为示例函数,可以根据具体的优化设计问题进行修改。
关于无约束优化各种方法

E(k)
x(k [g (
)[x(k ) ]T k ) ]T x(k )
H (k )g (k )[g (k ) ]T H (k ) [g (k ) ]T H (k )g (k )
变尺度法
DFP变尺度法现代公认的较好的算法之一。 DFP法、BFGS算法是基于牛顿法的思想又作了 重要改进。这种算法仅用到梯度,不必计算海赛阵及 其逆矩阵,但又能使搜索方向逐渐逼近牛顿方向,具 有较快的收敛速度。
akf
( xk )]
min a
f [xk
af
( xk )]
min( ) a
§4-1 最速下降法
f
( x ) k1
f [xk
akf
( xk )] min a
f [xk
af ( xk )解析法:根据极值点必要条件。
首次迭代时,H (0) I , S (k) f (x(k) ) , 即为梯度法,
§3.5 牛顿法和变尺度法
这样避免计算二阶导数及Hesse矩阵的逆矩阵,而利用了牛顿法的优点。
§3.5 牛顿法和变尺度法
构造变尺度矩阵的递推公式:
H (k1) H (k) E(k) , 其中: E(k)为第k次迭代时的修正矩阵。
黄金分割法
牛顿法
抛物线法
§4-1 最速下降法
相邻 两个 搜索 方向 互相 垂直
最速下降法的搜索路径
f
( xk1)
f [xk
akf
( xk )] min a
f [xk
af ( xk )]
min( ) a
根据一元函数极值的必要条件及
复合函数求导公式得
'( ) f [ xk kf ( xk )] T f ( xk ) 0
鲍威尔法的基本原理

鲍威尔法的基本原理在数学优化领域,鲍威尔法(Powell's Method)是一种求解无约束优化问题的重要方法。
它以其独特的思路和有效的性能,在众多优化算法中占据了一席之地。
要理解鲍威尔法,首先得清楚什么是无约束优化问题。
简单来说,就是在没有任何限制条件的情况下,寻找一个函数的最小值或最大值。
比如说,我们有一个函数 f(x),目标就是找到那个能让 f(x)取到最小或最大的 x 值。
鲍威尔法的核心思想在于通过一系列的线性搜索来逐步逼近最优解。
它不是一下子就找到最终的答案,而是一步一步地靠近。
具体来看,鲍威尔法从一个初始点开始。
这个初始点可以是随意选择的,但通常会根据问题的特点和一些先验知识来进行合理的设定。
然后,它会沿着一组给定的方向进行搜索。
这些方向是怎么来的呢?一开始,鲍威尔法会选择一组固定的线性无关的方向。
比如说,在二维空间中,可能就是 x 轴和 y 轴的方向;在三维空间中,可能就是 x、y、z 轴的方向。
随着算法的进行,这些方向会不断地更新和优化。
在每次的迭代中,鲍威尔法会沿着当前的方向进行线性搜索,找到函数值下降最快的点。
这个过程就像是在黑暗中摸索,沿着一个方向走,看看哪里更低。
当完成一轮沿着所有给定方向的搜索后,鲍威尔法会根据这一轮搜索的结果来更新方向。
它会把这一轮中函数值下降最多的方向保留下来,然后用新产生的方向替换掉原来的某个方向。
新产生的方向是通过把这一轮搜索的起点和终点连接起来得到的。
这样做的目的是为了让新的方向更能反映函数的特性,从而更有效地引导搜索朝着最优解的方向前进。
比如说,如果在一轮搜索中,沿着某个方向函数值下降得特别多,那么这个方向就被认为是比较好的方向,会被保留。
而新产生的方向则是基于这一轮搜索的整体效果,希望能够捕捉到函数的变化趋势,更好地指导下一轮的搜索。
鲍威尔法的一个重要特点是它不需要计算目标函数的导数。
这在一些情况下是非常有用的,因为计算导数可能会很复杂,甚至有时候根本无法计算。
第六节_无约束优化方法 鲍威尔

结论:从不同的点出 发沿某一方向分别对 函数作两次一维搜索 ,得到两个极小点, 那么这两个极小点的 连线方向与该方向对 G共轭
二、鲍威尔基本算法
鲍 威 尔 基 本 算 法 的 搜 索 过 程 ( 二 维 )
二、鲍威尔基本算法
鲍 威 尔 基 本 算 法 的 搜 索 过 程 ( 三 维 )
鲍威尔基本算法的步骤:
m max[ F ( xik1 ) F ( xik )] Fm1 Fm (1≤m≤n)
k k k x d x 及与之相对应的两个点 m 1 和 m ,并以 m 表示两点
的连线方向。
(4)关键点函数值
k k k xn 2 x x 1 n 0
k F1 F ( x0 ) k F3 F ( xn 1 ) k F2 F ( xn )
7.9883 x* x 5.9981
5 2
f * f ( x*) 7.95025
§4.5
3. 方法评价:
坐标轮换法
• 方法简单,容易实现。 • 当维数增加时,效率明显下降。
收敛慢,以振荡方式逼近最优点。
•
受目标函数的性态影响很大。 如图 a) 所示,二次就收敛到极值点; 如图 b) 所示,多次迭代后逼近极值点;
按照以下两种情况处理: 1) 上式中至少一个不等式成立,则第k+1轮的 基本方向仍用老方向组d1k、d2k、 • • • 、 dnk。 k+1轮的初始点取 x0k+1=xnk F2<F3 x0k+1=xn+1k F2F3
2)两式均不成立,则淘汰函数值下降最大的方向, 并用第k轮的新生方向补入k+1轮基本方向组的最后, 即k+1轮的方向组为d1k、d2k 、 • • • 、 dm-1k、 dm+1k 、 • • • 、dnk、 dk 。
机械优化设计鲍威尔法

机械优化设计鲍威尔法
机械优化设计鲍威尔法(Powell method)是一种常用的非线性优化
算法,它以鲍威尔的名字命名,用于解决无约束非线性优化问题。
该方法
在各个领域都有广泛的应用,如工程优化设计、机器学习等。
下面将详细
介绍机械优化设计鲍威尔法的原理及应用。
鲍威尔法的具体步骤如下:
1.初始化参数:选择初始设计参数和方向。
2.寻找一维极小值点:沿着方向找到目标函数在该方向上的极小值点。
3.更新方向:通过比较前后两个极小值点的差异来更新方向。
4.迭代优化:重复步骤2和步骤3,直到达到指定的收敛条件。
鲍威尔法的优点是收敛速度较快、计算量较小,同时可以处理非线性
的优化问题。
然而,该方法也存在一些不足之处,如可能陷入局部最优解、对初值敏感等。
机械优化设计鲍威尔法在工程领域中有广泛的应用。
例如,在机械结
构设计中,可以利用鲍威尔法来优化结构参数,以满足特定的性能指标。
在汽车工业中,可以使用鲍威尔法来优化车辆的燃油效率和性能。
在航空
航天领域,可以利用该方法来优化飞行器的飞行性能。
此外,该方法还可
以用于机器学习中的参数优化,如调整神经网络的权重和偏置等。
总之,机械优化设计鲍威尔法是一种常用的非线性优化算法,通过迭
代逼近最优解。
虽然该方法有一些不足之处,但在实际应用中具有广泛的
适用性,尤其在工程优化设计和机器学习等领域。
通过使用该方法,可以
优化设计参数,改进性能指标,提高工程效率和产品质量。
无约束优化搜索方法鲍威尔法(齐童)
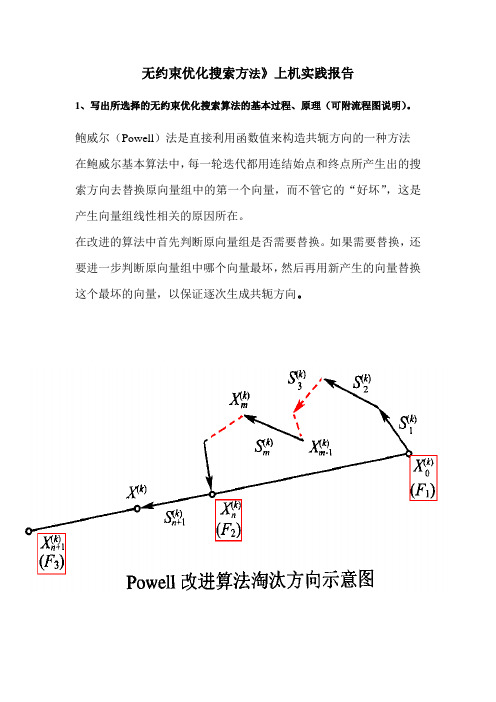
无约束优化搜索方法》上机实践报告1、写出所选择的无约束优化搜索算法的基本过程、原理(可附流程图说明)。
鲍威尔(Powell)法是直接利用函数值来构造共轭方向的一种方法在鲍威尔基本算法中,每一轮迭代都用连结始点和终点所产生出的搜索方向去替换原向量组中的第一个向量,而不管它的“好坏”,这是产生向量组线性相关的原因所在。
在改进的算法中首先判断原向量组是否需要替换。
如果需要替换,还要进一步判断原向量组中哪个向量最坏,然后再用新产生的向量替换这个最坏的向量,以保证逐次生成共轭方向。
2、程序计算结果分析:中间各步骤的结果分析及与理论计算结果分析对比。
算例:ff=x[0]*x[0]+2*x[1]*x[1]-4*x[0]-2*x[0]*x[1];(1)鲍威尔改进算法C++程序清单:#include "stdio.h"#include "stdlib.h"#include "math.h"double objf(double x[]){double ff;ff=x[0]*x[0]+2*x[1]*x[1]-4*x[0]-2*x[0]*x[1];return(ff);}void jtf(double x0[ ],double h0,double s[ ],int n,double a[ ],double b[ ]){int i;double *x[3],h,f1,f2,f3;for (i=0;i<3;i++)x[i]=(double *)malloc (n*sizeof(double));h=h0;for(i=0;i<n;i++)*(x[0]+i)=x0[i];f1=objf(x[0]);for(i=0;i<n;i++)*(x[1]+i)=*(x[0]+i)+h*s[i];f2=objf(x[1]);if(f2>=f1){h= -h0;for (i=0;i<n;i++)*(x[2]+i)=*(x[0]+i);f3=f1;for(i=0;i<n;i++){*(x[0]+i)= *(x[1]+i);*(x[1]+i)= *(x[2]+i);}f1=f2;f2=f3;}for(;;){h=2. *h;for(i=0;i<n;i++)*(x[2]+i)=* (x[1]+i) +h*s[i];f3= objf(x[2]);if(f2<f3)break;else{ for(i=0;i<n;i++){*(x[0]+i)= *(x[1]+i);*(x[1]+i)= *(x[2]+i);}f1=f2;f2=f3;}}if(h<0. )for(i=0;i<n;i++){a[i]=*(x[2]+i);b[i]=*(x[0]+i);}elsefor(i=0;i<n;i++){a[i]=*(x[0]+i);b[i]=*(x[2]+i);}for(i=0;i<3;i++)free(x[i]);}double gold(double a[],double b[],double eps,int n,double xx[]) {int i;double f1,f2,*x[2],ff,q,w;for(i=0;i<2;i++)x[i]=(double*)malloc (n*sizeof(double));for(i=0;i<n;i++){*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);}f1=objf(x[0]);f2=objf(x[1]);do{if(f1>f2){for(i=0;i<n;i++){b[i]=*(x[0]+i);*(x[0]+i)=*(x[1]+i);}f1=f2;for(i=0;i<n;i++)*(x[1]+i)=a[i]+0.382*(b[i]-a[i]);f2=objf(x[1]);}else{for(i=0;i<n;i++){a[i]=*(x[1]+i);*(x[1]+i)=*(x[0]+i);}f2=f1;for(i=0;i<n;i++)*(x[0]+i)=a[i]+0.618*(b[i]-a[i]);f1=objf(x[0]);}q=0;for(i=0;i<n;i++)q=q+(b[i]-a[i])*(b[i]-a[i]);w=sqrt(q);}while(w>eps);for(i=0;i<n;i++)xx[i]=0.5*(a[i]+b[i]);ff=objf(xx);for(i=0;i<2;i++)free(x[i]);return(ff);}double oneoptim(double x0[],double s[],double h0,double epsg,int n,double x[]){double *a,*b,ff;a=(double *)malloc(n*sizeof(double));b=(double *)malloc(n*sizeof(double));jtf(x0,h0,s,n,a,b);ff=gold(a,b,epsg,n,x);free(a);free(b);return(ff);}double powell(double p[],double h0,double eps,double epsg,int n,double x[]){int i,j,m;double *xx[4],*ss,*s;double f,f0,f1,f2,f3,fx,dlt,df,sdx,q,d;ss=(double *)malloc(n*(n+1)*sizeof(double)); s=(double *)malloc(n*sizeof(double));for (i=0;i<n;i++){for (j=0;j<=n;j++)*(ss+i*(n+1)+j)=0;*(ss+i*(n+1)+i)=1;}for (i=0;i<4;i++)xx[i]=(double *)malloc(n*sizeof(double));for (i=0;i<n;i++)*(xx[0]+i)=p[i];for(;;){for (i=0;i<n;i++){*(xx[1]+i)=*(xx[0]+i);x[i]=*(xx[1]+i);}f0=f1=objf(x);dlt=-1;for (j=0;j<n;j++){for (i=0;i<n;i++){*(xx[0]+i)=x[i];*(s+i)=*(ss+i*(n+1)+j);}f=oneoptim(xx[0],s,h0,epsg,n,x);df=f0-f;if(df>dlt){dlt=df;m=j;}}sdx=0.;for (i=0;i<n;i++)sdx=sdx+fabs(x[i]-(*(xx[1]+i)));if(sdx<eps){free(ss);free(s);for (i=0;i<4;i++)free(xx[i]);return(f);}for (i=0;i<n;i++)*(xx[2]+i)=x[i];f2=f;for (i=0;i<n;i++){*(xx[3]+i)=2.*(*(xx[2]+i)-(*(xx[1]+i))); x[i]=*(xx[3]+i);}fx=objf(x);f3=fx;q=(f1-2*f2+f3)*(f1-f2-dlt)*(f1-f2-dlt); d=0.5*dlt*(f1-f3)*(f1-f3);if((f3<f1)||(q<d)){if(f2<=f3)for (i=0;i<n;i++)*(xx[0]+i)=*(xx[2]+i);elsefor (i=0;i<n;i++)*(xx[0]+i)=*(xx[3]+i);}else{for (i=0;i<n;i++){*(ss+(i+1)*(n+1))=x[i]-(*(xx[1]+i));*(s+i)=*(ss+(i+1)*(n+1));}f=oneoptim(xx[0],s,h0,epsg,n,x);for(i=0;i<n;i++)*(xx[0]+i)=x[i];for (j=m+1;j<=n;j++)for (i=0;i<n;i++)*(ss+i*(n+1)+j-1)=*(ss+i*(n+1)+j);}}}void main(){double p[]={1,1};double ff,x[2],x1,x2,f;ff=powell(p,0.3,0.001,0.0001,2,x);printf("shuchuzuiyoujie:\n");x1=x[1];x2=x[2];f=ff;printf("x1=%f,x2=%f,f=%f\n",x1,x2,f); getchar();}(2)运行结果为:算例1ff=x[0]*x[0]+x[1]*x[1]+x[0]+x[0]*x[1]输出结果:shuchuzuiyoujieú║x1=0.333246,x2=0.333246,f=-0.333333算例2ff=3*x[0]*x[0]+6*x[1]*x[1]+2*x[0]+(x[0]+5)*x[1]输出结果:shuchuzuiyoujieú║x1=-0.394357,x2=-0.394357,f=-1.253521感想本次上机让我感触颇多,让我学会了使用鲍威尔法进行无约束优化问题的分析,感谢老师对我的指导。
鲍威尔法VB程序设计

鲍威尔法实验报告姓名:刘阳阳学号:1201013009鲍威尔法程序设计1 方法(算法)介绍1.1 方法原理简介鲍威尔法——多维无约束优化算法是在无约束优化算法之一,首先选取一组共轭方向,从某个初始点出发,求目标函数在这些方向上的极小值点,然后以该点为新的出发点,重复这一过程直到获得满意解,其优点是不必计算目标函数的梯度就可以在有限步内找到极值点。
鲍威尔法是以共轭方向为基础的收敛较快的直接法之一,是一种十分有效的算法。
在无约束方法中许多算法都是以共轭方向作为搜索方向,它们具有许多特点。
根据构造共轭方向的原理不同,可以形成不同的共轭方向法。
基本算法1)任选一初始点x0,再选两个线性无关的向量,如坐标轴单位向量e1=[1,0]T 和e2=[0,1]T作为初始搜索方向。
2)从x0出发,顺次沿e1,e2作一维搜索,得x10,x20点,两点连线得一新方向d1=x20-x0。
用d1代替e1形成两个线性无关向量d1 ,e2 ,作为下一轮迭代的搜索方向。
再x20 出发,沿d1 作一维搜索得点x01,作为下一轮迭代的初始点。
3)从x1 出发,顺次沿,e2。
d1 作一维搜索,得到点x11,x21,两点连线得一新方向:d2=x21-x11。
4)沿d2d2作一维搜索得点.x2 ,即是二维问题的极小点x*把二维情况的基本算法扩展到n维,则鲍威尔基本算法的要点是:在每一轮迭代中总有一个始点(第一轮的始点是任选的初始点)和n个线性独立的搜索方向。
从始点出发顺次沿n个方向作一维搜索得一终点,由始点和终点决定了一个新的搜索方向。
用这个方向替换原来n个方向中的一个,于是形成新的搜索方向组。
替换的原则是去掉原方向组的第一个方向而将新方向排在原方向的最后。
此外规定,从这一轮的搜索终点出发沿新的搜索方向作一维搜索而得到的极小点,作为下一轮迭代的始点。
这样就形成算法的循环。
1.2 程序设计框图1.3程序说明本程序使用VB程序语言设计,在该程序中插入command模块picture模块利用矩阵函数语句迭代计算出鲍威尔最小值并将之在picture模块中显示出2 例题计算2.1 例题:用鲍威尔法求f(x1,x2)=10*(x1+x2-5)^2+(x1-x2)^22.2 计算结果与分析VB程序计算结果如图:经演算迭代后得到结果为:X0^2= 2.49952.5091 F0=f0(x0^2)=0.0008可见已足够接近极值点x*=(2.5,2.5)T 及极小值f(x*)=02.3 结论经验算鲍威尔法VB程序计算结果正确且为最优解。
《最优化设计》PPT课件

x* = [0 0]T f(x* ) =0
---
(3)
5
§4-2 最速下降法
(4)
图4-3表示例4-1的搜索路径,目标函数等值线为椭圆。 若进行代换
y1 = x1 y2 = 5x2
则 f(x1, x2) 变为(y1, y2),等值线为一族同心圆。因为圆上
任一点的负梯度方向都指向圆心,因此沿负梯度方向经过 一次一维搜索即可找到最优点。
无约束优化方法可分为两大类:1)不求导数的直接法, 主要有随机方法和直接搜索方法;2)求导数的间接法,按 所求导数的最高阶数又可分为一阶方法和二阶方法。二阶 方法很少采用。
图4-1为无约束极小化算法的粗框图。在§1-4 中已给 出了优化算法的一般搜索迭代公式
xk+1= xk+xk (1-15)
xk+1= xk+kdk (1-16)
2 0
f x 0
1
2T
2
0
0 1
4
100T
50
2T
1 2
4 0100
0
4
1 50
T
100
0T
对照梯度法和牛顿法迭代公式,可以看出只相差一项 海赛矩阵的逆矩阵。因此,牛顿法是对梯度法的进一步修 正。事实上,梯度法是对目标函数f(x)在点xk的一阶(线性) 近似,而牛顿法是对f(x)在点xk 的二阶(二次)近似。
---
9
§4-4 共轭方向及共轭方向法
(1)
共轭方向的概念
二次正定函数的一般形式为:
fx1xTG xbTxc
2
式中,G为 nn 阶对称正定矩阵,b=[b1, b2, ,bn]T 为常矢
坐标轮换法

3.从
X
k 0
出发,分别沿
S
k i
(i
1,2,
n)
作一维搜索,依次得n个极小点X
k i
,
计算各相邻极小点目标函数的差值 ,
并找出其中的最大差值及其相应的方向:
km
max{ f
(
X
k i1
f
(
X
k i
)
f
(
X
k m1
)
f
(
X
k m
)
i 1,2 n}
S
k m
X
k m
Xk m 1
X
k 0
1
X
k 0
1
或
f
(
X
k 0
1
)
f
(
X
k 0
)
f
(
X
k 0
1
)
2
则可终止迭代,得
X
k 0
1
为最优点,输出结
果
X k 1 0
X*
,
f
(
X
k 1 0
)
f (X *)
;
否则,置
X k 1 0
X0
,k 1 k
;返回第
3步。
3.共轭方法法及其构成
坐标轮换法的收敛速
度很慢,原因在于搜索
方向总是平行于坐标轴,
不适应函数的变化情况。
若将一轮的起点和末点
连接起来,形成一个新
的搜索方向
S2
,由右图可知,从这个搜索方向出发可以极大的
现代设计方法第六章 优化设计方法 (1-4)无约束优化 单形替换法

选取 X 1 , X 2 , X 3 为顶点作初始单纯形。 计算各顶点的函数值 f ( X 1 ) ,f ( X 2 ) ,f ( X 3 ) 。 计算形心点 X 4 、反射点 X 5 、扩张点 X 6 。
函数值比较, 顶点替换, 单纯形变换形状位置。
三、单形替换法的具体实例
目标函数 f ( X ) = 4( x1 − 5) 2 + ( x 2 − 6) 2 的极小值求解过程动画演示
X1X 4 方向上的所有点都比最差点差。
缩边:
这时不能沿着此方向进行搜索,应该以最好点为中心,将单纯形 进行缩边,使顶点 X 1 , X 2 向 X 3 移近一半的距离,得到新的单纯 形 { X 3 , X 9 , X 10 } ,在此基础上继续进行寻优。
二、单形替换法的实现过程
⑤
f ( X ) > f ( X1)
二、单形替换法的实现过程
反射、扩张、收缩、缩边
二、单形替换法的实现过程
设 二 维 目 标 函 数 为 f ( X ) = f ( x1 , x 2 ) ,在 平 面 x1 − x 2 上 X 1 , X 2 , X 3 为 线 性 独 立 三 个 点 ,并 以 它 们 为 顶 点 构 造 初 始 单 纯 形 — — 三 角 形 。计 算 这 三 个 顶 点处的函数值 f (X1) , f (X 2) , f (X 3) 并作比较。
X3
X 5 代替 X 1 构 成 新 的单纯
形 {X 2 , X 3 , X 5 } 。
x1
X1 函数值下降方向 O
二、单形替换法的实现过程
③
f ( X1) > f ( X 5 ) ≥ f ( X 2 )
若反射点的函数值 f ( X 5 ) 小于最差点的函数值 f ( X1 ) 但大于次差点的函数值 f ( X 2 )
优化设计鲍威尔法 ppt课件

优化设计鲍威尔法
冶金机械教研室 吕勇 lvyong@教一楼512
武汉科技大学机械自动化学院
现代设计方法
• 找出前一轮迭代法中函数值下降最多的方向 m及下降量△m,即:
△m=max{[f(Xk(i))-f(Xk(i+1))](i=0,1,…,n-1)} = f(Xk(m-1))-f(Xk(m))
k+1次循环方向组时,不用淘汰前一循环中的
第一个方向S1(k)的办法,而是计算函数值并根
据是否满足条件计算:
S k (n)
➢ f1=f(Xk(0))
X2
f3
➢ f2=f(Xk(n)) ➢ f3=f(Xk(n+2))
X (n2) k
f2
X (n1) k
X k (n)
f1
2
X
(0) k
1
X
(1) k
X1
S1(1)=e1=[1,0]T S2(1)=e2=[0,1]T
优化设计鲍威尔法
冶金机械教研室 吕勇 lvyong@教一楼512
武汉科技大学机械自动化学院
S (1)
X2
模式方向
现代设计方法
S (2)
X
(1) 0
X
(2) 1
X (3) 0
X
(2) 2
X
(1) 2
S (1)
X
(2) 0
优化设计鲍威尔法
武汉科技大学机械自动化学院
现代设计方法
§5.4.3 鲍威尔法( Powell法)
• 两次平行搜索产生一个共轭方向,Powell法 也是一种共轭方向法,能在有限步长内极 小化一个二次函数,是直接搜索方法中使 用效果最佳的一种方法。
• 对于维数n<20的目标函数求最优化问题, 此法可获得满意效果。
优化设计 约束和无约束优化

无约束优化方法1.坐标轮换法2.鲍威尔法3.梯度法4.牛顿法5.变尺度法1.坐标轮换法坐标轮换发是一种不计算函数梯度,而是通过函数值本身,即可求出寻优方向,因而也称为直接寻优法.在以后提到的鲍威尔法(Powell)法也属于直接寻优法。
对于坐标轮换法,我们做个比喻:如果我们在北京的老城区找一个地方,我们可以沿着经纬线去找。
这个比喻为我们提供了一种思路,既可以取坐标的方向为寻优的方向,这就是坐标轮换法。
它在每次搜索中,只允许一个变量的变化,其余量保持不变,即沿着坐标方向轮流进行搜索的方法。
该方法把多变量的优化问题轮流转化成一系列单变量的优化问题。
对应于n 个变量的寻优函数,若在第轮沿第k 个坐标第i 个坐标方向ki i S e =进行搜索,则迭代公式为1(0,1,...,1,2,...,)k k k k i i i i X X S k i n α-=+==其中搜索方向取坐标方向,即k i i S e =(1,2,...,i n =)。
若0k k n X X -‖‖<ε,则*kn X X ←,否则10k kn X X +←,进行下一轮的搜索,一直到满足精度要求为止。
其搜索路径如图所示这种方法的收敛效果与目标函数等值线形有很大关系。
如果目标函数为二元二次函数,其等值线为圆或长轴平行于坐标轴的椭圆时,此方法很有效,经过两次搜索即可以达到最优点,如图所示。
如果等值线为长轴不平行于坐标轴的椭圆,则需多次迭代才能达到最优点,但因坐标轮换法是坐标方向搜索而不是沿脊线搜索,所以就终止到脊线上而不能找到最优解。
从上述分析可以看出,采用坐标轮换法只能轮流沿着坐标的方向搜索,尽管也能使函数值步步下降,但经过曲折迂回的路径才能达到极值点;尤其极值点附近步长很小,收敛很慢,所以坐标轮换法不是一种很好的搜索方法。
但是可以构造很好的搜索策略,下面讨论的鲍威尔法就是这种情况。
例题:已知22121212()10460f X x x x x x x =+---+,设初始点:(0)[0,0]T X=,精度0.1=ε,用最优步长法的坐标轮换法求目标函数的最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2)再沿新生方向作一维搜 索,完成第一轮的迭代。 以后每轮的基本方向组是 将上轮的第一个方向淘汰 ,上轮的新生方向补入本 轮的最后而构成: d2k , d3k , …… dnk , dk
0
以
x
1 1
为新起点,沿e2方向一维搜索
x1 2x1 12e25 021 0 52
以最优步长原则确定α2,即为极小化
m in F (x 1 1 )2 2 1 02 6 0 2 4.5
x
1 2
5
4
.
5
对于第一轮按终止条件检验
x1 2x0 1 524.526.7
计算5轮后,有 x25x05 0.0413
§4.5 坐标轮换法
计算步骤:
⑴任选初始点,确定搜索方向
x 第一轮的起点
1 0
,置n个坐标轴方向矢量为单位坐标矢量
1
0
e1
0
0
0
1
e2
0
0
0
0
en
0
1
§4.5 坐标轮换法
⑵迭代计算
xik xik1 ikei
k为迭代轮数的序号,取k=1,2,……; i为该轮中一维搜索的序号,取i=1,2,……n 步长α一般通过一维优化方法求出其最优步长。
结论:从不同的点出 发沿某一方向分别对 函数作两次一维搜索 ,得到两个极小点, 那么这两个极小点的 连线方向与该方向对 G共轭
二、鲍威尔基本算法
鲍 威 尔 基 本 算 法 的 搜 索 过 程 ( 二 维 )
二、鲍威尔基本算法
维鲍 )威
尔 基 本 算 法 的 搜 索 过 程 ( 三
鲍威尔基本算法的步骤:
故近似优化解为x* x257.9883 5.9981
f*f(x*)7.95025
§4.5 坐标轮换法
3. 方法评价:
• 方法简单,容易实现。 • 当维数增加时,效率明显下降。
收敛慢,以振荡方式逼近最优点。
• 受目标函数的性态影响很大。
如图 a) 所示,二次就收敛到极值点; 如图 b) 所示,多次迭代后逼近极值点; 如图 c) 所示,目标函数等值线出现山脊(或称陡 谷),若搜索到 A 点,再沿两个坐标轴以±t0步长测 试,目标函数值均上升,计算机判断 A 点为最优点。 事实上发生错误。
§4.6 鲍威尔方法
鲍威尔方法是直接搜索法中一个十分 有效的算法。该算法是沿着逐步产生的共 轭方向进行搜索的,因此本质上是一种共 轭方向法。
§4.6 鲍威尔方法
一、共轭方向的生成
x k , x k 1 为两个极小点
根据梯度与等值面之间关系可知
d j
T
gk
0
dj
T
gk1 0
dj
T
(gk1gk)0
§4.6 鲍威尔方法
一、共轭方向的生成
对于二次函数,x k , x k 1 两点处
的梯度可表示为
gk Gxk b gk1 Gxk1b
gk1gkG (xk1xk)
代入到公式:
dj
T
(gk1gk)0
§4.6 鲍威尔方法
一、共轭方向的生成
d jT (g k 1 g k ) d jT G (x k 1 x k ) 0
若在第k轮的优化搜索过程中出现1k=0,则方向dk表
示为d2k、 d3k 、 • • • 、 dnk的线性组合,以后的各次搜索 将在降维的空间进行,无法得到n维空间的函数极小值, 计算将失败。
如图所示为一个 三维优化问题的 示例,设第一轮
中1 =0 ,则新
生方向与e2 、e3 共面,随后的各 环方向组中,各 矢量必在该平面 内,使搜索局限 于二维空间,不 能得到最优解。
鲍威尔基本算法的缺陷:
可能在某一轮迭代中出现基本方向组为线性相关的矢 量系的情况。如第k轮中,产生新的方向:
dk=xnk-x0k=1kd1k+ 2kd2k + • • • + nkdnk
式中, d1k、d2k 、 • • • 、 dnk为第k轮基本方向组矢
量, 1k 、 2k、 • • • 、 nk为各方向的最优步长。
流
x xik f←f(x)
程
图
i←i+1
N i=n?
k←k+1
x* xnk Y
Y
xnk x0k ?
N
x0k 1 xnk
结束
例:用坐标轮换法求下列目标函数的无约束最优解。
F (x ) x 1 2 x 2 2 x 1 x 2 1x 1 0 4 x 2 60
给定初始点
x0
0
0
,精度要求ε=0.1
第四章 无约束优化方法
4.1 最速下降法 4.2 牛顿型方法 4.3 共轭梯度法 4.4 变尺度法 4.5 坐标轮换法 4.6 鲍威尔方法 4.7 单形替换法
§4.5 坐标轮换法
一. 坐标轮换法: 1. 基本思想:
每次搜索只允许一个变量 变化,其余变量保持不变, 即沿坐标方向轮流进行搜 索的寻优方法。它把多变 量的优化问题轮流地转化 成单变量(其余变量视为 常量)的优化问题,因此 又称这种方法为变量轮换 法。此种方法只需目标函 数的数值信息而不需要目 标函数的导数。
解:做第一轮迭代计算
沿e1方向进行一维搜索 x11 x01 1e1
式中,x
1 0
为第一轮的起始点,取
x
1 0
x0
x11 0011001
按最优步长原则确定最优步长α1,即极小化
m inF (x 1 1 )1 2 1 01 6 0
此问题可由某种一维优化方法求出α1:
21100
1 5
x
1 1
5
⑶判断是否中止迭代
应该是一轮迭代 的始点和终点, 不是某搜索方向 的前后迭代点。
xnk x0k ?
如满足,迭代中止, 并输出最优解
否则,令k←k+1 返回步骤(2)
最优解 x* x k F*F(x*)
开始
给定 x00 ,ε
坐
K←1
标
i←1
轮
换
法
沿ei方向一维搜索αi
的
xik xik1ikei
计算x0k 、 x1k、 • • • 、 xnk、xk、xn+1k 各点的函数值, 记作:
x3
x1 1=0
2e2
S1
e3
S1
e2
x2 3e3
鲍威尔基本算法的退化
三、鲍威尔修正算法
在某轮已经取得的n+1个方向中,选取n个线性无关的 并且共轭程度尽可能高的方向作为下一轮的基本方向组
鲍威尔修正算法的搜索方向的构造:在第k轮的搜索中
, x0k 为初始点,搜索方向为d1k、d2k 、 • • • 、 dnk,产生 的新方向为dk ,此方向的极小点为xk。沿dk方向移动得到点 xn+1k=2xnk-x0k , 称之为x0k对xnk的映射点。
