必修二第一章章末复习教案

合集下载

必修二第一章章末复习课件

1．1992年至1993年，该城市的人口增长率是( A )
A．16.7%
B．14.3%
C．0.9%
D．1
读甲、乙两国人口变化曲线图，完成2～3题。 2．关于甲、乙两国人口增长模式类型的叙述，正确的是( D ) A．1900—1950年，两国人口增长模式皆为“高高低”模式 B．1850—1950年，甲国人口增长模式为“高高低”模式 C．1900—1950年，乙国人口增长模式为过渡模式 D．20世纪末甲国的人口增长模式为“三低”模式 3．从图中可看出，人口增长模式的转变开始于( B ) A．出生率的下降 B．死亡率的下降 C．自然增长率的下降 D．自然增长率的上升
至今仍没结束，人口问题严重
（二）“高－低－高”模式主要原因：工业化生产方式代替手工劳动
生产力水平提高
医疗卫生事业迅速发展
特点：
粮食产量大幅度增加 1. 人口死亡率下降； 2. 人口自然增长率很高；
3. 人口增长迅速；
代表国家：20世纪50年代，普遍存在于大多数发展中国家。如尼日利亚
（三）“低－低－低”模式（现代模式） “低出生率－低死亡率－低人口自然增长率” 原因：生产力发展现代科学知识的普及医疗卫生技术的进步人类生活水平和文化水平的提升人的生育观念和生育行为也发生较大的变化
20世纪90年代以来有许多学者从不同角度对我国人口数量及人口容量进行了预测，表中内容为一些学者的预测数据，读表，回答8～9题。
预测2050年人口数量将达到依农业资源最大供养的人口数量依粮食生产能力最多供养的人口数量依小康消费水平最适宜供养的人口数量
约14～15亿约15～16亿 15.1亿或16.6亿约8～9亿
下图为2001—2050年部分国家迁入人口统计图(含预测)。读图完成6～7题。

必修2第1章第1-2节复习学案

必修2第1章人口与环境复习学案第1节人口增长模式【课标要求】分析不同人口发展模式的主要特点及地区分布。

【学习目标】1、了解人口增长模式类型。

2、掌握世界人口增长在不同发展阶段的主要特点。

3、结合实例，说明不同地区人口增长的主要特点。

【自主探究】一、人口增长1．历程：在人口增长图中，人口增长曲线呈“__________”形，在历史上，有的时期人口增长得__________，有的时期人口增长得__________。

2．人口自然增长率：指一定时期内人口__________与__________相减的得数。

第2节人口合理容量【学习目标】1、了解人口爆炸的事实。

2、了解地球的环境承载力、人口合理容量的概念以及人口容量的特点。

3、理解资源、环境对人口的限制性。

4、理解环境承载力与人口合理容量的区别。

【学习重点】1、环境对人口的限制性。

2、环境承载力中的人口规模与人口合理容量的差别。

3、人口容量的三特点。

【自主复习】一、“人口爆炸”1．描述对象：20世纪出现的近100多年来世界人口______的现象。

2．人口的指数增长：即世界人口的“__”形曲线增长，特点是开始时数量比较____，但很快就会________________。

二、环境的限制性1．原因⎩⎪⎨⎪⎧ ⑤ 是人类生产生活资料的主要来源人口的急剧增长，社会经济发展→对⑥ 的需求与日俱增人们生活水平不断提高→资源的⑦ 增加21．人口容量(1)概念：指在一定的自然资源和____________条件下，一个国家或地区所能容纳的________人口数量。

(2)特点：__________、相对性、__________。

如果某地的人口数量与相当，表明人口与其赖以生存的物质资源基本协调。

一个国家或地区的人口控制目标应该低于，并以此作为人口控制的最终警戒线。

2．人口合理容量：指在有效和______地利用资源、环境并获得最大______效益的情况下，一定地区所能容纳的人口数量。

高中数学北师大版必修二学案：第一章章末复习课

学习目标1.整合知识结构，梳理知识网络，进一步巩固、深化所学知识.2.熟练掌握平行关系与垂直关系，能自主解决一些实际问题.3.掌握几何体的三视图与直观图，能计算几何体的表面积与体积．1．空间几何体的结构特征及其侧面积和体积2.空间几何体的三视图与直观图(1)三视图是观察者从三个不同位置观察同一个空间几何体而画出的图形；它包括主视图、左视图、俯视图三种．画图时要遵循“长对正、高平齐、宽相等”的原则．注意三种视图的摆放顺序，在三视图中，分界线和可见轮廓线都用实线画出，不可见轮廓线用虚线画出．熟记常见几何体的三视图．画组合体的三视图时可先拆，后画，再检验．(2)斜二测画法：主要用于水平放置的平面图形或立体图形的画法．它的主要步骤：①画轴；②画平行于x、y、z轴的线段分别为平行于x′、y′、z′轴的线段；③截线段：平行于x、z轴的线段的长度不变，平行于y轴的线段的长度变为原来的一半．三视图和直观图都是空间几何体的不同表示形式，两者之间可以互相转化.(3)转化思想在本章应用较多，主要体现在以下几个方面①曲面化平面，如几何体的侧面展开，把曲线(折线)化为线段．②等积变换，如三棱锥转移顶点等．③复杂化简单，把不规则几何体通过分割，补体化为规则的几何体等．3．四个公理公理1：如果一条直线上的________在一个平面内，那么这条直线上所有的点都在这个平面内.公理2：过________________________的三点，有且只有一个平面．公理3：如果两个不重合的平面有一个公共点，那么它们有且只有____________________________．公理4：平行于同一条直线的两条直线互相________． 4．直线与直线的位置关系⎩⎨⎧共面直线⎩⎪⎨⎪⎧异面直线：不同在一个平面内，没有公共点5．平行的判定与性质(1)直线与平面平行的判定与性质(2)面面平行的判定与性质α∥β，a β (3)空间中的平行关系的内在联系6．垂直的判定与性质(1)直线与平面垂直a⊥b，bα(b为α内的________直线)a⊥m，a⊥n，m、nα，________________(2)平面与平面垂直的判定与性质定理⎭⎪⎬⎪⎫l βl ⊥α⇒α⊥β⎭⎪⎬⎪⎫α⊥βα∩β＝a l βl ⊥a⇒l ⊥α(3)空间中的垂直关系的内在联系7．空间角(1)异面直线所成的角①定义：设a，b是两条异面直线，经过空间任一点O作直线a′∥a，b′∥b，把a′与b′所成的____________________叫作异面直线a，b所成的角(或夹角)．②范围：设两异面直线所成角为θ，则________________．(2)二面角的有关概念①二面角：从一条直线和由这条直线出发的__________所组成的图形叫作二面角．②二面角的平面角：以二面角的棱上任意一点为端点，在两个半平面内分别作________________的两条射线，这两条射线所成的角叫作二面角的平面角．类型一由三视图求几何体的表面积与体积例1某几何体的三视图如图所示，则该几何体的体积为()A ．12B ．18C ．24D ．30反思与感悟 (1)以三视图为载体的几何体的表面积问题，关键是分析三视图确定几何体中各元素之间的位置关系及数量．(2)多面体的表面积是各个面的面积之和，组合体的表面积问题要注意衔接部分的处理． (3)旋转体的表面积问题注意其侧面展开图的应用．跟踪训练1 已知某几何体的三视图如图所示，则该几何体的体积为( )A.8π3 B ．3π C.10π3D ．6π类型二平行问题例2 如图所示，四边形ABCD 是平行四边形，PB ⊥平面ABCD ，MA ∥PB ，PB ＝2MA .在线段PB上是否存在一点F，使平面AFC∥平面PMD？若存在，请确定点F的位置；若不存在，请说明理由．反思与感悟(1)证明线线平行的依据①平面几何法(常用的有三角形中位线、平行四边形对边平行)；②公理4；③线面平行的性质定理；④面面平行的性质定理；⑤线面垂直的性质定理．(2)证明线面平行的依据①定义；②线面平行的判定定理；③面面平行的性质定理．(3)证明面面平行的依据①定义；②面面平行的判定定理；③线面垂直的性质定理；④面面平行的传递性．跟踪训练2如图，AB是圆O的直径，P A垂直圆O所在的平面，C是圆O上的点．(1)求证：BC⊥平面P AC；(2)设Q为P A的中点，G为△AOC的重心，求证：QG∥平面PBC.类型三垂直问题例3如图所示，在四棱锥P－ABCD中，P A⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，P A＝AB＝BC，E是PC的中点．证明：(1)CD⊥AE；(2)PD⊥平面ABE.反思与感悟(1)两条异面直线相互垂直的证明方法①定义；②线面垂直的性质定理．(2)直线和平面垂直的证明方法①线面垂直的判定定理；②面面垂直的性质定理．(3)平面和平面相互垂直的证明方法①定义；②面面垂直的判定定理．跟踪训练3如图，斜三棱柱ABC－A1B1C1的底面是直角三角形，∠ACB＝90°，点B1在底面ABC上的射影恰好是BC的中点，且BC＝CA＝AA1.(1)求证：平面ACC1A1⊥平面B1C1CB；(2)求证：BC1⊥AB1.类型四空间角问题例4如图，在正方体ABCD－A1B1C1D1中，E，F，M，N分别是A1B1，BC，C1D1和B1C1的中点．(1)求证：平面MNF⊥平面ENF；(2)求平面MEF与NEF的夹角的正切值．反思与感悟(1)面面垂直的证明要化归为线面垂直的证明，利用垂直关系的相互转化是证明的基本方法．(2)找二面角的平面角的方法有以下两种：①作棱的垂面；②过一个平面内一点作另一个平面的垂线，过垂足作棱的垂线．跟踪训练4如图，在圆锥PO中，已知PO⊥底面⊙O，PO＝2，⊙O的直径AB＝2，C是AB的中点，D为AC的中点．(1)证明：平面POD⊥平面P AC；(2)求二面角B－P A－C的余弦值．1．如图所示，观察四个几何体，其中判断正确的是()A．①是棱台B．②是圆台C．③是棱锥D．④不是棱柱2．设m，n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题：①若m⊥α，n∥α，则m⊥n；②若α∥β，β∥γ，m∥α，则m∥γ；③若m∥α，n∥α，则m∥n；④若α⊥γ，β⊥γ，则α∥β.其中正确命题的序号是()A．①B．②和③C．③和④D．①和④3．如图所示，在正方体ABCD－A1B1C1D1中，下面结论错误的是()A．BD∥平面CB1D1B．AC1⊥BDC．AC1⊥平面CB1DD．异面直线AD与CB1所成的角为45°4．某几何体的三视图如图所示(单位：cm)，则该几何体的表面积是______cm2，体积是________cm3.5. 已知正方体ABCD－A1B1C1D1，O是底面ABCD对角线的交点．求证：(1)C1O∥平面AB1D1；(2)A1C⊥平面AB1D1.1.转化思想是证明线面平行与垂直的主要思路，其关系为2．研究空间几何体，需在平面上画出几何体的直观图或三视图，由几何体的直观图可画它的三视图，由三视图可得到其直观图，同时可以通过作截面把空间几何问题转化成平面几何问题来解决．另外，圆柱、圆锥、圆台的表面积公式，我们都是通过展开图、化空间为平面的方法得到的，求球的切接问题通常也是由截面把空间问题转化为平面问题来解决．★答案☆精析知识梳理1．互相平行四边形互相平行多边形有一个公共顶点平行于棱锥底面矩形的一边一条直角边平行于圆锥底面底面和截面半圆的直径半圆面3．两点不在同一条直线上一条过该点的公共直线平行 4．平行相交任何 5．(1)a ∩α＝∅ a α， bα， a ∥ba ∥α a ∥α，a β， α∩β＝b (2)α∩β＝∅ a β，b β， a ∩b ＝P ， a ∥α，b ∥αα∥β α∩γ＝a β∩γ＝b6．(1)任意 m ∩n ＝O a ⊥α b α a ∥b (2)垂线7．(1)①锐角(或直角) ②0°<θ≤90° (2)①两个半平面 ②垂直于棱题型探究例1 C [由俯视图可以判断该几何体的底面为直角三角形，由主视图和左视图可以判断该几何体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的．在长方体中分析还原，如图(1)所示，故该几何体的直观图如图(2)所示．在图(1)中，111ABC A B C V 棱柱－＝S △ABC ·AA 1＝12×4×3×5＝30，111P A B C V －棱锥＝13111A B C S ·PB 1＝13×12×4×3×3＝6.故几何体ABC －P A 1C 1的体积为30－6＝24.故选C.] 跟踪训练1 B [将三视图还原为直观图求体积．由三视图可知，此几何体(如图所示)是底面半径为1，高为4的圆柱被从母线的中点处截去了圆柱的14，所以V ＝34×π×12×4＝3π.]例2 解当点F 是PB 的中点时，平面AFC ∥平面PMD ，证明如下：如图连接AC 和BD 交于点O ，连接FO ，则PF ＝12PB .∵四边形ABCD 是平行四边形， ∴O 是BD 的中点．∴OF ∥PD . 又OF平面PMD ，PD 平面PMD ，∴OF ∥平面PMD .又MA 綊12PB ，∴PF綊MA.∴四边形AFPM是平行四边形．∴AF∥PM.又AF平面PMD，PM平面PMD.∴AF∥平面PMD.又AF∩OF＝F，AF平面AFC，OF平面AFC.∴平面AFC∥平面PMD.跟踪训练2证明(1)由AB是圆O的直径，得AC⊥BC，由P A⊥平面ABC，BC平面ABC，得P A⊥BC.又P A∩AC＝A，P A平面P AC，AC平面P AC，所以BC⊥平面P AC.(2)连接OG并延长交AC于点M，连接QM，QO，由G为△AOC的重心，得M为AC中点．由Q为P A中点，得QM∥PC，又O为AB中点，得OM∥BC.因为QM∩MO＝M，QM平面QMO，MO平面QMO，BC∩PC＝C，BC平面PBC，PC平面PBC，所以平面QMO∥平面PBC.因为QG平面QMO，所以QG∥平面PBC.例3证明(1)在四棱锥P－ABCD中，∵P A⊥底面ABCD，CD平面ABCD，∴P A⊥CD.∵AC⊥CD，P A∩AC＝A，∴CD⊥平面P AC.而AE平面P AC，∴CD⊥AE.(2)由P A＝AB＝BC，∠ABC＝60°，可得AC＝P A.∵E是PC的中点，∴AE⊥PC.由(1)知，AE⊥CD，且PC∩CD＝C，∴AE⊥平面PCD.而PD平面PCD，∴AE⊥PD.∵P A⊥底面ABCD，AB底面ABCD，∴P A⊥AB.又∵AB⊥AD且P A∩AD＝A，∴AB⊥平面P AD，而PD平面P AD，∴AB⊥PD.又∵AB∩AE＝A，∴PD⊥平面ABE.跟踪训练3证明(1)设BC的中点为M，∵点B1在底面ABC上的射影恰好是点M，∴B1M⊥平面ABC. ∵AC平面ABC，∴B1M⊥AC.又∵BC⊥AC，B1M∩BC＝M，∴AC⊥平面B1C1CB.又∵AC平面ACC1A1，∴平面ACC1A1⊥平面B1C1CB.(2)连接B1C.∵AC⊥平面B1C1CB，∴AC⊥BC1.在斜三棱柱ABC－A1B1C1中，∵BC＝CC1.∴四边形B1C1CB是菱形，∴B1C⊥BC1.又∵B1C∩AC＝C，∴BC1⊥平面ACB1，∴BC1⊥AB1.例4(1)证明连接MN，∵N，F均为所在棱的中点，∴NF ⊥平面A 1B 1C 1D 1.而MN 平面A 1B 1C 1D 1，∴NF ⊥MN .又∵M ，E 均为所在棱的中点，∴△C 1MN 和△B 1NE 均为等腰直角三角形．∴∠MNC 1＝∠B 1NE ＝45°，∴∠MNE ＝90°，∴MN ⊥NE ，∴MN ⊥平面NEF .而MN 平面MNF ，∴平面MNF ⊥平面ENF .(2)解在平面NEF 中，过点N 作NG ⊥EF 于点G ，连接MG .由(1)知MN ⊥平面NEF ，又EF 平面NEF ，∴MN ⊥EF .又MN ∩NG ＝N ，∴EF ⊥平面MNG ，∴EF ⊥MG .∴∠MGN 为平面MEF 与平面NEF 的夹角．设该正方体的棱长为2，在Rt △NEF 中，NG ＝NE ·NF EF ＝233， ∴在Rt △MNG 中，tan ∠MGN ＝MN NG＝2233＝62.∴平面MEF 与平面NEF 的夹角的正切值为62. 跟踪训练4 (1)证明连接OC .∵PO ⊥底面⊙O ，AC 底面⊙O ，∴AC ⊥PO .∵OA ＝OC ，D 是AC 的中点，∴AC ⊥OD .又∵OD ∩PO ＝O ，∴AC ⊥平面POD .又∵AC 平面P AC ，∴平面POD ⊥平面P AC .(2)解在平面POD 中，过点O 作OH ⊥PD 于点H .由(1)知，平面POD ⊥平面P AC ，∴OH ⊥平面P AC .又∵P A 平面P AC ，∴P A ⊥OH .在平面P AO 中，过点O 作OG ⊥P A 于点G ，连接HG ，则有P A ⊥平面OGH ，∴P A ⊥HG .故∠OGH 为二面角B －P A －C 的平面角．∵C 是AB 的中点，AB 是直径，∴OC ⊥AB .在Rt △ODA 中，OD ＝OA ·sin 45°＝22. 在Rt △POD 中，OH ＝PO ·OD PD ＝PO ·OD PO 2＋OD 2＝2×222＋12＝105. 在Rt △POA 中，OG ＝PO ·OA P A ＝PO ·OA PO 2＋OA 2＝2×12＋1＝63. 在Rt △OHG 中，sin ∠OGH ＝OH OG ＝10563＝155. ∴cos ∠OGH ＝1－sin 2∠OGH＝ 1－1525＝105. 故二面角B －P A －C 的余弦值为105. 当堂训练1．C 2.A3．C4．80 40解析由三视图可知该几何体由一个正方体和一个长方体组合而成，上面正方体的边长为2 cm ，下面长方体的底面边长为4 cm ，高为2 cm ，其直观图如图所示，其表面积S ＝6×22＋2×42＋4×2×4－2×22＝80(cm 2)．体积V ＝2×2×2＋4×4×2＝40(cm 3)．5．证明 (1)连接A 1C 1，设A 1C 1∩B 1D 1＝O 1，连接AO 1，∵ABCD －A 1B 1C 1D 1是正方体，∴A 1ACC 1是平行四边形，∴A1C1∥AC且A1C1＝AC，又O1，O分别是A1C1，AC的中点，∴O1C1∥AO且O1C1＝AO，∴四边形AOC1O1是平行四边形，∴C1O∥AO1，AO1平面AB1D1，C1O平面AB1D1，∴C1O∥平面AB1D1.(2)∵CC1⊥平面A1B1C1D1，B1D1平面A1B1C1D，∴CC1⊥B1D1，又∵A1C1⊥B1D1，CC1∩A1C1＝C1，∴B1D1⊥平面A1C1CA，∵A1C平面A1C1CA，∴A1C⊥B1D1，同理可证A1C⊥AB1，又B1D1∩AB1＝B1，∴A1C⊥平面AB1D1.。

人教版高中数学必修二教案第一章+空间几何体复习

第一学期高二年级数学（文科）教案项目内容第1章空间几何体复习课题修改与创新（共 1 课时）通过总结和归纳空间几何体的知识，能够使学生综合运用知识解决有教学关问题，培养学生分析、探究和思考问题的能力，激发学生学习数学的兴目标趣，培养其分类讨论的思想和提高其抽象思维能力. 教学重点：①空间几何体的结构特征. 教学②由三视图还原为实物图. 重、③面积和体积的计算. 难点教学难点：①由三视图还原为实物图. ②组合体的结构特征. 教学多媒体课件准备一、导入新课：我们生活的世界，存在各式各样的物体，它们大多是由具有柱、锥、台、球等形状的物体组成的.认识和把握柱体、锥体、台体、球体的几何结构特征，是我们认识空间几何体的基础.教师引出课题.二、讲授新课：教学过提出问题程 1.本章接触到的空间几何体是单一的柱体、锥体、台体、球体，或者是它们的简单组合体.你能说出较复杂的几何体（如你身边的建筑物）的结构吗？ 2.对于空间几何体，可以有不同的分类标准.你能从不同的方面认识柱、锥、台、球等空间几何体吗？你分类的依据是什么？ 3.为了研究空间几何体，我们需要在平面上画出空间几何体.空间几何体有哪些不同的表现形式？4.利用斜二测画法，我们可以画出空间几何体的直观图.你能回顾用斜二测画法画空间几何体的基本步骤吗？5.计算空间几何体的表面积和体积时，要充分利用平面几何知识，把空间图形转化为平面图形，特别是柱、锥、台体侧面展开图.请同学们回顾柱、锥、台体的侧面展开图是什么？如何计算它们的表面积？柱、锥、台体的体积之间是否存在一定的关系？ 6.球是比较特殊的空间几何体，它的表面积公式和体积公式是什么？7.画出本章的知识结构图. 活动：让学生自己回顾所学知识或结合课本，重新对知识整合，对没有思路的学生，教师可以提示按课本的章节标题来分类.对于画知识结构图，学生可能比较陌生，教师可以引导学生先画一个本班班委的结构图或学校各个处室的关系结构图，待学生了解了简单的画法后，再画本章的知识结构图. 讨论结果：1.略.以实际情况来确定. 2.按围成几何体的面是否是平面分为：棱柱棱柱柱体圆柱多面体棱锥棱锥棱台锥体按底面的情况分为：简单几何体圆锥简单几何体圆柱棱台圆锥台体旋转体圆台圆台球球体 3.空间几何体有两种表现形式：三视图和直观图. 4.略. 5. 结构特棱柱棱锥棱台圆柱圆锥圆台球征平行由三角由梯侧面展不可展四边形拼接形拼矩形扇形扇环开图开形成接成表面积的计算各个面的面积之和就是表面积方法柱、锥、台体的体积之间的关系：柱体和锥体可以看作由台体变化得到.柱体可以看作是上、下底面相同的台体，锥体可以看作是有一个底面是一个点的台体.柱体和锥体的体积公式都可以看作由台体的体积公式演变而来. 426.半径为R的球，其表面积为S=4πR，体积V=. 表33R7.本章的知识结构图如图1所示. 图1 应用示例例1 下列几何体是台体的是（）图2 活动：学生回顾台体的结构特征. 分析：A中的“侧棱”没有相交于一点，所以A不是台体；B中的几何体没有两个平行的面，所以B不是台体；很明显C是棱锥，D是台体. 答案：D 点评：本题主要考查台体的结构特征.像这样的概念辨析题，主要是依靠对简单几何体的结构特征的准确把握. 变式训练1.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括（） A.一个圆台、两个圆锥 B.两个圆台、一个圆柱 C.两个圆台、一个圆柱 D.一个圆柱、两个圆锥分析：因为梯形的两底平行，故另一底旋转形成了圆柱面，而两条腰由于与旋转轴相交，故旋转形成了锥体，因此得到一个圆柱、两个圆锥. 答案：D2.下列三视图表示的几何体是（）图3 A.圆台 B.棱锥 C.圆锥 D.圆柱分析：由于俯视图是两个同心圆，则这个几何体是旋转体，又侧视图和正视图均是等腰梯形，所以该几何体是圆台. 答案：A3.下列有关棱柱的说法：①棱柱的所有的棱长都相等；②棱柱的所有的侧面都是长方形或正方形；③棱柱的侧面的个数与底面的边数相等；④棱柱的上、下底面形状、大小相同. 正确的有______________. 分析：棱柱的所有面都是平的，所有侧棱长都相等，但底面上的棱与侧棱不一定相等，其侧面都是平行四边形，只有当棱柱是直棱柱时，侧面才是矩形，侧面个数与底面边数相等，棱柱的上、下底面是全等的多边形，由此可知③④正确. 答案：③④例2 (2006福建高考，理5)已知正方体外接球的体积是，那么正方3体的棱长等于（）234222A. B. C. 3343D. 3活动：学生思考交流正方体和球的结构特征，教师可以借助于信息技术，展示图形. 分析：过正方体的相对侧棱作球的截面，可得正方体的对角线是球的直径.3a3a设正方体的棱长为a，球的半径为R，则有2R=，所以R=，则243a32433()，解得a=. 3233答案：D 点评：球与其他几何体的简单组合体问题，通常借助于球的截面来明确构成组合体的几何体的结构特征及其联系，本题利用正方体外接球的直径是正方体的对角线这一隐含条件使得问题顺利获解.空间几何体的表面积和体积问题是高考考查的热点之一.主要以选择题或填空题形式出现，也不排除作为解答题中的最后一问，题目难度属于中、低档题，以考查基础知识为主，不会出现难题.其解决策略是利用截面或展开图等手段，转化为讨论平面图形问题，结合平面几何的知识来求解. 变式训练 1.（2005全国高考卷Ⅰ，理5）如图4（1）所示，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE、△BCF均为正三角形，EF∥AB，EF=2，则该多面体的体积为（）4323A. B.C. D. 3233(1) (2) 图4 分析：如图4(2)所示，过B作BG⊥EF于G，连接CG，则CG⊥EF，BF=1，12223△BCG中，BG=，BC边上的高为，而S=×1×=, △BCG2222421212∴V=.同理过A作AH⊥EF于H，则有V=，显F—BCGE—AHD342242422然BCG—ADH为三棱柱，∴V=×1=，则由图4(2)可知BCG—ADH442V=V+V+V=. ADE—BCFF—BCG E—答案：A 点评：本题求几何体体积的方法称为割补法，AHDBCG—ADH3经常应用这种方法求多面体体积.割补法对空间想象能力的要求很高且割补法的目的是化不规则为规则.因此可以说割补法是一种综合的方法，这和我们高考的理念和命题原则是相通的，高考题中出现这样的问题也是很正常的，所以这将是高考对立体几何这部分知识命题的方向. 2.（2007广东中山高三期末统考，文6）某个容器的底部为圆柱，顶部为圆锥，其正视图如图5所示，则这个容器的容积为（）图5 7833mm3A.B. C.3π m 333D.12π m分析：由该容器的正视图可知，圆柱的底面半径为1 m，高为2 m，圆锥33的底面半径为1 m，高为1 m.则圆柱的体积为2π m，圆锥的体积为m，373m所以该容器的容积为. 3答案：A 点评：三视图是新课标高考的新增内容，在高考中会重点考查，在该知识点出题的可能性非常大，应予以重视.此类题目的解题关键是利用三视图获取体积公式中所涉及的基本量的有关信息，这要依靠对三视图的理解和把握. 3.（2007广东佛山一模，理4）如图6所示，一个简单空间几何体的三视图其正视图与侧视图是边长为2的正三角形、俯视图轮廓为正方形，则其体积是（）图6 842433A. B. C. D. 3336分析：根据三视图可知该几何体是正四棱锥，且底面积是4，高为正视图1433等边三角形的高，所以体积为. 33答案：B 课堂小结：本节课复习了： 1.第一章知识及其结构图. 2.三视图和体积、面积的有关问题. 3.空间几何体的概念.布置作业：课本本章复习参考题A组 7、8、9. 板书设计教学反思。

整合新课标人教A版必修二第一章空间几何体复习教案

第一章空间几何体使我们很好地把握空间几何体的性质．由空间几何体可以画出它的三视图，同样，由三视图可以想象出空间几何体的形状，两者之间可以相互转化．若某几何体的三视图如图所示，则这个几何体的直观图可以是( )A B C D【思路点拨】选项――――→验证三视图――――→对照选择【解析】所给选项中，A 、C 选项的正视图、俯视图不符合，D 选项的侧视图不符合，只有B选项符合．【答案】 B如图1－2，某几何体的正视图是平行四边形，侧视图和俯视图都是矩形，则该几何体的体积为()A．63B．9 3C．12 3 D．18 3【解析】由三视图可知该几何体为一个平行六面体(如图)，其底面是边长为3的正方形，高为22－12＝3，所以该几何体的体积为93，故选B.【答案】 B1.在计算中应注意各数量之间的关系及各元素之间的位置关系，特别是特殊的柱、锥、台，要注意其中矩形、梯形及直角三角形等重要的平面图形的作用．2．常见的计算方法(1)公式法：根据题意直接套用表面积或体积公式求解．(2)割补法：割补法的思想是：通过分割或补形，将原几何体分割成或补成较易计算体积的几何体，从而求出原几何体的体积．(3)等体积变换法：等积变换法的思想是：从不同的角度看待原几何体，通过改变顶点和底面，利用体积不变的原理，来求原几何体的体积．已知三棱锥A－BCD的表面积为S，其内有半径为r的内切球O(球O与三棱锥A－BCD的每个面都相切，即球心O到A－BCD每个面的距离都为r)，求三棱锥A－BCD的体积．【思路点拨】分析三棱锥A－BCD的体积与以O为顶点，各个面为底面的4个小棱锥体积间的关系．【规范解答】连接AO ，BO ，CO ，DO ，则三棱锥A －BCD 被分割成为四个小三棱锥：O －ABC ，O －ABD ，O －ACD ，O －BCD ，并且这四个小三棱锥的顶点都为O ，高都为r ，底面分别为△ABC ，△ABD ，△ACD ，△BCD .故有V A －BCD ＝V O －ABC ＋V O －ABD ＋V O －ACD ＋V O －BCD＝13S △ABC ·r ＋13S △ABD ·r ＋13S △ACD ·r ＋13S △BCD ·r＝13(S △ABC ＋S △ABD ＋S △ACD ＋S △BCD )r ＝13Sr .某三棱锥的三视图如图1－3所示，该三棱锥的表面积是 ( )图1－3A ．28＋6 5B ．30＋6 5C ．56＋12 5D ．60＋12 5【解析】由三棱锥的三视图可得三棱锥的直观图如图(1)所示．图(1) 图(2)S △ACD ＝12×AC ×DM ＝12×5×4＝10.S △ABC ＝12×AC ×BC ＝12×5×4＝10.在△CMB 中，∠C ＝90°，∴|BM |＝5.∵DM ⊥面ABC ，∴∠DMB ＝90°，∴|DB |＝42＋52＝41，∴△BCD 为直角三角形，∠DCB ＝90°，∴S △BCD ＝12×5×4＝10.在△ABD 中，如图(2)，S △ABD ＝12×25×6＝65，∴S 表＝10＋10＋10＋65＝30＋6 5.故选B.【答案】 B1.转化与化归的思想方法是数学中最基本的思想方法，所谓转化与化归思想是指把待解决的问题(或者说未知解的问题)转化归结为已有知识范围内可解的问题的一种数学意识．立体几何中的有关问题，一般转化为平面问题来解决，其途径主要有以下两种：一是多面体常转化到它的底面、侧面、对角面内，而旋转体主要是利用轴截面；二是将多面体的表面或旋转体的侧面展开．如图1－4，长方体ABCD —A 1B 1C 1D 1中，AB ＝a ，BC ＝b ，BB 1＝c ，并且a ＞b ＞c ＞0.求沿着长方体的表面自A 到C 1的最短线路的长．图1－4【思路点拨】长方体表面展开→平面内两点间的距离【规范解答】将长方体相邻两个面展开有下列三种可能，如图．三个图形(1)(2)(3)中AC 1的长分别为：a ＋b2＋c 2＝a 2＋b 2＋c 2＋2ab ， a 2＋b ＋c2＝a 2＋b 2＋c 2＋2bc ， a ＋c 2＋b 2＝a 2＋b 2＋c 2＋2ac .∵a ＞b ＞c ＞0.∴ab ＞ac ＞bc ＞0. 故最短线路的长为a 2＋b 2＋c 2＋2bc .圆柱的轴截面是边长为5 cm 的正方形ABCD ，从A 到C 圆柱侧面上的最短距离为( )A ．10 cm B.52π2＋4 cm C ．5 2 cm D ．5 π2＋1 cm【解析】如图所示，沿母线BC 展开，曲面上从A 到C 的最短距离为平面上从A 到C 的线段的长．∵AB ＝BC ＝5，∴A ′B ＝AB ＝12×2π×52＝52π.∴A ′C ＝A ′B 2＋BC 2＝254π2＋25＝5π24＋1＝52 π2＋4.【答案】 B2．函数与方程思想函数与方程思想是指将抽象的数学问题转化为函数的性质或解方程(组)等问题解决，在立体几何中求几何体的高、棱长、侧面积、体积等往往利用这一思想方法．一个圆锥底面半径为R ，高为3R ，求圆锥的内接正四棱柱表面积的最大值．【思路点拨】画出该几何体组合体的轴截面，利用相似三角形的知识建立等量关系，借助函数的知识求其最值．【规范解答】如图所示，△SAB为圆锥的一个轴截面，且该轴截面经过正四棱柱的对角面，DF为棱柱的底面对角线．设正四棱柱的高为h，底面正方形边长为a，则DE＝2 2a.∵△SDE∽△SAO，∴DEAO＝SESO.∵AO＝R，SO＝3R，∴22aR＝3R－h3R，∴h＝3R－62a.∴S表＝2a2＋4ah＝2a2＋4a⎝⎛⎭⎪⎫3R－62a.整理得S表＝(2－26)⎝⎛⎭⎪⎫a－3R6－12＋6R26－1(0<a<2R)．∵2－26<0，3R6－1<2R，∴当a＝3R6－1时，S表有最大值，为6R26－1，即圆锥的内接正四棱柱表面积的最大值为6R2 6－1，即6＋5R2.将一个底面圆的直径为2，高为1的圆柱截成横截面为长方形的棱柱(如图1－5)，设这个长方形截面的一条边长为x，对角线长为2，截面的面积为A.图1－5(1)求面积A以x为自变量的函数式；(2)求出截得棱柱的体积的最大值．【解】(1)横截面如图，由题意得A＝x·4－x2(0<x<2)．(2)棱柱的体积V＝A ·h＝x ·4－x2＝－x2－2＋4，由(1)知0<x<2，所以，当x＝2时，V取最大值，其值为2.3．数形结合思想数形结合思想的实质是将抽象的数学语言与直观的图形结合起来，通过对图形的认识，实现数与形的转化，使问题化抽象为具体，化难为易．求函数f (x )＝x 2＋4＋x 2－10x ＋34的最小值．【思路点拨】结合函数解析式的结构特征，将代数问题转化为几何问题．【规范解答】依题意：f (x )＝x 2＋22＋－x 2＋32，构造长方体ABCD －A 1B 1C 1D 1，其三条棱长分别为AB ＝2，BC ＝3，BB 1＝5(如图(1))，设BE ＝x.(1) (2)则AE ＝x 2＋22，EC 1＝－x 2＋32，所以f (x )＝AE ＋EC 1.这样，原题求函数f (x )的最小值，就转化为在长方体AC 1的棱BB 1上找一点E ，使折线AEC 1的长度最短．将长方体侧面展开(如图(2))．连接AC 1，显然AE ＋EC 1≥AC 1且AC 1＝＋2＋52＝52，即f (x )min ＝5 2. 即函数f (x )＝x 2＋4＋x 2－10x ＋34的最小值是52.若半球内有一内接正方体，则这个半球的表面积与正方体的表面积之比为________．【解析】设半球的半径为R ，内接正方体的棱长为a ，过正方体的对角面作出它的截面图，如图．OE ＝OF ＝OD ＝R ，BC ＝AD ＝a ，AB ＝CD ＝2a ，所以OA ＝22a .在△OAD 中，OD 2＝OA 2＋AD 2，即R 2＝a 22＋a 2＝32a 2，所以R 2a 2＝32. 又S 半球S 正方体＝12×4πR 2＋πR 26a 2＝π2·R 2a 2＝π2×32＝3π4，所以应填3π∶4. 【答案】3π∶4。

高一语文人教版必修二第一单元期末复习导学案

高一语文人教版必修二第一单元期末复习导学案1班级姓名组别一、学习目标：1、熟悉第一单元三篇文章的作者背景及主要内容。

2、积累文章中的重点词语和理解文章中的重点语句的含义。

3、提升自己的语言表达能力和鉴赏文字的能力。

二、基础知识检测：1、下列词语中加点字注音全都正确的一项是( )A.眷．恋（ｊｕàｎ）恬．适（ｔｉáｎ）羁．绊（ｊī）驾驭．（ｙù）B.厦．门（ｘｉà）混．沌（ｈùｎ）椽．子（ｃｈｕáｎ）驯．鸽（ｘúｎ）C.穿著．（ｚｈｕó）平仄．（ｚè）颓．废（ｔｕǐ）廿．四（ｎｉàｎ）D.隽．永（ｊùｎ）歧．韵（ｑí）椭．圆（ｔｕǒ）啼．唱（ｄǐ）2、下列选项中加点的字注音全对的一项是( )A陆蠡．(lǐ) 涸．(hé)辙揠．( àn )苗助长淅．(xī )沥B猗．( yī )郁抑．(yì)郁蕈．(xùn )菌婆娑．(suō)C.瞥．(piē)见茎．(jǐng)叶纤．(xiān)细脉络．(luò)D移徙．(xǐ) 葱茏．(lóng) 囚系．(jì)嵌．(qiàn)着3．下列加粗字注音正确的一项是（）A．倩（qiān）影媛（yuàn）女鹢（yì）首袅娜（nuó）B．羞涩（sè）蟋蟀（shuai）啼（tí）唱婆娑（shuō）C．陪衬（chèn）瞥（piē）见肋（lèi )骨澄（dēng）清D．宛（wǎn）然颤（zhàn)栗氛（fēn围创（chuāng）伤4．下列各句中没有错别字的一项是( )A．金碧辉煌萧索秋蝉厮叫B．疏疏落落传诵搅尽脑汁凋零C．放荡不羁落寞隐逸恬适点缀D．意境姿态洪流训鸽渲染5、下列各句中，加点成语使用不恰当的一项是( )A．有些家长，自己喜欢吃喝玩乐，混混沌沌．．．．地过日子，孩子就容易成为如此父母的镜子。

必修二第一章学案

必修二《人口的变化》复习学案【课时进度】必修二第一章【复习指南】重点知识：1.1人口的数量变化(A) 人口的自然增长。

(B)人口增长模式的主要特点、地区分布。

(C)利用图表分析人口增长模式。

1.2人口的空间变化(A)人口的迁移。

(B)影响人口迁移的因素。

1.3人口的合理容量(A) 对环境人口容量的不同估计。

(B) 环境承载力、环境人口容量、人口合理容量；环境人口容量的影响因素。

【知识总结】第一节人口的变化一、人口的自然增长1. 一个地区人口的自然增长，是由 ________________ 和 _____________ 共同决定的2. 时间世界人口数量变化的总趋势是不断____________________________________10万年以来农业革命前：人口增长及其______________________的人口增长农业革命期间：人口增长______________________工业革命后：人口增长速度明显________________________100 年来世界人口的增长：以前所未有的速度___________________________ 我国人口的突出特点是______________________ 大3. 空间__________________________________________ 世界人口增长地区上是发达国家：人口增长_____________ ，有的国家还出现_________________ ，女口： __________________________________________________________发展中国家：人口增长_______ ，原因是______________________________二、人口增长模式及其转变1.人口增长模式是由 _____________ 、、___________ 三项指标构成2.模式原始型：岀生率，死亡率，自然增长率传统型：出生率，死亡率，自然增长率现代性：岀生率，死亡率，自然增长率3.分布发达国家：型大多数发展中国家：____________________ 型全球：由_______________ 型向__________________ 的过渡阶段中国：基本实现从_________________ 型向 _______________________ 转变第二节人口的空间变化一、人口的迁移1. 概念：人的2. 分类：在、或范围内发生变化3.国际概念：人口跨并改变达到一疋时间(通常为年人口迁移活动迁移19 世纪前总特点：_____________________________________________________迁出区：_________________ ，迁入区______________________原因：__________________________________________________意义：__________________________________________________ 二战后新特点：______________________________________________________________ 迁出区：____________________ ，迁入区：_____________________________原因：______________________________________________________________意义：______________________________________________________________ 4. 国内概念：在范围内，人口从一个地区向另一个地区移居的现象人口古代：深受统治者及其行政力量的束缚迁移新中国到20世纪特点：80年代中期流向：20世纪80特点:年代中期以来流向:、影响人口迁移的因素__.日疋 ___________________________________________________________________________________ 二是__________________________________________________________________________ 第三节人口的合理容量一、地球最多能养活多少人-----环境人口容量1. 环境承载力概念：环境能___________________ 供养的人口数量衡量指标：__________________________________________2. 环境人口容量概念：__________________________________________________________制约因素： _____________ （__________ 相关）______________ （ _________ 相关）_____________________________ （__________ 相关）估计结果：__________________ 、、 _______________________地球的环境人口容量在____________________ 亿左右二、地球上适合养活多少人-------- 人口的合理容量1. 人口的概念：____________________________________________________________合理容量意义：它对于制定一个地区或一个国家的________________ 和___________有着重要意义，进而影响区域饿经济社会发展战略2. 保持人口合理容量的紧迫性①全人类共同面临的_________ 、、______________②发达国家___________________________________________________________________③发展中国家_________________________________________________________________ 【巩固练习】一•单项选择题1. 10万年以来世界人口数量不断增长，但是在不同的历史时期，人口数量增长的特点是不相同的，下列说法正确的是A. 农业革命之前，人口数量增长较快B. 农业革命之后，人口数量高速增长，一直到工业革命前C•农业革命到工业革命前，人口数量总体来说在增加，但后期速度减慢甚至停止增长D.工业革命后，人口数量减少2. 一个地区人口数量的变化，主要有哪两个变化原因①人口的自然增长率②人口的出生率③人口的死亡率④人口迁移A .①②B .②③C .③④D .①④3. 下列国家中属于人口超过1亿且政府仍然大力推广鼓励生育政策的是A. 日本B .中国 C.印度 D.英国4. 目前，多数发达国家的人口增长状况是人口比左■畫2• ■1 e( )C. ①D.④( )C. ①D.④自然增长率 D. 生育率A 快速增长B •负增长C •接近零增长 D.零增长5. 为了缓和人口压力，我国应采取下图人口增长模式中的下图反映四个国家的人口出生率和死亡率，回答6〜7题6. 其中人口增长模式属于“传统型”的国家是A. ③B.②7. 当今世界，发达国家的人口增长模式类似于A.③B.②8. 在人口增长模式转变过程中，先转变的是A.出生率B. 死亡率C.C. 20世纪70年代知识青年“上山下乡”一一气候因素D. 巴勒斯坦人迁往西亚其他国家——水源因素 12. 关于我国“民工潮”的叙述，正确的是A. 我国农业机械化的普及，使农村大量剩余劳动力外流B. 城乡和地区间巨大的收入差距是引起民工流动的根本原因C. 大量民工的涌入，给城市环境造成巨大的压力，不利于城市经济的发展D. 使大城市人口老龄化严重 13.第二次世界大战以后，国际人口迁移表现出新的特点有（）①人口从发展中国家流向发达国家②短期流动的人口减少定居移民增多③欧洲由人口迁入地区变为人口迁出地区④拉丁美洲由人口迁入变为人口迁出地区⑤ 20世纪70年代以来，西亚和北非石油输出国也从境外招募了大批外籍工人A ①③⑤B .①②③④C .①④⑤D .①②③④⑤ 14.随着人类社会的发展，对人口迁移的影响作用逐步增强的是（）A.自然环境因素 B .政治因素 C.婚姻家庭因素D.社会经济因素下图为人口迁移示意。

必修2第一章教学设计

教学设计5 6教学设计2.根据金属元素最高价氧化物对应化水物碱性强弱。

碱性越强，则原金属元素的金属性越强。

3.可以根据对应阳离子氧化性强弱判断。

金属阳离子氧化性越弱，则元素金属性越强。

[过渡]刚才我们以典型的金属一族为例，下面我们以典型的非金属为例。

看看他们的性质有原子结构间是否存在联系？探究点二：卤族元素的有什么样的递变规律？展示卤素单质的物理性质：请大家根据表，总结出卤素单质在颜色、状态、密度、熔沸点、溶解性等各方面的递变规律。

大家能否根据卤素原子的结构特点来解释一下卤素单质在性质上的相似性与递变性呢?【教师】下面请同学们看表格：卤素单质与氢气的反应。

从中我们得出什么结论？[教师]我们可以通过金属与盐溶液的置换反应可以比较金属的强弱，通过卤素间的置换反应实验，比较非金属的氧化性的强弱。

[实验1]、[实验2]［小结］卤素单质随着原子核电荷数的递增，在物理性质和化学性质方面，均表现出一定的相似性和递变性。

但一般之中有特殊。

由此可见同一主族元素性质具有一定的相似性和递变性。

由此，我们得出非金属性强弱的判断依据：1. 与氢气反应生成气态氢化物难易；2.单质的氧化性（或离子的还原性）；3.最高价氧化物的水化物（H n RO m）的酸性强弱；4.非金属单质间的置换反应。

（四）反思总结、当堂检测教师组织学生反思总结本节主要内容，并进行当堂检测。

（五）发导学案、布置预习我们已经学习了碱金属和卤族元素的递变规律，同主族元素性质的递变规律，进而知道了元素强弱的判断依据教学设计（3）离子指的是带电的原子或原子团。

带正电荷的粒子叫阳离子，带负电荷的粒子叫阴离子。

当质子数(核电荷数)＞核外电子数时，该粒子是阳离子，带正电荷；当质子数(核电核数＜核外电子数时，该粒子是阴离子，带负电荷。

（4）原子组成的表示方法2、核素和同位素（1）核素：具有一定数目的质子和一定数目的中子的原子叫核素。

如如氢元素有11H、21H、31H三种不同核素。

高中化学人教版必修二高中化学第一章章末复习教案1

优质资料---欢迎下载第一章物质结构元素周期律章末复习【教学目标】一、知识与能力1、掌握元素周期律的实质即元素周期表的结构2、掌握同一周期内元素性质的递变规律与原子结构的关系，同一主族内元素性质递变规律和原子结构的关系。

3、理解原子的组成及同位素的概念。

掌握原子序数、核电荷数、质子数、中子数、核外电子数的相互关系4、短周期元素为例，掌握核外电子排布的规律。

5、理解离子键、共价键的含义，了解分子作用力、氢键的作用。

二、过程与方法能初步具有总结元素递变规律的能力；能把元素的性质、元素周期位置与组成的粒子结构初步联系起来，并能较熟练地运用；培养学生科学的分析推理能力。

三、情感态度与价值观对“位、构、性”的分析，培养学生综合、辩证、创新的精神；使学生初步意识到物质的结构决定物质的性质；科学地、辩证地看问题。

教学重点：元素周期律的实质；“位-构-性”三者之间的关系；原子的组成及同位素的概念；掌握原子序数、核电荷数、质子数、中子数等之间的关系；理解离子键、共价键的涵义。

教学难点： “位-构-性”三者之间的关系；原子序数、核电荷数、质子数、中子数、核外电子数之间的相互关系；用电子式表示离子化合物或共价化合物形成过程。

【基础知识自查】知识点11．原子结构（1）原子的构成原子原子核核外电子（2）核素(原子)符号表示A Z X表示质子数为_________、质量数为___________、中子数为_________的核素原子，如氘__________。

（3）微粒中的“各数”间的关系①质量关系：质量数(A )＝_____________＋___________________②电性关系⎩⎪⎨⎪⎧原子(A Z X )：核外电子数＝质子数(Z )＝核电荷数＝原子序数阴离子(AZX n －)：核外电子数＝Z ＋n阳离子(A ZX n ＋)：核外电子数＝Z －n2．元素、核素、同位素（3）氢元素的三种核素11H ：名称为__________，不含中子 21H ：用字母_______表示，名称为____________或重氢 31H ：用字母___________表示，名称为____________或超重氢练习：1．2016年1月5日，江西省国土资源厅宣布，该省地质工作者在浮梁县发现超大型钨铜矿。

高中数学必修二第一章章末复习提升公开课教案课件课时训练练习教案课件

1．空间几何体的结构特征(1)棱柱：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边互相平行．棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形．棱台是棱锥被平行于底面的平面所截而成的．这三种几何体都是多面体．(2)圆柱、圆锥、圆台、球分别是由平面图形矩形、直角三角形、直角梯形、半圆面旋转而成的，它们都称为旋转体．在研究它们的结构特征以及解决应用问题时，常需作它们的轴截面或截面．(3)由柱、锥、台、球组成的简单组合体，研究它们的结构特征实质是将它们分解成多个基本几何体．2．空间几何体的三视图与直观图(1)三视图是观察者从三个不同位置观察同一个空间几何体而画出的图形；它包括正视图、侧视图、俯视图三种．画图时要遵循“长对正、高平齐、宽相等”的原则．注意三种视图的摆放顺序，在三视图中，分界线和可见轮廓线都用实线画出，不可见轮廓线用虚线画出．熟记常见几何体的三视图．画组合体的三视图时可先拆，后画，再检验．(2)斜二测画法为：主要用于水平放置的平面图形或立体图形的画法．它的主要步骤：(1)画轴；(2)画平行于x、y、z轴的线段分别为平行于x′、y′、z′轴的线段；(3)截线段：平行于x、z轴的线段的长度不变，平行于y轴的线段的长度变为原来的一半．三视图和直观图都是空间几何体的不同表示形式，两者之间可以互相转化，这也是高考考查的重点；根据三视图的画法规则理解三视图中数据表示的含义，从而可以确定几何体的形状和基本量．3．几何体的侧面积和体积的有关计算柱体、锥体、台体和球体的侧面积和体积公式球S球面＝4πR3题型一三视图与直观图例1将正方体如图(1)所示截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的侧视图为()答案B解析还原正方体后，将D1，D，A三点分别向正方体右侧面作垂线．D1A的投影为C1B，且为实线，B1C被遮挡应为虚线．跟踪演练1若某几何体的三视图如图所示，则这个几何体的直观图可以是()答案B解析所给选项中，A、C选项的正视图、俯视图不符合，D选项的侧视图不符合，只有B 选项符合．题型二几何体的表面积与体积例2如图所示，已知三棱柱ABCA′B′C′，侧面B′BCC′的面积是S，点A′到侧面B′BCC′的距离是a，求三棱柱ABCA′B′C′的体积．解连接A′B，A′C，如图所示，这样就把三棱柱分割成了两个棱锥．设所求体积为V ，显然三棱锥A ′ABC 的体积是13V . 而四棱锥A ′BCC ′B ′的体积为13Sa ，故有13V ＋13Sa ＝V ，即V ＝12Sa . 跟踪演练2 某几何体的三视图如图所示，则该几何体的体积为( )A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π答案 A解析将三视图还原为原来的几何体，再利用体积公式求解．原几何体为组合体：上面是长方体，下面是圆柱的一半(如图所示)，其体积为V ＝4×2×2＋12π×22×4＝16＋8π. 题型三转化与化归思想例3 如图所示，圆台母线AB 长为20 cm ，上、下底面半径分别为5 cm 和10 cm ，从母线AB 的中点M 拉一条绳子绕圆台侧面转到B 点，求这条绳子长度的最小值．解如图所示，作出圆台的侧面展开图及其所在的圆锥．连接MB ′，P 、Q 分别为圆台的上、下底面的圆心．在圆台的轴截面中，∵Rt △OP A ∽Rt △OQB ，∴OA OA ＋AB ＝P A QB， ∴OA OA ＋20＝510.∴OA ＝20(cm)．设∠BOB ′＝α，由扇形弧BB ′的长与底面圆Q 的周长相等，得2×10×π＝2×OB ×π×α360°，即20π＝2×(20＋20)π×α360°，∴α＝90°. ∴在Rt △B ′OM 中，B ′M ＝OM 2＋OB ′2＝302＋402＝50(cm)，即所求绳长的最小值为50 cm.跟踪演练3 圆柱的轴截面是边长为5 cm 的正方形ABCD ，从A 到C 圆柱侧面上的最短距离为( )A ．10 cm B.52π2＋4 cm C ．5 2 cm D ．5π2＋1 cm答案 B解析如图所示，沿母线BC 展开，曲面上从A 到C 的最短距离为平面上从A 到C 的线段的长．∵AB ＝BC ＝5，∴A ′B ＝AB ＝12×2π×52＝52π. ∴A ′C ＝A ′B 2＋BC 2＝ 254π2＋25＝5π24＋1＝ 52π2＋4(cm)．研究空间几何体，需在平面上画出几何体的直观图或三视图，由几何体的直观图可画它的三视图，由三视图可得到其直观图，同时可以通过作截面把空间几何问题转化成平面几何问题来解决．另外，圆柱、圆锥、圆台的表面积公式，我们都是通过展开图、化空间为平面的方法得到的，求球的切接问题通常也是由截面把空间问题转化为平面问题来解决．活动目的：教育学生懂得“水”这一宝贵资源对于我们来说是极为珍贵的，每个人都要保护它，做到节约每一滴水，造福子孙万代。

高中数学必修二第一章完整全部教案及导学案经典练习

第一章空间几何体第1课时多面体的结构特征1.通过观察实例，理解并掌握棱柱、棱锥、棱台的定义和结构特征．(重点)2.理解棱柱、棱锥、棱台的结构特征及其关系．(易错点)3.在描述和判断几何体结构特征的过程中，培养学生的观察能力和空间想象能力．(难点)空间几何体阅读教材P2～P3前三自然段，完成下列问题．基本概念【提示】至少有4个面.多面体阅读教材P3后两个自然段和P4的内容，完成下列问题．基本概念多面体定义图形及表示相关概念棱柱有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱如图可记作：棱柱ABCD－A′B′C′D′底面(底)：两个互相平行的面侧面：其余各面侧棱：相邻侧面的公共边顶点：侧面与底面的公共顶点棱锥有一个面是多边形，其余各面都是有一个公共顶点的三底面(底)：多边形面角形，由这些面所围成的多面体叫做棱锥如图可记作：棱锥S－ABCD侧面：有公共顶点的各个三角形面侧棱：相邻侧面的公共边顶点：各侧面的公共顶点续表多面体定义图形及表示相关概念棱台用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫做棱台如图可记作：棱台ABCD－A′B′C′D′上底面：原棱锥的截面下底面：原棱锥的底面侧面：其余各面侧棱：相邻侧面的公共边顶点：侧面与上(下)(1)由六个面围成的封闭图形只能是五棱锥．()(2)两个底面平行且相似，其余各面都是梯形的多面体是棱台．()【解析】(1)不正确，由六个面围成的封闭图形有可能是四棱柱；(2)不正确，两个底面平行且相似，其余各面都是梯形的多面体．侧棱不一定相交于一点，所以不一定是棱台．【答案】(1)×(2)×[探究问题]1．说出它们有何共同特点？分别说出它们几何体的名称．2．有一个面是多边形，其余各面都是三角形的几何体一定是棱锥吗？3．棱台的各侧棱的延长线相交于一点吗？为什么？[探究成果]对多面体概念的理解(1)多面体是由平面多边形围成的，不是由圆面或其他曲面围成的，也不是由空间多边形围成的．(2)我们所说的多面体包括它内部的部分，故多面体是一个“封闭”的几何体．(3)棱柱的侧棱互相平行且相等，侧面都是平行四边形．(4)棱锥的侧棱有公共点，侧面都是三角形．(5)棱台各侧棱延长后必相交于一点，否则不是棱台．关键词：底面、侧棱、侧面下列关于棱柱的说法：(1)所有的面都是平行四边形；(2)每一个面都不会是三角形；(3)两底面平行，并且各侧棱也平行；(4)被平面截成的两部分可以都是棱柱．其中正确说法的序号是________．【思路点拨】根据棱柱的定义进行判断．【自主解答】(1)错误，棱柱的底面不一定是平行四边形；(2)错误，棱柱的底面可以是三角形；(3)正确，由棱柱的定义易知；(4)正确，棱柱可以被平行于底面的平面截成两个棱柱，所以说法正确的序号是(3)(4)．【答案】(3)(4)有关棱柱的结构特征问题的解题策略(1)紧扣棱柱的结构特征进行有关概念辨析①两个面互相平行；②其余各面是四边形；③相邻两个四边形的公共边互相平行．求解时，首先看是否有两个平行的面作为底面，再看是否满足其他特征．(2)多注意观察一些实物模型和图片便于反例排除．[变式训练]1．下列说法正确的是()A．棱柱的面中，至少有两个互相平行B．棱柱中两个互相平行的平面一定是棱柱的底面C．棱柱中各条棱长都相等D．棱柱的侧面是平行四边形，但它的底面一定不是平行四边形【解析】棱柱的两个底面互相平行，A正确．【答案】 A关键词：底面、截面下列关于棱锥、棱台的说法：(1)用一个平面去截棱锥，底面和截面之间的部分组成的几何体叫棱台；(2)棱台的侧面一定不会是平行四边形；(3)由四个面围成的封闭图形只能是三棱锥；(4)棱锥被平面截成的两部分不可能都是棱锥，其中正确说法的序号是________．【思路点拨】已知条件→联想空间图形→紧扣定义→得出结论【自主解答】(1)错误，若平面不与棱锥底面平行，用这个平面去截棱锥，棱锥底面和截面之间的部分不是棱台；(2)正确，棱台的侧面一定是梯形，而不是平行四边形；(3)正确，由四个面围成的封闭图形只能是三棱锥；(4)错误，如图所示四棱锥被平面截成的两部分都是棱锥．【答案】(2)(3)判断棱锥、棱台结构特征的两个方法(1)举反例法：结合棱锥、棱台的定义举反例直接判断关于棱锥、棱台结构特征的某些说法不正确．(2)直接法：[变式训练]2．下面描述中，不是棱锥的结构特征的为()A．三棱锥有四个面是三角形B．棱锥都是有两个面是互相平行的多边形C．棱锥的侧面都是三角形D．棱锥的侧棱相交于一点【解析】根据棱锥的结构特征，知棱锥中不存在互相平行的多边形，故B错．【答案】 B关键词：几何体如图1－1－1长方体ABCD－A1B1C1D1.图1－1－1(1)这个长方体是棱柱吗？如果是，是几棱柱？为什么？(2)用平面BCFE把这个长方体分成两部分后，各部分的几何体还是棱柱吗？若是棱柱指出它们的底面与侧棱．【思路点拨】观察图形→紧扣概念→得出结论→回答问题【自主解答】(1)这个长方体是棱柱，是四棱柱，因为它满足棱柱的定义．(2)截面BCFE右侧部分是三棱柱，它的底面是△BEB1与△CFC1，侧棱是EF，B1C1，BC.截面左侧部分是四棱柱．它的底面是四边形ABEA1与四边形DCFD1，侧棱是AD，BC，EF，A1D1.1．解答本题的关键是正确掌握棱柱的几何特征，本题易出现认为所分两部分的几何体一个是棱柱，一个是棱台的错误．2．在利用几何体的概念进行判断时，要紧扣定义，注意几何体间的联系与区别，不要认为底面就是上下位置，如此题，底面也可放在前后位置．[变式训练]3．从长方体的一个顶点出发的三条棱上各取一点E、F、G，过此三点作长方体的截面，那么截去的几何体是________．【解析】如图所示，所截去的几何体是三棱锥．【答案】三棱锥1．判断一个几何体是何种几何体，一定要紧扣柱、锥、台的结构特征，判断时要充分发挥空间想象能力，必要时做几何模型，通过演示进行准确判断．2．棱柱、棱锥、棱台的关系在运动变化的观点下，棱柱、棱锥、棱台之间的关系可以用下图表示出来(以三棱柱、三棱锥、三棱台为例)．1．下列四个几何体为棱台的是()【解析】棱台的底面为多边形，各个侧面为梯形，侧棱延长后又交于一点，只有C项满足这些要求．【答案】 C2．下列几何体中棱柱有()图1－1－2A．5个B．4个C．3个D．2个【解析】由棱柱定义知，①③为棱柱．【答案】 D3．如图1－1－3所示，在三棱台A′B′C′－ABC中，截去三棱锥A′－ABC，则剩余部分是( )图1－1－3A．三棱锥B．四棱锥C．三棱柱D．组合体【解析】剩余部分是四棱锥A′－BB′C′C.【答案】 B4．根据下列关于空间几何体的描述，说出几何体的名称．(1)由6个平行四边形围成的几何体；(2)由7个面围成，其中一个面是六边形，其余6个面都是有一个公共顶点的三角形；(3)由5个面围成的几何体，其中上、下两个面是相似三角形，其余三个面都是梯形，并且这些梯形的腰延长后能相交于一点．【解】(1)这是一个上、下底面是平行四边形，四个侧面也是平行四边形的四棱柱．(2)这是一个六棱锥，其中六边形面是底，其余的三角形面是侧面．(3)这是一个三棱台，其中相似的两个三角形面是底面，其余三个梯形面是侧面．反思小结：学生基本能够掌握多面体的基本结构，没有什么难点，能达到预期目标第2课时旋转体和简单组合体的结构特征学科：数学年级：高一班级217-228班主备教师：单祖培参与教师：刘英华，沈琼梅，王丝然，樊明文，尹继叶，张露平审定教师：沈琼梅旋转体阅读教材P5～P6“探究”以上部分，完成下列问题．基本概念旋转体结构特征图形表示圆柱以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体叫做圆柱．旋转轴叫做圆柱的轴；垂直于轴的边旋转而成的圆面叫做圆柱的底面；平行于轴的边旋转而成的曲面叫做圆柱的侧面；无论旋转到什么位置，不垂直于轴的边都叫做圆柱侧面的母线我们用表示圆柱轴的字母表示圆柱，左图可表示为圆柱OO′圆锥以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的面所围成的旋转体叫做圆锥我们用表示圆锥轴的字母表示圆锥，左图可表示为圆锥SO圆台用平行于圆锥底面的平面去截圆锥，底面与截面之间的部分叫做圆台我们用表示圆台轴的字母表示圆台，左图可表示为圆台OO′续表旋转体结构特征图形表示球以半圆的直径所在直线为旋转轴，半圆面旋转一周所形成的旋转体叫做球体，简称球．半圆的圆心叫做球的球心，半圆的半径叫做球的半径，半圆的直径叫做球的直径球常用球心字母进行表示，左图可表示为球O【思考】类比圆柱、圆锥的形成过程，圆台可以由平面图形旋转形成吗？【提示】(1)圆台可以看作是直角梯形以垂直于底边的腰所在的直线为旋转轴，其他三边旋转一周而成的曲面所围成的旋转体；(2)圆台也可以看作是等腰梯形以其底边的中线所在的直线为轴各边，旋转半周形成的曲面所围成的几何体．简单组合体阅读教材P6“探究”下面部分及P7“练习”以上部分，完成下列问题．1．简单组合体的概念由简单几何体组合而成的几何体叫做简单组合体．2．简单组合体的构成形式有两种基本形式：一种是由简单几何体拼接而成的；另一种是由简单几何体截去或挖去一部分而成的．【思考】图1－1－8如图1－1－8所示的组合体是由哪些简单几何体构成的？【提示】该组合体上面是一个四棱锥，下面是一个四棱柱，因此该组合体的结构特征是四棱锥和四棱柱的一个组合体．[探究问题]1．上述几何体与棱柱、棱锥和棱台有何不同？2．如何形成上述几何体的曲面？3．球与球面有何区别？【探究提示】1．与棱柱、棱锥和棱台的不同之处在于它们是由平面和曲面围成．2．可将半圆、直角三角形、矩形和直角梯形绕一边为轴旋转而成．3．球与球面是完全不同的两个概念，球是指球面所围成的空间，而球面只指球的表面部分．[探究成果]1．以直角三角形斜边所在的直线为旋转轴，其余两边旋转成的曲面围成的旋转体不是圆锥．2．球是旋转体，球的表面是旋转体形成的曲面，球是球面及其内部空间组成的几何体．3．圆台的两个性质①圆台的母线所在直线共点，所以任意两条母线确定的截面为一等腰梯形；②与上、下底面都相交的截面不一定是梯形，更不一定是等腰梯形．关键词：旋转轴、母线、轴截面给出下列说法：(1)以直角三角形的一条边所在直线为轴，其余两边旋转形成的曲面围成的几何体是圆锥；(2)以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)经过圆锥任意两条母线的截面是等腰三角形；(4)圆锥侧面的母线长有可能大于圆锥底面圆直径，其中正确说法的序号是________．【思路点拨】根据圆锥的定义及结构特征判断．【自主解答】(1)不正确，因为当直角三角形绕斜边所在直线旋转得到的旋转体就不是圆锥，而是两个同底圆锥的组合体；(2)正确，以等腰三角形底边上的中线所在直线为轴，将三角形旋转形成的曲面围成的几何体是圆锥；(3)正确，如图所示，经过圆锥任意两条母线的截面是等腰三角形；(4)正确，如图所示，圆锥侧面的母线长有可能大于圆锥底面圆半径的2倍(即直径)．【答案】(2)(3)(4)1．判断简单旋转体结构特征的方法(1)明确由哪个平面图形旋转而成．(2)明确旋转轴是哪条直线．2．简单旋转体的轴截面及其应用(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量．(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想．[变式训练]1．下列命题中正确的是()A．圆台的任意两条母线的延长线可能相交，也可能不相交B．夹在圆柱的两个平行截面间的几何体是一个旋转体C．圆锥截去一个小圆锥后剩余部分是圆台D．通过圆台侧面上一点，有无数条母线【解析】A错误，圆台的母线延长线相交于一点．B错误，没有说明这两个平行截面与底面的位置关系，当这两个平行截面与底面平行时正确，其他情况则是错误的．D错误，通过圆台侧面上一点，只有一条母线，故选C.【答案】 C关键词：拼接截去或挖去分割描述下列几何体的结构特征．图1－1－10【思路点拨】观察各组合体，利用多面体或旋转体的定义与结构特征，结合简单组合体的两种基本构成形式，入手分析．【自主解答】图(1)所示的几何体是由两个圆台拼接而成的组合体；图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体；图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体．组合体的构成形式和识别方法：组合体是由简单几何体拼接、截去或挖去一部分而成的，因此，要仔细观察组合体的组成和结构，结合柱、锥、台、球的几何结构特征对原组合体进行分割．[变式训练]2．观察下面的简单组合体，你能说出它们各由哪些简单几何体组合而成的吗？图1－1－11【解】图(1)是一个六棱柱与一个圆柱的组合体，图(2)是一个圆柱挖去一个圆锥的组合体．关键词：旋转几何体图1－1－12如图1－1－12，四边形ABCD为直角梯形，试作出绕其各条边所在的直线旋转所得到的几何体．【思路点拨】注意所旋转的图形特点，结合其选定的轴易于解决问题．【自主解答】以边AD所在直线为旋转轴旋转，形成的几何体是圆台，如图(1)所示．以边AB所在直线为旋转轴旋转，形成的几何体是一个圆锥和一个圆柱拼接而成的几何体，如图(2)所示．以边CD所在直线为旋转轴旋转，形成的几何体是一个圆柱挖掉一个圆锥构成的几何体，如图(3)所示．以边BC所在直线为旋转轴旋转，形成的几何体是由一个圆台挖掉一个圆锥构成的几何体和一个圆锥拼接而成，如图(4)所示．由平面图形作旋转体的技巧：(1)要作出一个平面图形绕某一条直线旋转一周所形成的几何体，一般是先作出这个平面图形的各顶点(如果是半圆形，则取垂直于这条直线的半径的端点)关于这条直线的对称点，再把这些相互对称的两点用圆弧连结起来，也就得出相应的几何体，进而便可判定它是由哪些简单的旋转体所组成的几何体．(2)对一个平面图形进行旋转时，所选取的轴不同所得旋转体也不同，对所得几何体要借助圆柱、圆锥、圆台的结构特征进行分析．[变式训练]3．如图1－1－13，第一排中的图形绕虚线旋转一周，能形成第二排中的某个几何体，请把一、二排中相应的图形用线连起来．图1－1－13【答案】(1)—C (2)—B (3)—D (4)—A1．圆柱、圆锥、圆台的关系如图所示．2．处理台体问题常采用还台为锥的补体思想．3．处理组合体问题常采用分割思想．4．重视圆柱、圆锥、圆台的轴截面在解决几何量中的特殊作用，切实体会空间几何平面化的思想．1．(2014·宁德高一检测)将一个等腰梯形绕着它的较长的底边所在的直线旋转一周，所得的几何体包括( )A．一个圆台、两个圆锥B．两个圆台、一个圆柱C．两个圆台、一个圆锥D．一个圆柱、两个圆锥【解析】应由两个圆锥，一个圆柱构成，如图所示：【答案】 D2．(2014·兰州高一检测)下列几何体是台体的是()A B C D【解析】台体包括棱台和圆台两种，A的错误在于四条侧棱没有交于一点．B的错误在于截面与圆锥底面不平行．C是棱锥．结合棱台和圆台的定义可知D正确．【答案】 D3．(2014·兰州高一检测)图1－1－14是由第________个平面图形旋转得到的．图1－1－14【解析】因为题图为一个圆台和一个圆锥的组合体，因此平面图形应是由一个直角三角形和一个直角梯形构成的．由此可知①、②、④不正确．③正确．【答案】③图1－1－154．如图1－1－15，AB为圆弧BC所在圆的直径，∠BAC＝45°.将这个平面图形绕直线AB 旋转一周，得到一个组合体，试说明这个组合体的结构特征．【解】如图所示，这个组合体是由一个圆锥和一个半球体拼接而成的．反思总结: 学生基本掌握旋转体的基本结构，能达到预期目标。

必修2第一章教案4.doc

学科：数学主备人：吕旭授课人: 审核人:课前认识垂直是一种非帘重要的位迸关系，它不仅应用较多，而且是平行关系的的转化手段，可以说垂直关系是立体儿何的核心内容之一，也是高考的热点内容引入在现实牛活小，我们经常看到一些直线与平面垂直的现象，例如：“旗杆与地而，大桥的桥柱和水而等的位置关系”，你能举出一些类似的例子吗？然后让学生回忆、思考、讨论、教师对学牛•的活动给予评价，接着教师指出：一条直线与一个平血垂直的意义是什么？并通过分析旗杆与它在地面上的射影的位置关系引出课题内容。

研探新知1、为使学生学会从“感性认识”到“理性认识”过程屮获収新知，可再借助长方体模型让学生感知直线与平面的垂直关系。

然后教师引导学生用“平面化”的思想来思考问题：从直线与直线垂直、直线与平面平行等的定义过程得到启发，能否用一条直线垂玄于一个平面内的直线来定义这条直线与这个平曲垂直呢？并组织学生交流讨论，概括其定义。

如果直线L与平面a内的任意一条直线都垂直，我们就说直线L与平而a互相垂宜，记作L丄a ,肓线L叫做平面a的垂线，平面a叫做直线L的垂面。

如图2. 3-1,直线与平面垂直时，它们唯一公共点P叫做垂足。

并对画示表示进行说明。

L图2-3-12、老师提出问题,让学生思考:(1)问题：虽然可以根据定义判定直线与平面垂直，但这种方法实际上难以实施。

有没有比较方便可行的方法来判断肓•线和平面垂直呢？（2）师生活动：请同学们准备一块三角形的纸片，我们一起来做如图2.3-2试验：iiAABC的顶点A翻折纸片，得到折痕AD, 将翻折后的纸片竖起放置在桌面上（BD、DC与桌血接触），问如何翻折才能保证折痕AD •桌面所在平面垂直？图2. 3-2（3）归纳结论：引导学生根据直观感知及已有经验（两条相交直线确定一个平面），进行合情推理，获得判定定理：—•条直线与一个平而内的两条相交直线都垂直，则该直线与此平而垂直。

老师特别强调：a）定理中的“两条相交直线”这一条件不可忽视; b）定理体现了“直线少平面垂直”与“直线与直线垂直”互相转化的数学思想。

4、粤教版必修二第一章章末总结教学设计

必修二第一章章末复习教案（简案）学习目标：1、掌握建立思维导图的方法。

2、掌握本章常见知识点。

学习重点：1、建立本章思维导图。

2、会用本章知识解答有关问题。

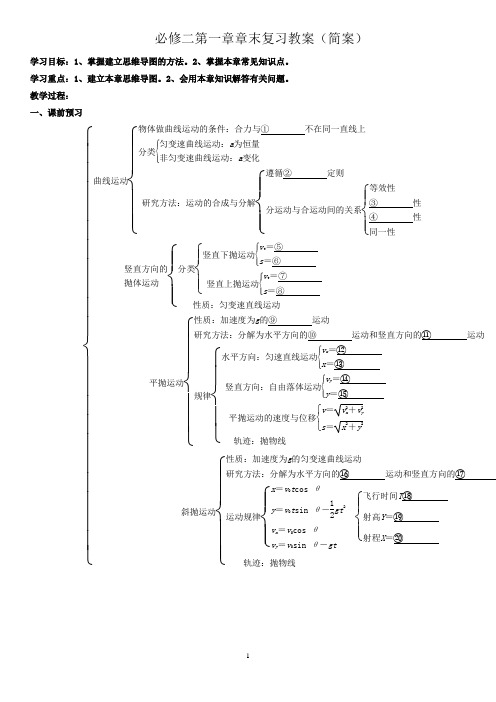
教学过程：一、课前预习⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧曲线运动⎩⎪⎪⎨⎪⎪⎧物体做曲线运动的条件：合力与① 不在同一直线上分类⎩⎪⎨⎪⎧匀变速曲线运动：a 为恒量非匀变速曲线运动：a 变化研究方法：运动的合成与分解⎩⎪⎨⎪⎧遵循② 定则分运动与合运动间的关系⎩⎪⎨⎪⎧等效性③ 性④ 性同一性竖直方向的抛体运动⎩⎪⎨⎪⎧分类⎩⎪⎨⎪⎧竖直下抛运动⎩⎪⎨⎪⎧v t＝⑤s ＝⑥竖直上抛运动⎩⎪⎨⎪⎧v t＝⑦s ＝⑧ 性质：匀变速直线运动平抛运动⎩⎪⎪⎨⎪⎪⎧性质：加速度为g 的⑨ 运动研究方法：分解为水平方向的⑩ 运动和竖直方向的⑪ 运动规律⎩⎪⎨⎪⎧水平方向：匀速直线运动⎩⎪⎨⎪⎧v x＝⑫ x ＝⑬ 竖直方向：自由落体运动⎩⎪⎨⎪⎧v y＝⑭ y ＝⑮ 平抛运动的速度与位移⎩⎨⎧v ＝v 2x ＋v2ys ＝x 2＋y 2轨迹：抛物线斜抛运动⎩⎪⎪⎨⎪⎪⎧性质：加速度为g 的匀变速曲线运动研究方法：分解为水平方向的⑯ 运动和竖直方向的⑰运动规律⎩⎪⎨⎪⎧x ＝v 0t cos θy ＝v 0t sin θ－12gt 2v x ＝v 0cos θv y＝v 0sin θ－gt ⎩⎪⎨⎪⎧飞行时间T ⑱射高Y ＝⑲ 射程X ＝⑳ 轨迹：抛物线[答案填写] ①速度方向 ②平行四边形 ③独立 ④等时 ⑤v 0＋gt ⑥v 0t ＋12gt 2 ⑦v 0－gt ⑧v 0t －12gt 2⑨匀变速曲线 ⑩匀速直线 ⑪自由落体 ⑫v 0 ⑬v 0t ⑭gt ⑮12gt 2⑯匀速直线 ⑰竖直上抛⑱2v 0sin θg ⑲v 20sin 2θ2g ⑳v 20sin 2θg二、曲线运动的轨迹和合外力的关系练习1、(单选)以一定速度上升的热气球里面坐着一个人，这个人相对于热气球水平向右抛出一物体，能正确表示该物体相对于地面的运动轨迹的是（）三、关联速度问题：“绳联物体”的速度分解问题1、“绳联物体”指物体拉绳(杆)或绳(杆)拉物体的问题(下面为了方便，统一说“绳”)，要注意以下两点： (1)物体的实际速度一定是合速度，分解时两个分速度方向应取沿绳方向和垂直于绳方向． (2)由于绳不可伸长，一根绳两端物体沿绳方向的速度分量相等． 2．常见的速度分解模型练习2 如图所示，以速度v沿竖直杆匀速下滑的物体A用轻绳通过定滑轮拉物体B，当绳与水平面夹角为θ时，物体B的速度为( )A．v B.v /sin θC．vcos θ D．vsin θ练习3 如图所示，AB杆和墙的夹角为θ时，杆的A端沿墙下滑的速度大小为v1，B端沿地面的速度大小为v2，则v1、v2的关系是( )A．v1＝v2 B．v1＝v2cos θC．v1＝v2tan θ D．v1＝v2sin θ四、竖直上抛运动的处理方法：分步骤处理、整体处理练习4、如图,一人站在h=10m高的阳台上将一小球以v0=10m/s的初速度竖直向上抛出,不计空气阻力,g取10m/s2,求小球从抛出到落地所经历的时间。