第二题 指派问题
第4章整数规划——指派问题

4 指派问题
解: 可行解{c12=0, c24 =0, c31 =0, c43 =0}是一个独立零元素组, c12=0, c24 =0, c31 =0, c43 =0分别称 为独立零元素; {c12=0, c23 =0, c31 =0, c44 =0}也 是一个独立零元素组,而{c14=0, c23 =0, c31 =0, c44 =0}就不是独立零元素 组.
4 指派问题
1)对新矩阵中所有不含“*”元素的行打√ ; 2)对打√的行中,所有打×零元素所在的列打√; 3)对所有打√列中标记“*”元素所在行打√; 4)重复上述2),3)步,直到不能进一步打√为止; 5)对未打√的每一行划一直线,对已打√的每一列划一纵线, 即得到覆盖当前0元素的最少直线数。 第四步:对矩阵未被直线覆盖过的元素中找最小元素,将打 √行的各元素减去这个最小元素,将打√列的各元素加上这个最小 元素(以避免打√行中出现负元素),这样就增加了零元素的个 数,返回第二步。 【例5】 求解例1和例2
X (2)
都是指派问题的最优解。
4 指派问题
4.3 指派问题的求解 指派问题既是一类特殊的整数规划问题,又是特殊的运输问 题,因此可以用多种相应的解法来求解,然而这些解法都没有充 分利用指派问题的特殊性质,有效地减少计算量,直到1955年库 恩(W. W. Kuhn)提出的匈牙利法才有效地解决了指派问题。 匈牙利法的理论基础 定义2 独立零元素组 在效率矩阵中,有一组在不同行不同 列的零元素,称为独立零元素组,其每个元素称为独立零元素。 5 0 2 0 2 3 0 0 C 【例4】 已知效率矩阵 0 5 6 7 4 8 0 0 求其独立零元素组。
0 , 不 指 派 Ai 承 建 商 店 B j x ij ( i , j 1, 2 ,3, 4 ,5 ) 1, 指 派 Ai 承 建 商 店 B j
数学建模模版之指派问题2

三. 求最大化指派问题 (max cx) 1. 可以将之最小化 min - cx . 2. 为方便起见,可令
c~ij M cij 0 , M max { cij } 转化为 min c~x.
对第5行打√, 检查第5行,对第1列打√,检查第一列
对第3行打√, 检查第3行,打√操作终止。
画线:没打√的行划横线和打√的列划竖线。
Step 4. 变换新矩阵 B (bij ), 使零元素增加 : ①在B中没被直线覆盖的各元 素中找出最小元素 ;
②对B中没被画直线的各行减 去;对B中已画直线的 各列加上
⑤ 对于没有√的行画横线,对所有打√号的列画竖线, 产生覆盖所有零元素的最少直线,直线数目应等于
0 的个数。
例: 5 0 2 0 2 2 3 0 0 0
B 0 10 5 7 5 9 8 0 0 4 0 6 3 6 2
5 0 2 0 2 2 3 0 0 0 0 10 5 7 5√ 9 8 0 0 4 0√ 6 3 6 2√
1, (i, j) J xij
0, (i, j) J
为指派问题的最优指派决策.
二、匈牙利法的步骤
Step 1. 将C零元素化,得到矩阵B,使B中每行每列中均有 零元素 ① C中的各行减该行最小元素; ② C中的各列减该列最小元素;
例: (本章例3,n=4)
-4 -2
3 14 10 5 -3
k (可正、可负)后,形成新矩阵 B (bij )nn ,则以B为效益矩 阵的指派问题与原问题 有相同的最优解 , 但新问题的最优值 ~z *与原问题的最优值 z *满足~z * k z * ( 你能证明吗?)
指派问题——匈牙利法

• 若资源多,事件少,则增加一些虚拟 事件,这些虚拟事件被资源实现的费用( 成本、效率)取值为0;
非标准形式的指派问题
(3) 一个资源可以做多件事的指派问题
若某资源可以用来做几件事件,则 可将该资源化作相同的几个资源来接 受指派,这几个“资源”做同一事件的 费用(效率)系数取相同值;
例 下列矩阵中,最少3条直线覆盖了所有0元 素,因此可判定矩阵有3个独立0元素。
0 1 3 4 2 0 6 0 0 5 9 3 2 7 0 6
指派问题的匈牙利解法——步骤
Step 1. 每行减去该行的最小数, 每列减去该 列的最小数,使矩阵每行每列均有0元素;
Step 2. 寻找独立0元素
• 从单个0元素的行(列)开始,给0加圈,记作◎,然 后划去所在列(行)的其它0元素,记为;重复进 行,直到处理完所有列(行)的单个0元素;
• 练习例题:甲乙丙丁四个人,A、B、C、D四 项任务,不同的人做不同的工作效率不同, 表中数据为时耗,如何指派不同的人去做不 同的工作使效率最高?
数模: minZ=ΣΣcijxij Σxij=1 i=1,…,n Σxij=1 j=1,…,n Xij=0或1
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
(1) 最大化指派问题
设效率矩阵为 C (cij )nn ,其中最大元素 为 m,令矩阵 B (bij )nn , bij m cij ,则 以 B为效率矩阵的最小化指派问题和以C为 效率矩阵的原最大化指派问题有相同的最优 解;
非标准形式的指派问题
运筹学__指派问题

•下面要证明M m. 如图假定覆盖所有0元素的m条直线 有r行、c列,m=r+c.
所有r行上不在j1,…,jc列上的0元 素个数≥ r,这些0元素至少有r个位
于不同列
同理:所有c列上不在i1,…,ir行上
j1 j2
的0元素个数≥c ,且这些0元素至
少有c个位于不同
i1 i2
ir jc
若上述两部分0个数总和为S,则S≥m;其中有m 个,又它们必无重复元素,彼此独立,则SM,故 有m≤M, 故可得M=m.
覆盖所有“0”元素的最少直线数 = 独立的“0”元素 的最多个数
推论1:覆盖所有“0”元素的直线数≥ 不同行不同列的“0”元素的最多个数(m)
推论2:覆盖所有“0”元素的最少直线数≥ 不同行不同列的“0”元素的个数
定理2说明: 1. 只要表中含有不同行或不同列的“0”元素,
都可以通过直线覆盖的方式来找到它们 2. 当覆盖直线的最少条数达到m条时,
(二)算法的基本原理 匈牙利数学家狄·康尼格(D·Konig)证明的两个定理
定理1 如果从指派问题效率矩阵[cij]的每一行元素中分别 减去(或加上)一个常数ui(被称为该行的位势), 从每一列分别减去(或加上)一个常数vj(称为该列的位势) 得到一个新的效率矩阵[bij], 若其中bij=cij-ui-vj,
一、指派问题的数学模型
(一)举例
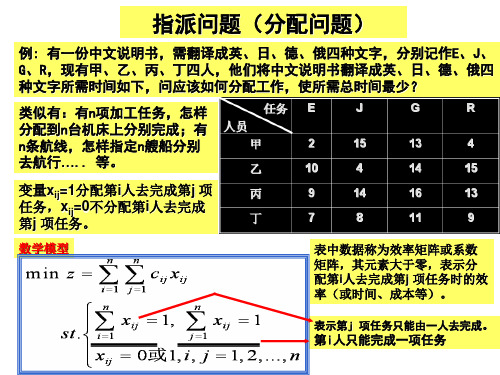
例7: 有一份中文说明书, 要分别译成英、日、德、俄四种文字, 分别记作E 、 J 、 G 、 R ,交与甲、乙、丙、丁 四个人去完成. 因个人专长不同, 他们完成翻译不同语种的说明书所需的时间(h)如表所示. 应如何指派,使四个人分别完成这四项任务总时间为最小?
任务 人员
将其代入目标函数中得到zb=0,它一定是最小值。 ❖ 这就是以(bij)为系数矩阵的指派问题的最优解。
指派 问题

指派问题(Assignment Problem )1. 标准指派问题的提法及模型指派问题的标准形式是:有n 个人和n 件事,已知第i 个人做第j 件事的费用为cij (i ,j=1,2,…,n ),要求确定人和事之间的一一对应的指派方案,使完成这n 件事的总费用最小。
设n2个0-1变量1,i j 0,i j ij x ⎧=⎨⎩若指派第个人做第件事若不指派第个人做第件事(i,j=1,2,…, n) 数学模型为:1111min 1.101,,1,2,,n nij iji j nij i n ij j ijZ c x x s t x x or i j n =====⎧=⎪⎪⎪=⎨⎪⎪==⎪⎩∑∑∑∑ 其中矩阵C 称为是效率矩阵或系数矩阵。
其解的形式可用0-1矩阵的形式来描述,即 (xij)n ⨯n 。
标准的指派问题是一类特殊的整数规划问题,又是特殊的0-1规划问题和特殊的运输问题。
1955年W. W. Kuhn 利用匈牙利数学家D. Konig 关于矩阵中独立零元素的定理, 提出了解指派问题的一种算法, 习惯上称之为匈牙利解法。
2. 匈牙利解法匈牙利解法的关键是指派问题最优解的以下性质:若从指派问题的系数矩阵C=(cij )的某行(或某列)各元素分别减去一个常数k ,得到一个新的矩阵C ’=(c ’ij),则以C 和C ’为系数矩阵的两个指派问题有相同的最优解。
(这种变化不影响约束方程组,而只是使目标函数值减少了常数k ,所以,最优解并不改变。
)对于指派问题,由于系数矩阵均非负,故若能在在系数矩阵中找到n 个位于不同行和不同列的零元素(独立的0元素),则对应的指派方案总费用为零,从而一定是最优的。
匈牙利法的步骤如下:步1:变换系数矩阵。
对系数矩阵中的每行元素分别减去该行的最小元素;再对系数矩阵中的每列元素分别减去该列中的最小元素。
若某行或某列已有0元素,就不必再减了(不能出现负元素)。
步2:在变换后的系数矩阵中确定独立0元素(试指派)。
指派问题

指派问题 运输问题
1. 指派问题(Assignment Problem)
有n项任务由n个人完成,每项任务交给一个人,每人都有一项 任务。由i个人完成j项任务的成本(或效益)为cij。求使总成本 最小(或总效益最大)的分配方案。
设:
0 第i个人不从事第j项任务 x ij 1 第i个人被指派完成第j项任务
1
8 7
2
10 8
3
9Hale Waihona Puke 1143 25
6 9
船
3
4 5
2
7 10
4
7 8
6
5 10
4
2 3
4
7 11
匈牙利法(Hungarian Method)
1.写出行数和列数相同的成本矩阵; 2.压缩成本矩阵:每一行的所有成本均减去行里面 最小的成本,然后每一列的所有成本均减去列里 面最小的成本,使新的成本矩阵每一行每一列至 少有一个为0; 3.以最少的直线(水平或者垂直)划掉所有的0, 若所用直线数与行数相同,则已经找到最优解, 可以跳到第5步,否则就进行第4步; 4.找到没有被划掉的最小的数值,从所有没有被划 掉的数值中减去这一数值,而所有被划掉2次的 划线数值加上这一数值。返回第3步; 5.根据0的位置确定最佳指派方案。
销售 人员
指派问题3 (Assignment Problem)
7项工作分别分派给7个设备的成本若下表所示, 应如何分派?
成本 1 2 3 1 68 14 54 2 48 64 10 3 57 71 54 设备 4 48 50 13 5 84 24 8 6 10 10 9 7 77 84 8
任务
4 5 6 7
一个销售经理要分派6个销售人员负责不同地区 的销售,这些销售人员有不同的关系和能力,他们 的期望销售额如下表所示,应如何分派?
二次指派问题的理论与算法

二次指派问题的理论与算法二次指派问题的理论与算法一、什么是二次指派问题二次指派问题是在计算机最优化理论中常见的一个问题。
它的基本结构由资源的使用者、被指派的资源以及求解的目标组成。
它的主要任务是尽可能将资源高效地指派给不同的使用者,以达到令行知名的目标。
二次指派问题已被用于机器人任务指派,交通路线指派,被指派任务的决策,人工智能规划,医疗工作调度系统以及众多其他等实际应用。
二、二次指派问题的理论二次指派问题具有四个重要的理论框架:最优性条件、正交性原理、资源分配一致性以及决策规划的综合理论。
1、最优性条件:指在给定的实力限制下,总是能找到一个最优的解决方案。
2、正交性原理:指给定资源规模、使用者能力以及求解目标之后,需要找到每一个使用者和资源之间的唯一正交解,以达到最优化效果。
3、资源分配一致性:指在使用者之间的资源分配是一致的,也就是说资源的分配要保持一致。
4、决策规划的综合理论:指要根据不同的实力限制以及指派的资源,采用决策规划的综合理论来进行资源指派,并且获得最佳的分配结果。
三、二次指派问题的算法对于二次指派问题,一般有四种不同的算法进行解决:单层搜索、直觉式搜索、混合算法以及哈密顿算法。
1、单层搜索:指以不断地遍历节点/路径为基础,深度优先搜索或广度优先搜索等手段,最终找到最优解。
2、直觉式搜索:采用极大量的迭代来收敛到最优解,是一种速度较快的搜索算法。
3、混合算法:将单层搜索和总结式搜索融合在一起,形成一种综合性的搜索技术,使搜索效率较高。
4、哈密顿算法:是一种图形搜索的算法,它通过图搜索的思想,搜索出一条遍历所有点的最佳路径,来获取最优解。
四、总结二次指派问题在最优化理论中被广泛应用,它包括四个重要的理论框架:最优性条件、正交性原理、资源分配一致性以及决策规划的综合理论;而其解决的算法也常用单层搜索、直觉式搜索、混合算法以及哈密顿算法等。
未来在二次指派问题中,仍需不断追求更高性能、更有效率和更全面性的算法方法,使指派任务更加高效。
指派问题(经典运筹学)

1 1 c 11 2 c 21 … i c i1 … n c n1 2
c 12 c 22 ci2 cn2
…
1 2 3 4
6 20 10
21
25 14 0
5
x6
解:x i
1
2
0
不在第i个地区建站
i=1,2, …,6
Z表示全区消防站总数
2 6 1 x3 x4 1 s.t x3 x4 x5 1 x x x 1 4 5 6 x i 0 ,1 i 1, 2 , , 6
一、决策问题与0-1变量
决策变量
xi
x i 是否做第
i 件事 i 1, 2 , , n
1 0
做第i件事 不做第i件事
x1 x 2 x n k
n件事中必须做k件并只做k件事 n件事中最多做k件事 n件事中至少做k件事
x1 x 2 x n k x1 x 2 x n k
当n=4时, 有16变量,8个约束方程
例:现有4份工作,4个人应聘,由 于各人技术专长不同,他们承担 各项工作所需费用如下表所示, 且规定每人只能做一项工作,每 一项工作只能由一人承担,试求 使总费用最小的分派方案。
工作
Z表示总费用
max Z 3 x11 5 x12 4 x13 5 x14 6 x 21 7 x 22 6 x 23 8 x 24 8 x 31 9 x 32 8 x 33 10 x 34 10 x 41 10 x 42 9 x 43 11 x 44
指派问题详解

第一章绪论1、指派问题的背景及意义指派问题又称分配问题,其用途非常广泛,比如某公司指派n个人去做n 件事,各人做不同的一件事,如何安排人员使得总费用最少?若考虑每个职工对工作的效率(如熟练程度等),怎样安排会使总效率达到最大?这些都是一个企业经营管理者必须考虑的问题,所以该问题有重要的应用价值.虽然指派问题可以用0-1规划问题来解,设X(I,J)是0-1变量, 用X(I,J)=1表示第I个人做第J件事, X(I,J)=0表示第I个人不做第J件事. 设非负矩阵C(I,J)表示第I个人做第J件事的费用,则问题可以写成LINGO程序SETS:PERSON/1..N/;WORK/1..N/;WEIGHT(PERSON, WORK): C, X ;ENDSETSDATA:W=…ENDDATAMIN=@ SUM(WEIGHT: C*X);@FOR(PERSON(I): @SUM(WORK(J):X(I,J))=1);@FOR(WORK(J): @SUM(PERSONM(I):X(I,J))=1);@FOR(WEIGHT: @BIN(X));其中2*N个约束条件是线性相关的, 可以去掉任意一个而得到线性无关条件.但是由于有N^2个0-1变量, 当N很大时,用完全枚举法解题几乎是不可能的. 而已有的0-1规划都是用隐枚举法做的,计算量较大. 对于指派问题这种特殊的0-1规划,有一个有效的方法——匈牙利算法,是1955年W. W. Kuhn利用匈牙利数学家D.König的二部图G的最大匹配的大小等于G的最小顶点覆盖的大小的定理提出的一种算法,这种算法是多项式算法,计算量为O(N3).匈牙利算法的基本原理是基于以下两个定理.定理1设C=(C ij)n×n是指派问题的效益矩阵,若将C中的任一行(或任一列)减去该行(或该列)中的最小元素,得到新的效率矩阵C’,则C’对应的新的指派问题与原指派问题有相同的最优解.证明:设X’是最优解, 即@SUM(WEIGHT: C*X’)<= @SUM(WEIGHT: C*X), 则当C中任一行或任一列减去该行或该列的最小数m时,得到的阵C’还是非负矩阵, 且@SUM(WEIGHT: C’*X’)<=@SUM(WEIGHT: C*X)-m=@SUM(WEIGHT: C’*X)定理2效率矩阵C中独立的0元素的最多个数等于覆盖所有0元素的最少直线数. 当独立零元素的个数等于矩阵的阶数时就得到最优解.3、理论基础定义:图G的一个匹配M是图G中不相交的边的集合. 属于匹配M中的边的所有端点称为被该匹配M饱和, 其他的顶点称为M-未饱和的. 如果一个匹配M 饱和了图G的所有顶点,则称该匹配M是一个完全匹配. 可见顶点数是奇数的图没有完全匹配. 一个匹配M称为是极大匹配, 如果它不能再扩张成更大的一个匹配. 一个匹配称为是最大匹配, 如果不存在比它更大的匹配.定义:对于一个匹配M, 图G的一个M-交替路是图G中的边交替地在M中及不在M中的边组成. 从M-未饱和点出发到M-为饱和点结束的M-交替路称为一条M-增广路. 把M-增广路中不是M中的边改成新的匹配M’中的边, 把M-增广路中M中的边不作为M’中的边, 在M-增广路以外的M中的边仍作为M’中的边, 则M’的大小比M大1. 故名M-增广路. 因此最大匹配M不存在M-增广路.定义:若图G和图H有相同的顶点集V, 我们称G和H的对称差,记为G∆H,是一个以V为顶点集的图, 但其边集是G和H的边集的对称差: E(G∆H)=E(G) ∆E(H)=E(G)⋂E(H)-(E(G)⋃E(H))=(E(G)-E(H)) ⋂ (E(H)-E(G))定理: (Berge, 1957) 图G的一个匹配M是最大匹配,当且仅当G中没有M-增广路.证明: 我们只要证明, G中没有M-增广路时, M是最大匹配. 用反证法, 若有一个比M大的匹配M’. 令G的一个子图F, E(F)=M∆M’, 因M和M’都是匹配, F的顶点的最大度数至多是2, 从而F由不相交的路和环组成, 它们的边交替地来自M和M’, 于是F中的环的长度是偶数. 由于M’比M大, F中存在一个连通分支,其中M’中的边数大于M中的边数. 这个分支只能是起始和终止的边都在M’中. 而这就是一条G中的M-增广路. 与假设矛盾. 证毕.定理(Hall, 1935)设G是一个二部图, X和Y是其二分集, 则存在匹配M 饱和X当且仅当对于X中的任意子集S, Y 中与S中的点相邻的点组成的集合N(S)中元素的个数大于等于集合S中元素的个数.证明:必要性是显然的. 对于充分性, 假设 |N(S)|≥|S|, ∀S⊂X, 考虑G的一个最大匹配M, 我们用反证法,若M没有饱和X, 我们来找一个集合S不满足假设即可. 设u∈X是一个M-未饱和顶点, 令S⊂X和T⊂Y分别是从u出发的M-交替路上相应的点.我们来证明M中的一些边是T到S-u上的一个匹配. 因为不存在M-增广路,T中的每个点是M-饱和的. 这意味着T中的点通过M中的边到达S中的一个顶点. 另外, S-u中的每个顶点是从T中的一个顶点通过M中的一条边到达的. 因此M 中的这些边建立了T与S-u的一个双射, 即|T|=|S-u|. 这就证明了M中的这些边是T到S-u上的一个匹配,从而意味着T⊂N(S), 实际上, 我们可证明T=N(S). 这是因为连接S和Y-T中的点y的边是不属于M的, 因为不然的话, 就有一条到达y的M-增广路, 与y∉T矛盾. 故|N(S)|=|T|=|S-u|=|S|-1<|S|, 与假设矛盾.当X与Y的集合的大小相同时的Hall定理称为婚姻问题,是由Frobenius(1917)证明的.推论: k-正则的二部图(X的每一点和Y的每一点相关联的二部图)(k>0)存在完全匹配.证明: 设二分集是X,Y. 分别计算端点在X和端点在Y的边的个数, 得k|X|=k|Y|, 即|X|=|Y|.因此只要证明Hall的条件成立即可. 使X饱和的匹配就是完全匹配. 考虑∀S⊂X, 设连接S与N(S)有m条边, 由G的正则性, m=k|S|. 因这m条边是与N(S)相关联的, m≤k|N(S)|, 即k|S|≤ k|N(S)|, 即|N(S)|≥|S|. 这就是Hall的条件.用求M-增广路的方法来得到最大匹配是很费时的. 我们来给出一个对偶最优化问题.定义:图G的一个顶点覆盖是集合S⊂V(G), 使得G的每条边至少有一个端点在S中. 我们称S中的一个顶点覆盖一些边, 若这个顶点是这些边的公共端点.因为匹配的任意两条边不能被同一个顶点覆盖, 所以顶点覆盖的大小不小于匹配的大小: |S|≥|M|. 所以当|S|=|M| 时就同时得到了最大的匹配和最小的顶点覆盖.定理(König [1931],Egerváry[1931])二部图G的最大匹配的大小等于G的最小顶点覆盖的大小.证明: 设M是G的任一个匹配, 对应的二分集是X,Y. 设U是一个最小的顶点覆盖, 则|U|≥|M|, 我们只要由顶点覆盖U来构造一个大小等于|U|的匹配即完成证明. 令R=U⋃X, T=U⋃Y, 令H, H’分别是由顶点集R⋂(Y-T)及T⋂(X-R)诱导的G的子图. 我们应用Hall的定理来证明H有一个R到Y-T中的完全匹配,H’有一个从T到X-R中的完全匹配. 再因这两个子图是不相交的, 这两个匹配合起来就是G中的一个大小为|U|的匹配.因为R⋂T是G的一个覆盖, Y-T与X-R之间没有边相联接. 假设S⊂R, 考虑在H中S的邻接顶点集N(S), N(S) ⊂Y-T. 如果|N(S)|<|S|, 因为N(S)覆盖了不被T覆盖的与S相关联所有边, 我们可以把N(S) 代替S作为U中的顶点覆盖而得到一个更小的顶点覆盖. U的最小性意味着H中Hall条件成立. 对H'作类似的讨论得到余下的匹配. 证毕.最大匹配的增广路算法输入: 一个二分集为X,Y的二部图G,一个G中的匹配M, X中的M-未饱和顶点的集合U.思路: 从U出发探求M-交替路,令S⊂X,T⊂Y为这些路到达过的顶点集. 标记S中不能再扩张的顶点. 对于每个x∈(S⋂T)-U, 记录在M-增广路上位于x前的点.初始化: S=U,T=∅.叠代: 若S中没有未标记过的顶点, 结束并报告T⋂(X-S)是最小顶点覆盖而M是最大匹配.不然, 选取S中未标记的点x, 考虑每个y∈N(x)且xy∉M, 若y是M-未饱和的, 则得到一个更大的匹配,它是把xy加入原来的匹配M得到的,将x从S中去除. 不然, y是由M中的一条边wy相连接的, w∈X, 把y加入T(也有可能y本来就在T中), 把w加入S. w未标记, 记录w前的点是y. 对所有关联到x的边进行这样的探索后, 标记x. 再次叠代.定理: 增广路算法可以得到一个相同大小的匹配和顶点覆盖.证明: 考虑这个算法终止的情况, 即标记了S中所有的点. 我们要证明R=T⋂(X-S)是大小为|M|的一个顶点覆盖.从U出发的M-交替路只能通过M中的边进入X中的顶点, 所以S-U中的每个顶点通过M与T中的顶点匹配, 并且没有M中的边连接S和Y-T. 一旦一条M-交替路到达x∈S, 可以继续沿着任何未饱和的边进入T, 由于算法是对于x的所有邻域顶点进行探索才终止的,所以从S 到Y-T 没有未饱和边. 从而S 到Y-T 没有边, 证明了R 是一个顶点覆盖.因为算法是找不到M-增广路时终止, T 的每一个顶点是饱和的. 这意味着每个顶点y ∈T 是通过M 匹配与S 中的一个顶点. 由于U ⊂S, X-S 的每个顶点是饱和的, 故M 中与X-S 相关联的边不和T 中的点相连接. 即它们与是饱和T 的边不同的, 这样我们可见M 至少有|T|+|X-S|条边. 因不存在一个比顶点覆盖更大的匹配, 所以有|M|=|T|+|X-S|=|R|.设二部图G 的二分集X 和Y 都是n 个元素的点集, 在其边j i y x 上带有非负的权ij w , 对于G 的一个匹配M, M 上各边的权和记作w(M).定义: 一个n ×n 矩阵A 的一个横截(transversal)是A 中的n 个位置, 使得在每行每列中有且只有一个位置(有的文献中把横截化为独立零元素的位置来表示).定义: 指派问题就是给定一个图G=n n K ,(完全二部图, 即每个X 中的顶点和Y 中的每个顶点有边相连接的二部图)的边的权矩阵A, 求A 的一个横截, 使得这个横截上位置的权和最大. 这是最大带权匹配问题的矩阵形式.定义: 对于图G=n n K ,,设其二分集是X ,Y ,给定G 的边j i y x 的n ×n 权矩阵W={ij w }.考虑G 的子图v u G ,, 设其二分集是U ⊂X ,V ⊂Y, 边集是E(v u G ,), 对于子图v u G ,的带权覆盖u,v 是一组非负实数{i u },{j v },使得ij j i w v u ≥+,)(,v u j i G E y x ∈∀, v u G ,的带权覆盖的费用是∑∑+j i v u 记为C(u,v), 最小带权覆盖问题就是求一个具有最小费用C(u,v)的带权覆盖u,v.引理: 若M ⊂E(v u G ,)是一个带权二部子图v u G ,的最大匹配, 且u, v 是v u G ,的带权覆盖, 则C(u,v)≥w(M). 而且, C(u,v)=w(M)当且仅当ij j i w v u =+,M y x j i ∈∀. 这时M 是v u G ,最大带权匹配, u,v 是v u G ,的最小带权覆盖, 定义这时的v u G ,为G 的相等子图(equality subgraph ).证明: 因为匹配M 中的边是不相交的, 由带权覆盖的定义就得C(u,v)≥w(M). 而且C(u,v)=w(M)当且仅当ij j i w v u =+,M y x j i ∈∀成立. 因一般地有C(u,v)≥w(M).所以当C(u,v)=w(M)时. 意味着没有一个匹配的权比C(u,v)大, 也没有一个覆盖的费用比w(M)小.Kuhn 得到一个指派问题的算法,命名为匈牙利算法, 为的是将荣耀归于匈牙利数学家König 和Egerv áry.指派问题的匈牙利算法(Kuhn[1955], Munkres[1957]):输入G=n n K ,的边的权矩阵A, 及G 的二分集X,Y.初始化: 任取一个可行的带权覆盖,例如)(max ij ji w u =,0=j v ,建立G 的相等子图v u G ,, 其二分集是X, Y ’⊂Y, 求v u G ,的一个最大匹配M. 这个匹配的权和w(M)=C(u,v), M 的带权覆盖是具有最小费用的.叠代: 如M 是G 的一个完全匹配, 停止叠代, 输出最大带权匹配M. 不然, 令U 是X 中的M-未饱和顶点. 令S ⊂X, T ⊂Y 是从U 中顶点出发的M-交替路到达的顶点的集合.令},:min{T Y y S x w v u j i ij j i -∈∈-+=ε.对于所有的S x i ∈, 将i u 减少ε, 对于所有的T y j ∈,将j v 增加ε,形成新的带权覆盖u ’,v ’及对应的新的相等子图v u G '',.如果这个新的相等子图含有M-增广路, 求它的最大匹配M ’, 不然不改变M 再进行叠代.定理: 匈牙利算法能找到一个最大权匹配和一个最小费用覆盖.证明: 算法由一个覆盖开始,算法的每个叠代产生一个覆盖,仅在相等子图有一个完全的匹配为止。
指派问题例题

• 第四步 划线——无行、打列划线
• 第五步 造0——直线未覆盖旳元素,减
去其最小值,交叉点上加最小元素,产
生新旳0元素,Go to 2
0 6 2 1 -1 5 1 0 0 4 0
Cij= 0 5 3 1 -1 0 4 2 0 3 1 0
0001
1 0 1
2 0 2
1320
2 3 2 2 2 1
数模: minZ=ΣΣcijxij Σxij=1 i=1,…,n Σxij=1 j=1,…,n Xij=0或1
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
指派问题解法—匈牙利法
• 解:类似运送问题旳最小元素法
• 第一步 造0——各行各列减其最小元素
4 10 7 5 -4 0 6 3 1 6 2 1
+1
• 最优2 7 6 3 -2 0 5 4 1 0 5 3 1
3 3 4 4 -3 0 0 1 1 0 0 1
4 6 6 3 -3 1 3 3 0 1 3 2
-1
• 第二步 圈0——寻找不同行不同列旳0元素,
圈之。 所在行和列其他0元素划掉
• 第三步 打——无旳行打,打行上0列打
,打列上行打,打行上0列打 …
指派问题
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
最大流问题
v1
5,2
5,5 5,5
vs 6,4 v2
4,2
v4 6,6
v3
2,2
4,2 vt
5,3
指派问题——匈牙利法
• 练习例题:甲乙丙丁四个人,A、B、C、D 四项任务,不同旳人做不同旳工作效率不同, 表中数据为时耗,怎样指派不同旳人去做不 同旳工作使效率最高?
第二题 指派问题

0Ø 4 4 0◎ 6
总费用为=7+9+4+3+5=28
分配问题与匈牙利法
Ø0 Ø0 3 ◎0 3
1
6
0Ø 2
◎0
3 2 0◎ 0Ø 3
2
◎0
2
3
Ø0
0◎ 4 4 0Ø 6
总费用为=8+9+4+3+4=28
分配问题与匈牙利法
课堂练习:用匈牙利法求解下列指派问题。
练习1:
练习2:
0 13 11 2
6
0
10
11
0 5 7 4
0 1 4 2
2)试指派(找独立0元素) 4 2
0 13 7 0
6
0
6
9
0 5 3 2
0 1 0 0
0Ø 13 7 ◎0
6
◎0
6
9
0◎ 5 3 2
0Ø
1
◎0
Ø0
独立0元素的个数为4 , 指派问题的最优指 派方案即为甲负责D工作,乙负责B工作, 丙负责A工作,丁负责C工作。这样安排 能使总的工作时间最少,为4+4+9+11 =28。
7 9 10 12
1
3
12
16
1
7
15 16 14 15
1 1 1 2 1 5 1 6
3 8 2 10 3
8
7
29
7
6 4 2 7 5
最少时间为105。
分配问题与匈牙利法
例4.6 有一份中文说明书,需译成英、日、德、俄四种文字, 分别记作A、B、C、D。现有甲、乙、丙、丁四人,他们将 中文说明书译成不同语种的说明书所需时间如下表所示,问 如何分派任务,可使总时间最少?
指派问题优秀课件

A由甲或丙完毕,乙和丁效率设为M C由丙或丁完毕, 甲和乙效率设为M E由甲,乙或丁完毕,丙效率设为M 虚设一种人,丙和丁旳最小值作为虚 设人旳效率系数,所以应虚设一行为
(34 27 28 23 45)
min 0 0 4 2
列变换
0 13 7 0 60 69
0 5 3 2
0 1 0 0
环节二、试指派(找独立旳0元素)
(记独立0元素个数为m,矩阵阶数为n.当m=n 时,问题到此结束.m<n旳情况下一题讨论)
0 0 0 1
0 6
0 0
13 0 5 1
7 6 3 0
0
9
所以:最优解为0 1
19 18 6 0 13 最终一列减去5 19 18 6 0 8
17 0 1 13 5
17 0 1 13 0
1
19
7
0
22
1 19 7 0 17
0 0 0 0 M
0 0 0 0 M
因为M是一种较大旳数,减去5后来 仍为一种较大旳数,所以仍以M表达
找独立旳0元素并试指派
0 4 6 17 7
ABC D E
甲
25
29
31
42
37
乙
39
38
26
20
33
丙 34 27 28 40 32
丁 24 42 30 23 45
要求:
1、E必须完毕,其他一人一项
2、一人完毕两项,其他一人一 项
3、A由甲或丙完毕,C由丙或 丁完毕。E由甲,乙或丁完毕, 丙或丁完毕两项,其 他一 人一项
• 分析:
0
0
0
此时m=n=4,
0 找到了最优解
软考指派问题计算

软考指派问题计算
软考指派问题是一种常见的组合优化问题,通常涉及到将一组任务分配给一组工人,以最小化总成本或最大化总效益。
解决指派问题的一种常见方法是使用匈牙利算法。
以下是使用匈牙利算法解决指派问题的基本步骤:
1. 创建代价矩阵:将问题抽象为一个二维矩阵,其中每个元素表示将某个任务分配给某个工人的成本或者效益。
代价矩阵的大小为n行m列,其中n
表示任务的数量,m表示工人的数量。
2. 寻找增广路径:从代价矩阵中寻找增广路径,即从某一行或某一列出发,沿着矩阵的边缘移动,直到回到起始位置。
在寻找增广路径的过程中,需要不断更新代价矩阵。
3. 构造增广矩阵:在增广路径上,将代价矩阵中对应位置的元素减去最小值,并将路径上的其他元素设置为最大值。
这样构造的增广矩阵与原代价矩阵具有相同的行和列。
4. 求解最小二等分问题:将增广矩阵分为两个子矩阵,分别代表左半部分和右半部分。
求解这两个子矩阵对应的最小二等分问题,即找到一个分割线,使得左半部分和右半部分的元素总和最小。
5. 确定最佳分配方案:根据最小二等分问题的解,确定最佳的分配方案。
如果最小二等分问题的解为0,则说明已经找到了最优解;否则,需要重复步骤2-4,直到找到最优解。
通过以上步骤,可以求解指派问题并找到最优的分配方案。
需要注意的是,指派问题的解并不一定是整数解,可能是小数或者分数。
在实际应用中,需要根据具体问题和要求来确定是否需要取整或者进行其他处理。
5-02 指派问题

例 求下表所示效率矩阵的指派问题的最小解。 表
任 务 人员 甲 乙 丙 丁 戊 A 12 8 7 15 4 B 7 9 17 14 10 C 9 6 12 6 7 D 7 6 14 6 10 E 9 6 9 10 9
解
按上述第一步,将这系数矩阵进行变换。
min 12 7 9 7 9 7 5 0 2 0 8 9 6 6 6 6 2 3 0 0 7 17 12 14 9 7 0 10 5 7 15 14 6 6 10 6 9 8 0 0 4 10 7 10 9 4 0 6 3 6 2 0 2 4 5
• 经第一步变换后,系数矩阵中每行每列都已有 了0元素;但需找出n个独立的0元素。若能找 出,就以这些独立0元素对应解矩阵(xij)中的 元素为1,其余为0,这就得到最优解。当n较 小时,可用观察法、试探法去找出n个独立0元 素。若n较大时,就必须按一定的步骤去找, 常用的步骤为:
• (1) 从只有一个0元素的行(列)开始,给这个0 元素加圈,记作◎。这表示对这行所代表的人, 只有一种任务可指派。然后划去◎所在列(行) 的其他0元素,记作Φ 。这表示这列所代表的 任务已指派完,不必再考虑别人了。 • (2) 给只有一个0元素列(行)的0元素加圈,记 作◎;然后划去◎所在行的0元素,记作Φ 。 • (3) 反复进行(1),(2)两步,直到所有0元素 都被圈出和划掉为止。
• 令这直线数为l。若l<n,说明必须再变 换当前的系数矩阵,才能找到n个独立的 0元素,为此转第四步:若 l=n ,而 m<n , 应回到第二步(4),另行试探。 • 在上例中,对矩阵①按以下次序进行: • 先在第五行旁打√,接着可判断应在第1 列下打√,接着在第3行旁打√。经检查 不再能打√了。对没有打√行,画一直 线以覆盖0元素,已打√的列画一直线以 覆盖0元素。得
指派问题——精选推荐

指派问题设有n 项工作需分配给n 个人去做,每人做一项,由于各人的工作效率不同,因而完成同一工作所需时间也就不同,设人员i 完成工作j 所需时间为ij C (称为效率矩阵),问如何分配工作,使完成所有工作所用的总时间最少?这类问题称为指派问题(assignment problem ),也称最优匹配问题,它是一类重要的组合优化问题。
用10-变量ij x 表示分配情况,1=ij x 表示指派第i 个人完成第j 项任务,0=ij x 表示不分配。
则上述问题可以表示为如下10-线性规划:⎪⎪⎩⎪⎪⎨⎧======∑∑∑∑====10,,2,1,1,,2,1,1..min1111或ij nj ij ni ij n i nj ijij x n i x nj x t s x C z其中第一个约束条件表示每项工作只能指派给一个人做,第二个约束条件表示每个人只能做一项工作。
求解指派问题的常用方法是Kuhn 于1955年给出的算法,称为匈牙利算法。
由于指派问题的模型是比较典型的10-规划线性规划,可以用LINGO 很方便地求解。
例:分配甲、乙、丙、丁、戊去完成A、B、C、D、E五项任务,每人完成一项,每项任务只能由一个人去完成,五个人分别完成各项任务所需时间如下表所示,试作出任务分配使总时间最少。
解:MODEL:SETS:WORKER/W1..W5/;JOB/J1..J5/;LINKS(WORKER,JOB):C,X;ENDSETSDA TA:C=8,6,10,9,12,9,12,7,11,9,7,4,3,5,8,9,5,8,11,8,4,6,7,5,11;ENDDA TAMIN=@SUM(LINKS:C*X);@FOR(WORKER(I):@SUM(JOB(J):X(I,J))=1); @FOR(JOB(J):@SUM(WORKER(I):X(I,J))=1); @FOR(LINKS:@BIN(X));END。
指派问题
9
Ø
6
3
6
5
从只有一个0元素的列开始, 给这个0元素加圈,记
5 2
3 10 8
2 0 5 0
0 0 7 0
2 0 2 4
9
Ø
6
3
6
5
然后划去所在的行的其他0元素, 记作Ø。
5 2
3 10 8
2 0 5 0
Ø
0 7 0
2 0 2 4
9
Ø
6
3
6
5
从只有一个0元素的列开始, 给这个0元素加圈,记
对没有打行画横线,有打列 画纵线,就得到覆盖所有0元素的 最少直线数。
的个数m=4,而n=5, m<n,转下一步。
第四步:在没有被直线覆 盖的部分中找出最小元素, 然后在打行各元素都减 去这最小元素,而在打 列中各元素都加上这最小 元素,以保证原来0元素 不变,这样得到新的系数 矩阵(它的最优解和原问 题相同)。若得到n个独 立的0元素,则已经得到 最优解。否则回到第三步 重复进行。
5 2
3 10 8
2 0 5 0
Ø
0 7 0
2
2 4
9
Ø
6
3
6
5
然后划去所在的行的其他0元素, 记作Ø。
5 2
3 10 8
2
Ø Ø
7 0
2
Ø
5 0
2 4
9
Ø
6
3
6
5
从只有一个0元素的列开始, 给这个0元素加圈,记
5 2
3 10 8
2
Ø Ø
lingo 指派问题

Lingo 作业题1、指派问题设有n 个人, 计划作n 项工作, 其中ij c 表示第i 个人做第j 项工作的收益,求一种指派方式,使得每个人完成一项工作,使总收益最大.现6个人做6项工作的最优指派问题,其收益矩阵如表所示,请给出合理安排.一、问题分析根据第一题的题意我们可以知道,此题的最终目标是让我们建立一种数学模型来解决这个实际生活中的问题,此题意简而言之就是为了解决6个人做6项工作的指派最优问题,从而使题目中的ij C 收益等达到所需要的目的。
在题目中曾提到:每个人完成一项工作。
其意思就是每人只能做一项工作且每项工作只能做一人做。
二、符号说明此题属于最优指派问题,引入如下变量:题目中说:ij C 表示第i 个人做第j 项工作的收益。
例如56C 则表示第5个人做第6项工作。
即6611max ij ij i j z xy c ===∑∑s.t.:611ij i C==∑ ,j=1,2,3,···,6611ij j C==∑ ,i=1,2,3,···,6 01ij C =或 ,i,j=1,2,3,···,6此题需要求出最大值最优(最大值),即需要使用max ,表示最大。
在编程过程中“@bin (x )”是“限制x 为0或1”。
三、建立模型此题属于最优指派问题,与常见的线性问题极为类似。
因此,使用Lingo软件。
由于“每人只能做一项工作且每项工作只能做一人做”故采用0-1规划求得优。
四、模型求解(一)常规程序求解Lingo输入框:max=20*c11+15*c12+16*c13+5*c14+4*c15+7*c16+17*c21+15*c22+33*c23+12*c24+8*c25+6*c26+9*c31+12*c32+18*c33+16*c34+30*c35+13*c36+12*c41+8*c42+11*c43+27*c44+19*c45+14*c46+0*c51+7*c52+10*c53+21*c54+10*c55+32*c56+0*c61+0*c62+0*c63+6*c64+11*c65+13*c66;c11+c12+c13+c14+c15+c16=1;c21+c22+c23+c24+c25+c26=1;c31+c32+c33+c34+c35+c36=1;c41+c42+c43+c44+c45+c46=1;c51+c52+c53+c54+c55+c56=1;c61+c62+c63+c64+c65+c66=1;c11+c21+c31+c41+c51+c61=1;c12+c22+c32+c42+c52+c62=1;c13+c23+c33+c43+c53+c63=1;c14+c24+c34+c44+c54+c64=1;c15+c25+c35+c45+c55+c65=1;c16+c26+c36+c46+c56+c66=1;@bin(c11);@bin(c12);@bin(c13);@bin(c14);@bin(c15);@bin(c16);@bin(c21);@bin(c22);@bin(c23);@bin(c24);@bin(c25);@bin(c26);@bin(c31);@bin(c32);@bin(c33);@bin(c34);@bin(c35);@bin(c36);@bin(c41);@bin(c42);@bin(c43);@bin(c44);@bin(c45);@bin(c46);@bin(c51);@bin(c52);@bin(c53);@bin(c54);@bin(c55);@bin(c56);@bin(c61);@bin(c62);@bin(c63);@bin(c64);@bin(c65);@bin(c66);Lingo输出(结果)框:Global optimal solution found.Objective value: 142.0000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced CostC11 1.000000 -20.00000C12 0.000000 -15.00000C13 0.000000 -16.00000C14 0.000000 -5.000000C15 0.000000 -4.000000C21 0.000000 -17.00000 C22 0.000000 -15.00000 C23 1.000000 -33.00000 C24 0.000000 -12.00000 C25 0.000000 -8.000000 C26 0.000000 -6.000000 C31 0.000000 -9.000000 C32 0.000000 -12.00000 C33 0.000000 -18.00000 C34 0.000000 -16.00000 C35 1.000000 -30.00000 C36 0.000000 -13.00000 C41 0.000000 -12.00000 C42 0.000000 -8.000000 C43 0.000000 -11.00000 C44 1.000000 -27.00000 C45 0.000000 -19.00000 C46 0.000000 -14.00000 C51 0.000000 0.000000 C52 0.000000 -7.000000 C53 0.000000 -10.00000 C54 0.000000 -21.00000 C55 0.000000 -10.00000 C56 1.000000 -32.00000 C61 0.000000 0.000000 C62 1.000000 0.000000 C63 0.000000 0.000000 C64 0.000000 -6.000000 C65 0.000000 -11.00000 C66 0.000000 -13.00000Row Slack or Surplus Dual Price1 142.0000 1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000013 0.000000 0.000000(二)循环语句求解Lingo输入框:model:sets:gz/A1..A6/:a;ry/B1..B6/:b;yw(gz,ry):xy,x;endsetsdata:a=1,1,1,1,1,1;b=1,1,1,1,1,1;xy=20 15 16 5 4 7,17 15 33 12 8 6,9 12 18 16 30 13,12 8 11 27 19 14,0 7 10 21 10 32,0 0 0 6 11 13;enddatamax=@sum(yw:xy*x);@for(gz(i):@sum(ry(j):x(i,j))=1);@for(ry(j):@sum(gz(i):x(i,j))=1);@for(yw(i,j):@bin(x(i,j)));EndLingo输出(结果)框Global optimal solution found.Objective value: 142.0000Extended solver steps: 0Total solver iterations: 0Variable Value Reduced Cost A( A1) 1.000000 0.000000 A( A2) 1.000000 0.000000 A( A3) 1.000000 0.000000 A( A4) 1.000000 0.000000 A( A5) 1.000000 0.000000 A( A6) 1.000000 0.000000 B( B1) 1.000000 0.000000 B( B2) 1.000000 0.000000B( B4) 1.000000 0.000000 B( B5) 1.000000 0.000000 B( B6) 1.000000 0.000000 XY( A1, B1) 20.00000 0.000000 XY( A1, B2) 15.00000 0.000000 XY( A1, B3) 16.00000 0.000000 XY( A1, B4) 5.000000 0.000000 XY( A1, B5) 4.000000 0.000000 XY( A1, B6) 7.000000 0.000000 XY( A2, B1) 17.00000 0.000000 XY( A2, B2) 15.00000 0.000000 XY( A2, B3) 33.00000 0.000000 XY( A2, B4) 12.00000 0.000000 XY( A2, B5) 8.000000 0.000000 XY( A2, B6) 6.000000 0.000000 XY( A3, B1) 9.000000 0.000000 XY( A3, B2) 12.00000 0.000000 XY( A3, B3) 18.00000 0.000000 XY( A3, B4) 16.00000 0.000000 XY( A3, B5) 30.00000 0.000000 XY( A3, B6) 13.00000 0.000000 XY( A4, B1) 12.00000 0.000000 XY( A4, B2) 8.000000 0.000000 XY( A4, B3) 11.00000 0.000000 XY( A4, B4) 27.00000 0.000000 XY( A4, B5) 19.00000 0.000000 XY( A4, B6) 14.00000 0.000000 XY( A5, B1) 0.000000 0.000000 XY( A5, B2) 7.000000 0.000000 XY( A5, B3) 10.00000 0.000000 XY( A5, B4) 21.00000 0.000000 XY( A5, B5) 10.00000 0.000000 XY( A5, B6) 32.00000 0.000000 XY( A6, B1) 0.000000 0.000000 XY( A6, B2) 0.000000 0.000000 XY( A6, B3) 0.000000 0.000000 XY( A6, B4) 6.000000 0.000000 XY( A6, B5) 11.00000 0.000000 XY( A6, B6) 13.00000 0.000000 X( A1, B1) 1.000000 -20.00000 X( A1, B2) 0.000000 -15.00000 X( A1, B3) 0.000000 -16.00000 X( A1, B4) 0.000000 -5.000000X( A1, B6) 0.000000 -7.000000 X( A2, B1) 0.000000 -17.00000 X( A2, B2) 0.000000 -15.00000 X( A2, B3) 1.000000 -33.00000 X( A2, B4) 0.000000 -12.00000 X( A2, B5) 0.000000 -8.000000 X( A2, B6) 0.000000 -6.000000 X( A3, B1) 0.000000 -9.000000 X( A3, B2) 0.000000 -12.00000 X( A3, B3) 0.000000 -18.00000 X( A3, B4) 0.000000 -16.00000 X( A3, B5) 1.000000 -30.00000 X( A3, B6) 0.000000 -13.00000 X( A4, B1) 0.000000 -12.00000 X( A4, B2) 0.000000 -8.000000 X( A4, B3) 0.000000 -11.00000 X( A4, B4) 1.000000 -27.00000 X( A4, B5) 0.000000 -19.00000 X( A4, B6) 0.000000 -14.00000 X( A5, B1) 0.000000 0.000000 X( A5, B2) 0.000000 -7.000000 X( A5, B3) 0.000000 -10.00000 X( A5, B4) 0.000000 -21.00000 X( A5, B5) 0.000000 -10.00000 X( A5, B6) 1.000000 -32.00000 X( A6, B1) 0.000000 0.000000 X( A6, B2) 1.000000 0.000000 X( A6, B3) 0.000000 0.000000 X( A6, B4) 0.000000 -6.000000 X( A6, B5) 0.000000 -11.00000 X( A6, B6) 0.000000 -13.00000Row Slack or Surplus Dual Price1 142.0000 1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000012 0.000000 0.00000013 0.000000 0.000000五、模型结果通过以上的应用Lingo模型求解,得出结论:第1项工作由第1个人来完成。
指派问题

0 1 X= 0 0
1 0 0 0
0 0 0 1
0 0 1 、丁 做第三项, 最高总分Z=92+95+90+80=357
人数和工作数不相等的指派问题
• 像处理不平衡运输问题那样,根据情况,虚设人,或者虚设 工作任务。虚设人完成工作的费用以及任何人完成虚设工作 的费用取零(理解为这些费用实际不会发生)。这样一来, 便可将人数和工作数不相等的指派问题转化为标准形式的指 派问题。
2 2 0 0
0 1 2 1
0 0 0 1
• 步骤三:找出独立零元素。
4 ◎ 0 2 0 Φ
2 ◎ 0 Φ 0 2 1 Φ 0 0 2 ◎ 0 Φ 0 1 1 ◎
4 Φ 0 2 0 ◎
2 ◎ 0 Φ 0 2 1 ◎ 0 0 2 Φ 0 ◎ Φ 0 1 1
' M cij ,其中 M max cij ,则 令 cij
1i , j n
n
n
i 1 j 1
' ' z cij xij (M cij xij ) M xij cij xij Mn z ' i 1 j 1 i 1 j 1 i 1 j 1 i 1 j 1
• 找独立0元素,常用的步骤为:
从只有一个0元素的行开始,给该行中的0元素加圈,记作◎ 。
然后划去◎ 所在列的其它0元素,记作Ø ;这表示该列所代 表的任务已指派完,不必再考虑别人了。依次进行到最后一 行。
从只有一个0元素的列开始(画Ø的不计在内),给该列中的0
元素加圈,记作◎;然后划去◎ 所在行的0元素,记作Ø , 表示此人已有任务,不再为其指派其他任务了。依次进行到 最后一列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 8 8 7 6 4 8 4 9 10
2 10 3 2 9 7 2 7 5 2 3 5 6 9 10
分配问题与匈牙利法
答案:
Page 19
7 13 15 11
9 12 16 12
10 16 14 15
12 17 15 16
0 2 15 13 4 2 10 4 14 15 4 6 0 9 14 16 13 9 0 7 8 11 9 7 2)试指派(找独立0元素) 13 11 2 0 10 11 5 7 4 1 4 2 4 2
分配问题与匈牙利法
2)试指派(找独立0元素)
Page 12
2 2 4 4 0
0 4 2 4 5 0 3 0 1 0 1 3 0 3 5 1 2 3 0 5
2 2 4 4 0 ◎
◎ 0
5 1 0 Ø 2
4 2 4 0 0 Ø 3 ◎ ◎ 1 3 0 3 5 1 3 Ø 5 0
√
√
分配问题与匈牙利法
Page 14
1 2 4 3 ◎ 0
◎
0 6 2 Ø 0
3 √ ◎ √ 0 3 √ √ Ø 0 3 3 Ø 5 0 3 Ø 0 ◎ 0 2 1 3 1 4
√ √
l =m=4 < n=5
选择直线外最小元素为1, 直线外元素减1,直线交 点元素加1,其他保持不 变,得到新的系数矩阵。
任务 人员 甲 A 25 B 29 C 31 D 42 E 37
乙
丙 丁
39
34 24
38
27 42
26
28 36
20
40 23
33
32 45
戊
0
0
0
0
M
分配问题与匈牙利法
用匈牙利法求出最优指派方案为:
0 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0
7 9 8 7 4
5 12 5 3 6
9 7 4 6 7
8 11 6 9 5
11 5 97 94 63 11 4
2 2 4 4 0
0 4 3 6 5 0 4 2 1 0 2 5 0 3 6 3 2 3 1 7 -1 -2
分配问题与匈牙利法
3 4 3 0 0 1 0 5 2 0 4 4 0 2 6 0
0 1 0 0
Page 7
试指派
3 ◎ 2 2
4 3 1 Ø ◎ 4 6 ◎
◎
5 4 Ø
得到4个独立零元素, 所以最优解矩阵为:
0 0 1 0 0 0 1 0 0 0 1 0
48
3 8 8 7 6 4 8 4 9 10
2 10 3 2 9 7 2 7 5 2 3 5 6 9 10 21
分配问题与匈牙利法
非标准型的指派问题: 匈牙利法的条件是:模型求最小值、效率cij≥0。
Page 20
当遇到各种非标准形式的指派问题时,处理方法是先将 其转化为标准形式,然后用匈牙利法来求解。
任务 人员 A B C D
甲
乙 丙
6
4 3
7
5 1
11
9 10
2
8 4
丁
5
9
8
2
分配问题与匈牙利法
解:1)变换系数矩阵,增加0元素。
6 4 (c ij ) 3 5 7 11 2 2 5 9 8 4 1 10 4 1 9 8 2 2
4 0 2 3 5 9 0 1 5 4 0 9 3 7 6 0
分配问题与匈牙利法
1. 最大化指派问题
Page 21
处理方法:设m为最大化指派问题系数矩阵C中最大元素。 令矩阵B=(m-cij)nn则以B为系数矩阵的最小化指派问题和 原问题有相同的最优解。 例4.9 某人事部门拟招聘4人任职4项工作,对他们综合考评的 得分如下表(满分100分),如何安排工作使总分最多。
分配问题与匈牙利法
Page 10
例4.8 已知五人分别完成五项工作耗费如下表,求最优分 配方案。
任务 人员 甲 乙 丙 A 7 9 8 B 5 12 5 C 9 7 4 D 8 11 6 E 11 9 8
丁
戊
7
4
3
6
6
7
9
5
6
11
分配问题与匈牙利法
解:1)变换系数矩阵,增加0元素。
Page 11
0 1 X= 0 0 1 0 0 0 0 0 0 1
Page 22
5 0 5 7
0 0 1 0
即甲安排做第二项工作、乙做第三项、丙做第四项、丁做 第三项, 最高总分Z=92+95+90+80=357
分配问题与匈牙利法
2. 不平衡的指派问题
Page 23
当人数m大于工作数n时,加上m-n项虚拟工作,例如:
5 1 1 8 6 3 9 6 14 4 2 1 0 3 1 7 5 1 9 10 0 5 3 0 11 6 8 14 17 0 4 5 0 6 3 2 1 0 0 0 0 0 0
Page 16
Ø 0
3
Ø 0 ◎ 0 2
Ø 0
6 2 ◎ 0 4
2 0 Ø 3
◎ 0
4
3 ◎ 0 3 Ø 0 6
总费用为=7+9+4+3+5=28
分配问题与匈牙利法
Page 17
0 Ø 1 3 2 0 ◎
Ø 0
3
Ø 0 ◎ 0 2
◎
0 2 0 Ø 3
Ø 0
甲 85 乙 95 C= 丙 82 丁 86 92 73 90 87 78 95 83 79 90 90 80 88
分配问题与匈牙利法
解: M=95,令 C (95 c ij )
10 3 22 0 8 17 C = 13 12 16 9 5 15 用匈牙利法求解C’,最优解为:
Page 3
即甲-B,乙-D,丙-E,丁-A, 任务C放弃。 最少时间为105。
分配问题与匈牙利法
Page 4
例4.6 有一份中文说明书,需译成英、日、德、俄四种文字, 分别记作A、B、C、D。现有甲、乙、丙、丁四人,他们将 中文说明书译成不同语种的说明书所需时间如下表所示,问 如何分派任务,可使总时间最少?
即完成4个任务的总时间最少 为:2+4+1+8=15
分配问题与匈牙利法
Page 8
例4.7 已知四人分别完成四项工作所需时间如下表,求最优 分配方案。
任务
人员 甲 A 2 B 15 C 13 D 4
乙
丙 丁
10
9 7
4
14 8
14
16 11
15
13 9
分配问题与匈牙利法
解:1)变换系数矩阵,增加0元素。
Page 9
0 13 7 0 6 0 6 9 0 5 3 2 0 1 0 0
0 Ø 6 0 ◎ Ø 0
13 7 ◎ 0 ◎ 6 9 0 5 3 2 1 ◎ Ø 0 0
独立0元素的个数为4 , 指派问题的最优指 派方案即为甲负责D工作,乙负责B工作, 丙负责A工作,丁负责C工作。这样安排 能使总的工作时间最少,为4+4+9+11 =28。
6 2 ◎ 0 4
4
3 ◎ 0 3 Ø 0 6
总费用为=8+9+4+3+4=28
分配问题与匈牙利法
课堂练习:用匈牙利法求解下列指派问题。 练习1: 练习2:
Page 18
7 13 15 11
9 12 16 12
10 16 14 15
12 17 15 16
√
分配问题与匈牙利法
Ø 0 1 3 2 ◎ 0
◎
Page 15
0 6 2 Ø 0
3 Ø 0 3 ◎ 0 Ø 4 4 0 6 3 ◎ 0 0 Ø 2 0 Ø 2 ◎ 0 3
总费用为 =5+7+6+6+4=28
注:此问题有多个最优解
分配问题与匈牙利法
◎ 0 1 3 2 0 Ø
独立0元素的个数l=4<5,故画直线调整矩阵。
分配问题与匈牙利法
Page 13
2 2 4 4 ◎ 0
◎
0 5 1 Ø 0
4 ◎ 0 3 1 Ø 2 3 0 5 4 Ø 0 ◎ 0 3 2 3 1 5
√
选择直线外的最小元素 为1;直线外元素减1, 直线交点元素加1,其 他保持不变。
当人数m小于工作数n时,加上n-m个人,例如
15 20 10 9 6 5 4 7 10 13 16 17
15 6 10 0 20 5 13 0 10 4 16 0 9 7 17 0
分配问题与匈牙利法
3. 一个人可做几件事的指派问题
Page 24
若某人可做几件事,则将该人化作相同的几个“人”来接受 指派,且费用系数取值相同。 例如:丙可以同时任职A和C工作,求最优指派方案。
甲 乙 丙 15 20 10 9 6 5 4 7 10 13 16 17
15 6 10 10 20 5 13 13 10 4 16 16 9 7 17 17
Page 6
4 ◎ 2 3
5 4 ◎ √ Ø 4 1 ◎ 4 3 √ 7 1 Ø √
独立零元素的个数m等于最少 直线数l,即l=m=3<n=4;
