用C++或C语言编写出100以内所有互为质数的勾股数
(2021年整理)c语言求100以内素数

(完整版)c语言求100以内素数编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)c语言求100以内素数)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)c语言求100以内素数的全部内容。
(完整版)c语言求100以内素数编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望(完整版)c语言求100以内素数这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为 <(完整版)c语言求100以内素数〉这篇文档的全部内容.//C语言:求100以内素数。
#include<stdio。
h>void main(){int i,j;for(i=2;i〈=100;i++){int t=1;for(j=2;j〈i;j++){if(i%j==0){t=0;break;}}if(t==1)printf(”%d ",i);}}合肥学院13—软工(1)班。
100-300的回文素数c语言

回文素数是指一个数从前往后和从后往前读都是一样的素数。
在这里,我们需要找到100到300之间的所有回文素数。
以下是一个简单的C语言程序来查找100到300之间的回文素数:```c#include <stdio.h>#include <math.h>int main() {printf("回文素数有:\n");for (int i = 100; i <= 300; i++) {if (isprime(i) && isprime(reverse(i))) {printf("%d\n", i);}}return 0;}int isprime(int n) {if (n <= 1) {return 0;}for (int i = 2; i <= sqrt(n); i++) {if (n % i == 0) {return 0;}}return 1;}int reverse(int n) {int rev = 0;while (n > 0) {rev = (rev * 10) + (n % 10);n /= 10;}return rev;}```这个程序首先定义了一个`isprime`函数来检查一个数是否是素数。
然后,它定义了一个`reverse`函数来获取一个数的反转。
在`main`函数中,它循环遍历100到300之间的所有数,并检查它们是否是回文素数。
如果是,则打印出来。
C语言循环例题

1.//输出a和b之间的所有素数, 10个素数为一行输出#include<stdio.h>#include<stdlib.h>#include<math.h>int panDuanSuShu(int x) //判断x是否是素数{int i,m,flag; //flag为1表示是素数,flag为0表示不是素数 m=(int)sqrt(x);if(x==2){ flag=1;}else{for(i=2;i<=m;i++){if(x%i==0){flag=0;break;}}if(i>m){ flag=1; }}return flag;}int shuChuSuShu(int a,int b){int i,k=0;//i是循环变量,k表示已经输出了k个素数for(i=a;i<=b;i++){if(panDuanSuShu(i)==1){printf("%6d",i);k++;if(k%10==0){ printf("\n");}}}printf("\n");return k;}int main(){int a,b,t;while(a<2||b<2){printf("重新输入n和m:");scanf("%d%d",&a,&b);}if(a>b){ t=a;a=b;b=t; }printf("%d和%d之间共有%d个素数",a,b,shuChuSuShu(a,b));printf("\n\n");return 0;}2.//用户输入2个数,输出这2个数之间所有的超素数//超素数(质数)的概念:7193是素数,719是素数,71是素数,7是素数,则7193是素数#include<stdio.h>#include<stdlib.h>#include<math.h>int isPrime(int n)//判断某数是否是素数{int i,f,m=(int)sqrt(n);if(n==1) f=0;else{for(i=2;i<=m;i++){if(n%i==0)break;}if(i>m) f=1;else f=0;}return f;}int supperPrime(int n)//判断某数是否是超素数{int t=n;while(t>0){if(isPrime(t)==1)t=t/10;elsebreak;}}void printSupperPrime(int a,int b)//输出a到b之间所有的超素数{int i,m=0;for(i=a;i<=b;i++){if(supperPrime(i)){ printf("%8d",i);m++;if(m%5==0)printf("\n");}}printf("\n");}int main(){int a,b,t;printf("input a,b:");scanf("%d%d",&a,&b);while(a<2 || b<2){printf("input a,b:");scanf("%d%d",&a,&b);}if(a>b) {t=a;a=b;b=t;}printSupperPrime(a,b);printf("\n");//system("pause");return 0;}3.//满足a*a+b*b==c*c的a,b,c三个数,称为勾股数//编程输出100以内的所有勾股数#include<stdio.h>#include<stdlib.h>int gouGuShu(){int x=0;for(int a=1;a<=100;a++)for(int b=a;b<=100;b++)for(int c=b;c<=100;c++)if(x%4==0)printf("\n");printf("%4d%4d%4d ",a,b,c);x++;}return x;}int main(){printf("\n\n 100以内的勾股数共有:%d个。
最新100以内的勾股数

1100以内的勾股数:2i=3 j=4 k=53i=5 j=12 k=134i=6 j=8 k=105i=7 j=24 k=256i=8 j=15 k=177i=9 j=12 k=158i=9 j=40 k=419i=10 j=24 k=2610i=11 j=60 k=6111i=12 j=16 k=2012i=12 j=35 k=3713i=13 j=84 k=8514i=14 j=48 k=5015i=15 j=20 k=2516i=15 j=36 k=3917i=16 j=30 k=3418i=16 j=63 k=6520i=18 j=80 k=82 21i=20 j=21 k=29 22i=20 j=48 k=52 23i=21 j=28 k=35 24i=21 j=72 k=75 25i=24 j=32 k=40 26i=24 j=45 k=51 27i=24 j=70 k=74 28i=25 j=60 k=65 29i=27 j=36 k=45 30i=28 j=45 k=53 31i=30 j=40 k=50 32i=30 j=72 k=78 33i=32 j=60 k=68 34i=33 j=44 k=55 35i=33 j=56 k=65 36i=35 j=84 k=9138i=36 j=77 k=8539i=39 j=52 k=6540i=39 j=80 k=8941i=40 j=42 k=5842i=40 j=75 k=8543i=42 j=56 k=7044i=45 j=60 k=7545i=48 j=55 k=7346i=48 j=64 k=8047i=51 j=68 k=8548i=54 j=72 k=9049i=57 j=76 k=9550i=60 j=63 k=8751i=65 j=72 k=975253勾股数的常用套路54所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a, 55b,c)。
100以内的勾股数

100以内的勾股数100以内的勾股数:i=3 j=4 k=5i=5 j=12 k=13i=6 j=8 k=10i=7 j=24 k=25i=8 j=15 k=17i=9 j=12 k=15i=9 j=40 k=41i=10 j=24 k=26i=11 j=60 k=61i=12 j=16 k=20i=12 j=35 k=37i=13 j=84 k=85i=14 j=48 k=50i=15 j=20 k=25i=15 j=36 k=39i=16 j=30 k=34i=16 j=63 k=65i=18 j=24 k=30i=18 j=80 k=82i=20 j=21 k=29i=20 j=48 k=52i=21 j=28 k=35i=21 j=72 k=75i=24 j=32 k=40i=24 j=45 k=51i=24 j=70 k=74i=25 j=60 k=65i=27 j=36 k=45i=28 j=45 k=53i=30 j=40 k=50i=30 j=72 k=78i=32 j=60 k=68i=33 j=44 k=55i=33 j=56 k=65i=35 j=84 k=91i=36 j=48 k=60i=36 j=77 k=85这是最经典的一个套路,而且由于两个连续自然数必然互质,所以用这个套路得到的勾股数组全部都是互质的。
2、当a为大于4的偶数2n时,b=n2-1, c=n2+1也就是把a的一半的平方分别减1和加1,例如:n=3时(a,b,c)=(6,8,10)n=4时(a,b,c)=(8,15,17)n=5时(a,b,c)=(10,24,26)n=6时(a,b,c)=(12,35,37)... ...这是次经典的套路,当n为奇数时由于(a,b,c)是三个偶数,所以该勾股数组必然不是互质的;而n为偶数时由于b、c是两个连续奇数必然互质,所以该勾股数组互质。
所以如果你只想得到互质的数组,这条可以改成,对于a=4n (n>= 2), b=4*n^2-1, c=4*n^2+1,例如:n=2时(a,b,c)=(8,15,17)n=3时(a,b,c)=(12,35,37)n=4时(a,b,c)=(16,63,65)... ...========Edward补充========对于N 为质因数比较多的和数时还可以参照其质因数进行取相应的勾股数补充,即1个N会有多对的勾股数,例如:n=9时(a,b,c)=(9,24,25)or (9,12,15) --------3* (3,4,5)n=12时(a,b,c)= (12,35,37) or (12,16,20) ----- 4*(3,4,5)=========ShangJingbo补充=======还有诸如此类的勾股数,20、21、29;119、120、169;696、697、985;4059、4060、5741;23660、23661、33461;137903 137904 195025803760 803761 11366894684659 4684660 6625109常见的几种通式:(1) (3,4,5), (6,8,10)… …3n,4n,5n (n是正整数)第3 / 4页(2) (5,12,13),(7,24,25), (9,40,41)… …2n +1, 2n^2 +2n, 2n^2 +2n +1 (n是正整数)(3) (8,15,17), (12,35,37) … …2^2*(n+1),[2(n+1)]^2-1,[2(n+1)]^2+1 (n是正整数)(4)m^2-n^2,2mn,m^2+n^2 (m、n均是正整数,m>n)观察分析上述的勾股数,可看出它们具有下列二个特点:1、直角三角形短直角边为奇数,另一条直角边与斜边是两个连续自然数。
100以内的勾股数

100以内的勾股数: i=3 j=4 k=5 i=5 j=12 k=13 i=6 j=8 k=10 i=7 j=24 k=25 i=8 j=15 k=17 i=9 j=12 k=15 i=9 j=40 k=41 i=10 j=24 k=26 i=11 j=60 k=61 i=12 j=16 k=20 i=12 j=35 k=37 i=13 j=84 k=85 i=14 j=48 k=50 i=15 j=20 k=25 i=15 j=36 k=39 i=16 j=30 k=34 i=16 j=63 k=65 i=18 j=24 k=30 i=18 j=80 k=82 i=20 j=21 k=29 i=20 j=48 k=52
i=48 j=55 k=73 i=48 j=64 k=80 i=51 j=68 k=85 i=54 j=72 k=90 i=57 j=76 k=95 i=60 j=63 k=87 i=65 j=72 k=97 勾股数的常用套路 所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数( a,b,c)。 即 a^2+b^2=c^2,a,b,c∈N2 又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数 n 得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是 a,b ,c互质的勾股数组。 关于这样的数组,比较常用也比较实用的套路有 以下两种: 1、当 a 为大于 1 的奇数 2n+1时,b=2*n^2+2*n, c=2*n^2+2*n+1。 实际上就是把 a 的平方数拆成两个连续自然数,例 如: n=1时(a,b,c)=(3,4,5)
用c语言编写编写输出1到100之间的素数?

用c语言编写编写输出1到100之间的素数?
素数是指只能被1和自身整除的正整数,而其他正整数则被称为合数。
在本问题中,我们需要编写一个程序,以输出1到100之间的素数。
编写程序的步骤如下:
Step 1:了解1到100之间的素数的定义以及判断方法。
在这里,我们需要先明确什么是素数。
一个正整数n是否为素数,可以通过判断它是否可以被2到n-1的任意整数整除来得到。
如果n能被任意一个2到n-1的整数整除,那么它就不是素数,否则就是素数。
Step 2:开始编写程序
我们可以通过以下代码来实现1到100之间的素数输出:
```
#include <stdio.h>
该程序中,我们首先定义了两个循环变量i和j,用来枚举1到100之间的所有数。
然后,在外层循环中,我们假设当前枚举的数是素数,即flag=1。
在内层循环中,我们枚举2到i-1之间的所有数,并判断i是否能被这些数整除。
如果存在可以整除的数,则将flag 设置为0,即当前枚举的数不是素数。
最后,在外层循环结束后,当flag=1时,我们输出当前枚举的数。
这样,就完成了1到100之间的素数输出。
Step 3: 总结
在本问题中,我们学习了如何在C语言中编写程序来输出1到100之间的素数。
我们需要用到循环结构和条件语句来进行判断和输出。
同时,我们也需要熟悉素数的定义,以便能够在程序中进行判断。
希望这里的程序代码和思路能够对大家的学习和实践有所帮助。
C语言中判断素数(求素数)的思路与方法实例

C语⾔中判断素数(求素数)的思路与⽅法实例⽬录前⾔思路1实现:思路2实现:《C与指针》4.14-2:补充:判断素数的4种⽅法实例总结前⾔素数⼜称质数。
所谓素数是指除了 1 和它本⾝以外,不能被任何整数整除的数,例如17就是素数,因为它不能被 2~16 的任⼀整数整除。
思路1):因此判断⼀个整数m是否是素数,只需把 m 被 2 ~ m-1 之间的每⼀个整数去除,如果都不能被整除,那么 m 就是⼀个素数。
思路2):判断⽅法还可以简化。
m 不必被 2 ~ m-1 之间的每⼀个整数去除,只需被 2 ~ 之间的每⼀个整数去除就可以了。
如果m 不能被 2 ~ 间任⼀整数整除,m 必定是素数。
例如判别 17 是是否为素数,只需使 17 被 2~4 之间的每⼀个整数去除,由于都不能整除,可以判定 17 是素数。
原因:因为如果 m 能被 2 ~ m-1 之间任⼀整数整除,其⼆个因⼦必定有⼀个⼩于或等于,另⼀个⼤于或等于。
例如 16 能被2、4、8 整除,16=2*8,2 ⼩于 4,8 ⼤于 4,16=4*4,4=√16,因此只需判定在 2~4 之间有⽆因⼦即可。
思路1实现:#include <stdio.h>int main() {int n;printf("请输⼊⼀个1-100之间的整数:\n");scanf("%d", &n);int m = 0;for (int i = 2; i < n; i++ ) {if(n % i == 0) {m++;}}if (m == 0) {printf("%d是素数\n", n);} else {printf("%d不是素数\n", n);}return 0;}思路2实现:#include <stdio.h>#include <math.h>int main() {int n;printf("请输⼊⼀个1-100之间的整数:\n");scanf("%d", &n);int i = 0;int q = sqrt(n);for (i = 2; i <= q; i++ ) {if(n % i == 0) {break;}}if (i > q) {printf("%d是素数\n", n);} else {printf("%d不是素数\n", n);}return 0;}《C与指针》4.14 - 2:打印1~100之间所有质数:#include <stdio.h>int main() {int num, divisor;printf("1, 2");for (num = 3; num <= 100; num += 2) {for(divisor = 3; divisor < num; divisor +=2 ) {if (num % divisor == 0) {break;}}if(divisor >= num) {printf(", %d", num);}}printf("\n");return 0;}结果:1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97补充:判断素数的4种⽅法实例#include<stdio.h>#include<math.h>//⽅法⼀:从1-n挨个判断;bool isPrimel_1(int n){ for(int i=2;i<n;i++)if(n%i==0)return false;return true;}//⽅法⼆:将被判断数n,进⾏开⽅作为判断结束的条件,//因为开⽅后的数,是n的最⼤因⼦,最⼤因⼦之后的数对判断该数是否是素数没有意义。
C语言循环例题

1、//输出a与b之间的所有素数, 10个素数为一行输出#include<stdio、h>#include<stdlib、h>#include<math、h>int panDuanSuShu(int x) //判断x就是否就是素数{int i,m,flag; //flag为1表示就是素数,flag为0表示不就是素数 m=(int)sqrt(x);if(x==2){ flag=1;}else{for(i=2;i<=m;i++){if(x%i==0){flag=0;break;}}if(i>m){ flag=1; }}return flag;}int shuChuSuShu(int a,int b){int i,k=0;//i就是循环变量,k表示已经输出了k个素数for(i=a;i<=b;i++){if(panDuanSuShu(i)==1){printf("%6d",i);k++;if(k%10==0){ printf("\n");}}}printf("\n");return k;}int main(){int a,b,t;printf("输入a与b,以便求a与b之间的所有素数\n");scanf("%d%d",&a,&b);while(a<2||b<2){printf("重新输入n与m:");scanf("%d%d",&a,&b);}if(a>b){ t=a;a=b;b=t; }printf("%d与%d之间共有%d个素数",a,b,shuChuSuShu(a,b));printf("\n\n");return 0;}2、//用户输入2个数,输出这2个数之间所有的超素数//超素数(质数)的概念:7193就是素数,719就是素数,71就是素数,7就是素数,则7193就是素数#include<stdio、h>#include<stdlib、h>#include<math、h>int isPrime(int n)//判断某数就是否就是素数{int i,f,m=(int)sqrt(n);if(n==1) f=0;else{for(i=2;i<=m;i++){if(n%i==0)break;}if(i>m) f=1;else f=0;}return f;}int supperPrime(int n)//判断某数就是否就是超素数{int t=n;while(t>0){if(isPrime(t)==1)t=t/10;elsebreak;}if(t==0) return 1;else return 0;}void printSupperPrime(int a,int b)//输出a到b之间所有的超素数{int i,m=0;for(i=a;i<=b;i++){if(supperPrime(i)){ printf("%8d",i);m++;if(m%5==0)printf("\n");}}printf("\n");}int main(){int a,b,t;printf("input a,b:");scanf("%d%d",&a,&b);while(a<2 || b<2){printf("input a,b:");scanf("%d%d",&a,&b);}if(a>b) {t=a;a=b;b=t;}printSupperPrime(a,b);printf("\n");//system("pause");return 0;}3、//满足a*a+b*b==c*c的a,b,c三个数,称为勾股数//编程输出100以内的所有勾股数#include<stdio、h>#include<stdlib、h>int gouGuShu(){int x=0;for(int a=1;a<=100;a++)for(int b=a;b<=100;b++)for(int c=b;c<=100;c++)if(a*a+b*b==c*c){if(x%4==0)printf("\n");printf("%4d%4d%4d ",a,b,c);x++;}return x;}int main(){printf("\n\n 100以内的勾股数共有:%d个。
质数c语言程序

质数c语言程序质数(Prime Number),又称素数,指在大于1的自然数中,除了1和自身以外没有其他因数的自然数。
在计算机编程中,使用C语言编写一个判断质数的程序是非常常见的任务。
下面我将为您介绍如何用C语言编写一个判断质数的程序。
首先,我们需要明确判断质数的条件。
一个数是否为质数可以通过判断它能否被大于1小于该数的平方根的所有自然数整除来确定。
如果这些自然数都不能整除该数,则该数是质数。
接下来,我们将上述条件转化为C语言程序。
假设我们要判断的数为num,我们可以采用以下步骤:1. 导入必要的头文件在程序的开头,我们需要包含<stdio.h>头文件,该头文件提供了输入输出操作的函数。
我们可以使用其中的printf和scanf函数来进行输入输出操作。
2. 获取输入的数字使用scanf函数获取用户输入的数字,并将其存储在num变量中。
例如:```int num;printf("请输入一个整数: ");scanf("%d", &num);```3. 判断质数编写一个用于判断质数的函数,例如isPrime。
该函数接受一个整数作为参数,并返回一个布尔类型的值,如果该数为质数则返回true,否则返回false。
函数的实现如下:```#include <stdbool.h>bool isPrime(int num) {if (num <= 1) {return false; // 1以下的数不是质数}for (int i = 2; i * i <= num; i++) {if (num % i == 0) {return false; // 可以被整除,不是质数}}return true; // 未能被整除,是质数}```4. 调用判断质数的函数并输出结果在主函数中调用isPrime函数,并根据返回值输出相应的结果。
例如:```if (isPrime(num)) {printf("%d是质数。
C语言求勾股数

C语言求勾股数问题描述求100以内的所有勾股数。
所谓勾股数,是指能够构成直角三角形三条边的三个正整数(a,b,c)。
问题分析根据“勾股数”定义,所求三角形三边应满足条件a2 + b2 = c2。
可以在所求范围内利用穷举法找出满足条件的数。
算法分析采用穷举法求解时,最容易想到的一种方法是利用3个循环语句分别控制变最a、b、c的取值范围,第1层控制变量a,取值范围是1〜100。
在a值确定的情况下再确定b值,即第2层控制变量b,为了避免结果有重复现象,b的取值范围是a+1〜100。
a、b的值已确定,利用穷举法在b+1〜100范围内一个一个的去比较,看当前c值是否满足条件a2 + b2 = c2,若满足,则输出当前a、b、c的值,否则继续寻找。
主要代码如下:1.//...2.for(a=l; a<=100; a++)/*确定a的取值*/3.for(b=a+l; b<=100; b++)/*确定b的取值*/4.for(c=b+l; c<=100; c++)/*确定c的取值*/5.if(a*a+b*b==c*c)6.printf("%d\t%d\t%d\n", a, b, c)/*判断三个变量是否满足勾股数条件*/7.//...但是上述算法的效率比较低,根据a2 + b2 = c2这个条件,在a、b值确定的情况下,没必要再利用循环一个一个去寻找c值。
若a、b、c是一组勾股数,则a2 + b2的平方根一定等于c,c的平方应该等于a、b的平方和,所以可将的平方根赋给c,再判断c的平方是否等于。
根据“勾股数”定义将变量定义为整型,a2 + b2的平方根不一定为整数,但变量c 的类型为整型,将一个实数赋给一个整型变量时,可将实数强制转换为整型(舍弃小数点之后的部分)然后再赋值,这种情况下得到的c的平方与原来的的值肯定不相等,所以可利用这一条件进行判断。
下面是完整的代码:1.#include<stdio.h>2.#include<math.h>3.int main()4.{5.int a, b, c, count=0;6.printf("100以内的勾股数有:\n");7.printf(" a b c a b c a b c a bc\n");8./*求100以内勾股数*/9.for(a=1; a<=100; a++)10.for(b=a+1; b<=100; b++)11.{12. c=(int)sqrt(a*a+b*b);/*求c值*/13.if(c*c==a*a+b*b && a+b>c && a+c>b && b+c>a && c<=100)/*判断c的平方是否等于a2+b2*/14.{15.printf("%4d %4d %4d ", a, b, c);16. count++;17.if(count%4==0)/*每输出4组解就换行*/18.printf("\n");19.}20.}21.22.printf("\n");23.return0;24.}运行结果:。
c语言 题目

c语言题目
当然可以,以下是一个简单的C语言题目:
题目:找出1到100之间的所有素数。
这是一个简单的C语言程序,用于找出1到100之间的所有素数:
c复制代码
#include<stdio.h>
int main() {
int i, j;
for (i = 2; i <= 100; i++) {
int isPrime = 1;
for (j = 2; j < i; j++) {
if (i % j == 0) {
isPrime = 0;
break;
}
}
if (isPrime) {
printf("%d ", i);
}
}
return0;
}
这个程序通过两个嵌套的for循环来找出1到100之间的所有素数。
外部循环从2开始,一直循环到100。
内部循环从2开始,一直循环到当前外部循环的数减1,检查当前数是否能够被整除。
如果能够被整除,则将isPrime变量设置为0,并跳出内部循环。
如果isPrime变量仍然为1,则当前数是素数,将其打印出来。
100以内的勾股数规律整理
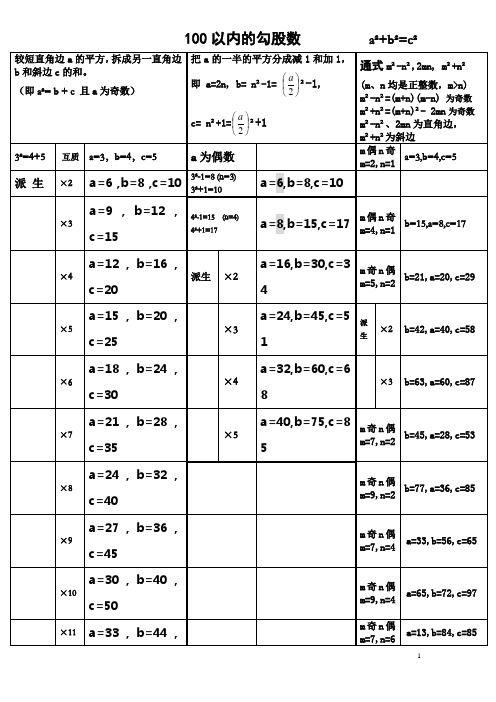
1
的平方, 较短直角边 a 的平方,拆成另一直角边 把 a 的一半的平方分成减 1 和加 1,
通式 m²-n²,2mn, m²+n² m²
的和。 (即 b 和斜边 c 的和。 即 a²= b + c 且 a 为 ( 奇数) ) 奇数)
a c= n²+1= ²+1 n²+1= 2
a=2n, 即 a=2n,
×2
8²-1=63 (n=8) 1=63 +1=65 8²+1=65
9²=40+41
互质
派 生
11² 11²=60+61
×2
9²-1=80 (n=9) 1=80 +1=82 9²+1=82 10² 10²-1=99 (n=10) 10² 10²+1=101
a=18,b=80,c=82 a=18,b=80,c=82 18,b=80,c= a=20,b=99,c=101 a=20,b=99,c=101 m 偶 n 奇 a=11,b=60,c=61 20,b=99,c= a=11 b=60,c=61 11, 60,c=
生
a=32,b=60, a=32,b=60,c=68 32,b=60 a=40,b=75, a=40,b=75,c=85 40,b=75
m奇n偶 b=45,a=28,c=53 45,a=28,c= b=45,a=28,c=53 m=7,n=2 m奇n偶 77,a=36,c= ,a=36,c=85 b=77,a=36,c=85 m=9,n=2 m奇n偶 a=33,b=56,c=65 33,b=56,c= a=33,b=56,c=65 m=7,n=4 m奇n偶 a=65,b=72,c=97 65,b=72,c= a=65,b=72,c=97 m=9,n=4 m奇n偶 a=13,b=84,c=85 13,b=84,c= a=13,b=84,c=85 m=7,n=6 奇数±奇数= ∵奇数±奇数=偶数 偶数±偶数= 偶数±偶数=偶数 奇数±偶数= 奇数±偶数=奇数 奇数×偶数= 奇数×偶数=偶数 奇数×奇数= 奇数×奇数=奇数 又∵ =(m+n)² 斜边 m²+n²=(m+n)²- 2mn 直角边 2mn 为偶数 =(m+n)(m直角边 m²-n²=(m+n)(m-n) 三边不能同偶 同偶基本勾 同偶, 三边不能 同偶 , 同偶基本勾 股数就不互质了 就不互质了, 股数就不互质了, m+n≠ 即 m+n≠偶数 不能同奇数、不能同偶 ∴m、n 不能同奇数、不能同偶 ∴m、n 为一奇一偶
100以内所有质数的输出
100以内所有质数的输出1.什么是质数?⼜称素数,只能被1和它本⾝整除的⾃然数,即除了1和它本⾝作为约数,没有别的约数了。
--->从2开始到这个数-1都不能被这个数本⾝整除。
2.⽅式⼀:package cn.tust.cycle;/** 输出50000以内的质数** */public class PrimeNumber {public static void main(String[] args) {boolean isFlag = true ;long starttime = System.currentTimeMillis();//遍历这50000个数for(int i = 2;i<=50000;i++) {//质数就是只能被1和它本⾝整除的⾃然数for(int j=2;j<i;j++) {if(i%j == 0) {isFlag = false;}}if(isFlag ==true) {System.out.println(i);}isFlag = true;}long endtime = System.currentTimeMillis();System.out.println("所花费的时间是:"+(endtime-starttime));}}输出结果:所花费的时间是:5637ms⽅式⼀中当i能够整除某⼀个j时,即当isFlag第⼀次被赋值false的时候,就不要再进⾏j的循环了,可以直接进⾏下⼀次的i的循环。
2.1 优化1:package cn.tust.cycle;/** 输出50000以内的质数** */public class PrimeNumber {public static void main(String[] args) {boolean isFlag = true ;long starttime = System.currentTimeMillis();//遍历这50000个数for(int i = 2;i<=50000;i++) {//质数就是只能被1和它本⾝整除的⾃然数for(int j=2;j<i;j++) {if(i%j == 0) {isFlag = false;break; //优化1:只对⾮质数的⾃然数是有效的}}if(isFlag ==true) {System.out.println(i);}isFlag = true;}long endtime = System.currentTimeMillis();System.out.println("所花费的时间是:"+(endtime-starttime));}}输出结果:所花费的时间是:544ms2.2优化2:package cn.tust.cycle;/** 输出50000以内的质数** */public class PrimeNumber {public static void main(String[] args) {boolean isFlag = true ;long starttime = System.currentTimeMillis();//遍历这50000个数for(int i = 2;i<=50000;i++) {//质数就是只能被1和它本⾝整除的⾃然数for(int j=2;j<Math.sqrt(i);j++) { //优化2:对本⾝就是质数和不是质数的⾃然数都有效if(i%j == 0) {isFlag = false;break; //优化1:只对⾮质数的⾃然数是有效的}}if(isFlag ==true) {System.out.println(i);}isFlag = true;}long endtime = System.currentTimeMillis();System.out.println("所花费的时间是:"+(endtime-starttime));}}输出结果:所花费的时间是:69ms3.⽅式⼆:public class PrimeNumberTest2 {public static void main(String[] args) {long startTime = System.currentTimeMillis();label:for(int i=2;i<50000;i++) {for(int j=2;j<Math.sqrt(i);i++) {if(i%j == 0) {continue label;}System.out.println(i);}}long endTime = System.currentTimeMillis();System.out.println("所花费的时间是:"+(endTime-startTime));}}为什么要在内循环中将循环的次数修改为i的平⽅根?解答:以97为例,当97去除以某个数的时候,那么结果很定也在2-97的这根坐标轴上,除以2的时候得到48.5,所以48之后的数就不⽤再去循环了,因为与48之后的数配对的都是⼤于1⼩于2的数;当除到这个数的平⽅根的时候,得到的结果也是这个数的平⽅根,当再往上除的时候,所得结果都是刚才已经配对过的数,即都是刚才的除数,所以循环只要到Math.sqrt(i)就⾏。
100以内的勾股数

100以内的勾股数:i=3j=4k=5i=5j=12k=13i=6j=8k=10i=7j=24k=25i=8j=15k=17i=9j=12k=15i=9j=40k=41i=10j=24k=26i=11j=60k=61i=12j=16k=20i=12j=35k=37i=13j=84k=85i=14j=48k=50i=15j=20k=25i=15j=36k=39i=16j=30k=34i=16j=63k=65i=18j=24k=30i=18j=80k=82i=20j=21k=29i=20j=48k=52i=21j=28k=35i=21j=72k=75i=24j=32k=40i=24j=45k=51i=24j=70k=74i=25j=60k=65i=27j=36k=45i=28j=45k=53i=30j=40k=50i=30j=72k=78i=32j=60k=68i=33j=44k=55i=33j=56k=65i=35j=84k=91i=36j=48k=60i=36j=77k=85i=39j=52k=65i=39j=80k=89i=40j=42k=58i=40j=75k=85i=42j=56k=70i=45j=60k=75i=48j=55k=73i=48j=64k=80i=51j=68k=85i=54j=72k=90i=57j=76k=95i=60j=63k=87i=65j=72k=97勾股数的常用套路所谓勾股数,一般是指能够构成直角三角形三条边的三个正整数(a,b,c)。
即a^2+b^2=c^2,a,b,c∈N又由于,任何一个勾股数组(a,b,c)内的三个数同时乘以一个整数n得到的新数组(na,nb,nc)仍然是勾股数,所以一般我们想找的是a,b,c互质的勾股数组。
关于这样的数组,比较常用也比较实用的套路有以下两种:1、当a为大于1的奇数2n+1时,b=2*n^2+2*n,c=2*n^2+2*n+1。
