3-刚体平面运动
大物刚体力学-3

C
v A = 2vo
vB = vD = 2vo (方向如图) 方向如图)
点瞬时静止) (C点瞬时静止) 点瞬时静止
7
vC = 0
在刚体上任取一点P,其速度为
v v v ′ vP = vO + vP v v ′ Q vP = rω , vo = rω
v v ′ ∴ vP = vo
由图得
0
v ′ vP
20
力的三要素:大小、方向、作用点。 力的三要素:大小、方向、作用点。 对刚体而言,力的三要素:大小、方向、作用线。 对刚体而言,力的三要素:大小、方向、作用线。 若力的作用线通过质心, 若力的作用线通过质心,则该力对质心轴的力矩为 零,故该力仅产生质心加速度。 故该力仅产生质心加速度。 应 用:
根据质心运动定律,有
v mg cosθ − N = m R+r
2 c
(1)
15
v v 以小球和大球为系统,外力 N , f 不做功机械 能守恒,取地面为重力势能零点,则有
1 2 1 mg ( R + r ) = mg ( R + r ) cosθ + mvc + I cω 2 2 2
由题意为纯滚动,所以
§7.5 刚体平面运动的动力学
复习: 复习:
刚体上任一质元的运动轨迹都平行于某一 平 面,这种运动称为刚体的平面平行运动。 刚体的平面平行运动。 刚体的平面平行运动 特点:刚体上每一质元的运动轨迹都是平面曲 特点: 线,且各平面互相平行;刚体在运动中转轴始终 保持平行且垂直于某一固定平面。
1
• 刚体平面平行运动的描述(运动学) 刚体平面平行运动的描述(运动学)
r r 如所示, 是一对力偶。 如所示,力 F 和 F '是一对力偶。则对质心轴所 形成的力矩为: 形成的力矩为: r r r r r 方向? M = r × F + r '× F ' 方向?
理论力学第4章 刚体的平面运动

独立的参变量。
2021/7/17
.
13
xAxA(t) yAyA(t) φφ(t)
称为刚体平面运动方程
对于每一瞬时 t ,都可以求出对应的 xA, yA, ,
平面图形S 在该瞬时的位置也就确定了。
2021/7/17
.
14
3.平面运动分解为平移和转动
当平面图形S上的点A不动时,则刚体作定轴转动, 当平面图形S上 的角 不变时,则刚体作平移。
思考: 下列运动是否可能?
V
V
v
V
V
v
V
v
2021/7/17
.
55
2) 加 速 度 投 影 形 式
aBaAaB n A aBA
当 0时aB n A 0
a
BA
a
n B
A
aA
[aB]AB[aA]AB
当 0 时 a B n A 0a B AB.A A a A
有[aB]A B[aA]A B
2021/7/17
车轮相对定系(Oxy)的平面运动(绝对运动)
车厢(动系 A x y ) 相对定系的平移(牵连运动) 车轮相对车厢(动系 A x y )的转动(相对运动)
2021/7/17
.
18
2021/7/17
.
19
转动部分的角度、角速度、角加速度与基点的选择无关。
φ1 φ2
ω1 ω2 1 2
平移部分的轨迹、速度与加速度都与基点的选择有关。
称点A为基点 平面图形的平面运动(绝对运动)可以看成是平面图形 一方面随基点A的平移(牵连运动),另一方面图形又绕 基点的转动(相对运动)的合成运动。
2021/7/17
刚体的平面运动

Northeastern University
§8-2
求平面图形内各点速度的基点法
平面图形内任意A、B两点间速度关系: v ' MO
vB v A vBA
vM
vO '
MB
O' A
vO '
大小 vBA AB 方向 垂直于 AB,朝向图形转动的一方
PAG 9
y'
o'
x'
Northeastern University
§8-1
刚体平面运动的概述和运动分解
y
任意平面运动的分析 在平面图形上任取一点O 做为基点; 在O点假想地做一个平移 参考系Oxy;
y'
x' O'
o
x
平面图形运动时,动坐标轴O'x' 轴、O'y' 轴始终分别 平行于定坐标轴Ox 轴、Oy 轴。 随着基点的平移
用一个平行于固定平面的平面 截割连杆; 截面S :一个平面图形 过平面图形上任一点作垂直于 图形的直线; 刚体作平面运动 直线作平移
连 杆
平面图形上各点的运动可以代 表刚体内所有点的运动。 刚体的平面运动可简化为平面 图形在它的自身平面内运动。
S
PAG 7
Northeastern University
vO '
M
动系:O'x'y' (平移坐标系)
牵连运动:随O'点的平移 相对运动:绕O'点的圆周运动 绝对运动: 两个运动的合成 vM ve vr vO' vMO'
理论力学课件-刚体平面运动

作速度 vA、vB的垂线,交点P即为该瞬时的
速度瞬心。
③ 已知某瞬时图形上两点A 、B 的速度 vA vB且 ⊥连线 AB, 则连线 AB与速度矢 vA、vB 端点连线的交点P即速度瞬心。 (a)
vA vB (a) 若vA 与vB 同向,则 AB
v A vB (b) 若v A 与vB 反向, 则 AB
但各点的加速度并不相等。 设匀角速度为,则 aB aB n AB 2 () 而 ac 的方向沿AC,故
aB ac ,瞬时平动与平动不同。
4. 速度瞬心法 利用速度瞬心求平面图形上点的速度的方法,称速度瞬心法。 平面图形任一瞬时的运动可以视为绕速度瞬心的瞬时转动, 故速度瞬心又称为平面图形的瞬时转动中心。 若P点为速度瞬心,则任意一点A的速度大小为 vA AP , 方向 AP,指向与 一致。 5. 注意的问题 ① 速度瞬心在平面图形上的位置不是固定的,而是随时间 不断变化的。在任一瞬时是唯一存在的。 ② 速度瞬心处速度为零,但加速度不一定为零,不同于定轴 转动。 ③ 刚体作瞬时平动时,虽然各点速度相同,但各点加速度 不一定相同,不同于刚体作平动。
vB v A / sin
在B点做 速度平行四边形,如图示。
l / sin 45 2l ()
vBA vActg l ctg45 l
AB vBA / AB l / l (
)
根据速度投影定理 vB AB vA AB vB sin vA vB vA / sin
n 其中 aa aB , ae aA , ar aBA aBA aBA
于是
aB a A aBA aBA
n
aB a A aBA aBA n 其中:aBA AB ,方向 AB,指向与 一致; aBA n AB 2,方向沿AB,指向A点。
刚体的平面运动

• 当f=0°时,vA与vBA 均垂直于OB连 • 线,vA与vBA也垂直于vB,按速度平行四 • 边形合成法则,应有 • vB=0。
•当f=90°时,vA与vB方向一致, •vBA垂直于AB,其速度平行四边形应为一直线, •显然有 vB=vA=rw •而 vBA=0。 •则此时杆AB的角速度wAB为零,
•
例1 曲柄连杆机构如图所示,OA=r,AB=1.73r。 如曲柄OA以匀角速度w转动,求当f=60°、0°和 90°时点B的速度。 • 解:连杆AB作平面运动,以点A为基点,点B的 速度为 • vB=vA+vBA
• 点B的速度为 vB=vA+vBA • 其中 vA=rw, 方向与OA垂直, • vB 沿OB方向, vBA与AB垂直。 • 可以作出其速度平行四边形。 当f=60°时,由于AB=1.73OA,OA恰好与AB垂 直,其速度平行四边形如图所示, 解出 : vB=vA/cos30°=1.15rw
• • • •
单独轮子作平面运动时,可在轮心O′处固 连一个平动坐标系x′o′y′,同样可把轮 子这种较为复杂的平面运动分解为平动和 转动两种简单运动。
一、研究平面运动的方法
• 1、动坐标系 • 对于任意的平面图形,可在图形上任取一点 O′为基点作为动系原点,建立跟随基点平动的坐 标系x′o′y′。 • 于是平面图形S的绝对运动可看成是: • 跟随基点的平动和绕基点的转动的合成。
若图形上某点I vI=0 ,选此点
为基点,则其它各点的速度
vB=vI+vBI=vBI
• 2、瞬时速度中心 • ①定义:一般情况下,在每一瞬时,平面图形上 • 都唯一地 存在一个速度为零的点。此点称为瞬 时速度中心。
②证明:如果点M在vA的垂线AN上 (由vA到AN的转向与图形的转向 一致),由图中看出,vA和vMA 在同一直线,而方向相反,故vM 的大小为 vM=vA-w·AM
理论力学刚体的平面运动

车轮的平面运动
刚体的平面运动可以 分解为随基点的平动 和绕基点的转动.
随基点A的平动
绕基点A'的转动
平面图形S在t时间内从位置I运动到位置II
以A为基点: 随基点A平动到A'B''后, 绕基点A'转 1角到A'B' 以B为基点: 随基点B平动到A''B'后, 绕基点B'转 2 角到A'B' 图中看出:AB A'B'' A''B' ,1 2 于是有
3
vC vB vCB
大小 ? l l 2
方向 ?
vC vB2 vC2B 1.299 m s 方向沿BD杆向右
例3 曲柄连杆机构如图所示,OA =r, AB= 3。r 如曲柄OA以匀角速度ω转动。
求:当 60,0,90时点B的速度。
已知:OA r, AB
求:当机构在图示位置时,夹板AB的角速度。
已知:AB 600mm, OE 100mm, 10 rad s , BC GD 500mm, 求:
AB
解: 1 杆GE作平面运动,瞬心为 C1
OG 800mm 500mm sin 15 929.4mm
EC1 OC1 OE 3369mm
解: 1 AB作平面运动。
vB AB vA
vB cos 30 OA
OA
vB cos 30 0.2309 m s
已知
求
OA
vE
100mm,OA
2
rad
s
, CD
3CB, CD
《理论力学》第八章刚体的平面运动

刚体的平面运动特点
刚体的平面运动具有 连续性,即刚体上任 意一点的运动轨迹都 是连续的。
刚体的平面运动具有 周期性,即刚体的运 动轨迹可以是周期性 的。
刚体的平面运动具有 对称性,即刚体的运 动轨迹可以是对称的。
02
刚体的平面运动分析
刚体的平动分析
平动定义
刚体在平面内沿着某一确定方向作等速直线运动。
详细描述
通过综合分析动能和势能的变化,可以深入理解刚体在平面运动中的能量转换过程。例 如,当刚体克服重力做功时,重力势能转化为动能;当刚体克服摩擦力做功时,机械能 转化为内能。这种能量转换过程遵循能量守恒定律,即系统总能量的变化等于外界对系
统所做的功与系统内能变化之和。
06
刚体的平面运动的实例分析
刚体的平面运动通常可以分为两种类型:纯滚动和滑动。在 纯滚动中,刚体只滚不滑,刚体上任意一点在任意时刻都位 于一个固定的圆周上。在滑动中,刚体既滚又滑,刚体上任 意一点在任意时刻都位于一个变化的圆周上。
刚体的平面运动分类
纯滚动
刚体只滚不滑,刚体上任意一点 在任意时刻都位于一个固定的圆 周上。
滑动
刚体既滚又滑,刚体上任意一点 在任意时刻都位于一个变化的圆 周上。
势能定理
总结词
势能定理描述了势能与其他形式的能量转换的关系。
详细描述
势能定理指出,在刚体的平面运动过程中,非保守力(如摩擦力、空气阻力等)对刚体所做的功等于系统势能的 减少量。非保守力做正功时,系统势能减少;非保守力做负功时,系统势能增加。
动能和势能的综合分析
总结词
在刚体的平面运动中,动能和势能的综合分析有助于理解运动过程中能量的转换和守恒。
做平动,这种运动也是复合运动。
刚体平面运动

第十章刚体的平面运动一、内容提要1、基本概念(1)刚体的平面运动的定义刚体运动时,若其上任一点至某个固定平面的距离保持不变,则称该刚体作平面运动。
(2)刚体的平面运动的简化刚体的平面运动可以简化为平面图形在自身平面内的运动。
(3)刚体平面运动方程为x o'=f1(t) , y o'=f2(t) , ϕ=f3(t) ,(4)刚体平面运动的分解平面图形的运动可以分解为随基点的平动和绕基点的转动。
2、平面图形上各点的速度(1)基点法(速度合成法)V M= V O+V MO(2)速度投影法(V M)MO=(V O)MO(3)速度瞬心法V M=MC∙ω(C点为速度瞬心)3、平面图形上各点的加速度加速度分析主要用基点法(加速度合成法)a M= a O+aτMO+a n MOaτMO =MO∙ε方向垂直于MO,并与ε的转向一致。
a n MO =MO∙ω2 方向由点M指向基点O。
二、基本要求1、熟练掌握平面图形上各点的速度的求解。
2、熟练掌握平面图形上各点的加速度的求解。
三、典型例题例如图所示平面机构,由四杆依次铰接而成。
已知AB=BC=2R,C D=DE=R,AB杆和DE杆分别以匀角速度ω1与ω2绕A、E轴转动。
在图示瞬时,AB与CD铅直,BC与DE水平。
4142 试求该瞬时BC 杆转动的角速度和C 点加速度的大小。
解 AB 杆和DE 杆作定轴转动,BC 杆CD 杆均作平面运动。
(1)求BC 杆的角速度ωBC 因为V B =2R ω1 , V D =R ω2 分别以B 点和D 点为基点,分析C 点速度,有V C = V B + V CB (1)V C = V D + V CD (2) 所以 V B + V CB = V D + V CD (3) 沿BC 方向投影式(3)得V B = V CD则CD 杆的角速度ωCD = V CD /CD=V B /R=2ω1 (逆时针) 沿DC 方向投影式(3)得V CB = V D则BC 杆的角速度ωBC = V CB /BC=V D /2R=0.5ω2 (逆时针)(2)求C 点的加速度a C 因为a B =a B n =2R ω12 ,a D =a D n =R ω22分别以B 点和D 点为基点,分析C 点加速度,有 a C = a B + a CB τ + a CB n (4)a C =a D +a CD τ+a CD n (5)所以 a B + a CB τ + a CB n =a D +a CD τ+a CD n (6) 沿CD 方向投影式(6)得a B n - a CB τ = a CD na CB τ=a B n - a CD n =2R ω12-R(2ω1)2=-2R ω12又将式(4)分别沿x 、y 轴投影式得a Cx =-a CD n =-2R ωBC 2= -0.5R ω22a Cy =-a B n + a CB τ = -2R ω12-2R ω12= - 4R ω12故C 点加速度大小a C =22cy cx a a +=4241642ωω+R43。
刚体的平面运动

由此的结论:平面图形内任一点的速度等于该点随图 形绕瞬时速度中心转动的速度。
vA vAC AC
vB vBC BC
vD vDC DC
7.2
平面运动刚体上各点的速度(瞬心法)
三、确定速度瞬心位臵的方法
1. 平面图形沿一固定表面作无滑动的滚动。
B
v
A
vB
C
例如: 曲柄连杆机构中连杆AB的运 动,A点作圆周运动,B点作直线 运动,因此,AB 杆的运动既不是 平动也不是定轴转动,而是平面运 动.
7.1
刚体平面运动的描述
刚体的平面运动是工程上常见的一种运动,这是 一种较为复杂的运动.对它的研究可以在研究刚体的 平动和定轴转动的基础上,通过运动合成和分解的方 法,将平面运动分解为上述两种基本运动.然后应用 合成运动的理论,推导出平面运动刚体上一点的速度 和加速度的计算公式.
vA vO vAO vO vBO
解:取点O为基点,则点C的速度
vDO
vD
vO
vO
ω vO
vC vO vCO vCO R
vB
因轮纯滚动,所以vC=0,则
vCO
0 vO R
vBO 点D: vDO
点B:
vAO R vO v A 2vO R vO vB 2vO R vO vD 2vO
点A:
vO R
7.2
平面运动刚体上各点的速度(基点法)
例:曲柄长OA=r=40cm,以匀角速度ω=5rad/s转动。连杆 AB长l=200cm,求当曲柄与水平线成45º 角时,滑块B的速 度及连杆AB的角速度。
7.2
vA
平面运动刚体上各点的速度(基点法)
《刚体的平面运动 》课件

鲁棒性分析
分析控制系统对参数变化和外部干扰的鲁棒 性表现。
05
刚体的平面运动的展望
刚体的平面运动的发展趋势
理论研究的深入
随着数学和物理学理论的不断发展,人们对刚体的平面运动的理 解将更加深入,这有助于推动相关领域的研究和应用。
航空航天领域
在航空航天领域,刚体的平面运动对于飞行器的姿态调整和机动性有着 至关重要的作用,未来随着空间探索的深入,其应用前景将更加广阔。
03
医疗器械
刚体的平面运动在医疗器械领域也有着广泛的应用,例如在手术机器人
中用于精确控制手术器械的动作,提高手术的精度和安全性。
刚体的平面运动的挑战与机遇
挑战
刚体的平面运动的研究和应用面临着 一些挑战,如精确控制、稳定性、复 杂环境下的适应性等问题,需要不断 探索和创新来解决。
自动化生产线
刚体的平面运动在自动化生产线中起到关键作用, 如传送带、机器人手臂等。
机械设备的维护和检修
刚体的平面运动在机械设备的维护和检修中也有应 用,如对机械设备进行定位和调整。
航空航天中的应用
飞机起降系统
刚体的平面运动在飞机起降系统中起 到关键作用,如飞机滑行、转向等。
航天器对接
航空航天器的制造和测试
刚体的平面运动的重要性
实际应用
刚体的平面运动在实际生活中广泛存 在,如机械设备的运作、车辆的行驶 等。
理论意义
刚体的平面运动是刚体运动的基础, 对于理解更复杂的刚体运动形式具有 重要意义。
刚体的平面运动的基本原理
平移原理
刚体在平面内沿直线进行平移时,其上任意一点都沿着该直线进行等距离的移 动。
旋转原理
详细描述
在实际的物理问题中,刚体往往不会只进行平动或转动,而是同时进行这两种运动。这种复杂的平面运动形式通 常包括椭圆运动、抛物线运动等。这种复杂的运动形式通常需要综合考虑平动和转动的共同作用,以确定刚体的 最终运动轨迹。
刚体的平面运动

9.1 刚 体 平 面 运 动 的 简 化 及 其 分 解
如图所示,由图可知: 如图所示,由图可知:
∆ϕ = ∆ϕ ′
∆ϕ ∆ϕ ′ ω ′ = lim 而 ω = lim ∆t →0 ∆t ∆t →0 ∆t
B A
B′′
∆ϕ ∆ϕ ′
B′
A′
A′′
所以
ω = ω′
类似地
α = α′
即:在任一瞬时,图形绕其平面内任何点转动的角 在任一瞬时, 速度和角加速度都相同。亦即: 速度和角加速度都相同。亦即:角速度和角加速度 与基点的位置的选择无关。于是可以直接称为平面 与基点的位置的选择无关。于是可以直接称为平面 运动的角速度和角加速度
第八章 刚体的平面运动
1、刚体平面运动的概述和运动分 、 2、平面图形内各点的速度分析 、 3、平面图形上各点的加速度分析 、
一、刚体平面运动的定义 8.1 刚 体 平 面 运 动 的 概 述 和 运 动 分 解
ω
B
O
O
r vO
O
ω
A
O1
观察上述刚体的运动发现,它们在运动的过程 观察上述刚体的运动发现, 中有一个共同的特征, 当刚体运动时, 中有一个共同的特征,即:当刚体运动时,刚体内 任一点至某一固定平面的距离始终保持不变。 任一点至某一固定平面的距离始终保持不变。具备 这样一个特征的刚体的运动称为刚体的平面运动 刚体的平面运动, 这样一个特征的刚体的运动称为刚体的平面运动, 简称平面运动 平面运动。 简称平面运动。
r r r vB = v A + vBA
o
B点的速度合成矢量图如图所示。建立如图的投影 坐标,由速度合成矢量式,将各矢量投影到轴上得
0 = −v A + vBA sin 30
《刚体的平面运动》课件

刚体平动的实例分析
总结词
刚体平动的实例分析主要介绍了刚体在平面内沿某一方向做直线运动的情况,包 括匀速平动和加速平动。
详细描述
刚体平动的实例分析中,我们可以通过观察汽车在路面上行驶、火车在铁轨上飞 驰等实际现象,理解刚体平动的概念和特点。同时,通过分析匀速平动和加速平 动的动力学特征,可以深入了解刚体的平动运动规律。
03
刚体的平面运动的动力学
刚体的平动的动力学方程
平动的动力学方程:$F = ma$
描述刚体在平面内平动时的加速度和力之 间的关系。 适用于刚体在平面内直线运动或曲线运动 的情况。 考虑了刚体的质量对运动的影响。
刚体的定轴转动的动力学方程
定轴转动的动力学方程:$T = Ialpha$
描述刚体绕固定轴转动时的角加速度和力 矩之间的关系。 适用于分析刚体在平面内定轴转动的情况 。 考虑了刚体的转动惯量对运动的影响。
特点
刚体上任意一点的速度方 向都与该固定轴线平行, 且各点的速度大小相等。
应用
许多机械的运动可以简化 为刚体的定轴转动,如车
轮、电机转子等。
刚体的平面运动
定义
刚体在平面内既有平动又有定轴转动的运 动。
特点
刚体的运动轨迹是一个平面曲线,同时具 有平动和定轴转动的特征。
应用
许多复杂的机械运动可以简化为刚体的平 面运动,如曲柄连杆机构、凸轮机构等。
刚体的平面运动的运动学方程
平面运动定义
刚体在平面内既有平动又有定轴转动 。
运动学方程
解释
该方程描述了刚体在平面内既有平动 又有定轴转动的复杂运动,需要综合 考虑平动和定轴转动的运动学方程来 描述其运动轨迹。
需要将平动和定轴转动的运动学方程 结合起来,描述刚体在平面内的运动 轨迹。
理论力学—刚体平面运动

试求:该瞬时滑块B的速度和AB杆的角速度。
B
O
A
R
O1
解:用速度合成法(基点法)求解。
取A 为基点,B 点的速度为
vB v A vBA
式中:vA r 方向与OA相垂直。
vBA方向与AB杆垂直,大小未知
第二章 刚体的平面运动
§2.1. 刚体平面运动的简化 §2.2. 用分析方法研究平面图形的运动 §2.2.1. 运动方程
§2.2.2.平面图形的角位移、角速度 角加速度
§2.2.3. 平面图形上点的运动分析
*§2.3. 用矢量方法研究平面图形的运动 §2.3.1 平面平动 §2.3.2 定轴转动 *§ 2.3.3 平面图形上点的速度关系 *§2.3.4. 平面图形上点的加速度关系
Z
Y A1
S
A
A2
X
简化
Y
S A
X
§2.2 分析法研究平面图形的运动
2.2.1.运动方程
一、确定图形位置
自由的平面图形S,其位置的确定 可由其上任一线段AB 的位置来确定。
AB 位置由下述方法确定:
y
建立与参考空间固连
B
直角坐标Oxy
x A
A
A点坐标:xA, yA
O
y
A
x
方位角(AB与固定线 Ox夹角)
求解B 点的速度、加速度。
§2.3. 矢量法研究平面图形的运动
2.3.1、平面平动
平面平动特征
刚体上任意线段AB在移动
B
B'
过程中方向不变。
平动刚体上点的速度与加速度 rB A
理论力学刚体的平面运动

A的速度为
vA vO vAO 2vO
B的速度为
vB vO2 vBO2 2vO
同理,可得D的速度为
A
vDO
vD
D vO O
vO
vAO
vA
vO B vO
vCO
C
vBO vO
vB
vD 2vO
9.3.2 速度投影法
应用矢量投影定理,将该矢量式 vB vA vBA向
AB连线投影 。
vA cos vB cos
结论:刚体的平面运动可以 简化为平面图形S 在其自身 平面内的运动。
9.1.3 刚体的平面运动方程
在平面图形S内建立平面直角坐标系Oxy,为确定
平面图形 S 在任意瞬时 t 的位置,只须确定其上任意
线段 AB 的位置,而线段 AB 的位置可由点 A 的坐标
xA,yA 和线段 AB 与 x 轴(或 y 轴)的夹角j 来确定。
9.1.2 平面运动的简化
⑴ 作平面Ⅱ∥定平面Ⅰ且与 刚体相交成一平面图形S 。当刚体 运动时,平面图形S 始终保持在平 面Ⅱ内。平面Ⅱ称为平面图形S 自 身所在平面。
⑵ 在刚体上任取⊥平面图形S 的直线A1A2 , A1A2 作平动,其上各 点都具有相同的运动。
⑶ A1A2 和图形S 的交点 A 的运动可代表全部A1A2 的运动, 而平面图形S 内各点的运动即可代表全部刚体的运动。
[vB ]AB [v A ]AB
(9-3)
速度投影定理:平面图形上任意两点的速度在 这两点连线上的投影相等。速度投影定理是刚体上任 意两点间的距离保持不变的必然结果。适用于任何形 式的刚体运动。
应用速度投影定理求速度的方法称为速度投影 法。
例9-4 用速度投影法求例9-1中点B的速度。
刚体平面运动的概念和简化

刚体的运动\刚体平面运动的概念和简化
1.2 刚体平面运动的简化
由刚体平面运动的定义,可将平面运动 进行简化。设平面Ⅰ为某一固定平面,作平 面Ⅱ与平面Ⅰ平行,平面Ⅱ与刚体相交成一 平面图形S,如图所示。当刚体作平面运动 时,平面图形S始终在平面Ⅱ内运动。若在 刚体内任取一条与平面图形S垂直的直线A1A2, 显然该直线作平移,因此直线上各点都具有 相同的运动,这样直线A1A2与平面图形S的交 点A的运动即可代表直线上各点的运动。由 于A1A2是任取的,所以刚体内所有点的运动 都可以由平面图形S上相应点的运动来代表。 于是,平面图形S的运动就可代表整个刚体 的运动,即刚体的平面力学
刚体的运动\刚体平面运动的概念和简化
刚体平面运动的概念和简化
1.1 刚体平面运动的概念
刚体的平面运动是一种比平行移动和定轴转动复杂的运动,在 工程实际中会经常遇到,例如车轮沿直线轨道的滚动,曲柄连杆机 构中连杆(蓝色杆)的运动。这些刚体的运动既不是平移也不是定 轴转动,但是这些刚体的运动有一个共同的特征,那就是当刚体运 动时,刚体内任一点至某一固定平面的距离始终保持不变,即刚体 内的任一点都在平行于某一固定平面的平面内运动。刚体的这种运 动称为平面运动。
目录
理论力学
刚体的平面运动-3
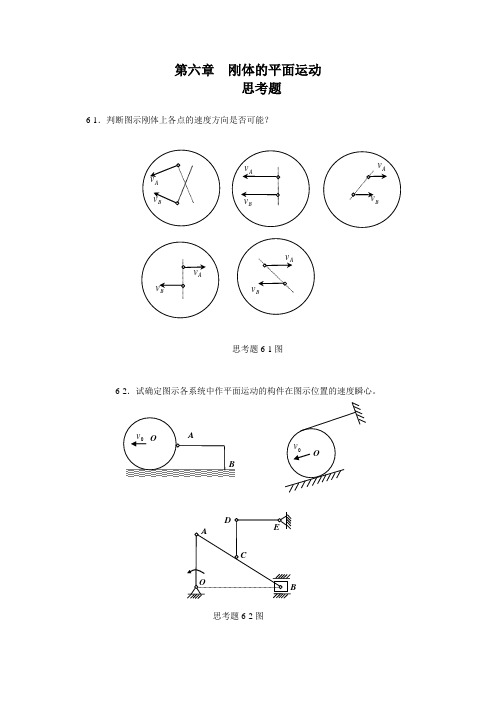
第六章 刚体的平面运动思考题6-1.判断图示刚体上各点的速度方向是否可能?6-2.试确定图示各系统中作平面运动的构件在图示位置的速度瞬心。
思考题6-2图B思考题6-1图6-3.某瞬时平面图形上A 、B 两点的速度矢分别为A v 和B v ,则该瞬时AB 连线上中点C 的速度矢为()2B A C v v v +=,请问此式是否正确?。
6-4.平面图形瞬时平动时,其上任意两点的加速度在这两点连线上的投影相等。
这种说法是否正确?为什么?6-5.刚体的平动和定轴转动都是平面运动的特例吗?刚体的平动与某瞬时刚体瞬时平动有何区别?6-6.刚体的平面运动通常分解为哪两个运动?它们与基点的选取有无关系?用基点法求平面图形上各点的加速度时,要不要考虑科氏加速度?6-7.如图所示机构中,能否根据A 、B 两点的速度A v 、B v 的方向,按图示的方法确定速度瞬心I 的位置,为什么?6-8.图示杆AB 沿墙角在铅直平面滑落时,试画出其动瞬心轨迹和定瞬心轨迹。
思考题6-7图思考题6-8图第六章 刚体的平面运动习 题6-1 筛子的摆动由曲柄连杆机构带动。
已知曲柄OA 的转速40 r/min, 0.3m, n OA BC BE ===。
求图示瞬时筛子CD 的速度。
6-2 杆AB 的A 端沿水平线以等速v 运动,运动时杆恒与一半径为R 的半圆周相切,如图所示,如杆与水平线间的交角为θ,试以角θ表示杆的角速度。
6-3 图示曲柄连杆机构中,曲柄OA 长20cm ,以匀角速度010rad/s ω=转动,连杆AB 长100cm ,求在图示位置时连杆的角速度与角加速度以及滑块B 的加速度。
6-4 在图示曲柄连杆机构中,曲柄OA 绕轴O 转动,其角速度为0ω,角加速度为0α,在某瞬时曲柄与水平线间成60°角,而连杆AB 与曲柄OA 垂直。
滑块B 在圆形槽内滑动,此时半径O 1B 与连杆AB 间夹角为30°。
如果1, , 2OA r AB O B r ===,求该瞬时,滑块B 的切向和法向加速度。
哈工大_理论力学课件第09章3

r r vA // vB ,且不垂直于AB r r r vB = vA + vAB r ⇒ vBA = 0 ⇒ωAB = 0 r r r ⇒ vB = vA = vM
瞬时平移(瞬心在无穷远处) 瞬时平移(瞬心在无穷远处)
纯滚动(只滚不滑) 纯滚动(只滚不滑)约束
运动方程
x = r (ωt − sinωt ) y = r (1− cosωt )
第九章
刚体的平面运动
§9-1 刚体平面运动的概述和运动分解
1、平面运动
在运动中, 在运动中, 刚体上的任意一点与某一固定平面始终保持 相等的距离,这种运动称为平面运动 平面运动。 相等的距离,这种运动称为平面运动。
平面运动 = 平面图形的运动
=
2、运动方程
广义坐标
xA , y A , ϕ
运动方程
1、 解: 1、轮Ⅱ作平面运动
基点:A 基点
r r r 2、 D = vA + vDA = 0 v
vDA = vA = ωO ( r + r2 ) 1
r vDA vA ω = = = ωO 1+ 1 Ⅱ DA r2 r2 r r r 3、 vB = vA + vBA
大小 ?ωO ( r + r2 ) ω r2 1 Ⅱ 方向 √ √ √
r r r vB = vA + vBA
沿AB连线方向上投影 连线方向上投影
r r ( vB ) AB = ( vA ) AB
同一平面图形上任意两点的速度在这两点连线上 的投影相等。 的投影相等。
如图所示的平面机构中,曲柄OA长 例9-5 如图所示的平面机构中,曲柄 长 100mm,以角速度 转动。 ,以角速度ω=2rad/s转动。连杆 带动摇杆 转动 连杆AB带动摇杆 CD,并拖动轮E沿水平面纯滚动。已知:CD=3CB, ,并拖动轮 沿水平面纯滚动。已知: , 沿水平面纯滚动 图示位置时A,B,E三点恰在一水平线上,且 图示位置时 三点恰在一水平线上, CD⊥ED, OA⊥AB ⊥ ⊥ 求:此瞬时点 的速度。 此瞬时点E的速度 的速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
vA
A
AB
vB
vA
B
“ ”向投影
vBA
vB sin vBA
3 R v BA 3 v BA 1 AB AB 3
7
例2
BC=l
vC vB
8
解: (1)[BDC]
以C为基点, v B v C v BC
vC 0 r
vC v B sin v BC v B cos
vE
vB vA R vC
[轮E], 瞬心I点,D点速度方向如图
I
E
vD vE E DI R
(a)
[杆CD], 由速度投影法: vC cos60 vD cos15
1 vD 0.37R 代入(a)式: vE 2
vD 0.52R
方向水平向左
23
重要的概念
大小:
rA
x
AB
vB v A vBA
4
一、基点法
平面运动刚体内任意两点 速度关系:
y
y ' vBA
A B
vB
B
vA vA
x'
vB v A vBA
vBA AB
可求解有两个速度 未知量(大小、方向) 的问题
o
x
A为基点,B为同一刚体上的任意点。
5
二、速度投影法
解:[AB],取A为基点
vB v A vBA R vA 2 3 R O vB ቤተ መጻሕፍቲ ባይዱ cos cos 3
vBA vA tan vBA R tan 1 3 AB R cot 法2 由投影法 vB cos vA R
R 2 3 R vB cos 3
(1)
(2)
B
vB
问题:某瞬时速度瞬心是否唯一? 唯一
v B' I A (5)纯滚动
15
16
例3:确定图示机构中AB杆在该瞬时的速度瞬心
vA
A O (1)
I
vA
B
A
B O (2) O
vA
A
vB
B I
vB
vB
(3)
速度瞬心的特点: 速度瞬心是平面图形(或其延伸平面)中的一点
1、瞬时性——不同的瞬时,有不同的速度瞬心;
v D 70 r 3
vDC 21 sin cos 与水平线的夹角: vD 14
10
如何解释 这种现象
?
离车轮与地面接触处近的钢丝看得清,离 得远的钢丝看不清,甚至看不见。
11
回顾:平面图形上任意两点速度关系
基点法: vB v A vBA
缺点: 计算比较繁琐。
角加速度和A点的加速度。
t a AO n R a AO aO vO O n a IO t a IO
A
x
y
O aO v R R
取O为基点,加速度基点法:
a A aO a AO a
x:
y:
2 v n a Ay a AO 2R O R
n AO
若要求瞬心加速度呢? 2 vO y : aIy x : aIx 0 R
aB
2 a r BA 0
3 2 3 2 l 0 ( r l ) 0 27 27
因:
a BA AB l
AB
a 3 3 2 8 3 2 BA ( ) 0 0 l 3 27 27
28
例 一长为L的刚性杆AB, B端靠墙, A端着地,并以速度 v 匀速向右运动, 求杆AB 的转动角加速度、端部B 点 的加速度。
位置描述:
基线
x A f1 (t ) y A f 2 (t )
o
x
为常量
f (t )
* *
刚体的角速度、角
加速度是唯一的 !
3
刚体的角速度和角加速度
f ' (t ) f (t )
A
BA BA
aA
x
a 其中: BA AB
n aBA AB 2
基
点:A
刚体上点:B
n aB a A a a BA BA
25
例:已知半径为R圆盘在地面上 纯滚动,图示瞬时轮心的速度为 vO和加速度aO,求圆盘的角速度、
解:因为圆盘纯滚动
vO R
上式两边对时间 t 求导
x
定义:某瞬时,平面图形或延伸平面内必存在一点,其速度在该瞬
时为零,该点称为瞬时速度中心(I),简称速度瞬心。
注意:速度瞬心可能在平面图形内部或延伸平面内。
13
由基点法: vB v A vBA
问题:若选速度瞬心为基点,情况将如何呢?
取速度瞬心I为基点,平面图形上B点的速度:
问题:某瞬时,是否存在一个速度为零的点
?
12
8.2.3. 速度瞬心法
1. 方法推导
由 欲使
y
vB v A vBA vB 0
A
vBA
B
vA vA
vA
只需 vBA v A
因为 vBA rAB
o
rAB 大小:
rAB v A 所以B相对A点的矢径 rAB满足:
D
B
vB v A B cot R R 20
例6:半径为R的圆轮在水平面上
作纯滚动,杆BC一端B与轮缘铰 接,滑块C沿 f=30°的斜槽滑动。
解:[轮O], A为瞬心,则B点速度如图
vB 2RO 2vO
已知在图示瞬时(B处于最高点,
=60°),圆轮中心的速度为v0。
试求该瞬时滑块C的速度。
vA
vB
解:[AB杆], 速度投影法:
vA r vB v A r
vC
vA cos30 vB cos30
BC I
方向垂直BF向下 [BC杆], 速度投影法: vB cos30 vC cos30 vC vB r I为BC杆瞬心, v B r BC BI L
y
vB v A vBA
上式两边分别投影到AB连线上:
y ' vBA
A B
vB
B
A
vB AB vA AB
vB cos B vA cos A
o
vA
x'
x
若A、B两点速度方向已知,则有:
6
例1:已知OA杆的角速度,求图示瞬时滑块B的 速度和 AB杆的角速度。OA R, 600 , AB OA
a BA
B
I
vB
AB
vA 3 v IA 2
x
B
解:[AB]
n a BA
aB
n aB a A a a BA BA n aB a a BA BA
60°
O A
vA
an BA AB AB
2
60°
O A
“x”:
n 0 a cos 30 a sin 30 BA BA
求杆B端的速度、杆的角速度、 杆中点D的速度和圆盘的角速
解:[AB杆],
I为AB杆的速度瞬心
度。AB=L
vA vA AB AI L sin
vA
A
vD vB
AB
I
vB BI AB vA cot vA vD DI AB 2 sin
[轮B], 接触点为瞬心
• 刚体角速度与角加速度与基点的选择无关
• 速度瞬心具有唯一性
• 基点法或瞬心法是针对同一刚体
• 瞬时平移只是某一瞬时
24
第三节 平面运动刚体的加速度
研究平面运动刚体上各点加速度之间的关系。
基点法
因为
y
y'
a BA
B
n aBA
x'
vB v A ω rAB
A
dv B dv A 对t求导 dt dt α rAB ω (ω rAB ) o a B a a a n
2 vB 0 r 3
AB
vB 2r0 AB
3R
v BC BC l
BC r0
3l
BC
9
(2)求D点的速度 以C为基点
v D v C v DC
v DC DC BC
r 0 3
vD 2 vC 2 vDC 2 2vC vDC sin
n a B a A+ a + a BA BA
O
aB
速度分析;瞬心法:
v AB AB l 0 AO 0 3 AB 3
2 a r 其中: A 0
n 2 a BA AB AB
将各项向AB方向投影:“n”
a B cos30 =a
n AB 2 l 0 , 9
B
O
v0 所以: R
所以:
vO
D
vB BA 2 Rv0
A
vC CA 2 Rv0
vD DA 2 Rv0
方向如图所示
18
现在: 你能解 释这种现象吗
?
因为车轮与地面接触点为速度瞬心,离它越近的
钢丝速度越小,离得越远的钢丝速度越大。
19
例5:已知 AB 杆A点的速度,
