多边形面积奥数
5年级奥数多边形面积计算公式例题解析

【内容概述】正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题.通过恰当地分割与拼补进行计算的面积问题.【例题】1.如图6-1,每一个小方格的面积都是l平方厘米,那么用粗线围成的图形的面积是多少平方厘米?[分析与解]方法二:如下图,先求出粗实线外格点内的图形的面积,有①=3÷2=1.5,②=2÷2=1,③=2÷2=1,④=2÷2=1,⑤=2÷2=1,⑥=2÷2=1,还有三个小正方形,所以粗实线外格点内的图形面积为1.5+1+1+1+1+1+3=9.5,而整个格点阵所围成的图形的面积为16,所以粗线围成的图形的面积为:16-9.5=6.5(平方厘米).2.如图6-2,如果每一个小三角形的面积是l平方厘米,那么四边形ABCD的面积是多少平方厘米?[分析与解]正三角形方形格点阵中多边形面积公式:×单位正三角形面积,其中N为图形内格点数,L为图形周界上格点数.有N=9,L=4,所以用粗线围成的图形的面积为:(9×2+4-2)×1=20(平方厘米).方法二:如下图,我们先数出粗实线内完整的小正三角形有10个,而将不完整的小正三角形分成4部分计算,其中①部分对应的平行四边形面积为3,所以①部分的面积为1.5,②、③、④部分对应的平行四边形面积分别为2,8,6,所以②、③、④部分的面积分别为1,4,3。
所以粗实线内图形的面积为10+2+1+4+3=20(平方厘米).3.如果图6-3是常见的一副七巧板的图,图6-4是用这副七巧板的7块板拼成的小房子图,那么,第2块板的面积等于整幅图的面积的几分之几?第4块板与第7块板面积的和等于整幅图的面积的几分之几?[分析与解]如下图,我们在图6-3中标出图6-4中各块图形的位置.设整个七巧板的组成的正方形的边长为1,显然整幅图形的面积为1,且有第2块的面积为=.有S3=S4,S2=S5=S7=2S3,有2、3、4、5、7五块图形的面积之和为,所以S 4=,S7=.所以第2块板的面积等于整幅图面积的,第4块板与第7块板面积和为整幅图面积的.4.把正三角形每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形.再将这个六角形的各个“角”(即小正三角形)的两边三等分,又以它们的中间段向外作更小的正三角形,这样就得到图6-5所示的图形.如果这个图形面积是1,那么原来的正三角形面积是多少?[分析与解]如下图,我们将图6-5分成若干个大小、形状完全相同的小正三角形,注意到图6-5由40块小正三角形组成,而原来的正三角形由27块小正三角形组成.120块小正三角形的面积为1,所以每块为,那么原来的正三角形由81块小正三角形组成,其面积显然为.方法二:如下图,我们把图5-6中的三角形分成A、B、C三种,设A形正三角形面积为t,则B、C两种正三角形的面积依次为t、t.在图5-6中,A种、B种、C种正三角形的个数依次为1,3,12,所以图5-6中图形的面积为t+3×t+12×t=t.所以有t=,而原来的正三角形即为三角形A,所以原来的正三角形的面积为.5.如图6-6,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?[分析与解]如下图,我们将图6-6分成大小、形状相同的三角形,有正六边形ABCDEF包含有24个小正三角形,而阴影部分MNP包含有9个小正三角形.正六边形ABCDEF的面积为6,所以每个小正三角形的面积为6÷24=,所以三角形MNP的面积为9×=2.25(平方厘米).6.把同一个三角形的三条边分别五等分、七等分,适当连接这些分点,便得到了若干个面积相等的小三角形.已知图6-7中阴影部分的面积是294平方分米,那么图6-8中的阴影部分的面积是多少平方分米?[分析与解]在图6-7中,原正三角形被分成25个小正三角形,而阴影部分含有12个小正三角形,所以每个小正三角形的面积为294÷12=24.5,所以原正三角形的面积为24.5×25=612.5(平方分米).而在图6-8中,原正三角形被分成49块,而阴影部分含有16块,所以阴影部分的面积为612.5÷49×16=200(平方分米).7.图6-9是5×5的方格纸,小方格的面积是l平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求选出的点中任意3点都不在同一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么所围图形的面积是多少平方厘米?[分析与解]我们知道满足题意的7个点可以组成一个七边形,适当的切去正方形的一个角可以得到一个五边形,切出2个角可以得到一个六边形,切去3个角可以得到七边形.为了使最后留下的七边形的面积尽可能大,那么切去的3个角面积应尽可能的小.如下切法得到的七边形的面积最大,为25-3×0.5=23.5(平方厘米).8.在图6-10中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是多少平方厘米?[分析与解]如下图,连接IG,有四边形ADGI为正方形,易知FG=FC=3(厘米),所以DG=DF-FG=9-3=6(厘米),于是S△HIG =×S正方形AIGD=×62=9.而四边形IGFB为长方形,有BF=AD=DG=6(厘米),GF=3(厘米),所以S长方形IGFB=6×3=18.阴影部分面积为△HIG与长方形IGFB的面积和,即为9+18=27(平方厘米).解法二:如下图,为了方便叙述,将图6-10中某些交点标上字母.易知三角形BIE、CGF、AIH、DGH均为等腰直角三角形.先求出等腰直角三角形AHI、CGF的面积,在用已知的等腰三角形ABC的面积与其作差,即为需求阴影部分的面积.有S△ABC =S△DEF=×DF×DF=,S△CGF=×CF×CF=.因为CF=FG=3,所以DG=DF-FG=6.如下图,可以将4个三角形DGH拼成一个边长为DG的正方形.所以,S△DGH =×DG×DG=9,而S△AIH=S△DGH=9,所以S阴影BFGHI=S△ABC-S△CGF-S△AIH=--9=27(平方厘米).即阴影部分的面积为27平方厘米.9.如图6-1l,在长方形ABCD中,O是长方形的中心,BC长20厘米,AB长12厘米,DE=4AE,CF=3DF,那么阴影部分的面积是多少平方厘米?[分析与解]我们只用先求出四边形ADFO的面积,在将其减去两个三角形AEO、EFO的面积和,即为所求阴影部分的面积.而四边形ADFO的面积等于两个三角形AOD、ODF的面积和.由题意知AE=4,ED=16,DF=3,FC=9.即阴影部分的面积为39平方厘米.10.如图6-12,大正方形的边长为l0厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?[分析与解]如下图,我们将大正方形中的所有图形分成A、B两种三角形.其中含有A形三角形8个,B形三角形16个,其中阴影部分含有A形三角形4个,B形三角形8个.所以,阴影部分面积恰好为大正方形面积的,即为×10×10=50(平方厘米).11.如图6-13,ABCD是边长为8厘米的正方形,梯形AEBD的对角线相交于O,三角形.AOE的面积比三角形BOD的面积小16平方厘米,则梯形AEBD的面积是多少平方厘米?[分析与解]如下图,将梯形AEBD内4个三角形的面积分别记为①、②、③、④.在梯形AEBD中,有△EBD、△ABD同底等高,所以有S△EBD =S△ABD,即③+②=①+②.显然有①=③.由题意知S△BOD -S△AOE=16,即②-④=16,于是有(①+②)-(③+④)=16.已知①+②=S△ABD=×8×8=32,所以③+④=(①+②)-16=16.所以有S梯形AEBD=(①+②)+(③+④)=32+16=48(平方厘米).评注:在任意梯形ABCD中,两条对角线将其分成四块,记它们的面积为①、②、③、④,有:Ⅰ.①=③,Ⅱ.②:④=BC2:AD2,Ⅲ.①×③=②×④.12.如图6-14,ABCD是长方形,长AD等于7.2厘米,宽AB等于5厘米,CDEF 是平行四边形.如果BH的长是3厘米,那么图中阴影部分面积是多少平方厘米?[分析与解]S 平行四边形CDEF =DC ×BC =5×7.2=36,HC =BC -BH =7.2-3=4.2,所以S △CDH =×CD ×HC =×5×4.2=10.5.S 阴影=S 平行四边形CDEF -S △CDH =36-10.5=25.5(平方厘米).13.如图6-15,已知一个四边形的两条边的长度和三个角,那么这个四边形的面积是多少?[分析与解] 将AD 、BC 延长交于E ,有∠EDC =45°,∠ECD =90°,所以△CDE 为等腰直角三角形,有EC =DC .而∠EDC =45°,∠EAB =90°,所以△ABE 也是等腰直角三角形,有EA =AB .有S △ABE =×AB ×EA =,S △EDC =×EC ×DC =.有S 四边形ABCD =S △ABE -S △CDE =-=20.14.图6-16是边长为1的正方形和一个梯形拼成的“火炬”.梯形的上底长1.5米,A为上底的中点,B为下底的中点,线段AB恰好是梯形的高,长为0.5米,CD长为米.那么图中阴影部分的面积是多少平方米?[分析与解]为了方便叙述,将下图中一些点标上字母.延长AB交正方形边EF 于H点,过D作AH的垂线,交AH于G点.我们先求出梯形JICK与正方形IFEC的面积和,再求出三角形AFH、AGD与矩形GHED的面积和,将前者与后者作差所得到的值即为所求阴影部分的面积.15.从一块正方形木板锯下宽为米的一个木条以后,剩下的面积是平方米.问锯下的木条面积是多少平方米?[分析与解]我们画出示意图a,则剩下的木块为图b,将4块剩下的木块如下拼成一个正方形得到图c.我们称AB为长,AD为宽,有长与宽的差为,所以图c中心的小正方形边长为,于是大正方形AEHK的面积为×4+×==×,所以AK长为.即,长+宽=,综合长-宽=,得长=,于是锯去部分的木条的面积为×==(平方米).。
五年级奥数讲义-多边形面积计算二(附答案)

五年级奥数-多边形的面积计算二学员编号: 年 级:小五 课 时 数:学员姓名: 辅导科目:奥数 学科教师: 课程主题:多边形的面积计算二 授课时间:学习目标教学内容知识点一(多边形的面积) 【知识梳理】【典型例题】例题精讲例1. 如图△ABC 中,D 是BC 的中点,AC=3EC 。
已知三角形CDE 的面积是6平方厘米,那么三角形ABC 的面积是多少?答案: 362cm例2. 如下图所示,两个完全相同的直角三角形部分重叠,已知AB=10厘米,BD=4cm ,EF=3cm ,求阴影部分的面积。
G 答案:连接AF, =ACGFAEFS SS阴影即可求出,得34A FB D C③ ① EBDCE A知识精讲例3. 直角梯形ABCD 的上底AB=10,高DA=8.,下底上的线段ED=6。
求阴影部分面积。
(单位:厘米)答案:ADFS=6*8/2=24=BCFS例4. 把例3 的问题改为:梯形ABCD 的面积是多少平方厘米? 答案:ADFS=24,ABFS=8*10/2-24=16, BCFS=24AF:FC=16:24=2:3ADFS:DCFS=2:3, DCFS=36S=24+24+16+36=100平方厘米【同步练习】1、在平行四边形ABCD 的一角有一个△AEF 。
已知AB=4AF,AD=3AE,△AEF 的面积是5平方厘米,求平行四边形ABCD 的面积。
答案:连接BE,BD,AB=4AF, AEBS=4 AEFS=20,AD=3AE, ADBS=3AEBS=60, S=2ADBS =1202、已知△ABC 的面积是1平方厘米,把AB ,BC ,CA 分别延长2倍到D 、E 、F ,求△DEF 的面积。
答案:连BF,DC,AE,CE=BD=BF=2, S=198A C10 6 BD EF3、下图由两个相同的直角梯形重叠在一起,求图中阴影部分的面积。
(单位:厘米)答案:45厘米4、在下图中,正方形ABCD 的边长为5厘米,又△CEF 的面积比△ADF 的面积大5平方厘米。
最新小学奥数 多边形的面积

小学奥数多边形的面积我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算,图形及计算公式如下:正方形面积=边长×边长=a2,长方形面积=长×宽=ab,平行四边形面积=底×高=ah,圆面积=半径×半径×π=πr2,扇形面积=半径×半径×π×圆心角的度数÷360°在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲和后面的两讲中,我们将学习如何计算它们的面积。
例1小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出大正方形边长=(16+4)÷2=10(厘米),小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2如左下图所示,四边形ABCD与DEFG都是平行四边形,证明它们的面积相等。
分析与证明:这道题两个平行四边形的关系不太明了,似乎无从下手。
我们添加一条辅助线,即连结CE(见右上图),这时通过三角形DCE,就把两个平行四边形联系起来了。
在平行四边形ABCD中,三角形DCE 的底是DC,高与平行四边形ABCD边DC上的高相等,所以平行四边形ABCD的面积是三角形DCE的两倍;同理,在平行四边形DEFG中,三角形DCE的底是DE,高与平行四边形DEFG边DE上的高相等,所以平行四边形DEFG的面积也是三角形DCE的两倍。
多边形面积奥数

第十讲格点与切割备考导航格点面积及切割是竞赛考试的一个难点知识,本讲将学习正方形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题。
通过恰当地分割与拼补进行计算的面积问题。
利用格点求图形的面积有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形的面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
格点面积公式=中间格点数+图形一周的格点数÷2﹢1典型例题【例1】图中相邻两格点问的距离均为1厘米,三个多边形的面积分别是多少平方厘米?【例2】图中每个小正方形的面积均为2平方厘米,阴影多边形的面积是多少平方厘米?【例3】如图所示,如果每个小等边三角形的面积都是1平方厘米,四边形ABCD和三角形EFG的面积分别是多少平方厘米?【例4】如图所示,在正方形ABCD内部有一个长方形EFGH,已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米。
求长方形EFGH的面积。
【例5】如图所示,大正方形的边长为10厘米。
连接大正方形的各边中点得到一个小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连。
请问:图中阴影部分的面积总和等于多少平方厘米?【例6】如图,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,求阴影部分的面积。
【例7】如图所示,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD 中点,P是EF中点。
请问:三角形MNP的面积是多少平方厘米?【例8】已知大的正六边形面积是72平方厘米,按图中不同方式切割(切割点均为等分点),形成的阴影部分面积各是多少平方厘米?小试身手(1)下图是一个三角形点阵,其中能连出的最小的等边三角形的面积为l平方厘米。
三个多边形的面积分别为多少平方厘米?(2)图中,五个小正方形的边长都是2厘米,求三角形ABC的面积(3)如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?星级挑战(一)夯实基础★★★1、图中相邻两格点问的距离均为l厘米,三个阴影图形的面积分别是多少平方厘米?2、图中每个小正方形的面积是2平方厘米,阴影部分面积是多少平方厘米?3、图中每个小正三角形的面积是4平方厘米,阴影部分面积是多少平方厘米?4、图中每个小正方形的边长为1厘米,阴影部分的面积是多少平方厘米?5、下图的数字分别表示对应线段的长度,试求这个多边形的面积。
奥数拓展第六讲:多边形的面积综合-数学五年级上册含参考答案

奥数拓展第六讲:多边形的面积综合-数学五年级上册一、选择题1.比较下面阴影部分的面积,()是错误的。
①②③④A.图①中阴影部分的面积等于图②中阴影部分的面积B.图②中阴影部分的面积等于图③中阴影部分的面积C.图③中阴影部分的面积不等于图④中阴影部分的面积的是()。
A.面积变大B.面积变小C.面积不变D.无法确定4.七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,把一幅七巧板按如图①所示进行1~7编号,1~7号分别对应着七巧板的七块。
图②所示的“天鹅”是由这幅七巧板拼成的,“天鹅”头颈由3号和6号块构成,其面积为3,则图①大正方形的边长为()。
A.8 B.6 C.4 D.25.将一个梯形割补成一个三角形(如图所示),面积和原来相比(),周长与原来相比()。
A.不变;变大B.不变;变小C.变小;变大D.无法确定6.如图中两个正方形的边长分别是6厘米和4厘米,阴影部分的面积是()平方厘米。
A.20 B.18 C.16 D.22二、填空题7.下图中ABCD是梯形,ABED是平行四边形,其中几个三角形面积如图所示(单位:平方厘米),阴影部分的面积是( )平方厘米。
8.图中ABCD为正方形,E为AB的中点,阴影部分的面积是21cm2,正方形ABCD的面积是( )cm2。
9.如图,在三角形ABC 中,D 是边AB 的中点,可知AD =BD ,则三角形BCD 与三角形ACD 的面积相等。
(1)如图①,在三角形ABC 中,D 、E 分别是AB 和AC 两边的中点。
已知三角形ADE 的面积是2cm 2,则三角形ABC 的面积是( )cm 2。
(2)如图②,在三角形ABC 中,把AB 边三等分、AC 边四等分。
已知三角形ADE 的面积是2cm 2,则三角形ABC 的面积是( )cm 2。
(3)如图③,在平行四边形ABCD 中,把AB 边五等分、AD 边六等分。
已知平行四边形ABCD 的面积是15cm 2,则三角形AEF 的面积是( )cm 2。
五年级奥数基础教程-多边形的面积小学

多边形的面积我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算,图形及计算公式如下:正方形面积=边长×边长=a2,长方形面积=长×宽=ab,平行四边形面积=底×高=ah,圆面积=半径×半径×π=πr2,扇形面积=半径×半径×π×圆心角的度数÷360°在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲和后面的两讲中,我们将学习如何计算它们的面积。
例1小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出大正方形边长=(16+4)÷2=10(厘米),小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2如左下图所示,四边形ABCD与DEFG都是平行四边形,证明它们的面积相等。
分析与证明:这道题两个平行四边形的关系不太明了,似乎无从下手。
我们添加一条辅助线,即连结CE(见右上图),这时通过三角形DCE,就把两个平行四边形联系起来了。
在平行四边形ABCD中,三角形DCE的底是DC,高与平行四边形ABCD边DC上的高相等,所以平行四边形ABCD的面积是三角形DCE的两倍;同理,在平行四边形DEFG中,三角形DCE的底是DE,高与平行四边形DEFG边DE上的高相等,所以平行四边形DEFG的面积也是三角形DCE的两倍。
五年级数学上册 第六单元 多边形的面积同步奥数(附答案)

第六单元多边形的面积同步奥数1.平行四边形的面积例题1.如下图,已知平行四边形ABCD的周长是22.4厘米。
求平行四边形ABCD的面积是多少平方厘米? D A练习1.如图所示,平行四边形ABCD的周长是75厘米,以BC为底的高是14厘米,以CD为底的高是16厘米,求平行四边形ABCD的面积。
2.三角形的面积等积法:1.同底等高型:如果两个三角形的底相同,且能够证明出高相等,则这两个三角形面积相等。
2.同高等底型:如果两个三角形的高相同,且能够证明出底相等,则这两个三角形面积相等。
例题1.找出下图中哪些三角形的面积是相等的。
A D练习1.找出找出下图中哪些三角形的面积是相等的。
例题2.下图中的ABCD和CEFG分别是边长为8和6的正方形,连接BD、DF、FB形成△BDF,求阴影部分BDF的面积。
(单位:厘米)练习2.如图中大小正方形的边长分别是9厘米和5厘米,求阴影部分的面积。
例题3.在图中,正方形ABCD和正方形CEFG形AEG和三角形BDF的面积分别是多少?A D练习3.如图,甲、乙两图形都是正方形,它们的边长分别是5厘米和6厘米,求阴影部分的面积。
例题4.正方形ABCD的面积为9平方厘米,正方形EFGH的面积为64平方厘米。
如图所示,边BC落在EH上。
已知三角形ACG的面积为6.75平方厘米,则三角形ABE的面积为多少平方厘米?A D练习4.已知正方形ABCD边长为10,正方形BEFG边长为6,求阴影部分的面积。
A DB EC H例题5.如图所示,在四边形ABCD中,M和N分别是AB和CD的中点。
如果四边形ABCD的面积是40,那么BNDM的面积是多少? A练习5.如图所示,在四边形ABCD中,M和N分别是AD和BC的中点。
如果四边形ABCD的面积是28,那么BNDM的面积是多少? D3.梯形面积例题1.将一个底边BC长16厘米的直角三角形ABC向右平移6厘米,再向下平移1.5厘米,得到一个图形(如下图),求阴影部分的面积。
奥数技巧解密多边形面积题

奥数技巧解密多边形面积题多边形面积问题是数学竞赛中常见的一个考点,解决多边形面积题需要一定的技巧和方法。
在这篇文章中,我们将揭开一些奥数技巧,帮助你更好地理解和解决多边形面积题。
一、三角形的面积计算三角形是最简单的多边形,常被用来解决面积问题。
计算三角形面积的常用方法是利用底边和高的关系,公式为:面积 = 1/2 ×底边 ×高。
其中,底边和高可以通过画图或者已知条件得出。
例如,给定一个三角形ABC,已知底边AB的长度为6,高CD的长度为4。
我们可以直接使用面积公式得出三角形的面积:面积 = 1/2× 6 × 4 = 12。
因此,三角形ABC的面积为12平方单位。
二、矩形和正方形的面积计算矩形和正方形都属于多边形,其面积计算方法是基于长和宽的乘积。
对于一个矩形或正方形,面积 = 长 ×宽。
这个公式相信大家都非常熟悉。
举个例子,假设一个矩形的长为5,宽为3。
我们可以直接使用面积公式得出矩形的面积:面积 = 5 × 3 = 15。
因此,该矩形的面积为15平方单位。
三、正多边形的面积计算正多边形指的是所有边和角都相等的多边形。
解决正多边形的面积问题需要利用正多边形的性质。
以下是计算正多边形面积的一种常见方法:1. 确定正多边形的边长和边数;2. 将正多边形分割成若干个等边三角形;3. 计算一个等边三角形的面积;4. 将三角形的面积乘以正多边形的边数。
假设我们要计算一个正六边形的面积,已知边长为4。
首先,我们将正六边形分割成六个等边三角形。
然后,我们计算一个等边三角形的面积。
对于一个等边三角形,边长为4,我们可以利用三角形的高和底边计算面积。
在这里,三角形的高等于边长乘以正弦60度(正六边形内角的一半)。
因此,三角形的高为4 × sin 60° = 4 × √3 / 2 = 2√3。
接下来,我们可以使用三角形的面积公式计算一个等边三角形的面积:面积 = 1/2 ×底边 ×高= 1/2 × 4 × 2√3 = 4√3。
五年级数学奥数专题正多边形面积

五年级数学奥数专题正多边形面积五年级数学奥数专题:正多边形面积正多边形是指所有边相等,所有角相等的多边形。
在五年级研究数学奥数时,正多边形的面积是一个重要的专题。
本文将介绍如何计算正多边形的面积以及一些相关的特性和应用。
正多边形的面积公式正多边形的面积可以通过以下公式计算:面积 = (边长 ×边长) × (n / 4) × tan(π / n)其中,边长表示正多边形的边长,n表示正多边形的边数,π表示圆周率(约等于3.14)。
这个公式可以帮助我们计算任意正多边形的面积。
实例演练让我们通过一个实际的例子来演示如何计算正多边形的面积。
假设我们有一个正六边形,边长为5厘米。
我们可以使用上面的公式计算它的面积:面积= (5 × 5) × (6 / 4) × tan(π / 6)现在我们来计算具体数值:面积= 25 × (6 / 4) × tan(π / 6)≈ 25 × 1.5 × tan(π / 6)≈ 25 × 1.5 × 0.577≈ 21.718 厘米²所以,这个正六边形的面积约为21.718平方厘米。
正多边形的特性和应用除了计算面积,正多边形还有一些特性和实际应用:1. 边数相等的正多边形具有相等的内角和外角;2. 正多边形可以用来拼接图形,如拼接多个正方形来形成六边形;3. 在建筑和设计中,正多边形常用于构建对称和美观的结构。
总结正多边形的面积计算是五年级数学奥数的重要专题。
我们可以使用面积公式来计算正多边形的面积,其中需要知道边长和边数。
正多边形还有一些特性和应用,例如相等的内角和外角,以及在建筑和设计中的应用。
通过研究这些内容,我们可以更好地理解和应用正多边形的知识。
[参考资料]。
奥数题关于图形面积
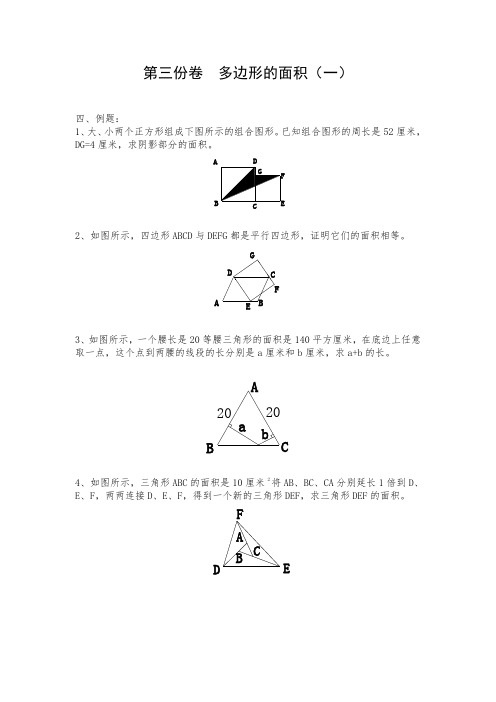
第三份卷 多边形的面积(一)四、例题: 1、大、小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
ABD2、如图所示,四边形ABCD 与DEFG 都是平行四边形,证明它们的面积相等。
ABC D FG3、如图所示,一个腰长是20等腰三角形的面积是140平方厘米,在底边上任意取一点,这个点到两腰的线段的长分别是a 厘米和b 厘米,求a+b 的长。
ABCab20204、如图所示,三角形ABC 的面积是10厘米2将AB 、BC 、CA 分别延长1倍到D 、E 、F ,两两连接D 、E 、F ,得到一个新的三角形DEF ,求三角形DEF 的面积。
CF DEA B5、一个正方形,将它的一边截去15厘米,另一边截去10厘米,剩下的长方形比原来正方形的面积减少了1750平方厘米,求剩下的长方形的面积。
甲乙丙15106、红、黄、绿三块同样大小的正方形纸片,放在一个正方形盒的底部,它们之间互相叠合(见图),知露在外面的部分中,红色面积是20,黄色面积是14,绿色面积是10,求正方形盒子底部的面积。
黄红绿7、如图所示,两个相同的直角三角形重叠在一起,求阴影部分的面积?AB F8、如图所示,平行四边形ABCD 的边BC 长10厘米,直角三形ECB 的直角边EC 长8厘米,已知阴影部分的面积比三角形EFG 的面积大10平方厘米,求平行四边形ABCD 的面积。
D五、练习:1、等腰直角三角形的面积是20平方厘米,在其中做一个最大的正方形,求这个正方形的面积。
2、如图所示,平行四边形ABCD的周长是75厘米,以BC为底的高是14厘米,以CD为底的高是16厘米,求平行四边形ABCD的面积。
AB C D14163、如图所示,在一个正方形水池的周围,环绕着一条宽2米的小路,小路的面积是80平方米,正方形水池的面积是多少?水池4、如图所示,一个长方形被一线段分成三角形和梯形两部分,它们的面积差是28平方厘米,梯形的上底长是多少?7105、如图所示,在三角形ABC中,BD=DF=FC,BE=EA,若三角形EDF的面积是1,则三角形ABC的面积是多少?AEB D CF6、一个长方形的周长是28厘米,如果它的长和宽分别增长3厘米,那么得到的新长方形比原来的面积增加了多少平方厘米?7、如图所示,四边形ABCD面积是1,将BA、CB、DC、AD分别延长一倍到E、F、G、H,连接E、F、G、H,问:得到的新四边形EFGH的面积是多少?A BCDEFGH8、如图所示,等腰直角三形ABC 的腰是10厘米,以C 为圆心、CF 为半径画弧线EF ,组成扇形C ,如果图中甲、乙两部分的面积相等,那么扇形所在的圆的面积是多少?甲乙A CEF9、如图所示,是两个相同的直角梯形重叠在一起,求阴影部分的面积?10、如图所示,扇形ABD 的半径是4厘米,甲比乙的面积大3.44平方厘米,求直角梯形ABCD 的面积?ABCD甲乙11、如图所示,三角形ABC ,D 、E 分别是所在边的中点,求四边形ADFE 的面积?A BC D E F82第四份卷 多边形的面积(二)二、例题1、求下图中阴影部分的面积。
多边形面积奥数题

人教版五年级上册数学第六单元《多边形面积》奥数题一.选择题1.一个梯形的上底、下底、高分别扩大2倍,它的面积扩大()倍。
A.2B.4C.6D.82.边长相等的小正方形拼成下面的图形,其中面积最小的是()。
3.一个梯形的上底4.4米,高10米,面积为55平方米.这个梯形的下底是(用方程解)()。
A.6.6米B.6米C.4.6米D.5米4.如下图,有两个面积相等的长方形,两个阴影部分的面积关系为()。
A.a>bB.a<bC.a=b5.一个正方形边长是6真米,如果把它的边长增加2厘米,则它的面积增加()。
A.4B.12C.28二.判断题1.n个同样的平行四边形一定能拼成一个较大的平行四边形。
()2.一个梯形的上底是6米,下底是8米,面积是42平方米,它的高是6米。
()3.面积大的三角形比面积小的三角形的底长些。
()4.同底等高的两个三角形,形状不一定相同,但它们的面积一定相等。
()5.把平行四边形木框拉成长方形,周长没变,面积变大了。
()三.填空题1.沿着平行四边形的一条高剪开,然后拼成一个长方形,这个长方形的长等于平行四边形的(),长方形的宽等于平行四边形的()。
因此,平行四边形的面积等于(),用字母表示是()。
2.一张平行四边形贺卡,底为5cm,高为2.6cm,这张贺卡的面积是()。
3.梯形的上底是4cm,下底是5.2cm,高是2.5cm,面积是()平方厘米。
4.如图的小花瓶中,1个小正方形的面积是1平方厘米,那么整个花瓶的面积是()平方厘米。
5.两个完全一样的梯形可以拼成一个()形。
1.计算下列图形的面积。
(单位:厘米)2.求下面图形涂色部分的面积。
(单位:厘米)五.作图题1.在下面的钉子图上画一个平行四边形、一个五边形和一个六边形。
1.如图是一块长方形草地,长16m、宽10m,中间有两条路,一条是平行四边(一边长2m),一条是长方形(宽2m)。
求草地的面积。
2.如图,这是一个铝合金框组成的鱼缸,侧面的每个面都是正方形,且边长为25厘米。
五年级奥数-图形周长及多边形面积计算(附答案)

数学学科教师辅导教案学员编号: 年 级:小五 课 时 数:学员姓名: 辅导科目:数 学 学科教师: 课程主题:图形的周长及多边形面积计算 授课时间:学习目标教学内容知识点一(图形的周长) 【知识梳理】【典型例题】例1. 求下列图形的周长。
(单位:厘米) (10+15)*2=50例2. 如图,在长方形ABCD 中,EFGH 是正方形,AH=12厘米,FC=10厘米。
求长方形ABCD 的周长。
C=(AD+CD)*2=(AH+HD+CD)*2=(AH+GC+FG)*2=(AH+FC)*2=(12+10)*2=44AB CDEF G H1015知识精讲例3. 如右图,把5个同样的小长方形拼成一个大长方形,已知小长方形的长是9cm ,拼成的大长方形的周长是多少厘米? ( 66 )例3. 如右图,七个相同的小长方形拼成了一个大长方形,已知大长方形的周长是68cm ,小长 方形的周长是多少厘米?( 28 )【同步练习】1、求下图的周长。
( 82 )2、如下图所示,长方形ABCD 中,AB=18cm ,截去正方形EBCF 后,求剩下的长方形AEFD 的周长。
( 36 )用四个一样的长方形和一个小正方形(如下图)拼成一个大正方形,大、小正方形的面积分别是64平分厘米和4平分厘米,长方形的长和宽各是多少厘米?( 5厘米,3厘米 )DA BCE F19 1304、如图是由两个相同的正方形和三个相同的长方形组成的,它的周长为104厘米,其中每个长方形的长都是宽的1.5倍,小长方形的周长是多少厘米?设小正方形的边长为a,得a为8(8+1.5*8)*2=405、求下图的周长。
(单位:分米)(64)6、如下图,一个正方形是由4个同样的长方形和一个小正方形拼成的,已知长方形的长是8厘米,小正方形的边长是3cm,求大正方形的周长。
( 52 )38210 20②①③知识点二(多边形面积计算) 【知识梳理】【典型例题】例题精讲例1. 已知正方形的对角线长10厘米,求正方形的面积。
五年级数学上册课件同步奥数培优多边形面积的计算(苏教版)共17张

它们的面积公式还记得吗?
长方形= 长×宽
S= ab
正方形= 边长×边长 S= a2
平行四边形= 底×高 S= ah
三角形= 底×高÷2 S= ah÷2
梯形
梯形= (上底+下底)×高÷2 S= (a+b)h÷2
2024/7/29
3
知道平行四边形的面积和高,底怎么去求? 底= 平行四边形面积÷高 高= 平行四边形面积÷底
空白的面积= 8×8÷2+(8+6)×6÷2=74(平方厘米)
阴影部分的面积= 正方形①②-空白 100-74=26(平方厘米)
2024/7/2答9 :阴影部分的面积是26平方厘米。
9、求右图中阴影部分的面积。(单位:厘米)
阴影部分怎样去求?
阴影部分是什么图形? 不规则图形 4 1
能直接求出吗?
视察:阴影部分和 空白部分有什么关系?
答:阴影部分的面积是30平方厘米。
6、下图长方形中,E,F分别是AD和DC的中点。已知AB=10厘米, BC=8厘米,那么阴影部分的面积是多少平方厘米?
D 1
8E 3
A
10 F
已知条件是什么? C AE=DE =8÷2=4(厘米) 2 DF=CF =10÷2=5(厘米)
S阴影= S总- S空白
B
长方形ABCD S①+S②+S③
A
D
1 8
E
2
B
C F6
排空法 尝试着自己做一下吧! S阴影= S总- S空白 100 S①7+0S②
S正方形ABCD=100平方厘米
正方形ABCD边长= 10厘米
S①: 8×10÷2=40(平方厘米) S②: 6×10÷2=30(平方厘米)
五年级奥数专题二十:多边形的面积

五年级奥数专题二十:多边形的面积关键词:多边正方面积边长周长多边形奥数正方形之和厘米我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算,图形及计算公式如下:正方形面积=边长×边长=a2,长方形面积=长×宽=ab,平行四边形面积=底×高=ah,圆面积=半径×半径×π=πr2,扇形面积=半径×半径×π×圆心角的度数÷360°在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲和后面的两讲中,我们将学习如何计算它们的面积。
例1小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出大正方形边长=(16+4)÷2=10(厘米),小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2如左下图所示,四边形ABCD与DEFG都是平行四边形,证明它们的面积相等。
分析与证明:这道题两个平行四边形的关系不太明了,似乎无从下手。
我们添加一条辅助线,即连结CE(见右上图),这时通过三角形DCE,就把两个平行四边形联系起来了。
在平行四边形ABCD中,三角形DCE的底是DC,高与平行四边形ABCD边DC上的高相等,所以平行四边形ABCD的面积是三角形DCE的两倍;同理,在平行四边形DEFG 中,三角形DCE的底是DE,高与平行四边形DEFG边DE上的高相等,所以平行四边形DEFG的面积也是三角形DCE的两倍。
苏教版五年级上册同步奥数培优 第三讲多边形的面积(等积变形)

苏教版五上同步奥数培优第三讲多边形的面积(等积变形)【知识概述】三角形面积的公式是底×高÷2,两个三角形只要是底和高分别相等,它们的面积就相等,而这两个三角形的形状不一定完全相同,例如,下面的两个三角形面积就是相等的。
在解答一些平面图形的面积4时,我们可以巧用等底等高两个三角形面积相等的方法来解答。
例题1:四边形ABCD中,M为AB的中点,N为CD的中点,如果四边形ABCD的面积是80平方厘米,求阴影部分BNDM的面积是多少平方厘米。
练习一:1.如图,六边形ABCDEF的面积是16平方厘米,M,N,P,Q分别是AB,CD,DE,AF的中点。
求图中阴影部分的面积。
2.如图,平行四边形的面积为50平方厘米,P是其中任意一点,求阴影部分面积。
3.如图,正方形的边长是6厘米,E,H是所在边的二等分点,F, G,L,M是所在边的三等分点,求阴影部分的面积和。
例2:如下图,三角形ABC为等边三角形,D为AB边上的中点。
已知三角形BDE的面积为5平方厘米。
求等边三角形ABC的面积。
练习二: 1.如图,平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,平行四边形的面积是多少平方厘米?2.如图,已知长方形ABCD,三角形ABG的面积为20平方厘米,三角形CDQ的面积为35平方厘米,求阴影部分的面积是多少平方厘米。
3.如图,在一个等边三角形中任意取一点P,连接PA,PB,PC,过P点作三角形三边的垂线,E,F,G分别为垂足。
三角形ABC被分成6个三角形。
已知三角形ABC的面积为40平方厘米,求图中阴影部分的面积。
例3:下图中正方形ABCD的边长是4厘米,长方形DEFG的长DG=5厘米,问长方形的宽DE为多少厘米?练习三:1.如图,两个相同的直角三角形叠放在一起,求阴影部分的面积。
(单位:分米)2.如图,ABCD为长方形,AB=10厘米,BC=6厘米,E,F分别为AB,AD的中点,且FG=2CGE。
(完整版)五年级奥数专题二十:多边形的面积

an dAl l t h i ng si nt he i rb ei n ga re g五年级奥数专题二十:多边形的面积关键词:多边 正方 面积 边长 周长 多边形 奥数 正方形 之和 厘米我们已经学习过三角形、正方形、长方形、平行四边形、梯形以及圆、扇形等基本图形的面积计算,图形及计算公式如下: 正方形面积=边长×边长=a 2, 长方形面积=长×宽=ab , 平行四边形面积=底×高=ah , 圆面积=半径×半径×π=πr 2,an dAl l t h i ng si nt he i rb ei n ga re go od fo r 扇形面积=半径×半径×π×圆心角的度数÷360° 在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲和后面的两讲中,我们将学习如何计算它们的面积。
例1 小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG 部分重合了。
用组合图形的周长减去DG ,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出 大正方形边长=(16+4)÷2=10(厘米), 小正方形边长=(16-4)÷2=6(厘米)。
e an dAl l t h i ng si nt he i rb ei n ga 两个正方形的面积之和减去三角形ABD 与三角形BEF 的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
例2如左下图所示,四边形ABCD 与DEFG 都是平行四边形,证明它们的面积相等。
苏教版五年级上册同步奥数培优 第二讲 多边形的面积 (面积计算)

苏教版五年级上册同步奥数培优第2讲多边形的面积(面积计算)知识概述:在数学课上我们已经掌提了几种基本图形的面积计算方法:正方形的面积=边长×边长,S=a²长方形的面积=长×宽,S=ab平行四边形的面积=底×高,S=ah三角形的面积=底×高÷2,S=ah÷2梯形的面积=(上底十下底)×高÷2,S=(a+b)h÷2由两个或多个简单的基本几何图形可以组合成一个组合图形、要计算一个组合图形的面积,就要根据图形的基本关系,运用分解、组合、平移、旋转、割补、添辅助线等几种方法来思考。
例1、已知平行四边形的面积是28平方厘米,求阴影部分的面积。
练习:1.下图的梯形中,阴影部分面积是150平方厘米,求梯形的面积。
2.已知平行四边形的面积是48平方厘米,求阴影部分的面积。
3.如果用铁丝固成如下图一样的平行四边形,需要用铁丝多少厘米?(单位:厘米)例2:下图中甲和乙都是正方形,求阴影部分的面积。
(单位:厘米)练习:1.求右图中阴影部分的面积。
(单位:厘米)2.求右图中阴影部分的面积。
(单位:厘米)3.如图所示,四边形ABCD是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积。
例3:如图所示,甲三角形的面积比乙三角形的面积大6平方厘米,求CE的长度。
练习:1.四边形ABCD是一个长为10厘米,宽为6厘米的长方形,三角形ADE的面积比三角形CEF的面积大10平方厘米。
求CF的长是多少厘米?2.平行四边形ABCD的底边长BC=10厘米,直角三角形BCE的直角边EC长8厘米,已知阴影部分的面积比三角形EFG的面积大10平方厘米。
求CF的长。
3.正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,求:(1)三角形DEF的面积; (2)CF的长例4:两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少。
小学奥数之多边形面积

组合图形是由两个或两个以上的简单几何图形组成,组合形式有两种:一是拼接组合,二是重叠组合。
要正确解答组合图形的面积应该注意以下几个点:1、切实掌握相关简单图形的概念、公式,牢固建立空间观念;2、仔细观察,认真思考,看清所求图形是哪几个基本图形组成的;3、适当采用增加辅助线解决问题;4采用割、补、分解、代换等方法,多角度去思考,把握整体和部分之间的关系,将复杂问题简单化。
例题1、小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
例题2、如左下图所示,一个腰长是20厘米的等腰三角形的面积是140厘米2,在底边上任意取一点,这个点到两腰的垂线段的长分别是a厘米和b厘米。
求a+b的长。
例题3、如左下图所示,三角形ABC的面积是10厘米2,将AB,BC,CA分别延长1倍到D,E,F,两两连结D,E,F,得到一个新的三角形DEF。
求三角形DEF的面积。
(若改为CA,AB,BC分别延长1,2,3倍到F,D,E,)例题4、一个正方形,将它的一边截去15厘米,另一边截去10厘米,剩下的长方形比原来正方形的面积减少1725厘米2,求剩下的长方形的面积。
例题5、两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积。
例题6、在右图中,平行四边形ABCD的边BC长10厘米,直角三角形ECB的直角边EC长8厘米。
已知阴影部分的总面积比三角形EFG的面积大10厘米2,求平行四边形ABCD的面积巩固1:在右图中,AB=8厘米,CD=4厘米,BC=6厘米,三角形AFB比三角形EFD的面积大18厘米2。
求ED的长。
例题8、左下图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积。
补充:梯形中的蝴蝶原理课后作业:1、下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积2、.如右图所示,一个长方形被一线段分成三角形和梯形两部分,它们的面积差是28厘米2,梯形的上底长是多少厘米?3、在下图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分别为6厘米、4厘米,DF的长是多少厘米?4下图是一块长方形公园绿地,绿地长24米,宽16米,中间有一条宽为2米的道路,求草地(阴影部分)的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十讲格点与切割
备考导航
格点面积及切割是竞赛考试的一个难点知识,本讲将学习形格点阵中多边形面积的计算公式,出现在各种形状的格点阵中的直线形的面积问题,以及借助构造格点阵求解的几何问题。
通过恰当地分割与拼补进行计算的面积问题。
利用格点求图形的面积有两种思路,一是直接将图形分成若干个面积单位,然后通过计算有多少个面积单位来求图形的面积;二是将某些图形转化成长方形的面积来求。
当然还可以将这两种方法结合起来,求出某些较复杂图形的面积。
格点面积公式=中间格点数+图形一周的格点数÷2﹢1
典型例题
【例1】图中相邻两格点问的距离均为1厘米,三个多边形的面积分别是多少平方厘米?
【例2】图中每个小形的面积均为2平方厘米,阴影多边形的面积是多少平方厘米?
【例3】如图所示,如果每个小等边三角形的面积都是1平方厘米,四边形ABCD和三角形EFG的面积分别是多少平方厘米?
【例4】如图所示,在形ABCD部有一个长方形EFGH,已知形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米。
求长方形EFGH的面积。
【例5】如图所示,大形的边长为10厘米。
连接大形的各边中点得到一个小形,将小形每边三等分,再将三等分点与大形的中心和一个顶点相连。
请问:图中阴影部分的面积总和等于多少平方厘米?
【例6】如图,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,求阴影部分的面积。
【例7】如图所示,正六边形ABCDEF的面积是6平方厘米,M是AB中点,N是CD 中点,P是EF中点。
请问:三角形MNP的面积是多少平方厘米?
【例8】已知大的正六边形面积是72平方厘米,按图中不同方式切割(切割点均为等分点),形成的阴影部分面积各是多少平方厘米?
小试身手
(1)下图是一个三角形点阵,其中能连出的最小的等边三角形的面积为l平方厘米。
三个多边形的面积分别为多少平方厘米?
(2)图中,五个小形的边长都是2厘米,求三角形ABC的面积
(3)如图,在两个相同的等腰直角三角形中各作一个形,如果形A的面积是36平方厘米,那么形B的面积是多少平方厘米?
星级挑战
(一)夯实基础★★★
1、图中相邻两格点问的距离均为l厘米,三个阴影图形的面积分别是多少平方厘米?
2、图中每个小形的面积是2平方厘米,阴影部分面积是多少平方厘米?
3、图中每个小正三角形的面积是4平方厘米,阴影部分面积是多少平方厘米?
4、图中每个小形的边长为1厘米,阴影部分的面积是多少平方厘米?
5、下图的数字分别表示对应线段的长度,试求这个多边形的面积。
(单位:厘米)
6、如图,形网格的总面积等于96平方厘米,求阴影图形的面积。
(二)冲刺名校★★★★
7、图中每个小形的边长为1厘米,阴影部分的面积是多少平方厘米?
8、下图为一个边长为2厘米的形,分别连接顶点与对应边中点。
围成的阴影部分的面积为多少平方厘米?
9、如图所示,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少平方厘米?(单位:厘米)
10、如图所示,这个多边形六条边的长度分别是1、2、3、4、5、7。
问:这个图形的面积最大可能是多少?
(三)勇夺冠军★★★★★
11、正三角形ABC的面积是1平方米,将三条边分别向两端各延长一倍,连结六个端
点得到一个六边形(如右图),求六边形的面积。
C
B A
12、下图是一个4×4的方格纸,请用六种不同的方法将它分割成完全相同的两部分,
但要保持每个小方格的完整。
本周作业或通知:
第十一讲 平面组合图形
备考导航
三角形、长方形、形、平行四边形、梯形、菱形、圆和扇形等图形被称之为基本图形或
规则图形。
由两个或多个简单的基本几何图形可以组合成一个组合图形,要计算组合图形的
面积,就要根据图形的基本关系, 常用的基本方法有:直接计算法、切割法、排空法、添
补法等。
典型例题
【例1】如果用铁丝围成如下图一样的平行四边形,需要用铁丝多少厘米?
【例2】图中的四边形均为形,按图中所示数据,(单位:厘米)求阴影部分的面积?
【例3】右图是两个相同的直角三角形叠在一起,求阴影部分的面积。
【例4】如下图,AB=14cm,BC=11cm,CD=11cm,AD=14cm ,点M到各边的距离都是4.5厘米,这个四边形面积是多少?
【例5】如图,是长方形与平行四边形组成的图形,阴影部分的面积是168平方厘米,则AB的长度为多少?
【例6】如图,平行四边形ABCD中,BC=10cm,直角三角形ECB的边EC=8cm,已知阴影部分的总面积比三角形EFG的面积大10cm2,求平行四边形ABCD的面积。
【例7】如图,三个边长为10,12,8的形拼在一起,直线CB将整个图形的面积平分,
求线段AB的长度?
【例8】在四边形ABCD中(见左下图),线段BC长6cm,∠ABC为直角,∠BCD 为135°,而且点A到边CD的垂线段AE的长为12cm,线段ED的长为5cm,则四边形ABCD的面积是平方厘米。
小试身手
(1)下图是一个五边形,已经AB=AE,BC=CD=8cm,∠A、∠C、∠D都是直角,求这个图形的面积。
(2)如图,三角形甲比三角形乙的面积多3cm2,那么a等于多少厘米?
(3)图中,有四条线段的长度已经知道,还有两个角是直角,那么四边形ABCD(阴影部分)的面积是多少?
星级挑战
(一)夯实基础★★★
1、王大伯利用一面墙围成一个鸡圈(如图)已知所用篱笆全长12m,请你帮王大伯算出这个鸡圈的面积是多少m2?
2、一个平行四边形的周长是74cm(如图),以CD为底时,它的高是18cm,BC是24cm,求它的面积?
3、求下列各图中阴影部分的面积。
(单位:厘米)
墙3m
鸡圈
4、如图,直角梯形ABCD 的周长为102cm ,高AD=10cm ,斜边BC=18cm ,求梯形ABCD 的面积。
5、下图是一块长方形草地,长方形的长是16,宽是10。
中间有两条道路,一条是长方形,一条是平行四边形,那么有草部分的面积(阴影部分)有多大?
6、下图中 ABCD 是 6×8的长方形,AF 长是4,求阴影部分三角形AEF 的面积。
(二)冲刺名校★★★★
7、求下面图形中梯形ABCD 的面积。
(单位:厘米)BC =8厘米,∠AED =90°
8、下图是一个平行四边形和一个长方形所组成的图形,数据如图所示,求阴影部分的面积? A B
D C A D
B E 3 5 4
9、四边形ABCD中,AC和BD互相垂直,AC=18厘米,BD=13厘米,求四边形面积。
10、下图ABCD为直角梯形,AB的长为10cm,求梯形的面积。
(三)勇夺冠军★★★★★
11、如图所示,直角三角形ABC由红、绿两个直角三角形和一个黄色长方形拼成。
AE=25cm,BF=20cm.问黄色的长方形的面积是多少平方厘米?
红4
绿黄
6
12、P是长方形ABCD一点,三角形PAB的面积等于5,三角形PBC的面积等于13.问三角形PBD的面积是多少?
数学乐园
隔壁分银
只闻隔壁客分银,不知人数不知银,
四两一份多四两,半斤一份少半斤。
试问各位能算者,多少客人多少银?本周作业或通知:。
