Random Walk Definition - Boston University随机游走的定义-波士顿大学
效率场假说与随机漫步

效率市场假说与随机漫步在理解效率市场时要防止两个极端。
一个极端是把效率市场等同于平稳的市场。
在有些人的印象中,在半强式效率市场中,证券价格等于证券价值,因此证券价格的变动应该是有秩序的、平稳的。
实际上,由于没有人能准确地找出证券价值,而只能根据现有的信息对其进行判断或预期,而这种预期又取决于有关公司未来的现金流、投资者的风险厌恶度、投资机会等方面的信息。
由于利好或利空信息的出现总体上说带有很大的随机性,因此股价的变动在很大程度上也是随机的。
以世界上效率程度最高的美国股票市场为例,受利好或利空消息的影响,一天之内涨跌超过20%,甚至超过40%的股票并不是罕见的。
例如,2001年9月17日,美国股市在美国遭受恐怖主义袭击而关闭4天重新开盘后,美国航空公司因有两架被劫持客机撞上纽约世贸大楼, 其股价在开盘半小时之内就暴跌了46.43%, 这并不是美国股市投机性强的表现,而恰恰是其效率高的表现。
因此,我们不能简单地以股价是否稳定作为判断股市是否有效的标准,而要看这种波动是由于市场操纵引起的还是由于市场由于新信息的出现而对股票价值的判断变化引起的。
另一个极端是把效率市场等同于随机漫步(Random Walk )。
随机漫步理论的鼻祖是法国数学家巴契利尔(Bachelier ),后来因萨缪尔森(Samuelson )的著名论文“适当预期的价格随机波动的证据”而几乎成了效率市场假说的代名词。
随机漫步理论认为,证券价格的变动是完全不可预测的。
随机漫步可以用公式(1)表示:t t t S S ε=--1ln ln (1)其中S 表示证券价格, εt 表示随机误差项,它是个鞅过程,即0)|(1=-t t I E ε,1-t I 表示时刻t-1的信息集合。
在公式(1)中用证券价格(S t )的自然对数而不是用证券价格本身可以保证不会出现证券价格为负的情况,从而可以避免有限责任问题。
t t t-1t-1lnS lnS lnS lnS -=表示以连续复利表示的证券收益率。
医学网络平台分析 随机游走

Random Walk是扩散过程的基础,因此它被广 泛地用于对物理和化学等扩散现象的模拟上。
在应用数学上,Random Walk是利用随机因 素模拟真实的动力系统的常用方法。图 (a)和 (b)分别显示的是Random Walk在二维和三维 空间的模拟图。
此外,Random Walk又是设计随机算法的一 个非常广泛的工具,其中一个典型的例子就是 “马尔可夫链蒙特卡罗”法(MCMC)。 MCMC是解决近似计算问题一种重要方法,它能 以比确定性算法快指数级的速度提供解决问题的 最好随机方法,目前已经被广泛地应用在统计领 域。
W:图的列向量归一化的邻接矩阵。 P0:初始概率向量,对于每一个种子结点,以相
等的概率分配,向量中各元素之和为1。
r:游走者返回种子结点的概率(重启动概率), r的值越接近于0,表示随机游走方法考虑图的
全局结构特征越多。
P t 1
0
t
t
t
t
5 0.1 * P5 0.9 * P8 * (1 / 4) 0.9 * P6 * (1 / 2) 0.9 * P7 * (1 / 2) 0.9 * P4 * (1 / 3)
随后,Brin 和Page 利用PageRank 技术成 立了Google 公司,而今天Google已经在人们 的日常生活中显示出巨大影响,所以可以毫不 夸张地说Random Walk改善了今天的生活。下 图为PageRank 的一般描述示意图,边上显示 的是转移概率,而网页上除了ID 外显示的是页 片的Rank 值。
这里我们给出一些可以参考的理论著作:一 个比较好的关于图上的Random Walk 的理论 研究综述是由Lovász 给出的;
Lovász, L, Random walks on graphs: a survey. In Combinatorics, Paul Erdos is eighty, Vol.2, pp. 353–397, 1993.
随机漫步法则 -回复

随机漫步法则-回复什么是随机漫步法则?随机漫步法则(Random Walk Theory)是一种数学模型,用于描述一个物体在随机不规则的方向上移动的趋势。
这一概念最早于1900年由法国数学家路易斯·巴舍利耶(Louis Bachelier)提出,后来由肖尔测试(Maurice Kendall)和彼得·斯帕卡(Peter Whittle)等学者进一步发展和应用。
随机漫步法则的基本假设是,物体在每一步中的移动是完全随机的,不受任何外部因素的限制或干扰,且每一步的移动都是独立的。
换句话说,物体在下一步的移动方向和距离与前一步的移动无关,完全由随机因素决定。
因此,随机漫步被认为是一种无记忆性的行为。
随机漫步的应用领域广泛。
在金融领域,随机漫步法则被用来模拟股票市场中的价格波动。
根据随机漫步的理论,股票价格的变动是无法预测的,其未来的走势与过去的走势无关。
在自然科学领域,随机漫步法则被用来解释分子的扩散行为、人口迁移模式等现象。
随机漫步法则有几个基本特征。
首先,随机漫步的路径通常是不规则的,例如,一个随机漫步者在一个广场上可能会呈现一条曲线状的路径。
其次,随机漫步的路径长度可能非常不稳定,有时会是短程的,有时则会是长程的。
最后,随机漫步的路径通常是对称的,也就是说,沿某一特定方向的移动与沿相反方向的移动是等可能发生的。
随机漫步法则也具有一些局限性。
首先,它忽略了物体内部的结构和作用力的影响,只关注移动的随机性。
因此,在某些情况下,随机漫步的模型可能无法准确描述物体的移动。
其次,由于随机漫步是基于概率的,它不能提供确定性的预测,只能给出可能的结果。
虽然随机漫步法则并不能解决一些具体问题,但它在许多领域中被广泛使用,并且具有重要的意义。
它为研究随机过程、模拟和估计提供了理论基础,对于理解和解释一些看似随机的现象是非常有帮助的。
此外,随机漫步法则也为其他更复杂的模型和理论提供了参考和基础。
总结起来,随机漫步法则是一种数学模型,用来描述一个物体在随机的方向上移动的趋势。
随机漫步理论

随机漫步(Random Walk)思想最早由 Karl Pearson在1905年提出,它是一种不规则的变动形式,在变动过程当中的每一步都是随机的。
通常来说,随机漫步被假定为具有马尔可夫链的性质,也即是每一个步骤具有“无记忆”的特性,换句话说,每一次变动都不会影响别的变动。
除此之外,还有许多更加复杂的随机漫步。
在维度方面,随机漫步处于图和面上,或者维度更多的结构中,例如群。
如果考虑到时间参数,一些随机漫步过程是标记为非连续时间,例另一些随机漫步过程则采用随机时间,例如X t,并且作为连续时间段;这样的例子包括drunkard's walk和Lévy flight等等。
随机漫步过程通常与扩散模型和马尔可夫过程相联系,它的一些性质,例如dispersal distributions, first-passage times 和 encounter rates, 已经得到了非常深入的研究。
一维随机漫步这是一个简单的随机漫步例子,它的特征是每次变化的“量”是一个整数,从零开始,每一步变化记作+1或者-1。
下面的图采用一个例子,根据掷硬币来产生随机步骤,头像记作1,背面记作-1:掷5次后的最终位置如上所示。
但是如果我们想比较正式地定义这个过程,我们可以首先认为不同的时间点(上例中为每次掷硬币)为一个整数线,然后我们确立一系列独立随机变量:每一个变量均有50%的概率值为1或者-1,如上所述,我们可以得到:分别表示初始位置为0,以及中间某一位置为前面所有步骤变化量的总和。
于是,集合可以称为在上的简单随机漫步。
该集合是所以1和-1的相加,并计算出漫步距离。
的期望值为0,也即是说,如果掷硬币的次数增加,每次掷硬币所得到的值的平均数会趋向于0,有限次数相加的期望值为:考虑到,变换成另一个类似的计算公式则为:这样显示了在n次漫步后,期望的转换距离为,大约为。
事实上,我们能够知道:如果允许无数次随机漫步,整个过程设定的边界能够有多少次会被经过?在上的简单随机漫步能够在无限次数中经过所有的点,这样的过程有不同的名字 level-crossing phenomenon, recurrence或者the gambler's ruin。
第六讲-有效市场假说

– 利用基本面分析的相关信息进行检验 – 市场异象:市盈率、小公司效应、账面-市值比 – 收益公告后的价格变化趋势 – 对半强式EMH的检验还没有取得一致意见!
29
三、市场有效性检验(续)
小 公 司 效 应
30
-
三、市场有效性检验(续)
账 面 市 值 比 效 应
31
13
一、随机漫步(续)
• 问题:为什么说股市随机漫步体现了市场 有效性?
• 市场竞争越充分,投资分析越深入,信息 扩散越快速,股市越呈现为随机漫步!
14
一、随机漫步(续)
• 据此可将有效市场假说(EMH)分为三种 形式
弱有效形式 半强有效形式 强有效形式
15
二、有效市场假说的含义
• 技术分析:寻找股价的周期变化特征和预 测模式
• 技术分析成功的关键是机敏地发现股票向 新的均衡调整的动力,并充分利用这一调 整的时间差获得投资机会
– 例:量化投资、统计套利、趋势分析、均值回 复等等
44
五、技术分析(续)
• 在很多方面,技术分析的基本假设和理论 基础与行为金融相通
– 如:“过度反应”导致的均值回复效应、“处 置效应”导致的动量效应等等
56
二、债券的收益率(续)
• 实现复利收益率
• 如果每期息票支付的 再投资收益率不同于 到期收益率,那么, 投资于该债券最终实 现的收益率也不同于 到期收益率(参见 p297,例14-5)
57
二、债券的收益率(续)
– 1、没有告诉人们如何利用市场非理性获利 – 2、研究方法过于松散,缺乏理论体系,过于经
验导向(如:强调实验方法!) – 3、行为学者们用于解释异常现象的非理性观点
Random Walk Definition - Boston University随机游走的定义-波士顿大学

Almost there
• A strong component of a directed graph G is a subgraph C of G where for each edge eij there is a directed path from i to j and from j to i.
Markov Chain Definitions
• Define vector qt (q1t,q2 t, ,qn t) • where the i-th entry is the probability that
the chain is in state t
• Note: qt1 qt P
fij
r(t) ij
t0
• Consider how many steps to get from state i
to j. hij tri(jt) given fij 1 hij ,otherwise t0
Even More Definitions
• Consider fii • State i is called transient fii < 1 • State i is called persistent if fii = 1 • If state i is persistent and hii is infinite then i
• Next move does not depend on previous moves, formally
P X t 1 r j |X 0 [ i 0 , X 1 i 1 ,X . t . i ] . P X , t 1 r j |X t [ i ] P ij
随机游走

随机游走本来是“物理上布朗运动”相关的分子,还是微观粒子的运动形成的一个模型。
现在过多的谈到随机游走假说是数理金融中最重要的假设,它把有效市场的思想与物理学中的布朗运动联系起来,由此而来的一整套的随机数学方法成为构建数理金融的基石。
(其研究的机理已经在股票研究中应用很广泛)编辑本段何谓随机游走?“随机游走”(random walk)是指基于过去的表现,无法预测将来的发展步骤和方向。
这一术语应用到股市上,则意味着股票价格的短期走势不可预知,意味着投资咨询服务、收益预测和复杂的图表模型全无用处。
在华尔街上,“随机游走”这个名词是个讳语,是学术界杜撰的一个粗词,是对专业预言者的一种侮辱攻击。
若将这一术语的逻辑内涵推向极致,便意味着一只戴上眼罩的猴子,随意向报纸的金融版面掷一些飞镖,选出的投资组合就可与投资专家精心挑选出的一样出色编辑本段随机游走模型随机游走模型的提出是与证券价格的变动模式紧密联系在一起的。
最早使用统计方法分析收益率的著作是在1900年由路易·巴舍利耶(Louis Bachelier)发表的,他把用于分析赌博的方法用于股票、债券、期货和期权。
在巴舍利耶的论文中,其具有开拓性的贡献就在于认识到随机游走过程是布朗运动。
1953年,英国统计学家肯德尔在应用时间序列分析研究股票价格波动并试图得出股票价格波动的模式时,得到了一个令人大感意外的结论:股票价格没有任何规律可寻,它就象“一个醉汉走步一样,几乎宛若机会之魔每周仍出一个随机数字,把它加在目前的价格上,以此决定下一周的价格。
”即股价遵循的是随机游走规律。
随机游走模型有两种,其数学表达式为:Y t =Y t-1 +e t ①Y t =α+Y t-1 +e t ②式中:Y t 是时间序列(用股票价格或股票价格的自然对数表示); e t 是随机项,E(e t )=0;Var(e t )=σ 2 ;α是常数项。
模型①称为“零漂移的随机游走模型”,即当天的股票价格是在前一天价格的基础上进行随机变动。
Random Walk Definition - Boston University随机游走的定义-波士顿大学共36页

Questions
• How many steps to get from u to v • How many steps to get back to initial node • How many steps to visit every node • Easy questions to answer if we consider a
• Define vector qt (q1t,q2 t,,qn t) • where the i-th entry is the probability that
the chain is in state t
• Note: qt1 qt P
• Notice that we can then calculate everything given q0 and P.
• Expected number of steps to visit every
node in a regular graph is
n1
(n 1)1/ i
i1
Triangle Example
Vo (1, 0, 1/2, 1/4, ... )
V1 (1/2, 0, 1/4, 3/8, ...)
V2 (1/2, 0, 1/4, 3/8, ...)
simple example
Regular Gumber of steps to get from vertex u to v in a regular graph is n-1,
• The expected number of steps to get back to starting point is n for a regular graph.
Transition Matrix
马尔可夫链蒙特卡洛方法中的随机漫步尺度调整技巧(四)

马尔可夫链蒙特卡洛方法中的随机漫步尺度调整技巧马尔可夫链蒙特卡洛方法(MCMC)是一种重要的统计学习方法,广泛应用于贝叶斯推断、机器学习和大数据分析等领域。
在MCMC方法中,随机漫步(Random Walk)是一种常用的采样算法,而随机漫步的尺度调整技巧则是保证算法收敛性和采样效率的重要手段。
一、随机漫步的基本原理随机漫步是一种基于概率的随机移动方式,其核心思想是在当前位置附近随机选择一个新的位置,并以一定的概率接受这个新位置作为下一步的移动位置。
在MCMC方法中,随机漫步被应用于参数空间的遍历和采样,通过不断地在参数空间中进行随机移动,最终收敛到目标分布。
在随机漫步的过程中,尺度的调整是至关重要的。
尺度过大会导致接受概率过低,采样效率低下;尺度过小则会导致在参数空间中长时间徘徊,同样会影响采样效率。
因此,如何合理地调整随机漫步的尺度成为了MCMC方法中的一个重要问题。
二、随机漫步尺度调整技巧1. 自适应尺度调整自适应尺度调整是一种常见的随机漫步尺度调整技巧。
在这种技巧中,随机漫步的尺度会随着采样的进行而自动调整。
具体而言,可以根据接受率来动态地调整尺度大小,以保证接受率在一个合理的范围内。
这样的方法能够有效地平衡随机漫步的探索性和利用性,提高采样效率。
2. 方差调整在一些MCMC算法中,如Metropolis-Hastings算法,参数空间中的随机漫步是通过一个高斯分布来实现的。
在这种情况下,可以通过调整高斯分布的方差来控制随机漫步的尺度。
通常情况下,可以根据接受率来动态地调整高斯分布的方差,以保证接受率的稳定性。
这种方法简单有效,易于实现。
3. 多尺度随机漫步在一些复杂的参数空间中,不同方向上的尺度可能存在差异。
因此,可以考虑使用多尺度随机漫步技巧,即在不同方向上采用不同的尺度来进行随机漫步。
这样的方法能够更好地适应参数空间的结构,提高采样效率。
三、随机漫步尺度调整技巧的应用随机漫步尺度调整技巧在MCMC方法的各个领域都有着广泛的应用。
随机游走

RMR实例
随机游走概述
一维随机游走
一维随机游走
上述问题可以用杨辉三角来看:
当n趋于无穷的时候,就可以与中心极限定理相联系
一维随机游走模拟结果图:
高维随机游走模拟
二维模拟:
一个25000步伐的二维随机游走
三维模拟:
高斯随机游走
带重启的随机游走(RWR)
• Random walk with restart :从一个节点开始,在每一步游 走时面临两个选择:或者移动到一个随机选择的邻点;或 者跳回起点。 • RWR最初是为图像分割而提出的一个算法,它反复的探究 一个网络的总体结构去估计两个节点之间的亲和力程度 (亲和力分数),这个算法只考虑一个参数 r :“重启概率” (1-r的概率移动到某个邻点) 这个过程反复迭代进行下去直到走遍所有节点,此时得到的 概率向量包含所有节点与起点的亲和力分数。 另外,RWR的起点也可以选择一个起点集合(多个起点组成 的集合)。
随机游走(Random Walk)
问题直观:
• 有个醉汉走在回家路上,由于酒醉未醒,分不清家往哪边走。假如 家在东面n的位置,醉汉处在m(m<n)位置。醉汉每一个时间单位 走一步,向东(家的方向)或者向西(酒吧的方向)的概率皆为 1/2。 这个醉汉的行为就可用random walk 来模拟。
ห้องสมุดไป่ตู้
这是一个简单的一维随机游走问题模型,从这个模型中我们可以对随机游走 有一个直观上的感受:每一步都是随机的。
什么是随机游走
随机游走是由一系列随机步伐(steps)所形成的活动模型。 比如: 液体或空气中分子的运动; 动物的觅食; 股票的价格波动; 一个赌徒的财产状况… 这些都可以模型为random walks(尽管现实中他们可能不是真 正的随机) • Karl Pearson在1905年第一次提出了random walk,如今已被应 用在诸多领域:生态学、经济学、心理学、计算机科学、物 理学、化学、生物学等。
Random Walk Definition - Boston University随机游走的定义-波士顿大学

1i n, i 0
– for 1i n, fii1anhd ii1/i
– Given N(i,t) number of time chain visits state i in t steps
V2 (1/2, 0, 1/4, 3/8, ...)
• Consider probabilities of being at a particular vertex at each step in walk.
• Each of these can be consider a vector,
V (1 ,o 0 ,0 )V , (1 1 /2 ,1 /4 ,1 /4 ),...
Almost there
• A strong component of a directed graph G is a subgraph C of G where for each edge eij there is a directed path from i to j and from j to i.
• Notice that we can then calculate everything given q0 and P.
More Definitions
• Consider question where am I after t steps, define t-step probability P i(tj)PX rt[j|X oi]
• We can express hitting time in terms of
commute time as
随机游走模型(RandomWalkMobility)
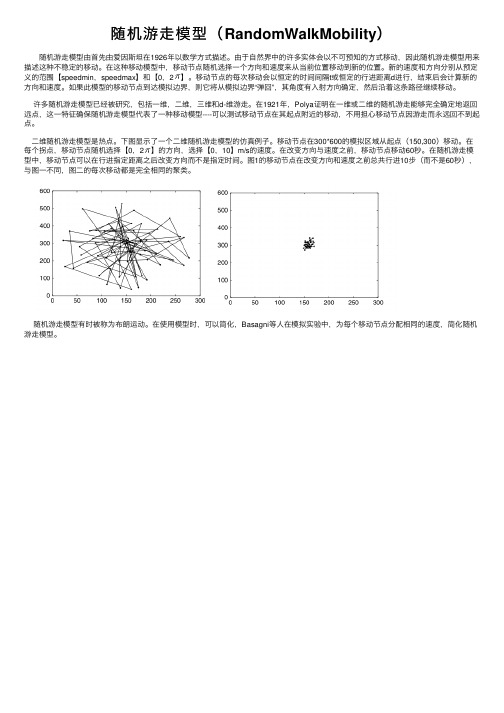
随机游⾛模型(RandomWalkMobility)随机游⾛模型由⾸先由爱因斯坦在1926年以数学⽅式描述。
由于⾃然界中的许多实体会以不可预知的⽅式移动,因此随机游⾛模型⽤来描述这种不稳定的移动。
在这种移动模型中,移动节点随机选择⼀个⽅向和速度来从当前位置移动到新的位置。
新的速度和⽅向分别从预定义的范围【speedmin,speedmax】和【0,2】。
移动节点的每次移动会以恒定的时间间隔t或恒定的⾏进距离d进⾏,结束后会计算新的⽅向和速度。
如果此模型的移动节点到达模拟边界,则它将从模拟边界“弹回”,其⾓度有⼊射⽅向确定,然后沿着这条路径继续移动。
许多随机游⾛模型已经被研究,包括⼀维,⼆维,三维和d-维游⾛。
在1921年,Polya证明在⼀维或⼆维的随机游⾛能够完全确定地返回远点,这⼀特征确保随机游⾛模型代表了⼀种移动模型----可以测试移动节点在其起点附近的移动,不⽤担⼼移动节点因游⾛⽽永远回不到起点。
⼆维随机游⾛模型是热点。
下图显⽰了⼀个⼆维随机游⾛模型的仿真例⼦。
移动节点在300*600的模拟区域从起点(150,300)移动。
在每个拐点,移动节点随机选择【0,2】的⽅向,选择【0,10】m/s的速度。
在改变⽅向与速度之前,移动节点移动60秒。
在随机游⾛模型中,移动节点可以在⾏进指定距离之后改变⽅向⽽不是指定时间。
图1的移动节点在改变⽅向和速度之前总共⾏进10步(⽽不是60秒),与图⼀不同,图⼆的每次移动都是完全相同的聚类。
随机游⾛模型有时被称为布朗运动。
在使⽤模型时,可以简化,Basagni等⼈在模拟实验中,为每个移动节点分配相同的速度,简化随机游⾛模型。
随机游走PPT课件

这个过程反复迭代进行下去直到走遍所有节点,此时得到的 概率向量包含所有节点与起点的亲和力分数。
另外,RWR的起点也可以选择一个起点集合(多个起点组成 的集合)。
随机游走(Random Walk)
问题直观:
•有个醉汉走在回家路上,由于酒醉未醒,分不清家往哪边走。假如家 在东面n的位置,醉汉处在m(m<n)位置。醉汉每一个时间单位走一 步,向东(家的方向)或者向西(酒吧的方向)的概率皆为1/2。 这 个醉汉的行为就可用random walk 来模拟。
这是一个简单的一维随机游走问题模型,从这个模型中我们可以对随机游走 有一个直观上的感受:每一步都是随机的。
.2ຫໍສະໝຸດ 随机游走概述 •.3
一维随机游走 •
.
4
一维随机游走
上述问题可以用杨辉三角来看:
当n趋于无穷的时候,就可以与中心极限定理相联系
一维随机游走模拟结果图:
.
5
高维随机游走模拟
二维模拟:
一个25000步伐的二维随机游走
三维模拟:
.
6
高斯随机游走 •
.
7
带重启的随机游走(RWR)
•Random walk with restart :从一个节点开始,在每一步游走 时面临两个选择:或者移动到一个随机选择的邻点;或者跳 回起点。
.
8
RMR实例 •
.
9
.
1
什么是随机游走
随机游走是由一系列随机步伐(steps)所形成的活动模型。 比如: 液体或空气中分子的运动; 动物的觅食; 股票的价格波动; 一个赌徒的财产状况…
随机漫步指标

随机漫步指标随机漫步指标是一种技术分析工具,用于预测股票价格趋势的变化。
该指标基于假设,即股票价格的变化是随机的,没有任何规律可言。
但是,该工具通过对价格变化进行统计分析,可以识别出趋势和反转点。
本文将详细介绍随机漫步指标的定义、计算方法、应用场景以及优缺点。
一、定义随机漫步指标(Random Walk Index)又称为RWI指标,它是通过比较当前价格与过去一段时间内的平均价格之间的差异来判断市场趋势是否转向的技术分析工具。
该指标基于假设,即股票价格在短期内是无规律波动的。
二、计算方法1. 计算真实波幅(TR)TR = MAX(High, PrevClose) - MIN(Low, PrevClose)其中High表示当日最高价,Low表示当日最低价,PrevClose表示前一日收盘价。
2. 计算随机漫步值(RWI)RWI = (Close - Avg) / TR其中Close表示当日收盘价,Avg表示过去N天内收盘价的平均值,N为用户自定义参数。
3. 计算随机漫步平均值(RWA)RWA = MA(RWI, M)其中MA表示移动平均线,M为用户自定义参数。
三、应用场景随机漫步指标主要用于判断市场趋势的转向和反转点的位置。
当RWI 值超过一定阈值时,意味着市场处于超买或超卖状态,可能会出现价格反转的机会。
此外,随机漫步指标还可以与其他技术分析工具结合使用,如移动平均线、相对强弱指数等。
四、优缺点1. 优点(1)随机漫步指标可以有效地识别市场趋势的转向和反转点。
(2)该指标计算简单,易于使用。
(3)随机漫步指标可以与其他技术分析工具结合使用,提高预测准确率。
2. 缺点(1)随机漫步指标只能适用于短期交易,无法预测长期趋势。
(2)该指标容易受到噪声干扰,需要结合其他技术分析工具进行综合分析。
(3)由于该指标基于假设,即股票价格变化是随机的,因此可能存在误判情况。
五、总结随机漫步指标是一种有效的技术分析工具,可以用于预测股票价格趋势的变化。
有效市场和投资者理性

有效市场假设的几种形式 (教材P295)
• 有效资本市场下的证券市场
证券价格曲线上任一点的价格均真实、准确地反映了 该证券及其发行人在该时点的全部信息。
1,根据有效资本市场理论,在一个有效的证券市场上,
的证券的实际价格,都应全面反映该证券的价值。
2,如果证券市场是有效的,则任何一个在该市场上交易
所谓有效,是指价格对信息的反映具有高效率,这种高效率不 仅指价格对信息反映的速度,还包括价格对信息反映的充分性 和准确性。
• 半强式有效假定
• 强式有效假定
一个市场是强有效的,如果价格反应了所有的信息,不管是公共的、私有的。 股价反映了全部与公司有关的信息,甚至包括仅为内幕人士所知道的信息。 意义和价值 在于从理论上确定理想市场的标准,为内幕交易的违法性提供理论上的根据。 强式有效假定是一种理想状态!
• Fama 的有效市场模型
‣ 大众已知的投资策略不能产生超额利润。 某些业绩表现突出的投资者仅仅是运气(因为公平赌局),过去的业绩不能代表将来。 ‣内幕信息往往不是内幕。 信息是否有用取决于是否真实,以及多少人知道。跟庄无效! ‣不应对有效市场的理论过分教条,而认为努力研究是不必要的。 ‣结论:市场有效,但创造性的工作会有应得到的报酬!
第二部分 资本资产定价-风险与收益的匹配
市场的有效性与投资者理性 资产组合原理 资本资产定价模型 因素模型 套利定价理论
02
有效市场的含义
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
define matrix M = DA
0 1/ 2 1/ 2
• For triangle d(i) = 2 so M = 1/ 2
0
1
/
2
1 / 2 1 / 2 0
• Note for triangle Pr[a to b] = Pr[b to a]
Markov Chains - Generalized Random Walks
• Notice the periodicity is the gcd of all cycles in G - closed walk
– Smallest walk is 2 go one step and come back – Since G is non-bipartite then there is odd length
Random Walks
Ben Hescott CS591a1
November 18, 2019
Random Walk Definition
• Given an undirected, connected graph G(V,E) with |V| = n, |E| = m a random “step” in G is a move from some node u to a randomly selected neighbor v. A random walk is a sequence of these random steps starting from some initial node.
then
N(i,t) lim t t
i
Random Walk is a Markov Chain
• Consider G a connected, non-bipartite, undirected graph with |V| = n, |E| = m. There is a corresponding Markov Chain
• A Markov Chain is a stochastic process defined on a set of states with matrix of transition probabilities.
• The process is discrete, namely it is only in one state at given time step (0, 1, 2, …)
• Consider probabilities of being at a particular vertex at each step in walk.
• Each of these can be consider a vector,
V (1 ,o 0 ,0 )V , (1 1 /2 ,1 /4 ,1 /4 ),...
• An ergodic Markov Chain is one where all states are aperiodic and non-null persistent
Fundamental Theorem of Markov Chains
• Given any irreducible, finite, aperoidic Markov Chain then all of the following hold
Clique n/2 nodes
n/2 node tail
• Here h u vO (n3)buh vt uO (n2)
Cover Time
move
Questions
• How many steps to get from u to v • How many steps to get back to initial node • How many steps to visit every node • Easy questions to answer if we consider a
to j. hij tri(jt) given fij 1 hij ,otherwise t0
Even More Definitions
• Consider fii • State i is called transient fii < 1 • State i is called persistent if fii = 1 • If state i is persistent and hii is infinite then i
• Define vector qt (q1t,q2 t, ,qn t) • where the i-th entry is the probability that
the chain is in state t
• Note: qt1 qt P
• Notice that we can then calculate everything given q0 and P.
More Definitions
• Consider question where am I after t steps, define t-step probability P i(tj)PX rt[j|X oi]
• Question is this my first time at node j?
– The chain is ergodic – There is a unique stationary distribution where for
1i n, i 0
– for 1i n, fii1anhd ii1/i
– Given N(i,t) number of time chain visits state i in t steps
• Expected number of steps to visit every
node in a regular graph is
n1
(n 1)1/ i
i1
Triangle Example
Vo (1, 0, 1/2, 1/4, ... )
V1 (1/2, 0, 1/4, 3/8, ...)
V2 (1/2, 0, 1/4, 3/8, ...)
• Next move does not depend on previous moves, formally
P X t 1 r j |X 0 [ i 0 , X 1 i 1 ,X . t . i ] . P X , t 1 r j |X t [ i ] P ij
Markov Chain Definitions
• Consider states of chain to be set of vertices
• Define transitional matrix to be
1/d(u) (u,erwise
Interesting facts
• MG is irreducible since G is connected and undirected
Almost there
• A strong component of a directed graph G is a subgraph C of G where for each edge eij there is a directed path from i to j and from j to i.
simple example
Regular Graphs
• The expected number of steps to get from vertex u to v in a regular graph is n-1,
• The expected number of steps to get back to starting point is n for a regular graph.
Hitting Time
• Generally hij, the expected number of steps needed before reaching node j when starting
from node i is the hitting time.
• The commute time is the expected number of steps to reach node j when starting from i and then returning back to i. Cuvhuvhvu
is null-persistent
• If state i is persistent and hii is not infinite then i is non-null-persistent
• Turns out every Markov Chain is either transient or non-null-persistent
cycle – GCD is then 1 so MG is aperiodic
Fundamental Theorem Holds
• So we have a stationary distribution, P =
• But Pvv P uvu
uv
• Good news, u d(u)2m
• Also get hii1u2md(u)
5
43
6
2
1 G
Points to note
• Processes is discrete • G is not necessarily planar • G is not necessarily fully connected • A walk can back in on itself • Can consider staying in same place as a
• A Markov Chain is irreducible if underlying graph G consists of a single strong component.
