数电习题解答 第1章
数电习题解(1-2章)

数电习题解答(1,2章)第一章数制与码制(教材p17)题1.2 将下列二进制整数转换为等值的十进制数。
(3)(10010111)2=1×27+1×24+1×22+1×21+1×20=151题1.4 将下列二进制数转换为等值的十进制数。
(2)(110.101)2=1×22+1×21+1×2-1+1×2-3=6.625题1.4 将下列二进制数转换为等值的八进制数和十六进制数。
(3)(101100.110011)2=(54.63)8, (101100.110011)2=()16题1.6 将下列十六进制数转换为等值的二进制数。
(2)(3D.BE)16=(111101.10111110)2题1.8将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后8位有效数字。
(2) (0.251)10≈(0.01000000)2=(0.40)16题1.9将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后4位有效数字。
(1) (25.7)10≈(11001.1011)2=(19.B)16题1.10 写出下列二进制数的原码、反码和补码。
(2) (+00110)2(+00110)原=000110, (+00110)反=000110, (+00110)补=000110.(3) (-1101)2(-1101)原=11101, (-1101)反=10010, (-1101)补=10011.题1.11 写出下列带符号位二进制数(最高位为符号位)的反码和补码。
(2) (001010)2(3) (111011)2(001010)2反码: 001010 , (001010)2补码: 001010(111011)2反码:100100, (111011)2补码:100101题1.12 用8位的二进制数补码表示下列十进制数。
数字电子技术答案 第1章 逻辑代数基础习题解答

X Y Z
F
图1.28 习题1-2(1)逻辑图
解:
X Y Z
00001111 00110011 01010101
00001111 11001100
11001111 01000101 01010101 00100000 01100101 F
11110000 00110011 10101010
真值表 X 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
CD AB 00 01 11 10 00 1 0 0 1 01 0 0 0 0 11 0 0 1 1 10 1 0 0 1
1-5 以卡诺图法化简下列函数,写成或-与表达式的形式。 (1) F AB (C D) A B DC 解: F (C D)( A C )( A D)( B D)( B C )
图1.29 习题1-2(6)的卡诺图
真值表 A 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 B 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 C 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 0
(2) F
A, B , C
m(1,2,5,7)
真值表 A 0 0 0 0 1 1 1 1 B 0 0 1 1 0 0 1 1 C 0 1 0 1 0 1 0 1 F 0 1 1 0 0 1 0 1
(3) F
W , X ,Y , Z
M (2,3,6,7,10,12)
真值表 W 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 X 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 Y 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 Z 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 F 1 1 0 0 1 1 0 0 1 1 0 1 0 1 1 1
数电--数电习题答案

数电--数电习题答案-CAL-FENGHAI.-(YICAI)-Company One1第1章习题答案1-1.按照集成度分类,试分析以下集成器件属于哪种集成度器件:(1)触发器;(2)中央处理器;(3)大型存储器;(4)单片计算机;(5)多功能专用集成电路;(6)计数器;(7)可编程逻辑器件。
解:(1)小规模;(2)大规模;(3)超大规模;(4)超大规模;(5)甚大规模;(6)中规模;(7)甚大规模。
1-2.将下列十进制数转换为二进制数、八进制数和十六进制数。
(1)45(2)78(3)(4)(5)65 (6)126解:(1)(45)10=(101101)2=(55)8=(2D)16(2)(78)10=(1111000)2=(170)8=(78)16(3)10=2=8=16(4)10=2=8=16(5)(65)10=(1100101)2=(145)8=(65)16(6)(126)10=(1111110)2=(176)8=(7E)161-3.将下列十六进制数转换为二进制数和十进制数。
解:(1)(49)16=(1001001)2=(73)10(2)(68)16=(1101000)2=(104)10(3)16=(1100101)2=(145)10(4)16=2=(84.)10(5)(35)16=(110101)2=(53)10(6)(124)16=(0)2=(292)101-4.将下列八进制数转换为二进制数和十进制数。
解:(1)(27)8=(010111)2=(23)10(2)(56)8=(101110)2=(46)10(3)8=2=10(4)8=2=10(5)(35)8=(11101)2=(29)10(6)(124)8=(1010100)2=(84)101-5.将下列二进制数转换为十六进制数、八进制和十进制数。
解:(1)(1110001)2=(71)16=(161)8=(113)10(2)2=16=8=10(3)2=16=8=10(4)(10001)2 =(11)16=(21)8=(17)10(5)(1010101)2=(55)16=(125)8=(85)101-6.试求出下列8421BCD码对应的十进制数。
数字电子技术基础第一章练习题及参考答案

第一章数字电路基础第一部分基础知识一、选择题1.以下代码中为无权码的为。
A. 8421BCD码B. 5421BCD码C.余三码D.格雷码2.以下代码中为恒权码的为。
A .8421BCD码B. 5421BCD码C.余三码D.格雷码3. 一位十六进制数可以用位二进制数来表示。
A. 1B.2C. 4D.164.十进制数25用8421BCD码表示为。
A .10 101B .0010 0101 C. 100101 D .101015.在一个8位的存储单元中,能够存储的最大无符号整数是。
A. (256) 10B. (127) 10C. (FF) 16D. (255) 106.与十进制数(53.5) 10等值的数或代码为。
A.(0101 0011. 0101)8421BCDB.(35. 8)16C.(110101. 1)2D.(65. 4)87.矩形脉冲信号的参数有。
A.周期B.占空比C.脉宽D.扫描期8.与八进制数(47. 3) 8等值的数为:A. (100111 . 011 )2B. (27. 6)16C. (27. 3 )16D. (1 00111 . 11 )29. 常用的BCD码有。
A.奇偶校验码B.格雷码C. 8421码D.余三码10 .与模拟电路相比,数字电路主要的优点有。
A.容易设计B.通用性强C.保密性好D.抗干扰能力强二、判断题(正确打,,错误的打X)1.方波的占空比为0. 5。
()2. 8421 码1001 比0001 大。
( )3.数字电路中用“ 1”和“ 0”分别表示两种状态,二者无大小之分。
()4.格雷码具有任何相邻码只有一位码元不同的特性。
()5.八进制数(18) 8比十进制数(18) 10小。
()6.当传送十进制数5时,在8421奇校验码的校验位上值应为1。
( )7.在时间和幅度上都断续变化的信号是数字信号,语音信号不是数字信号。
()8.占空比的公式为:q = t w / T,则周期T越大占空比q越小。
数字电路第1章习题解答

第1章 数字逻辑基础1-1 将下列二进制数转换为十进制数。
(1) 2(1101) (2) 2(10110110) (3) 2(0.1101) (4) 2(11011011.101) 解(1)3210210(1101)12120212(13)=⨯+⨯+⨯+⨯=(2)75421210(10110110)1212121212(182)=⨯+⨯+⨯+⨯+⨯= (3) 124210(0.1101)1212120.50.250.0625(0.8125)---=⨯+⨯+⨯=++= (4)76431013210(11011011.101)22222222 12864168210.50.125 (219.625)--=+++++++=+++++++= 1-2 将下列十进制数转换为二进制数和十六进制数(1) 10(39) (2) 10(0.625) (3) 10(0.24) (4) 10(237.375) 解(1)10216(39)(100111)(27)== (2) 10216(0.625)(0.101)(0.A)==(3)近似结果: 16210)3.0()00111101.0()24.0(D =≈ (4) 10216(237.375)(1110'1101.011)(0ED.6)== 1-3 将下列十六进制数转换为二进制数和十进制数(1) 16(6F.8) (2) 16(10A.C) (3) 16(0C.24) (4) 16(37.4) 解(1) 16210(6F.8)(1101111.1)(111.5)== (2) 16210(10A.C)(1'0000'1010.11)(266.75)== (3) 16210(0C.24)(1100.0010'01)(12.140625)== (4) 16210(37.4)(11'0111.01)(55.25)== 1-4 求出下列各数的8位二进制原码和补码(1) 10(39)- (2) 10(0.625) (3) 16(5B) (4) 2(0.10011)- 解(1)10(39)(1'0100111)(1'1011001)-==原码补码 (2) (0.1010000)(0.1010000)==10原码补码(0.625)(3) 16(5B)(01011011)(01011011)==原码补码(4) 2(0.10011)(1.1001100)(1.0110100)-==原码补码1-5 已知10X (92)=-,10Y (42)=,利用补码计算X +Y 和X -Y 的数值。
(完整版)《数字电子技术基础》第一章习题答案

第一章 逻辑代数及逻辑函数的化简1。
1、用布尔代数的基本公社和规则证明下列等式. 1、D B A DC D A BD B A +=+++证:左边=D B A DC D BD B A DC D A AD BD B A +=+++=++++=右边 2、C AB D A C AB D B A D AB +=++证:左边=C AB D A C AB B B D A +=++)(=右边 3、D B B DA C B D D BC +=++++))((证:左边=D B C B C DA B DA D BC B DA C B D BC +=++++=++++))((=右边 4、D B C B BC D A D C A ACD +=++++ 证:左边=B D B D A AD +=++=右边 5、))()((A C C B B A CA BC AB +++=++证:右边=AB BC AC A C B AC A C BC B AC AB ++=++=++++))(())((=左边 6、A C C B B A C B A ABC ++=+证:右边=C B A ABC A C BC C A B A A C C B B A A C C B B A +=+++=+++=))(())()(( 7、A C C B B A A C C B B A ++=++证:左边=A C C B B A C B B A A C A C C B B A ++=+++++=右边 8、)())()()((X W YZ Z Y Z Y X W Z Y +=++++证:左边=)())()((X W YZ Z Y X W Y Z YZ +=+++=右边 9、0))()()((=++++B A B A B A B A证:左边=0))((==++++A A B A B A A AB B A A =右边10、A D D C C B B A D C CD C B BC B A AB +++=+++))()(( 证:左边=D C B A ABCD D C CD C B A ABC +=++))((右边=))()()((A D D C C B B A A D D C C B B A ++++==D C B A ABCD AD C A D C BC C A B A +=++++))((=左边11、=⊕⊕C B A A ⊙B ⊙C证:左边=C B A ABC C B A C B A C B A AB C B A B A +++=+++)()( ==+++)()(C B C B A C B BC A A ⊙B ⊙C =右边 12、如果Y B X A BY AX B A +=+=⊕,证明0证:AB B A Y X X B Y A B A Y B X A BY AX +++++=++=+))((=X A Y B AB Y X X B Y A B A ++++++ =X A Y B X A Y B AB B A +=+++=右边1.2、求下列函数的反函数.1、B A AB F += 解:))((B A B A F ++=2、C B A C B A C AB ABC F +++=解:))()()((C B A C B A C B A C B A F ++++++++=3、)(D A C C B B A F +++= 解:))()((D A C C B B A F +++=4、))()((B A D C C D A B F +++= 解:B A D C C D A B F ++++=)(5、RST T S R T S R F ++= 解:))()((T S R T S R T S R F ++++++= 1.3、写出下列函数的对偶式.1、E DE C C A B A F ++++=))()(( 解:E E D C C A AB F )](['+++=2、B A D B C AB F = 解:B A D B C B A F ++++++='3、C B C A C B B A F +++++++= 解:BC C A BC B A F ='4、Z Y X Z XY F += 解:Z Y X Z Y X F ++++=' 1.4、证明函数F 为自对偶函数。
习题数电参考答案(终)

习题数电参考答案(终)第⼀章数字逻辑概论1.1 数字电路与数制信号1.1.1 试以表1.1.1所列的数字集成电路的分类为依据,指出下列IC器件属于何种集成度器件:(1)微处理器;(2)计数器;(3)加法器;(4)逻辑门;(5)4兆位存储器。
解:依照表1.1.1所⽰的分类,所列的五种器件:(1)、(5)属于⼤规模;(2)、(3)属于中规模;(4)属于⼩规模。
1.1.2⼀数字信号波形如图题1.1.2所⽰,试问该波形所代表的⼆进制数是什么?解:图题1.1.2所⽰的数字信号波形的左边为最⾼位(MSB),右边为最低位(LSB),低电平表⽰0,⾼电平表⽰1。
该波形所代表的⼆进制数为010110100。
1.1.3 试绘出下列⼆进制数的数字波形,设逻辑1的电压为5V,逻辑0的电压为0V。
(1)001100110011(2)0111010 (3)1111011101解:⽤低电平表⽰0,⾼电平表⽰1,左边为最⾼位,右边为最低位,题中所给的3个⼆进制数字的波形分别如图题1.1.3(a)、(b)、(c)所⽰,其中低电平为0V,⾼电平为5V。
1.1.4⼀周期性数字波形如图1.1.4所⽰,试计算:(1)周期;(2)频率;(3)占空⽐。
解:因为图题1.1.4所⽰为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms。
频率为周期的倒数,f=1/T=1/0.01s=100Hz。
占空⽐为⾼电平脉冲宽度与周期的百分⽐,q=1ms/10ms×100%=10%。
1.2 数制1.2.1 ⼀数字波形如图1.2.1所⽰,时钟频率为4kHz,试确定:(1)它所表⽰的⼆进制数;(2)串⾏⽅式传送8位数据所需要的时间;(3)以8位并⾏⽅式传送的数据时需要的时间。
解:该波形所代表的⼆进制数为00101100。
时钟周期T=1/f=1/4kHz=0.25ms。
串⾏⽅式传送数据时,每个时钟周期传送1位数据,因此,传送8位数据所需要的时间t=0.25ms×8=2ms。
《电子技术基础》数电部分课后习题解答

数字电子部分习题解答第1章 数字逻辑概论1.2.2 将10进值数127、2.718转换为2进制数、16进制数解:(2) (127)D = (1111111)B 此结果由127除2取余直至商为0得到。
= (7F)H 此结果为将每4位2进制数对应1位16进制数得到。
(4) (2.718)D = (10.1011)B 此结果分两步得到:整数部分--除2取余直至商为0得到;小数部分—乘2取整直至满足精度要求.= (2.B)H 此结果为以小数点为界,将每4位2进制数对应1位16进制数得到。
1.4.1 将10进值数127、2.718转换为8421码。
解:(2) (127)D = (000100100111)8421BCD 此结果为将127中每1位10进制数对应4位8421码得到。
(4) (2.718)D = (0010.0111 0001 1000)8421BCD 此结果为将2.718中每1位10进制数对应4位8421码得到。
第2章 逻辑代数2.23 用卡诺图化简下列各式。
解:(4) )12,10,8,4,2,0(),,,(∑=m D C B A LD C AB D C B A D C B A D C B A D C B A D C B A +++++= 对应卡诺图为:化简结果: D B D C L +=解:(6) ∑∑+=)15,11,55,3,1()13,9,6,4,2,0(),,,(d m D C B A L对应卡诺图为:化简结果: D A L +=第4章 组合逻辑电路4.4.7 试用一片74HC138实现函数ACD C AB D C B A L +=),,,(4.4.7 试用一片74HC138实现函数ACD C AB D C B A L +=),,,(。
解:将输入变量低3位B 、C 、D 接至74HC138的地址码输入端A 2、A 1、A 0 ,将输入变量高位A 接至使能端E 3,令012==E E ,则有:i i i Am m E E E Y ==123。
数电习题及解答

图 P2.7
题 2.7 解:
2.9 试写出图 P2.9 所示 CMOS 电路的输出逻辑表达式。
(a) 图 P2.9
(b)
题 2.9 解:
F1 A B A B ; F2 A B A B
2.11 试写出图 P2.11 中各 NMOS 门电路的输出逻辑表达式。
图 P2.11
0 1 1 1
0 1 1 1
证明 A B C AB AC
A
B
C
A B C
0 0 0 0 0 1 1 0
AB AC
0 0 0 0 0 1 1 0
0 0 0 0 1 1 1 1
(3)
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
证明 A B C A B C
(3) F ABC BC D A BD (4) F ( A, B, C , D) 题 1.15 解: (1) F A BC BC
m0,2,3,8,9,10,11,13
F B C A C B C
或
F B C B C A B
A
B
C
AB C
A BC
1 0 1
0 0 0
0 0 1
0 1 0
1 0 1
0 1 1 1 1
(4)
1 0 0 1 1
1 0 1 0 1
0 0 0 1 0
0 0 0 1 0
证明 AB AC A B AC
A
B
C
AB AC
A B AC
1 0 1 0 1 1 0 0
数字电路课后习题答案第一章

1INTRODUCTIONE X E R C I S E S O L U T I O N S1.2Three definitions of “bit”:(1) A binary digit (p. 1).(2)Past tense of “bite” (p. 1).(3) A small amount (pp. 6, 10).1.3ASIC Application-Specific Integrated CircuitCAD Computer-Aided DesignCD Compact DiscCO Central OfficeCPLD Complex Programmable Logic DeviceDAT Digital Audio TapeDIP Dual In-line PinDVD Digital Versatile DiscFPGA Field-Programmable Gate ArrayHDL Hardware Description LanguageIC Integrated CircuitIP Internet ProtocolLSI Large-Scale IntegrationMCM Multichip Module1–12DIGITAL CIRCUITSMSI Medium-Scale IntegrationNRE Nonrecurring EngineeringOK Although we use this word hundreds of times a week whether things are OK or not, we have probably rarely wondered about its history. That history is in fact a brief one, the word being first recorded in1839, though it was no doubt in circulation before then. Much scholarship has been expended on theorigins of OK, but Allen Walker Read has conclusively proved that OK is based on a sort of joke.Someone pronounced the phrase “all correct” as “oll (or orl) correct,” and the same person or someoneelse spelled it “oll korrect,” which abbreviated gives us OK. This term gained wide currency by beingused as a political slogan by the 1840 Democratic candidate Martin Van Buren, who was nicknamedOld Kinderhook because he was born in Kinderhook, New York. An editorial of the same year, refer-ring to the receipt of a pin with the slogan O.K., had this comment: “frightful letters . . . significant ofthe birth-place of Martin Van Buren, old Kinderhook, as also the rallying word of the Democracy of thelate election, ‘all correct’ .... Those who wear them should bear in mind that it will require their moststrenuous exertions ... to make all things O.K.” [From the American Heritage Electronic Dictionary(AHED), copyright 1992 by Houghton Mifflin Company]PBX Private Branch ExchangePCB Printed-Circuit BoardPLD Programmable Logic DevicePWB Printed-Wiring BoardSMT Surface-Mount TechnologySSI Small-Scale IntegrationVHDL VHSIC Hardware Description LanguageVLSI Very Large-Scale Integration1.4ABEL Advanced Boolean Equation LanguageCMOS Complementary Metal-Oxide SemiconductorJPEG Joint Photographic Experts GroupMPEG Moving Picture Experts GroupOK(see above)PERL According to some, it’s “Practical Extraction and Report Language.” But the relevant Perl FAQ entry, in perlfaq1.pod, says “never write ‘PERL’, because perl isn't really an acronym, apocryphal folkloreand post-facto expansions notwithstanding.” (Thanks to Anno Siegel for enlightening me on this.) VHDL VHSIC Hardware Description Language1.8In my book, “dice” is the plural of “die.”。
《数字电子技术基础》课后习题及参考答案

第1章习题与参考答案【题1-1】将下列十进制数转换为二进制数、八进制数、十六进制数。
(1)25;(2)43;(3)56;(4)78解:(1)25=(11001)2=(31)8=(19)16(2)43=(101011)2=(53)8=(2B)16(3)56=(111000)2=(70)8=(38)16(4)(1001110)2、(116)8、(4E)16【题1-2】将下列二进制数转换为十进制数。
(1)10110001;(2)10101010;(3)11110001;(4)10001000 解:(1)10110001=177(2)10101010=170(3)11110001=241(4)10001000=136【题1-3】将下列十六进制数转换为十进制数。
(1)FF;(2)3FF;(3)AB;(4)13FF解:(1)(FF)16=255(2)(3FF)16=1023(3)(AB)16=171(4)(13FF)16=5119【题1-4】将下列十六进制数转换为二进制数。
(1)11;(2)9C;(3)B1;(4)AF解:(1)(11)16=(00010001)2(2)(9C)16=(10011100)2(3)(B1)16=(1011 0001)2(4)(AF)16=(10101111)2【题1-5】将下列二进制数转换为十进制数。
(1)1110.01;(2)1010.11;(3)1100.101;(4)1001.0101解:(1)(1110.01)2=14.25(2)(1010.11)2=10.75(3)(1001.0101)2=9.3125【题1-6】将下列十进制数转换为二进制数。
(1)20.7;(2)10.2;(3)5.8;(4)101.71解:(1)20.7=(10100.1011)2(2)10.2=(1010.0011)2(3)5.8=(101.1100)2(4)101.71=(1100101.1011)2【题1-7】写出下列二进制数的反码与补码(最高位为符号位)。
《数电》教材习题答案 第1章习题答案
思考题与习题1-1 将下列二进制数转化为十进制数。
(1)(100101100)2=(300)10 (2)(101011)2=(43)10(3)(1111111)2=(127)10 (4)(1011110)2=(94)101-2 将下列十进制数转化为二进制数。
(1)(28)10=(11100)2 (2) (100)10=(1100100)2(3)(210)10=(11010010)2 (4)(321)10=(101000001)2 1-3 将八进制数34、567、4633转化为二进制数。
(34)8=(11100)2 (567)8=(101110111)2(4633)8=(100110011011)21-4 将二进制数转化为八进制数。
(1011010)2=(132)8 (11010011)2=(323)8 1-5 将二进制数转化为十六进制数。
(100100110101)2=(935)16 (1010110011)2=(2B3)16 1-6 将十六进制数转化为二进制数。
(7AF4)16=( 111101*********)2 (F9DE )16=(1111100111011110)2 1-7 将十进制数691用8421BCD 码表示。
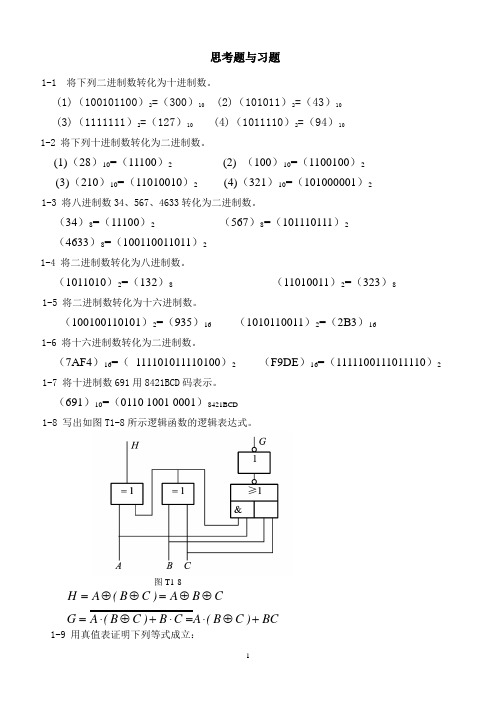
(691)10=(0110 1001 0001)8421BCD1-8 写出如图T1-8所示逻辑函数的逻辑表达式。
图T1-8BC)C B (A C B )C B (A G CB A )C B (A H +⊕⋅=⋅+⊕⋅=⊕⊕=⊕⊕= 1-9 用真值表证明下列等式成立:(1)A B + A B = (A +B )(A+B)可见,左式=右式,得证。
(2)A ⊕B =A ⊕B可见,左=右,得证。
(3)A ⊕0 = A可见,左式=右式,得证。
(4)A ⊕1 = A可见,左式=右式,得证。
1-10 利用公式和运算规则证明下列等式:(1)ABC + A BC + A B C = BC + AC证明:左=(ABC + A BC ) +( A B C +ABC )= BC + AC =右(2)C AB = AB + C证明:左=C AB C AB +=+=右(3)(A +B)(A + C)(B + C + D) = (A + B)(A + C)证明:将以上等式两边作对偶变换,可得到以下公式:AB +A C +BCD =AB +A C由常用公式四可知该式是成立的,则由对偶定理可知,对偶等式成立,则原等式也成立。
数字电子技术基础课后习题及答案

第1章习题与参考答案【题1-1】将以下十进制数转换为二进制数、八进制数、十六进制数。
〔1〕25;〔2〕43;〔3〕56;〔4〕78解:〔1〕25=〔11001〕2=〔31〕8=〔19〕16〔2〕43=〔101011〕2=〔53〕8=〔2B〕16〔3〕56=〔111000〕2=〔70〕8=〔38〕16〔4〕〔1001110〕2、〔116〕8、〔4E〕16【题1-2】将以下二进制数转换为十进制数。
〔1〕10110001;〔2〕10101010;〔3〕11110001;〔4〕10001000解:〔1〕10110001=177〔2〕10101010=170〔3〕11110001=241〔4〕10001000=136【题1-3】将以下十六进制数转换为十进制数。
〔1〕FF;〔2〕3FF;〔3〕AB;〔4〕13FF解:〔1〕〔FF〕16=255〔2〕〔3FF〕16=1023〔3〕〔AB〕16=171〔4〕〔13FF〕16=5119【题1-4】将以下十六进制数转换为二进制数。
〔1〕11;〔2〕9C;〔3〕B1;〔4〕AF解:〔1〕〔11〕16=〔00010001〕2〔2〕〔9C〕16=〔10011100〕2〔3〕〔B1〕16=〔1011 0001〕2〔4〕〔AF〕16=〔10101111〕2【题1-5】将以下二进制数转换为十进制数。
〔1〕1110.01;〔2〕1010.11;〔3〕1100.101;〔4〕1001.0101解:〔1〕〔1110.01〕2=14.25〔2〕〔1010.11〕2=10.75〔3〕〔1001.0101〕2=9.3125【题1-6】将以下十进制数转换为二进制数。
〔1〕20.7;〔2〕10.2;〔3〕5.8;〔4〕101.71解:〔1〕20.7=〔10100.1011〕2〔2〕10.2=〔1010.0011〕2〔3〕5.8=〔101.1100〕2〔4〕101.71=〔1100101.1011〕2【题1-7】写出以下二进制数的反码与补码〔最高位为符号位〕。
数电课后习题答案

部分习题答案第一章1.1(45)10=(101101)2=(55)8(129)10=(10000001)2=(201)8(538)10=(1000011010)2=(1032)8 (254.25)10=(11111110.01)2=(376.2)81.2 (1101)2=(13)10 (110101)2=(53)10 (1110101)2=(117)10 (10100110)2=(166)10 。
1.3 (27)10=(1B)16 , (43)10=(2B)16 , (125)10=(7D)16 , (254)10=(15E)16 ,312=(138)16 , (513)=(201)16 。
1.4 (1) (10100101)2=(425)8=(A5)16 。
(2) (10101111)2=(257)8=(AF)16 。
(3) (11001110111)2=(3167)8=(677)16 。
1.5 (1) (154)10=(10011010)2=(232)8=(9A)16 。
(2) (101011)2=(43)10=(53)8=(2B)16 。
(3) (7E)16=(126)10=(176)8=(1111110)2 。
1.6 (1) 1110,00001,0110101,110010,1110111,100001。
(2)+0011,+01010,-0001,-1111。
(3) 0111101,0001010,1000011,11010110。
(4) +1101,+1010,-00101,-010110。
(5) 01011110,10010010。
(6) 0111000,001010,1000100,110100。
(7) +111101,+001100,-01001,-01000。
1.7 (46)10=(1000110)8421BCD , (127)10=(100100111)8421BCD , (254)10=(1001010100)8421BCD , (893)10=(10001010100)8421BCD , (2.618)10=(10.011000011000)8421BCD 。
数字电子技术基础课后习题解答(一到三章张克农

第1章习题解答1.1把下列二进制数转换成十进制数①10010110;②11010100;③0101001;④10110.111;⑤101101.101;⑥0.01101。
[解] 直接用多项式法转换成十进制数① (10010110)B = (1⨯2 7+1⨯24 + 1⨯22 +1⨯21)D = (150)D=150② (11010100)B = 212③ (0101001)B = 41④ (10110.111)B = 22.875⑤ (101101.101)B = 45.625⑥ (0.01101)B = 0.406251.2把下列十进制数转换为二进制数①19;② 64;③ 105;④ 1989;⑤ 89.125;⑥ 0.625。
[解] 直接用基数乘除法① 19= (10011)B② 64= (1000000)B③ 105 = (1101001)B④ 1989 = (11111000101)B⑤ 89.125 = (1011001.001)B⑥ 0.625= (0.101)B1.3把下列十进制数转换为十六进制数① 125;② 625;③ 145.6875;④0.5625。
[解]直接用基数乘除法① 125 = (7D)H② 625 = (271)H③ 145.6875= (91.B)H④ 0.56255=(0.9003)H1.4把下列十六进制数转换为二进制数① 4F;② AB;③ 8D0;④ 9CE。
[解]每位十六进制数直接用4位二进制数展开① (4F)H= (1001111)B② (AB)H= (10101011)B 2 19 余数2 9 …… 1 ……d02 4 …… 1 ……d12 2 ……0 ……d22 1 ……0 ……d32 0 …… 1 ……d4图题1.2 ①基数除法过程图12③ (8D0)H = (100011010000)B ④ (9CE)H = (100111001110)B 1.5 写出下列十进制数的8421BCD 码 ① 9;② 24;③ 89;④ 365。
习题数电参考答案(终)

第一章数字逻辑概论1.1 数字电路与数制信号1.1.1 试以表1.1.1所列的数字集成电路的分类为依据,指出下列IC器件属于何种集成度器件:(1)微处理器;(2)计数器;(3)加法器;(4)逻辑门;(5)4兆位存储器。
解:依照表1.1.1所示的分类,所列的五种器件:(1)、(5)属于大规模;(2)、(3)属于中规模;(4)属于小规模。
1.1.2一数字信号波形如图题1.1.2所示,试问该波形所代表的二进制数是什么?解:图题1.1.2所示的数字信号波形的左边为最高位(MSB),右边为最低位(LSB),低电平表示0,高电平表示1。
该波形所代表的二进制数为010110100。
1.1.3 试绘出下列二进制数的数字波形,设逻辑1的电压为5V,逻辑0的电压为0V。
(1)001100110011(2)0111010 (3)1111011101解:用低电平表示0,高电平表示1,左边为最高位,右边为最低位,题中所给的3个二进制数字的波形分别如图题1.1.3(a)、(b)、(c)所示,其中低电平为0V,高电平为5V。
1.1.4一周期性数字波形如图1.1.4所示,试计算:(1)周期;(2)频率;(3)占空比。
解:因为图题1.1.4所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms。
频率为周期的倒数,f=1/T=1/0.01s=100Hz。
占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms×100%=10%。
1.2 数制1.2.1 一数字波形如图1.2.1所示,时钟频率为4kHz,试确定:(1)它所表示的二进制数;(2)串行方式传送8位数据所需要的时间;(3)以8位并行方式传送的数据时需要的时间。
解:该波形所代表的二进制数为00101100。
时钟周期T=1/f=1/4kHz=0.25ms。
串行方式传送数据时,每个时钟周期传送1位数据,因此,传送8位数据所需要的时间t=0.25ms×8=2ms。
数字电路第1章习题解答

数字电路第1章习题解答第1章数字逻辑基础1-1将下列二进制数转换为十进制数。
(1)(1101)2(2)(10110110)2(3)(0.1101)2(4)(11011011.101)2求解(1)(1101)2?1?23?1?22?0?21?1?20?(13)10(2)(10110110)52?1?27?1?2?1?24?1?22?1?21?(182)10(3)(0.1101)2?1?2?1?1?2?2?1?2?4?0.5?0.25?0.0625?(0.8125)10(4)(11011011.101)7?12?2?26?24?23?21?20?2?2?3?128?64?16?8?2?1?0.5?0.125?(219.625)1 01-2将下列十进制数转换为二进制数和十六进制数(1)(39)10(2)(0.625)10(3)(0.24)10(4)(237.375)10求解1)(39)10?(100111)2?(27)16(2)(0.625)10?(0.101)2?(0.a)163)对数结果:(0.24)10?(0.00111101)2?(0.3d)16(4)(237.375)10?(1110'1101.011)2?(0ed.6)161-3将以下十六进制数切换为二进制数和十进制数(1)(6f.8)16(2)(10a.c)16(3)(0c.24)16(4)(37.4)16解1)(6f.8)16?(1101111.1)2?(111.5)10(2)(10a.c)16?(1'0000'1010.11)2?(266.75)10(3)(0c .24)16?(1100.0010'01)2?(12.140625)10(4)(37.4)16?(11'0111.01)2?(55.25)101-4算出以下各数的8十一位二进制原码和补码(1)(?39)10(2)(0.625)10(3)(5b)16(4)(?0.10011)2解1)(?39)10?(1'0100111)原码?(1'1011001)补码(2)(0.625)10?(0.1010000)原码?(0.1010000)补码1(((((3)(5b)16?(01011011)原码?(01011011)补码(4)(?0.10011)2?(1.1001100)原码?(1.0110100)补码1-5未知x?(?92)10,y?(42)10,利用补码排序x+y和x-y的数值。
