2016年中考数学应用题专题复习(可编辑修改word版)

合集下载

2016中考数学应用题汇编及答案

中考应用题大题题型汇总1.我国中东部地区雾霾天气趋于严重，环境治理已刻不容缓．我市某电器商场根据民众健康需要,代理销售某种家用空气净化器，其进价是200元/台．经过市场销售后发现：在一个月内，当售价是400元/台时，可售出200台，且售价每降低10元，就可多售出50台．若供货商规定这种空气净化器售价不能低于300元/台，代理销售商每月要完成不低于450台的销售任务．(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量 x的取值范围；(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大？最大利润是多少？2.湿地风景区特色旅游项目:水上游艇.旅游人员消费后风景区可盈利10元/人,每天消费人员为500人.为增加盈利,准备提高票价,调查发现,在其他条件不变的情况下,票价每涨1元,消费人员就减少 20人.（1）现该项目要保证每天盈利6000元，同时又要旅游者得到实惠，那么票价应涨价多少元？（2）若单纯从经济角度看，票价涨价多少元，能使该项目获利最多？3.临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.调查发现,零售单价每降0.1元，每天可多卖出100只粽子.为了使每天获得的利润更多，该店决定把零售单价下降m（0<m<1）元.(1)零售单价降价后,该店每天可售出只粽子,利润为元。

（2）在不考虑其他因素的条件下，当m定为多少时，才能使该店每天获取的利润是420元，且卖出的粽子更多？4.某校九年级准备购买一批笔奖励优秀学生,在购买时发现，每只笔可以打九折,用360元钱购买的笔,打折后购买的数量比打折前多10本.（1）求打折前每支笔的售价是多少元？（2）由于学生的需求不同,学校决定购买笔和笔袋共80件,笔袋每个原售价为10元,两种物品都打八折,若购买总金额不低于400元,且不高于405元,问有哪几种购买方案？（3）在（2）的条件下,求购买总金额的最小值.5.一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元，若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：（1）甲、乙两组工作一天，商店各应付多少钱？（2）已知甲单独完成需12天，乙单独完成需24天，单独请哪个组，商店所需费用最少？（3）若装修完后，商店每天可赢利200元，你认为如何安排施工更有利于商店？请你帮助商店决策。

2016年全国中考数学试题汇编-----分式和分式方程

2016年全国中考数学试题汇编-----分式和分式方程（2016，成都）分式方程=1的解为（）A．x=﹣2 B．x=﹣3 C．x=2 D．x=3【考点】分式方程的解．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【解答】解：去分母得：2x=x﹣3，解得：x=﹣3，经检验x=﹣3是分式方程的解，故选B．（2016，成都）化简：（x﹣）÷．【考点】分式的混合运算．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．【解答】解：原式=•=•=x+1．(2016,百色)A、B两地相距160千米，甲车和乙车的平均速度之比为4：5，两车同时从A地出发到B地，乙车比甲车早到30分钟，若求甲车的平均速度，设甲车平均速度为4x千米/小时，则所列方程是（）A．﹣=30 B．﹣=C．﹣=D． +=30【考点】由实际问题抽象出分式方程．【分析】设甲车平均速度为4x千米/小时，则乙车平均速度为5x千米/小时，根据两车同时从A地出发到B地，乙车比甲车早到30分钟列出方程即可．【解答】解：设甲车平均速度为4x千米/小时，则乙车平均速度为5x千米/小时，根据题意得，﹣=．故选B．(2016,毕节)为加快“最美毕节”环境建设，某园林公司增加了人力进行大型树木移植，现在平均每天比原计划多植树30棵，现在植树400棵所需时间及原计划植树300棵所需时间相同，设现在平均每天植树x棵，则列出的方程为（）A． B． C． D．【考点】由实际问题抽象出分式方程．【分析】设现在平均每天植树x棵，则原计划每天植树（x﹣30）棵，根据：现在植树400棵所需时间=原计划植树300棵所需时间，这一等量关系列出分式方程即可．【解答】解：设现在平均每天植树x棵，则原计划每天植树（x﹣30）棵，根据题意，可列方程： =，故选：A．(2016,毕节)若a2+5ab﹣b2=0，则的值为 5 ．【考点】分式的化简求值．【分析】先根据题意得出b2﹣a2=5ab，再由分式的减法法则把原式进行化简，进而可得出结论．【解答】解：∵a2+5ab﹣b2=0，∴﹣===5．故答案为：5．（2016，黑龙江龙东地区）．关于x的分式方程=3的解是正数，则字母m的取值范围是（）A．m＞3 B．m＞﹣3 C．m＞﹣3 D．m＜﹣3【考点】分式方程的解．【分析】分式方程去分母转化为整式方程，由分式方程解为正数确定出m的范围即可．【解答】解：分式方程去分母得：2x﹣m=3x+3，解得：x=﹣m﹣3，由分式方程的解为正数，得到﹣m﹣3＞0，且﹣m﹣3≠﹣1，解得：m＜﹣3，故选D（2016，荆门）要使式子有意义，则x的取值范围是（）A．x＞1 B．x＞﹣1 C．x≥1 D．x≥﹣1【考点】二次根式有意义的条件．【分析】直接利用二次根式有意义的条件进而得出x﹣1≥0，求出答案．【解答】解：要使式子有意义，故x﹣1≥0，解得：x≥1．则x的取值范围是：x≥1．故选：C．（2016，荆门）化简的结果是（）A． B． C．x+1 D．x﹣1【考点】分式的混合运算．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果．【解答】解：原式=÷=•=，故选A（2016，随州）．先化简，再求值：（﹣x+1）÷，其中x=﹣2．【考点】分式的化简求值．【分析】首先将括号里面的通分相减，然后将除法转化为乘法，化简后代入x的值即可求解．【解答】解：原式=[﹣]•=•=，当x=﹣2时，原式===2．（2016，随州）某校学生利用双休时间去距学校10km的炎帝故里参观，一部分学生骑自行车先走，过了20min后，其余学生乘汽车沿相同路线出发，结果他们同时到达．已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度和汽车的速度．【考点】分式方程的应用．【分析】求速度，路程已知，根据时间来列等量关系．关键描述语为：“一部分学生骑自行车先走，过了20min后，其余学生乘汽车沿相同路线出发，结果他们同时到达”，根据等量关系列出方程．【解答】解：设骑车学生的速度为x千米/小时，汽车的速度为2x千米/小时，可得：，解得：x=15，经检验x=15是原方程的解，2x=2×15=30，答：骑车学生的速度和汽车的速度分别是每小时15km，30km．（2016，常德）先化简，再求值：（），其中x=2．【考点】分式的化简求值．【分析】先算括号里面的，再算除法，最后把x的值代入进行计算即可．【解答】解：原式=[+]÷[﹣]=÷=÷=•=，当x=2时，原式==．（2016，常德）某服装店用4500元购进一批衬衫，很快售完，服装店老板又用2100元购进第二批该款式的衬衫，进货量是第一次的一半，但进价每件比第一批降低了10元．（1）这两次各购进这种衬衫多少件？（2）若第一批衬衫的售价是200元/件，老板想让这两批衬衫售完后的总利润不低于1950元，则第二批衬衫每件至少要售多少元？【考点】分式方程的应用；一元一次不等式的应用．【分析】（1）设第一批T恤衫每件进价是x元，则第二批每件进价是（x﹣10）元，再根据等量关系：第二批进的件数=×第一批进的件数可得方程；（2）设第二批衬衫每件售价y元，由利润=售价﹣进价，根据这两批衬衫售完后的总利润不低于1950元，可列不等式求解．【解答】解：（1）设第一批T恤衫每件进价是x元，则第二批每件进价是（x﹣10）元，根据题意可得：，解得：x=150，经检验x=150是原方程的解，答：第一批T恤衫每件进价是150元，第二批每件进价是140元，（件），（件），答：第一批T恤衫进了30件，第二批进了15件；（2）设第二批衬衫每件售价y元，根据题意可得：30×+15（y﹣140）≥1950，解得：y≥170，答：第二批衬衫每件至少要售170元．（2016，娄底）函数y=的自变量x的取值范围是（）A．x≥0且x≠2 B．x≥0 C．x≠2 D．x＞2【考点】函数自变量的取值范围．【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．【解答】解：由题意得，x≥0且x﹣2≠0，解得x≥0且x≠2．故选A．（2016，娄底）先化简，再求值：（1﹣）•，其中x是从1，2，3中选取的一个合适的数．【考点】分式的化简求值．【分析】先括号内通分，然后计算除法，最后取值时注意使得分式有意义，最后代入化简即可．【解答】解：原式=•=．当x=2时，原式==﹣2．（2016，娄底）甲、乙两同学的家及学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校、乙同学骑自行车去学校．已知甲步行速度是乙骑自行车速度的，公交车的速度是乙骑自行车速度的2倍．甲乙两同学同时从家发去学校，结果甲同学比乙同学早到2分钟．（1）求乙骑自行车的速度；（2）当甲到达学校时，乙同学离学校还有多远？【考点】一元一次方程的应用．【分析】（1）设乙骑自行车的速度为x米/分钟，则甲步行速度是x米/分钟，公交车的速度是2x米/分钟，根据题意列方程即可得到结论；（2）300×2=600米即可得到结果．【解答】解：（1）设乙骑自行车的速度为x米/分钟，则甲步行速度是x米/分钟，公交车的速度是2x米/分钟，根据题意得+=﹣2，解得：x=300米/分钟，经检验x=300是方程的根，答：乙骑自行车的速度为300米/分钟；（2）∵300×2=600米，答：当甲到达学校时，乙同学离学校还有600米．（2016，吉林）解方程： =．【考点】解分式方程．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【解答】解：去分母得：2x﹣2=x+3，解得：x=5，经检验x=5是分式方程的解．（2016，泰州）函数中，自变量x的取值范围是．【考点】函数自变量的取值范围；分式有意义的条件．【分析】根据分式有意义的条件是分母不为0；令分母为0，可得到答案．【解答】解：根据题意得2x﹣3≠0，解可得x≠，故答案为x≠．（2016，泰州）（﹣）÷．【考点】分式的混合运算．【分析】先将括号内的分式通分，进行减法运算，再将除法转化为乘法，然后化简即可．【解答】解：（﹣）÷=（﹣）•=•=．（2016，无锡）分式方程=的解是x=4 ．【考点】分式方程的解．【分析】首先把分式方程=的两边同时乘x（x﹣1），把化分式方程为整式方程；然后根据整式方程的求解方法，求出分式方程=的解是多少即可．【解答】解：分式方程的两边同时乘x（x﹣1），可得4（x﹣1）=3x解得x=4，经检验x=4是分式方程的解．故答案为：x=4．（2016，大连）A、B两地相距200千米，甲车从A地出发匀速开往B 地，乙车同时从B地出发匀速开往A地，两车相遇时距A地80千米．已知乙车每小时比甲车多行驶30千米，求甲、乙两车的速度．【考点】分式方程的应用．【专题】应用题．【分析】根据题意，可以设出甲、乙的速度，然后根据题目中的关系，列出相应的方程，本题得以解决．【解答】解：设甲车的速度是x千米/时，乙车的速度为（x+30）千米/时，解得，x=60，则x+30=90，即甲车的速度是60千米/时，乙车的速度是90千米/时．【点评】本题考查分式方程的应用，解题的关键是明确题意，找出所求问题需要的条件，发现题目中的数量关系，列出相应的方程．（2016，丹东）某商场购进甲、乙两种商品，乙商品的单价是甲商品单价的2倍，购买240元甲商品的数量比购买300元乙商品的数量多15件，求两种商品单价各为多少元？【考点】分式方程的应用．【分析】设甲商品的单价为x元，乙商品的单价为2x元，根据购买240元甲商品的数量比购买300元乙商品的数量多15件列出方程，求出方程的解即可得到结果．【解答】解：设甲商品的单价为x元，乙商品的单价为2x元，根据题意，得﹣=15，解这个方程，得x=6，经检验，x=6是所列方程的根，∴2x=2×6=12（元），答：甲、乙两种商品的单价分别为6元、12元．（2016，内地新疆班）两个小组同时从甲地出发，匀速步行到乙地，甲乙两地相距7500米，第一组的步行速度是第二组的1.2倍，并且比第二组早15分钟到达乙地．设第二组的步行速度为x千米/小时，根据题意可列方程是（）A．﹣=15 B．﹣=C．﹣=15 D．﹣=【考点】由实际问题抽象出分式方程．【分析】根据第二组的速度可得出第一组的速度，依据“时间=路程÷速度”即可找出第一、二组分别到达的时间，再根据第一组比第二组早15分钟（小时）到达乙地即可列出分式方程，由此即可得出结论．【解答】解：设第二组的步行速度为x千米/小时，则第一组的步行速度为1.2x千米/小时，第一组到达乙地的时间为：7.5÷1.2x；第二组到达乙地的时间为：7.5÷x；∵第一组比第二组早15分钟（小时）到达乙地，∴列出方程为：﹣==．故答案为D．（2016，内地新疆班）计算（1﹣）（x+1）的结果是x ．【考点】分式的混合运算．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，约分即可得到结果．【解答】解：原式=•（x+1）=x，故答案为：x（2016，呼和浩特）先化简，再求值：﹣÷，其中x=﹣．【考点】分式的化简求值.【分析】先算除法，再算加减，最后把x的值代入进行计算即可．【解答】解：原式=﹣•=+==，当x=﹣时，原式==﹣（2016，呼和浩特）某一公路的道路维修工程，准备从甲、乙两个工程队选一个队单独完成．根据两队每天的工程费用和每天完成的工程量可知，若由两队合做此项维修工程，6天可以完成，共需工程费用385200元，若单独完成此项维修工程，甲队比乙队少用5天，每天的工程费用甲队比乙队多4000元，从节省资金的角度考虑，应该选择哪个工程队？【考点】分式方程的应用．【分析】设甲队单独完成此项工程需要x天，乙队单独完成需要（x+ 5）天，然后依据6天可以完成，列出关于x的方程，从而可求得甲、乙两队单独完成需要的天数，然后设甲队每天的工程费为y元，则可表示出乙队每天的工程费，接下来，根据两队合作6天的工程费用为385200元列方程求解，于是可得到两队独做一天各自的工程费，然后可求得完成此项工程的工程费，从而可得出问题的答案．【解答】解：设甲队单独完成此项工程需要x天，乙队单独完成需要（x+5）天．依据题意可列方程： +=，解得：x1=10，x2=﹣3（舍去）．经检验：x=10是原方程的解．设甲队每天的工程费为y元．依据题意可列方程：6y+6（y﹣4000）=385200，解得：y=34100．甲队完成此项工程费用为34100×10=341000元．乙队完成此项工程费用为30100×15=451500元．答：从节省资金的角度考虑，应该选择甲工程队．（2016，西宁）化简：，然后在不等式x≤2的非负整数解中选择一个适当的数代入求值．【考点】分式的化简求值；一元一次不等式的整数解．【分析】首先利用分式的混合运算法则将原式化简，然后解不等式，选择使得分式有意义的值代入求解即可求得答案．【解答】解：原式====∵不等式x≤2的非负整数解是0，1，2∵（x+1）（x﹣1）≠0，x+2≠0，∴x≠±1，x≠﹣2，∴把x=0代入．（2016，青岛）A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为（）A．﹣=1 B．﹣=1C．﹣=1 D．﹣=1（2016，青岛）化简：﹣（2016，威海）函数y=的自变量x的取值范围是（）A．x≥﹣2 B．x≥﹣2且x≠0C．x≠0D．x＞0且x≠﹣2【考点】函数自变量的取值范围．【分析】根据被开方数大于等于0，分母不等于0列式计算即可得解．【解答】解：由题意得，x+2≥0且x≠0，解得x≥﹣2且x≠0，故选：B．（2016，威海）某校进行期末体育达标测试，甲、乙两班的学生数相同，甲班有48人达标，乙班有45人达标，甲班的达标率比乙班高6%，求乙班的达标率．【考点】分式方程的应用．【分析】设乙班的达标率是x，则甲班的达标率为（x+6%），根据“甲、乙两班的学生数相同”列出方程并解答．【解答】解：设乙班的达标率是x，则甲班的达标率为（x+6%），依题意得： =，解这个方程，得x=0.9，经检验，x=0.9是所列方程的根，并符合题意．答：乙班的达标率为90%．实数a，b在数轴上对应点的位置如图所示，化简|a|+的结果是（）A．﹣2a+b B．2a﹣b C．﹣b D．b【考点】二次根式的性质及化简；实数及数轴．【分析】直接利用数轴上a，b的位置，进而得出a＜0，a﹣b＜0，再利用绝对值以及二次根式的性质化简得出答案．【解答】解：如图所示：a＜0，a﹣b＜0，则|a|+=﹣a﹣（a﹣b）=﹣2a+b．故选：A．（2016，潍坊）若关于x的方程+=3的解为正数，则m的取值范围是（）A．m＜B．m＜且m≠C．m＞﹣D．m＞﹣且m≠﹣【考点】分式方程的解．【分析】直接解分式方程，再利用解为正数列不等式，解不等式得出x的取值范围，进而得出答案．【解答】解：去分母得：x+m﹣3m=3x﹣9，整理得：2x=﹣2m+9，解得：x=，∵关于x的方程+=3的解为正数，∴﹣2m+9＞0，级的：m＜，当x=3时，x==3，解得：m=，故m的取值范围是：m＜且m≠．故选：B ．（2016，烟台）先化简，再求值：（﹣x ﹣1）÷，其中x=，y=．【考点】分式的化简求值．【分析】首先将括号里面进行通分，进而将能分解因式的分解因式，再化简求出答案．【解答】解：（﹣x ﹣1）÷，=（﹣﹣）×=×=﹣，把x=，y=代入得：原式=﹣=﹣1+（2016·山西）甲、乙两个搬运工搬运某种货物，已知乙比甲每小时多搬运600kg ，甲搬运5000kg 所用的时间及乙搬运8000kg 所用的时间相等，求甲、乙两人每小时分别搬运多少kg 货物．设甲每小时搬运xkg 货物，则可列方程为（ B ）A ．x x 80006005000=- B ．60080005000+=x x C ．x x 80006005000=+ D ．60080005000-=x x 考点：分式方程的应用分析：设甲每小时搬运xkg 货物，则甲搬运5000kg 所用的时间是：x5000，根据题意乙每小时搬运的货物为x +600，乙搬运8000kg 所用的时间为6008000+x再根据甲搬运5000kg 所用的时间及乙搬运8000kg 所用的时间相等列方程解答：甲搬运5000kg 所用的时间及乙搬运8000kg 所用的时间相等，所以60080005000+=x x故选B ．（2016·山西）先化简，在求值：112222+---x xx x x ，其中x =-2．考点：分式的化简求值分析：先把分子分母因式分解，化简后进行减法运算解答：原式=1)1)(1()1(2+-+--x xx x x x ……………………………（2分） =112+-+x xx x ……………………………（3分） =1+x x……………………………（4分）当x =-2时，原式=21221=+--=+x x（2016，陕西）化简：（x ﹣5+）÷．【考点】分式的混合运算．【分析】根据分式的除法，可得答案．【解答】解：原式=•=（x ﹣1）（x ﹣3）=x2﹣4x+3．（2016，广安）某市为治理污水，需要铺设一段全长600m的污水排放管道，铺设120m后，为加快施工进度，后来每天比原计划增加20m，结果共用11天完成这一任务，求原计划每天铺设管道的长度．如果设原计划每天铺设xm管道，那么根据题意，可列方程．【考点】由实际问题抽象出分式方程．【分析】根据题目中的数量关系，可以列出相应的方程，本题得以解决．【解答】解：由题意可得，，化简，得，故答案为：．（2016，广安）先化简，再求值：（﹣）÷，其中x 满足2x+4=0．【考点】分式的化简求值．【分析】原式括号中利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出已知方程的解得到x的值，代入计算即可求出值．【解答】解：原式=•=，由2x+4=0，得到x=﹣2，则原式=5．（2016，凉山州）关于x的方程无解，则m的值为（）A．﹣5 B．﹣8 C．﹣2 D．5【考点】分式方程的解．【分析】分式方程去分母转化为整式方程，由分式方程无解得到x+1=0，求出x的值，代入整式方程求出m的值即可．【解答】解：去分母得：3x﹣2=2x+2+m，由分式方程无解，得到x+1=0，即x=﹣1，代入整式方程得：﹣5=﹣2+2+m，解得：m=﹣5，故选A（2016，凉山州）先化简，再求值：，其中实数x、y满足．【考点】分式的化简求值；二次根式有意义的条件．【分析】原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，根据负数没有平方根求出x及y的值，代入计算即可求出值．【解答】解：原式=•=，∵y=﹣+1，∴x﹣2≥0，2﹣x≥0，即x﹣2=0，解得：x=2，y=1，则原式=2．（2016，昆明）计算：﹣= ．【考点】分式的加减法．【分析】同分母分式加减法法则：同分母的分式相加减，分母不变，把分子相加减；再分解因式约分计算即可求解．【解答】解：﹣===．故答案为：．（2016，昆明）八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（）A．﹣=20 B．﹣=20 C．﹣=D．﹣=【考点】由实际问题抽象出分式方程．【分析】根据八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，可以列出相应的方程，从而可以得到哪个选项是正确的．【解答】解：由题意可得，﹣=，故选C．（2016，衢州）当x=6时，分式的值等于﹣1 ．【考点】分式的值．【分析】直接将x的值代入原式求出答案．【解答】解：当x=6时， ==﹣1．故答案为：﹣1（2016，绍兴）解分式方程： +=4．【考点】解分式方程．【分析】观察可得方程最简公分母为（x﹣1），将方程去分母转化为整式方程即可求解．【解答】解：方程两边同乘（x﹣1），得：x﹣2=4（x﹣1），整理得：﹣3x=﹣2，解得：x=，经检验x=是原方程的解，故原方程的解为x=．（2016，台州）化简的结果是（）A．﹣1 B．1 C．D．【考点】约分．【分析】根据完全平方公式把分子进行因式分解，再约分即可．【解答】解： ==；故选D．（2016，台州）解方程：﹣=2．【考点】解分式方程．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【解答】解：去分母得：x+1=2x﹣14，解得：x=15，经检验x=15是分式方程的解．（2016，温州）若分式的值为0，则x的值是（）A．﹣3 B．﹣2 C．0 D．2【考点】分式的值为零的条件．【分析】直接利用分式的值为0，则分子为0，进而求出答案．【解答】解：∵分式的值为0，∴x﹣2=0，∴x=2．故选：D．（2016，安徽）方程=3的解是（）A．﹣B．C．﹣4 D．4【考点】分式方程的解．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【解答】解：去分母得：2x+1=3x ﹣3，解得：x=4，经检验x=4是分式方程的解，故选D ．（2016，北京）如果a +b =2,那么代数2()b aa a a b--的值是（A ） 2 （B ）-2 （C ） 12 （D ）−12答案：A考点：分式的运算，平方差公式。

2016年中考数学真题试题及答案(word版)

（2）共12种情况，有6种情况两次摸到相同颜色棋子，所以概率为． 24. 解：（1）设第一批购进水果x千克，则第二批购进水果2.5千克，依
据题意得：，解得x=200，经检验x=200是原方程的解，∴x+2.5x=700，答：这两批水果功够进700千克；（2）设售价为每千克a元，则：， 630a≥7500×1.26，∴ ，∴a≥15，答：售价至少为每千克15元． 25. （1）证明：在△GAD和△EAB中，∠GAD=90°+∠EAD， ∠EAB=90°+∠EAD， ∴∠GAD=∠EAB，又∵AG=AE，AB=AD，∴△GAD≌△EAB， ∴EB=GD；（2）EB⊥GD，理由如下：连接BD，由（1）得：∠ADG=∠ABE，则在△BDH中， ∠DHB=180°-（∠HDB+∠HBD）=180°-90°=90°，∴EB⊥GD；（3）设BD与AC交于点O，∵AB=AD=2在Rt△ABD中，DB= ， ∴EB=GD= ． 26. 解：（1）由y=0得，ax2-2ax-3a=0，∵a≠0，∴x2-2x-3=0，解得 x1=-1，x2=3， ∴点A的坐标（-1，0），点B的坐标（3，0）；（2）由y=ax2-2ax-3a，令x=0，得y=-3a，∴C（0，-3a），又 ∵y=ax2-2ax-3a=a（x-1）2-4a，得D（1，-4a），∴DH=1，CH=-4a（-3a）=-a，∴-a=1，∴a=-1，∴C（0，3），D（1，4），设直线CD的解析式为y=kx+b，把C、D两点的坐标代入得，，解得， ∴直线CD的解析式为y=x+3；（3）存在．由（2）得，E（-3，0），N（-
保密 ★ 启用前
2016年中考真题数学试卷
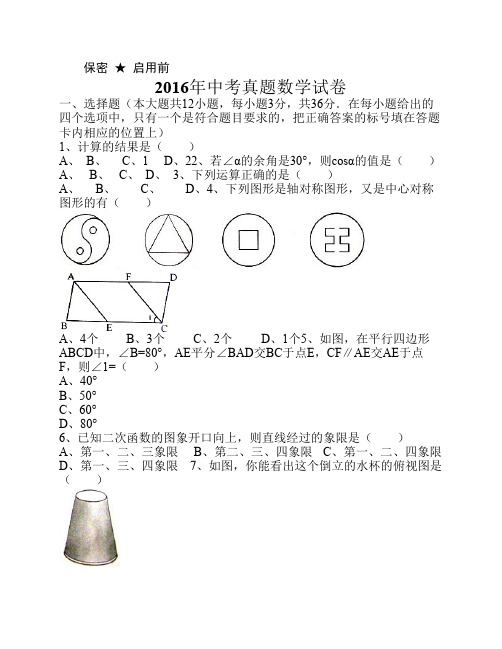
一、选择题（本大题共12小题，每小题3分，共36分．在每小题给出的四个选项中，只有一个是符合题目要求的，把正确答案的标号填在答题卡内相应的位置上） 1、计算的结果是（） A、 B、 C、1 D、22、若∠α的余角是30°，则cosα的值是（） A、 B、 C、 D、 3、下列运算正确的是（） A、 B、 C、 D、4、下列图形是轴对称图形，又是中心对称图形的有（）

(广东省)2016-2019年数学中考试题及答案(可编辑修改word版)

2016 年广东省中考数学试卷一、选择题（共10 小题，每小题3 分，满分30 分）1．（3 分）﹣2 的相反数是（）A．2 B．﹣2 C． D．﹣2．（3 分）如图所示，a 与b 的大小关系是（）A．a＜b B．a＞b C．a=b D．b=2a3．（3 分）下列所述图形中，是中心对称图形的是（）A．直角三角形B．平行四边形C．正五边形D．正三角形4．（3 分）据广东省旅游局统计显示，2016 年4 月全省旅游住宿设施接待过夜游客约27700000 人，将27700000 用科学记数法表示为（）A．0.277×107 B．0.277×108 C．2.77×107 D．2.77×1085．（3 分）如图，正方形ABCD 的面积为1，则以相邻两边中点连线EF 为边正方形EFGH 的周长为（）A． B．2C．+1 D．2 +16．（3 分）某公司的拓展部有五个员工，他们每月的工资分别是3000 元，4000 元，5000 元，7000 元和10000 元，那么他们工资的中位数是（）A．4000 元B．5000 元C．7000 元D．10000 元7．（3 分）在平面直角坐标系中，点P（﹣2，﹣3）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限8．（3 分）如图，在平面直角坐标系中，点A 的坐标为（4，3），那么cosα 的值是（）A．B．C．D．9．（3 分）已知方程x﹣2y+3=8，则整式x﹣2y 的值为（）A．5 B．10 C．12 D．1510．（3 分）如图，在正方形ABCD 中，点P 从点A 出发，沿着正方形的边顺时针方向运动一周，则△APC 的面积y 与点P 运动的路程x 之间形成的函数关系图象大致是（）A． B． C． D．二、填空题（共6 小题，每小题4 分，满分24 分）11．（4 分）9 的算术平方根是．12．（4 分）分解因式：m2﹣4= ．13．（4 分）不等式组的解集是．14．（4 分）如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC，已知圆锥的高h 为12cm，OA=13cm，则扇形AOC 中的长是cm（计算结果保留π）．15．（4 分）如图，矩形ABCD 中，对角线AC=2，E 为BC 边上一点，BC=3BE，将矩形ABCD 沿AE 所在的直线折叠，B 点恰好落在对角线AC 上的B′处，则AB= ．16．（4 分）如图，点P 是四边形ABCD 外接圆上任意一点，且不与四边形顶点重合，若AD 是⊙O 的直径，AB=BC=CD．连接PA、PA、PC，若PA=a，则点A 到PB 和PC 的距离之和AE+AF= ．三、解答题（共3 小题，每小题6 分，满分18 分）17．（6 分）计算：|﹣3|﹣（2016+sin30°）0﹣（﹣）﹣1．18．（6 分）先化简，再求值：•+，其中a= ﹣1．19．（6 分）如图，已知△ABC 中，D 为AB 的中点．（1）请用尺规作图法作边AC 的中点E，并连结DE（保留作图痕迹，不要求写作法）；（2）在（1）的条件下，若DE=4，求BC 的长．四、解答题（共3 小题，每小题7 分，满分21 分）20．（7 分）某工程队修建一条长1200m 的道路，采用新的施工方式，工效提升了50%，结果提前4 天完成任务．（1）求这个工程队原计划每天修建道路多少米？（2）在这项工程中，如果要求工程队提前2 天完成任务，那么实际平均每天修建道路的工效比原计划增加百分之几？21．（7 分）如图，Rt△ABC 中，∠B=30°，∠ACB=90°，CD⊥AB 交AB 于D，以CD 为较短的直角边向△CDB 的同侧作Rt△DEC，满足∠E=30°，∠DCE=90°，再用同样的方法作Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC，∠ HCI=90°．若AC=a，求CI 的长．22．（7 分）某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：（1）这次活动一共调查了名学生；（2）补全条形统计图；（3）在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于度；（4）若该学校有1500 人，请你估计该学校选择足球项目的学生人数约是人．五、解答题（共3 小题，每小题9 分，满分27 分）23．（9 分）如图，在直角坐标系中，直线y=kx+1（k≠0）与双曲线y=（x＞0）相交于点P（1，m ）．（1）求k 的值；（2）若点Q 与点P 关于直线y=x 成轴对称，则点Q 的坐标是Q（）；（3）若过P、Q 二点的抛物线与y 轴的交点为N（0，），求该抛物线的函数解析式，并求出抛物线的对称轴方程．24．（9 分）如图，⊙O 是△ABC 的外接圆，BC 是⊙O 的直径，∠ABC=30°，过点B 作⊙O 的切线BD，与CA 的延长线交于点D，与半径AO 的延长线交于点E，过点A 作⊙O 的切线AF，与直径BC 的延长线交于点F．（1）求证：△ACF∽△DAE；（2）若S△AOC=，求DE 的长；（3）连接EF，求证：EF 是⊙O 的切线．25．（9 分）如图，BD 是正方形ABCD 的对角线，BC=2，边BC 在其所在的直线上平移，将通过平移得到的线段记为PQ，连接PA、QD，并过点Q 作QO⊥BD，垂足为O，连接OA、OP．（1）请直接写出线段BC 在平移过程中，四边形APQD 是什么四边形？（2）请判断OA、OP 之间的数量关系和位置关系，并加以证明；（3）在平移变换过程中，设y=S△OPB，BP=x（0≤x≤2），求y 与x 之间的函数关系式，并求出y 的最大值．2016 年广东省中考数学试卷一、选择题（共10 小题，每小题3 分，满分30 分）1．（3 分）（2016）﹣2 的相反数是（）A．2 B．﹣2 C． D．﹣【考点】相反数．【分析】根据相反数的意义，只有符号不同的数为相反数．【解答】解：根据相反数的定义，﹣2 的相反数是2．故选：A．【点评】本题考查了相反数的意义．注意掌握只有符号不同的数为相反数，0 的相反数是0．2．（3 分）（2016•广东）如图所示，a 与b 的大小关系是（）A．a＜b B．a＞b C．a=b D．b=2a【考点】有理数大小比较．【分析】根据数轴判断出a，b 与零的关系，即可．【解答】根据数轴得到a＜0，b＞0，∴b＞a，故选A【点评】此题是有理数大小的比较，主要考查了识别数轴上的点表示的数，也是解本题的难点．3．（3 分）（2016•广东）下列所述图形中，是中心对称图形的是（）A．直角三角形B．平行四边形C．正五边形D．正三角形【考点】中心对称图形．【分析】根据中心对称图形的定义对各选项分析判断即可得解．【解答】解：A、直角三角形不是中心对称图形，故本选项错误；B、平行四边形是中心对称图形，故本选项正确；C、正五边形不是中心对称图形，故本选项错误；D、正三角形不是中心对称图形，故本选项错误．故选B．【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180 度后两部分重合．4．（3 分）（2016•广东）据广东省旅游局统计显示，2016 年4 月全省旅游住宿设施接待过夜游客约27700000 人，将27700000 用科学记数法表示为（）A．0.277×107 B．0.277×108 C．2.77×107 D．2.77×108【考点】科学记数法—表示较大的数．【分析】科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数．确定n 的值时，整数位数减1 即可．当原数绝对值＞10 时，n 是正数；当原数的绝对值＜1 时，n 是负数．【解答】解：将27700000 用科学记数法表示为2.77×107，故选C．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n 的形式，其中1≤|a|＜10，n 为整数，表示时关键要正确确定a 的值以及n 的值．5．（3 分）（2016•广东）如图，正方形ABCD 的面积为1，则以相邻两边中点连线EF 为边正方形EFGH 的周长为（）A． B．2C．+1 D．2 +1【考点】正方形的性质．【分析】由正方形的性质和已知条件得出BC=CD==1，∠BCD=90°，CE=CF= ，得出△CEF 是等腰直角三角形，由等腰直角三角形的性质得出EF 的长，即可得出正方形EFGH 的周长．【解答】解：∵正方形ABCD 的面积为1，∴BC=CD==1，∠BCD=90°，∵E、F 分别是BC、CD 的中点，∴CE=BC= ，CF= CD=，∴CE=CF，∴△CEF 是等腰直角三角形，∴EF= CE=，∴正方形EFGH 的周长=4EF=4×=2 ；故选：B．【点评】本题考查了正方形的性质、等腰直角三角形的判定与性质；熟练掌握正方形的性质，由等腰直角三角形的性质求出EF 的长是解决问题的关键．6．（3 分）（2016•广东）某公司的拓展部有五个员工，他们每月的工资分别是3000元，4000 元，5000 元，7000 元和10000 元，那么他们工资的中位数是（）A．4000 元B．5000 元C．7000 元D．10000 元【考点】中位数．【分析】找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．【解答】解：从小到大排列此数据为：3000 元，4000 元，5000 元，7000 元，10000 元，5000 元处在第3 位为中位数，故他们工资的中位数是5000元．故选B．【点评】本题属于基础题，考查了确定一组数据的中位数的能力．一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．7．（3 分）（2016•广东）在平面直角坐标系中，点P（﹣2，﹣3）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限【考点】点的坐标．【分析】根据各象限内点的坐标特征解答即可．【解答】解：点P（﹣2，﹣3）所在的象限是第三象限．故选C．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）8．（3 分）（2016•广东）如图，在平面直角坐标系中，点A 的坐标为（4，3），那么cosα 的值是（）A． B． C． D．【考点】锐角三角函数的定义；坐标与图形性质．【分析】利用勾股定理列式求出OA，再根据锐角的余弦等于邻边比斜边列式即可．【解答】解：由勾股定理得OA==5，所以cosα=．故选D．【点评】本题考查了锐角三角函数的定义，坐标与图形性质，勾股定理，熟记概念并准确识图求出OA 的长度是解题的关键．9．（3 分）（2016•广东）已知方程x﹣2y+3=8，则整式x﹣2y 的值为（）A．5 B．10 C．12 D．15【考点】等式的性质．【分析】根据等式的性质1：等式两边同时加上﹣3，可得x﹣2y=5．【解答】解：由x﹣2y+3=8 得：x﹣2y=8﹣3=5，故选A【点评】本题考查了等式的性质，非常简单，属于基础题；熟练掌握等式的性质是本题的关键，也运用了整体的思想．10．（3 分）（2016•广东）如图，在正方形ABCD 中，点P 从点A 出发，沿着正方形的边顺时针方向运动一周，则△APC 的面积y 与点P 运动的路程x 之间形成的函数关系图象大致是（）A． B． C． D．【考点】动点问题的函数图象．【专题】动点型；函数思想．【分析】分P 在AB、BC、CD、AD 上四种情况，表示出y 与x 的函数解析式，确定出大致图象即可．【解答】解：设正方形的边长为a，当P 在AB 边上运动时，y=ax；当P 在BC 边上运动时，y=a（2a﹣x）=﹣ax+a2；当P 在CD 边上运动时，y= a（x﹣2a）= ax﹣a2；当P 在AD 边上运动时，y=a（4a﹣x）=﹣ax﹣2a2，大致图象为：故选C．【点评】此题考查了动点问题的函数图象，解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．二、填空题（共6 小题，每小题4 分，满分24 分）11．（4 分）（2016•广东）9 的算术平方根是 3 ．【考点】算术平方根．【分析】9 的平方根为±3，算术平方根为非负，从而得出结论．【解答】解：∵（±3）2=9，∴9 的算术平方根是|±3|=3．故答案为：3．【点评】本题考查了数的算式平方根，解题的关键是牢记算术平方根为非负．12．（4 分）（2016•广东）分解因式：m2﹣4= （m+2）（m﹣2）．【考点】因式分解-运用公式法．【专题】计算题．【分析】本题刚好是两个数的平方差，所以利用平方差公式分解则可．平方差公式：a2﹣b2=（a+b）（a﹣b）．【解答】解：m2﹣4=（m+2）（m﹣2）．故答案为：（m+2）（m﹣2）．【点评】本题考查了平方差公式因式分解．能用平方差公式进行因式分解的式子的特点是：两项平方项；符号相反．13．（4 分）（2016•广东）不等式组的解集是﹣3＜x≤1．【考点】解一元一次不等式组．【专题】计算题．【分析】分别解两个不等式得到x≤1和x＞﹣3，然后利用大小小大中间找确定不等式组的解集．【解答】解：，解① 得x≤1，解②得x＞﹣3，所以不等式组的解集为﹣3＜x≤1．故答案为﹣3＜x≤1．【点评】本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．14．（4 分）（2016•广东）如图，把一个圆锥沿母线OA 剪开，展开后得到扇形AOC，已知圆锥的高h 为12cm，OA=13cm，则扇形AOC 中的长是10π cm（计算结果保留π）．【考点】圆锥的计算；弧长的计算．【分析】根据的长就是圆锥的底面周长即可求解．【解答】解：∵圆锥的高h 为12cm，OA=13cm，∴圆锥的底面半径为=5cm，∴圆锥的底面周长为10πcm，∴扇形AOC 中的长是10πcm，故答案为：10π．【点评】本题考查了圆锥的计算，解题的关键是了解圆锥的底面周长等于展开扇形的弧长，难度不大．15．（4 分）（2016•广东）如图，矩形ABCD 中，对角线AC=2，E 为BC 边上一点，BC=3BE，将矩形ABCD 沿AE 所在的直线折叠，B点恰好落在对角线AC 上的B′ 处，则AB= ．【考点】矩形的性质；翻折变换（折叠问题）．【分析】先根据折叠得出BE=B′E，且∠AB′E=∠B=90°，可知△EB′C 是直角三角形，由已知的BC=3BE 得EC=2B′E，得出∠ACB=30°，从而得出AC 与AB 的关系，求出AB 的长．【解答】解：由折叠得：BE=B′E，∠AB′E=∠B=90°，∴∠EB′C=90°，∵BC=3BE，∴EC=2BE=2B′E，∴∠ACB=30°，在Rt△ABC 中，AC=2AB，∴AB= AC= ×2 = ，故答案为：．【点评】本题考查了矩形的性质和翻折问题，明确翻折前后的图形全等是本题的关键，同时还运用了直角三角形中如果一条直角边是斜边的一半，那么这条直角边所对的锐角是30°这一结论，是常考题型．16．（4 分）（2016•广东）如图，点P 是四边形ABCD 外接圆上任意一点，且不与四边形顶点重合，若AD 是⊙O 的直径，AB=BC=CD．连接PA、PA、PC，若PA=a，则点A 到PB 和PC 的距离之和AE+AF= a ．【考点】圆周角定理；勾股定理；解直角三角形．【分析】如图，连接OB、OC．首先证明∠AOB=∠BOC=∠COD=60°，推出∠APB= ∠AOB=30°，∠APC= ∠AOC=60°，根据AE=AP•sin30°，AF=AP•sin60°，即可解决问题．【解答】解：如图，连接OB、OC．∵AD 是直径，AB=BC=CD，∴==，∴∠AOB=∠BOC=∠COD=60°，∴∠APB= ∠AOB=30°，∠APC= ∠AOC=60°，在Rt△APE 中，∵∠AEP=90°，∴AE=AP•sin30°=a，在Rt△APF 中，∵∠AFP=90°，∴AF=AP•sin60°=a，∴AE+AF= a．故答案为a．【点评】本题考查圆周角定理、锐角三角函数等知识，解题的关键是学会添加常用辅助线，学会利用直角三角形解决问题，属于中考常考题型．三、解答题（共3 小题，每小题6 分，满分18 分）17．（6 分）（2016•广东）计算：|﹣3|﹣（2016+sin30°）0﹣（﹣）﹣1．【考点】实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．【专题】计算题．【分析】根据实数的运算顺序，首先计算乘方，然后从左向右依次计算，求出算式|﹣3|﹣（2016+sin30°）0﹣（﹣）﹣1的值是多少即可．【解答】解：|﹣3|﹣（2016+sin30°）0﹣（﹣）﹣1=3﹣1+2=2+2=4．【点评】（1）此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到有的顺序进行．另外，有理数的运算律在实数范围内仍然适用．（2）此题还考查了零指数幂的运算，要熟练掌握，解答此题的关键是要明确：①a0=1（a≠0）；②00≠1．（3）此题还考查了特殊角的三角函数值，要牢记30°、45°、60°角的各种三角函数值．（4）此题还考查了负整数指数幂的运算，要熟练掌握，解答此题的关键是要明确：①a﹣p=（a≠0，p 为正整数）；②计算负整数指数幂时，一定要根据负整数指数幂的意义计算；③当底数是分数时，只要把分子、分母颠倒，负指数就可变为正指数．18．（6 分）（2016•广东）先化简，再求值：•+ ，其中a=﹣1．【考点】分式的化简求值．【专题】计算题；分式．【分析】原式第一项约分后两项通分并利用同分母分式的加法法则计算，得到最简结果，把a 的值代入计算即可求出值．【解答】解：原式=•+=+==，当a= ﹣1 时，原式=== +1．【点评】此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．19．（6 分）（2016•广东）如图，已知△ABC 中，D 为AB 的中点．（1）请用尺规作图法作边AC 的中点E，并连结DE（保留作图痕迹，不要求写作法）；（2）在（1）的条件下，若DE=4，求BC 的长．【考点】三角形中位线定理；作图—基本作图．【分析】（1）作线段AC 的垂直平分线即可．（2）根据三角形中位线定理即可解决．【解答】解：（1）作线段AC 的垂直平分线MN 交AC 于E，点 E 就是所求的点．（2）∵AD=DB，AE=EC，∴DE∥BC，DE= BC，∵DE=4，∴BC=8．【点评】本题考查基本作图、三角形中位线定理等知识，解题的关键是掌握线段垂直平分线的作法，记住三角形的中位线定理，属于中考常考题型．四、解答题（共3 小题，每小题7 分，满分21 分）20．（7 分）（2016•广东）某工程队修建一条长1200m 的道路，采用新的施工方式，工效提升了50%，结果提前4 天完成任务．（1）求这个工程队原计划每天修建道路多少米？（2）在这项工程中，如果要求工程队提前2 天完成任务，那么实际平均每天修建道路的工效比原计划增加百分之几？【考点】分式方程的应用．【分析】（1）设原计划每天修建道路x 米，则实际每天修建道路1.5x 米，根据题意，列方程解答即可；（2）由（1）的结论列出方程解答即可．【解答】解：（1）设原计划每天修建道路x 米，可得：，解得：x=100，经检验x=100 是原方程的解，答：原计划每天修建道路100 米；（2）设际平均每天修建道路的工效比原计划增加y%，可得：，解得：y=20，经检验y=20 是原方程的解，答：实际平均每天修建道路的工效比原计划增加百分之二十．【点评】本题考查了由实际问题抽象出分式方程，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程．21．（7 分）（2016•广东）如图，Rt△ABC 中，∠B=30°，∠ACB=90°，CD⊥AB 交AB 于D，以CD 为较短的直角边向△CDB 的同侧作Rt△DEC，满足∠E=30°，∠D C E=90°，再用同样的方法作Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC，∠HCI=90°．若AC=a，求CI 的长．【考点】勾股定理；含30 度角的直角三角形．【分析】在Rt△ACD 中，利用30 度角的性质和勾股定理求CD 的长；同理在Rt△ECD 中求FC 的长，在Rt△FCG 中求CH 的长；最后在Rt△HCI 中，利用30 度角的性质和勾股定理求CI 的长．【解答】解：在Rt△ACB 中，∠B=30°，∠ACB=90°，∴∠A=90°﹣30°=60°，∵CD⊥AB，∴∠ADC=90°，∴∠ACD=30°，在Rt△ACD 中，AC=a，∴AD= a，由勾股定理得：CD==，同理得：FC=×=，CH=×=，在Rt△HCI 中，∠I=30°，∴HI=2HC= ，由勾股定理得：CI==，答：CI 的长为．【点评】本题考查了勾股定理和直角三角形含30°角的性质，在直角三角形中，30°角所对的直角边等于斜边的一半，这一性质经常运用，必须熟练掌握；同时在运用勾股定理和直角三角形含30°角的性质时，一定要书写好所在的直角三角形，尤其是此题多次运用了这一性质．22．（7 分）（2016•广东）某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：（1）这次活动一共调查了 250 名学生；（2）补全条形统计图；（3）在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于 108 度；（4）若该学校有1500 人，请你估计该学校选择足球项目的学生人数约是 480 人．【考点】条形统计图；用样本估计总体；扇形统计图．【分析】（1）由“足球”人数及其百分比可得总人数；（2）根据各项目人数之和等于总人数求出“篮球”的人数，补全图形即可；（3）用“篮球”人数占被调查人数的比例乘以360°即可；（4）用总人数乘以样本中足球所占百分比即可得．【解答】解：（1）这次活动一共调查学生：80÷32%=250（人）；（2）选择“篮球”的人数为：250﹣80﹣40﹣55=75（人），补全条形图如图：（3）选择篮球项目的人数所在扇形的圆心角为：×360°=108°；（4）估计该学校选择足球项目的学生人数约是：1500×32%=480（人）；故答案为：（1）250；（3）108；（4）480．【点评】本题考查了条形统计图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．五、解答题（共3 小题，每小题9 分，满分27 分）23．（9 分）（2016•广东）如图，在直角坐标系中，直线y=kx+1（k≠0）与双曲线y= （x＞0）相交于点P（1，m ）．（1）求k 的值；（2）若点Q 与点P 关于直线y=x 成轴对称，则点Q 的坐标是Q（ 2，1 ）；（3）若过P、Q 二点的抛物线与y 轴的交点为N（0，），求该抛物线的函数解析式，并求出抛物线的对称轴方程．【考点】反比例函数与一次函数的交点问题；待定系数法求二次函数解析式．【分析】（1）直接利用图象上点的坐标性质进而代入求出即可；（2）连接PO，QO，PQ，作PA⊥y 轴于A，QB⊥x 轴于B，于是得到PA=1，OA=2，根据点Q 与点P 关于直线y=x 成轴对称，得到直线y=x 垂直平分PQ，根据线段垂直平分线的性质得到OP=OQ，根据全等三角形的性质得到QB=PA=1，OB=OA=2，于是得到结论；（3）设抛物线的函数解析式为y=ax2+bx+c，把P、Q、N（0，）代入y=ax2+bx+c，解方程组即可得到结论．【解答】解：（1）∵直线y=kx+1 与双曲线y=（x＞0）交于点A（1，m），∴m=2，把A（1，2）代入y=kx+1 得：k+1=2，解得：k=1；（2）连接PO，QO，PQ，作PA⊥y 轴于A，QB⊥x 轴于B，则PA=1，OA=2，∵点Q 与点P 关于直线y=x 成轴对称，∴直线y=x 垂直平分PQ，∴OP=OQ，∴∠POA=∠QOB，在△OPA 与△OQB 中，，∴△POA≌△QOB，∴QB=PA=1，OB=OA=2，∴Q（2，1）；故答案为：2，1；（3）设抛物线的函数解析式为y=ax2+bx+c，∵过P、Q 二点的抛物线与y 轴的交点为N（0，），∴，解得：，∴抛物线的函数解析式为y=﹣x2+x+ ，∴对称轴方程x=﹣=．【点评】本题考查了一次函数和反比例函数的交点问题，全等三角形的判定和性质，解题需把点的坐标代入函数解析式，灵活利用方程组求出所需字母的值，从而求出函数解析式，熟练掌握待定系数法求函数的解析式是解题的关键．24．（9 分）（2016•广东）如图，⊙O 是△ABC 的外接圆，BC 是⊙O 的直径，∠ ABC=30°，过点B 作⊙O 的切线BD，与CA 的延长线交于点D，与半径AO 的延长线交于点E，过点A 作⊙O 的切线AF，与直径BC 的延长线交于点F．（1）求证：△ACF∽△DAE；（2）若S△AOC=，求DE 的长；（3）连接EF，求证：EF 是⊙O 的切线．【考点】相似形综合题．【分析】（1）根据圆周角定理得到∠BAC=90°，根据三角形的内角和得到∠ ACB=60°根据切线的性质得到∠ OAF=90°，∠DBC=90°，于是得到∠ D=∠ AFC=30°由相似三角形的判定定理即可得到结论；（2）根据S△AOC= ，得到S△ACF= ，通过△ACF∽△DAE，求得S△DAE= ，过A 作AH⊥DE 于H，解直角三角形得到AH=DH= DE，由三角形的面积公式列方程即可得到结论；（3）根据全等三角形的性质得到OE=OF，根据等腰三角形的性质得到∠OFG=（180°﹣∠EOF）=30°，于是得到∠AFO=∠GFO，过O 作OG⊥EF 于G，根据全等三角形的性质得到OG=OA，即可得到结论．【解答】（1）证明：∵BC 是⊙O 的直径，∴∠BAC=90°，∵∠ABC=30°，∴∠ACB=60°∵OA=OC，∴∠AOC=60°，∵AF 是⊙O 的切线，∴∠OAF=90°，∴∠AFC=30°，∵DE 是⊙O 的切线，∴∠DBC=90°，∴∠D=∠AFC=30，∵∠DAE=ACF=120°，∴△ACF∽△DAE；（2）∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°，∴∠CAF=30°，∴∠CAF=∠AFC，∴AC=CF∴OC=CF，∵S△AOC= ，∴S△ACF= ，∵∠ABC=∠AFC=30°，∴AB=AF，∵AB= BD，∴AF= BD，∴∠BAE=∠BEA=30°，∴AB=BE=AF，∴=，∵△ACF∽△DAE，∴=（）2=，∴S△DAE= ，过A 作AH⊥DE 于H，∴AH= DH= DE，∴S△ADE= DE•AH=×•DE2= ，∴DE= ；（3）∵∠EOF=∠AOB=120°，在△AOF 与△BOE 中，，∴△AOF≌△BEO，∴OE=OF，∴∠OFG= （180°﹣∠EOF）=30°，∴∠AFO=∠GFO，过O 作OG⊥EF 于G，∴∠OAF=∠OGF=90°，在△AOF 与△OGF 中，，∴△AOF≌△GOF，∴OG=OA，∴EF 是⊙O 的切线．【点评】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，切线的判定和性质，圆周角定理，直角三角形的性质，证得△ACF∽△DAE 是解题的关键．25．（9 分）（2016•广东）如图，BD 是正方形ABCD 的对角线，BC=2，边BC 在其所在的直线上平移，将通过平移得到的线段记为PQ，连接PA、QD，并过点Q 作QO⊥BD，垂足为O，连接OA、OP．（1）请直接写出线段BC 在平移过程中，四边形APQD 是什么四边形？（2）请判断OA、OP 之间的数量关系和位置关系，并加以证明；（3）在平移变换过程中，设y=S△OPB，BP=x（0≤x≤2），求y 与x 之间的函数关系式，并求出y 的最大值．【考点】四边形综合题．【分析】（1）根据平移的性质，可得PQ，根据一组对边平行且相等的四边形是平行四边形，可得答案；（2）根据正方形的性质，平移的性质，可得PQ 与AB 的关系，根据等腰直角三角形的判定与性质，可得∠PQOPQO，根据全等三角形的判定与性质，可得AO 与OP 的数量关系，根据余角的性质，可得AO 与OP 的位置关系；（3）根据等腰直角三角形的性质，可得OE 的长，根据三角形的面积公式，可得二次函数，根据二次函数的性质，可得到答案．【解答】（1）四边形APQD 为平行四边形；（2）OA=OP，OA⊥OP，理由如下：∵四边形ABCD 是正方形，∴AB=BC=PQ，∠ABO=∠OBQ=45°，∵OQ⊥BD，∴∠PQO=45°，∴∠ABO=∠OBQ=∠PQO=45°，∴OB=OQ，在△AOB 和△OPQ 中，∴△AOB≌△POQ（SAS），∴OA=OP，∠AOB=∠POQ，∴∠AOP=∠BOQ=90°，∴OA⊥OP；（3）如图，过O 作OE⊥BC 于E．①如图1，当P 点在B 点右侧时，则BQ=x+2，OE=，∴y=×•x，即y=（x+1）2﹣，又∵0≤x≤2，∴当x=2 时，y 有最大值为2；②如图2，当P 点在B 点左侧时，则BQ=2﹣x，OE= ，∴y=×•x，即y=﹣（x﹣1）2+，又∵0≤x≤2，∴当x=1 时，y 有最大值为；综上所述，∴当x=2 时，y 有最大值为2；【点评】本题考查了二次函数综合题，利用平行四边形的判定是解题关键；利用全等三角形的判定与性质是解题关键；利用等腰直角三角形的性质的出OE 的长是解题关键，又利用了二次函数的性质．2017 年广东省中考数学试卷一、选择题（本大题共10 小题，每小题3 分，共30 分）1．5 的相反数是（）A．B．5 C．﹣D．﹣52.“一带一路”倡议提出三年以来，广东企业到“一带一路”国家投资越来越活跃，据商务部门发布的数据显示，2016 年广东省对沿线国家的实际投资额超过4000000000 美元，将4000000000 用科学记数法表示为（）A．0.4×109B．0.4×1010C．4×109D．4×10103.已知∠A=70°，则∠A 的补角为（）A．110°B．70° C．30° D．20°4.如果2 是方程x2﹣3x+k=0 的一个根，则常数k 的值为（）A．1 B．2 C．﹣1 D．﹣25.在学校举行“阳光少年，励志青春”的演讲比赛中，五位评委给选手小明的平分分别为：90，85，90，80，95，则这组数据的众数是（）A．95 B．90 C．85 D．806.下列所述图形中，既是轴对称图形又是中心对称图形的是（）A．等边三角形B．平行四边形C．正五边形D．圆7.如图，在同一平面直角坐标系中，直线y=k1x（k1≠0）与双曲线y=（k2≠0）相交于A，B 两点，已知点A 的坐标为（1，2），则点B 的坐标为（）A．（﹣1，﹣2）B．（﹣2，﹣1）C．（﹣1，﹣1）D．（﹣2，﹣2）8．下列运算正确的是（）A．a+2a=3a2B．a3•a2=a5 C．（a4）2=a6D．a4+a2=a49.如图，四边形ABCD 内接于⊙O，DA=DC，∠CBE=50°，则∠DAC 的大小为（）A．130°B．100°C．65° D．50°10.如图，已知正方形ABCD，点E 是BC 边的中点，DE 与AC 相交于点F，连接BF，下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（）。

2016年全国中考数学真题分类一元二次方程及应用(习题解析)

2016年全国中考数学真题分类一元二次方程及其应用一、选择题8．（2016浙江衢州，8，3分）已知关于的一元二次方程x2－2x－k＝0有两个不相等的实数根，则实数k的取值范围是（）A．k≥1 B．k＞1 C．k≥－1 D．k＞－1【答案】D9．（2016山东烟台，9，3分）若x1，x2是一元二次方程x2﹣2x﹣1=0的两个根，则x12﹣x1+x2的值为（）A．﹣1 B．0 C．2 D．3【答案】D8．（2016山东青岛，8，3分）输入一组数据，按下列程序进行计算，输出结果如表： x 20.5 20.6 20.7 20.8 20.9输出﹣13.75 ﹣8.04 ﹣2.31 3.44 9.21分析表格中的数据，估计方程（x+8）2﹣826=0的一个正数解x的大致范围为（）A．20.5＜x＜20.6 B．20.6＜x＜20.7 C．20.7＜x＜20.8 D．20.8＜x＜20.9【答案】C9. （2016兰州，9，4分）公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m2，求原正方形空地的边长，设原正方形的空地的边长为x m，则可列方程为（）C. (x-1) (x-2) =18D. x 2+3x+16=0 【答案】C1．(2016江西，5，3分）设βα,是一元二次方程0122=-+x x 的两个根，则αβ的值是（）． A. 2 B. 1 C. -2 D. -1【答案】 D.5. （2016兰州，5，4分）一元二次方程x 2+2x+1=0的根的情况是（） A. 有一个实数根 B. 有两个相等的实数根 C. 有两个不想等的实数根 D. 没有实数根【答案】B7．（2016四川自贡，7，4分）已知关于x 的一元二次方程x 2+2x ﹣（m ﹣2）=0有实数根，则m 的取值范围是（） A ．m ＞1B ．m ＜1C ．m ≥1D ．m ≤1【答案】C ．5.（2016，浙江金华，5,3分）一元二次方程2320x x --=的两根为12x x ，，则下列结论正确的是（ )A. 1212x x =-=，B. 121,2x x ==-C. 123x x +=D. 122x x = 【答案】C2.(2016浙江丽水，6，3分）下列一元二次方程没有实数根的是（） A ．x 2+2x+1=0 B ．x 2+x+2=0 C ．x 2﹣1=0 D ．x 2﹣2x ﹣1=0【答案】B ．3.(2016福州，12，3分)下列选项中，能使关于x 的一元二次方程ax 2－4x ＋c ＝0一定有实数根的是( )A ．a ＞0B ．a ＝0C ．c ＞0D ．c ＝0 【答案】DA.无实数根B.有一正根一负根C.有两个正根D.有两个负根答案：C.5.（2016山东枣庄，5，3分）已知关于x 的方程230x x a ++=有一个根为-2，则另一个根为（） A ．5 B ．－1 C ．2 D ．－5 【答案】B6.（2016山东枣庄，8，3分）若关于x 的一元二次方程2210x x kb -++=有两个不相等的实数根,则一次函数y kx b =+的图象可能是 ( ) 【答案】B9．(2016年湖北荆门，9，3分)已知3是关于x 的方程x 2－(m ＋1)x ＋2m ＝0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC 的两条边长，则△ABC 的周长为( ) A ．7 B ．10 C ．11 D ．10或11 [答案]D7. (2016四川乐山，9,3分）若t 为实数，关于x 的方程2420x x t -+-=的两个非负实数根为a 、b ，则代数式22(1)(1)a b --的最小值是（）()A 15- ()B 16- ()C 15 ()D 16答案：A8.8．（2016台州， 8，4分）有x 支球队参加篮球比赛，共比赛了45场，每两队之间都比赛一场，则下列方程中符合题意的是（）A ．1(1)452x x -= B ．1(1)452x x += C ．(1)45x x -= D ．(1)45x x += 【答案】A 9. 10. 11.12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 二、填空题1.（2016聊城，14,3分）如果关于x 的一元二次方程0132=--x kx 有两个不相等的实根，那么k的取值范围是【答案】049≠-k k 且（2016山东菏泽，12，3分）已知m 是关于x 的方程x 2﹣2x ﹣3=0的一个根，则2m 2﹣4m= ．【答案】 62.（2016山东德州，15，4分）方程2230x x x --=12的两个根为x ,x ，则22=12x +x答案：134. 12.（2016湖北黄石，12，3分）关于x 的一元二次方程01222=+-+m x x 的两实数根之积为负，则实数m 的取值范围是_______________. 【答案】21>m 14.（2016江苏淮安，14，3分）若关于x 的x 2+6x+k=0一元二次方程有两个相等的实数根，则k ＝ . 【答案】93.．(2016四川宜宾，14，3分)已知一元二次方程x 2＋3x －4＝0的两根为x 1，x 2，则x 12＋x 1x 2＋x 22＝______． [答案]1314．（2016湖南长沙，14，3分）若关于x 的一元二次方程x 2﹣4x ﹣m=0有两个不相等的实数根，则实数m 的取值范围是．答案：m ＞﹣4．4.（2016四川广安，14，3分）某市为治理污水，需要铺设一段全长600m 的污水排放管道，铺设120m ，为加快施工速度，后来每天比原计划增加20m ，结果共有11天完成这一任务，求原计划每天铺设管道的长度．如果设原计划每天铺设x m 管道，那么根据题意，可列方程 ▲ ．【答案】120x ＋600－120x ＋20＝11（或120x ＋480x ＋20＝11）．13．（2016江苏连云港，13，3分）已知关于x 的方程x 2+x+2a ﹣1=0的一个根是0，则a= ．答案：．7.8.9.10.11.12.13.14.15.16.17.18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.38. 39. 三、解答题1.（2016兰州，21(2)，5分）2y 2+4y=y+2【答案】原方程可化为2,2+3y-2=0，解得y 1=2;y 2=-22．（2016，山东淄博，19，5分）解方程：x 2+4x ﹣1=0．解：∵x 2+4x ﹣1=0 ∴x 2+4x=1 ∴x 2+4x+4=1+4 ∴（x+2）2=5 ∴x=﹣2±∴x 1=﹣2+，x 2=﹣2﹣．17．（2016·山西，17，7分）解方程：93222-=-x x ）（考点：解一元二次方程分析：方法一：观察方程，可先分解因式，然后提取x -3，利用公式法求解方法二：将方程化为一般式，利用公式法求解解答：解法一：原方程可化为)3)(3(322-+=-x x x ）（……………………………（1分） 0)3)(3()3(22=-+--x x x ． ……………………………（2分） 0)]3()3(2)[3(=+---x x x ． ……………………………（3分） 0)9-)(3(=-x x ． ……………………………（4分） ∴ x -3=0或x -9=0． ……………………………（5分） ∴ 31=x ，92=x ． ……………………………（7分）解法二：原方程可化为027122=+-x x ……………………………（3分）这里a =1，b =-12，c =27． ∵0362714)12(422>=⨯⨯--=-ac b ∴2612123612±=⨯±=x ． ……………………………（5分）因此原方程的根为 31=x ，92=x ． ……………………………（7分）1.(2016年甘肃白银、张掖，21，8分)已知关于x 的方程x 2＋mx ＋m －2＝0． (1)若此方程的一个根为1，求m 的值；(2)求证：不论m 取何实数，此方程都有两个不相等的实数根．解：(1)将x ＝1代入原方程，得 12＋1·m ＋m －2＝0．解得m ＝12．(2)△＝m 2－4(m －2)＝m 2－4m ＋8＝(m －2)2＋4．无论m 取何实数，(m －2)2＋4＞0，即△＞0，所以原方程有两个不相等的实数根．21．（2016湖北孝感，21，9分）已知关于x 的一元二次方程0122=-+-m x x 有两个实数根1x ，2x ．（1）求m 的取值范围；（4分）（2）当2122216x x x x =+时，求m 的值．（5分）解：（1）∵原方程有两个实数根，∴△＝)1(4)2(2---m ≥0……………………………2分444+-m ≥0 ∴m ≤2……………………………4分（2）∵221=+x x ，121-=m x x……………………………5分又2122216x x x x =+∴212122162)(x x x x x x =-+，08)(21221=-+x x x x ……………………6分 ∴0)1(822=--m ，0884=+-m……………………………7分∴23=m ． ∵223<=m ，∴符合条件的m 的值为23．……………………………9分2.（2016四川成都，15（2），6分）已知关于x 的方程3x 2+2x ﹣m=0没有实数解，求实数m 的取值范围．（2）∵3x 2+2x ﹣m=0没有实数解， ∴b 2﹣4ac=4﹣4×3（﹣m ）＜0，解得：m ＜，故实数m 的取值范围是：m ＜．20．（2016四川南充，20，8分）已知关于x 的一元二次方程x 2﹣6x+（2m+1）=0有实数根．（1）求m 的取值范围；（2）如果方程的两个实数根为x 1，x 2，且2x 1x 2+x 1+x 2≥20，求m 的取值范围．解：（1）根据题意得△=（﹣6）2﹣4（2m+1）≥0，解得m ≤4；（2）根据题意得x 1+x 2=6，x 1x 2=2m+1，而2x 1x 2+x 1+x 2≥20，所以2（2m+1）+6≥20，解得m ≥3，而m ≤4，所以m 的范围为3≤m ≤4．（2016四川巴中，27，7分）随着国家“惠民政策”的陆续出台，为了切实让老百姓得到实惠，国家卫计委通过严打药品销售环节中的不正当行为，某种药品原价200元/瓶，经过连续两次降价后，现在仅卖98元/瓶，现假定两次降价的百分率相同，求该种药品平均每场降价的百分率．由题意得：200（1﹣x）2=98解得：x1=1.7（不合题意舍去），x2=0.3=30%．答：该种药品平均每场降价的百分率是30%．19、3.（2016山东济宁，19，8分）某地2014年为做好“精度扶贫”工作，投入1280万元用于异地安置，并规划投入资金逐年增加，2016年在2014年的基础上增加投入资金1600万元.（1）从2014年到2016年该地投入异地安置资金的年平均增产率为多少？（2）在2016年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前1000户（含第1000户）每户每天补助8元，1000户以后每天每户补助5元.按租房400天计算，试求今年该地至少有多少户享受到优先搬租房奖励？解：（1）设年平均增产率为x，则有1280（1+x）2=1280+1600，解得，x1=50%,x2=-2.5（不合题意，舍去）所以从2014年到2016年年平均增产率为50%.（2）设有y户享受到优先搬租房奖励,则有400[1000×8+5（x-1000）]≥5000000，解得，x≥1900. 所以今年该地至少有1900户享受到优先搬租房奖励.4.5.6.7.8.9.10.11.12.13.14.15.16.2016年全国中考数学精品文档18.19.20.21.22.23.24.25.26.27.28.29.30.31.32.33.34.35.36.37.38.39.11。

2016中考数学试题及答案解析

2016中考数学试题及答案解析2016年中考数学已经结束，本文将对本次考试试题出现的知识点进行解析，帮助考生对数学考点更加清晰明确。

2016年中考数学试题及答案解析一、单项选择题1.斐波那契数列(第n项满足公式 Fn=Fn-1+Fn-2)中，第25项的值为（A. 1250B. 1280C. 1290D. 1300答案：D，解析：F1=1，F2=1，F3=2，那么F25=F24+F23=750+550=1300。

2.若复数z=（6-3i）*（2+i），z的共轭复数为（A. 8-3iB. 8+3iC. 6-iD. 6+i答案： B. 8+3i，解析：z的共轭复数即为z的根号共轭复数，即(6-3i)(2+i)的根号共轭复数为(6+3i)(2-i)，得到结果8＋3i。

3.下列函数中的值正确的连续12点的解析式是(A. y=x^2-3x+7B. y=3x^2+2x-1C. y=(x-2)^2-5x+7D. y=x^2+7答案： C，解析：根据函数y=(x-2)^2-5x+7，它的x取值为0，1，2，3，4，5，6，7，8，9，10，11，且y均为正数，因此其值正确。

二、解答题4.一家公司把罐装蜂蜜装入木箱，每个木箱里装有六个罐装蜂蜜，每罐蜂蜜重1.5Kg，请计算出20个木箱装蜂蜜重量是多少答案：20*6*1.5kg=180kg。

解析：每个木箱里装6个罐装蜂蜜，每个蜂蜜罐重1.5Kg，20个木箱装蜂蜜重量计算为：20*6*1.5kg=180kg。

5.若△ABC的面积为40，AB=4，BC=6，则BC角度数是（答案：60°. 解析：△ABC的面积为40，AB=4，BC=6，则AB:BC=2:3，可利用海伦公式求出其BC角α，即：α=arccos(2/3)=60°。

(完整word版)2016年中考数学压轴题70题精选(含答案及解析),推荐文档

2016年中考数学压轴题70题精选(含答案)【001】如图13，二次函数y x px q( p 0)的图象与x轴交于A、B两点，与y轴交于点C( 0, -1),5A ABC的面积为4(1)求该二次函数的关系式；(2 )过y轴上的一点M (0, m)作y轴的垂线，若该垂线与A ABC的外接圆有公共点，求m的取值范围；(3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。

【002】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B ( 4, 0)、C (8 , 0)、D (8 , 8)抛物线y=ax2+bx过A、C两点.(1) 直接写出点A的坐标，并求出抛物线的解析式；(2) 动点P从点A出发•沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动.速度均为每秒1个单位长度，运动时间为t秒•过点P作PE丄AB交AC于点E,①过点E作EF丄AD 于点F,交抛物线于点G当t为何值时，线段EG最长？②连接EQ.在点P、Q运动的过程中，判断有几个时刻使得厶CEQ是等腰三角形？请直接写出相应的t值。

【003】抛物线y ax2 bx c(a 0)的顶点为M，与x轴的交点为A、B (点B在点A的右侧)，△ ABM的三个内角/ M、/ A> Z B所对的边分别为m、a、b。

若关于x的一元二次方程(m a)x2 2bx (m a) 0 有两个相等的实数根。

(1)判断△ ABM的形状，并说明理由。

(2)当顶点M的坐标为(一2,—1)时，求抛物线的解析式，并画出该抛物线的大致图形。

(3)若平行于x轴的直线与抛物线交于C、D两点，以CD为直径的圆恰好与x轴相切，求该圆的圆心坐标。

k【004】一次函数y ax b的图象分别与x轴、y轴交于点M,N，与反比例函数y 的图象相交于点xA, B •过点A分别作AC x轴，AE y轴，垂足分别为C,E ;过点B分别作BF x轴，BD y轴，垂足分别为F， D, AC与BD交于点K，连接CD •k(1 )若点A , B 在反比例函数y 仝的图象的同一分支上，如图1，试证明:x① S 四边形AEDKS 四边形CFBK ；② AN BM •k-的图象的不同分支上，如图 2,则AN 与BM 还相等吗？试证 x明你的结论.(2) 连接BM ，如图2,动点P 从点第A2出题图沿折线ABC 方向第25个单位/秒的速度向终点 C 匀速运动，设△ PMB 的面积为S(S 工0)，点P 的运动时间为t 秒，求S 与t 之间的函数关系式(要求写出自变量 t 的取值范围)；(3) 在(2)的条件下，当t 为何值时，/ MPB 与/ BCO 互为余角，并求此时直线 OP 与直线AC 所夹锐角的正切值.【006】如图，抛物线y ax 2 bx 3与x 轴交于A, B 两点，与y 轴交于C 点，且经过点(2, 3a)，对称轴是直线x 1，顶点是M . (1 )求抛物线对应的函数表达式； (2)经过C,M 两点作直线与x 轴交于点N ，在抛物线上是否存在这样的点 P ，使以点P , A, C , N 为顶点的四边形为平行四边形？若存在，请求出点P 的坐标；若不存在，请说明理由；(3) 设直线y x 3与y 轴的交点是D ，在线段BD 上任取一点E (不与B , D 重合)，经过 A, B, E 三点的圆交直线BC 于点F ，试判断△ AEF 的形状，并说明理由；(2)若点A ，B 分别在反比例函数S MK C F【005】如图1 ,在平面直角坐标系中，点点C 在x 轴的正半轴上，直线 AC 交y 轴于点(1)求直线AC 的解析式; y+ Ny，点A 的坐标为(一3, 4), O仝标原点，四边形ABCqE 校y 轴于点x ~ D K(4) 当E 是直线y x 3上任意一点时，(3)中的结论是否成立？(请直接写出结论).如图9，已知正比例函数和反比例函数的图象都经过点I{(第26题A(3,3).x函数和反比例函数的解析式;OA 向下平移m)，求m 的值和这个一次函数的解析式;y I【007】(2 )把A O (1 )求 M(3)第(2)问中的一次函数的图象与x轴、y轴分别交于C、D,求过A、B、D三点的二次函数的解析式;(4)在第(3)问的条件下，二次函数的图象上是否存在点E,使四边形OECD的面积S与四边形OABD过点B作圆0的切线交DC的延长线于点P，判断点P是否在抛物线上，说明理由. NC分(3)yA(4,0, B(1,0, C(0, 2)三点.(1 )A(2三角形与F .-动点，过【009】如图,P作PM x轴，垂足为M，是否存在P点，使得以A, P, M为顶点的△OAC 相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；(3)在直线AC上方的抛物线上有一点D,使得△ DCA的面积最大，求出点D的坐标.【010】如图，抛物线y ax2 bx 4a经过A( (1)求抛物线的解析式; B •(2)已知点D(m, m 1)在第一象限的抛物线上，求点D关于直线BC对称的点的坐标;⑴求二次函数的解析式；⑵在该抛物线的对称轴上找一点 P ,使PA+PD 最小，求出点P 的坐标；⑶在抛物线上是否存在点 0,使厶QAB 与厶ABC 相似？如果存在，求出点 Q 的坐标；如果不存在，请说明理由.【012】如图，已知抛物线y x 2 bx c 经过A(1,0) , B(0,2)两点，顶点为D . (1) 求抛物线的解析式；(2) 将厶OAB 绕点A 顺时针旋转90。

2016年全国中考数学真题分类分式方程及其应用(习题解析)

2016年全国中考数学真题分类分式方程及其应用一、选择题1．（2016安徽，5，4分）方程=3的解是（）A．﹣ B．C．﹣4 D．4【考点】分式方程的解．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：2x+1=3x﹣3，解得：x=4，经检验x=4是分式方程的解，故选D．2．（2016甘肃定西，8，3分）某工厂现在平均每天比原计划多生产50台机器，现在生产800台所需时间与原计划生产600台机器所需时间相同．设原计划平均每天生产x台机器，根据题意，下面所列方程正确的是（）A． =B． =C． =D． =【分析】根据题意可知现在每天生产x+50台机器，而现在生产800台所需时间和原计划生产600台机器所用时间相等，从而列出方程即可．【解答】解：设原计划平均每天生产x台机器，根据题意得： =，故选：A．【点评】此题主要考查了列分式方程应用，利用本题中“现在平均每天比原计划多生产50台机器”这一个隐含条件，进而得出等式方程是解题关键．3.（2016广东深圳，9，3分）施工队要铺设一段全长2000米，的管道，因在中考期间需停工两天，实际每天施工需比原来计划多50米，才能按时完成任务，求原计划每天施工多少米。

设原计划每天施工x米，则根据题意所列方程正确的是（）A.25020002000=+-x x B.22000502000=-+x x C.25020002000=--x x D.22000502000=--xx 【答案】A4．（2016广西贺州，8，3分）若关于x 的分式方程2x －a x －2＝12的解为非负数，则a 的取值范围是（）A ．a ≥1B ．a ＞1C ．a ≥1且a ≠4D ．a ＞1且a ≠4 【答案】C5.（2016河北，12，2分）在求3x 的倒数的值时，嘉淇同学将3x 看成了8x ，她求得的值比正确答案小5.依上述情形，所列关系式成立的是（） A ．11538x x =- B ．11538x x =+ C ．1853x x =- D ．1853x x =+答案:B解析：根据题意，3X 的倒数比8X 的倒数大5，故选B 项。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

小专题五：应用题专题复习一、方程与方程组型1．（2015•平谷区二模）列方程或方程组解应用题：为开阔学生的视野在社会大课堂活动中，某校组织初三年级学生参观科技馆，原计划租用45 座客车若干辆，但有15 人没有座位；若租用同样数量的60 座客车，则多出一辆车，且其余客车恰好坐满．求该校初三年级有学生多少人？原计划租用多少辆45 座客车？2．（2015•岳池县模拟）一辆汽车从A 地驶往B 地，前路为普通公路，其余路段为高速公路，已知汽车在普通公路上行驶的速度为60km/h，在高速路上行驶的速度为100km/h，汽车从A 地到B 地一共行驶了2.2h，普通公路和高速公路各是多少km？3．（2015•长沙）现代互联网技术的广泛应用，催生了快递行业的高度发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10 万件和12.1 万件，现假定该公司每月投递的快递总件数的增长率相同．（1）求该快递公司投递总件数的月平均增长率；（2）如果平均每人每月最多可投递0.6 万件，那么该公司现有的21 名快递投递业务员能否完成今年6 月份的快递投递任务？如果不能，请问至少需要增加几名业务员？4．（2015•淮安）水果店张阿姨以每斤2 元的价格购进某种水果若干斤，然后以每斤4 元的价格出售，每天可售出100 斤，通过调查发现，这种水果每斤的售价每降低0.1 元，每天可多售出20 斤，为保证每天至少售出260 斤，张阿姨决定降价销售．（1）若将这种水果每斤的售价降低x 元，则每天的销售量是斤（用含x 的代数式表示）；（2）销售这种水果要想每天盈利300 元，张阿姨需将每斤的售价降低多少元？5．（2016•安徽模拟）2014 年西非埃博拉病毒疫情是自2014 年2 月开始爆发于西非的大规模病毒疫情，截至2014 年12 月02 日，世界卫生组织关于埃博拉疫情报告称，几内亚、利比里亚、塞拉利昂、马里、美国以及已结束疫情的尼日利亚、塞内加尔与西班牙累计出现埃博拉确诊、疑似和可能感染病例17290 例，其中6128 人死亡．感染人数已经超过一万，死亡人数上升趋势正在减缓，在病毒传播中，每轮平均1 人会感染x 个人，若1 个人患病，则经过两轮感染就共有81 人患病．（1）求x 的值；（2）若病毒得不到有效控制，三轮感染后，患病的人数会不会超过700 人？6．（2016•凉山州模拟）某县2013 年公共事业投入经费40000 万元，其中教育经费占15%，2015 年教育经费实际投入7260 万元，若该县这两年教育经费的年平均增长率相同．（1）求该县这两年教育经费平均增长率；（2）若该县这两年教育经费平均增长率保持不变，那么2016 年教育经费会达到8000 万元吗？二、不等式与不等式组型7．（2010 春•三元区校级期中）某学校为学生安排宿舍，现有住房若干间，若每间5 人，则还有14 人安排不下，若每间7 人，则有一间不足7 人．问学校至少有几间房可以安排学生住宿？可以安排住宿的学生有多少人？8．（2015•甘孜州）一水果经销商购进了A，B 两种水果各10 箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：箱，B 种水果两店各5 箱，请你计算出经销商能盈利多少元？（2）在甲、乙两店各配货10 箱（按整箱配送），且保证乙店盈利不小于100 元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？9．（2015•黔东南州）去冬今春，我市部分地区遭受了罕见的旱灾，“旱灾无情人有情”．某单位给某乡中小学捐献一批饮用水和蔬菜共320 件，其中饮用水比蔬菜多80 件．（1）求饮用水和蔬菜各有多少件？（2）现计划租用甲、乙两种货车共8 辆，一次性将这批饮用水和蔬菜全部运往该乡中小学．已知每辆甲种货车最多可装饮用水40 件和蔬菜10 件，每辆乙种货车最多可装饮用水和蔬菜各20 件．则运输部门安排甲、乙两种货车时有几种方案？请你帮助设计出来；（3）在（2）的条件下，如果甲种货车每辆需付运费400 元，乙种货车每辆需付运费360 元．运输部门应选择哪种方案可使运费最少？最少运费是多少元？三、函数综合型10．（2015•衢州）高铁的开通，给衢州市民出行带来了极大的方便，“五一”期间，乐乐和颖颖相约到杭州市的某游乐园游玩，乐乐乘私家车从衢州出发1 小时后，颖颖乘坐高铁从衢州出发，先到杭州火车站，然后再转车出租车取游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开衢州的距离y（千米）与乘车时间t（小时）的关系如图所示．请结合图象解决下面问题：（1）高铁的平均速度是每小时多少千米？（2）当颖颖达到杭州火车东站时，乐乐距离游乐园还有多少千米？（3）若乐乐要提前18 分钟到达游乐园，问私家车的速度必须达到多少千米/小时？11．（2016•安徽模拟）为加大对残疾人补助力度，改善残疾人的生活水平，2015 年安徽省提高了对残疾人的补助标准，一级、二级救助标准由每人每年726 元增加到每人每年800 元；三级残疾人救助标准由每人每年360 元增加到每人每年400 元．某县有大量一级、二级和三级残疾人.2014 年共投入补助经费1446 万元.2015 年提高补助标准后投入补助经费1600 万元．（1）2015 年该县的一级、二级和三级残疾的人数没有任何变化，则2015 年该县的一级、二级残疾人共多少万人？三级残疾人共多少万人；（2）2015 年该县决定对一级、二级残疾人进行养老保险的补助，一级残疾人每人每年养老保险补助480 元，二级残疾人每人每年300 元．已知二级残疾人的数量不低于一级残疾人的4 倍，则该县最多需要投入残疾人养老保险的补助多少万元？12．（2015•莱芜）今年我市某公司分两次采购了一批大蒜，第一次花费40 万元，第二次花费60 万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500 元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500 元，第二次的采购数量是第一次采购数量的两倍．（1）试问去年每吨大蒜的平均价格是多少元？（2）该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8 吨大蒜，每吨大蒜获利1000 元；若单独加工成蒜片，每天可加工12 吨大蒜，每吨大蒜获利600 元．由于出口需要，所有采购的大蒜必需在30 天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？13．（2016•安徽模拟）音乐喷泉（图1）可以使喷水造型随音乐的节奏起伏变化而变化．某种音乐喷泉形状如抛物线，设其出水口为原点，出水口离岸边18m，音乐变化时，抛物线的顶点在直线y=kx 上变动，从而产生一组不同的抛物线（图2），这组抛物线的统一形式为y=ax2+bx．（1）若已知k=1，且喷出的抛物线水线最大高度达3m，求此时a、b 的值；（2）若k=1，喷出的水恰好达到岸边，则此时喷出的抛物线水线最大高度是多少米？（3）若k=3，a=﹣，则喷出的抛物线水线能否达到岸边？14．（2015•湖北）为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40 元．超市规定每盒售价不得少于45 元．根据以往销售经验发现；当售价定为每盒45 元时，每天可以卖出700 盒，每盒售价每提高1 元，每天要少卖出20 盒．（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？（3）为稳定物价，有关管理部门限定：这种粽子的每盒售价不得高于58 元．如果超市想要每天获得不低于6000 元的利润，那么超市每天至少销售粽子多少盒？15.某公司生产的某种时令商品每件成本为20 元，•经过市场调研发现，这种商品在未来40天内的日销售量m（件）与时间t（天）的关系如表所示：时间t/天 1 3 6 10 36 …日销售量m/件94 90 84 76 24 …1 未来40 天内，前20 天每天的价格y1（元/件）与时间t（天）的函数关系式为y1= t+254（1≤t≤20 且t 为整数），后20 天每天的价格y2（元/件）与时间t（天）的函数关系式为y2=－1t+40（21≤t≤40 且t 为整数）．下面我们就来研究销售这种商品的有关问题：2（1）认真分析表中的数据，用所学过的一次函数，二次函数，反比例函数的知识确定一个满足这些数据的m（件）与t（天）之间的函数关系式；（2）请预测未来40 天中哪一天的日销售利润最大，最大日销售利润是多少？（3）在实际销售的前20 天中，该公司决定每销售一件商品就捐赠a 元利润（a<4）给希望工程．公司通过销售记录发现，前20 天中，•每天扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a 的取值范围．四、几何类应用题16、某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90∘，AC=80 米，BC=60 米。

(1) 若入口E 在边AB 上，且与A. B 等距离，求从入口E 到出口C 的最短路线的长；(2) 若线段CD 是一条水渠,且D 点在边AB 上,已知水渠的造价为10 元/米,则D 点在距A 点多远处时，此水渠的造价最低，最低造价是多少?17、如图,公路MN 与PQ 在点P 处交汇,且∠QPN=30∘,点A 处有一住宅小区,AP=160 米。

假设卡车行驶时,周围100 米以内(包括100 米)会受到噪声的影响，(1) 那么卡车在公路MN 上沿PN 方向行驶时，小区是否会受到噪声影响?如果受影响，请说明理由。

(2) 已知卡车行驶速度为18 千米/时，那么小区受影响的时间为多少?18、某人在公路a 上向东行走,在A 处测得公路旁的建筑物C 在北偏东60°方向, 前进50m 到达B 处,又测得建筑物C 在北偏东45°方向,继续前进,此人在行走过程中,离建筑物C 的最近距离是多少（结果保留根号）。