2-2逻辑代数的基本定律和规则
逻辑代数的基本定律和规则

逻辑代数的基本定律和规则一、逻辑代数的基本公式(一)、逻辑常量运算公式(二)、逻辑变量、常量运算公式变量A的取值只能为0或为1,分别代入验证。
二、逻辑代数的基本定律逻辑代数的基本定律是分析、设计逻辑电路,化简和变换逻辑函数式的重要工具。
这些定律和普通代数相似,有其独特性。
(一)、与普通代数相似的定律交换律、结合律、分配律(二)、吸收律与学生一同验证以上四式。
第④式的推广:由表4可知,利用吸收律化简逻辑函数时,某些项或因子在化简中被吸收掉,使逻辑函数式变得更简单。
(三)、摩根定律三、逻辑代数的三个重要规则(一)、代入规则对于任一个含有变量A的逻辑等式,可以将等式两边的所有变量A用同一个逻辑函数替代,替代后等式仍然成立。
这个规则称为代入规则。
代入规则的正确性是由逻辑变量和逻辑函数值的二值性保证的。
例题:(二)、(三)、若两函数相等,其对偶式也相等。
(可用于变换推导公式)。
讨论三个规则的正确性。
逻辑涵数的公式化简法一、化简的意义与标准1、化简逻辑函数的意义根据逻辑问题归纳出来的逻辑函数式往往不是最简逻辑函数式,对逻辑函数进行化简和变换,可以得到最简的逻辑函数式和所需要的形式,设计出最简洁的逻辑电路。
这对于节省元器件,优化生产工艺,降低成本和提高系统的可靠性,提高产品在市场的竞争力是非常重要的。
2、逻辑函数式的几种常见形式和变换3、逻辑函数的最简与-或式对与或式而言:最简:二、逻辑函数的代数化简法1、并项法三、代数化简法举例在实际化简逻辑函数时,需要灵活运用上述几种方法,才能得到最简与-或式.四、作业:。
逻辑代数的基本定律及规则2010.9.23

_ _ _
_
_ _
_
三变量最小项的编号
长春理工大学软件学院
最大项
最大项标准式是以“或与”形式出现的标准式。 最大项: 对于一个给定变量数目的逻辑函数, 所有变 量参加相“或”的项叫做最大项。 在一个最大项中, 每个 变量只能以原变量或反变量出现一次。 例如, 一个变量A有二个最大项: (2 ) A, A。
例题:化简函数
AB + AC + BC = AB + AC
F = ABC + AD + C D + BD
F = ABC + AD + C D + BD
= ABC + ( A + C ) D + BD
= AC ⋅ B + AC ⋅ D + BD
= AC ⋅ B + AC ⋅ D
= ABC + AD + C D
最小项
2 n 个最小项。最小项通 以此类推,n变量共有
常用 mi 表示。 最小项标准式:全是由最小项组成的“与或” 式,便是最小项标准式(不一定由全部最小项 组成)。 例如:
F ( ABC ) = A B C + BC + A C = A B C + ABC + A BC + AB C + AB C = ∑ m(0,3,4,6,7)
长春理工大学软件学院
逻辑代数的基本定律及规则
对合律: A = A
冗余律: AB + A C + BC = AB + A C
长春理工大学软件学院
逻辑代数的基本定律及规则
3 基本规则
代入规则:任何一个含有变量A的等式,如果将所有 出现A的位置都用同一个逻辑函数代替,则等式仍然 成立。这个规则称为代入规则。 反演规则:对于任何一个逻辑函数F,想要得到F的反 函数,只需要将F中的所有“·”换成“+”,“+”换 成“·”,“0”换成“1”,“1”换成“0”,原变量换成反 变量,反变量换成原变量。 长春理工大学软件学院
逻辑代数的基本定律

逻辑代数的基本定律逻辑代数的基本定律是指逻辑代数中的基础规则和定理,这些定理是逻辑代数中最基本的概念和方法。
逻辑代数是用数学方法来处理逻辑问题的一种方法,它将逻辑问题转化为数学问题,从而可以用数学方法来解决。
逻辑代数的基本定律主要包括以下几个方面:1. 同一律同一律是指一个逻辑表达式和它自身相与(或相或)的结果不变。
即A ∧ T = A,A ∨ F = A。
这个定律的意思是,当逻辑表达式与真值或假值相与(或相或)时,结果不变。
例如,如果有一个逻辑表达式A ∧ T,它与真值T 相与的结果仍然是A。
同样地,如果有一个逻辑表达式A ∨ F,它与假值 F 相或的结果仍然是 A。
2. 恒等律恒等律是指一个逻辑表达式与一个恒等式相与(或相或)的结果相等。
即A ∧ A = A,A ∨ A = A。
这个定律的意思是,当逻辑表达式与一个恒等式相与(或相或)时,结果相等。
例如,如果有一个逻辑表达式A ∧ A,它与恒等式 A 相与的结果仍然是A。
同样地,如果有一个逻辑表达式A ∨ A,它与恒等式 A 相或的结果仍然是 A。
3. 交换律交换律是指一个逻辑表达式中的两个变量相与(或相或)的顺序可以交换。
即A ∧ B = B ∧ A,A ∨ B = B ∨ A。
这个定律的意思是,当逻辑表达式中的两个变量相与(或相或)时,它们的顺序可以交换。
例如,如果有一个逻辑表达式A ∧ B,它与表达式B ∧ A 相与的结果是相等的。
同样地,如果有一个逻辑表达式A ∨ B,它与表达式B ∨ A 相或的结果是相等的。
4. 结合律结合律是指一个逻辑表达式中的多个变量相与(或相或)时,可以任意加括号,而结果不变。
即A ∧ (B ∧ C) = (A ∧ B) ∧ C,A ∨ (B ∨ C) = (A ∨ B) ∨ C。
这个定律的意思是,当逻辑表达式中有多个变量相与(或相或)时,可以任意加括号,而结果不变。
例如,如果有一个逻辑表达式A ∧ (B ∧ C),它与表达式(A ∧ B) ∧ C 相与的结果是相等的。
数字电子技术基础教程
第6页/共55页
2.2 逻辑代数的基本定律和规则
反演律 吸收律
A B AB
A AB A
A B A B A (A B) A
A B A B A
(A B)(A B) A
A AB A B
A(A B) AB
冗余律
AB AC BC AB AC
(A+B)(A+C)(B C) (A+B)(A+C)
F AB
2.或非逻辑
F AB
A
F
&
B
与非门
A
F
B
或非门
3. 与或非逻辑
&
F AB CD
第20页/共55页
异或逻辑与同或逻辑
4.异或逻辑
F A B AB AB
A
=1
F
B
5.同或逻辑 F=A ⊙ B= AB AB
A
=
F
B
AB F
00 0 01 1 10 1 11 0
AB F
00 1 01 0 10 0 11 1
② 任意两个i0最小项之积恒i为0A0B,C任·意AB两C个=最0大项之
和恒等于1 。
mi m j 0(i j)
Mi M j 1(i j)
③ n 变量的每一个最小(大)项有n 个相邻项
(相邻项是指两个最小项只有一个因子互为反变
量,其余因子均相同,又称为逻辑相邻项)。
第32页/共55页
2.6 逻辑代数的K诺图
ABC ABC ABC
最大项表达式:
F ( A B C)( A B C)( A B C)
第28页/共55页
最大项的Mi表示
n个变量可以构成2n个最大项。最大项用符号Mi表示。与 最小项恰好相反,对于任何一个最大项,只有一组变量 取值使它为0,而变量的其余取值均使它为1。
第2章逻辑代数基础
同时,函数F的值为“0”。
便于获得逻辑电路图
逻辑表达式的简写:
1.“非”运算符下可不加括号,如
,
等。
2.“与”运算符一般可省略,如A·B可写成AB。
3.在一个表达式中,如果既有“与”运算又有“或”运 算,则按先“与”后“或”的规则进行运算,可省去括号,如 (A·B)+(C·D)可写为AB+CD。
注意:(A+B)·(C+D)不能省略括号,即不能写成A+B·C+D!
A
FA
1
FA
F
(a)我国常用传统符号
(b)国际流行符号 非门的逻辑符号
(c)国家标准符号
2.1.3 逻辑代数的复合运算
“与”、“或”、“非”三种基本逻辑运算按不同的方 式组合,还可以构成“与非”、“或非”、“与或非”、 “同或”、“异或”等逻辑运算,构成复合逻辑运算。对应 的复合门电路有与非门、或非门、与或非门、异或门和同或 门电路。
能实现基本逻辑运算的电路称为门电路,用基本的门电 路可以构成复杂的逻辑电路,完成任何逻辑运算功能,这些 逻辑电路是构成计算机及其他数字系统的重要基础。
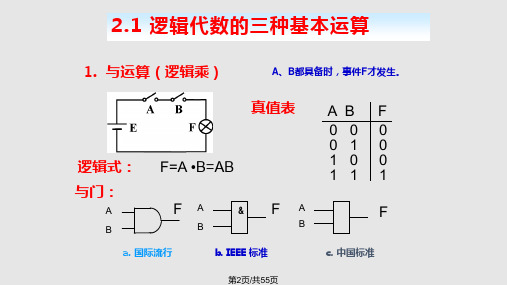
实现“与”运算关系的逻辑电路称为“与”门。
A
A
A
&
B
F B
F B
F
(a)我国常用传统符号
(b)国际流行符号 与门的逻辑符号
(c)国家标准符号
2.1.2 逻辑代数的基本运算
2.逻辑值0和1是用来表征矛盾的双方和判断事件真伪 的形式符号,无大小、正负之分。
2.1.1 逻辑代数的定义
逻辑代数L是一个封闭的代数系统,它由一个逻辑变量集 K,常量0和1以及“或”、“与”、“非”三种基本运算所 构成,记为L={K,+,·,-,0,1}。该系统应满足下列公理。
逻辑代数的运算法则

逻辑代数的运算法则逻辑代数又称布尔代数。
逻辑代数与普通代数有着不同概念,逻辑代数表示的不是数的大小之间的关系,而是逻辑的关系,它仅有0、1两种状态。
逻辑代数有哪些基本公式和常用公式呢?1.变量与常量的关系与运算公式 一、基本公式A·1=AA·0=0或运算公式A+0=A A+1=101律2.与普通代数相似的定律与运算公式A·B=B·A 或运算公式A+B=B+A交换律A·(B·C)=(A·B)·C A+(B+C)=(A+B)+C 结合律A·(B+C)=A·B+A·C A+(B·C)=(A+B)(A+C)分配律3.逻辑代数特有的定律与运算公式或运算公式互补律重叠律(同一律) 反演律(摩根定律)0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+ 非非律(还原律)AA =A A A =⋅A A A =+真值表证明摩根定律0001101111111100结论:BA B A +=⋅ 以上定律的证明,最直接的办法就是通过真值表证明。
若等式两边逻辑函数的真值表相同,则等式成立。
【证明】公式1AB A AB =+B A AB +)(B B A += 互补律1⋅=A 01律A= 合并互为反变量的因子【证明】公式2AAB A =+AB A +)(B A +=1 01律A= 吸收多余项【证明】公式3BA B A A +=+B A A +BA AB A ++=B A A A )(++= 互补律BA += 消去含有另一项的反变量的因子【证明】CA AB BC C A AB +=++BC A A C A AB )(+++=BC C A AB ++ 分配律BC A ABC C A AB +++= 吸收多余项公式2互补律CA AB += 公式2逻辑代数的运算法则一、基本公式二、常用公式A·1=AA·0=0A+0=A A+1=1 1.变量与常量的关系01律2.与普通代数相似的定律交换律A·B=B·A A+B=B+A结合律 分配律3.逻辑代数特有的定律互补律A·A=A A+A=A 重叠律(同一律)反演律(摩根定律)0=⋅A A 1=+A A BA B A +=⋅BA B A ⋅=+非非律(还原律)AA =AB A AB =+.1AAB A =+.2BA B A A +=+.3CA AB BC C A AB +=++.4A·(B·C )=(A·B )·C A+(B+C )=(A+B )+C A·(B+C )=A·B+A·CA +(B·C )=(A+B )(A+C )谢谢!。
第二章 逻辑代数基础

A B A B
______
A (B C) A (B C) A B C
__________ _____
A ( B C ) A B C A B C
________
3.反演定理
对于任意一个逻辑式 Y ,若将其中所有的“•”换成 “+”, “+”换成“•”,0换成1,1换成0,原变量 __ 换成反变量,反变量换成原变量,则得到的结果就是 Y
2、非逻辑真值表 A 0 1 Y
3 、非逻辑函数式
Y=A 或: Y A
1
0
4、 非逻辑符号
A
1
Y
或: 5 、 非逻辑运算 0=1 1=0
四、 几种最常见的复合逻辑运算
1 、 与非 Y=A B A B & Y
A 0 0 1 1
B 0 1 0 1
Y 1 1 1 0
3 、 同或 Y= AB+A B =A⊙B A B Y
(还原律)
证明: A B A B A ( B B ) A 1 A
4.
A ( A B) A
(吸收律)
证明: A ( A B) A A A B A A B A (1 B) A 1 A
5. A B A C B C A B A C
c. 非非律: ( A) A
A+A=A
d. 吸收律:A + A B = A
A (A+B) = A
A AB A B
e. 摩根定律: ( AB) A B
A .B A B 反演律(摩根定律): A B A B
逻辑代数中的基本定律和公式

逻辑代数中的基本定律和公式
逻辑代数是一种用来研究逻辑的数学,它通过使用变元和逻辑公式来描述逻辑系统,它被用来解释和分析许多不同类型的逻辑结构。
它还可以帮助我们理解计算机语言、逻辑设计和许多其他类型的数学理论。
基本定律和公式是逻辑代数的基础,它们用来描述一个逻辑系统的行为。
以下是一些常见的定律和公式:* 交换律:如果A和B是同类元素,则A+B = B+A。
* 结合律:如果A、B和C是同类元素,则A+(B+C)=(A+B)+C。
* 分配率:如果A、B和C是同类元素,则A(B+C)= AB + AC。
* 吸收律:如果A和B是同类元素,则A+AB=A。
* 对立律:如果A是一个元素,则A+ A'=
1,其中A'是A的补充。
* 析取律:如果A和B是同类元素,则A+B'=A'B。
* 推理律:如果A和B是同类元素,则A→B = A'+B。
* 合取律:如果A和B是同类元素,则A+B = A'B'。
这些定律和公式提供了一种方法来描述逻辑系统的行为,这些定律和公式可以用来构建逻辑系统,并且可以用来解释和分析逻辑系统的行为。
它们也可以用来构建计算机语言,并用来解释和分析计算机语言的行为。
因此,我们可以看出,逻辑代数中的基本定律和公式是一种非常重要的工具,它们可以帮助我们理解和分析逻辑系统,也可以帮助我们理解和分析计算机语言的行为。
此外,它们还可以用来解释和分析许多不同类型的逻辑结构。
因此,逻辑代数中的基本定律和公式是一种非常重要的研究工具,它们可以帮助我们理解和探索逻辑系统的行为,从而有助于我们更好地理解和设计逻辑系统。
逻辑代数的基本定律和常用公式

逻辑代数的基本定律与常用公式1、基本定律逻辑代数就是一门完整的科学。
与普通代数一样,也有一些用于运算的基本定律。
基本定律反映了逻辑运算的基本规律,就是化简逻辑函数、分析与设计逻辑电路的基本方法。
(1)交换律(2)结合律(3)分配律(4)反演律(德·摩根定律)2、基本公式(1)常量与常量(2)常量与变量(3)变量与变量3、常用公式除上述基本公式外,还有一些常用公式,这些常用公式可以利用基本公式与基本定律推导出来,直接利用这些导出公式可以方便、有效地化简逻辑函数。
(1)证明:上式说明当两个乘积项相加时,若其中一项(长项:A·B)以另一项(短项:A)为因子,则该项(长项)就是多余项,可以删掉。
该公式可用一个口诀帮助记忆:“长中含短,留下短”。
(2)证明:上式说明当两个乘积项相加时,若她们分别包含互为逻辑反的因子(B与),而其她因子相同,则两项定能合并,可将互为逻辑反的两个因子(B与)消掉。
(3)证明:上式说明当两项相加时,若其中一项(长项:·B)包含另一项(短项:A)的逻辑反()作为乘积因子,则可将该项(长项)中的该乘积因子()消掉。
该公式可用一个口诀帮助记忆:“长中含反,去掉反”。
例如:(4)证明:上式说明当3项相加时,若其中两项(AB与C)含有互为逻辑反的因子(A与),则该两项中去掉互为逻辑反的因子后剩余部分的乘积(BC)称为冗余因子。
若第三项中包含前两项的冗余因子,则可将第三项消掉,该项也称为前两项的冗余项。
该公式可用一个口诀帮助记忆:“正负相对,余(余项)全完”。
例:。
逻辑代数的基本定律及规则

逻辑代数的基本定律及规则文章来源:互联网作者:佚名发布时间:2012年05月26日浏览次数: 1 次评论:[已关闭] 功能:打印本文一、逻辑代数相等:假定F、G都具有n个相同变量的逻辑函数,对于这n个变量中的任意一组输入,如F和G都有相同的输出值,则称这两个函数相等。
在实际中,可以通过列真值表来判断。
二、逻辑代数的基本定律:在逻辑代数中,三个基本运算符的运算优先级别依次为:非、与、或。
由此推出10个基本定律如下:1.交换律A+B=B+A;A·B=B·A2.结合律A+(B+C)=(A+B)+C;A·(BC)=(AB)·C3.分配律A·(B+C)=AB+AC;A+BC=(A+B)·(A+C)4.0-1律A+0=A;A·1=AA+1=1 ;A·0=05.互补律A+=1 ;A·=06.重叠律A·A=A;A+A=A7.对合律=A8.吸收律A+AB=A;A·(A+B)=AA+B=A+B;A·(+B)=ABAB+B=B;(A+B)·(+B)=B9.反演律=·;=+10.多余项律AB+C+BC=AB+C;(A+B)·(+C)·(B+C)=(A+B)·(+C)上述的定律都可用真值表加以证明,它们都可以用在后面的代数化简中。
三、逻辑代数的基本规则:逻辑代数中有三个基本规则:代入规则、反演规则和对偶规则。
1.代入规则:在任何逻辑代数等式中,如果等式两边所有出现某一变量(如A)的位置都代以一个逻辑函数(如F),则等式仍成立。
利用代入规则可以扩大定理的应用范围。
例:=+,若用F=AC代替A,可得=++2.反演规则:已知函数F,欲求其反函数时,只要将F式中所有的“·”换成“+”,“+”换成“·”;“0”换成“1”,“1”换成“0”时,原变量变成反变量,反变量变成原变量,便得到。
2逻辑代数入门基础

第2章逻辑代数基础2.1 概述一、算术运算和逻辑运算在数字电路中,二进制数码不仅可以表示数值的大小,而且可以表示事物的状态,当两个二进制数码表示两个数值大小时,它们之间可进行数值运算,即算术运算。
当两个二进制数码表示不同逻辑状态时,它们之间的因果关系可进行逻辑运算。
算术运算与逻辑运算有本质的差别,下面重点介绍逻辑运算的各种规则。
二、几个基本概念1、逻辑状态表示法一种状态高电位有真是美生 1 0另一种状态低电位无假非丑死 0 12、两种逻辑体制1 高电位低电位0 低电位高电位正逻辑负逻辑3、高低电平的规定正逻辑负逻辑2.2 逻辑代数中的三种基本运算1、与逻辑(与运算)(逻辑乘)与逻辑的定义:仅当决定事件(Y)发生的所有条件(A,B,C,…)均满足时,事件(Y)才能发生。
表达式为:Y=ABC开关A,B串联控制灯泡Y2、或逻辑(或运算)或逻辑的定义:当决定事件(Y )发生的各种条件(A ,B ,C ,…)中,只要有一个或多个条件具备,事件(Y )就发生。
表达式为:Y=A+B+C+…开关A ,B 并联控制灯泡YA 、B 都断开,灯不亮。
A 断开、B 接通,灯亮。
A 接通、B 断开,灯亮。
A 、B 都接通,灯亮。
两个开关只要有一个接通,灯就会亮。
逻辑表达式为:Y=A+B功能表3(A )满足时,开关A 控制灯泡YA 断开,灯亮。
A 接通,灯灭。
功 能 表Y=A4((((1、代入定理:任何一个含有变量A A的位置都用同一个逻辑函数代替,则等式仍然成立。
这个规则称为代入定理。
例如,已知等式,用函数Y=AC代替等式中的A,根据代入规则,等式仍然成立,即有:(2)反演定理:对于任何一个逻辑表达式Y,如果将表达式中的所有“·”换成“+”,“+”换成“·”,“0”换成“1”,“1”换成“0”,原变量换成反变量,反变量换成原变量,那么所得到的表达式就是函数Y的反函数Y(或称补函数)。
这个规则称为反演定理。
逻辑代数的基本定律和规则

(3)、对偶规则: 首先了解什么是对偶式;
对偶式:已知函数为 F ,将 F 中的所有 “·” 换为 “+”,“+” 换为 “·” ,0 换为 1 ,1 换为 0,变 量保持不变。得到的函数式就是原函数的对偶式 F′。 F AB C 例: F ' A BC
F ( A B)( A C 1) F ' AB AC 0
◇与非逻辑表达式: F A B ◇与非门逻辑符号:A B& NhomakorabeaF
A B
F
A B
F
◇与非门真值表:
A B F A B 0 0 1 0 1 1 1 0 1 1
与非门运算顺序是: 有0为1,全1为0
先与后非
1 0
即:当输入A、B中,只要有一个 0,输出就是 1,只有输入全为 1时, 输出才是0。
D 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
F 1 1 1 0 1 1 1 0 1 1 1 0 0 0 0 0
F AB CD ◇工作波形图:
A B C D F
A,B为两个单刀双掷开关。 灯亮的条件是:一个开关打在上 220V F 面,另一个开关打在下面。两个开关 同时打在上面或者下面,则灯不亮。 假设: ★取F=1列与项逻辑式。 真值表: 开关打在上面为1 ★如果输入变量是“1”,记原 开关打在下面为0 A B F 变量。如果输入变量是“0”, 记反变量。 灯亮为1 0 0 0 灯灭为0 0 1 1 ★对任何一种输入变量组合, 异或运算特点: 1 0 1 变量之间是“与”运算。 相异为1,相同为0 1 1 0 ★各组合之间是“或”逻辑关 系。 F AB AB A B ◇由真值表写出逻辑表达式:
逻辑代数的基本公式、定律和规则

逻辑代数的基本公式、定律和规则示例文章篇一:《逻辑代数的基本公式、定律和规则》一、逻辑代数的基本公式1. 常量之间的运算公式- 0和1是逻辑代数中的两个常量。
0就像是黑暗,1就像是光明。
在逻辑代数里,0 + 0 = 0,这就好比两个黑暗加在一起还是黑暗呀。
那0 + 1 = 1呢,就好像黑暗里来了一点光明,那结果就是光明啦。
1 + 1 = 1,这可能有点奇怪,可这就像两个光明加在一起还是光明,不会变得更亮啦。
- 0×0 = 0,这很好理解,就像两个没有东西相乘还是没有东西。
0×1 = 0,就像没有东西和有东西相乘,结果就是没有东西。
1×1 = 1,有东西和有东西相乘还是有东西嘛。
2. 变量与常量的运算公式- 对于变量A,A + 0 = A。
这就像你有一个东西A,再加上没有东西(0),那还是你原来的东西A呀。
A + 1 = 1,不管你原来有什么东西A,再加上光明(1),那结果就是光明(1)啦。
- A×0 = 0,不管你是什么东西A,和没有东西(0)相乘,结果就是没有东西(0)。
A×1 = A,就像你有东西A,和有东西(1)相乘,结果还是你原来的东西A。
3. 同一律、互补律等公式- 同一律就是A×A = A,A + A = A。
比如说你有一个苹果A,那一个苹果乘以一个苹果还是一个苹果,一个苹果加上一个苹果还是一个苹果(在逻辑代数的概念里哦)。
- 互补律是A×A' = 0,A+A' = 1。
A'就像是A的反面。
如果A是白天,A'就是黑夜。
白天和黑夜不能同时存在(A×A' = 0),而白天或者黑夜肯定有一个存在(A+A' = 1)。
二、逻辑代数的基本定律1. 交换律- 在逻辑代数里,加法交换律是A + B = B + A,就像你有苹果A和香蕉B,先数苹果再数香蕉,和先数香蕉再数苹果,总数是一样的。
(完整版)逻辑代数的运算规则

逻辑代数的运算规则逻辑代数的基本定律逻辑代数的三个规则1、代入规则在任一逻辑等式中,如果将等式两边所有出现的某一变量都代之以一个逻辑函数,则此等式仍然成立,这一规则称之为代入规则。
2、反演规则已知一逻辑函数F,求其反函数时,只要将原函数F中所有的原变量变为反变量,反变量变为原变量;“+”变为“·”,“·”变为“+”;“0”变为“1”;“1”变为“0”。
这就是逻辑函数的反演规则。
3、对偶规则已知一逻辑函数F,只要将原函数F中所有的“+”变为“·”,“·”变为“+”;“0”变为“1”;“1”变为“0”,而变量保持不变、原函数的运算先后顺序保持不变,那么就可以得到一个新函数,这新函数就是对偶函数F'。
其对偶与原函数具有如下特点:1.原函数与对偶函数互为对偶函数;2.任两个相等的函数,其对偶函数也相等。
这两个特点即是逻辑函数的对偶规则。
逻辑运算的常用公式逻辑代数的总结基本逻辑运算:与(或称“积”)---符号(&、•、无、∧、∩)或(或称“和”)---符号(| 、+、∨、∪)非(或称“反”)---符号(! 、)10-1律:0•A=0 0+A=11•A=A 1+A=A同一律:A•A=A A+A=A互补律:A•A=0 A+A=0反演律A•B =A+B A+B=A•还原律A =A√⊕⊙••+A=02、常用公式交换律:A•B=B•A A+B=B+A结合律:A•(A•B)=(A•B)•C A+(A+B)=(A+B)+C 分配律:A•(A+B)=A•B+A•C A+(A•B)=(A+B)•(A+C) 吸收律:A•(A+B)=AB A+(A•B)=ABA•B+(A•B)=A (A+B)•(A+B)=A。
逻辑代数基本定律

逻辑代数基本定律逻辑代数是一门研究逻辑关系的数学分支。
在逻辑代数中,有许多基本定律可以帮助我们理解和分析逻辑关系。
本文将介绍逻辑代数的基本定律,希望能够以生动、全面、有指导意义的方式来展示这些定律的重要性和应用。
第一个基本定律是交换律。
交换律告诉我们,对于逻辑运算而言,两个表达式的次序不会影响最终的结果。
也就是说,无论是与运算还是或运算,两个表达式的顺序都可以随意交换。
这一定律的生动例子可以是两个朋友来到一个餐馆,无论他们是坐在一起还是分开坐,最后都是一起进餐,结果是一样的。
第二个基本定律是结合律。
结合律告诉我们,在逻辑运算中,无论是与运算还是或运算,多个表达式可以按照不同的方式组合,最终的结果都是一样的。
例如,对于三个命题A、B和C,无论我们是先对A和B进行与运算,再与C进行与运算,还是先对B和C进行与运算,再与A进行与运算,最终的结果都是一样的。
第三个基本定律是分配律。
分配律告诉我们,在逻辑运算中,一个逻辑表达式可以与一个逻辑运算的结果进行分配,同时保持逻辑等价。
这一定律在代数中也有类似的应用。
例如,对于命题A、B和C,我们可以将A与B进行或运算,再与C进行与运算,结果与先将A和C 进行与运算,再将B和C进行与运算,然后将两个结果进行或运算,得到的结果是一样的。
第四个基本定律是德·摩根定律。
德·摩根定律告诉我们,在逻辑运算中,当取反运算作用于一个由与和或运算构成的复合命题时,先取反再进行与运算,等价于先将每个部分取反,然后再进行或运算;先取反再进行或运算,等价于先将每个部分取反,然后再进行与运算。
这一定律的一个生动的例子是在布尔代数中,将一个复杂的逻辑表达式进行简化时,可以通过应用摩根定律来实现。
综上所述,逻辑代数的基本定律帮助我们理解和分析逻辑关系。
交换律告诉我们顺序不影响结果,结合律告诉我们组合方式不影响结果,分配律告诉我们运算的分配方式不影响结果,摩根定律告诉我们取反运算的顺序可以改变。
第二章 逻辑代数基础

上页 下页 返回 17
第2章
2.3 复 合 逻 辑
1.与非逻辑
F = AB
2.或非逻辑 F = A+B
3. 与或非逻辑
F = AB+CD
A &F
A
F
B
B
与非门
A
F
≥1
B
或非门
A
B&
F
C
D
与或非门
上页 下页 返回 18
第2章
2.3 复 合 逻 辑
4.异或逻辑—相同为‘0’,相异为‘1’
F = A B =A B + A B
A) F1= [( A+ B) •C + D]( A+ C)
B) F2= A•B •C •D •E
[例2] 求下列函数的对偶函数 A)F1= AB+ C •D + AC B) F2= A+ B + C + D + E
A) F1*=[( A+ B) •C + D]( A+ C)
B) F2*=A•B •C •D •E
n个变量有2n个最小项,记作mi 3个变量有23(8)个最小项
n个变量的最小项,有n个相邻项
最小项 ABC ABC ABC ABC A BC A BC AB C ABC
二进制数 000 001 010 011 100 101 110 111
十进制数 0 1 2
3
45 67
编号
m0 m1 m2
m3
m4 m5
A⊕A⊕A⊕A⊕…⊕A = ? A (A的个数为奇数)
An-1⊕An-2⊕…⊕A0 = ?
0 (Ai中‘1’的个数为偶数) 1 (Ai中‘1’的个数为奇数)
逻辑代数基础

Y AC AB
AC( B B) AB(C C)
ABC ABC ABC ABC ABC ABC ABC m5 m6 m7
例1:画出 Y AC AB 的卡诺图
Y ABC ABC ABC m5 m6 m7
输入变量 BC 00 A 0 0 1 00 01 11 10 m0 m1 m3 m2 m4 m5 m7 m6 0
0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
② 最小项的性质 对于任意一个最小项,只有一组变量取值使 它的值为1,而在变量取其它各值时,这个 最小项的值都是零; 不同的最小项,使它的值为1的那组变量取 值也不同; 对于变量的同一组取值,任意两个最小项 的乘积为零; 对于变量的同一组取值,所有最小项的逻辑 或为1。
第2章 逻辑代数基础
§2.1 逻辑代数 § 2.2 逻辑函数表达式的形式与变换 §2.3逻辑函数的化简
§2.1逻辑代数的基本规则和定理
逻辑代数(又称布尔代数),它是分析和 设计逻辑电路的数学工具。虽然它和普通代 数一样也用字母表示变量,但变量的取值只 有“0”,“1”两种,分别称为逻辑“0”和逻 辑 “1”。这里“0”和“1”并不表示数量的大小, 而是表示两种相互对立的逻辑状态。
③最小项的编号
注:下标与编码所对应的十进制数值相同
④函数的最小项表达式
将逻辑函数表达式化成一组最小项之和,称为 最小项表达式。任何一个函数均可表达成 唯一的 最小项之和。 如:
L( A, B, C ) ( AB AB C ) AB
( AB A B C ) AB AB ABC AB ABC A BC ABC ABC m3 m5 m 6 m 7 m(3,5,6,7)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
逻辑代数基础
逻辑函数的有4种常用的表示方法:
真值表、逻辑函数式、卡诺图、逻辑图。
作业题: 2. 5 2.6
对偶规则:两个函数式相等,则它们的对偶式也相等。 变换时注意:(1) 变量不改变 (2) 不能改变原来的运算顺序 A + AB = A
A· (A + B) = A
应用对偶规则可将基本公式和定律扩展。
逻辑代数基础
小结
逻辑代数是分析和设计逻辑电路的重要工具。 逻辑代数的公式与定律中,除常量之间及常 量与变量之间的运算外,还有交换律、结合 率、分配律、吸收律、摩根定律等。 逻辑代数的规则有代入规则、反演规则和对偶 规则。
逻辑代数基础
(二) 逻辑代数的特殊定理
吸收律 A + AB = A
A + AB = A (1 + B) = A
逻辑代数基础
(二) 逻辑代数的特殊定理
吸收律 A + AB = A 推广公式:
摩根定律(又称反演律) 推广公式: A B A· B A+B A B A+B A · B 0 0 1 1 0 0 1 1 0 1 1 1 0=1 0,则 B 0 = C 吗? 思考:(1) 若已知 A + B A+C 1 0 1 1 1 0 0 0 (2) 若已知 AB = AC,则 B = C 吗? 1 1 0 0 1 1 0 0
变换时注意: (1) 不能改变原来的运算顺序。 (2) 反变量换成原变量只对单个变量有效,而长非 号保持不变。
原运算次序为 可见,求逻辑函数的反函数有两种方法: 利用反演规则或摩根定律。
逻辑代数基础
(三) 对偶规则
对任一个逻辑函数式 Y,将“· ”换成 “+”,“+”换成“· ”,“0”换成 “1”,“1”换成“0”,则得到原逻 辑函数式的对偶式 Y 。
逻辑变量与常量的运算公式
0–1律 0+A=A 1+A=1 1· A=A 0· A=0 重迭律 A+A=A A· A=A 互补律 还原律
逻辑代数基础
二、基本定律
(一) 与普通代数相似的定律
交换律 结合律 分配律 A+B=B+A (A + B) + C = A + (B + C) A (B + C) = AB + AC A· B=B· A (A · B) · C=A· (B · C) A + BC = (A + B) (A + C) 普通代数没有! 逻辑等式的 证明方法 利用真值表
利用基本公式和基本定律
逻辑代数基础
[例] 证明等式 A + BC = (A + B) (A + C) 解: 真值表法 A B C A + BC (A + B) (A + C) 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 公式法 右式 = (A + B) (A + C) 用分配律展开 = AA + AC + BA + BC = A + AC + AB + BC = A (1 + C + B) + BC =A· 1 +BC = A + BC
逻辑代数基础
三、重要规则
(一) 代入规则
A A A 将逻辑等式两边的某一变量均用同 一个逻辑函数替代,等式仍然成立。Leabharlann A均用 代替 A均用 代替
B均用C代替 利用代入规则能扩展基本定律的应用。
逻辑代数基础
(二) 反演规则
对任一个逻辑函数式 Y,将“· ”换成 “+”,“+”换成“· ”,“0”换成“1”, “1”换成“0”,原变量换成反变量,反变量 换成原变量,则得到原逻辑函数的反函数 Y 。
逻辑代数基础
第2章
逻辑代数基础
逻辑代数的基本定律和规则 小结
逻辑代数基础
2.2
逻辑代数的基本定律和规则
主要要求:
掌握逻辑代数的基本公式和基本定律。 了解逻辑代数的重要规则。
逻辑代数基础
一、基本公式
逻辑常量运算公式 0· 0=0 0· 1=0 1· 0=0 1· 1=1 0+0=0 0+1=1 1+0=1 1+1=1
