数模_全国一等奖__A题__储油罐的变位识别与罐容表标定
数模全国一等奖储油罐的变位识别与罐容表标定

储油罐的变位识别与罐容表的标定摘要本文研究储油罐的变位识别与罐容表的标定。
分别以小椭圆型油罐和实际卧式储油罐为研究对象,运用高等数学的积分的知识,分别建立罐体变位前后罐内油体积与油高读数之间的积分模型,使用Matlab 软件得出结论。
对于问题一,以小椭圆型储油罐为研究对象,在无变位时,小椭圆型储油罐为规则的椭球柱体,可利用解析几何与高等数学的知识建立油罐内体积与油高读数之间的积分模型,得出罐体无变位时的理论值。
当罐体发生纵向变位时,小椭圆型储油罐的截面不再是规则的几何形体,但根据倾角α及所给小椭圆型罐体的尺寸,可得其截面面积的表达式,利用高等数学中积分的方法,根据不同油高,建立了模型一,得到了储油量和油高的关系公式。
最后,根据实验数据的处理,用拟合的方法,修正了某些系统误差的影响,计算出罐体变位后油位高度间隔1cm 的罐容表的标定值。
对于问题二,由于实际储油罐内没油的高度不同,我们将其分为五种情况分别讨论,并对每种情况建立积分公式,得出罐内油体积与油位高度及变位参数(纵向倾斜角α和横向偏转角β)之间的函数关系式,利用所给的实验数据,运用最小二乘法,建立非线性规划模型212arg ,(((,,)(,,)))min (,,)nii i i V H V HOilData error OilData αβαβαβαβ-==--∑用Matlab 非线性规划求解得出使得总体误差最小的α与β值:α=2.12°,β=4.06°。
通过α与β的数值计算出出油量理论值与实测值的平均相对误差小于0.5% 。
对模型进行了较为充分的正确性验证和稳定性验证:在α与β的值为0时,其计算出来的罐容值与理论值完全吻合,说明模型在体积计算上是正确的;当对油高进行0.1%的扰动时,α的值变化也在0.1%左右,说明α的稳定性很好,但是β的值从4.06°变成了3.75°,变化了大约8%,所以我们详细分析了β的数学表达式,从理论上分析了影响其稳定性的因素。
全国大学生数学建模竞赛A题获奖—储油罐的变位识别与罐容表标定收集资料

2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是:A题储油罐的变位识别与罐容表标定我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):日期:2010年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型,在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据,最后分析误差及评价模型的合理性。
对于问题一的任一种情形,我们均建立笛卡尔坐标系,当储油罐无变位时,利用微元法得到体积关于h的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
全国数学建模大赛题目

附件2:实际储油罐的检测数据
2010高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
B题 2010年上海世博会影响力的定量评估
2010年上海世博会是首次在中国举办的世界博览会。从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台。请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。按照有关规定,需要定期对罐容表进行重新标定。图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
全国大学生数学建模竞赛A题获奖—储油罐的变位识别与罐容表标定

2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是:A题储油罐的变位识别与罐容表标定我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):日期:2010年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型,在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据,最后分析误差及评价模型的合理性。
对于问题一的任一种情形,我们均建立笛卡尔坐标系,当储油罐无变位时,利用微元法得到体积关于h的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
A题 储油罐的变位识别与罐容表标定
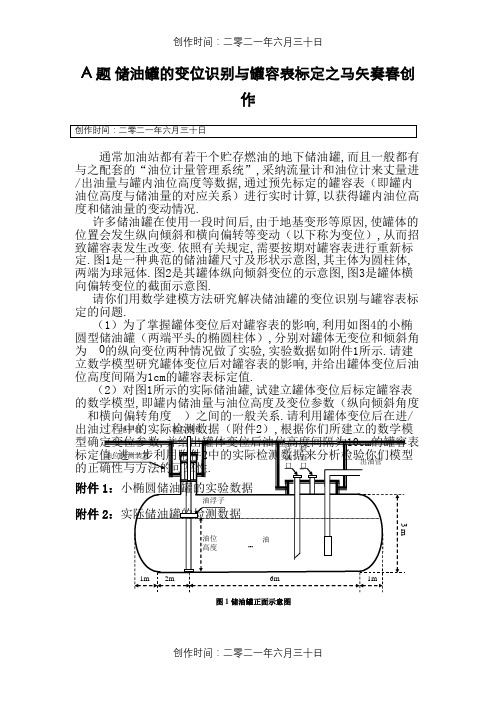
A 题 储油罐的变位识别与罐容表标定之马矢奏春创作创作时间:二零二一年六月三十日通常加油站都有若干个贮存燃油的地下储油罐,而且一般都有与之配套的“油位计量管理系统”,采纳流量计和油位计来丈量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以获得罐内油位高度和储油量的变动情况.许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变动(以下称为变位),从而招致罐容表发生改变.依照有关规定,需要按期对罐容表进行重新标定.图1是一种典范的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体.图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图.请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题.(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为0的纵向变位两种情况做了实验,实验数据如附件1所示.请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值.(2)对图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系.请利用罐体变位后在进/型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值.进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性.附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据油油浮子出油管 油位探测装置 注油口 检查口地平线 2m 6m1m 1m3 m油位高度图1 储油罐正面示意图油位探针油位探针地平线 图2 储油罐纵向倾斜变位后示意图(b) 小椭圆油罐截面示意图水平线17cm(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图油位探针(a )无偏转倾斜的正截面图油位探针。
(推荐)数学建模A题--储油罐的变位识别与罐容表标定的论

储油罐的变位识别与罐容表标定摘要本文主要探讨了储油罐的变位识别与罐容表标定的问题。
本文通过建立合适的坐标系,使用二重积分的方法和近似积分、坐标变换等技巧,求解了小椭圆储油罐和实际储油罐在发生变位时储油量与油高变化的函数关系,从而分析了罐体变位后对罐容表的影响,并对数据结果和误差进行了详实的分析。
本文在模型的建立与求解的过程中始终遵循化繁为简的原则,最先考虑简化的基本模型,再通过变换推导出实际的模型。
在第一问中,我们首先假设油罐壁的厚度为零,并通过二重积分的计算了小椭圆储油罐在无变位情况下的理论储油量。
其次我们通过运用几何原理通过坐标变换利用现有模型计算了小椭圆储油罐在纵向倾斜后的理论储油量。
在进行误差分析时,我们发现误差非线性,且误差数量级较大,得出油罐壁的厚度应不为零的结论,且经过理论分析油量3()V O d =,故我们用三次多项式拟合误差曲线()f H ,并通过'()()()V H V H f H =-修正了油量的计算公式。
经检验,修正后模型的计算值与实际值十分吻合,模型准确度很高。
并且,我们用修正后的模型V'(H)对油罐进行了标定。
在第二问中,我们利用了问题一中的模型求解罐身中的油量体积,并通过二重积分给出了油罐凸头部分油量的计算公式,其中,在油罐发生纵向倾斜时,我们队凸头部分的油量进行了合理的近似计算。
并且,我们通过坐标变换,给出了211()((,,((),))V H f f H f H αββα==))的变位参数修正形式。
在求解变为参数α、β时,我们通过最小二乘法拟合()V H ,求出了 2.1258, 4.6814αβ︒︒==。
将此变位参数代入模型中进行检验,得出理论计算值与实际值的相对误差限为5.006%,平均相对误差为0.029%,模型准确可靠。
最后我们用所得模型对油罐进行了标定。
关键词:储油罐 油量 倾斜 标定问题的重述与分析1、问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
2010全国赛A题

12010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数, 并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
(先检测误差补偿的可靠性,然后进行计算0-10,10-20…..)附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据地平线 图1 储油罐正面示意图油位探针2误差补偿公式:油位探针地平线 图2 储油罐纵向倾斜变位后示意图(b) 小椭圆油罐截面示意图水平线1.2m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线油位探针(a )无偏转倾斜的正截面图。
2010A(国家一等奖)解析

题目: 储油罐的变位识别与罐容表标定【摘 要】本文根据题目要求,针对具体问题建立相应的数学模型,并对问题进行精确求解,逐层深入比较题给数据与理论求解值同时分析它们之间的关系,据此得出合理的结论。
对于问题一,首先,采用截面法建立数学模型对无变位及有变位的理论油容量与油位高度之间的关系表达式。
然后,根据附件1所给的无变位进油时油高求出对应理论油量并与所给实际油量值相比较,发现两者的相对偏差σ基本成一稳定值3.371%,并根据两者之间的关系求出理论油量的修正函数,同时将偏差函数运用于无变位出油中,通过比较相邻两时刻绝对出油量的相对误差(均值为41021.3-⨯)检验修正函数的正确性。
接着,根据对应倾斜变位进油油高的校正理论油量与实际油量相比较,分析得出纵向变位时液位较小时罐容表读数偏小,液位较高时读数偏大的结论。
最后运用MATLAB 编写程序对变位后罐容按油位高度间隔为1cm 的进行标定,结果见附表1。
对于问题二,由于横向倾斜不影响体积的计算,只影响油面高度实际值h 与罐容表测量值*h 之间的关系。
于是,先根据三重积分与截面法计算只有纵向倾斜的情况下罐容与倾斜角度α和h 的关系),(h f V y α=。
然后,根据油面高度与横向偏转角度β及*h 关系),(*h f h β=得罐内储油量与油位高度及纵向倾斜角度α和横向偏转角度β之间的一般关系),,(*h f V y βα=。
取0,0==βα(无变位时),根据附件2中油位高度计算出相应油量,发现与附件所给油量容积几乎完全一致。
接着利用附件2中实际出油量与理论出油量的差值的平方和最小的条根据误差最小原则选取)244.4,129.2(==βα,求得罐容表标定值部分数据量与理论出油量近似相等,验证模型的正确性和可靠性。
并进行了模型推广,进行了基于MATLAB 的GUI 设计。
关键词:截面法,三重积分,遍历法,NDEPSO 算法,GUI 设计一问题的重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
2010数学建模A题答案论文 储油罐的变位识别与罐容表标定

摘要
储油罐作为加油站常用的贮存设施,对油品在不同液面高度时的贮油量进行精确的 计量变得尤为重要,本文讨论了,加油站卧式储油罐的变位识别与罐容表标定问题。其 主要方法是参考卧式储油罐罐内油品体积标定测量技术,结合几何关系及积分计算,建 立储油罐内储油量,油位高度及变位参数(纵向倾斜角 与横向倾斜角 )之间的关系 模型。然后分析模型,在油位高度一定时,由储油量确定变位参数 与 的值,即为对 储油罐进行变位识别;在变位参数 与 一定时,根据油位高度可确定储油量,即为对 罐容表(罐内油位高度与储油量之间对应的函数关系表达式)进行标定。
地平线
油位探针
油位探测装置
注检 油查 口口
出油管
油浮子
3m
油位
油
高度
1m 2m
6m
1m
图 1 储油罐正面示意图
-2-
地平线 油位探测装置
油位探针
油浮子
注检 油查 口口
出油管
油
α
图 2 储油罐纵向倾斜变位后示意图
水平线
地平线
油位探针
油位探测装置
地平线 油位探针
油 油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图
-6-
S ' a2 / 2 (a h' )a sin( / 2)
公式(2)
从而求得所求截面面积: S ( a2 / 2 (a h')a sin( / 2)) cos
公式(3)
将式(3)带入式(1)求得: V ( a2 / 2 (a h' )a sin( / 2))l cos
首先,结合上述因素及汽油热膨胀系数,建立模型并对模型进行修正,修正热膨胀 所带来的计算误差。代入附表实际测量数据验证模型。
全国大学生数学建模竞赛A题获奖—储油罐的变位识别与罐容表标定精品

2010高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是:A题储油罐的变位识别与罐容表标定我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.2.3.指导教师或指导教师组负责人(打印并签名):日期:2010年9月12日赛区评阅编号(由赛区组委会评阅前进行编号):2010高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):储油罐的变位识别与罐容表标定摘要本文通过对储油罐中油位高度及变位参数之间的不同情形的储油量进行分析并建立相应的数学模型,在该过程中先利用投影法、截面法及微元法得出储油量与油位高度及变位参数的函数关系。
再由Matlab编程可知各高度储油量的理论数据,最后分析误差及评价模型的合理性。
对于问题一的任一种情形,我们均建立笛卡尔坐标系,当储油罐无变位时,利用微元法得到体积关于h的公式,当储油罐发生变位时,根据储油罐中油量的多少分成三种情形,就每一类利用微元法得到体积关于h的公式。
代人附件1实验数据中的高度得到储油罐中的理论油量V。
根据理论油量及实际油量得出误差,判断误差所服从的分布,再利用相对误差进行误差分析并评价模型的合理性。
由上述得到储油罐发生变位时体积关于h的公式我们给出了罐体变位后油位高度间隔为1cm的罐容表标定值(即进/出油量与罐内油位高度的表格)。
储油罐的变位识别和罐容表标定问题(2010年数学建模竞赛A题论文)

储油罐的变位识别和罐容表标定问题摘要储油罐使用一段时间后,由于地基变形等原因罐体发生纵向倾斜和横向偏转,导致罐容表发生改变,需要对其重新标定。
本文建立了积分模型和非线性回归模型,解决了储油罐的变位识别和罐容表标定问题。
为了得到罐体变位对灌容表的影响,首先通过积分得到储油量与油高之间的方程。
在求该关系过程中,先将有变位情况的油高转化为无变位的油高,通过求无变位状态下的储油量来求变位后的储油量,得到积分模型。
利用实验数据对模型进行检验,发现无变位状态下进出油时理论计算值与实测值的相对误差约为定值3.49%,而倾斜4.1°时相对误差随着油高的减小而增大,最大为5%,这是因为倾斜下油高较小时底部储油并不引起油浮子变化,从而导致相对误差大。
该误差可能来源于测量误差、温度等外界因素影响,而积分模型没有考虑这些因素,因此在函数关系的基础上建立非线性回归模型,用MATLAB7.1进行拟合得到回归方程,并进行系数的区间估计和残差检验,最大残差为6L,最大相对误差为3.06%。
因此,利用非线性回归模型按油高分三段得到油位高度间隔1cm的罐容表标定值。
问题二中考虑到纵、横变位对灌容表的影响是独立的,变位影响增量可叠加,得到无变位状态下的油高与变位后的油高及纵横变位参数之间的关系=。
先不考虑两端球冠,按照问题一的求解思路可得到中间柱体储(,,)H H hαβ油量与油高的关系。
然后对两端球冠单独积分,将得到的油量与柱体油量相加得到储油罐总油量方程(,,)=。
根据实际数据,采用非线性拟合,利用TaylorV V hαβ级数对复杂的函数关系式进行简化,从而实现对变位参数的点估计,得到的系数为变位参数的函数,反解即可得到变位参数值:α=2.57°,β=4.82°。
接着将变位参数反代回(,,)=得到变位情况下的罐容表函数,然后按间隔10cmV V hαβ的油高标定罐容表。
又对实际数据进行了多项式拟合,比较两种方式得到的函数值与实际值的残差分布情况,说明用积分模型标定罐容表的方法是可行的。
A题储油罐的变位识别与罐容表标定
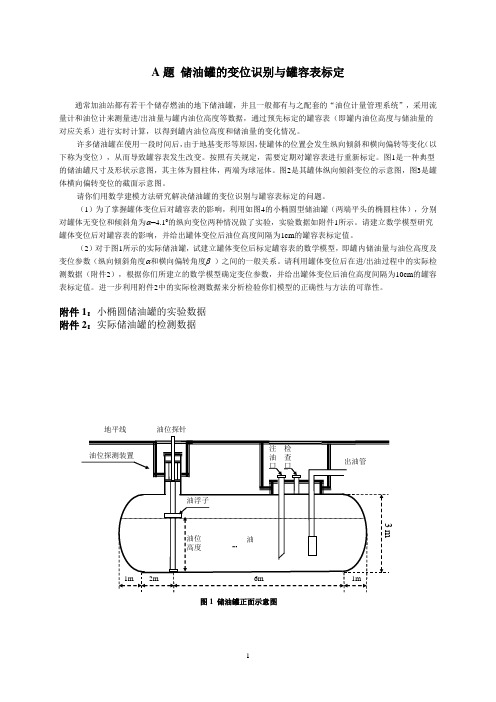
A题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据油位探针地平线油位探针地平线图2 储油罐纵向倾斜变位后示意图图3 储油罐截面示意图(b)横向偏转倾斜后正截面图地平线地平线垂直线油位探针(a)无偏转倾斜的正截面图油位探针变位储油罐的罐容表标定模型摘要:加油站的地下储油罐会出现变位的情况,计量储油罐油量的罐容表需要重新标定。
2010A 数学建模国家一等奖

储油罐的变位识别与罐容表标定问题的探讨摘要通常加油站都有多个储存燃油的地下储油罐。
许多储油罐在使用一段时间后,由于 种种原因,罐体的位置会发生变位,从而导致罐容表发生改变,给计量工作带来一定误 差。
因此用数学建模方法研究解决储油罐的变位识别与罐容表标定问题具有重要意义。
对于问题一,分别进行了精确理论推演与数值模拟求解,均取得很好效果。
第一步,在罐体无变位时,利用元素法用定积分求出油位高度与油量体积之间的关 系式 )] 1 / ( ) 1 / ( 1 2 / ) 1 / arcsin( [ 2 - - - + + - = b h b h b b b h b al v p ,用其计算的理论值与实验 测量值之间有偏差(测量误差),于是分析建立了测量误差和油位高度之间的显著回归 函数: h e 13493 . 0 01203 . 0 + - = ,将函数对上述关系式进行修正得到无变位的数学模型, 模型的精确度可以达到99.5%。
第二步,给定倾角纵向变位时,根据油位高度的不同,分三种情形建立了油量与油 位高度之间二重积分模型。
利用 MATLAB 求解得到表达式,然后给出了测量误差与油位 高度之间的显著回归函数: 2 2 39739 . 0 58340 . 0 12424 . 0 h h e - + -= ,将其对上述表达式进 行修正,从而建立出精确度可达到99.6%的数学模型。
第三步,对于罐体变位后对罐容表的影响,我们认为有两部分:其一是理论公式计 算上的变化,通过对有变位与无变位的积分表达式做差,结合泰勒公式,得到体积改变 量与油高和倾角的关系式;其二是测量误差的变化。
对前面的表达式进行分析,给出测 量误差 e v D 与油高h 和倾角a 的函数关系形式,然后确定函数中的参数,最后得到了在 任意纵向倾角情况下的误差项模型:01203 . 0 30852 . 4 ) 6511 . 30 13493 . 0 ( 9435 . 38 7611 . 11 2 / 3 2 - - + + - = D a a a a h h h v e 此模型对前两种有无变位的测量误差都具有显著回归效果。
全国数学建模历年赛题

2010年全国大学生数学建模竞赛题目A题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为a=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度a和横向偏转角度b)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台。
请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力。
A题 储油罐的变位识别与罐容表标定全集文档

A题储油罐的变位识别与罐容表标定全集文档(可以直接使用,可编辑实用优质文档,欢迎下载)A题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据油位探针地平线油位探针地平线(b) 小椭圆油罐截面示意图水平线(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线垂直线(a )无偏转倾斜的正截面图英语动词三态变化表——“动词原形”、“过去式”、“过去分词”一、“三态同形”(AAA)二、过去分词和动词原形同型(ABA)三、过去式和过去分词同型(ABB)四、三态不同型(ABC)(1)字母变化in-an-un(2)词尾变化ear-ore-orn(3)过去式以-ew结尾;过去分词以-wn结尾(4)过去分词以-en结尾(5)其他p.s. 动词原形(simple form);过去式(past form);过去分词(past participle)未完成过去时特殊动词变位简单将来时特殊动词变位条件式现在时动词变位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
储油罐的变位识别与罐容表的标定摘要本文研究储油罐的变位识别与罐容表的标定。
分别以小椭圆型油罐和实际卧式储油罐为研究对象,运用高等数学的积分的知识,分别建立罐体变位前后罐内油体积与油高读数之间的积分模型,使用Matlab 软件得出结论。
对于问题一,以小椭圆型储油罐为研究对象,在无变位时,小椭圆型储油罐为规则的椭球柱体,可利用解析几何与高等数学的知识建立油罐内体积与油高读数之间的积分模型,得出罐体无变位时的理论值。
当罐体发生纵向变位时,小椭圆型储油罐的截面不再是规则的几何形体,但根据倾角α及所给小椭圆型罐体的尺寸,可得其截面面积的表达式,利用高等数学中积分的方法,根据不同油高,建立了模型一,得到了储油量和油高的关系公式。
最后,根据实验数据的处理,用拟合的方法,修正了某些系统误差的影响,计算出罐体变位后油位高度间隔1cm 的罐容表的标定值。
对于问题二,由于实际储油罐内没油的高度不同,我们将其分为五种情况分别讨论,并对每种情况建立积分公式,得出罐内油体积与油位高度及变位参数(纵向倾斜角α和横向偏转角β)之间的函数关系式,利用所给的实验数据,运用最小二乘法,建立非线性规划模型212arg ,(((,,)(,,)))min (,,)nii i i V H V HOilData error OilData αβαβαβαβ-==--∑用Matlab 非线性规划求解得出使得总体误差最小的α与β值:α=2.12°,β=4.06°。
通过α与β的数值计算出出油量理论值与实测值的平均相对误差小于0.5% 。
对模型进行了较为充分的正确性验证和稳定性验证:在α与β的值为0时,其计算出来的罐容值与理论值完全吻合,说明模型在体积计算上是正确的;当对油高进行0.1%的扰动时,α的值变化也在0.1%左右,说明α的稳定性很好,但是β的值从4.06°变成了3.75°,变化了大约8%,所以我们详细分析了β的数学表达式,从理论上分析了影响其稳定性的因素。
根据得到的变位参数计算出实际罐体变位后油位高度间隔为10cm 的罐容表的标定值。
最后,本文对模型的优缺点进行了评价,并讨论模型的推广。
关键字:储油罐;变位识别;罐容表标定;非线性规划一.问题重述通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
根据上述所述,求解下列问题:(1)为了掌握罐体变位后对罐容表的影响,利用小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.1°的纵向变位两种情况做了实验。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据,根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用实际检测数据来分析检验你们模型的正确性与方法的可靠性。
二.问题分析本文研究罐容表的读数与储油罐的变位的关系。
借助高等数学积分的方法,求出储油量与油高读数的函数关系式,并对倾斜的储油罐进行容量标定。
1.对问题一的分析问题一中用小椭圆储油罐分别对罐体无变位和纵向倾斜进行实验,研究变位对罐容表的影响,因此我们分别建立变位前和变位后的罐容表读数与罐内油体积的函数关系式,通过函数关系式计算出理论值,再与所给的实际值相比较,得出其相对误差,然后通过分析系统误差进行修正,出罐体变位后油位高度间隔为1cm的罐容表的标定值。
2.对问题二的分析问题二中是以实际储油罐为研究对象,不仅考虑了储油罐的纵向倾斜,而且还考虑了横向偏转,为了使问题简化,我们先只考虑纵向倾斜,由于储油罐的形体不规则,所以我们将它分成如图1所示的三部分,分别算出每部分的体积与罐容表读数的函数关系式,然后对其求和。
再考虑横向偏转,建立它与所给的油高的函数关系式。
然后将二者进行综合考虑得出变位后罐容表读数与储油罐内油体积的函数关系式,通过关系式和所给数据,运用最小二乘法,通过MATLAB程序,搜索出α和β的最小误差解,再对模型的稳定性和正确性进行评定,最后给出高度间隔10cm的罐容表的标定值。
图1 油罐分区域积分示意图三.模型假设假设一:数据是储油罐的内壁参数。
假设二:忽略温度、压力对汽油的密度的影响。
假设三:储油罐在偏移的过程中,油位探针始终与油罐底面垂直。
假设四:对卧式储油罐来说,不考虑其长期埋在地下所发生的蠕变。
假设五:累加进出油量数据是准确可靠的。
四.符号说明H: 对应于罐容表读数的液面实际高度。
H: 球冠中与油罐圆柱左侧底面距离为x处的油高。
1R: 球冠中与油罐左侧底面相距为x处的小圆半径。
2H:球冠中与油罐圆柱右侧底面距离为x处的油高。
2R:球冠中与油罐右侧底面相距为x处的小圆半径。
3R: 储油罐圆柱部分的底面半径。
1R: 球冠所在球体的大圆半径。
H:第i条数据所对应的罐容表读数。
iOilData:用于分析的油量进出数据。
a: 椭圆长半轴长。
b: 椭圆短半轴长。
n: 用于分析的进出油测量数据个数。
h:罐容表读数。
五. 模型的建立与求解5.1 模型一的建立与求解问题一要求研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
5.1.1 计算未变位和变位的理论罐内油位高度与储油量的关系利用高等数学中微元法求体积的方法建立罐容表读数与罐内油体积的函数关系式的模型。
(1) 在无变位的情况下,储油罐内的油所占空间为柱体,其体积为 V S L = (1) 其中S 为柱体底面面积,L 为柱体的长度。
2hbS x dy -=⎰(2)底面椭圆方程为 22221x y a b += (3)22a x b y b=-(4)将(4)代入(2),得到222hba Sb y dy b-=-⎰ (5)其积分解析表达式为 22221(arcsin )2a h S hb h b b b b π=-++ (6) 其中, h H b =-(7)如图图2微元法求椭圆切面面积221[()(2)arcsin(1)]2a H S H b H b H b b b b π=--+-+(8) 221[()(2)arcsin(1)]2a H V L Hb H b H b b b b π=--+-+(9)图3 油罐无倾斜时示意图(2)当油罐发生纵向偏转时,油罐中油所占空间为一倾斜柱体,如图4所示:图4 油罐偏移示意图 如图4所示,根据几何关系可知,'(0.4)tan h H x α=--(10)又根据油面的高度不同,可分为以下三种情况:图5 情况1:低油位若油面位于图5所示位置,则:22 1022[(0.4tan tan)(0.4tan)0.4tan tan1arcsin]2aV H x b b H bbH x bb b dxbαααααααπ=+---+-++--+⎰(H+0.4tan)/tan(11)图6 情况2:正常油位若油面位于图6所示位置,则:2.45222022[(0.4tan tan)(0.4tan)0.4tan tan1arcsin]2aV H x b b H bbH x bb b dxbαααααπ=+---+-++--+⎰(12)图7 情况3高油位若油面位于图7位置,则:2.4530.4(1.2H)/tan 22[(tan tan 1arcsin ]2aV abL x b bx b b b dxb απααπ--=---+⎰(13)由上述公式知,油罐的变位会对罐内油高与储油量的对应关系(罐容表),产生较大的影响。
综合式(11)-(13),可以得到模型1如下:()0222.4502[(0.4tan tan 0.4tan tan 1arcsin ] H<2.05*tan 2[(0.4tan tan ()arcsin a H x b bH x b b b dx b a H x b bV H H b ααααααπααα+--+--+++--=++⎰⎰(H+0.4tan )/tan ,当0<22.450.4(1.2H)/tan 220.4tan tan 1] (H 1.2-0.4tan )2[(tan tan 1arcsin] (H 1.2)2x b b dx b a abL x b b x b b b dx b αααπααπααπα--⎧⎪⎪⎪⎪⎨--+≤≤---++≤⎰,当2.05*tan ,当1.2-0.4tan <⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩(14)5.1.2 应用试验数据对理论关系式进行修正当无变位进油时,我们可以根据式(9)221[(arcsin(1)]2a H V L Hb b b b b π=--+对每一个油位高度求出其理论储油量;另根据累加进油量和罐内油量初值,可求得实际储油量。
由于理论储油量和实测数据之间存在一定的系统误差,所以我们用线性回归方式得到修正系数 m = 1.035。
因此,无变位实际体积的修正计算公式为:221[(arcsin(1)]/2f a H V L H b b b m b b π=--+(15) 对不同高度用式(14)计算对应的体积f V 和实测值进行对比验证,平均误差为0.01%,达到较好的计算精度(图8)。
参考数据见附表1图8当罐体有α=4.1°倾斜角的纵向变位时,利用模型1我们对每一实验数据给出的油高计算其理论储油量。
系统误差校正:所谓系统误差,是由于原始读数不准确造成的,其原因可能是仪表不准确、罐体变形或者进油出油管道和仪表占据一定的容积。
虽然我们不知道具体的原因,但是我们通过统计分析可以一定程度上消除系统误差。
方法如下:根据实验数据中累加进油量和罐内油量初始值求出实际储油量,与模型计算值进行比较,用二阶多项式拟合储油量差值和油高。
20.00040.5834124.24,0.9773dv H H Relative =-+-=(16)这两列数据的相关系数达到0.977,有理由采用此多项式对模型的计算值进行系统误差修正。
图9 系统误差和油高的拟合对于试验中变位时,数据中的油高均处在5.1中正常油位情况,模型一中其他两种情况没有涉及。
