小升初数学组合图形总复习题
2013小升初数学总复习试题 组合图形

2013小升初数学总复习试题组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
2014年小升初数学总复习试题:组合图形

组合图形1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
不规则或组合平面图形阴影部分面积计算-2024年小升初数学复习热点题型专项训练(通用版)(含解析)
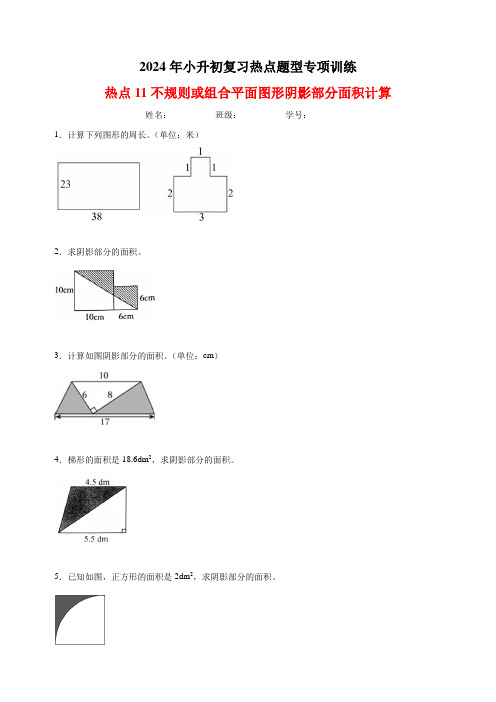
2024年小升初复习热点题型专项训练热点11不规则或组合平面图形阴影部分面积计算姓名:_________ 班级:_________ 学号:_________1.计算下列图形的周长。
(单位:米)2.求阴影部分的面积。
3.计算如图阴影部分的面积。
(单位:cm)4.梯形的面积是18.6dm2,求阴影部分的面积。
5.已知如图,正方形的面积是2dm2,求阴影部分的面积。
6.求阴影部分的周长。
7.求下列组合图形的面积。
(单位:cm)8.计算如图中阴影部分的面积。
9.计算下边阴影图形的周长。
10.求组合图形的面积。
(单位:米)11.求组合图形的面积。
(单位:cm)12.求图中阴影部分的面积(单位:厘米)13.如图中阴影部分的面积是多少?14.求如图阴影部分的周长和面积。
15.求阴影部分的面积(单位:厘米)。
16.求下面图形中阴影部分的面积。
17.求图中涂色部分的面积。
(单位:厘米)18.如图中,大圆的半径等于小圆的直径。
请计算阴影部分的周长。
19.计算如图阴影部分的面积。
20.求图形中阴影部分的面积。
(单位:分米)21.求下面图形阴影部分的周长和面积。
22.求下图中阴影部分的周长和面积。
23.求图中阴影部分的面积。
(单位:厘米)( 取3.14)24.求阴影部分的面积。
(单位:厘米)25.求下面图中阴影部分的面积(单位:厘米)。
26.计算如图所示图形阴影部分的面积。
(单位:厘米;圆周率取3.14)27.求下面图形中阴影部分的周长和面积。
28.计算如图所示图形阴影部分的面积。
(单位:厘米;圆周率取3.14)29.求出下图中阴影部分的面积。
(单位:米)30.求出前两个图形的面积和第三个图形中涂色部分的面积。
参考答案1.122米;12米【分析】(1)长方形的周长=(长+宽)×2,代入数据即可解答;(2)把这个图形上方的小线段分别向上、向左及向右平移,则这个图形的周长就是边长为3米的正方形的周长,据此利用正方形的周长公式即可解答。
小升初数学复习几何图形—专题14《圆与组合图形》(原卷版)

几何图形—专题14《圆与组合图形》一.选择题1.(2018秋•浦东新区期末)如图,扇形OAB的圆心角为90︒,且半径为R,分别以OA,OB为直径在扇形内作半圆,P和Q分别表示两个阴影部分的面积,那么P和Q的大小关系是()A.P Q=B.P Q<D.无法确定>C.P Q2.如图,直径AB为12的半圆,绕A点逆时针旋转60︒,此时点B旋转到点B',则图中阴影部分的面积是()A.12πB.24πC.6πD.36π3.三张边长都是12厘米的正方形铁皮,分别按下图剪下不同规格的圆片.哪种剪法最浪费材料?( )A.第一种B.第二种C.第三种D.三种浪费得同样多4.如图,半圆周上任意一点P,连接AP、BP,APB∠的度数是()A.大于90︒B.小于90︒C.等于90︒D.不确定二.填空题5.(2018•株洲)如图,一枚半径为1cm的圆形游戏币在边长为4cm的正方形内任意移动,则在正方形内,cmπ取3.14)游戏币不能到达的部分面积为2(6.(2016•天津)如图,三角形ABC是等腰直角三角形,D是圆周上的一点,圆心角BOD是120︒已知AB 边的长是6cm,阴影部分的面积是2cm.7.(2015•碑林区校级模拟)如图,在等腰直角三角形ABC中,90∠=︒,点D为AB的中点,已知扇形EADC和扇形FBD的圆心分别为点A、点B,且2AC=,则图中阴影部分的面积为.8.(2014•湖南模拟)图中扇形的半径6∠=︒,AC垂直OB于C,那么图中阴影AOB==厘米.45OA OBπ=部分的面积是平方厘米.( 3.14)9.如图,半圆的面积是39.25平方厘米,圆的面积是28.26平方厘米,那么图中空白部分的面积是平方厘米.三.应用题10.如图,有3个完全相同的圆,其中A、B被固定住,圆C紧贴着A、B这两个圆沿顺时针方向无滑动滚动.当圆C 再滚动出发点P 时,它绕自己的圆心转了多少圈?四.操作题11.在一个等边三角形内画一个最大的圆,再在这个圆内画一个最大的等边三角形.写出这两个等边三角形的面积比.五.解答题12.(2017•邛崃市模拟)如图,正方形ABCD 的边长为4cm ,点E 在BC 上,四边形BEFG 也是正方形,以点B 为圆心,BA 长为半径画弧AC .连结AF 、CF 、AF 与BC 交于点H ,试求图中阴影部分的面积.13.(2017秋•长沙月考)如图,半圆1S 的面积是14.13平方厘米,圆2S 面积是6.28平方厘米.长方形(阴影)的面积是多少平方厘米?14.(2016秋•铜仁市月考)求如图阴影部分的面积.(单位:厘米)15.(2015春•尚志市期末)如图,圆的周长是12.56厘米,A、B的长度是8厘米,阴影部分的面积是多少平方厘米?16.(2015•南京模拟)底边和高都是6厘米的等腰三角形,分别以高的长为直径画圆,以底的一半长为直径画两个半圆,求阴影部分的面积.17.(2015•泸州校级模拟)求阴影部分的面积.18.(2014•陕西)如图所示,在一个长方形纸片上截出一个半圆和一个小圆,它们恰好能围成一个圆锥,已知长方形的长为8厘米,则纸片剩余部分面积为多少?( 近似值3)19.(2013秋•铜仁市月考)如图,圆的周长是25.12厘米,圆的面积正好和长方形的面积相等,这个长方形的长时多少厘米?20.(2011秋•江油市期末)长方形的面积等于圆的面积,已知长方形的周长是16.56厘米.求阴影部分的周长及面积.。
六年级下册数学-小升初平面图形组合专项试题-s1-人教版

-小升初平面图形组合专项试题-人教版一、解答题(题型注释)(1)(2)2.仔细数一数,填一填。
(1)右图是由个小三角形拼成的。
(2)右图有个三角形。
(3)右图共有个正方形。
3.根据游戏的需要,幼儿园阿姨用两个长8米、宽4米的长方形地垫先后拼成一个长方形游戏垫和一个正方形游戏垫(如图所示),拼成的长方形游戏垫和正方形游戏垫的周长分别是多少?4.如图,长方形中,,,三角形的面积为平方厘米,求长方形的面积.5.如图在中,,求的值.6.请你画出已学过的4种图形,使它们的面积相等,并计算出它们的面积.7.为了迎接“六•一”儿童节,学校做了一幅长方形的宣传画,长7米,宽50分米.这幅宣传画的周长和面积各是多少?8.如下图,在三角形ABC中,DC=2BD,CE=3AE,阴影部分的面积是20平方厘米,求三角形ABC的面积。
9.如下图,是一块长方形草地,长方形的长是14米,宽是12米。
中间有三条宽为2米的道路,两条是长方形,一条是平行四边形。
则草地的面积有多大?10.如图(1)(2)(3)(4)都是由9个边长为1厘米的正方形组成的3×3平方厘米的正方形,其中的阴影四边形的面积分别记为,,和,则,,ABCD:2:3BE EC=:1:2DF FC=DFG2ABCDAB CDEFGABC△12DC EA FBDB EC FA===GHIABC△的面积△的面积IHGFED CBA和中最小的与最大的和是多少平方厘米?参数答案1.(1)解:(2)解:【解析】1.根据题干的要求画图相应图形。
2.(1)4(2)3(3)5【解析】2.3.解:拼成长方形的周长是:(8+8+4)×2=20×2=40(米)答:拼成的长方形游戏垫的周长是40米.拼成后正方形的周长是:8×4=32(米)答:拼成的正方形游戏垫的周长是32米【解析】3.用两个长8米,宽4米的长方形,拼成一个大长方形,这个大长方形的长是(8+8)米,宽是4米;拼成正方形的边长是8米,然后根据长方形的周长公式:C=(a+b)×2,正方形的周长公式:C=4a,代入数据解答即可.4.72【解析】4.连接,.因为,,所以.因为,,所以平方厘米,所以平方厘米.因为,所以长方形的面积是平方厘米.5.17【解析】5.连接BG,设1份,根据燕尾定理,,得(份),(份),则(份),因此,同理连接AI、CH得,,所以如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.6.16平方厘米AE FEAB CDEFG:2:3BE EC=:1:2DF FC=3111()53210DEF ABCD ABCDS S S=⨯⨯=V长方形长方形12AED ABCDS S=V长方形11::5:1210AG GF==510AGD GDFS S==V V12AFDS=V16AFD ABCDS S=V长方形ABCD 72IHGFED CBABGCS△=::2:1AGC BGCS S AF FB==△△::2:1ABG AGCS S BD DC==△△2AGCS=△4ABGS=△7ABCS=△27AGCABCSS=△△27ABHABCSS=△△27BICABCSS=△△7222177GHIABCSS---==△△【解析】6.试题分析:此题没有具体数据,答案不唯一:把每个方格的长度看作1厘米,这里可以指定画面积为16平方厘米的正方形与长方形,则正方形的边长是4厘米,长方形的长可以是8厘米,则宽就是2厘米,梯形的上底是4厘米,下底是12厘米,高是2厘米,三角形的底是8厘米,高是4厘米,由此即可画图解:根据题干分析画图如下:答:它们的面积都是16平方厘米.7.24米,35平方米【解析】7.试题分析:根据长方形的周长=(长+宽)×2,长方形的面积=长×宽,代入数据即可解答.解:50分米=5米,(7+5)×2=24(米),7×5=35(平方米),答:这幅画的周长是24米,面积是35平方米.8.120平方厘米【解析】8.本题考查三角形面积和比的相关知识。
2024年小升初数学精讲专题专题16 组合图形的周长与面积(基础卷)
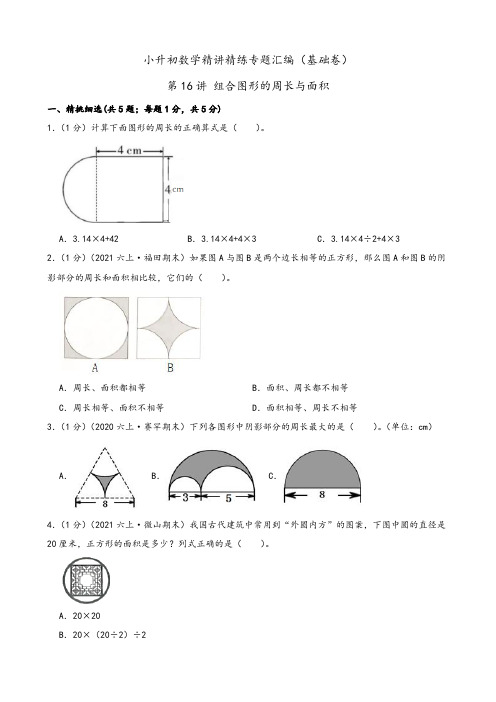
小升初数学精讲精练专题汇编(基础卷)第16讲组合图形的周长与面积一、精挑细选(共5题;每题1分,共5分)1.(1分)计算下面图形的周长的正确算式是()。
A.3.14×4+42 B.3.14×4+4×3 C.3.14×4÷2+4×32.(1分)(2021六上·福田期末)如果图A与图B是两个边长相等的正方形,那么图A和图B的阴影部分的周长和面积相比较,它们的()。
A.周长、面积都相等B.面积、周长都不相等C.周长相等、面积不相等D.面积相等、周长不相等3.(1分)(2020六上·赛罕期末)下列各图形中阴影部分的周长最大的是()。
(单位:cm)A. B. C.4.(1分)(2021六上·微山期末)我国古代建筑中常用到“外圆内方”的图案,下图中圆的直径是20厘米,正方形的面积是多少?列式正确的是()。
A.20×20B.20×(20÷2)÷2C.20×(20÷2)÷2×25.(1分)(2021六上·温江期末)如图,大圆内有3个大小不等的小圆,这四个圆的圆心都在同一直线上,若大圆的直径是5厘米,则三个小圆的周长之和是()厘米.A.7.85 B.15.7 C.31.4 D.78.5二、仔细想,认真填(共8题;每空1分,共9分)6.(1分)(2022六下·巧家期中)请算出下面面图形的面积是cm2。
7.(2分)(2020六上·合山期末)一个半圆,它的半径是r,它的直径是,周长是。
8.(1分)(2020六上·赛罕期末)如图所示,圆的直径20cm,阴影部分的面积是cm2。
9.(1分)(2020六上·福田月考)如图,半圆的半径是2分米,则封闭图形的周长为分米。
10.(1分)(2020·海安模拟)如图,在一大一小两个正方形拼成的图形中,阴影部分的面积是50平方厘米,则小正方形的面积是平方厘米。
2024年人教版六年级下册数学小升初分班考专题:图形的拼组(含答案)

2024年人教版六年级下册数学小升初分班考专题:图形的拼组一、单选题1.下图是一个长3厘米、宽与高都是2厘米的长方体。
将它挖掉一个棱长1厘米的小正方体,它的表面积( )。
A.比原来大B.比原来小C.不变D.无法确定2.在一个长、宽、高分别是30厘米、25厘米、60厘米的长方体箱子里,最多能装进棱长1分米的立方体( )个。
A.45B.30C.36D.723.城市义工协会开展垃圾分类宣传进社区活动。
他们计划在下面右边这张直角梯形卡纸上剪出如左边那样大小的三角形制作宣传标志(如下图),最多可以剪出( )个这样的三角形。
A.3B.4C.5D.64.如图,把一个底面半径4分米、高8分米的圆柱切开并拼成一个近似的长方体。
下面说法中错误的是( )A.长方体的体积与圆柱的体积相等B.长方体的底面积等于圆柱的底面积C.长方体的高等于圆柱的高D.长方体的表面积等于圆柱的表面积5.一个长9厘米、宽6厘米、高3厘米的长方体,切割成3个体积相等的长方体,表面积最大可增加( )A.36平方厘米B.72平方厘米C.108平方厘米D.216平方厘米6.在一个棱长为1dm的正方体的8个角上,各锯下一个棱长为1cm的正方体,现在它的表面积和原来比( )。
A.不变B.减少C.增加D.无法确定二、填空题7.在一块边长是20cm的正方形纸上画一个最大的圆,这个圆的面积是 cm2。
8.用三个完全一样的正方体,拼成一个长方体,长方体的表面积是70平方分米,原来一个正方体的表面积是 平方分米。
9.用3个棱长2分米的正方体拼成一个长方体。
这个长方体的体积是 立方分米,表面积是 平方分米。
10.如图,这个圆的直径是6厘米,把这个圆剪拼成一个近似的长方形,那么这个长方形的宽约 厘米,长方形的长约是 厘米。
11.一个正方体的棱长总和是24厘米,这个正方体的体积是 立方厘米,用两个这样的正方体拼成一个长方体,这个长方体的表面积是 平方厘米.12.如图形体是由棱长为1厘米的小正方体搭拼成的,它的表面积是 平方厘米,至少还需要 个这样的小正方体,才能搭拼成棱长为3厘米的一个正方体.13.一个高5厘米的圆柱体,沿底面直径将圆柱体锯成两块,其表面积增加40平方厘米,原来这个圆柱体的体积是 立方厘米。
小升初数学总复习专题分类训练卷 圆、组合图形的面积

小升初数学总复习专题分类训练卷圆、组合图形的面积第一部分知识梳理字母意义:O 圆心,r 半径,d 直径,π 圆周率,C 周长,S 面积特征:同一圆内,所有的半径、直径都分别相等,直径等于半径的2倍对称性:圆是轴对称图形,圆的直径所在的直线是圆的对称轴1.圆圆的周长计算公式:C=πd=2πr ,半圆周长计算公式:C半圆=πr+2r=(π+2)r圆的面积计算公式推导过程:将圆沿着直径等分成若干个扇形(偶数份),再拼成一个近似的长方形(分成的扇形越多,越接近长方形),长方形的长相当于圆的周长一半(πr),宽相当与圆的半径,圆的面积等于长方形的面积。
所以:S圆=S长方形=πr×r=πr2概念:两个半径不等的同心圆之间的部分称之为圆环。
各部分名称:①外圆:圆环中较大的圆叫做外圆,其半径通常用R表示。
2.圆环②内圆:圆环中较小的圆叫做内圆,其半径通常用r表示。
③环宽:外圆到内圆的距离叫做环宽环宽=R—r圆环的面积计算方法:外圆的面积与内圆的面积之差是圆环的面积。
即:S圆环=S外圆—S内圆,S圆环=π(R2 —r2)弧:圆上任意两点间的部分叫做弧3.扇形圆心角:弧的两个端点与圆心连结,所得两条半径的夹角叫圆心角扇形:由圆心角的两条半径和圆心角所对的弧组成的图形叫扇形割补(平移)法组合图形的面积加减法计算策略1 旋转、对称法4.组合图形的要求阴影先求空白面积计算包含与排除组合图形的面积总面积=两部分面积和-重叠部分面积计算策略2 巧添辅助线等积转化(代换)第二部分精讲点拨例1判断下列各题是否正确:(1)圆的周长是直径的3.14倍。
()(2)圆是轴对称图形,直径是圆的对称轴。
()(3)世界上第一位把圆周率精确到七位小数的人物是祖冲之。
()举一反三:1.填空题:(1)经过圆心并且两端都在圆上的线段叫做圆的(),圆有()条直径。
(2)圆的面积推导公式是:将圆分成若干个扇形,再拼成一个近似的长方形,长方形的长相当于圆的(),长方形的宽相当于圆的(),所以圆的面积公式为()。
苏教版小升初数学总复习试题组合图形

2018小升初数学专题1、求下列组部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)
部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
组合图形的面积(二)-小升初六年级数学下册第一轮总复习人教版

小升初第一轮总复习—空间与图形组合图形的面积(二)✎一、选择1.下面图形是由边长a cm的正方形组成,则阴影部分的面积是()cm2A. 4a2B. 3a2C. 2a2D. 1.5a22.图中,将两个正方形放在一起,大、小正方形的边长分别为l0,6,则图中阴影部分面积为()A. 42B. 40C. 38D. 363.某正方形园地是由边长为1米的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是.()A. B. C. D.4.如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰CD以D为中心逆时针旋转90°至DE,连AE、CE,则△ADE的面积是()A. 1B. 2C. 3D. 45.如图,将三角形ABC的BA边延长1倍到D,CB的边延长2倍到E,AC边延长1倍到F,如果三角形ABC的面积等于1,那么三角形DEF的面积是()A. 10B. 18C. 9D. 116.如图,平行四边形的面积是3.6平方厘米,阴影部分的面积是()A. 1.2平方厘米B. 3.6平方厘米C. 1.8平方厘米D. 7.2平方厘米7.第()个图形中涂色部分的面积不能用“2r×2r-πr2”来表示.A. B. C. D.8.如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米,图中阴影部分的面积是()A. 44平方厘米B. 60平方厘米C. 100平方厘米D. 144平方厘米9.如图,三角形ADF与三角形ABE、四边形AFCE的面积相等,BC=9厘米,CD=6厘米,求阴影部分的面积()A. 5(平方厘米)B. 25(平方厘米)C. 15(平方厘米)D. 10(平方厘米)10.以正方形ABCD的顶点A为圆心,以边长为半径,画一个圆,已知正方形的面积为16平方米,则S阴影=()A. 55平方米B. 3.44平方米C. 50平方米D. 5平方米11.如图所示:任意四边形ABCD,E是AB中点,F是CD中点,已知四边形ABCD面积是10,则阴影部分的面积是()A. 5B. 6C. 7D. 812.比较下面两个图形,说法正确的是()A. 甲、乙的面积相等,周长也相等B. 甲、乙的面积相等,但甲的周长长C. 甲、乙的周长相等,但乙的面积大D. 甲、乙的面积相等,它们周长不一定相等13.在图中的平行四边形中,甲的面积()乙的面积。
小升初数学图形与几何知识点分类复习《图形拼组问题》大题量附答案

小升初数学图形与几何知识点分类复习《图形拼组问题》一、选择题1.想要把一个长方形纸板剪成2个长方形纸板后,剪成的两个长方形纸板周长的和与原来长方形纸板的周长相比()。
A.增加了B.减少了C.与原来相等2.用两个完全一样的直角三角形拼成一个平行四边形,可以拼成两种平行四边形,问拼成的两个平行四边形面积相等吗?()A.相等B.不相等C.无法确定3.两个()的三角形可以拼成一个平行四边形。
A.形状相同B.面积相等C.周长相等D.等底等高4.两个周长是12厘米的正方形,拼成一个长方形,这个长方形的周长是()厘米。
A.24B.96C.185.把一个长10cm、宽8cm、高6cm的长方体,切成两个相等的长方体,它们的表面积之和比原来最多增加()平方厘米。
A.480B.160C.96D.806.先放两个正方体,在两个正方体的上面放两个圆柱,在两个圆柱的上面放一个长方体,在长方体上面放一个球,放对了的是()。
A.①B.①C.①7.在一张长方形纸上剪一刀,把它分成两部分,这两部分的形状不可能是()。
A.直角三角形B.等边三角形C.正方形D.直角梯形8.用20个相同的小正方形可以拼成()种长方形,20的因数有()个。
A.3;6B.4;5C.4;6D.5;69.左边的图形是用()个组成的。
A.4B.5C.610.把一张长方形的纸对折三次,折痕间的关系是()。
A.互相平行B.互相垂直C.可能互相平行,也可能互相垂直11.两个()的梯形一定能拼成一个平行四边形。
A.面积相等B.形状相同C.完全一样12.认真观察下图,共有()个。
A.6B.7C.813.以下几个图形中,不能单独密铺的是()。
A.B.C.D.14.下图中的大长方形是由4个完全相同的长方形拼成的,那么阴影部分与空白部分的面积比是()。
A.3①4B.4①5C.3①8D.3①515.一根绳子对折2次后,每段长4米,对折3次后,每段长()。
A.2米B.4米C.8米16.把一张圆形纸片剪拼成一个近似的梯形(如图),这个梯形的上、下底之和相当于圆的()。
【小升初】2020六年级下册数学总复习试题-组合图形的面积专项练 全国版(含答案)

组合图形的面积一、单选题1.如图中的阴影部分面积是()平方厘米A. 144B. 72C. 18D. 无法确定2.如图中阴影部分的面积是()平方厘米.(单位:厘米)A. 132B. 14.25C. 289D. 28.53.等腰梯形的一内角为45°,高等于上底,下底为9,那么梯形的面积为()。
A. 27B. 18C. 36D. 244.图中阴影部分的面积是()平方厘米.A. 24B. 28C. 325.下面三幅图的阴影部分的面积相比较,( )的面积大。
A. 图(1)大B. 图(2)大C. 图(3)大D. 同样大二、填空题6.求图中阴影部分的面积为________ (结果保留π).7.已知如图中三角形的面积是10平方厘米,图中圆的面积是________平方厘米.组合图形的面积是________平方厘米9.求下列图形的面积是________dm2。
(单位:dm)10.图中正方形的面积是12平方厘米,圆的面积是________平方厘米.11.计算下面图形阴影部分的面积________.(单位:厘米)12.(2015•长沙)如图,两个正方形的边长分别是8厘米和4厘米,则阴影部分的面积是________平方厘米.13.先求右面图形中涂色部分的面积,再求小正方形的面积.涂色面积________平方分米,小正方形面积________平方分米.平行四边形AFEB的面积S=________平方厘米平行四边形CFED的面积S=________平方厘米15.下图表示的是一间房子侧面墙的形状.它的面积是________平方米.16.求下面各图阴影部分的面积(1)________(2)________17.计算下面图形的面积________.(单位:厘米)18.有一条引水渠穿过了一块麦地,这块地的总面积是引水渠占去的面积的________倍?19.把一个长12厘米,宽8厘米的长方形纸片剪下一个最大的正方形,剩下部分的面积是________平方厘米.20.求阴影部分的面积.________平方厘米21.大正方形边长为8厘米,小正方形边长为4厘米,阴影部分的面积是________平方厘米。
小升初圆与组合图形面积专题(含解析)

小学数学圆与组合图形面积专题1.如图所示,大正方形与小正方形的面积之差为50平方厘米,阴影部分的面积是( )平方厘米.A .33.5πB .37.5πC .40πD .47.5π2.如图中,三角形ABC 是等腰直角三角形,图中阴影部分和空白部分的面积相比较,()A .阴影部分的面积大B .空白部分的面积大C .面积一样大D .无法判断3.计算如图阴影部分面积,正确的列式是( )A .266 3.14() 3.142⨯-⨯B .22166 3.14() 3.1422⨯⨯-⨯C .2216[6 3.14() 3.14]22⨯⨯-⨯D .1(62 3.146 3.14)2⨯⨯⨯-⨯4.下面是两张同样大小的正方形纸,分别剪出不同规格的圆片,剩下的面积( )A .第一张纸剩下的面积大B .第二张纸剩下的面积大C .两张纸剩下的面积一样大5.如图,长方形ABCD 的面积是26m ,圆的面积是 2m6.如图两个圆的半径都是4厘米,涂色部分的面积之和是 平方厘米.7.长方形里有两个圆(如图),阴影部分的面积是27cm ,那么一个圆的面积是 平方厘米.8.如图,这个图形的周长是 厘米.9.如图阴影部分的面积是25cm ,环形的面积是 2cm .三.计算题(共7小题)10.如图中正方形的边长为4cm ,求阴影部分的面积.11.求如图阴影部分的面积.(单位:厘米)12.计算如图图形中阴影部分的面积.13.求如图阴影部分的面积.14.求图中阴影部分面积.15.如图中,已知圆的周长是25.12厘米,圆的面积与长方形的面积相等,图中阴影部分的面积是多少平方厘米?cm16.求阴影部分的面积.(单位:)17.求如图阴影部分的面积和周长.面积:.周长:.18.如图,三角形ABC是等腰直角三角形,8C∠=︒,求:==,45AB AC cm(1)弧AD的长度;(2)图中阴影部分的面积.19.如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知==厘米,求阴影部分的面积.AB BC1020.如图,ABCD是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积.21.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为多少平方厘米?22.如图所示的多边形是由一个三角形和三个长方形组成的.已知三个长方形的面积分别是12平方厘米、4平方厘米和6平方厘米.三角形面积是多少平方厘米?23.公园里有一块长方形的草坪,为方便游客,在草坪中间开辟了两条小路(如图).现在m草坪的面积是多少?(单位:)24.如图,已知大圆半径为6cm,四个小圆的面积相等.阴影部分面积是多少平方厘米?(分合割补法)25.一个容积为550mL的水瓶,里面装了一些水,正放时,水面高20cm,倒放时,空气高7.5cm.求水有多少升?26.如图是直角三角形中有一个内接正方形,求图中阴影部分的面积.单位:厘米.提示:分拆图形时常用“分割、填补、组合、旋转”等方法.27.如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C 到边AB的垂线CE长为10厘米,求四边形ABCD的面积.28.图形计算(1)求下图阴影部分的周长和面积.(单位:厘米)(2)三条边长分别是6厘米、8厘米、10厘米的直角三角形.将它的最短边对折到斜边相重合,(如图)图中阴影部分面积是 平方厘米.29.如图,1S 的面积比2S 的面积大多少?30.图中正方形的边长是10厘米,三角形甲的面积比三角形乙的面积少20平方厘米,求线段AB 的长.圆与组合图形面积专题参考答案与试题解析一.选择题(共4小题)1.如图所示,大正方形与小正方形的面积之差为50平方厘米,阴影部分的面积是( )平方厘米.A .33.5πB .37.5πC .40πD .47.5π【解答】解:235037.5()4cm ππ⨯⨯= 答:阴影部分的面积是37.5π平方厘米. 故选:B .2.如图中,三角形ABC 是等腰直角三角形,图中阴影部分和空白部分的面积相比较,()A .阴影部分的面积大B .空白部分的面积大C .面积一样大D .无法判断【解答】解:根据分析可得,②=③+④=三角形ABC 面积的一半,①=③那么,空白部分的面积=②+③=三角形ABC 面积的一半+③ 阴影部分的面积=①+④=③+④=三角形ABC 面积的一半 所以,空白部分的面积大; 故选:B .3.计算如图阴影部分面积,正确的列式是( )A .266 3.14() 3.142⨯-⨯B .22166 3.14() 3.1422⨯⨯-⨯C .2216[6 3.14() 3.14]22⨯⨯-⨯D .1(62 3.146 3.14)2⨯⨯⨯-⨯【解答】解:2216[6 3.14() 3.14]22⨯⨯-⨯127 3.142=⨯⨯ 42.39=(平方厘米)答:阴影部分面积是42.39平方厘米; 故选:C .4.下面是两张同样大小的正方形纸,分别剪出不同规格的圆片,剩下的面积( )A .第一张纸剩下的面积大B .第二张纸剩下的面积大C .两张纸剩下的面积一样大 【解答】解:第一张纸剩下的面积是:244 3.14(42)⨯-⨯÷ 16 3.144=-⨯ 1612.56=- 3.44=第二张纸剩下的面积是:244 3.14(422)4⨯-⨯÷÷⨯ 16 3.1414=-⨯⨯ 1612.56=- 3.44=所以两张纸剩下的一样多.答:剪完圆后,两张纸剩下的一样多. 故选:C .二.填空题(共5小题)5.如图,长方形ABCD 的面积是26m ,圆的面积是 9.42 2m【解答】解:623÷=(平方米) 3.1439.42⨯=(平方米)答:圆的面积是9.42平方米. 故答案为:9.42.6.如图两个圆的半径都是4厘米,涂色部分的面积之和是 12.56 平方厘米.【解答】解:23.1444⨯÷ 50.244=÷12.56=(平方厘米)答:阴影部分的面积是12.56平方厘米. 故答案为:12.56.7.长方形里有两个圆(如图),阴影部分的面积是27cm ,那么一个圆的面积是 21.98 平方厘米.【解答】解:设圆的半径为r 厘米, 227r r ⨯÷=27r =3.14721.98⨯=(平方厘米)答:一个圆的面积是 21.98平方厘米.故答案为:21.98.8.如图,这个图形的周长是 23.98 厘米.【解答】解:3.1462 3.1482(86)⨯÷+⨯÷+-9.4212.562=++23.98=(厘米)答:这个图形的周长是 23.98厘米.故答案为:23.98.9.如图阴影部分的面积是25cm ,环形的面积是 31.4 2cm .【解答】解:设大圆的半径为R ,小圆的半径为r ,因为2211522R r -=, 则2210R r -=,环形的面积:223.14()R r ⨯-3.1410=⨯31.4=(平方厘米)答:环形的面积是31.4平方厘米.故答案为:31.4.三.计算题(共7小题)10.如图中正方形的边长为4cm ,求阴影部分的面积.【解答】解:244 3.14(42)⨯-⨯÷16 3.144=-⨯1612.56=-23.44()cm =答:阴影部分的面积是23.44cm .11.求如图阴影部分的面积.(单位:厘米)【解答】解:633-=(厘米)(63)32+⨯÷272=÷13.5=(平方厘米)答:阴影部分的面积是13.5平方厘米.12.计算如图图形中阴影部分的面积.【解答】解:222020 3.14204 3.14(202)2⨯-⨯÷+⨯÷÷400314157=-+243=(平方厘米)答:阴影部分的面积是243平方厘米.13.求如图阴影部分的面积.【解答】解:26226()cm ⨯÷=答:阴影部分的面积是26cm .14.求图中阴影部分面积.【解答】解:8822⨯÷÷6422=÷÷16=(平方厘米)答:图中阴影部分的面积是16平方厘米.15.如图中,已知圆的周长是25.12厘米,圆的面积与长方形的面积相等,图中阴影部分的面积是多少平方厘米?【解答】解:半径:25.12 3.1424÷÷=(厘米)233.1444⨯⨯3.1412=⨯37.68=(平方厘米)答:阴影部分的面积是37.68平方厘米.16.求阴影部分的面积.(单位:)cm【解答】解:(47)42+⨯÷112=⨯22=(平方厘米)答:阴影部分的面积是22平方厘米.四.解答题(共14小题)17.求如图阴影部分的面积和周长.面积:9平方厘米.周长:.【解答】解:面积:6(62)2⨯÷÷632=⨯÷9=(平方厘米)周长:3.14626⨯÷+9.426=+15.42=(厘米)故答案为:9平方厘米,15.42厘米.18.如图,三角形ABC是等腰直角三角形,8AB AC cm==,45C∠=︒,求:(1)弧AD的长度;(2)图中阴影部分的面积.【解答】解:(1)因为45n=︒,8r=厘米所以弧AD的长为:45 3.148180⨯⨯2 3.14=⨯6.28=(厘米)答:弧AD的长度6.28厘米.(2)22 180 3.144145 3.148(88)3602360⨯⨯⨯⨯-⨯⨯-8 3.14(328 3.14)=⨯--⨯16 3.1432=⨯-18.24=(平方厘米)答:阴影部分的面积是18.24平方厘米.19.如图,三角形ABC是等腰直角三角形,D是圆周的中点,BC是半圆的直径,已知10AB BC==厘米,求阴影部分的面积.【解答】解:连接BD 、OD 、OA ,由于DO BC ⊥,AB BC ⊥,所以//DO AB , 则AOD BOD S S ∆∆=,而阴影部分的面积AOB AOD BOD S S S ∆∆=+-扇形,AOB BOD BOD S S S ∆∆=+-扇形, 211101*********()242222π=⨯⨯÷+⨯⨯-⨯⨯ 2519.62512.5=+-,32.125=(平方厘米).20.如图,ABCD 是一个长方形草坪,长20米,宽14米,中间有一条宽2米的曲折小路,求小路的面积.+⨯-⨯=(平方米),【解答】解:小路面积为:(2014)22264答:小路的面积是64平方米.21.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为多少平方厘米?【解答】解:如图,,阴影部分A的面积等于空白部分B的面积,阴影部分C的面积等于空白部分D的面积,所以阴影部分的面积和等于正方形面积的一半,⨯÷=(平方厘米)4428答:图中阴影部分的面积为8平方厘米.22.如图所示的多边形是由一个三角形和三个长方形组成的.已知三个长方形的面积分别是12平方厘米、4平方厘米和6平方厘米.三角形面积是多少平方厘米?【解答】解:如图,设三角形面积为x平方厘米,则2:126:4x=x⨯=⨯42126x=872x÷=÷887289x=答:三角形面积是9平方厘米.23.公园里有一块长方形的草坪,为方便游客,在草坪中间开辟了两条小路(如图).现在m草坪的面积是多少?(单位:)⨯-⨯+⨯+⨯,【解答】解:2012(212220)22240(2440)4=-++,=-+,240644=(平方米);180答:现在草坪的面积是180平方米.24.如图,已知大圆半径为6cm,四个小圆的面积相等.阴影部分面积是多少平方厘米?(分合割补法)【解答】解:阴影部分的面积:(62)(62)2⨯⨯⨯÷,12122=⨯÷,1442=÷,272()cm =.答:阴影部分的面积是72平方厘米.25. 一个容积为550mL 的水瓶,里面装了一些水,正放时,水面高20cm ,倒放时,空气高7.5cm .求水有多少升?【解答】解:因为水的体积是不变的,瓶内空余部分的体积也是不变的, 所以水体积是空余部分体积的8207.53÷=倍, 885505504008311⨯=⨯=+毫升0.4=升, 答:水有0.4升.26.如图是直角三角形中有一个内接正方形,求图中阴影部分的面积.单位:厘米.提示:分拆图形时常用“分割、填补、组合、旋转”等方法.【解答】解:根据题干分析可得:18122108⨯÷=(平方厘米), 答:图中阴影部分的面积是108平方厘米.故答案为:108平方厘米.27.如图四边形ABCD 中,角DAB 和角DCB 都是直角,边CD 和边BC 的长度相等,从点C到边AB 的垂线CE 长为10厘米,求四边形ABCD 的面积.【解答】解:将三角形CEB 以C 点为中心顺时针旋转90度,如下图,四边形ABCD 的面积与新得到的正方形相等,所以面积为:1010100⨯=(平方厘米). 答:四边形ABCD 的面积是100平方厘米.28.图形计算(1)求下图阴影部分的周长和面积.(单位:厘米)(2)三条边长分别是6厘米、8厘米、10厘米的直角三角形.将它的最短边对折到斜边相重合,(如图)图中阴影部分面积是 6 平方厘米.【解答】解:(1)如图,阴影部分的周长:903.141022 3.1410231.415.747.1360︒⨯÷⨯+⨯⨯⨯=+=︒(厘米); 两个直角等腰三角形的面积:(直角边2+直角边22)210÷=(斜边2)2100250÷=÷=(平方厘米);阴影部分的面积:2903.141078.55028.5360︒⨯⨯-=-=︒(平方厘米). 答:阴影部分的周长是47.1厘米,面积是28.5平方厘米.(2)阴影部分大直角边长:1064-=(厘米);阴影部分小直角边长:623÷=(厘米);阴影部分面积:4326⨯÷=(平方厘米).答:图中阴影部分面积是6平方厘米.故答案为:(1)47.1厘米,28.5平方厘米;(2)629.如图,1S 的面积比2S 的面积大多少?【解答】解:如图:12S S -12()()BCGF BCGF S S S S =+-+ABC BCGE S S =-10(68)2106=⨯+÷-⨯7060=-10=(平方厘米)答:1S 的面积比2S 的面积大10平方厘米.30.图中正方形的边长是10厘米,三角形甲的面积比三角形乙的面积少20平方厘米,求线段AB 的长.【解答】解:三角形甲的面积比三角形乙的面积小20平方厘米;根据图形可得:三角形DCB的面积比正方形CDEA的面积大20平方厘米,所以三角形DCB的面积为:10102010020120⨯+=+=(平方厘米)又因为正方形的边长10CD=厘米所以CB的长度是:12021024⨯÷=(厘米)所以AB的长度为:241014-=(厘米)答:AB的长度是14厘米.。
六年级下册数学试题-小升初复习讲练:组合图形的体积(含答案)sc

组合图形的体积尊典题探究例1.棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的体积是10立方厘米,表面积是36平方厘米.例2.计算体积.(单位:厘米)例3.有一个深4分米的长方体容器,其内侧底面为边长3分米的正方形.当容器底面的一边紧贴桌面倾斜如图时,容器内的水刚好不溢出.容器内的水有22.5升.例4.有一个棱长是10厘米的正方体木块,在它的上、左、前三个面中心分别穿一个3厘米见方的孔,直至对面.求穿孔后木块的体积.演练方阵A档(巩固专练)选择题(共5小题)1.如图,三个半径分别为1米、1.5米和2米的同轴圆柱,每个圆柱高0.5米,这三个圆柱组成一个立体图形,这个立体图形的表面积是()平方米.卜,]米I2来—iA.42.39B.39.25C.36.11D.25.123.把一个底面直径为a,高为a的圆柱恰好放入正方体盒子里,此时盒子剩余空间()A-(1-2L)a3B-(1-—)a3C'(1-2L)a3D,(1- —)a3 3412244.两个棱长1分米的正方体并成一个长方体,并成的长方体的表面积()原两个正方体的表面积之和.A.大于B.小于C.等于5.用两根完全相同的圆柱形木料分别制作成右图中的两个模型(图中涂色部分),甲与乙的体积相比()C.相等二.填空题(共13小题)6.如图中,每个小长方体的体积都是1立方厘米,那么图形的体积是,表面积是-7.如图,是一个直立于水平面上的几何体(它是圆柱的一部分,下底面为圆面,单位:cm).则这个几何体的体积为cm3.(计算结果保留兀)8.有一个草堆,上部是一个圆锥,下部是一个圆柱,圆锥高1.5m,底面半径2m,圆柱高3m,底面半径2m,这个草堆的体积是m3.9.(•富源县)如图有个棱长为20cm的正方体木箱堆放在墙角的形状,这些木箱的体积是_____________cm3.10.(•北京)一支未用过的圆柱形铅笔,长18厘米,体积是9立方厘米.使用一段时间后,变成了如图的样子.这时体积是多少立方厘米?11.(•万州区)以直角梯形的上底为轴旋转一周,所得的立体图形的体积是立方厘米.(兀值取整数3)12.如图,计算出它的体积为单位:厘米.A.n(24-2)2x3x(1+1)B./ix22x3x(1+1)33C.n(2+2)2xlx(3+3)D.形(2+2)2x3xlx4.3313.以棱长10厘米的正方体的一个面,挖去一直径为4厘米的圆孔(挖去的圆孔为圆柱体),则挖去后这个物体的体积是立方厘米.14.如图1,是三个直立于水平面上的形状完全相同的几何体(下底面为圆面.单位:cm).将它们拼成如图2的新几何体,则该新几何体的体积为cn?.(计算结果保留兀)15.(•崇文区)一个长20厘米、宽10厘米、高20厘米的无盖长方体玻璃容器,里面盛有一些红色溶液.小明想知道溶液的深,他将一根底面边长5厘米,长1米的长方形木条垂直插入到容器底部,取出后量得木条被染红的部分长16厘米.原来容器内红色溶液深_厘米.16.(•大安区)一根长方体木料,横截面是边长10厘米的正方形.从这根木料上截下6厘米长的一段,切削成一个最大的圆锥.圆锥的体积是cn?,约占截下这段长方体木料体积的_____________%(百分号前面保留一位小数).17.(•武汉模拟)已知某几何体的三视图如图所示,则该几何体的体积为(结果保留71)18.最早将圆周率精确地计算到小数点后面7位,请借助圆周率计算立体图形(如图)的侧面积为平方厘米.6chl4cm2c mB档(提升精练)一.解答题(共9小题)1.(•临川区)有一个粮仓,它们上面是圆锥体,下面是圆柱体,已知圆柱的底面周长是18.84米,高为4米,圆锥的高是1米,则这个粮仓的体积是多少立方米?2.(•汉阳区)如图是丰裕粮仓示意图.如果每立方米稻谷重600千克,这个粮仓可储存稻谷多少千克?3.(•龙泉驿区)请计算零件的表面积和体积(正方体棱长10cm,圆柱的半径r=4cm,高h=6cm).4.(»±海)如图,(单位:dm)是一块零件的铜铸毛坯,每立方分米铜重8.9千克,这块零件铸铁毛坯的重量是多少吨?5.(•广州模拟)有一根长20厘米,半径为2厘米的圆钢,在它的两端各钻了一个深为4厘米,底面半径为2厘米的圆锥形小孔做成一个零件,如图这个零件的体积是多少立方厘米?6.(•陆良县模拟)每立方厘米的钢重7.8克,求下面一段钢管约重多少千克?(得数保留一位小数)(单位:厘米)(/]。
六年级下册数学试题-小升初复习讲练:组合图形的面积 (含答案)sc

组合图形的面积典题探究例1.已知一个五边形的三条边的长和四个角,如图所示,那么,这个五边形的面积是.例2.如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.若三角形EFC的面积为a,则梯形ABCD的面积是.例3.如图,每个小方格的面积是1cm2,那么△ABC的面积是cm2.例4.如图等腰三角形中阴影部分的面积是.例5.求右图直角梯形中阴影部分的面积.(单位:厘米)例6.求阴影部分的面积.(单位,厘米)演练方阵A档(巩固专练)一.选择题(共15小题)1.如图中,阴影部分的面积甲()乙.A.大于B.小于C.等于D.无法确定2.如图中阴影甲的面积比阴影乙的面积大多少()A.6(平方厘米)B.8(平方厘米)C.4(平方厘米)D.10(平方厘米)3.由四个相同的直角三角形和中间的小正方形拼成的一个大正方形(如图).如果直角三角形的两条直角边的长分别是3厘米和2厘米,大正方形的面积是()平方厘米.A.13 B.14 C.15 D.254.图中阴影部分的面积之和是()平方厘米.A.20 B.24 C.26 D.305.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是()A.8+8×B.5+5×C.5×8×D.××6.如图,涂色部分面积是长方形面积的()A.B.C.无法计算7.下图中梯形ABCD的面积是40平方分米,三角形ABC的面积是25平方分米,则三角形BCD的面积是()A.25平方分米B.15平方分米C.40平方分米8.如图,黑色部分的面积为96平方厘米,则空白部分的面积为()A.96 B.240 C.120 D.1009.(•南城县)图中阴影部分占总面积的()A.B.C.D.10.(•泉州)下列各图中的正方形面积相等,图()的阴影面积与另外三图不同.A.B.C.D.11.(•康县)如图中,两三角形的面积之和占长方形面积的()A.B.C.D.12.(•徐水县)在一长方形草地里有一条宽1米的曲折小路,如图所示,小路的面积是()平方米.A.10 B.20 C.3013.(•揭阳)下面三幅图中,正方形的边长相等,这些图形中阴影部分的面积()大.A.图(1)B.图(2)C.图(3)D.一样大14.(•崇文区)从甲、乙两块厚度、边长均相等的正方形钢板上冲制出一些圆形(如图,每块上的圆形大小分别相同),剩下的边角料重量相比,下面说法正确的是()A.甲重B.乙重C.重量相等15.(•秀屿区)从一个长为3,宽为2的长方形中擦去一个直径为1的圆(如图,单位厘米),下列表示各平方厘米数中最接近阴影部分的面积是()A.6B.5C.4二.填空题(共13小题)16.大小正方形如图.小正方形边长a厘米,阴影面积是_________平方厘米.17.如图,大正方形边长为8cm,小正方形边长为6cm,则阴影部分的面积是_________.18.如图正方形ABCD边长是10厘米,长方形EFGH的长为8厘米,宽为5厘米.阴影部分甲与阴影部分乙的面积差是_________平方厘米.19.如图所示,正六边形ABCDEF的面积是36平方厘米,AG=AB,CH=CD,则四边形BCHG的面积是_________平方厘米.20.如图,有一块正方形的草坪,周边用边长为6分米的方砖铺了一条宽15分米的小路(如图阴影部分),共用方砖300块.则小路所围草坪的面积是_________平方分米.21.如图,长方形ABCD的面积是100平方厘米,M在AD边上,且AM=AD,N在AB 边上,且AN=BN.那么,阴影部分的面积等于_________平方厘米.22.如图,ABCD是长方形,图中的数是各部分的面积数,则图中阴影部分的面积为_________.23.(•江油市模拟)图中阴影部分为2cm,AB:AE=4:1,长方形ABCD面积为_________24.(•长沙模拟)下列图形的边长为2厘米,阴影部分面积相等的图形有_________.25.一个机器零件,形状如图阴影所示,这个机器零件的面积是_________dm2.26.如图,在边长相等的五个正方形中,画了两个三角形,三角形A的面积是15平方厘米,那么三角形B的面积是_________平方厘米.27.如图,已知三角形ABC的面积等于18平方厘米,∠ABC、∠DEC都是直角,AC=8厘米,BD=2DC.DE的长是_________厘米.28.如图,平行四边形中阴影A的面积是6平方厘米,阴影B的面积占平行四边形面积的,平行四边形面积是_________平方厘米.B档(提升精练)一.选择题(共15小题)1.(•剑川县模拟)一块边长是4米的正方形草地上,一条对角线的两个顶点各有1棵树,树上各栓1只羊,绳长4米,两头羊都能吃到的草地面积为()平方米.A.6.28 B.9.12 C.12.56 D.50.242.下列图形的面积是()A.800 B.700 C.750 D.6003.(•郑州模拟)如图,将四条长为16cm,宽为2cm的长方形垂直相交平放在桌面上,则桌面被盖住的面积是()A.72cm2B.128cm2C.20cm2D.112cm24.(•牡丹江)如图,四边形ABCD是一个梯形,由三个直角三角形拼成,它的面积是()平方厘米.A.1.92 B.16 C.4D.85.下列图形中,每个小正方形都是边长1cm,图中阴影面积最大的是()A.B.C.6.如图所示:任意四边形ABCD,E是AB中点,F是CD中点,已知四边形ABCD面积是10,则阴影部分的面积是()A.5B.6C.7D.87.(2004•宜兴市)如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米.图中阴影部分的面积是()A.44平方厘米B.60平方厘米C.100平方厘米D.144平方厘米8.(•万州区)如图中,阴影部分的面积占平行四边形面积的()A.B.C.D.9.(•河西区)如图长方形ABEF中AF=10分米,其中梯形ABCG、平行四边形CDFG和三角形DEF的面积比为3:1:1,DE=()分米.A.2B.C.4D.10.(•济源模拟)甲、乙、丙三名小朋友用相同的正方形手工纸剪成圆形,甲剪了一个最大的扇形,乙剪了一最大的圆,丙剪了四个最大的圆.(如图)三个人中对手工纸的利用率情况是()A.甲最高B.乙最高C.丙最高D.三人相同11.(•开化县模拟)如图A、B分别是长方形长和宽的中点,阴影部分面积是长方形的()A.B.C.D.12.(•无锡)用三张边长都是8厘米的正方形铁皮,分别按如图剪下不同规格的圆片.哪张铁皮剩下的废料多?()A.甲铁皮剩下的废料多B.乙铁皮剩下的废料多C.丙铁皮剩下的废料多D.剩下的废料同样多13.(•广东模拟)右图中三角形a,b的面积都是长方形面积的,则阴影部分面积是长方形面积的()A.B.C.D.14.(•中山模拟)如图,图中每个圆的直径都为2cm,阴影部分的周长和的面积各是()A.2π﹣4 π﹣4 B.4π4πC.2π4﹣πD.4715.(•湛江模拟)如图所示,甲和乙两幅图的阴影面积相比,下列说法正确的是()A.甲>乙B.甲<乙C.甲=乙二.填空题(共13小题)16.(•成都)如图,阴影部分的面积是_________.17.(•常熟市)如图:三角形的面积为5平方厘米,求圆的面积是_________平方厘米.18.(•阜阳模拟)如图,求涂色部分的面积是_________平方分米.19.(•台湾模拟)如图正方形的边长为10公分,四边形ABCD的面积为6平方公分,那么,阴影部分的面积为_________平方公分.20.(•广州模拟)在如图中,平行四边形的面积是80平方厘米,图中A、B两个三角形的面积比是_________,阴影部分的面积是_________平方厘米.21.(•雁江区模拟)图中阴影部分的面积是_________cm2,周长是_________cm.22.(•广州)如图ABCD是一个长方形,AB=10厘米,AD=4厘米,E、F分别是BC、AD 的中点,G是线段CD上意一点,则图中阴影部分的面积为_________.23.(•东莞)如图,B、C分别是正方形边上的中点,己知正方形的周长是80厘米.阴影部分的面积是_________平方厘米.24.(•中山模拟)在半径为10cm的圆内,C为AO的中点,则阴影的面积为_________.25.(•泸州模拟)如图,以直角三角形的直角边长20厘米为直径画一个半圆,阴影部分①的面积比②的面积小16平方厘米.BC=_________.26.(•长沙模拟)如图的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是_________平方厘米.27.(•长沙模拟)如图,长方形ABCD中,AB=12厘米,BC=8厘米,平行四边形BCEF的一边BF交CD于G,若梯形CEFG的面积为64平方厘米,则DG长为_________.28.(•顺德区模拟)如图是两个一样的直角三角形重叠在一起,图中阴影部分面积是_________.C档(跨越导练)一.填空题(共9小题)1.(•揭阳)图中,平行四边形ABCD的面积是32cm2阴影部分的面积是_________cm2.2.(•广西)如图中,梯形的下底是12厘米,高是5厘米.阴影部分的面积是_________平方厘米.3.(•绍兴县)图中三角形ABC三个顶点上都是半径为1厘米的圆,图中阴影部分的面积是_________.4.(•河北)如图是一个长方形,面积是18平方厘米,P是长方形内任意一点,图中两个阴影部分的面积和是_________平方厘米.5.(•渠县)求阴影部分面积.(单位:cm)6.(•上海)如图中,两个正方形的边长分别为6cm和4cm,求阴影部分的面积.(4%)7.(•长汀县)图中3号图形的面积占七巧板面积的_________.8.(•游仙区模拟)一个圆形纸片,直径是8厘米,把它剪成一个最大的正方形,剪掉的面积是_________平方厘米.9.(•河西区)如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是_________厘米.二.解答题(共13小题)10.(•绍兴县)求图中阴影部分的面积(单位:厘米)11.(•乐清市)左图正方形边长为2厘米.以顶点A为圆心边长AB为半径作圆弧,再分别以AB、AC为直径作半圆弧.求阴影部分面积.12.(•延边州)求图中阴影部分的面积.(单位:厘米)13.(•麟游县)求图中阴影部分的面积(单位:厘米)14.(•金沙县)如图,求阴影部分的面积.已知:r=10cm.15.(•东莞)如图:阴影2比阴影1面积大2.75平方厘米,圆的半径5厘米;求BC的长.16.(•重庆)已知S圆=S长方形求阴影部分周长和面积.17.(•长寿区)第1、2题求阴影部分周长和面积,第3﹣6题只求阴影部分面积.18.(•宁波)如图,直角梯形中,高是5厘米,下底是14厘米,求阴影部分的面积?19.(•天柱县)如图中,小正方形边长为1分米,大正方形边长为2分米,阴影部分面积是多少?20.(•康县模拟)求下列图形的阴影部分的面积.21.(•紫金县)(1)求阴影部分周长(2)求图阴影部分的面积.22.(•郑州)草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(如图).问:这只羊能够活动的范围有多大?组合图形的面积答案典题探究例1.已知一个五边形的三条边的长和四个角,如图所示,那么,这个五边形的面积是18.考点:组合图形的面积;等积变形(位移、割补).分析:根据题意,过点E作BC的垂线于点F,延长CB、EA交点G,因∠AED=135°,所以∠AEF=45°,在三角形EFG中,∠EFG=90°,所以∠EGF=45°,EF=FG=5,即三角形EFG是等腰直角三角形,在三角形ABG中,∠AGB=45°,∠BAG=90°,所以∠ABG=45°,那么三角形ABG是等腰直角三角形,根据三角形、四边形的面积公式可计算出各自的面积,最后再用长方形CDEF的面积加上等腰直角三角形EFG再减去等腰直角三角形ABG即可,列式解答即可得到答案.解答:解:三角形EFG的面积是:5×5÷2=12.5,长方形CDEF的面积是2×5=10,延长出的三角形ABG的面积是:3×3÷2=4.5,组合图形的面积是:12.5+10﹣4.5=18,答这个五边形的面积是18.点评:解答此题的关键是将组合图形的两条边延长分为三角形和长方形,然后再减去延长部分所得到的面积即可.例2.如图,梯形ABCD中,BC=2AD,E、F分别为BC、AB的中点.连接EF、FC.若三角形EFC的面积为a,则梯形ABCD的面积是6a.考点:组合图形的面积.专题:平面图形的认识与计算.分析:如图,连接AE,因为BC=2AD,E为BC的中点,所以四边形AECD是平行四边形,且三角形ABE和平行四边形AECD等底等高,所以平行四边形的面积是这个三角形的面积的2倍,又因为三角形EFC的面积为a,所以三角形BEF的面积也是a,又因为F是AB的中点,所以可得三角形ABE的面积是2a,则平行四边形的面积就是2a×2=4a,据此即可解答问题.解答:解:连接AE,因为BC=2AD,E为BC的中点,所以四边形AECD是平行四边形,且三角形ABE和平行四边形AECD等底等高,所以平行四边形的面积是这个三角形的面积的2倍,又因为三角形EFC的面积为a,所以三角形BEF的面积也是a,又因为F是AB的中点,所以可得三角形ABE的面积是2a,则平行四边形的面积就是2a×2=4a,所以这个梯形的面积是2a+4a=6a.答:则梯形ABCD的面积是6a.故答案为:6a.点评:此题考查了高一定时,三角形的面积与底成正比例的性质以及等底等高的平行四边形是三角形的面积的2倍的灵活应用.例3.如图,每个小方格的面积是1cm2,那么△ABC的面积是8.5cm2.考点:组合图形的面积;三角形的周长和面积.分析:△ABC的面积为长方形RPCQ的面积减三角形ARB的面积减三角形BPC的面积再减三角形CQA的面积,将数据代入公式即可求解.解答:解:如图所示,S△ARB=S长方形ARBH=×6=3(平方厘米),S△BPC=S长方形BPCE=×5=2.5(平方厘米),S△CQA=S长方形CQAF=×12=6(平方厘米),则,S△ABC=S长方形﹣S△ARB﹣S△BPC﹣S△CQA,=20﹣3﹣2.5﹣6,=8.5(平方厘米).故答案为:8.5.点评:此题主要考查组合图形的面积,关键是将图形进行合理的分割.例4.如图等腰三角形中阴影部分的面积是 2.86.考点:组合图形的面积.专题:平面图形的认识与计算.分析:如图所示,阴影部分的面积等于两条直角边为4的等腰直角三角形的面积减去两条直角边为2的等腰直角三角形的面积,再减去半径为2的圆面积的四分之一,据此计算即可解答.解答:解:4÷2=24×4÷2﹣2×2÷2﹣3.14×22÷4=8﹣2﹣3.14=2.86答:阴影部分的面积是2.86.点评:本题主要考查组合图形的面积,解答本题的关键是找出图中阴影部分是哪几部分相减得到的.例5.求右图直角梯形中阴影部分的面积.(单位:厘米)考点:组合图形的面积;三角形的周长和面积;梯形的面积;圆、圆环的面积.专题:压轴题;平面图形的认识与计算.分析:用梯形底面积减去半径是2厘米的圆面积的四分之一,减去一个底是4﹣2=2厘米,高是2厘米的三角形的面积,得到的差就是阴影部分的面积.解答:解:(3+4)×2÷2﹣3.14×22×﹣(4﹣2)×2÷2,=7﹣3.14﹣2,=1.86(平方厘米);答:阴影部分的面积是1.86平方厘米.点评:本题考查了梯形,圆,三角形的面积公式的掌握与运用情况,同时也考查了学生的计算能力.例6.求阴影部分的面积.(单位,厘米)考点:组合图形的面积.专题:压轴题.分析:我们可以右边的小阴影割后移动到左边补上,从图中可以观察到,割补后只要用长方形AODE的面积减去三角形AOC的面积就是整个阴影部分的面积.解答:解:由图知,经过割补后,S阴=S AOED﹣S AOC,=3×6﹣3×3÷2,=18﹣4.5,=13.5(平方厘米);故答案:13.5平方厘米.点评:此题考查了组合图形的面积和割补的思想.演练方阵A档(巩固专练)一.选择题(共15小题)1.如图中,阴影部分的面积甲()乙.A.大于B.小于C.等于D.无法确定考点:组合图形的面积.分析:根据题意甲乙均为三角形,那么在梯形ABCD中,三角形ABC与三角形BCD是等底等高的三角形,所以它们的面积相等,甲部分的面积等于三角形ABC减去三角形BCO,乙部分的面积等于三角形BCD的面积减去三角形BCO的面积,因为三角形ABC与三角形BCD面积相等,所以三角形ABO的面积等于三角形CDO的面积,即甲的面积=乙的面积.解答:解:如图:三角形ABC与三角形BCD是等底等高的三角形,所以三角形ABC的面积等于三角形BCD的面积,甲的面积等于三角形ABC﹣三角形BCO,乙的面积等于三角形BCD﹣三角形BCO,所以甲的面积等于乙的面积.故选:C.点评:解答此题的关键是把甲乙两部分的面积放在同底等高的两个三角形中,同底等高的两个三角形的面积相等,然后去掉共同拥有的三角形BCO,所剩面积也会相等.2.如图中阴影甲的面积比阴影乙的面积大多少()A.6(平方厘米)B.8(平方厘米)C.4(平方厘米)D.10(平方厘米)考点:组合图形的面积.专题:平面图形的认识与计算.分析:求阴影甲与阴影乙的面积差,实际上是求大三角形与正方形的面积差,将数据代入三角形和正方形的面积公式即可求解.解答:解:(6+8)×6÷2﹣6×6,=14×6÷2﹣36,=42﹣36,=6(平方厘米);答:阴影甲的面积比阴影乙的面积大6平方厘米.故选:A.点评:解答此题的关键是明白:求阴影甲与阴影乙的面积差,实际上是求大三角形与正方形的面积差.3.由四个相同的直角三角形和中间的小正方形拼成的一个大正方形(如图).如果直角三角形的两条直角边的长分别是3厘米和2厘米,大正方形的面积是()平方厘米.A.13 B.14 C.15 D.25考点:组合图形的面积.专题:平面图形的认识与计算.分析:由图意可知:中间小正方形的边长为3﹣2=1厘米,则大正方形的面积=直角三角形的面积×4+小正方形的面积,代入数据即可求解.解答:解:3×2÷2×4+(3﹣2)×(3﹣2),=12+1,=13(平方厘米);答:大正方形的面积是13平方厘米.故选:A.点评:由三角形的直角边长求出小正方形的边长,是解答本题的关键.4.图中阴影部分的面积之和是()平方厘米.A.20 B.24 C.26 D.30考点:组合图形的面积.专题:平面图形的认识与计算.分析:等底等高的三角形的面积相等,由图形可知,图中两个空白三角形的面积相等,根据三角形的面积公式:s=ah÷2,把数据代入公式求出两个空白三角形的面积,再根据长方形的面积公式:s=ab,把数据代入公式求出长方形的面积,然后用长方形的面积减去两个空白三角形的面积即可.据此解答.解答:解:8×6﹣6×4÷2×2=48﹣24=24(平方厘米),答:阴影部分的面积是24平方厘米.故选:B.点评:解决此题的关键是利用等积转换,即等底等高的三角形面积相等,用长方形减去空白面积就是阴影面积,5.如图是由面积都是5平方厘米的8个三角形组成,图中阴影部分的面积是多少平方厘米?列式是()A.8+8×B.5+5×C.5×8×D.××考点:组合图形的面积.专题:平面图形的认识与计算.分析:如图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×,据此解答即可.解答:解:如上图所示,三角形②的面积是5,而三角形①的面积是三角形②面积的一半,则阴影部分的面积是5+5×,故选:B.点评:将阴影部分进行分割,再据已知条件,即可求出阴影部分的面积.6.如图,涂色部分面积是长方形面积的()A.B.C.无法计算考点:组合图形的面积;分数的意义、读写及分类.专题:平面图形的认识与计算.分析:设长方形的长和宽分别为a和b,两个三角形的高之和正好等于长方形的宽,即等于b,则两个阴影三角形的面积和为a(b1+b2)=ab,所以涂色部分面积是长方形面积的.解答:解:设长方形的长和宽分别为a和b,则两个阴影三角形的面积和为ab,所以涂色部分面积是长方形面积的.故选:B.点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.7.下图中梯形ABCD的面积是40平方分米,三角形ABC的面积是25平方分米,则三角形BCD的面积是()A.25平方分米B.15平方分米C.40平方分米考点:组合图形的面积;三角形的周长和面积.专题:平面图形的认识与计算.分析:根据图知道用梯形ABCD的面积减去三角形ABC的面积即可求出三角形BCD的面积.解答:解:40﹣25=15(平方分米),答:三角形BCD的面积15平方分米;故选:B.点评:关键是根据图得出梯形ABCD的面积减去三角形ABC的面积就是三角形BCD的面积.8.如图,黑色部分的面积为96平方厘米,则空白部分的面积为()A.96 B.240 C.120 D.100考点:组合图形的面积.专题:平面图形的认识与计算.分析:根据平行四边形的面积公式S=ah,得出h=S÷a,由此求出黑色部分的高,即长方形的宽,再根据图得出空白部分的面积等于长方形的面积减去黑色部分的面积,由此再利用长方形的面积公式解答.解答:解:96÷8=12(厘米)(20+8)×12﹣96=28×12﹣96=336﹣96=240(平方厘米)答:空白部分的面积是240平方厘米;故选:B.点评:本题主要是灵活利用平行四边形的面积公式与长方形的面积公式解答.9.(•南城县)图中阴影部分占总面积的()A.B.C.D.考点:组合图形的面积.分析:把阴影部分的图形进行拼凑,把①放到②处,即可得到阴影部分的面积是总面积的.解答:解:由图可知阴影部分的面积是,故选:A.点评:本题把图形进行拼凑,即可得到答案.10.(•泉州)下列各图中的正方形面积相等,图()的阴影面积与另外三图不同.A.B.C.D.考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:从图中可以看出阴影部分的面积=正方形的面积﹣圆的面积.观察图形可发现:四个正方形是全等的,面积是相等;A、C、D三个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这三个图形中阴影部分的面积相等,得出答案.解答:解:由图可知:从左到右A、C、D的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,根据等量减去等量差相等的原理得这三个图形中阴影部分的面积相等.故选:B.点评:此题考查了面积及等积变换,将阴影面积转化为易求的图形的面积的差或和是解题的常用方法.11.(•康县)如图中,两三角形的面积之和占长方形面积的()A.B.C.D.考点:组合图形的面积;分数的意义、读写及分类.专题:压轴题;分数和百分数.分析:假设每个小正方形的面积是1,则2个小三角形的面积都是,2个小三角形的面积和就为1,而长方形的面积为4,于是问题容易得解.解答:解:假设每个小正方形的面积是1,则2个小三角形的面积都是,2个小三角形的面积和就为1,而长方形的面积为4,1÷4=,所以两三角形的面积之和占长方形面积的;故选:C.点评:解答此题的关键是:利用假设法先求出两个三角形的面积和,问题即可得解.12.(•徐水县)在一长方形草地里有一条宽1米的曲折小路,如图所示,小路的面积是()平方米.A.10 B.20 C.30考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:我们把图形进行分割,把①②③排在一起就是一个长方形长是11米,宽是1米,把④⑤⑥图形沿着大长方形的宽排列,得到的长方形的长(10﹣1)米,宽是1米的长方形.解答:解:画图如下:11×1+(10﹣1)×1,=11+9,=20(平方米);故选:B.点评:本题运用长方形的面积公式进行就即可,即“长×宽=面积”.13.(•揭阳)下面三幅图中,正方形的边长相等,这些图形中阴影部分的面积()大.A.图(1)B.图(2)C.图(3)D.一样大考点:组合图形的面积;圆、圆环的面积.分析:这三幅图中,正方形的边长相等,说明正方形的面积相等,求这些图形中阴影部分的面积,都可以认为是从正方形的面积里减去同一个圆的面积,由此得解.解答:解:正方形的边长相等,说明三幅图正方形的面积相等,里面的圆的半径也相等;(1)阴影部分的面积=正方形的面积﹣4×圆的面积;(2)阴影部分的面积=正方形的面积﹣2×圆的面积;(3)阴影部分的面积=正方形的面积﹣圆的面积;所以这些图形中阴影部分的面积一样大.故选:D.点评:此题属于求组合图形的面积,要求阴影部分的面积,就从外面图形面积里减去里面的小图形的面积.14.(•崇文区)从甲、乙两块厚度、边长均相等的正方形钢板上冲制出一些圆形(如图,每块上的圆形大小分别相同),剩下的边角料重量相比,下面说法正确的是()A.甲重B.乙重C.重量相等考点:组合图形的面积;圆、圆环的面积.分析:要解决剩下的边角料重量相比问题,根据题干,只要比较出剩下的边角料的面积大小即可,剩下面积大的重,由此只要求得甲乙两个图中的阴影部分的面积即可解决问题.解答:解:设甲乙两个正方形的边长为12,则甲中圆的半径为:12÷2÷2=3,乙中的圆的半径为12÷3÷2=2,甲剩下的部分为:12×12﹣3.14×32×4,=144﹣113.04,=30.96;乙剩下的部分为:12×12﹣3.14×22×9,=144﹣113.04,=30.96,所以甲乙剩下部分的面积相等,故选:C.点评:此题考查了在正方体中切割等圆的方法,得出每个圆的半径是解决此类问题的关键.15.(•秀屿区)从一个长为3,宽为2的长方形中擦去一个直径为1的圆(如图,单位厘米),下列表示各平方厘米数中最接近阴影部分的面积是()A.6B.5C.4考点:组合图形的面积.专题:压轴题;平面图形的认识与计算.分析:我们运用长方形的面积减去圆的面积就是阴影部分的面积,得出的差再与下列选项进行比较再进行选择.解答:解:3×2﹣3.14×(1÷2)2,=6﹣0.785,=5.215(平方厘米);5.215与5最接近.故选:B.点评:本题考查了长方形及圆的面积公式的掌握与运用情况,同时考查了数的大小比较和近似数.二.填空题(共13小题)16.大小正方形如图.小正方形边长a厘米,阴影面积是a2平方厘米.考点:组合图形的面积.分析:如图所示,连接BC,则三角形ABC和三角形CEB等底等高,则二者的面积相等,它们分别去掉公共部分三角形CFB,剩余部分的面积仍然相等,即三角形CEF的面积和三角形ABF的面积相等,于是阴影部分就转化成了小正方形的面积的一半,问题得解.解答:解:连接BC,则S△ABC=S△CEB,于是S△ABC﹣S△CFB=S△CEB﹣S△CFB,即S△ABF=S△CEF,所以阴影部分的面积=a2;故答案为:a2.点评:解答此题的关键是作出辅助线,将阴影部分的面积转化成小正方形的面积的一半,问题即可得解.17.如图,大正方形边长为8cm,小正方形边长为6cm,则阴影部分的面积是32平方厘米.。
小升初真题专练组合图形的面积小学数学六年级下册人教版(含答案)

小升初真题特训:组合图形的面积-小学数学六年级下册人教版学校:___________姓名:___________班级:___________考号:___________1A.(1)号面积最大B.(2)号面积最大二、填空题7.(2020·江苏南通·统考小升初真题)如图,大正方形被分成了4个相同的三角形和一个小正方形。
大正a b ,则小正方形的面积是()平方厘米。
方形的周长为24厘米,已知:2:18.(2021·全国·小升初真题)(汉阳区)如图,将两个正三角形重叠作出一个星形,在重叠的图形中再作出一个小星形,即阴影部分,已知大星形的面积是40cm2,那么小星形的面积是_____.9.(2020·北京海淀·小升初真题)如图,已知大正方形的面积是a,则小正方形的面积是___________。
10.(2020·北京海淀的面积的面积=的面积=,由此发现,,15.(2020·全国·小升初真题)5平方分米.三、图形计算20.(2022·湖北十堰·统考小升初真题)如图,两个正方形的边长分别是10cm和4cm,求阴影部分的面积。
21.(2022·山东临沂·统考小升初真题)求如图阴影部分的面积。
四、解答题22.(2022·湖南长沙·长沙市开福区青竹湖湘一外国语学校校考小升初真题)如图,大小正方形的边长分别是5厘米、3厘米,求三角形DBF的面积。
23.(2020·江苏常州·校考小升初真题)如下图所示,把三角形DBE沿线段AC折叠,得到一个多边形27.(2021·浙江宁波·小升初真题)28.(2020春·辽宁·六年级统考小升初模拟)如下图,一张边长为4cm的正方形纸,从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩余部分面积是多少?29.(2021春·江苏·六年级统考小升初模拟)如图,一块长方形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪.草坪的面积是多少平方米?(单位:米)30.(2020·河北·小升初真题)李大爷家承包了如图所示的一块地,请你帮他计算一下这块地的面积(单位,米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、求下列组合图形阴影部分的面积。
2、①求它的周长和面积。
(单位:厘米)②圆的周长是18.84cm,求阴影部分面积。
③长方形的面积和圆的面积相等,已知圆④求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
⑤下图中长方形长6cm,宽4cm,已知阴影⑥图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑦平行四边形的面积是30cm2,⑧一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑨已知AB=8cm,AD=12cm,三角形ABE和三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
⑩梯形上底8cm,下底16cm,阴影⑾求阴影部分面积。
(单位:cm)部分面积64cm2,求梯形面积。
⑿梯形面积是48平方厘米,阴影部分比空白⒀阴影部分比空白部分大6cm2,求S 阴。
部分12平方厘米,求阴影部分面积。
3、求下列图形的体积。
(单位:厘米)。
