小升初数学讲义:第八讲 组合图形和阴影部分计算 (2)
小升初复习专题求阴影部分面积.doc

2017年小升初复习专题•求阴影部分面积(含答案)□标:巩固小学儿何图形计算公式,并通过专题复习,加强学生对于图形面积计算的灵活运用。
1、儿何图形计算公式:1)正方形:周长=边长x4 C=4a面积=边长x边长S=axa2)正方体:表面积二棱长x棱长x6 S表=axax6体积=棱长x棱长x棱长V二axaxa3)长方形:周长=(长+宽)x2 C=2(a+b)面积二长x宽S=ab4)长方体:表面积=(长x宽+长x高+宽X|nj)x2 S=2(ab+ah+bh)体积=长乂宽x高V=abh 5)三角形:面积=底><高十2 s=ah-i-26)平行四边形:面积二底x高s=ah7)梯形:面积=(上底+下底)XiSj-i-2 s=(a+b)xh-r28)圆形:周长二直径xn=2xnx半径C=nd=2nr面积二半径x半径xll9)圆柱体:侧面积二底面周长x高表面积二侧面积+底面积x2体积二底面积><高10)圆锥体:体积二底面积x拓十32.面积求解大致分为以下儿类:>从整体图形中减去局部;>割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例2•正方形面积是7平方厘米,求阴影部分的面积。
例1•求阴影部分的面积。
(单位:厘米)例3•求图中阴影部分的面积。
(单位:厘米)⑶例9•求阴影部分的面积。
(单位:厘米)例10•求阴影部分的面积。
(单位:厘米)例5•求阴影部分的面积。
(单位: 厘米) 例6•如图:已知小圆半径为2厘米,大圆半径 是小圆的3倍,问:空口部分屮比乙的面积多 多少厘米?(6)例7•求阴影部分的面积。
(单位: 厘米) 例&求阴影部分的面积。
(单位:厘米)(8)(10)例17•图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18•如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
小升初数学复习专题:求阴影部分面积(含答案解析)

解题公式、方法1、几何图形计算公式:1) 正方形:周长=边长 ×4 C=4a面积 = 边长 × 边长 S=a×a2) 正方体:表面积 = 棱长 × 棱长 ×6 S 表 = a×a×6体积 = 棱长 × 棱长 × 棱长 V=a×a×a3) 长方形:周长 =(长 + 宽)×2 C=2(a+b)面积 = 长 × 宽 S=ab4) 长方体:表面积 =(长 × 宽 + 长 × 高 + 宽 × 高)×2 S=2(ab+ah+bh)体积 = 长 × 宽 × 高 V=abh5) 三角形:面积 = 底 × 高 ÷2 s=ah÷26) 平行四边形:面积 = 底 × 高 s=ah7) 梯形:面积 =(上底 + 下底)× 高 ÷2 s=(a+b)×h÷28) 圆形:周长 = 直径 ×Π=2×Π× 半径 C=Πd=2Πr面积 = 半径 × 半径 ×Π9) 圆柱体:侧面积 = 底面周长 × 高表面积 = 侧面积 + 底面积 ×2体积 = 底面积 × 高10) 圆锥体:体积 = 底面积 × 高 ÷32、面积求解大致分为以下几类:Ø 从整体图形中减去局部;割补法:将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
练习题例 1. 求阴影部例 2. 正方形面分的面积。
(单位: 厘米) 积是 7 平方厘米,求阴影部分的面积。
(单位: 厘米)例 3. 求图中阴影部分的面积。
小升初组合图形复习

倍,问:空白部分甲圆的面积。
圆,
圆面积,
[π+ππ]
π(116
解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边
π
为半径的圆的一部分,求阴影部分的面
解法二:右上面空白部分为小正方形面积减去小圆面积,
,问:阴影部分甲比乙面积小多少?
圆
例33.求阴影部分的面积。
(单位:厘米)
解:用大圆的面积减去长方形面积再加上一个以2为半径的圆ABE 面积,
例34.求阴影部分的面积。
(单位:厘米)
解: 阴影部分为两个半圆面积减去两个弓形面积,结果为
例35.如图,三角形OAB 是等腰三角形,OBC 是扇形,OB=5厘米,求阴
影部分的面积。
解:将两个同样的图形拼在一起成为圆减等腰直角三角形
1、求下列组合图形阴影部分的面积。
⑥图中阴影①比阴影②面积小
⑦平行四边形的面积是30cm
⑧一个圆的半径是4cm,求阴影部分面积。
⑨已知AB=8cm ,AD=12cm ,三角形ABE 和三角形ADF 的面积,各占长方形ABCD 的1/3,求三角形AEF 的面积。
⑩梯形上底8cm ,下底16cm ,阴影部分面积64cm2,求梯形面积。
(11)阴影部分面积。
(单位:cm )
⑿梯形面积是48平方厘米,阴影部分比空白部分12平方厘米,求阴影部分面积。
⒀阴影部分比空白部分大6cm 2
,求S 阴。
3、求下列图形的体积。
(单位:厘米)。
小升初复习专题求阴影部分面积(含答案)

小升初复习专题求阴影部分面积(含答案)2017年小升初复专题-求阴影部分面积(含答案)本专题旨在巩固小学几何图形计算公式,并通过复加强学生对于图形面积计算的灵活运用。
首先列出了几何图形计算公式,包括正方形、正方体、长方形、长方体、三角形、平行四边形、梯形、圆形、圆柱体和圆锥体。
然后介绍了面积求解的大致分类方法,包括从整体图形中减去局部和割补法,强调了观察图形特点并选择合适的方法求解图形面积的重要性。
例题部分包含多个图形,要求求出阴影部分的面积,其中有些题目给出了已知条件,有些则需要自行推导。
学生需要灵活运用所学过的基本的平面图形的面积求解方法,根据图形特点选择合适的方法求解阴影部分的面积。
以下是例题部分,已经修正了格式错误并删除了明显有问题的段落:例1.求阴影部分的面积。
(单位:厘米)图片显示了一个正方形,其中一角被割去,求剩余部分的面积)解:由于正方形是一个规则图形,我们可以直接计算出整个正方形的面积,然后减去被割去的部分的面积即可。
设正方形边长为a,则正方形的面积为a×a,被割去的部分是一个直角三角形,底边长为a,高为a/2,面积为a×a/2×1/2=a²/4.将两个面积相减,得到阴影部分的面积为3a²/4.例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)图片显示了一个正方形,其中一角被割去,求剩余部分的面积)解:设正方形边长为a,则根据题意可得a²=7,解得a=√7.同样地,我们可以计算出被割去的部分的面积为a²/4=7/4.将整个正方形的面积减去被割去的部分的面积,得到阴影部分的面积为21/4.例3.求图中阴影部分的面积。
(单位:厘米)图片显示了一个矩形,其中一角被割去,求剩余部分的面积)解:设矩形长为a,宽为b,则根据题意可得a=6,b=4.被割去的部分是一个直角三角形,底边长为4,高为2,面积为4×2/2=4.将整个矩形的面积减去被割去的部分的面积,得到阴影部分的面积为20.例4.求阴影部分的面积。
小升初组合图形面积计算

权威小升初之---阴影部分面积计算【知识精讲】1.常用公式长方形面积= 正方形面积= 平行四边形面积=三角形面积= 梯形面积=长方形周长= 正方形周长=2.等积代换最常用的等积变换是三角形,要熟记下面的结论:1 等底等高的两个三角形面积相等;2 两条平行线间的距离处处相等;3 底在同一条直线上并且相等,两底分别所对的两个三角形的两个角的顶点是同一个点或在与底平行的直线上,则这两个三角形面积相等;4 若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形的几倍。
1、扇形、环形的面积计算1、(2010成外一)甲乙两人分别绕右图的内圆(半径为30米)和外圆(半径为50米)跑步.①两人各跑一圈相差多少米?(π≈3)②求图中阴影部分的面积?(π≈3)2、右图所示是人行道的转弯处,已知弧AA’和BB’都是45°圆心角所对的弧,AA1的半径为8米,人行道宽为2米,求ABB’A’的面积。
. 3、求下图中阴影部分的面积。
(单位:米)4、(2012成外)圆的半径是4cm,阴影部分的面积是14πcm2,求图中三角形的面积.2、割补法1、(2010成外一)图中阴影部分的面积是()平方厘米。
2、(2012成都西川中学)如图所示,正方形ABCD的边长为10cm,以CD为直径作半圆,E为半圆周上的中点,F为BC的中点,求阴影部分的面积。
3、(2009成都西川中学)求下列图形中阴影部分的面积。
4、 (2009成都西川中学)图中正方形ABCD的边长为3厘米,正方形CEFG的边长为4 厘米。
5、 (2012成都七中嘉祥)如图是边长6的正方形和梯形拼成的“火炬”,梯形的上底长9m,A为上底的中点,B为下底的中点,线段AB恰好是梯形的高且长为3m,CD长为2m。
那么,图中阴影部分的面积是多少㎡?6、(2010成都七中嘉祥)如图,若长方形APHM、BNHP、CQHN的面积分别为7、4、6,则阴影部分的面积是多少?7、(2010成都实外一)如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积。
小升初复习专题求阴影部分面积(含答案)(2020年九月整理).doc

2017年小升初复习专题-求阴影部分面积(含答案)目标:巩固小学几何图形计算公式,并通过专题复习,加强学生对于图形面积计算的灵活运用。
1、几何图形计算公式:1)正方形:周长=边长×4 C=4a 面积=边长×边长S=a×a2)正方体:表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3)长方形:周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4)长方体:表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5)三角形:面积=底×高÷2 s=ah÷26)平行四边形:面积=底×高s=ah7)梯形:面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形:周长=直径×Π=2×Π×半径C=Πd=2Πr 面积=半径×半径×Π9)圆柱体:侧面积=底面周长×高表面积=侧面积+底面积×2 体积=底面积×高10)圆锥体:体积=底面积×高÷32、面积求解大致分为以下几类:➢从整体图形中减去局部;➢割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
小升初图形阴影部分面积教案包含答案

小升初图形阴影部分面积(专题)课堂引导:问题: 大家的小学生活马上就要结束了,在小学中我们学习过哪些几何图形呢知识点回顾:正方形的面积=长方形的面积=梯形的面积=三角形的面积=圆的面积=大家想一想,我们还有哪些面积公式没有想到扇形的面积=平行四边形的面积=互动环节:我画大家猜,怎样计算下列阴影部分的面积目的:引导学生初步掌握阴影部分面积的计算方法。
涂色面积=长方形面积+三角形面积涂色部分面积=长方形面积+半圆面积×2涂色部分面积=长方形面积+圆形面积涂色面积=正方形面积+半圆面积涂色面积=外圆面积—内圆面积涂色面积=正方形面积—圆形面积涂色面积=半圆面积—三角形面积涂色面积=外半圆面积—内半圆面积问题:一、序号为1、2、3、6的图形,它们的阴影部分面积是怎样计算大家有没有发现什么规律!引导学生回答出来:涂色部分面积是几个简单图形面积的差二、那么序号为4、5、7的图形,它们的阴影部分的面积又是怎样计算根据题意引导学生回答:涂色部分面积是几个简单图形面积的和经典题型【例题1】:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【试一试】:1、边长分别为3厘米与5厘米的两个正方形拼在一起(如图)。
求阴影部分的面积。
2、求图形阴影部分面积(单位:厘米)【例题2】:求组合图形的面积。
(单位:厘米)【分析与解答】:上图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.4÷2=2(米)4×4+2×2×3.14÷2=22.28(平方厘米)【试一试】:长方形长6厘米,宽4厘米,求阴影部分的面积。
【分析与解答】:上图中,若求阴影部分的面积,只需先求出长方形面积再减去里面圆的面积即可.4÷2=2(米)6×4-2×2×3.14=11.44(平方厘米)【例题】3、计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.4、求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.【试一试】:求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.【例题】5.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.【试一试】:求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.【例题】6、求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.【试一试】:如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.【例题】7、求阴影部分面积(单位:厘米)8、求阴影部分面积(单位:厘米)【试一试】:求阴影部分的面积。
六年级上册数学讲义-小升初培优:第08讲 等积变形(解析版)全国通用

第八讲等积变形1、理解并掌握等积变形的思想方法;2、能正确运用等积变形的思想方法解决一些实际问题;3、让学员在操作、观察、讨论、归纳等数学活动过程中,体会等积变形、转化等数学思想方法。
我们已经知道三角形面积的计算公式:三角形面积=底×高÷2从这个公式可以发现:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:面积相同三角形有无数多个不同的形状。
在实际问题的研究中,我们还会常常用到以下结论:(1)等底等高的两个三角形面积相等。
(2)夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,那么ACD BCDS S∆∆=;反之,如果ACD BCDS S∆∆=,则可知直线AB平行于CD。
(备注:长方形和正方形的对边就是一组平行线。
)讲演者:得分:如图,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米。
求长方形的宽。
【解析】连接AG,则可以依据题目条件求出三角形AGB的面积,因为DG已知,进而可以求三角形AGD的高,也就是长方形的宽,问题得解。
解答:长方形的宽的长是6.4厘米。
讲演者:得分:如图已知正方形ABCD和正方形DEFM,且正方形ABCD的边长为8分米。
请问图中阴影部分的面积是多少平方分米?【解析】连结FD。
根据等底等高的三角形面积相等可得S△AFD=S△FDC,而△FHD是它们的公共部分,因此,△AHD与△HCD的面积相等,从而得到△AFC=S△AHC+S△HCD=S△ADC=0。
正方形ABCD面积依此即可求。
解答:图中阴影部分的面积是32平方分米。
如图,已知梯形ABCD的面积为5,DA与EB平行,ED与CA平行,求四边形EDAC的面积。
【解析】连接EA、DB,根据平行线间的距离处处相等,和等底等高的三角形的面积相等,可得△EDC的面积=△EDA的面积、△EDA的面积=△DAB的面积、△DAB的面积=△CAB的面积;据此可得△EDC的面积=△CAB的面积;据此可得四边形EDAC的面积=△EDC的面积+△CDA的面积=△CAB的面积+△CDA的面积=梯形ABCD的面积=5。
小升初专题之组合图形面积

一、几种常用求组合图形面积的方法: 1、旋转的思想方法。
将所给图形中的某一部分绕一个固定点旋转一定(或适当)的角度,变为较明显的简单而又直观的图形。
2.移动的思想方法。
A .点的移动:将图中的某一点看作一个“动点”沿直线移动,使原来分着的空白部分合并在一起变成一个简单明了的图形。
B .面的移动:将所给图形中的某个图形沿直线上下左右移动,把复杂的图形转化成简单的图形,使原来面积不等变成相等。
3.翻折的思想方法。
将所给图形的某一部分以某一直线为对称轴翻折,使原来复杂的图形变为直观图形。
【例题讲解】例1、如图,长方形的长是8厘米、宽是6厘米、A 和B 是宽的中点,求长方形内阴影部分的面积。
例2、下面的长方形是一块草坪,中间有两条宽1米的走道。
求植草的面积。
BB例3、下图是一块长方形草地。
长方形长16米、宽10米,中间有两条宽2米的道路,两条都是平行四边形。
求有草部分的面积。
【知识反馈】1、求图中阴影部分的面积。
(单位:厘米)2、梯形草坪(如下图),有一平形四边形人行道,求人行道的面积是多少平方米?80米50米16102203、一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如下图阴影所示部分,红条宽都是2厘米。
问:这条手帕白色部分的面积是多少?7、下图是一块长方形草地。
长方形长30米、宽15米,中间有两条宽3米的道路,一条是长方形,另一条是平行四边形。
求有草部分的面积。
8、如图,ABCD 是直角梯形,AD=4cm,BC=6cm,AB=3cm 求阴影部分的面积和。
(单位:厘米)3033DA 439、下图中,边长为10和15的两个正方形并放在一起,求三角形ABC (阴影部分)的面积。
小升初数学课程:第八讲组合图形和阴影部分计算
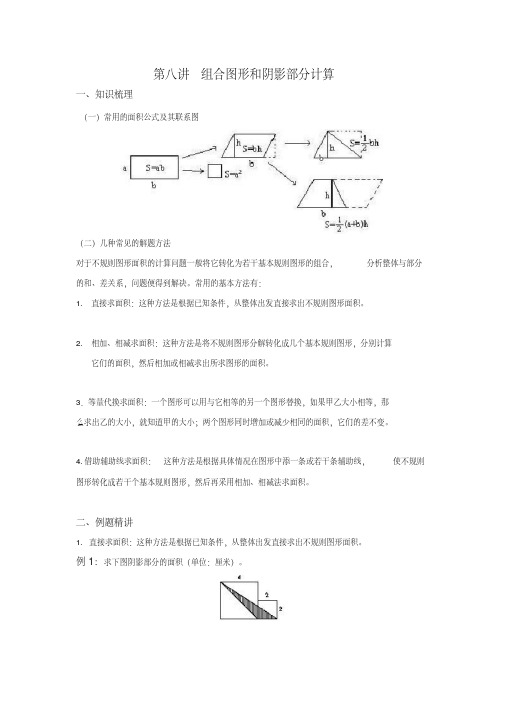
第八讲组合图形和阴影部分计算一、知识梳理(一)常用的面积公式及其联系图(二)几种常见的解题方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:1.直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出所求图形的面积。
3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
二、例题精讲1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)变式1:如图,求下列图形总面积【解析】如图所示,该图形由三角形和平行四边形组成。
面积=三角形面积+平行四边形面积故总面积=10*32*1/2+20*32=800变式2:如图求下列图形总面积【解析】该图形由一个梯形和直角三角形组成。
总面积=(6+20)*15*1/2+3*4*1/2=201例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:+=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)变式1:如图,两个正方形边长分别为9厘米、6厘米,求图中阴影部分面积。
小升初数学课程:第八讲 组合图形和阴影部分计算
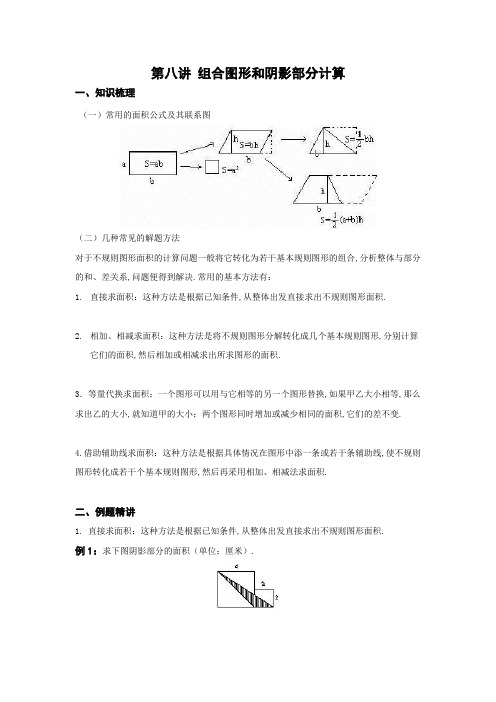
第八讲组合图形和阴影部分计算一、知识梳理(一)常用的面积公式及其联系图(二)几种常见的解题方法对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:1.直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加或相减求出所求图形的面积.3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变.4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积.二、例题精讲1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.例1:求下图阴影部分的面积(单位:厘米).解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)变式1:如图,求下列图形总面积【解析】如图所示,该图形由三角形和平行四边形组成.面积=三角形面积+平行四边形面积故总面积=10*32*1/2+20*32=800变式2:如图求下列图形总面积【解析】该图形由一个梯形和直角三角形组成.总面积=(6+20)*15*1/2+3*4*1/2=201例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?解答:两个正方形的面积:+=41(平方厘米)三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)阴影部分的面积:41-33=8(平方厘米)变式1:如图,两个正方形边长分别为9厘米、6厘米,求图中阴影部分面积.【解析】解法一:把题中两个正方形拼成的图形分解成三个部分,两个空白的三角形和阴影部分.阴影部分面积就等于两个正方形的面积和减去两个空白三角形的面积:9×9+6×6-9×9÷2-(9+6)×6÷2﹦31.5(平方厘米).解法二:在原图上添加一条辅助线,如下图.阴影部分面积就等于两个正方形面积和的一半减去蓝色三角形的面积:(92+62)÷2-9×6÷2﹦31.5(平方厘米).变式2:长方形的长是8厘米,宽是5厘米,DE是2厘米,CF是1.5厘米,求阴影三角形的面积.【解析】原长方形被线段AE,EF,AF分解成了4个小三角形.先求出原长方形的面积为:5×8=40(平方厘米)再求出3个空白直角三角形的面积:三角形ADE的面积:2×5÷2﹦5(平方厘米);三角形ABF的面积:8×(5-1.5)÷2﹦14(平方厘米);三角形CEF的面积:(8-2)×1.5÷2﹦4.5(平方厘米).所以阴影三角形的面积为:40-5-14-4.5﹦16.5(平方厘米)例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米.已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米.平行四边形ABCD的面积:8×6÷2+8=32(平方厘米)变式1:求阴影部分面积【解析】如图阴影部分是一个梯形,上底为小正方形的边长,下底为大正方形边长.故面积=(4+8)*4*1/2=24变式2:求阴影部分面积【解析】如图阴影部分面积可以看做正方形面积的合减去三角形.面积=6*6+4*4-6*10*1/2=22例4:如图,长方形的长是8厘米,宽是5厘米,DE是2厘米,CF是1.5厘米,求阴影三角形的面积.【解析】原长方形被线段AE,EF,AF分解成了4个小三角形.先求出原长方形的面积为:5×8=40(平方厘米)再求出3个空白直角三角形的面积:三角形ADE的面积:2×5÷2﹦5(平方厘米);三角形ABF的面积:8×(5-1.5)÷2﹦14(平方厘米);三角形CEF的面积:(8-2)×1.5÷2﹦4.5(平方厘米).所以阴影三角形的面积为:40-5-14-4.5﹦16.5(平方厘米).变式1:如图所示是两个相同的直角梯形重叠在一起,求阴影部分的面积.(单位:厘米)【解析】两个相同的梯形总面积相等,重叠部分面积也相等,等量减等量,则阴影部分面积与图形下方下底20厘米,高8厘米的梯形面积也是相等的.图形下方梯形的上底为:20-5﹦15(厘米)所以这个梯形的面积即阴影部分面积为:(20+15)×8÷2﹦140(厘米).变式2:如图,正方形边长为10,A、B在正方形的边上,并且AB=9,A下移3,B左移2,然后分别作水平线与竖直线得C、D,求四边形ABCD的面积.【解析】原长方形被分割成了6个小三角形,因为E、F、G分别是AB、BC、CD的中点,所以3个阴影三角形分别与其相邻的3个空白三角形面积相等.所以阴影部分总面积就等于长方形面积的一半:36÷2﹦18(平方厘米).例5:求阴影部分的面积.(单位:厘米)解:[π+π-π]=π(116-36)=40π=125.6平方厘米变式1:求阴影部分的面积.(单位:厘米)【解析】把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米变式2:求阴影部分的面积.(单位:厘米)【解析】平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米三、课堂总结在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形.就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法.此次课主要教会学生使用抽象性的思维,能够把图形分解开.四、课后作业1.求下列各图中阴影部分的面积:【解析】(1)如左下图所示,将左下角的阴影部分分为两部分,然后按照右下图所示,将这两部分分别拼补在阴影位置.可以看出,原题图的阴影部分等于右下图中AB弧所形成的弓形,其面积等于扇形OAB与三角形OAB的面积之差.π×4×4÷4-4×4÷2=4.56.(2)在题图虚线分割的两个正方形中,右边正方形的阴影部分是半径为5的四分之一个圆,在左边正方形中空白部分是半径为5的四分之一个圆.如下图所示,将右边的阴影部分平移到左边正方形中.可以看出,原题图的阴影部分正好等于一个正方形的面积,为5×5=25.2.在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几.【解析】(1)割补法从顶点作底边上的高,得到两个相同的直角三角形.将这两个直角三角(2)拼补法将两个这样的三角形拼成一个平行四边形(下页左上图).积和平行四边行面积同时除以2,商不变.所以原题阴影部分占整个图形面(3)等分法将原图等分成9个小三角形(见右上图),阴影部分占3个小三角形,注意,后两种方法对任意三角形都适用.也就是说,将例题中的等腰三角形换成任意三角形,其它条件不变,结论仍然成立.3.如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分).求这个梯形的面积.【解析】因为不知道梯形的高,所以不能直接求出梯形的面积.可以从等腰直角三角形与正方形之间的联系上考虑.将四个同样的等腰直角三角形拼成一个正方形(上页右下图),图中阴影部分是边长9厘米与边长5厘米的两个正方形面积之差,也是所求梯形面积的4倍.所以所求梯形面积是(9×9-5×5)÷4=14(厘米2).4.在左下图的直角三角形中有一个矩形,求矩形的面积.【解析】题中给出了两个似乎毫无关联的数据,无法沟通与矩形的联系.我们给这个直角三角形再拼补上一个相同的直角三角形(见右上图).因为A与A′,B与B′面积分别相等,所以甲、乙两个矩形的面积相等.乙的面积是4×6=24,所以甲的面积,即所求矩形的面积也是24.5.下图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40厘米2.求乙正方形的面积.【解析】如果从甲正方形中“挖掉”和乙正方形同样大的正方形丙,所剩的A,B,C三部分之和就是40厘米2(见左下图).把C割下,拼补到乙正方形的上面(见右上图),这样A,B,C三块就合并成一个长20厘米的矩形,面积是40厘米2,宽是40÷20=2(厘米).这个宽恰好是两个正方形的边长之差,由此可求出乙正方形的边长为(20-2)÷2=9(厘米),从而乙正方形的面积为9×9=81(厘米2).。
小升初专题平面组合图形的面积计算

平面图形面积————圆的面积专题简析:在进行组合图形的面积计算时,要仔细观察,认真思考,看清组合图形是由几个基本单位组成的,还要找出图中的隐蔽条件与已知条件和要求的问题间的关系;并且同学们应该牢记几个常见的圆与正方形的关系量:在正方形里的最大圆的面积占所在正方形的面积的错误!,而在圆内的最大正方形占所在圆的面积的错误!,这些知识点都应该常记于心,并牢牢掌握例题1;求图中阴影部分的面积单位:厘米;分析如图所示的特点,阴影部分的面积可以拼成1/4圆的面积;62××1/4=平方厘米练习11.求下面各个图形中阴影部分的面积单位:厘米;2.求下面各个图形中阴影部分的面积单位:厘米;例题2;求图中阴影部分的面积单位:厘米;分析阴影部分通过翻折移动位置后,构成了一个新的图形如图所示;从图中可以看出阴影部分的面积等于大扇形的面积减去大三角形面积的一半;×42×1/4-4×4÷2÷2=平方厘米练习21、计算下面图形中阴影部分的面积单位:厘米,正方形边长4;2、计算下面图形中阴影部分的面积单位:厘米,正方形边长4;1 2例题3;如图19-10所示,两圆半径都是1厘米,且图中两个阴影部分的面积相等;求长方形ABO1O的面积;分析因为两圆的半径相等,所以两个扇形中的空白部分相等;又因为图中两个阴影部分的面积相等,所以扇形的面积等于长方形面积的一半如图19-10右图所示;所以×12×1/4×2=平方厘米练习31、如图所示,圆的周长为厘米,AC两点把圆分成相等的两段弧,阴影部分1的面积与阴影部分2的面积相等,求平行四边形ABCD的面积;2、如图所示,AB=BC=8厘米,求阴影部分的面积;例题4;如图所示,图中圆的直径AB是4厘米,平行四边形ABCD的面积是7平方厘米,∠ABC=30度,求阴影部分的面积得数保留两位小数;分析阴影部分的面积等于平行四边形的面积减去扇形AOC的面积,再减去三角形BOC的面积;半径:4÷2=2厘米扇形的圆心角:180-180-30×2=60度扇形的面积:2×2××60/360≈平方厘米三角形BOC的面积:7÷2÷2=平方厘米7-+=平方厘米练习41、如图,三角形ABC的面积是平方厘米,圆的直径AC=6厘米,BD:DC=3:1;求阴影部分的面积;2、如图所示,求阴影部分的面积单位:厘米;得数保留两位小数;3、如图所示,求阴影部分的面积单位:厘米;得数保留两位小数;1 2 3例题5;如图所示,求图中阴影部分的面积;分析解法一:阴影部分的一半,可以看做是扇形中减去一个等腰直角三角形如图,等腰直角三角形的斜边等于圆的半径,斜边上的高等于斜边的一半,圆的半径为20÷2=10厘米×102×1/4-10×10÷2×2=107平方厘米解法二:以等腰三角形底的中点为中心点;把图的右半部分向下旋转90度后,阴影部分的面积就变为从半径为10厘米的半圆面积中,减去两直角边为10厘米的等腰直角三角形的面积所得的差;20÷22×1/2-20÷22×1/2=107平方厘米练习51、如图所示,求阴影部分的面积单位:厘米2、如图所示,用一张斜边为29厘米的红色直角三角形纸片,一张斜边为49厘米的蓝色直角三角形纸片,一张黄色的正方形纸片,拼成一个直角三角形;求红蓝两张三角形纸片面积之和是多少例题6如图所示,求图中阴影部分的面积单位:厘米;分析解法一:先用长方形的面积减去小扇形的面积,得空白部分a的面积,再用大扇形的面积减去空白部分a的面积;如图所示;×62×1/4-6×4-×42×1/4=平方厘米解法二:把阴影部分看作1和2两部分如图20-8所示;把大、小两个扇形面积相加,刚好多计算了空白部分和阴影1的面积,即长方形的面积;×42×1/4+×62×1/4-4×6=平方厘米练习61、如图所示,三角形ABC是直角三角形,AC长4厘米,BC长2厘米;以AC、BC为直径画半圆,两个半圆的交点在AB边上;求图中阴影部分的面积;2、如图所示,图中平行四边形的一个角为600,两条边的长分别为6厘米和8厘米,高为厘米;求图中阴影部分的面积;例题7;在图中,正方形的边长是10厘米,求图中阴影部分的面积;分析先用正方形的面积减去一个整圆的面积,得空部分的一半如图所示,再用正方形的面积减去全部空白部分;空白部分的一半:10×10-10÷22×=平方厘米阴影部分的面积:10×10-×2=57平方厘米练习71、求下面各图形中阴影部分的面积单位:厘米;2、求右面各图形中阴影部分的面积单位:厘米;3、求右面各图形中阴影部分的面积单位:厘米;例题8;在正方形ABCD中,AC=6厘米;求阴影部分的面积;分析这道题的难点在于正方形的边长未知,这样扇形的半径也就不知道;但我们可以看出,AC是等腰直角三角形ACD的斜边;根据等腰直角三角形的对称性可知,斜边上的高等于斜边的一半如图所示,我们可以求出等腰直角三角形ACD的面积,进而求出正方形ABCD的面积,即扇形半径的平方;这样虽然半径未求出,但可以求出半径的平方,也可以把半径的平方直接代入圆面积公式计算;既是正方形的面积,又是半径的平方为:6×6÷2×2=18平方厘米 阴影部分的面积为:18-18×÷4=平方厘米答:阴影部分的面积是平方厘米;练习81、 如图所示,图形中正方形的面积是50平方厘米,分别求出每个图形中阴影部分的面积;2、 如图所示,正方形中对角线长10厘米,过正方形两个相对的顶点以其边长为半径分别做弧;求图形中阴影部分的面积试一试,你能想出几种办法;例题9;在图的扇形中,正方形的面积是30平方厘米;求阴影部分的面积;分析阴影部分的面积等于扇形的面积减去正方形的面积;可是扇形的半径未知,又无法求出,所以我们寻求正方形的面积与扇形面积的半径之间的关系;我们以扇形的半径为边长做一个新的正方形如图所示,从图中可以看出,新正方形的面积是30×2=60平方厘米,即扇形半径的平方等于60;这样虽然半径未求出,但能求出半径的平方,再把半径的平等直接代入公式计算;×30×2×1/4-30=平方厘米答:阴影部分的面积是平方厘米;练习91、 如图所示,平行四边形的面积是100平方厘米,求阴影部分的面积;2、如图所示,O 是小圆的圆心,CO 垂直于AB,三角形ABC 的面积是45平方厘米,求阴影部分的面积;上面所举的例子只是常见的圆的组合图形面积解法,在以后的练习中,还希望同学们能举一反三,总结自己的学习方法与心得与体会,达到举一反三的效果圆的面积与组合圆积专题训练一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是3.,,这个正方形E D C B A 4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.保留两位小数5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B 长40厘米, BC 长 厘米. 6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积为 . 7.扇形的面积是平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中单位:厘米,两个阴影部分面积的和是 平方厘米. 11.如图,阴影部分的面积是 .12.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.13.在一个半径是厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.π取,结果精确到1平方厘米 14.右图中三角形是等腰直角三角形,阴影部分的面积是 平方厘米.15.如图所求,圆的周长是厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是厘米.)14.3(=π16.如图,151=∠的圆的周长为厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .17.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .18.图中,ADB 的面积的311倍,那么,CAB ∠是 度. 20.,以圆弧为分界线的甲、乙两部分的面6C B A O 4512 15 20 C ② ① A B 2 1 211., BC 是半圆的直径,已知:AB =BC 14.3=π12.如图2的面积是平方厘米.那么长方形阴影 13.如图1521=∠=,那么阴影部分的面积是多少平方厘米)14.3(≈π4个顶点,它们的公共点是该正方形的1厘米,那么阴影部分的总面积是多少平方厘米。
初小数学衔接讲义8(图形的计算)
2016年暑期初小数学衔接讲义8(图形的计算)
学校班级姓名
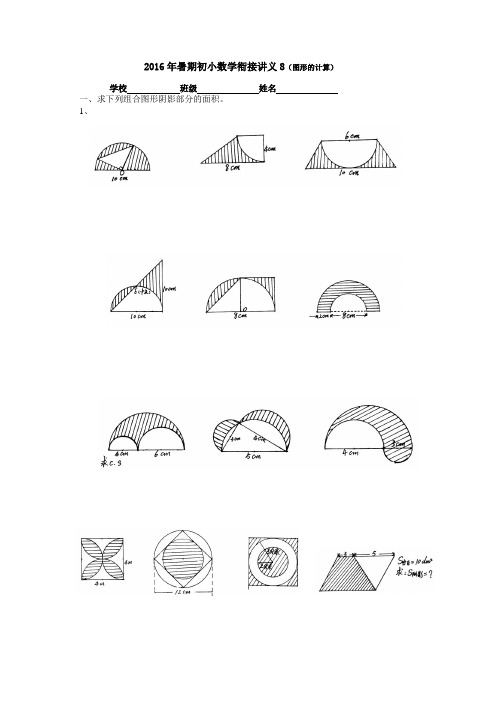
一、求下列组合图形阴影部分的面积。
1、
(本题高为3)
2、①长方形的面积和圆的面积相等,已知圆②求直角三角形中阴影部分的面积。
的半径是3cm,求阴影部分的周长和面积。
(单位:分米)
③下图中长方形长6cm,宽4cm,已知阴影④图中阴影①比阴影②面积小48平方厘米,
①比阴影②面积少3cm2,求EC的长。
AB=40cm,求BC的长。
⑤平行四边形的面积是30cm2,⑥一个圆的半径是4cm,求阴影部分面积。
求阴影部分的面积。
⑦已知AB=8cm,AD=12cm,三角形ABE和三角形ADF 的面积,各占长方形ABCD的1
3
,
求三角形AEF的面积。
⑧梯形上底8cm,下底16cm,阴影部分面积64cm2,求梯形面积
⑨梯形面积是48平方厘米,阴影部分比空白⑩阴影部分比空白部分大6cm2,求S阴。
部分少12平方厘米,求阴影部分面积。
二、解答题
1、个正方形(如图),边长分别是1米、2米、3米、4米、5米。
问图中白色部分面积与阴影部分面积的比是几比几?
2、篱笆靠墙围一块花圃(如图),如果用这个篱笆改围成一个靠墙的正方形,正方形的面积是多少?
3、下图是长方体的表面展开图,这个纸盒的用料面积至少是多少平方厘米?(单位:厘米)
4、图中,直角三角形AOB的面积是12平方厘米,那么圆的面积是多少平方厘米?
5、上右图中,三角形ABO的面积(S1)是11平方厘米,O为圆心,半径长5厘米,求阴影部
分的面积。
(完整word版)小升初数学阴影面积专题

小升初数学阴影面积专题
一、 考点、热点回顾
1、 面积单位:平方厘米(2cm )/平方分米(2dm )/平方米(2m )
2、 基本面积公式:长方形ab S = 正方形2a S =
3、 梯形 2)(÷⨯+=h b a S S=(a+b)h ÷2 菱形 2÷⨯b a
圆2r S π= 扇形 ︒
÷=3602r n S π 二、典型例题
例1:图中阴影部分面积为
例2:如图长方形ABCD 的面积是16平方厘米,三角形ABE 和三角形ADF 的面积分别是
3平方厘米和4平方厘米,则阴影部分的面积为
变式训练:如例2图,长方形ABCD 的面积是35平方厘米,三角形ABE 和三角形ADF 的
面积分别是5平方厘米和7平方厘米,则阴影部分的面积为
例3:计算下列图形的阴影面积
⑴ 已知半圆半径为2cm
⑵
⑶
⑷
⑸图中阴影①比阴影②面积小48平方,AB=40cm,求BC的长。
⑹梯形面积是48平方厘米,阴影部分比空白部分
少12平方厘米,求阴影部分面积。
三、习题练习
1、求第一图和第三图阴影部分面积
4、已知AB=8cm,AD=12cm,三角形ABE和
三角形ADF的面积,各占长方形ABCD的
1/3,求三角形AEF的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八讲组合图形和阴影部分计算
一、知识梳理
(一)常用的面积公式及其联系图
(二)几种常见的解题方法
对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有:
1.直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
2.相加、相减求面积:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算
它们的面积,然后相加或相减求出所求图形的面积。
3.等量代换求面积:一个图形可以用与它相等的另一个图形替换,如果甲乙大小相等,那么求出乙的大小,就知道甲的大小;两个图形同时增加或减少相同的面积,它们的差不变。
4.借助辅助线求面积:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法求面积。
二、例题精讲
1. 直接求面积:这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例1:求下图阴影部分的面积(单位:厘米)。
解答:通过分析发现它就是一个底是2、高是4的三角形,其面积直接可求为:×2×4=4(平方厘米)
变式1:如图,求下列图形总面积
【解析】如图所示,该图形由三角形和平行四边形组成。
面积=三角形面积+平行四边形面积
故总面积=10*32*1/2+20*32=800
变式2:如图求下列图形总面积
【解析】该图形由一个梯形和直角三角形组成。
总面积=(6+20)*15*1/2+3*4*1/2=201
例2:正方形甲的边长是5厘米,正方形乙的边长是4厘米,阴影部分的面积是多少?
解答:两个正方形的面积:+=41(平方厘米)
三个空白三角形的面积和:(5+4)×5÷2+4×4÷2+5×(5-4)÷2=33(平方厘米)
阴影部分的面积:41-33=8(平方厘米)
变式1:如图,两个正方形边长分别为9厘米、6厘米,求图中阴影部分面积。
【解析】解法一:把题中两个正方形拼成的图形分解成三个部分,两个空白的三角形和阴影部分。
阴影部分面积就等于两个正方形的面积和减去两个空白三角形的面积:
9×9+6×6-9×9÷2-(9+6)×6÷2﹦31.5(平方厘米)。
解法二:在原图上添加一条辅助线,如下图。
阴影部分面积就等于两个正方形面积和的一半减去蓝色三角形的面积:
(92+62)÷2-9×6÷2﹦31.5(平方厘米)。
变式2:长方形的长是8厘米,宽是5厘米,DE是2厘米,CF是1.5厘米,求阴影三角形
的面积。
【解析】原长方形被线段AE,EF,AF分解成了4个小三角形。
先求出原长方形的面积为:5×8=40(平方厘米)
再求出3个空白直角三角形的面积:
三角形ADE的面积:2×5÷2﹦5(平方厘米);
三角形ABF的面积:8×(5-1.5)÷2﹦14(平方厘米);
三角形CEF的面积:(8-2)×1.5÷2﹦4.5(平方厘米)。
所以阴影三角形的面积为:40-5-14-4.5﹦16.5(平方厘米)
例3:平行四边形ABCD的边BC长8厘米,直角三角形ECB的直角边EC长为6厘米。
已知阴影部分的总面积比三角形EFG的面积大8平方厘米,平行四边形ABCD的面积是多少?
解答:阴影部分的总面积比三角形EFG的面积大8平方厘米,分别加上梯形FBCG,得出的平行四边形ABCD比三角形EBC的面积大8平方厘米。
平行四边形ABCD的面积:8×6÷2+8=32(平方厘米)
变式1:求阴影部分面积
【解析】如图阴影部分是一个梯形,上底为小正方形的边长,下底为大正方形边长。
故面积=(4+8)*4*1/2=24
变式2:求阴影部分面积
【解析】如图阴影部分面积可以看做正方形面积的合减去三角形。
面积=6*6+4*4-6*10*1/2=22
例4:如图,长方形的长是8厘米,宽是5厘米,DE是2厘米,CF是1.5厘米,求阴影三
角形的面积。
【解析】原长方形被线段AE,EF,AF分解成了4个小三角形。
先求出原长方形的面积为:5×8=40(平方厘米)
再求出3个空白直角三角形的面积:
三角形ADE的面积:2×5÷2﹦5(平方厘米);
三角形ABF的面积:8×(5-1.5)÷2﹦14(平方厘米);
三角形CEF的面积:(8-2)×1.5÷2﹦4.5(平方厘米)。
所以阴影三角形的面积为:40-5-14-4.5﹦16.5(平方厘米)。
变式1:如图所示是两个相同的直角梯形重叠在一起,求阴影部分的面积。
(单位:厘米)
【解析】两个相同的梯形总面积相等,重叠部分面积也相等,等量减等量,则阴影部分面积与图形下方下底20厘米,高8厘米的梯形面积也是相等的。
图形下方梯形的上底为:20-5﹦15(厘米)
所以这个梯形的面积即阴影部分面积为:
(20+15)×8÷2﹦140(厘米)。
变式2:
如图,正方形边长为10,A、B在正方形的边上,并且AB=9,A下移3,B左移2,然后分别作水平线与竖直线得C、D,求四边形ABCD的面积。
【解析】原长方形被分割成了6个小三角形,因为E、F、G分别是AB、BC、CD的中点,所以3个阴影三角形分别与其相邻的3个空白三角形面积相等。
所以阴影部分总面积就等于长方形面积的一半:
36÷2﹦18(平方厘米)。
例5:求阴影部分的面积。
(单位:厘米)
解:[π+π-π]
=π(116-36)=40π=125.6平方厘米
变式1:求阴影部分的面积。
(单位:厘米)
【解析】把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,
所以阴影部分面积为:2×3=6平方厘米
变式2:求阴影部分的面积。
(单位:厘米)
【解析】
平移左右两部分至中间部分,则合成一个长方形,
所以阴影部分面积为2×1=2平方厘米
三、课堂总结
在组合图形中,除了多边形外,还有由圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
就是在多边形的组合图形中,为了计算面积,有时也要用到割补的方法。
此次课主要教会学生使用抽象性的思维,能够把图形分解开。
四、课后作业
1.求下列各图中阴影部分的面积:
2.在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(见右图),求图中阴影部分的面积占整个图形面积的几分之几。
【
3.如左下图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长9厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
4.在左下图的直角三角形中有一个矩形,求矩形的面积。
5.下图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40厘米2。
求乙正方形的面积。
