3-形态折叠共15页
三浦叠法大全10种叠法

以下是10种三浦折叠法:
1. 折叠式:将纸张从中间对折,然后展开,将底部向上折叠,再次从中间对折,展开后将两侧向内折叠。
2. 菱形折叠式:将纸张对折后展开,然后将底部向上折叠,再次对折后展开,将两侧向内折叠,形成菱形形状。
3. 三角折叠式:将纸张从底部向上折叠,形成一个三角形,然后从三角形顶部再次向内折叠,形成两个三角形。
4. 十字折叠式:将纸张从中间对折,然后展开,将两侧向内折叠,形成十字形状。
5. 风车折叠式:将纸张从中间对折,然后展开,将底部向上折叠,再次从中间对折,展开后将两侧向内折叠,形成风车形状。
6. 平行四边形折叠式:将纸张从顶部向下折叠,形成一个平行四边形,然后将两侧向内折叠,形成更小的平行四边形。
7. 蝴蝶折叠式:将纸张从顶部向下折叠,形成蝴蝶形状,然后将底部向上折叠,再次形成蝴蝶形状。
8. 卷心菜折叠式:将纸张从顶部向下折叠,形成卷心菜形状,然后将两侧向内折叠,形成更小的卷心菜形状。
9. 圆锥折叠式:将纸张从顶部向下折叠,形成圆锥形状,然后将底部向上折叠,再次形成圆锥形状。
10. 圆柱折叠式:将纸张从顶部向下折叠,形成圆柱形状,然后将两侧向内折叠,形成更小的圆柱形状。
以上是10种三浦折叠法供您参考。
小小折纸趣题,浓浓数学味道——折叠正三角形的三种方法

小小折纸趣题,浓浓数学味道——折叠正三角形的三种方法折叠正三角形的三种方法世界上最古老的数学书籍『九章算术』,在第九章里,就提到"三角形",在折叠正三角形之前,它首先提到了折叠六边形与四边形,它也被誉为折纸趣题的里程碑。
折叠正三角形这个问题,直到现代化学习,才有了可解释的数学理论,而且有三种折叠方法可以折叠成正三角形:折叠形状、折叠类型和最终折叠。
第一种折叠形状,也称为"兴建形折叠",是把正三角形折叠成三角形臂的结构,它分析过程是先把正三角形折分为两个小三角形,然后再把这两个小三角形再折叠成一个小三角形,三角形臂被折叠出来,折叠完成之后,就变成了正三角形。
第二种折叠类型,也称为"六边形"折叠,是把原来的正三角形分为三个平行的六边形,分别把三个六边形折叠成三个全等的正三角形,折叠完成之后,就变成了美丽的正三角形。
第三种折叠方法,也就是最终折叠,是把三角形的两个对边分别折叠成直角,借助等边斜角的性质,它可以产生出两个直角,这种折叠方法也可以折出美丽的正三角形,它在九章算术中也得到了提及,当然,它以后也被传播出去,成为很多小折纸趣题的最终答案。
折叠正三角形的三种方法,这三种手法都能折出正三角形,这三种方法可谓是无以伦比,因为它们在数学理论上都是正确的,折叠也都十分简单,也都很容易掌握,只要用心去学习,就可以把它们都学会,这就是折纸趣题难中之难,而又有益于促进数学知识的学习。
另外,折叠正三角形,它可以让我们对三角函数、图形学、空间几何等数学知识有更深刻的体会,也可以结合折纸实现应用,培养孩子的动手能力,激发孩子的科学创造力。
总之,折叠正三角形的三种方法,都很重要、都十分独特,它不仅可以用于教学、也可以用于娱乐,它。
折立体三角形的方法

折立体三角形的方法
折立体三角形的方法通常有以下几种:
1. 折法一:平面折叠法
这种方法适用于折纸立体三角形。
首先,在一个平面纸上绘制一个等边三角形。
然后,沿着三角形的边缘线将纸折叠起来,将三角形折叠成立体的形状。
2. 折法二:平行角折法
这种方法适用于折纸立体三角形。
首先,在一个平面纸上绘制一个等腰三角形。
然后,根据等腰三角形的性质,在三角形的底边上选择一个点,使它与顶点连线相交,并且使得与底边平行的线段上有与底边等长的线段。
接下来,将这两个线段连接起来,形成一个平行四边形。
最后,将纸沿着这个平行四边形的边缘线折叠起来,将三角形折叠成立体的形状。
3. 折法三:垂直角折法
这种方法适用于折纸立体三角形。
首先,在一个平面纸上绘制一个等腰直角三角形。
然后,根据等腰直角三角形的性质,在较短的直角边上选择一个点,使它与直角边连线相交。
接下来,将与直角边相等长度的线段连接这两个点,形成一个垂直扇形。
最后,将纸沿着这个垂直扇形的边缘线折叠起来,将三角形折叠成立体的形状。
以上是折立体三角形的几种常见方法,不同的方法适用于不同的情况和要求。
在
折叠过程中,需要注意折痕的位置和方向,以确保折叠后的形状准确无误。
三折页折叠方法

三折页折叠方法
三折页是一种常用的折纸形式,可以用于制作卡片、传单等。
以下是三折页的折叠方法:
1. 将一张长方形的纸张竖向放置,确保折痕清晰。
2. 将纸张的右上角向下折叠至左下角,形成一条折痕。
3. 将纸张的左上角向右下角折叠,形成第二条折痕。
4. 将纸张的右下角向左折叠至左上方,形成第三条折痕。
5. 最后将纸张展开,就可以看到三条折痕,这就是三折页的折叠方法。
通过以上步骤,你可以轻松地完成三折页的折叠。
如有需要,还可以在折叠好的三折页上添加内容或装饰,使其更加美观和实用。
微生物 第二章 原核生物细胞的形态与结构

第二章原核生物的形态、构造和功能P12-41第一节细菌细菌:是一类细胞细短(直径约0.5um,长0.5~5um)、结构简单、胞壁坚韧、二分裂繁殖、水生性强的单细胞原核生物(周德庆版P13)生活特性:喜温暖、潮湿、富含有机物微碱环境(大多数)腐生或寄生,好氧或厌氧,自养或异养一、细菌的形态与大小P121、基木形态:3种(球状杆状、螺旋状)在自然界中,杆菌最常见,球菌次之,而螺旋状的最少。
2、大小:度量细菌大小的单位是微米级(um)球状:0.5~1mm(直径)光学显微镜、油镜观察)杆状:0.2~1mm(直径)X1~80mm(长度)螺旋状:0.3~1mm(直径)X1~50mm(长度)(长度是菌体两端点之间的距离,而非实际长度)3、测定方法:显微镜测微定:显微照相后根据放大倍数进行测算4、细菌大小测量结果的影响因素1)个体差异;2)干燥、固定后的菌体会一般由于脱水而比活菌体缩短1/3-1/4;3)染色方法的影响,一般用负染色法观察的菌体较大;4)幼龄细菌一般比成熟的或老龄的细菌大;5)环境条件,如培养基中渗透压的改变也会导致细胞大小的变化。
简单染色法正染色革兰氏染色法鉴别染色法抗酸性染色法芽孢染色法死菌姬姆萨染色法负染色:荚膜染色法等细菌染色法周德庆版P15活菌:用美蓝或TTC(氧化三苯基四氮唑)等作活菌染色二、细菌的细胞结构与功能P14一般构造(一)细胞壁概念:是紧贴细胞质膜外侧的一层厚实、坚韧的外被。
主要成分:肽聚糖构成细胞壁的功能:1)固定细胞外形和提高机械强度,保护细胞免受渗透压等外力损伤2)为细胞的生长、分裂和鞭毛运动所必需;3)渗透屏障,阻拦大分子有害物质(水解酶和某些抗生素)进入细胞;4)赋予细菌特定的抗原性、致病性和对抗生素和噬菌体的敏感性。
1、革兰氏阳性细菌细胞壁特点:厚度大(20-80nm)化学组分简单,一般只含90%肽聚糖和10%磷壁酸。
(1)肽聚糖(peptidoglycan,金黄色葡萄球菌为例)特点:由25-40层左右的网格状分子,交联度75%,厚20~80nm。
数学活动 折纸做60°,30°,15°的角 ppt课件

13
勤学 诚实 育人 报国
五、变式练习 学以致用
问题9 在图中找出所有30°和60°的角?
A
R
D
EH
O
F
B
C
A O
M E
P B
R
ppt课件
D N F Q C
14
勤学 诚实 育人 报国
五、变式练习 学以致用
问题10 用矩形卡片如何剪出等边三角形?
怎样剪出的等边三角形面积才是最大的?
A
R
D
A
O
M
O
E
ppt课件
16
勤学 诚实 育人 报国
五、变式练习 学以致用
(2)将矩形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的 点F处,折痕为BE(如图①);再沿过点E的直线折叠,使点D 落在BE上的点H处,折痕为EG(如图②);再展平纸片(如图 ③).求图③中∠1 的大小.
A
E
DA
E
DA
E
D
H
1
B
CB F
A
R
D
问题6 你能说出以上操作的依据吗?
O
证明:对折矩形ABCD
E 1
4
F
23
∴ AB=2BE,∠1=90°
B
C
∵ 以BR为折痕折叠,使点A落在EF上
∴ AB=BO, ∠2=∠3
∴ BO=2BE
又∵ ∠1=90°
∴ ∠4=30°
∵ ∠ABO=90°- ∠4=60°
∴∠2=∠3=30°
ppt课件
9
勤学 诚实 育人 报国
F
CB G
C FG
图①
图②
图③
ppt课件
正方体11种折叠方法

探究正方体的展开图
将一个正方体的表面沿某些棱剪开,展成一个平面,共有哪些不同的图形呢?只从本质上讲,有以下三类共11种。
一、“141型”(共6种)
特点:这类展开图中,最长的一行(或一列)有4个正方形(图1~图6)。
理解:有4个面直线相连,其余2个面分别在“直线”两旁,位置任意。
二、“231型”与“33型”(共4种)
特点:这类展开图中,最长的一行(或一列)有3个正方形(如图7~图10)。
理解:在“231型”中,“3”所在的行(列)必须在中间,“2”、“1”所在行(列)分属两边(前后不分),且“2”与“3”同向,“1”可以放在“3”的任意一个正方形格旁边,这种情况共有3种,而“33型”只有1种。
三、“222型”(只有1种)
特点:展开图中,最多只有2个面直线相连(图11)。
评注:⑴将上面11个图中的任意一个,旋转一定角度或翻过来,看上去都与原图似有不同,但这只是图形放置的位置或方式不同。
实际上,它与原图能够完全重合,不能算作一个独立的新图,而从上面11个图中任取两个,不论怎样操作(旋转、翻折、平移等),它们都不可能完全重合,即彼此是独立的、不同的图形。
⑵对于由大小一样的六个正方形通过边对齐相连组成的平面图,如果图中含有“一”字型、“7”字型、“田”字型、“凹”字型,就一定不能折成正方体。
概括地说,只要不符合上述“141”、“231”和“33”、“222”的特点,就不能折成正方体。
如图12,如果将其看作“231”型,那么,无论怎么看,“2”和“3”都不是同向,故不能折成正方体。
其实,它属于“123”(或“321”)型。
折叠,形态,结构:综述折叠理论在建筑中的应用

l 机械工程 l
…
…
一一
r 一 一 一 一 一 一 一 I
l
设计
l
…
…
一
一
r 一 一 一 一 一 一 一 l
I
筑
l
每寰 聪 chitec ture/ ;I
、
2.作为 概念 的折 叠 理论 和折 叠理 论 在建 筑中 的 分径 与交 融 图示
@
二、分径 与交融— —建筑中折叠 理论 的哲思与数理
折 纸的出现可 以视为折叠发展 的一 个标志 。-  ̄EAg发明为折叠提 供了 良好的物质 媒介 ,折纸可 以将折叠技 术具象化并 留存下来 。纸 在发明初期非 常昂 贵 ,此 时折纸作品只作 为仪式用A, O ̄-L器 ,只追求形式 精美 。这种情 况下 ,折叠技术 得到了纯粹原 理性探索 。关于折纸最早 的记录是 日本平安时代 (公元 794—1185年 )-3 ̄用于庆典的折 纸模型 。此次记录之后 的很长一段 时间里 ,折 纸都缓慢地 以艺 术形式存 在着 ,并没有理论 的实质进步 。直到 18世 纪末 , 折叠原理 才被人们关 注 ,此时折纸 艺术也开始 复苏 。近 50年间 .折纸 无论 作为游戏还是 艺术 ,在世 界各国都得 到了长足 发展 。依托 折纸 ,折叠 背后 的 原 理 也 逐 渐 引 发 了 哲 学 家 和 数 学 家 的兴 趣 。
、兰FOLD, /:, 囊 , 建筑学、 Arch Ji ̄ec[ure
I 天体物理
-…
…
一
r一 一
I
-…
一 一 一一
生物学
…
一 I
j
一
r一 一
I
染色体的形态和结构
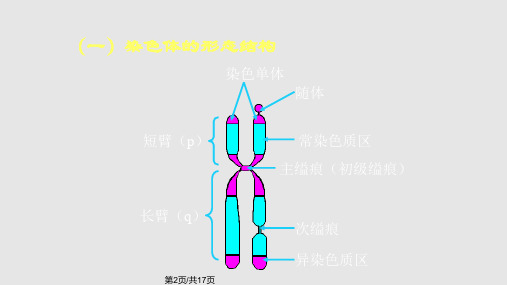
核酸 DNA RNA
蛋白质5-0.1
1 0.5-1.5
第9页/共17页
三、染色体的结构 1.一级结构
核小体是染色质的基本结构单位,为染色质的 一级结构, 10nm。
第10页/共17页
核小体
第11页/共17页
2 .二级结构: 螺线管是染色质的二级结
构,6个核小体缠绕一圈形成的 中空性管. 外30nm; 内10nm, 组蛋白H1位于螺旋管内侧。
第12页/共17页
内10nm 组蛋白H1
第13页/共17页
染色质的二级结构:螺线管
第14页/共17页
3 .三级结构:
超螺线管为染色质的三级结构, 它是由螺旋管进一步盘曲而形成。
4 .四级结构:
超螺线管进一步折叠成为四级结 构—染色单体。(DNA分子长度压缩至 1/8000~1/10 000)。
动粒结构域
主
缢
痕
模
式
图
配对结构域
第4页/共17页
随体
染色体的臂上凹陷缩窄 形成次缢痕,与核仁的 形成有关,称为核仁组 织区(NOR)。
第5页/共17页
端粒(telomere)
第6页/共17页
端粒(telomere)
端粒是存在于染色体末端的特化部位。通常 由一简单重复的序列组成,进化上高度保守。可以保 护染色体末端不被降解,并防止与其它染色体的末端 融合。 正常染色体每复制一次,端粒序列减少50-100 个bp,因而端粒也被称为细胞的生命钟,当端粒缩短到 一定程度,即是细胞衰老的标志。
生殖细胞、胚胎干细胞和肿瘤细胞含有端粒 酶,可以使端粒恢复原长。
第7页/共17页
端粒酶
端粒酶是一种由蛋白质和RNA组成的核糖核蛋 白酶。具有延长端粒末端重复序列的功能,如果端粒 酶活性丧失,端粒将逐渐缩短,从而导致细胞衰老。
三棱柱折叠方法

三棱柱折叠方法引言三棱柱是一种具有三个平行且相等的侧面的立体形状,它有着独特的几何特性。
在本文中,我们将探讨三棱柱的折叠方法,以及折叠后的形态和性质。
一、三棱柱的基本构造三棱柱由两个底面和三个侧面组成。
底面是两个全等的多边形,而侧面是由这两个多边形的对应边所组成的三个矩形。
三棱柱的高度是连接两个底面的垂直线段。
二、三棱柱的折叠方法1. 折叠底面将三棱柱的两个底面对折。
将其中一个底面的边与另一个底面的边对齐,然后沿着这条对折线将两个底面折叠在一起。
这样,底面的形状将变为一个多边形的一部分。
2. 折叠侧面接下来,将三个侧面按照一定的顺序对折。
首先,将一个侧面沿着底面的一边对折,使得这个侧面与底面垂直。
然后,将另外两个侧面依次对折,使得它们与底面平行。
最后,将这三个折叠好的侧面沿着底面的边对齐,使得它们形成一个完整的形状。
3. 完成折叠将三个折叠好的侧面按照一定的顺序对齐,使得它们形成一个平面图形。
这样,三棱柱就完成了折叠过程,变为一个平面图形。
这个平面图形可以用来表示三棱柱折叠后的形态和性质。
三、折叠后的形态和性质1. 形态经过折叠后,三棱柱变为一个平面图形。
这个平面图形由两个多边形和三个矩形组成。
两个多边形是底面的一部分,而三个矩形是侧面的一部分。
折叠后的形态可以用平面图形来表示,使得观察和研究更加方便。
2. 性质经过折叠后,三棱柱的性质也发生了变化。
折叠后的平面图形具有以下性质:- 底面的形状:折叠后的底面形状是一个多边形的一部分。
这个多边形的形状与原来的底面相似,但不完全相同。
- 侧面的形状:折叠后的侧面形状是三个矩形的一部分。
这三个矩形的形状与原来的侧面相似,但不完全相同。
- 高度的变化:经过折叠后,三棱柱的高度没有改变。
折叠后的平面图形仍然具有原来的高度。
四、应用领域三棱柱的折叠方法在很多领域都有应用。
以下是其中几个例子:1. 几何学:三棱柱的折叠方法可以用来研究和探索几何形状的性质和变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形体折叠
——法兰克福莱伯斯托克园折叠变形后的单体建筑(埃森曼)
形体折叠
西班牙的MartinezLapeiniz-TorresArouiteetoS设计的 Visitors Center位于大学校园内而比邻一个公园。设计者 希望建筑不是切断基地的体量而是景观的延续。
的现象,折叠是一种普遍的物质 构造,如山川、江河、岩石、组 织、大脑等等。这些启发许多新 一代建筑师……
形体折叠
界面折叠
空间折叠
这种形状不是自然界所特有的,他来自与一种数学模型,体现了现代技术 的魅力,成为了一个别具特色的折叠表现主义景观建筑。
界面折叠——某展示馆设计方案
空间折叠——朱苏图书馆和库哈斯的杜会空间
折叠既是组织功能也是制造连续的空间工具。库哈斯在巴黎的图书馆竞 赛中,用“社会魔毯” 来形容建筑连续的楼板,倾斜的楼板既与下层也与 上层一致,形成连续的路径,图书馆的体验变成了一种城市景观的感觉。
Visitors Center模型及草图
形体折叠——某展示馆设计方案
形体折叠(电脑模型)
界面折叠——BBC音乐中心(FOA)
通过折叠转换的手法,使地板、屋面、墙面形成一个连续的界面,传统意 义上的地板、屋面和墙消失了,空间形态呈现出连续、弯曲、流动的特征。
界面折叠——Springteeture-Biwa住宅
空间折叠——朱苏图书馆和库哈斯的杜会空间
几个不同的空间被融合在一起,其最基本特征是空间地面的非水平面 化。在满足使用功能要求的前提下,非水平面化的折叠手法包容了内部与 外部、水平与垂直的对立关系,消解了重力对层和对人的支配关系。
空间折叠(方式示例)
非线性建筑的形式特征 ——形态折叠
褶皱是一种自然界比比皆是
藤原秀萍一直努力用连续的波形钢来做建筑。用扭曲,缠绕的方法,全异于 传统的建造思维。在他雕塑般的建筑中,人们对建筑的习惯认知受到挑战。我们 无法确定某一段表面属于内或者外,而且当我们站在带子形成的的平台上,
藤原秀萍的日本城市公园小品建筑(公共厕所,建筑通过将镀锌压型钢板 进行螺旋形卷曲而形成的三度空间,组织出了男、女卫生间及管理用房。
