机电传动系统的运动学基础全解
第章机电传动系统的动力学基础

2.1.3 转矩方向的确定
1) TM与n正方向一致 TL与n正方向相反
2) TM与n正方向相反 TL与n正方向一致
或1) TM与n方向一致 TL与n方向相反
2) TM与n方向相反 TL与n方向一致
TM取“+”号(拖动转矩TM) TL取“+”号(制动转矩TL) TM取“-”号(制动转矩TM) TL取“-”号(拖动转矩TL) TM与n同号(拖动转矩TM) TL与n同号(制动转矩TL) TM与n异号(制动转矩TM) TL与n异号(拖动转矩TL)
风机
起重机
生产机械转矩分为:摩擦阻力产生的和重力作用产生的。
摩擦阻力产生的转矩为反抗性转矩,其作用方向与n相反, 为制动转矩。
重力产生的转矩为位能性转矩,其作用方向与n无关,提 升时为制动转矩;下放时为拖动转矩。
2.1 动力学方程式
单轴机电传动系统如图所示:
+ω
TL
+TM
TM ω 传动系统图
生产机械
Tm
l 恒与运动方向相反,阻碍运动
T
Tm
电动机轴
n
(b) TL为位能转矩时, l 作用方向恒定,与运动方向无关
l 如:卷扬机起吊重物等
思考:TL方向
负载的机械特性指:n=f(TL)关系
TL为反抗转矩,负载转矩由摩擦力 产生,其特点:大小恒定(与n无 关);作用方向与运动方向相反。
2.3.1 定义
同一转轴上负载转矩和转速之间的函数关系。
2.3.2 分类
n f(TL)
• 恒转矩型机械特性(TL为常数) • 恒功率型机械特性(P为常数) • 离心式通风机型机械特性 • 直线型机械特性
《机电传动技术》 第二章 机电传动系统的动力学基础

当干扰使n↑时,干扰消除后希望n↓这时如TM-TL<0则负加速 当干扰使n↓时,干扰消除后希望n↑这时如TM-TL>0则正加速 例:a、b两点 a点,当n↑时, TM↓,当干扰消除后 由于TM-TL<0,所以n↓ b点,当n↑时, TM↑,当干扰消除后 由于TM-TL>0,所以n↑,直到a点处平衡。
机电传动控制
机电传动系统的动力学基础
机电传动系统的运动方程
单轴机电传动系统
dω dn TM − TL = J =k dt dt
意义:Tm与TL之差将产生加速度 当Tm > TL时,加速 当Tm < TL时,减速 当Tm = TL时,匀速(平衡)
(TM − TL = Td )
3、TM与TL的正反 以转速的方向为准(n) TM:与n同向时为正(拖动) 反之为负(制动) TL :与n反向时为正(制动) 反之为负(拖动) 例:提升重物 启动:Tm为正, TL正 制动: TL为正,Tm为负
TM − TL = Td
− TM − TL = Td
生产机械的机械特性
机械特性: 生产机械转轴(电机轴)上的负载转矩和转 速之间的函数关系。 1、恒转矩型机械特性 特点: 负载转矩为常数, TL =C 反抗转矩 位能转矩
与n同号(总制动)摩擦、切削力
方向一定吊重物
2、离心式通风机型机械特性 、 特点: TL = Cn 2 ,负载转矩与转速平方成正比
END
1、电动机和生产机械的机械特性 曲线应有交点
此处:Tm=TL(匀速) 例:曲线1和2,附合这个条件,有a、b交点 曲线1和3,不附合
2、当有外加干扰使n变化时,干扰消除后n应能自行恢 复到原状态。 该条件的判断原则是: 该条件的判断原则是 当n ↑, TM < TL 由运动方程看
机电传动系统的动力学基础
a点: TM − TL = 0 点 当负载突然增加后
TM − TL' < 0 TM ' − TL &g; = 0
当负载波动消除后
TM − TL = 0
点为系统的稳定平衡点。 故a点为系统的稳定平衡点。 点为系统的稳定平衡点 同理b点不是稳定平衡点。 同理 点不是稳定平衡点。 点不是稳定平衡点
符合稳定运行条件的平衡点称为稳定平衡点。 符合稳定运行条件的平衡点称为稳定平衡点。
§2.4机电传动系统的稳定运行条件
分析举例1 分析举例 右图是异步电动机拖动 直流他励发电机工作时 的机械特性。 的机械特性。 n’ 点是不是稳定平衡点? b点是不是稳定平衡点? nb 为什么? 为什么? 由系统稳定运行时 1)电动机与直流他励发电机 TM=TL TM’TL’ 生产机械) (生产机械)的机械特性 曲线是否有交点, 曲线是否有交点, 点为系统的稳定平衡点。 故b点为系统的稳定平衡点。 点为系统的稳定平衡点 系统受到干扰, 2)系统受到干扰,干扰消除后 能否恢复原态的原则来判别。 能否恢复原态的原则来判别。
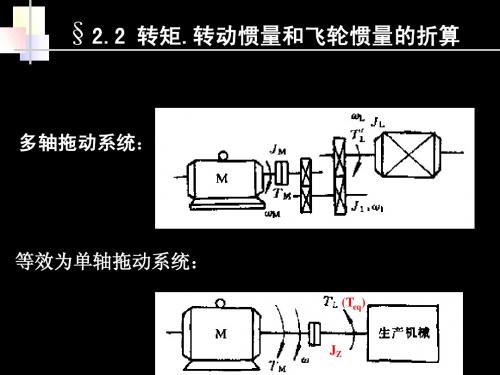
转矩.转动惯量和飞轮惯量的折算 §2.2 转矩 转动惯量和飞轮惯量的折算
三、转动惯量和飞轮惯量的折算
当速比j较大时,可用适当加大电动机轴转动惯量或 飞轮惯量来考虑中间传动机构转动惯量或飞轮惯量的影响。
折算到电动机轴上的总转动惯量(工程简化式) J =δJ + J / j 2 Z M L L
机电传动系统动力学基础讲诉课件

提出改善机电传动系统稳定性的措施 ,如优化系统参数和增加阻尼等。
稳定性分析方法
分析机电传动系统的稳定性,包括时 域分析和频域分析等方法。
04
机电传动系统动态响应仿真
仿真软件介绍
ANSYS Maxwell
一款强大的电磁场仿真软件,适 用于电机、发电机、变压器等设
备的电磁场分析。
ADAMS
机械系统动力学仿真软件,可对机 电系统进行运动学和动力学分析。
。
刚体动力学
总结词
研究刚体运动规律的学科
详细描述
刚体动力学是研究刚体运动规律的学 科,主要研究刚体的平动、转动和复 合运动等规律。刚体动力学在机械系 统、机器人、航空航天等领域有着广 泛的应用。
弹性力学基础
总结词
研究弹性物体变形和力的关系的学科
VS
详细描述
弹性力学是研究弹性物体变形和力的关系 的学科,主要研究弹性体的应力、应变和 位移等物理量之间的关系。弹性力学在机 械设计、材料科学、航空航天等领域有着 广泛的应用。
SolidWorks/Adams
用于建立和仿真机电传动系统的机械结构,支持多种优化算法和运 动学分析。
THANKS
感谢观看
分析系统的稳态性能,如电压 、电流、转矩等。
动态分析
分析系统的动态响应特性,如 启动、制动、调速等过程中的 性能表现。
优化设计
根据仿真结果对系统进行优化 设计,提高性能和效率。
故障诊断与预测
通过仿真分析系统可能出现的 故障模式和原因,为实际运行 中的故障诊断和预防提供依据
。
05
机电传动系统优化设计
机电传动系统动力学基础讲诉课件
目录
• 机电传动系统概述 • 机电传动系统动力学基础 • 机电传动系统动态特性分析 • 机电传动系统动态响应仿真 • 机电传动系统优化设计
第2章 机电传动系统的动力学基础1汇总

TL 470.4N m
解(1) TL
TLL c M
TL
c j
470.4 34.1N m 0.92 3 5
解:(2)飞轮矩的折算
GDZ2
(GDM2
GD12 ) (GD22
GD32 )
1 j12
(GD42
GDL2 )
1 jL2
(294 29.4) (78.4 49) 1 (196 450.8) 1 ]
方向相同。
不论n为正向还是负向,TL作用方向都不变。 设n为正时负载转矩阻碍运动,则特性在第一、四象限。
位能转矩
不难理解,在运动方程式中,反抗转矩TL的符号总是与 n 相同 为正;位能转矩TL的符号则有时与n 相同,有时与n相反。
离心式通风机型机械特性
TL Cn 2
虚线表示在有摩擦负载 的实际情况
n为负方向时TL为负,特性在第三象限。
2.位能转矩 ✓转矩大小恒定不变;
✓作用方向不变,与运动方向无关,即在某一方向阻 碍运动而在另一方向促进运动。
卷扬机起吊重物时,由于重物的作用方向永远向着地心,所 以,由它产生的负载转矩永远作用在使重物下降的方向,当电动
机拖动重物上升时,TL与n的方向相反;当重物下降时,TL和n的
一、单轴拖动系统
电动机 (M)
TL 生产机械
TM 图2.1 单轴拖动系统
MM
+TL
TM TL n c d / dt 0 TM TL n c d / dt 0
静态(稳态)
动态(加速 或减速)
单轴机电传动系统的运动方程式
TM
TL
J
d
dt
J m 2 mD2 / 4
(2.1)
G mg
2第二章 机电传动系统的动力学基础

n -TL 0 TL T
n
0
TL T
(a)反抗性负载
(b)位能性负载
(2)离心式通风机型负载特性(TL=Cn2) 按离心力原理工作,如离心式通风机,水泵。 (3)直线型负载特性(TL=Cn)如发电机的负载 与转速的关系
n
n
0
离心式通风机负载特性
TL 0
直线型负载特性
TL
(4)恒功率型负载特性( TL=K/n )如电动 机、发动机的转速和转矩的关系。
TL
C பைடு நூலகம்M
TL ' L
TL ' /(C j )
起重机提升重物: TL 9.55 Fv /( c nM ) 起重机下放重物: TL 9.55 Fv c / nM
'
飞轮转矩的折算(重要)
(根据能量守恒原则,即各轴上的动能之和等于折算到电机 轴之后的动能)
一、执行机构旋转运动时有:
输入功率:PM TLM 输出功率: PL Fv 传动效率: 起重机提升重物: c Fv /( TL w M )
起重机下放重物: ' c TL w M /( Fv )
折算转矩:起重机提升重物: TL 9.55 Fv /( c nM )
起重机下放重物: TL 9.55 Fv ' c / nM
(+ )
d TM TL J dt
2.2 转矩、转动惯量和飞轮转矩的 折算
目的:生产中的机电系统大多是多轴拖 动系统,在分析此类系统时要将其转化 为单轴拖动系统。因此,需将多轴拖动 系统的动力参数折算到电机轴上。 原则:转矩(功率守恒);转动惯量 (能量守恒)。
负载转矩的折算(重要)
机电传动系统的动力学基础课件

机电传动系统的发展趋势
01
高效节能
提高系统的能源利用效率,降低 能源消耗。
03
智能化与网络化
将传感器、控制器和执行器等智 能设备集成到系统中,实现系统
的智能化和网络化。
02
高精度控制
采用先进的控制算法和传感器技 术,实现高精度的位置和速度控
通过优化机电传动系统的设计和控制算法,可以提高机器人的性能和智能化程度, 拓展其应用领域。
在数控机床中的应用
数控机床是现代制造业的核心设 备之一,机电传动系统在数控机
床中发挥着重要的作用。
数控机床需要实现高精度、高效 率、高可靠性的加工,机电传动 系统的性能和控制精度直接决定
了机床的加工质量和效率。
前馈控制
通过预测系统输入的变化来提前调整系统输出 ,以减小未来的误差。
补偿控制
通过引入外部信号来抵消系统内部的干扰或扰动。
PID控制算法及其实现
1 2
P(比例)
根据误差的大小来调整输出,以减小误差。
I(积分)
对过去的误差进行累积并调整输出,以消除长期 误差。
3
D(微分)
根据误差的变化率来调整输出,以预测未来的误 差。
机电传动系统的动力学基础课件
目录
• 机电传动系统概述 • 机电传动系统的动力学模型 • 机电传动系统的稳定性分析 • 机电传动系统的控制策略与实现 • 机电传动系统的仿真研究与实验验证 • 机电传动系统的应用实例
01
机电传动系统概述
机电传动系统的基本组成
电机
作为动力源,将电能转化为机械能。
传动机构
频域分析法
通过分析系统的频率响应函数来判断系统是否稳定。如果频率响应 函数的极点都位于复平面的左半部分,则系统是稳定的。
机电传动控制2、机电传动的动力学基础

详细描述
机电传动系统是将电能转换为机械能以驱动机械设备 运转的系统。它主要由电机、传动机构和控制装置三 部分组成。电机是将电能转换为机械能的核心部件, 通过电机的旋转运动实现机械能的输出;传动机构则 是将电机的输出与机械设备连接,实现减速、变速或 传递扭矩等功能;控制装置则是控制电机的启动、停 止、调速等操作,以实现对机械设备的精确控制。
该系统通常采用交流伺服电机驱动, 通过高精度编码器和反馈控制系统实 现精确的位置和速度控制。
此外,该系统还具有强大的故障诊断 和安全保护功能,以保障设备和操作 人员的安全。
工业机器人机电传动控制系统
工业机器人是自动化生产线上 不可或缺的重要设备,其机电 传动控制系统是实现高精度、
高效率、高可靠性的关键。
该系统通常采用直流伺服电机 驱动,通过高精度编码器和反 馈控制系统实现精确的位置和
速度控制。
工业机器人的机电传动控制系 统还具有高刚度、低惯量、低 摩擦等特性,以确保稳定、准 确的运动轨迹。
此外,该系统还具有强大的故 障诊断和安全保护功能,以保 障设备和生产线的稳定运行。
风力发电机的机电传动控制系统
机电传动控制2
contents
目录
• 机电传动系统概述 • 机电传动的动力学基础 • 机电传动系统的控制原理 • 机电传动系统的设计方法 • 机电传动控制系统的实现 • 机电传动控制系统的应用实例
01 机电传动系统概述
机电传动系统的定义与组成
总结词
机电传动系统是由电机、传动机构和控制装置组成的 ,用于实现机械能与电能之间转换的系统。
机电传动系统的分类
• 总结词:根据应用领域和功能特点,机电传动系统可分为直流电机传动、交流 电机传动、步进电机传动和伺服电机传动等类型。
第二章 机电传动系统的运动学基础

−TM − TL
G D 2 dn = 375 dt
2.1
单轴拖动系统的运动方程式
TM、TL 、n的参考方向
例2:提升重物过程如下图示,写出运动方程式. 2:提升重物过程如下图示,写出运动方程式.
(a)中 (a)中: TM为正, TL为正。
GD 2 dn TM − TL = 375 dt
TM为拖动转矩,TL为制动转矩。
式中: GDM 2GD12GDL 2 分别为电动机轴,中间传动轴, 分别为电动机轴,中间传动轴,
生产机械轴上的飞轮转矩. 生产机械轴上的飞轮转矩.
2.2 多轴拖动系统的简化 计算举例
例3 机电传动系统如图所示. 机电传动系统如图所示. 已知每根轴的飞轮转矩和转速, 已知每根轴的飞轮转矩和转速,如下所示:
TM =TL时传动系统处于恒速运动的这种状态被称为稳态。
2.动态(TM ≠ TL时): 动态(
TM > TL时:
TM < TL时:
Td = J
Td = J
dω < 0, 即 dt
dω > 0 即 dt
dω > 0 , 传动系统加速运动。 dt
dω < 0, dt
传动系统减速运动。
TM ≠TL 时传动系统处于加速或减速运动的这种状态被称为动态。
TM − TL
G D 2 dn = 375 dt
……工程计算式
GD2-飞轮转矩,且J=1/4(GD2); 飞轮转矩,
2.1
单轴拖动系统的运动方程式
传动系统的状态
根据运动方程式可知:运动系统有两种不同的运动状态:
1.稳态(TM = TL时) 稳态( :
dω Td = J = 0 即 dt
机电传动控制机电传动系统的运动学基础解读

符合稳定运行条件的平衡点称为稳定平衡点。
分析举例
异步电动机 的机械特性
交点a
? a、b两点是
否为稳定平衡点
生产机械 的机械特 性
交点b
a点: TM ? TL ? 0
当负载突然增加后 TM ? TL' ? 0 TM' ? TL' ? 0
当负载波动消除后 TM' ? TL ? 0 TM ? TL ? 0
拖动转距,否则为制动转距。
2. TL的符号与性质
当TL的实际作用方向与n的方向相同时,取与n相反的符号; 当TL的实际作用方向与n的方向相反时,取与n相同的符号; 当TL的实际作用方向与n的方向相同(符号相反)时, TL为拖
动转距,否则为制动转距。
举例:如图所示电动机拖动重物上升和下降。
重物上升
TM为正 TL为正
dt
?0
即 dω ? 0 dt
传动系统以恒速运动。
TM =TL时传动系统 处于恒速运动的这种状 态被称为稳态。
2.动态( TM ? TL时):
TM ? TL时:
Td?0
即 d ? ? 0 , 加速运动。
dt
TM ? TL时: T d
?
J
d?
dt
? 0,
即 d ? ? 0 , 减速运动。
dt
TL─ 负载转矩(N.m);
? ─ 角速度(rad/s );
J ─ 转动惯量(kg.m 2);
t ─ 时间(s );
Td
?
J d?
dt
?
J 2? dn
60 dt
─ 动态转矩(N.m)。
三、传动系统的状态 根据运动方程式可知:运动系统有两种不同的运动状态:
第二章机电传动系统动力学基础课件

总目录 章目录 返回 上一页 下一页
解: 这是折算到低速轴 TM / TM jc TM nn31 c 132.3Nm
电机与拖动
GDZ 2
GD12
(
n1 n3
)
2
GD22
(
n2 n3
)2
GD32
3675Nm2
由公式可得生产机械轴上的加速度为:
dnL dt
电气控制系统的发展概况
电机与拖动
3) 可编程序控制器(PLC)
是继电器常规控制技术与微机技术的结合,是一台按开关 量输入的工业控制专用计算机;
具有逻辑运算功能,定时/计数功能,数字运算功能,通信功 能.
4) 计算机数字控制系统
1952年美国出现第一台数控铣床,1958年出现加工中 心,20世纪70年代CNC应用于数控机床和加工中心,80年代 出现了柔性制造系统(FNS);
TM
GDZ 2
电动机
等效负载
TL
j1η1 1
工作机构
j2η2 GDL2
GD2
GD2
GD2 1
GD2 L
Z
M
j2
j2
1
L
式中:GD2 、GD2 、GD2 分别为电动机轴,中间传动轴,生
M
1
L
产机械轴上的飞轮转矩。
总目录 章目录 返回 上一页 下一页
二、三轴直线运动折算到电动机轴上
1.负载转矩的折算
提高了生产机械的通用性和效率,实现机械加工全盘自动 化.
总目录 章目录 返回 上一页 下一页
3. 本课程的性质和任务
电机与拖动
1) 课程性质 该课程是机械类专业的一门必修的专业基础课,
是机电一体化人才所需电知识的驱体. 2) 课程内容
02机电传动系统的动力学基础

29
2.3.4 恒功率型机械特性
机械的负载转矩TL与转速n成反比,即TL =K/n,或 K=TLn cc P为常数。
例如:车床加工,在粗加工时, 切削量大,负载阻力大 ,开低速;在精加工时,切削量小,负载阻力小,开高速 。当选择这样的方式加工时,不同转速下,切削功率基本 不变。
30
除了上述几种类型的生产机械外,还有一些生产机械具有 各自的转矩特性,如带曲柄连杆机构的生产机械,它们的 负载转矩TL是随转角α而变化的,而球磨机、碎石机等生 产机械,其负载转矩则随时间作无规律的随机变化,等等 。
16
度。
折算到电动机轴上的总飞轮转矩为:
2 Z
GD
GD
2 M
GD j
2 1
2 1
GD j
2 L
2 L
式中,GD2M、GD21、GD2L—电动机轴、中间传动轴、生 产机械轴上的飞轮转矩。 说明: 当速比 j 较大时,中间传动机构的转动惯量J1或 飞轮转矩GD21 ,在折算后占整个系统的比重不大,实际 工程中为了计算方便起见,多用适当加大电动机轴上的转 动惯量JM或飞轮转矩GD2M的方法,来考虑中间传动机构 的转动惯量J1或飞轮转矩GD21 的影响,
1
1 .当 T M T L 时, n 常数 , dn / dt 0 ; 或 =常数 , d / dt 0 , 这种运动状态称为静态 态)或稳态 ( 稳定运转状态 )。
2
(相 对静止 状
当 T M T L 时 , 速度 ( n 或 ) 就要 发要 变化,产生 加速或减速。
11
电动机拖动生产机械运动时的传动效率:
c
输出功率 输入功率 T ' L L
机电传动系统的动力学基础课件

机电传动系统的应用
工业自动化生产线
在工业自动化生产线上,机电传 动系统广泛应用于各种机械设备 的驱动,如传送带、机械手、包
装机等。
交通运输
在交通运输领域,机电传动系统主 要用于电动汽车、轨道交通、船舶 和飞机等交通工具的驱动。
电机优化设计
1 2
电机效率优化
通过改进电机材料、优化电机结构设计、提高制 造精度等方式,提高电机的效率,减少能源浪费 。
电机尺寸优化
在满足性能要求的前提下,尽量减小电机的体积 和重量,以便在有限的空间内安装更多的电机。
3
电机可靠性优化
通过优化电机的散热设计、提高电机的耐久性和 稳定性,从而提高电机的可靠性,减少故障率。
交流电机
交流电机是一种将交流电能转换为机械能的装置,分为异步 电机和同步电机两大类,广泛应用于工业、农业、商业等各 个领域。
齿轮传动实例分析
圆柱齿轮传动
圆柱齿轮传动是最常见的齿轮传动形式之一,具有传动效率高、传动比准确等优点,广泛应用于各种 机械传动系统中。
行星齿轮传动
行星齿轮传动是一种比较复杂的齿轮传动形式,具有承载能力大、传动比范围广等优点,常用于高速 重载的场合,如航空发动机等。
组成
主要由电动机、传动机构、执行机构等部分组成。电动机作为动力源,将电能 转换为机械能;传动机构则将电动机的动力传递到执行机构;执行机构则负责 完成具体的机械动作。
机电传动系统的分类
按传动方式
可分为机械传动、液压传动、气压传动、电气传动等类型。其中,电气传动又可 分为直流电气传动和交流电气传动。
机电传动控制 第2章 机电传动系统的运动学基础

四、TM、TL 、n的参考方向 因为电动机和生产机械以共同的转速旋转,所以一般以ω (或n)的转动方向为参考来确定转矩的正负。 拖动转距促进运动;制动转距阻碍运动。 1. TM的符号与性质 当TM的实际作用方向与n的方向相同时,取与n相同的符号; 当TM的实际作用方向与n的方向相反时,取与n相反的符号; 当TM的实际作用方向与n的方向相同(符号相同)时, TM 为拖动转距,否则为制动转距。 2. TL的符号与性质 当TL的实际作用方向与n的方向相同时,取与n相反的符号; 当TL的实际作用方向与n的方向相反时,取与n相同的符号; 当TL的实际作用方向与n的方向相同(符号相反)时, TL 为拖动转距,否则为制动转距。
二、负载转矩的折算
11
河北工程大学
Hebei University of Engineering
对于旋转运动,假设电动机以ωM角速度旋转,生产机械的负 载转矩TL折算到电动机轴上的负载转矩为Teq,而生产机械转动速 度为ωL 。则传动机构的输入功率Peq和输出功率PL分别为:
P eq M Teq
J mr
2
1 1 1 1 2 2 2 2 E mv m r mr J 2 2 2 2 2
例:滑冰时,手臂伸展人转慢,手臂抱紧人转快。
机电传动控制
二、运动方程式
5
河北工程大学
Hebei University of Engineering
在机电系统中,TM、TL、(或n)之间的函数关系称为运 动方程式。根据动力学原理,三者的函数关系如下:
机电传动控制
9
河北工程大学
Hebei University of Engineering
举例:如图所示电动机拖动重物匀速上升或匀速下降。 设重物上升时速度n的符号为正,下降时n的符号为负。
机电传动系统的运动学基础全解课件

机电传动系统的发展趋势与前沿技术
随着能源紧缺和环境保护意识的提高,高效节能和绿色环 保成为机电传动系统的发展趋势。
矢量控制、直接转矩控制、自适应控制等先进控制策略以 及新型电机、变速器、离合器等关键零部件的应用,为机 电传动系统的发展提供了新的机遇。
数字化设计与仿真技术、网络化控制技术、智能制造技术 等前沿技术的融合应用,将进一步推动机电传动系统的智 能化和自动化发展。
3
牛顿第三定律
对于每一个作用力总有一个大小相等、 方向相反的反作用力。在机电传动系统 中,这个定律用来分析系统内各部件之 间的相互作用力,以及这种相互作用力 对系统整体运动状态的影响。
动量定理、动能定理及其在机电传动系统中的应用
动量定理
物体动量的变化等于作用于它的外力的冲量。在机电传动系统中,这个定理用来分析系统在受到外力作用后, 其动量的变化情况以及这种变化对系统运动状态的影响。
02
机电传动系统的动力学基础
牛顿运动定律及其在机电传动系统中的应用
1
牛顿第一定律
物体总保持匀速直线运动或静止状态, 直到有外力改变这种状态。在机电传动 系统中,这个定律用来分析系统的平衡 状态以及在外力作用下的运动状态变化 。
2
牛顿第二定律
物体的加速度与作用于它的力成正比, 与它的质量成反比。在机电传动系统中 ,这个定律用来分析系统的受力情况, 以及根据受力情况推算出系统的运动状 态变化。
5. 结果分析
对仿真结果进行分析,得 出结论。
动力学仿真的应用实例及效果评价
要点一
应用实例
要点二
效果评价
例如,通过动力学仿真优化了机器人的运动性能;通过仿 真发现了电机控制中的问题并提出了解决方案等。
机电传动控制基础课后题答案

折算到电机轴上的静态转矩:
TL
9.55 F v2
c nM
9.55 100 0.37 0.83 950
0.448
N •m
折算到电动机轴上整个拖动系统的飞轮惯量GDZ2
GDZ2
GDM2
GD12
j
2 1
(
GDL2 j1 j2 )2
365
G v2 nM2
1.1 GDM2
365
F v2 nM2
(2)电动机拖动位能性恒转矩负载,要求以-300r/min速度下放重 物,采用倒拉反接制动,电枢回路应串多大电阻?若采用能耗制动, 电枢回路应串多大电阻?
(3)想使电机以n=-1200r/min速度,在再生发电制动状态下,下 放重物,电枢回路应串多大电阻?若电枢回路不串电阻,在再生发 电制动状态下,下放重物的转速是多少?
n) 9.55Ke N 2
TL
- Ra
( 220 1200) 9.55 0.2082
0.208
49
- 0.4 0.8
不串电阻时的制动转速:
n
UN KeN
Ra
9.55Ke
N
2
TL
220 0.208
0.4 9.55 0.2082
49 1105 r/min
习题与思考
3.4 直流电动机一般为什么不允许直接启动?如直接启动 会发生什么问题?应采用什么方法启动比较好?
N •m
3.11一台他励直流电动机的名牌数据为:
PN=5.5kW,UN=110V, IN=62A
nN=1000r/min ,
试绘制出它的固有机械特性曲线:
解:
Ra
0.75
UnN n2
PN
机电传动系统的运动学基础全解课件

用于需要较大扭矩和较小的减速比的场合。
机电传动系统的应用
工业自动化生产线
组成
主要由电机、减速器、联轴器、 传动轴等部件组成,其中电机是 核心部件,负责将电能转换为机 械能。
机电传动系统的分类
按电机类型分类
可分为直流电机传动系统和交流电机传动系统。直流电机具有良好的调速性能,适用于 需要精确控制速度的场合;交流电机结构简单、维护方便,适用于高效率、大扭矩的场
合。
按减速器类型分类
动力学的基本问题
质点运动问题
如何求解质点在力作用下的运动轨迹、速度和加速度。
刚体转动问题
如何求解刚体在力矩作用下的转动轨迹、角速度和角加速度。
弹性力学问题
如何求解弹性物体在力作用下的变形和应力分布。
04
机电传动系统的控制原理
控制系统的基本概念
控制系统
01
由控制器、受控对象和反馈通路组成,用于实现某一特定功能
03
机电传动系统的动力学分析
动力学的基本概念
动量
系统动量的定义,以及动量守恒 定律。
动能
系统动能的定义,以及动能守恒定 律。
力
力的定义,以及力的分类(保守力 、非保守力等)。
动力学的基本定理
牛顿第三定律
阐述了作用力和反作用力的关系。
动量定理
阐述了动量的变化与外力之间的关系。
动能定理
阐述了动能的变化与外力做功之间的关系。
某工厂的传送带系统,设计时考虑了 高效、稳定和易于维护的原则,实际 运行中取得了良好的效果。
第二章机电传动系统的动力学基础

习题与试探题第二章机电传动系统的动力学基础说明机电传动系统运动方程中的拖动转矩,静态转矩和动态转矩。
拖动转矩是由电动机产生用来克服负载转矩,以带动生产机械运动的。
静态转矩确实是由生产机械产生的负载转矩。
动态转矩是拖动转矩减去静态转矩。
从运动方程式如何看出系统是处于加速,减速,稳态的和静态的工作状态。
T M-T L>0说明系统处于加速,T M-T L<0 说明系统处于减速,T M-T L=0说明系统处于稳态(即静态)的工作状态。
试列出以下几种情形下(见题图)系统的运动方程式,并说明系统的运动状态是加速,减速,仍是匀速?(图中箭头方向表示转矩的实际作用方向)T M TT M=T L T M< T LT M-T L>0说明系统处于加速。
T M-T L<0 说明系统处于减速T M T L T M T LT M> T L T M> T L系统的运动状态是减速系统的运动状态是加速T M T L T T LT M= T L T M= T L系统的运动状态是减速系统的运动状态是匀速多轴拖动系统什么缘故要折算成单轴拖动系统?转矩折算什么缘故依据折算前后功率不变的原那么?转动惯量折算什么缘故依据折算前后动能不变的原那么?因为许多生产机械要求低转速运行,而电动机一样具有较高的额定转速。
如此,电动机与生产机械之间就得装设减速机构,如减速齿轮箱或蜗轮蜗杆,皮带等减速装置。
因此为了列出系统运动方程,必需先将各转动部份的转矩和转动惯量或直线运动部份的质量这算到一根轴上。
转矩折算前后功率不变的原那么是P=Tω, p不变。
转动惯量折算前后动能不变原那么是能量守恒MV=ω2什么缘故低速轴转矩大,高速轴转矩小?因为P= Tω,P不变ω越小T越大,ω越大T 越小。
什么缘故机电传动系统中低速轴的GD2逼高速轴的GD2大得多?因为P=Tω,T=G∂D2/375. P=ωG∂D2/375. ,P不变转速越小GD2越大,转速越大GD2越小。
第二章 机电传动系统的动力学基础PPT课件

TL/负载转矩
上的转矩
负载旋
L
转
角速度
M电动机轴角速度
c
P
/ L
TL/L
(c传动效率)
PM TLM
TL=TcL/ML
= TL/
cj
(
j速比)
9
五、负载转矩的折算
5.2 直线运动
PM TLM
PL/ F
PM电动机轴功率
F直线运动部件的负载 TL负力载力F在电动机轴上产生
JZ
JM
J1 j12
JL
j
2 L
JM、J1、J L 分别为电动机轴、中间传动轴、生产机械运动轴上的转动惯量;
j1
M 1
电动机轴与中间传动轴之间的速度比;
jL
M L
电动机轴与生产机械运动轴之间的速度比;
M、1、L 分别为电动机轴、中间传动轴、生产机械运动轴的旋转角速度;
制动减速
❖ 当制动减速时,TM的作用方向与n的方向相反, 故TM的符号与n的符号相反,TM取负;而TL的 作用方向与n的方向相反,故TL的符号与n的符 号相同, TL取正。TM、 TL、n的方向如图(b) 所示 .
TM
TL
J
2
60
dn dt
GD 2 375
dn dt
0(减速)
7
四、多轴拖动系统的组成
14
7.3 离心式通风机型负载特性曲线
虚线表示 在有摩擦 负载的实 际情况
TL Cn2 负载转矩与n的 二次方成正比
15
7.4 直线型负载特性曲线
实验室中模拟负 载用的他励电动 机,当励磁电流 和电枢电阻固定 不变时,其电磁 转矩与转速成正 比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.稳态(TM TL时):
Td
J
d
dt
0即
dω dt
0,ω为常数,传动系统以恒速运动。
TM =TL时传动系统处于恒速运动的这种状态被称为稳态。
2.动态(TM TL时):
TM
TM
TL时:Td
TL时:Td
J J
d
dt
d
dt
0即 0, 即
d
dt
d
dt
0,传动系统加速运动。 0,传动系统减速运动。
假设n为正时TL阻碍运动,则n为负时TL一定促进运动,特性 在第一、四象限。
不难理解,在运动方程式中,反抗转矩TL的符号总是与 n 相 同;位能转矩TL的符号则有时与n 相同,有时与n相反。
二、离心式通风型机械特性
离心式通风型机械特性是按离心力
原理工作的,如离心式鼓风机、水泵等,
它们的负载转矩TL的大小与速度n的平
拖动转距,否则为制动转距。
2. TL的符号与性质
当TL的实际作用方向与n的方向相同时,取与n相反的符号; 当TL的实际作用方向与n的方向相反时,取与n相同的符号; 当TL的实际作用方向与n的方向相同(符号相反)时, TL为拖
动转距,否则为制动转距。
举例:如图所示电动机拖动重物上升和下降。 设重物上升时速度n的符号
出转矩TM,用来克服负载转矩TL ,带动生产机械以角速度ω(或速
度n)进行运动。
二、运动方程式
在机电系统中,TM、TL、(或n)之间的函数关系称为运动方
程式。
根据动力学原理,TM、TL、(或n)之间的函数关系如下:
TM
TL
J
d
dt
J 2 dn ……运动方程式
60 dt TM TL Td ……转矩平衡方程式
为正,下降时n的符号为负。
当重物上升时:
TM为正,TL为正。
TM、TL、n的方向如图(a)
所示。运动方程式为:
TM
TL
J
2
60
dn dt
因此重物上升时,TM为拖动转矩,TL为制动转矩。
当重物下降时: TM为正, TL为正。 TM、TL、n的方向如图(b)所示。运动方程式为:
TM
TL
J
2
60
dn dt
方成正比,即:
TL Cn2
其中:C为常数。
三、直线型机械特性
直线型机械特性的负载转矩TL的 大小与速度n的大小成正比,即 :
TL Cn 其中:C为常数。
四、恒功率型机械特性
恒功率型机械特性的负载转矩TL的大小与速度n的大小成正比,
即
TL
C n
其中:C为常数。如图所示。
2.4 机电系统稳定运行的条件 机电传动系统中,电动机与生产机械连成一体,为了使系统运
二、负载转矩的折算
假设电动机以ωM角速度旋转,负载转矩TL折算到电动机轴
上的负载转矩为Teq,而生产机械的转动速度为ωL 。则电动机输
出功率PM和负载所需功率PL分别为:
PM M • Teq
PL L •TL
考虑传动机构在传输功率的过程中有损耗,这个损耗可用效率
ηc来表示,且
C
减速机构的输出功率 减速机构的输入功率
TM TL 时传动系统处于加速或减速运动的这种状态被称为动 态。
四、TM、TL 、n的参考方向(2) 因为电动机和生产机械以共同的转速旋转,所以,一般以ω
(或n)的转动方向为参考来确定转矩的正负。
拖动转距促进运动;制动转距阻碍运动。
1. TM的符号与性质
当TM的实际作用方向与n的方向相同时,取与n相同的符号; 当TM的实际作用方向与n的方向相反时,取与n相反的符号; 当TM的实际作用方向与n的方向相同(符号相同)时, TM为
2.位能转矩 , 其特点为: ✓转矩大小恒定不变; ✓作用方向不变,与运动方向无关,即在某一方向阻碍运动而 在另一方向促进运动。
卷扬机起吊重物时,由于重物的作用方向永远向着地心,所 以,由它产生的负载转矩永远作用在使重物下降的方向,当电动 机拖动重物上升时,TL与n的方向相反;当重物下降时,TL和n的 方向相同。
行合理,就要使电动机的机械特性与生产机械的机械特性尽量相配 合。特性配合好的一个起码要求是系统能稳定运行。
一、机电系统稳定运行的含义
1. 系统应能一定速度匀速运行; 2. 系统受某种外部干扰(如电压波动、负载转矩波动等)使运 行速度发生变化时,应保证在干扰消除后系统能恢复到原来的运 必要条件 电动机的输出转矩TM和负载转矩TL大小相等,方向相反。 从T—n坐标上来看,就是电动机的机械特性曲线 n=f(TM)和生 产机械的机械特性曲线 n=f(TL)必须有交点,交点被称为平衡点。
恒转矩型机械特性根据其特点可分为反抗转矩和位能转矩两种。 分别如图所示:
1.反抗转矩:又称摩擦性转矩,其特点如下:
✓转矩大小恒定不变; ✓ 作用方向始终与速度n的方向相反,当n的方向发生变化 时,它的作用方向也随之发生变化,恒与运动方向相反,即 总是阻碍运动的。
按关于转矩正方向的约定可知,反抗转矩恒与转速n取相同的 符号,即n为正方向时TL为正,特性在第一象限;n为负方向时TL为 负,特性在第三象限。
TLL TeqM
则生产机械上的负载转矩折算到电动机轴上的等效转矩为:
Teq
TLL c M
TL
c j
式中:ηc—电动机拖动生产机械运动时的传动效率;
j M L
—传动机构的总传动比
2.3 生产机械的机械特性 在同一轴上,负载转矩和转速之间的函数关系,称为生产机
械的机械特性。 一、恒转矩型机械特性
即:
TL
TM
J
2
60
dn dt
因此重物下降时,TM为制动转矩,TL为拖动转矩。
2.2 多轴拖动系统的简化 一、多轴拖动系统的组成 电动机通过减速机构(如减速齿轮箱、蜗轮蜗杆等)与生产机
械相连,如图所示:
为了对多轴拖动系统进行运行状态的分析,一般是将多轴拖动 系统等效折算为单轴系统。
折算的原则是:静态时,折算前后系统总的传输功率不变。
TM ─ 电动机的输出转矩(N.m); TL─ 负载转矩(N.m);
J ─ 转动惯量(kg.m2); n ─ 速度(r/min);
─ 角速度(rad/s);
t ─ 时间(s );
Td
J
d
dt
J
2
60
dn dt
─
动态转矩(N.m)。
三、传动系统的状态
根据运动方程式可知:运动系统有两种不同的运动状态:
第二章 机电传动系统的运动学基础 ✓机电传动系统的运动方程式; ✓ 了解几种典型生产机械的负载特性; ✓ 了解机电传动系统稳定运行的条件以及学会分析实际 系统的稳定性。
2.1 单轴拖动系统的运动方程式 一、单轴拖动系统的组成
电动机
电动机的驱动对象
系统结构图
连接件
转距方向
电动机M通过连接件直接与生产机械相连,由电动机M产生输
