初中函数综合试题附答案

合集下载

初二函数试题及答案

初二函数试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项是函数y=2x+3的值域？A. {x|x∈R}B. {y|y∈R}C. {(x, y)|x∈R, y∈R}D. {y|y=2x+3, x∈R}答案：D2. 函数y=f(x)=x^2-4x+3的图象开口方向是：A. 向上B. 向下C. 向左D. 向右答案：A3. 函数y=-x^2+6x-8的顶点坐标是：A. (1, -7)B. (3, -1)C. (3, 1)D. (1, 7)答案：B4. 函数y=\frac{1}{x}的图象在第几象限？A. 第一象限B. 第二象限C. 第三象限D. 第四象限答案：B5. 下列函数中，哪一个是奇函数？A. y=x^2B. y=x^3C. y=x+1D. y=x^2-1答案：B二、填空题（每题3分，共15分）1. 函数y=3x-7的图象与x轴的交点坐标是______。

答案：(\frac{7}{3}, 0)2. 函数y=\frac{1}{2}x+1的图象与y轴的交点坐标是______。

答案：(0, 1)3. 函数y=x^2-6x+5的对称轴是直线______。

答案：x=34. 函数y=-2x+1的一次项系数是______。

答案：-25. 函数y=x^3-3x^2+3x-1的图象在x=1处的切线斜率是______。

答案：-1三、解答题（每题5分，共20分）1. 已知函数y=2x-1，求当x=2时，y的值。

答案：当x=2时，y=2*2-1=3。

2. 求函数y=x^2-4x+3的最小值。

答案：函数y=x^2-4x+3可以写成y=(x-2)^2-1，因此当x=2时，函数取得最小值-1。

3. 已知函数y=x-1，求该函数的反函数。

答案：反函数为y=x+1。

4. 已知函数y=\frac{1}{x}，求该函数在x=-2处的导数值。

答案：函数y=\frac{1}{x}的导数为y'=-\frac{1}{x^2}，因此在x=-2处的导数值为y'=\frac{1}{4}。

初中函数测试题及答案

初中函数测试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项不是函数的定义？A. 函数是数集到数集的映射B. 函数是一种特殊的关系C. 函数是一种运算D. 函数是数集到数集的对应关系答案：C2. 如果一个函数的自变量x的取值范围是x>0，那么下列哪个选项是正确的？A. 函数的定义域为所有实数B. 函数的定义域为非负实数C. 函数的定义域为正实数D. 函数的定义域为负实数答案：C3. 函数y=2x^2+3x+1的图像是：A. 抛物线B. 直线C. 双曲线D. 圆答案：A4. 下列哪个函数是奇函数？A. y=x^2B. y=x^3C. y=x^4D. y=x答案：D5. 函数y=1/x的图像在第一象限内：A. 向右上方倾斜B. 向左上方倾斜C. 向右下方倾斜D. 向左下方倾斜答案：B6. 如果函数f(x)=x^2-4x+3，那么f(1)的值是多少？A. -2B. 0C. 2D. 4答案：A7. 函数y=3x-2的图像与y轴的交点坐标是：A. (0, -2)B. (0, 3)C. (2, 0)D. (-2, 0)答案：A8. 函数y=1/x的图像经过第几象限？A. 第一象限和第三象限B. 第二象限和第四象限C. 第一象限和第二象限D. 第三象限和第四象限答案：A9. 函数y=x+1与y=x-1的图像之间的距离是：A. 1B. 2C. 3D. 4答案：B10. 函数y=x^2的图像在x=0处的切线斜率是：A. 0B. 1C. 2D. -1答案：A二、填空题（每题4分，共20分）1. 函数y=2x+3的图像在x=2时的y值是_________。

答案：72. 如果函数f(x)=x^2-6x+8，那么f(3)的值是_________。

答案：13. 函数y=1/x的图像在x=-1处的切线斜率是_________。

答案：-14. 函数y=x^3-3x^2+2的图像在x=1处的切线斜率是_________。

函数试题及答案初二

函数试题及答案初二一、选择题1. 函数的概念是什么？A. 变量之间的关系B. 变量的值C. 变量的集合D. 变量的映射答案：D2. 函数的自变量和因变量分别代表什么？A. 自变量是函数的输入，因变量是函数的输出B. 自变量是函数的输出，因变量是函数的输入C. 自变量和因变量都是函数的输入D. 自变量和因变量都是函数的输出答案：A3. 下列哪个选项是函数的表示方法？A. 列表B. 表格C. 公式D. 图像答案：C4. 函数的值域是指什么？A. 函数的所有可能输入值B. 函数的所有可能输出值C. 函数的自变量范围D. 函数的因变量范围答案：B5. 如果一个函数的自变量是x，因变量是y，那么函数可以表示为：A. y = f(x)B. x = f(y)C. f = y(x)D. f = x(y)答案：A二、填空题1. 函数是定义在某个非空数集上的一个______到另一个非空数集上的一个______。

答案：映射2. 函数的自变量可以取任意实数，那么这个函数的定义域是______。

答案：全体实数3. 如果一个函数的图像是一条直线，那么这个函数是______函数。

答案：线性4. 函数y = 2x + 3的值域是______。

答案：全体实数5. 函数y = x^2的图像是一个______。

答案：抛物线三、解答题1. 已知函数f(x) = 3x - 2，求f(5)的值。

答案：将x=5代入函数f(x) = 3x - 2，得到f(5) = 3*5 - 2 = 15 - 2 = 13。

2. 已知函数g(x) = x^2 - 4x + 3，求g(2)的值。

答案：将x=2代入函数g(x) = x^2 - 4x + 3，得到g(2) = 2^2 -4*2 + 3 = 4 - 8 + 3 = -1。

3. 已知函数h(x) = 2x + 1，求h(-3)的值。

答案：将x=-3代入函数h(x) = 2x + 1，得到h(-3) = 2*(-3) + 1 = -6 + 1 = -5。

初三中考数学函数综合题含答案

初三中考数学函数综合题含答案一、单选题1．函数32x y x +=-中，自变量x 的取值范围是（） A ．3x >-B ．3x ≥-且2x ≠C ．2x ≠D ．3x >-且2x ≠2．如图，函数y ax b =+和y kx =的图象交于点P ，则根据图象可得，关于x 、y 的二元一次方程组0ax y b kx y -+=⎧⎨-=⎩的解是（）A ．42x y =-⎧⎨=-⎩B ．42x y =⎧⎨=⎩C ．24x y =-⎧⎨=-⎩D ．24x y =⎧⎨=⎩3．若反比例函数1k y x-=，当0x >时，y 随x 的增大而减小，则k 的取值范围是（） A ．1k >B ．1k <C ．1k >-D ．1k <-4．将抛物线()2321y x =-+先向右平移2个单位长度，再向下平移2个单位长度，平移后所得的抛物线解析式是（） A ．()2341y x =-- B ．()2343y x =-+ C ．233y x =+D ．231y x =-5．抛物线213y x =的开口方向、对称轴分别是（）A ．向上，x 轴B ．向上，y 轴C ．向下，x 轴D ．向下，y 轴 6．二次函数y ＝x 2＋6x ＋4的对称轴是（） A ．x ＝6B ．x ＝﹣6C ．x ＝﹣3D ．x ＝47．下列y 关于x 的函数中，一次函数为（） A ．()2y a x b =-+B ．()211y k x =++C ．2y x=D ．221y x =+8．一次函数y kx b =+的图象与直线23y x =+平行，且与y 轴的交点为(0,2)，则一次函数的表达式为（） A ．23y x =+B ．22y x =+C ．23y x =-+D ．22y x =-+9．已知抛物线y ＝ax 2＋bx ＋c （a ≠0）的顶点为（2，4），有以下结论：①当a >0时，b 2－4ac >0；②当a >0时，ax 2＋bx ＋c≥4；③若点（-2，m ）,（3，n ）在抛物线上，则m <n ；④若关于x 的一元二次方程ax 2＋bx ＋c ＝0的一根为－1，则另一根为5．其中正确的是（） A ．①②B ．①④C ．②③D ．②④10．已知点A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）都在反比例函数y kx=（k ＜0）的图象上，且x 1＜x 2＜0＜x 3，则y 1，y 2，y 3的大小关系是（） A ．y 2＞y 1＞y 3 B ．y 3＞y 2＞y 1 C ．y 1＞y 2＞y 3 D ．y 3＞y 1＞y 211．已知y =kx +b ，当x =2时，y =-2；当x =3时，y =0．则（）A ．k =2，b =-6B ．k =-6，b =2C ．k =-2，b =6D ．k =-2，b =-612．抛物线y ＝﹣2（x ﹣3）2﹣4的顶点坐标是（）A ．（﹣3，4）B ．（﹣3，﹣4）C ．（3，﹣4）D ．（3，4）13．将一次函数23y x =-的图象沿y 轴向上平移3个单位长度后，所得图象的函数表达式为（） A ．2y x = B ．26y x =- C ．53y x =- D ．3y x =-- 14．二次函数22(3)1y x =-+-的顶点坐标是（）A ．(31)， B ．(13)-， C ．(3,1)-D ．(3,1)--15．已知A （﹣11,3y ），B （﹣21,2y ），C （1，y 3）是一次函数y ＝b ﹣3x 的图象上三点，则y 1、y 2、y 3的大小关系为（） A ．y 3＜y 1＜y 2B ．y 3＜y 2＜y 1C ．y 1＜y 2＜y 3D ．y 2＜y 1＜y 3二、填空题16．一次函数(27)2y k x =-+中，y 随x 的增大而减小，则k 的取值范围是___________． 17．将直线213y x =-+向上平移3个单位后所得直线解析式为_______．18．已知点(2,)A m 在一次函数53y x =+的图象上，则m 的值是__．19．已知一次函数(1)2y m x m =-+-的图象经过平面直角坐标系中的第一、三、四象限，那么m 的取值范围是______．20．若函数y ＝（m ﹣2）x +|m |﹣2是正比例函数，则m ＝_____．三、解答题21．如图，抛物线y ＝ax 2+3x +c 经过A (﹣1，0)，B (4，0)两点，并且与y 轴交于点C ．(1)求此抛物线的解析式； (2)直线BC 的解析式为；(3)若点M 是第一象限的抛物线上的点，且横坐标为t ，过点M 作x 轴的垂线交BC 于点N ，设MN 的长为h ，求h 与t 之间的函数关系式及h 的最大值；(4)在x 轴的负半轴上是否存在点P ，使以B ，C ，P 三点为顶点的三角形为等腰三角形？如果存在；如果不存在，说明理由．22．如图，抛物线y ＝ax 2+bx +3与x 轴交于A （﹣1，0）、B （3，0）两点，抛物线的对称轴l 与x 轴交于M 点．(1)求抛物线的函数解析式；(2)设点P 是直线l 上的一个动点，当PA +PC 的值最小时，求PA +PC 长；(3)已知点N （0，﹣1），在y 轴上是否存在点Q ，使以M 、N 、Q 为顶点的三角形与△BCM 相似？若存在；若不存在，请说明理由．23．已知二次函数222y x x m =-+-的图象与x 轴有交点，求非负整数m 的值． 24．已知抛物线y ＝12x 2﹣x ﹣32与x 轴交于点A ，点B （点A 在点B 左侧）． (1)求点A ，点B 的坐标；(2)用配方法求该抛物线的顶点C 的坐标，判断△ABC 的形状，并说明理由；(3)在抛物线的对称轴上是否存在点P ，使以点O 、点C 、点P 为顶点的三角形构成等腰三角形？若存在，请直接写出点P 的坐标；若不存在，请说明理由． 25．已知抛物线222y x mx m =--．(1)求证：对任意实数m ，抛物线与x 轴总有交点． (2)若该抛物线与x 轴交于1,0A ，求m 的值．【参考答案】一、单选题 1．B 2．A3．A 4．A 5．B 6．C 7．B 8．B 9．D 10．A 11．A 12．C 13．A 14．D 15．A 二、填空题16．72k < 17．243y x =-+18．1319．2m >20．-2三、解答题21．(1)234y x x =-++ (2)4y x =-+(3)h 与t 之间的函数关系式为：()2404h t t t =-+<<，h 的最大值为4(4)在x 轴的负半轴上存在点()4,0P -或()4P -，使以B ，C ，P 三点为顶点的三角形为等腰三角形，理由见解析【解析】【分析】（1）把A (﹣1，0)，B (4，0) 代入抛物线解析式，即可求解；（2）根据抛物线解析式求出点C 的坐标，再利用待定系数法，即可求解；（3）根据题意可得点()2,34M t t t -++，点(),4N t t -+，从而得到24MN t t =-+，再根据二次函数的性质，即可求解；（4）分三种情况：当PC =BC 时，当PB =BC 时，当PC =PB 时，即可求解． (1)解：∵抛物线y ＝ax 2+3x +c 经过A (﹣1，0)，B (4，0)两点，∴3016340a c a c -+=⎧⎨+⨯+=⎩，解得：14a c =-⎧⎨=⎩， ∴抛物线的解析式为234y x x =-++； (2)解：当0x =时，4y =， ∴点()0,4C ，设直线BC 的解析式为()0y kx b k =+≠，把点B (4，0)，()0,4C 代入得：404k b b +=⎧⎨=⎩，解得：14k b =-⎧⎨=⎩，∴直线BC 的解析式为4y x =-+； (3) 解：如图，∵点M 是第一象限的抛物线上的点，且横坐标为t ，∴点()2,34M t t t -++，∵MN ⊥x 轴， ∴点(),4N t t -+，∴()()223444MN t t t t t =-++--+=-+，∴()()2242404h t t t t =-+=--+<<， ∴当2t =时，h 的值最大，最大值为4； (4)解：在x 轴的负半轴上存在点P ，使以B ，C ，P 三点为顶点的三角形为等腰三角形，理由如下：当PC =BC 时， ∵OC ⊥BP ， ∴OP =OB ，∵点B (4，0)，点P 在x 轴的负半轴上， ∴点()4,0P -；当PB =BC 时， ∵B (4，0)，()0,4C ， ∴OC =4，OB =4，∴BP BC ==∴4OP BP OB =-=， ∵点P 在x 轴的负半轴上，∴点()4P -；当PC =PB 时，点P 位于BC 的垂直平分线上， ∵OB =OC =4，∴点O 位于BC 的垂直平分线上， ∴此时点P 与点O 重合，不合题意，舍去；综上所述，在x 轴的负半轴上存在点()4,0P -或()4P -，使以B ，C ，P 三点为顶点的三角形为等腰三角形．【点睛】本题主要考查了求二次函数和一次函数的解析式，二次函数的图象和性质，等腰三角形的性质，熟练掌握用待定系数法求二次函数和一次函数的解析式，二次函数的图象和性质，等腰三角形的性质是解题的关键． 22．(1)y ＝﹣x 2+2x +3(2)PA +PC 的长为(3)存在，点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭，理由见解析【解析】【分析】（1）当x ＝0时，y ＝3，可得C （0，3）．再设设抛物线的解析式为y ＝a （x +1）（x ﹣3）（a ≠0），利用待定系数法，即可求解；（2）连接PA 、PB 、PC ，根据轴对称性可得PA ＝PB ．从而得到PA +PC ＝PC +PB ．进而得到当点P 在线段BC 上时，PC +AP 有最小值．即可求解；（3）先求出抛物线的对称轴，可得点()1,0M ，再由点N （0，﹣1），B （3，0），C （0，3）．可得2,45,45MN BC BM CBM MNO ===∠=︒∠=︒，可得∠CBM =∠MNO ，然后分三种情况讨论，即可求解． (1)解：把x ＝0代入得：y ＝3， ∴C （0，3）．设抛物线的解析式为y ＝a （x +1）（x ﹣3）（a ≠0），将点C 的坐标代入上式得：3＝﹣3a ，解得：a ＝﹣1．∴抛物线的解析式为y ＝-（x +1）（x -3）=﹣x 2+2x +3． (2)解：如图，连接PA 、PB 、PC ，∵点A 与点B 关于直线l 对称，点P 在直线l 上， ∴PA ＝PB ． ∴PA +PC ＝PC +PB ． ∵两点之间线段最短，∴当点P 在线段BC 上时，PC +AP 有最小值． ∵OC ＝3，OB ＝3， ∴BC ＝32∴PA +PC 的最小值＝32 (3)解：存在，理由：抛物线的对称轴为直线x ＝﹣2ba＝1． ∵抛物线的对称轴l 与x 轴交于M 点． ∴点()1,0M ，∵点N （0，﹣1），B （3，0），C （0，3）． ∴OM =ON =1，OB =OC =3，∴2,32,2,45,45MN BC BM CBM MNO ===∠=︒∠=︒， ∴∠CBM =∠MNO ，当点Q 在点N 下方时，∠MNQ =135°，不符合题意， ∴点Q 在点N 上方，设点Q 的坐标为（0，n ）．则QN =n +1， ∵以M 、N 、Q 为顶点的三角形与△BCM 相似， ∴∠QMN =∠CMB 或∠MQN =∠CMB ，当1Q MN CMB ∠=∠时，1Q MNCMB ，如图（2），∴1Q N MNBC BM=， ∴12232n +=，解得：2n =， ∴点()10,2Q ；当2MQ N CMB ∠=∠时，2MQ NCMB ，如图（3），∴2Q N MN MB BC=， ∴12232n +=13n =-，∴点210,3Q ⎛⎫- ⎪⎝⎭，综上所述，点Q 的坐标为()0,2或10,3⎛⎫- ⎪⎝⎭．【点睛】本题主要考查了二次函数的综合题，相似三角形的判定和性质，两点之间，线段最短，待定系数法求二次函数解析式等知识，熟练掌握二次函数的图象和性质，相似三角形的判定和性质，利用数形结合思想解答是解题的关键． 23．0或1或2或3 【解析】【分析】根据二次函数y =x 2-2x +m -2的图象与x 轴有交点，根据Δ≥0列出m 的不等式，求出m 的取值范围即可．【详解】解：∵二次函数y =x 2-2x +m -2的图象与x 轴有交点， ∴Δ=4-4（m -2）≥0， ∴m ≤3， ∵m 为非负整数， ∴m =0或1或2或3．【点睛】本题主要考查了抛物线与x 轴交点的知识，解答本题的关键是根据二次函数y =x 2-2x +m -2的图象与x 轴有交点列出m 的不等式，此题难度不大． 24．(1)A （-1，0），B （3，0）(2)点C 的坐标为（1，-2），ABC 为等腰直角三角形，理由见解析(3)点P 的坐标为（1，2），2)，(1,2)或3(1,)4-【解析】【分析】（1）把0y =代入到21322y x x =--得，213022x x --=，解得13x =，21x =-，又因为点A 在点B 的左侧，即可得；（2）21322y x x =--配方得21(1)22y x =--，即可得点C 的坐标为（1，-2），根据点A ，B ，C 的坐标得4AB =，AC ，BC =AC =BC ，又因为2224+=，所以222AC BC AB +=，即可得90ACB ∠=︒，从而得出ACB △是等腰直角三角形；（3）当点P 与点C 关于x 轴对称时，OC =OP ，OCP △为等腰三角形，即可得点P 的坐标（1，2），当CO CP =时，CP =，即可得点P 的坐标为2)或(1,2)，当OP CP =时，点P 在OC 的垂直平分线上，设点(1,)P a ，点P 交x 轴于点D ，在Rt ODP 中，根据勾股定理得，222(2)1a a +=+，解得34a =-，即可得点P 的坐标为3(1,)4-，综上，即可得． (1)解：把0y =代入到21322y x x =--得， 213022x x --= 2230x x --= (3)(1)0x x -+=解得13x =，21x =-， ∵点A 在点B 的左侧，∴A （-1，0），B （3，0）． (2) 解：21322y x x =-- =21(3)2x x -- =21(1)22x x -+- =21(1)22x --∴点C 的坐标为（1，-2），ABC 为等腰直角三角形，理由如下：∵A （-1，0），B （3，0），C （1，-2）， ∴3(1)4AB =--=，22(11)(02)8AC =----=， 22(31)(02)8BC =---=，∴AC =BC ， ∵222(8)(8)4+=， ∴222AC BC AB +=， ∴90ACB ∠=︒，∴ACB △是等腰直角三角形． (3)解：当点P 与点C 关于x 轴对称时，OC =OP ，OCP △为等腰三角形， ∴点P 的坐标为（1，2）；当CO CP =时，22(10)(20)5CP =-+-=， ∴点P 的坐标为(1,52)-或(1,52)--；当OP CP =时，点P 在OC 的垂直平分线上，设点(1,)P a ，如图所示，点P 交x 轴于点D ，在Rt ODP 中，根据勾股定理得，222(2)1a a +=+，22441a a a ++=+34a =- ∴点P 的坐标为3(1,)4-；综上，点P 的坐标为（1，2），2)，(1,2)或3(1,)4-．【点睛】本题考查了二次函数与三角形的综合，解题的关键是掌握二次函数的性质，等腰三角形的判定与性质．25．(1)见解析(2)122,1m m =-=【解析】【分析】（1）令0y =，得到关于x 的一元二次方程，根据一元二次方程根的判别式判断即可；（2）令1x =，0y =，解一元二次方程即可求得m 的值(1)令0y =，则有2220x mx m --=222890m m m ∆=+=≥即，对于任意实数方程2220x mx m --=总有两个实数根，∴对任意实数m ，抛物线与x 轴总有交点．(2)解：∵抛物线222y x mx m =--与x 轴交于1,0A ，∴202m m =--解得122,1m m =-=【点睛】本题考查了二次函数与坐标轴交点问题，掌握一元二次方程根的判别式以及解一元二次方程是解题的关键．。

初中函数练习题及答案

初中函数练习题及答案初中函数练习题及答案导语：函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。

以下是初中函数练习题及答案的内容，仅供参考学习。

初中函数练习题及答案一、选一选，慧眼识金（每小题3分，共２４分）1．下列函数关系式：①,y=-2x ② y=-2/x , ③y=-2x2, ④y=2 , ⑤y=2x-1.其中是一次函数的是（）（Ａ）①⑤ （Ｂ）①④⑤（Ｃ）②⑤ （Ｄ）②④⑤2．一个正比例函数的图象经过点（2，-1），那么这个正比例函数的表达式为（）（Ａ）y=2x （Ｂ）y=-2x（Ｃ）xy21 （Ｄ）xy2 1３．函数y=-3x-6中，当自变量x增加１时，函数值y就（）（Ａ）增加３（Ｂ）减少３（Ｃ）增加１（Ｄ）减少１４.在同一直角坐标系中，对于函数：①y=-x-1 ②y=x+1 ③y=-x+1 ④y=-2(x+1)的图象，下列说法正确的是（）（Ａ）通过点（－１，０）的是①和③ （Ｂ）交点在y轴上的是②和④（Ｃ）互相平行的是①和③ （Ｄ）关于x轴平行的是②和③５．一次函数y=-3x+6的图象不经过（）（Ａ）第一象限（Ｂ）第二象限（Ｃ）第三象限（Ｄ）第四象限６．已知一次函数y=ax+4与y＝bx-2的图象在x轴上交于同一点，则a b 的值为（）（Ａ）４（Ｂ）－２（Ｃ）-2/1 （Ｄ）2/1７．小明、小强两人进行百米赛跑，小明比小强跑得快，如果两人同时跑，小明肯定赢，现在小明让小强先跑若干米，图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系，根据图象判断：小明的速度比小强的速度每秒快A、1米B、1.5米C、2米D、2.5米８．如图中的图象（折线ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s（千米）和行驶时间t（小时）之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为3 80 千米/时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有（）A、1个B、2个C、3个D、4个二、填一填,画龙点睛(每小题 4分,共32分)1．某种储蓄的月利率为0.15%，现存入1000元，则本息和y （元）与所存月数x之间的函数关系式是 .2. 一次函数y= -2x+4的图象与x轴交点坐标是，与y轴交点坐标是与坐标轴围成的三角形面积是。

初中函数专题试题及答案

初中函数专题试题及答案一、选择题（每题3分，共30分）1. 下列函数中，哪一个是一次函数？A. $ y = x^2 $B. $ y = 2x + 3 $C. $ y = \frac{1}{x} $D. $ y = x^3 - 2x $答案：B2. 函数 $ y = 3x - 5 $ 的图象与x轴的交点坐标是：A. $ (0, -5) $B. $ (5, 0) $C. $ (-5, 0) $D. $ (0, 5) $答案：C3. 如果函数 $ y = 2x + 1 $ 在 $ x = 2 $ 时的值为5，那么$ x = 1 $ 时的值是：A. 3B. 4C. 2D. 1答案：A4. 函数 $ y = -\frac{1}{2}x + 3 $ 的斜率是：A. $ \frac{1}{2} $B. $ -\frac{1}{2} $C. $ \frac{3}{2} $D. $ -3 $答案：B5. 函数 $ y = 4x^2 $ 的顶点坐标是：A. $ (0, 0) $B. $ (0, 4) $C. $ (2, 0) $D. $ (0, -4) $答案：A6. 函数 $ y = x^2 - 6x + 9 $ 可以写成完全平方的形式：A. $ (x - 3)^2 $B. $ (x + 3)^2 $C. $ (x - 3)^2 + 3 $D. $ (x + 3)^2 - 3 $答案：A7. 函数 $ y = 2x^2 - 8x + 7 $ 的最小值是：A. 1B. 3C. 7D. 无法确定答案：A8. 函数 $ y = \frac{1}{x} $ 的图象是：A. 一条直线B. 两条直线C. 一个双曲线D. 一个抛物线答案：C9. 函数 $ y = 3x^2 + 2x - 5 $ 的对称轴是：A. $ x = -\frac{2}{3} $B. $ x = \frac{2}{3} $C. $ x = -1 $D. $ x = 1 $答案：B10. 函数 $ y = 2x + 3 $ 和 $ y = -x + 1 $ 的交点坐标是：A. $ (-2, -1) $B. $ (2, 5) $C. $ (-1, 1) $D. $ (1, 3) $答案：C二、填空题（每题4分，共20分）11. 函数 $ y = 2x + 1 $ 在 $ x = -1 $ 时的值为 _______。

初中数学函数专题练习及答案

初中数学函数专题练习及答案函数专题讲稿二次函数：1.抛物线 $y=- (x-1)^2+3$ 的顶点坐标为 $(1,3)$。

2.抛物线 $y=x^2-2x+1$ 的顶点坐标是 $(1,0)$。

3.抛物线$y=2x^2+6x+c$ 与$x$ 轴的一个交点为$(1,0)$，则这个抛物线的顶点坐标是 $(-1,-2)$。

4.二次函数 $y=(x-1)^2+2$ 的最小值是 $2$。

5.已知二次函数 $y=-x^2+2x+c$ 的对称轴和 $x$ 轴相交于点 $(1,0)$，则 $m$ 的值为 $1$。

6.抛物线 $y=x^2-2x+3$ 的对称轴是直线 $x=1$。

7.将抛物 $y=-(x-1)$ 向左平移 $1$ 个单位后，得到的抛物线的解析式是 $y=-x^2$。

8.把抛物线 $y=x^2+bx+c$ 向右平移 $3$ 个单位，再向下平移 $2$ 个单位，所得图像的解析式是 $y=x^2-3x+5$，则有$b=3$，$c=4$。

9.已知抛物线 $y=x^2+(m-1)x+(m-2)$ 与 $x$ 轴相交于 $A$，且线段 $AB=2$，则 $m$ 的值为 $2$。

10.一个满足条件的二次函数解析式是 $y=-x^2$。

11.若抛物线 $y=x^2+2x+a$ 的顶点在 $x$ 轴的下方，则$a$ 的取值范围是 $a<1$。

12.已知二次函数 $y=ax^2+bx+c$，且 $a0$，则一定有$b^2-4ac<0$。

利用图像：1.若直线 $y=m$（$m$ 为常数）与函数 $y=4$ 的图像恒有三个不同的交点，则常数 $m$ 的取值范围是 $m>4$。

2.阴影部分的面积相等的是 $①②$。

3.若 $A(-\frac{13}{4},1)$，$B(-1,y_2)$，$C(\frac{5}{3},y_3)$ 为二次函数 $y=-x^2-4x+5$ 的图象上的三点，则 $y_1>y_2>y_3$。

初三中考数学函数综合题含答案

初三中考数学函数综合题含答案一、单选题1．已知点A （1，y 1），B （2，y 2）在抛物线y =（x +1）2+2上，则下列结论正确的是（）． A ．122y y >> B ．212y y >> C ．122y y >>D ．212y y >>2．抛物线y ＝14（x ﹣6）2+3的顶点坐标是（）A ．（6，﹣3）B ．（6，3）C ．（﹣6，3）D ．（﹣6，﹣3） 3．抛物线y =2（x -1）2-3的顶点坐标是（） A ．()1,3-- B ．()1,3- C ．()1,3- D ．()1,3 4．一次函数y ＝－2x ＋5的图像不经过的象限是（）A ．一B ．二C ．三D ．四 5．将函数y ＝2x 的图象向上平移4个单位后，下列各点在平移后的图象上的是（） A ．()1,5 B ．()0,4 C ．()1,3- D ．()2,3- 6．在直角坐标系的x 轴的负半轴上，则点P 坐标为（）A ．()4,0-B ．()0,4C ．()0,3-D ．()1,0 7．直线7y x =--一定不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限8．下列各点中，在反比例函数2y x=-图象上的是-（）A ．(21)，B ．233⎛⎫⎪⎝⎭， C ．(21)--， D ．(12)-，9．已知点()11,A x y ，()22,B x y 在直线()0y kx b k =+≠上，当12x x <时，12y y >，且0kb <，则直线()0y kx b k =+≠在平面直角坐标系中的图象大致是（）A ．B ．C ．D ．10．下列一次函数中，y 随x 的增大而减小的是（） A ．y ＝x ﹣3 B ．y ＝1﹣x C ．y ＝2x D ．y ＝3x +2 11．下列二次函数中，对称轴是直线1x =的是（）A ．21y x =+B ．()221y x =+C ．()21y x =-+D ．()231y x =--12．反比例函数y ＝2x的图象位于（）A ．第一、三象限B ．第二、三象限C ．第一、二象限D ．第二、四象限13．如图，△ABC 中，点B ，C 是x 轴上的点，且A （3，2），以原点O 为位似中心，作△ABC 的位似图形△A ′B ′C ′，且△ABC 与A ′B ′C ′的相似比是1：2，则点A ′的坐标是（）A ．（﹣6，﹣4）B ．（﹣1.5，﹣1）C ．（1.5，1）或（﹣1.5，﹣1）D ．（6，4）或（﹣6，﹣4）14．已知点P （a ，a ﹣1）在平面直角坐标系的第四象限，则a 的取值范围在数轴上可表示为（） A ．B ．C ．D ．15．要得到抛物线()2321y x =-++可以将抛物线232y x =-+（） A ．先向右平移2个单位，再向上平移1个单位 B ．先向右平移2个单位，再向下平移1个单位C ．先向左平移2个单位，再向上平移1个单位D ．先向左平移2个单位，再向下平移1个单位二、填空题16．已知点(),P m n 在一次函数1y x =+的图象上，则n m -=______．17．已知某函数图像过点（－1，1），写出一个符合条件的函数表达式：______．18．将一次函数123=+y x 向上平移5个单位长度后得到直线AB ，则平移后直线AB 对应的函数表达式为______．19．将抛物线22(3)y x m =-+向右平移3个单位，再向上平移1个单位后恰好经过点(2,3)，则m 值是 __．20．若抛物线y =x 2+bx +经过点A （0，5），B （4，5），则其对称轴是直线______三、解答题21．已知抛物线y ＝－（x －m ）2＋1与x 轴的交点为A ，B （B 在A 的右边），与y 轴的交点为C ．(1)写出m ＝1时与抛物线有关的三个正确结论．(2)当点B 在原点的右边，点C 在原点的下方时，是否存在△BOC 为等腰三角形的情形？若存在，求出m 的值；若不存在，请说明理由． (3)请你提出两个对任意的m 值都能成立的正确命题．22．在平面直角坐标系xOy 中，点()11,A x y ，()22,B x y 在抛物线()2210y ax ax a =-+>上，其中12x x < (1)求抛物线的对称轴；(2)若122x x a +=-，比较1y 与2y 的大小关系，并说明理由．23．如图，在平面直角坐标系中，二次函数243y ax x =+-图象的顶点是A ，与x 轴交于B ，C 两点，与y 轴交于点D ．点B 的坐标是()1,0．(1)求A ，C 两点的坐标，并根据图象直接写出当0y >时x 的取值范围；(2)将图象向上平移m 个单位后，二次函数图象与x 轴交于E ，F 两点，若6EF =，求m 的值．24．一抛物线以()1,9-为顶点，且经过x 轴上一点()4,0-，求该抛物线解析式及抛物线与y 轴交点坐标．25．已知抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)，点P 为抛物线上的一点． (1)求此抛物线的解析式；(2)若点P 的横坐标为2，则点P 到x 轴的距离为．【参考答案】一、单选题 1．D 2．B 3．C 4．C 5．B 6．A 7．A 8．D 9．C 10．B 11．D 12．A 13．D 14．C 15．D 二、填空题 16．117．y ＝-x （答案不唯一） 18．y =13x +719．-3020．2x = 三、解答题21．(1)抛物线的对称轴为直线x =1，抛物线与x 轴的两个交点为（0，0），（2，0），抛物线开口向下 (2)存在，2(3)无论m 为何值，函数的始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点【解析】【分析】（1）当m =1时，y =-（x -1）2+1，根据()2y a x h k =-+的性质写出三个结论即可；（2）求得C （0，1-m 2），根据点B 在原点的右边，点C 在原点的下方，可得m ＞1，根据等腰三角形的性质可得1+m =m 2-1，解方程求解即可；（3）根据()2y a x h k =-+的性质，可知无论m 为何值，函数的始终有最大值1；无论m为何值，函数始终与x 轴有两个不同的交点． (1)解：当m =1时，y =-（x -1）2+1， ∴抛物线的对称轴为直线x =1，令0y =，-（x -1）2+1=0，解得120,2x x ==，抛物线与x 轴的两个交点为（0，0），（2，0），抛物线开口向下； (2)存在，理由如下：令x =0，则y =1-m 2， ∴C （0，1-m 2），令y =0，则x =1+m 或x =m -1， ∴B （1+m ，0），∵点B 在原点的右边，点C 在原点的下方， ∴1+m ＞0，1-m 2＜0， ∴m ＞1，∵△BOC 为等腰三角形， ∴1+m =m 2-1，解得m =2或m =-1（舍）， ∴m =2； (3)无论m 为何值，函数始终有最大值1；无论m 为何值，函数始终与x 轴有两个不同的交点．【点睛】本题考查了()2y a x h k =-+的性质，等腰三角形的性质，解一元二次方程，二次函数与坐标轴交点问题，掌握()2y a x h k =-+的性质是解题的关键． 22．(1)直线1x = (2)12y y >，见解析【解析】【分析】（1）将解析式整理成顶点式，直接写出对称轴；（2）方法一：利用作差法，将12y y -表示出来，再进行判断正负，据此判断大小即可；方法二：判断12,y y 距离对称轴的大小，根据函数增减性判断． (1)解：∵()222111y ax ax a x a =-+=--+， ∴抛物线的对称轴为直线1x = (2)方法一：()()221211222121y y ax ax ax ax -=-+--+，()()22122122ax ax ax ax =-+-，()()12122a x x x x =-+-， ()212a x x =--，∵0a >，12x x <， ∴120y y ->，即12y y >，方法二：∵0a >，122x x a +=-， ∴122x x +<， ∴1212x x +<，又∵抛物线对称轴是直线1x =，开口向上，且12x x <， ∴1211x x ->-， ∴12y y >．【点睛】本题主要考查二次函数中系数的运用，以及比较函数值的大小，熟练掌握二次函数的基础运算是解题的关键．23．(1)(2,1)A ，(3,0)C ，当0y >时，13x <<． (2)8m = 【解析】【分析】（1）利用待定系数法求出a ，再求出点C 的坐标即可解决问题．（2）由题意得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，由12|6|x x -=可得出答案．(1)解：把(1,0)B 代入243y ax x =+-，得043a =+-，解得1a =-，2243(2)1y x x x ∴=-+-=--+，)1(2,A ∴，对称轴为直线2x =，B ，C 关于2x =对称，(3,0)C ∴，∴当0y >时，13x <<．(2)解：抛物线向上平移m 个单位，可得抛物线的解析式为243y x x m =-+-+，设二次函数图象与x 轴交于1(E x ，0)，2(F x ，0)两点，则124x x +=，123x x m =-，12||6x x ∴-=，212()36x x ∴-=，21212()436x x x x ∴+-=，164(3)36m ∴-⨯-=，8m ∴=．【点睛】本题考查了抛物线与x 轴的交点，二次函数的性质和二次函数图象上点的坐标特征，解决问题的关键是能够把二次函数的一般形式化为顶点式． 24．y =﹣x 2-2x ＋8；抛物线与y 轴交点为()0,8 【解析】【分析】知道顶点和抛物线上一点，可以用抛物线的顶点式求答；【详解】解：设抛物线解析式为()2y a x h k =-+，依题意1h =-，9k =，将()4,0-代入()219y a x =++中，得099a =+，解得1a =-，∴抛物线解析式为()219y x =-++，即y =﹣x 2-2x ＋8；令0x =，则8y =，∴抛物线与y 轴交点为()0,8．【点睛】本题考查待定系数法求二次函数的解析式；在知道顶点坐标的时候，利用顶点式求二次函数解析式十分方便． 25．(1)223y x x =-- (2)3 【解析】【分析】（1）把点A (0，﹣3)，代入抛物线解析式，即可求解；（2）根据抛物线()214y x =--的对称轴为直线1x =，可得点P 和点A (0，﹣3)关于直线1x =对称，从而得到点的纵坐标为-3，即可求解．(1)解：∵抛物线y ＝（x ﹣1）2+k 与y 轴相交于点A (0，﹣3)， ∴()2301k -=-+，解得：4k =-，∴此抛物线的解析式为()221423y x x x =--=--； (2)解：∵抛物线()214y x =--的对称轴为直线1x =， ∴点P 和点A (0，﹣3)关于直线1x =对称， ∴点的纵坐标为-3， ∴点P 到x 轴的距离为3．【点睛】本题主要考查了求二次函数的解析式，利用抛物线的对称性求函数值，熟练掌握利用待定系数法求函数解析式的步骤是解题的关键．。

中考数学总复习《函数》专项测试卷-附参考答案

中考数学总复习《函数》专项测试卷-附参考答案一、单选题(共12题；共24分)1．如图所示，抛物线L：y=ax2+bx+c（a<0）的对称轴为x=5，且与x轴的左交点为（1,0）则下列说法正确的有（）①C（9,0）；②b+c＞-10；③y的最大值为-16a；④若该抛物线与直线y=8有公共交点，则a的取值范围是a≤ 1 2．A．①②③④B．①②③C．①③④D．①④2．若y+3与x-2成正比例，则y是x的()A．正比例函数B．不存在函数关系C．一次函数D．以上都有可能3．关于函数y＝2x﹣1，下列结论成立的是（）A．当x＜0时，则y＜0B．当x＞0时，则y＞0C．图象必经过点（0，1）D．图象不经过第三象限4．关于一次函数y＝x＋2，下列说法正确的是（）A．y随x的增大而减小B．经过第一、三、四象限C．与y轴交于（0，2）D．与x轴交于（2，0）5．点P(3，y1)、Q (4，y2)是二次函数y=x2−4x+5的图象上两点，则y1与y2的大小关系为（）A．y1>y2B．y1<y2C．y1=y2D．无法确定6．快、慢两车分别从甲、乙两地同时出发，相向匀速行驶，两车在途中相遇时都停留了一段时间，然后分别按原速度原方向匀速行驶，快车到达乙地后休息半小时后，再以另一速度原路匀速返回甲地（掉头的时间忽略不计），慢车到达甲地以后即停在甲地等待快车．如图所示为快、慢两车间的距离y （千米）与快车的行驶时间x（小时）之间的函数图象．则下列说法：①两车在途中相遇时都停留了1小时；②快车从甲地去乙地时每小时比慢车多行驶40km；③快车从乙地返回甲地的速度为120km/h；④当慢车到达甲地的时候，快车与甲地的距离为400km．其中正确的有（）A．4B．3C．2D．17．如图，动点A在抛物线y=−x2+2x+3(0≤x≤3)上运动，直线l经过点（0,6），且与y轴垂直，过点A做AC⊥ l于点C，以AC为对角线作矩形ABCD，则另一对角线BD的取值范围正确的是（）A．2≤BD≤3B．3≤BD≤6C．1≤BD≤6D．2≤BD≤68．如图，在平面直角坐标系中，函数y=kx,y=−2x的图像交于A,B两点，过A作y轴的垂线，交函数y=3x的图像于点C，连接BC，则ΔABC的面积为（）A．2B．3C．5D．69．如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点是A，对称轴是直线x＝1，且抛物线与x轴的一个交点为B（4，0）；直线AB的解析式为y2＝mx+n（m≠0）．下列结论：①2a+b＝0；②abc＞0；③方程ax2+bx+c＝mx+n有两个不相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，则则y1＞y2，其中正确的是（）A．①②B．①③⑤C．①④D．①④⑤10．如图，矩形ABCD中，AB=3，BC=4，点P从A点出发，按A→B→C的方向在AB和BC上移动，记PA=x，点D到直线PA的距离为y，则y关于x的函数大致图象是（）A．B．C．D．11．如图，在平面直角坐标系中，ΔA1A2A3，ΔA3A4A5，ΔA5A6A7，…都是等边三角形，其边长依次为2，4，6，…，其中点A1的坐标为(2，0)，点A2的坐标为(1，−√3)，点A3的坐标为(0，0)，点A4的坐标为(2，2√3)，…，按此规律排下去，则点A2020的坐标为()A．(1，−1009√3)B．(1，−1010√3)C．(2，1009√3)D．(2，1010√3)12．如图，二次函数y=-x2+bx+c 图象上有三点A(-1，y1 )、B(1，y2) 、C（2，y3），则y1，y2，y3大小关系为（）A．y1＜y3＜y2B．y3＜y1＜y2C．y1＜y2＜y3D．y2＜y1＜y3二、填空题(共6题；共6分)13．点P(1,1)向左平移两个单位后恰好位于双曲线y=k x上，则k=．14．将二次函数y=−x2+3的图像向下平移5个单位长度，所得图像对应的函数表达式为．15．如图，已知A1（1，0），A2（1，1），A3（﹣1，1），A4（﹣1，﹣1），A5（2，﹣1）…，则点A2021的坐标为.16．请写出一个二次函数，使它的图象同时满足下列两个条件：①开口向下，②与y轴的交点是（0，1），你写出的函数表达式是．17．若点P(n，1)，Q(n+6，3)在正比例函数图象上，请写出正比例函数的表达式. 18．在−3，−2，−1，4，5五个数中随机选一个数作为一次函数y=kx−3中k的值，则一次函数y=kx−3中y随x的增大而减小的概率是.三、综合题(共6题；共67分)19．3−√(−3)2+|√3−2|（1）计算：(−1)2021+√16+√−27（2）如图所示的是某学校的平面示意图，已知旗杆的位置是(−1，2)，实验室的位置是(2，3)．①根据所给条件建立适当的平面直角坐标系，并用坐标表示食堂，宿舍楼和大门的位置．②已知办公楼的位置是(−2，1)，教学楼的位置是(3，1)，在①中所画的图中标出办公楼和教学楼的位置．20．汽车出发1小时后油箱里有油40L，继续行驶若干小时后，在加油站加油若干升（加油时间忽略不计）．图象表示出发1小时后，油箱中剩余测量（y）与行驶时间t（h）之间的关系．（1）汽车行驶h后加油，中途加油L；（2）求加油前油箱剩余量y与行驶时间t的函数关系式；（3）若加油前后汽车都以80km/h匀速行驶，则汽车加油后最多能行驶多远？21．凤凰单丛（枞）茶，是潮汕的名茶，已有九百余年的历史．潮汕人将单丛茶按香型分为黄枝香、芝兰香、桃仁香、玉桂香、通天香、鸭屎香等多种．清明采茶季后，某茶叶店准备购买通天香和鸭屎香两种单丛茶进行销售，已知若购买4千克通天香单丛和3千克鸭屎香单丛需要2500元，购买2千克通天香单丛和5千克鸭屎香单丛需要2300元．（1）求通天香、鸭屎香两种茶叶的单价分别为多少元？（2）茶叶专卖店计划购买通天香、鸭屎香两种单丛茶共80千克，总费用不多于26000元，并且要求通天香茶叶数量不能低于10千克，那么应如何安排购买方案才能使总费用最少，最少费用应为多少元？22．为落实“双减”政策，丰富课后服务的内容，某学校计划到甲、乙两个体育专卖店购买一批新的体育用品，两个商店的优惠活动如下：甲：所有商品按原价8.5折出售；乙：一次购买商品总额不超过300元的按原价付费，超过300元的部分打7折．设需要购买体育用品的原价总额为x元，去甲商店购买实付y甲元，去乙商店购买实付y乙元，其函数图象如图所示.（1）分别求y甲，y乙关于x的函数关系式；（2）两图象交于点A，求点A坐标；（3）请根据函数图象，直接写出选择去哪个体育专卖店购买体育用品更合算．23．直线y=kx+b经过A（0，-3）)和B（-3，0）两点．（1）求这个一次函数的解析式；（2）画出图象，并根据图象说明不等式kx+b<0的解集．24．“龟兔首次赛跑”之后，输了比赛的兔子没有气馁，总结反思后，和乌龟约定再赛一场，下面的函数图象表示“龟兔再次赛跑”时，则乌龟所走路程y1（米）和兔子所走的路程y2（米）分别与乌龟从起点出发所用的时间x（分）之间的函数图象，根据图象解答下列问题：（1）“龟兔再次赛跑”的路程是米，兔子比乌龟晚走了分钟，乌龟在途中休息了分钟，“龟兔再次赛跑”获胜的是．（2）分别求出乌龟在途中休息前和休息后所走的路程y1关于时间x的函数解析式，并写出自变量x的取值范围．（3）乌龟和兔子在距离起点米处相遇．参考答案1．【答案】B 2．【答案】C 3．【答案】A 4．【答案】C 5．【答案】B 6．【答案】B 7．【答案】D 8．【答案】C 9．【答案】B 10．【答案】C 11．【答案】D 12．【答案】A 13．【答案】-114．【答案】y =−x 2−2 15．【答案】（506，﹣505）16．【答案】y =−x 2+x +1 （不唯一） 17．【答案】y =13x 18．【答案】3519．【答案】（1）解：原式=−1+4−3−3+2−√3=−1−√3（2）解：①根据题意，建立如图所示的平面直角坐标系，如下：∴食堂(−4，4)，宿舍楼（-5，1），大门(1，−1) ②办公楼和教学楼的位置如图所示．20．【答案】（1）4；35（2）解：设y 与x 的函数关系式为y ＝kt+b 把（1，40）和（4，10）代入得{k +b =404k +b =10解得 {k =−10b =50∴加油前油箱剩余油量y 与行驶时间t 的函数关系式y ＝﹣10t+50（3）解：由图象知，汽车加油前行驶了3小时，则用油40﹣10＝30（L ） ∴汽车行驶1小时耗油量为 303＝10（L/h ）加油后邮箱中剩余油量45L ，可以行驶 4510 ×80＝360（km ）．∴汽车加油后最多能行驶360km ．21．【答案】（1）解：设通天香茶叶每千克为x 元，鸭屎香茶叶每千克为y 元，根据题意，得{4x +3y =25002x +5y =2300解得{x =400y =300∴通天香茶叶每千克为400元，鸭屎香茶叶每千克为300元．（2）解：设购买通天香茶叶m 千克，鸭屎香茶叶（80－m ）千克，总费用w 元根据题意，得400m +300(80−m)≤26000 解得m ≤20 ∵m ≥10∴m 的取值范围是：10≤m ≤20总费用w =400m +300(80−m)=100m +24000 ∵100>0∴w 随着m 的增大而增大∴当m ＝10时，则w 最少，w 最少＝1000＋24000＝25000（元）∴通天香茶叶购进10千克，鸭屎香茶叶购进70千克，总费用最少为25000元．22．【答案】（1）解：由题意可得，y 甲=0.85x ；乙商店：当0≤x≤300时，则y 乙与x 的函数关系式为y 乙=x ；当x ＞300时，则y 乙=300+（x-300）×0.7=0.7x+90 由上可得，y 乙与x 的函数关系式为y 乙={x(0≤x ≤300)0.7x +90(x ＞300)（2）解：由{y 甲＝0.85xy 乙＝0.7x +90，解得{x ＝600y 乙＝510点A 的坐标为（600，510）；（3）解：由点A 的意义，当买的体育商品标价为600元时，则甲、乙商店优惠后所需费用相同，都是510元结合图象可知当x ＜600时，则选择甲商店更合算；当x=600时，则两家商店所需费用相同；当x ＞600时，则选择乙商店更合算．23．【答案】（1）解：将A(0，−3)，B(−3，0)代入y =kx +b 得{b =−3−3k +b =0解得：k =−1，b =−3∴y =−x −3一次函数的解析式为：y =−x −3．（2）解：作图如下：由图象可知：直线从左往右逐渐下降，即y 随x 的增大而减小当x =−3时∴kx +b <0的解集为：x >−3．24．【答案】（1）1000；40；10；兔子（2）解：设乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1＝kx ∴600＝30k ，解得k ＝20∴乌龟在途中休息前所走的路程y 1关于时间x 的函数解析式为y 1＝20x （0≤x≤30）设乌龟在途中休息后所走的路程y 1关于时间x 的函数解析式为y 1＝k′x+b∴{40k ′+b =60060k ′+b =1000，解得{k ′=20b =−200∴乌龟在途中休息后所走的路程y1关于时间x的函数解析式为y1＝20x﹣200（40≤x≤60）；（3）750第11页共11。

初中数学二次函数综合题及答案(经典题型)印.pdf

二次函数试题
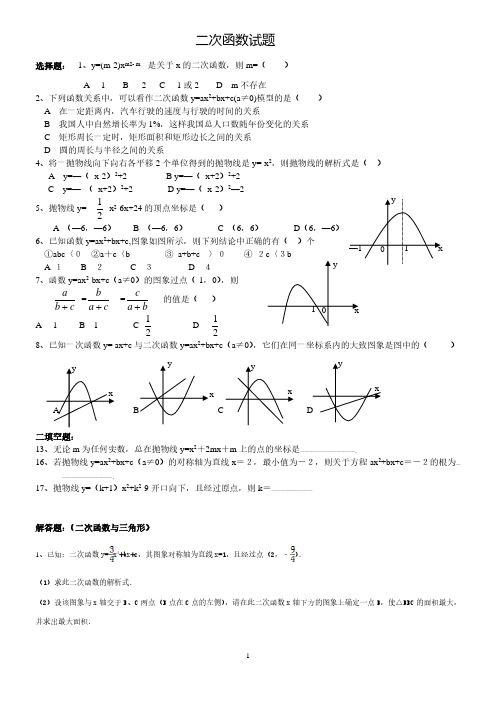
选择题： 1、y=(m-2)xm2- m 是关于 x 的二次函数，则 m=（）
A -1 B 2 C -1 或 2 D m 不存在
2、下列函数关系中，可以看作二次函数 y=ax2+bx+c(a≠0)模型的是（）
A 在一定距离内，汽车行驶的速度与行驶的时间的关系
B 我国人中自然增长率为 1%，这样我国总人口数随年份变化的关系
a
b
=
b+c a+c
A -1 B 1
ቤተ መጻሕፍቲ ባይዱ
c
=
a+b 1
C
2
的值是（）
1
D-
2
-1 0
x
8、已知一次函数 y= ax+c 与二次函数 y=ax2+bx+c（a≠0），它们在同一坐标系内的大致图象是图中的（
x ）
y
y
y
y
x
A
B
x
x
x
C
D
二填空题： 13、无论 m 为任何实数，总在抛物线 y=x2＋2mx＋m 上的点的坐标是————————————。 16、若抛物线 y=ax2+bx+c（a≠0）的对称轴为直线 x＝２，最小值为－２，则关于方程 ax2+bx+c＝－２的根为—
且交点 M 始终位于抛物线上 A、C 两点之间时，试探究：当 n 为何值时，四边形 AMCN 的面积取得最大值，并求出这个最大
值．
y
y
l:x＝n
M
A
A
O
B
D
C x
O
B
C
N
x
D
6、如图所示，在平面直角坐标系中，四边形 ABCD 是直角梯形，BC∥AD，∠BAD=90°，BC 与 y 轴相交于点 M，且 M 是 BC

9年级学生函数试卷加答案【含答案】

9年级学生函数试卷加答案【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列函数中，哪个函数是增函数？A. y = -2x + 3B. y = x^2C. y = 1/xD. y = -x^32. 如果函数f(x) = x^3 3x + 2，那么f(-1)的值是？A. -2B. 0C. 2D. 43. 下列哪个函数是奇函数？A. y = x^2B. y = x^3C. y = |x|D. y = sin(x)4. 函数y = 2^x的图像是？A. 上升的直线B. 下降的直线C. 上升的曲线D. 下降的曲线5. 如果函数f(x) = x^2 + 2x + 1，那么它的顶点坐标是？A. (-1, 0)B. (-1, 1)C. (1, 0)D. (1, 1)二、判断题（每题1分，共5分）1. 所有的线性函数都是一次函数。

（）2. 函数y = x^3在x = 0处有极值。

（）3. 偶函数的图像关于y轴对称。

（）4. 如果函数f(x)在区间(a, b)上单调递增，那么它在整个实数域上也是单调递增的。

（）5. 函数y = ax^2 + bx + c的图像是一个抛物线，无论a的值是正是负。

（）三、填空题（每题1分，共5分）1. 如果函数f(x) = x^2 4x + 3，那么f(2)的值是______。

2. 函数y = 3x 2的图像是一条______。

3. 如果函数f(x) = x^3 6x^2 + 9x，那么f'(x)的值是______。

4. 函数y = |x|的图像在x = 0处______。

5. 如果函数f(x) = (x 1)^2，那么它的顶点坐标是______。

四、简答题（每题2分，共10分）1. 简述一次函数的定义及其图像特点。

2. 什么是函数的单调性？如何判断一个函数的单调性？3. 简述二次函数的定义及其图像特点。

4. 什么是函数的奇偶性？如何判断一个函数的奇偶性？5. 简述函数的极值概念及其求法。

初中函数综合试题及答案

初中函数综合试题及答案一、选择题（每题3分，共30分）1. 函数y=2x+3的图象是一条直线，其斜率k和截距b分别是（）A. k=2, b=3B. k=3, b=2C. k=-2, b=3D. k=-3, b=22. 若函数y=x^2-4x+3的最小值是-1，则x的值是（）A. 2B. 3C. 4D. 53. 函数y=-2x+1与y=-x-1的交点坐标是（）A. (0,1)B. (1,-1)C. (-1,-3)D. (2,-3)4. 函数y=x+1/x的值域是（）A. (-∞,-2]∪[2,+∞)B. (-∞,-1]∪[1,+∞)C. (-∞,0)∪(0,+∞)D. (-∞,-1)∪(1,+∞)5. 函数y=x^3-3x^2+2在区间(1,2)上是（）A. 增函数B. 减函数C. 先增后减D. 先减后增6. 若函数y=x^2+2x-3与x轴有两个交点，则这两个交点的横坐标之和是（）A. -2B. 2C. -4D. 47. 函数y=1/x的图象关于（）A. 原点对称B. y轴对称C. x轴对称D. 直线y=x对称8. 函数y=x^2-6x+8的顶点坐标是（）A. (3, -1)B. (3, 1)C. (-3, 1)D. (-3, -1)9. 函数y=2x-1与直线y=3x+2平行的条件是（）A. 斜率不相等B. 斜率相等C. 截距不相等D. 截距相等10. 函数y=x^2-4x+m的图象与x轴有两个交点，则m的取值范围是（）B. m<4C. m≥4D. m≤4二、填空题（每题3分，共15分）1. 函数y=x^2-6x+8的对称轴是直线x=______。

2. 若函数y=x^2-4x+3的图象向上平移2个单位，则新的函数解析式为y=______。

3. 函数y=-2x+1与y=-x-1的交点坐标是(1,-1)，因此函数y=-2x+1的图象经过点______。

4. 函数y=x+1/x在x=1处的导数为______。

初中函数综合试题(卷)(附答案解析解析)

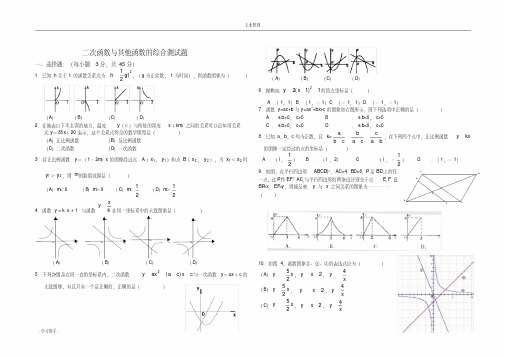
二次函数与其他函数的综合测试题一、选择题：（每小题3分，共45分）1．已知h 关于t 的函数关系式为221gt h，（g 为正常数，t 为时间），则函数图象为（）（A ）（B ）（C ）（D ）2．在地表以下不太深的地方，温度y （℃）与所处的深度x （k m ）之间的关系可以近似用关系式y ＝35x ＋20表示，这个关系式符合的数学模型是（）（A ）正比例函数（B ）反比例函数．（C ）二次函数（D ）一次函数3．若正比例函数y ＝（1－2m ）x 的图像经过点A （1x ，1y ）和点B （2x ，2y ），当1x ＜2x 时1y ＞2y ，则m 的取值范围是（）（A ）m ＜0（B ）m ＞0（C ）m ＜21（D ）m ＞214．函数y = k x + 1与函数xyk 在同一坐标系中的大致图象是（）OxyOxyOxyOxy（A ）（B ）（C ）（D ）5．下列各图是在同一直角坐标系内，二次函数c xc aax y )(2与一次函数y ＝a x ＋c 的大致图像，有且只有一个是正确的，正确的是（）（A ）（B ）（C ）（D ）6．抛物线1)1(22x y的顶点坐标是（）A ．（1，1）B ．（1，－1）C ．（－1，1）D ．（－1，－1）7．函数y =a x +b 与y =a x 2+bx +c 的图象如右图所示，则下列选项中正确的是（）A ． a b >0， c>0 B． a b <0， c>0 C ． a b >0， c<0 D ． a b <0， c<08．已知a ，b ，c 均为正数，且k=bac cab cba ，在下列四个点中，正比例函数kxy 的图像一定经过的点的坐标是（）A ．（l ，21） B ．（l ，2） C ．（l ，－21） D．（1，－1）9．如图，在平行四边形ABCD 中，AC=4，B D=6，P 是BD 上的任一点，过P 作EF ∥AC ，与平行四边形的两条边分别交于点E ，F ．设BP =x ，EF =y ，则能反映y 与x 之间关系的图象为……………（）10．如图4，函数图象①、②、③的表达式应为（）（A ）x y 25，2x y，xy 4（B ）x y 25，2x y ，x y 4（C ）x y25，2xy，xy4A BCDEFP（D ）x y25，2x y，xy411．张大伯出去散步，从家走了20分钟，到一个离家900米的阅报亭，看了10分钟报纸后，用了15分钟返回到家，下面哪个图形表示张大伯离家时间与距离之间的关系（）12．二次函数y =x 2-2x +2有（）A ．最大值是 1B ．最大值是 2C ．最小值是 1 D．最小值是 213．设A （x 1，y 1）、B （x 2，y 2）是反比例函数y =x2图象上的两点，若x 1<x 2<0，则y 1与y 2之间的关系是（）A ．y 2< y 1<0B ．y 1< y 2<0C ．y 2> y 1>0D ．y 1> y 2>0 14．若抛物线y =x 2-6x +c 的顶点在x 轴上，则c 的值是 ( )A ． 9B ． 3C ．-9D ． 015．二次函数2332xxy 的图象与x 轴交点的个数是（）A ．0个B ．1个C ．2个D ．不能确定二、填空题：（每小题3分，共30分）1．完成下列配方过程：122px x＝________________22px x＝____________2x；2．写出一个反比例函数的解析式，使它的图像不经过第一、第三象限：_________．3．如图，点P 是反比例函数2y x上的一点，P D ⊥x 轴于点D ，则△P OD 的面积为；4、已知实数m 满足022mm，当m =___________时，函数11m x m xym的图象与x 轴无交点．5．二次函数)1()12(22m x m x y 有最小值，则m ＝_________；6．抛物线322xxy向左平移5各单位，再向下平移2个单位，所得抛物线的解析式为___________；7．某商场销售一批名牌衬衫，平均每天可售出20件，每件可盈利40元．为了扩大销售量，增加盈利，采取了降价措施，经调查发现如果每件计划降价1元，那么商场平均每天可多售出2件．若商场平均每天要赢利1200元，则每件衬衫应降价__________；8．某学生在体育测试时推铅球，千秋所经过的路线是二次函数图像的一部分，如果这名学生出手处为A （0，2），铅球路线最高处为B （6，5），则该学生将铅球推出的距离是________；9．二次函数)0(2a c bxaxy的图像与x 轴交点横坐标为－2，b ，图像与y 轴交点到圆点距离为3，则该二次函数的解析式为___________；10．如图，直线)0(2k kxy与双曲线xk y在第一象限内的交点R ，与x 轴、y 轴的交点分别为P 、Q ．过R 作RM ⊥x 轴，M 为垂足，若△OPQ 与△PRM 的面积相等，则k 的值等于．三、解答题：（1－3题，每题7分，计21分；4－6题每题8分，计24分；本题共45分）1已知二次函数c bx xy 2的图像经过A （0，1），B （2，－1）两点．（1）求b 和c 的值；（2）试判断点P （－1，2）是否在此函数图像上？2．已知一次函数y kx k 的图象与反比例函数8yx的图象交于点P (4，n )．（1）求n 的值．（2）求一次函数的解析式．3．看图，解答下列问题．（1）求经过A 、B 、C 三点的抛物线解析式；x第3题图y P DO（2）通过配方，求该抛物线的顶点坐标和对称轴；（3）用平滑曲线连结各点，画出该函数图象．4．已知函数y=x2+bx-1的图象经过点（3，2）（1）求这个函数的解析式；（2）画出它的图象，并指出图象的顶点坐标；（3）当x>0时，求使y≥２的x的取值范围．5．某工厂设门市部专卖某产品，该产品每件成本40元，从开业一段时间的每天销售统计中，随机抽取一部分情况如下表所示：每件销售价（元）50 60 70 75 80 85 …每天售出件数300 240 180 150 120 90 …假设当天定的售价是不变的，且每天销售情况均服从这种规律．（1）观察这些统计数据，找出每天售出件数y与每件售价x（元）之间的函数关系，并写出该函数关系式．（2）门市部原设有两名营业员，但当销售量较大时，在每天售出量超过168件时，则必须增派一名营业员才能保证营业有序进行，设营业员每人每天工资为40元．求每件产品应定价多少元，才能使每天门市部纯利润最大（纯利润指的是收入总价款扣除成本及营业员工资后的余额，其它开支不计）6．如图，一单杠高 2.2米，两立柱之间的距离为 1.6米，将一根绳子的两端栓于立柱与铁杠结合处，绳子自然下垂呈抛物线状．（1）（2）（1）一身高0.7米的小孩站在离立柱0.4米处，其头部刚好触上绳子，求绳子最低点到地面的距离；（2）为供孩子们打秋千，把绳子剪断后，中间系一块长为0.4米的木板，除掉系木板用去的绳子后，两边的绳长正好各为2米，木板与地面平行．求这时木板到地面的距离（供选用数据：36.3≈１.8，64.3≈１.9，36.4≈２.1）7．已知抛物线y＝－x2＋mx－m＋2．（Ⅰ）若抛物线与x轴的两个交点A、B分别在原点的两侧，并且AB＝5，试求m的值；（Ⅱ）设C 为抛物线与y 轴的交点，若抛物线上存在关于原点对称的两点M 、N ，并且△MNC的面积等于27，试求m 的值．参考答案：一、选择题： 1．A 2．D 3．D 4．B 5．D 6．A 7．D 8．A9．A 10．C 11．D 12．C 13．C 14．A 15．C 二、填空题：1．2p ，21p ，p ，21p．2y =x2 3． 1 4．2或－1 5．45 6．1082x xy7．10元或20元8．6＋52 9．3412xxy或3412x xy 10．22三、解答题：1．2．解：（1）由题意得：84n，2.n （2）由点P （4，2）在ykxk 上，24,kk 25k．一次函数的解析式为2255yx．3．解：（1）由图可知A （－1，－1），B （0，－2），C （1，1）设所求抛物线的解析式为y ＝ax 2＋bx ＋c依题意，得121ab c c abc，，解得212a b c，，∴y ＝2x 2＋x －2．（2）y ＝2x 2＋x －2＝2（x ＋41）2－817∴顶点坐标为（－41，817），对称轴为x ＝－41（3）图象略，画出正确图象4．解：（1）函数y =x 2+bx -1的图象经过点（3，2）∴9+3b -1=2，解得b =-2 ．∴函数解析式为y =x 2-2x -1（2）y =x 2-2x -1=(x -1)2-2 ，图象略，图象的顶点坐标为（1，-2）（3）当x =3 时，y =2，根据图象知，当x ≥３时，y ≥２∴当x >0时，使y ≥２的x 的取值范围是x ≥3．5．解：（1）由统计数据知，该函数关系为一次函数关系，每天售出件数y 与每件售价x 之间的函数关系为：x y 6600．（2）当168y时，6006168x ，解得：72x；设门市部每天纯利润为z①当72x时，168y52807063406600402xx x z当70x时，5280maxz②当72x 时，168y 53207062406600402x x x z 70x 时，y 随x 的增大而减少72x时，52965320262max z 5280529672x当时，纯利润最大为5296元．6．（1）（2）解：（1）如图，建立直角坐标系，设二次函数解析式为y ＝ax 2＋c∵D （－0.4，0.7），B （0.8，2.2），∴．＝＋，＝＋2.264.07.016.0c a c a ∴．＝，＝2.0528c a ∴绳子最低点到地面的距离为0.2米．（2）分别作EG ⊥AB 于G ，FH ⊥AB 于H ，AG ＝21（AB －EF ）＝21（1.6－0.4）＝0.6．在Rt △AGE 中，AE ＝2，EG ＝22AG AE －＝226.02＝64.3≈1.9．∴ 2.2－1.9＝0.3（米）．∴木板到地面的距离约为0.3米．7．解： (I)设点Ａ（x 1，0），B (x 2，0) ，则x 1，x 2是方程x 2－mx ＋m －2＝0的两根．∵x 1 ＋x 2＝m ，x 1·x 2 =m－2 ＜0 即m ＜2；又AB ＝∣x 1 x 2∣＝121245x x x x 2（+），∴m 2－4m＋3=0 ．解得：m =1或m =3(舍去) ，∴m 的值为 1 ．（II ）设M (a ，b )，则N (－a ，－b ) ．∵M 、N 是抛物线上的两点，∴222,2.a ma m b ama m b L L ①②①＋②得：－2a 2－2m ＋4＝0 ．∴a 2＝－m ＋2．∴当m ＜2时，才存在满足条件中的两点M 、N ．∴2am ．这时M 、N 到y 轴的距离均为2m ，又点C 坐标为（0，2－m ），而S △M N C = 27 ，∴2×12×（2－m ）×2m =27 ．∴解得m =－7 ．。

初中数学九年级总复习《函数》专项试卷含详解答案

AP，当点 P 满足 DP+AP的值最小时， P 点坐标为
．
第 11 题图
第 12 题图
第 13 题图
第 14 题图
12. 如图，在平面直角坐标系中，正方形 ABOC和正方形 DOFE的顶点 B，F 在 x
轴上，顶点
C，D 在 y 轴上，且
S△ADF＝ 4，反比例函数
??=
??
（
x＞
0）的图象经
??
《函数》总复习试卷含答案
一、选择题（本大题共 10 小题，每小题 3 分，共 30 分）
1．在函数 ??= √??+1中，自变量 x 的取值范围是（
）
??-2
A． x＞﹣ 1 B ．x≥﹣ 1 C ．x＞﹣ 1 且 x≠2 D ．x≥﹣ 1 且 x≠ 2
2．如图，若一次函数 y=kx+b 的图象与两坐标轴分别交于 A，B 两点，点 A 的坐
22. （本小题满分 10 分）某实验学校为开展研究性学习，准备购买一定数量的两人学习桌和三人学习桌，如果购买 3 张两人学习桌和 1 张三人学习桌需 220 元；如果购买 2 张两人学习桌和 3 张三人学习桌需 310 元．
（1）求两人学习桌和三人学习桌的单价；（2）学校欲投入资金不超过 6000 元，购买两种学习桌共 98 张，以至少满足
第 23-24 题每小题 12 分， 25 题 14 分，共 96 分）
17. （本小题满分 8 分）
对于给定的两个函数，任取自变量 x 的一个值，当 x＜1 时，它们对应的函
数值互为相反数：当 x≥1 时，它们对应的函数值相等，我们称这样的两个
函数互为相关函数，例如：一次函数 y=x-4 ，它的相关函数为 ??=

初中函数综合试题(卷)(附答案解析)

初中函数综合试题(卷)(附答案解析)一、单选题1．函数32x y x +=-中，自变量x 的取值范围是（） A ．3x >- B ．3x ≥-且2x ≠ C ．2x ≠ D ．3x >-且2x ≠2．将抛物线y ＝x 2向右平移3个单位，再向上平移2个单位，得到的抛物线是（）A ．y ＝（x +3）2﹣2B ．y ＝（x +3）2+2C ．y ＝（x ﹣3）2﹣2D ．y ＝（x ﹣3）2+2 3．二次函数y ＝2x 2﹣1的图象的顶点坐标是（）A ．（﹣1，0）B ．（1，0）C ．（0，1）D ．（0，﹣1） 4．在直角坐标系的x 轴的负半轴上，则点P 坐标为（）A ．()4,0-B ．()0,4C ．()0,3-D ．()1,05．已知（﹣3，y 1），（﹣2，y 2），（1，y 3）是二次函数y ＝﹣2x 2﹣8x +m 图象上的点，则（） A ．y 2＞y 1＞y 3 B ．y 2＞y 3＞y 1 C ．y 1＜y 2＜y 3 D ．y 3＜y 2＜y 1 6．点A （3,-5）在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．抛物线22y x =-的图象可能是（）A ．B ．C ．D ．8．下列的各点中，在反比例函数5y x=图象上的点是（） A ．()2,4B ．()1,5C ．1,22⎛⎫ ⎪⎝⎭D ．11,23⎛⎫ ⎪⎝⎭9．下列各点中，在反比例函数2y x=-图象上的是-（）A ．(21)，B ．233⎛⎫⎪⎝⎭， C ．(21)--， D ．(12)-，10．一次函数 y ＝－2x +2 经过点（a ，2）则 a 的值为（） A ．－1 B ．0C ．1D ．211．下列二次函数中，对称轴是直线1x =的是（）A ．21y x =+B ．()221y x =+C ．()21y x =-+D ．()231y x =--12．在直角坐标系中，已知(1,0)A 、(1,2)B --、(2,2)C -三点坐标，若以A 、B 、C 、D 为顶点的四边形是平行四边形，那么D 的坐标不可以是（） A ．(2,0)- B ．(0,4) C ．(4,0) D ．(0,4)- 13．点P 在第四象限，它到x 轴，y 轴的距离分别为2，5，则点P 的坐标为（）A ．()2,5B ．()2,5-C ．()5,2-D ．()5,2-14．点（3，2）在反比例函数y ＝kx（x ＞0）上，则下列不可能在该函数图像上的点是（） A ．（2，3）B ．（﹣2，﹣3）C ．（2，﹣3）D ．（﹣3，﹣2）15．亮亮每天都要坚持体育锻炼，某天他跑步到离家较近的秀湖公园，看了一会喷泉表演然后慢慢走回家，如图能反映当天亮亮离家的距离y 随时间x 变化的大致图象是（）A ．B ．C ．D ．二、填空题16．已知y 关于x 的函数()224y m x m =++-是正比例函数，则m 的值是______．17．在平面直角坐标系中，一次函数y ＝kx +b 和y ＝mx +n 相交于点（2，﹣1），则关于x ，y 的方程组y kx by mx n=+⎧⎨=+⎩的解是______．18．若y 关于x 的函数y ＝﹣7x ＋2＋m 是正比例函数，则m ＝_____． 19．抛物线()223y x =+-可以由抛物线2y x 先向左平移2个单位，再向下平移___________个单位得到的．20．抛物线231y ax x =+-的顶点在x 轴上，那么=a ______．三、解答题21．已知抛物线()220y ax bx b b a =++-≠．(1)若b ＝2a ，求抛物线的对称轴； (2)若a ＝1，且抛物线的对称轴在y 轴右侧． ①当抛物线顶点的纵坐标为1时，求b 的值；②点()13,y -，()21,y -，()33,y 在抛物线上，若132y y y >>，请直接写出b 的取值范围． 22．海鲜市场某销售商销售一种成本为6元/千克的海产品，市场调查反映，若按12元/千克销售，每天可售出200千克，如调整价格，销售价每降低1元，每天可多售出50千克．设每千克的售价为()12x x ≤元，每天的销售量为y 千克． (1)求y 与x 之间的关系式；(2)当售价定为多少元时，每天能获得最大利润？并求出最大利润． 23．已知二次函数2361y x x =-++． (1)用配方法化成()2y a x h k =-+的形式； (2)直接写出该二次函数图象的对称轴和顶点坐标．24．已知抛物线y ＝ax 2+bx ﹣1经过点A (1，2)、B (﹣3，2)两点． (1)求该抛物线的解析式．(2)当﹣2≤x ≤2时，请直接写出y 的取值范围．25．在平面直角坐标系xOy 中，已知二次函数图像的顶点为()1,2A -，且经过()3,0B -． (1)求二次函数的解析式；(2)将该二次函数图像向右平移几个单位，可使平移后所得图像经过坐标原点？并直接写出平移后所得图像与x 轴的另一个交点的坐标．【参考答案】一、单选题 1．B 2．D 3．D 4．A 5．A 6．D 7．A 8．B 9．D 10．B 11．D12．B 13．D 14．C 15．B 二、填空题 16．217．21x y =⎧⎨=-⎩18．﹣2 19．320．94- 三、解答题21．(1)抛物线的对称轴为直线x ＝－1 (2)①23b =-；②－2<b <0．【解析】【分析】（1）根据抛物线对称轴公式求解即可；（2）①先根据抛物线对称轴在y 轴右侧求出0b <，再根据抛物线顶点坐标公式求解即可；②根据抛物线的增减性以及对称性求解即可． (1)解：抛物线的对称轴为直线2b x a=-， ∵b ＝2a ， ∴x ＝－1，∴抛物线的对称轴为直线x ＝－1． (2)解：①当a ＝1时，抛物线解析式为22y x bx b b =++-， ∴抛物线的对称轴为直线2bx =-，∵抛物线的对称轴在y 轴右侧， ∴02b->， ∴0b <，∵该抛物线顶点的纵坐标为1， ∴()22414b b b --=，解得：123b =-，22b =，又∵b <0， ∴23b =-．②∵抛物线对称轴在y 轴右侧，且132y y y >>，抛物线对称轴为直线2bx =-，且抛物线开口向上∴13022b -+<-<， ∴20b -<<．【点睛】本题主要考查了二次函数的性质，熟知二次函数的增减性，对称轴公式，顶点坐标公式是解题的关键． 22．(1)50800y x =-+(2)当售价定为11元，每天能获得最大利润，最大利润为1250元【解析】【分析】（1）根据题意即可直接列出关于x 、y 的等式，再整理即可；（2）设每天的利润为w 元，根据题意可列出关于w 、x 的等式，整理，再根据二次函数的性质即可解答． (1)根据题意得：()2001250y x =+-⨯ 整理，得：50800y x =-+∴y 与x 之间的关系为50800y x =-+； (2)设每天的利润为w 元，根据题意得：()()650800w x x =--+ ∴()250111250w x =--+ ∵500-<∴抛物线开口向下，∴当11x =时，有最大利润1250元．答：当售价定为11元，每天能获得最大利润，最大利润为1250元．【点睛】本题考查一次函数和二次函数的实际应用．根据题意找出等量关系，列出等式是解题关键．23．(1)()2314y x =--+(2)对称轴为1x =，顶点坐标为()1,4 【解析】【分析】（1）利用完全平方公式进行配方即可；（2）依据配方后的解析式即可得到结论． (1)解：()22361314y x x x =-++=--+． (2) 解：()2314y x =--+∴对称轴为1x =，顶点坐标为()1,4【点睛】本题考查了二次函数顶点式2()y a x h k =-+的顶点坐标为(),h k ，掌握顶点式求顶点坐标是解题的关键． 24．(1)y ＝x 2+2x ﹣1 (2)﹣2≤y ≤7 【解析】【分析】（1）把A 点和B 点坐标代入y ＝ax 2+bx ﹣1得到关于a 、b 的方程组，再解方程组可确定抛物线解析式；（2）利用配方法得到抛物线的对称轴为直线x ＝﹣1，顶点坐标为（﹣1，﹣2），利用二次函数的性质，x ＝﹣1时，y 的值最小，而x ＝2时y ＝7，从而得到y 的取值范围． (1)将A （1，2）、B （﹣3，2）代入y ＝ax 2+bx ﹣1，得129312a b a b +-=⎧⎨--=⎩，解得12a b =⎧⎨=⎩， ∴抛物线的解析式为y ＝x 2+2x ﹣1； (2)∵y ＝x 2+2x ﹣1＝（x +1）2﹣2，∴抛物线的对称轴为直线x ＝﹣1，顶点坐标为（﹣1，﹣2），当x ＝2时，y ＝（2+1）2﹣2＝7，所以当﹣2≤x ≤2时，y 的取值范围为﹣2≤y ≤7．【点睛】本题考查了待定系数法求二次函数的解析式：在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式．也考查了二次函数的性质．25．(1)21322y x x =--+(2)()4,0 【解析】【分析】（1）根据题意设出二次函数的顶点式，然后用待定系数法求解即可；（2）根据题意设出平移后的表达式为()21122y x m =-+-+，将原点()0,0代入即可求出平移后的表达式，当0y =时，即可求出与x 轴的另一个交点的坐标． (1)解：设二次函数的表达式为：()()2102y a x a =+≠+ 将()3,0B -代入得：420a +=解得：12a =-∴()21122y x =-++，即21322y x x =--+； (2)解：设将该二次函数图像向右平移()>0m m 个单位， ∴平移后的表达式为()21122y x m =-+-+， ∵平移后所得图像经过坐标原点，∴将原点()0,0代入得，()2100122m =-+-+，即()21122m -=，解得：123,1m m ==-(舍去)， ∴3m =，∴平移后的表达式为()21222y x =--+，当0y =时，即()212202x --+=，解得：120,4x x ==，∴平移后所得图像与x 轴的交点坐标为()0,0和()4,0， ∴平移后所得图像与x 轴的另一个交点的坐标为()4,0．【点睛】本题考查二次函数图象的平移，待定系数法求二次函数表达式，二次函数与一元二次方程的联系等知识点，牢记相关的知识点是解此类题的关键．。

初中函数综合试题附答案

初二函数试题及答案

初中函数测试题及答案

函数试题及答案初二

初三中考数学函数综合题含答案

初中函数练习题及答案

初中函数专题试题及答案

初中数学 函数专题练习及答案

初三中考数学函数综合题含答案

中考数学总复习《函数》专项测试卷-附参考答案

初中数学二次函数综合题及答案(经典题型)印.pdf

9年级学生函数试卷加答案【含答案】

初中函数综合试题及答案

初中函数综合试题(卷)(附答案解析解析)

初中数学九年级总复习《函数》专项试卷含详解答案

初中函数综合试题(卷)(附答案解析)

初中数学函数专题练习及答案