加减乘除运算求x方法
向量的加减乘除运算

向量的加减乘除运算向量是数学中的重要概念,它在物理、工程、计算机科学等领域有着广泛的应用。
在进行向量运算时,我们常常需要进行加减乘除的操作。
本文将详细介绍向量的加减乘除运算及其相关概念。
一、向量的表示方式向量可以用不同的表示方式进行表达,最常见的有坐标表示和向量表示方法。
1. 坐标表示:在二维直角坐标系中,向量可以表示为(x,y),分别代表向量在x轴和y轴上的分量。
在三维空间中,向量可以表示为(x,y,z),分别代表向量在x轴、y轴和z轴上的分量。
2. 向量表示:向量可以用箭头进行表示,箭头的长度代表向量的模,箭头的方向代表向量的方向。
二、向量的加法运算向量的加法运算是指将两个向量合并为一个新的向量。
向量的加法满足交换律和结合律。
设有向量A和向量B,它们的加法运算表示为:A + B = C,C为结果向量。
向量的加法运算可以使用坐标相加的方法或三角形法则进行计算。
三、向量的减法运算向量的减法运算是指从一个向量中减去另一个向量,得到一个新的向量。
向量的减法可以看作是加法的逆运算。
设有向量A和向量B,它们的减法运算表示为:A - B = D,D为结果向量。
向量的减法运算可以使用将被减向量取相反数,然后进行加法运算的方式进行计算。
四、向量的数乘运算向量的数乘运算是指将向量的每个分量与一个数相乘。
数乘可以改变向量的长度和方向。
设有向量A和一个实数k,向量的数乘运算表示为:k * A = E,E为结果向量。
在坐标表示中,向量的数乘可以直接将向量的每个分量与数k相乘。
在向量表示中,向量的数乘可以通过改变箭头的长度来表示。
五、向量的除法运算向量的除法运算并没有一个直接的定义和运算规则。
在向量运算中,我们通常使用乘法的逆运算来代替除法运算。
设有向量A和一个非零实数k,向量的除法运算可以用乘法的逆运算表示为:A / k = (1/k) * A。
六、向量的加减乘除综合运算在实际问题中,我们往往需要对向量进行多种运算的组合。
正态分布加减乘除计算公式

正态分布是一种广泛应用于统计学和量化金融的概率分布,其在自然界和人类活动中
的很多现象中都有应用。
在进行正态分布的加减乘除计算时,需要使用相应的公式和
方法。
下面是正态分布的加减乘除计算公式的介绍:
1. 正态分布加减法计算公式:
假设X和Y是两个正态分布随机变量,其均值分别为μx和μy,标准差为σx和σy,
则其和或差的分布仍然是正态分布。
具体而言,若Z = X ± Y,其均值为μz = μx ± μy,标准差为σz = √(σx^2 + σy^2)。
2. 正态分布乘法计算公式:
假设X和Y是两个正态分布随机变量,其均值分别为μx和μy,标准差为σx和σy,
则其积的分布服从形状不同的正态分布。
具体而言,若Z = X *Y,其均值为μz=μx*μy,标准差为σz=|μx| * σy + |μy| * σx。
在计算标准差时要考虑到乘积中每个因子的符号。
3. 正态分布除法计算公式:
假设X和Y是两个正态分布随机变量,其均值分别为μx和μy,标准差为σx和σy,
则其商的分布也是一个正态分布。
具体而言,若Z = X / Y,则其均值为μz = μx / μy,
标准差为σz = |μx /μy| * √[(σx / μx)^2 + (σy / μy)^2- 2ρ(σx / μx)(σy / μy)],其中ρ是X和
Y的相关系数。
需要注意的是,正态分布的计算公式和方法可能因为问题的具体条件而略有不同,同
时也需要注意在计算过程中避免舍入误差和数值不稳定性等问题。
函数极限的四则运算法则

函数极限的四则运算法则函数极限是数学中重要的概念之一,它在数学分析和微积分中有着广泛的应用。
四则运算法则指的是对函数进行加减乘除运算时,其极限的运算规则。
在本文中,我们将对四则运算法则进行详细的说明。
1.加法法则:如果有两个函数 f(x) 和 g(x),且它们的极限都存在,则它们的和的极限等于两个极限的和,即lim(x→a) [f(x) + g(x)] = lim(x→a)f(x) + lim(x→a) g(x)。
证明如下:假设lim(x→a) f(x) = L1,lim(x→a) g(x) = L2,我们需要证明lim(x→a) [f(x) + g(x)] = L = L1 + L2根据极限的定义,我们可以找到两个足够小的正数ε1和ε2,使得当0<,x-a,<δ1时,有,f(x)-L1,<ε1,当0<,x-a,<δ2时,有,g(x)-L2,<ε2取δ = min{δ1, δ2},则当 0 < ,x-a,< δ 时,有,f(x) - L1,< ε1 且,g(x) - L2,< ε2此时,我们可以将不等式,f(x)-L1,+,g(x)-L2,<ε1+ε2转化为不等式,f(x)+g(x)-(L1+L2),<ε1+ε2根据极限的定义,当,f(x) + g(x) - (L1 + L2),< ε1 + ε2 时,有,x - a,< δ,即证明了lim(x→a) [f(x) + g(x)] = L1 +L22.减法法则:如果有两个函数 f(x) 和 g(x),且它们的极限都存在,则它们的差的极限等于两个极限的差,即lim(x→a) [f(x) - g(x)] = lim(x→a) f(x) - lim(x→a) g(x)。
证明方法与加法法则类似,略。
3.乘法法则:如果有两个函数 f(x) 和 g(x),且它们的极限都存在,则它们的乘积的极限等于两个极限的乘积,即lim(x→a) [f(x) * g(x)] =lim(x→a) f(x) * lim(x→a) g(x)。
整式的加减乘除法则总结

整式的加减乘除法则总结一、整式的定义整式是由数字、字母和运算符号(加号、减号、乘号)通过运算得出的式子。
例如,2x - 5y + 3 是一个整式。
二、整式的加法法则整式加法法则可以总结为下列两条规则:1.对于整式的同类项进行合并,即将相同字母的幂次相同的项合并。
例如:2x - 3x + 4x + 5 可以合并为 3x + 5。
2.对合并后的同类项进行系数相加。
例如:3x - 2y + 4x - 5y 可以合并为 7x - 7y。
三、整式的减法法则整式减法法则是整式加法法则的特例,即将减号后面的各项取相反数后,按整式加法法则进行运算。
例如:5x^2 - 3x + 2y - (2x^2 - 4x + 3y) = 5x^2 - 3x + 2y - 2x^2 + 4x - 3y = 3x^2 + x - y。
四、整式的乘法法则整式乘法法则可以总结为下列规则:1.将两个整式的每一项按照乘法分配律进行相乘。
例如:(2x - 3)(4x + 5) 可以按乘法分配律展开为 2x(4x + 5) - 3(4x + 5) = 8x^2 + 10x - 12x - 15 = 8x^2 - 2x - 15。
2.将展开后的各项进行合并。
例如:3x(2x - 1) + 5y(3x + 2y) 可以合并为 6x^2 - 3x^2 + 15xy + 10y^2。
五、整式的除法法则整式除法法则可以总结为下列规则:1.将除法转化为乘法。
即将被除数乘以除数的倒数。
例如:(4x^2 + 8x) / 2x 可以转化为 (4x^2 + 8x) * (1 / 2x)。
2.化简分式。
例如:(4x^2 + 8x) * (1 / 2x) 可以化简为 2x + 4。
六、整式的总结通过以上的总结,可以得出整式的加减乘除法则:1.加法法则:合并同类项后,进行系数相加。
2.减法法则:减号后面的各项取相反数,按照整式加法法则进行运算。
3.乘法法则:按乘法分配律展开,并合并同类项。
对数加减乘除运算法则

对数加减乘除运算法则对数的世界,听起来是不是有点高深莫测?它和我们的生活息息相关,就像你每天早上喝的咖啡一样不可或缺。
要知道,对数其实就是一种“倒过来的乘法”。
你听到这个,是不是觉得有点新鲜?就像把冰淇淋倒过来一样,瞬间又变得有趣了。
我们经常用对数来解决那些庞大、复杂的数字问题。
比如,你想计算一个数字的幂,这时候对数就像是个好帮手,能把难题变得简单得多。
用对数,哎哟,那真是省心又省力,仿佛在数学的海洋中找到了救生圈。
说到对数的加减乘除,那可真是一门艺术。
我们可以把对数看成是数学的调味料,加点儿进去,瞬间让菜肴变得美味可口。
咱们得知道对数加法的法则,简单来说就是“对数相加,底数相乘”。
听起来是不是有点像做菜?把两种食材混合在一起,最后出来的就是新的一道菜。
比如,log_a(x) + log_a(y) = log_a(xy),这就好比你把两种不同的果汁混在一起,最后得到一杯全新的果汁。
这种感觉,真是妙不可言。
然后说说减法。
对数减法也是一门技巧,公式是“对数相减,底数相除”。
像是在厨房里,把一个大蛋糕切成两半,最后剩下的那一块就是你的成果。
想想,log_a(x)log_a(y) = log_a(x/y),是不是觉得很简单?就像把一杯果汁倒掉一部分,最后剩下的就是你要的味道。
学会这些,你会发现,数学原来也是可以很轻松的,根本不是什么高不可攀的存在。
说到乘法,那可就更有趣了。
对数的乘法法则可真是个好帮手!我们知道,两个数相乘,换成对数后就是加起来。
这就像在学校里组队比赛,大家一起努力,最终的成绩才会更好。
你想想,log_a(xy) = log_a(x) + log_a(y),合起来就是个强大的组合,正如一群小伙伴齐心协力,一起打怪升级。
数学在这里也变得生动活泼,谁说它只能是枯燥的公式?再来讲讲除法,哇,这也太简单了。
对数的除法就像是把食材分给大家一样,分享的乐趣让人心情愉悦。
这里的法则是log_a(x/y) = log_a(x) log_a(y),一听就知道是一个公平的游戏。
加减乘除速算法

加减乘除速算法,为孩子打开一个神奇有趣的数学世界加法的神奇速算法一、加大减差法1、口诀前面加数加上后面加数的整数,减去后面加数与整数的差等于和。
2、例题1376+98=1474 计算方法:1376+100-23586+898=4484 计算方法:3586+1000-1025768+9897=15665 计算方法:5768+10000-103二、求只是数字位置颠倒两个两位数的和1、口诀一个数的十位数加上它的个位数乘以11等于和2、例题47+74=121 计算方法:(4+7)x 11=12168+86=154 计算方法:(6+8)x 11=15458+85=143 计算方法:(5+8)x 11=143减法的神奇速算法一、减大加差法1、例题321-98=223计算方法:减100,加28135-878=7257计算方法:减1000,加12291321-8987= 82334计算方法:减10000,加10132、总结被减数减去减数的整数,再加上减数与整数的差,等于差。
二、求只是数字位置颠倒两个两位数的差1、例题74-47=27计算方法:(7-4)x9=2783-38=45计算方法:(8-3)x9=4592-29=63计算方法:(9-2)x9=632、总结被减数的十位数减去它的个位数乘以9,等于差。
三、求只是首尾换位,中间数相同的两个三位数的差1、例题936-639=297计算方法:(9-6)x9=27注意!27中间必须加9,即为差297723-327=396计算方法:(7-3)x9=36注意!36中间必须加9,即为差396873-378=495计算方法:(8-3)x9=45注意!45中间必须加9,即为差4952、总结被减数的百位数减去它的个位数乘以9,(差的中间必须写9)等于差。
四、求互补两个数的差1、例题73-27=46计算方法:(73-50)x2=46613-387=226计算方法:(613-500)x2=2268112-1888=6224计算方法:(8112-5000)x2=62242、总结两位互补的数相减,被减数减50乘以2;三位互补的数相减,被减数减500乘以2;四位互补的数相减,被减数减5000乘以2;以此类推......乘法的神奇速算法一、十位数相同,个位数互补的两位数乘法1、口诀十位加一乘十位,个位相乘写后边(未满10补零)。
小学数学解方程10种方法,解方程其实很简单(经典集锦)

小学解方程10种方法汇总一、未知数加减乘除1.形如x+a=b或x-a=b的方程。
(遇加同减,遇减同加)例1 x+7=19 遇加同减解:x+7-7=19-7 两边同时减去7X=12例2 x-6=19 遇减同加解:x-6+6=19+6 两边同时加上6x=252.利用等式解形如ax=b或x÷a=b(a不等于0)的方程。
(遇乘同除,遇除同乘)例1 7x=63 遇乘同除解:7x÷7=63÷7两边同时除以7x=9例2 x ÷7=9 遇除同乘解:x÷7×7=9×7两边同时乘以7x=633.利用等式解形如ax+b=c、ax-b=c或x÷a+b=c、x÷a-b=c(a不等于0)的方程。
(混合运算,先加减再乘除:能计算的要先计算)例1 2x+5=29 有乘法和加法,先算加法,遇加同减解:2x+5-5=29-5 两边同时减去52x=24 遇乘同除2x÷2=24÷2两边同时除以2x=12例2 5x-6=24 有乘法和减法,先算减法,遇减同加解: 5x-6+6=24+6 两边同时加上65x=30 遇乘同除5x÷5=30÷5两边同时除以5x=6例3 x÷7+3=10 有除法和加法,先算加法,遇加同减解:x÷7+3-3=10-3 两边同时减去3x÷7=7 遇除同乘x÷7×7=7×7两边同时乘以7x=49例4 x÷10-6=9 有除法和减法,先算减法,遇减同加x÷10-6+6=9+6 两边同时加上6x÷10=15遇除同乘x÷10×10=15×10两边同时乘以10x=150二、未知数被加上或被减去;4.未知数被加上a+x=b,a+bx=c(解法同上)5.形如b-x=c、b-ax=c的方程。
从左到右运算法则

从左到右运算法则1. 算术运算在算术运算中,从左到右运算法则是最基本的运算规则之一。
我们通常按照从左到右的顺序进行加减乘除等运算,以求得正确的结果。
例如,对于表达式 3 + 4 * 2,我们先进行乘法运算,再进行加法运算,得到11作为最终结果。
2. 代数运算在代数运算中,从左到右运算法则同样适用。
当我们进行代数式的化简或求解等操作时,也需要按照从左到右的顺序进行计算。
例如,对于表达式2x + 3y - 4z,我们先计算2x,再计算3y,最后计算-4z,以得到最简形式的代数表达式。
3. 函数运算在函数运算中,从左到右运算法则同样发挥着重要作用。
当我们对函数进行组合、求导或积分等操作时,也需要按照从左到右的顺序进行计算。
例如,对于复合函数f(g(x)),我们先计算g(x),再计算f(g(x)),以得到最终结果。
4. 统计运算在统计学中,从左到右运算法则同样被广泛应用。
当我们进行数据分析、概率计算或假设检验等统计操作时,也需要按照从左到右的顺序进行计算。
例如,在计算均值、方差或回归系数时,我们需要按照从左到右的顺序进行相应的计算步骤。
5. 数列运算在数列运算中,从左到右运算法则同样非常重要。
当我们对数列进行求和、求极限或求导等操作时,也需要按照从左到右的顺序进行计算。
例如,在计算等差数列的和时,我们需要先计算每一项的值,再进行求和运算,以得到最终结果。
总结起来,从左到右运算法则是数学中一种非常重要的运算次序约定,它确保了数学运算的准确性和一致性。
无论是在算术、代数、函数、统计还是数列运算中,我们都需要遵循从左到右的顺序进行计算,以获得正确的结果。
掌握和应用从左到右运算法则,对于理解和解决各种数学问题都具有重要的意义。
矩阵的加减乘除运算法则

矩阵的加减乘除运算法则矩阵是数学中重要的一种数学工具,在各种领域中广泛应用,矩阵是用数的方阵表示的,并且还有着加减乘除等运算法则。
本文将详细介绍矩阵的加减乘除运算法则。
一、矩阵加减法矩阵加减法的定义:假设矩阵A和矩阵B都是同一维度的矩阵,令矩阵C等于A加上B,矩阵C中的第i行第j列的元素等于A中第i行第j列的元素加上B中第i行第j列的元素,即:C(i,j) = A(i,j) + B(i,j)相应地,如果要使用矩阵B从矩阵A中减去,我们将B的所有元素取反并将它与矩阵A相加。
矩阵加减法的性质:1.加法的交换律和结合律:对于任何两个同维度的矩阵A和B,我们有以下性质:A +B = B + A (交换律)(A + B) + C = A + (B + C) (结合律)2.加法的单位元:对于任何矩阵A,我们有:A + 0 = A其中0是一个全0矩阵,即元素全部为0。
3.加法的逆元:每个矩阵都存在一个负数矩阵-B,使得A + B = 0,其中0是一个全0矩阵。
二、矩阵乘法矩阵乘法的定义:对于两个矩阵A和B,如果A的列数等于B的行数,则将它们相乘,得到一个新矩阵C,C的行数等于A的行数,列数等于B的列数。
对于C中的每个元素,都是A的相应行和B的相应列中元素的乘积之和。
下面是矩阵乘法的公式:C(i,j) = A(i,1) * B(1,j) + A(i,2) * B(2,j) + ... + A(i,n) * B(n,j)其中,n是矩阵A的列数,也是矩阵B的行数。
矩阵乘法的性质:1.乘法的结合律:如果矩阵A,B和C的维度满足AB和BC都有定义,则有:(A * B) * C = A * (B * C)2.分配律:对于任意矩阵A,B和C,以及任意标量c,我们有:(A + B) * C = A * C + B * CA * (B + C) = A * B + A * Cc * (A * B) = (c * A) * B = A * (c * B)3.不满足交换律:一般情况下,矩阵乘法不满足交换律,即AB不等于BA,因为乘法顺序导致的行列不匹配。
小学四年级解方程的方法详解

小学四年级解方程的方法详解方程:含有未知数的等式叫做方程。
如4x-3=21,6x-2(2x-3)=20方程的解:使方程成立的未知数的值叫做方程的解。
如上式解得x=6解方程:求方程的解的过程叫做解方程。
解方程的依据:方程就是一架天平,“=”两边是平衡的,一样重!1. 等式性质:(1)等式两边同时加上或减去同一个数,等式仍然成立;(2)等式两边同时乘以或除以同一个非零的数,等式仍然成立。
2. 加减乘除法的变形:(1) 加法:a + b = 和则 a = 和-b b = 和-a例:4+5=9 则有:4=9-5 5=9-4(2) 减法:被减数a –减数b = 差则:被减数a = 差+减数b 被减数a-差= 减数b 例:12-4=8则有:12=8+4 12-8=4(3) 乘法:乘数a ×乘数b = 积则:乘数a = 积÷乘数b 乘数b= 积÷乘数a 例:3×7=21则有:3=21÷7 7=21÷3(4) 除法:被除数a ÷除数b = 商则:被除数a= 商×除数b 除数b=被除数a ÷商例:63÷7=9 则有:63=9×7 7=63÷9解方程的步骤:1、去括号:(1)运用乘法分配律;(2)括号前边是“-”,去掉括号要变号;括号前边是“+”,去掉括号不变号。
2、移项:法1——运用等式性质,两边同加或同减,同乘或同除;法2——符号过墙魔法,越过“=”时,加减号互变,乘除号互变。
注意两点:(1)总是移小的;(2)带未知数的放一边,常数值放另一边。
3、合并同类项:未知数的系数合并;常数加减计算。
4、系数化为1:利用同乘或同除,使未知数的系数化为1。
5、写出解:未知数放在“=”左边,数值(即解)放右边;如x=66、验算:将原方程中的未知数换成数,检查等号两边是否相等!注意:(1)做题开始要写“解:”(2)上下“=”要始终对齐【例1】x-5=13 x-5=13法1 解:x-5+5=13+5 法2 解:x=13+5x=18 x=18【例2】3(x+5)-6=18 3(x+5)-6=18法1 解: 3x+3×5-6=18 法2 解:3x+3×5-6=183x+15-6=18 3x+15-6=183x+9=18 3x+9=183x+9-9=18-9 3x=18-93x=9 3x=93x÷3=9÷3 x=9÷3x=3 x=3【例3】3(x+5)-6=5(2x-7)+2解: 1.去括号:3x+3×5-6=5×2x-5×7+23x+15-6=10x-35+23x+9=10x-332.移项:33+9=10x-3x (注意:移小的,如-33, 3x)3.合并同类项:42=7x4.系数化为1:42÷7=7x÷76=x5.写出解:x=66.验算:3×(6+5)-6=5(2x6-7)+23×11-6=5×5+227=27√解方程练习(写出详细过程):4+x=7 x+6=9 4+x=7+54+x-2=7 x-6=9 17-x=9x-6=9+3 9+3=17-x 16+2x =24+x4x=16 15=3x 4x+2=1824-x =15+2x 2+5x=18+3x 6x-2=3x+103(x+6) =2+5x 2(2x-1)=3x+10 30-4(x-5)=2x-162(x+4) -3=2+5x 100-3(2x-1)=3-4x 30+4(x-5)=2x-2620x-50=50 28+6 x =88 32-22 x =1024-3 x =3 10 x ×(5+1)=60 99 x =100- x36÷ x=18 x÷6=12 56-2 x =2036÷ x-2=16 x÷6+3=9 56-3x =20-x4y+2=6 x+32=76 3x+6=1816+8x=40 2x-8=8 4x-3×9=298x-3x=105 x-6×5=42+2x 2x+5=7 ×3 2(x+3)+3=13 12x-9x=9 6x+18=4856x-50x=30 5x=15(x-5)78-5x=2832y-29y=3 5(x+5)=15 89 – 9x =80 100-20x=20+30x 55x-25x=60 76y÷ 76=1 23y÷ 23=23 4x-20=0 80y+20=100-20y 53x-90=16 2x+9x=11 12(y-1)=2480÷ 5x=100 7x÷ 8=14 65x+35=10019y+y=40 25-5x=15 79y+y=8042x+28x=140 3x-1=8-2x 90y-90=90-90y 80y-90=70÷ 30 78y+2y=160 88-4x=80-2x9÷(4x)=1 20x=40 – 10x 65y-30=10051y-y=100 85y+1=y+86 45x-50=40-45x二、列方程解应用题:(一)口算:a+2a= 3c+5c= 4m-2m= X+3x=5x-x= 6x-2x= 1.5x-x= 3.6x+1.4x=(二)用方程表示数量关系:1.火车每小时行120千米,汽车每小时a千米,火车每小时比汽车快6千米。
加减乘除合并同类项与化简

加减乘除合并同类项与化简在数学中,合并同类项是一种常见的运算技巧,用于简化代数表达式。
当我们需要进行加减乘除的运算时,合并同类项可以帮助我们更方便快捷地求解问题。
本文将介绍如何进行加减乘除合并同类项与化简。
一、加法与减法中的合并同类项在进行加法与减法运算时,合并同类项可以将具有相同字母指数的项合并为一个项。
例如:1. 合并同类项:2x + 3x = (2 + 3)x = 5x2. 合并同类项:4a - 6a = (4 - 6)a = -2a通过上述例子可以看出,当字母的指数相同时,我们可以将系数相加或相减,字母指数不变。
二、乘法中的合并同类项在进行乘法运算时,合并同类项的方法与加法与减法类似。
我们将具有相同字母指数的项的系数相乘,并将字母指数保持不变。
例如:1. 合并同类项:2a × 3a = (2×3)(a×a) = 6a^22. 合并同类项:-5b^2 × 4b^2 = (-5×4)(b^2×b^2) = -20b^4通过上述例子可以看出,合并同类项时,我们将系数相乘,字母指数不变。
三、除法中的合并同类项在进行除法运算时,合并同类项的方法也与乘法类似。
我们将除数与被除数中具有相同字母指数的项的系数相除,并将字母指数保持不变。
例如:1. 合并同类项:8x^2 ÷ 4x = (8 ÷ 4)(x^2 ÷ x) = 2x2. 合并同类项:-12y^3 ÷ -3y^2 = (-12 ÷ -3)(y^3 ÷ y^2) = 4y通过上述例子可以看出,合并同类项时,我们将系数相除,字母指数不变。
四、化简代数表达式在复杂的代数表达式中,我们常常需要通过合并同类项来化简表达式,使其更为简洁。
例如:1. 表达式:3x + 4 - 2x + 5x首先,合并相同字母的项:(3x - 2x + 5x) + 4然后,将具有相同字母指数的项的系数相加:6x + 4最终化简后的表达式为:6x + 42. 表达式:2a^2b - b^2 + a^2b + 3ab^2 - 4a^2b首先,合并相同字母的项:(2a^2b + a^2b - 4a^2b) + (-b^2 + 3ab^2)然后,将具有相同字母指数的项的系数相加:-a^2b + 3ab^2 - b^2最终化简后的表达式为:-a^2b + 3ab^2 - b^2通过以上例子可以看出,通过合并同类项与化简代数表达式,我们可以更清晰地表达数学问题,使其更易于理解与求解。
小学数学解方程10种方法,解方程其实很简单(经典集锦)

小学解方程10种方法汇总一、未知数加减乘除1.形如x+a=b或x-a=b的方程。
(遇加同减,遇减同加)例1 x+7=19 遇加同减解:x+7-7=19-7 两边同时减去7X=12例2 x-6=19 遇减同加解:x-6+6=19+6 两边同时加上6x=252.利用等式解形如ax=b或x÷a=b(a不等于0)的方程。
(遇乘同除,遇除同乘)例1 7x=63 遇乘同除解:7x÷7=63÷7两边同时除以7x=9例2 x ÷7=9 遇除同乘解:x÷7×7=9×7两边同时乘以7x=633.利用等式解形如ax+b=c、ax-b=c或x÷a+b=c、x÷a-b=c(a不等于0)的方程。
(混合运算,先加减再乘除:能计算的要先计算)例1 2x+5=29 有乘法和加法,先算加法,遇加同减解:2x+5-5=29-5 两边同时减去52x=24 遇乘同除2x÷2=24÷2两边同时除以2x=12例2 5x-6=24 有乘法和减法,先算减法,遇减同加解: 5x-6+6=24+6 两边同时加上65x=30 遇乘同除5x÷5=30÷5两边同时除以5x=6例3 x÷7+3=10 有除法和加法,先算加法,遇加同减解:x÷7+3-3=10-3 两边同时减去3x÷7=7 遇除同乘x÷7×7=7×7两边同时乘以7x=49例4 x÷10-6=9 有除法和减法,先算减法,遇减同加x÷10-6+6=9+6 两边同时加上6x÷10=15遇除同乘x÷10×10=15×10两边同时乘以10x=150二、未知数被加上或被减去;4.未知数被加上a+x=b,a+bx=c(解法同上)5.形如b-x=c、b-ax=c的方程。
积分的加减乘除运算法则

积分的加减乘除运算法则积分是微积分中的重要概念,常用于求解曲线下的面积、曲线的长度、体积等问题。
积分的运算法则包括加法法则、减法法则、乘法法则和除法法则。
这些法则是计算积分时的基本规则,下面分别进行详细介绍。
1. 加法法则:若 f(x) 和 g(x) 在区间 [a, b] 上可积,则有∫[a, b] (f(x) + g(x)) dx = ∫[a, b] f(x) dx + ∫[a, b] g(x) dx这个法则可以理解为对函数的积分是可加的,即两个函数的和的积分等于它们分别的积分之和。
2. 减法法则:若 f(x) 和 g(x) 在区间 [a, b] 上可积,则有∫[a, b] (f(x) - g(x)) dx = ∫[a, b] f(x) dx - ∫[a, b] g(x) dx类似于加法法则,对函数的积分也是可减的,即两个函数的差的积分等于它们分别的积分之差。
3. 乘法法则:若 f(x) 和 g(x) 在区间 [a, b] 上可积,则有∫[a, b] f(x)g(x) dx = ∫[a, b] f(x) dx * ∫[a, b] g(x) dx乘法法则是指积分运算的乘法,即两个函数的积的积分等于它们分别的积分之积。
4. 除法法则:若 f(x) 和 g(x) 在区间 [a, b] 上可积,且 g(x) 不为零,则有∫[a, b] (f(x) / g(x)) dx = ∫[a, b] f(x) dx / ∫[a, b] g(x) dx除法法则是指积分运算的除法,即两个函数的商的积分等于它们分别的积分之商。
这几个积分运算法则是求解积分时常用的基本规则,可以通过这些法则将复杂的积分问题化简为简单的积分计算。
在实际应用中,我们可以根据具体的问题选择合适的法则来进行积分运算,从而得到最终的结果。
需要注意的是,积分运算法则的使用条件是函数在积分区间上是可积的,即函数在该区间上是连续的且没有间断点。
对于一些特殊的函数,如含有间断点的函数或者不连续函数,需要额外的方法进行处理,比如按区间进行分段求解,或者使用广义积分的概念来进行计算。
函数单调性加减乘除判定口诀
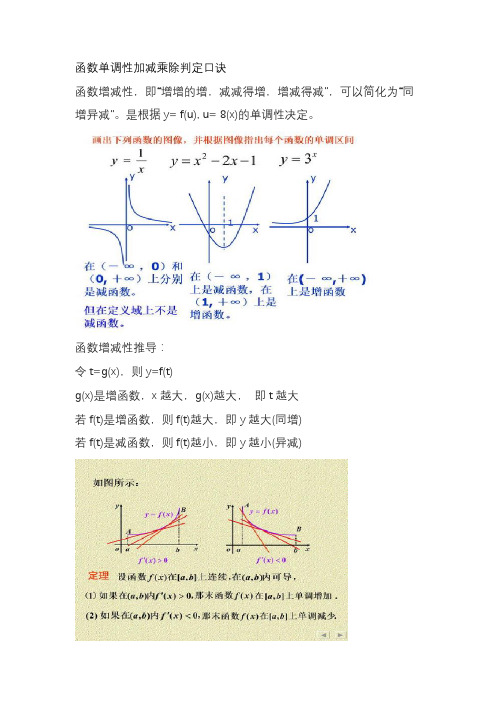
函数单调性加减乘除判定口诀
函数增减性,即“增增的增,减减得增,增减得减”,可以简化为“同增异减”。
是根据y= f(u), u= 8(x)的单调性决定。
函数增减性推导:
令t=g(x),则y=f(t)
g(x)是增函数,x越大,g(x)越大,即t越大
若f(t)是增函数,则f(t)越大,即y越大(同增)
若f(t)是减函数,则f(t)越小,即y越小(异减)
增函数与减函数的四则运算函数性质(增减性)不要求推倒过程,用简洁的等式关系表达即可比如增-增=x。
增函数与减函数的四则运算函数性质(增减性)不要求推倒过程,用简洁的等式关系表达即可。
指数对数函数增减性判断的方法是:(1)底数大于1时,它们是增函数;(2)底数大于零且小于1时,它们是减函数。
扩展资料:y=f[g(x)]型函数可以看作由两个函数y=f(u)和u=g (x)复合而成,一般称其为复合函数。
其中y=f(u)为外函数,u=g(x)为内函数。
若内、外函数的增减性相同,则原复合函数为增函数;相反则为减函数,即复合函数,单调性遵从同增异减的原则。
x代入原方程简便运算口诀

x代入原方程简便运算口诀解方程,真容易;
为什么?我来答;
性质1,加减等;
性质2,乘除等;
性质1来性质2,
用得对来终结果;
方程左,未知数;
方程右,终结果;
你要问我最难忘的是什么,
那就是中间等号要对齐,
检验里,需注意,
左开始,右结束,
先列式,再代入,
最后记得要所以。
2、方程方程是等式,必须含有未知数。
未知数值就是解,能使方程左右平。
解方程儿是过程,可以求出未知数。
要解方程很容易,同加同减同乘除。
未知在左数在右,解出方程带入验。
遇到复杂方程式,先找关系定整体。
慢慢清理身边数,只留未知才能算,
未知项前是减除,先加或乘未知项,
转换之后左右换,才能轻松把他算。
解方程技巧:
1、方程的左右两边同时加上或减去同一个数,方程的解不变。
2、方程的左右两边同时乘同一个不为0的数,方程的解不变。
3、方程的左右两边同时除以同一个不为0的数,方程的解不变。
4、根据加减乘除法各部分之间的关系解方程。
(1)根据加法中各部分之间的关系解方程。
(2)根据减法中各部分之间的关系解方程在减法中,被减速=差+减数。
(3)根据乘法中各部分之间的关系解方程在乘法中,一个因数=积/另一个因数例如:列出方程,并求出方程的解。
(4)根据除法中各部分之间的关系解方程。
解完方程后,需要
通过检验,验证求出的解是否成立。
