电子科大《信号与系统》考卷汇总
2015-2016年电子科技大学考研试题858信号与系统

(4) 若要从 y3 (t ) 中恢复出 y2 (t ) ,确定线性时不变系统 h2 (t ) 的频率响应 H2 ( jw)
七、(10 分)已知一个连续时间线性时不变系统是稳定系统,系统的单位冲击响应为偶信号,
系统函数为 H (S ) ,并满足下面条件,确定该系统的系统函数及收敛域。 (1) H (S ) 在有限的 S 平面内只有 4 个极点,没有零点 (2) h (-t ) 的拉普拉斯变换的一个极点为 S = 1 (3) h (t ) e j2t 的拉普拉斯变换的一个极点为 S = 0
电子科技大学 2015 年攻读硕士学位研究生入学考试试题
考试科目:858 信号与系统
注:所有答案必须写在答题纸上,写在试卷或草稿纸上均无效。
一、单项选择题(共 25 分,每题 5 分)
1、 下面说法正确的是( )
A) 连续时间周期信号与连续时间周期信号的和一定是周期信号
B) 离散时间周期信号与离散时间周期信号的和一定是周期信号
0
£
n £ M -1 其它n值
,则输出
y[n]
不为
0
的点数最多为___
______________。
2、 已知连续时间线性时不变系统的单位阶跃响应为 s (t ) = e-tu(t) ,则该系统的单位冲击响应
h (t ) 为_________________。 3、 x (t ) 的拉普拉斯变换 X (S ) 存在,且 X (S ) 为有理表达式,在有限的 S 平面内,只存在பைடு நூலகம்4
十 、( 15 分 ) 已 知 连 续 时 间 线 性 时 不 变 系 统 可 由 线 性 常 系 数 微 分 方 程
d
2 y(t
dt 2
杭州电子科技大学信号与系统真题2000-2009
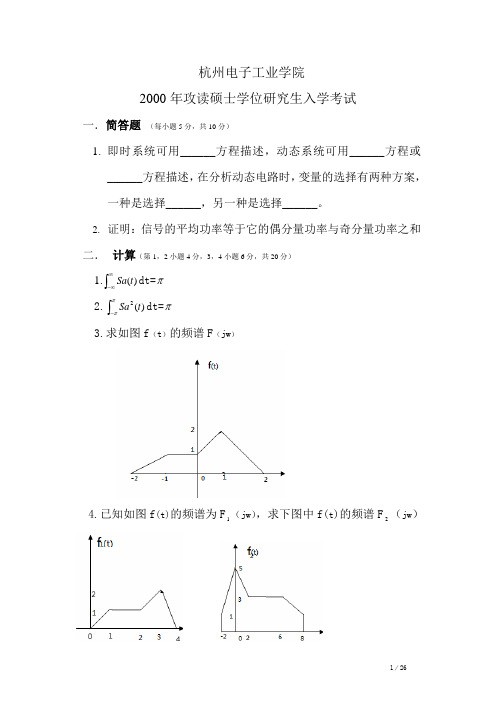
7. 已 知 线 性 时 不 变 系 统 的 输 入 — 输 出 方 程 为
r (t ) = ∫ e −(t −τ ) e(τ )dτ 则其冲击响应 h(t)为________
−∞
8.
e −αt u (t ) * sin tu (t ) = ________
9. 已知某连续系统的零点为 1;极点为 0,-3;冲激响应的终
要求:1 画出其信号流图; 2 写出其状态方程。(12 分)
某些地方难免出错,敬请见谅。 其中2001年真题以及历年答案本人没有找到, 如果谁有可以跟我联系。 做出一份比较完整的考研试卷帮助大家Q:305942916
7/26
杭州电子工业学院 2003 年攻读硕士学位研究生入学考试 《信号与系统》 (共九大题)
e − t u (t ) * sin t u (t ) =_______
3 £ [(1 + 2t )e −t ] = ________ 4 £ −1 ⎢
⎤ s+3 ⎥ =________ 3 ⎣ ( s + 1) ( s + 2) ⎦ ⎡
5 若 F [ f (t )] = F ( w) ,则 F[(1-t)f(1-t)]=_________ 6 已 知 系 统 函 数 H(s)= r(t)=_________
五. (8 分)系统如图所示,试画出其流图表示,并求转移函数 H(s) =
Y (s) 。 X ( s)
六. (10 分)信号的频谱如图所示,若此信号通过下图系统,试绘出 A、B、C、D 各点信号的频谱图形,设理想滤波器截止频率均为 W 0 ,
2/26
通带内传输值为 1,相移为零,且 W 0 >>W c .
值为-10,则该系统函数为 H(S)=________
西安电子科技大学信号与系统期末考试题
F(s)
s 1 2
k 题20图
s
1
2
∑ Y(s)
第0-12页
■
©西安电子科技大学电路与系统教研中心
1 2π
f 2 (t 3) dt
F (j ) dω
2
1 F (j ) dω 2 π
(B) (D)
1 2π
1 2π
F (j ) dω
j 3
2
F (j ) e
dω
第0-5页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
第0-10页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2005期末考试试题
(10分)19、如题19图所示电路,uL(t)和iR(t)为输出, uS(t)、iS(t)为输入,选iL(t)和uC(t)为状态变量。试列写状 态方程与输出方程。
2Ω uL a
1 F 3
iL
uS(t)
1 H 2
1 (k ),f (k) 2 2
k
= 1(–< k< ),
。
第0-7页
■
©西安电子科技大学电路与系统教研中心
信号与系统 电子教案
2005期末考试试题
Ⅲ、计算题(共6小题,50分)
请你写出简明解题步骤;只有答案得0分。非通用符号请 注明含义。
(10分)16、题16图所示因果系统, (1) 求系统函数H(z); (2) 求单位序列响应h(k); (3) 列写该系统的输入输出差分方程; (4) 判断该系统是否稳定。
4
t 题4图
2020西安电子科技大学《信号与系统》期末考试试题

答案+我名字学习中心/函授站 _姓名学号西安电子科技大学网络与继续教育学院2020 学年上学期《信号与系统》期末考试试题(综合大作业)题号一二三总分题分 32 30 38得分考试说明:1、大作业试题于 2020 年 4 月 23 日公布,2020 年 4 月 24 日至 2020 年 5 月 10 日在线上传大作业答卷(一张图片对应一张 A4 纸答题纸),要求拍照清晰、上传完整;2、考试必须独立完成,如发现抄袭、雷同均按零分计;3、答案须用《西安电子科技大学网络与继续教育学院标准答题纸》手写完成,要求字迹工整、卷面干净。
须知:符号(t)、(k)分别为单位阶跃函数和单位阶跃序列。
LTI 表示线性时不变。
为加法器。
一、单项选择题(共 8 小题,每小题 4 分,共 32 分)__ _ 1、等于 ( )t(A) 1 (B) (C) (D) 0 ( ) t ( ) t__ _ 2、等于 ( )ii(A) 1 (B) 0 (C) (D) ) (k ( ) k___ 3、等于A B C D ( ) t '( ) t ( ) a t1( ) ta__ _4、、波形如图 4 所示,则1 ( )f t2 ( )f t1 2( ) ( )* ( ) f t f t f t (2) f(A) (B) 1 (C) (D) 21232___5、和的波形如图 5 所示,则1 ( )f k2 ( )f k1 2( ) ( )* ( ) f k f k f k ( 1) f(A) 0 (B) 1 (C) 2 (D) 3__ _6、已知则其单边拉普拉斯变换的象函数 ( ) sin2 ( ) f t t t ( ) F s (A) (B) (C) (D)11 s2( 1) 4ss24ss224 s7、已知的频谱函数,则 ( ) f t1( )2jF jj( ) f t(A) (B) (C) (D)2( )te t23tt e2( ) 3tt e ( ) t8、已知则其双边 Z 变换的象函数等于1( ) ( ) 2 ( 1)2kf k k k( ) F zA 不存在BC D122z zzz122z zzz122z zzz二、填空题(共 6 小题,每小题 5 分,共 30 分)。
信号与系统试卷电科专业
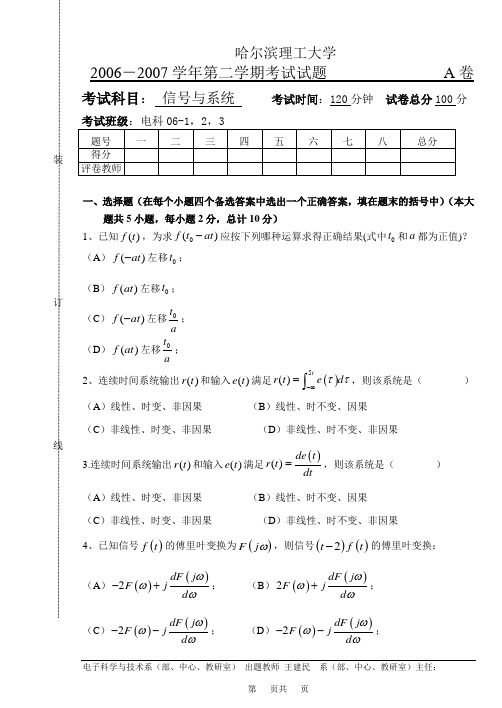
哈尔滨理工大学2006-2007学年第二学期考试试题 A 卷考试科目: 信号与系统 考试时间:120分钟 试卷总分100分一、选择题(在每个小题四个备选答案中选出一个正确答案,填在题末的括号中)(本大题共5小题,每小题2分,总计10分)1、已知()f t ,为求0()f t at -应按下列哪种运算求得正确结果(式中0t 和a 都为正值)? (A )()f at -左移0t ; (B )()f at 左移0t ; (C )()f at -左移0t a; (D )()f at 左移t a; 2、连续时间系统输出()r t 和输入()e t 满足()5()tr t e d ττ-∞=⎰,则该系统是( )(A )线性、时变、非因果 (B )线性、时不变、因果 (C )非线性、时变、非因果 (D )非线性、时不变、非因果 3.连续时间系统输出()r t 和输入()e t 满足()()de t r t dt=,则该系统是( ) (A )线性、时变、非因果 (B )线性、时不变、因果 (C )非线性、时变、非因果 (D )非线性、时不变、非因果4、已知信号()f t 的傅里叶变换为()F j ω,则信号()()2t f t -的傅里叶变换:(A )()()2dFj F j d ωωω-+; (B )()()2dF j F j d ωωω+;(C )()()2dF j F jd ωωω--; (D )()()2dF j F j d ωωω--;5、已知信号()f t 的傅里叶变换为()F j ω,则信号()2tf t 的傅里叶变换:(A )122dF j d ωω⎛⎫ ⎪⎝⎭-; (B )122dF j d ωω⎛⎫ ⎪⎝⎭; (C )()()2dF j F jd ωωω--; (D )()()2dF j F j d ωωω--; 6、连续周期信号的频谱具有( )(A )连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 7、连续非周期信号的频谱具有( )(A )连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 8、系统()()2r t e t =是(A )稳定系统、可逆系统 (B )稳定系统、非可逆系统 (C )非稳定系统、可逆系统 (D )非稳定系统、非可逆系统 9、系统()()5r t e t =-是(A )稳定系统、可逆系统 (B )稳定系统、非可逆系统 (C )非稳定系统、可逆系统 (D )非稳定系统、非可逆系统 二、填空题(每空2分,共20分) 1、()()0j t e t t t dt ωδδ∞--∞--⎡⎤⎣⎦⎰= ;2、()sin 6t t t dt πδ∞-∞⎛⎫+- ⎪⎝⎭⎰= ;3、确定信号()()210060Sa t Sa t +的最低抽样率 ,奈奎斯特间隔 ;4、确定信号()()210080Sa t Sa t +的最低抽样率 ,奈奎斯特间隔 ;哈尔滨理工大学2006-2007学年第二学期考试试题 A 卷5、确定信号()()1T n t t nT δδ∞=-∞=-∑的傅里叶变换 。
电子科技大学2014-2015 学年第 1 学期信号与系统期 末 考试 A 卷

电子科技大学2014-2015 学年第 1 学期期末考试A 卷课程名称:信号与系统考试形式:一页纸开卷考试日期:20 15年 1 月 15 日考试时长: 120 分钟课程成绩构成:平时 10 %,半期考试 20 %,实验 10 %,期末 60 %本试卷试题由二部分构成,共 5 页。
题号一二合计1234得分得分一、选择填空题(共30分,共 6问,每问5分)1.Consider two signals and , as shown in Figure 1. The Fourier transform of is . Then the Fourier transform ofshould be().(a)(b)(c)(d)Figure 1 The waveforms of and2. The convolution sum ( ).(a) (b) (c) (d) not existed3. Consider a stable discrete-time system, whose system function is a rational function and has only two poles:. The positions of zeros are unknown. The impulse response of the system must be ( ).(a) finite duration (b) right-sided (c) left-sided (d) two sided4.The relation between the input and the output of a causal continuous-time LTI system is described by the differential equation . The system is ().(a) Low-pass filter (b) Band-pass filter (c) High-pass filter (d) Band-stop filter5.The Fourier transform of the signal is shown in Figure 2.The signal may beFigure 2(a) real and even (b) real and odd(c) pure imaginary and odd (d) pure imaginary and even6. The Laplace Transform of is ().(a) , (b) ,(c) , (d) ,二、计算题(共70分)得分1.(15 points)Suppose and are both band-limited signals, where.Impulse-train sampling is performed on to obtain , as shown inFigure 3 where .Deduce the value of so that for .Specify the range ofvalues for the sampling period T which ensures that =.32.( 18 points ) Consider an LTI system with unit impulseresponse .The input signal ,where is the unit stepfunction.得分(a) Sketch. (b) Determine the magnitude and phase responseof this system. (c) Determine the output .3(17分)A causal continuous-time LTI system is given in Figure 4.(a)Determine the range of the constant K toensure that the system is stable.(b)If K=2, determine the unit step response.1/S-31/S-2KFigure 44(20 分)Suppose that we are given the following information about a causal discrete-time LTI system:(1)If the input is ,then the output is .(2)The value of the unit impulse response at n=0 is .Solve the following problems:(a) Determine the system function ,and indicate its ROC.(b) Draw a block diagram representation of this system.(c) Determine the unit impulse response .(d) Suppose. Determine the range of real numberso that is the unit impulse response of a stable system.。
电子科大历年信号与系统考研试题

2. 试求系统的单位冲激响应 ht ;
3. 若输入 x t et , t ,试求系统的输出 y t ;
4. 该系统是否稳定,是否因果。
xt
1/ s
1/ s
yt
2
2005年信号与系统考研试题
五、(16分)某离散时间系统的差分方程为:
yn 5 yn 1 1 yn 2 f n 1
电子科技大学
2008 年攻读硕士学位研究生入学试题
考试科目:836 信号与系统和数字电路
1.(15 分)完成下列卷积和与卷积积分的运算:
⑴.已知 x1n n n 1, x2 n 2n un 1 un 2
计算 xn x1n x2 n ,并画出 xn的波形;
⑵.已知 x1 t ut u t 2 , x2 t x1 2t
2009年信号与系统考研试题
试求出 xt 并画出其波形。
2.
(15
分)已知信号
x
t
sin
t
t
2
和
g
t
x nTS
t
nTS
,TS
2 3
,其傅里
叶变换分别为 X j 和 G j 。为确保 G j 1.5X j , 0 ,求出0 的最大
值。
3. (9 分) 实基带信号 xt 具有频谱 X j 0 , 100 ,假定 y t xt e jct ,试
3. 画出系统的幅频特性曲线,说明这是一个什么类型的系统。
R
Vi
Vo
R
C
2007年信号与系统考研试题
1. (10 分)某离散时间系统的输入为 xn,输出为 yn ,其输入输出关系为
y
电子科大信号与系统期中考试试卷及答案11-12学年

………密………封………线………以………内………答………题………无………效……电子科技大学二零 一 一 至二零 一 二 学年第 一 学期期 中 考试SIGNALS AND SYSTEMS 课程考试题 卷 ( 120 分钟) 考试形式: 闭卷 考试日期 20 11 年 月 日课程成绩构成:平时 10 分, 期中 20 分, 实验 10 分, 期末 60 分1(56points).Each of the following questions may have one or two right answers, justify your answers and write it in the blank. (1)()cos 221πδ+∞-∞-=⎰t t dt ( d ).(a) 1 (b) -1 (c) 0.5 (d) -0.5(2) The fundamental period of the signal []23cos sin 32ππ⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦x n n n is ( a ). (a) 12N = (b) 6N = (c) 8N = (d) 24N = (3) Let ()1tx t e -= and ()()()14k x t x t t k δ+∞=-∞=*-∑. The Fourier series coefficients of ()x t may be ( a ).(a) {} and Im 0-==k k k a a a (b) {} and Im 0-=-=k k k a a a (c) {} and Re 0-==k k k a a a (d) {} and Re 0k k k a a a -=-=(4) Consider an LTI system with unit impulse response ()h t illustrated in Figure 1, if the input is ()()d t x t dtδ=, the output () 0.5t y t =- is( b ).(a) -1 (b) 1 (c) -0.5 (d) 0.5(5) The convolution integral ()222t te e u t -*=( c ).(a) 2 (b)214te (c)212te (d)()212te u t(6) Which of the following systems is an linear system ( a ). In each example, []y n denotes the system output and []x n is the systeminput.(a) [][][]cos y n n x n = (b) [][]{}cos 3y n x n = (c) [][]()ln y n x n = (d) [][]2y n x n =(7) Which of the following systems are causal and stable system ( ad ). In each example, ()h t denotes the impulse response of thefollowing systems.(a) ()()()13h t t t δδ=-+- (b) ()()()0.5cos 2t h t t e u t =- (c) ()()()13h t t t δδ=+++ (d) ()()()cos 2t h t t e u t -=-(8) Determine the following signals which have finite total energy ( bc ). (a) []()[]1x n n u n =+ (b) ()()23tx t eu t -=+(c) []()[]1cos /32nx n n u n π⎛⎫= ⎪⎝⎭(d) () , tx t e t =-∞<<+∞tFigure 1………密………封………线………以………内………答………题………无………效……(9) Consider a continuous-time LTI system whose frequency response is ()()sin /2Hj ωωω=. If we know the output ()y t to some periodicinput signals are ()0y t =. The fundamental period of the input signal may be ( ac ). (a) 1T = (b) 2T = (c) 0.5T = (d) 3T =2(12points). A continuous-time signal ()32-+x t is illustrated in Figure 2.(a) Determine the signal ()x t . (b) Sketch and label carefully ()x t .3(10 points).Consider an LTI system whose response to the signal ()t x 1 in Figure 3 is the signal ()t y 1 illustrated in Figure 4. Determine the response of the system to the input ()t x 2 depicted in Figure 5 .4(12 points). Consider a continuous-time LTI system whose frequency response ()H j ω is illustrated in Figure 6. If the input signal()1cos 3sin 6ππ=++x t t t , determine the output of the system.12Figure 3ωFigure 6tFigure 2………密………封………线………以………内………答………题………无………效……14(10points). Consider an LTI system whose input []x n and unit impulse response []h n are given by []{}1,0,1,1,0,1x n n =-=-,[]{}2,1,3,2,2,3,4,5h n n ==. Determine the output [][][]n h n x n y *= of this system.《信号与系统》半期考试评分标准说明1.填空题(56分)⑴. (d) ⑵ (a) ⑶ (a) ⑷ (b) ⑸ (c) ⑹ (a) ⑺ (ad) ⑻ (bc) ⑼ (ac) ⑽ (ab) 本部分评分规则:1) 选择题共14个正确答案,1-6题为单选,7-10题为双选; 2) 若只填写了1个答案,正确得4分,错误得0分;3) 若填写了2个答案,2个正确得8分,1个正确、1个错误得4分,2个错误得0分;4) 若填写了3个答案,2个正确、1个错误得4分,1个正确、2个错误得2分,3个错误得0分; 5) 若填写了4个答案,得0分。
电子科大《信号与系统》考卷汇总

x t
cos 4 t
2
w t
H ( j )
2
w t
5 4
1
4
5
0
1
y t
H ( j )
X j
1
4
0
Figure 2 5
0
y t
5 4
Figure 1
0
信号与系统试卷
2004年7月
2. (
10points来自G j 15 X j for 0 ,
x t
h 1 t
r1 t
r2 t
H 2 j
y t
p t
Figure 2
信号与系统试卷
4. (15 points) The system function of an LTI system is
2
(a)Specify the range of values for the sampling period T which ensures that r1 t is recoverable from
r2 t .
(b) If T
1 second, sketch the spectrum of r1 t and r2 t . 20
Attention: You must answer the following questions in English.
信号与系统试卷 2005 1.( 12 points)The spectrum X j of the signal x t is depicted in Figure 1.
the output y t 1 . (a) Determine the system function H s , then indicate the ROC of H s . (b) Determine the unit impulse response h t of this system, is this system causal? (c) For the input x t te u t , compute the output y t .
1999年电子科技大学信号与系统考研试题 831
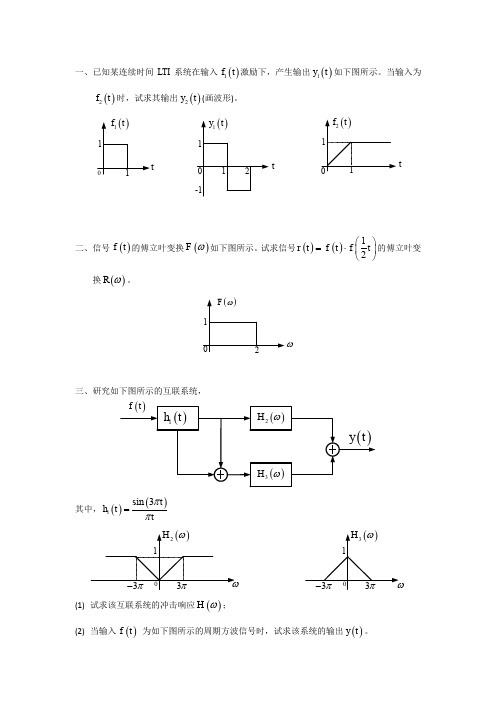
f 2 t 时,试求其输出 y2 t (画波形)。
f1 t
1
y1 t
1 1 1 2
f2 t
1
t
0 -1
t
0
1
t
二、信号 f t 的傅立叶变换 F 如下图所示。试求信号 r t f t f t 的傅立叶变 换 R 。
1、 求具有这一特性的连续时间 LTI 系统的系统函数 H s , 做其零极点图, 并标明收敛域; 2、 求该系统的冲激响应 h t ; 3、 写出描述该系统的数学模型(常系数微分方程); 4、 画出该系统的模拟框图; 5、 当输入 f t e
2t
t 时,求输出 y t 。
f t 又可写成 f t I t cos 2 fot Q t sin 2 f ot 。试设计一个系统,能够很方便
的从 f t 中获得 I t 和 Q t 。
被称为一节全通系统。试用解析房或者几何法证明之。
七、脉冲幅度调制 PAM 系统如下图所示,该系统的输出是 PAM 信号 f 0 t 。
f t
r t
p t
h0 t
PAM系统
f0 t
H
y t
图中 p t
n
t nT , h t 如下图所示:
F
1 2
1 0 2
三、研究如下图所示的互联系统,
f t
h1 t
H 2
电子科大《信号与系统》考卷汇总

高通滤波器
允许高频信号通过,抑制低频信号,用于提 取高频成分。
带通滤波器
允许某一频段的信号通过,抑制其他频段的 信号,用于提取特定频率范围的信号。
陷波滤波器
抑制特定频率的信号,用于消除特定频率的 干扰。
05
CATALOGUE
系统的频域分析
系统的频域响应
频域响应的定义
系统的频域响应是指在频域中描述系统对输入信号的响应特性。
实现信号处理算法的工具
实现信号处理算法需要使用专业的工具和软件,如MATLAB、Python等。这些工具提供了丰富的函数库 和工具箱,方便用户进行信号处理和分析。
系统设计中的信号处理技术
系统设计中的信号处 理需求
在系统设计中,信号处理技术是 必不可少的。系统中的信号可能 受到噪声、干扰和其他因素的影 响,导致信号质量下降。因此, 需要进行信号处理以提取有用信 息,提高信号质量。
过程。
02
调制解调技术的分类
调制解调技术可以分为模拟调制和数字调制两大类,模拟调制包括调频
、调相和调幅等,数字调制包括振幅键控、频率键控和相位键控等。
03
调制解调技术的应用
调制解调技术广泛应用于通信、雷达、声呐和遥控等领域,是实现信号
传输和处理的关键技术之一。
06
CATALOGUE
信号与系统的综合应用
信号的时移
将信号在时间轴上移动一定的时间,可以得到一 个新的信号。
信号的展缩
将信号的幅度进行放大或缩小,可以得到一个新 的信号。
信号的反转
将信号在时间轴上进行翻转,可以得到一个新的 信号。
03
CATALOGUE
系统的时域分析
系统的时域响应
瞬态响应
西安电子科技大学811信号与系统通信原理专业课考研真题答案 74页

A2
σ
2 n
得 Pe
1 2
erfc(
A 2σn
)
1 2
erfc
r 2
3. (1) 框图见附录;
(2) 见图 12-2;
(3)
B 1.5 fc , η
RB B
fc 1.5 f
c
2 3
B/Hz
sMSK (t) 0 1 1 0 0 1 t
4. (1) 789 为正→ C1 1 ; 512 789 1024
9. 3;3【解析】码重指码组中非零元素的个数;码距指两个码组 ci 、 cj 之间不同比特的个数。
10. 载波同步、位同步、帧同步 【解析】载波同步是相干解调的基础;位同步是正确取样判决的基础; 而接收端在收到比特流后,必须能够正确地找出帧定界符,以便知道哪些比特构成一个帧,接收端 找到了帧定界符并确定帧的准确位置就是完成了帧同步。
二、简答题
1. ①幅度失真、相位失真;②见附录;③均衡技术。 2. ①见附录;② +1 0 0 0 +V -1 +1 -B 0 0 -V +1 0 0 0 -1
【解析】编码规则见附录。 3. ①原理框图见附录;
·3·
②工作原理:以 2PSK 信号为例,来分析采用平方环的情况。2PSK 信号平方后得到
θ (t)
→位于第七段→ C2C3C4 110 ;
π
789 512 32
8
......
21 →位于序号为
8
的量化级
2
t
→ C5C6C7C8 1000
-π
∴编码器的输出码组为 11101000。
由 D(n1) D(n2 ) σ 2 以及概率论知识, D(x) D(an1 bn2 ) a2D(n1) (b)2 D(n2 ) σ2 (a2 b2 )
第四章考题电子科技大学信号与系统858期末复习

2012
11. (16 points) Let X ( j) denotethe Fourier transformof
the signal x(t) depicted in Figure 1.
a).Determine the expression of ReX ( j).
b). Determinethe valueof h2 (t)dt. -
c).Determinethe convolution integral
y(t)
k 0
k
1 1
sin(2kt
)
h(t).
Solution
16.
a)H(j
)
j,
0,
2 , if the input x(t) is
t
depictedin Figure,determinetheoutput y(t).
x(t)
…… -3
1
-1
1
……
3
5
t
Solution
17. y(t) cos2t cost
18. x(t) e j0t ,
h(t) u(t 1) u(t 1),
Solution
1.H(jω)来自 j,
0
0, 0
x(t)
e j0t
1
e j30t
1
e j30t
1
j 0 t
e4
1
j0 t
e4
2j
2j
2
2
y(t)
ak H (
k
信号与系统题库(完整版)

信号与系统题目部分,(卷面共有200题,0.0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x[n]如下图所示,则x[n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad sπ,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk --+)u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。
