单元滚动检测卷(七)
青岛版四年级数学上册第六、七单元跟踪检测卷

第六、七单元跟踪检测卷一、用心思考,正确填写。
(每空1分,共22分)1.小玲从家到学校每分钟走70米,需要12分钟,小玲家到学校的距离是( )米,利用公式( )×( )=( )来计算。
2.一辆汽车5小时行驶420千米,平均每小时行驶多少千米?这是已知( )和( )求( ),结果是( )。
3.一瓶饮料的价格是8元,买10瓶这样的饮料需要( )元,120元能买这种饮料( )瓶。
4.计算9×240-40÷5时,( )和( )可以同时计算,计算结果是( )。
如果把运算顺序改为先求差,再求积,最后求商,则式子变为( )。
5.80÷(8+12)×2的计算结果是( ),如果去掉小括号,计算结果是( )。
6.在里填上“>”“<”或“=”。
23+17×8(23+17)×8 256-(56-34)256-56-34 42×7÷642÷6×7 180÷15×3180÷(15×3) 7.小刚2分钟能做18道口算题,照这样的速度,5分钟能做( )道,做完90道需要( )分钟。
二、仔细推敲,判断对错。
(对的打“√”,错的打“×”。
每题1分,共4分)1.58+37-58+37=0 ( )2.小明平均每分钟折12架纸飞机,可以写作12架/分。
( ) 3.在混合运算中,必须按照先算乘除法后算加减法的顺序计算。
( ) 4.花同样的钱买两种货物,A种货物买的数量多,B种货物买的数量少,说明A种货物的单价便宜些。
( ) 三、反复比较,择优录取。
(选择正确答案的序号填入括号,每空1分,共7分)1.在计算350÷[7×(45-40)]时,第一步求的是( )。
A.积B.商C.差2.汽车每小时行驶75千米,4小时行驶300千米,下列算式各表示什么意义?(1)4×75=300(千米)表示求( )。
单元滚动检测卷(五)

单元滚动检测卷(五)[测试范围:第八单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.若一个多边形的每一个外角都等于40°,则这个多边形的边数是(C) A.7B.8C.9 D.10【解析】∵360°÷40°=9,∴这个多边形的边数是9.2.如图5-1,▱ABCD中,AE平分∠DAB,∠B=100°,则∠AED=(D)图5-1A.100°B.80°C.60°D.40°【解析】在▱ABCD中,∵AD∥BC,∴∠DAB=180°-∠B=180°-100°=80°.∵AE平分∠DAB,∴∠DAE=∠EAB=12∠DAB=40°.又∵AB∥DC,∴∠AED=∠EAB=40°.3.如图5-2,下列四组条件中,不能判定四边形ABCD是平行四边形的是(C)图5-2A.AB=DC,AD=BCB.AB∥DC,AD∥BCC.AB∥DC,AD=BCD.AB∥DC,AB=DC【解析】根据平行四边形的判定定理,A、B、D均符合判定平行四边形的条件,C则不能判定是平行四边形.4.如图5-3,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有(D)图5-3A.2条B.4条C.5条D.6条【解析】∵在矩形ABCD中,AC=16,∴AO=BO=CO=DO=12×16=8.∵AO=BO,∠AOB=60°,∴△AOB是等边三角形,∴AB=AO=8,∴CD=AB=8,∴共有6条线段长度为8.5.下列命题是假命题的是(C) A.平行四边形的对边相等B.四条边都相等的四边形是菱形C.矩形的两条对角线互相垂直D.等腰梯形的两条对角线相等6.已知菱形的边长和一条对角线的长均为2 cm,则菱形的面积为(D) A.3 cm2B.4 cm2C. 3 cm2D.2 3 cm2【解析】菱形的边长和一条对角线的长相等,则这条对角线把菱形分成两个全等的等边三角形,所以S菱形=12×32×2×2×2=23(cm2).选D.7.如图5-4,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是(C)图5-4A.24 B.16C.413 D.2 38.顺次连结矩形四边中点所得的四边形一定是(C) A.正方形B.矩形C.菱形D.等腰梯形【解析】如图,连结AC,BD,在△ABD中,∵AH=HD,AE=EB,∴EH=12BD,同理FG=12BD,HG=12AC,EF=12AC.第8题答图又∵在矩形ABCD中,AC=BD,∴EH=HG=GF=FE,∴四边形EFGH为菱形.9.如图5-5所示,矩形纸片ABCD 中,AB =6 cm ,BC =8 cm ,现将其沿EF 对折,使得点C 与点A 重合,则AF 的长为( B )图5-5A.258 cm B.254cm C.252 cmD .8 cm【解析】 设AF =x cm ,则DF =(8-x )cm ,∵矩形纸片ABCD 中,AB =6 cm ,BC =8 cm ,现将其沿EF 对折,使得点C 与点A 重合, ∴DF =D ′F . 在Rt △AD ′F 中, ∵AF 2=AD ′2+D ′F 2,∴x 2=62+(8-x )2,解得x =254(cm).10.如图5-6,正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE =22.5°,EF ⊥AB ,垂足为F ,则EF 的长为( C )图5-6A .1B. 2 C .4-2 2D .32-4【解析】 在正方形ABCD 中, ∠ABD =∠ADB =45°. ∵∠BAE =22.5°,∴∠DAE=90°-∠BAE=90°-22.5°=67.5°.在△ADE中,∠AED=180°-45°-67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4.∵正方形的边长为4,∴BD=42,∴BE=BD-DE=42-4.∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=22BE=22×(42-4)=4-2 2.故选C.第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图5-7,梯形ABCD中,AD∥BC,AD=4,AB=5,BC=10,CD的垂直平分线交BC于E,连结DE,则四边形ABED的周长等于__19__.图5-7【解析】∵CD的垂直平分线交BC于E,∴DE=CE,∴四边形ABED的周长=AD+AB+BE+DE=AD+AB+BE+CE=AD+AB +BC.∵AD=4,AB=5,BC=10,∴四边形ABED的周长=4+5+10=19.12.菱形ABCD中,若对角线长AC=8 cm,BD=6 cm,则边长AB=__5__cm.【解析】设菱形ABCD的对角线AC与BD相交于点O,∵菱形ABCD中,对角线长AC=8 cm,BD=6 cm,∴AO=12AC=4 cm,BO=12BD=3 cm.∵菱形的对角线互相垂直,∴在Rt△AOB中,AB=AO2+BO2=42+32=5(cm).13.如图5-8,在四边形ABCD中,已知AB=CD,再添加一个条件__答案不唯一,如AB∥CD或AD=BC或∠A+∠D=180°或∠B+∠C=180°__(写出一个即可),使四边形ABCD是平行四边形(图形中不再添加辅助线).图5-8【解析】添加的条件可以是另一组对边AD与BC相等,也可以是AB与CD 这一组对边平行.14.在四边形ABCD中,AB=DC,AD=BC,请再添加一个条件,使四边形ABCD 是矩形.你添加的条件是__∠A=90°或∠B=90°或∠C=90°或∠D=90°或AC=BD(答案不唯一,写出一种即可)__(写出一种即可).【解析】填其中任一内角为90°或对角线相等即可.15.如图5-9,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离是__4__ cm.图5-9【解析】∵BD平分∠ABC,又∵PE⊥AB,PE=4 cm,∴点P到BC的距离为4 cm.16.如图5-10,在梯形ABCD中,DC∥AB,∠A+∠B=90°.若AB=10,AD =4,DC=5,则梯形ABCD的面积为__18__.图5-10【解析】 作CE ∥AD 交AB 于E ,CF ⊥AB 于F ,则易证CE ⊥CB ,BC =52-42=3, ∴CF =CE ·BC BE =125,∴S 梯形ABCD =5+102×125=18.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.在四边形ABCD 中,∠D =60°,∠B 比∠A 大20°,∠C 是∠A 的2倍,求∠A ,∠B ,∠C 的大小.解:设∠A =x ,则∠B =x +20°,∠C =2x .由四边形内角和定理得x +(x +20°)+2x +60°=360°,解得x =70°, ∴∠A =70°,∠B =90°,∠C =140°.18.如图5-11,四边形ABCD 是平行四边形,E ,F 分别是BC ,AD 上的点,∠1=∠2.求证:△ABE ≌△CDF .图5-11证明:∵四边形ABCD 是平行四边形, ∴∠B =∠D ,AB =CD ,∴在△ABE 与△CDF 中,⎩⎨⎧∠1=∠2,AB =CD ,∠B =∠D ,∴△ABE ≌△CDF (ASA ).19.如图5-12,四边形ABCD是菱形,对角线AC与BD相交于点O,∠ACD =30°,BD=6.(1)求证:△ABD是正三角形;(2)求AC的长(结果可保留根号).图5-12解:(1)证明:∵AC是菱形ABCD的对角线,∴AC平分∠BCD.∵∠ACD=30°,∴∠BCD=60°.∵∠BAD与∠BCD是菱形的一组对角,∴∠BAD=∠BCD=60°.∵AB,AD是菱形的两条边,∴AB=AD.∴△ABD是正三角形.(2)∵O为菱形对角线的交点,∴AC=2OC,OD=12BD=3,∠COD=90°.在Rt△COD中,ODOC=tan∠OCD=tan30°,∴OC=ODtan30°=333=3 3.∴AC=2OC=6 3.答:AC的长为6 3.20.如图5-13,四边形ABCD是矩形,E是AB上一点,且DE=AB,过C作CF⊥DE,垂足为F.(1)猜想AD与CF的大小关系;(2)请证明上面的结论.图5-13解:(1)AD=CF.(2)证明:∵四边形ABCD是矩形,∴CD∥AE,AB=CD.∴∠AED=∠FDC.∵DE=AB,∴DE=AB=CD.又∵CF⊥DE,∴∠CFD=∠A=90°.∴△ADE≌△FCD(AAS).∴AD=CF.21.已知:如图5-14,在▱ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连结EF,分别交AB,CD于点M,N,连结DM,BN.(1)求证:△AEM≌△CFN;(2)求证:四边形BMDN是平行四边形.图5-14证明:(1)∵四边形ABCD是平行四边形,∴∠DAB=∠BCD,∴∠EAM=∠FCN.又∵AD∥BC,∴∠E=∠F.∵AE=CF,∴△AEM≌△CFN.(2)由(1)得AM=CN,又∵四边形ABCD是平行四边形,∴AB綊CD,∴BM綊DN,∴四边形BMDN是平行四边形.22.如图5-15,△ABC中,∠B=90°,AB=6 cm,BC=8 cm.将△ABC沿射线BC方向平移10 cm,得到△DEF,A,B,C的对应点分别是D,E,F,连结AD,求证:四边形ACFD是菱形.图5-15证法一:∵∠B=90°,AB=6 cm,BC=8 cm,∴AC=AB2+BC2=10 cm.由平移变换的性质得CF=AD=10 cm,DF=AC=10 cm,∴AD=CF=AC=DF,∴四边形ACFD是菱形.证法二:由平移变换的性质得AD∥CF,AD=CF=10 cm,∴四边形ACFD是平行四边形.∵∠B=90°,AB=6 cm,BC=8 cm,∴AC=AB2+BC210 cm,∴AC=CF,∴平行四边形ACFD是菱形.23.已知:如图5-16,四边形ABCD的对角线AC,BD交于点O,BE⊥AC于点E,DF⊥AC于点F,点O既是AC的中点,又是EF的中点.(1)求证:△BOE≌△DOF;(2)若OA=12BD,则四边形ABCD是什么特殊四边形?请说明理由.图5-16解:(1)证明:∵BE⊥AC,DF⊥AC,∴∠BEO=∠DFO=90°.∵点O是EF的中点,∴OE=OF.又∵∠DOF=∠BOE,∴△BOE≌△DOF(ASA).(2)四边形ABCD是矩形.理由如下:∵△BOE≌△DOF,∴OB=OD.又∵OA=OC,∴四边形ABCD是平行四边形.∵OA=12BD,OA=12AC,∴BD=AC,∴▱ABCD是矩形.24.已知△ABC为等边三角形,点D为直线BC上一动点(点D不与B,C重合),以AD为边作菱形ADEF(A,D,E,F按逆时针排列),使∠DAF=60°,连结CF.(1)如图5-17(1),当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图5-17(2),当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC,CF,CD之间存在的数量关系,并说明理由;(3)如图5-17(3),当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC,CF,CD之间存在的数量关系.(1)(2)(3)图5-17解:(1)①∵△ABC是等边三角形,∴AB=AC,∠BAC=60°.∵四边形ADEF为菱形,∴AD=AF.∵∠BAC=∠DAF=60°,∴∠BAC-∠DAC=∠DAF-∠DAC,即∠BAD=∠CAF,∴△ABD≌△ACF,∴BD=CF.②∵AC=BC=BD+CD,且由①知BD=CF,∴AC=CF+CD.(2)不成立.存在的数量关系为:CF=AC+CD.理由:由(1)同理可得△ABD≌△ACF,∴BD=CF.∵BD=BC+CD=AC+CD,∴CF=AC+CD.(3)CD=AC+CF.补全图形如图所示.第24题答图。
单元滚动检测卷(三)

单元滚动检测卷(三)[测试范围:第五单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.如图3-1,在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度后,那么平移后对应的点A′的坐标是(C)图3-1A.(-2,-3)B.(-2,6)C.(1,3) D.(-2,1)2.当x>0时,函数y=-5x的图象在(A)A.第四象限B.第三象限C.第二象限D.第一象限3.在平面直角坐标系中,下列函数的图象经过原点的是(C)A.y=-x+3 B.y=5 xC.y=2x D.y=-2x2+x-74.二次函数y=ax2+bx+c(a≠0)的图象如图3-2所示,则函数值y<0时x的取值范围是(C)图3-2A.x<-1B.x>3C.-1<x<3D.x<-1或x>3【解析】由图象可知,当-1<x<3时,函数图象在x轴的下方,此时y<0.5.如图3-3,正比例函数y1与反比例函数y2相交于点E(-1,2),若y1>y2>0,则x的取值范围在数轴上表示正确的是(A)图3-3图3-46.把抛物线y=12x2-1先向右平移1个单位,再向下平移2个单位,得到的抛物线的解析式为(B)A.y=12(x+1)2-3B.y=12(x-1)2-3C.y=12(x+1)2+1D.y=12(x-1)2+17.关于二次函数y=2(x-3)2+1有下列说法:①其图象的开口向下;②其图象的对称轴为直线x=-3;③其图象顶点坐标为(3,-1);④当x<3时,y随x的增大而减小.则其中正确的有(A) A.1个B.2个C.3个D.4个【解析】①∵a=2>0,∴图象的开口向上,故本说法错误;②图象的对称轴为直线x=3,故本说法错误;③图象顶点坐标为(3,1),故本说法错误;④当x<3时,y随x的增大而减小,故本说法正确.综上所述,说法正确的只有1个.故选A.8.某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是(C)图3-5【解析】根据某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间,休息时油量不发生变化,再次出发后油量继续减小,即可得出符合要求的图象.9.如图3-6,二次函数y =ax 2+bx +c 的图象与y 轴正半轴相交,其顶点坐标为⎝ ⎛⎭⎪⎫12,1,下列结论:①ac <0;②a +b =0;③4ac -b 2=4a ;④a +b +c <0.其中正确结论的个数是( C )图3-6A .1B .2C .3D .4【解析】 根据图象可知: ①a <0,c >0,∴ac <0正确; ②∵顶点横坐标等于12,∴-b 2a =12, ∴a +b =0正确;③∵顶点纵坐标为1,∴4ac -b 24a =1, ∴4ac -b 2=4a ,正确;④当x =1时,y =a +b +c >0,错误. 正确的有3个,故选C.10.某公园草坪的防护栏是由100段形状相同的抛物线组成的.为了牢固起见,每段护栏需要间距0.4 m 加设一根不锈钢的支柱,防护栏的最高点距底部0.5 m(如图3-7),则这条防护栏需要不锈钢支柱的总长度至少为 ( C )A .50 mB .100 mC .160 mD .200 m图3-7【解析】 建立如图所示的直角坐标系.设抛物线解析式为y =a (x +1)(x -1), 将点(0,0.5)的坐标代入得a =-0.5, ∴y =-0.5x 2+0.5. 当x =0.2时,y =0.48; 当x =0.6时,y =0.32,第10题答图∴每一段护栏需用支柱的长度为2×(0.48+0.32)=1.6(m),1.6×100=160(m),选C.第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.在平行四边形ABCD 中,已知点A (-1,0),B (2,0),D (0,1),则点C 的坐标为__(3,1)__.【解析】 如图,∵平行四边形ABCD 中,已知点A (-1,0),B (2,0),D (0,1),∴AB =CD =2-(-1)=3,DC ∥AB ,第11题答图∴点C 的横坐标是3,纵坐标和点D 的纵坐标相等,是1, ∴点C 的坐标是(3,1).12.如图3-8,一次函数y 1=ax +b (a ≠0)与反比例函数y 2=kx (k ≠0)的图象交于A (1,4),B (4,1)两点,若y 1>y 2,则x 的取值范围是__1<x <4或x <0__.图3-8【解析】 根据图象,当x <0或1<x <4时,一次函数的图象在反比例函数的图象上方,即y 1>y 2.13.已知一次函数y =kx +b (k ≠0)经过(2,-1),(-3,4)两点,则它的图象不经过第__三__象限.14.如图3-9,已知二次函数y =x 2+bx +c 的图象经过点(-1,0),(1,-2),当y 随x 的增大而增大时,x 的取值范围是__x ≥12__.图3-9【解析】 依题意有⎩⎨⎧0=(-1)2-b +c ,-2=1+b +c ,解得⎩⎨⎧b =-1,c =-2,∴y =x 2-x -2,对称轴为x =12,∴当x ≥12时,y 随x 的增大而增大.15.二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)图象的对称轴是直线x =1,其图象的一部分如图3-10所示.对于下列说法:①abc <0;②当-1<x <3时,y >0;③3a +c <0;④a -b +c <0,其中正确的是__①③④__(把正确的序号都填上).图3-10【解析】 根据图象可得:a <0,b >0,c >0, 则abc <0,故①正确;当-1<x <3时图象上有的点在x 轴的上方,有的点在x 轴的下方,故②错误; 根据图示知,该抛物线的对称轴是直线x =1,即-b2a =1,则b =-2a ,那么当x =-1时,y =a -b +c =a +2a +c =3a +c <0,故③正确;当x =-1时,对应的二次函数图象上的点一定在x 轴的下方,因而其纵坐标a -b +c <0,故④正确.16.抛物线y =ax 2+bx +c 上部分点的横坐标x ,纵坐标y 的对应值如下表:__①③④__(①抛物线与x 轴的一个交点为(3,0);②抛物线y =ax 2+bx +c 的最大值为6; ③抛物线的对称轴是x =12;④在对称轴左侧,y 随x 的增大而增大. 【解析】 观察可知抛物线对称轴为x =12,设抛物线解析式为y =a ⎝ ⎛⎭⎪⎫x -122+h ,把(-2,0)和(0,6)的坐标代入,得 ⎩⎪⎨⎪⎧0=a ⎝ ⎛⎭⎪⎫-522+h ,6=a ⎝ ⎛⎭⎪⎫-122+h , 解得⎩⎪⎨⎪⎧a =-1,h =254,∴y =-⎝ ⎛⎭⎪⎫x -122+254,∴正确的有①③④.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.常用的确定物体位置的方法有两种.如图3-11,在4×4个边长为1的正方形组成的方格中,标有A,B两点.请你用两种不同方法表述点B相对点A 的位置.图3-11解:方法1:用有序实数对(a,b)表示.比如:以点A为原点,水平向右方向为x轴正方向,竖直向上方向为y轴正方向,建立直角坐标系,则B(3,3).方法2:用方向和距离表示.比如:B点位于A点的东北方向(北偏东45°等均可),距离A点32处.18.在直角坐标系xOy中,直线l过(1,3)和(3,1)两点,且与x轴,y轴分别交于A,B两点.(1)求直线l的函数关系式;(2)求△AOB的面积.图3-12解:(1)设直线l的函数关系式为y=kx+b(k≠0),把坐标(3,1),(1,3)代入,得⎩⎨⎧3k +b =1,k +b =3,解方程组得⎩⎨⎧k =-1,b =4,∴直线l 的函数关系式为y =-x +4; (2)当x =0时,y =4, ∴B (0,4);当y =0时,-x +4=0, 解得x =4, ∴A (4,0),∴S △AOB =12AO ·BO =12×4×4=8.19.已知点P (2,2)在反比例函数y =kx (k ≠0)的图象上. (1)当x =-3时,求y 的值; (2)当1<x <3时,求y 的取值范围.解:(1)∵点P (2,2)在反比例函数y =kx (k ≠0)的图象上, ∴2=k2,即k =4,∴反比例函数的解析式为y =4x , ∴当x =-3时,y =-43.(2)∵当x =1时,y =4;当x =3时,y =43,又反比例函数y =4x 在x >0时y 值随x 值的增大而减小,∴当1<x <3时,y 的取值范围为43<y <4.20.一名男生推铅球,铅球行进高度y (单位:m)与水平距离x (单位:m)之间的关系是y =-112x 2+23x +53,铅球运行路线如图3-13所示. (1)求铅球推出的水平距离;(2)通过计算说明铅球行进高度能否达到4 m?图3-13解:(1)当y =0时,-112x 2+23x +53=0, 解得x 1=10,x 2=-2(不合题意,舍去), 所以铅球推出的水平距离是10米.(2)y =-112x 2+23x +53=-112(x 2-8x +16-16)+53 =-112(x 2-8x +16)+53+43=-112(x -4)2+3, 当x =4时,y 取最大值3,所以铅球行进高度不能达到4 m ,最高只能达到3 m.21.如图3-14,二次函数y =ax 2+bx 的图象经过A (1,-1),B (4,0)两点. (1)求这个二次函数解析式;(2)点M 为坐标平面内一点,若以点O ,A ,B ,M 为顶点的四边形是平行四边形,请直接写出点M 的坐标.图3-14解:(1)∵二次函数y =ax 2+bx 的图象经过A (1,-1),B (4,0)两点, ∴⎩⎨⎧a +b =-1,16a +4b =0,解得⎩⎪⎨⎪⎧a =13,b =-43,∴二次函数的解析式为y =13x 2-43x .(2)根据题意,得M 1(3,1),M 2(-3,-1),M 3(5,-1).22.如图3-15,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =m x的图象交于一、三象限内的A ,B 两点,直线AB 与x 轴交于点C ,点B 的坐标为(-6,n ),线段OA =5,E 为x 轴正半轴上一点,且tan ∠AOE =43.(1)求反比例函数的解析式;(2)求△AOB 的面积.图3-15解:(1)如图,过点A 作AD ⊥x 轴于点D ,第22题答图在Rt △AOD 中,tan ∠AOE =AD OD =43,设AD =4x ,OD =3x ,又OA =5,∴在Rt △AOD 中,根据勾股定理可得AD =4,OD =3,∴A (3,4).把A (3,4)的坐标代入反比例函数y =m x 的解析式中,解得m =12,则反比例函数的解析式为y =12x ;(2)把点B 的坐标(-6,n )代入y =12x 中,解得n =-2,则点B 的坐标为(-6,-2).把A (3,4)和B (-6,-2)的坐标分别代入一次函数y =kx +b (k ≠0)的解析式中,得⎩⎨⎧3k +b =4,-6k +b =-2,解得⎩⎪⎨⎪⎧k =23,b =2,则一次函数的解析式为y =23x +2.∵点C 在x 轴上,令y =0,得x =-3,即OC =3,∴S △AOB =S △AOC +S △BOC =12×3×4+12×3×2=9.23.在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y (个)与销售单价x (元/个)之间的对应关系如图3-16所示.(1)试判断y 与x 之间的函数关系,并求出函数关系式;(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w (元)与销售单价x (元/个)之间的函数关系式;(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.图3-16解:(1)y 是x 的一次函数,设y =kx +b ,∵一次函数的图象过点(10,300),(12,240),∴⎩⎨⎧10k +b =300,12k +b =240,解得⎩⎨⎧k =-30,b =600,∴y =-30x +600.当x =14时,y =180;当x =16时,y =120,即点(14,180),(16,120)均在函数y =-30x +600的图象上,∴y 与x 之间的函数关系式为y =-30x +600.(2)w =(x -6)(-30x +600)=-30x 2+780x -3 600,即w 与x 之间的函数关系式为w =-30x 2+780x -3 600.(3)由题意,得6(-30x +600)≤900,解得x ≥15.w =-30x 2+780x -3 600图象的对称轴为x =-7802×(-30)=13, ∵a =-30<0,∴抛物线开口向下,当x ≥15时,w 随x 的增大而减小,∴当x =15时,w 最大=1 350,即以15元/个的价格销售这批许愿瓶可获得最大利润1 350元.24.在平面直角坐标系xOy 中,抛物线y =mx 2-2mx -2(m ≠0)与y 轴交于点A ,其对称轴与x 轴交于点B .(1)求点A ,B 的坐标;(2)设直线l与直线AB关于该抛物线的对称轴对称,求直线l的解析式;(3)若该抛物线在-2<x<-1这一段位于直线l的上方,并且在2<x<3这一段位于直线AB的下方,求该抛物线的解析式.图3-17解:(1)对于y=mx2-2mx-2,当x=0时,y=-2,∴A(0,-2).抛物线的对称轴为x=--2m2m=1,∴B(1,0).(2)易得A点关于对称轴x=1的对称点为A′(2,-2),第24题答图则直线l经过点A′,B.设直线l的解析式为y=kx+b,则⎩⎨⎧2k +b =-2,k +b =0,解得⎩⎨⎧k =-2,b =2, ∴直线l 的解析式为y =-2x +2.(3)∵抛物线的对称轴为x =1,抛物线在2<x <3这一段与抛物线在-1<x <0这一段关于对称轴x =1对称,结合图象可以观察到抛物线在-2<x <-1这一段位于直线l 的上方,在-1<x <0这一段位于直线l 的下方,∴抛物线与直线l 的其中一个交点横坐标为-1,由直线l 的解析式为y =-2x +2,当x =-1时,y =-2×(-1)+2=4,则抛物线过点(-1,4),故当x =-1时,m +2m -2=4,解得m =2,∴抛物线的解析为y =2x 2-4x -2.。
《高考总复习单元滚动卷》简介

学习过程中,不可避免地伴随着遗忘。
“艾宾浩斯遗忘曲线”告诉我们,知识的遗忘是有规律的,遵循“先快后慢”的原则。
在一轮复习过程中,“滚动复习”模式能加深对知识前后、左右的联系,对于夯实基础、防止遗忘,效果是十分明显的。
针对以上思路,我们经过探索,编写了这套深具“滚动复习”特点的备考试卷。
本试卷立足教材基础知识,科学划分单元、合理编排试题,并有侧重地进行滚动复习。
特点如下:一、全面系统,立足一轮复习。
一轮复习,主要是对教材基础知识的梳理,强调复习的全面性、系统性。
本书以单元(章)为单位命制试卷,注重知识点的合理搭配,关注大纲和考试说明的要求,关注学习中的薄弱环节,关注重点、难点以及高考热点。
二、精心命题,拓展前沿视野。
题目来源:百强名校、重点中学2010届高三最新模拟、联考、质检、月考等试题;教育专家、一线名师的原创题和改编题;近年高考卷中典型性强的试题等。
充分保证了试题的前瞻性、新颖性,使学生练有所得,备考事半功倍。
三、滚动测试,减少知识遗忘。
所谓“滚动测试”,就是后面的习题中,兼顾考查前面的知识点。
这种考查不是简单的重复,而是对与本单元知识结合最为紧密、高考中常综合命题的知识的滚动考查。
每一部分结束,还适当安排综合检测卷,进行“小综合”训练。
四、温馨栏目,有助轻松备考。
本书设有“动感地带”栏目,包括学习方法、趣味知识、答疑解惑等内容,关注考生的学习、生活和心理。
这个栏目只是个桥梁,通过在线答疑、书信往来、电话沟通等,编辑老师与考生进行互动,扫除诸多备考路上的障碍。
这套试卷共10科,包括语文、文科数学、理科数学、英语、物理、化学、生物、政治、历史、地理。
单册定价:15.00元。
一轮备考最佳方法——滚动复习,知识积累就像“滚雪球”!。
单元滚动检测卷(六)

单元滚动检测卷(六)[测试范围:第九单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.下列结论正确的是(B) A.长度相等的两条弧是等弧B.半圆是弧C.相等的圆心角所对的弧相等D.弧是半圆【解析】A、根据圆的某些概念的相关定义,能够完全重合的弧是等弧,故本选项错误,B、弧分为优弧、劣弧、半圆,故本选项正确;C、根据在同圆或等圆内,相等的圆心角所对的弧相等,故本选项错误;D、弧分为优弧、劣弧、半圆,故本选项错误.2.如图6-1,已知⊙O的半径OA=10 cm,弦AB=16 cm,P为弦AB上的一个动点,则OP的最短距离为(B)图6-1A.5 cm B.6 cmC.8 cm D.10 cm【解析】当OP为垂线段,即OP⊥AB时,OP为最短,∴AP=BP=12AB=12×16=8(cm),而OA=10 cm,在Rt△OAP中,OP=OA2-AP2=102-82=6(cm).故选B.3.如图6-2是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB 宽为8 cm,水的最大深度为2 cm,则该输水管的半径为(C)图6-2A.3 cm B.4 cmC.5 cm D.6 cm【解析】如图所示,过点O作OD⊥AB于点D,连结OA.∵OD⊥AB,∴AD=12AB=12×8=4 (cm).设OA=r,则OD=r-2,第3题答图在Rt△AOD中,OA2=OD2+AD2,即r2=(r-2)2+42,解得r=5 cm.故选C.4.如图6-3,AB是⊙O的直径,∠AOC=110°,则∠D=(B)图6-3A.25°B.35°C .55°D .70°5.已知⊙O 1与⊙O 2外切,⊙O 1的半径R =5 cm ,⊙O 2的半径r =1 cm ,则⊙O 1与⊙O 2的圆心距是( D )A .1 cmB .4 cmC .5 cmD .6 cm【解析】 外切两圆的圆心距等于两圆半径的和,所以O 1O 2=R +r =5 cm + 1 cm =6 cm.6.用半径为3 cm ,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( D )A .2π cmB .1.5 cmC .π cmD .1 cm7.如图6-4,半圆O 的直径AB =10,弦AC =6 cm ,AD 平分∠BAC ,则AD 的长为( A )图6-4A .4 5 cmB .3 5 cmC .5 5 cmD .4 cm【解析】 如图,连结OD ,OC ,作DE ⊥AB 于E ,OF ⊥AC 于F .第7题答图∵∠CAD =∠BAD (角平分线的定义), ∴CD ︵=BD ︵,∴∠DOB =∠OAC =2∠BAD . 又∵OA =OD ,∠AFO =∠DEO =90°, ∴△AOF ≌△ODE ,∴OE =AF =12AC =3 cm.在Rt △DOE 中,DE =OD 2-OE 2=4 cm , 在Rt △ADE 中,AD =DE 2+AE 2=4 5 cm.故选A.8.如图6-5,P A ,PB 是⊙O 的切线,AC 是⊙O 的直径,∠P =40°,则∠BAC 的度数是( B )图6-5A .10°B .20°C .30°D .40°【解析】 ∵P A ,PB 是⊙O 的切线,∴P A =PB ,∠OAP =90°,∴∠P AB =∠ABP ,又∠P =40°,∴∠P AB =70°,∴∠BAC =90°-70°=20°. 9.如图6-6,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连结BC ,若∠ABC =120°,OC =3,则BC ︵的长为( B )图6-6A .πB .2πC .3πD .5π【解析】 连结OB ,第9题答图∵AB 与⊙O 相切于点B ,∴∠ABO =90°. ∵∠ABC =120°, ∴∠OBC =30°.∵OB =OC ,∴∠OCB =30°, ∴∠BOC =120°,∴BC ︵的长为120π×3180=2π,故选B.10.如图6-7,MN 是半径为1的⊙O 的直径,点A 在⊙O 上,∠AMN =30°,B 为AN ︵的中点,点P 是直径MN 上一个动点,则P A +PB 的最小值为( B )图6-7A .2 2 B. 2 C .1D .2第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.图6-8中圆心角∠AOB =30°,弦CA ∥OB ,延长CO 与圆交于点D ,则∠BOD =__30°__.图6-812.平面上有⊙O 及一点P ,P 到⊙O 上的点的距离最长为6 cm ,最短为2 cm ,则⊙O 的半径为__4或2__cm.【解析】 当点P 在圆内时,则直径=6+2=8(cm),因而半径是4 cm ;当点P在圆外时,直径=6-2=4(cm),因而半径是2 cm.所以⊙O的半径为4 cm或2 cm.13.当宽为3 cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图6-9所示(单位:cm),那么该圆的半径为__256__cm.图6-9【解析】连结OA,过点O作OD⊥AB于点D,∵OD⊥AB,∴AD=12AB=12×(9-1)=4,设OA=r,则OD=r-3,在Rt△OAD中,OA2-OD2=AD2,即r2-(r-3)2=42,解得r=256cm.第13题答图14.如图6-10,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.已知正三角形的边长为1,则“凸轮”的周长等于__π__.图6-10【解析】 ∵△ABC 为正三角形,∴∠A =∠B =∠C =60°,AB =AC =BC =1, ∴AB ︵=BC ︵=AC ︵=60π×1180=π3,根据题意可知凸轮的周长为三个弧长的和, 即凸轮的周长=AB ︵+BC ︵+AC ︵=3×π3=π.15.底面半径为1,高为3的圆锥的侧面积等于__2π__. 【解析】 ∵高线长为3,底面半径是1, ∴由勾股定理知:母线长=(3)2+1=2, ∴圆锥侧面积=π×1×2=2π.16.如图6-11所示,AB 是⊙O 的直径,点D 在⊙O 上,∠AOD =130°,BC ∥OD 交⊙O 于点C ,则∠A =__40°__.图6-11【解析】 ∵∠AOD =130°, ∴∠BOD =50°, 又∵OD ∥BC ,∴∠ABC =∠BOD =50°, 又∵AB 为直径, ∴∠C =90°, ∴∠A =40°.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.中华民族的科学文化历史悠久、灿烂辉煌,我们的祖先几千年前就能在生产实践中运用数学.1 300多年前,我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图6-12).经测量,桥拱下的水面距拱顶6 m时,水面宽34.64 m,已知桥拱跨度是37.04 m,运用你所学的知识计算出赵州桥的大致拱高.(运算时取37.04≈147,34.64≈203)图6-12解:如图,设圆弧所在圆的圆心为O,第17题答图AB=37.04≈147 m,CD=34.64≈20 3 m,GE=6 m.在Rt△OCE中,OE=OG-6,CE=103,∵OC2=CE2+OE2,∴OC2=(103)2+(OC-6)2,∴OC=28(m),∴OA=28.在Rt△OAF中,AF=77,∴OF=OA2-AF2=282-(77)2=21(m).∴拱高GF=28-21=7(m).18.如图6-13,⊙O的半径为4 cm,点P是⊙O外一点,OP=6 cm,求:图6-13(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?(分别作出图形,并解答)解:(1)若两圆外切,则小圆⊙P的半径为6-4=2 (cm).第18题答图(2)若两圆内切,则大圆⊙P的半径为6+4=10 (cm).19.如图6-14,实线部分是半径为15 m的两条等弧组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心,求游泳池的周长.图6-14解:设两个圆的交点分别为C,D,连结O1C.O1D2,O2C,O2D,则易证四边形O,CO2D是菱形,所以∠CO1D=∠CO2D=120°,所以两条等弧所对的圆心角均为360°-120°=240°.则游泳池的周长为2×nπr180=2×240π×15180=40π(m).20.如图6-15,⊙O经过菱形ABCD的三个顶点A,D,C,且与AB相切于点A.(1)求证:BC为⊙O的切线;(2)求∠B的度数.图6-15解:(1)证明:如图,连结AO,CO.∵AB是⊙O的切线,∴OA⊥AB.∴∠BAO=90°.∵四边形ABCD是菱形,∴AB=BC.∵AO=CO,BO=BO,∴△BAO≌△BCO(SSS).∴∠BCO=∠BAO=90°,即OC⊥BC.∴BC为⊙O的切线.第20题答图(2)如图,连结OD,则∠AOC=2∠ADC.由(1)知∠BAO=∠BCO=90°,且四边形ABCO的内角和为360°,∴∠B+∠AOC=360°-∠BAO-∠BCO=180°,即∠B+2∠ADC=180°.∵四边形ABCD是菱形,∴∠B=∠ADC.∴∠B+2∠B=180°.∴∠B=60°.21.如图6-16,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.(1)求证:P A为⊙O的切线;(2)若OB=5,OP=253,求AC的长.图6-16解:(1)设AC与OP相交于点H,∵AB是⊙O的直径,∴∠ACB=90°.∵OP∥BC,∴∠AHO=∠ACB=90°,∴∠AOH+∠OAH=90°.∵∠P=∠OAH,∴∠AOH+∠P=90°,∴∠OAP=90°,即OA⊥AP,∴P A为⊙O的切线.(2)在Rt△OAP中,OA=OB=5,OP=25 3,∴AP=OP2-OA2=20 3.∵S△OAP =12OA·AP=12OP·AH.∴AH =OA ·AP OP =5×203253=4.∵OH ⊥AC ,∴AC =2AH =8.22.如图6-17,将一块三角板和半圆形量角器按图中方式叠放,三角板一边与量角器的零刻度线所在直线重合,重叠部分的量角器弧(AB ︵)对应的圆心角(∠AOB )为120°,OC 的长为2 cm ,求三角板和量角器重叠部分的面积.图6-17解:∵∠AOB =120°,∴∠BOC =60°.在Rt △OBC 中,OC =2 cm ,∠BOC =60°,∴∠OBC =30°,∴OB =4 cm ,BC =2 3 cm ,则S 扇形OAB =120π×42360=16π3,S △OBC =12OC ·BC =23,故S 重叠=S 扇形OAB +S △OBC =16π3+2 3.23.已知:如图6-18,在梯形ABCD 中,AD ∥BC ,DA =DC ,以点D 为圆心,DA 长为半径的⊙D 与AB 相切于点A ,与BC 交于点F ,过点D 作DE ⊥BC ,垂足为E .(1)求证:四边形ABED 为矩形;(2)若AB =4,AD BC =34,求CF 的长.图6-18解:(1)∵⊙D 与AB 相切于点A ,∴AB ⊥AD .∵AD ∥BC ,DE ⊥BC ,∴DE ⊥AD ,∴∠DAB =∠ADE =∠DEB =90°,∴四边形ABED 为矩形.(2)∵四边形ABED 为矩形,∴DE =AB =4.∵DA =DC ,∴点C 在⊙D 上.∵点D 为圆心,DE ⊥BC ,∴CF =2EC .∵AD BC =34,设AD =3k (k >0),则BC =4k ,∴BE =3k ,EC =BC -BE =4k -3k =k ,DC =AD =3k .在Rt △DEC 中,由勾股定理得DE 2+EC 2=DC 2,∴42+k 2=(3k )2,∴k 2=2.∵k >0,∴k =2,∴CF =2EC =2 2.24.如图6-19,AB 是⊙O 的直径,C 是半圆O 上的一点,AC 平分∠DAB ,AD ⊥CD ,垂足为D ,AD 交⊙O 于E ,连结CE .(1)判断CD 与⊙O 的位置关系,并证明你的结论;(2)若E 是AC ︵的中点,⊙O 的半径为1,求图中阴影部分的面积.图6-19解:(1)CD 与⊙O 相切,理由如下:∵AC 为∠DAB 的平分线,∴∠DAC =∠BAC .∵OA =OC ,∴∠OAC =∠OCA ,∴∠DAC =∠OCA ,∴OC ∥AD .∵AD ⊥CD ,∴OC ⊥CD ,∴CD 与⊙O 相切;(2)连结OE ,∵E 是AC ︵的中点,∴AE ︵=EC ︵,∴S 弧形AE ︵=S 弧形EC ︵,∴S 阴影=S △DEC .∵∠DAC =∠BAC ,∴EC ︵=BC ︵,即AE ︵=EC ︵=BC ︵.∴∠AOE =∠EOC =∠BOC =60°.又∵OE =OC ,∴△EOC 是等边三角形, ∴EC =OC =1,∠ECO =∠EOC =60°, ∴∠ECD =90°-∠ECO =30°.在Rt △EDC 中,∠ECD =30°,EC =1,∴ED =12EC =12,CD =EC 2-ED 2=32, ∴S 阴影=S △DEC =12ED ·CD =12×12×32 =38.。
部编版语文小学四年级上册单元试卷含答案(全册)

部编版语文小学四年级上册单元试卷含答案(全册)统编版四年级语文上册第一单元检测卷一、基础知识(42分)1.认真拼一拼,把字写漂亮。
(10分)zhújiàn。
pàn wàng。
kuān kuòzhuāng jia。
fēng súpútao。
shàshíchéng shúgǔn dòng。
zhāo dài2.分清这些字,分别组词。
(10分)堤()犹()震()剧()坑()提()优()振()据(。
)炕()3.补充词语,并选词填空。
(8分)风()浪()山()地()()天()地水天()()人()人()若()若()1)今天是个航海的好天气,海面上______________。
2)XXX还没有来,海塘大堤上早已______________。
4.按要求写句子。
(7分)1)月光是那样柔和,照亮了高高的点苍山,照亮了村头的大青树,也照亮了,照亮了村间的大道和小路……(仿写排比句)(3分)漫步在公园里,只见灿烂的阳光洒在_____________,洒在_____________,还洒在______________……2)霎时,潮头奔腾西去。
(用加点词造句)(2分)__________________________________________________ _______________(3)自古以来,人们把钱塘江大潮称为世界奇迹。
(改写成“被”字句)______________________________________________________ ___________5.我会查字典。
(4分)鼎”字用部首查字法,先查____部,再查____画,第六笔笔画的名称是:________。
“鼎”字在字典中的解释有:①古代煮工具的器物;②锅;③合理,正在。
在“人声鼎沸”一词当选第______种解释。
人教版数学高一单元测试卷第一、二章_滚动性检测含解析

C.-x3+x2D.x3-x2
答案:B
解析:令x<0,则-x>0,∴f(-x)=x2(1+x),又f(-x)=f(x),∴f(x)=x2(1+x)=x3+x2.
7.已知函数f(x)= 那么f(ln2)的值是()
A.0 B.1
C.ln(ln2) D.2
答案:B
解析:∵ln2<1,∴f(ln2)=eln2-1=2-1=1.
∴log2(a+9)<3=log28,
∴0<a+9<8,∴-9<a<-1.
(2)当a=1时,f(x)=log2(x2+4x+5),
令t=x2+4x+5,则t=(x+2)2+1≥1,
解:∵B⊆A,当B=∅时,得2m-1>m+1,m>2,
当B≠∅时,得 解得-1≤m≤2.
综上所述,m的取值范+5).
(1)若f(1)<3,求a的取值范围;
(2)若a=1,求函数f(x)的值域.
解:(1)∵f(1)=log2(a+9),
答案:C
解析:∵f(x)在R上是偶函数,
∴f(-π)=f(π),f(-4)=f(4),而3<π<4且f(x)在(0,+∞)上是增函数.
∴f(3)<f(π)<f(4),即f(3)<f(-π)<f(-4).
6.已知函数f(x)是定义在R上的偶函数,当x>0时,f(x)=x2(1-x),则当x<0时,f(x)=()
A.(-1,0)∪(0,1)
B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞)
D.(-∞,-1)∪(0,1)
答案:C
解析:由题意可得 或 解得 或 ⇒a>1或-1<a<0.
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
单元滚动检测卷(七)
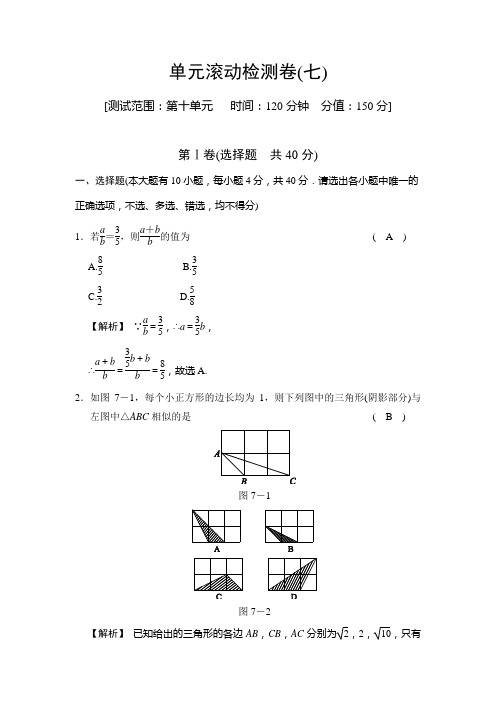
单元滚动检测卷(七)[测试范围:第十单元 时间:120分钟 分值:150分]第Ⅰ卷(选择题 共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的 正确选项,不选、多选、错选,均不得分) 1.若a b =35,则a +b b 的值为( A )A.85B.35C.32D.58【解析】 ∵a b =35,∴a =35b , ∴a +b b =35b +bb =85,故选A.2.如图7-1,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC 相似的是( B)图7-1图7-2【解析】 已知给出的三角形的各边AB ,CB ,AC 分别为2,2,10,只有选项B 的各边分别为1,2,5与它的各边对应成比例.故选B.3.如图7-3所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC CD=ABBC;④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的个数为(C)A.1 B.2C.3 D.4【解析】有3个.①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.③中两组对应边的比相等,∠A不是对应边的夹角,故不正确.④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,故选C.图7-3图7-44.如图7-4是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C 处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(B) A.6米B.8米C.18米D.24米【解析】∵△ABP∽△CDP,∴ABCD=BPPD,∴CD=1.2×121.8=8(米).故选B.5.手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是(D)图7-5【解析】虽然矩形的四个角相等,但每条边长减去同一个常数后,对应边不一定成比例,故选D.6.若△ABC∽△DEF,△ABC与△DEF的相似比为1∶2,则△ABC与△DEF 的周长比为(B) A.1∶4 B.1∶2C.2∶1 D.1∶ 2【解析】相似三角形的周长比等于相似比,故选B.7.如图7-6,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD∶AB =3∶4,AE=6,则AC等于(D)图7-6A.3 B.4C.6 D.8【解析】∵DE∥BC,∴ADAB=AEAC,∴34=6AC,解得AC=8.8.如图7-7,P AB,PCD为⊙O的两条割线,AD,BC相交于点E,则图中相似三角形共有(C)图7-7A .0对B .1对C .2对D .3对【解析】 ∵∠BEA =∠DEC ,∠B =∠D , ∴△ABE ∽△CDE .∵∠B =∠D ,∠P =∠P ,∴△PBC ∽△PDA , ∴共有两对相似三角形.9.如图7-8,直角梯形ABCD 中,AB ∥CD ,∠C =90°,∠BDA =90°,AB =a ,BD =b ,CD =c ,BC =d ,AD =e ,则下列等式成立的是( A )图7-8A .b 2=acB .b 2=ceC .be =acD .bd =ae【解析】 ∵CD ∥AB ,∴∠CDB =∠DBA ,又∵∠C =∠BDA =90°, ∴△CDB ∽△DBA ,∴CD DB =BC AD =BDAB , 即c b =d e =b a , ∴b 2=ac ,故选A.10.如图7-9,在平行四边形ABCD 中,AC 与BD 交于点O ,E 为OD 的中点,连结AE 并延长交DC 于点F ,则DF ∶FC =( D )图7-9A.1∶4 B.1∶3C.2∶3 D.1∶2第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图7-10,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为__1.5__m.图7-1012.如图7-11所示,DE是△ABC的中位线,则△ADE与△ABC的面积比为__1∶4__.图7-1113.如图7-12,在▱ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F,若ABBC=35,则AFAC=__38__.图7-12【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EBC=∠AEB.∵BE 是∠ABC 的角平分线, ∴∠EBC =∠AEB =∠ABE , ∴AB =AE .∵AB BC =35,∴AE BC =35.∵AD ∥BC ,∴△AFE ∽△CFB ,∴AE BC =AF FC =35,∴AFAC =AF AF +FC =33+5=38.14.如图7-13所示,⊙O 的两弦AB ,CD 交于点P ,连结AC ,BD ,得S △ACP ∶S △DBP =16∶9,则AC ∶BD =__4∶3__.图7-13【解析】 相似三角形对应边的比等于面积比的算术平方根.由同弧所对的圆周角相等,易知∠B =∠C ,∠D =∠A , ∴△ACP ∽△DBP , ∴⎝ ⎛⎭⎪⎫AC BD 2=S △ACP S △DBP =169, ∴AC BD =169=43.15.如图7-14,△ABC 中,点D 在边AB 上,满足∠ACD =∠ABC ,若AC =2,AD =1,则DB =__3__.【解析】 由于∠ACD =∠ABC ,∠BAC =∠CAD ,所以△ADC ∽△ACB ,所以AC AB =AD AC ,即AB ·AD =AC 2,则AB =AC 2AD=4,所以BD =AB -AD =3.图7-14图7-1516.如图7-15,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是2,cos A的值是4结果保留根号).【解析】∵△ABC中,AB=AC=1,∠A=36°,∴∠ABC=∠ACB=180°-∠A2=72°.∵BD是∠ABC的平分线,∴∠ABD=∠DBC=12∠ABC=36°,∴∠A=∠ABD=∠DBC=36°,∠BDC=∠C=72°.又∵∠C=∠C,∴△ABC∽△BDC,∴ACBC=BCCD.设AD=x,则BD=BC=AD=x,则1x=x1-x,解得x=-5-12(舍去)或x=5-12,故x=5-1 2.过点D作DE⊥AB于点E,∵AD=BD,∴E为AB的中点,即AE=12AB=12.在Rt△AED中,cos A=AEAD=125-12=5+14.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.已知x2=y3=z4,(1)求x-2yz的值;(2)若x+3=z-y,求x的值.解:由x2=y3=z4,设x=2k,y=3k,z=4k,则(1)x-2yz=2k-6k4k=-1.(2)x+3=z-y可化为2k+3=k,∴2k+3=k2,即k2-2k-3=0,∴k=3或k=-1,经检验,k=-1不符合题意,∴k=3,从而x=2k=6,即x=6.18.如图7-16,△ABC∽△DAB,AB=8,BC=12,求AD的长.图7-16解:∵△ABC∽△DAB,∴BCAB=ABAD.∵AB=8,BC=12,∴128=8AD,∴AD=16 3.19.如图7-17,四边形ABCD是平行四边形,点F在BA的延长线上,连结CF交AD于点E.(1)求证:△CDE∽△F AE;(2)当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF.图7-17证明:(1)∵四边形ABCD是平行四边形,∴CD∥AB,即CD∥F A,∴△CDE∽△F AE;(2)∵△CDE∽△F AE,DE=EA,∴△CDE≌△F AE,∴CD=AF,∴BF=2CD.∵BC=2CD,∴BF=BC,∴∠F=∠BCF.20.已知:如图7-18,在△ABC中,∠C=90°,点D,E分别在边AB,AC 上,DE∥BC,DE=3,BC=9.(1)求ADAB的值;(2)若BD=10,求sin A的值.图7-18 解:(1)∵DE∥BC,∴△ADE∽△ABC,∴ADAB=DEBC.又∵DE=3,BC=9,∴ADAB=39=13.(2)根据(1)中ADAB=DEBC得ADAD+BD=DEBC.∵BD=10,DE=3,BC=9,∴ADAD+10=3 9,∴AD=5,∴AB=3AD=15,∴sin A=BCAB=915=35.21.如图7-19,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD 相似,已知AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比.图7-19解:(1)由已知得MN=AB,MD=12AD=12BC,∵矩形DMNC与矩形ABCD相似,∴DMAB=MNBC.∵MN=AB,DM=12AD,BC=AD,∴12AD2=AB2,∴由AB=4,得AD=42;(2)矩形DMNC与矩形ABCD的相似比为DMAB=224=22.22.已知如图7-20,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连结BD,AE⊥BD,垂足为E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.图7-20解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC.∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC.(2)∵AB=AD,又AE⊥BD,∴BE=DE,∴BD=2BE.由△ABE∽△DBC,得ABBD=BEBC.∵AB=AD=25,BC=32,∴252BE=BE32,∴BE=20,∴AE=AB2-BE2=252-202=15.23.如图7-21,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB =12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;图7-21 解:(1)∵AB=DB,∴∠BDA=∠BAD.又∵∠BDA和∠BCA是弧AB所对的圆周角,∴∠BDA=∠BCA.∴∠BCA=∠BAD.(2)∵在Rt△ABC中,AB=12,BC=5,∴AC=AB2+BC2=13.又∵∠BAC和∠BDC是弧BC所对的圆周角,∴∠BAC=∠BDC.∵∠ABC=∠DEB=90°,∠BAC=∠BDC,∴△ACB∽△DBE.∴ABDE=ACBD.∴DE=AB·BDAC=12×1213=14413.24.如图7-22,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.图7-22(1)当PE⊥AB,PF⊥BC时,如图(1),则PEPF的值为________;(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图(2),求PEPF的值;(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP∶PC=1∶2时,如图(3),PEPF的值是否有变化?证明你的结论.解:(1)3(2)如图(1),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,则∠PHE=∠PGB =∠PGF=90°.由(1)得PHPG= 3.第24题答图(1)又∵∠ABC=90°,∴四边形PHBG为矩形,∴∠HPG=90°,∴∠HPE+∠EPG=90°,又∵∠EPF=∠EPG+∠GPF=90°,∴∠HPE=∠GPE=α,又∵∠EHP=∠PGF=90°,∴Rt△PHE∽Rt△PGF,∴PEPF=PHPG,∴PEPF= 3.(3)PEPF的值有变化.证明:如图(2),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,第24题答图(2)(3)则∠AHP=∠ABC=∠PGC=90°,∴HP∥BC,∴∠APH=∠PCG,∴△APH∽△PCG,∴PHCG=APPC=12.在Rt△PCG中,∠PCG=30°,tan∠PCG=PGCG,∴PGCG=3 3,∴CG=3PG,∴PH3PG=12,∴PHPG=3 2.同(2)中可证得PEPF=PHPG=32.。
单元滚动检测卷(一)

单元滚动检测卷(一)[测试范围:第一单元及第二单元 时间:120分钟 分值:150分]第Ⅰ卷(选择题 共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分) 1.四个数-1,0,12,2中为无理数的是( D )A .-1B .0 C.12D. 22.在-3,-1,0,2这四个数中,最小的数是( A )A .-3B .-1C .0D .23.若x 是2的相反数,|y |=3,则x -y 的值是 ( D )A .-5B .1C .-1或5D .1或-54.已知a <c <0<b ,则abc 与0的大小关系是 ( C )A .abc <0B .abc =0C .abc >0D .无法确定【解析】 由a <c <0<b 知a ,c 为负数,b 为正数,则abc >0,故选C. 5.我国南海某海域探明可燃冰储量约有194亿立方米,194亿用科学记数法表示为( A )A .1.94×1010B .0.194×1010C .19.4×109D .1.94×1096.有理数a ,b 在数轴上的位置如图1-1所示,则a +b 的值( A )图1-1A .大于0B .小于0C .小于aD .大于b【解析】 观察图象知-1<a <0,b >1,所以a +b >0. 7.下列计算正确的是( A )A .a 6÷a 3=a 3B .(a 2)3=a 8C .(a -b )2=a 2-b 2D .a 2+a 2=a 48.如果(2a -1)2=1-2a ,则( B )A .a <12 B .a ≤12 C .a >12 D .a ≥129.化简⎝ ⎛⎭⎪⎫x -2x -1x ÷⎝ ⎛⎭⎪⎫1-1x 的结果是( B )A.1x B .x -1 C.x -1x D.x x -1【解析】 ⎝⎛⎭⎪⎫x -2x -1x ÷⎝ ⎛⎭⎪⎫1-1x=x 2-2x +1x ÷x -1x=(x -1)2x ·x x -1=x -1,故选B.10.设a =19-1,a 在两个相邻整数之间,则这两个整数是( C )A .1和2B .2和3C .3和4D .4和5【解析】 ∵16<19<25,即4<19<5, ∴4-1<19-1<5-1,即3<19-1<4, 故a 在3,4两个整数之间.第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分) 11.(1)-3的相反数是__3__;-3的倒数是__-13__.(2)H7N9禽流感病毒的直径大约为0.0000000805米,用科学记数法表示为__8.1×10-8__米(保留两位有效数字).12.(1)计算:12+(-1)-1+(3-2)0=. (2)计算(50-8)÷2的结果是__3__. 13.(1)函数y =2-x +1x +1中自变量x 的取值范围是__x ≤2且x ≠-1__. (2)若等式⎝⎛⎭⎪⎫x 3-20=1成立,则x 的取值范围是__x ≥0且x ≠12__. 【解析】 本题含有0次幂及二次根式.根据0次幂底数不为0,二次根式被开方数为非负数,列不等式求解. 即x3≥0且x3-2≠0,解得x ≥0且x ≠12.14.(1)分解因式:3a 2-12=__3(a +2)(a -2)__. (2)分解因式:-a 3+a 2b -14ab 2=__-a ⎝ ⎛⎭⎪⎫a -12b 2__.【解析】 当一个多项式是三项式时,应先提公因式,然后尝试用完全平方公式或平方差公式分解因式.-a 3+a 2b -14ab 2=-a ⎝ ⎛⎭⎪⎫a 2-ab +14b 2=-a ⎝ ⎛⎭⎪⎫a -12b 2.15.(1)若实数a ,b 满足:||3a -1+b 2=0,则a b =__1__. (2)已知1a -1b =12,则ab a -b 的值是__-2__.【解析】 由1a -1b =12,得b -a ab =12, ∴abb -a =2, ∴aba -b=-2. 16.先找规律,再填数: 11+12-1=12, 13+14-12=112, 15+16-13=130, 17+18-14=156, ……则12 013+12 014-__11 007__=12 013×2 014.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.如图1-2,一只蚂蚁从点A 沿数轴向右直爬2个单位到达点B ,点A 表示-2,设点B 所表示的数为m ,求m 的值.图1-2解:由题意得m =2- 2.18.计算:(1-3)0+|-2|-2cos 45°+⎝ ⎛⎭⎪⎫14-1.解:原式=1+2-2×22+4=5.19.按下面的程序计算:输入x =3,请列式计算出结果.输入x →立方→-x →÷2→答案图1-3解:按程序写出算式为(x 3-x )÷2,当x =3时,原式=(33-3)÷2=12. 20.先化简,再求值:(1+a )(1-a )+(a -2)2, 其中a =-3.解:原式=1-a 2+a 2-4a +4=-4a +5,当a =-3时,原式=12+5=17. 21.若x ,y 为实数,且|x +1|+y -1=0,求⎝ ⎛⎭⎪⎫x y 2 013的值.解:∵|x +1|≥0,y -1≥0, 且|x +1|+y -1=0,∴x +1=0,y -1=0,解得x =-1,y =1, ∴⎝ ⎛⎭⎪⎫x y 2 013=(-1)2 013=-1. 22.先化简,再求值:⎝ ⎛⎭⎪⎫x +1x 2-1+x x -1÷x +1x 2-2x +1,其中x =2. 解:原式=x +1+x (x +1)(x +1)(x -1)×(x -1)2x +1=(x +1)2(x +1)(x -1)×(x -1)2x +1 =x -1.把x =2代入x -1=2-1=1.23.把四张形状,大小完全相同的小长方形卡片(如图1-4)不重叠的放在一个底面为长方形(长为m cm ,宽为n cm)的盒子底部(如图1-5),盒子底面未被卡片覆盖的部分用阴影表示,求图中两块阴影部分的周长的和.图1-4图1-5解:设小长方形的宽为x cm,则长为(m-2x)cm,则两阴影部分周长之和为2[(m-2x)+(n-2x)]+2{2x+[n-(m-2x)]}=2(m+n-4x+4x+n-m)=2×2n=4n.24.我国古代的许多数学成果都曾位居世界前列,其中“杨辉三角”就是一例.如图1-6,这个三角形的构造法则是:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等.(1)根据上面的规律,写出(a+b)5的展开式;(2)利用上面的规律计算:25-5×24+10×23-10×22+5×2-1.图1-6【解析】(1)由图依次补充第五行,第六行的系数,即可得(a+b)5=a5+5a4b +10a3b2+10a2b3+5ab4+b5.(2)要计算的式子为6项,且2的指数依次递减.又-1=(-1)5.结合(a+b)5展开式系数规律,可得原式为(2-1)5=1.解:(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.(2)原式=25+5×24×(-1)+10×23×(-1)2+10×22×(-1)3+5×2×(-1)4+(-1)5=(2-1)5=1.。
2022《单元滚动检测卷》高考物理(江苏专用)精练 第七章 恒定电流 Word版含答案

单元滚动检测七恒定电流考生留意:1.答卷前,考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上.2.本次考试时间90分钟,满分100分.3.请在密封线内作答,保持试卷清洁完整.一、单项选择题:本题共7小题,每小题4分,共计28分,每小题只有一个选项符合题意.1.两根材料相同的均匀导线A和B,其长度分别为L和2L,串联在电路中时沿长度方向电势的变化如图1所示,则A和B导线的横截面积之比为( )图1A.2∶3B.1∶3 C.1∶2D.3∶12.如图2所示,电源电动势E=36V,内阻r=1Ω,电灯上标有“6V,12W”的字样,直流电动机线圈电阻R =2Ω.接通电源后,电灯恰能正常发光,下列说法正确的是()图2A.电路中的电流大小为6AB.电动机产生的热功率为56WC.电动机的机械效率约为85.7%D.电源的输出功率为72W3.QQ是一款流行的互联网即时通讯工具,新版本QQ推出了“在线时长”新功能,用户通过积累在线时长可以获得更高等级、享受更多服务,很多网友为追求虚拟的等级而纯粹地开机在线,造成大量的电能铺张.如图3所示是某网友QQ界面的电脑屏幕抓拍图,请你估算他升到下一级还要消耗多少电能(假定QQ用户使用台式电脑)( ) 图3A.0.2kW·h B.2kW·hC.20kW·h D.200kW·h4.如图4所示的电路中,开关闭合时,灯L1、L2正常发光.由于电路消灭故障,灯L1突然变亮,灯L2变暗,电流表的读数变小.则发生的故障可能是( )图4A.R1断路B.R2断路C.R3断路D.R4断路5.如图5所示的电路中,R1、R2、R3是定值电阻,R4是光敏电阻,其阻值随光照强度的增加而减小.当开关S 闭合且没有光照射时,电容器C不带电.当用强光照射R4且电路稳定时,与无光照时比较下列说法正确的是( )图5A.电容器C的下极板带正电B.R3两端电压降低C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源供应的总功率变小6.如图6所示,a、b、c为不同材料做成的电阻,b与a的长度相等,横截面积是a的两倍;c与a的横截面积相等,长度是a的两倍.当开关闭合后,三个抱负电压表的示数关系是U1∶U2∶U3=1∶1∶2.关于三种材料的电阻率ρa、ρb、ρc,下列说法中正确的是( )图6A.ρa是ρb的2倍B.ρa是ρc的2倍C.ρb是ρc的2倍D.ρc是ρa的2倍7.在如图7甲所示的电路中,电源电动势为3.0V,内阻不计,L1、L2为相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示,R为定值电阻,阻值为7.5Ω.当开关S闭合后( )图7A.L1的电阻为112ΩB.L1消耗的电功率为7.5WC.L2的电阻为7.5ΩD.L2消耗的电功率为7.5W二、多项选择题:本题共5小题,每小题4分,共计20分.每小题有多个选项符合题意.全部选对得4分,选对但不全的得2分,错选或不答得0分.8.如图8(a)所示电路中,R2为一阻值非线性变化的滑动变阻器,移动滑片转变滑动变阻器接入电路中的长度x(x为图中a与滑片之间的距离),得到如图(b)所示的定值电阻R1两端的电压U1与x的关系.a、b、c为滑动变阻器上等间距的三个点,当滑片从a移到b和从b移到c时,电流表A的示数变化分别为ΔI ab和ΔI bc,电压表V2的示数变化分别为ΔU ab和ΔU bc,电阻R1的功率变化分别为ΔP1ab和ΔP1bc,电源的总功率变化分别为ΔP ab和ΔP bc,则下列说法正确的是( )图8 A.ΔI ab=ΔI bc B.ΔU ab=ΔU bcC.ΔP1ab<ΔP1bc D.ΔP ab>ΔP bc9.已知将电阻R1与R2分别接在同一电池组的两极时消耗的电功率相同,电池组向两个电阻供电时的电流分别是I1和I2,电池组内阻消耗的功率分别是P1′和P2′,电池组的效率分别是η1和η2,电阻两端的电压分别是U1和U2,若I1<I2,则有( )A.R1>R2B.U1>U2C.η1>η2D.P1′>P2′10.压敏电阻的阻值会随所受压力的增大而减小,某同学利用压敏电阻的这种特性设计了一个探究电梯运动状况的装置,该装置的示意图如图9所示,将压敏电阻平放在电梯内,其受压面对上,在受压面上放一物体m,电梯静止时电流表示数为I0,当电梯做四种不同的运动时,电流表示数分别如图10甲、乙、丙和丁所示,下列推断中正确的是( )图9图10A.甲图表示电梯可能做匀速直线运动B.乙图表示电梯可能做匀加速上升运动C.丙图表示电梯可能做匀加速上升运动D.丁图表示电梯可能做变减速下降运动11.如图11所示,电流表A1(0~3A)和A2(0~0.6A)是由两个相同的电流计改装而成,现将这两个电流表并联后接入电路中.闭合开关S,调整滑动变阻器,下列说法中正确的是( )图11A.A1、A2的读数之比为1∶1B.A1、A2的读数之比为5∶1C.A1、A2的指针偏转角度之比为1∶1D.A1、A2的指针偏转角度之比为1∶512.如图12所示电路中,电源电动势为E,内阻为r,当滑动变阻器R2的滑动端向右滑动后,抱负电流表A1、A2的示数变化量的确定值分别为ΔI1、ΔI2,抱负电压表示数变化量的确定值为ΔU.下列说法中正确的是( )图12A.电压表V的示数减小B.电流表A2的示数减小C.ΔU与ΔI1的比值肯定小于电源内阻rD.ΔU与ΔI2的比值肯定小于电源内阻r三、简答题(共计12分)13.(6分)试验电流表有内阻,可等效为抱负电流表与电阻的串联.测量试验电流表G1内阻r1的电路如图13所示.供选择的仪器如下:①待测电流表G1(0~5mA,内阻约为300Ω);②电流表G2(0~10mA,内阻约为100Ω);③定值电阻R1(300Ω);④定值电阻R2(10Ω);⑤滑动变阻器R3(0~1000Ω);⑥滑动变阻器R4(0~20Ω);⑦干电池(1.5V);⑧开关S及导线若干.图13(1)定值电阻应选________,滑动变阻器应选________.(在空格内填写序号)(2)用连线连接实物图.(图14)图14(3)补全试验步骤:①按电路图连接电路,________________________________________________________;②闭合开关S,移动滑动触头至某一位置,记录G1、G2的读数I1、I2;③________________________________________________________________________;④以I2为纵坐标,I1为横坐标,在图15中作出相应图线.图15(4)依据I2-I1图线的斜率k及定值电阻,写出待测电流表的内阻的表达式__________________.14.(6分)A、B同学都用如图16甲所示的电路测电源电动势E、内阻r以及R1的阻值.试验器材有:待测电源E,待测电阻R1,电压表V(量程为2.0V,内阻很大),电阻箱R(0~99.99Ω),单刀单掷开关S1,单刀双掷开关S2,导线若干.图16(1)A同学测量电阻R1的试验步骤如下,请在下面横线的空白处将他的操作补充完整.闭合S1,将S2切换到a,调整电阻箱,读出其示数R0和对应的电压表示数U1,保持电阻箱阻值不变,________,读出电压表的示数U2,则电阻R1的表达式为R1=______.(2)B同学已经测得电阻R1=5.2Ω,连续测电源电动势E和内阻r的值.该同学的做法是:闭合S1,将S2切换到a,多次调整电阻箱,读出多组电阻箱示数R和对应的电压表示数U,由测得的数据绘出了如图乙所示的1 U -1R图线,则待测电源电动势E=______V,内阻r=______Ω.(计算结果小数点后均保留两位数字)四、计算题:本题共4小题,共计40分.解答时请写出必要的文字说明、方程式和重要的演算步骤,只写出最终答案的不能得分,有数值计算的题,答案中必需明确写出数值和单位.15.(8分)如图17所示电路中,电动势E=12V,内阻r=2Ω,指示灯R L的阻值为16Ω,电动机M线圈电阻R M为2Ω.当开关S闭合时,指示灯R L的电功率P=4W.求:图17(1)流过电流表A的电流;(2)电动机M输出的机械功率.16.(10分)如图18所示,电源电动势E=6V,内阻r=1Ω,电阻R1=2Ω,R2=3Ω,R3=7.5Ω,电容器的电容C=4μF.开关S原来断开,现在合上开关S到电路稳定,试问这一过程中通过电流表的电荷量是多少?图1817.(10分)如图19甲所示的电路中,R1、R2均为定值电阻,且R1=100Ω,R2阻值未知,R3为一滑动变阻器.当其滑片P从左端滑至右端时,测得电源的路端电压随电源中流过的电流变化图线如图乙所示,其中A、B两点是滑片P在变阻器的两个不同端点得到的.求:图19(1)电源的电动势和内阻;(2)定值电阻R2的阻值;(3)滑动变阻器的最大阻值.18.(12分)在如图20所示的电路中,R1=2Ω,R2=R3=4Ω,当开关K接a时,R2上消耗的电功率为4W,当开关K接b时,电压表示数为4.5V,试求:图20(1)开关K接a时,通过电源的电流和电压表的示数;(2)电源的电动势和内电阻;(3)当开关K接c时,通过R2的电流.答案精析 1.B 2.C 3.B 4.A 5.A 6.C 7.C8.AB 9.ABC 10.ACD 11.BC 12.BC13.(1)③ ⑥ (2)见解析图 (3)①将滑动触头移至最左端 ③多次移动滑动触头,记录相应的G 1、G 2的读数I 1、I 2 (4)r 1=(k -1)R 1解析 (1)依据试验的电路原理图,若定值电阻与待测电流表内阻大约相同,试验中两电流表可同时达到满偏,读数误差较小;滑动变阻器接受分压接法时,应选用阻值适当小一些的变阻器,调整便利. (2)连线时要留意:电表的正、负接线柱不能接反,如图所示.(3)在闭合开关前应将滑动变阻器滑动触头移至最左端以爱护电表.试验中要多次测量,减小偶然误差.(4)依据串、并联电路规律可知,I 2=I 1+I 1r 1R 1=R 1+r 1R 1I 1,即k =R 1+r 1R 1,所以r 1=(k -1)R 1.14.(1)将S 2切换到bU 2-U 1U 1R 0 (2)1.43 0.80 解析 (1)当S 2接a 时,电压表测R 两端的电压,当S 2接b 时,电压表测R 1及R 两端的总电压,则R 1两端的电压为U 2-U 1,此时流过R 1的电流为U 1R 0,由欧姆定律可得R 1=U 2-U 1U 1R 0. (2)由题意可知,此试验中可读出电阻箱的示数R ,而电压表测出R 两端的电压,由闭合电路欧姆定律可得E =U R(R +R 1+r ), 变形可得1U =R 1+r E ·1R +1E.由数学学问可得:1E=0.7V -1,则E ≈1.43V ;R 1+r E =2.8-0.70.5V -1·Ω, 解得内阻r =0.80Ω. 15.(1)2A (2)7.5W解析 (1)对指示灯依据焦耳定律,P =I 2L R L ,解得I L =0.5A 路端电压为U =I L R L ,解得U =8V设流过电流表的电流为I ,依据闭合电路欧姆定律,U =E -Ir 解得I =E -Ur=2A. (2)电动机支路的电流为I M ,I M =I -I L 电动机总功率为P M =UI M =12W 电动机输出机械功率为P M 出=P M -I 2M R M 解得P M 出=7.5W. 16.1.92×10-5C解析 S 断开时的等效电路如图甲所示,电容器C 两端电压U 为电阻R 2两端电压U 2,则U 2=ER 1+R 2+r·R 2=3V电容器C 的电荷量Q =CU =CU 2=1.2×10-5C .且a 板带正电,b 板带负电S 闭合时的等效电路如图乙所示,电容器C 两端电压U ′为电阻R 1两端电压U 1′ 有R 外=R 3(R 1+R 2)R 3+(R 1+R 2)=3Ω电阻R 1中的电流I 1′=ER 外+r ·R 外R 1+R 2=0.9A电阻R 1两端电压U 1′=I 1′R 1=1.8V电容器C 的电荷量Q ′=CU ′=CU 1′=7.2×10-6C 且a 板带负电,b 板带正电通过电流表的电荷量ΔQ =Q +Q ′=1.92×10-5C. 17.(1)20V 20Ω (2)5Ω (3)300Ω解析 (1)题图乙中AB 延长线,交U 轴于20V 处,交I 轴于1.0A 处,所以电源的电动势为E =20V ,内阻r =EI 短=20Ω. (2)当P 滑到R 3的右端时,电路参数对应图乙中的B 点,即U 2=4V 、I 2=0.8A ,得R 2=U 2I 2=5Ω.(3)当P 滑到R 3的左端时,由图乙知此时U 外=16V ,I 总=0.2A ,所以R 外=U 外I 总=80Ω 由于R 外=R 1R 3R 1+R 3+R 2,所以滑动变阻器的最大阻值为:R 3=300Ω. 18.(1)1A 4V (2)6V 2Ω (3)0.5A解析 (1)K 接a 时,R 1被短路,外电阻为R 2,依据电功率公式P =I 2R 可得通过电源电流I 1=PR 2=1A ,再依据P =U 2R可得电压表的示数U 1=PR 2=4V.(2)K 接a 时,有E =U 1+I 1rK 接b 时,R 1和R 2串联,R 外=R 1+R 2=6Ω 通过电源电流I 2=U 2R 外=0.75A 这时有:E =U 2+I 2r ,解得:E =6V ,r =2Ω. (3)当K 接c 时,R 2、R 3并联,R 23=R 2R 3R 2+R 3=2Ω R 总=R 1+r +R 23=6Ω总电流I 3=E R 总=1A ,通过R 2的电流I ′=12I 3=0.5A.。
中考数学单元滚动检测试卷(七)含答案(第10单元)

单元滚动检测卷(七)【测试范围:第十单元 时间:100分钟 分值:100分】 一、选择题(每题5分,共30分) 1.若a b =35,则a +b b 的值为( A )A.85B.35C.32D.58【解析】 ∵a b =35,∴a =35b ,∴a +b b =35b +b b =85.2.如图1,每个小正方形的边长均为1,则下列选项中的三角形(阴影部分)与图1中△ABC 相似的是( B )【解析】 已知给出的三角形的各边AB ,CB ,AC 分别为2,2,10,只有选项B 的各边分别为1,2,5与它的各边对应成比例.故选B. 3.如图2,给出下列条件:①∠B =∠ACD ;②∠ADC =∠ACB ;③AC CD =AB BC ;④AC 2=AD ·AB .能够单独判定△ABC ∽△ACD 的条件的个数为( C )A .1个B .2个C .3个D .4个【解析】 有3个.①∠B =∠ACD ,再加上∠A 为公共角,可以根据有两组角对应相等的两个三角形相似来判定;②∠ADC =∠ACB ,再加上∠A 为公共角,可以根据有两组角对应相等的两个三角形相似来判定;③中两组对应边的比相等,∠A 不是对应边的夹角,故不能判定;④可以根据两组对应边的比图1图2相等且对应边的夹角相等的两个三角形相似来判定.故选C.4.如图3,梯形ABCD 中,AD ∥BC ,∠B =∠ACD =90°,AB =2,DC =3,则△ABC 与△DCA 的面积比为( C )图3A .2∶3B .2∶5C .4∶9D.2∶ 35.[·哈尔滨]如图4,在△ABC 中,D ,E 分别为AB ,AC 边上的点,DE ∥BC ,BE 与CD 相交于点F ,则下列结论一定正确的是( A )图4A.AD AB =AE ACB.DF FC =AE ECC.AD DB =DE BCD.DF BF =EF FC【解析】 A .∵DE ∥BC ,∴AD AB =AEAC .故正确;B.∵DE ∥BC ,∴△DEF ∽△CBF ,∴DF FC =DE BC =AEAC .故错误;C .∵DE ∥BC ,∴AD AB =DE BC .故错误;D.∵DE ∥BC ,∴△DEF ∽△CBF ,∴DF FC =EFBF .故错误.故选A.6.[·宁波模拟]如图5,⊙O 是△ABC 的外接圆,已知AD 平分∠BAC 交⊙O 于点D ,AD =5,BD =2,则DE 的长为( D )A.35B.425C.225D.45【解析】 ∵AD 平分∠BAC ,∴∠BAD =∠DAC ,∵∠DBC =∠DAC , ∴∠DBC =∠BAD ,∴△ABD ∽△BED ,∴AD BD =BD DE ,∴DE =BD 2AD =45.故选D. 二、填空题(每题5分,共30分)7.[·山西模拟]《孙子算经》是我国古代重要的数学著作,成书于约一千五百年前,其中有道歌谣算题:“今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?”歌谣的意思是:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五,同时立一根一尺五的小标杆,它的影长五寸(提示:丈和尺是古代的长度单位,1丈=10尺,1尺=10寸),可以求出竹竿的长为__45__尺. 【解析】 设竹竿的长度为x 尺,∵竹竿的影长=一丈五尺=15尺,标杆长=一尺五寸=1.5尺,影长五寸=0.5尺,∴x 15=1.50.5,解得x =45,即竹竿的长为45尺.8.如图6,AD =DF =FB ,DE ∥FG ∥BC ,则S Ⅰ∶S Ⅱ∶S Ⅲ=__1∶3∶5__. 【解析】 ∵DE ∥FG ∥BC ,∴△ADE ∽△AFG ∽△ABC ,∵AD =DF =FB ,∴AD ∶AF ∶AB =1∶2∶3,∴S △ADE ∶S △AFG ∶S △ABC =1∶4∶9,∴S Ⅰ∶S Ⅱ∶S Ⅲ=1∶3∶5.图6图79.如图7,△ABC 中,D 为AB 边上的一点,要使△ABC ∽△AED 成立,还需要添加一个条件为__∠ADE =∠C 或∠AED =∠B 或AD AC =AEAB (答案不唯一,合理即可)__.【解析】∵∠B=∠AED,∠A=∠A,∴△ABC∽△AED,同理,可由∠ADE=∠C或ADAC=AEAB得出△ABC∽△AED.10.如图8,⊙O的两弦AB,CD交于点P,连结AC,BD,得S△ACP∶S△DBP=16∶9,则AC∶BD=__4∶3__.【解析】相似三角形对应边的比等于面积比的算术平方根.由同弧所对的圆周角相等,易知∠B=∠C,∠D=∠A,∴△DBP∽△ACP,∴⎝⎛⎭⎪⎫ACBD2=S△ACPS△DBP=169,∴ACBD=169=43.11.如图9,△ABO中,∠AOB=90°,点A在第一象限,点B在第四象限,且AO∶BO=1∶ 2.若点A(x0,y0)的坐标满足y0=1x0,则点B(x,y)的坐标x,y 所满足的关系式为__y=-2x__.图9 第11题答图【解析】设点B在反比例函数y=kx(k<0)上,如答图,分别过点A,B作AC,BD分别垂直y轴于点C,D,∵∠ACO=∠BDO=90°,∠AOC+∠BOD=90°,∠AOC+∠OAC=90°,∴∠OAC=∠BOD,∴△AOC∽△OBD,∴S△AOCS△BOD=⎝⎛⎭⎪⎫OAOB2=⎝⎛⎭⎪⎫122=12,∵点A(x0,y0)的坐标x0,y0满足y0=1x0,∴S△AOC=12,∴S△BOD=1,∴k=-2,∴点B(x,y)的坐标x,y所满足的关系式为y=-2x.12.[·杭州一模]如图10,△ABC是定圆O的内接三角形,AD为△ABC的高线,图8AE 平分∠BAC 交⊙O 于E ,交BC 于G ,连结OE 交BC 于F ,连结OA ,在下列结论中,①CE =2EF ;②△ABG ∽△AEC ;③∠BAO =∠DAC ;④AB ·ACAD为常量.其中正确的有__②③④__.图10第12题答图【解析】 ∵∠BCE 的度数不一定为30°,∴Rt △CEF 中,CE =2EF 不一定成立,故①错误;∵AE 平分∠BAC ,∴∠BAG =∠EAC ,又∵∠ABG =∠AEC ,∴△ABG ∽△AEC ,故②正确;如答图所示,延长AO 交⊙O 于点H ,连结BH ,∵AH 是⊙O 直径,AD ⊥BC ,∴∠ABH =90°,∠ADC =90°,∴∠H +∠BAH =90°,∠DAC +∠ACD =90°,∵∠H =∠ACD ,∴∠BAH =∠DAC ,故③正确;∵∠BAH =∠DAC ,∠ABH =∠ADC ,∴△ABH ∽△ADC, ∴AH AC =ABAD ,即AH =AB ·AC AD ,又∵AH 为常量,∴ AB ·ACAD 为常量,故④正确.综上,正确的有②③④. 三、解答题(共40分)13.(8分)如图11,△ABC ∽△DAB ,AB =8,BC =12,求AD 的长.解:∵△ABC ∽△DAB , ∴BC AB =AB DA .又∵AB =8,BC =12,图11∴128=8AD ,∴AD =163.14.(10分)如图12,在△ABC 中,D 是BC 边的中点,DE ⊥BC 交AB 于点E ,AD =AC ,EC 交AD 于点F .求证:(1)△ABC ∽△FCD ; (2)FC =3EF .证明:(1)∵AD =AC , ∴∠ADC =∠ACB , ∵BD =CD ,DE ⊥BC ,∴∠B =∠ECB ,∴△ABC ∽△FCD ; (2)∵△ABC ∽△FCD ,∴BC CD =ACFD , ∵D 是BC 边的中点,∴BC =2CD ,∴FD AC =12,∴AD =AC =2FD ,∵∠ACD =∠ADC ,∠B =∠FCD ,∠ACF +∠FCD =∠ACD ,∠EAD +∠B =∠ADC ,∴∠EAD =∠ACE ,∴△EAF ∽△ECA , ∴EA EC =EF EA =AF CA =12,∴EC =2EA =4EF , ∴FC =3EF .15.(10分)[·海曙区模拟]如图13,C 为⊙O 上的一点,P 为直径AB 延长线上的一点,BH ⊥CP 于H ,交⊙O 于D ,∠PBH =2∠P AC . (1)求证:PC 是⊙O 的切线; (2)若sin P =23,求BHBD 的值.图12图13 第15题答图解:(1)证明:如答图,连结OC , ∵OA =OC ,∴∠P AC =∠OCA , ∴∠COP =∠P AC +∠OCA =2∠P AC , ∵∠PBH =2∠P AC ,∴∠COP =∠PBH ,∴OC ∥BH ,∵BH ⊥CP ,∴OC ⊥CP ,∴PC 是⊙O 的切线;(2)如答图,作OG ⊥DH 于点G .设⊙O 的半径为2a ,在Rt △OCP 中,sin P =23,OC ⊥CP ,∴OP =3a ,∴PB =OP -OB =a ,∵OG ⊥BD ,∴BG =12BD ,△OBG ∽△PBH , ∴BH BG =BP OB =12,∴BH BD =14.16.(12分)[·宁波一模]如图14,四边形ABCD 内接于⊙O ,AB 是⊙O 的直径,AC 和BD 相交于点E ,且DC 2=CE ·CA . (1)求证:BC =CD ;(2)分别延长AB ,DC 交于点P ,若PB =OB ,CD =22,求⊙O 的半径.图14第16题答图解:(1)证明:∵DC 2=CE ·CA ,∴DC CE =CADC ,而∠ACD =∠DCE , ∴△CAD ∽△CDE ,∴∠CAD =∠CDE ,∵∠CAD =∠CBD , ∴∠CDB =∠CBD ,∴BC =CD ;(2)如答图,连结OC ,设⊙O 的半径为r , ∵CD =CB ,∴CD ︵=CB ︵,∴∠BOC =∠BAD , ∴OC ∥AD ,∴PC CD =PO OA =2rr =2, 又∵CD =22,∴PC =2CD =42, ∵∠PCB =∠P AD ,∠CPB =∠APD , ∴△PCB ∽△P AD ,∴PC P A =PB PD ,即423r =r62,∴r =4(负值舍去),即⊙O 的半径为4.。
单元滚动检测卷(八)

单元滚动检测卷(八)[测试范围:第十一单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.如图8-1,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tan A的值为(B)图8-1A.2 B.1 2C.55 D.255【解析】tan A=BCAC=12,选B.2.计算2sin 45°的结果等于(B)A. 2 B.1C.22 D.12【解析】2sin45°=2×22=1,选B.3.如图8-2,若∠A=60°,AC=20 m,则BC大约是(结果精确到0.1 m)(B)图8-2A .34.64 mB .34.6 mC .28.3 mD .17.3 m【解析】 ∵∠A =60°,∠C =90°, ∴∠B =30°,∴AB =2AC . ∵AC =20 m , ∴AB =40 m ,∴BC =AB 2-AC 2= 1 600-400= 1 200=203≈34.6(m),故选B. 4.已知∠A 是锐角,sin A =35,则5cos A =( A )A .4B .3 C.154D .55.计算:cos 245°+tan60°·cos30°等于( C )A .1B . 2C .2D. 3【解析】 原式=⎝ ⎛⎭⎪⎫222+3×32=12+32=2.故选C.6.如图8-3,在Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点D ,已知AC =5,BC =2,那么sin ∠ACD =( A )图8-3A.53B.23C.255D.52【解析】 在Rt △ABC 中, ∵AB 2=AC 2+BC 2, ∴AB =3.∵∠ACD +∠BCD =90°,∠B +∠BCD =90°,∴∠ACD=∠B.∴sin∠ACD=sin B=ACAB=53.7.河堤横断面如图8-4所示,堤高BC=5米,迎水坡AB的坡比是1∶3(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是(A)图8-4A.53米B.10米C.15米D.103米【解析】在Rt△ABC中,BC=5米,tan A=1∶3;∴AC=BC÷tan A=53米.故选A.8.如图8-5,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°,已知滑梯AB的长为3 m,点D,B,C在同一水平地面上,那么加长后的滑梯AD的长是(C)图8-5A.2 2 m B.2 3 mC.3 2 m D.3 3 m【解析】假设AC=x,∴BC=x.∵滑梯AB的长为3 m,∴2x2=9,解得x=322.∵∠D=30°,∴2AC=AD,∴AD=3 2.故选C.9.某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/时的速度沿北偏西60°方向航行23小时到达B 处,那么tan ∠ABP =( A )A.12B .2 C.55D.255【解析】 ∵灯塔A 位于客轮P 的北偏东30°方向,且相距20海里, ∴P A =20.∵客轮以60海里/时的速度沿北偏西60°方向航行23小时到达B 处, ∴∠APB =90°,BP =60×23=40, ∴tan ∠ABP =AP BP =2040=12.故选A.10.如图8-6,△ABC 中,AC =5,cos B =22,sin C =35,则△ABC 的面积是( A )图8-6A.212 B .12 C .14D .21【解析】 作AD ⊥BC 于D , ∵sin C =35,AC =5,∴AD =3,DC =4, 又∵cos B =22, ∴∠B =45°=∠BAD , ∴BD =AD =3,∴BC =7,∴S△ABC =12BC·AD=12×7×3=212,选A.第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.∠α的补角是120°,则∠α=__60°__,sin α=2.【解析】∠α=180°-120°=60°,∴sin α=sin 60°=3 2.12.如图8-7,△ABC的顶点都在方格纸的格点上,则sin A=5.图8-7【解析】过点C作CD⊥AB交AB的延长线于点D,设小正方形的边长为1,在Rt△ACD中,CD=2,AC=25,∴sin A=CDAC=225=55.13.图8-8是市民广场到解百地下通道的手扶电梯示意图,其中AB,CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是5 2 m,则乘电梯从点B到点C上升的高度h是__5__m.图8-8【解析】作CE⊥AB交AB的延长线于E,则∠CBE=180°-135°=45°,∴CE=BC·sin45°=52×22=5.14.计算:sin 230°+cos 230°-tan 245°=__0__.【解析】 原式=⎝ ⎛⎭⎪⎫122+⎝ ⎛⎭⎪⎫322-12=14+34-1=0.故答案是0.15.如图8-9,在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,过D 点作AB 的垂线交AC 于点E ,BC =6,sin A =35,则DE =__154__. 【解析】 ∵BC =6,sin A =BC AB =35, ∴AB =10,∴AC =102-62=8. ∵D 是AB 的中点,∴AD =12AB =5. 易证△ADE ∽△ACB , ∴DE BC =AD AC ,即DE 6=58, 解得DE =154,故答案为154.图8-9图8-1016.如图8-10,将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,如果AB BC =23,那么tan ∠DCF 的值是2. 【解析】 ∵四边形ABCD 是矩形, ∴AB =CD ,∠D =90°.∵将矩形ABCD 沿CE 折叠,点B 恰好落在边AD 的F 处,∴CF =BC .∵AB BC =23,∴CD CF =23. 设CD =2x ,CF =3x , ∴DF =CF 2-CD 2=5x , ∴tan ∠DCF =DF CD =5x 2x =52.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.计算:12-⎝ ⎛⎭⎪⎫-12-1-tan 60°+3-8+||3-2.【解析】 先化简每一项,再计算. 解:原式=23+2-3-2+2-3=2. 18.先化简,再求值:⎝ ⎛⎭⎪⎫1x +2-1÷x 2+2x +1x 2-4,其中x =tan 60°-1.解:原式=1-(x +2)x +2÷(x +1)2(x +2)(x -2)=-x -1x +2·(x +2)(x -2)(x +1)2=-x -2x +1.当x =tan60°-1=3-1时, 原式=-3-1-23-1+1=-3-33=3-1.19.如图8-11,在△ABC 中,∠C =90°,sin A =45,AB =15,求△ABC 的周长和tan A 的值.图8-11解:在Rt △ABC 中,∠C =90°,AB =15,sin A =BC AB =45,∴BC =12,AC =AB 2-BC 2=152-122=9, ∴△ABC 的周长=AB +AC +BC =36, tan A =BC AC =43.20.如图8-12,在△ABC 中,∠C =90°,AD 是角平分线,且∠BAC =60°,AD =10,求AB 的值.图8-12解:∵在△ABC 中,∠C =90°,∠BAC =60°, ∴∠B =30°, ∴AB =2AC . ∵AD 是角平分线, ∴∠DAC =∠BAD =30°. ∵AD =10,∴AC =53, ∴AB =10 3.21.已知不等臂跷跷板AB 长4 m .如图①,当AB 的一端A 碰到地面时,AB 与地面的夹角为α;如图②,当AB 的另一端B 碰到地面时,AB 与地面的夹角为β.求跷跷板AB 的支撑点O 到地面的高度OH (用含α,β的式子表示).图8-13解:在Rt △AHO 中,sin α=OHOA , ∴OA =OHsin α.在Rt△BHO中,sin β=OHOB,∴OB=OHsin β.∵AB=4,∴OA+OB=4,即OHsin α+OHsin β=4,∴OH=4sin αsin βsin α+sin β(m).22.一测量爱好者,在海边测量位于正东方向的小岛高度AC.如图8-14所示,他先在点B测得山顶A点的仰角是30°,然后沿正东方向前行62米到达D 点,在点D测得山顶A点的仰角为60°(B,C,D三点在同一水平面上,且测量仪的高度忽略不计).求小岛的高度AC.(结果精确到1米,参考数据:2≈1.4,3≈1.7)图8-14解:在Rt△ABC中,∠ABC=30°,tan∠ABC=AC BC,∴BC=ACtan∠ABC=AC33=3AC.在Rt△ADC中,∠ADC=60°,tan∠ADC=AC DC,∴DC=ACtan∠ADC=AC3=33AC.由题意,得BD=BC-DC=3AC-33AC=62,解得AC=313≈53(米),即小岛的高度AC约为53米.23.如图8-15,一段河坝的横断面为梯形ABCD,试根据图中的数据,求出坝底宽AD(i=CE∶ED,单位:m).图8-15解:如图所示,过点B作BF⊥AD,可得矩形BCEF,∴EF=BC=4,BF=CE=4.在Rt△ABF中,∠AFB=90°,AB=5,BF=4,由勾股定理可得:AF=52-42=3.又∵Rt△CED中,i=CEED=12,∴ED=2CE=2×4=8,∴AD=AF+FE+ED=3+4+8=15(米).第23题答图24.如图8-16,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A,B两地之间的距离为12海里.求A,C两地之间的距离.(参考数据:2≈1.41,3≈1.73,6≈2.45,结果精确到0.1海里)图8-16解:如图,过点B作BD⊥CA,交CA的延长线于点D.第24题答图由题意,得∠ACB=60°-30°=30°,∠ABC=75°-60°=15°,∴∠DAB=∠ACB+∠ABC=45°在Rt△ADB中,AB=12,∠BAD=∠ABD=45°,∴BD=AD=AB sin∠BAD=6 2.在Rt△BCD中,∠BCD=30°,tan∠BCD=BDCD,∴CD=BDtan∠BCD=6233=6 6.∴AC=CD-AD=66-62≈6.2(海里).答:A、C两地之间的距离约为6.2海里.。
单元滚动检测卷(四)

单元滚动检测卷(四)[测试范围:第六单元及第七单元时间:120分钟分值:150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的正确选项,不选、多选、错选,均不得分)1.如图4-1,△ABC中,AB=AC,∠B=70°,则∠A的度数是(D)图4-1A.70° B.55°C.50°D.40°2.下列四个图中,∠1大于∠2的是(D)图4-23.如图4-3,在直角三角形ABC中,∠C=90°,AB=10,AC=8,点E,F 分别为AC和AB的中点,则EF=(A)图4-3A.3 B.4C.5 D.6【解析】∵在直角三角形ABC中,∠C=90°,AB=10,AC=8,∴BC=102-82=6.∵点E,F分别为AC,AB的中点,∴EF是△ABC的中位线,∴EF=12BC=12×6=3.故选A.4.如图4-4,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为(C)图4-4A.4 B.6C.16 D.55【解析】由于a,b,c都是正方形,∴AC=CD,∠ACD=90°;∵∠ACB+∠DCE=∠ACB+∠BAC=90°,即∠BAC=∠DCE,∠ABC=∠CED=90°,AC=CD,∴△ACB≌△CDE,∴AB=CE,BC=DE;在Rt△ABC中,由勾股定理,得AC2=AB2+BC2=AB2+DE2,即S b=S a+S c=5+11=16.5.如图4-5,AC=BC=10 cm,∠B=15°,AD⊥BC于点D,则AD的长为(C)图4-5A.3 cm B.4 cmC.5 cm D.6 cm【解析】∵AC=BC,∴∠B=∠BAC=15°,∴∠ACD=∠B+∠BAC=15°+15°=30°,∴在Rt△ACD中,AD=12AC=12×10=5(cm).6.如图4-6,AD,BE是锐角△ABC的高,相交于点O,若BO=AC,BC=7,CD=2,则AO的长为(B)图4-6A.2 B.3C.4 D.5【解析】∵AD,BE是锐角△ABC的高,∴∠ACB+∠DBO=∠ACB+∠DAC=90°,∴∠DBO=∠DAC.又∵BO=AC,∠BDO=∠ADC=90°,∴△BDO≌△ADC,∴BD=AD,DO=CD.∵BD=BC-CD=5,∴AD=5,∴AO=AD-OD=AD-CD=3.7.如图4-7,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连结DE,则△CDE的周长为(C)图4-7A.20 B.12C.14 D.13【解析】∵AB=AC,AD平分∠BAC,BC=8,∴AD⊥BC,CD=BD=12BC=4.∵点E为AC的中点,∴DE=CE=12AC=5,∴△CDE的周长=CD+DE+CE=4+5+5=14.故选C.8.如图4-8,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB 于点O,交AC于点D,连结BD.下列结论错误的是(C)图4-8A.∠C=2∠AB.BD平分∠ABCC.S△BCD=S△BODD.点D为线段AC的黄金分割点【解析】A:∵∠A=36°,AB=AC,∴∠C=∠ABC=72°,∴∠C=2∠A,故本选项结论正确;B:∵DO是AB的垂直平分线,∴AD=BD,∴∠A=∠ABD=36°,∴∠DBC=72°-36°=36°=∠ABD,∴BD是∠ABC的角平分线,故本选项结论正确;C:根据已知不能推出△BCD的面积和△BOD的面积相等,故本选项结论错误;D:∵∠C=∠C,∠DBC=∠A=36°,∴△CBD∽△CAB,∴BCAC=CDBC,∴BC2=CD·AC.∵∠C=72°,∠DBC=36°,∴∠BDC=72°=∠C,∴BC=BD.∵AD=BD,∴AD=BC,∴AD2=CD·AC,即点D是线段AC的黄金分割点,故本选项结论正确.故选C.9.如图4-9所示,AB=AC,要说明△ADC≌△AEB,需添加的条件不能是(D)图4-9A.∠B=∠C B.AD=AEC.∠ADC=∠AEB D.DC=BE10.如图4-10,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处.下面结论错误的是(B)图4-10A.AB=BE B.AD=DCC.AD=DE D.AD=EC【解析】根据折叠的性质可得AD=DE=EC,AB=BE,显然DC是等腰Rt △DEC的斜边,不可能有DC=DE=AD,故选B.第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图4-11,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,则∠FED=__32__度,∠EFD=__58__度.图4-11【解析】∵AC=DF,BC=EF,∠BAC=∠EDF=90°,∴△ABC≌△DEF,∴∠FED=∠CBA=32°,∠EFD=90°-32°=58°.12.如图4-12,AB=AC,要使△ABE≌△ACD,应添加的条件是__答案不唯一,如∠C=∠B或∠AEB=∠ADC或∠CEB=∠BDC或AE=AD或CE=BD__(添加一个条件即可).图4-1213.如图4-13,在△ABC 中,AB =5 cm ,AC =3 cm ,BC 的垂直平分线分别交AB ,BC 于D ,E ,则△ACD 的周长为__8__cm.图4-13【解析】 △ACD 的周长为AD +DC +AC ,又因为DE 垂直平分BC ,所以DC =BD ,所以AD +DC +AC =AD +BD +AC =AB +AC =5+3=8(cm). 14.如图4-14,∠DEF =60°,AB =BC =CD =DE =EF ,则∠A =__15__度.图4-14【解析】 ∵AB =BC , ∴∠A =∠ACB ,∴∠CBD =∠A +∠ACB =2∠A . ∵BC =CD =DE =EF ,∴同理可得∠DCE =∠A +∠ADC =3∠A , ∠EDF =∠A +∠AED =4∠A . ∵DE =EF ,∠DEF =60°, ∴△DEF 是等边三角形, ∴∠EDF =4∠A =60°, ∴∠A =15°.15.如图4-15所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S 1=258π,S 2=2π,则S 3是__9π8__.图4-1516.如图4-16是一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②′,…,然后依此类推,若正方形①的边长为64 cm ,则第4个正方形的边长为图4-16【解析】 根据题意:第一个正方形的边长为64 cm ; 第二个正方形的边长为22×64=322(cm); 第三个正方形的边长为22×322=32(cm); ……此后,每一个正方形的边长是上一个正方形的边长的22, 所以第n 个正方形的边长为64×⎝ ⎛⎭⎪⎫22n -1(cm),则第4个正方形的边长为64×⎝ ⎛⎭⎪⎫223=16 2 cm.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23 题每题12分,第24题14分,共80分)17.如图4-17,在△ABC 中,已知∠ABC =46°,∠ACB =80°,延长BC 至D ,使CD =CA ,连结AD ,求∠BAD 的度数.图4-17解:∵∠ACB=80°,∴∠ACD=180°-∠ACB=180°-80°=100°.又∵CD=CA,∴∠CAD=∠D.∵∠ACD+∠CAD+∠D=180°,∴∠CAD=∠D=40°,∴∠BAD=180°-∠ABC-∠D=180°-46°-40°=94°.18.如图4-18,DE是△ABC的AB边的垂直平分线,分别交AB,BC于D,E,AE平分∠BAC,若∠B=30°,求∠C的度数.图4-18解:∵DE是AB边的垂直平分线,∴EA=EB,∴∠ABE=∠1.∵∠B=30°,∴∠1=30°.又∵AE平分∠BAC,∴∠2=∠1=30°,即∠BAC=60°,∴∠C=180°-∠BAC-∠B=90°.19.如图4-19,在离水面高度为5 m的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒0.5 m的速度收绳.(1)8秒后船向岸边移动了多少米?(2)写出还没收的绳子的长度s米与收绳时间t秒的函数关系式.图4-19解:(1)如图,假设8秒后,船到达D位置,连结CD,∵AC=5 m,∠CBA=30°,∴CB=2AC=10 m,此人以每秒0.5 m的速度收绳,则8秒后收回的绳子长为0.5×8=4 (m),∴CD=10-4=6(m).第19题答图在Rt△ACD中,AD=CD2-AC2=62-52=11(m),在Rt△ACB中,AB=CB2-AC2=100-25=53(m),则BD=AB-AD=(53-11)m.(2)s=10-0.5t(0≤t≤10).20.如图4-20,△ABC中,AB=AC,BD⊥AC,CE⊥AB.求证:BD=CE.图4-20【解析】证明BD,CE所在的两个三角形全等.证明:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°.在Rt △ABD 和Rt △ACE 中,∠ADB =∠AEC =90°,∠A =∠A ,AB =AC ,∴△ABD ≌△ACE ,∴BD =CE .21.如图4-21,点D ,E 在△ABC 的边BC 上,AB =AC ,BD =CE .求证:AD =AE .图4-21证明:∵AB =AC ,∴∠B =∠C .在△ABD 与△ACE 中,⎩⎨⎧AB =AC ,∠B =∠C ,BD =CE ,∴△ABD ≌△ACE ,∴AD =AE .22.如图4-22,AB ∥CD ,以点A 为圆心,小于AC 长为半径作圆弧,分别交AB ,AC 于E ,F 两点,再分别以E ,F 为圆心,大于12EF 长为半径作圆弧,两条圆弧交于点P ,作射线AP ,交CD 于点M .图4-22(1)若∠ACD =114°,求∠MAB 的度数;(2)若CN ⊥AM ,垂足为N ,求证:△ACN ≌△MCN .【解析】 (1)根据AB ∥CD ,∠ACD =114°,得出∠CAB =66°,再根据AM是∠CAB的平分线,即可得出∠MAB的度数.(2)根据∠CAM=∠MAB,∠MAB=∠CMA,得出∠CAM=∠CMA,再根据CN⊥AM,CN=CN,即可得出△ACN≌△MCN.解:(1)∵AB∥CD,∴∠ACD+∠CAB=180°,又∵∠ACD=114°,∴∠CAB=66°.由作法可知,AM是∠CAB的平分线,∴∠MAB=12∠CAB=33°.(2)证明:由作法可知,AM是∠CAB的平分线,∴∠MAB=∠CAM.∵AB∥CD,∴∠MAB=∠CMA,∴∠CAM=∠CMA.又∵CN⊥AD,∴∠CNA=∠CNM=90°,又∵CN=CN,∴△ACN≌△MCN.23.如图4-23,在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,过D点作DE⊥DF,交AB于E,交BC于F.若AE=4,FC=3,求EF 的长.图4-23【解析】连结BD,构造全等三角形,利用勾股定理求解.解:连结BD,∵∠ABC=90°,AB=BC,D为AC边上的中点,∴∠ABD =12∠ABC =45°=∠A =∠C ,∠ADB =∠CDB =90°.又∵∠EDF =90°,∴∠EDB +∠BDF =∠BDF +∠CDF =90°,∴∠EDB =∠CDF .又∠EBD =∠DCF =45°,BD =12AC =CD ,∴△EBD ≌△FCD ,∴BE =FC =3.又AE +BE =BF +FC ,∴AE =BF =4,∴在Rt △EBF 中,EF =BE 2+BF 2=5.24.如图4-24,已知在△ABC 中,AB =AC ,∠BAC =90°,分别过B ,C 向过A 的直线作垂线,垂足分别为E ,F .(1)如图①,过A 的直线与斜边BC 不相交时,求证:EF =BE +CF ;(2)如图②,过A 的直线与斜边BC 相交时,其他条件不变,若BE =10,CF =3,求EF 的长.图4-24解:(1)证明:∵BE ⊥EA ,CF ⊥AF ,∴∠BAC =∠BEA =∠CFE =90°,∴∠EAB +∠CAF =90°,∠EBA +∠EAB =90°,∴∠CAF =∠EBA .在△ABE 和△AFC 中,⎩⎨⎧∠BEA =∠AFC =90°,∠EBA =∠CAF ,AB =AC ,∴△BEA ≌△AFC ,∴EA =FC ,BE =AF ,∴EF =EA +AF =FC +BE .(2)解:∵BE ⊥EA ,CF ⊥AF ,∴∠BAC =∠BEA =∠CFE =90°,∴∠EAB +∠CAF =90°,∠ABE +∠EAB =90°, ∴∠CAF =∠ABE .在△ABE 和△ACF 中,⎩⎨⎧∠BEA =∠AFC =90°,∠EBA =∠CAF ,AB =AC ,∴△BEA ≌△AFC ,∴EA =FC =3,BE =AF =10,∴EF =AF -EA =10-3=7.。
(原创连载)统编版五年级上册第七单元测试(市统考真题模板,含答案)

原创连载,侵权必究统编版五年级上册市第七单元标准化试题(含答案)时间:90分钟满分:100分班级 ________ 姓名________ 学号________ 分数________卷首语:绿树红花,莲叶田田,大雁南飞,雪花飞舞,“四时景物皆成趣”。
其实我们皆风景,因为我们或文静,或活泼,或幽默;有喜,有忧,有笑,有泪,有花,有果。
今天,我们何不以最美的答题状态,完成这份检测,亮出自己最美的风景呢?第一部分:积累运用(43.5分)一、卷面整洁。
(2分)二、根据拼音或积累,在相应位置书写相关内容。
(22.5分)1.读拼音,写词语:(10分)hóng yùn yíng huǒdàyàn xīn kuàng shén yízǒu láng wèi miǎn róng shùyìng jiēbùxiá2.“山一程,水一程,,。
”出自代词人的《》。
词中“”一句点明了作者身在行军途中,“,。
”则写出了将士的思乡之情。
3.《山居秋暝》中含蓄地表达诗人远离官场、洁身自好、归隐山林的生活志向的诗句是: “,”;运用动静结合的手法描写雨后秋景的两句诗是:“,。
”4.我能从“,。
”中感受到桃红水碧、鹭飞鱼肥的江南美景。
5.竹林里传来一阵阵欢声笑语,那是天真无邪的姑娘们洗衣归来的声音。
这情景会让你想到王维的诗句:“,。
”6.《枫桥夜泊》一诗中,描写寒山寺的夜半钟声的诗句是: ,。
7. (国家)(作者)写的《四季之美》中描写春天黎明天空的语句是:“东方,,飘着红紫,红紫的彩云。
”8.“那‘鸟的天堂’的确是鸟的天堂啊!”这句话中不加引号的“鸟的天堂”指 ,加引号的“鸟的天堂”指。
三、下面各小题均有A、B、C、D四个备选答案,请按题目要求选择一个正确的答案,将序号填在“( )”里。
人教版小学四年级上册语文单元试卷全册

人教版小学四年级上册语文单元试卷全册LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】人教版小学四年级上册语文第一单元检测试题班级: 姓名: 得分:识字·写字(30%)一、看拼音写词语。
10分hu ī fù zhào yào fèi téng gu ī l ǜ fèng xì( )( ) ( ) ( ) ( ) càn làn jìng jì y ī jiù l ǒng zhào shù sh āo( ) ( ) ( ) ( ) ( )二、用“√”给带点的字选择正确的读音。
9分 闷.雷(mēn mèn) 踮.着脚(diǎn diān) 号.叫(háo hào) 兴.奋(xīng xìng) 答.应(yīng yìng) 堤.岸(dī tī) 停泊.(pō bó) 树干.(gān gàn) 不可计数.(shǔ shù)三、把下列词语补充完整。
5分若( )若现 漫天( )地 齐头并( ) 不可计( ) ( )首东望横( )江面 风平( )静 水天相( ) 一争高( ) 人声鼎( )四、照样子,把下列句子写具体。
6分例:那么多的绿叶,一簇堆另一簇上面,不留一点儿缝隙。
1.那么多的鸟儿, 。
2. 的岩石上绽开了 的花朵。
例:午后一点左右,从远处传来隆隆的响声,好像闷雷滚动。
3.高高的瀑布从上游山峡里倾泻下来,像。
阅读·积累 70%一、判断下列说法,对的打“√”,错的打“×”。
3分1.观赏钱塘江大潮是在夏天。
( )2.《火烧云》是作家萧红写的。
( ) 3.“鸟的天堂”是一棵枝繁叶茂的大榕树。
( )二、把下面的句子按一定顺序整理成一段通顺的话。
滚动练综合检测卷七年级下册答案2022英语第八单元第一章仁爱

滚动练综合检测卷七年级下册答案2022英语第八单元第一章仁爱【听力材料】:(Text 1)W: What’s new with you,Jack?M:Well,I met a really nice woman.We’ve been going out for three months and things look good now.(Text 2)M: When did you first find the door broken and things missing?W:After I got up,around 5:20.Then I called the police station.(Text 3)W: Pass me the flour,please.M:Which tin is it in?W:The one at the end of the shelf.It’s slightly smaller than the others.M:Oh,right.(Text 4)W:Do you know why George hasn’t come yet?M:Yes.He was planning to come,but his wife’s father fell downsome stairs and they had to take him to a hospital.W:I’m sorry to hear that.(Text 5)W:Hi,Tony.How did your experiment go yesterday?M: Well,it wasn’t as easy as I had thought.I have to continue doing it tonight.(Text 6)M:Is that Ann?W:Yes.M:This is Mike.How are things with you?W:Oh,very well,but I’m very busy.M:Busy? But you’ve finished all your exams?W:Yes,but I have to help my little sister with her foreign language.M:How about coming out with me this evening?There’s a new film on.W:I’m afraid I can’t.A friend of mine is coming from the south and I have to go to the station to meet him.M:What a pity!How about the weekend then?W:No,I’ve arranged to go to an art exhibition with my parents.M:What about next week sometime?W:Maybe.(Text 7)W:I hear there will be a football competition between all senior schools next month.Is that so?M:That’s true.W:Would you please go into some more details?M:Well,the competition will be held in our school and it will begin on August 11.The competition will last a whole week.W:Anything else?M:Yes,both the girls and boys competition will be held at the same time.The girls competition will be held in the morning and the boys competition will be held in the afternoon.W:Yes? Sounds exciting.M:We are both members of our school football team.We should be ready for it.W:Of course.It’s a long time since we had the last football competition last time.I’m really looking forward to anothercompetition.M:Me,too.(Text 8)W: Excuse me.I am from STM.We are carrying out a survey on the traffic in our city.Do you mind if I ask you some questions?M:No,not at all.Go ahead.W:Good,thanks.What do you do,sir?M:I am a teacher.I teach children French.W:Great.Do you live far from the school? I mean,how do you usually go to work?M:Well,mostly by car.But once in a while,I prefer to ride my bike.You know,I live quite far from the school,about 20 miles.And I have to spend about an hour riding to school.But it only takes me less than a quarter of an hour to drive my car,unless the traffic is very bad.W:I see.Does this happen often? I mean the bad traffic.M:Yes,sure! I often get stuck on the way,and the problem’s getting worse and worse.W:That’s all of my questions.Thank you very much.M:You are welcome.(Text 9)M: Customer service.Andney Grant speaking.How may I help you?W:I can’t believe this is happening.I called and ordered a 32?inch bag last Friday.But today I found that you sent me a 24?inch one.I was planning to use that bag during our vacation in Mexico,but it doesn’t seem possible any more because we will take off on Saturday.It’s only two days away.What am I supposed to do?M:I’m really sorry,madam. I’ll check right away.Would you please tell me your order number?W:It’s CE2938.M:Just a minute.I do apologize,madam.There did seem to be a mistake.I’ll have the correct size bag sent to you by overnight mail right away.It will arrive in time for your Saturday trip.Again I apologize for any inconvenience caused by our mistake.I promise it won’t happen again.W:OK.Well,thank you.M:Thank you,madam,for choosing Linch mail.I hope you will have a wonderful vacation.(Text 10)I wasn’t too fond of the lecture classes of 400 students in my general course.Halfway through my second term when I was considering whether or not to come back in the fall,I went on the Internet and came across Americorp.Then I joined in an organization,and that’s what I did last school year.I worked on making roads,building a house,serving as a teacher’s assistant and working as a camp officer in several projects in South Carolina and Florida.It’s been a great experience,and I’ve almost learned more than what I could have in college since I didn’t really want to be at that school and wasn’t interested in my major anyway,I thought this was better for me.After 1,700 hours of service I received 4,750 dollars.I can use that to pay off the money I borrowed from the bank or for what is needed when I go back to school this fall at Columbus State in Ohio.Classes are smaller there and I’ll be majoring in German education.After working with the kids,now I know,I want to be a teacher.一、听力第一节(共5小题,每小题1分)听下面5段对话。
单元滚动检测卷(二)

单元滚动检测卷(二)[测试范围:第三单元及第四单元 时间:120分钟 分值:150分]第Ⅰ卷(选择题 共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的 正确选项,不选、多选、错选,均不得分)1.方程x 2-3x =0的解为( D )A .x =0B .x =3C .x 1=0,x 2=-3D .x 1=0,x 2=32.一元二次方程x 2+x -2=0根的情况是( A ) A .有两个不相等的实数根B .有两个相等的实数根C .无实数根D .无法确定3.分式方程2x -2-1x =0的根是 ( D ) A .x =1B .x =-1C .x =2D .x =-24.由方程组⎩⎨⎧2x +m =1,y -3=m可得出x 与y 的关系是 ( A )A .2x +y =4B .2x -y =4C .2x +y =-4D .2x -y =-4【解析】 两方程相加得2x +m +y -3=1+m ,故2x +y -3=1,所以2x +y=4.5.如图2-1,A ,B 两点在数轴上表示的数分别为a ,b ,下列式子成立的是( C )图2-1A .ab >0B .a +b <0C .(b -1)(a +1)>0D .(b -1)(a -1)>0【解析】 由a ,b 两点在数轴上的位置可知:-1<a <0,b >1,∴ab <0,a +b >0,故A ,B 错误;∵-1<a <0,b >1,∴b -1>0,a +1>0,a -1<0,故C 正确,D 错误.故选C.6.不等式组⎩⎨⎧2-x ≥1,2x -1>-7的解集在数轴上表示正确的是 ( D )图2-27.关于x 的方程mx -1=2x 的解为正实数,则m 的取值范围是( C )A .m ≥2B .m ≤2C .m >2D .m <2 【解析】 原方程可化为(m -2)x =1,∴x =1m -2,由题意,得m -2>0, ∴m >2,选C.8.某药品经过两次降价,每瓶零售价由168元降为128元,已知两次降价的百分率相同,设每次降价的百分率为x ,根据题意列方程得 ( B )A .168(1+x )2=128B .168(1-x )2=128C .168(1-2x )=128D .168(1-x 2)=1289.为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地调查了10 000人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人,如果设这10 000人中,吸烟者患肺癌的人数为x ,不吸烟者患肺癌的人数为y ,根据题意,下面列出的方程组正确的是( B ) A.⎩⎨⎧x -y =22x ×2.5%+y ×0.5%=10 000B.⎩⎪⎨⎪⎧x -y =22x 2.5%+y 0.5%=10 000 C.⎩⎨⎧x +y =10 000x ×2.5%-y ×0.5%=22D.⎩⎪⎨⎪⎧x +y =10 000x 2.5%-y 0.5%=2 10.对于非零的两个实数a ,b ,规定a ⊗b =1b -1a ,若1⊗(x +1)=1,则x 的值为( D )A.32B.13C.12 D .-12【解析】 依题意可列方程1x +1-1=1, ∴x =-12,故选D.第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.若代数式2x -1-1的值为零,则x =__3__.12.(1)方程组⎩⎨⎧2x +3y =7,x -3y =8的解是__⎩⎨⎧x =5,y =-1__.(2)方程x 2-2x -1=0的解是. 13.不等式组⎩⎪⎨⎪⎧x -4≤1x +12>2,的解集是__3<x ≤5__. 14.解方程:4x x -2-1=32-x,则方程的解是__x =-53__. 15.已知如图2-3所示的图形的面积为24.根据图中的条件,可列出方程:__答案不唯一,如(x +1)2=25__.图2-3【解析】 此图形的面积等于两个正方形的面积的差,据此可以列出方程. 根据题意,得(x +1)2-1=24,即:(x +1)2=25.故答案为:(x +1)2=25.16.已知关于x 的方程x 2+mx -6=0的一个根为2,则这个方程的另一个根是__-3__.【解析】 ∵方程x 2+mx -6=0的一个根为2,设另一个为a ,∴2a =-6,解得a =-3,则方程的另一个根是-3.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.解方程:(1)x 2-2x -1=0;(2)2x =32x -1. 解:(1)x =-(-2)±(-2)2-4×1×(-1)2∴x =2±222.∴x 1=1+2,x 2=1- 2.(2)解:通分得,2(2x -1)=3x .4x -2=3x .x =2.经检验,x =2是原方程的根.18.用代入消元法解方程组⎩⎨⎧x -y =2, ①3x +5y =14. ②解:由①,得x =y +23.将③代入②,得3(y +2)+5y =14.解得y =1.把y =1代入③,得x =3.∴原方程组的解为⎩⎨⎧x =3,y =1. 19.解不等式组:⎩⎪⎨⎪⎧3x >x -2,x +13>2x . 解:由3x >x -2,得x >-1.由x +13>2x ,得x <15.∴不等式组的解集为-1<x <15.20.某渔船出海捕鱼,2010年平均每次捕鱼量为10吨,2012年平均每次捕鱼量为8.1吨,求2010~2012年每年平均每次捕鱼量的年平均下降率.解:设2010~2012年每年平均每次捕鱼量的年平均下降率为x ,根据题意,得10(1-x )2=8.1.x 1=0.1=10%,x 2=1.9(不符合题意,舍去).答:2010~2012年每年平均每次捕鱼量的年平均下降率为10%.21.方程x 2-9x +18=0的两个根是等腰三角形的底和腰,求这个等腰三角形的周长.解:x 2-9x +18=0,∴(x -3)(x -6)=0,∴x -3=0,x -6=0,∴x 1=3,x 2=6,当等腰三角形的三边是3,3,6时,3+3=6,不符合三角形的三边关系定理, ∴此时不能组成三角形,当等腰三角形的三边是3,6,6时,此时符合三角形的三边关系定理,周长是3+6+6=15.22.如图2-4,邻边不等的矩形花圃ABCD (其中BC >AB ),它的一边AD 利用已有的围墙,另外三边所围的栅栏的总长度是6 m .若矩形的面积为4 m 2,求AB 的长度.(可利用的围墙长度超过6 m).图2-4解:AB 的长度是1.23.苏州某旅行社组织甲、乙两个旅游团分别到西安、北京旅游.已知这两个旅游团共有55人,甲旅游团的人数比乙旅游团的人数的2倍少5人.问甲、乙两个旅游团各有多少人?解:设甲旅游团有x 人,乙旅游团有y 人,依题意,得⎩⎨⎧x +y =55,x =2y -5,解得⎩⎨⎧x =35,y =20.答:甲、乙两个旅游团分别有35人、20人.24.为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A 、B 两种型号的学习用品共1 000件,已知A 型学习用品的单价为20元,B 型学习用品的单价为30元.(1)若购买这批学习用品共用了26 000元,则购买A 、B 两种学习用品各多少件?(2)若购买这批学习用品的钱不超过28 000元,则最多购买B 型学习用品多少件?解:(1)法1:设购买A 型学习用品x 件,购买B 型学习用品(1 000-x )件,根据题意,得20x +30(1 000-x )=26 000,解得x =400,1 000-400=600.法2:设购买A 型学习用品x 件,购买B 型学习用品y 件,根据题意,得⎩⎨⎧x +y =1 00020x +30y =26 000, 解得⎩⎨⎧x =400y =600, 答:购买A 型学习用品400件,购买B 型学习用品600件.(2)设购买B 型学习用品m 件,则购买A 型学习用品为(1 000-m )件,由题意可得20(1 000-m )+30m ≤28 000,解得m ≤800,所以最多购买B 型学习用品800件.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单元滚动检测卷(七)第Ⅰ卷选择题(共50分)1.(温州市2019届高三9月选考适应性测试)下列过程会释放出热量的是()A.浓硫酸稀释B.水的分解C.硝酸铵溶于水D.冰的融化答案A解析浓硫酸稀释放热,故A正确;水的分解吸热,故B错误;硝酸铵溶于水吸热,故C 错误;冰的融化吸热,故D错误。
2.氢能是一种理想的“绿色能源”,以下有关氢能开发的方式中最理想的是()A.大量建设水电站,用电力分解水制取氢气B.利用化石燃料燃烧放热,使水高温分解产生氢气C.在催化剂作用下,利用太阳能分解水制取氢气D.利用铁等金属与酸反应产生氢气答案C解析A项,消耗大量的电能,错误;B项,产生大量污染物,且造成能量的浪费,错误;C项,太阳能无污染,且取之不尽用之不竭,正确;D项,消耗大量的金属,错误。
3.(浙江省“七彩阳光”联盟2019届高三上学期期初联考)下列化学反应属于放热反应的是A.浓硫酸溶于水B. 镁溶于盐酸C.石灰石煅烧D.Ba(OH)2·8H2O晶体与NH4Cl晶体混合答案B解析浓硫酸溶于水是物理变化,而非化学变化,故不属于放热反应,选项A错误;镁溶于盐酸发生反应生成氯化镁和氢气且放出大量的热,属于放热反应,选项B正确;石灰石在高温条件下煅烧发生分解反应,属于吸热反应,选项C错误;Ba(OH)2·8H2O晶体与NH4Cl晶体混合属于吸热反应,选项D错误。
4.下列反应中生成物总能量高于反应物总能量的是()A.碳酸钙受热分解B.乙醇燃烧C.铝粉和氧化铁反应D.氧化钙溶于水答案A解析碳酸钙受热分解是吸热反应,生成物的总能量高于反应物总能量,A正确;乙醇燃烧是放热反应,B错误;铝粉和氧化铁反应是放热反应,C错误;氧化钙溶于水放热,D错误。
5.下列关于燃料充分燃烧的说法中,错误的是()A.氧气量充足,燃烧充分B.固体燃料块越大燃烧越充分C.液体燃料燃烧时可以雾状喷出D.温度必须达到着火点答案B解析固体燃料块越大,接触面积小,燃烧越不充分,B错误;液体燃料燃烧时可以雾状喷出增大反应物接触面积,加快反应速率,C正确。
6.(浙江省名校协作体2019届高三上学期考试)下列说法不正确的是()A.煤属于生物质能B.氢气是理想的绿色能源C.地沟油可加工成航空煤油D.沼气属于可再生能源答案A解析煤属于化石能源,故A错误;氢气燃烧后生成水,且氢气是可再生能源,故是理想的燃料,故B正确;沼气可以通过发酵而制得,属于可再生能源,故D正确。
7.(宁波市十校2019届高三9月联考)下列说法不正确的是()A.人类在远古时代就通过燃烧植物的方式开始利用生物质能B.氢能是理想的绿色能源,但人们只能将氢气的化学能转化为热能C.煤中含有硫元素,大量的直接燃烧煤会引起酸雨等环境问题D.太阳能以光和热的形式传送到地面,人们可以直接利用这些光和热答案B解析人类燃烧植物的方式获得热能,是开始利用生物质能的最早方式,故A正确;还可以让氢气构成燃料电池,使化学能转化成电能,故B错误;煤中含有硫元素,燃烧时产生SO2,引起酸雨等环境问题,故C正确;人们可以直接利用光和热,如太阳能热水器,故D正确。
8.(2019·金华市东阳中学高三月考)为消除目前燃料燃烧时产生的环境污染,同时缓解能源危机,有关专家提出了利用太阳能制取氢能的构想。
下列说法正确的是()A.H2O的分解反应是放热反应B.氢能源已被普遍使用C.2 mol H2O具有的总能量低于2 mol H2和1 mol O2的能量D.氢气不易贮存和运输,无开发利用价值答案C解析氢气燃烧生成水是放热反应,则水的分解反应是吸热反应,A项错误;由于氢气的获得目前还没有更好的技术,所以氢能源还没有被普通使用,B项错误;因为水的分解反应是吸热反应,所以2 mol液态H2O具有的总能量低于2 mol H2和1 mol O2的能量,C项正确;氢气属于新能源,具有很好的开发价值,D项错误。
9.(2019·浙江省嘉兴市高三模拟)下列对于太阳能、生物质能和氢能利用的说法不正确的是A.芒硝晶体(Na2SO4·10H2O)白天在阳光下曝晒后失水、分解吸热,夜里重新结晶放热,实现了太阳能转化为化学能继而转化为热能B.将植物的秸秆、枝叶、杂草和人畜粪便加入沼气发酵池中,在富氧条件下,经过缓慢、复杂、充分的氧化反应最终生成沼气,从而有效利用生物质能C.生活、生产中大量应用氢能源,首先要解决由水制备氢气的能耗、氢气的储存和运输等问题D.垃圾焚烧处理厂把大量生活垃圾中的生物质能转化为热能、电能,减轻了垃圾占地给城市造成的压力,改善了城市的环境答案B解析芒硝在白天光照下失水,是太阳能转化为化学能,晚上重新结晶放热,是化学能转化成热能,故A正确;将植物的秸秆、枝叶、杂草和人畜粪便加入沼气发酵池中,应在厌氧条件下进行,故B错误;氢能源开发利用过程中需要解决的问题是探索廉价制氢气的方法和怎样解决氢气的储存、运输问题,故C正确;利用垃圾发电可将生活垃圾中的生物质能转化为热能、电能等,故D正确。
10.沼气是一种新能源,它的主要成分是甲烷。
0.5 mol CH4完全燃烧生成CO2和H2O(l)时,放出445 kJ热量,则下列热化学方程式中正确的是()A.2CH4(g)+4O2(g)===2CO2(g)+4H2O(l)ΔH=890 kJ·mol-1B.CH4(g)+2O2(g)===CO2(g)+2H2O(l)ΔH=890 kJ·mol-1C.CH4(g)+2O2(g)===CO2(g)+2H2O(l)ΔH =-890 kJ·mol -1 D.12CH 4(g)+O 2(g)===12CO 2(g)+H 2O(l) ΔH =-890 kJ·mol -1答案 C解析 0.5 mol CH 4完全燃烧生成CO 2和液态水时放出445 kJ 的热量,则1 mol CH 4完全燃烧生成CO 2和液态水时放出890 kJ 的热量,因此热化学方程式是CH 4(g) + 2O 2(g)===CO 2(g) + 2H 2O(l) ΔH =-890 kJ·mol -1,故选项是C 。
11.(2019·嘉兴市高三检测)下列有关热化学方程式的叙述正确的是( )A .己知2H 2(g)+O 2(g)===2H 2O(g) ΔH =-483.6 kJ·mol -1,则H 2的标准燃烧热为-241.8 kJ·mol -1B .已知C(石墨,s)===C(金刚石,s) ΔH >0,则金刚石比石墨稳定C .含20.0 g NaOH 的稀溶液与稀盐酸完全中和,放出28.7 kJ 的热量,则该反应的热化学方程式为NaOH(aq)+HCl(aq)===NaCl(aq)+H 2O(l) ΔH =-57.4 kJ·mol -1D .已知 2SO 2(g)+O 2(g)2SO 3(g) ΔH =-Q kJ·mol -1(Q >0),则将2 mol SO 2(g)和10 mol O 2(g)置于一密闭容器中充分反应后放出Q kJ 的热量答案 C解析 燃烧热是1 mol 可燃物完全燃烧生成稳定的氧化物所释放的热量,水应为液态,故A 错误;ΔH >0说明此反应是吸热反应,即金刚石的能量大于石墨,物质能量越低,越稳定,即石墨比金刚石稳定,故B 错误;1 mol 氢氧化钠完全反应放出热量为28.70.5kJ =57.4 kJ ,故C 正确;此反应是可逆反应,不能完全进行到底,放出的热量小于Q ,故D 错误。
12.(2019·金华市东阳中学高三月考)已知:2CO(g)+O 2(g)===2CO 2(g) ΔH =-565.2 kJ·mol -1,下列说法不正确的是( )A .CO(g)+12O 2(g)===CO 2(g) ΔH =-282.6 kJ·mol -1 B .2 mol CO(g)与1 mol O 2(g)反应生成2 mol CO 2(s)放出热量小于565.2 kJC .相同条件下,2 mol CO(g)和1 mol O 2(g)的总能量大于2 mol CO 2(g)的总能量D .拆开2 mol CO 和1 mol O 2的化学键所需总能量低于形成2 mol CO 2化学键所放出总能量 答案 B解析 1 mol 一氧化碳燃烧放出的热量为282.6 kJ ,则反应热的化学方程式为CO(g)+12O 2(g)===CO 2(g) ΔH =-282.6 kJ·mol -1,故A 正确;气体变成固体要放出热量,所以2 molCO(g)与1 mol O2(g)反应生成2 mol CO2(s)放出的热量大于565.2 kJ,故B错误;正反应是放热反应,所以反应物的总能量高于生成物的总能量,所以2 mol CO(g)和1 mol O2(g)的总能量大于2 mol CO2(g)的总能量,故C正确;根据化学反应的实质,因为该反应为放热反应,则拆开反应物化学键所吸收的总能量小于形成生成物化学键所放出的总能量,故D正确。
13.(金华市2019届高三9月十校联考)用Cl2生产某些含氯有机物时会产生副产物HCl。
利用反应A,可实现氯的循环利用:4HCl(g)+O2(g)2Cl2(g)+2H2O(g)ΔH=-115.6 kJ·mol-1已知:Ⅰ.反应A中,4 mol HCl被氧化,放出115.6 kJ的热量。
下列说法正确的是()A.升高温度能提高HCl的转化率B.加入催化剂,能使该反应的焓变减小C.1 mol Cl2转化为2 mol Cl原子放出243 kJ热量D.断裂H2O(g)中1 mol H—O键比断裂HCl(g)中1 mol H—Cl键所需能量高答案D解析升高温度,平衡逆向移动,HCl的转化率减小,故A错误;加入催化剂,反应的焓变不变,故B错误;根据提示,1 mol Cl2转化为2 mol Cl原子吸收243 kJ热量,故C错误;E(H—O)、E(H—Cl)分别表示H—O的键能、H—Cl的键能,反应中,4 mol HCl被氧化,放出115.6 kJ的热量,反应热ΔH=反应物的总键能-生成物的总键能,故:4×E(H—Cl)+498 kJ·mol-1-[2×243 kJ·mol-1+4×E(H—O)]=-115.6 kJ·mol-1,整理得,4E(H—Cl)-4E(H—O)=-127.6 kJ·mol-1,即E(H—O)-E(H—Cl)=31.9 kJ·mol-1,故断开1 mol H—O键比断开1 mol H—Cl键所需能量高,故D正确。
