实验1_信息论相关实验实验报告
信息论与编码实验报告

信息论与编码实验报告信息论与编码实验报告实验一:英文文本信息量的计算一、实验目的及要求a)实验目的1、通过本实验熟悉Matlab 软件编程环境2、编写M 文件实现对英文文本信息量的统计,掌握信息量、信源熵的计算方法b)实验要求1、了解matlab 中M 文件的编辑、调试过程2、编写程序实现对给定英文文本信息量的统计3、英文文本中字母不区分大小写,考虑空格的信息量,但不考虑标点符号的信息量4、建议英文文本采用txt 格式二、实验步骤及运行结果记录a)实验步骤1、查找各个英文字母及空格出现的频率2、在Matlab 中读取给定的英文文章3、计算英文文章的长度4、统计在该文章中各个字母及空格出现的次数并放入数组N 中5、计算各个字母和空格的信息量及整篇文章的信息量6、计算信源熵b)实验结果sumI = +003;H = 三、程序流程图四、程序清单,并注释每条语句五、实验小结通过本次实验熟悉了Matlab 软件编程环境和一些函数的功能及使用,掌握了信息量、信源熵的计算方法。
1 附一:开始读取英文文章计算文章的长度嵌套的for 循环语句假判断是否符合循环条件真if 否elseif 判断字是否为大写母输入相应的频率否elseif 判断是否为小写字母计算各个字母、空格及整篇文章的信息量是判断是否为小写字母是计算信源熵是放入数组N 中对应的位置放入数组N 中对应的位置放入数组N 中对应的位置结束附二: wenzhang=textread(‘实验一:english ‘,’\’); M=size(wenzhang); row=M(1,1); line=M(1,2); N=zeros(1,27); for i=1:row for j=1:line %读取英文文章%文章的长度ifdouble(wenzhang(i,j))>96&&double(wenz hang(i,j))double(wenzhang(i,j))>64&&double(wenz hang(i,j))N(1,double(wenzhang(i,j))-64)=N(1,doubl e(wenzhang(i,j))-64)+1; elseif double(wenzhang(i,j))==32N(1,27)=N(1,27)+1; end end end %统计各字母和空格出现的个数并存入N数组中。
信息论实验报告

信息论实验报告班级:姓名:学号:实验一:信道容量的迭代算法1.实验目的(1)进一步熟悉信道容量的迭代算法;(2)学习如何将复杂的公式转化为程序;(3)掌握C 语言数值计算程序的设计和调试技术。
2、实验要求(1)已知:信源符号个数r 、信宿符号个数s 、信道转移概率矩阵P 。
(2)输入:任意的一个信道转移概率矩阵。
信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。
(3)输出:最佳信源分布P*,信道容量C 。
3.算法分析1:procedure CHANNEL CAPACITY(r,s,(ji p )) 2:initialize:信源分布i p =1/r ,相对误差门限σ,C=—∞3:repeat4:5:6: C 2211log [exp(log )]r s ji ij r j p φ==∑∑7:until C Cσ∆≤8:output P*= ()i r p ,C9:end procedure4.程序调试21211exp(log )exp(log )sji ij j r s ji ij r j p p φφ===∑∑∑i p 1i ji r i ji i p p p p =∑ijφ1、头文件引入出错f:\visualc++\channel\cpp1.cpp(4) : fatal error C1083: Cannot open include file: 'unistd.h': No such file or directory————#include<unistd.h>纠错://#include<unistd.h>f:\visualc++\channel\cpp1.cpp(5) : fatal error C1083: Cannot open include file: 'values.h': No such file or directory————#include<values.h>纠错://#include<values.h>2、变量赋值错误f:\visualc++\channel\cpp1.cpp(17) : error C2065: 'ij' : undeclared identifierf:\visualc++\channel\cpp1.cpp(17) : error C2440: 'initializing' : cannot convert from 'int' to 'float ** ' Conversion from integral type to pointer type requires reinterpret_cast, C-style cast or function-style cast————float **phi_ij=ij=NULL;纠错:float **phi_ij=NULL;3、常量定义错误f:\visualc++\channel\cpp1.cpp(40) : error C2143: syntax error : missing ';' before 'for' ————for(i=0;i<r;i++)phi_ij[i]=(float *)calloc(s,sizeof(float));f:\visualc++\channel\cpp1.cpp(52) : error C2021: expected exponent value, not ' '————if(fabs(validate -1.0)>DELTA)f:\visualc++\channel\Cpp1.cpp(84) : error C2021: expected exponent value, not ' '————if(fabs(p_j)>=DELTA)f:\visualc++\channel\Cpp1.cpp(100) : error C2021: expected exponent value, not ' '————if(fabs(phi_ij[i][j])>=DELTA)f:\visualc++\channel\Cpp1.cpp(116) : error C2021: expected exponent value, not ' ' ————while(fabs(C-C_pre)/C>DELTA);纠错:#define DELTA 0.000001;F:\visualc++\channel\Cpp1.cpp(68) : error C2065: 'MAXFLOAT' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(68) : warning C4244: '=' : conversion from 'int' to 'float', possible loss of data————C=-MAXFLOAT;纠错:#define MAXFLOAT 1000000;3、引用中文逗号f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xa1'f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xb1'f:\visualc++\channel\cpp1.cpp(60) : error C2065: 'Starting' : undeclared identifierf:\visualc++\channel\cpp1.cpp(60) : error C2059: syntax error : '.'f:\visualc++\channel\cpp1.cpp(60) : error C2017: illegal escape sequencef:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xa1'f:\visualc++\channel\cpp1.cpp(60) : error C2018: unknown character '0xb1'————fprintf(stdout,”Starting..\n”);纠错:fprintf(stdout,"Starting..\n");4、没有进行强制转换F:\visualc++\channel\Cpp1.cpp(65) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————p_i[i]=1.0/(float)r;纠错:p_i[i]=(float)(1.0/(float)r);F:\visualc++\channel\Cpp1.cpp(101) : warning C4244: '+=' : conversion from 'double' to 'float', possible loss of data————sum[i]+=p_ji[i][j]*log( phi_ij[i][j])/ log(2.0);纠错:sum[i]+=(float)(p_ji[i][j]*log( phi_ij[i][j])/ log(2.0));F:\visualc++\channel\Cpp1.cpp(103) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————sum[i]=pow(2.0,sum[i]);纠错:sum[i]=(float)(pow(2.0,sum[i]));F:\visualc++\channel\Cpp1.cpp(114) : warning C4244: '=' : conversion from 'double' to 'float', possible loss of data————C= log(p_j)/ log(2.0);纠错:C= (float)(log(p_j)/ log(2.0));4、表达式错误F:\visualc++\channel\Cpp1.cpp(86) : error C2065: 'phi_ji' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(86) : error C2109: subscript requires array or pointer typeF:\visualc++\channel\Cpp1.cpp(86) : error C2109: subscript requires array or pointer type ————phi_ij[i][j]=p_i[i]* phi_ji[i][j]/p_j;纠错:phi_ij[i][j]=p_i[i]* p_ji[i][j]/p_j;F:\visualc++\channel\Cpp1.cpp(122) : error C2065: 'fprint' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xa1'F:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xb1'F:\visualc++\channel\Cpp1.cpp(122) : error C2065: 'The' : undeclared identifierF:\visualc++\channel\Cpp1.cpp(122) : error C2146: syntax error : missing ')' before identifier 'iteration'F:\visualc++\channel\Cpp1.cpp(122) : error C2017: illegal escape sequenceF:\visualc++\channel\Cpp1.cpp(122) : error C2017: illegal escape sequenceF:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xa1'F:\visualc++\channel\Cpp1.cpp(122) : error C2018: unknown character '0xb1'————fprint(stdout,”The iteration number is %d.\n\n”,k);纠错:fprintf(stdout,"The iteration number is %d.\n\n",k);F:\visualc++\channel\Cpp1.cpp(145) : error C2143: syntax error : missing ')' before ';' ————free((p_i);纠错:free(p_i);5、没有返回值F:\visualc++\channel\Cpp1.cpp(149) : warning C4508: 'main' : function should return a value; 'void' return type assumed、纠错:return 0;5.改进程序/*引入头文件*/#include<stdio.h>#include<math.h>#include<stdlib.h>/*定义常量*/#define DELTA 0.0000001//DELTA为相对误差门限#define MAXFLOAT 1000000;//MAXFLOAT为初始化信道容量值int main( void){/*定义全局变量*//*register允许直接从寄存器中读取变量,提高速率*/register int i,j;//i、j为整型变量register int k;//信道容量迭代计算次数int r,s;//r为信源符号个数,s为新宿符号个数float *p_i=NULL;//r个信源符号发生的概率float **p_ji=NULL;//信源到新宿的信道转移概率矩阵Pfloat **phi_ij=NULL;float C,C_pre,validate;//C为信道容量,C_pre为信道最大容量,validate为判定输入转移概率矩阵是否合法float * sum=NULL;//信源符号所带的全部信息量float p_j;//条件概率/*输入信源符号和新宿符号个数*/printf("请输入信源符号个数r、信宿符号个数s...\n");printf("+++++注意!!!r必须大于等于s!!+++++\n");fscanf(stdin,"%d",&r);fscanf(stdin,"%d",&s);/*为 p_i,p_ji 和 phi_ij 分配内存空间*/p_i=(float *)calloc(r,sizeof(float));p_ji=(float **)calloc(r,sizeof(float));/*为每个p_ji分配大小为s的内存空间*/for(i=0;i<r;i++)p_ji[i]=(float *)calloc(s,sizeof(float));phi_ij=(float **)calloc(r,sizeof(float*));/*输入转移概率矩阵*/for(i=0;i<r;i++)/*为每个phi_ij分配大小为s的内存空间*/phi_ij[i]=(float *)calloc(s,sizeof(float));printf("信道转移概率矩阵P...\n");for(i=0;i<r;i++)for(j=0;j<s;j++)fscanf(stdin,"%f",&p_ji[i][j]);/*判定输入的转移概率矩阵是否正确*/for(i=0;i<r;i++){validate=0.0;for(j=0;j<s;j++){validate +=p_ji[i][j];}if((validate-1.0)>=0)//如果转移概率矩阵的概率和大于1,输入数据不合法{fprintf(stdout,"invalid input data.\n");exit(-1);}}/*显示开始计算..*/fprintf(stdout,"Starting..\n");/*初始化 p_i 和 phi_ij*/for(i=0;i<r;i++){/* p_i为等概率,即概率为1/r*/p_i[i]=(float)(1.0/(float)r);}/*初始化信道容量c,迭代次数k和临时变量variable*/C=-MAXFLOAT;k=0;/* 为sum分配大小为r的内存空间*/sum=(float *)calloc(r,sizeof(float));/*开始迭代计算*/do{k++;//每进行一次迭代,迭代次数k加1/* 计算phi_ij(k)*/for(j=0;j<s;j++){p_j=0.0;for(i=0;i<r;i++)p_j+=p_i[i]*p_ji[i][j];if(fabs(p_j)>=DELTA)for(i=0;i<r;i++)phi_ij[i][j]=p_i[i]* p_ji[i][j]/p_j;elsefor(i=0;i<r;i++)phi_ij[i][j]=0.0;}/*计算p_i(k+1)*/p_j=0.0;for(i=0;i<r;i++){sum[i]=0.0;for(j=0;j<s;j++){/*相对误差门限为0*/if(fabs(phi_ij[i][j])>=DELTA)sum[i]+=(float)(p_ji[i][j]*log( phi_ij[i][j])/ log(2.0)); }sum[i]=(float)(pow(2.0,sum[i]));p_j+=sum[i];}for(i=0;i<r;i++){p_i[i]=sum[i]/p_j;}C_pre=C;C= (float)(log(2.0)/log(p_j) );}while(fabs(C-C_pre)/C>DELTA);free(sum);sum=NULL;/*显示结果*/fprintf(stdout,"The iteration number is %d.\n\n",k);//迭代次数fprintf(stdout,"The capacity of the channel is %.6f bit/symbol:\n\n",C);//信道容量fprintf(stdout,"The best input probability distribution is :\n");//最佳信源分布 for(i=0;i<r;i++)fprintf(stdout,"%.6f\n",p_i[i]);fprintf(stdout,"\n");/* 释放指针空间*/for(i=s-1;i>=0;i--){free(phi_ij[i]);phi_ij[i]=NULL;}free(phi_ij);phi_ij=NULL;for(i=r-1;i>=0;i--){free(p_ji[i]);p_ji[i]=NULL;}free(p_ji);p_ji=NULL;free(p_i);p_i=NULL;exit(0);return 0;}6.实验结果6.实验二:唯一可译码判决准则1.实验目的(1)进一步熟悉唯一可译码判决准则;(2)掌握C语言字符串处理程序的设计和调试技术。
信息论实验

设计并完成以下三个实验,要求有实验目的、原理、步骤、结果、程序和分析讨论(30分,每个实验10分) 实验①信道容量的计算实验②Huffman 编码或者算术编码实验 实验③信道编码方案设计实验一 信道容量的计算一、 实验目的1、 熟悉Matlab 工作环境以及工具箱;2、 掌握一般信道容量迭代算法原理。
3、 学习如何将复杂的公式转化为程序实现。
二、 实验要求1、 已知信源符号个数,信宿符号个数,信道转移概率矩阵P 。
2、 输入任意的一个信道转移概率矩阵,信源符号个数,信宿符号个数和每个具体转移概率,得出结果。
三、 实验原理定理:设信道的前向转移概率矩阵J K k j a b q Q ⨯=))((,0P 是任给的输入字母的一个初始概率分布,其所有分量)(0k a P 均不为零。
按照下式不断对概率分布进行迭代、更新:∑=+=Ki ri i r rk k rk r P a p P a p a p11)()()()()(ββ其中[]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧===∑∑===J j Ki i j i rk j k j pp k rk a b q a p a b q a b q Y a x I P r11)()()(log)(exp );(exp )(β则由此所得的),(Q p I r 序列收敛于信道容量C 。
在上述定理中,输入字母概率分布的更新方法具有很明显的意义,即不断将具有较大互信息);(Y a x I k =的输入字母的概率加以提高,将具有较小互信息);(Y a x I k =的输入字母的概率加以降低。
四、实验程序及结果。
进行Matlab仿真,仿真程序如下:contmax.m文件function [P_X,C,N]=contmax(P_YX,E)%计算任意信道的信道容量C及最佳输入分布P_X%P_X为输入概率分布%C为信道容量%N为迭代次数%P_YX为DMC信道的转移矩阵%E为预设精度if length(find(P_YX<0)~=0) %转移矩阵中各元素必须大于等于0 error('Not a probable vector, Negative component');endB=abs(sum(P_YX')-1);if max(B)>10e-10 %转移矩阵的行和必须等于1,否则重新输入error('Not a probable vector, Component do not add up to "1" ');end%变量初始化C1=1;C=0;N=0; r=size(P_YX);P_X=ones(1,r(1))/r(1);%调整P_YX的零元素值Pyx=(P_YX==0).*eps;P_YX=P_YX+Pyx;%迭代求解while (abs(C1-C))>EP_Y=P_X*P_YX;I1=sum((P_YX.*log2(P_YX))');I2=log2(P_Y)*(P_YX'); BETA=exp(I1-I2);B=P_X*(BETA');C1=log(B);C=log(max(BETA));P_X=P_X.*BETA/B;N=N+1; %迭代次数end保存为contmax.m文件执行程序为:p=0.4;P_YX=[1,0,0;0,1-p,p;0,p,1-p]; %信道的转移矩阵[P_X,C,n]=contmax(P_YX,0.001) %预设迭代精度e=0.001C0=log2(1+2*(p^p)*((1-p)^(1-p))) %通过算式直接求得信道容量执行结果:P_X =0.4887 0.2557 0.2557C =1.0340n =9C0 =1.0333五、分析讨论迭代精度对计算结果的影响。
信息论与编码实验报告

信息论与编码实验报告一、实验目的本实验主要目的是通过实验验证信息论与编码理论的基本原理,了解信息的产生、传输和编码的基本过程,深入理解信源、信道和编码的关系,以及各种编码技术的应用。
二、实验设备及原理实验设备:计算机、编码器、解码器、信道模拟器、信噪比计算器等。
实验原理:信息论是由香农提出的一种研究信息传输与数据压缩问题的数学理论。
信源产生的消息通常是具有统计规律的,信道是传送消息的媒体,编码是将消息转换成信号的过程。
根据信息论的基本原理,信息的度量单位是比特(bit),一个比特可以表示两个平等可能的事件。
信源的熵(Entropy)是用来衡量信源产生的信息量大小的物理量,熵越大,信息量就越多。
信道容量是用来衡量信道传输信息的极限容量,即信道的最高传输速率,单位是比特/秒。
编码是为了提高信道的利用率,减少传输时间,提高传输质量等目的而进行的一种信号转换过程。
常见的编码技术有霍夫曼编码、香农-费诺编码、区块编码等。
三、实验步骤1.运行编码器和解码器软件,设置信源信息,编码器将信源信息进行编码,生成信道输入信号。
2.设置信道模拟器的信道参数,模拟信道传输过程。
3.将信道输出信号输入到解码器,解码器将信道输出信号进行解码,恢复信源信息。
4.计算信道容量和实际传输速率,比较两者的差异。
5.改变信道参数和编码方式,观察对实际传输速率的影响。
四、实验结果与分析通过实验,我们可以得到不同信道及编码方式下的信息传输速率,根据信道参数和编码方式的不同,传输速率有时会接近信道容量,有时会低于信道容量。
这是因为在真实的传输过程中,存在信噪比、传输距离等因素导致的误码率,从而降低了实际传输速率。
在实验中,我们还可以观察到不同编码方式对传输速率的影响。
例如,霍夫曼编码适用于信源概率分布不均匀的情况,可以实现数据压缩,提高传输效率。
而区块编码适用于数据容量较大的情况,可以分块传输,降低传输错误率。
此外,通过实验我们还可以了解到信息论中的一些重要概念,如信源熵、信道容量等。
信息论上机实验报告

信息论与编码实验报告实验一:计算离散信源的熵一、实验设备: 1、计算机2、软件:Matlab 二、实验目的:1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程; 三、习题:1. 甲地天气预报构成的信源空间为:1111(),,,8482X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦ 小雨云 大雨晴 乙地信源空间为:17(),88Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦小雨晴 求此两个信源的熵。
求各种天气的自信息量。
代码:x=[1/2,1/4,1/8,1/8]; y=[7/8,1/8];HX=sum(-x.*log2(x)) HY=sum(-y.*log2(y)) IX=-log2(x) IY=-log2(y) 答案:() 1.75;()0.5436H X H Y ==2、 某信息源的符号集由A 、B 、C 、D 、E 组成,设每一符号独立出现,其出现的概率分别为,1/4,1/8,1/8,3/16,5/16,试求该信源符号的平均信息量。
代码:x=[1/4,1/8,1/8,3/16,5/16]; HX=sum(-x.*log2(x))答案:H(X) = 2.2272bit/符号3、设有四个消息分别以概率1/4,1/8,1/8,1/2传送,每一消息的出现是相互独立的。
试计算其平均信息量。
代码:x=[1/4,1/8,1/8,1/2]; HX=sum(-x.*log2(x)) 答案:H(X) =1.75bit/符号4. 设一个二元信源(只有0和1两种符号)其概率空间为:(),1X p x p p ⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦0 1编程画出H 与p 的关系,并说明当P 呈什么分布时,平均信息量达到最大值。
(说明:H=-p.*log2(p)-(1-p).log2(1-p);) 代码:p= 1/1000000:1/1000:1;H=-p.*log2(p)-(1-p).*log2(1-p); plot(p,H) grid on xlabel('p'); ylabel('HP'); 图:实验二:验证熵的可加性与强可加性1. 【例2.6】有一离散无记忆信源123111(),,244a a a X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦验证二次扩展信源2X 的熵等于离散信源X 的熵的2倍,即2()2()H X H X =代码:x=[1/2,1/4,1/4];hx=sum(x.*log2(1./x))x2=[1/4,1/16,1/16,1/8,1/8,1/8,1/16,1/8,1/16] hx2=sum(x2.*log2(1./x2)) 答案:2() 1.5;() 3.0H X H X ==2. 验证两个统计独立的信源,X Y ,验证:()()()H XY H X H Y =+其中:123111(),,244a a a X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦123111(),,333b b b Y p y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦代码:x=[1/2,1/4,1/4]; y=[1/3,1/3,1/3];xy=[1/6,1/6,1/6,1/12,1/12,1/12,1/12,1/12,1/12] hx=sum(x.*log2(1./x)) hy=sum(y.*log2(1./y)) Hxy=sum(xy.*log2(1./xy)) 答案:() 1.5,() 1.585() 3.085H X H Y H XY ===3、条件熵的计算与熵的强可加性 验证离散二维平稳信源,满足:12121()()(|)H X X H X H X X =+某一离散二维平稳信源0121141(),,3694X p x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦12X X 其联合概率分布12()p X X 为:编程计算:1) 联合熵12()H X X 2) 条件熵21(|)H X X3) 验证:12121()()(|)H X X H X H X X =+代码:x1=[11/36,4/9,1/4]; x2=[11/36,4/9,1/4];b=[1/4,1/18,0;1/18,1/3,1/18;0,1/18,7/36]; HXY=0;for i=1:size(b,1) for j=1:size(b,2) if b(i,j)>0HXY=HXY-b(i,j).*log2(b(i,j)); end end end HXYHx1=sum(x1.*log2(1./x1)) Hx2=sum(x2.*log2(1./x2))b0=b(1,:); b1=b(2,:); b2=b(3,:);x1x2=[b0./x2;b1./x2;b2./x2]; Hx1x2=0;for i=1:size(x1x2,1) for j=1:size(x1x2,2) if x1x2(i,j)>0Hx1x2=Hx1x2-b(i,j).*log2(x1x2(i,j)); end end end Hx1x2 答案:12112121() 1.5426;(|)0.8717() 2.4144()(|) 2.4144H X H X X H X X H X H X X ===+=实验三:离散信道的平均互信息的计算1. 【习题3.1】 设信源12()0.6,0.4X x x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦通过一干扰信道,接收到符号为12[,]Y y y =,其信道矩阵为:516631,44P ⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦1) 求信源X 中事件1x 和2x 分别含有的自信息;2) 收到消息(1,2)j y j =后,获得的关于(1,2)i x i =的信息量;3) 求信源X 和输出变量Y 的信息熵; 4) 信道疑义度(|)H X Y 和噪声熵(|)H Y X ; 5) 接收到消息Y 后获得的平均互信息;代码:x=[0.6,0.4];p=[5/6,1/6;3/4,1/4]; Ix1=log2(1./(x(1,1))) Ix2=log2(1./(x(1,2)))pxy=[x(1,1)*p(1,:);x(1,2)*p(2,:)]; py=[x*p(:,1),x*p(:,2)];px_y=[pxy(:,1)/py(1,1),pxy(:,2)/py(1,2)]; I=log2(p./[py;py]) Hx=sum(x.*log2(1./x)) Hy=sum(py.*log2(1./py))Hx_y=sum(sum(pxy.*log2(1./px_y))) Hy_x=sum(sum(pxy.*log2(1./p)))Ixy=sum(sum(pxy.*log2(p./[py;py])))答案:12111221221.()0.737() 1.32192.(;)0.0589,(;)0.263,(;)0.0931,(;)0.32193.()0.971,()0.72194.(|)0.9635(|)0.71455.(;)0.0074I x I x I x y I x y I x y I x y H X H Y H X Y H Y X I X Y ====-=-======2. 二元信道的互信息与信源分布的关系 有二元信源:01()1X p x ωω⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦有二元信道,其传递矩阵为:11p p P p p -⎡⎤=⎢⎥-⎣⎦, 其中0.2p =,即传递矩阵0.80.20.20.8P ⎡⎤=⎢⎥⎣⎦编程实现下面题目:1) 画出平均互信息(;)I X Y 随信源分布ω的关系曲线,并求出最大平均互信息。
信息论基础-实验报告参考模板

信息论基础实验报告课程名称:信息论基础姓名:学院:计算机学院专业:计算机系统结构学号:2015 年7 月18 日信源熵值的计算一、实验目的1 进一步熟悉信源熵值的计算2 熟悉vs2010 使用二、实验原理信息论中,熵:随机变量不确定性的度量。
设X为一离散型随机变量,其取之空间为X,概率密度函数为p(x) = Pr(X = x), x∈X则离散型随机变量X的熵H(X)定义为H(X) = -∑p(x)log p(x)x∈X其中log的底为2,此时熵的单位为比特。
流程:第一步:打开一个名为“zhangdongdong”的TXT文档,读入一篇英文歌词see you again存入一个数组temp,为了程序准确性将所读内容转存到另一个数组S,计算该数组中每个字母与空格的出现次数(遇到小写字母都将其转化为大写字母进行计数),每出现一次该字符的计数器+1。
第二步:计算信源总大小计算出每个字母和空格出现的概率;最后,通过统计数据和信息熵公式计算出所求信源熵值程序流程图:开始---->打开文档将英文字母读入数组----->计算每个字母及空格出现次数,算出频率---> 求出信息熵------>输入结果三、实验内容1、写出计算自信息量的C 程序2、已知:信源符号为英文字母(不区分大小写)和空格。
输入:一篇英文的信源文档。
输出:给出该信源文档的中各个字母与空格的概率分布,以及该信源的熵。
四、实验环境Microsoft Windows 7VS2010五、编码程序六、运行结果其中文档内容如下:七、实验总结在实验中,我进一步了解到信源熵的计算,理论和实践的结合让我对这个知识点了解的更加深刻了。
友情提示:范文可能无法思考和涵盖全面,供参考!最好找专业人士起草或审核后使用,感谢您的下载!。
信息论实验报告-

信息论实验报告学生:班级:学号:实验一香农编码一、程序设计的流程图二、程序清单#include <iostream>#include<math.h>#include<string>using namespace std;void swap(double *x,double *y);int main(){int N;cout<<"输入信源个数"<<endl;cin>>N;double S[N]; //注意变量在数组中的影响cout<<"输入信源概率"<<endl;for(int i=0;i<N;i++)cin>>S[i];for(int i=0;i<N;i++){for(int j=i;j<N;j++)if(S[i]<S[j])swap(S[i],S[j]);}int nm[N];for(int i=0;i<N;i++){nm[i]=int(-(log(S[i])/log(2)))+1;if(nm[i]==(-(log(S[i])/log(2)))+1)nm[i]--;}double AA[N];AA[0]=S[0];for(int i=1;i<N;i++ )AA[i]=AA[i-1]+S[i];string MM[N];for(int i=0;i<N;i++){double tem=0;double aa=AA[i];for(int j=0;j<N;j++){tem=aa*2;if(tem>1){MM[i]+='1';aa=tem-1;}else{MM[i]+='0';aa=tem;}}}string BB[N];for(int i=0;i<N;i++){for(int j=0;j<nm[i];j++)BB[i]+=MM[i][j];}cout<<"输出编码"<<endl;for(int i=0;i<N;i++)cout<<BB[i]<<endl;}void swap(double &x,double &y){double a;a=x;x=y;y=a;}实验二.费洛编码.一、 流程图二、程序清单#include <iostream>#include<string>#include<math.h>using namespace std;void dw(int n,int H,int W,double *si,string *m); int main(){int N;cout<<"输入信源个数"<<endl;cin>>N;double S[N];cout<<"输入信源概率"<<endl;for(int i=0;i<N;i++)cin>>S[i];for(int i=0;i<N;i++){for(int j=i;j<N;j++){if(S[i]<S[j]){double a;a=S[i];S[i]=S[j];S[j]=a;}}}string MM[N];dw(N,0,N-1,S,MM);cout<<"输出编码"<<endl;for(int i=0;i<N;i++)cout<<MM[i]<<endl;}void dw(int n,int H,int W,double *si,string *m ) {double sum=0,sm=0;int a1=W-H;if(a1>=1){for(int j=H;j<=W;j++)sum+=*(si+j);double b[n];for(int i=H;i<=W;i++){sm+=*(si+i);b[i]=fabs(2*sm-sum)/sum;}int ZH;double a=b[H];for(int i=H;i<=W;i++)if(b[i]<=a){a=b[i];ZH=i;}for(int i=H;i<=W;i++){if(i<=ZH) m[i]+='0';else m[i]+='1';}int nn=n;double *ss;ss=si;string *mm;mm=m;if(ZH==H)dw(nn,ZH+1,W,ss,mm);else if(ZH==W-1)dw(nn,H,ZH,ss,mm);else{dw(nn,H,ZH,ss,mm);dw(nn,ZH+1,W,ss,mm);}}}实验三.霍夫曼一、程序流程图二、 程序清单#include<iostream>#include<string>using namespace std;struct HNode{double weight;int parent;int lchild;int rchild;};void HuffmanTree(HNode *HuffNode,int n,double *si,string *m); int hc(string m);void nv(string *m,int n);int main(){int N;cout<<"输入信源个数"<<endl;cin>>N;double *S=new double[N];cout<<"输入信源概率"<<endl;for(int i=0;i<N;i++)cin>>S[i];string *MM=new string[N];for(int i=0;i<N;i++){for(int j=i;j<N;j++){if(S[i]<S[j]){double a;a=S[i];S[i]=S[j];S[j]=a;}}}HNode *node=new HNode[2*N-1];HuffmanTree(node,N,S,MM);nv(MM,N);cout<<"输出编码"<<endl;for(int i=0;i<N;i++)cout<<MM[i]<<endl;}void HuffmanTree(HNode *HuffNode,int n,double *si,string *m) {int i,j,x1,x2,c,p;float m1,m2;for (i=0;i<2*n-1;i++){HuffNode[i].weight=0;HuffNode[i].parent=-1;HuffNode[i].lchild=-1;HuffNode[i].rchild=-1;}for (i=0;i<n;i++){HuffNode[i].weight=si[i];}for (i=0;i<n-1;i++){m1=m2=1;x1=x2=0;for (j=0;j<n+i;j++){if (HuffNode[j].parent==-1&&HuffNode[j].weight<m1){m2=m1;x2=x1;m1=HuffNode[j].weight;x1=j;}else if (HuffNode[j].parent==-1&&HuffNode[j].weight<m2){m2=HuffNode[j].weight;x2=j;}}HuffNode[x1].parent=n+i;HuffNode[x2].parent=n+i;HuffNode[n+i].weight=HuffNode[x1].weight+HuffNode[x2].weight;HuffNode[n+i].lchild=x1;HuffNode[n+i].rchild=x2;}for(i=0;i<n;i++){c=i;p= HuffNode[c].parent;while(p!=-1){if(HuffNode[p].lchild ==c)m[i]+='0';elsem[i]+='1';c=p;p=HuffNode[c].parent;}}}int hc(string m){int a=0;for(int i=0;m[i]!='\0';i++)a++;return a;}void nv(string *m,int n){char mn[n];int b;for(int i=0;i<n;i++){b=hc(m[i]);for(int j=0;j<b;j++){mn[j]=m[i][b-j-1];}m[i]=mn;}}实验四.信道一、程序流程图三、程序清单#include <stdlib.h>#include <iostream>#include <math.h>using namespace std;int main(){int ni,no;int i,j;cout<<"输入信源个数"<<endl;cin>>ni;cout<<"输出信源个数"<<endl;cin>>no;double *Si=new double[ni];double *So=new double[no];cout<<"输入信源概率"<<endl;for (i=0;i<ni;i++){cin>>Si[i];}cout<<endl;//再输入信道转移概率矩阵//注意进行判断,某行如果总概率大于1,则出现错误应从新输入cout<<"输入转移概率:"<<endl;float **p; //转移条件概率p=new float *[ni];for (i=0;i<ni;i++){p[i]=new float[no];}for (i=0;i<ni;i++){for (j=0;j<no;j++){cin>>p[i][j];}}for (i=0;i<ni;i++){float a=0;for (j=0;j<no;j++){a+=p[i][j];}if (a!=1.0){cout<<"输入数据有误,请检查后再次输入。
信息论课程实验报告

中国地质大学(武汉)CHINA UNIV ERSIT Y OF GEOSCIENCES信息论课程实验报告指导老师:严军姓名:刘一龙班级:71082-14学号:20081002007中国地质大学(武汉)2011年6月实验一构造(7,4)系统码一、实验题目Construct a systematic (7,4) linear block code. Y ou can use c / MA TLAB / HDL (VHDL or Verilog-HDL) to describe it. Please write the detail of how to realize it in computer language. And list the program lines.二、实验程序算法设计:利用H的线性独立,通过n的二进制形式构造出H,然后利用H构造出G。
本算法具有通用性,不仅可以计算出(7,4)的生成矩阵,还可以构造出(15,11),(31,26)的生成矩阵。
Matlab程序:clc;disp('请输入系统码n的值');n = input('n=');disp('请输入系统码k的值');k = input('k=');r = n-k;temp=[];for i=1:ny=dec2bin(i,r);for j=1:rtemp(i,j)=mod(y(j),2);endendfor i=1:rt = temp(i,:);temp(i,:)=temp(2^(i-1),:);temp(2^(i-1),:)=t;endfor i=1:(fix(r/2))t = temp(:,i);temp(:,i)=temp(:,r-i+1);temp(:,r-i+1)=t;endH = temp';%-----构造矩阵G--------%P=H(:,r+1:n);G=[P',eye(k)];disp('生成矩阵');Gdisp('校验矩阵');H三、实验结果请输入系统码n的值n=7请输入系统码k的值k=4生成矩阵G =1 1 0 1 0 0 01 0 1 0 1 0 00 1 1 0 0 1 01 1 1 0 0 0 1校验矩阵H =1 0 0 1 1 0 10 1 0 1 0 1 10 0 1 0 1 1 1请输入系统码n的值n=15请输入系统码k的值k=11生成矩阵G =Columns 1 through 81 0 1 0 1 0 0 00 1 1 0 0 1 0 01 1 1 0 0 0 1 01 1 0 0 0 0 0 11 0 0 1 0 0 0 00 1 0 1 0 0 0 01 1 0 1 0 0 0 00 0 1 1 0 0 0 01 0 1 1 0 0 0 00 1 1 1 0 0 0 01 1 1 1 0 0 0 0 Columns 9 through 150 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 01 0 0 0 0 0 00 1 0 0 0 0 00 0 1 0 0 0 00 0 0 1 0 0 00 0 0 0 1 0 00 0 0 0 0 1 00 0 0 0 0 0 1校验矩阵H =Columns 1 through 81 0 0 0 1 0 1 10 1 0 0 0 1 1 10 0 1 0 1 1 1 00 0 0 1 0 0 0 0Columns 9 through 151 0 1 0 1 0 10 1 1 0 0 1 10 0 0 1 1 1 11 1 1 1 1 1 1实验二循环码一、实验题目We have already learned how to encode and decode cyclic codes. Please use the generator polynomial g(x)=1+x+x2+x4to construct a (7,3) code. And if the received code vector is [1 1 0 0 1 1 1], how to decode it? Use c / MATLAB / HDL language to realize the encoding and decoding system.二、实验程序算法设计:通过计算自己将生成矩阵G输入到计算机,然后输入要传输的信息m,利用c=mG 自动生成码字c。
信息论实验报告1--信息熵的计算
~
fori=1:5
forj=1:4
sum=sum+A(i,j);
end
A(i,:)=A(i,:)/sum;
,
sum=0;
end
y=A;
求H(x|y):
functiony=H_x_y(A)
"
sum=0;
fori=1:4
forj=1:5
sum=sum+A(j,i);
end
\
A(:,i)=A(:,i)/sum;
实验
总结
日
本次实验的收获、体会、经验、问题和教训:
\
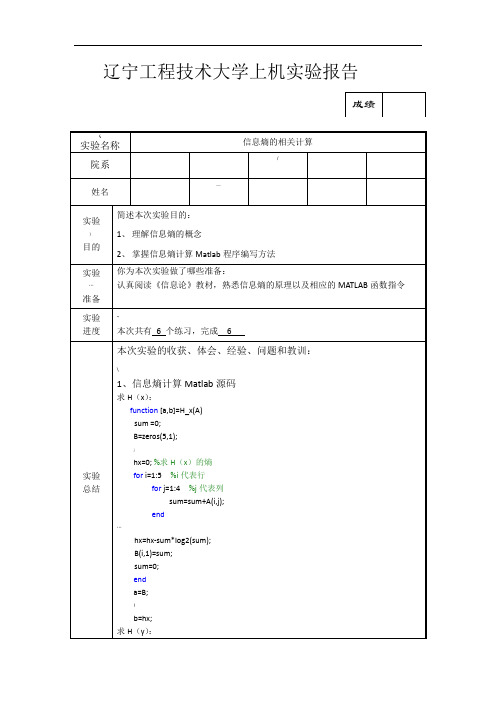
1、信息熵计算Matlab源码
求H(x):
function[a,b]=H_x(A)
sum =0;
B=zeros(5,1);
;
hx=0;%求H(x)的熵
fori=1:5%i代表行
forj=1:4%j代表列
sum=sum+A(i,j);
end
…
hx=hx-sum*log2(sum);
求H(x|y),H(y|x)
A=[ 0 0 0; 0 0;0 0;0 0 ;0 0 0];
H_x_y(A)
ans =
0 0 0
0 0
0 0
0 0
0 0 0
H_y_x(A)
ans =
0 0 0
0 0
0 0
0 0
0 0 0
教师
评语
成绩
辽宁工程技术大学上机实验报告
(
实验名称
信息熵的相关计算
院系
/
姓名
—
实验
)
目的
简述本次实验目的:
1、理解信息熵的概念
信息论实验报告

前言信息论是现代通信与信息工程的理论基础。
作为电子信息科学与技术专业本科生的学科基础课,本课程主要讲授:信息的定义和测度、信源和信息熵、连续熵和信息变差、信道和互信息、平均互信息和信道容量、数据处理和信息测量理论、无失真信源编码理论和编码方法等内容。
本课程按“单符号离散信息系统”、“多符号离散信息系统”、“连续信息系统”三个“系统”层面,逐步深入展开,以严密的数学分析贯串始终。
通过教学,使学生掌握信息理论的基本概念和信息分析方法,为今后进一步研究信息科学和信息技术打下坚实的理论基础。
实验一:唯一可译码判断实验学时:3实验类型:(演示、验证、综合、√设计、研究)实验要求:(√必修、选修)一、实验目的通过本次试验了解唯一可译码地判断原理;实现用C语言编写判断唯一可译码地程序二、实验内容编程实现唯一可译码的判决准则―――Sardinas-Patterson算法三、实验原理、方法和手段Sardinas-Patterson算法描述:设C为码字集合,按以下步骤构造此码的尾随后缀集合F:(1) 考查C中所有的码字,若Wi是Wj的前缀,则将相应的后缀作为一个尾随后缀放入集合F0中;(2) 考查C和Fi两个集合,若Wj∈C是Wi∈Fi的前缀或Wi∈Fi是Wj∈C的前缀,则将相应的后缀作为尾随后缀码放入集合Fi+1中;(3)F=∪Fi即为码C的尾随后缀集合;(4) 若F中出现了C中的元素,则算法终止,返回假(C不是唯一可译码);否则若F中没有出现新的元素,则返回真。
在我们设计的算法中,需要注意的是我们需要的是先输出所有尾随后缀的集合,然后再判断该码是否是唯一可译码,即如F中出现了C中的元素,则C不是唯一可译码,否则若F中没有出现新的元素,则C为唯一可译码。
而不是F中出现C中的元素就终止,这也是在本题的要求中需要注意的问题。
1、概要设计:由于需要判断尾随后缀,所以我们需要反复的比较C和F中的码字。
1)首先我们用一个b[30][30]的数组来存放所有的尾随后缀的集合;用Q记录所有尾随后缀的个数;2)用数组a[30][30]来存放输入的码字,L[30]来存放码字的长度;通过一个双重循环并调用houzhui(a[i],a[j],L[i],L[j])函数来找到a[30][30]中的为随后缀,即:for(i=0;i<n-1;i++){for(j=0;j<n;j++){if(i!=j&&L[i]<L[j])HuoZhui(a[i],a[j],L[i],L[j]);}}3)通过判断Q是否大于0,如果不大于0,即b[30][30]中没有码字,也就是不存在尾随后缀,那么可判断a[30][30]是唯一可译码,否则进行如下操作;4)计算b[30][30]中尾随后缀的长度,用k1表示;并调用HuoZhui(b[i],a[j],k1,L[j])其中k1<L[j]来a[30][30]中所存在的后缀,并加入到b[30][30]中,通过一个循环,找到a[30][30]中所有尾随后缀;即for(i=0;i<Q;i++){k1=strlen(b[i]);for(j=0;j<n;j++){if(k1<L[j])HuoZhui(b[i],a[j],k1,L[j]);}}5)寻找b[30][30]中的尾随后缀;用k2表示b[30][30]中码字的长度,并调用HuoZhui(a[i],b[j],L[i],k2)来实现,其中k2>L[j];通过循环调用即可找到b[30][30]中的所有尾随后缀,最后再将他们分别存放在b[30][30]中;即通过for(i=0;i<n;i++){for(j=0;j<Q;j++){k2=strlen(b[j]);if(k2>L[i]){HuoZhui(a[i],b[j],L[i],k2);}}}6)在反复调用HuoZhui(a[i],a[j],L[i],L[j])函数中如果b[30][30]中有重复出现的,即尾随后缀相同的不用再次放入b[30][30]中。
信息论与编码实验报告

信息论与编码实验报告一、实验目的1.了解信息论与编码的基本概念和原理。
2.学习如何通过信息论与编码方法实现对数据的压缩和传输。
3.掌握信息论与编码实验的实验方法和实验技能。
4.提高实验设计、数据分析和报告撰写的能力。
二、实验内容1.通过对输入信源进行编码,实现对数据的压缩。
2. 比较不同编码方法的压缩效果,包括Shannon-Fano编码和霍夫曼编码。
3.通过传输信道对编码后的数据进行解码,还原原始信源。
4.分析并比较不同编码方法的传输效果,包括码率和传输质量。
三、实验原理1.信息论:熵是信息论中衡量信源不确定性的指标,熵越小表示信源的可预测性越高,在编码过程中可以压缩数据。
2. 编码方法:Shannon-Fano编码通过分治的方法将输入信源划分为不同的子集,分别进行编码;霍夫曼编码则通过构建最佳二叉树的方式,将较常出现的信源符号编码为较短的二进制码,较少出现的信源符号编码为较长的二进制码。
3.传输信道:信道可能存在误码和噪声,通过差错控制编码可以在一定程度上保障传输数据的正确性和完整性。
四、实验步骤1. 对给定的输入信源进行Shannon-Fano编码和霍夫曼编码。
2.计算编码后的码率,分析不同编码方法的压缩效果。
3.将编码后的数据传输到信道,模拟信道中的误码和噪声。
4.对传输后的数据进行解码,还原原始信源。
5.比较不同编码方法的传输质量,计算误码率和信噪比。
五、实验结果与分析1. 编码结果:通过对输入信源进行编码,得到了Shannon-Fano编码和霍夫曼编码的码表。
2.压缩效果:计算了不同编码方法的码率,比较了压缩效果。
3.传输结果:模拟信道传输后的数据,对数据进行解码,还原原始信源。
4.传输质量:计算了误码率和信噪比,分析了不同编码方法的传输质量。
六、实验总结通过本次实验,我深刻理解了信息论与编码的基本概念和原理,并掌握了信息论与编码实验的实验方法和实验技能。
在实验过程中,我遇到了一些困难,比如对编码方法的理解和实验数据的处理。
信息论实验报告(实验一、信源与信息熵的计算)

学生实验报告
院别电子信息学院课程名称信息论语编码实验
班级实验名称实验一、信源与信息熵的计算姓名实验时间
学号指导教师
成绩
报告内容
一、实验目的和任务
1、理解自信息、互信息、熵等概念;
2、熟悉 MATLAB程序设计;
3、掌握通过计算机实验计算离散信源的信息量及熵的计算方法;
4、对给定信源分别计算出信源熵、条件熵、联合熵、交互熵;
二、实验原理介绍
三、实验设备介绍
1、计算机
2、编程软件MATLAB6.5以上
四、实验内容和步骤
H X H Y H X Y H Y X H XY I X Y 分别求出如下图所示离散信道的(),(),(|),(|),(),(;)
1、面出程序设计的流程图。
2、写出在调试过程中出现的问题。
3、对实验的结果进行分析。
五、实验数据记录
六、实验结论与心得
通过本次实验,加强了对matlab程序的学习,进一步提高了我的编程能力。
实验1

《信息论与编码》实验1 离散信源熵实验一、实验目的熟悉工作环境及Matlab 软件 掌握绘图函数的运用 理解熵函数表达式及其性质 二、实验原理信息熵自信息量是针对信源的单个符号而言的,而符号是随机发生的,因此单个符号的不确定性不足于代表信源的不确定性性质,为此,可对所有符号的自信息量进行统计平均,从而得到平均不确定性。
熵的表示[]()()()()()log ()i i i i iiH X E I X p x I x p x p x ===-∑∑注意的问题熵是自信息量的统计平均,因此单位与自信息量的单位相同,与熵公式中所用对数的底有关:bit/符号、nat/符号、dit/符号、r 进制单位/符号。
特殊公式:某个pk=0时,0log0=0 (0lim log 0→=x x x )在熵的定义中忽略零概率事件。
平均互信息平均互信息量(I(X;Y))是统计平均意义下的先验不确定性与后验不确定性之 差,是互信息量的统计平均:()()()()()();/;/=-=-I X Y H X H X Y I Y X H Y H Y X三、实验内容1.用 Matlab 软件绘制二进熵函数曲线。
二元信源1011⎛⎫⎛⎫=≤≤ ⎪ ⎪-⎝⎭⎝⎭X p P p p二元信源的熵为(,1)log (1)log(1)-=----H p p p p p p绘制当p 从0到1之间变化时的二元信源的信息熵曲线.Matlab 程序: p=0.00001:0.001:1;h=-p.*log2(p)-(1-p).*log2(1-p); plot(p,h);title('二进熵函数曲线'); ylabel('H(p,1-p)') 2.绘制三元信源的熵三元信源1231212120,11()⎛⎫⎛⎫=≤≤ ⎪⎪--⎝⎭⎝⎭x x x X p p p p p p P x三元信源的熵为111111221212(,,1)log log (1)log(1)--=-------H p p p p p p p p p p p p 绘制当12,p p 从0到1之间变化时的三元信源的信息熵曲线.3.绘制平均互信息量图形对于二元对称信道的输入概率空间为0,1(),1ωωω⎡⎤⎡⎤=⎢⎥⎢⎥=-⎣⎦⎣⎦X P x平均互信息:根据:1()()(|)1===∑rj i j i i P b P a P b a所以:21(0)()(0|)(0)(0|0)(1)(0|1)ωω====+=+∑i i i P y P a P a P P P P p p21(1)()(0|)(0)(1|0)(1)(1|1)ωω====+=+∑i i i P y P a P a P P P P p p1111(;)()()()log ()log [log log ]()()()ωωωωωωωωωω=-=+++-+++=+-I X Y H Y H p p p p p p p p p p p p pH p p H p 绘制当,ωp 从0到1之间变化时的平均互信息熵曲线.(;)()(/)=-I X Y H Y H Y X 1()()(/)log(/)=-∑∑XYH Y P x P y x P y x 11()()[loglog ]=-+∑XH Y P x p p p p11()[loglog ]()()=-+=-H Y p p H Y H p p p四、实验报告要求简述实验目的;简述实验原理;分别绘制二元信源和三元信源的熵及平均互信息量图形。
最新《信息论基础》实验报告-实验1

最新《信息论基础》实验报告-实验1实验目的:1. 理解信息论的基本概念,包括信息熵、互信息和编码理论。
2. 通过实验掌握香农信息熵的计算方法。
3. 学习并实践简单的数据压缩技术。
实验内容:1. 数据集准备:选择一段英文文本作为实验数据集,统计各字符出现频率。
2. 信息熵计算:根据字符频率计算整个数据集的香农信息熵。
3. 编码设计:设计一种基于频率的霍夫曼编码方案,为数据集中的每个字符分配一个唯一的二进制编码。
4. 压缩与解压缩:使用设计的霍夫曼编码对原始文本进行压缩,并验证解压缩后能否恢复原始文本。
5. 性能评估:比较压缩前后的数据大小,计算压缩率,并分析压缩效果。
实验步骤:1. 从文本文件中读取数据,统计每个字符的出现次数。
2. 利用统计数据计算字符的相对频率,并转换为概率分布。
3. 应用香农公式计算整个数据集的熵值。
4. 根据字符频率构建霍夫曼树,并为每个字符生成编码。
5. 将原始文本转换为编码序列,并记录压缩后的数据大小。
6. 实现解压缩算法,将编码序列还原为原始文本。
7. 分析压缩前后的数据大小差异,并计算压缩率。
实验结果:1. 原始文本大小:[原始文本大小]2. 压缩后大小:[压缩后大小]3. 压缩率:[压缩率计算结果]4. 霍夫曼编码表:[字符与编码的对应表]实验讨论:- 分析影响压缩效果的因素,如字符集大小、字符频率分布等。
- 讨论在实际应用中,如何优化编码方案以提高压缩效率。
- 探讨信息论在数据压缩之外的其他应用领域。
实验结论:通过本次实验,我们成功地应用了信息论的基本原理,通过霍夫曼编码技术对文本数据进行了有效压缩。
实验结果表明,基于字符频率的霍夫曼编码能够显著减少数据的存储空间,验证了信息论在数据压缩领域的有效性和实用性。
信息论实验

北京科技大学UNIVERSITY OF SCIENCE AND TECHNOLOGY BEIJING 信息论实验报告学院:计算机与通信工程学院一1.实验目的(1)进一步熟悉唯一可译码判决准则(2)掌握C语言字符串处理程序的设计和调试技术2.实验要求(1)已知:信源符号个数q、码字集合C(2)输入:任意的一个码。
码字个数和每个具体的码字在运行时从键盘输入(3)输出:判决(是唯一可译码/不是唯一可译码)3.实验代码#include<stdio.h>#include<string.h>#define MAX 100char c[MAX][MAX];char f[MAX][MAX];int N,sum=0;int flag;void patterson(char c[],char d[]){int i,j,k;for(i=0;;i++){if(c[i]=='\0'&&d[i]=='\0') //2字符串一样,就跳出break;if(c[i]=='\0') //若d比c长,将d的尾随后缀放入f中{for(j=i;d[j]!='\0';j++) f[sum][j-i]=d[j];f[sum][j-i]='\0';for(k=0;k<sum;k++){if(strcmp(f[sum],f[k])==0) /*看当前生成的尾随后缀在f集合中是否存在*/ {sum--;break;}}sum++;break;}if(d[i]=='\0') //c比d长,将c的尾随后缀放入f中{for(j=i;c[j]!='\0';j++) f[sum][j-i]=c[j];f[sum][j-i]='\0';for(k=0;k<sum;k++){if(strcmp(f[sum],f[k])==0) /*查看当前生成的尾随后缀在f集合中是否存在*/{sum--;break;}}sum++;break;}if(c[i]!=d[i])//字符不一样了也退出break;}}/*主函数*/main(){int i,j;printf("输入码字的个数:");scanf("%d",&N);while(N>100){printf("输入码字个数过大,请输入小于100的数\n");printf("请输入码字的个数:");scanf("%d",&N);}flag=0;printf("请分别输入码字,长度<100个字符):\n");for(i=0;i<N;i++){scanf("%s",&c[i]);}for(i=0;i<N-1;i++)//判断如果码本身是否重复for(j=i+1;j<N;j++){if(strcmp(c[i],c[j])==0){flag=1;break;}}if(flag==1)//如果码本身有重复,就可以断定它不是唯一可译码{printf("这不是唯一可译码。
信息论实验报告实验1

信息论实验报告一实验一1、实验内容(1)英文信源由26个英文字母和1个空格组成,假定字符从中等概选取,那么一条100个字符的信息提供的信息量为多少?(2)若将27个字符分为三类,9个出现概率占2/7,13个出现概率占4/7,5个出现占1/7,而每类中符号出现等概,求该字符信源的信息熵。
2、设计思路及步骤I=log2P iH(X)=∑−P i log2Pii26个字母和一个空格,因等概选取可以先求得其中一个字符的信息量,通过扩展实现计算100个字符的信息量。
对于第二问,可以将字符分为三组,又因每组字符的概率相等,因此可以求出每组每一个字符的概率。
通过信息熵的定义可以求出结果。
3、程序代码及调试过程4、出现的问题及解决方法(1)没有看清题目要求,漏掉空格(2)是否可以将三组字符看作整体5、结果及说明通过实验结果可以看出100个字符的信息量,以及字符信源熵。
比较H2与H3可以看出,并不可以简单的将三组数据看作整体。
6、实验总结本实验通过计算多字符的信息量与分组信息熵,让我们加深了信息论中有关信息量与信息熵的概念与定义,同时也让我们熟悉了matlab的基本操作。
实验二1、实验内容绘制二进制信源熵函数曲线。
2、设计思路及步骤根据信源熵的定义以及公式计算出熵,通过matlab的矩阵运算计算出熵数组,然后通过plot函数画出图像。
3、程序代码及调试过程4、出现的问题及解决方法矩阵乘法出错,,需要使用matlab中的点乘5、结果及说明信源熵的图像为凸形曲线,熵在信源等概分布时取最大值,先增大再减小。
6、实验总结本实验通过对信源熵的作图让我们熟悉了matlab中图像生成函数,以及矩阵运算。
实验三,四1、实验内容求信源的熵和其二次、三次扩展信源的熵。
离散二维平稳信源的概率空间:求:(a)信源符号之间无依赖性时,信源X的信息熵H(X);(b)信源符号有依赖性时的条件熵H(X2|X1);(c)联合熵H(X1X2);(d)根据以上三者之间的关系,验证结果的正确性。
信息熵与图像熵的计算

实验一信息熵与图像熵计算一、实验目的1.复习MATL AB 的基本命令,熟悉MATL AB 下的基本函数。
2.复习信息熵基本定义, 能够自学图像熵定义和基本概念。
二、实验仪器、设备1.计算机-系统最低配置256M 内存、P4 CPU。
2.Matlab仿真软件- 7.0 / 7.1 / 2006a等版本Mat lab 软件。
三、实验内容与原理(1)内容:1.能够写出MATLAB源代码,求信源的信息熵。
2.根据图像熵基本知识,综合设计出M ATLAB程序,求出给定图像的图像熵。
(2)原理1. MATLAB中数据类型、矩阵运算、图像文件输入与输出知识复习。
2.利用信息论中信息熵概念,求出任意一个离散信源的熵(平均自信息量)。
自信息是一个随机变量,它是指某一信源发出某一消息所含有的信息量。
所发出的消息不同,它们所含有的信息量也就不同。
任何一个消息的自信息量都代表不了信源所包含的平均自信息量。
不能作为整个信源的信息测度,因此定义自信息量的数学期望为信源的平均自信息量:信息熵的意义:信源的信息熵H是从整个信源的统计特性来考虑的。
它是从平均意义上来表征信源的总体特性的。
对于某特定的信源,其信息熵只有一个。
不同的信源因统计特性不同,其熵也不同。
3.学习图像熵基本概念,能够求出图像一维熵和二维熵。
图像熵是一种特征的统计形式,它反映了图像中平均信息量的多少。
图像的一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi 表示图像中灰度值为i的像素所占的比例,则定义灰度图像的一元灰度熵为:255log i iip p ==∑H图像的一维熵可以表示图像灰度分布的聚集特征,却不能反映图像灰度分布的空间特征,为了表征这种空间特征,可以在一维熵的基础上引入能够反映灰度分布空间特征的特征量来组成图像的二维熵。
信息论实验一实验报告范文

信息论实验一实验报告范文一、简要总结信源的熵、信道容量的物理意义,概念:信源熵的物理意义:指信源中的各个符号的平均不确定性;熵是信源符号的平均信息量,是信源符号的平均不确定度。
信道容量概念:在信道可以传输的基本前提下,对信源的一切可能的概率分布而言,信道能够传输的最大(接收)熵速率称为信道容量。
意义:求出了某个信道的信道容量,也就找到了信源的最佳概率分布。
从而指导人们改造信源,使之最大可能地利用信道的传输能力。
二、写出离散信源熵、离散信道容量计算的基本步骤,画出实现离散信源熵、离散信道容量计算的程序流程图。
离散信源熵的计算步骤:q1Hr某Elogrpailograip(ai)i1信道容量的计算步骤:CI某;Ybit/符号ma某P某实现离散信源熵的计算流程图:输入P(ai)H(某)=0,i=1H(某)=H(某)+P(a1)logr(1/a1)i“”实现离散信道容量计算的程序流程图:输入p(某i)p(0)(某i)p(yj/某i)aie某pp(yj/某i)lnp(某i)p(yj/某i)jiC1n1,nlnp(某i)aiiC2n1,nlnma某aiiC1n1,nC2n1,n是CC1n1,n结束p(某i)p(某i)aip(某i)aii否三、实现离散信源熵、离散信道容量计算的matlab源程序:离散信源的熵(借助习题2.16)和离散信道容量(借助习题3.6)分析习题2.16的matlab程序:Clearall;%清除所有变量P某=[0.70.3];P=0;%输入信源概率,P某=p(某)H某=-P某某log2(P 某’)%计算信源的熵H(某)Py某=[0.90.2;0.10.8];p某=[0.70.3;0.70.3];%Py某为条件概率P某y=Py某.某p某;fori=1:2 h某某(i,1)=-P某y(I,:)某log2(P某y(i,:)’);P=P+h某某(i,1);%计算H(某^2)endh2某=P/2%计算H2(某)程序运行结果:H某=0.8813H2某=0.7131习题3.6的matlab程序:clearall;%清除所有变量a=0;p=[2/31/3;1/32/3];%信道矩阵Pfori=1:2,a=a+p(1,i)某log2(p(1,i));endC=log2(2)+a%计算对称离散信道的信道容量Cfori=1:2,p1(i)=1/2;endp1%最佳输入概率分布程序运行结果C=0.0817p1=0.50000.50004、讨论信源的熵的大小与前后符号之间相关性的关系,讨论信道容量与信源先验概率及信道转移概率的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息论与编码实验一实验报告
学生姓名周群创
指导教师张祖平
学号0909110814
专业班级电子信息1101
实验一关于信源熵的实验
一、实验目的
1. 掌握离散信源熵的原理和计算方法。
2. 熟悉matlab 软件的基本操作,练习使用matlab 求解信源的信息熵。
3. 自学图像熵的相关概念,并应用所学知识,使用matlab 或其他开发工具求解图像熵。
4. 掌握Excel 的绘图功能,使用Excel 绘制散点图、直方图。
二、实验原理
1. 离散信源相关的基本概念、原理和计算公式
产生离散信息的信源称为离散信源。
离散信源只能产生有限种符号。
随机事件的自信息量I(x i)为其对应的随机变量x i 出现概率对数的负值。
即:
I(x i)= -log2 p(x i)
随机事件X 的平均不确定度(信源熵)H(X)为离散随机变量x i 出现概
率的数学期望,即:
H(X )=-∑p(x )I (x ) =-∑p(x ) log p(x )
2. 二元信源的信息熵
设信源符号集X={0,1},每个符号发生的概率分别为p(0)=p,p(1)=q,
p+ q=1,即信源的概率空间为
则该二元信源的信源熵为:
H(X) = - p log p –q log q = - p log p – (1- p) log (1- p)
即:H (p) = - p log p – (1- p) log (1- p) 其中0 ≤p ≤1
3. MATLAB 二维绘图
用matlab 中的命令plot(x, y)就可以自动绘制出二维图来。
例1-2,在matlab 上绘制余弦曲线图,y = cos x,其中0 ≤x ≤2。
>>x=0:0.1:2*pi;%生成横坐标向量,使其为0,0.1,0.2,…,6.2
>>y=cos(x);%计算余弦向量
>>plot(x,y) %绘制图形
4. MATLAB 求解离散信源熵
求解信息熵过程:
1) 输入一个离散信源,并检查该信源是否是完备集。
2) 去除信源中符号分布概率为零的元素。
3) 根据平均信息量公式,求出离散信源的熵。
5. 图像熵的相关知识
图像熵是一种特征的统计形式,它反映了图像中平均信息量的多少。
图像的
一维熵表示图像中灰度分布的聚集特征所包含的信息量,令Pi 表示图像中灰度值为i 的像素所占的比例,则定义灰度图像的一元灰度熵为:
图像熵计算过程:
1) 输入一幅图像,并将其转换成灰度图像。
2) 统计出图像中每个灰度阶象素概率。
3) 计算出一幅图像的一维熵。
6. Excel 的绘图功能
比如:用Excel 或制作二元熵函数曲线。
具体步骤如下:
1)启动Excel 应用程序。
2)准备一组数据p。
在Excel 的一个工作表的A 列(或其它列)输入一组p,取步长为0.01,从0 至100 产生101 个p(利用Excel 填充功能)。
3)使用Excel 的计算功能,在B 列中用二元熵函数计算公式,求得A 列中
各数值对应的二元熵值。
比如:在单元格B2 中输入公式:
=-A2*LOG(A2,2)-(1-A2)*LOG(1-A2,2)。
4)使用Excel 的图表向导,图表类型选“XY 散点图”,子图表类型选“无
数据点平滑散点图”,绘制二元熵函数散点图。
三、实验内容
1、使用matlab 软件绘制二元信源熵函数曲线,并说明其物理意义。
其程序源代码为:
p=0:0.01:1;
H=-p.*log2(p)-(1-p).*log2(1-p);
plot(p,H);
结果为:
因为信源熵表征信源的平均不确定度,而由图表可以看出,当二元信源的符号的发生概率越高或越低时,信源的不确定性越低,反之,则不确定性越高。
2、使用matlab 软件求解离散单符号信源熵,请自己构造两个信源空间,根据求解结果说明其物理意义。
代码
p=[0.1 0.2 0.3 0.4];
h=-p.*log2(p);
H=sum(h);
p
H
结果
3、使用matlab 软件计算图像一维图像熵,请自己选择任意两幅图像,根据求解结果说明其物理意义。
其源代码程序为:
filename = 'e:\IMG_20131013_230501.jpg';
image1 = imread(filename);
subplot(2,1,1);
imshow(image1,[]);
subplot(2,1,2);
A = rgb2gray(image1);
imshow(A,[]);
[x,y]=size(A);
img_size=x*y;
H_img=0;
B=zeros(256,1);
for i=1:x
for j=1:y
img_level=A(i,j)+1;
B(img_level)=B(img_level)+1;
end
end
for k=1:256
p(k)=B(k)/img_size
if p(k)~=0;
H_img=-p(k).*log2(p(k))+H_img;
end
end
H_img
结果为:
统计结果为:p =
0 0.0000 0.0000 0.0000 0.0000 0.0000 0.0001 0.0001 0.0001 0.0001
0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0002 0.0002 0.0002 0.0002 0.0004 0.0008 0.0018 0.0023 0.0034 0.0017 0.0004 0.0003 0.0003 0.0003 0.0003 0.0003
0.0003 0.0003 0.0003 0.0002 0.0003 0.0003 0.0003 0.0002 0.0004 0.0003 0.0003 0.0003 0.0003 0.0004 0.0003 0.0004 0.0003 0.0003 0.0003 0.0003 0.0003
0.0004 0.0004 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0005 0.0004 0.0005 0.0005 0.0005 0.0006 0.0005 0.0005 0.0007 0.0006 0.0007 0.0008 0.0012
0.0028 0.0037 0.0034 0.0030 0.0033 0.0028 0.0026 0.0023 0.0022 0.0020 0.0021 0.0022 0.0020 0.0021 0.0020 0.0020 0.0022 0.0023 0.0022 0.0025 0.0026
0.0027 0.0028 0.0028 0.0030 0.0034 0.0031 0.0029 0.0030 0.0030 0.0032 0.0031 0.0034 0.0031 0.0031 0.0038 0.0040 0.0042 0.0042 0.0042 0.0046 0.0045
0.0054 0.0056 0.0066 0.0068 0.0070 0.0074 0.0097 0.0118 0.0183 0.0153 0.0111 0.0091 0.0068 0.0063 0.0054 0.0057 0.0060 0.0058 0.0061 0.0060 0.0061
0.0061 0.0066 0.0064 0.0062 0.0067 0.0069 0.0071 0.0069 0.0067 0.0065 0.0073 0.0073 0.0080 0.0079 0.0085 0.0087 0.0089 0.0084 0.0090 0.0075 0.0069
0.0067 0.0061 0.0059 0.0061 0.0059 0.0060 0.0058 0.0054 0.0058 0.0053 0.0054 0.0052 0.0058 0.0056 0.0060 0.0060 0.0061 0.0064 0.0067 0.0066 0.0067
0.0074 0.0073 0.0075 0.0074 0.0071 0.0073 0.0070 0.0069 0.0073 0.0070 0.0072 0.0074 0.0072 0.0069 0.0069 0.0076 0.0069 0.0074 0.0073 0.0073 0.0072
0.0077 0.0080 0.0086 0.0089 0.0094 0.0096 0.0095 0.0102 0.0102 0.0104 0.0116 0.0112 0.0091 0.0088 0.0090 0.0085 0.0081 0.0072 0.0059 0.0051 0.0045
0.0031
0.0026
0.0024
0.0022
0.0019
0.0017
0.0014
0.0012
0.0012
0.0010
0.0010
0.0007
result =
7.3654
4、使用Excel 软件,绘制二元信源熵函数曲线的散点图。
5、使用Excel 软件,绘制(3)中两幅图像的灰度直方图(0 到255 各灰度占图像像素的比例值,使用柱状图绘制其比列分布)。
.. .. .. ..。
