一次函数及特殊四边形的存在性问题[培优拓展]
一次函数之平行四边形存在性问题

一次函数与平行四边形1.线段中点公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点P 的坐标为 (2,22121y y x x ++) 例:如图,已知点A (-2,1),B (4,3),则线段AB 的中点P 的坐标是________.2.线段的平移平面内,线段AB 平移得到线段A'B' ,则①AB ∥A'B' ,AB =A'B' ;②AA'∥BB',AA'= BB'. 如图,线段AB 平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________.%例:如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)、D (x 4,y 4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标"例:如图,已知□ABCD 中A (-2,2),B (-3,-1), C (3,1),则点D 的坐标是________. 方法一:利用线段平移总结:x 1-x 2= x 4-x 3,y 1-y 2= y 4-y 3 或者 x 4-x 1= x 3-x 2,y 4-y 1= y 3-y 2 等方法二:利用中点公式总结:x 1+x 3= x 2+x 4,y 1+y 3= y 2+y 4类型一:三定一动例1 、如图,平面直角坐标中,已知中A(-1,0),B(1,-2),C (3,1),点D是平面内一动点,若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.*总结:三定一动问题,可以通过构造中点三角形得以解决.说明:若题中四边形ABCD是平行四边形,则点D的坐标只有一个结果________【例1】.一次函数y =x +3与y =﹣x +q 的图象都过点A (m ,0),且与y 轴分别交于点B 、C .(1)试求△ABC 的面积;(2)点D 是平面直角坐标系内的一点,且以点A 、C 、B 、D 为顶点的四边形是平行四边形,请直接写出点D 的坐标;(3)过△ABC 的顶点能否画一条直线,使它能平分△ABC 的面积若能,求出直线的函数关系式,若不能,说明理由.【解答】解:(1)将点A (m ,0)代入y =x +3中,得$m +3=0,解得m =﹣3,即点A (﹣3,0),将点A (﹣3,0)代入y =﹣x +q 中,得q =﹣3,∴点B (0,3)、C (0,﹣3),故S =12×BC ×AO =9;(2)满足条件的D 点坐标为D (﹣3,6)、D (﹣3,﹣6)、D (3,0);(3)若过点A ,则得直线l :y =0;若过点C ,则得直线l :y =﹣3x ﹣3;@若过点B ,则得直线l :y =3x +3.例2.如图,在平面直角坐标系xOy 中,已知直线PA 是一次函数y =x +m (m >0)的图象,直线PB 是一次函数y =﹣3x +n (n >m )的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点.(1)用m 、n 分别表示点A 、B 、P 的坐标及∠PAB 的度数;(2)若四边形PQOB 的面积是112,且CQ :AO =1:2,试求点P 的坐标,并求出直线PA 与PB的函数表达式;(3)在(2)的条件下,是否存在一点D ,使以A 、B 、P 、D 为顶点的四边形是平行四边形若存在,求出点D 的坐标;若不存在,请说明理由.【解答】解:(1)在直线y =x +m 中,令y =0,得x =﹣m .∴点A (﹣m ,0).…在直线y =﹣3x +n 中,令y =0,得x =x 3. ∴点B (x 3,0). 由{x =x +x x =−3x +x ,得{x =x −x 4x =x +3x 4,∴点P (x −x 4,x +3x 4). 在直线y =x +m 中,令x =0,得y =m ,∴|﹣m |=|m |,即有AO =QO .又∵∠AOQ =90°,∴△AOQ 是等腰直角三角形,∴∠PAB =45°.(2)∵CQ :AO =1:2,,∴(n ﹣m ):m =1:2,整理得3m =2n ,∴n =32m , ∴x +3x 4=32x +3x 4=98m , 而S 四边形PQOB =S △PAB ﹣S △AOQ =12(x 3+m )×(98m )−12×m ×m =1132m 2=112, 解得m =±4,∵m >0,∴m =4,∴n =32m =6,∴P (12,92). !∴PA 的函数表达式为y =x +4,PB 的函数表达式为y =﹣3x +6.(3)存在.过点P 作直线PM 平行于x 轴,过点B 作AP 的平行线交PM 于点D 1,过点A 作BP 的平行线交PM 于点D 2,过点A 、B 分别作BP 、AP 的平行线交于点D 3.①∵PD 1∥AB 且BD 1∥AP ,∴PABD 1是平行四边形.此时PD 1=AB ,易得x 1(132,92); ②∵PD 2∥AB 且AD 2∥BP ,∴PBAD 2是平行四边形.此时PD 2=AB ,易得x 2(−112,92);③∵BD 3∥AP 且AD 3∥BP ,此时BPAD 3是平行四边形.】∵BD 3∥AP 且B (2,0),∴y BD 3=x ﹣2.同理可得y AD 3=﹣3x ﹣12{x =x −2x =−3x −12, 得{x =−52x =−92,∴x 3(−52,−92).3.如图,在等边△ABC 中,BC =8cm ,射线AG ∥BC ,点E 从点A 出发沿射线AG 以1cm /s 的速度运动,同时点F 从点B 出发沿射线BC 以2cm /s 的速度运动,设运动时间为t (s ).(1)连接EF ,当EF 经过AC 边的中点D 时,求证:△ADE ≌△CDF ;(2)填空:#①当t 为 s 时,以A 、F 、C 、E 为顶点的四边形是平行四边形;②当t 为 s 时,四边形ACFE 是菱形.【解答】(1)证明:∵AG ∥BC ,∴∠EAD =∠DCF ,∠AED =∠DFC ,∵D 为AC 的中点,∴AD =CD ,∵在△ADE 和△CDF 中,{∠xxx =∠xxx∠xxx =∠xxx xx =xx,∴△ADE ≌△CDF (AAS );(2)解:①当点F 在C 的左侧时,根据题意得:AE =tcm ,BF =2tcm ,·则CF =BC ﹣BF =6﹣2t (cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AECF 是平行四边形,即t =8﹣2t ,解得:t =83; 当点F 在C 的右侧时,根据题意得:AE =tcm ,BF =2tcm ,则CF =BF ﹣BC =2t ﹣8(cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AEFC 是平行四边形,即t =2t ﹣8,]解得:t =8;综上可得:当t =83或8s 时,以A 、C 、E 、F 为顶点四边形是平行四边形.②若四边形ACFE 是菱形,则有CF =AC =AE =8,则此时的时间t =8÷1=8(s );故答案是:83或8;8.|4.已知,Rt △OAB 的两直角边OA 、OB 分别在x 轴和y 轴上,如图1,A ,B 坐标分别为(﹣2,0),(0,4),将△OAB 绕O 点顺时针旋转90°得△OCD ,连接AC 、BD 交于点E .(1)求证:△ABE ≌△DCE .(2)M 为直线BD 上动点,N 为x 轴上的点,若以A ,C ,M ,N 四点为顶点的四边形是平行四边形,求出所有符合条件的M 点的坐标.(3)如图2,过E 点作y 轴的平行线交x 轴于点F ,在直线EF 上找一点P ,使△PAC 的周长最小,求P 点坐标和周长的最小值.【分析】(1)由A 、B 的坐标可求得AO 和OB 的长,由旋转的性质可求得OC 、OD 的长,从而可求得∠AEB =90°,再由勾股定理可求得CD 和AB 的长,可求得AB =CD ,可证得△ABE ≌△DCE ;(2)由B 、D 坐标可求得直线BD 解析式,当M 点在x 轴上方时,则有CM ∥AN ,则可求得M 点纵坐标,代入直线BD 解析式可求得M 点坐标,当M 点在x 轴下方时,同理可求得M 点纵坐标,则可求得M 点坐标;)(3)由AE =DE 可知A 、D 关于EF 对称,连接CD 交EF 于点P ,则P 点即为满足条件的点,由C 、D 坐标可求得直线CD 的解析式,则可求得P 点坐标,利用勾股定理可分别求得AC 和CD 的长,则可求得此时△PAC 的周长.【解答】解:(1)∵A (﹣2,0),B (0,4),∴OA =2,OB =4,∵将△OAB 绕O 点顺时针旋转90°得△OCD ,∴OC =OA =2,OD =OB =4,AB =CD ,∴∠ACO =∠ECB =∠CBE =45°,∴∠CEB =90°,∴∠AEB =∠CED ,且CE =BE ,在Rt △ABE 和Rt △DCE 中:{xx =xx xx =xx∴Rt △ABE ≌Rt △DCE (HL );(2)由(1)可知D (4,0),且B (0,4),∴直线BD 解析式为y =﹣x +4,当M 点在x 轴上方时,则有CM ∥AN ,即CM ∥x 轴,∴M 点到x 轴的距离等于C 点到x 轴的距离,∴M 点的纵坐标为2,在y =﹣x +4中,令y =2可得x =2,∴M (2,2);当M 点在x 轴下方时,同理可得M 点的纵坐标为﹣2,(在y =﹣x +4中,令y =﹣2可求得x =6,∴M 点的坐标为(6,﹣2);综上可知M 点的坐标为(2,2)或(6,﹣2);(3)由(1)可知AE =DE ,∴A 、D 关于直线EF 对称,连接CD 交EF 于点P ,则PA =PD , ∴PA +PC =PD +PC =CD ,∴满足△PAC 的周长最小,∵C (0,2),D (4,0),∴可设直线CD 解析式为y =kx +2,∴4k +2=0,解得k =−12, ∴直线CD 解析式为y =−12x +2,∵A (﹣2,0),D (4,0),∴F (1,0),即直线EF 解析式为x =1,在y =−12x +2中,令x =1可得y =32, ∴P (1,32), 在Rt △AOC 中,由勾股定理可求得AC =2√2, 在Rt △COD 中,由勾股定理可求得CD =√22+42=2√5, ∴PA +PC +AC =CD +AC =2√5+2√2, 即△PAC 的周长最小值为2√5+2√2.。
一次函数中四边形存在性问题 2022-2023学年八年级数学下学期期末复习专练(人教版)(解析版)
一次函数中的四边形存在性问题【题型1 平行四边形的存在性问题】1.(2023•襄阳模拟)如图,直线l 1:y =−34x +b 分别与x 轴、y 轴交于A 、B 两点,与直线l 2:y =kx ﹣6交于点C (2,32). (1)点A 坐标为( , ),B 为( , )(2)在线段BC 上有一点E ,过点E 作y 轴的平行线交直线l 2于点F ,设点E 的横坐标为m ,若四边形OBEF 是平行四边形时,求出此时m 的值.【分析】(1)先将点C 坐标代入直线l 1中,求出直线l 1的解析式,令x =0和y =0,即可得出结论;(2)先求出直线l 2的解析式,表示出点E ,F 的坐标,在判断出OB =EF ,建立方程求解,即可得出结论;【解答】解:∵点C(2,32)在直线l1:y=−34x+b上,∴−34×2+b=32,∴直线l1的解析式为y=−34x+3,令x=0,∴y=3,∴B(0,3),令y=0,∴−34x+3=0,∴x=4,∴A(4,0),故答案为:4,0,0,3;(2)∵点C(2,32)在直线l2:y=kx﹣6上,∴2k﹣6=32,∴k=154,∴直线l2的解析式为y=154x﹣6,∵EF∥y轴,点E的横坐标为m,∴点F的横坐标为m,∵点E l1上,∴E(m,−34m+3),∵点F在直线l2:y=154x﹣6上,∴F(m,154m﹣6),∵四边形OBEF是平行四边形,且BO∥EF,∴OB=EF,EF=−34m+3﹣(154m﹣6)=3,∴m=4 3;【点评】此题是一次函数综合题,主要考查了待定系数法,平行四边形的性质,三角形的面积公式,利用方程的思想解决问题是解本题的关键.2.(2022春•涟水县校级月考)如图,平行四边形ABCD 在直角坐标系中,点B 、点C 都在x 轴上,其中OA =8,OB =6,AD =12,E 是线段OD 的中点.(1)直接写出点C ,D 的坐标;(2)求直线AE 的关系式;(3)平面内是否存在一点F ,使以A 、D 、E 、F 为顶点的四边形是平行四边形?若存在,请直接写出点F 的坐标;若不存在,请说明理由.【分析】(1)根据平行四边形的性质得AD =BC =12,AD ∥BC ,根据题意可得OC =6,点A 的坐标为(0,8),点D 的坐标为(12,8),即可得点C 的坐标为(6,0);(2)根据E 是线段OD 的中点得E (6,4),设直线AE 的关系式为:y =kx +b ,根据直线AE 经过点A ,点E ,即可得{b =86x +b =4,进行计算即可得; (3)分情况讨论:①当EF 为平行四边形的边时,根据对边相等即可得;②当EF 为平行四边形的对角线时,根据对角线互相平分即可得.BC【解答】解:(1)∵四边形ABCD 是平行四边形,∴AD =BC =12,AD ∥BC ,∵点B 、C 都在x 轴上,点A 在y 轴上,OA =8,OB =6,∴OC =BC ﹣OB =12﹣6=6,点A 的坐标为(0,8),点D 的坐标为(12,8),∴点C 的坐标为(6,0);(2)∵E 是线段OD 的中点,∴E (6,4),设直线AE 的关系式为:y =kx +b ,∵直线AE 经过点A ,点E ,∴{b =86x +b =4, 解得{b =8k =−23, ∴直线AE 的关系式:y =−23x +8;(3)存在,F坐标为(﹣6,4)或(18,4)或(6,12),①如图所示,当EF为平行四边形的边时,EF=AD=12,∴点F的坐标为:(﹣6,4)或(18,4),②如图所示,当EF为平行四边形的对角线时,则DG=AG=6,FG=GE=4,即点F的坐标为:(6,12),综上,点F的坐标为:(﹣6,4)或(18,4)或(6,12).【点评】本题考查了平行四边形的判定与性质,一次函数的性质,解题的关键是掌握并灵活运用这些知识点.3.(2022春•昌江县期末)如图,直线y=﹣x+4分别交x轴、y轴于A、B两点,直线BC与x轴交于点C (﹣2,0),P是线段AB上的一个动点(点P与A、B不重合).(1)求直线BC所对应的函数表达式;(2)设动点P的横坐标为t,△POA的面积为S.①求出S与t的函数关系式,并写出自变量t的取值范围;②在线段BC上存在点Q,使得四边形COPQ是平行四边形,求此时点Q的坐标.【分析】(1)根据直线y =﹣x +4分别交x 轴、y 轴于A 、B 两点,直线BC 与x 轴交于点C (﹣2,0),可以得到点B 的坐标,从而可以得到直线BC 的函数表达式;(2)①根据题意,可以用含t 的代数式表示出点P 的坐标,从而可以得到S 与t 的函数关系式,并写出自变量t 的取值范围;②根据题意和平行四边形的性质,可以用含t 的代数式表示出点Q 的坐标,再根据OC =PQ ,即可得到点Q 的坐标.【解答】解:(1)∵直线y =﹣x +4分别交x 轴、y 轴于A 、B 两点,∴点A 的坐标为(4,0),点B 的坐标为(0,4),设直线BC 所对应的函数表达式为y =kx +b ,{b =4−2k +b =0, 解得,{k =2b =4, 即直线BC 所对应的函数表达式是y =2x +4;(2)①∵点O (0,0),点A (4,0),∴OA =4,∵动点P 的横坐标为t ,△POA 的面积为S ,P 是线段AB 上的一个动点(点P 与A 、B 不重合), ∴动点P 的纵坐标为﹣t +4,∴S =4×(−t+4)2=−2t +8, 即S 与t 的函数关系式是S =﹣2t +8(0<t <4);②过点P 作PQ ∥x 轴,交BC 于点Q ,∵点P 的坐标为(t ,﹣t +4),∴点Q 的纵坐标为﹣t +4,∵点Q 在直线y =2x +4上,∴﹣t +4=2x +4,得x =﹣0.5t ,∵四边形COPQ是平行四边形,OC=2,∴OC=PQ,∴2=t﹣(﹣0.5t),解得,t=4 3,∴点Q的坐标为(−23,83).【点评】本题是一道一次函数综合题,主要考查一次函数的性质、平行四边形的性质、待定系数法求一次函数解析式,三角形的面积,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.4.(2023春•鲤城区校级期中)如图1,在平面直角坐标系中,直角梯形OABC的顶点A的坐标为(4,0),直线y=−14x+3经过顶点B,与y轴交于顶点C,AB∥OC.(1)求顶点B的坐标;(2)如图2,直线l经过点C,与直线AB交于点M,点O'与点O关于直线l对称,连接CO′并延长交直线AB于第一象限的点D,当CD=5时,求直线l的解析式;(3)在(2)条件下,点P在直线l上运动,点Q在直线OD上运动,当四边形PBCQ是平行四边形时,求点P的坐标.【分析】(1)根据AB∥OC,可得点B的横坐标为4,再代入y=−14x+3,即可求解;(2)过C点作CN⊥AB于N,可得到∠DCM=∠DMC,从而得到CD=MD=5,再求出OC=3,DN=3,从而得到NM=5﹣3=2,继而得到AM=1,可得到点M(4,1),即可求解;(3)连接OD,先求出D点坐标为(4,6),可得直线OD解析式为y=32x,设P点坐标为(a,−12a+3),Q点坐标为(b,32b),然后根据平行四边形对角线互相平分,即可求解.【解答】解:(1)∵A(4,0),AB∥OC,∴点B的横坐标为4,把x=4代入y=−14x+3中,得y=2,∴B(4,2);(2)如图,过C点作CN⊥AB于N,∵AB∥OC,∴∠OCM=∠DMC,∵点O'为点O关于直线l的对称点,∴∠DCM=∠OCM,∴∠DCM=∠DMC,∴CD=MD=5,∵y=−14x+3,当x=0时,y=3,∴点C(0,3),∴OC=3,∵CN=OA=4,∴DN=√CD2−CN2=√52−42=3,∴NM=5﹣3=2,∴AM=AN﹣NM=3﹣2=1,∴M(4,1),设直线l解析式y=kx+b把C(0,3),M(4,1)代入得:{3=b 1=4k +b, 解得:{k =−12b =3,∴直线l 的解析式为:y =−12x +3;(3)如图,连接OD ,∵AD =AM +MD =1+5=6,AD ∥OC ,A 点坐标为(4,0),∴D 点坐标为(4,6),设OD 直线解析式为y =kx ,将(4,6)代入可得4k =6,解得k =32,∴直线OD 解析式为y =32x ,∵点P 在直线l 上运动,点Q 在直线OD 上运动,∴设P 点坐标为(a ,−12a +3),Q 点坐标为(b ,32b),∵四边形PBCQ 是平行四边形,∴平行四边形对角线互相平分,{4+b 2=a+022+32b 2=−12a+3+32, 解得:{a =5b =1, 当a =5时,−12a +3=−12×5+3=12,∴P 点坐标为(5,12).【点评】本题主要考查了一次函数与四边形的综合题,熟练掌握一次函数的图象和性质,平行四边形的性质是解题的关键.【题型2 矩形的存在性问题】1.如图,在平面直角坐标系xOy中,已知直线l与直线y=2x平行,且直线l与x、y轴分别交于点A(﹣1,0)、点B,点C(1,a)在直线l上.(1)求直线l的表达式以及点C的坐标;(2)点P在y轴正半轴上,点Q是坐标平面内一点,如果四边形P AQC为矩形,求点P、Q的坐标.【分析】(1)根据题意设直线l的解析式为y=2x+b,代入A(﹣1,0)求得b,即可求得直线l的解析式,然后代入C(1,a),就可求得a的值;(2)先证得Q在y轴上,根据勾股定理求得AB,然后根据矩形的性质即可求得P、Q的坐标.【解答】解:(1)∵直线l与直线y=2x平行,∴直线l的斜率为2,设直线l的解析式为y=2x+b,∵直线l经过A(﹣1,0),∴2×(﹣1)+b=0,解得b=2,∴直线l的表达式为y=2x+2,∵点C(1,a)在直线l上,∴a=2×1+2=4;(2)∵y=2x+2,∴B(0,2),∵A(﹣1,0),C(1,4),∴AB=BC,∵四边形P AQC为矩形,点P在y轴正半轴上,∴Q点在y轴负半轴上,∵A(﹣1,0),∴AB=√12+22=√5,∴PB=QB=√5,∴P(0,2+√5),Q(0,2−√5).【点评】本题考查了两条直线相交或平行问题,待定系数法求一次函数的解析式,矩形的性质,熟练掌握矩形的对角线相等且互相平分是解题的关键.2.(2023•阜阳三模)如图,四边形OABC是矩形,点A、C分别在x轴、y轴上,△ODE是△OCB绕点O 顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,点B的坐标为(﹣2,4).(1)求直线BD的表达式;(2)求△DEH的面积;(3)点M在x轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)根据矩形的性质和旋转的性质可得点D坐标,再利用待定系数法求直线BD的表达式即可;(2)先利用待定系数法求出直线OE 的解析式,再联立{y =12x y =−23x +83,求出点H 坐标,再根据△DEH 的面积=12DE ⋅HG 求解即可;(3)先求出点F 坐标,以点D 、F 、M 、N 为顶点的四边形是矩形,分情况讨论:①当FD 是矩形的对角线时,②当FD 为矩形的边时,分别求出点M 的坐标,根据平移的性质即可确定点N 坐标.【解答】解:(1)在矩形ABCO 中,∠OCB =90°,∵点B 坐标为(﹣2,4),∴OC =4,BC =2,根据旋转的性质可得,OD =OC =4,DE =BC =2,∠ODE =∠OCB =90°,∴点D 坐标为(4,0),点E 坐标为(4,2),设直线BD 的解析式为y =kx +b (k ≠0,k ,b 为常数),代入点B (﹣2,4),点D (4,0),得{−2k +b =44k +b =0, 解得{k =−23b =83, ∴直线BD 的解析式为y =−23x +83;(2)过点H 作HG ⊥DE 于点G ,如图所示:设直线OE 的解析式为y =mx (m ≠0,m 为常数),代入点E (4,2),得4m =2,解得m =12, ∴直线OE 的解析式为y =12x ,联立{y =12x y =−23x +83,解得{x =167y =87, ∴点H 坐标为(167,87), ∴HG =4−167=127, ∵DE =2,∴△DEH 的面积=12DE ⋅HG =12×2×127=127; (3)存在点N ,点N 坐标为(4,83)或(209,−83),理由如下: 当x =0时,y =−23x +83=83,∴点F 坐标为(0,83), 以点D 、F 、M 、N 为顶点的四边形是矩形,分情况讨论:①当FD 是矩形的对角线时,如图所示:此时M 点与点O 重合,∴N 点坐标为(4,83); ②当FD 为矩形的边时,如图所示:设OM =m ,在Rt △OMF 中,根据勾股定理,得MF 2=m 2+(83)2,∵DF 2=42+(83)2,MF =4+m , 在Rt △MDF 中,根据勾股定理,得MF 2+DF 2=DM 2,∴m 2+(83)2+42+(83)2=(m +4)2,解得m =169, ∴点M 坐标为(−169,0), 根据平移的性质,可得点N 坐标为(209,−83), 综上所述,点N 坐标为(4,83)或(209,−83). 【点评】本题考查了一次函数的综合题,涉及待定系数法求解析式,旋转的性质,矩形的性质,三角形的面积,存在性问题等,本题综合性较强,难度较大.3.(2020春•香坊区校级月考)如图,在平面直角坐标系中,矩形OABC 的顶点A 、C 分别落在x 轴、y 轴正半轴上,点E 在边OA 上,点F 在边OC 上,且AE =EF ,已知B (6,8),F (0,2√3 ).(1)求点E 的坐标;(2)点E 关于点A 的对称点为点D ,点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,设P 点的运动时间为t 秒,△PBD 的面积为S ,用含t 的代数式表示S ;(3)在(2)的条件下,点M 为平面内一点,点P 在线段BC 上运动时,作∠PDO 的平分线交y 轴于点N ,t 为何值时,四边形DPNM 为矩形?并求此时点M 的坐标.【分析】(1)先确定出点A 的坐标,进而得出OA ,最后在Rt △OEF 中,利用勾股定理求出OE 即可得出点E 的坐标;(2)分两种情况,用三角形的面积公式即可解决问题;(3)先利用对称求出点D 的坐标,进而得出OD ,由角平分线的性质定理得出DP =OD 求出点P 的坐标,进而求出直线PD ,MD 的解析式,再利用勾股定理求出点N 的坐标,进而得出直线MN 的解析式,联立直线DM和MN的解析式即可得结论.【解答】解:(1)在矩形OABC中,BC∥OA,B(6,8),∴A(6,0),∴OA=6,设OE=a,∴EF=AE=OA﹣OE=6﹣a,∵F(0,2√3),∴OF=2√3,在Rt△AEF中,根据勾股定理得,OE2+OF2=EF2,∴a2+12=(6﹣a)2,∴a=2,∴E(2,0);(2)由(1)知,E(2,0),∴AE=4,∵点D是点E关于点A的对称点,∴D(10,0),∵BC∥OA,B(6,8),OC=AB=8,∴P(t,8),PB=|t﹣6|①当点P在边BC上时,如图1,∴0≤t<6,∴PB=6﹣t,∴S=S△PBD=12PB•OC=12×(6﹣t)×8=﹣4t+24,②当点P在CB的延长时,如图2,∴t>6,∴PB=t﹣6,∴S=S△PBD=12PB•OC=12×(t﹣6)×8=4t﹣24,即:S={−4t+24(0<t<6) 4t−24(t>6),(3)如图3,由(2)知,D(10,0),∴OD =10,∵四边形DPNM 是矩形,∴∠DPN =90°=∠DON ,∴NP ⊥DP ,NO ⊥OD ,∵DN 是∠PDO 的平分线,∴NO =NP ,在Rt △NDO 和Rt △NDP 中,{DN =DN NO =NP, ∴Rt △NDO 和Rt △NDP (HL ),∴DP =OD =10,∵P (t ,8),D (10,0),∴DP 2=(t ﹣10)2+64=100,∴t =16(由于点P 在线段BC 上,所以舍去)或t =4,∴P (4,8),∵D (10,0),∴DP 的解析式为y =−43x +403,∵DM ⊥DP ,∴直线DM 的解析式为y =34x 152①,设N (0,n ),∴ON =n ,∴PN =n ,CN =OC ﹣ON =8﹣n ,∵P (4,8),∴CP =4,在Rt △CNP 中,根据勾股定理得,CN 2+CP 2=PN 2,∴(8﹣n )2+16=n 2,∴n =5,∴N (0,5),∵PD ∥NM ,∴直线NM 的解析式为y =−43x +5②,联立①②解得,x=6,y=﹣3,∴M(6,﹣3).【点评】此题是四边形综合题,主要考查了矩形的性质,角平分线的性质定理,待定系数法,勾股定理,解(1)的关键是利用勾股定理求出OE,解(2)的关键是分两种情况讨论计算,解(3)的关键是求出点P的坐标.【题型3 菱形的存在性问题】1.(2023春•江阴市期中)将矩形OABC如图所示放置在第一象限,点B的坐标为(3,4),一次函数y=−23x+b的图象与边OC、AB分别交于点D、E,并且满足OD=BE,点M是线段DE上的一个动点.(1)填空:b=;(2)设点N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点M的坐标.【分析】(1)分别表示出D和E点的坐标,根据OD=BE列出等式即可求出b的值;(2)分当OD为菱形一边时和当OD为菱形一条对角线时两种情况,根据菱形邻边相等或对角线的对称性等特点找到等量列出等式即可求出M点坐标.【解答】解:(1)∵点B的坐标为(3,4),矩形OABC放置在第一象限,∴A(3,0),C(0,4),D(0,b),E(3,b﹣2),∵OD=BE,∴b=4﹣(b﹣2),∴b=3;(2)①当OD 为菱形一边时,OD =OM ,如图所示:设M(m ,3−23m), ∴m 2+(3−23m)2=32,解得,m =3613<3或m =0(不合题意,舍去),∴M(3613,1513);②当OD 为菱形一条对角线时,过OD 中点P 作PM ⊥OD 交直线CE 于点M ,∴点M 的纵坐标为32, ∴32=−23c +3, ∴c =94<3,∴点M(94,32),综上,符合条件的点M 有两个,其坐标分别为(94,32)或(3613,1513).【点评】本题属于一次函数综合题,考查了一次函数基本性质以及菱形的基本性质等知识,熟练掌握好一次函数的基本性质以及平面直角坐标系中点的综合变化,并能将菱形特点与平面直角坐标系坐标变化相互结合,灵活运用是解决本题的关键.2.(2023•赫山区校级一模)如图,在平面直角坐标系中,直线y =12x +3分别与x 轴、y 轴交于点B ,C ,且与直线y =−12x 交于A .(1)分别求出A ,B ,C 的坐标;(2)若D 是线段OA 上的点,且△COD 的面积为3,求直线CD 的函数解析式;(3)在(2)的条件下,设P 是射线CD 上的点,在平面内是否存在点Q ,使以O ,C ,P ,Q 为顶点的四边形是菱形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.【分析】(1)由函数图象上点的坐标特征直接求解即可;(2)求出D 点坐标,再由待定系数法求解即可;(3)设P (t ,t +3),Q (x ,y ),根据对角线的情况,再分三种情况讨论即可.【解答】解:(1)令x =0,y =3,∴C (0,3),令y =0,x =﹣6,∴B (﹣6,0),联立方程组{y =12x +3y =−12x , 解得{x =−3y =32, ∴A (﹣3,32); (2)由 S △COD =12OC ⋅ℎOC =12×3ℎOC =3,∴h OC =2,∴当x =﹣2时,y =1,∴D (﹣2,1),设直线CD 的函数解析式为y =kx +b (k ≠0),∴{b =3−2k +b =1, 解得{k =1b =3, ∴直线CD 的函数解析式为y =x +3;(3)存在点Q ,使以O ,C ,P ,Q 为顶点的四边形是菱形,理由如下:设P (t ,t +3),Q (x ,y ),①当PQ 为菱形对角线时,OP =PC ,∴{t +x =0t +3+y =3t 2+(t +3)2=t 2+t 2,解得{ t =−32x =32y =32, ∴Q (32,32); ②当PO 为菱形对角线时,CO =PC ,∴{t =xt +3=y +39=t 2+t 2,解得{ t =32√2x =32√2y =32√2(舍){ t =−32√2x =−32√2y =−32√2, ∴Q (−32√2,−32√2);③当PC 为菱形对角线时,OP =OC ,∴{t =xt +6=y t 2+(t +3)2=9,解得{t =0x =0y =6(舍)或{t =−3x =−3y =3,∴Q (﹣3,3);综上所述:满足条件的点Q 的坐标是(32,32)或(−32√2,−32√2)或(﹣3,3). 【点评】本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质,菱形的判定及性质,分类讨论是解题的关键.3.(2023春•新吴区期中)如图矩形OABC 的顶点A 、C 分别在x 轴、y 轴的正半轴上,点B 的坐标为(5,7),一次函数y =−13x +5的图象与边OC 、AB 分别交于D 、E 两点,点M 是线段DE 上的一个动点.(1)则BE 的长为 ;(2)连接OM ,若△ODM 的面积为152,求点M 的坐标;(3)在(2)的条件下,设点P 是x 轴上一动点,点Q 是平面内的一点,以O 、M 、P 、Q 为顶点的四边形是菱形,直接写出点Q 的坐标.【分析】(1)把点E 的横坐标代入一次函数解析式求出纵坐标得到AE 的长度,进而得到BE =AB ﹣AE 的长度;(2)根据△ODM 的面积为152列方程求解即可;(3)画出菱形,找到点Q 的位置,根据菱形的性质分情况分别计算即可.【解答】解:(1)∵四边形OABC 是矩形,∴AB ⊥x 轴,∵B (5,7),AB =7,∴E 点的横坐标为5,∵一次函数y =−13x +5的图象过点E ,∴当x =5时,y =−53+5=103,∴AE =103,∴BE =AB ﹣AE =7−103=113,故答案为:113;(2)∵一次函数y =−13x +5的图象交y 轴于点D ,∴当x =0时,y =5,∴D (0,5),∴OD =5,∵△ODM的面积为15 2,∴12×5×x M=152,∴x M=3,当x=3时,y=−13×3+5=4,∴M(3,4);(3)∵M(3,4),∴OM=√32+42=5,如图,当OM为菱形的边长时,QM∥x轴,QM=OM=5,∴Q(﹣2,4)或(8,4);如图,当OP是菱形的对角线时,MQ⊥x轴于点F,FQ=FM=4,∴Q(3,﹣4);如图,当OM是菱形对角线时,QM∥x轴,QM=OQ,设Q(q,4),∵QM2=OQ2,∴(3﹣q)2=q2+42,解得:q=−7 6,∴Q (−76,4);综上所述,点Q 的坐标为:(﹣2,4)或(8,4)或(3,﹣4)或(−76,4). 【点评】本题考查一次函数综合题,考查分类讨论的思想,画出菱形,找到点Q 的位置,根据菱形的性质分情况分别计算是解题的关键.4.(2022春•荔湾区校级期中)如图1,在平面直角坐标系中,直线L 2:y =−12x +6与L 1:y =12x 交于点A ,分别与x 轴、y 轴交于点B 、C .(1)分别求出点A 、B 、C 的坐标;(2)若D 是线段OA 上的点,且△COD 的面积为12,求直线CD 的函数表达式;(3)在(2)的条件下,设P 是直线CD 上的点,在平面内是否存在其它点Q ,使以O 、C 、P 、Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.【分析】(1)构建方程组确定交点A 的坐标,利用待定系数法确定B ,C 两点坐标即可.(2)设D (m ,12m ),利用三角形的面积公式,构建方程求出m 的值,再利用待定系数法即可解决问题. (3)分三种情形:根据OC =PC ,设P (m ,12m ),利用两点间距离公式,构建方程求出m 即可.如图2﹣1中,当OC 为菱形的对角线时,OC 垂直平分线段P ′Q ′,利用对称性解决问题即可.当OC =OP 时,P ″(6,0),Q ″(6,6).【解答】解:(1)由{y =−12x +6y =12x,解得{x =6y =3, ∴A (6,3).∵y =−12x +6与分别与x 轴、y 轴交于点B 、C , ∴C (0,6),B (12,0);(2)设D (m ,12m ), 由题意:OC =6,△COD 的面积为12,∴12×6×m =12, ∴m =4,∴D (4,2),∵C (0,6),设直线CD 的解析式为y =kx +b ,则有{4k +b =2b =6, 解得{k =−1b =6, ∴直线CD 的解析式为y =﹣x +6;(3)当四边形OCPQ ∴OC =PC =6,设P (m ,﹣m +6),∴m 2+m 2=36,∴m =3√2或﹣3√2,∴P (3√2,﹣3√2+6),∵PQ ∥OC ,PQ =OC ,∴Q (3√2,﹣3√2),如图2﹣1中,当OC 为菱形的对角线时,OC 垂直平分线段P ′Q ′,易知P ′(3,3),Q ′(﹣3,3),∴满足条件的点Q ′的坐标为(﹣3,3).当OC =OP 时,P ″(6,0),Q ″(6,6).综上所述,满足条件的点Q 的坐标为(3√2,﹣3√2)或(﹣3,3)或(6,6).【点评】本题属于一次函数综合题,考查了待定系数法,三角形的面积,菱形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.【题型4 正方形的存在性问题】1.(2022•前进区二模)△P AC在平面直角坐标系中的位置如图所示,AP与y轴交于点B(0,2),点P的坐标为(﹣1,3),线段OA,OC的长分别是方程x2﹣9x+14=0的两根,OC>OA.(1)求线段AC的长;(2)动点D从点O出发,以每秒1个单位长度的速度沿x轴负半轴向终点C运动,过点D作直线l与x轴垂直,设点D运动的时间为t秒,直线l扫过四边形OBPC的面积为S,求S与t的关系式;(3)M为直线l上一点,在平面内是否存在点N,使以A,P,M,N为顶点的四边形为正方形?若存在,请直接写出点的坐标;若不存在,请说明理由.【分析】(1)解方程可求得OA,OC的长,则可求得A、C的坐标,利用两点之间的距离公式即可求解;(2)分两种情况:①当0<t≤1时;②当1<t≤7时,利用梯形的面积公式即可求解;(3)分两种情况:①AP为正方形的对角线时,②AP为正方形的边时,根据正方形以及等腰直角三角形的性质,可求得N点坐标.【解答】解:(1)解方程x2﹣9x+14=0可得x=2或x=7,∵线段OA,OC的长分别是方程x2﹣9x+14=0的两根,且OC>OA,∴OA=2,OC=7,∴AC=2+7=9,∴线段AC的长为:7;(2)①如图,当0<t≤1时,点E(﹣t,t+2),∴S=S梯形OBDE =12t(2+t+2)=12t2+2t(0<t≤1);②如图,当1<t≤7时,设直线CP解析式为:y=mx+n,∵C(﹣7,0),点P的坐标为(﹣1,3),代入得{−7m+n=0−m+n=3,解得:{m=12n=72,∴直线CP解析式为:y=12x+72;设E(﹣t,−12t+72),∴DE=−12t+72,∴S=S梯形OBPH+S梯形HPED=12×(2+3)×1+12(t﹣1)(−12t+72+3)=−14t2+72t−34(1<t≤7),∴S=12t2+2t(0<t≤1)或S=−14t2+72t−34(1<t≤7);(3)存在,分两种情况:①AP为正方形的对角线时,如图,∵A(2,0),B(0,2),∴∠OAB=45°,∵四边形AMPN是正方形,∴∠P AN=45°,∠NAM=90°,∴∠OAB+∠P AN=90°,∴点M在x轴上,NA⊥x轴,NP∥c轴,∴N(2,3);②AP为正方形的边时,如图,∵∠OAB=45°,四边形AMPN是正方形,∴∠NAO=∠OAB=45°,AP=AN,∴HN=PH=3,∴N(﹣1,﹣3),∵MH=AH=3,∴M(﹣4,0),∴N(﹣4,0)或(﹣1,﹣3),综上可知,存在满足条件的N点,其坐标为(2,3)或(﹣4,0)或(﹣1,﹣3).【点评】本题考查了一次函数的性质、一元二次方程、勾股定理、待定系数法、正方形的性质等知识.在(1)中求得OA、OC的长是解题的关键,在(2)中求得P点坐标是解题的关键,在(3)中分类思想的运用是解题的关键.2.如图,在平面直角坐标系中,OB和OC的长是方程x2﹣15x+36=0的两个根,且OB<OC.∠BAC=90°,D是x轴上一点,且将△ADC沿AD翻折,AC恰好落在y轴上的AE处.(1)求点A的坐标;(2)求直线CE的解析式;(3)M是直线AC上一点,在平面上是否存在一点N,使以A,B,M,N为顶点的四边形为正方形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)解方程得出OB和OC的值,证△AOB∽△COA,根据线段比例关系求出OB即可确定B 点的坐标;(2)由(1)得出C点和E点的坐标,用待定系数法求出直线CE的解析式即可;(3)用待定系数法求出直线AC的解析式,平移AC过B点,设出N点坐标,根据BN=AB确定N点坐标即可.【解答】解:(1)解方程x2﹣15x+36=0,得x=3或x=12,∵OB<OC,∴OB=3,OC=12,∵∠BAO+∠ABO=90°,∠BAO+∠CAO=90°,∴∠ABO =∠CAO ,又∵∠AOB =∠COA =90°,∴△AOB ∽△COA ,∴OB OA =OA OC ,∴OA =√OB ⋅OC =√3×12=6,∴A (0,6);(2)由(1)知A (0,6),C (12,0),∴AC =√62+122=6√5,∴OE =AC ﹣OA =6√5−6,∴E (0,6﹣6√5),设直线CE 的解析式为y =kx +b ,代入C 点和E 点坐标得{12k +b =0b =6−6√5, 解得{k =12√5−12b =6−6√5, ∴直线CE 的解析式为y =(12√5−12)x +6﹣6√5;(3)存在点N ,使以A ,B ,M ,N 为顶点的四边形为正方形,理由如下:①若M 点在线段AC 上,∵∠BAM =90°,∴存在四边形ABNM 为正方形,设直线AC 的解析式为y =sx +t ,代入A 点和C 点的坐标得{t =612s +t =0, 解得{s =−12t =6,∴直线AC 的解析式为y =−12x +6,平移直线AC与直线BN重合,则直线BN得解析式为y=−12x+m,∵B(﹣3,0),∴m=−3 2,即直线BN得解析式为y=−12x−32,设N(n,−n2−32),∵四边形ABNM是正方形,∴BN2=AB2,即(n+3)2+(−n2−32)2=32+62,解得n=3或n=﹣9(舍去),故N点得坐标为(3,﹣3),②若M点在CA延长线上,由①知,此时N点也在直线y=−12x−32上,设N(p,−p2−32),∵四边形ABNM是正方形,∴BN2=AB2,即(p+3)2+(−p2−32)2=32+62,解得p=3(舍去)或p=﹣9,故N点得坐标为(﹣9,3),∴点N的坐标为(3,﹣3)或(﹣9,3)时四边形ABNM是正方形.【点评】本题主要考查一次函数的综合题型,熟练掌握待定系数法求函数解析式及一次函数的性质是解题的关键.3.(2021春•柳南区校级期末)如图,直线L 1:y =x +1与直线L 2:y =﹣x +5相交于点C 直线L 1与x 轴相交于点A ,直线L 2与x 轴相交于点B .(1)求三角形ABC 的面积;(2)若经过点C 的一条直线交x 轴于D ,直线CD 把三角形ABC 分成两个三角形,且这两个三角形面积的比为1:2,请直接写出点D 的坐标;(3)假设G 是直线y =x +1上的点,在坐标平面上是否存在一点Q ,使以A ,B ,Q ,G 为顶点的四边形是正方形,若存在求出点Q 的坐标,若不存在请说明理由.【分析】(1)利用待定系数法求出A 、B 、C 三点坐标即可解决问题;(2)分两种情形分别求解即可;(3)分两种情形讨论①在L 1上取点G (G 异于A ),且CG =CA ,在L 2上取点Q (Q 异于B ),且CQ =CB ,可以证明四边形ABGQ ②当G 与C 重合时,以AB 为对称轴作G 的对称点Q ,于是四边形AQBG 为正方形.【解答】解:(1)在y =x +1中,当y =0时,则x =﹣1∴A (﹣1,0)在y =﹣x +5中当y =0时,则x =5B (5,0)∴AB =OA +OB =6,由{y =x +1y =−x +5解得{x =2y =3, ∴C (2,3)∴作CE⊥x轴于E.∴E(2,0)∴CE=3∴S△ABC=12•AB•CE=12×6×3=9,(2)由题意A(﹣1,0),B(5,0),AD=2BD或BD=2AD,可得D(1,0)或D(3,0).(3)设y=x+1交y轴于F,则F(0,1).∴OF=OA∴∠OAF=45°同理∠ABC=45°∴∠ACB=90°∴CA=CB,在L1上取点G(G异于A),且CG=CA,在L2上取点Q(Q异于B),且CQ=CB∴CG=CA=CQ=CB,又∵AG⊥BQ,∴四边形ABGQ为正方形,又∵A(﹣1,0)AB=AQ=6当G与C重合时,以AB为对称轴作G的对称点Q,于是四边形AQBG为正方形.又∵G(2,3),∴Q(2,﹣3)综合上述:Q(﹣1,6)或Q(2,﹣3).【点评】本题考查一次函数综合题、三角形的面积、正方形的性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题,属于中考压轴题.【题型5 四边形存在性的压轴题】1.(2023春•宜兴市期中)如图,在平面直角坐标系中,已知A(0,4),点B、C都在x轴上,BC=12,AD∥BC,CD所在直线的函数表达式为y=﹣x+9,E是BC的中点,点P是BC边上一个动点.(1)当PB=时,以点P、A、D、E为顶点的四边形为平行四边形;(2)点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.【分析】(1)若以点P、A、D、E为顶点的四边形为平行四边形,则AD=PE,有两种情况:①当P在E的左边,利用已知条件可以求出BP的长度;②当P在E的右边,利用已知条件也可求出BP的长度;(2)以点P、A、D、E为顶点的四边形能构成菱形.由(1)知,当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形,根据已知条件分别计算一组邻边,证明它们相等即可证明是菱形.【解答】解:(1)∵AD∥BC,点A坐标是(0,4),CD所在直线的函数关系式为y=﹣x+9,∴D点的纵坐标为4,y=4时,4=﹣x+9,x=5,∴D点的横坐标为5,∵CD所在直线的函数关系式为y=﹣x+9,y=0时,0=﹣x+9,x=9,∴C(9,0),∴OC=9,作DN⊥BC交于N,如图1所示,则四边形OADN为矩形,∴CN=OC﹣ON=OC﹣AD=9﹣5=4,DN=4,∴△DNC为等腰直角三角形,∴CD=√42+42=4√2,若以点P、A、D、E为顶点的四边形为平行四边形,则AD=PE=5,有两种情况:①当P在E的左边,∵E是BC的中点,∴BE=6,∴PB=BE﹣PE=6﹣5=1;②当P在E的右边,PB=BE+PE=6+5=11;故当PB=1或11时,以点P、A、D、E为顶点的四边形为平行四边形,故答案为:1或11;(2)点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能构成菱形,理由如下:①当BP=1时,此时CN=DN=4,NE=5﹣3=2,∴DE=√DN2+NE2=√42+22=2√5≠AD,故不能构成菱形.②当BP=11时,以点P、A、D、E为顶点的四边形是平行四边形,∴EP=AD=5,过D作DN⊥BC于N,如图2所示:由(1)得:DN=CN=4,∴NP=BP﹣BN=BP﹣(BC﹣CN)=11﹣(12﹣4)=3.∴DP=√DN2+NP2=√42+32=5,∴EP=DP=AD=5,故此时平行四边形PDAE是菱形,即以点P、A、D、E为顶点的四边形能构成菱形.【点评】本题是一次函数综合题,考查了等腰直角三角形的判定与性质、勾股定理、平行四边形的判定、矩形的判定、菱形的判定等知识,解题的关键是学会用分类讨论的思想思考问题,灵活运用所学知识解决问题,属于中考压轴题.2.如图,已知直线y=−1x+3与x轴,y轴分别交于点A,B,以AB为直角边,∠B为直角作等腰直角三2角形ABC(点C在第一象限).(1)求点A,B,C坐标;(2)点D A,B,C,D四点围成的四边形为正方形时,求点D坐标;(3)点P为x轴上一动点,点Q为线段AC上一动点,是否存在四边形BP AQ为平行四边形?若存在,求出P,Q点的坐标,若不存在,说明理由.【分析】(1)利用待定系数法求出A,B的坐标,过点C作CH⊥y轴于点H.构造全等三角形求出点C 的坐标;(2)利用正方形的性质,平移变换的性质求解即可;(3)求出直线AC 的解析式,再利用平行四边形的性质求解即可.【解答】解:(1)对于直线y =−12x +3,令y =0,得到x =6,∴A (6,0),令x =0,得到y =3,∴B (0,3),∴OA =6,OB =3,过点C 作CH ⊥y 轴于点H .∵∠BHC =∠CBA =∠AOB =90°,∴∠CBH +∠ABO =90°,∠ABO +∠BAO =90°,∴∠CBH =∠BAO ,在△BHC 和△AOB 中,{∠BHC =∠AOB∠CBH =∠BAO BC =AB,∴△BHC ≌△AOB (AAS ),∴CH =OB =3,BH =AO =6,∴OH =9,∴C (3,9);(2)∵四边形ABCD 是正方形,∴BC =AD ,BC ∥AD ,∵点B 向右平移3个单位,向上平移6个单位得到点C ,∴点A 向右平移3个单位,向上平移6个单位得到点D ,∴D (9,6);(3)∵A (6,0),C (3,9),设直线AC 的解析式为y =kx +b ,则有{6k +b =03k +b =9, 解得{k =−3b =18, ∴直线AC 的解析式为y =﹣3x +18,∵四边形APBQ 是平行四边形,∴BQ ∥AP ,BQ =AP ,∴Q(5,3),∴BQ=AP=5,∴P(1,0).【点评】本题属于一次函数综合题,考查了一次函数的性质,正方形的性质,平行四边形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.3.(2023•武陵区一模)如图,在平面直角坐标系中,直线AB交x轴于点A(﹣2,0),交y轴于点B(0,4),直线y=kx+b经过点B且交x轴正半轴于点C,已知△ABC面积为10.(1)点C的坐标是(,),直线BC的表达式是;(2)如图1,点E为线段AB中点,点D为y轴上一动点,连接DE,以DE为直角边作等腰直角三角形△EDF,且DE=DF,在点的运动过程中,当点F落在直线BC上时,求点D的坐标;(3)如图2,若G为线段BC上一点,且满足S△ABG=S△ABO,点M为直线AG上一动点,在x轴上是否存在点N,使以点B,C,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)由△ABC 面积为10,可得AC =5,即可求C 点坐标,再将点B 与C 代入y =kx +b ,解二元一次方程组可求y =−43x +4;(2)当D 点在E 上方时,过点D 作MN ⊥y 轴,过E 、F 分别作ME 、FN 垂直与x 轴,与MN 交于点M 、N ,由△EDF 是等腰直角三角形,可证得△MED ≌△NDF (AAS ),设D (0,y ),F (m ,−43m +4),E (﹣1,2),由ME =y ﹣2,MD =1,DN =y ﹣2,NF =1,得到m =y ﹣2,y =1+(−43m +4)=5−43m ,求出D (0,237);当点D 在点E 下方时,过点D 作PQ ⊥y 轴,过P 、Q 分别作PE 、FQ 垂直与x 轴,与PQ 交于点P 、Q ,同理可证△PED ≌△QDF (AAS ),设D (0,y ),F (m ,−43m +4),得到PE =2﹣y ,PD =1,DQ =2﹣y ,QF =1,所以m =2﹣y ,1=−43m +4﹣y ,求得D (0,﹣1); (3)连接OG ,由S △ABG =S △ABO ,可得OG ∥AB ,求出AB 的解析式为y =2x +4,所以OG 的解析式为y=2x ,可求出G (65,125),进而能求出AG 的解析式为y =34x +32,设M (t ,34t +32),N (n ,0), ①当BC 、MN 分别为对角线时,BC 的中点为(32,2),MN 的中点为(t+n 2,38t +34),求得N (−13,0);②当BM 、CN 分别为对角线时,BM 的中点为(t 2,38t +114),CN 的中点为(3+n 2,0),求得N (−313,0);③当BN 、CM 分别为对角线时,BN 的中点为(n 2,2),CM 的中点为(t+32,38t +34),求得N (193,0).【解答】解:(1)∵△ABC 10,∴12×AC ×OB =12×AC ×4=10, ∴AC =5,∵A (﹣2,0),∴C (3,0),将点B 与C 的坐标代入y =kx +b ,可得{b =43k +b =0, ∴{k =−43b =4,∴y =−43x +4,故答案为(3,0),y =−43x +4;(2)当D 点在E 上方时,过点D 作MN ⊥y 轴,过E 、F 分别作ME 、FN 垂直于x 轴,与MN 交于点M 、N ,。
一次函数平行四边形存在性
平行四边形存在性知识点睛1.存在性问题处理框架:①研究背景图形.②根据不变特征,确定分类标准.③分析特殊状态的形成因素,画出符合题意的图形并求解.④结果验证.2.平行四边形存在性问题特征举例:①三定一动,连接定点出现三条定线段.定线段分别作为平行四边形的________,利用________确定点的坐标.②两定两动,连接定点出现一条定线段.若定线段作为平行四边形的________,则通过________确定点的坐标;若定线段作为平行四边形的________,则定线段绕________旋转,利用________________确定点的坐标.精讲精练1.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y轴正半轴上,且OB=2OC.若M是坐标平面内一点,且以点M,A,B,C为顶点的四边形是平行四边形,则点M的坐标为_____________________.2.如图,在平面直角坐标系中,已知A(3,0),B(0,1),C(2,2),若D是坐标平面内一点,且以点A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为______________.3.如图,在平面直角坐标系中,直线23y x=+与坐标轴分别交于点A,B,点C在y轴正半轴上,且12OAAC=,直线CD⊥AB于点P,交x轴于点D.在坐标平面内是否存在点M,使得以点B,P,D,M为顶点的四边形是平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.4.如图,在平面直角坐标系中,直线334y x=-+与x轴、y轴分别交于点A,B,点C的坐标为(0,2-).若点D在直线AB上运动,点E在直线AC上运动,当以点O,A,D,E为顶点的四边形是平行四边形时,求点D的坐标.5.如图,在平面直角坐标系中,四边形OABC是直角梯形,6. 如图,在平面直角坐标系中,四边形OABC 是矩形,顶点A ,C 分别在x 轴、y 轴上,顶点B 的坐标为(3,4),点E 在OC 边上,点F 的坐标为(2,4).将矩形OABC 沿直线EF 折叠,点C 落在AB 边上的点G 处,若点N 在x 轴上,则直线EF 上是否存在点M ,使得以点F ,G ,M ,N 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.【参考答案】知识点睛1.①对角线平移②边平移对角线其中点中点坐标公式 精讲精练1.(3,2),(-3,2),(5,-2)2.(5,1),(-1,3),(1,-1)3.存在(3),(-,3),(-3)4.(125,65),(285,-65)5.存在(-3,0),(7,0),(3,0)6.存在(3,(1,,(1+,8。
一次函数中的(特殊图形)存在性问题(解析版)八年级数学上册同步考点归类培优题库

专题十五 一次函数中的(特殊图形)存在性问题考点一 直角三角形存在性问题【方法点拨】分类讨论哪个角为直角,一般分三种情况,简称“两垂线+一圆”1.如图1,在平面直角坐标系中,点A 坐标为(﹣4,4),点B 的坐标为(4,0).(1)求直线AB 的解析式;(2)点M 是坐标轴上的一个点,若AB 为直角边构造直角三角形△ABM ,请求出满足条件的所有点M 的坐标;(3)如图2,以点A 为直角顶点作∠CAD =90°,射线AC 交x 轴的负半轴与点C ,射线AD 交y 轴的负半轴与点D ,当∠CAD 绕点A 旋转时,OC ﹣OD 的值是否发生变化?若不变,直接写出它的值;若变化,直接写出它的变化范围(不要解题过程).【思路点拨】(1)由A 、B 两点的坐标利用待定系数法可求得直线AB 的解析式;(2)分别过A 、B 两点作AB 的垂线,与坐标轴的交点即为所求的M 点,再结合相似三角形的性质求得OM 的长即可求得点M 的坐标;(3)过A 分别作x 轴和y 轴的垂线,垂足分别为E 、F ,可证明△AEC ≌△AFD ,可得到EC =FD ,从而可把OC ﹣OD 转化为FD ﹣OD ,再利用线段的和差可求得OC ﹣OD =OE +OF =8;【解析】解:(1)设直线AB 的解析式为:y =kx +b (k ≠0).∵点A (﹣4,4),点B (0,2)在直线AB 上,∴{−4k +b =4b =2,解得{k =−12b =2, ∴直线AB 的解析式为:y =−12x +2;(2)∵△ABM 是以AB 为直角边的直角三角形,∴有∠BAM =90°或∠ABM =90°,①当∠BAM =90°时,如图1,过A 作AB 的垂线,交x 轴于点M 1,交y 轴于点M 2,则可知△AEM 1∽△BEA ,∴M 1E AE =AE BE ,由(1)可知OE =OB =AE =4,∴M 1E 4=48,解得M 1E =2, ∴OM 1=2+4=6,∴M 1(﹣6,0),∵AE ∥y 轴,∴M 1EM 1O =AEOM 2,即26=4OM 2,解得OM 2=12,∴M 2(0,12);②当∠ABM =90°时,如图2,过B 作AB 的垂线,交y 轴于点M 3,设直线AB交y轴于点E,则由(1)可知E(0,2),∴OE=2,OB=4,由题意可知△BOE∽△M3OB,∴OEOB =OBOM3,即24=4OM3,解得OM3=8,∴M3(0,﹣8),综上可知点M的坐标为(﹣6,0)或(0,12)或(0,﹣8);(3)不变.理由如下:过点A分别作x轴、y轴的垂线,垂足分别为G、H,如图3.则∠AGC=∠AHD=90°,又∵∠HOC=90°,∴∠GAH=90°,∴∠DAG+∠DAH=90°,∵∠CAD=90°,∴∠DAG+∠CAG=90°,∴∠CAG=∠DAH.∵A (﹣4,4),∴OG =AH =AG =OH =4.在△AGC 和△AHD 中{∠AGC =∠AHD AG =AH ∠CAG =∠DAH∴△AGC ≌△AHD (ASA ),∴GC =HD .∴OC ﹣OD =(OG +GC )﹣(HD ﹣OH )=OG +OH =8.故OC ﹣OD 的值不发生变化,值为8.【点睛】本题为一次函数的综合应用,涉及知识点有待定系数法、全等三角形的判定和性质、相似三角形的判定和性质及分类讨论思想等.在(1)中注意待定系数法的应用步骤,在(2)中确定出M 点的位置是解题的关键,在(3)中构造三角形全等是解题的关键.本题考查知识点较多,综合性较强,难度适中.2.已知,如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求经过点E 、D 的直线解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G ,使得EF =2GO ,请求出此时OG 的长度.(3)对于(2)中的点G ,在直线ED 上是否存点P ,使得点P 与点D 、G 构成的△DPG 是直角三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【思路点拨】(1)只要证明△ADE ∽△BCD ,可得AD BC =AE DB ,求出AE 即可解决问题;(2)由△ADE ≌△RDG ,可得AF =RG ,设OG =m ,则AF =GR =2﹣m ,构建方程即可解决问题;(3)分两种情形①作GP ⊥BE 于P ,则△PDG 是直角三角形.②作P ′G ⊥DG 交直线DE 于P ′,则△DGP ′是直角三角形.分别根据一次函数利用方程组确定交点坐标即可;【解析】解:(1)如图1中,∵四边形ABCO 是矩形,∴∠OAB =∠B =90°,∵∠AOD =∠DOC =45°,∴OA =AD =2,DB =1,∵DE ⊥DC ,∴∠EDC =90°,∴∠ADE +∠BDC =90°,∵∠BDC +∠BCD =90°,∴∠ADE =∠DCB ,∴△ADE ∽△BCD ,∴AD BC =AE DB ,∴AE =1,∴E (0,1),设直线DE 的解析式为y =kx +b ,则有{b =12k +b =2, 解得{k =12b =1∴直线DE 的解析式为y =12x +1(2)如图2中,作DR ⊥OC 于R .易知△ADE≌△RDG,∴AF=RG,设OG=m,则AF=GR=2﹣m,∴EF=1+2﹣m=3﹣m,∵EF=2OG,∴3﹣m=2m,∴m=1,∴OG=1.(3)如图3中,①作GP⊥BE于P,则△PDG是直角三角形.∵G(1,0),GP⊥BE,∴直线PG的解析式为y=﹣2x+2,由{y =12x +1y =−2x +2,解得{x =25y =65, ∴P (25,65). ②作P ′G ⊥DG 交直线DE 于P ′,则△DGP ′是直角三角形,∵直线DG 的解析式为y =2x ﹣2,∴直线GP ′的解析式为y =−12x +12,由{y =−12x +12y =12x +1,解得{x =−12y =34, ∴P ′(−12,34), 综上所述,满足条件的点P 坐标为(25,65)或(−12,34). 【点睛】本题考查一次函数综合题、旋转变换、全等三角形的判定和性质.相似三角形的判定和性质、直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形和相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.考点二 等腰三角形存在性问题【方法点拨】分类讨论哪两条边相等,一般分三种情况,简称“两圆+一中垂线”1.如图1,在平面直角坐标系中,O 是坐标原点,长方形OACB 的顶点A 、B 分别在x 轴与y 轴上,已知OA =6,OB =10.点D 为y 轴上一点,其坐标为(0,2),点P 从点A 出发以每秒2个单位的速度沿线段AC ﹣CB 的方向运动,当点P 与点B 重合时停止运动,运动时间为t 秒.(1)当点P 经过点C 时,求直线DP 的函数解析式;(2)①求△OPD 的面积S 关于t 的函数解析式;②如图②,把长方形沿着OP 折叠,点B 的对应点B ′恰好落在AC 边上,求点P 的坐标.(3)点P 在运动过程中是否存在使△BDP 为等腰三角形?若存在,请求出点P 的坐标;若不存在,请说明理由.【思路点拨】(1)设直线DP 解析式为y =kx +b ,将D 与C 坐标代入求出k 与b 的值,即可确定出解析式;(2)①当P 在AC 段时,三角形ODP 底OD 与高为固定值,求出此时面积;当P 在BC 段时,底边OD 为固定值,表示出高,即可列出S 与t 的关系式;②当点B 的对应点B ′恰好落在AC 边上时,关键勾股定理即可求出此时P 坐标;(3)存在,分别以BD ,DP ,BP 为底边三种情况考虑,利用勾股定理及图形与坐标性质求出P 坐标即可.【解析】解:(1)∵OA =6,OB =10,四边形OACB 为长方形,∴C (6,10).设此时直线DP 解析式为y =kx +b ,把(0,2),C (6,10)分别代入,得{b =26k +b =10, 解得{k =43b =2则此时直线DP 解析式为y =43x +2;(2)①当点P 在线段AC 上时,OD =2,高为6,S =6;当点P 在线段BC 上时,OD =2,高为6+10﹣2t =16﹣2t ,S =12×2×(16﹣2t )=﹣2t +16;②设P (m ,10),则PB =PB ′=m ,如图2,∵OB ′=OB =10,OA =6,∴AB ′=√OB′2−OA 2=8,∴B ′C =10﹣8=2,∵PC =6﹣m ,∴m 2=22+(6﹣m )2,解得m =103 则此时点P 的坐标是(103,10);(3)存在,理由为: 若△BDP 为等腰三角形,分三种情况考虑:如图3,①当BD =BP 1=OB ﹣OD =10﹣2=8,在Rt △BCP 1中,BP 1=8,BC =6,根据勾股定理得:CP 1=√82−62=2√7,∴AP 1=10﹣2√7,即P 1(6,10﹣2√7);②当BP 2=DP 2时,此时P 2(6,6);③当DB =DP 3=8时,在Rt △DEP 3中,DE =6,根据勾股定理得:P 3E =√82−62=2√7,∴AP 3=AE +EP 3=2√7+2,即P 3(6,2√7+2),综上,满足题意的P 坐标为(6,6)或(6,2√7+2)或(6,10﹣2√7).【点睛】此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,坐标与图形性质,等腰三角形的性质,勾股定理,利用了分类讨论的思想,熟练掌握待定系数法是解本题第一问的关键.2.如图①,在平面直角坐标系中,△AOB的边OA在x轴上,点A坐标为(14,0),点B在第一象限,∠BAO=45°,AB=8√2.D为射线OB上一点,过D作直线l∥y轴交OA于E,交射线AB于G.(1)求B点坐标;(2)当D为线段OB中点时,在直线l上找点P,当△PBD为等腰三角形,请直接写出P点坐标;(3)如图②,F为AO中点,当S△BDF=2S△BDG时,求D点坐标.【思路点拨】(1)先求出BH=AH=8,进而求出OH=6,即可得出结论;(2)先设出点P坐标,进而表示出DP,BP,BD,再分三种情况讨论建立方程求解即可得出结论;(3)先求出OF,直线OB,AB的解析式,进而设出点D的坐标,表示出S△BDG=12|m﹣14|×|6﹣m|,S△BDF =|143m﹣28|,最后用面积关系建立方程求解即可得出结论.【解析】解:(1)如图①,过点B作BH⊥OA于H,∵∠BAO=45°,AB=8√2,∴BH=AH=1√2AB=8,∵A(14,0),∴OA=14,∴OH=OA﹣AH=6,∴B(6,8);(2)∵DE ⊥OA ,∴DE ∥BH ,∵点D 是OB 中点,∴DE =12BH =4,OE =12OH =3,∴D (3,4),设P (3,m ),∵B (6,8),∴DP =|m ﹣4|,BD =5,BP 2=(m ﹣8)2+9,∵△PBD 为等腰三角形,∴①DP =BD ,∴|m ﹣4|=5,∴m =9或m =﹣1,∴P (3,9)或(3,﹣1),②DP =BP ,∴(m ﹣4)2=(m ﹣8)2+9,∴m =578, ∴P (3,578)③BD =BP ,∴25=(m ﹣8)2+9,∴m =4(舍)或m =12,∴P (3,12),即:满足条件的点P (3,9)或(3,﹣1)或(3,578)或(3,12);(3)如图由(1)知,B (6,8),∴直线OB 的解析式为y =43x ,∵A (14,0),∴直线AB 的解析式为y =﹣x +14,∵点F 是OA 中点,∴OF =12OA =7,设点D (m ,43m ),∴G (m ,﹣m +14), ∴S △BDG =12|﹣m +14−43m |×|6﹣m |=12|m ﹣14|×|6﹣m |, S △BDF =|S △BOF ﹣S △DOF |=|12×7×8−12×7×43m |=|143m ﹣28|,∵S △BDF =2S △BDG ,∴|143m ﹣28|=212|m ﹣14|×|6﹣m |, ∴m =4或m =8, ∴D (4,163)或(8,323).【点睛】此题是三角形综合题,主要考查了勾股定理,等腰三角形的性质,三角形的面积公式,分类讨论的思想,解本题的关键是用方程的思想解决问题.考点三 等腰直角三角形存在性问题【方法点拨】分类讨论哪个角为直角且哪两条边相等1.正方形OABC 的边长为1,把它放在如图所示的直角坐标系中,点M (t ,0)是x 轴上一个动点(t ≥1),连接BM ,在BM 的右侧作正方形BMNP ;直线DE 的解析式为y =2x +b ,与x 轴交于点D ,与y 轴交于点E ,当△PDE 为等腰直角三角形时,点P 的坐标是 (2,4)或(2,1) .【思路点拨】过点P 作PF ⊥BC 交CB 的延长线于点F ,根据同角的余角相等可得∠ABM =∠FBP ,然后利用“角角边”证明△ABM 和△FBP 全等,根据全等三角形对应边相等可得BF =AB ,PF =AM ,然后根据正方形OABC 的边长为2以及点M (t ,0)表示出点P 的坐标,再利用直线DE 的解析式求出点D 、E 的坐标,然后分①DE 是斜边时,利用勾股定理以及两点间的距离公式分别表示出PD 、PE 、DE 的平方,再根据等腰直角三角形的三边关系,②PD 是斜边时,过点P 作PF ⊥y 轴于点F ,然后利用“角角边”证明△EDO 和△PEF 全等,根据全等三角形对应边相等可得EF =DO ,PC =EO ,然后用b 、t 表示并求解即可得到点P 的坐标.【解析】解:如图,过点P 作PF ⊥BC 交CB 的延长线于点F ,∵四边形OABC 与四边形BMNP 都是正方形,∴∠ABM +∠MBF =90°,∠FBP +∠MBF =90°,∴∠ABM =∠FBP ,在△ABM 和△FBP 中,{∠ABM =∠FBP∠BAM =∠F =90°BM =BP,∴△ABM ≌△FBP (AAS ),∴BF =AB ,PF =AM ,∵正方形OABC 的边长为1,点M (t ,0),∴BF =1,PF =t ﹣1,点P 到x 轴的距离为t ﹣1+1=t ,∴点P 的坐标为(2,t ),又∵当y =0时,2x +b =0,解得x =−b 2,当x =0时,y =b ,∴点D (−b 2,0),E (0,b ),①DE 是斜边时,PD 2=(b 2+2)2+t 2,PE 2=(b ﹣t )2+22,DE 2=(b 2)2+b 2, ∵△PDE 是等腰直角三角形,∴PD 2=PE 2,且PD 2+PE 2=DE 2,即(b 2+2)2+t 2=(b ﹣t )2+22,且(b 2+2)2+t 2+(b ﹣t )2+22=(b 2)2+b 2, 14b 2+2b +4+t 2=b 2﹣2bt +t 2+4,且14b 2+2b +4+t 2+b 2﹣2bt +t 2+4=14b 2+b 2, 整理得,b =83(t +1)且t 2﹣b (t ﹣1)+4=0,∴t 2−83(t +1)(t ﹣1)+4=0,整理得,t 2=4,解得t 1=2,t 2=﹣2(舍去),∴点P 的坐标是(2,2);②PD 是斜边时,∵△PDE 是等腰直角三角形,∴PE ⊥DE ,且PE =DE ,过点P 作PF ⊥y 轴于点F∵∠DEO +∠PEO =90°,∠DEO +∠EDO =90°,∴∠PEO =∠EDO ,在△EDO 和△PEF 中,{∠PEO =∠EDO ∠DOE =∠EFP =90°PE =DE,∴△EDO ≌△PEF (AAS ),∴EF =DO =b 2,PC =EO =b ,又∵点P (2,t ),∴b =2,b ﹣t =b 2,解得t=b2=12×2=1,∴点P坐标为(2,1),此时点C、F重合,点M、A重合,综上所述,点P的坐标为(2,4)或(2,1).故答案为:(2,2)或(2,1).【点睛】本题是一次函数的综合题型,主要利用了全等三角形的判定与性质,等腰三角形的性质,直线与坐标轴的交点的求解,勾股定理的应用,综合题但难度不大,要注意分情况讨论.2.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(a,﹣a),与y轴交于点B(0,b),其中a,b满足(a+2)2+√b−3=0.(1)求直线l2的解析式;(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;(3)已知平行于y轴且位于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.【思路点拨】(1)由偶次方及被开方数非负,可求出a 、b 的值,进而可得出点A 、B 的坐标,由点A 、B 的坐标,利用待定系数法即可求出直线l 2的解析式;(2)由△AOP 和△AOB 等底及S △AOP =S △AOB ,可得出点P 到AO 的距离与点B 到AO 的距离相等,分点P 在l 1的右侧及点P 在l 1的左侧两种情况考虑:①当点P 在l 1的右侧时,设点P 为P 1,则P 1B ∥l 1,根据平行线的性质结合点B 的坐标可得出直线P 1B 的解析式,再利用一次函数图象上点的坐标特征可求出点P 1的坐标;②当点P 在l 1的左侧时,设点P 为P 2,设直线y =5与直线l 1交于点E ,利用一次函数图象上点的坐标特征可求出点E 的坐标,再由点E 为P 1P 2中点,可求出点P 2的坐标;(3)设动直线为x =t ,由题可得﹣2<t <0,则点M 的坐标为(t ,﹣t ),点N 的坐标为(t ,12t +3),进而可得出MN 的长度.分∠NMQ =90°、∠MNQ =90°及∠MQN =90°三种情况,利用等腰直角三角形的性质可求出点M 、N 、Q 的坐标,此题得解.【解析】解:(1)∵a 、b 满足(a +2)2+√b −3=0,∴a +2=0,b ﹣3=0,∴a =﹣2,b =3,∴点A 的坐标为(﹣2,2),点B 的坐标为(0,3).设直线l 2的解析式为y =kx +c (k ≠0),将A (﹣2,2)、B (0,3)代入y =kx +c ,得:{−2k +c =2c =3,解得:{k =12c =3, ∴直线l 2的解析式为y =12x +3.(2)∵S △AOP =S △AOB ,∴点P 到AO 的距离与点B 到AO 的距离相等,且点P 位于l 1两侧(如图1).①当点P 在l 1的右侧时,设点P 为P 1,则P 1B ∥l 1,∴直线P 1B 的解析式为:y =﹣x +3,当y =5时,有﹣x +3=5,解得:x =﹣2,∴点P 1的坐标为(﹣2,5);②当点P 在l 1的左侧时,设点P 为P 2,设直线y =5与直线l 1交于点E ,则点E 的坐标为(﹣5,5),∵点E 为P 1P 2中点,∴点P 2的坐标为(﹣8,5).综上所述:点P 的坐标为(﹣2,5)或(﹣8,5).(3)设动直线为x =t ,由题可得﹣2<t <0,则点M 的坐标为(t ,﹣t ),点N 的坐标为(t ,12t +3), ∴MN =32t +3(如图2).①当∠NMQ =90°时,有MN =MQ ,即32t +3=﹣t , 解得:t =−65,∴点M 的坐标为(−65,65). ∵MQ ∥x 轴,∴点Q 的坐标为(0,65); ②当∠MNQ =90°时,有MN =NQ ,即32t +3=﹣t , 解得:t =−65,∴点N 的坐标为(−65,125). ∵NQ ∥x 轴,∴点Q 的坐标为(0,125);③当∠MQN =90°时,点Q 到MN 的距离=12MN ,即﹣t =12×(32t +3),解得:t =−67,∴点M 的坐标为(−67,67),点N 的坐标为(−67,187).∵△MNQ 为等腰直角三角形,∴点Q 的坐标为(0,127).综上所述:点Q 的坐标为(0,65)或(0,125)或(0,127).【点睛】本题考查了待定系数法求一次函数解析式、偶次方及被开方数的非负性、三角形的面积、一次函数图象上点的坐标特征以及等腰直角三角形,解题的关键是:(1)根据点的坐标,利用待定系数法求出一次函数解析式;(2)分点P 在l 1的右侧及点P 在l 1的左侧两种情况求出点P 的坐标;(3)分∠NMQ =90°、∠MNQ =90°及∠MQN =90°三种情况,利用等腰直角三角形的性质求出点Q 的坐标.3.在平面直角坐标系xOy 中,直线l 1:y =k 1x +2√3与x 轴、y 轴分别交于点A 、B 两点,OA =√3OB ,直线l 2:y =k 2x +b 经过点C (1,−√3),与x 轴、y 轴和线段AB 分别交于点E 、F 、D 三点.(1)求直线l 1的解析式;(2)如图①:若EC =ED ,求点D 的坐标和△BFD 的面积;(3)如图②:在坐标轴上是否存在点P ,使△PCD 是以CD 为底边的等腰直角三角形,若存在,请直接写出点P 的坐标;若不存在,请说明理由.【思路点拨】(1)求出点A的坐标,利用待定系数法即可解决问题;(2)如图1中,作CM⊥OA于M,DN⊥CA于N.由△CME≌△DNE(AAS),推出CM=DN由C(1,−√3),可得CM=DN=√3,再利用待定系数法即可解决问题;(3)分点P在y轴或x轴两种情形分别求解即可解决问题;【解析】解:(1)∵直线y=k1x+2√3与y轴B点,∴B(0,2√3),∴OB=2√3,∵OA=√3OB=6,∴A(6,0),把A(6,0)代入y=k1x+2√3得到,k1=−√33,∴直线l1的解析式为y=−√33x+2√3.(2)如图1中,作CM⊥OA于M,DN⊥CA于N.∵∠CME=∠DNE=90°,∠MEC=∠NED,EC=DE,∴△CME≌△DNE(AAS),∴CM=DN∵C (1,−√3),∴CM =DN =√3,当y =√3时,√3=−√33x +2√3, 解得x =3,∴D (3,√3),把C (1,−√3),D (3,√3)代入y =k 2x +b ,得到{k 2+b =−√33k 2+b =√3, 解得{k 2=√3b =−2√3, ∴直线CD 的解析式为y =√3x ﹣2√3,∴F (0,﹣2√3),∴S △BFD =12×4√3×3=6√3.(3)①如图③﹣1中,当PC =PD ,∠CPD =90°时,作DM ⊥OB 于M ,CN ⊥y 轴于N .设P (0,m ).∵∠DMP =∠CNP =∠CPD =90°,∴∠CPN +∠PCN =90°,∠CPN +∠DPM =90°,∴∠PCN =∠DPM ,∵PD =PC ,∴△DMP ≌△NPC (AAS ),∴CN =PM =1,PN =DM =m +√3,∴D (m +√3,m +1),把D 点坐标代入y =−√33x +2√3,得到:m +1=−√33(m +√3)+2√3,解得m =4√3−6,∴P (0,4√3−6).②如图③﹣2中,当PC=PC,∠CPD=90时,作DM⊥OA于M,CN⊥OA于N.设P(n,0).同法可证:△DMP≌△PNC,∴PM=CN=√3,DM=PN=n﹣1,∴D(n−√3,n﹣1),把D点坐标代入y=−√33x+2√3,得到:n﹣1=−√33(n−√3)+2√3,解得n=2√3∴P(2√3,0).综上所述,满足条件的点P坐标为(0,4√3−6)或(2√3,0)【点睛】本题属于一次函数综合题,考查了待定系数法,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数解决问题,属于中考压轴题.4.如图1,在平面直角坐标系中,A(a,0),B(0,b),且a,b满足b=√a2−4+√4−a2+16a+2(1)求直线AB的解析式;(2)第一象限内是否存在一点M,使△ABM是等腰直角三角形,若存在,求出点M的坐标;若不存在,请说明理由;(3)如图2过点A的直线y=kx﹣2k交y轴负半轴于点P,N点的横坐标为﹣1,过点N的直线y=k2x−k2交AP于点M,交x轴于点C,求证:NC=MC.【思路点拨】(1)由二次根式的被开方数是非负数可以求得a 、b 的值.则易求点A 、B 的坐标.设直线AB 的方程为y =kx +b (k ≠0),将其分别代入该解析式列出关于k 、b 的方程组,通过解方程组即可求得它们的值;(2)需要分类讨论:当AB 为底和当AB 为腰时,分别求得点M 的坐标;(3)将y =kx ﹣2k 与y =k 2x −k 2联立求出M 的坐标为(3,k ),由条件可求得N 的坐标为(﹣1,﹣k ),C 的坐标为(1,0),作CG ⊥x 轴于G 点,MH ⊥x 轴于H 点,可证△NGC ≌△MHC ,得NC =MC .【解析】解:(1)依题意,得:{a 2−4≥04−a 2≥0a +2≠0,解得a =2;则b =4.所以A (2,0),B (0,4),设直线AB 解析式为y =kx +b (k ≠0),将A 与B 坐标代入得:{2k +b =0b =4, 解得:{k =−2b =4, 则直线AB 的解析式为y =﹣2x +4;(2)如图1,分三种情况:①如图1,当BM ⊥BA ,且BM =BA 时,过M 作MN ⊥y 轴于N ,∵BM ⊥BA ,MN ⊥y 轴,OB ⊥OA ,∴∠MBA =∠MNB =∠BOA =90°,∴∠NBM +∠NMB =90°,∠ABO +∠NBM =90°,∴∠ABO =∠NMB ,在△BMN 和△ABO 中{∠MNB =∠BOA ∠NMB =∠ABO BM =AB,∴△BMN ≌△ABO (AAS ),MN =OB =4,BN =OA =2,∴ON =2+4=6,∴M 的坐标为(4,6 );②如图2当AM ⊥BA ,且AM =BA 时,过M 作MN ⊥x 轴于N ,△BOA ≌△ANM (AAS ),同理求出M 的坐标为(6,2);③如图4,当AM⊥BM,且AM=BM时,过M作MN⊥X轴于N,MH⊥Y轴于H,则△BHM≌△AMN,∴MN=MH,设M(x,x),由勾股定理得,(x﹣2)2+x2=(4﹣x)2+x2,解得,x=3;∴M点的坐标为(3,3)综上所知M点的坐标为(4,6)(6,2)(3,3);(3)将y=kx﹣2k与y=k2x−k2联立求出M的坐标为(3,k),由条件可求得N的坐标为(﹣1,﹣k),C的坐标为(1,0),作CG⊥x轴于G点,MH⊥x轴于H点,可证△NGC≌△MHC,得NC=MC.【点睛】本题主要考查对一次函数图象上点的坐标特征,等腰直角三角形性质,用待定系数法求正比例函数的解析式,全等三角形的性质和判定,二次根式的性质等知识点的理解和掌握,综合运用这些性质进行推理和计算是解此题的关键.。
中考数学“特殊四边形的存在性问题”题型解析

中考数学“特殊四边形的存在性问题”题型解析由抛物线上的点构成特殊四边形的问题,需要根据特殊四边形的性质与判定去确定点的坐标,然后求解 . 具体而言,解该类题时,我们要根据题目中的条件,科学地进行分类,然后画出图形,再根据这个四边形的性质或判定求出这点的坐标,若这一点是根据特殊四边形的特性得到的坐标,我们还应将这一点代入到抛物线的解析式中去验证是否是抛物线上的点 .本节主要来讨论下特殊四边形:平行四边形、菱形、矩形的存在性问题 .类型一:平行四边形问题【例题1】如图,抛物线y = 1/2 x^2 + bx + c 经过点A(-1,0)和点B(3,0),同时交y 轴于点C .(1)求抛物线的解析式;(2)若点Q 在y 轴上,点P 在抛物线上,且以A , B , Q , P 为顶点的四边形是平行四边形,求满足条件的点P 的坐标 .【分析】(1)根据抛物线经过A , B 两点即可求得b , c 的值,可解题;(2)以A , B , Q , P 为顶点的四边形是平行四边形,则点P 横坐标为4 或- 4,将x = 4 或- 4 代入抛物线解析式即可求得y 的值,即可解题 .【解析】(1)把A(-1,0),B(3,0)代入y = 1/2 x^2 + bx + c 中,∴抛物线的解析式是y = 1/2 x^2 - x - 3/2 .(2)①当AB 为边时,只要PQ∥AB 且PQ = AB = 4 即可 .又知点Q 在y 轴上,∴点P 的横坐标为4 或- 4 ,这时符合条件的点P 有两个,分别记为P1 , P2,把x = 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 5/2 ,把x = - 4 代入y = 1/2 x^2 - x - 3/2 ,得y = 21/2 ,此时P1(4 , 5/2),P2(- 4 , 21/2);②当AB 为对角线时,只要线段PQ 与线段AB 互相平分即可 .又知点Q 在y 轴上,且线段AB 中点的横坐标为1,∴点P 的横坐标为2,这时符合条件的P 只有一个记为P3 ,而且当x = 2 时,y = - 3/2 ,此时P3(2,- 3/2),综上,满足条件的P 为P1(4 , 5/2),P2(- 4 , 21/2),P3(2,-3/2).类型二:菱形问题【例题2】如图,在平面直角坐标系中,点O 为坐标原点,直线y = -x + b 与坐标轴交于C,D 两点,直线AB 与坐标轴交于A , B 两点,线段OA , OC 的长是方程x^2 - 3x + 2 = 0 的两个根(OA > OC).(1)求点A , C 的坐标;(2)直线AB 与直线CD 交于点E,若点E 是线段AB 的中点,反比例函数y = k/x (k ≠0 )的图象的一个分支经过点E,求k 的值;(3)在(2)的条件下,点M 在直线CD 上,坐标平面内是否存在点N,使以点B , E , M , N 为顶点的四边形是菱形?若存在,请直接写出满足条件的点N 的坐标;若不存在,请说明理由 .【分析】(1)利用分解因式法解一元二次方程x^2 - 3x + 2 = 0 即可得出OA , OC 的值,再根据点所在的位置即可得出A , C 的坐标;(2)根据点C 的坐标利用待定系数法即可求出直线CD 的解析式,根据点A , B 的横坐标结合点E 为线段AB 的中点即可得出点E 的横坐标,将其代入直线CD 的解析式中即可求出点E 的坐标,再利用待定系数法即可求出k 的值;(3)假设存在,设点M 的坐标为(m , - m + 1), 分别以BE 为边、BE 为对角线来考虑 .根据菱形的性质找出关于m 的方程,解方程即可得出点M 的坐标,再结合点B , E 的坐标即可得出点N 的坐标 .【解析】(1)x^2 - 3x + 2 = (x - 1)(x - 2)= 0 ,∴x1 = 1 , x2 = 2 ,∵OA > OC ,∴OA = 2 , OC = 1 ,∴A(-2,0),C(1,0);(2)将C(1,0)代入y = - x + b 中,得0 = - 1 + b , 解得b = 1 ,∴直线CD 的解析式为y = - x + 1 .∵点E 为线段AB 的中点,A(-2,0),B 的横坐标为0 ,∴点E 的横坐标为- 1 .∵点E 为直线CD 上一点,∴E(-1,2).将点E(-1,2)代入y = k/x (k ≠0 )中,得2 = k / -1 , 解得k = -2 ;(3)假设存在,设点M 的坐标为(m , - m + 1),以点B , E , M , N 为顶点的四边形是菱形分两种情况(如上图所示)类型三:矩形问题【例题3】【解题策略】这三道例题分别呈现了运动变化过程中的平行四边形、菱形、矩形的存在性问题,三道例题的思路都是要依据特殊四边形的性质构图并建立方程求点的坐标 .特别地,由于菱形任意三个顶点组成的三角形都是等腰三角形,因此可将菱形问题转化为等腰三角形的存在性问题;而矩形问题则可转化为直角三角形的问题,要注意体会相关知识之间的联系 .。
一次函数与四边形存在性问题

一次函数与四边形存在性【学习目标】1.熟练运用一次函数解决特殊四边形存在问题;2.体会数形结合的思想方法;体会一次函数与几何图形的内在联系.平行四边形问题:(注意点的顺序)1.给三点,先连接三点构成三角形;然后以每边为对角线构造平行四边形;以中点公式或者平移法求点坐标。
2.给两点,分为边和对角线讨论,充分利用平行四边形对边平行且相等,对角线平分两个全等三角形来做。
1.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为.(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为.(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.2.已知点A、B、C、D可以构成平行四边形,且点A(-1,0),点B(0,3),点C(3,0),则第四个顶点D的坐标为_________________________;xy BCA O举一反三:1.如图,在平面直角坐标系xOy 中,直线交y 轴于点A ,交x 轴于点B ,以线段AB 为边作菱形ABCD (点C 、D 在第一象限),且点D 的纵坐标为9. (1)求点A 、点B 的坐标; (2)求直线DC 的解析式;(3)除点C 外,在平面直角坐标系xOy 中是否还存在点P ,使点A 、B 、D 、P 组成的四边形是平行四边形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系中,函数122+=x y 的图像分别交x 轴、y 轴于A 、B 两点.过点A 的直线交y 轴正半轴于点C ,且点C 为线段OB 的中点. (1)求直线AC 的表达式;(2)如果四边形ACPB 是平行四边形,求点P 的坐标.3. 如图10,直线102+-=x y 与x 轴交于点A ,又B 是该直线上一点,满足OA OB =, (1)求点B 的坐标;(2)若C 是直线上另外一点,满足AB=BC ,且四边形OBCD 是平行四边形,试画出符合要求的大致图形,并求出点D 的坐标.4.已知:如图,平面直角坐标系中有一个等腰梯形ABCD ,且AD ∥BC ,AB=CD ,点A 在y 轴正半轴上,点B 、C 在x 轴上(点B 在点C 的左侧),点D 在第一象限,AD=3,BC=11,梯形的高为2,双曲线y=经过点D ,直线y=kx +b 经过A 、B 两点.O BA x yD(1)求点A、B、C、D的坐标;(2)求双曲线y=和直线y=kx+b的解析式;(3)点M在双曲线上,点N在y轴上,如果四边形ABMN是平行四边形,求点N的坐标.5.如图1,在平面直角坐标系中,点A的坐标为(﹣4,4),点B的坐标为(0,2).(1)求直线AB的解析式;(2)以点A为直角顶点作∠CAD=90°,射线AC交x轴的负半轴于点C,射线AD交y轴的负半轴于点D.当∠CAD绕着点A旋转时,OC﹣OD的值是否发生变化?若不变,求出它的值;若变化,求出它的变化范围;(3)如图2,点M(﹣4,0)是x轴上的一个点,点P是坐标平面内一点.若A、B、M、P四点能构成平行四边形,请写出满足条件的所有点P的坐标(不要解题过程).菱形问题:(注意点的顺序)一般给两点,一动点在某直线上,另一点在平面直角坐标系中。
一次函数与平行四边形存在性问题

一次函数与平行四边形存在性问题1.坐标系中的平行四边形:(1)对边平行且相等2. 线段中点坐标公式平面直角坐标系中,点A坐标为(x1,y1),点B坐标为(x2,y2),则线段AB的中点坐标为(221xx+,221yy+).2.1平行四边形顶点坐标公式□ABCD的顶点坐标分别为A(x A,y A)、B(x B,y B)、C(x C,y C)、D(x D,y D),则:x A+x C=x B+x D;y A+y C=y B+y D.证明:如图2,连接AC、BD,相交于点E.∵点E为AC的中点,∴E点坐标为(2CA xx+,2CA yy+).又∵点E为BD的中点,∴E点坐标为(2DB xx+,2DB yy+).∴x A+x C=x B+x D;y A+y C=y B+y D.即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.以上两条可统一为:总结:平面直角坐标系中,平行四边形两组相对顶点的横坐标之和相等,纵坐标之和相等方法归纳:1、列出四个点坐标2、分三组对角线讨论列方程组,解方程组3、验证点是否符合题意如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(m﹣6)2+=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处(1)求线段OD的长;(2)求点E的坐标;(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐标.如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B 的坐标分别A(32-,0)、B(32-,2),∠CAO=30°.(1)求对角线AC所在的直线的函数表达式;(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.如图1,在平面直角坐标系中,直线l1:y=x+1与y轴交于点A,过B(6,1)的直线l2与直线l1交于点C(m,﹣5).(1)求直线l2的解析式;(2)若点D是第一象限位于直线l2上的一动点,过点D作DH∥y轴交l1于点H.当DH=8时,试在x轴上找一点E,在直线l1上找一点F,使得△DEF的周长最小,求出周长的最小值;(3)如图2,将直线l2绕点A逆时针旋转90°得到直线l3,点P是直线l3上一点,到y轴的距离为2且位于第一象限.直线l2与x轴交于点M,与y轴交于点N,将△OMN沿射线NM方向平移2个单位,平移后的△OMN记为△O'M'N'.在平面内是否存在一点Q,使得以点M′,C,P,Q顶点的四边形是平行四边形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.如图1,在平面直角坐标系xOy中,直线l2:y=﹣x+与x轴交于点B,与直线l1:y=x+b交于点C,C 点到x轴的距离CD为2,直线l1交x轴于点A.(1)求直线l1的函数表达式;(2)如图2,y轴上的两个动点E、F(E点在F点上方)满足线段EF的长为,连接CE、AF,当线段CE+EF+AF 有最小值时,求出此时点F的坐标以及CE+EF+AF的最小值;(3)如图3,将△ACB绕点B逆时针方向旋转60°,得到△BGH,使点A与点H对应,点C与点G对应,将△BGH沿着直线BC平移,平移后的三角形为△B′G′H′,点M为直线AC上的动点,是否存在分别以C、O、M、G′为顶点的平行四边形,若存在,请求出M的坐标;若不存在,说明理.。
专题04 一次函数中的特殊平行四边形存在性问题(解析版)

专题04一次函数中的特殊平行四边形存在性问题类型一、菱形问题(1)如图1,请直接写出点A 的坐标,并求出直线AB 的解析式.(2)如图2,直线2y x b =+是线段AB 的垂直平分线,垂足为点D ,且交y 轴于点C ,连接BC 线CD 上的一动点,当点P 使得32ACP ACD S S =△△时,请求出符合条件的点P 坐标.(3)在(2)的条件下,若点P 在直线CD 上且在第三象限内,在平面内是否存在其它点Q ,使得以点P 、Q 为顶点的四边形是菱形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)()0,2A ,122y x =-+(2)()3,3或者()3,9--(1)求A C 、两点坐标;(2)若点M 是直线CB 上一点,且(3)点P 是y 轴上的点,在坐标平面内是否存在点直接写出点Q 坐标,若不存在,请说明理由.【答案】(1)(1,0)A ,(3,0)C -∵(1,0),(0,3),(3,0),,A B C M m ⎛- ⎝∴1(3)4AC =--=,3OB =,MD ∴23ABC S = ,12ACM S AC MD = △∴(,3)F m ,BF m =,33MF =∵90ABC ∠=︒,∴90ABM ∠=︒,即ABM 是直角三角形,∴AB BP PQ AQ ===∴()1,2Q ;②如图所示,以AP 为对角线,四边形同理,AB BP PQ ==∴()1,2Q -;③如图所示,以AB 为对角线,四边形在Rt AOB △中,OA =∴根据菱形的性质可知,∵30ABO ∠=︒,∴30PAH QAH ∠=∠=∴AB BQ QP AP ====∴(0,3),(1,0)P Q --;综上所述,点P 是y 轴上的点,坐标平面内存在点为()1,2或()1,2-或21,⎛ ⎝∴存在,点Q 坐标为(1,(1)如图1,求点E 坐标和直线CE 的解析式;(2)点P 为x 轴正半轴上的动点,设OP t =.①如图2,当点P 在线段OA (不包含端点A ,O )上运动时,过点P 作直线l ∥y 的线段长为d .求d 关于t 的函数关系式,并直接写出自变量t 的取值范围;∵OP t=,∴31,6,,43 G t t H t t ⎛⎫⎛-+-+ ⎪⎝⎭⎝∴136634d t t⎛⎫=-+--+=⎪⎝⎭②当CE 为对角线时,如图,∵四边形CPEG 是菱形,∴设CP PE n ==,则OP =在直角三角形O C P 中,根据勾股定理可得当CE 为边时,如图,∵四边形CEPG 是菱形,∴∵CG PE ∥,∴(10,6G 综上,点G 的坐标是25⎛【点睛】本题考查了矩形的性质、菱形的性质、勾股定理、折叠的性质、待定系数法求一次函数的解析式等知识,具有较强的综合性,熟练掌握相关图形的性质、熟练掌握待定系数法求一次函数的解析式、灵活应用数形结合思想是解题的关键.类型二、矩形存在性问题(1)求直线BD的表达式;(2)求OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【答案】(1)2833 y x =+(2)64 21(3)存在,N点坐标为208,93⎛⎫-⎪⎝⎭或104,3⎛⎫--⎪⎝⎭或84,3⎛⎫⎪⎝⎭【分析】(1)根据旋转的性质求出D点坐标,根据矩形的性质求出B 析式即可;(2)分别求出80,,(4,2)3F E⎛⎫⎪⎝⎭,先确定直线OE的解析式,从而求出∵MF FD FO MD ⊥⊥,,∴90MFD ∠=°,FOM DOF ∠=∠(1)求A,B,C三点的坐标;(2)点D是折线B A C--上一动点.①如图(1),当点D是线段AB的中点时,在y轴上找一点E,使ED EB+最小;用直尺和圆规画出点位置(保留作图痕迹,不要求写作法和证明),并求出点E的坐标;点D 是AB 的中点,(0,6)A ,(6,0)B ,(3,3)D \,6,90OA OB AOB ==∠=︒ ,AOB ∴ 为等腰直角三角形,即BAO ∠=∠在BOF 与AOC 中,FBO CAO ∠=∠⎧类型三、正方形存在性问题(1)求点A ,点B 的坐标;(2)若AOC BCP S S =△△,求点P 的坐标;(3)若点E 是直线54y x =上的一个动点,在平面内是否存在点F ,使四边形APEF 点E 的坐标;若不存在,请说明理由.99⎝⎭②当点P 在点E 的右侧时,如图同理可得AMP PNE ≌△△,∴6NE PM ==,NP AM =,即65684m n m n +=⎧⎪⎨-=-⎪⎩解得:16m =,5204m =,【点睛】本题考查了一次函数综合问题,一次函数与坐标轴交点问题,正方形的性质,三角形面积问题,坐标与图形,熟练掌握一次函数的性质,数形结合是解题的关键.例2.如图,在平面直角坐标系中,直线(0k ≠)交于点P ,4OC OD OA ==(1)求直线CD 的解析式;(2)连接OP 、BC ,若直线AB 上存在一点Q ,使得(3)将直线CD 向下平移1个单位长度得到直线,直线角坐标系中,是否存在点M ,使以点O ,E ,N ,M 标;若不存在,请说明理由.【答案】(1)4y x =-+;∵3AC=,点P的坐标为∴12PQC P S AC y=⨯+△∴点N 的坐标为(0,3),∴点M 的坐标为(3,3);当3OE =作为矩形OEMN ∴点F 的坐标为3(,0)2,∵tan 11OEN ∠=-=,∴45OEN ∠=︒,∵ON NE ⊥,∴ONE ∆是等腰直角三角形,(1)求直线l 的解析式;(2)求证:ABC 是等腰直角三角形;(3)将直线l 沿y 轴负方向平移,当平移恰当的距离时,直线与存在点P ,使得A B P ''△是等腰直角三角形,请直接写出所有符合条件的点【答案】(1)142y x =-+∴90DPE A PB ''∠=∠=︒,∴A PD B PE ''∠=∠,∵90A FP CEB ''∠=∠=︒,∴A FP CEB '' ≌,∴4,PE PF A F B E ''===,此时点P 的坐标为()44--,;同理此时点P 的坐标为()44-,;如图,若以点B '为直角顶点时,过点P 作同理A OB B GP ''' ≌,∴44OB PG OF t '====+,B '∴8t =-或0(舍去),∴8B G OA ''==,∴12OG =,∴此时点P 的坐标为()412--,;如图,若以点B '为直角顶点时,过点同理PB M A B O ''' ≌,∴44B M B O t ''===+,82PM OA t '==+,∴0=t (舍去);如图,若以点A '为直角顶点时,同理A PF B A O ''' ≌,∴,PF A O B O A F '''==,∴4482t t --=---,解得:8t =-,∴8PF =,此时点P 的坐标为()48-,;如图,若以点A '为直角顶点时,同理A PF B A O ''' ≌,(1)求直线1l的解析式;(2)设2P m(,),求ABP的面积S (3)当ABP的面积为3时,则以点【答案】(1)114y x =-+(2)当12m>时,21S m=-;当m90CBF PBE CFB PEB BC BP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩,∴CBF PBE AAS ≌().∴2BF CF PE EB ====.∴426OF OB BF =+=+=.∴62C (,);如图3,PBC 是等腰直角三角形,∴PE CE =,∴22C (,-),∴以点B 为直角顶点作等腰直角BPC △,点C 的坐标是62(,)或22(,-).当123m -=时,1m =-,可得21P (,-),同法可得32C (,)或52-(,).综上所述,满足条件的点C 坐标为62(,)或22(,-)或(3,2)或52(,-).【点睛】本题考查一次函数与几何的综合应用,同时考查了等腰三角形的性质,全等三角形的判定和性质.正确的求出函数解析式,利用数形结合和分类讨论的思想,进行求解,是解题的关键.2.如图1,在平面直角坐标系中,△ABO 为直角三角形,∠ABO =90°,∠AOB =30°,OB =3,点C 为OB 上一动点.∵将△OAB绕点O顺时针旋转,∴BO=B'O=3,∠AOB=∠A'OB'=30°,∵将△OAB绕点O顺时针旋转,∴∠BOB'=∠AOA'=90°,OB=OB'=3,∴点B'在y轴上,∴点B'(0,-3),如图,由中心对称的性质可得:点B'的坐标综上所述:点B '的坐标()03-,或332⎛- ⎝,【点睛】本题考查了含30度角的直角三角形的性质,旋转的性质,一次函数的性质等知识,中心对称的性质,利用分类讨论思想解决问题是解题的关键..如图,在平面直角坐标系中,直线y =与直线CD 交于点(),3A m .(1)求直线AB 的解析式;(2)点E 是射线CD 上一动点,过点E 作EF y ∥轴,交直线平行四边形,请求出点E 的坐标;(3)设P 是射线CD 上一点,在平面内是否存在点Q ,使以直接写出点Q 的坐标;若不存在,请说明理由.∵()0,3B -,()0,6C ∴直线PQ 的解析式是直线32y =,M 令362y x =-+=,解得92x =,∴点P 的坐标是93,22⎛⎫ ⎪⎝⎭,设点P 的坐标是(,6b b -+∵BC BP =,即()20b -解得:9b =或0b =(此时点∴点P 的坐标是()9,3-∴9PQ BC ==,设点P 的坐标是(,b b -+解得:922b =或b =-又∵9PQ =,∴点Q 的坐标是综上所述:点Q 的坐标为:【点睛】本题考查待定系数法求直线的解析式,一次函数的图象与性质,平行四边形的性质,菱形的性质,(2)迁移应用:如图2,将一块等腰直角的三角板(3)拓展应用:如图3,在平面直角坐标系内,已知直线【答案】(1)见解析;(2)点【详解】(1)证明:∵90ACB ∠=︒,AD l ⊥,∴90ACB ADC ∠=∠=︒,∵ACE ADC CAD ∠=∠+∠,ACE ACB BCE ∠=∠+∠,∴CAD BCE ∠=∠,∵90ADC CEB ∠=∠=︒,AC BC =,∴()AAS ACD CBE ≌ ,∴AD CE =,CD BE =;(2)解:如图2,过点F 作FM y ⊥轴,垂足为M ,过点G 作GN x ⊥轴于点N ,交MF 的延长线于J ,∵()3,1G -,∴3ON =,1GN =,由已知可得OG GF =,且90OGF ∠=︒,∵FM y ⊥轴,GN x ⊥轴,∴90JMO MON JNO ∠=∠=∠=︒,∴四边形JMON 是矩形,∴90ONG FJG ∠=∠=︒,JM ON =,∴90FGJ OGN OGN GON ∠+∠=∠+∠=︒,∴FGJ GON ∠=∠,∵OG GF =,90ONG FJG ∠=∠=︒,∴()AAS GJF ONG ≌ ,∴3GJ ON ==,1JF GN ==,∴3JM ON ==,过点3P 作3P E x ⊥轴于点E ,由(1)知3P EN NOM ≌ ,∴33P E ON ==,1NE OM ==,∴314OE =+=,∴()343P ,,同理可得()42,3P -.综上所述点P 的坐标为()34,或()32-,或()41,或(()2,1--).【点睛】本题主要考查了一次函数的应用,正方形的判定和性质,矩形的判定和性质,三角形全等的判定和性质,余角的性质,解题的关键是作出辅助线构造全等三角形,熟练掌握全等三角形的判定方法.5.如图,在平面直角坐标系中,一次函数(0)y kx b b =+≠的图象经过(1,0)A -,(0,2)B ,D 三点,点D 在x 轴上方,点C 在x 轴正半轴上,且5OC OA =,连接,BC CD ,已知2ADC ABC S S =△△.(1)求直线AB 的表达式;(2)求点D 的坐标;(3)在线段AD CD ,上分别取点M ,N ,使得MN x ∥轴,在x 轴上取一点P ,连接MN NP MP ,,,是否存(1)求直线1l 的函数表达式;(2)在平面直角坐标系中有一点()5,P m ,使得S (3)点M 为直线1l 上的动点,过点M 作y 轴的平行线,交直角三角形,请直接写出满足条件的点M 的坐标.【答案】(1)26y x =-+;(2)点P 坐标为()5,2或()5,8;则||M MN x t ==,∴36t t -=,∴32t =或3t =,∴332,M ⎛⎫ ⎪⎝⎭或()3,0M ,综上所述,点M 的坐标为618,55⎛⎫ ⎪⎝⎭或()6,6-或⎛ ⎝。
【教学设计】八下数学专题复习--以一次函数为载体的平行四边形的存在性问题
1八下数学专题复习--以一次函数为载体的平行四边形的存在性问题一、教学目标 1. 知识目标:探索以一次函数为载体的平行四边形的存在性问题,并能熟练应用。
2. 能力目标:经历探索以一次函数为载体的平行四边形的存在性问题,提高学生对问题的探究能力和对知识的综合应用能力。
3. 情感目标:在探究中发展学生的探究意识和合作交流的习惯,感受平行四边形与三角形知识的密切联系,体会数学的数形结合思想、分类思想和转化思想。
二、教学重难点1. 重点:找三定一动类型的动点位置。
2. 难点:求三定一动类型的动点坐标。
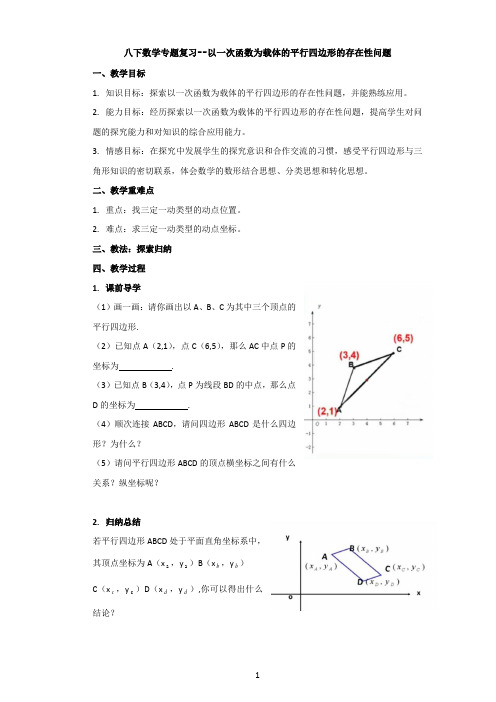
三、教法:探索归纳四、教学过程1. 课前导学(1)画一画:请你画出以A 、B 、C 为其中三个顶点的平行四边形.(2)已知点A (2,1),点C (6,5),那么AC 中点P 的坐标为 .(3)已知点B (3,4),点P 为线段BD 的中点,那么点D 的坐标为 .(4)顺次连接ABCD ,请问四边形ABCD 是什么四边形?为什么?(5)请问平行四边形ABCD 的顶点横坐标之间有什么关系?纵坐标呢?2. 归纳总结若平行四边形ABCD 处于平面直角坐标系中,其顶点坐标为A (x a ,y a )B (x b ,y b )C (x c ,y c )D (x d ,y d ),你可以得出什么结论?2 3. 例题讲解已知A 、B 、C 三点的坐标分别为(3,7),(1,2),(6,4),求点D 的坐标使四边形ABCD 成为平行四边形。
4. 变式训练已知A 、B 、C 三点的坐标分别为(3,7),(1,2),(6,4),求点D 的坐标使以A 、B 、C 、D 为顶点的四边形成为成为平行四边形。
5. 比较总结例题和变式在解题中有什么区别?6. 进阶训练如图,若点A (2,1),B (5,1),C 在过点A 的直线y=2x-3上,且以A 、B 、C 为其中三个顶点的平行四边形的面积为6.求平行四边形顶点D 的坐标.7. 拓展提升在平面直角坐标系中,点A (2,1),B (5,1),点C 在直线y=2x-3上运动,问:在直线y=0.5x 上是否存在一点D ,使得以A 、B 、C 、D 为顶点的四边形是平行四边形?若存在,求出点D 的坐标;若不存在,请说明理由.五、板书设计八下数学专题复习--以一次函数为载体的平行四边形的存在性问题 找①类型:三定一动、两定两动②分类标准:对角线↓求①中点坐标法②平移法③全等法六、教学反思。
一次函数平行四边形存在性

1平行四边形存在性Ø知识点睛1.存在性问题处理框架:①研究背景图形.②根据不变特征,确定分类标准.③分析特殊状态的形成因素,画出符合题意的图形并求解.④结果验证.2.平行四边形存在性问题特征举例:①三定一动,连接定点出现三条定线段.定线段分别作为平行四边形的________,利用________确定点的坐标.②两定两动,连接定点出现一条定线段.若定线段作为平行四边形的________,则通过________确定点的坐标;若定线段作为平行四边形的________,则定线段绕________旋转,利用________________确定点的坐标.Ø精讲精练1.如图,在平面直角坐标系中,点A 的坐标为(1,0),点B 的坐标为(4,0),点C 在y 轴正半轴上,且OB =2OC .若M 是坐标平面内一点,且以点M ,A ,B ,C 为顶点的四边形是平行四边形,则点M 的坐标为_____________________.2.如图,在平面直角坐标系中,已知A (3,0),B (0,1),C (2,2),若D 是坐标平面内一点,且以点A ,B ,C ,D 为顶点的四边形是平行四边形,则点D 的坐标为______________.CB A yOxxC BAy O3. 如图,在平面直角坐标系中,直线323y x =+与坐标轴分别交于点A ,B ,点C 在y 轴正半轴上,且12OA AC =,直线CD ⊥AB 于点P ,交x 轴于点D .在坐标平面内是否存在点M ,使得以点B ,P ,D ,M 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.xy ABCD OPxy ABCD OP4. 如图,在平面直角坐标系中,直线334y x =-+与x 轴、y 轴分别交于点A ,B ,点C 的坐标为(0,2-).若点D 在直线AB 上运动,点E 在直线AC 上运动,当以点O ,A ,D ,E 为顶点的四边形是平行四边形时,求点D 的坐标.的坐标.y xCB AO5. 如图,在平面直角坐标系中,四边形OABC 是直角梯形,是直角梯形,BC ∥OA ,∠OCB =90°,AB =5,BC =1,直线112y x =-+经过点A ,且与y轴交于点D .若M 是直线AD 上的一个动点,则在x 轴上是否存在点N ,使得以点O ,B ,M ,N 为顶点的四边形是平行四边形?若存在,求出点N 的坐标;若不存在,请说明理由.标;若不存在,请说明理由.y xCB AO y x DC BA O y xD C BAO6. 如图,在平面直角坐标系中,在平面直角坐标系中,四边形四边形OABC 是矩形,顶点A ,C 分别在x 轴、y 轴上,顶点B 的坐标为(3,4),点E 在OC 边上,点F 的坐标为(2,4).将矩形OABC 沿直线EF 折叠,点C 落在AB 边上的点G 处,若点N 在x 轴上,则直线EF 上是否存在点M ,使得以点F ,G ,M ,N 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.GF OAB C E xy GFOAB CE xy【参考答案】Ø 知识点睛 1. ①对角线①对角线 平移②边②边 平移平移 对角线对角线 其中点其中点 中点坐标公式 Ø 精讲精练1. (3,2),(-3,2),(5,-2) 2. (5,1),(-1,3),(1,-1) 3. 存在存在 (53,3),(33-,3),(3-,-3) 4. (125,65),(285,-65) 5. 存在存在 (-3,0),(7,0),(3,0) 6. 存在存在 (4333-,3),(4313-,3-),(4313+,83-) 。
专题55 一次函数背景下的图形存在性问题(解析版)

例题精讲考点一:一次函数中等腰三角形存在性问题【例1】.如果一次函数y=﹣x+6的图象与x轴、y轴分别交于A、B两点,M点在x轴上,并且使得以点A、B、M为定点的三角形是等腰三角形,则M点的坐标为(﹣8,0)或(﹣2,0)或(18,0)或(﹣,0).解:一次函数y=﹣x+6中令x=0,解得y=6;令y=0,解得x=8,∴A(8,0),B(0,6),即OA=8,OB=6,在直角三角形AOB中,根据勾股定理得:AB=10,分四种情况考虑,当BM=BA时,由BO⊥AM,根据三线合一得到O为MA的中点,此时M1(﹣8,0);当AB=AM时,由AB=10,得到OM=﹣2或18,此时M2(﹣2,0),M3(18,0);当MA=MB时,∵A(8,0),B(0,6),∴AB的中点的坐标为(4,3),设直线AB的垂直平分线的解析式为y=x+b,代入(4,3)得3=+b,解得b=﹣,∴直线AB的垂直平分线的解析式为y=x﹣,令y=0,解得x=,此时M4(,0).综上,这样的M点有4个,分别为(﹣8,0)或(﹣2,0)或(18,0)或(,0).故答案为(﹣8,0)或(﹣2,0)或(18,0)或(,0).变式训练【变1-1】.如图,在平面直角坐标系中,直线MN的函数解析式为y=﹣x+3,点A在线段MN上且满足AN=2AM,B点是x轴上一点,当△AOB是以OA为腰的等腰三角形时,则B点的坐标为(2,0)或(,0)或(,0).解:∵在y=﹣x+3中,令x=0,则y=3;令y=0,则﹣x+3=0,解得x=3,∴N(3,0),M(0,3),∴OM=ON=3,∵AN=2AM,∴A(1,2),∴OA==,当AO=OB时,则OB=,∴点B的坐标为(﹣,0)或(,0);②当AO=AB时,设点B的坐标为(m,0),则=,整理得,(1﹣m)2=1,解得m=2或m=0(舍去),∴点B的坐标为(2,0).综上所述:点B的坐标为(2,0)或(,0)或(,0).【变1-2】.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.(1)求点C的坐标.(2)若P是x轴上的一个动点,直接写出当△OPC是等腰三角形时P的坐标.解:(1)联立两直线解析式成方程组,得,解得:,∴点C的坐标为(4,4);(2)设点P(m,0),而点C(4,4),点O(0,0);PC2=(m﹣4)2+16,PO2=m2,OC2=42+42=32;当PC=PO时,(m﹣4)2+16=m2,解得:m=4;当PC=OC时,同理可得:m=0(舍去)或8;当PO=OC时,同理可得:m=±4;故点P的坐标为(4,0)或(8,0)或(4,0)或(﹣4,0).考点二:一次函数中直角三角形存在性问题【例2】.已知点A、B的坐标分别为(2,2)、(5,1),试在x轴上找一点C,使△ABC为直角三角形.解:当△ABC为直角三角形时,设点C坐标为(x,0),分三种情况:①如果A为直角顶点,则AB2+AC2=BC2,即(2﹣5)2+(2﹣1)2+(2﹣x)2+22=(5﹣x)2+1,解得:x=,②如果B为直角顶点,那么AB2BC2=AC2,即(2﹣5)2+(2﹣1)2+(5﹣x)2+1=(2﹣x)2+22,解得x=,③如果C为直角顶点,那么AB2=AC2+BC2,即(2﹣5)2+(2﹣1)2=(2﹣x)2+22+(5﹣x)2+1,解得x=3或4,综上可知,使△PAB为直角三角形的点C坐标为(,0)或(,0)或(3,0)或(4,0).变式训练【变2-1】.如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P 是x轴上的一点,且满足△ABP是直角三角形,则点P的坐标是(1,0)或(3,0).解:∵一次函数y=kx+1的图象过点A(1,2),∴2=k+1,解得k=1,∴一次函数的解析式为y=x+1.∴当∠APB=90°时,P1(1,0);当∠BAP=90°时,∵一次函数的解析式为y=x+1,∴设直线AP的解析式为y=﹣x+b,∵A(1,2),∴2=﹣1+b,解得b=3,∴直线AP的解析式为y=﹣x+3,∴当y=0时,x=3,∴P2(3,0).综上所述,点P的坐标是(1,0)或(3,0).【变2-2】.如图,已知一次函数y=x﹣2的图象与y轴交于点A,一次函数y=4x+b的图象与y轴交于点B,且与x轴以及一次函数y=x﹣2的图象分别交于点C、D,点D的坐标为(﹣2,﹣4).(1)关于x、y的方程组的解为.(2)求△ABD的面积;(3)在x轴上是否存在点E,使得以点C,D,E为顶点的三角形是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x﹣2的图象与一次函数y=4x+b的图象交于点D,且点D的坐标为(﹣2,﹣4),∴关于x、y的方程组的解是,∴关于x、y的方程组的解是,故答案为:;(2)把点D的坐标代入一次函数y=4x+b中得:﹣8+b=﹣4,解得:b=4,∴B(0,4),∵A(0,﹣2),∴AB=4﹣(﹣2)=6,==6;∴S△ABD(3)存在,如图1,当点E为直角顶点时,过点D作DE⊥x轴于E,∵D(﹣2,﹣4),∴E(﹣2,0);当点C为直角顶点时,x轴上不存在点E;当点D为直角顶点时,过点D作DE⊥CD交x轴于点E,作DF⊥x轴于F,设E(t,0),当y=0时,4x+4=0,∴x=﹣1,∴C(﹣1,0),∵F(﹣2,0),∴CE=﹣1﹣t,EF=﹣2﹣t,∵D(﹣2,﹣4),∴DF=4,CF=﹣1﹣(﹣2)=1,在Rt△DEF中,DE2=EF2+DF2=42+(﹣2﹣t)2=t2+4t+20,在Rt△CDF中,CD2=12+42=17,在Rt△CDE中,CE2=DE2+CD2,∴(﹣1﹣t)2=t2+4t+20+17,解得t=﹣18,∴E(﹣18,0),综上,点E的坐标为:(﹣2,0)或(﹣18,0).考点三:一次函数中平行四边形存在性问题【例3】.如图,已知一次函数y=kx+b的图象经过A(1,3),B(﹣2,﹣1)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.解:(1)将A(1,3)、B(﹣2,﹣1),代入y=kx+b得:,解得,∴一次函数的表达式为y=x+;(2)在y=x+中,令x=0得y=,∴OD=,=OD•|x A|=××1=,∴S△AODS△BOD=OD•|x B|=××2=,=S△BOD+S△AOD=;∴△AOB的面积S△AOB(3)存在,理由如下:在y=x+中,令y=0得y=﹣,∴C(﹣,0),设M(m,n),而B(﹣2,﹣1),O(0,0),①以OB、CM为对角线,则OB的中点即是CM的中点,如图:∴,解得,∴M(﹣,﹣1);②以BC、OM为对角线,则BC的中点即是OM的中点,如图:∴,解得,∴M(﹣,﹣1);③以BM、CO为对角线,则BM的中点即是CO的中点,如图:∴,解得,∴M(,1);综上所述,M的坐标为:(﹣,﹣1)或(﹣,﹣1);或(,1).变式训练【变3-1】.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,∴∠OBC=∠ECD.∵将线段CB绕着点C顺时针旋转90°得到CD,∴BC=CD.在△BOC和△CED中,,∴△BOC≌△CED(AAS).(2)解:∵直线y=﹣x+3与x轴、y轴相交于A、B两点,∴点B的坐标为(0,3),点A的坐标为(6,0).设OC=m,∵△BOC≌△CED,∴OC=ED=m,BO=CE=3,∴点D的坐标为(m+3,m).∵点D在直线y=﹣x+3上,∴m=﹣(m+3)+3,解得:m=1,∴点D的坐标为(4,1),点C的坐标为(1,0).∵点B的坐标为(0,3),点C的坐标为(1,0),∴直线BC的解析式为y=﹣3x+3.设直线B′C′的解析式为y=﹣3x+b,将D(4,1)代入y=﹣3x+b,得:1=﹣3×4+b,解得:b=13,∴直线B′C′的解析式为y=﹣3x+13,∴点C′的坐标为(,0),∴CC′=﹣1=,∴△BCD平移的距离为.(3)解:设点P的坐标为(0,m),点Q的坐标为(n,﹣n+3).分两种情况考虑,如图3所示:①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P1的坐标为(0,);当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P2的坐标为(0,);②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P的坐标为(0,).综上所述:存在,点P的坐标为(0,)或(0,).考点四:一次函数中矩形存在性问题【例4】.Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求线段AB的长;(2)求直线CE的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,在直角△AOB中,AB===10;(2)∵BC平分∠ABO,CD⊥AB,AO⊥BO,∴OC=CD,设OC=x,则AC=8﹣x,CD=x.∵△ACD和△ABO中,∠CAD=∠BAO,∠ADC=∠AOB=90°,∴△ACD相似于△ABO,∴,即,解得:x=3.即OC=3,则C的坐标是(﹣3,0).设AB的解析式是y=kx+b,根据题意得解得:则直线AB的解析式是y=x+6,设CD的解析式是y=﹣x+m,则4+m=0,则m=﹣4.则直线CE的解析式是y=﹣x﹣4;(3)①当AB为矩形的边时,如图所示矩形AM1P1B,易知BC的直线方程为y=2x+6,设M1(m,2m+6),P1(x,y),因为A(﹣8,0),B(0,6),则AM12=(m+8)2+(2m+6)2,=5m2+40m+100,BM12=m2+(2m+6﹣6)2=5m2,AB=10,根据AB2+AM12=BM12得100+5m2+40m+100=5m2,m=﹣5,∴M1(﹣5,﹣4),根据平移规律可以解得P1(3,2)②当AB为矩形的对角线时,此时有AB2=AM22+BM22,即100=5m2+40m+100+5m2,m =﹣4或m=0(舍去),∴M2(﹣4,﹣2),根据平移规律可以解得P2(﹣4,8)综上可得,满足条件的P点的坐标为P1(3,2)或P2(﹣4,8).变式训练【变4-1】.如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2﹣4x+3=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求点H到x轴的距离;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)x2﹣4x+3=0,解得:x=3或1,故BC=1,OC=3,即点C(0,3)、点A(﹣1,0),则点B(﹣1,3),点D(3,0),点E(3,1),将B、D点的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线BD的表达式为:y=﹣x+…①;(2)同理可得:直线OE的表达式为:y=x…②,联立①②并解得:y=,即点H到x轴的距离为:;(3)直线BD的表达式为:y=﹣x+,则点F(0,),①当FD是矩形的一条边时,当点M在x轴上时,∵MF⊥BD,则直线MF的表达式为:y=x+,当y=0,x=﹣,即点M(﹣,0),点F向右平移3个单位向下平移单位得到D,则点M向右平移3个单位向下平移单位得到N,则点N(,﹣);当点M在y轴上时,同理可得:点N(﹣3,﹣);②当FD是矩形的对角线时,此时点M在原点O,则点N(3,);综上,点N的坐标为:(,﹣)或(﹣3,﹣)或(3,).考点五:一次函数中菱形存在性问题【例5】.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.(1)求点C的坐标;(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M 的坐标;(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=x+6,令x=0,得到y=6,∴B(0,6),令y=0,得到x=﹣8,∴A(﹣8,0).∵A(﹣8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB==10,过点C作CH⊥AB于H,设OC=t,∵BC平分∠ABO,∠AOB=90°,∴CH=OC=t,=S△ABC+S△BCO,∵S△ABO∴OA•OB=AB•CH+OC•OB,∴6×8=10t+6t,∴t=3,∴OC=3,∴C(﹣3,0);(2)设线BC的表达式为:y=kx+b,∵B(0,6),C(﹣3,0),∴直线BC的表达式为:y=2x+6,设点M(m,2m+6)、N(n,2n+6),过点M作MF⊥x轴于点F,过点N作NE⊥x轴于点E,∵△AMN为等腰直角三角形,故AM=AN,∵∠NAE+∠MAF=90°,∠MAF+∠AMF=90°,∴∠NAE=∠AMF,∵∠AFM=∠NEA=90°,AM=AN,∴△FMA≌△EAN(AAS),∴EN=AF,MF=AE,即﹣2n﹣6=m+8,2m+6=8+n,解得:m=﹣2,n=﹣6,故点M的坐标为(﹣2,2)、点N(﹣6,﹣6);由于M,N的位置可能互换,故点N的坐标为(﹣2,2)、点M(﹣6,﹣6);综上所述,点M的坐标为(﹣2,2)或(﹣6,﹣6);(3)设点P(0,p),∴BP2=(p﹣6)2,AP2=82+p2,①当AB是边时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴BP=AB=10,BP′=AB=10,OB=OP″,∵B(0,6),∴P(0,16),P′(0,﹣4),P″(0,﹣6),∵A(﹣8,0),∴Q(﹣8,10),Q′(﹣8,﹣10),Q″(8,0);②当AB是对角线时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴AP=BP,∴BP2=AP2,∴(p﹣6)2=82+p2,解得p=﹣,∴P(0,﹣),∵A(﹣8,0),B(0,6),∴Q(﹣8,);综上所述,点Q的坐标为(﹣8,10)或(﹣8,﹣10)或(8,0)或(﹣8,).变式训练【变5-1】.如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,﹣2),与直线CD交于点A(m,2).(1)求直线AB的解析式;(2)点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)设P是射线CD上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)∵点A(m,2)在直线y=x+4上∴m+4=2解得m=﹣2∴点A的坐标为(﹣2,2)设直线AB的解析式为y=kx+b∴解得∴直线AB的解析式为y=﹣2x﹣2;(2)如图1,由题意设点E的坐标为(a,a+4),则∵EF∥y轴,点F在直线y=﹣2x﹣2上∴点F的坐标为(a,﹣2a﹣2)∴EF=|a+4﹣(﹣2a﹣2)|=|3a+6|,∵以点O、C、E、F为顶点的四边形是平行四边形,且EF∥OC∴EF=OC∵直线y=x+4与y轴交于点C∴点C的坐标为(0,4)∴OC=4,即|3a+6|=4解得:a=﹣或a=﹣∴点E的坐标为(﹣,)或(﹣,);(3)如图2,当BC为对角线时,点P,Q都是BC的垂直平分线,且点P和点Q关于BC对称,∵B(0,﹣2),C(0,4),∴点P的纵坐标为1,将y=1代入y=x+4中,得x+4=1,∴x=﹣3,∴P''(﹣3,1),∴Q''(3,1)当CP是对角线时,CP是BQ的垂直平分线,设Q(m,n),∴BQ的中点坐标为(,),代入直线y=x+4中,得+4=①,∵CQ=CB,∴m2+(n﹣4)2=36②,联立①②得,(舍)或,∴Q'(﹣6,4),当PB是对角线时,PC=BC=6,设P(c,c+4),∴c2+(c+4﹣4)2=36,∴c=3(舍)或c=﹣3,∴P(﹣3,﹣3+4),设Q(d,e)∴(﹣3+0)=(0+d),(﹣3+4﹣2)=(e+4),∴d=﹣3,e=﹣3﹣2,∴Q(﹣3,﹣3﹣2),即:点Q的坐标为(3,1),(﹣6,4)或(﹣3,﹣3﹣2).1.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为(﹣8,0)(3,0)(2,0)(,0).解:当x=0时,y=4,当y=0时,x=﹣3,即A(﹣3,0),B(0,4),OA=3,OB=4,由勾股定理得:AB=5,有三种情况:①以A为圆心,以AB为半径交x轴于两点,此时AC=AB=5,C的坐标是(2,0)和(﹣8,0);②以B为圆心,以AB为半径交x轴于一点(A除外),此时AB=BC,OA=OC=3,C的坐标是(3,0);③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),A(﹣3,0),B(0,4),∵AC=BC,由勾股定理得:(a+3)2=a2+42,解得:a=,∴C的坐标是(,0),故答案为:(﹣8,0)(3,0)(2,0)(,0).2.如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2(,0),P3(﹣,0),P4(,0).解:设P(x,0),当OA=AP时,∵A(2,1),∴P1(4,0);当OA=OP时,∵A(2,1),∴OA==,∴P2(,0),P3(﹣,0);当AP=OP时,∵P(x,0),(2,1),∴(2﹣x)2+12=x2,解得x=,∴P4(,0).综上所述,P点坐标为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).故答案为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).3.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y 的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为(3,2)(﹣3,2)(5,﹣2).解:如图,①当BC为对角线时,易求M1(3,2);②当AC为对角线时,CM∥AB,且CM=AB.所以M2(﹣3,2);③当AB为对角线时,AC∥BM,且AC=BM.则|M y|=OC=2,|M x|=OB+OA=5,所以M3(5,﹣2).综上所述,符合条件的点D的坐标是M1(3,2),M2(﹣3,2),M3(5,﹣2).故答案为:(3,2)(﹣3,2)(5,﹣2).4.如图,一次函数y=k2x+b的图象与y轴交于点B,与正比例函数y=k1x的图象相交于点A(3,4),且OA=OB.(1)分别求出这两个函数的解析式;(2)求△AOB的面积;(3)点P在x轴上,且△POA是等腰三角形,请直接写出点P的坐标.解:(1)∵正比例函数y=k1x的图象经过点A(3,4),∴3k1=4,∴k1=,∴正比例函数解析式为y=x.如图1中,过A作AC⊥x轴于C,在Rt△AOC中,OC=3,AC=4,∴AO==5,∴OB=OA=5,∴B(0,﹣5),∴,解得,∴一次函数的解析式为y=3x﹣5.(2)如图1中,过A作AD⊥y轴于D,∵A(3,4),∴AD=3,=;∴S△AOB(3)当OP=OA时,P1(﹣5,0),P2(5,0),当AO=AP时,P3(6,0),当PA=PO时,线段OA的垂直平分线为y=﹣,∴,满足条件的点P的坐标(﹣5,0)或(5,0)或(6,0)或.5.直线l1交x轴于点A(6,),交y轴于B(0,6).(1)如图,折叠△AOB,使BA落在y轴上,折痕所在直线为l2,直线l2与x轴交于C 点,求C点坐标及l2的解析式;(2)在直线l1上找点M,使得以M、A、C为顶点的三角形是等腰三角形,求出所有满足条件的M点的坐标.解:∵点A(6,0),交y轴于B(0,6).∴OA=6,OB=6,∴tan∠OAB==,∴∠OAB=30°,∴∠OBA=60°,∵折叠△AOB,∴∠OBC=∠ABC=30°,∴BC=2OC,BO=OC=6,∴OC=2,∴点C(2,0),设直线BC解析式为:y=kx+b,解得:∴直线BC解析式为:y=﹣x+6;(2)当点M与点B重合时,由(1)可知:∠AMC=∠MAC=30°,∴CM=AC,∴△ACM是等腰三角形,∴当M为(0,6)时,△ACM是等腰三角形,∵OC=2,OA=6,∴AC=4,若AM=AC=4,如图1:过点M作MH⊥AC,∵∠MAH=30°,∴MH=AM=2,AH=2MH=6,∴OH=6﹣6或6+6,∴点M(6﹣6,2)或(6+6,﹣2)若AM=MC,如图2,过点M作MH⊥AC,∵AM=MC,MH⊥AC,∴AH=CH=2,∴OC=4,∵∠MAH=30°,∴AH=MH,∴MH=2,∴点M(4,2),综上所述:点M(6﹣6,2)或(6+6,﹣2)或(4,2)或(0,6).6.在平面直角坐标系中,直线y=kx+8k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).(1)求点A的坐标;(2)如图1,将直线AB绕点B逆时针旋转45°交x轴于点C,求直线BC的解析式;(3)在(2)的条件下,直线BC上有一点M,坐标平面内有一点P,若以A、B、M、P 为顶点的四边形是菱形,请直接写出点P的坐标.解:(1)令y=kx+8k=0,解得x=﹣8,故点A的坐标为(﹣8,0);(2)过点A作AD⊥AB交BC于点D,过点A作y轴的平行线交过点B与x轴的平行线于点M,交过点D与x轴的平行线于点N,∵∠ABC=45°,故△ABD为等腰直角三角形,则AD=AB,∵∠BAM+∠DAN=90°,∠DAN+∠ADN=90°,∴∠BAM=∠ADN,∵∠BMA=∠AND=90°,∴△BMA≌△AND(AAS),∴AN=BM=8,ND=AM=6,故点D的坐标为(﹣2,﹣8),设直线BC的表达式为y=kx+b,则,解得,故直线BC的表达式为y=7x+6;(3)设点M的坐标为(m,7m+6),点P(s,t),而点A、B的坐标分别为(﹣8,0)、(0,6),①当AB是边时,点A向右8个单位向上6个单位得到点B,同样,点M(P)向右8个单位向上6个单位得到点P(M),且AB=BP(AB=BM),则或,解得或或(不合题意的值已舍去);故点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2);②当AB是对角线时,由中点坐标公式和AM=BM得:,解得,故点P的坐标为(﹣7,7);综上,点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2)或(﹣7,7).7.如图,在平面直角坐标系中,一次函数的图象与x轴交于点A(﹣4,0),与y轴交于点B,且与正比例函数y=x的图象交于点C(m,6).(1)求一次函数的解析式;(2)求△BOC的面积;(3)在x轴上是否存在一点P,使得△ABP是等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.解:(1)∵将点C(m,6)代入y=x,∴6=m,∴m=4,∴C(4,6),设一次函数的解析式为y=kx+b,∴,∴,∴y=x+3;(2)在y=x+3中,令x=0得y=3,∴B(0,3),=OB•|x C|=×3×4=6;∴S△BOC(3)在x轴上存在一点P,使得△ABP是等腰三角形,理由如下:∵A(﹣4,0),B(0,3),∴AB=5,OA=4,当B为等腰三角形顶角顶点时,P点与A点关于y轴对称,∴P(4,0);当A为等腰三角形顶角顶点时,AP=AB=5,∴P(﹣9,0)或P(1,0);当P为等腰三角形顶角顶点时,设P(t,0),∵PA=PB,∴(t+4)2=t2+9,解得t=﹣,∴P(﹣,0),综上所述:P点坐标为(﹣9,0)或(1,0)或(4,0)或(﹣,0).8.如图,已知一次函数y=x+m的图象与x轴交于点A(﹣6,0),交y轴于点B.(1)求m的值与点B的坐标(2)问在x轴上是否存在点C,使得△ABC的面积为16?若存在,求出点C的坐标;若不存在,说明理由.(3)问在x轴是否存在点P,使得△ABP为等腰三角形,求出点P坐标.(4)一条经过点D(0,2)和直线AB上的一点的直线将△AOB分成面积相等的两部分,请求出这条直线的函数表达式.解:(1)把点A(﹣6,0)代入y=x+m,得m=8,∴点B坐标为(0,8).(2)存在,设点C坐标为(a,0),由题意•|a+6|•8=16,解得a=﹣2或﹣10,∴点C坐标(﹣2,0)或(﹣10,0).(3)如图1中,①当AB=AP时,AP=AB==10,可得P1(﹣16,0),P2(4,0).②当BA=BP时,OA=OP,可得P3(6,0).③当PA=PB时,∵线段AB的垂直平分线为y=﹣x+,可得P4(,0),综上所述,满足条件的点P坐标为(﹣16,0)或(4,0)或(6,0)或(,0).(4)如图2中,设过点D的直线交AB于E,设E(b,),由题意BD•(﹣b)=××6×8,∴b=﹣4,∴点E坐标(﹣4,),设直线DE的解析式为y=kx+b则有,解得,∴这条直线的函数表达式y=﹣x+2.9.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P(2,a).(1)求点A、B的坐标;(2)若Q为x轴上一动点,△APQ为等腰三角形,直接写出Q点坐标;(3)点C在直线AB上,过C作CE⊥x轴于E,交直线OP于D,我们规定若C,D,E 中恰好有一点是其他两点所连线段的中点,则称C,D,E三点为“和谐点”,求出C,D,E三点为“和谐点”时C点的坐标.解:(1)当x=0时,y=﹣x+2=2,∴点B的坐标为(0,2);当y=0时,有﹣x+2=0,解得:x=4,∴点A的坐标为(4,0);(2)∵一次函数y=﹣x+2的图象交直线y=kx于P(2,a).∴a=﹣×2+2=1,∴点P的坐标为(2,1),设点Q(m,0),而点A、P的坐标分别为:(4,0)、(2,1),则AP==,AQ=|4﹣m|,PQ=,当AP=AQ时,则=|4﹣m|,解得m=4±,∴点Q(4±,0);当AP=PQ时,=,解得m=0或4(舍去),∴点Q(0,0);当PQ=AQ时,即=|4﹣m|,解得:m=,∴点Q(,0);综上,点Q的坐标为(4±,0)或(0,0)或(,0);(3)∵y=kx过P(2,1).∴2k=1,解得k=,∴y=x,设点C的坐标为(n,﹣n+2),则点D的坐标为(n,n),点E的坐标为(n,0),∴CD=|﹣n+2﹣n|=|2﹣n|,DE=|n|,CE=|﹣n+2|=|n﹣2|,当D为CE的中点时,CD=DE,∴|2﹣n|=|n|,解得n=或4(舍去),∴点C的坐标为(,);当C为DE的中点时,CD=CE,∴|2﹣n|=|n﹣2|,解得n=或0(舍去),∴点C的坐标为(,);当E为CD的中点时,DE=CE,∴|n|=|n﹣2|,无解;综上,C,D,E三点为“和谐点”时C点的坐标为(,)或(,).10.如图所示,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4).(1)求△AOB的面积;(2)动点M从A点以每秒1个单位的速度沿x轴向左移动,求△COM的面积S与M的移动时间t之间的函数关系式;(3)当动点M在x轴上移动的过程中,在平面直角坐标系中是否存在点N,使以点A,C,N,M为顶点的四边形为菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)令y=0,,解得x=.令x=0,y=.∴A(,0),B(0,).=.∴△AOB的面积为12.(2)∵动点M从A点以每秒1个单位的速度沿x轴向左移动,∴AM=t.当0≤t≤时,OM=,OC=.∴==.当t>时,OM=t﹣.∴==.综上,△COM的面积S与M的移动时间t之间的函数关系式:S=.(3)在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形.①当AC,AM为菱形的边时,情况一:如图1,当点M在点A的左侧时,Rt△AOC中,=,∴NC=AC=.∵NC∥AM,∴点N(,).情况二,如图1′,当点M在点A的右侧时,由情况一同理可得点N的坐标为.②当AC为菱形的对角线时,如图2,此时M,O重合,四边形OANC为正方形,则点N(,).③如图3,当AC为菱形的边,AM为菱形的对角线时,此时点C,N关于x轴对称,∴点N(0,﹣).综上,在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形,此时点N的坐标为:(,),,(,),(0,﹣).11.如图,直线y=﹣x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且OC=OB.(1)求点A的坐标及直线BC的函数关系式;(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=﹣x+4,令x=0的y=4,令y=0得x=4,∴A(4,0),B(0,4),∴OB=OA=4,∵OC=OB,∴OC=3,∴C(﹣3,0),设直线BC的解析式为y=kx+b,则有,解得,∴直线BC的解析式为y=x+4.(2)如图1中,当点M在点A的左边时,∵OB=OA=4,∠AOB=90°,∴∠ABO=45°,∴∠CBO+∠MBA=∠MBA+∠MBO=45°,∴∠CBO=∠OBM,∵∠CBO+∠BCO=90°,∠BMO+∠OBM=90°,∴∠BCO=∠BMO,∴BC=BM,OC=OM=3,∴M(3,0),作点M关于直线AB的对称点N,作直线BN交x轴于M1,则∠M1BA=∠MBA,点M1满足条件.∵N(4,1),B(0,4),∴直线BN的解析式为y=﹣x+4,令y=0,得x=,∴M1(,0),综上所述,满足条件的点M的坐标为(3,0)或(,0).(3)如图2中,∵BC==5,当BC为菱形的边时,四边形CP1Q1B,四边形CP3Q3B,四边形BCQ2P2是菱形,此时Q1(﹣5,4),Q3(5,4),Q2(0,4),当BC是菱形的对角线时,四边形CP4BQ4是菱形,可得Q4(﹣,4).综上所述,满足条件的点Q的坐标为(﹣5,4)或(5,4)或(0,﹣4)或.12.已知,一次函数y=的图象与x轴、y轴分别交于点A、点B,与直线y=相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)求点C到直线l的距离.=S△BCP,求点P的坐标.(3)若S△AOC(4)若点E是直线y=上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,请直接写出点E的坐标.解:(1)∵一次函数y=的图象与x轴、y轴分别交于点A、点B,∴令y=0,则=0,∴x=8,令x=0,则y=6,∴点A、B的坐标分别为:(8,0)、(0,6);(2)解:得,,∴点C(3,),则C到直线l的距离为6﹣=;=×8×=15=S△BCP=×BP×(y P﹣y C)=BP×,(3)∵S△AOC解得:BP=,故点P(,6)或(﹣,6);(4)设点E(m,m)、点P(n,6);①当∠EPA=90°时,当点P在y轴右侧时,当点P在点E的左侧时,如图1,∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°,∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS),则ME=PN=6,MP=AN,即m﹣n=6,m﹣6=8﹣n,解得:m=,当点P在点E的右侧时,如图,同理可得m=16,当∠EAP=90°时,当点P在y轴左侧时,如图2,同理可得:m﹣8=6,m=8﹣n,解得:m=14,故点E(14,);故点E(,)或(14,)或(16,20);如图3,同理可得:△AMP≌△ANE(AAS),故MP=EN,AM=AN=6,即m=n﹣8,|8﹣m|=6,解得:m=2或14(不合题意舍去),故点E(2,);综上,E(,)或(16,20)或(2,)或(14,).13.如图,在平面直角坐标系xOy中,直线y=﹣x+与y=x相交于点A,与x轴交于点B.(1)求点A,B的坐标;(2)在平面直角坐标系xOy中,是否存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C的坐标;如果不存在,请说明理由;(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.解:(1)∵直线y=﹣x+与y=x相交于点A,∴联立得,解得,∴点A(1,1),∵直线y=﹣x+与x轴交于点B,∴令y=0,得﹣x+=0,解得x=3,∴B(3,0),(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.①如图1,过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,∵AC∥x轴,OC∥AB,∴四边形CABO是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(﹣2,1),②如图2,过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,∵AC∥x轴,BC∥AO,∴四边形CAOB是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(4,1),③如图3,过点O作平行于AB轴的直线,过点B作平行于AO的直线,两直线交于点C,∵OC∥AB,BC∥AO,∴四边形CBAO是平行四边形,∵A(1,1),B(3,0),∴AO=BC,OC=AB,作AE⊥OB,CF⊥OB,易得OE=EF=FB=1,∴C(2,﹣1),(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(﹣,﹣),②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(,),③如图6,当OB=DB时,∵∠AOB=∠ODB=45°,∴DB⊥OB,∵OB=3,∴D(3,3),④如图7,当DO=DB时,作DE⊥x轴,交x轴于点E∵∠AOB=∠OBD=45°,∴OD⊥DB,∵OB=3,∴OE=,AE=,∴D(,).综上所述,在直线OA上,存在点D(﹣,﹣),D(,),D(3,3)或D(,),使得△DOB是等腰三角形,14.如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)(1)求直线AB的函数的表达式;(2)直接写出不等式(kx+b)﹣ax<0的解集;(3)求△AOC的面积;(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.解:(1)依题意得:,解得,∴所求的一次函数的解析式是y=﹣x+2.(2)观察图形可知:不等式(kx+b)﹣ax<0的解集;x<﹣1.(3)对于y=﹣x+2,令y=0,得x=2∴C(1,0),∴OC=2.=×2×3=3.∴S△AOC(4)①当点P与B重合时,OP1=OC,此时P1(0,2);②当PO=PC时,此时P2在线段OC的垂直平分线上,P2(1,1);③当PC=OC=2时,设P(m.﹣m+2),∴(m﹣2)2+(﹣m+2)2=4,∴m=2±,可得P3(2﹣,),P4(2+,﹣),综上所述,满足条件的点P坐标为:(1,1)或(0,2)或P(2+,﹣)或(2﹣,).15.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.(1)直接写出k的值为﹣1;(2)如图2,C为x轴负半轴上一点,过C点的直线l2:经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QM⊥x轴分别交直线l1、l2于M、N,且MN=2MQ,求t的值;(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.解:(1)把A(4,0)代入y=kx+4,得0=4k+4.解得k=﹣1.故答案是:﹣1;(2)∵在直线y=﹣x+4中,令x=0,得y=4,∴B(0,4),∵A(4,0),∴线段AB的中点P的坐标为(2,2),代入,得n=1,∴直线l2为,∵QM⊥x轴分别交直线l1、l2于M、N,Q(t,0),∴M(t,﹣t+4),,∴,MQ=|﹣t+4|=|t﹣4|,∵MN=2MQ,∴,分情况讨论:①当t≥4时,,解得:t=10.②当2≤t<4时,,解得:.③当t<2时,,解得:t=10>2,舍去.综上所述:或t=10.(3)在x轴上取一点P(1,0),连接BP,作PQ⊥PB交直线BN于Q,作QR⊥x轴于R,∴∠BOP=∠BPQ=∠PRQ=90°,∴∠BPO=∠PQR,∵OA=OB=4,∴∠OBA=∠OAB=45°,∵M(﹣1,0),∴OP=OM=1,∴BP=BM,∴∠OBP=∠OBM=∠ABN,∴∠PBQ=∠OBA=45°,∴PB=PQ,∴△OBP≌△RPQ(AAS),∴RQ=OP=1,PR=OB=4,∴OR=5,∴Q(5,1),∴直线BN的解析式为,将N(5m,3m+2)代入,得3m+2=﹣×5m+4解得,∴.16.如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM 的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,2),Q3(1,﹣2),Q4(1,).17.如图1,在平面直角坐标系中.直线与x轴、y轴相交于A、B两点,动点C 在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当直线B′C′经过点D时,求点D的坐标;(3)若点P在y轴上,点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,∴∠BCO=∠CDE,在△BOC和△CED中,。
一次函数中的图形存在性问题归类同步讲义培优

一次函数中的图形存在性问题归类同步讲义培优一次函数的存在性问题在解决存在性问题时,通常需要根据已知条件探索状态是否存在,主要考查运动的结果。
在一次函数的背景下,可以采取以下思考方向:1.将函数信息(坐标或表达式)转化为几何信息;2.分析特殊状态的形成因素,画出符合题意的图形;3.根据图形的几何特征建立等式来解决问题;4.举例不变特征,如等腰直角三角形、等腰三角形和全等三角形等;5.在函数背景下研究存在性问题,先将函数信息转化为几何信息,然后按照存在性问题来处理。
以下是几道相关的例题:1.已知直线 $y=-\frac{1}{3}x+3$ 与 $x$ 轴、$y$ 轴分别交于 $A$、$B$ 两点,点 $P$ 是第一象限内的点,由点 $P$、$O$、$B$ 组成了一个含 $60^\circ$ 角的直角三角形。
求点$P$ 的坐标。
2.已知直线 $y=kx-4$ 与 $x$ 轴、$y$ 轴分别交于 $B$、$C$ 两点,且 $\frac{OC}{OB}=\frac{4}{3}$。
1)求点 $B$ 的坐标和 $k$ 的值;2)若点$A$ 是第一象限内直线$y=kx-4$ 上的一个动点,则当点 $A$ 运动到什么位置时,$\triangle AOB$ 的面积是 $6$?3)在(2)成立的情况下,是否存在 $x$ 轴上的一点 $P$,使 $\triangle POA$ 是等腰三角形?若存在,求出点 $P$ 的坐标;若不存在,请说明理由。
3.平面直角坐标系中,直角梯形 $OABC$ 的边 $OC$、$OA$ 分别与 $x$ 轴、$y$ 轴重合,$AB\parallel OC$,$\angle AOC=90^\circ$,$\angle BCO=45^\circ$,$BC=62$,点$C$ 的坐标为 $(-9,0)$。
1)求点 $B$ 的坐标;2)若直线 $BD$ 交 $y$ 轴于点 $D$,且 $OD=3$,求直线 $BD$ 的表达式;3)若点 $P$ 是(2)中直线 $BD$ 上的一个动点,是否存在点 $P$,使以 $O$、$D$、$P$ 为顶点的三角形是等腰三角形?若存在,求出点 $P$ 的坐标;若不存在,请说明理由。
16四边形之存在性问题二培优班讲义
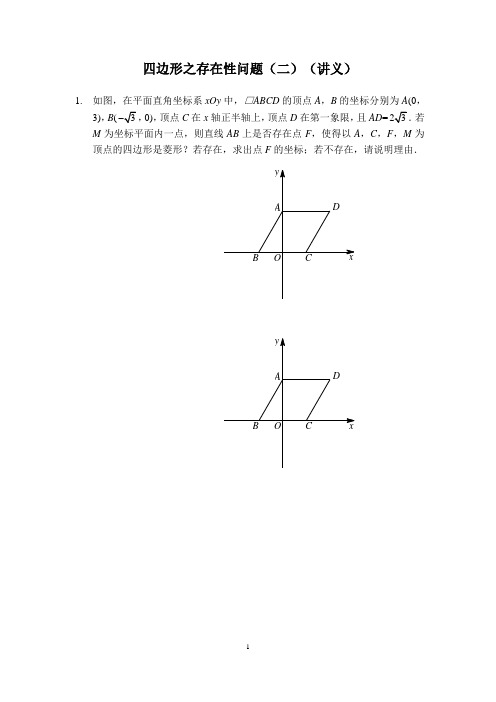
四边形之存在性问题(二)(讲义)1.如图,在平面直角坐标系xOy中,□ABCD的顶点A,B的坐标分别为A(0,2.如图,在平面直角坐标系xOy中,直角梯形OABC的顶点A在y轴正半轴上,顶点C的坐标为(18,0),A B∥O C,∠OCB=45°,且BC=(1)求点B的坐标.(2)直线BE与线段OA交于点E,且OE=6.若P是直线BE上的一动点,则在坐标平面内是否存在点Q,使得以O,E,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.3.4.如图,在平面直角坐标系xOy中,矩形OABC的顶点A,C分别在x轴、y轴的正半轴上,顶点B的坐标为(8,6).若点D在第一象限内的直线l:26=-y x 上,点P在AB边上,AP=m,Q为坐标平面内一点,且以C,P,D,Q为顶点的四边形是正方形,求m的值.三、回顾与思考【参考答案】1.存在,12(F F 2.(1)B (-6,12);(2)存在,1234(66)((33)Q Q Q Q ---,或或或,3.存在,1234(1228)(416)(1414)(22)N N N N --,或,或,或, 4.存在,142633m m m ===,或四边形之存在性问题(二)(随堂测试)1. 如图,在平面直角坐标系中,直线l 1分别与x 轴、y 轴交于点A ,B ,直线l 2与直线l 1交于点C ,已知B (0,6),C (4,2),若P 为坐标平面内一点,则在直线l 1上是否存在一点Q ,使以O ,B ,P ,Q 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.【参考答案】1.存在,1234(60)((33)Q Q Q Q--+,或或或,四边形之存在性问题(二)(作业)1.如图,平面直角坐标系中,矩形OABC的对角线AC=12,AO=6,把矩形沿直线DE对折使点C落在点A处,DE与AC相交于点F,若M为坐标平面内一点,则在直线DE上是否存在点N,使以O,F,M,N为顶点的四边形是菱形?若存在,求出点N的坐标;若不存在,请说明理由.2. 如图,在平面直角坐标系中,直线y 1=2x 与直线y 2=-6x +48交于点A ,另有一直线平行于x 轴,分别交线段OA ,AB 于M ,N 两点,点R 在x 轴上,在坐标平面内,是否存在这样的点Q ,使得以R ,M ,N ,Q 为顶点的四边形是正【参考答案】1.存在,123433(06)(3N N N N ---++,或,或 2.存在,12336129(0)(0)(6)552Q Q Q ,或,或,。
一次函数与矩形存在性问题

一次函数与矩形存在性问题本文讨论一次函数与矩形存在性的问题,并探讨其中的关系和特点。
引言一次函数是指具有形式为 y = ax + b 的函数,其中 a 和 b 均为常数,且 a 不等于 0。
矩形是一个具有四个直角的四边形,其中所有内角均为 90 度。
在数学中,我们经常会遇到一次函数与矩形的相关问题,例如确定一次函数是否与某个矩形相交或相切。
问题分析一次函数与矩形相交或相切的存在性取决于函数的斜率和截距与矩形的边界条件之间的关系。
以下是一些常见情况的分析结果:1. 当函数的斜率为正时,如果函数的截距小于矩形最低边的上端点,并且截距大于矩形最高边的下端点,则函数与矩形相交或相切。
2. 当函数的斜率为负时,如果函数的截距大于矩形最低边的上端点,并且截距小于矩形最高边的下端点,则函数与矩形相交或相切。
3. 当函数的斜率为零时,如果函数的截距在矩形最低和最高边的下、上端点之间,则函数与矩形相交或相切。
需要注意的是,以上分析仅适用于矩形的上、下、左、右四条边界条件,对于矩形内部的情况则不予考虑。
实例分析为了更好地理解一次函数与矩形存在性问题,我们来看一个具体的实例。
假设有一条直线方程为 y = 2x + 3,并且有一个矩形的四个顶点坐标分别为 A(1, 2),B(4, 5),C(6, 1) 和 D(3, -2)。
我们可以根据上述分析方法来判断这条直线是否与该矩形相交或相切。
根据函数的斜率和截距,我们可以得知该直线的斜率为 2,截距为 3。
然后我们可以根据矩形的边界条件来判断:1. 矩形的最低边为 AB,上端点为 B(4, 5)。
根据情况 1,我们可以知道直线的截距必须小于 B 的 y 坐标,即 3 < 5,所以该直线与矩形 AB 边相交或相切。
2. 矩形的最高边为 CD,下端点为 D(3, -2)。
根据情况 1,我们可以知道直线的截距必须大于 D 的 y 坐标,即 3 > -2,所以该直线与矩形 CD 边相交或相切。
一次函数存在性问题

专题4.3一次函数中的四边形存在性问题1.如图,在平面直角坐标系中,直线13:2l y x m =+与直线2l 交于点(2,3)A -,直线2l 与x 轴交于点(4,0)C ,与y 轴交于点B ,将直线2l 向下平移5个单位长度得到直线3l ,3l 与y 轴交于点D ,与1l 交于点E ,连接AD .(1)求直线2l 的解析式;(2)求ADE ∆的面积;(3)在平面直角坐标系中存在点P ,使得以A 、E 、D 、P 为顶点的四边形是平行四边形,请直接写出点P 的坐标.2.如图,平面直角坐标系中,O 是坐标原点,直线15(0)y kx k =+≠经过点(3,6)C ,与x 轴交于点A ,y 轴交于点B ,线段CD 平行于x 轴,交直线34y x =于点D ,连接OC ,AD .(1)求证:四边形OADC 是平行四边形;(2)动点P 从点O 出发,沿对角线OD 以每秒1个单位长度的速度向点D 运动,直到点D 为止;动点Q 同时从点D 出发,沿对角线DO 以每秒1个单位长度的速度向点O 运动,直到点O 为止.设两个点的运动时间均为t 秒.当点P ,Q 运动至四边形CPAQ 矩形时,请求此时t 的值.3.如图,在平面直角坐标系中,把矩形OBCD 沿对角线OC 所在直线折叠,点B 落在点B '处,OB '与CD 相交于点E ,4BC =,对角线OC 所在直线的函数表达式为2y x =.(1)求证:ODE ∆≅△CB E ';(2)请写出CE 的长和B '的坐标;(3)F 是直线OC 上一个动点,是矩形OBCD 边上一点(包括顶点).是否存在点G 使得G ,F ,B ',C 所组成的四边形是平行四边形?如果不存在,请说明理由;如果存在,直接请求出F 的坐标.4.如图,在平面直角坐标系中,直线364y x =+与x 轴交于点A ,与y 轴交于点B ,把AOB ∆沿BC 翻折,点O 恰好落在AB 边的点D 处,BC 为折痕.(1)求线段AB 的长;(2)求直线BC 的解析式;(3)若M 是射线BC 上的一个动点,在坐标平面内是否存在点P ,使以A 、B 、M 、P 为顶点的四边形是矩形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.5.如图,在平面直角坐标系中,直线24y x =+交坐标轴于点C ,D ,:1:2AD OD =,以OA 和OC 为邻边作矩形OABC ,点E 是直线AB 上一动点.(1)写出点B 的坐标;(2)连接DE ,若DE 平分ADC ∠,求出点E 的坐标;(3)若点F 是纵轴(y 轴)左侧任意一点,是否存在以C ,D ,E ,F 为顶点的四边形是矩形,若存在,直接写出点F6.如图,平面直角坐标系中,直线y =+与坐标轴交于点A 、B .点C 在x 轴的负半轴上,且:1:2AB AC =.(1)求A 、C 两点的坐标;(2)若点M 从点C 出发,以每秒1个单位的速度沿射线CB 运动,连接AM ,设ABM ∆的面积为S ,点M 的运动时间为t ,写出S 关于t 的函数关系式,并写出自变量的取值范围;(3)点P 是y 轴上的点,在坐标平面内是否存在点Q ,使以A 、B 、P 、Q 为顶点,且以AB 为边的四边形是菱形,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,O 为原点,已知直线443y x =-+与x 轴交于点A ,与y 轴交于点B .(Ⅰ)点A 的坐标为,点B 的坐标为;(Ⅱ)如图①,若点(,)M x y 在线段AB 上运动(不与端点A 、B 重合),连接OM ,设AOM ∆的面积为S ,写出S 关于x 的函数解析式,并写出自变量x 的取值范围;(Ⅲ)如图②,若四边形OADC OD 的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次函数与特殊四边形的存在性问题
(培优专题)
1.(2015春•通州区校级期中)如图,在直角坐标系中,A(0,1),B(0,3),P是x轴上一动点,在直线y=x上是否存在点Q,使以A、B、P、Q为顶点的四边形为平行四边形?若存在,画出所有满足情况的平行四边形,并求出对应的P、Q的坐标;若不存在,请说明理由.
2.(2015春•北京校级期中)已知直线y=x+3分别交x轴、y轴于点A、B.
(1)求∠BAO的平分线的函数关系式;(写出自变量x的取值范围)
(2)点M在已知直线上,点N在坐标平面内,是否存在以点M、N、A、O为顶点的四边形为菱形?若存在,请直接写出点N的坐标;若不存在,说明理由.
3.(2010秋•吴江市校级期中)已知:如图,在矩形ABCD中,点E在AD边上,AE>DE,BE=BC,点O是线段CE的中点.
(1)试说明CE平分∠BED;
(2)在直线AD上是否存在点F,使得以B、C、F、E为顶点的四边形是菱形?如果存在,试画出点F的位置,并作适当说明;如果不存在,请说明理由.
4.如图,在平面直角坐标系xOy,直线y=x+1与y=﹣2x+4交于点A,两直线与x轴分别交于点B和点C,D是直线AC上的一个动点,直线AB上是否存在点E,使得以E,D,O,A为顶点的四边形是平行四边形?若存在,求出点E 的坐标;若不存在,请说明理由.
5.如图,点A的坐标是(2,1),点B的坐标是(5,1),过点A的直线l的表达式为y=2x+b,点C在直线l上运动,在直线OA上是否存在一点D,使得
以A,B,C,D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
6.(2012春•雨花区校级期末)如图,已知等边△ABC的边长为2,顶点A、B 分别在x轴、y轴的正半轴上移动.
(1)当OA=时,求点C的坐标.
(2)在(1)的条件下,求四边形AOBC的面积.
(3)是否存在一点C,使线段OC的长有最大值?若存在,请求出此时点C
的坐标;若不存在,请说明理由.
7.(2012春•石狮市期末)如图,在平面直角坐标系中,直线y=﹣分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
(1)填空:b= ;
(2)求点D的坐标;
(3)点M是线段AB上的一个动点(点A、B除外),试探索在x上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标.
8.(2014秋•朝阳区期末)如图,四边形ABCD为矩形,点D与坐标原点重合,点C在x轴上,点A在y轴上,点B的坐标是(8,12),矩形ABCD沿直线EF折叠,点A落在BC边上的G处,点E,F分别在AD,AB上,且F点的坐
标是(5,12).
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)坐标系内是否存在点M,使以点A,E,F,M为顶点的四边形为平行四
边形?若存在,求出点M的坐标;若不存在,请说明理由.
9.(2014•伊春模拟)如图,矩形OABC在坐标系中,OA>OC,矩形面积为12,对角线AC的长为5.
(1)求A,C的坐标;
(2)若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;
(3)在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形?若存在,请直接写出点G的坐标;若不存在,请说明理由.
10.(2011春•张家港市期末)如图,OB是矩形OABC的对角线,点B的坐标为(3,6).D、E分别是OC、OB上的点,OD=5,OE=2EB,过D、E的直线交x 轴于点F.
(1)点E的坐标为;
(2)求直线DE的解析式;
(3)若点M是线段DF上的一个动点,在x轴上方的平面内是否存在另一个点N,使得以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.
11.(2007秋•成都期末)如图,在平面直角坐标系中,已知矩形OABC的两个
顶点A、B 的坐标分别A(,0)、B(,2),∠CAO=30°.
(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四
边形?若存在,求出点P的坐标;若不存在,请说明理由.
12.(2014•金华模拟)如图,在平面直角坐标系中,直线l:分别
交x轴、y轴于A、B两点.点C(2,0)、D(8,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:3.设矩形CDEF与△ABO重叠部分的面积为S.(1)求点E、F的坐标;
(2)求s与b的函数关系式,并写出自变量的取值范围;
(3)若把点O关于直线l的对称点记为点G,在直线l上下平移的过程中,平面上是否存在这样的点P,使得以A、P、E、G为顶点的四边形为菱形?若存在,求出点P的坐标;若不存在,说明理由.
13.如图,在平面直角坐标系中,已知A(0,4),B(2,3).
(1)求出直线AB的解析式;
(2)点P是直线AB上的一个动点,在平面直角坐标系内,是否存在另一个点Q,使得以A,O,P,Q为顶点的四边形是菱形(AP为其中一个边)?若存在,请求出点Q的坐标;若不存在,请说明理由.
14.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴、y轴交于A、B两点,点C是线段AB的中点,点D在线段OC上,OD=2CD.
(1)点C的坐标为;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以为O、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
多年的财务工作实践给了我巨大的舞台来提高自已观察问题、分析问题、处理问题的能力,使我的业务水平和工作能力得到了长足的进步,但我也清醒地认识到,自己的工作中
还存在许多不足之处,今后,我将更加注意学习,努力克服工作中遇到的困难,进一步提高职业道德修养,提高业务学识和组织管理水平,为全县交通事业的发展作出新的贡献。
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求。
