高中物理竞赛复赛专题角动量及其守恒定律36页PPT

角动量守恒教学ppt课件

i
12
M外 Mi外 ri Fi
i
i
----各质点所受外力矩的矢量和称为质点系所受合外力矩
M内 Mi内 (ri fij ) 0
i
i
ji
----各质点所受内力矩的矢量和
（证明如下：）
Fi
m2
m1
mi
fij ri
f ji m j
0
rj
13
内力总是成对出现的，所以内力矩也是成对出
：质量线密度
线积分
对质量面分布的刚体： dm dS
：质量面密度
对质量体分布的刚体：dm dV
：质量体密度
面积分
体积分 26
计算转动惯量 I 的三条有用的定理：
（1）叠加定理:对同一转轴 I 有可叠加性
I Ii
I mr mr mr
m2
I
r1
m1
r2 r3
m3
转轴
（2）平行轴定理: I Ic md 2
常矢量
7
若 M 0 ，则 L 常矢量
M 0
的条件是
— 质点角动量守恒定律
F 0
或 F 过固定点：有心力
（如行星受的万有引力）
角动量守恒定律是物理学的基本定
律之一，它不仅适用于宏观体系，也适用于微观体系，而且在高速低速范围均适用。
8
角动量守恒定律可导出行星运动的开
普勒第二定律：
L
（书P79页例3.1）
i
与内力矩无关 v
守恒条件 M i 0 i
20
§3.3 定轴转动刚体的角动量转动惯量一、定轴转动刚体的角动量
把刚体看作非常多质元构成的质点系，第i个质元对原点o
z v vvi

角动量守恒定律ppt课件

数学补充知识：
点积
abba
aaa2
叉积
a b b a
a a 0
c ( a b ) a ( b c ) b ( a c )
点积的微商叉积的微商
c ( a b ) a ( b c ) b ( c a )
d(a b )a db da b
L
Or v
（对圆心的）角动量：
m
L r p r ( m v ) m r v (r v )
大小：
L mrv
方向：满足右手关系，向上。
2.行星在绕太阳公转时的椭圆轨道运动
对定点（太阳）的角动量：
v
L r p m (r v)
大小： Lmvsrin
v
r
r
Sun
方向：满足右手关系，向上。
L dm trv m ( a c o ti s b si t jn )
( asit in bco t j) s
m m ( a a k c bb (2 恒矢o t k 量 ) a ss b 2 i t k ) n
M
dL
0
!
dt
或由 M rF 直接计算力矩
r a co ti s b sit j n
(1)对C点的角动量是否守恒？
(2)对O点的角动量是否守恒？
C T
O
mg C'
(3)对竖直轴CC'的角动量是否守恒？
请同学思考！
质点系的角动量定理和角动量守恒定律
1.一对作用力、反作用力对定点（定轴）的合力
矩等于零。
证明：
M 1r1f1
M 2r2f2
r2
f2
r
M 1 M 2 r 1 f 1 r 2 f 2

高中物理奥林匹克竞赛专题--第3章-角动量定理和刚体的转动(共44张PPT)

21
例3-3 如图，均质圆形薄板放在水平桌面上，板的半径为R，
板与桌面间的滑动摩擦系数为，令圆板以角速度0开始绕
通过板心且与板面垂直的光滑固定轴O旋转，问圆板转动多
少周后停止？（圆板转动惯量 I mR2 / 2 ）
RO
0
22
摩擦力矩：注意圆板与桌面间摩擦力分布在全部水平接触面上，与转轴等距的细圆环上各点摩擦力对轴的力臂相等；细圆环半径不同，摩擦力对轴的力臂不同，用积分计算总力矩。
垂直轴 11
平行轴定理质量为 m 的刚体，如果对其质心轴的转动惯量为 IC ，则对任一与该轴平行，相距为 d 的转轴的转动惯量：
I // IC md 2
刚体对各平行轴的不同转动惯量中，对质心轴的转动惯量最小。
垂直轴定理一个平面薄板刚体对垂直于平面的任一转轴的转动惯量,等于刚体对在平面内并与该垂直轴相交的任二正交轴转动惯量之和。
EkA

1 2
I
2
AA

1 2
(
2 3
m1R
2
)
2
R2

1 3
m1
2
EkB

1 2
I
2
BB

1 2
(
1 2
m2
r
2
)

r
2 2

1 4
m2
2
20
机械能守恒
1 2
m2 2
m2 gh
1 3
m1 2

1 4
m2 2

0
12m2 gh
4m1 9m2
可利用此装置及分析方法反过来测球壳或位于球壳处的其它不规则形状刚体的转动惯量。

高中物理奥林匹克竞赛专题--刚体角动量角动量守恒定律以及进动(29张ppt)

例2 A、B两圆盘绕各自的中心轴转动，角速度分别为
：A=50rad.s-1, B=200rad.s-1。已知A 圆盘半径
RA=0.2m, 质量mA=2kg, B 圆盘的半径RB=0.1m,
质量mB=4kg. 试求两圆盘对心衔接后的角速度 .
解：以两圆盘为系统，尽管在衔接过程中有重力、轴对圆盘支持力及轴向
u=50m/s远大于飞船的速率v(= r) ，所以此角动量近似地等于dm ru。在整个喷气过程
中喷出废气的总的角动量Lg应为
Lg＝ 0 mdm rumru
定轴转动刚体的角动量守恒定律
当宇宙飞船停止旋转时，其角动量为零。系统这时的总角动量L1就是全部排出的废气的总角动量，即为
L1Lg＝mru
刚体角动量和角动量守恒定律
1. 定轴转动刚体的角动量定理
刚体定轴转动定理：
Mz
d J
dt
由几个物体组成的系统，如果它们对同一给定
轴的角动量分别为、J11 、…J2，2
则该系统对该轴的角动量为：
Lz Jii
i1,2,
i
对于该系统还有 M Zdd LtZd dt i Jii
定轴转动刚体的角动量定理
在外力矩作用下，从 t0 t ，
E1 2JA2 A1 2JBB 21 2JAJB2
1.3 2140J
定轴转动刚体的角动量守恒定律
例题4-13 恒星晚期在一定条件下，会发生超新星爆发，这时星体中有大量物质喷入星际空间，同时星的内核却向内坍缩，成为体积很小的中子星。中子星是一种异常致密的星体，一汤匙中子星物体就有几亿吨质量！设某恒星绕自转轴每45天转一周，它的内核半径 R0 约为 2107m ，坍缩成半径 R 仅为 6103m的中子星。试求中子星的角速度。坍缩前后的星体内核均看作是匀质圆球。

《角动量守恒定律》课件

未来对于角动量守恒定律的研究和应用，将会推动物理学和科技领域的不断发展，为人类社会的进步提供更加坚实的理论基础和技术支持。
05
角动量守恒定律的拓展学习
与角动量相关的其他定律
角动量定理
描述角动量随时间变化的规律，即角动量定理。
拉格朗日定理
与角动量守恒定律相关的另一个重要定理，它描述了系统在保守力作用下的运动规律。
公式
L=r×p，其中L表示角动量，r表示位置矢量，p表示动量。
Байду номын сангаас
角动量守恒的条件
无外力矩作用
系统内力的力矩相互抵消，或者系统受到的外力矩为零。
孤立系统
系统与外界没有能量交换或相互作用，即系统处于孤立状态。
角动量守恒定律的应用场景
01
02
03
天体运动
行星绕太阳的旋转运动、卫星绕地球的运动等都遵循角动量守恒定律。
哈密顿原理
一个描述系统在保守力作用下最短路径的原理，与角动量守恒定律有密切联系。
角动量守恒定律的深入学习资源
《经典力学》教材
深入探讨角动量守恒定律的理论基础和应用，包括数学推导和实
例分析。
网络公开课
一些在线教育平台提供关于角动量守恒定律的深入学习课程，可以作为辅助学习资料。
学术论文
查阅相关学术论文，了解角动量守恒定律在前沿科学研究中的应用和最新研究成果。
们更好地设计和控制卫星轨道。
分子运动实例
总结词
分子转动是微观领域中角动量守恒的实例，对于理解化学反应机理和分子结构具有重要意义。
详细描述
分子转动是指分子中的原子或基团绕分子轴线的旋转运动。在分子转动过程中，分子的角动量是守恒的。这是因为分子内部没有摩擦力矩，从而保证了角动量的守恒。了解和利用角动量守恒定律，可以帮助我们更好地理解和预测化学反应机理和分子结构。

高二物理竞赛角动量角动量守恒课件(共13张PPT)

F
d
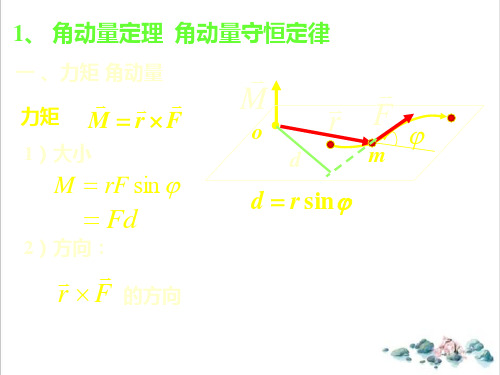
定义r：力对某点O的力矩等于力的作用点的矢
径与力F的矢量积 .
M rF
M
o•
r
F
M
m
注意：
M rF sin r F
4）当 F 0时
下列情况, M 0
A） r 0
B）Mo力•的方向r 沿矢F径的方向
m
sin 0 M
4）当 F 0时
下列情况, M 0
A） r 0
线运动或不能作直线运动。定义：力对某点O的力矩等于力的作用点的矢径与力F的矢量积.
Law of Conservation of Angular Momentum) Law of Conservation of Angular Momentum)
C) 力的方向与转轴平行
C) 力的方向与转轴平行
B）力的方向沿矢径的方向
4）角动量的定义并没有限定质点只能作曲线运动或不能作直线运动。
质点对选取的参考点的角动量等于其矢径与其动量之矢量积。
角动量、角动量守恒 ( Angular Momentum.
Law of Conservation of Angular Momentum)
Law of Conservation of Angular Momentum)
角动量、角动量守恒 ( Angular Momentum. Law
of Conservation of Angular Momentum)
一）角动量
例如天文上行星围绕太阳转。
定义：质点对选取的参考点的角动量等于其矢径 r 与其动量 mv之矢量积。用 L 表示。
L r mv
L
o•
r
mv
注意：1、为表示是对哪个参考点的角动量，通常将角动量L画在参考点上。

人大附中高中物理竞赛辅导课件(力学)运动定律：角动量定理、角动量守恒(共17张ppt)

解：已知
r
a
costi
b
sin
tj
v
dr dt
a
sin
ti
b
costj
L
r
mv
mab cos2 tk mab sin 2 tk
mabk
力径矩r：与M力o力对•F某的点矢rMO量的积F力.r矩等F于力的作用点的矢
d
m
d r sin
注意：
12））大方小向：Mr
rF sin F 的方向
Fd
L
r
mv
L
r
mv
L rmv sin rmv mr 2
质点作直线运动
Z Y
O
r
mv d
X
L L mv或r s：inLmmvvddkˆ
例线在一直质角量坐为标m下的的质矢点径沿为着：一r条空a间co曲s线t运i动，b s该in曲tj
其中a、b、皆为常数，求该质点对原点的角动量。
（河南名校竞赛班讲义）
对上式积分：
Mdt
dL
L2
L1
t1
L1
角动量定理（积分形式）
作用在质点系的角冲量等于系统角动量的增量。
三、角动量守恒定律
若则：
MdL合外0力矩 L0
恒矢量
dt
角动量守恒定律：若对某一参考点, 系统(质点)所
受合外力矩恒为零时，则此质点系(质点)对该参考
点的角动量将保持不变。
注意：1、角动量守恒定律是宇宙中普遍成立的定律，无论在宏观上还是微观领域中都成立。
j
M
O
L vZ0
X
mv (
v0ti
mgv 0 t
1

2020-2021学年高二物理竞赛角动量守恒课件

若人和转台的角速度分别为人 ,台
+ 人 m
因人和台原来都静止故角动量
M
台
X I人 I台 0(1)
mR 2 人
1 2
MR2台
0
人
M 2m
台 (2)
（2）式
×dt积分：
t
0 人dt
M 2m
t
0 台dt
+ 人 m X
t 0
人 dt
M 2m
t
0 台dt
台 M
人
M 2m
台
(3)
人台 2 (4)
（1）沙粒下落使转台的转动惯量发生变化
I I0 mr 2 .......(1)
其中
m dm t 2t.......(2) dt
所以 I 1 MR2 2tr 2 40 2t(kg.m2 ) 2
例5：质量为M＝20kg，半径为R＝2m的转台（可看作匀质圆盘）绕中心竖直轴以匀速ω0 匀速转动，今有沙粒以每秒2kg的速率（dm/dt=2kg/s）垂直落到转台上，在转台上粘附成一半径为r＝1m的圆环。求①试写出转台的转动惯量I随时间t的变化关系式；② 求当沙粒落到转台上使转台转速减到ω0/2 时所需要的时间。
l 2
后
末态的机械能
E2
0
Mg
l 2
l 2
(1
cos
)
mgl(1 cos )
M
M
E1
1 2
I 2
Mg
l 2
+
E2
0
Mg
l 2
l 2
(1
cos
)
mgl(1 cos )
依机械能守恒： E1 E2 (2)

高中物理竞赛复赛专题：角动量及其守恒定律共38页

39、没有不老的誓言，没有不变的承诺，踏上旅途，义无反顾。 40、对时间的价值没有没有深切认识的人，决不会坚韧勤勉。
46、我们若已接受最坏的，就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会，使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首，不会作诗也会吟。——孙洙 50、谁和我一样用功，谁就会和我一样成功。——莫扎特
高中物理竞赛复赛能”这个字(法语是一个字 )，只在愚人的字典中找得到。--拿破仑。 37、不要生气要争气，不要看破要突破，不要嫉妒要欣赏，不要托延要积极，不要心动要行动。 38、勤奋，机会，乐观是成功的三要素。(注意：传统观念认为勤奋和机会是成功的要素，但是经过统计学和成功人士的分析得出，乐观是成功的第三要素。

高二物理竞赛第3章第3讲定轴转动刚体的角动量转动惯量PPT(课件)

i
i
转动惯量
IZ mi Ri2 i
LZ ( mi Ri2 ) IZ i
转动惯量的计算： I mi Ri2 m R2dm i
平行轴定理
Iz Izc md 2
正交轴定理
Iz Ix Iy
l
1 12
ml
2
细圆棒轴通过中心
l
1 3
ml
2
细圆棒轴通过一端
I 1 mR2 2
圆盘轴垂直盘面通过中心
2 23
故细棒摆下角时的角速度为： 3g sin
重力的功 : A E mg l sin
l
p
பைடு நூலகம்
2
法二: 细棒摆动（即转
动）时，重力对0轴的
o
力矩为: 求:物体的加速度和定滑轮的角加速度，以及两边绳子中的张力。
一质量为m，速度为v的子弹射入距支点为a的棒内。刚体对定轴的角动量定理
l 若它与桌面间的滑动摩擦系数为μ，在t=0时，使圆柱体获得一个绕轴旋转的角速度ω。
一、刚体定轴转动的角动量定理
能包括所有的动能和势能.
对质点系而言角动量定理为：由系统角动量守恒(设向外为正方向)
注意：该定律不但适用于刚体，同样也适用于绕定轴转动的任意物体系统。处理刚体定轴转动问题与圆周运动角量描述类似例计算钟摆的转动惯量。（1）分别隔离和
dL dt
M外
2 质点系角动量守恒定律
角加速度：
lim
t 0
t
d
dt
处理刚体定轴转动问题与圆周运动角量描述类似
角量相同（角位移、角速度、角加速度）
线量不同
vi Ri ri
vi Ri
ai ai ainn

高中物理奥林匹克竞赛高分辅导角动量(共18张PPT)

1.051034 (kgm2s1)
此值为狄拉克h： h / 2
15 – 8 多普勒效应
第十五章机械波
例3 一质量 m 1.20104 kg 的登月飞船, 在离
月球表面高度 h 100km 处绕月球作圆周运动.飞船
采用如下登月方式 : 当飞船位于点 A 时,它向外侧短
时间喷气 , 使飞船与月球相切地到达点 B , 且OA 与
飞船在 A点喷出气体后, 在到
达月球的过程中, 机械能守恒
1 2
mv
2 A

G
mM m Rh

即
1 2
mvB2
vA2 vB2
G mM m 2G mMR 2G
Rh
mM R
vB B
R
O
v A v0
v u
A
h
vA 1615 m s1
于是
v

(
v
2 A

v02
点运动到b点，其速率
为 v 。(行星质量为m)
L

作直线bc垂直于oa，因t很小 ab ab s
s vt h ssin vt sin
t时间内扫过的面积
A 1 rh 1 rvt sin 1 mrv sin t
22
2m
15 – 8 多普勒效应
t2
L2
Mdt dL L2 L1 6
t1
L1
t2
Lx 2
写成分量式: M xdt dLx Lx2 Lx1
t1
Lx1
t2
Ly 2
M ydt dLy Ly2 Ly1
t1
Ly1

第角动量角动量守恒定律PPT课件

(练习二，17)
解设猴子、重物对地面的速度分别为
。
由猴、重物组成的系统角动量守恒，得
v1、v 2
v1 v2
R
∵ v1 v猴绳 v绳-地 v v绳-地
v1
v2
而 v绳地 v物地 v2 , 则 v1 v v2
∴
v2
v 2
第23页/共29页
机械能不守恒
力物的猴拉加，力由速于上和轻爬相绳过等各程m，处中1又g张，因力绳为相对猴等猴和，的物所拉相以力同在大质另于量一猴，端的绳重对重T1
[ C]
第9页/共29页
第五章角动量、角动量守恒定律
本章主要阐述三个问题：
1）角动量。 2）角动量守恒定律。 3）有心力与角动量守恒定律。 3）有心力与角动量守恒定律。
第10页/共29页
5-3 有心力与角动量守恒定律
自然界中有些力具有这样的性质：力的方向始终通过某一固定点，力的大小仅依赖于质点与这个点之间的距离。我们称这样的力为有心力，相应的固定点称为力心。例如，万有引力是有心力；静电作用力也是有心力。
作半径为的m圆轨道运动。取圆周上点R为参考点，如图所示，试求：①质P点
在图中点1处所受的力矩和质点的角动量
的力矩和质点的角动量。
；②质m点
在图中点2处所受
M1
L1
m
M2
L2
解 ① 力矩 M 1
2
在点1处，所m受引力指向点，故 P M 1 0
角动量 L1
由 m作圆周运动的动力学方程，可得速度
A 另离一端系向一右质，运量绳O动子，处到于达松位的弛置物状体态时。。物开O现体始A在速时使度，物的物体方m体以向位与与于0绳.位5d垂k置垂g直直0。处.的2试，5初求m速物度间体的在距处

高二物理竞赛角动量定理角动量守恒定律课件

的速率向东奔跑, 他感到风从北方吹来,当他奔跑的速率加倍时, 则感到风从东北方向吹来, 求风的速度。
或牛顿力学规律在伽利略变换下形式不变
A,B,C三个质点相互间有相对运动
M dL F dp
dt
dt
对质点系而言：（以两个质点为例）
设有质点m1 、 m2
分别受外力 F1 F2
外力矩 M1 M2
作用在质点系的角冲量等于系统角动量的增量。
三、角动量守恒定律
若则：
M合
dL
外
力
矩 0
0L
恒矢量
dt
M dL dt
角动量守恒定律：若对某一参考点, 系统(质点)所受合外力矩恒为零时，则此质点系(质点)对该参考点的角动量将保持不变。
注意：角动量守恒定律是宇宙中普遍成立的定律，无论在宏观上还是微观领域中都成立。
已知：
v sd = 10 正东
vcs
v fd = 10 v cs = 20
正西北偏西30o
•
vfd vsd
vcd vcs v sd
vcd 10 3 km / h 方向正北
vcs vcd
v fd v fc vcd
300
v fc v fd vcd
人地 cos 450
2人
地
4.23(m
s
1
)
质点动力学(二) 人地人地
450 450
风人
风地
二、力学的相对性原理
aAC aAB aBC
aBC 0, 同一质点的加速度在两个相互间作匀速 aAC aAB 直线运动的参照系中是相同的。
在牛顿力学中,力与参考系无关，质量与运动无关 F F