C均值聚类实验报告
kmeans作业实验报告

1.仔细阅读ppt,利用自己所熟悉的语言编写一 个c-means聚类算法,并运行ppt中的例子数据。
2.要求撰写实验报告。
3.完成后要检查代码。
1
2· 4 聚类的算法
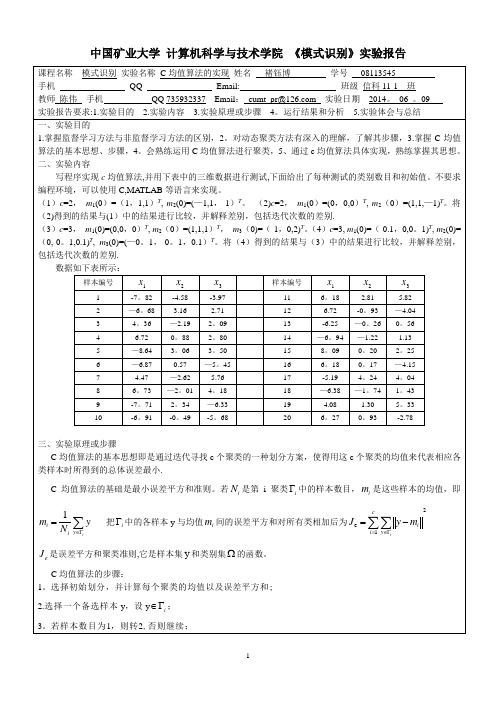
2.4.3 动态聚类法——C-均值法 ⒈ 条件及约定 x1, x2 ,, xN 设待分类的模式特征矢量集为: 类的数目C是事先取定的。 ⒉ 算法思想 该方法取定 C个类别和选取 C个初始聚类中 心,按最小距离原则将各模式分配到 C类中的某 一类,之后不断地计算类心和调整各模式的类别, 最终使各模式到其判属类别中心的距离平方之和 最小。 2
1 0 x2 ( )-( ) =1 Z1 (1) = 0 0
7
1 1 x2 Z 2 (1) ( ) ( ) 0 0 0 因为 x2 Z1 (1) > x2 Z 2 (1) , 所以 x2 Z 2 (1)
x3 Z1 (1) =1 < x3 Z 2 (1) 2 ,\ x3 Z1 (1) x4 Z1 (1) = 2 > x4 Z 2 (1) 1,\ x4 Z 2 (1) ... x20 与第二个聚类中心的距 同样把所有 x5、 x6、 ... x20 都属于 Z 2 (1) 离计算出来,判断 x5、 x6、
同理
因此分为两类:
一、 G 1 (1) ( x 1 , x 3 ), N 1 2 , N 2 18 二、 G 2 (1) ( x2 , x4 , x 5 ,... x20 )
8
10
9 8
X2
7 6
5
4
Z
(1) 2
x12
c均值算法c++实现实验报告

基于模糊C均值的聚类分析

• Columns 7 through 12
0.01486
0.015919 0.88683 0.082394
0.070257 0.97808
0.54463 0.0055741 0.2854 0.0068329 0.099713 0.009517
0.931 0.015668 0.94372
0.017272 0.020349 0.031376
0.035002 0.8824 0.053315
0.029278
• Columns 25 through 30
0.068372 0.026621 0.96861 0.96367 0.98434 0.006666 0.036258 0.03739 0.0060731 0.0085095 0.0033354 0.0069366 0.14864 0.86903 0.0092717 0.011597 0.0048348 0.95254 0.74673 0.066961 0.016046 0.016226 0.007487 0.033862
此时,目标函数在4.8339e+006处收敛, 算法结速
由得出的聚类中心矩阵及隶属度矩阵就 可以进行分类了:聚类中心矩阵有4行, 每一行代表一类及四类,3列,每一列代 表一种颜色;由隶属度矩阵中Columns 1 through 6为例:
0.033201 0.97007 0.029789 0.056082 0.92626 0.071666 0.029521 0.0058525 0.047123 0.020886 0.017596 0.020368 0.64897 0.0088617 0.84987 0.11948 0.023937 0.076162 0.28831 0.015217 0.073223 0.80355 0.032208 0.8318
模糊c均值聚类 地震 电阻率

模糊c均值聚类地震电阻率下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!地震勘探是一种常用的地球物理勘探方法,通过对地下介质的电阻率进行测量,可以有效地研究地壳结构和地质构造,为地质勘探和资源开发提供重要信息。
C均值聚类算法的C语言实现

C均值聚类算法的C语⾔实现/**C均值聚类算法的C语⾔实现Author:AnranWuDate:2020/11/25*/#include<stdio.h>#include<string.h>#include<math.h>#include<algorithm>using namespace std;typedef long long ll;const ll maxn=1e6+50;const double eps=1e-2;struct node{double x=0,y=0;}a[maxn],b[maxn],sum[maxn];int belong[maxn],cnt[maxn];double dis(node a,node b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));}int main(){int c,n;printf("请输⼊需要将模式分为的类别数 c :");scanf("%d",&c);printf("请输⼊模式总数 n :");scanf("%d",&n);//输⼊需要聚类的模式数printf("请输⼊各模式的两个特征点:\n");for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y);//输⼊每个模式的两个特征for(int i=1;i<=c;i++)b[i]=a[i];//选定初始的c个聚类中⼼int ans=0;//ans表⽰与上次聚类中⼼⼀致的聚类中⼼点数量,当所有聚类中⼼均不发⽣改变时循环结束while(ans<c){memset(cnt,0,sizeof(cnt));//cnt记录每⼀个类别有多少个模式属于该类for(int i=1;i<=n;i++){double minn=4e18;//计算该模式到每⼀个聚类中⼼的距离int mini=0;for(int j=1;j<=c;j++){double dis_to_center=dis(a[i],b[j]);if(dis(a[i],b[j])<minn){minn=dis_to_center;mini=j;}}belong[i]=mini;//选择距离最⼩的⼀个类加⼊该类cnt[mini]++;//更新该类中模式的数量}for(int i=1;i<=c;i++)sum[i].x=0,sum[i].y=0;for(int i=1;i<=n;i++){sum[belong[i]].x+=a[i].x;sum[belong[i]].y+=a[i].y;//计算新的聚类中⼼}ans=0;for(int i=1;i<=c;i++){sum[i].x/=cnt[i];sum[i].y/=cnt[i];//判断该聚类中⼼是否发⽣变化,eps控制容差值if((fabs(sum[i].x-b[i].x)<eps)&&(fabs(sum[i].y-b[i].y)<eps))ans++;b[i].x=sum[i].x;b[i].y=sum[i].y;//更新聚类中⼼}}printf("C均值聚类算法已经完成!\nc个类中⼼分别为\n");for(int i=1;i<=c;i++){printf("第%d类的聚类中⼼的两个特征值分别为 %.2lf %.2lf\n",b[i].x,b[i].y);}for(int i=1;i<=c;i++){printf("属于第%d类的点有:\n");for(int j=1;j<=n;j++){if(belong[j]==i)printf("%d号点 %.2lf %.2lf\n",j,a[j].x,a[j].y);}putchar(10);}}/*测试数据 #12200 01 00 11 12 11 22 23 26 67 68 66 77 78 79 77 88 89 88 99 9 */。
基于PSO的可能性C均值聚类算法的研究

f c o , h e t o t a du t n tepo eso ls r g ho g et g tegvn d t e , h e ut u t n tec ne p i s r aj s d i rc s f u t n .T ru hts n i a s t te r l n i r n e e h c e i i h e a s s
s o ta OPCM g rt m a r a e mprve e ti o e g n e s e d a d go a ptmiain b lt. h w h tPS l a o ih h s a g e t ri o m n n c nv r e c p e n l b lo i z t o a iiy
第2 卷 第9 7 期
文章 编 号 :0 6—94 ( 0 0 0 10 3 8 2 1 )9~0 7 17—0 4
计
算
机
仿
真
21年9 0 0 月
基 于 P O 的可 能 性 C均值 聚 类算 法 的研 究 S
高 颖, 王修 亮 , 陆旭 青 , 允锋 殷
( 北 工 业 大 学 水 下 信 息处 理 与控 制 重 点 实 验 室 , 西 西 安 7 07 ) 西 陕 10 2
me n lo i m o s s a s ag r h t n i .Ho e e ,i as a o ee t ,s c se sl al n ol c l p i m,s n i vt t o e w v r t loh ss med fcs u h a a i t f l i t o a t yo o mu e st i t i yo ii a o d t n n e d n o c n i e c f l se n e u t .F rt e a o e p o lms h a t l w m]o t — n t c n i o s a d l a i gt o ss n y o u tr g r s l i l i t c i s o h b v r b e ,t e p ri e s a c pi mi z t n a g r h c e i rv d t v i h m o o sbl t —me n l o t m ,w ih i a d P OP M.T e ai lo t m a b mp e o a od t e frp s i i si C o i n o i c a s ag r h i h c sn me S C h
模糊C均值(FuzzyC-Means)聚类论文:模糊C均值(FuzzyC-Means)聚类支..

模糊C均值(Fuzzy C-Means)聚类论文:模糊C均值(Fuzzy C-Means)聚类支持向量机(SVM) Laws纹理测同质性模型 Gabor滤波器【中文摘要】图像分割是图像处理的一个重要工具,一个有效的、前端的、复杂的算法。
它能够简化对图像的后续处理,并在视频和计算机视觉方面都有应用,如目标定位或识别、数据压缩、跟踪、图像检索等等。
虽然大量的图像分割算法已被广大研究者提出并改进,但是没有人提出一种完美的,适合于任何一种图像的分割算法,现有的方法都多少存在着方法或算法上的不足。
因此到目前为止,图像分割作为一个重要工具的同时,仍然是图像处理领域的一个具有挑战性的难题。
当前,对基于像素级、多特征、多种分割算法相结合的分割方法的研究,已经成为图像分割领域的热点。
通过认真总结,本文对模糊聚类算法和优于传统机器学习的支持向量机方法,从理论和实验结果等方面都进行了全面系统的比较和分析。
通过像素颜色,纹理等特征来描述图像的具体信息,并结合模糊C均值聚类(FCM,Fuzzy C-Means)算法和支持向量机(SVM)的方法展开实验,主要任务如下:1.本文对模糊聚类算法特别是模糊C均值聚类(FCM,Fuzzy C-Means)分割算法进行细致深入的研究探讨,并认真研究了模糊聚类图像分割算法中初始聚类类别数确定、初始聚类中心和隶属度函数的选择。
2.以模糊C均值聚类(FCM,Fuzzy C-Means)理论为基础,提出了一种结合laws纹理测度与自适应阈值的FCM聚类算法对图像进行分割。
通过大量实验对比表明,该算法与人的视觉感知系统一致性好,对噪声有良好的抑制效果,节省实验过程中程序运行的时间,提高图像分割速度。
3.通过核函数类型、核参数、惩罚因子等因素,对采用支持向量机(SVM)进行图像分割的方法的可行性进行了分析、研究,提出了一种基于无监督的支持向量机分类算法,为使用支持向量机方法(SVM)进行图像分割提供了依据。
模糊C均值聚类算法实现与应用

模糊C均值聚类算法实现与应用聚类算法是一种无监督学习方法,在数据挖掘、图像处理、自然语言处理等领域得到广泛应用。
C均值聚类算法是聚类算法中的一种经典方法,它将数据对象划分为若干个不相交的类,使得同一类中的对象相似度较高,不同类之间的对象相似度较低。
模糊C均值聚类算法是对C均值聚类的扩展,它不是将每个数据对象划分到唯一的类别中,而是给每个对象分配一个隶属度,表示该对象属于不同类的可能性大小。
本文主要介绍模糊C均值聚类算法的实现方法和应用。
一、模糊C均值聚类算法实现方法模糊C均值聚类算法可以分为以下几个步骤:1. 确定聚类数k与参数m聚类数k表示将数据分成的类别数目,参数m表示隶属度的度量。
一般地,k和m都需要手动设定。
2. 随机初始化隶属度矩阵U随机初始化一个k×n的隶属度矩阵U,其中n是数据对象数目,U[i][j]表示第j个对象隶属于第i个类别的程度。
3. 计算聚类中心计算每个类别的聚类中心,即u[i] = (Σ (u[i][j]^m)*x[j]) / Σ(u[i][j]^m),其中x[j]表示第j个对象的属性向量。
4. 更新隶属度对于每个对象,重新计算它对每个类别的隶属度,即u[i][j] = 1 / Σ (d(x[j],u[i])/d(x[j],u[k])^(2/(m-1))),其中d(x[j],u[i])表示第j个对象与第i个聚类中心的距离,k表示其他聚类中心。
5. 重复步骤3和4重复执行步骤3和4,直到满足停止条件,例如聚类中心不再变化或者隶属度矩阵的变化趋于稳定。
二、模糊C均值聚类算法应用模糊C均值聚类算法可以应用于多个领域,包括图像处理、文本挖掘、医学图像分析等。
下面以图像分割为例,介绍模糊C均值聚类算法的应用。
图像分割是图像处理中的一个重要应用,旨在将一幅图像分割成多个区域,使得同一区域内的像素具有相似度较高,不同区域之间的像素相似度较低。
常见的图像分割算法包括全局阈值法、区域生长法、边缘检测法等。
基于模糊C均值聚类的彩色图像分割方法研究的开题报告

基于模糊C均值聚类的彩色图像分割方法研究的开题报告一、选题背景图像分割是计算机视觉、图像处理领域研究的重要方向之一,是将一个复杂的图像分成若干个子区域,使得每个子区域的像素具有相同或相似的属性,从而达到人们所期望的目的。
图像分割应用广泛,如医学图像分析、遥感图像分析、自动驾驶、移动机器人导航等。
在图像分割算法中,模糊聚类算法因其能够处理模糊的图像信息而备受研究者关注。
模糊C均值聚类算法是模糊聚类算法的一种,其具有简单易实现的特点,适用于各种领域的图像分割。
在彩色图像分割中,模糊C均值聚类算法也被广泛应用。
然而,传统的模糊C均值聚类算法在彩色图像分割中存在一些问题,如难以处理颜色的相似度,以及对图像噪声不够鲁棒等。
因此,本次研究旨在探讨基于模糊C均值聚类算法的彩色图像分割方法,通过对算法进行改进和优化,提高其对颜色相似度的处理能力和噪声鲁棒性,以提高算法的可靠性和分割效果。
二、研究内容和方法1. 分析彩色图像的特点和分割需求,探究模糊C均值聚类算法在彩色图像分割中存在的问题和不足。
2. 提出一种基于模糊C均值聚类的彩色图像分割方法,并对其进行优化改进。
具体来说,可以采用以下方法:(1)基于颜色空间的特征提取方法,提高颜色相似度的处理能力;(2)利用自适应权重系数改进分类精度;(3)通过多次迭代优化算法效果,降低噪声对分割结果的影响。
3. 在多个数据集上进行实验验证,采用比较性分析、数值评价和视觉评价等方法,测试算法的可靠性和分割效果。
三、研究意义和预期成果本次研究将解决传统模糊C均值聚类算法在彩色图像分割中的问题和不足,提高其对颜色相似度的处理能力和噪声鲁棒性,实现对彩色图像的精确分割。
这将在医学图像分析、自动驾驶、环境监测等领域具有重要应用价值。
预期的研究成果包括:理论分析和彩色图像分割方法的设计方案、改进的模糊C均值聚类算法实现代码、测试数据集和实验结果分析等。
模糊C均值聚类及其有效性检验与应用研究

模糊C均值聚类及其有效性检验与应用研究一、内容概要本研究专注于模糊C均值聚类(Fuzzy Cmeans Clustering),这是一种在数据挖掘和模式识别领域广泛应用的无监督学习方法。
通过结合模糊理论和聚类技术,Fuzzy C均值聚类能够在模糊数据集中发现并提取有价值的信息。
引言: 介绍模糊集理论的基本概念,并阐述模糊C均值聚类算法的起源和基本原理,以及其在各领域的应用前景。
模糊C均值聚类算法: 详尽描述算法的具体步骤,包括初始化、模糊划分、聚类和迭代优化等,以及对初始聚类中心的选择和算法终止条件的设定进行深入探讨。
模糊C均值聚类的有效性检验: 探讨如何准确评估聚类结果的性能。
首先定义了聚类效果的评估指标,如轮廓系数和DaviesBouldin 指数,并提出了基于这些指标的聚类有效性检验方法。
案例分析: 通过实际应用案例,展示模糊C均值聚类算法在处理各类复杂数据集时的表现。
案例涵盖了图像分割、文档聚类和生物信息学等领域的数据分析。
应用研究: 探讨模糊C均值聚类算法在不同领域的应用潜力,如金融风控、智能交通和医疗诊断等。
针对特定应用场景,提出了一系列基于模糊C均值聚类的特征选择和降维策略。
结论: 总结研究成果,强调模糊C均值聚类算法在解决实际问题中的有效性和实用性,并指出未来研究方向,旨在进一步完善算法性能并拓展其应用领域。
本研究通过对模糊C均值聚类算法进行系统性的理论分析和案例验证,不仅揭示了其有效的聚类性能,还在多个实际应用领域展现出巨大的潜力和价值。
1.1 背景及意义随着计算机技术的不断发展,数据量呈现爆炸式增长,使得对数据的处理和分析变得越来越重要。
在众多数据处理方法中,聚类作为一种无监督学习方法,被广泛应用于各种领域,如图像处理、模式识别、文档聚类等。
传统的聚类算法如Kmeans、层次聚类等虽已取得一定的应用成果,但往往存在对初始中心点选择敏感、对噪声敏感、局部最优解等问题。
模糊C均值聚类(Fuzzy Cmeans Clustering,简称FCM)是一种基于模糊集理论和传统C均值聚类的改进算法。
模糊聚类实现鸢尾花(iris)分类实验报告

模糊聚类实现鸢尾花(iris)分类实验报告实验报告:模糊聚类实现鸢尾花(iris)分类一、实验目的本实验旨在通过模糊聚类算法对鸢尾花(iris)数据集进行分类,并比较其分类效果与传统的硬聚类算法。
二、实验原理模糊聚类是一种基于模糊集合理论的聚类分析方法。
与传统的硬聚类算法不同,模糊聚类能够为每个样本赋予一个隶属度,表示该样本属于某个簇的程度。
常用的模糊聚类算法包括模糊C-均值聚类(FCM)和概率模糊C-均值聚类(PFCM)。
三、实验步骤1. 数据准备:加载鸢尾花数据集,将数据分为特征和标签两部分。
2. 数据预处理:对特征数据进行归一化处理,使其满足模糊聚类的要求。
3. 构建模糊矩阵:根据给定的模糊参数,构建模糊矩阵。
4. 执行模糊聚类:使用模糊聚类算法对数据进行聚类,得到每个样本的隶属度矩阵。
5. 分类结果输出:根据隶属度矩阵和阈值,将样本分为不同的类别。
6. 评估分类效果:计算分类准确率、召回率等指标,评估分类效果。
四、实验结果以下是使用模糊C-均值聚类算法对鸢尾花数据集进行分类的结果:样本实际类别预测类别隶属度1 setosa setosa2 versicolor versicolor3 virginica virginica... ... ... ...150 setosa setosa151 versicolor versicolor152 virginica virginica通过观察上表,我们可以发现大多数样本被正确地分类到了所属的类别,且具有较高的隶属度。
具体分类准确率如下:setosa: 97%,versicolor: 94%,virginica: 95%。
可以看出,模糊聚类算法在鸢尾花数据集上取得了较好的分类效果。
五、实验总结本实验通过模糊聚类算法对鸢尾花数据集进行了分类,并得到了较好的分类效果。
与传统硬聚类算法相比,模糊聚类能够为每个样本赋予一个隶属度,更准确地描述样本属于各个簇的程度。
模式识别——C均值算法的实现【范本模板】
2
class 2: (—8.64,3.06, 3。50) (-6.25, -0.26,0.56)(—6.94, -1。22, 1.13) (—5.19, 4.24, 4.04)(-6。38,—1。74,1.43) (-6。 68,3。16,2。71)
m1(0)=(—0.1,0,0。1) T , m2(0)=(0,—0。1,0.1) T , m3(0)=(—0.1,-0.1,0.1) T
m2(0)=(1,1,1) T , m3(0)=(—1,0,2) T
current Je is:263.06184
after recalculate mean by 35 steps class 0: (-6。87, 0.57, —5.45) (-7。71, 2。34, —6.33) (—6。91, -0。49, -5。68) (-7。82,-4。58,-3,。97) class 1: (6。72, 0.88, 2。80) (4.47, —2。62, 5.76) (6.73, -2.01, 4.18) (6。18, 2。81, 5。82) (6。72, —0。93, -4。 04) (8。09, 0.20, 2.25) (6。18, 0.17, -4。15) (4.08, 1。30, 5.33) (6.27, 0。93, —2.78)(4。36,-2。19,2。09)
3。若样本数目为1,则转2,否则继续;
1
4.计算 j :j≠i 时, j
Nj N j 1
ymj
2;
j=i 时,
i
Ni Ni 1
y mi
2;
5.考查 j 中的最小者 k ,若 k i ,则把 y 从 i 移到 k 中;
6.重新计算聚类 i 和 k 的均值,并修改误差平方和;
颜色聚类实验报告

一、实验目的本次实验旨在通过颜色聚类算法,对一组图像中的颜色进行有效的分类和简化,从而降低图像的复杂度,提高图像处理的效率。
实验中将采用C-均值法和最大最小距离法进行颜色聚类,并对两种算法的性能进行比较。
二、实验内容与方法1. 数据准备实验数据为一组包含不同场景的图像,每张图像中包含多种颜色。
实验过程中,我们将提取每张图像的RGB颜色空间中的颜色向量。
2. 聚类算法(1)C-均值法C-均值法是一种基于距离的聚类算法,其基本思想是将数据集中的每个样本分配到距离最近的聚类中心,通过迭代优化聚类中心,使每个样本与其聚类中心的距离平方和最小。
(2)最大最小距离法最大最小距离法是一种基于最小距离的聚类算法,其基本思想是将数据集中的每个样本分配到距离最近的聚类中心,同时保持聚类中心之间的距离最大。
3. 实验步骤(1)提取图像颜色向量对每张图像进行颜色提取,得到其RGB颜色空间中的颜色向量。
(2)选择聚类算法分别采用C-均值法和最大最小距离法进行颜色聚类。
(3)设置聚类数目K根据实验需要,设置聚类数目K,通常取K为2或3。
(4)聚类结果分析分析两种聚类算法的聚类结果,包括聚类中心、样本分配情况等。
(5)图像简化将原始图像中的颜色向量替换为聚类中心,得到简化后的图像。
(6)误差计算计算简化后图像与原始图像的误差,包括失真度等指标。
三、实验结果与分析1. 聚类结果分析(1)C-均值法C-均值法将图像中的颜色向量分为2个或3个簇,每个簇对应一个聚类中心。
通过观察聚类中心,可以看出不同颜色簇的分布情况。
(2)最大最小距离法最大最小距离法同样将图像中的颜色向量分为2个或3个簇,聚类中心分布情况与C-均值法类似。
2. 图像简化效果分析通过将原始图像中的颜色向量替换为聚类中心,得到简化后的图像。
对比原始图像和简化后的图像,可以看出两种聚类算法在图像简化方面的效果。
3. 误差分析(1)失真度通过计算简化后图像与原始图像的失真度,可以评估图像简化的效果。
实验2 C均值实验

实验二K均值实验一.实验目的本实验的目的是使学生了解K均值聚类方法,掌握K均值聚类分析法的基本原理,培养学生实际动手和思考能力,为数据分析和处理打下牢固基础。
二.K均值聚类算法该算法以欧氏距离为基础,首先确定K个聚类中心,然后将所有样本就近归类,再对每个类计算均值作为新的聚类中心,再就近归类所有样本,再对每个类计算均值作为新的聚类中心,直到聚类中心不再变化,即两次的聚类中心相同为止。
最后将样本按最小距离原则归入最近的类。
例:样本分布如下图表所示。
可在取k=3时得到相应的聚类结果。
三.实验内容见右图所示,为二维点集。
四.实验步骤1、提取分类特征,确定特征值值域,确定特征空间;2、改编K均值聚类程序, 将所提取的样本的加以聚类;(取K=4),要求以任意的K个样本作为初始的K个中心。
提示:使用随机置换函数randomperm(N),取其前K个分量作为样本下标,对应的K个样本各成中心。
randPattern=randperm(N);for i=1:Kpattern(randPattern(i)).category=i;pattern(randPattern(i)).distance=0;%每个样本到中心点的距离center(i).feature=m_pattern(randPattern(i)).feature;center(i).index=i;center(i).patternNum=1;end3、用误差平方和准则(也可选用其他准则)加以评价,直到满意为止,即用不同K 值加以实验,直到找到一个合适的K值(即类数)为止。
提示:为便于计算误差平方和准则,每个样本增加存放其到中心点的距离成分distance附:1.求每个类的中心的函数:function y=CalCenter(center, pattern, N)[k,m]=size(pattern(1).feature);% k为样本行数,m为样本列数s=zeros(1,m);loccount=0;for i=1:Nif pattern(i).category==center.indexs=s+pattern(i).feature;loccounter=loccount+1;endendy.feature=s/loccount;y.index=center.index;y.patternNum=loccount;end2.K均值算法函数:(取k=2)sample=[ 0 0;3 8;2 2;1 1;5 3;4 8;6 3;5 4;6 4;7 5];[N,m]=size(sample);clc% K=2; %取k=2K=input('输入类数k='); %类数由输入给定iterNum=100;for i=1:Npattern(i).feature=sample(i,:);pattern(i).category=-1;endfor i=1:K %取前K个样本各成一类pattern(i).category=i;center(i).feature=pattern(i).feature;center(i).index=i;center(i).patternNum=1;endcount=0; % 循环次数change=1; % 用change控制循环,也由其作标志,记录是否进行了样本类别的改变% 若没有样本类别改变,两次的中心点也不改变while (count<iterNum & change==1)count=count+1;change=0;for i=1:N %对所有样本重新归类%计算各个样本到各个聚类中心的最小距离index=-1;mindis=inf;for j=1:Kdis=sqrt((pattern(i).feature-pattern(j).feature)*(pattern(i).feature-pattern(j).feature)');if dis<mindismindis=dis;index=j;endendif (pattern(i).category~=index)oldIndex=pattern(i).category; %记录原类号pattern(i).category=index; %归入新类if(oldIndex~=-1)center(oldIndex)=Calcenter(center(oldIndex),pattern,N);endcenter(index)=Calcenter(center(index),pattern,N);change=1;endendenddisp('显示中心:')for i=1:Kfprintf('center %d',center(i).index)disp(center(i).feature)%center(i).patternNumenddisp('显示样本的聚类:')for i=1:Nfprintf('pattern %d: category:%d, pattern: ',i,pattern(i).category)disp(pattern(i).feature)end。
C均值聚类实验报告

C 均值聚类实验报告一、C 均值聚类的算法原理聚类分析是指事先不知样本的类别,而利用样本的先验知识来构造分类器(无监督学习)聚类准则函数在样本相似性度量的基础上,聚类分析还需要一定的准则函数,才能把真正属于同一类的样本聚合成一个类的子集,而把不同类的样本分离开来。
如果聚类准则函数选得好,聚类质量就会高。
同时,聚类准则函数还可以用来评价一种聚类结果的质量,如果聚类质量不满足要求,就要重复执行聚类过程,以优化结果。
在重复优化中,可以改变相似性度量,也可以选用新的聚类准则。
误差平方和准则(最常用的)假定有混合样本集 ,采用某种相似性度量被聚合成c 个分离开的子集 ,每个子集是一个类, 它们分别包含个 样本 。
为了衡量聚类的质量,采用误差平方和聚类准则函数式中为类中样本的均值:是c 个子集合的中心,可以用来代表c 个类。
误差平方和 聚类准则函数是样本与集合中心的函数。
在样本集X 给定的情况下, 其取值取决于c 个集合“中心”。
它描述n 个试验样本聚合成c 个类时,所产生的总误差平方和 越小越好。
误差平方和准则适用于各类样本比较密集且样本数目悬殊不大的样本分布。
C-均值聚类算法的核心思想是通过迭代把数据对象划分到不同的簇中,以求目标数最小化,从而使生成的簇尽可能地紧凑和独立。
首先,随机选取k 个对象作为初始的k 个簇的质心;然后,将其余对象根据其与各个簇质心的距离分配到最近的簇;再求新形成的簇的质心。
12{,,...,}n X x x x =X cX X X ,.....,,21c n n n ,......,,21c J ∑∑==-=cj n k j k c jm x J 112||||j m ∑==jn j jjj xn m 11cj ,....,2,1=j m c J cJ这个迭代重定位过程不断重复,直到目标函数最小化为止。
C -均值聚类算法使用的聚类准则函数是误差平方和准则 : 为了使聚类结果优化,应该使准则最小化。
模式识别实验---C-均值算法与模糊C均值聚类的比较

实验一、C-均值算法与模糊C 均值聚类的比较一、实验目的1. 通过对算法的编程实现,加强对该算法的认识和理解,提高自身的知识水平和编程能力,认识模式识别在生活中的应用; 2. 深入理解C 均值和模糊C 均值的基本原理; 3. 采用两种分类方式进行仿真;二、 实验原理1.C 均值的原理;C 均值聚类算法是一种典型的无监督动态聚类算法。
该算法是在类别数目已知(=k )的条件下进行的,能够使聚类结果的距离平方和最小,即算法的基础是误差平方和准则。
其基本过程是建立初始的聚心和聚类,通过多次迭代,逐渐调整各类的聚心和各像元的类别,直至得到聚类准则约束下的最好结果为止。
本实验的具体过程如下:选择初始类别中心,假设有c 个类别,设置其中心分别为(1)(1)(1)12,,,c Z Z Z在第k 步迭代中,对于任何一个像元x(是一个N 维向量,N 是高光谱图像的波段数目),按如下方法把它调整到。
各类别中的某一个类别中去。
令d(x ,y)为向量x ,y 之间的距离,若:()()(,)(,)k k i j d x Z d x Z <=, j = 1 2 … c (j i ≠)则()k i x S ∈,其中()k i S 是以()k i Z 为中心的类。
由上一步得到的()k i S (i =1 2…c )个类别新的中心(1)k i Z +()(1)1k i k i x S iZ x N +∈=∑其中N i 是类别()k i S 的数目。
(1)k i Z +是按照最小J 的原则,J 的表达式为:()(1)1(,)k i ck ii x S J d x Z+=∈=∑∑对所有的i =1 2…c 。
如果,(1)()k k i i Z Z +=,则迭代结束(在程序中,则按照每个类别的对应的那些像素不再变化,则停止迭代),否则转到第二步继续迭代。
2.模糊C 均值的原理在数字图像由于存在混合像素的原因,也就是说一个像素中不仅存在一类地物,因而采用硬分类方式往往不合适,而模糊C 均值就是引入模糊集对每个像素的划分概率不单单是用0或1这样的硬分类方式,而是0和1之间的范围内(包括0和1)。
均值聚类算法试验目的通过本次试验学习用均值聚类分割彩色图像

均值聚类算法实验目的:通过本次实验学习用均值聚类分割彩色图像的方法。
实验方法:一聚类分析聚类分析按照某个相似测试将未标记的样本集分成若干个类,使同一类中的样本尽可能地相似,不同类中的样本尽可能地不相似。
确定数据集中样本相似性的常用方法是欧式距离。
按照聚类结果表现方式的不同,现有的聚类分析算法可以分为:硬聚类算法、模糊聚类算法和可能性聚类算法。
1 在硬聚类算法中,分类结果用样本对各类的隶属度表示。
样本对某个类别的隶属度只能是0 或1。
样本对某个类别的隶属度为1 表示样本属于该类;样本对某个类别的隶属度为0 则表示样本不属于该类。
样本只能属于所有类别中的某一个类别。
早期的聚类算法都是硬聚类算法。
传统的硬聚类算法包括:C-均值、ISODATA、FORGY、WISH 等。
硬聚类方法具有花费时间少的优点,缺点是:硬聚类割断了样本与样本之间的联系,无法表达样本在性态和类属方面的中介性,使得所得的聚类结果偏差较大,并且容易陷入局部最优解。
2 在模糊聚类算法中,分类结果仍旧用样本对各类的隶属度表示,只是样本对某个类别的隶属度在区间[0,l ]内取值,样本对所有类别的隶属度之和为1。
模糊聚类能够有效地对类与类之间有交叉的数据集进行聚类,所得的聚类结果明显要优于硬聚类,能更加客观和准确地反应现实世界的实际情况。
同与硬聚类算法相比,提高了算法的寻优概率,但模糊聚类的速度要比硬聚类慢。
3 可能性聚类算法中,分类结果以样本对各类的典型程度表示。
样本对某个类别的典型程度在区间[0,1]内取值。
可能性聚类算法是聚类分析与可能性理论的结晶。
第一个可能性聚类算法是R.Krishnapuram 和JM.Keller 在1993年提出的。
可能性聚类不仅顾及到每个样本与各个聚类中心的隶属关系,而且考虑到样本的典型性对分类结果的影响,能够对含有噪声的数据集进行聚类,抑制噪声能力很强。
研究表明:可能性聚类与传统的鲁棒性统计理论有密切的关系。
对数据进行聚类分析实验报告

对数据进行聚类分析实验报告基本要求用FAMALE.TXT、MALE.TXT和/或test2.txt的数据作为本次实验使用的样本集,利用C均值和分级聚类方法对样本集进行聚类分析,对结果进行分析,从而加深对所学内容的理解和感性认识。
二、实验要求1、把FAMALE.TXT和MALE.TXT两个文件合并成一个,同时采用身高和体重数据作为特征,设类别数为2,利用C均值聚类方法对数据进行聚类,并将聚类结果表示在二维平面上。
尝试不同初始值对此数据集是否会造成不同的结果。
2、对1中的数据利用C均值聚类方法分别进行两类、三类、四类、五类聚类,画出聚类指标与类别数之间的关系曲线,探讨是否可以确定出合理的类别数目。
3、对1中的数据利用分级聚类方法进行聚类,分析聚类结果,体会分级聚类方法。
4、利用test2.txt数据或者把test2.txt的数据与上述1中的数据合并在一起,重复上述实验,考察结果是否有变化,对观察到的现象进行分析,写出体会三、实验步骤及流程图根据以上实验要求,本次试验我们将分为两组:一、首先对FEMALE与MALE中数据组成的样本按照上面要求用C均值法进行聚类分析,然后对FEMAL E MALE test2中数据组成的样本集用C均值法进行聚类分析,比较二者结果。
二、将上述两个样本用分即聚类方法进行聚类,观察聚类结果。
并将两种聚类结果进行比较。
一、(1)、C均值算法思想C均值算法首先取定C个类别和选取C个初始聚类中心,按最小距离原则将各模式分配到C类中的某一类,之后不断地计算类心和调整各模式的类别,最终使各模式到其判属类别中心的距离平方之和最小(2))实验步骤第一步:确定类别数C,并选择C个初始聚类中心。
本次试验,我们分别将C的值取为2和3。
用的是凭经验选择代表点的方法。
比如:在样本数为N时,分为两类时,取第1个点和第INT N/2 1个点作为代表点;分为三类时,取第1、INT N/3 1、INT 2N/3 1个点作为代表点;第二步:将待聚类的样本集中的样本逐个按最小距离规则分划给C个类中的某一类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 均值聚类实验报告一、C 均值聚类的算法原理聚类分析是指事先不知样本的类别,而利用样本的先验知识来构造分类器(无监督学习)聚类准则函数在样本相似性度量的基础上,聚类分析还需要一定的准则函数,才能把真正属于同一类的样本聚合成一个类的子集,而把不同类的样本分离开来。
如果聚类准则函数选得好,聚类质量就会高。
同时,聚类准则函数还可以用来评价一种聚类结果的质量,如果聚类质量不满足要求,就要重复执行聚类过程,以优化结果。
在重复优化中,可以改变相似性度量,也可以选用新的聚类准则。
误差平方和准则(最常用的)假定有混合样本集 ,采用某种相似性度量被聚合成c 个分离开的子集 ,每个子集是一个类, 它们分别包含个 样本 。
为了衡量聚类的质量,采用误差平方和聚类准则函数式中为类中样本的均值:是c 个子集合的中心,可以用来代表c 个类。
误差平方和 聚类准则函数是样本与集合中心的函数。
在样本集X 给定的情况下, 其取值取决于c 个集合“中心”。
它描述n 个试验样本聚合成c 个类时,所产生的总误差平方和 越小越好。
误差平方和准则适用于各类样本比较密集且样本数目悬殊不大的样本分布。
C-均值聚类算法的核心思想是通过迭代把数据对象划分到不同的簇中,以求目标数最小化,从而使生成的簇尽可能地紧凑和独立。
首先,随机选取k 个对象作为初始的k 个簇的质心;然后,将其余对象根据其与各个簇质心的距离分配到最近的簇;再求新形成的簇的质心。
12{,,...,}n X x x x =X cX X X ,.....,,21c n n n ,......,,21c J ∑∑==-=cj n k j k c jm x J 112||||j m ∑==jn j jjj xn m 11cj ,....,2,1=j m c J cJ这个迭代重定位过程不断重复,直到目标函数最小化为止。
C -均值聚类算法使用的聚类准则函数是误差平方和准则 : 为了使聚类结果优化,应该使准则最小化。
二、C 均值聚类的实现步骤 C -均值算法步骤:① 给出n 个混合样本,令,表示迭代运算次数,选取c 个初始聚合中心② 计算每个样本与聚合中心的距离:若 则 ③令 计算新的集合中心: 计算误差平方和 值:④ 对每个聚合中的每个样本,计算:表示 减少的部分 。
表示 增加的部分: 若 ,则把样本移到聚合中心 中,并修改聚合中心和 值。
⑤ 判断:若 则 ,返回④。
否则,算法结束。
c J c J 1=I (1),1,2,...,;j Z j c =(,()),1,2,...,;1,2,...,.k j D x Z I k n j c ==1,2,...,(,())min {(,()),1,2,...,},k i k j j c D x Z I D x Z I k n ===;ki x ω∈12,I I =+=()11(2),1,2,...,;jn j jkk jZ xj c n ===∑c J ∑∑==-=cj n k i i k c jZ x J 112)(||)2(||)2(()2||()||,1,2, (1)i i ii k i i n x Z I i c n ρ=-=-ii ρc J ()2||()||,1,2, (1)i ij k j j n x Z I j c j in ρ=-=≠+ij ρc J }{min ij ij ilρρ≠=ii il ρρ<)(i k xl ωc J])([11)()1()(i k i i i i x I Z n I Z I Z --+=+])([11)()1()(i k l l j l x I Z n I Z I Z -++=+)()()1(il ii c c I J I J ρρ--=+(1)(),c c J I J I +<1+=I I三. 编写的程序:#include <cfloat>#include <iostream>#include <iomanip>#include <fstream>#include <ctime>#include <cmath>using namespace std;double distance(double a[4], double b[4]){// TODO: 改马氏距离double d0 = a[0]-b[0];double d1 = a[1]-b[1];double d2 = a[2]-b[2];double d3 = a[3]-b[3];return sqrt(d0*d0+d1*d1+d2*d2+d3*d3);}int main(){// 读取数据double data[150][4];ifstream f("data.txt");for(int i=0; i<150; i++)f>>data[i][0]>>data[i][1]>>data[i][2]>>data[i][3];f.close();// 归一化double m[4] = {DBL_MAX, DBL_MAX, DBL_MAX, DBL_MAX};double M[4] = {-DBL_MAX, -DBL_MAX, -DBL_MAX, -DBL_MAX};for(i=0; i<150; i++)for(int j=0; j<4; j++){if(data[i][j]<m[j])m[j]=data[i][j];if(data[i][j]>M[j])M[j]=data[i][j];}for(i=0; i<150; i++)for(int j=0; j<4; j++)data[i][j] = (data[i][j]-m[j]) / (M[j]-m[j]);// 打乱// TODO: 使用随机排序int rightLabels[150];for(i=0; i<50; i++)rightLabels[i] = 0;for(i=50; i<100; i++)rightLabels[i] = 1;for(i=100; i<150; i++)rightLabels[i] = 2;srand(time(NULL));for(i=0; i<150; i++){int j = rand()%150;double tmp;tmp = data[i][0]; data[i][0] = data[j][0]; data[j][0] = tmp;tmp = data[i][1]; data[i][1] = data[j][1]; data[j][1] = tmp;tmp = data[i][2]; data[i][2] = data[j][2]; data[j][2] = tmp;tmp = data[i][3]; data[i][3] = data[j][3]; data[j][3] = tmp;int tmp2;tmp2 = rightLabels[i];rightLabels[i] = rightLabels[j];rightLabels[j] = tmp2;}// 分类int labels[150];double Z[3][4] = {data[0][0], data[0][1], data[0][2], data[0][3], data[1][0], data[1][1], data[1][2], data[1][3],data[2][0], data[2][1], data[2][2], data[2][3]};int iterations = 0;while(true){//cout<<setw(10)<<Z[0][0]<<setw(10)<<Z[0][1]<<setw(10)<<Z[0][2]<<setw(10)<<Z[0][3]< <endl//<<setw(10)<<Z[1][0]<<setw(10)<<Z[1][1]<<setw(10)<<Z[1][2]<<setw(10)<<Z[1][3]<<end l//<<setw(10)<<Z[2][0]<<setw(10)<<Z[2][1]<<setw(10)<<Z[2][2]<<setw(10)<<Z[2][3]<<end l// <<endl;// cin.get();iterations++;// 最小距离分类到labelfor(int i=0; i<150; i++){double d0 = distance(Z[0], data[i]);double d1 = distance(Z[1], data[i]);double d2 = distance(Z[2], data[i]);if((d0<d1)&&(d0<d2))labels[i] = 0;else if(d1<d2)labels[i] = 1;elselabels[i] = 2;}// 计算均值为新聚类中心到Zdouble sum[3][4] = {0.0};int count[3] = {0};for(i=0; i<150; i++){int label = labels[i];sum[label][0]+=data[i][0];sum[label][1]+=data[i][1];sum[label][2]+=data[i][2];sum[label][3]+=data[i][3];count[label]++;}bool changed = false;for(i=0; i<3; i++)for(int j=0; j<4; j++){if(Z[i][j] != sum[i][j] / count[i])// 可以加入e比较{Z[i][j] = sum[i][j] / count[i];changed = true;}}// 聚类中心没改变则退出if(!changed)break;}// 输出int count[3] = {0};for(i=0; i<150; i++){cout<<data[i][0]<<"\t"<<data[i][1]<<"\t"<<data[i][2]<<"\t"<<data[i][3]<<"\t"<<labels[i]<<" \t"<<(char)(rightLabels[i]+'A')<<endl;count[labels[i]]++;}cout<<endl<<"iterations: "<<iterations<<endl<<"label0 count: "<<count[0]<<endl<<"label1 count: "<<count[1]<<endl<<"label2 count: "<<count[2]<<endl;cin.get();return 0;}四.运行结果:0.166667 0.166667 0.389831 0.375 0 B0.138889 0.416667 0.067797 0 1 A0.472222 0.083333 0.677966 0.583333 0 C0.583333 0.333333 0.779661 0.875 2 C0.25 0.875 0.084746 0 1 A0.194444 0 0.423729 0.375 0 B0.194444 0.583333 0.084746 0.041667 1 A0.5 0.375 0.627119 0.541667 0 B0.416667 0.291667 0.525424 0.375 0 B0.75 0.5 0.627119 0.541667 2 B0.138889 0.458333 0.101695 0.041667 1 A0.25 0.291667 0.491525 0.541667 0 B0.333333 0.625 0.050848 0.041667 1 A0.666667 0.416667 0.677966 0.666667 2 B0.444444 0.416667 0.542373 0.583333 0 B0.194444 0.541667 0.067797 0.041667 1 A0.361111 0.291667 0.542373 0.5 0 B0.666667 0.541667 0.79661 1 2 C0.194444 0.625 0.101695 0.208333 1 A0.25 0.583333 0.067797 0.041667 1 A0.361111 0.333333 0.661017 0.791667 0 C0.805556 0.416667 0.813559 0.625 2 C0.416667 0.291667 0.694915 0.75 0 C0.388889 0.375 0.542373 0.5 0 B0.361111 0.416667 0.525424 0.5 0 B0.361111 0.208333 0.491525 0.416667 0 B 0.611111 0.333333 0.610169 0.583333 0 B 0.694444 0.5 0.830508 0.916667 2 C 0.583333 0.5 0.59322 0.583333 2 B 0.388889 0.333333 0.59322 0.5 0 B 0.527778 0.583333 0.745763 0.916667 2 C 0.361111 0.416667 0.59322 0.583333 0 B 0.555556 0.541667 0.627119 0.625 2 B0.5 0.333333 0.627119 0.458333 0 B 0.166667 0.666667 0.067797 0 1 A 0.222222 0.208333 0.338983 0.416667 0 B 0.527778 0.333333 0.644068 0.708333 2 C 0.194444 0.583333 0.101695 0.125 1 A 0.583333 0.375 0.559322 0.5 0 B 0.194444 0.5 0.033898 0.041667 1 A 0.222222 0.541667 0.118644 0.166667 1 A 0.083333 0.5 0.067797 0.041667 1 A 0.416667 0.291667 0.491525 0.458333 0 B 0.222222 0.625 0.067797 0.083333 1 A 0.111111 0.5 0.050848 0.041667 1 A 0.222222 0.75 0.152542 0.125 1 A 0.305556 0.416667 0.59322 0.583333 0 B 0.638889 0.375 0.610169 0.5 0 B 0.666667 0.416667 0.711864 0.916667 2 C 0.722222 0.458333 0.661017 0.583333 2 B 0.166667 0.208333 0.59322 0.666667 0 C 0.833333 0.375 0.898305 0.708333 2 C 0.333333 0.25 0.576271 0.458333 0 B 0.722222 0.458333 0.694915 0.916667 2 C 0.333333 0.166667 0.457627 0.375 0 B 0.555556 0.583333 0.779661 0.958333 2 C 0.416667 0.291667 0.694915 0.75 0 C 0.555556 0.375 0.779661 0.708333 2 C 0.472222 0.416667 0.644068 0.708333 2 C 0.166667 0.458333 0.084746 0.041667 1 A 0.388889 0.208333 0.677966 0.791667 0 C 0.944444 0.25 1 0.916667 2 C 0.777778 0.416667 0.830508 0.833333 2 C 0.416667 0.833333 0.033898 0.041667 1 A 0.805556 0.666667 0.864407 1 2 C 0.611111 0.416667 0.711864 0.791667 2 C 0.611111 0.5 0.694915 0.791667 2 C 0.333333 0.208333 0.508475 0.5 0 B 0.138889 0.583333 0.101695 0.041667 1 A0.694444 0.333333 0.644068 0.541667 2 B 0.194444 0.625 0.050848 0.083333 1 A 0.583333 0.458333 0.762712 0.708333 2 C 0.111111 0.5 0.101695 0.041667 1 A 0.694444 0.416667 0.762712 0.833333 2 C 0.388889 0.333333 0.525424 0.5 0 B 0.416667 0.25 0.508475 0.458333 0 B 0.166667 0.458333 0.084746 0 1 A 0.138889 0.583333 0.152542 0.041667 1 A 0.611111 0.416667 0.762712 0.708333 2 C 0.083333 0.458333 0.084746 0.041667 1 A 0.305556 0.708333 0.084746 0.041667 1 A 0.722222 0.458333 0.745763 0.833333 2 C 0.583333 0.291667 0.728814 0.75 2 C 0.805556 0.5 0.847458 0.708333 2 C 0.333333 0.166667 0.474576 0.416667 0 B 0.555556 0.541667 0.847458 1 2 C 0.722222 0.5 0.79661 0.916667 2 C 0.444444 0.416667 0.694915 0.708333 2 C 0.222222 0.625 0.067797 0.041667 1 A 0.666667 0.458333 0.627119 0.583333 2 B 0.333333 0.916667 0.067797 0.041667 1 A 0.222222 0.708333 0.084746 0.125 1 A 0.333333 0.125 0.508475 0.5 0 B0.5 0.416667 0.661017 0.708333 2 C 0.527778 0.083333 0.59322 0.583333 0 B 0.916667 0.416667 0.949153 0.833333 2 C 0.611111 0.416667 0.813559 0.875 2 C 0.666667 0.208333 0.813559 0.708333 2 C 0.222222 0.75 0.101695 0.041667 1 A 0.444444 0.5 0.644068 0.708333 2 B 0.055556 0.125 0.050848 0.083333 1 A 0.305556 0.791667 0.118644 0.125 1 A 0.027778 0.416667 0.050848 0.041667 1 A 0.861111 0.333333 0.864407 0.75 2 C 0.083333 0.583333 0.067797 0.083333 1 A0 0.416667 0.016949 0 1 A 0.472222 0.583333 0.59322 0.625 2 B 0.138889 0.416667 0.067797 0.083333 1 A 0.305556 0.583333 0.118644 0.041667 1 A 0.222222 0.75 0.084746 0.083333 1 A 0.555556 0.125 0.576271 0.5 0 B0.5 0.333333 0.508475 0.5 0 B 0.388889 0.416667 0.542373 0.458333 0 B0.666667 0.458333 0.576271 0.541667 2 B0.388889 0.75 0.118644 0.083333 1 A1 0.75 0.915254 0.7916672 C0.944444 0.75 0.966102 0.875 2 C0.083333 0.666667 0 0.041667 1 A0.5 0.25 0.779661 0.541667 0 C0.194444 0.416667 0.101695 0.041667 1 A0.361111 0.375 0.440678 0.5 0 B0.944444 0.416667 0.864407 0.916667 2 C0.25 0.625 0.084746 0.041667 1 A0.027778 0.375 0.067797 0.041667 1 A0.277778 0.708333 0.084746 0.041667 1 A0.638889 0.416667 0.576271 0.541667 0 B0.555556 0.208333 0.661017 0.583333 0 B0.5 0.416667 0.610169 0.541667 0 B0.388889 0.25 0.423729 0.375 0 B0.222222 0.583333 0.084746 0.041667 1 A0.944444 0.333333 0.966102 0.791667 2 C0.583333 0.333333 0.779661 0.833333 2 C0.555556 0.208333 0.677966 0.75 2 C0.555556 0.291667 0.661017 0.708333 2 C0.194444 0.666667 0.067797 0.041667 1 A0.472222 0.083333 0.508475 0.375 0 B0.416667 0.333333 0.694915 0.958333 2 C0.555556 0.333333 0.694915 0.583333 0 C0.472222 0.291667 0.694915 0.625 0 B0.305556 0.583333 0.084746 0.125 1 A0.166667 0.416667 0.067797 0.041667 1 A0.583333 0.5 0.728814 0.916667 2 C0.388889 1 0.084746 0.125 1 A0.527778 0.375 0.559322 0.5 0 B0.472222 0.375 0.59322 0.583333 0 B0.194444 0.125 0.389831 0.375 0 B0.027778 0.5 0.050848 0.041667 1 A0.305556 0.791667 0.050848 0.125 1 A0.666667 0.458333 0.779661 0.958333 2 C0.666667 0.541667 0.79661 0.833333 2 Citerations: 9label0 count: 48label1 count: 50label2 count: 52说明: 左边前4列是规格化的样本,第5列是识别结果,第6列是正确结果.。
