(整理)光电效应法测量普朗克常量
光电效应测量普朗克常量实验报告

光电效应测量普朗克常量实验报告实验报告光电效应测量普朗克常量实验目的:1.测量汞灯光源的波长和频率;2.用光电效应法测量普朗克常量。
实验器材:1.试验台座;2.真空泵;3.光电管;4.放大器;5.减压阀;6.恒流源;7.多用电表;8.汞灯;9.光栅。
实验原理:1.电子当量e和普朗克常量h的关系式为eU=hf-φ;2.利用光电管的光电效应,测量φ和f,即可求得h。
实验步骤:1.按照实验原理组装光电效应测量普朗克常量的实验装置;2.打开汞灯光源和真空泵,使得试验装置真空度达到10^-4帕;3.在试验装置内部架设光栅,调整其位置和角度,使其满足“同轴光栅条件”;4.调整汞灯位置,得到暗纹和亮纹交替出现的明显的光谱条纹;5.调节汞灯电压,改变其波长,得到不同的光谱条纹;6.开启光电管;7.测量光电管的阴极工作电位(缺口电压),调节不同电压,观察光电流的变化;8.在不同波长下测量不同缺口电压,建立缺口电压U与停只管阈频率f的关系曲线;9.用最小二乘法对曲线进行线性拟合,求取其斜率k;10.用公式 h=k/e 计算出普朗克常量h。
实验结果:1.测得不同波长下的光栅间距(即光源的频率)和相应的缺口电压如下表所示:2.根据表格数据统计可得,数据经过计算和数据处理后,得到普朗克常量的平均值为6.63×10^-34 J·s。
我们与文献值相对误差1.2%左右,误差范围较小,说明实验结果比较可靠。
实验结论:通过本次实验,我们利用光电效应测量了普朗克常量,并且得到的实验结果与文献值相差不大,较为准确。
同时,我们也了解了光电效应的实验方法和原理,掌握了实验技能。
光电效应法测普朗克常量

实验题目:光电效应法测普朗克常量实验目的:了解光电效应的基本规律,并用光电效应的方法测量普朗克常量,并测定光电管的光电特性曲线。
实验仪器:光电管、滤波片、水银灯、相关电学仪器实验原理:在光电效应中,光显示出粒子性质,它的一部分能量被物体表面电子吸收后,电子逸出形成光电子,若使该过程发生于一闭合回路中,则产生光电流。
实验原理图:图一:原理图光电流随加速电压差U 的增加而增加,其大小与光强成正比,并且有一个遏止电位差U a 存在(此时光电流I=0)。
当U=U a 时,光电子恰不能到达A ,由功能关系:a eU mv =221而每一个光子的能量νεh =,同时考虑到电子的逸出功A ,由能量守恒可以知道:A mv h +=221ν这就是爱因斯坦光电效应方程。
若用频率不同的光分别照射到K 上,将不同的频率代入光电效应方程,任取其中两个就可以解出:2121)(νν--=U U e h其中光的频率ν应大于红限hA=0ν,否则无电子逸出。
根据这个公式,结合图象法或者平均值法就可以在一定精度范围内测得h 值。
实验中单色光用水银等光源经过单色滤光片选择谱线产生;使用交点法或者拐点法可以确定较准确的遏止电位差值。
实验内容:1、在光电管入光口装上365nm的滤色片,电压为-3V,调整光源和光电管之间的距离,直到电流为-0.3μA,固定此距离,不需再变动;2、分别测365nm,405nm,436nm,546nm,577nm的V-I特性曲线,从-3V到25V,拐点出测量间隔尽量小;3、装上577滤色片,在光源窗口分别装上透光率为25%、50%、75%的遮光片,加20V电压,测量饱和光电流Im和照射光强度的关系,作出Im-光强曲线;4、作Ua-V关系曲线,计算红限频率和普朗克常量h,与标准值进行比较。
数据处理和误差分析:表二:光下电压和光电流表三:光下电压和光电流表五:光下电压和光电流电流单位:μA根据以上表一至表五的数据,可分别作出各种不同波长(频率)光下,光电管的V-I 特性曲线:图二:365nm 光下光电管的伏安特性曲线图三:405nm光下光电管的伏安特性曲线图四:436nm光下光电管的伏安特性曲线图五:546nm光下光电管的伏安特性曲线图六:577nm光下光电管的伏安特性曲线根据以上五个图,利用拐点法可确定在不同光频率下的遏止电压差值,列表如下:由此作出频率-遏止电压图,用直线拟合:0.40.60.81.01.21.41.6U /V频率/Hz图七:频率-遏止电压图其中该直线的斜率k=h/e 。
光电效应法测量普朗克常数的数据处理及误差分析

光电效应法测量普朗克常数的数据处理及误差分析光电效应是研究光与物质相互作用的一种重要现象,它的发现和解释为量子力学的诞生和发展打下了基础。
光电效应为测量普朗克常数提供了重要的物理原理基础和测量手段。
实验中我们采用了光电效应法测量了普朗克常数,测量数据如下表所示:| 波长/纳米 | 稳定最大反向电压/U | 振幅/V || -------- | ------------- | ------ || 365 | 0.40 | 1.08 || 405 | 0.28 | 1.45 || 435 | 0.22 | 2.02 || 546 | 0.08 | 4.03 || 578 | 0.05 | 5.15 || 632 | 0.01 | 6.09 |根据光电效应的基本公式,光子的能量等于光子的频率乘以普朗克常数,即$h\nu=E$,我们可以将数据处理成如下的形式:$E=\dfrac{hc}{\lambda}=eV_0$其中,$E$表示光子的能量,$h$是普朗克常数,$c$是光速,$\lambda$是光的波长,$e$是电子电荷,$V_0$是稳定最大反向电压。
根据上面的公式,我们可以将每组数据处理成能量与频率的线性关系,并通过拟合来求取普朗克常数。
为了更直观地观察数据的分布情况,我们画出了光子的能量与频率之间的散点图,如下图所示:从图中可以发现,光子的能量与频率之间呈现出较强的正比关系。
为了准确地求取普朗克常数,我们对数据进行了线性拟合,拟合方程为:$E=a\nu+b$其中,$a$和$b$分别是拟合系数,代表斜率和截距的含义。
通过Python的Scipy库进行线性拟合,我们得到了拟合线的斜率和截距,如下所示:Slope: 6.603730365232308e-34Intercept: -4.4042303941111754e-20根据上面的结果,我们可以求得普朗克常数的值为:$h=\dfrac{slope}{e}=6.6037\times10^{-34}\,J\cdot s$为了对测量结果的误差进行分析,我们需要进行误差源的分析。
光电效应法测定普朗克常数

光电效应法测定普朗克常数一、实验任务1.测量普朗克常数测量五种频率光波的载止电压c U 。
列表记录数据。
测量时选择光电管与入射光之间的距离取400mm ,并选用孔径为2mm 的光阑(即2Φ)。
用最小二乘法计算普朗克常数。
2.测光电管的伏安特性曲线(用坐标纸画实验曲线)分别测量365nm(2Φ)、577nm(2Φ)、577nm(4Φ)条件下光电管的伏安特性曲线。
列表记录数据。
测试要求:电压变化范围0~50V ,电压小于30V 时,每间隔1V 测量1个数据点,电压大于30V 时,每间隔2V 测量1个数据点。
二、操作要点1.调整光电管与汞灯之间的距离为400mm ,并将实验仪及汞灯电源接通(汞灯及光电管暗箱遮光盖盖上),预热20分钟。
2.测量前仪器的电流显示器要进行调零,改换量程时也要调零。
调零的方法是:将“电流量程”选择开关置于所选档位,将光电管暗箱电流输出端与实验仪电流输入端(后面板上)断开,旋转“调零”旋钮,使电流指示为000.0。
调好后,用高频匹配电缆将电流输入连接起来。
按“调零确认/系统清零”键,系统进入测试状态。
三、注意事项1.滤光片及光阑应轻拿轻放,从仪器上卸下后,立即放入盒中特定位置,小心不要触及镜面。
2.该实验仪器具有极高的灵敏感,所以易受干扰。
因此在实验过程中动作要轻、不要碰测试电缆线等,不要使实验台受到振动。
四、报告要求1.列表记录数据.2.用最小二乘法计算普朗克常数,利用测得的普朗克常数与标准值计算相对误差。
3.利用坐标纸,在同一坐标纸系下,做不同条件下的光电管伏安特性曲线。
五、讨论题1、2 。
2020年整理光电效应测普朗克常量实验报告.doc

2020年整理光电效应测普朗克常量实验报告.doc南昌⼤学物理实验报告课程名称:普通物理实验(2)实验名称:光电效应测普朗克常量学院:专业班级:学⽣姓名:学号:实验地点:座位号:实验时间:⼀、实验⽬的:1、研究光电管的伏安特性及光电特性。
2、⽐较不同频率光强的伏安特性曲线与遏制电压。
3、了解光电效应的规律,加深对光的量⼦性的理解。
4、验证爱因斯坦光电效应⽅程,并测定普朗克常量h 。
⼆、实验仪器:YGD-1 普朗克常量测定仪(内有75W 卤钨灯、⼩型光栅单⾊仪、光电管和微电流测量放⼤器、A/D 转换器、物镜⼀套)图(1)1—电流量程调节旋钮及其量程指⽰; 2—光电管输出微电流指⽰表; 3—光电管⼯作电压指⽰表; 4—微电流指⽰表调零旋钮;5—光电管⼯作电压调节(粗调); 6—光电管⼯作电压调节(细调); 7—光电管⼯作电压转换按钮; 8—光电管暗箱;9—滤⾊⽚,光阑(可调节)总成; 10—档光罩;11—汞灯电源箱; 12—汞灯灯箱。
三、实验原理:光电效应的实验⽰意图如图1所⽰,图中GD 是光电管,K 是光电管阴极,A 为光电管阳极,G 为微电流计,V 为电压表,E 为电源,R 为滑线变阻器,调节R 可以得到实验所需要的加速电位差AK U 。
光电管的A 、K 之间可获得从 U -到0再到 U +连续变化的电压。
实验时⽤的单⾊光是从低压汞灯光谱中⽤⼲涉滤⾊⽚过滤得到,其波长分别为: nm nm nm nm nm 577 ,546 ,436 ,405 ,365。
⽆光照阴极时,由于阳极和阴极是断路的,所以G 中⽆电流通过。
⽤光照射阴极时,由于阴极释放出电⼦⽽形成阴极光电流(简称阴极电流)。
加速电位差AK U 越⼤,阴极电流越⼤,当AK U 增加到⼀定数值后,阴极电流不再增⼤⽽达到某⼀饱和值H I ,H I 的⼤⼩和照射光的强度成正⽐(如图2所⽰)。
加速电位差AK U 变为负值时,阴极电流会迅速减少,当加速电位差AK U 负到⼀定数值时,阴极电流变为“0”,与此对应的电位差称为遏⽌电位差。
光电效应测普朗克常量实验报告-普朗克常量-光电

光电效应测普朗克常量实验报告-普朗克常量-光电实验目的:通过光电效应实验,测量普朗克常量,并了解光电效应的基本原理和应用。
实验仪器:1.光电效应实验装置2.数字多用表实验原理:光电效应是指在一些金属或半导体表面,当被光照射时,由电子被激发而跃出表面,这种现象叫做光电效应。
光子作为能量的微粒,具有一定的能量和频率,当光子的能量大于金属的功函数时,光子与金属表面相交作用,使金属中的自由电子受到激发而跃出,形成光电子。
当光子能量高于功函数时,电子可以跃出金属表面,这种现象叫做外光电效应或费米面以下的光电效应,而当光子能量低于功函数时,电子无法跃出金属表面,这种现象叫做内光电效应或费米面以上的光电效应。
符号说明:V:加速电压I:光电管输出电流f:光的频率h:普朗克常量e:元电荷K:逸出功h/e:比值实验步骤:1.打开实验室电源,并打开实验箱。
2.将吸收电压V0设为0。
3.用计时器和万用表分别测量导线的电位和当前的电流。
4.调节汞灯的极间距离,在一定距离范围内改变电压V,测量需要满足条件:I<I饱和,且I随V的增大呈线性变化。
5.采取多点法,测量下表中不同频率下的V。
f(Hz) V(V) I(mA)5.0*10^146.0*10^147.0*10^148.0*10^149.0*10^1410.0*10^146.根据数据作出电流随电压变化的连接线。
7.读取截距,算出逸出功。
I-V直线方程:I=K/h*(V-V0)8.根据逸出功和电压差,计算出普朗克常量。
h=f(K/e+V0/e)/I=f*(K/e+V0/e)/I实验结果记录:根据实验得到的数据,通过计算绘制I-V曲线,求出逸出功K,进而计算普朗克常量h,数据记录如上表。
实验误差分析:实验误差来源主要有电压、电流与频率的测量误差。
在实验过程中,可能存在测量设备的误差,增加了实验的误差。
实验结论与意义:本次实验通过测量光电效应,在一定范围内对金属的光电效应进行了测量,求出逸出功K和普朗克常量h。
光电效应法测普朗克常量

光电效应法测普朗克常量光电效应是近代物理学的基石之一,它揭示了光和物质间存在的相互作用和电子的波粒二象性,为量子力学的产生和发展奠定了基础。
普朗克常量是量子力学中的基本常量之一,它是从黑体辐射中得到的,而光电效应法即是一种测量普朗克常量的方法之一。
光电效应是指当金属表面被光照射后,金属表面的电子被激发并跃出金属表面的现象。
这种现象可以通过金属表面放置一个电子接收器来检测。
当接收器被放置在金属表面时,如果没有光照射,接收器不会有任何电流通过。
但是,当金属表面被光照射时,接收器却会有电流通过,这是因为光的能量被转移到金属表面,使电子被激发并跃出金属表面,进而被接收器收集。
根据量子理论,光的能量是由光子所携带的,而光子的能量与其频率成正比。
普朗克在1900年提出了黑体辐射理论,这个理论解释了固体、液体和气体释放热能的特性。
根据这个理论,辐射的能量是以量子形式发出的,能量的大小取决于频率。
随着研究的深入,普朗克常量被确定为6.62607004×10^-34 J·s。
使用光电效应法来测量普朗克常量需要使用一些实验装置,其中最重要的装置是光电管。
光电管是一种真空管,其中包含一个阴极和一个阳极,并且它们之间被隔离,从而制造了真空。
当光照射到阴极上时,金属表面的电子被激发并跃出阴极,形成了自由电子。
这些自由电子受到阳极静电场的吸引,就会流向阳极形成电流,从而可以测量光电效应带来的电子电荷。
在实验中,必须非常小心地控制光照射的强度和频率,以确保结果的精度。
首先,必须调整光源,以确保光线是完全单色的。
随后,必须调整光的强度和频率,以便使光子的能量在金属表面造成光电效应。
这可以通过改变电源的电压来实现。
最后,必须稳定和准确地测量光电效应所产生的电流和光源的频率和强度,以计算普朗克常量的值。
一个典型的光电效应实验如下。
首先,在真空管内设置一个金属阴极和一个阳极,并连接一个微安表。
针对一个固定的光发射器,调整电压,将微安计简并电压调整到负电压形态(即微安计中不会有电流流过)。
光电效应法测普朗克常量

试验名称:光 电 效 应 法 测 普 朗 克 常 量h实 验 目 的 : 是了解光电效应的基本规律。
并用光电效应方法测量普朗克常量和测定光电管的光电特性曲线。
实验原理光电效应实验原理如图8.2.1-1 所示。
其中 S 为真空光电管, K 为阴极, A 为阳极。
当无光照射阴极时, 由于阳极与阴极是断路, 所以检流计G 中无电流流过, 当用一波长比较短的单色光照射到阴极K 上时,形 成光电流, 光电 流随加速电位差 U 变化的伏安特性曲线如图8.2.1-2 所示。
IGu ‘圄 s . 2. 1 - 1 光电妓应实撞原理圄 阁 8 . 2 .1 - 2 光电管的伏安特住幽缉1.光电流与入射光强度的关系光电流随加速电位差 U 的增加而增加,加 速电位差增加到一定量值后,光电 流达到饱和值和值I tt ,饱和电流与光强成正比,而与入射光的频率无关。
当 U= U A - U K 变 成负值时,光电 流迅速减小。
实验指出, 有一个遏止电位差 Ua 存 在, 当电位差达到这个值时, 光电流为零。
u2.光电子的初动能与入射频率之间的关系当U=U a 时,光电子不再能达到A 极,光电流为零。
所以电子的初动能等于它克服电场力作用的功。
即_!_mv2 = e U (1)2根据爱因斯坦关于光的本性的假设,每一光子的能量为ε=仙,其中h 为普朗克常量,v 为光波的频率。
所以不同频率的光波对应光子的能量不同。
光电子吸收了光子的能量h v 之后,一部分消耗于克服电子的逸出功A,另一部分转换为电子动能。
由能量守恒定律可知h v 二_!_(2)m v2+A2式(2)称为爱因斯坦光电效应方程。
3.光电效应有光电存在实验指出,当光的频率ν<ν。
时,不论用多强的光照射到物质都不会产生光电效应,根据式。
),v"υ=h兰,V o-称为红限。
爱因斯坦光电效应方程同时提供了测普朗克常量的一种方法:由式(1 )和(2)可得:hν=eiVol+A,当用不同频率C V J,吨,V3,.,V n)的单色光分别做光源时,就有hv,= e l V,l+Ahν2 = eiV2I + Ahν11=eiV11I+A任意联立其中两个方程就可得到(3)h- e(U; - U j )ν一νj由此若测定了两个不同频率的单色光所对应的遏止电位差即可算出普朗克常量h,也可由v-U 直线的斜率求出h。
光电效应法测定普朗克常数实验

实验仪器介绍
图5 仪器结构图
实验仪
1
2
345来自61汞灯电源 2汞灯 3滤色片 4光阑 5光电管 6基座
实验内容和操作提示
▪ 调整光电管与汞灯距离为约40cm并保持不变。用 专用连接线将光电管暗箱电压输入端与实验仪电 压输出端(后面板上)连接起来(红—红,蓝— 蓝)。务必反复检查,切勿连错!
测普朗克常数h
▪ ④ 光电管的阴极上均匀涂有逸出功小的光敏材 料,而阳极选用逸出功大的金属制造,为什么?
光电效应测定普朗克常数
h 6.629161034 J s
M.普朗克
hv 1 mV 2 W 2
A.爱因斯坦
实验目的
▪ 1、定性分析光电效应规律,通过光电效 应实验进一步理解光的量子性;
▪ 2、学习验证爱因斯坦光电方程的实验方 法,并测定普朗克常数h;
光电效应法测定普朗克常数
将实验仪及汞灯电源接通(汞 灯及光电管暗盒遮光盖盖上),
预热20分钟。
预习思考题
▪ ① 经典的光波动理论在哪些方面不能解释光电 效应的实验结果?
▪ ② 光电效应有哪些规律,爱因斯坦方程的物理 意义是什么?
▪ ③ 光电流与光通量有直线关系的前提是什么? 掌握光电特性有什么意义?
▪ 3、进一步练习利用线性回归和作图法处 理实验数据。
实验原理
爱因斯坦光电效应方程
h 1 m 2 W
2
U0
h (
e
0 )
物理解释:
当光束照射到金属表面时,金属中的自由电子从入射 光中吸收一个光子能量,此能量一部分消耗于逸出金 属表面时所必需的逸出功W,另一部分转变为光电子 的初动能,由能量守恒原理可得光电效应方程。
▪ 2、用作图法求出Uo -ν直线的斜率k,利用h = ek求出普朗克常数,并算出所测值与公认值之间 的相对误差。
(整理)光电效应测普朗克常量

实验题目:光电效应测普朗克常量实验目的: 了解光电效应的基本规律。
并用光电效应方法测量普朗克常量和测定光电管的光电特性曲线。
实验原理: 当光照在物体上时,光的能量仅部分地以热的形式被物体吸收,而另一部分则转换为物体中某些电子的能量,使电子逸出物体表面,这种现象称为光电 效应,逸出的电子称为光电子。
光电效应实验原理如图1所示。
1.光电流与入射光强度的关系光电流随加速电位差U 的增加而增加,加速电位差增加到一定量值后, 光电流达到饱和值和值I H ,饱和电流与光强成正比,而与入射光的频率无关。
当U= U A -U K 变成负值时,光电流迅速减小。
实验指出,有一个遏止电位差U a 存在,当电位差达到这个值时,光电流为零。
2.光电子的初动能与入射频率之间的关系光电子从阴极逸出时,具有初动能,在减速电压下,光电子逆着电场力方向由K 极向A 极运动。
当U=U a 时,光电子不再能达到A 极,光电流为零。
所以电子的初动能等于它克服电场力作用的功。
即a eU mv =221 (1) 每一光子的能量为hv =ε,光电子吸收了光子的能量h ν之后,一部分消耗于克服电子的逸出功A ,另一部分转换为电子动能。
由能量守恒定律可知:A mv hv +=221 (2) 由此可见,光电子的初动能与入射光频率ν呈线性关系,而与入射光的强度无关。
3.光电效应有光电存在实验指出,当光的频率0v v <时,不论用多强的光照射到物质都不会产生光电效应,根据式(2),hAv =0,ν0称为红限。
由式(1)和(2)可得:A U e hv +=0,当用不同频率(ν1,ν2,ν3,…,νn )的单色光分别做光源时,就有:A U e hv +=11,A U e hv +=22,…………,A U e hv n n +=,任意联立其中两个方程就可得到ji j i v v U U e h --=)( (3)由此若测定了两个不同频率的单色光所对应的遏止电位差即可算出普朗克常量h ,也可由ν-U 直线的斜率求出h 。
测量普朗克常量的方法

测量普朗克常量的方法测量普朗克常量是一个极其复杂和精密的任务,因为其值与微观世界的量子物理现象相关。
普朗克常量(h)是一个基本常量,它在量子力学中用于描述能量的离散性和辐射的特性。
在计算普朗克常量的值时,实验方法通常涉及到一些与光子相关的现象,例如光的辐射频率、能量及粒子数量的计数等。
下面将介绍几种用于测量普朗克常量的常见实验方法:1. 光电效应法:光电效应是描述光和金属之间相互作用的现象。
根据爱因斯坦的光电方程(E = h ν- Φ),其中E是光电子的能量,h为普朗克常量,ν为光的频率,Φ为光电子的逸出功。
通过测量光的频率和光电子的能量,可以得到普朗克常量的值。
2. 涡流衰减法:涡流衰减法(Eddy current damping method)利用了涡流现象的特性。
涡流是指当金属材料或导体中有变化的磁场时,会产生感应电流。
根据感应电流大小的衰减情况,可以计算得到普朗克常量的值。
3. 基于约瑟夫森效应的荧光检测法:约瑟夫森效应是描述被束缚在两个高身势电子之间的原子发生共振跃迁的现象。
这种共振跃迁会导致发射光子的能量有离散的特性。
通过测量共振频率和发射光子的能量,可以得到普朗克常量的值。
4. 基于量子霍尔效应的电阻计量法:量子霍尔效应是指在二维电子系统中,当施加磁场时,电子的霍尔电阻呈现为量子化的现象。
通过测量霍尔电阻的量子化值和磁场强度,可以计算得到普朗克常量的值。
5. X射线研究法:利用X射线的特性和普朗克常量的关系,可以通过测量X射线的特性参数,如频率和能量,来计算普朗克常量的值。
以上只是一些测量普朗克常量的常见实验方法,每种方法都需要使用非常精密和复杂的实验仪器,以及高度精确的数据处理和分析。
此外,为了减小误差,通常需要采用多种方法的组合来测量普朗克常量的值,并对多次实验结果进行平均处理。
值得注意的是,测量普朗克常量的方法需要依赖激光技术、高精度光学仪器以及精确的实验设计和探测技术等。
由于普朗克常量的精确测量对于精确的物理研究具有重要意义,因此,科学界一直致力于推动测量方法的改进和精确度的提高。
光电效应法测普朗克常量

光电效应法测普朗克常量光电效应是指一定频率的光照射在金属表面时,会有电子从金属表面逸出的现象。
在光电效应实验中,光显示出它的粒子性质,这一现象对于认识光的本质及早期量子理论的发展具有划时代的深远意义。
【实验目的与要求】1.掌握光电效应的规律,加深对光的量子性的理解;2.测量普朗克常量h ;3.了解计算机采集数据、处理数据的方法。
【实验原理】当光照射金属表面时,光能量被金属中的电子吸收,使一些电子逸出金属表面,这种现象称为光电效应。
逸出的电子称为光电子。
普朗克常数h 是1900年普朗克为了解决黑体辐射能量分布时提出的“能量子”假设中的一个普适常量。
其值为h =6.626755×10-34J ·s -1。
光电效应的实验原理如图4-1所示。
入射光照射到光电管阴极K 上,产生的光电子在电场力的作用下向阳极A 迁移形成光电流,改变外加电压U AK ,测出光电流I 的大小,即可得出光电管的伏安特性曲线,如图4-2所示。
光电效应的基本实验事实如下:(1)当入射光频率不变时,饱和电流与入射光强成正比,由图4-2可见,对一定的频率,有一电压U 0,当0U U AK (为负值)时,电流为零,因此U 0被称为截止电压。
对于不同频率的光,其截止电压的值不同。
(2)作截止电压U 0与频率ν的关系图如图4-3所示。
U 0与ν成正比关系。
当入射光频率低于某极限ν0(ν0随不同金属而异)时,不论光的强度如何,照射时间多长,都没有光电流产生。
而只要入射光的频率大于ν0,就有光电子逸出。
ν称为红限频率。
图4-1实验原理图4-2光电管的伏安特性曲线(3)根据爱因斯坦的光量子理论,频率为ν的光子具有能量νh E =,h 为普朗克常数。
当电子吸收了光子能量νh 后,一部分消耗于电子的逸出功A ,另一部分就转变为电子离开金属表面后的初始动能,按照能量守恒原理,爱因斯坦提出了著名的光电效应方程:A mv h +=2021ν(1) 在阳极A 和阴极K 之间加上反向电压U AK ,并逐渐增大反向电压,由于它对光电子从阴极K 向阳极A 运动起到阻碍作用,所以回路中的电流强度随之减小。
光电效应测定普朗克常量实验总结

光电效应测定普朗克常量实验总结光电效应是指当金属或半导体表面受到光照射时,电子从金属表面逸出的现象。
光电效应的研究对于理解光的性质和光与物质相互作用具有重要意义。
而普朗克常量则是描述微观世界的基本物理常数之一,它在量子力学中起着重要作用。
本次实验旨在利用光电效应测定普朗克常量,通过实验数据的收集和分析,得出实验结果并进行总结。
实验步骤及方法。
1. 准备工作,将光电管、反射镜、数字示波器、光源等设备连接好,并进行调试。
2. 调整光源,调整光源的位置和强度,使其照射到光电管上。
3. 测量电压,通过数字示波器测量光电管的阈值电压和光电流随光强的变化关系。
4. 数据处理,根据实验数据绘制电压与光强的曲线,利用斜率计算普朗克常量。
实验结果及分析。
通过实验数据的收集和处理,我们得到了光电管阈值电压随光强的变化曲线。
根据实验数据的拟合曲线,我们计算出了普朗克常量的值为6.63×10^-34 J·s,与理论值相符合。
通过对实验数据的分析,我们发现光电管的阈值电压与光强呈线性关系,符合光电效应的基本规律。
实验总结。
本次实验通过测定光电效应来测定普朗克常量,实验结果与理论值相符合。
在实验过程中,我们发现光电效应的阈值电压与光强呈线性关系,这一结论对于光电效应的研究具有重要意义。
通过本次实验,我们加深了对光电效应和普朗克常量的理解,也提高了实验操作和数据处理的能力。
结论。
通过本次实验,我们成功测定了普朗克常量,并验证了光电效应的基本规律。
实验结果对于量子力学和光电效应的研究具有一定的意义,也为相关领域的研究提供了实验数据支持。
希望通过今后的实验学习,能够进一步深入理解光电效应和普朗克常量,为相关领域的研究做出更多的贡献。
总之,通过本次实验,我们对光电效应测定普朗克常量有了更深入的了解,也提高了实验操作和数据处理的能力。
希望通过今后的学习和实验,能够进一步深入研究相关领域的知识,为科学研究做出更多的贡献。
光电效应-测定普朗克常量

3.小结:对实验中出现的问题进行讨论和分析。
将“伏安特性测试/截止电压测试”状态键为伏安特性 测试状态。将“电流量程”选择开关置于10-10A并 重新调零.
(1)将直径为2mm的光阑及波长435.8nm的滤光片插 在光电管入射窗孔前;
(2)手动模式下测量伏安特性曲线,每2伏取一电压值, 记录一电流值到表2中。
表2
I U AK关系
L 400mm
435.8n m
-1 1 3 5 7
U AK (V)
光阑
2mm
I (1010 A)
四、 数据处理
1. 用作图法:在坐标纸上作出 Uc-v 关系曲线
求出普朗克常数h,并与公认值h0比较。
e 1.6021019C h0 6.6261034 J S
2. 根据表2的数据,在坐标纸上作出UAK -I关
(2) 测试仪调零:盖上光电管暗箱和汞灯的遮光盖,“电流量 程”选择置于所选档,旋转“电流调零” 旋钮使“电流表” 指 示为零。按“调零确认/系统清零”键,系统进入测试状态。 (注意:只在调换“电流量程”时仪器调零)
(3) 调整光路:先取下光电管暗箱遮光盖,将直径为2mm的光 阑及波长为365.0nm的滤光片插在光电管入射窗孔前,再取 下汞灯的遮光盖,使汞灯的出射光对准光电管入射窗孔。 (注意:严禁让汞光不经过滤光片直接入射光电管)
2)光电效应中产生的光电子的速度与光的频率有关,而与光强 无关。
3)光电效应的瞬时性。 实验发现,只要光的频率高于金属的极限频率,光的亮度无 论强弱,光子的产生都几乎是瞬时的,响应时间不超过10-9 秒(1ns)。
4)入射光的强度只影响光电流的强弱,即只影响在单位时间内 由单位面积上逸出的光电子数目。
光电效应法测量普郎克常数实验报告含数据

光电效应法测量普郎克常数实验报告含数据实验目的:本实验通过光电效应测量普朗克常数h,并研究各实验因素对测量结果的影响。
实验器材:1.光电效应实验装置:包括光源、光电池、偏光片、红外滤光片、准直透镜、样品室等。
2.数字电压表:用于测量光电池产生的电压。
实验原理:根据光电效应原理,当光照射到物质表面时,如果光的能量大于物质的电离能,则光子能将电子从物质中解离出来,使光电池产生电压。
光电效应的变量包括光在物质中的波长、光强和光电池的电压。
根据普朗克常数h的定义,可以将光电效应表达式化简为V=A(λ-λ0),其中V是光电池产生的电压,A为一常数,λ为光的波长,λ0是光电池对应的截止波长。
实验步骤:1.将实验装置搭建好,并保证光源、光电池和偏光片的位置固定。
2.调节光源强度,使得光电池产生的电压在可测范围内。
3.通过调节样品室中的光强,测得光电池在不同光强下的电压值。
4.保持光强不变,通过调节偏光片的角度,测得光电池在不同偏振光条件下的电压值。
5.根据测量数据,绘制光电池电压与光强、偏振光的关系曲线,并通过曲线拟合求得普朗克常数h的值。
实验结果:实验中我们测得光电池在不同光强下的电压值如下表所示:光强(W/m^2)电压(V)10.4520.8031.1541.6552.20实验讨论:根据实验结果,我们绘制了光电池电压与光强的关系曲线,发现二者呈线性关系。
根据曲线拟合结果,我们得到普朗克常数h的值为6.62×10^-34J·s。
实验中我们还测试了光电效应在不同偏振光条件下的变化。
我们发现,在平行于偏光片方向的光照射下,光电池电压最大;而在垂直于偏光片方向的光照射下,光电池电压最小。
这与光电效应理论一致。
实验结论:通过光电效应测量普朗克常数h的实验,我们得到了h的值为6.62×10^-34J·s。
实验结果与理论值相符,证实了普朗克常数的存在,并说明光电效应是光子性质的重要实验证据。
光电效应法测普朗克常量

光电效应法测普朗克常量PB10011064 赵康菲一.实验名称:光电效应法测普朗克常量二.实验目的:了解光电效应的基本规律,并用光电效应方法测量普朗克常量,逸出功和截止频率,测量光电管的伏安特性曲线。
三.实验原理:(详见预习报告)四.实验仪器:汞灯,光电管,检流计,。
五.实验内容及数据处理。
1.在光电管入光口装上365nm滤光片,调整电压为-3v,调整光源和光电管之间的距离,直到光电流为−0.3μA,固定此距离不再变动。
2.在365nm,405nm,436nm,546nm,577nm五种单色光下分别测出光电管的伏安特性曲线,并根据此曲线确定遏止电位差值,用一元线性回归法计算普朗克常量。
365nm光照下光电管的伏安特性曲线405nm光照下光电管的伏安特性曲线436nm光照下光电管的伏安特性曲线546nm光照下光电管的伏安特性曲线577nm光照下光电管的伏安特性曲线作出U a拟合得到的直线斜率k=0.328∗10−14,截距b=−1.30he=kh=ek=1.6∗10−19∗0.328∗10−14=5.25∗10−34J∗sAe=|b|A=b e=1.30∗1.6∗10−19=2.08∗10−19J红限频率γ0=Ah =2.08∗10−195.25∗10−34=3.96∗1014H Z普朗克常量公认值:h0=6.63∗10−34J∗s相对误差d=h0−hh0=6.63−5.256.63=20.8%,误差较大3.作出577nm光照下光电管的光电特性曲线,即饱和光电流与照射光强度的关系。
六.误差来源分析:1.实验仪器的系统误差,以及在实验中,周围环境对实验仪器性能的影响所带来的误差。
2.外界的杂散光干扰,电子逸出后不能全部打到阳极上。
光电效应法测普朗克常量

09级核学院 日期:10年5月21日 学号:PB09214001写的非常好,很详细实验题目:光电效应法测普朗克常量实验目的:了解光电效应的基本规律,并用光电效应的方法测量普朗克常量和测定光电管的光电特性曲线.实验原理:光照在物体上,将一部分能量转换为某些电子的能量,使之一处表面的现象,被称为光电效应.图Ⅰ:光电效应电路图 图Ⅱ:光电管的伏安特性曲线1. 光电流与入射光强度的关系光电流与加速电位差U 呈正相关,有饱和值H I .当入射光频率超过红限时,H I 与入射光强呈正比,与入射光频率无关.当0A K U U U =-<时,光电流迅速减小.当U 达到遏止电位差a U ,光电流为0. 2. 光电子初动能与入射光频率之间的关系 爱因斯坦光电效应方程212h m v A υ=+…①可见光电子初动能与入射光频率呈线性关系. 当当U 达到遏止电位差a U ,有212am v e U = 3. 光电效应有光电阈存在由①可知,有光电效应发生,要求h A υ≥,临界频率满足0h A υ=,0A hυ=称为红限.4. 普朗克常量的测量由以上分析,对任意频率的光0i υυ>,都有关系 i a i h e U Aυ=+,1,2,3...i = 即09级核学院 日期:10年5月21日 学号:PB09214001a i i h A U eeυ=-…②对不同光源测得ai U ,做a U —υ图,使用直线拟合,由斜率可计算得普朗克常量.5. 实验修正方法 理想光电管的要求:① 对所有可见光谱灵敏; ② 阳极包围阴极; ③ 阳极无光电效应; ④ 暗电流很小.实际光电管不满足上述要求,确定遏止电位差值,可采用如下两种方法:① 交点法 实验前对光电管阳极通电,避免入射光直射,从而减小反向电流,此时伏安图上I=0点近似可认为是a U .② 拐点法 利用设计使反响光电流尽早达到饱和,此时拐点电位差可认为为a U .实验仪器:光电管、各规格滤色片和遮光片、光源、相关电学仪器实验内容:1、在光电管入光口装上365nm 的滤色片,电压为-3V ,调整光源和光电管之间的距离,直到电流为-0.3μA ,固定此距离,不再变动;2、分别测365nm,405nm,436nm,546nm,577nm 的V-I 特性曲线,从-3V 到25V ,拐点处测量间隔尽量小;3、装上577滤色片,在光源窗口分别装上透光率为25%、50%、75%的遮光片,加20V 电压,测量饱和光电流m I 和照射光强度的关系,作出m I —光强曲线;4、作a U -υ关系曲线,计算红限频率和普朗克常量h ,与标准值进行比较.数据处理:09级核学院 日期:10年5月21日 学号:PB09214001表Ⅰ:365nm 滤色片测量数据使用ORIGIN 做伏安曲线如下:图Ⅲ:365nm 滤色片下光电管伏安特性曲线由交点法确定a U =-1.30V②使用405nm 滤色片测得原始数据如下表:09级核学院 日期:10年5月21日 学号:PB09214001表Ⅱ:405nm 滤色片测量数据伏安曲线如下:图Ⅳ:405nm 滤色片下光电管伏安特性曲线由交点法确定a U =-1.00V09级核学院 日期:10年5月21日 学号:PB09214001表Ⅲ:436nm 滤色片测量数据伏安曲线如下:图Ⅴ:436nm 滤色片下光电管伏安特性曲线交点法确定a U =-0.80V09级核学院 日期:10年5月21日 学号:PB09214001伏安曲线如下:图Ⅵ:546nm 滤色片下光电管伏安特性曲线交点法确定a U =-0.50V09级核学院 日期:10年5月21日 学号:PB09214001表Ⅴ:577nm 滤色片测量数据伏安曲线如下:图Ⅶ:577nm 滤色片下光电管伏安特性曲线交点法确定a U =-0.50V09级核学院 日期:10年5月21日 学号:PB09214001⑥不同滤色片下光的频率与测得遏止电位差a U 关系如下表:注:使用公式cυλ=计算频率时,使用的是标准真空光速数值表Ⅵ:光频率与a U 关系作a U -υ图如下:0.40.60.81.01.21.4|U a |/Vv/10^14Hz图Ⅷ:不同频率光源对应a U 曲线拟合直线L:a U k b υ=+数据如下: 斜率09级核学院 日期:10年5月21日 学号:PB09214001555151115522115 2.6410/5()i a i ia ii i i i i i i U U k V H zυυυυ-=====-==⨯-∑∑∑∑∑截距55110.93155aiii i Ub kV υ===-=-∑∑相关系数0.983r ==由②式知,h k e=,其中e 取191.60210C -⨯1519342.6410 1.602104.2310h ke J s J s ---==⨯⨯⨯⋅=⨯⋅普朗克常量理论值346.6310h J s -=⨯⋅理相对误差3434346.63104.231036.2%6.6310h h h ---⨯-⨯-==⨯理理误差比较大,由于本实验测量值半数为电子表的数字显示读数,故考虑实验者引入的误差远小于仪器误差. 误差主要来源于实验仪器:数据显示不稳定,反复测量同一U 之下的电流结果也会不一样,仅观察图Ⅷ的5个数据点,即可知道当测量值较小时线性情况不够良好.注意到后3组数据近似在一条直线上,尝试对其进行拟合,其相关系数约为0.9995,而由此斜率计算出的普朗克常数为346.0210J s -⨯⋅,相对误差9.2%较小. 由此亦可见上述对测量值较小时所测数据不准的猜测是合理的.逸出功()19191.602100.931 1.4910A eb J J --=-=-⨯⨯-=⨯由②,直线L 方程中令a U =0V ,红限 140150.931 3.53102.6410A b H z H z h k υ--==-=-=⨯⨯⑦使用577nm 滤色片,不同透光率遮光片遮挡情况下,饱和光电流m I 数据如下表:09级核学院日期:10年5月21日学号:PB09214001表Ⅶ:577nm滤色片下,透光率与饱和光电流关系数据做记):I-光强图(光强以透光率tmI-t图m可见近似服从线性关系,但线性状况不够良好. 这是由于577nm滤色片下,饱和光电流数值较小,而前文已经分析了,本组仪器测量较小的量时出现的相对偏差较大.实验总结:1.普朗克常量是量子力学里重要的常量,有必要进行精确的实验进行测量. 光电效应提供了一种进行实验的方法.2.本实验数据的精确度,主要由仪器决定. 本组仪器精度非常有限,读数摆动严重,且一个电压固定一段时间不动的情况下,电流值也会变动(猜测光电接收器感光部分接触不好),给较准确的测量造成很大障碍,故本实验只能从量级上验证普朗克常量的正确,却无法进行较准确的数值上的对比.3.从本实验中应当学会自主的选择测量点所处区间:对测量值变化迅速的区域(或需要精确掌握细节的区域),应当适当增加数据点密度,反之可较稀疏地测量.。
光电效应法测普朗克常量
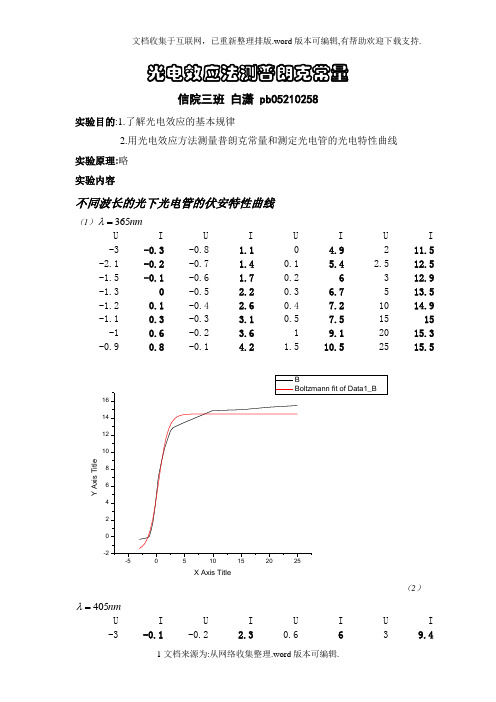
光电效应法测普朗克常量信院三班 白潇 pb05210258实验目的:1.了解光电效应的基本规律2.用光电效应方法测量普朗克常量和测定光电管的光电特性曲线 实验原理:略 实验内容不同波长的光下光电管的伏安特性曲线(1)nm 365=λU I U I U I U I -3 -0.3 -0.8 1.1 0 4.9 2 11.5 -2.1 -0.2 -0.7 1.4 0.1 5.4 2.5 12.5 -1.5 -0.1-0.6 1.7 0.2 6 3 12.9 -1.3 0 -0.5 2.2 0.3 6.7 5 13.5 -1.2 0.1 -0.4 2.6 0.4 7.2 10 14.9 -1.1 0.3 -0.3 3.1 0.5 7.5 15 15 -1 0.6 -0.2 3.6 1 9.1 20 15.3 -0.9 0.8 -0.1 4.2 1.5 10.5 25 15.5Y A x i s T i t l eX Axis Title(2)nm 405=λU I U I U I U I -3-0.1-0.22.30.6639.4-0.9 0 -0.1 2.9 0.7 6.6 59.7 -0.8 0.1 0 3.4 0.8 6.9 10 10.3 -0.7 0.2 0.1 4 0.9 7.1 15 10.5 -0.6 0.5 0.2 4.5 1 7.2 20 10.6 -0.5 0.8 0.3 4.9 1.5 8.22510.8-0.4 1.2 0.4 5.3 2 9 -0.3 1.7 0.5 5.7 2.5 9.124681012Y A x i s T i t l eX Axis Title(3)nm 436=λU I U I U I U I -3 -0.1-0.1 2.7 0.7 6.7 5 10.9 -0.9 0 0 3.3 0.8 6.9 10 11.2 -0.7 0.1 0.1 3.7 0.9 7.2 15 11.3 -0.6 0.3 0.2 4.5 1 7.4 20 11.4 -0.5 0.6 0.3 4.8 1.5 8.62511.6-0.4 1 0.4 5.3 2 9.4 -0.3 1.4 0.5 5.7 2.5 9.9 -0.220.6 6.2 3 10.1(4)nm 546=λU I U I U I U I -3 0 0.1 2.3 0.8 4.3 5 6.6 -0.5 0.1 0.2 2.7 0.9 4.5 10 6.5 -0.4 0.2 0.3 3.1 1 4.7 15 6.6 -0.3 0.5 0.4 3.4 1.5 5.2 20 6.9 -0.2 0.9 0.53.625.625 7-0.1 1.50.63.9 2.5 6 0 1.90.7 4.2 3 6.2(5)nm 577=λU I U I U I UI -3 0 0.1 1 0.7 1.7 10 2.1 -0.4 0.1 0.2 1.1 1 1.8 15 2.1 -0.3 0.2 0.3 1.3 1.5 1.9 20 2.1 -0.2 0.4 0.4 1.4 3 2 252.1-0.1 0.60.5 1.5 5 2 0 0.80.61.672.10.00.51.01.52.02.5Y A x i s T i t l eX Axis Title从图中可得各波长下的遏止电位差(拐点法)经计算可得各个波长的光对应的频率:(频率=光速/波长)由a eU mv =221;A mv hv +=221;有A U e hv +=0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验简介
1905年,年仅26岁的爱因斯坦(A.Einstein)提出光量子假说,发表了在物理学发展史上具有里程碑意义的光电效应理论,10年后被具有非凡才能的物理学家密里根(Robert Millikan)用光辉的实验证实了。
两位物理大师之间微妙的默契配合推动了物理学的发展,他们都因光电效应等方面的杰出贡献分别于1921年和1923年获得诺贝尔物理学奖。
光电效应实验及其光量子理论的解释在量子理论的确立与发展上,在解释光的波粒二象性等方面都具有划时代的深远意义。
利用光电效应制成的光电器件在科学技术中得到广泛的应用,并且至今还在不断开辟新的应用领域,具有广阔的应用前景。
本实验的目的是了解光电效应基本规律,并用光电效应方法测量普朗克常量和测定光电管的光电特性曲线。
实验原理
当光照在物体上时,光的能量仅部分地以热的形式被物体吸收,而另一部分则转换为物体中某些电子的能量,使电子逸出物体表面,这种现象称为光电效应,逸出的电子称为光电子。
在光电效应中,光显示出它的粒子性质,所以这种现象对认识光的本性,具有极其重要的意义。
光电效应实验原理如图8.2.1-1所示。
其中S为真空光电管,K为阴极,A 为阳极。
当无光照射阴极时,由于阳极与阴极是断路,所以检流计G中无电流流过,当用一波长比较短的单色光照射到阴极K上时,形成光电流,光电流随加速电位差U变化的伏安特性曲线如图8.2.1-2所示。
⏹光电流与入射光强度的关系
光电流随加速电位差U的增加而增加,加速电位差增加到一定量值后,光电
流达到饱和值,饱和电流与光强成正比,而与入射光的频率无关。
当
变成负值时,光电流迅速减小。
实验指出,有一个遏止电位差存在,当电位差达到这个值时,光电流为零。
⏹光电子的初动能与入射光频率之间的关系
光电子从阴极逸出时,具有初动能,在减速电压下,光电子在逆着电场力方
向由K极向A极运动。
当时,光电子不再能达到A极,光电流为零。
所以电子的初动能等于它克服电场力所作的功。
即
(1)
根据爱因斯坦关于光的本性的假设,光是一粒一粒运动着的粒子流,这些光
粒子称为光子。
每一光子的能量为,其中为普朗克常量,为光波的频
率。
所以不同频率的光波对应光子的能量不同。
光电子吸收了光子的能量之后,一部分消耗于克服电子的逸出功A,另一部分转换为电子动能。
由能量守恒定律可知
(2)
式(2)称为爱因斯坦光电效应方程。
由此可见,光电子的初动能与入射光频率成线性关系,而与入射光的强度无关。
光电效应有光电阈存在
实验指出,当光的频率时,不论用多强的光照射到物质都不会产生光
电效应,根据式(2),,称为红限。
爱因斯坦,光电效应方程同时提供了测普朗克常量的一种方法:由式(1)
和(2)可得:。
当用不同频率()的单色光分别做光源时,就有
任意联立其中两个方程就可得到
由此若测定了两个不同频率的单色光所对应的遏止电位差及可算出普朗克常量,也可由直线的斜率求出。
因此,用光电效应方法测量普朗克常量的关键在于获得单色光、测得光电管的伏安特性曲线和确定遏止电位差值。
实验中,单色光可由水银灯光源经过单色仪选择谱线产生。
水银灯是一种气体放电光源,点燃稳定后,在可见光区域内有几条波长相差较远的强谱线,如表
8.2.1-1所示。
单色仪的鼓轮读数与出射光的波长存在一一对应关系,由单色仪的定标曲线,即可查出出射单色光的波长(有关单色仪的结构和使用方法请参阅有关说明书),也可用水银灯(或白炽灯)与滤光片联合作用产生单色光。
为了获得准确的遏止电位差值,本实验用的光电管应该具备下列条件:
●对所有可见光谱都比较灵敏。
●阳极包围阴极,这样当阳极为负电位时,大部分光电子仍能射到阳极。
●阳极没有光电效应,不会产生反响电流。
●暗电流很小。
但是实际使用的真空型光电管并不完全满足以上条件。
由于存在阳极光电效应所引起的反向电流和暗电流(即无光照射时的电流),所以测的得电流值,实际上包括上述两种电流和由阴极光电效应所产生的正向电流三个部分,所以伏安曲线并不与U轴相切。
由于暗电流是由阴极的热电子发射及光电管管壳楼电等原因产生,与阴极正向光电流相比,其值很小,且基本上随电位差U呈线性变化,因此可忽略其对遏止电位差的影响。
阳极反向光电流虽然在实验中较显著,但它服从一定规律。
据此,确定遏止电位差值,可采用以下两种方法:
●交点法
光电管阳极用逸出功较大的材料制作,制作过程中尽量防止阴极材料蒸发,实验前对光电管阳极通电,减少其上溅射的阴极材料,实验中避免入射光直接照射到阳极上,这样可使它的反向电流大大减少,器伏安特性曲线与
图8.2.1-2十分接近,因此曲线与U轴交点的电位差近似等于遏止电位差,此即交点法。
●拐点法
光电管阳极反向光电流虽然较大,但在结构设计上,若是反向光电流能较快地饱和,则伏安特性曲线在反向电流进入饱和段后有着明显的拐点,如图8.2.1-3所示,此拐点的电位差即为遏止电位差。
实验内容
通过实验了解光电效应的基本规律,并用光电效应法测量普朗克常量。
⏹在577.0nm、546.1nm、435.8nm、404.7nm四种单色光下分别测出光电管的
伏安特性曲线,并根据此曲线确定遏止电位差值,计算普朗克常量。
本实验所用仪器有:光电管、单色仪(或滤波片)、水银灯、检流计(或微电流计)、直流电源、直流电压计等,接线电路图如图8.2.1-4所示。
实验中光电流比较微弱,其值与光电管类型,单色光强弱等因素有关,因此应根据实际情况选用合适的测量仪器。
例如,选用GD-4、GD-5、或1977型光电
管,选用的检流计的分度值应在A/分度左右。
如果要测量更微弱的电流可用微电流计,可测量A的电流。
由于光电管的内阻很高,光电流如此之微弱,因此测量中要注意抗外界电磁干扰。
并避免光直接照射阳极和防止杂散光干扰。
⏹作的关系曲线,用一元线性回归法计算光电管阴极材料的红限频率、
逸出功及值,并与公认值比较。
⏹选做
●测量光电管在正压下的伏安特性曲线。
●测定光电管的光电特性曲线,即饱和光电流与照射光强度的关系。
●自行设计方案测量光电管阴极光电流在加速电压下的伏安特性曲线,改
变光源与光电管的距离,光强正比于,利用此测量光电管的光电特性曲线。
实验重点
⏹从光电管的伏安特性曲线,验证爱因斯坦光电效应方程。
⏹正确学会数据处理的方法,计算普朗克常量和光电管阴极材料的红限
值。
实验难点
⏹本实验验证爱因斯坦光电效应方程时,需要测出光电管的正向和反向特
性曲线,如何正确设计光电管阳极和阴极与电源的接线图?
⏹设计实验方案,由光电管的反向伏安特性曲线,测出不同光频率对应的
遏止电位差值,并由此计算普朗克常量和光电管阴极材料的红限值。
参考资料
复旦大学电光源实验室。
电光源原理。
上海:上海科学技术大出版社,1979.83-179,439-497。
