主成分分析法在我国居民生活质量状况_多元统计分析报告
多元统计数据分析报告(3篇)

第1篇一、引言随着大数据时代的到来,数据量急剧增加,传统的统计分析方法已无法满足复杂数据关系的挖掘需求。
多元统计分析作为一种处理多个变量之间关系的方法,在社会科学、自然科学、工程技术等领域得到了广泛应用。
本报告旨在通过对某研究项目的多元统计分析,揭示变量之间的关系,为决策提供科学依据。
二、研究背景与目的本研究以某企业员工绩效评估数据为研究对象,旨在通过多元统计分析方法,探究员工绩效与个人特质、工作环境等因素之间的关系,为企业人力资源管理部门提供决策支持。
三、数据与方法1. 数据来源本研究数据来源于某企业员工绩效评估系统,包括员工的基本信息、个人特质、工作环境、绩效评分等。
2. 研究方法本研究采用以下多元统计分析方法:(1)描述性统计分析:对员工绩效、个人特质、工作环境等变量进行描述性统计分析,了解数据的分布情况。
(2)相关分析:分析变量之间的线性关系,找出相关系数较大的变量对。
(3)因子分析:将多个变量归纳为少数几个因子,揭示变量之间的内在关系。
(4)聚类分析:将员工根据绩效、个人特质、工作环境等因素进行分类,分析不同类别员工的特点。
(5)回归分析:建立员工绩效与个人特质、工作环境等因素之间的回归模型,分析各因素对绩效的影响程度。
四、数据分析结果1. 描述性统计分析通过对员工绩效、个人特质、工作环境等变量的描述性统计分析,得出以下结论:(1)员工绩效评分呈正态分布,平均绩效评分为75分。
(2)个人特质得分集中在中等水平,其中创新能力得分最高,稳定性得分最低。
(3)工作环境得分普遍较高,其中工作压力得分最低。
2. 相关分析通过对员工绩效、个人特质、工作环境等变量进行相关分析,得出以下结论:(1)绩效与创新能力、稳定性、工作环境等因素呈正相关。
(2)创新能力与稳定性呈负相关。
3. 因子分析通过对员工绩效、个人特质、工作环境等变量进行因子分析,得出以下结论:(1)提取了3个因子,分别对应创新能力、稳定性、工作环境。
多元统计实验报告

多元统计实验报告一、实验目的多元统计分析是统计学的一个重要分支,它能够处理多个变量之间的复杂关系。
本次实验的主要目的是通过实际操作和数据分析,深入理解多元统计分析的基本原理和方法,并掌握其在实际问题中的应用。
二、实验数据本次实验使用了一组来自某市场调研公司的数据集,包含了消费者的年龄、性别、收入、消费习惯等多个变量,共计_____个样本。
三、实验方法1、主成分分析(PCA)主成分分析是一种降维方法,它通过将多个相关变量转换为一组较少的不相关变量(即主成分),来简化数据结构并提取主要信息。
2、因子分析因子分析用于发现潜在的公共因子,这些因子能够解释多个观测变量之间的相关性。
3、聚类分析聚类分析将数据对象分组,使得同一组内的对象具有较高的相似性,而不同组之间的对象具有较大的差异性。
四、实验过程1、数据预处理首先,对原始数据进行了清洗和预处理,包括处理缺失值、异常值和数据标准化等操作,以确保数据的质量和可用性。
2、主成分分析使用统计软件进行主成分分析,计算出特征值、贡献率和累计贡献率。
根据特征值大于 1 的原则,确定了保留的主成分个数。
通过主成分载荷矩阵,解释了主成分的实际意义。
3、因子分析运用因子分析方法,提取公共因子,并通过旋转因子载荷矩阵,使得因子的解释更加清晰和具有实际意义。
计算因子得分,用于进一步的分析和应用。
4、聚类分析采用 KMeans 聚类算法,根据选定的变量对样本进行聚类。
通过不断调整聚类中心和重新分配样本,最终得到了较为合理的聚类结果。
五、实验结果与分析1、主成分分析结果提取了_____个主成分,它们累计解释了_____%的方差。
第一个主成分主要反映了_____,第二个主成分主要与_____相关,以此类推。
这为我们理解数据的主要结构提供了重要的线索。
2、因子分析结果成功提取了_____个公共因子,它们能够较好地解释原始变量之间的相关性。
每个因子所代表的潜在因素也得到了清晰的解释,有助于深入了解消费者的行为特征和市场结构。
《多元统计实验》主成分分析实验报告二

《多元统计实验》主成分分析实验报告三、实验结果分析6.5人均粮食产量x5,经济作物占农作物播种面积x6,耕地占土地面积比x7,果园与林地面积之比x8,灌溉田占1耕地面积比例x9等五个指标有较强的相关性, 人口密度x1,人均耕地面积x2,森林覆盖率x3,农民人均收入x4相关性也很强,再作主成分分析,求样本相关矩阵的特征值和主成分载荷。
λ11/2=2.158962,λ21/2=1.4455076,λ31/2 =1.0212708,λ41/2 =0.71233588,λ51/2 =0.5614001,λ61/2 =0.43887788,λ71/2 =0.33821497,λ81/2 =0.212900230,λ91/2=0.177406876。
确定主成分分析,前两个主成分的累积方差贡献率为75.01%,前三个主成分的累积方差贡献率为86.59%,按照累积方差贡献率大于80%的原则,主成分的个数取为3,前三个主成分分别为:Z*1=0.3432x*1-0.446x*3+0.376x*5+0.379x*6+0.432x*7+0.446x*9Z*2=0.368x*1-0.614x*2-0.61x*4-0.307x*5-0.1224x*6Z*3=-0.122x*6+0.246x*7-0.950x*8第一主成分在x*7,x*9两个指标上取值为正且载荷较大,可视为反映耕地占比和灌溉田占耕地面积比例的主成分,第二主成分在x*2和x*4这两个指标的取值为负,绝对值载荷最大,不能作为人均耕地和人均收入的主成分。
第三主成分,x*8这个指标取值为负且,载荷绝对值最大,不能反映果园与林地面积之比的主成分。
根据该图结果可以认为选取前两个指标作为主成分分析的选择是正确的。
将八个指标按前两个主成分进行分类:由结果可以得出森林覆盖率为一类,人口密度、果园与林地面积之比、耕地占土地面积比、灌溉田占耕地面积比为一类,经济作物占农作物播种面积比例、人均粮食产量、农民人均收入、人均耕地面积为一类。
多元统计课程实验报告

一、实验背景随着社会经济的发展和科学技术的进步,数据量日益庞大,如何从大量数据中提取有价值的信息,成为统计学研究的热点问题。
多元统计分析作为统计学的一个重要分支,通过对多个变量之间的关系进行分析,为决策者提供有力的数据支持。
本实验旨在通过实际操作,让学生熟练掌握多元统计分析方法,提高数据分析能力。
二、实验目的1. 掌握多元统计分析的基本概念和方法;2. 学会运用多元统计分析方法解决实际问题;3. 提高数据分析能力,为后续课程打下坚实基础。
三、实验内容本次实验以某城市居民消费数据为例,运用多元统计分析方法对其进行分析。
四、实验步骤1. 数据导入首先,将实验数据导入统计软件(如SPSS、R等)。
本实验采用SPSS软件,数据集包含以下变量:(1)收入(y):居民年收入;(2)教育程度(x1):居民最高学历;(3)年龄(x2):居民年龄;(4)家庭人口(x3):家庭人口数量;(5)住房面积(x4):家庭住房面积。
2. 描述性统计分析对数据集进行描述性统计分析,包括各变量的均值、标准差、最大值、最小值等。
3. 相关性分析运用皮尔逊相关系数、斯皮尔曼等级相关系数等方法,分析变量之间的相关关系。
4. 主成分分析运用主成分分析方法,提取主要成分,降低数据维度。
5. 聚类分析运用K-means聚类分析方法,将居民划分为不同的消费群体。
6. 随机森林回归分析运用随机森林回归分析方法,预测居民收入。
五、实验结果与分析1. 描述性统计分析根据描述性统计分析结果,可知居民年收入、教育程度、年龄、家庭人口、住房面积的平均值、标准差、最大值、最小值等。
2. 相关性分析通过相关性分析,发现收入与教育程度、年龄、家庭人口、住房面积之间存在显著的正相关关系。
3. 主成分分析根据主成分分析结果,提取出两个主成分,累计方差贡献率为84.95%,可以解释大部分的变量信息。
4. 聚类分析通过K-means聚类分析,将居民划分为3个消费群体。
应用多元统计分析实验报告之主成分分析
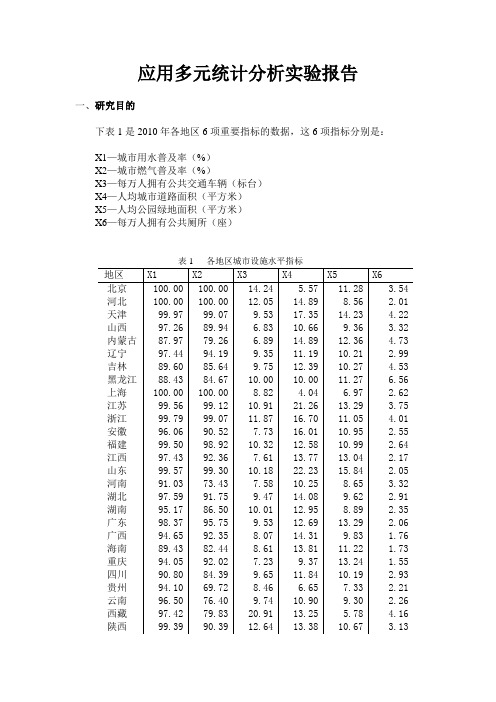
应用多元统计分析实验报告一、研究目的下表1是2010年各地区6项重要指标的数据,这6项指标分别是:X1—城市用水普及率(%)X2—城市燃气普及率(%)X3—每万人拥有公共交通车辆(标台)X4—人均城市道路面积(平方米)X5—人均公园绿地面积(平方米)X6—每万人拥有公共厕所(座)表1 各地区城市设施水平指标本次实验的研究目的是根据这些指标用主成分分析法对各地区城市设施水平进行综合评价和排序,得出结论并提出建议。
二、研究过程从标准化数据出发,首先计算这些指标的主成分,然后通过主成分的大小进行排序。
1.利用SPSS进行因子分析表2和表3分别是特征根(方差贡献率)和因子载荷阵的信息。
表3 因子载荷阵2.利用因子分析结果进行主成分分析 ⑴.表4是特征向量的信息表4 特征向量矩阵 z1 z2 z3 z4 z5 z6 x1 0.52 0.35 (0.31) (0.00) 0.08 0.70 x2 0.58 0.09 (0.19) 0.45 (0.37) (0.53) x3 0.17 0.67 0.26 (0.36) 0.41 (0.39) x4 0.43 (0.32) 0.32 (0.66) (0.41) 0.03 x5 0.41 (0.51) 0.25 0.21 0.68 (0.01) x6 (0.01) 0.23 0.79 0.43 (0.24) 0.28⑵.利用主成分得分进行综合评价时,从特征向量可以写出所有6个主成分的具体形式:Y1=0.52X1+0.68X2+0.17X3+0.43X4+0.41X5-0.01X6Y2=0.35X1+0.09X2+0.67X3-0.32X4-0.51X5+0.23X6 Y3=-0.31X1-0.19X2+0.26X3+0.32X4+0.25X5+0.79X6 Y4=0.00X1+0.45X2-0.36X3-0.66X4+0.21X5+0.43X6 Y5=0.08X1-0.37X2+0.41X3-0.41X4+0.68X5-0.24X6 Y6=0.70X1-0.53X2-0.39X3+0.03X4-0.01X5+0.28X6⑶.以特征根为权,对6个主成分进行加权综合,得出各地区的综合得分及排序,具体数据见表5.综合得分的计算公式是6161Y Y Y ii ∑∑+⋯+=λλλλ三、结果说明从表5可以看出,北京、天津。
主成分分析报告

主成分分析报告在当今的数据驱动的世界中,我们经常面临着处理大量复杂数据的挑战。
如何从这些海量的数据中提取有价值的信息,简化数据结构,发现潜在的模式和趋势,成为了数据分析领域的重要课题。
主成分分析(Principal Component Analysis,简称 PCA)作为一种强大的数据分析工具,为我们提供了一种有效的解决方案。
主成分分析是一种多元统计分析方法,其主要目的是通过对原始变量的线性组合,构建一组新的不相关的综合变量,即主成分。
这些主成分能够尽可能多地保留原始数据的信息,同时实现数据的降维。
让我们先来了解一下主成分分析的基本原理。
假设我们有一组观测数据,每个观测包含多个变量。
主成分分析的核心思想是找到一组新的坐标轴,使得数据在这些坐标轴上的投影具有最大的方差。
第一个主成分就是数据在方差最大方向上的投影,第二个主成分则是在与第一个主成分正交的方向上,具有次大方差的投影,以此类推。
为什么要进行主成分分析呢?首先,它能够帮助我们简化数据结构。
当我们面对众多相关的变量时,通过主成分分析可以将其归结为少数几个综合变量,从而减少数据的复杂性,便于后续的分析和处理。
其次,主成分分析可以去除数据中的噪声和冗余信息,突出数据的主要特征,有助于发现数据中的隐藏模式和关系。
此外,它还可以用于数据压缩和可视化,使得我们能够更直观地理解数据。
在实际应用中,主成分分析有着广泛的用途。
在图像处理领域,它可以用于图像压缩和特征提取,减少图像数据的存储空间,同时保留图像的主要特征。
在金融领域,主成分分析可以用于构建投资组合,通过对多个金融资产的分析,找出主要的影响因素,从而优化投资组合。
在生物学研究中,主成分分析可以用于分析基因表达数据,发现不同样本之间的差异和相似性。
接下来,我们来看看如何进行主成分分析。
首先,需要对原始数据进行标准化处理,以消除量纲的影响。
然后,计算数据的协方差矩阵或相关矩阵。
接着,通过求解特征值和特征向量,确定主成分的方向和权重。
基于主成分分析的我国城镇居民生活消费支出的研究剖析

基于主成分分析的我国城镇居民生活消费支出的研究陈忠磊,吴川东,杨礼锚,邓雍,黄廷朗(20122211012011,62,49,47,12)摘要:我国城镇居民的消费性支出在逐步提高的同时,不同地区之间的消费水平和支出结构仍存在较大差异。
全国各地的城镇居民生活消费的分布规律可以反映近年来在城镇化进行中各地居民的生活水平情况,通过选取相关的消费性支出指标,利用SPSS软件,对2012年我国31个省、市、自治区城镇居民家庭平均每人全年消费性支出的分布规律进行聚类分析和主成分分析,并进行了主成分得分综合排序,找出各地区城镇居民在消费性支出方面存在的差异,并提出相应缩小差异的建议。
关键词:消费性支出;聚类分析;主成分分析;综合评价近年来,随着我国经济的快速发展,城镇居民的收入不断增加,并且在国家连续出台住房、教育、医疗等各项改革措施和实施“刺激消费、扩大内需、拉动经济增长”经济政策的影响下,我国各地区城镇居民的消费支出也强劲增长,消费结构发生了巨大的变化,结构不合理现象也得到了一定程度的调整。
但是,由于各地区的经济发展不平衡及原有经济基础的差异,人民收入水平不同,各地区城镇间的消费性支出结构仍存在着明显差别。
为了进一步改善消费结构,正确引导消费,缩小消费性支出的地区差异,提高我国城市居民的消费水平和生活质量,有必要考察我国各地区城镇居民的消费性支出结构之间的异同并进行考察及系统分析研究,以期发现特点和规律,从宏观上把握各地区城镇居民的消费现状和不同地区消费水平的差异,为提高我国各地区消费水平和谐增长提供决策依据。
因此客观、准确、有效地分析这些地区差异具有重要的理论和实践指导意义。
为了研究全国各地区城镇居民人均年消费性支出的差异性和相似性,本文选取了全国31个省市自治区的相关数据,基于聚类分析、主成分分析等多元统计分析方法,运用SPSS 软件进行研究。
1主成分分析模型主成分分析是将多指标化为少数几个综合指标的一种统计方法,是由Pearson提出,后来被Hotelling发展起来的。
多元统计分析案例实验-使用SAS软件对我国各地区城镇居民消费性支出的主成分分析和聚类分析

实验三我国各地区城镇居民消费性支出的主成分分析和聚类分析一、实验目的1.掌握如何使用SAS软件来进行主成分分析和聚类分析;2.看懂和理解SAS输出的结果,并学会以此来作出分析;3.掌握对实际数据如何来进行主成分分析;4.对同一组数据使用五种系统聚类方法及k均值法,学会对各种聚类效果的比较,获取重要经验;5.掌握使用主成分进行聚类二、实验内容数据集sasuser.examp633中含有1999年全国31个省、直辖市和自治区的城镇居民家庭平均每人全年消费性支出的八个主要变量数据。
对这些数据进行主成分分析,可将这31个地区的前两个主成分得分标示于平面坐标系内,对各地区作直观的比较分析。
对同样的数据使用五种系统聚类方法及k均值法聚类,并对聚类效果作比较。
最后,对主成分的图形聚类和正规聚类的效果进行比较。
实验1进行主成分分析,根据前两个主成分得分所作的散点图对31个地区进行比较分析。
实验2分别使用最长距离法、中间距离法、两种类平均法、离差平方和法和k均值法进行聚类分析,并比较其聚类效果。
实验3主成分聚类,并与上述正规的聚类方法进行比较三、实验要求1.用SAS软件的交互式数据分析菜单系统完成主成分分析;2.完成五种系统聚类方法及k均值法,比较其聚类效果;3.根据前两个主成分得分的散点图作直观的聚类,并与上述正规的聚类方法进行比较。
四、实验指导1.进行主成分分析在inshigt中打开数据集sasuser.examp633,见图1。
选菜单过程如下:在图1中选分析⇒多元(Y X)⇒在变量框中选x1,x2,x3,x4,x5,x6,x7,x8(见图2)⇒Y⇒选输出⇒选主分量分析,主分量选项(见图3)⇒在图4中作图中的选择(主成分个数缺省时为“自动”选项,此时只输出特征值大于1的主成分)⇒确定⇒确定⇒确定图1图2图3图4 得到如图5、图6所示的结果:图5图6 从图5可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和87.8%,第一主成分1ˆy 在所有变量(除在*2x 上的载荷稍偏小外)上都有近似相等的正载荷,反映了综合消费性支出的水平,因此第一主成分可称为综合消费性支出成分。
农民生活水平进行主成分分析[技巧]
![农民生活水平进行主成分分析[技巧]](https://img.taocdn.com/s3/m/2fb9d9fd80c758f5f61fb7360b4c2e3f572725d5.png)
摘要 本文利用主成分分析对题中给出的十六个地区的农民在某年支出情况的抽样调查数据进行了分析,通过六个关键的综合指标对各地区农民生活水平进行主成分分析,并以主成分得分为基础,对各地区农民生活水平进行分类。
关键词 农民生活水平 主成分分析1、 问题的重述表1-1是我国16个地区农民在某年支出情况的抽样调查数据的汇总资料,每个地区都调查了反映每人平均生活消费支出情况的六个指标。
(1)试对调查资料中的16个地区的农民生活水平进行主成分分析,(2)并利用前两个主成分对16个地区的农民生活水平进行分类表1-1 16个地区的农民生活水平的调查数据 (单位:元)地区食品 (1X )衣着 (2X ) 燃料 (3X ) 住房 (4X ) 生活用品及其它 (5X ) 文化生活服务 (6X ) 北京 190.33 43.77 9.73 60.54 49.01 9.04 天津 135.20 36.40 10.47 44.16 36.49 3.94 河北 95.21 22.83 9.30 22.44 22.81 2.80 山西 104.78 25.11 6.40 9.89 18.17 3.25 内蒙古 128.41 27.63 8.94 12.58 23.99 3.27 辽宁 145.68 32.83 17.79 27.29 39.09 3.47 吉林 159.37 33.38 18.37 11.81 25.29 5.22 黑龙江 116.22 29.57 13.24 13.76 21.75 6.04 上海 221.11 38.64 12.53 115.65 50.82 5.89 江苏 144.98 29.12 11.67 42.60 27.30 5.74 浙江 169.92 32.75 12.72 47.12 34.35 5.00 安徽 153.11 23.09 15.62 23.54 18.18 6.39 福建 144.92 21.26 16.96 19.52 21.75 6.73 江西 140.54 21.50 17.64 19.19 15.97 4.94 山东115.8430.2612.2033.6133.773.85河南 101.18 23.26 8.46 20.20 20.50 4.302、模型的假设及符号说明2、1 模型的假设(1)各地区的农民生活水平是互为独立的,各指标之间也互为独立。
多元统计分析 实验报告

多元统计分析实验报告多元统计分析实验报告一、引言多元统计分析是一种研究多个变量之间关系的统计方法,可以帮助我们更全面地了解数据集中的信息。
本实验旨在通过多元统计分析方法,探索不同变量之间的关系,并分析其对研究结果的影响。
二、数据收集与处理在本实验中,我们收集了一份关于学生学业成绩的数据集。
数据集包括学生的性别、年龄、家庭背景、学习时间、考试成绩等多个变量。
为了方便分析,我们对数据进行了清洗和预处理,包括删除缺失值、标准化处理等。
三、描述性统计分析在进行多元统计分析之前,我们首先对数据进行了描述性统计分析。
通过计算各变量的均值、标准差、最小值、最大值等统计量,我们对数据的整体情况有了初步的了解。
例如,我们发现男生和女生的平均成绩存在差异,家庭背景与学习时间之间存在一定的相关性等。
四、相关性分析为了探索不同变量之间的关系,我们进行了相关性分析。
通过计算各个变量之间的相关系数,我们可以了解它们之间的线性关系强弱。
通过绘制相关系数矩阵的热力图,我们可以直观地观察到各个变量之间的相关性。
例如,我们发现学习时间与考试成绩之间存在较强的正相关关系,而年龄与考试成绩之间的相关性较弱。
五、主成分分析主成分分析是一种常用的降维方法,可以将多个相关变量转化为少数几个无关的主成分。
在本实验中,我们应用主成分分析方法对数据进行了降维处理。
通过计算各个主成分的解释方差比例,我们可以确定保留的主成分个数。
通过绘制主成分得分图,我们可以观察到不同变量在主成分上的贡献程度。
例如,我们发现第一主成分主要与学习时间和考试成绩相关,而第二主成分主要与家庭背景和性别相关。
六、聚类分析聚类分析是一种将样本按照相似性进行分类的方法,可以帮助我们发现数据集中的潜在模式和群体。
在本实验中,我们应用聚类分析方法对学生进行了分类。
通过选择适当的聚类算法和距离度量,我们可以将学生分为不同的群体。
通过绘制聚类结果的散点图,我们可以观察到不同群体之间的差异。
多元统计分析案例分析
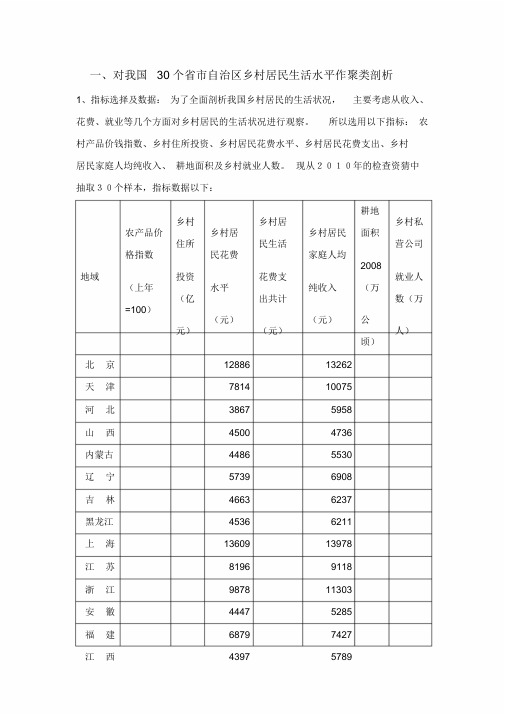
一、对我国30 个省市自治区乡村居民生活水平作聚类剖析1、指标选择及数据:为了全面剖析我国乡村居民的生活状况,主要考虑从收入、花费、就业等几个方面对乡村居民的生活状况进行观察。
所以选用以下指标:农村产品价钱指数、乡村住所投资、乡村居民花费水平、乡村居民花费支出、乡村居民家庭人均纯收入、耕地面积及乡村就业人数。
现从2010年的检查资猜中抽取30个样本,指标数据以下:耕地乡村乡村居乡村私农产品价乡村居乡村居民面积住所民生活营公司格指数民花费家庭人均2008地域投资花费支就业人(上年水平纯收入(万(亿出共计数(万=100)(元)(元)公元)(元)人)顷)北京12886 13262天津7814 10075河北3867 5958山西4500 4736内蒙古4486 5530辽宁5739 6908吉林4663 6237黑龙江4536 6211上海13609 13978江苏8196 9118浙江9878 11303安徽4447 5285福建6879 7427江西4397 5789山东5733 6990河南4061 5524湖北4758 5832湖南4513 5622广东5880 7890广西3561 4543海南3846 5275重庆3652 5277四川4748 5087贵州2926 3472云南3603 3952陕西3683 4105甘肃2975 3425青海3684 3863宁夏3894 4675新疆3590 4643数据根源:《中国统计年鉴2010》.2、将数据进行标准化变换:耕地乡村乡村居乡村私农产品价乡村居乡村居民面积住所民生活营公司格指数民花费家庭人均2008地域投资花费支就业人(上年水平纯收入(万(亿出共计数(万=100)(元)(元)公元)(元)人)顷)北京河北山西内蒙古辽宁吉林黑龙江上海江苏浙江安徽福建江西山东河南湖北湖南广东广西海南重庆四川贵州云南陕西甘肃宁夏新疆3、用K-均值聚类法对样本进行分类以下:聚类成员事例号地域聚类距离1 北京 12 天津 23 河北 34 山西 45 内蒙古 36 辽宁 27 吉林 38 黑龙江 39 上海 110 江苏 211 浙江 112 安徽 313 福建 214 江西 415 山东 316 河南 317 湖北 318 湖南 419 广东 220 广西 421 海南 422 重庆 423 四川 324 贵州 425 云南 326 陕西 427 甘肃 428 青海 429 宁夏 430 新疆 4分四类的状况下,最后分类结果以下:第一类:北京、上海、浙江。
多元统计分析报告范文

多元统计分析报告范文自己写的多元统计分析的报告,使用了聚类,主成分,因子分析方法,使用的软件有p和matlab聚类分析、主成分分析、因子分析的应用一、选题背景我曾参加过2022年的全国大学生数学建模竞赛,但是我们那时并没有深入的学习多元统计学方面的知识,当时做的时候只把前两问使用显著性分析和使用主成分分析进行了一些处理,通过上统计分析的课觉得这个题完全可以使用所学的知识解决,因此本文通过参考一些优秀的论文将这个题的整个过程详细的实现了一遍。
使用的分析工具有E某CLE2007,SPSS17.0中文版和MATLAB2022.a。
具体的题目如下:确定葡萄酒质量时一般是通过聘请有资质的评酒员进行品评。
每个评酒员在对葡萄酒进行品尝后对其分类指标打分,然后求和得到其总分,从而确定葡萄酒的质量。
酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系,葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。
附件1给出了某一年份一些葡萄酒的评价结果,附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据。
请尝试建立数学模型讨论下列问题:1.分析附件1中两组评酒员的评价结果有无显著性差异,哪一组结果更可信?4.分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响,并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量?二、分析过程1.问题一自己写的多元统计分析的报告,使用了聚类,主成分,因子分析方法,使用的软件有p和matlab表1(两种葡萄酒的得分情况)使用表1中得出的平均值,利用SPSS中的Kendall和调系数检验法对这两组评委的打分进行一致性检验,这里之所以选择Kendall和调系数检验法,随让一致性检验有多种方法,但是不同的方法使用范围是有限制的,而此方法正是用来检验多个评分者给分的一致性程度。
Kendall和调系数检验法原理和谐系数的计算公式:若评分中出现相同等级,则需要计算校正的系数,其公式为:SPSS操作步骤打开SPSS并导入处理之后的结果,选择菜单栏中的“分析”—>“非参数检验”—>“K个相关样本”—>“选择检验的数据”。
我国居民消费影响因素主成分回归分析

我国居民消费影响因素主成分回归分析根据已有的研究,总结影响消费的若干因素,在此基础上进行多重共线性诊断,并用主成分分析法消除变量之间的多重共线性,选择主成分,对我国居民消费进行回归,从而得出影响我国居民消费的主要因素,并在此基础上提出提高居民消费的建议。
标签:主成分分析;消费;需求F21引言出口、投资和消费一直被认为是拉动我国经济增长的“三驾马车”,然而回顾我国改革开放三十多年的经济增长过程,消费在我国经济增长过程发挥的作用仍有待加强。
事实上,与发达国家相比,我国的消费不足主要表现在居民消费不足。
自2000年以后,中国的消费率(最终消费支出占支出法GDP的比重)呈逐年下降的趋势,尤其是2007年以后,消费率下降并一直保持在50%以下;在中国的最终消费结构中,居民消费和政府消费呈现此消彼长的变化趋势,居民消费占总消费的比重从1995年的77%下降到2010年的71%,而在此期间,政府消费则从23%上升至29%;自2000年以来,中国居民的消费增长既落后于固定资产投资增长,也落后于经济(GDP)增长。
2文献回顾学术界对中国居民消费需求不足的原因进行了大量的研究,出现了不少富有启发性的和有价值的研究结论和研究方法。
概括而言,学者主要将我国居民消费不足的原因归纳为以下几点。
(1)收入分配不均抑制消费增长。
自改革开放以来,尤其是20世纪90年代至今,随着市场经济在我国的日益深入,东中西部、城乡之间、行业之间的收入分配差距日益扩大,中低收入人群的低支付能力使得总消费需求不足(毛盛勇,2007;邹红,喻开志,2011)。
(2)消费结构升级换代导致消费推迟。
尚不成熟的供给结构无法满足居民日益提高的消费结构,造成了消费推迟,影响居民消费增长(毛盛勇,2007;张红伟,吴瑾,2011)。
(3)保守的居民消费习惯减弱居民消费增长。
多数观点认为,由于长期的文化和经济发展原因,我国居民消费习惯与西方发达国家相比更加保守和谨慎(杭斌,2010),消费倾向偏低,具体表现为看重储蓄,厉行节约,不愿意负债消费。
多元统计分析与主成分分析的关系与应用

多元统计分析与主成分分析的关系与应用多元统计分析和主成分分析是统计学中两个重要的技术手段,它们在数据分析和统计建模中具有广泛的应用。
本文将探讨多元统计分析与主成分分析的关系以及它们在实际问题中的应用。
一、多元统计分析与主成分分析的关系多元统计分析是一种综合运用多种统计学方法和技术,研究多个变量之间关系的分析方法。
它旨在通过对大量的数据进行整合和分析,揭示不同变量之间的潜在结构和规律。
而主成分分析则是多元统计分析中常用的技术之一。
主成分分析(Principal Component Analysis,简称PCA)是一种通过降维的方法来简化数据集的技术。
它的基本思想是通过线性组合将原始数据变换为一组新的变量,这些新变量称为主成分,它们能够尽量保留原始数据的信息。
主成分分析通过将原始数据投影到主成分上,实现数据维度的压缩和去除冗余信息。
在多元统计分析中,主成分分析被广泛应用于数据预处理、变量选择和模型建立等环节。
通过主成分分析,可以将原始的高维数据转化为少数几个主成分,从而降低数据的维度,减少模型的复杂度,同时保留了原始数据中的主要信息,有助于提取数据的潜在结构和进行更有效的数据分析。
二、主成分分析的应用1. 数据可视化主成分分析可以帮助我们对高维数据进行可视化分析。
通过将数据投影到低维的主成分上,我们可以将原始数据在二维或三维空间中进行可视化展示。
这样可以更直观地观察数据之间的关系,发现异常值和聚类结构,为后续的模型建立提供重要的参考。
2. 数据预处理在建立统计模型之前,通常需要对数据进行预处理。
主成分分析可以作为一种预处理方法,通过去除原始数据中的冗余信息和噪声,减少数据维度,提高模型的建模效率和精度。
主成分分析还可以用于数据的标准化和归一化,使得不同变量之间具有可比性,更好地满足模型的要求。
3. 变量选择在众多的变量中选择对目标变量具有显著影响的变量是建立高效模型的关键一步。
主成分分析可以通过计算各个主成分的贡献率或者变量的负荷量,来评估每个变量对数据的影响程度。
主成分分析在区域农民生活水平评价中的应用

设 , , …
为原 有的P 指标, 如 性 合: = 个 考虑 下线 组 ∑%
} -1
(= , … , )为 新 指 标 。 i 12 p
的 样 本 方 差
Vr a
=
协 方 差
Cy , ) 见4( 1 , ,) 希望用较少新指标代替原来的 P o( = Jj , … p。 =2 个指标,就
要 求 它 们 含有 尽 可 能 多 的原 指 标 信 息且 互 不 相 关 指 标 中信 息量 的大 小通 常 用 该 指 标 的 方 差 来计 量 ,方 差 越 大 , 信 息 含 量 就 越 大 , 反 之 则 越 小 。
0 17 8 L 70
㈣ 6 8 x 3
x 4
x G
x 7
[ 关键词】 消费支出
主成分分析
指标体 系选取 了具有代表 性的各区域 能反映农 民每人平 均生 活消 费支 出的八
O 引言 、
主 成 分 分 析 是 一种 常 用 的 多元 统 计 分 析 方 法 , 相 对 于 其 他 统计 学 方
法, 它更强调用数据本 身来指导分析过程 , 而不是依 赖于事先给 定的某些 假 设 。其 主 要 目的是 希 望 用 较 少 的 变 量 去 解 释 原 始 资料 中 的 大 部 分 变 量 , 期望能将许 多相关性相对很高变量转化成彼此相独立 的变量 , 能从中选取 较原始变 量个数少而且能解释大部分资料 中的变量 的几个 新变量, 也就是 所谓的主成分 , 而这几个主成分也就是成为用来解释 资料 的综合性指标 。 生 活 消 费 指 标 体 系 是 描 述 和 度 量 国 民 生 活 水 平 的现 状 特 征 和 变 化 趋 势 的 , 一 个 指 标 都 从 不 同 的 层 次 、 面和 方 位 反 映 了 人 民生 活 水 平 的 某 每 侧 局部的特征 , 各指标之间既相互独立, 又相互关联 , 如果仅仅 单项比较或 简单叠加 , 都难 以准确 、 全面地综合反映人 民生活消 费水平 的客观 实际, 本 文将应用 主成分分析法对农 民生活消 费支 出指标体系 中各单项指标 的原 始 数据进行 加工 、 整理和分析 , 提取 出指标群 中具有表征 意义的少数特 征 指标 , 改善和简化观测系统, 从而实现对 各区域农民消费水平 的综合 分析、 比较 和 评 价 。 1实证研究方法设计 、
多元统计分析报告

多元统计分析课程设计主成分分析法在我国居民生活质量状况综合评价中的应用姓名:专业班级:学院:数学与系统科学学院学号:指导教师:山东科技大学2014年6月24日目录摘要 (1)1.问题及背景 (2)1.1背景提出 (2)2主成分分析概念与方法 (2)3主成分分析法在我国居民生活质量状况综合评价中的应用 (4)3.1原始数据 (4)3.2数据标准化 (5)3.3相关系数矩阵 (6)3.4特征方程及主成分确定 (6)3.5各特征值的单位特征向量 (6)3.6主成分值以及综合分值 (7)3.7各主成分上的得分 (8)3.8综合因子得分 (9)3. 9评价结果和排序 (9)4.聚类分析 (10)5 建议 (10)摘要改革开放以来,我国各地区间的经济发展速度有着明显差别,而人民的生活质量也因此产生了不同,本文用主成分分析法、聚类分析法,选取职工人均工资1()X ,人均居住面积2()X ,城市人口用水普及量3()X ,城市煤气普及量4()X ,人均拥有道路面积5()X ,人均绿地公共面积6()X ,批发零售贸易商品销售总额7()X ,旅游外汇收入8()X 8个指标,以综合因子的贡献率确定主成分和权重, 计算出主成分分值值以及综合分值,对全国31个省市居民的生活质量进行了简单的分析,得到以下结论:根据31个省市的综合分值可以将居民生活质量状况按照降序进行以下排序:上海、广东、北京、江苏、浙江、福建、天津、山东、重庆、辽宁、湖北、安徽、 湖 南、江西、山西、河北、陕西、四川、新疆、广西、青海、河南、云南、贵州、内蒙古、 宁夏、黑龙江、吉林、海南、甘肃、西藏。
关键词主成分分析法、聚类分析法、居民生活质量状况、综合评价使用软件:SPSS 17.0 Matlab 7.01.问题及背景1.1背景提出随着生产水平的的不断提高,我国居民生活水平不断提高,生活质量也在不断改进。
但是,受各地区生产力发展水平不平衡的影响,我国各地区居民生活质量也表现为不平衡。
应用多元统计分析实验报告之主成分分析

应用多元统计分析实验报告一、研究目的下表1是2010年各地区6项重要指标的数据,这6项指标分别是:X1—城市用水普及率(%)X2—城市燃气普及率(%)X3—每万人拥有公共交通车辆(标台)X4—人均城市道路面积(平方米)X5—人均公园绿地面积(平方米)X6—每万人拥有公共厕所(座)表1 各地区城市设施水平指标本次实验的研究目的是根据这些指标用主成分分析法对各地区城市设施水平进行综合评价和排序,得出结论并提出建议。
二、研究过程从标准化数据出发,首先计算这些指标的主成分,然后通过主成分的大小进行排序。
1.利用SPSS进行因子分析表2和表3分别是特征根(方差贡献率)和因子载荷阵的信息。
表3 因子载荷阵2.利用因子分析结果进行主成分分析 ⑴.表4是特征向量的信息表4 特征向量矩阵 z1 z2 z3 z4 z5 z6 x1 0.52 0.35 (0.31) (0.00) 0.08 0.70 x2 0.58 0.09 (0.19) 0.45 (0.37) (0.53) x3 0.17 0.67 0.26 (0.36) 0.41 (0.39) x4 0.43 (0.32) 0.32 (0.66) (0.41) 0.03 x5 0.41 (0.51) 0.25 0.21 0.68 (0.01) x6 (0.01) 0.23 0.79 0.43 (0.24) 0.28⑵.利用主成分得分进行综合评价时,从特征向量可以写出所有6个主成分的具体形式:Y1=0.52X1+0.68X2+0.17X3+0.43X4+0.41X5-0.01X6Y2=0.35X1+0.09X2+0.67X3-0.32X4-0.51X5+0.23X6 Y3=-0.31X1-0.19X2+0.26X3+0.32X4+0.25X5+0.79X6 Y4=0.00X1+0.45X2-0.36X3-0.66X4+0.21X5+0.43X6 Y5=0.08X1-0.37X2+0.41X3-0.41X4+0.68X5-0.24X6 Y6=0.70X1-0.53X2-0.39X3+0.03X4-0.01X5+0.28X6⑶.以特征根为权,对6个主成分进行加权综合,得出各地区的综合得分及排序,具体数据见表5.综合得分的计算公式是6161Y Y Y ii ∑∑+⋯+=λλλλ三、结果说明从表5可以看出,北京、天津。
多元统计分析实验报告

附录1:源程序
附录2:实验报告填写说明
1.实验项目名称:要求与实验教学大纲一致。
2.实验目的:目的要明确,要抓住重点,符合实验教学大纲要求。
3.实验原理:简要说明本实验项目所涉及的理论知识。
4.实验环境:实验用的软、硬件环境。
5.实验方案(思路、步骤和方法等):这是实验报告极其重要的内容。
概括整个实验过程。
对于验证性实验,要写明依据何种原理、操作方法进行实验,要写明需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验,在上述内容基础上还应该画出流程图、设计思路和设计方法,再配以相应的文字说明。
对于创新性实验,还应注明其创新点、特色。
6.实验过程(实验中涉及的记录、数据、分析):写明具体实验方案的具体实施步骤,包括实验过程中的记录、数据和相应的分析。
7.实验结论(结果):根据实验过程中得到的结果,做出结论。
8.实验小结:本次实验心得体会、思考和建议。
9.指导教师评语及成绩:指导教师依据学生的实际报告内容,给出本次实验报告的评价。
几种多元统计分析方法及其在生活中的应用

几种多元统计分析方法及其在生活中的应用一、本文概述随着大数据时代的到来,多元统计分析方法在各个领域中的应用日益广泛,其重要性和价值逐渐凸显。
本文旨在深入探讨几种主流的多元统计分析方法,包括主成分分析(PCA)、因子分析(FA)、聚类分析(CA)以及判别分析(DA)等,并阐述这些方法在生活实践中的具体应用。
我们将对每种多元统计分析方法进行详细介绍,包括其基本原理、实施步骤以及优缺点等方面。
通过这些基础知识的普及,为读者提供一个清晰的方法论框架,为后续的实际应用打下坚实基础。
我们将结合生活中的实际案例,详细阐述多元统计分析方法的应用场景。
这些案例可能涉及市场营销、医学诊断、社会调查、金融分析等多个领域,旨在展示多元统计分析方法在解决实际问题中的强大威力。
我们将对多元统计分析方法在生活中的应用前景进行展望,分析未来可能的发展趋势和挑战。
本文还将提出一些针对性的建议,以期推动多元统计分析方法在实践中的更广泛应用和发展。
通过本文的阐述,我们希望能够为读者提供一个全面、深入的多元统计分析方法及其在生活中的应用指南,为相关领域的研究和实践提供有益的参考。
二、多元统计分析方法介绍多元统计分析是一种在多个变量间寻找规律性的统计分析方法,其核心在于通过提取多个变量的信息,揭示出这些变量间的内在结构和相互关系。
以下是几种常见的多元统计分析方法及其特点。
多元回归分析:这种方法主要研究多个自变量对因变量的影响,旨在构建自变量与因变量之间的数学模型,并预测因变量的未来趋势。
多元回归分析可以帮助我们理解各个自变量对因变量的影响程度,以及这些影响是否显著。
主成分分析(PCA):PCA是一种降维技术,它通过正交变换将原始变量转换为线性无关的新变量,即主成分。
这些主成分按照其方差大小排序,前几个主成分通常可以代表原始数据的大部分信息。
PCA在数据压缩、特征提取和可视化等方面有广泛应用。
因子分析:因子分析通过提取公共因子来简化数据集,这些公共因子可以解释原始变量间的相关性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《多元统计分析》课程设计报告学生:峰学号:090090鹤090 学院: 理学院班级: 数学0题目: 主成分分析法在我国居民生活质量状况综合评价中的应用指导教师:辰职称: 教授红讲师2012 年 12 月 7 日一、问题分析1.1 问题及背景人均GDP达到1000美元,标志着我国居民生活水平迈上了一个新台阶,我国经济步入了一个崭新的发展时期。
然而,我国地域辽阔,人口众多,地区间经济发展很不平衡,城乡差距明显,经济发展的非均衡性已经严重威胁到我国经济的持续、健康发展。
若不妥善处理,将会成为制约我国经济发展的瓶颈因素。
事实上,东、中、西部地区的经济发展差距已是众所周知,并引起中央政府和有关部门的广泛重视。
但在地区间经济发展差距的背后,东、中、西部地区居民的生活质量究竟存在着多大的差距却鲜为人知。
随着生产力水平的不断提高,我国居民生活水平不断提高,生活质量也在不断改善。
但是,受各地生产力发展水平不平衡的影响,我国各地居民的生活质量也表现为不平衡。
利用主成分分析法对我国31个省市、自治区居民的生活状况进行评价分析。
为全面分析各地居民生活状况,可选取如下指标体系进行反应:职工人均工资、人均居住面积、城市人均用水普及量、城市煤气普及量、人均拥有道路面积、人均绿地公共面积、批发零售贸易商品销售总额、旅游外汇收入。
对我国居民生活质量问题的研究不仅是社会经济发展的客观要求,也是我国全面建设小康社会的迫切需要城市居民生活质量的评价体系,是依据中国城市居民生活的特征,并参阅国外生活质量评价研究的大量成果后构建的,集中体现了研究者的专业知识和对生活质量评价体系的理论构思,具有主观色彩,因此,有必要对理论遴选的评价指标进行隶属度分析、相关分析和辨别力分析等实证筛选,以增强评价指标的科学性、合理性和可操作性。
1.2 数据图1数据来源:《中国统计年鉴2009》二、主成分分析方法基本原理2.1 主成分分析定义主成分分析也称主分量分析,旨在利用降维的思想,把多指标转化为少数几个综合指标。
在实证问题研究中,为了全面、系统地分析问题,我们必须考虑众多影响因素。
这些涉及的因素一般称为指标,在多元统计分析中也称为变量。
因为每个变量都在不同程度上反映了所研究问题的某些信息,并且指标之间彼此有一定的相关性,因而所得的统计数据反映的信息在一定程度上有重叠。
在用统计方法研究多变量问题时,变量太 多会增加计算量和增加分析问题的复杂性,人们希望在进行定量分析的过程中,涉及的变量较少,得到的信息量较多。
2.2 主成分分析法方法简介主成分分析(Principal Component Analysis ,PCA ), 将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法。
又称主分量分析。
在实际课题中,为了全面分析问题,往往提出很多与此有关的变量(或因素),因为每个变量都在不同程度上反映这个课题的某些信息。
主成分分析首先是由K.皮尔森对非随机变量引入的,尔后H.霍特林将此方法推广到随机向量的情形。
信息的大小通常用离差平方和或方差来衡量。
主成分分析法是一种数学变换的方法, 它把给定的一组相关变量通过线性变换转成另一组不相关的变量,这些新的变量按照方差依次递减的顺序排列。
在数学变换中保持变量的总方差不变,使第一变量具有最大的方差,称为第一主成分,第二变量的方差次大,并且和第一变量不相关,称为第二主成分。
依次类推,I 个变量就有I 个主成分。
主成分分析是设法将原来众多具有一定相关性(比如P 个指标),重新组合成一组新的互相无关的综合指标来代替原来的指标。
主成分分析,是考察多个变量间相关性一种多元统计方法,研究如何通过少数几个主成分来揭示多个变量间的部结构,即从原始变量中导出少数几个主成分,使它们尽可能多地保留原始变量的信息,且彼此间互不相关.通常数学上的处理就是将原来P 个指标作线性组合,作为新的综合指标。
最经典的做法就是用1F (选取的第一个线性组合,即第一个综合指标)的方差来表达,即Var(1F )越大,表示1F 包含的信息越多。
因此在所有的线性组合中选取的F1应该是方差最大的,故称1F 为第一主成分。
如果第一主成分不足以代表原来P 个指标的信息,再考虑选取2F 即选第二个线性组合,为了有效地反映原来信息,1F 已有的信息就不需要再出现在2F 中,用数学语言表达就是要求0)F ,F (21=Cov ,则称2F 为第二主成分,依此类推可以构造出第三、第四,……,第P 个主成分。
p pi 22i 11i X a X a X a Fp +⋅⋅⋅⋅⋅⋅++=其中m),1,(i a , ,a ,a pi 2i 1i ⋅⋅⋅⋅=⋅⋅⋅⋅⋅为X 的协方差阵Σ的特征值所对应的特征向量,P 21X , ,X ,X ⋅⋅⋅⋅⋅是原始变量经过标准化处理的值,因为在实际应用中,往往存在指标的量纲不同,所以在计算之前须先消除量纲的影响,而将原始数据标准化,本文所采用的数据就存在量纲影响。
值和单位特征向量,0p 21≥≥⋅⋅⋅≥≥λλλ。
进行主成分分析主要步骤如下: 1. 指标数据标准化; 2. 指标之间的相关性判定; 3. 确定主成分个数m ; 4. 主成分i F 表达式; 5. 主成分i F 命名;其中Li 为p 维正交化向量,i Z 之间互不相关且按照方差由大到小排列,则称i Z 为X 的第I 个主成分。
设X 的协方差矩阵为Σ,则Σ必为半正定对称矩阵,求特征值i λ(按从大到小排序)及其特征向量,可以证明,i λ所对应的正交化特征向量,即为第I 个主成分i Z 所对应的系数向量i L ,而i Z 的方差贡献率定义为∑j i /λλ,通常要求提取的主成分的数量k 满足85.0/k>∑∑jλλ。
2.3主成分分析主要目的主成分分析主要目的是希望用较少的变量去解释原来资料中的大部分变异,将我们手中许多相关性很高的变量转化成彼此相互独立或不相关的变量。
通常是选出比原始变量个数少,能解释大部分资料中的变异的几个新变量,即所谓主成分,并用以解释资料的综合性指标。
由此可见,主成分分析实际上是一种降维方法。
三、问题求解第一步:录入数据,有以下变量:职工人均工资,人均居住面积,城市人口用水普及量,城市煤气普及量,人均拥有道路面积,人均绿地公共面积,批发零售贸易商品销售总额,旅游外汇收入,见图2图2第二步:选择功能模块图3第三步:将变量添加到Varicrible图4 第四步:输入信息图5图6图7图8 第五步:单击“OK”按钮,完成运算。
图9四、结果分析分析:第一列是列出八个原始变量,第二列是根据主成分分析初始解计算出变量共同度,第三列是是根据主成分分析最终解计算出变量共同度,这时由于因子变量个数少于原始变量个数,因此每个变量的共同度必然小于1。
例如,第一行中0.730表示m个因子变量共同解释掉原始变量“人均工资”方差72.2%。
分析:上表为SAS输出结果,从上表可以看出特征值和和贡献率。
从上表可以看出公共因子对原变量总体的描述情况。
可以看出前2个公共因子的的贡献率达到73.019%,所以提取2个公共因子就可以反映原变量的大部分信息。
分析:上图为公共因子碎石图,它的横坐标为公共因子数,纵坐标为公共因子的特征值。
可以看出前2个公共因子的特征值变化非常明显,到2个以后趋于平稳。
所以得出提取2个公共因子可以对原变量的信息描述有显著作用。
这与Communalities的结论也相符合。
Component Score CoefficientMatrixComponent1 2人均工资.216 -.272居住面积.200 -.人均用水.173 .134煤气普及.187 .170人均道路-.068 .460人均绿地.018 .426商品总额.249 -.064旅游外汇.213 -.040分析:该表格是因子得分矩阵,这是根据回归年算法计算出来的因子得分函数的系数,根据这个表格可得下面的因子得分函数8765432110.213x 0.249x 0.018x 0.068x -0.187x 0.173x 0.200x 0.216x F ++++++= 8765432120.040x -0.064x -0.426x 0.460x 0.170x 0.134x 0.010x --0.272x F ++++= SAS 将根据2个因子得分函数自动计算样本的2个因子得分,并且2个因子作为新变量,保存到SAS 窗口中。
第一主成分在人均拥有道路面积的系数上为负,其他为正,而且职工人居工资、人均居住面积、批发零售贸易商品销售总额、旅游外汇收入的系数绝对值比较大,说明第一主成分代表了我国居民生活质量状况针对职工人居工资、人均居住面积、批发零售贸易商品销售总额、旅游外汇收入和其他居民生活质量状况的反应指标之间的差异。
第二主成分在职工人均工资、人均居住面积、批发零售贸易商品销售总额、旅游外汇收入的系数上为负,其他为正,而且人均拥有道路面积和人居绿地公共面积的系数的绝对值比较大,说明第二主成分代表了我国居民生活质量状况针对人均公共设施需求(人均拥有道路面积和人居绿地公共面积)和其他居民生活质量状况的反应指标之间的差异。
五、总结第一主成得分较高的有北京、天津、上海、、、,这几个省份都是经济比较发达的地区,第一主成分代表的意义为我国居民生活质量状况针对职工人居工资、人均居住面积、批发零售贸易商品销售总额、旅游外汇收入和其他居民生活质量状况的反应指标之间的差异。
第二主成得分较高的有、、等地,由于第二主成分代表的意义为我国居民生活质量状况针对人均消费品普及量及人均公共设施需求,由此可见这几个地区非常注重人均公共设施需求及人均消费品普及量这些方面。
六、课程设计心得体会通过此次课程设计,使我更加扎实的掌握了有关主成分分析法在我国居民生活质量状况综合评价中的应用方面的知识,在设计过程中虽然遇到了一些问题,但经过一次又一次的思考,一遍又一遍的检查终于找出了原因所在,也暴露出了前期我在这方面的知识欠缺和经验不足。
实践出真知,通过亲自动手制作,使我们掌握的知识不再是纸上谈兵。
过而能改,善莫大焉。
在课程设计过程中,我们不断发现错误,不断改正,不断领悟,不断获龋最终的检测调试环节,本身就是在践行“过而能改,善莫大焉”的知行观。
这次课程设计终于顺利完成了,在设计中遇到了很多问题,最后在老师的指导下,终于游逆而解。
在今后社会的发展和学习实践过程中,一定要不懈努力,不能遇到问题就想到要退缩,一定要不厌其烦的发现问题所在,然后一一进行解决,只有这样,才能成功的做成想做的事,才能在今后的道路上劈荆斩棘,而不是知难而退,那样永远不可能收获成功,收获喜悦,也永远不可能得到社会及他人对你的认可!参考文献[1] 高惠璇.应用多元统计分析.北京:北京大学,2005[2] 高惠璇.实用统计方法与SAS系统.北京:北京大学,2001[3] 汪远征,徐雅静.SAS 软件与系统应用.北京:机械工业.2001[4] 梅长林.数据分析方法.北京:高等教育,2006. .. .. .源程序data CH12/princomp.sas ;input group RJGZ JZMJ RJYS MQPJ RJDL RJLD SPZE LYWH;card;56328 38.7 100 100 6.21 8.56 25832.4 445941748 28.31 100 100 14.39 8.92 9900.4 100124756 30.71 99.97 97.11 14.49 9.49 3976.5 27426114 21.47 82.03 74.25 12. 76 11.1 2127.9 57727729 26.39 96.89 92.38 9.95 9.37 8927.80 152623486 21.94 88.63 84.82 10.39 9.20 3040.4 21123046 21.72 84.24 79.45 9.28 9.46 2276.4 87056565 62.3 100 100 4.63 7.82 29712.5 497231667 44.05 99.88 98.23 20.28 13.11 20543.2 388034146 60.48 99.7 97.72 15.2 9.6 18270 302426363 29.88 95.11 87.6 14.15 9.29 3755.4 45425702 46.13 97.47 97.23 112.05 10.42 5743.4 239421000 37.56 96.49 90.18 11.06 10.6 1340.3 25226404 32.98 99.39 98.5 19.6 14.2 11775.8 139124816 31.69 85.56 66.91 9.90 8.2 4483.3 37422739 39.04 97.88 90.9 13.03 9.4 6183.6 44324870 40.72 94.57 84.26 12.01 7.96 2638.3 61733110 27.89 93.97 93.94 11.65 11.46 22348.8 917525660 31.75 92.87 84.04 11.83 8.61 1998.6 60221864 22.84 83.87 72.81 12.05 9.0 734.6 31426985 35.03 93.20 90.87 9.49 9.62 2891.2 45025038 34.94 88.09 81.09 10.78 8.74 4105.7 15424602 25.27 88.69 67.82 6.22 6.16 1076.5 11724030 27.44 95.22 76.1 12.09 7.62 3075.8 100847280 23.97 86.59 74.80 143.46 5.64 64.10 3125942 29.00 96.65 89.55 12.67 8.71 2487.4 66024017 19.87 87.85 65.32 10.37 7.87 1526 1630983 19.78 100 94.78 11.16 8.53 286.90 1030719 23.06 87.25 75.68 17.82 11 489.3 324687 22.78 92.82 88.61 12.47 7.912 863.3 136run;/程序文件:CH12/princomp.sas */proc princomp data=mylib.ch12_income out=income_out; /*把原始数据和主成分得分放入数据集var RJGZ JZMJ RJYS MQPJ RJDL RJLD SPZE LYWH;run;。
