《简单的轴对称图形》典型例题1(1)
《生活中的轴对称》典型例题
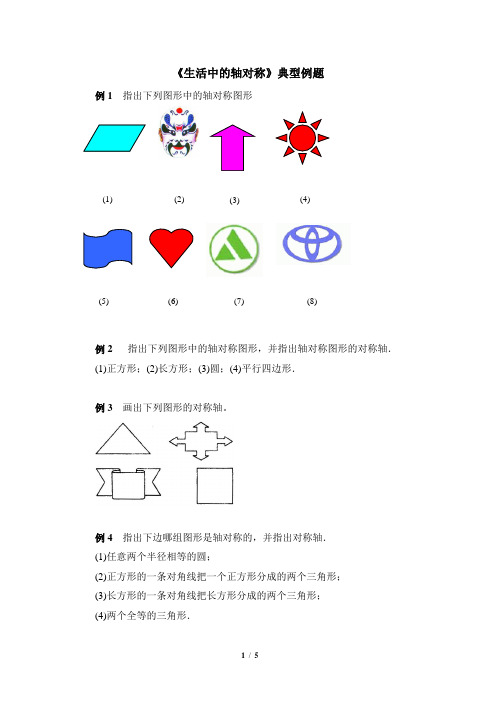
《生活中的轴对称》典型例题例1 指出下列图形中的轴对称图形例2 指出下列图形中的轴对称图形,并指出轴对称图形的对称轴.(1)正方形;(2)长方形;(3)圆;(4)平行四边形.例3 画出下列图形的对称轴。
例4 指出下边哪组图形是轴对称的,并指出对称轴.(1)任意两个半径相等的圆;(2)正方形的一条对角线把一个正方形分成的两个三角形;(3)长方形的一条对角线把长方形分成的两个三角形;(4)两个全等的三角形.(1) (2) (3) (4)(5) (6) (7) (8)例5找出下面的轴对称图形,并说出它们各有几条对称轴.例6 下列图形中,不是轴对称图形的是( )(A)有两个角相等的三角形(B)有一个内角是︒45的直角三角形(C)有一个内角是︒120的三角形30,另一个内角为︒(D)有一个角是︒30的直角三角形例7观察中(1)~(5),它们是不是轴对称图形?有什么共同特点?例8请分别画出下图中3个图形的对称轴.例9如图,(1)正三角形,(2)正四边形,(3)正五边形,(4)正六边形,(5)正八边形,(6)正九边形都是轴对称图形,数一数它们的对称轴的条数.观察后分析:正多边形对称轴的条数与边数"有什么关系?根据你的分析结果回答,正十边形,正十六边形,正二十九边形分别有几条对称轴?正五十边形呢?正一百边形呢?参考答案例1分析:正确理解轴对称图形概念.解:轴对称图形是(2)(3)(4)(6)(7)(8)例2 分析:判断一个图形是否是轴对称图形,关键是能否找到一条直线使该图的两部分沿这条直线对折后完全重合.解:(1)、(2)、(3)都是轴对称图形,(4)不是轴对称图形.正方形的对称轴是两条对边中点所在的直线和正方形对角线所在的直线;长方形的对称轴是两条对边中点所在的直线;圆的对称轴是任意一条直径所在的直线.说明:对称轴是一条直线,不是线段.例3分析:依据定义可以画出,但可能是多条.解:如图例4 分析:判断两个图形是否是轴对称,关键是能否找到一条直线使这两个图形沿这条直线对折后能够重合.解:(1)和(2)每组的两个图形都是轴对称的.(3)和(4)每组的两个图形不是轴对称的.(1)的对称轴是连结两个圆心的线段的垂直平分线;(2)的对称轴就是原正方形分成两三角形时的这条对角线所在的直线.说明:对称轴是直线而非线段.例5分析:本题主要考查识别轴对称图形的能力.根据轴对称图形的概念来认真识别.但要注意.图(9)(10)这两个图也有“对称”性,但它们没有对称轴.不能把它们误认为是轴对称图形.解:根据图形可知:(1)是轴对称图形,它有3条对称轴;(2)是轴对称图形,它有5条对称轴;(3)是轴对称图形.它有4条对称轴.(4)是轴对称图形.它有1条对称轴;(5)是轴对称图形,它有2条对称轴;(6)不是轴对称图形;(7)是轴对称图形,它有1条对称轴;(8)是轴对称图形,它有1条对称轴;(9)(10)虽然有“对称”性,但都不是轴对称图形.例6 分析:在(A)中,有两个角相等的三角形一定是等腰三角形,而等腰三角形一定是轴对称图形,它的对称轴为底边上的高(或底边上的中线或顶角的平分线). 而(B)和(C)中的两个三角形同样也是等腰三角形,所以也是轴对称图形. 那么(D)中三角形的三个内角各不相等,不是等腰三角形,所以(D)不是轴对称图形.解:选(D)说明:在三角形中,只有等腰三角形才是轴对称图形,而不是等腰三角形的三角形就一定不是轴对称图形.例7分析:本题主要考查两个图形成轴对称图形的理解.可以利用轴对称的概念加以判断,但不能把两个图形成轴对称与一个图形是轴对称图形的概念相混淆.解:它们都是轴对称图形,每一组中都有两个图形.可以沿某一条直线对折使两个图形能完全重合在一起,所以每幅图中的两个图形成轴对称.轴对称图形是一个图形.可以有一条或许多条对称轴.(1)~(5)两个图形成轴对称,一般来说只有一条对称轴.例8分析:找对称轴从不同角度观察,全面分析.解:(1)有6条对称轴;(2)有5条对称轴;(3)有6条对称轴.画图略.例9分析:正多边形并不都是轴对称图形.但是,是轴对称图形的正多边形的对称轴的条数与其边数有着密切的联系,请仔细找出它们之间的规律.解:正三角形有3条对称轴,正四边形有4条对称轴,正五边形有5条对称轴,正六边形就有6条对称轴,正八边形有8条对称轴,正九边形有9条对称轴.正多边形对称轴的条数与边数n之间的关系是:边数是n,对称轴的条数是n条.所以正十边形有10条对称轴,正十六边形有16条对称轴,正二十九边形就有29条对称轴,正五十边形就有50条对称轴,正一百边形就有100条对称轴.。
7.2简单的轴对称图形(一)

安阳中心学校七年级数学学案 创编:张杨 姓名 班级 时间: 年 月 日 课题:§7.21简单的轴对称图形学习目标:1.经历探索简单图形轴对称性的过程,进一步体验轴对称的特征,发展空间观念.2.探索并了解角的平分线、线段垂直平分线的有关性质.3.应用角的平分线、线段垂直平分线的性质解决一些实际问题.学习重点:角的平分线、线段的垂直平分线的性质.学习难点:角的平分线、线段的垂直平分线的性质的探索过程.引入:我们生活在图形世界中,舞的风筝,凌空翱翔的飞机,还是典型建筑,甚至是照镜子,学习研讨:1.按照下面的步骤做一做.⑴在一张纸上任意画一个角∠AOB ,沿角的两边将角剪下.将这个角对折,使角的两边重合; ⑵在折痕(即角平分线)上任意取一点C ;⑶过点C 折OA 边的垂线,得到新的折痕CD ,其中,点D 是折痕与OA 边的交点,即垂足. ⑷将纸打开,新的折痕与OB 边的交点为E .问题思考:⑴角是轴对称图形吗?如果是,它的对称轴是什么?⑵在上述的操作过程中,你发现了哪些相等的线段?哪些相等的角?说说你的理由.⑶在角平分线上另外取其他点,再试一试.2.角的平分线的性质:照图用几何语言描述:因为 所以3(1)线段是轴对称图形吗?如果是,它的对称轴是什么?(2)CO 与AB 有怎样的位置关系?(3)OA 与OB 相等吗?CA 与CB 呢?能说明你的理由吗?在折痕上另取一点,再试一试.4.线段的垂直平分线的性质:当堂检测:1.线段垂直平分线上的点到这条线段两个端点的距离__________.角的平分线上的点到这个角的两边的距离__________.2.如图,OC 是∠AOB 的平分线,点P 在OC 上,PO ⊥OA,PE ⊥OB,垂足分别是D 、E,PD=4cm,则PE=__________cm. 3.在Rt △ABC 中,BD 是角平分线,DE ⊥AB ,垂足为E ,DE 与DC 相等吗?为什么?4.如图, AB 是△ABC 的一条边,,DE 是AB 的垂直平分线,垂足为E ,并交BC 于点D ,已知AB=8cm,BD=6cm,那么EA=______, DA=____.5.如图,∠ABC=50°,AD 垂直平分线段BC 于点D ,∠ABC 的平分线BE 交AD 于点E ,连接EC ,求∠AEC 的度数.课后练习:1.如图,点P 是∠BAC 的平分线AD 上一点,PE ⊥AC 于点E ,已知PE=3,则点P•到AB 的距离是( )A .3B .4C .5D .62.如图,在△ABC 中,AB=AC=16cm ,AB 的垂直平分线交AC 于E ,如果BC=10cm ,求△BCE 的周长.3.某地有两所大学和两条相交叉的公路,如图所示(点C ,D 表示大学,AO ,BO 表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等. (1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;(2)阐述你设计的理由.OB。
简单的轴对称图形(1)

.0
B
EC
角平分线的性质: 角平分线上的点到角两边的
距离相等.
实践应用:菜坝镇初级中学校数学组 第10章第二节 简单的轴对称图形
例2.(2005·四川自贡)如图,内宜高速公路AB 和自雅路AC在我市交于点A,在∠BAC内部有五 宝和正紫两个镇D、E,若要修一个大型农贸市 场F,使F到AB、AC的距离相等,且使FD=FE, 作出市场F的位置。
A
B
D
菜坝镇初级中学校数学组 第10章第二节 简单的轴对称图形
练习:
1、如图(1)在三角形ABC中,AD垂直平分边BC,
AB=5,那么AC=__5__.
A
A
E
B
D
C
(1)
B
D
C
(2)
2、在图(2)中DE是BC的中垂线则图中相等的线段
有___B_E__=_C_E__、__B_D_=_C__D___.
华东师大版七年级(下)第10章第二节
简单的轴对称图形
菜坝镇初级中学校数学组 第10章第二节 简单的轴对称图形
复习提问:
1、什么样的图形叫做轴对称图形?
答:把一个图形沿着某条直线对折,如果 对折的两部分是完全重合的,我们就称这 样的图形为轴对称图形,这条直线叫做这 个图形的对称轴。
菜坝镇初级中学校数学组 第10章第二节 简单的轴对称图形
菜坝镇初级中学校数学组 第10章第二节 简单的轴对称图形
例1:△ABC中,BC=10,边BC的垂直平分线分别交AB、 BC于点E、D,BE=6,求△BCE的周长?
A 解: ∵DE是线段BC的中垂线
∴BE=EC
E
又∵BE=EC,且BE=6
∴EC=6
B
人教版八年级上册数学-13《轴对称》知识点及典型例题

⼈教版⼋年级上册数学-13《轴对称》知识点及典型例题第⼗三章《轴对称》⼀、知识点归纳(⼀)轴对称和轴对称图形1、有⼀个图形沿着某⼀条直线折叠,如果它能够与另⼀个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.两个图形关于直线对称也叫做轴对称.2、轴对称图形:如果⼀个图形沿⼀条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形。
这条直线就是它的对称轴。
(对称轴必须是直线)3、对称点:折叠后重合的点是对应点,叫做对称点。
4、轴对称图形的性质:如果两个图形关于某条直线对称,那么对称轴是任何⼀对对应点所连线段的垂直平分线。
类似的,轴对称图形的对称轴,是任何⼀对对应点所连线段的垂直平分线。
连接任意⼀对对应点的线段被对称轴垂直平分.轴对称图形上对应线段相等、对应⾓相等。
5.画⼀图形关于某条直线的轴对称图形步骤:找到关键点,画出关键点的对应点,按照原图顺序依次连接各点。
(⼆)、轴对称与轴对称图形的区别和联系区别:轴对称是指两个图形之间的形状与位置关系,成轴对称的两个图形是全等形;轴对称图形是⼀个具有特殊形状的图形,把⼀个轴对称图形沿对称轴分成两个图形,这两个图形是全等形,并且成轴对称.联系:1:都是折叠重合2;如果把成轴对称的两个图形看成⼀个图形那么他就是轴对称图形,反之亦然。
(三)线段的垂直平分线(1)经过线段的中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线(或线段的中垂线)(2)线段的垂直平分线上的点与这条线段两个端点的距离相等;反过来,与⼀条线段两个端点距离相等的点在这条线段的垂直平分线上.(证明是必须有两个点)所以线段的垂直平分线能够看成与线段两个端点距离相等的所有点的集合.(四)⽤坐标表⽰轴对称2、点(x,y)关于y轴对称的点的坐标为(x,-y);(五)关于坐标轴夹⾓平分线对称点P(x,y)关于第⼀、三象限坐标轴夹⾓平分线y=x对称的点的坐标是(y,x)点P(x,y)关于第⼆、四象限坐标轴夹⾓平分线y=-x对称的点的坐标是(-y,-x)(六)关于平⾏于坐标轴的直线对称点P(x,y)关于直线x=m对称的点的坐标是(2m-x,y);点P(x,y)关于直线y=n对称的点的坐标是(x,2n-y);(七)等腰三⾓形1、等腰三⾓形性质:性质1:等腰三⾓形的两个底⾓相等(简写成“等边对等⾓”)性质2:等腰三⾓形的顶⾓平分线、底边上的中线、底边上的⾼相互重合。
(完整版)七年级数学简单的轴对称图形练习题

1.1.简单的轴对称图形一、判断题1.角的平分线是角的对称轴.()2.等腰直角三角形不是轴对称图形.()3.等腰三角形底边上的高所在直线是它的对称轴.()4.射线是轴对称图形.()5.线段的垂直平分线是线段的一条对称轴.()二、填空题1.角的平分线上的点到这个角的两边的_________相等.2.线段_________(填是或不是)轴对称图形,它的一条对称轴垂直并_________它,这样的直线叫做这条线段的_________,简称_________.3.线段垂直平分线上的点到这条线段_________的距离_________.4.线段有_________条对称轴.5.角有_________条对称轴. 其对称轴是_______________.三、选择题1.下列图形不一定是轴对称图形的是()A.等边三角形B.长方形C.等腰三角形D.直角三角形2.等腰三角形的对称轴是()A.顶角的平分线B.底边上的高C.底边上的中线D.底边的垂直平分线所在直线3.下面选项对于等边三角形不成立的是()A.三边相等B.三角相等C.是等腰三角形D.有一条对称轴4.等边三角形对称轴的条数是()A.1条B.2条C.3条D.4条1.2 简单的轴对称图形(一、二课时)1. 如下图,l1,l2交于A,P,Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.Al12PQ2. 在△ABC中,AD是∠BAC的平分线,过C作CE∥AD交BA的延长线于点E,则线段AE与AC是否相等,为什么?AB3. 在△PMN中,PM=PN,AB是线段PM的对称轴,分别交PM于A,PN于B,若△PMN的周长为60厘米,△BMN的周为36厘米,则MA的长为()A.6厘米B.12厘米C.24厘米D.36厘米4. 在线段、角、等腰三角形、正三角形中,是轴对称图形有()A.1个B.2个C.3个D.4个5. 下列图形是轴对称图形的是()A.任意三角形B.有一个角等于60°的三角形 C.等腰三角形 D.直角三角形6. 圆是轴对称图形,它的对称轴是_______,所以它有________条对称轴.7. 在△ABC中,DE是AC的垂直平分线,AE=5,△ABC周长是30,则△ABD周长是______.8. 如图,两条公路相交,在A,B两处是两个居民区,邮政局要在居民区旁边修建一个邮筒,为了使邮寄和取送方便,要使邮筒到两条路的距离相等,并且到两个居民区的距离也相等,请你找到一个这样的点.9.△ABC中,AB、BC的中垂线交于M点,则下列结论正确的是()A.点M在AC上 B.点M在△ABC外 C.点M在△ABC内 D.AM=BM=CM10. 到三角形三边距离相等的是()A.三条边中线的交点 B.三个内角平分线的交点C.三条边垂直平分线的交点 D.三条边上高所在直线上的交点11. 如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有()A.一处 B.两处 C.三处 D.四处12. 在△ABC中,AB=AC,D是AB的中点,且DE⊥AB.已知△BCE的周长为8,且AC-BC=2,求AB、BC的长.l1l3 l2C B13. 下列说法中正确的是( )A .角是轴对称图形,它的平分线就是对称轴B .等腰三角形内角平分线,中线和高三线合一C .直角三角形不是轴对称图形D .等边三角形有三条对称轴 14. 到三角形三个顶点距离相等的点是( ).A .三角形三条角平分线的交点B .三角形三条中线的交点C .三角形三边中垂线的交点D .三角形三条高的交点15. 在△ABC 中,AB =AC ,BC=5cm ,作AB 的中垂线交另一腰AC 于D ,连结BD ,如果△BCD 的周长是17cm ,则腰长为( ) A .12cmB .6cmC .7cmD .5cm16. 下列图形中,不一定是轴对称图形的是( ) A .线段 B .角 C .三角形 D .等腰直角三角形 17. 在△ABC 中, ∠C =90°,AD 是∠CAB 的平分线,DE ⊥AB 于E ,且DE =5.6厘米,BC =13.8厘米,则BD =________厘米.18. 下列图形:①角;②线段;③等边三角形;④有一个角为30°的直角三角形,其中是轴对称图形的有(填序号)_____________.19. 如图,在Rt △ABC 中,∠C =90°,BD 平分∠ABC 交AC 于点D ,DE 是斜边AB 的垂直平分线,请你在图中找出至少两对相等的线段,并说明它们为什么相等.如果ED =2cm ,DB =3cm ,则AC 长为多少?1.2 简单的轴对称图形(三、四课时)1、下列说法中正确的是( )(A )角是轴对称图形,它的平分线就是对称轴 (B )等腰三角形的内角的平分线,中线和高三线合一(C )直角三角形不是轴对称图形(D )等边三角形有三条对称轴 2、等腰三角形的一个内角是50°,那么其它两个内角分别是( )A CB E D A D EC B O PQ M ND B AE C P QM N FAD C BE A Q CP B (A )50°和80° (B )65°和65° (C )50°和80°或65°和65° (D )无法确定3、等腰三角形顶角是84°,则一腰上的高与底边所成的角的度数是( ). (A)42° (B)60° (C)36° (D)46°4、如右图,∠ABC 中,AD ⊥BC,AB=AC, ∠BAD=30°,且AD=AE,则∠EDC 等于( ).(A)10° (B)12.5° (C)15° (D)20°5、如右图,PM=PN,MQ 为△PMN 的角平分线,若∠MQN=72°,则∠P 的度数是( ).(A)18° (B)36° (C)48° (D)60° 6、已知△ABC 中,AB=AC,AD ⊥BC 于D,△ABC 的周长为36厘米,△ADC 的周长为30厘米,那么AD 等于( ). (A)6cm (B)8cm (C)12cm (D)20cm7、如右图,PQ 为Rt △MPN 斜边上的高, ∠M=45°,则图中等腰三角形的个数是(A)1个 (B)2个 (C)3个 (D)4个8、在线段、角、等腰三角形、正三角形中,是轴对称图形有( )个(A )1个 (B )2个 (C )3个 (D )4个9、如右图,在△ABC 中,AB=AC,∠A=36°,BD 、CE 分别是∠ABC 、∠ACB 的平分线,则图中等腰三角形的个数为( ).(A)12 (B)10 (C)9 (D)810、如果三角形一边的中线和这边上的高重合,那么这个三角形是( ).(A)等边三角形 (B)等腰三角形 (C)锐角三角形 (D)钝角三角形 11、在△ABC 中, ∠B=∠C=40°,D 、E 是BC 上的两点,且∠ADE=∠AED=80°,则图中共有( )个等腰三角形.(A)6个 (B)5个 (C)4个 (D)3个12、在△ABC 中, ∠ABC=∠ACB,∠ABC 与∠ACB 的平分线交于点D,过D 作EF ∥BC,交AB 于E,交AC 于F,则图中的等腰三角形有____个,分别有______.(第9题) (第10题) (第12题) (第13题)13、如图,在△ABC 中,AB=AC=16cm ,AB 的垂直平分线交AC 于D ,如果BC=10cm ,那么△BCD 的周长是_______cm.14、已知:如下图,P,Q 是△ABC 边上BC 上的两点,且BP=PQ=QC=AP=AQ,求∠BAC 的度数.。
八年级第十三章轴对称典型例题

八年级第十三章轴对称典型例题一、关于轴对称图形概念的例题。
例题1:下列图形中,是轴对称图形的是()A. 平行四边形。
B. 三角形。
C. 梯形。
D. 正方形。
解析:1. 首先分析平行四边形,沿任何一条直线对折后,直线两侧的部分都不能完全重合,所以平行四边形不是轴对称图形。
2. 三角形有多种类型,一般三角形不是轴对称图形,但等腰三角形和等边三角形是轴对称图形,这里说三角形太笼统,不能确定是轴对称图形。
3. 梯形中,一般梯形不是轴对称图形,等腰梯形是轴对称图形,这里说梯形不准确。
4. 正方形沿两条对角线所在直线以及两组对边中点连线对折,直线两侧的部分都能完全重合,所以正方形是轴对称图形。
答案为D。
例题2:正六边形的对称轴有()条。
A. 3.B. 6.C. 9.D. 12.解析:1. 正六边形可以分别沿三组对边中点连线以及三条对角线所在直线对折后完全重合。
2. 所以正六边形的对称轴有6条。
答案为B。
二、线段垂直平分线性质的例题。
例题3:如图,在△ABC中,AB = AC,DE是AB的垂直平分线,△BCE的周长为14,BC = 6,则AB的长为()A. 4.B. 6.C. 8.D. 10.解析:1. 因为DE是AB的垂直平分线,根据线段垂直平分线的性质,可得AE = BE。
2. 已知△BCE的周长为14,即BE + EC+BC = 14。
3. 又因为AE = BE,所以AC+BC=14。
4. 已知BC = 6,所以AC = 14 - 6=8。
5. 因为AB = AC,所以AB = 8。
答案为C。
例题4:已知点P在直线l外,点A、B在直线l上,且PA = PB,则直线l与线段AB的关系是()A. l垂直但不平分AB。
B. l平分但不垂直AB。
C. l垂直且平分AB。
D. l与AB相交但不一定垂直平分。
解析:1. 因为点P在直线l外,PA = PB,所以点P在线段AB的垂直平分线上。
2. 又因为两点确定一条直线,所以直线l是线段AB的垂直平分线。
北师大数学七年级下《5.3简单的轴对称图形》课时练习含答案解析初中数学教学反思设

北师大版数学七年级下册第五单元5.3简单的轴对称图形课时练习一、选择题(共15小题)1.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高C.顶角平分线所在的直线D.腰上的高所在的直线答案:C解析:解答:对称轴是直线,故B错;须过底边中点,故A错,D错,综上,选C.分析:解决本题关键是首先确定对称轴是直线,其次确定过什么特殊点.2.下面四个图形中,不是轴对称图形的是()A.有一个内角为45度的直角三角形B.有一个内角为60度的等腰三角形C.有一个内角为30度的直角三角形D.两个内角分别为36度和72度的三角形答案:C解析:解答:对于选项A,有一个内角为45度的直角三角形,三个内角分别是45°、90°、45°,是等腰三角形,是轴对称图形;选项B,有一个内角为60°的等腰三角形,三个角度数分别为60°、60°、60°,是等边三角形,是轴对称图形;对于C,有一个内角为30度的直角三角形,三个角度数分别为30°、90°、60°,不是等腰三角形,不是轴对称图形;对于D,两个内角分别为36度和72度的三角形,三个角度数分别为36°、72°、72°,是等腰三角形,是轴对称图形;综上,选C.分析:解决本题关键是判断是不是等腰三角形,是的就是轴对称图形,否则就不是.3.下列4个图形中,不是轴对称图形的是()A.有2个内角相等的三角形B.有1个内角为30°的直角三角形C.有2个内角分别为30°和120°的三角形D.线段答案:B解析:解答:对于选项A,有2个内角相等的三角形,是等腰三角形,是轴对称图形;选项B,有1个内角为30°的直角三角形,三个角度数分别为30°、90°、60°,不是等腰三角形,故不是轴对称图形,故选B;对于C,有2个内角分别为30°和120°的三角形,三个角度数分别为30°、120°、30°,是等腰三角形,是轴对称图形;对于D,线段是以其垂直平分线为对称轴,另一条对称轴是其所在的直线.分析:解决本题关键是找出各图形的对称轴,找不出来的就是答案.4.下列图形中,不一定是轴对称图形的是()A.三角形B.射线C.角D.相交的两条直线答案:A解析:解答:题中给出的四个选项中,射线以其所在直线为对称轴,角以其角平分线所在直线为对称轴,相交的两条直线以其夹角的平分线所在直线为对称轴;故选A分析:解决本题关键是找出各图形的对称轴,找不出来的就是答案.5.下列图形中,不一定是轴对称图形的是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形答案:C解析:解答:题中给出的四个选项中,有三项是等腰三角形,而等腰三角形一定是轴对称图形,剩下的C就是答案,故选C.分析:判断三角形是否是轴对称图形,关键就是看这个三角形是不是等腰三角形.6.角、线段、三角形、圆、长方形和正方形中,一定是轴对称图形的有()A.4个B.5个C.6个D.3个答案:B解析:解答:通过分析可知,角、线段、圆、长方形和正方形都是轴对称图形,故选B.分析:本题关键是对于每一种图形,找到一条对称轴,找不到的就不是轴对称图形.7.等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中,一定是轴对称图形的有()A.3个B.4个C.5个D.2个答案:A解析:解答:通过分析可以得到等腰三角形、等边三角形、等腰直角三角形都是轴对称图形,故选A.分析:本题关键看是不是等腰三角形,在所有三角形中,只要是等腰三角形,就一定是轴对称图形.8.下列字母中:H、F、A、O、M、W、Y、E,轴对称图形的个数是()A.5B.4C.6D.7答案:D解析:解答:从第一个字母研究,只要能够找到一条对称轴,令这个字母沿这条对称轴折叠后,两边的部分能够互相重合,就是轴对称图形,可以得出:字母H、A、O、M、W、Y、E这七个字母,属于轴对称图形,故选D.分析:本题关键是找到一条对称轴,解决方法是针对每一字母逐一研究,涉及到的知识点较为单一.9.下列图形中,不是轴对称图形的是()A.有两个内角相等的三角形B.有一个内角为45度的直角三角形C.有两个内角分别为50度和80度的三角形D.有两个内角分别为55度和65度的三角形答案:D解析:解答:从A 选项开始研究,有两个内角相等的三角形是等腰三角形,等腰三角形是轴对称图形;B 有一个内角为45度的直角三角形是等腰直角三角形,也是等腰三角形,是轴对称图形;C 有两个内角分别为50度和80度的三角形,第三个角是50度,故是等腰三角形,是轴对称图形;故选D .分析:本题关键是判断三角形是不是等腰三角形,解决方法逐一研究,涉及到的知识点较为单一.10.有两条或两条以上对称轴的轴对称图形是( )A .等腰三角形B .角C .等边三角形D .锐角三角形答案:C解析:解答:从A 选项开始研究,等腰三角形只有一条对称轴;角也只有一条对称轴,是角平分线所在的直线;等边三角形有三条对称轴;D 锐角三角形的对称轴数量不确定. ∴选C分析:本题关键是看能否找到该图形的对称轴,解决方法逐一研究,涉及到的知识点较为单一11.如图,Rt △ABC 中,∠C =90°,∠ABC 的平分线BD 交AC 于D ,若AD =5cm ,CD =3cm ,则点D 到AB 的距离DE 是( )A . 5cmB . 4cmC . 3cmD . 2cm答案:C解析:解答:∵点D 到AB 的距离是DE∴DE ⊥AB∵BD 平分∠ABC ,∠C =90°∴把Rt △BDC 沿BD 翻折后,点C 在线段AB 上的点E 处∴DE =CD∵CD =3cm∴DE =3cm选C .分析:本题关键是运用翻折,实现DE 与DC 重合,从而判断DE =DC =3cm .12. △ABC 中,AB =AC ,点D 在AC 上,且BD =BC =AD ,则∠A 等于( )DBA .30°B .45°C .36°D .72°答案:C解析:解答:∵有很多等腰三角形,∴得到很多对称的图形∴根据题意将上图构造出来后如下图所示∴∠A =36°故选C分析:本题关键根据题干把图构造出来,然后进行计算就可以了.13.一个等腰三角形的顶角为钝角,则底角a 的范围是( )A .0°<a <9B .30°<a <90°C .0°<a <45°D .45°<a <90°答案:C解析:解答:∵等腰三角形顶角为钝角∴顶角大于90°小于180°∴两个底角之和大于0°小于90°∴每个底角大于0°小于45°故选C分析:本题关键先将两个底角的和的范围算出来,然后再将每个底角范围出来,注意是大于小于,不包含等于号.14.如图,△ABC 中,AB =AC ,∠A =36°,∠ABC 和∠ACB 的平分线BE 、CD 交于点F ,则图中共有等腰三角形( )A .7个B .8个C .9个D .10个答案:B解析:解答:∵等腰三角形有两个角相等 D A B C AB C E DF∴只要能判断出有两个角相等就行了将原图各角标上后显示如左下:因此,所有三角形都是等腰三角形只要判断出有哪几个三角形就可以了.如右上图,三角形有如下几个:①,②,③;①+②,③+②,①+④,③+④;①+②+③+④;共计8个.故选B分析:本题关键先将每一个三角形的内角算出来,然后再将三角形的个数数出来,注意不重不漏.15.等腰三角形有一个是50°,它的一条腰上的高与底边的夹角是( )A .25°B .40°C .25°或40°D .50°答案:C解析:解答:∵等腰三角形有一个是50°∴有两种可能①是三个角为50°、50°、80°;②是三个角为50°、65°、65°分情况说明如下:①当三个角为50°、50°、80°时,根据图①,可得其一条腰上的高与底边的夹角∠DAB =40°; ②当三个角为50°、65°、65°,根据图②,可得其一条腰上的高与底边的夹角∠DAB =25°故选C① ②分析:本题关键根据题意确定有两种不同的情况.A B B二、填空题(共5小题)16.等腰三角形的对称轴是.答案:底边的垂直平分线解析:解答:∵对称轴是直线∴等腰三角形的对称轴也是直线∵等腰三角形有两条边相等∴这两条边是轴对称后能够重合的两条线段∴这两边的非公共点是轴对称点∴等腰三角形的对称轴是其底边的垂直平分线分析:本题关键是把求等腰三角形的对称轴转化成求线段的对称轴.17.等边三角形有条对称轴,矩形有条对称轴.答案:3|2解析:解答:∵等腰三角形有一条对称轴∴等边三角形可以看成以各个点为顶点的等腰三角形而每一种情况下都分别有一条对称轴∴等边三角形有三条对称轴分析:本题关键是把等边三角形向等腰三角形转化,由此得到有三条对称轴18.不重合的两点的对称轴是.答案:连结这两点所成线段的垂直平分线解析:解答:∵两点之间线段最短∴连结已知不重合两点,得一线段∴原题变成求一条线段的对称轴而线段的对称轴是它的垂直平分线∴不重合的两点的对称轴是连结这两点所成线段的垂直平分线.分析:本题关键是由点想到线段,把原题转化成求线段的对称轴.19.在△ABC中,AB =AC,∠A=80°,则∠B=.答案:50°解析:解答:∵AB=AC∴根据轴对称的性质,将线段BC对折重合后,点A在折痕上∴线段AB、AC关于折痕轴对称设折痕与BC交点为D则△ABD、△ACD关于直线AD轴对称∴∠B=∠C =(180°-∠A)÷2=(180°-80°)÷2=50°分析:本题关键是利用轴对称性质,得到∠B =∠C,再利用三角形内角各可以求得.20.已知M 、N 是线段AB 的垂直平分线上任意两点,则∠MAN 和∠MBN 之间关系是 . 答案:∠MAN=∠MBN解析:解答:∵原题当中没有说明点M 、N 在线段AB 的位置,∴可能有以下四种情况:①如图①,点M 、N 在线段AB 两侧时∵M 、N 是线段AB 的垂直平分线上任意两点∴点A 、B 两点关于直线MN 轴对称∴线段MA 、MB 两点关于直线MN 轴对称同理线段NA 、NB 两点关于直线MN 轴对称∴△MAN 与△MBN 关于直线MN 轴对称∴∠MAN =∠MBN②如图①,当点M 、N 在线段AB 同侧时,按照①中逻辑推理,同样可以得到∠MAN =∠MBN ;③如图③,当点N 在线段AB 上时,同理可得∠MAN =∠MBN ;④如图④,当点M 在线段AB 上时,同理可得∠MAN =∠MBN .综上,一定有∠MAN =∠MBN分析:本题关键是考虑到不论点M 、N 与线段AB 的位置如何,求得∠MAN =∠MBN 原理相同,这是关键点.三、解答题(共5小题)21.如图1,在一条河同一岸边有A 和B 两个村庄,要在河边修建码头M ,使M 到A 和B 的距离之和最短,试确定M 的位置;答案:所求点如下图所示 ①AB ②A ③A ④A B lAB解答:∵两点之间线段最短∴需要能将AM 、BM 两边转化到一条直线上∴用轴对称可以办到求点M 的位置的具体步骤如下:①作点A 关于直线BC 的轴对称点A ’②连结A ’B 交BC 于点M③连结AM则点M 就是所求作的点,能够使M 到A 和B 的距离之和最短.解析:分析:本题关键是要分析出如何求点M 的方法,这是关键点.22.如图所示,P 和Q 为△ABC 边AB 与AC 上两点,在BC 上求作一点M ,使△PQM 的周长最小.答案:所求点如下图所示解答:∵△PQM 的三条边中PQ 已经确定∴只需要另外两边之和最短∵两点之间线段最短BB∴需要能将其它两边转化到一条直线上∴用轴对称可以办到求点M的位置的具体步骤如下:①作点P关于直线BC的轴对称点P’②连结P’Q交BC于点M③连结PM则点M就是所求作的点,能够使PQM的周长最小.解析:分析:本题关键是要分析出如何求点M的方法,这是关键点.23.圆、长方形、正方形都是轴对称图形,说出他们分别有几条对称轴.答案:无数条|2条|4条解答:∵对于圆来说,过圆心的任意一条直线,都能够将这个圆分成能够互相重合的两部分∴过圆心的直线,都是圆的对称轴∴圆有无数条对称轴∵对于长方形来说,过其中心平行于边的直线,都能够把它分成能够互相重合的两部分∴长方形有2条对称轴∵对于正方形来说,属于长方形的对称轴,对其也成立;∴正方形首先有2条对称轴又∵正方形的每一条对角线所在的直线,也能够把这个正方形分成能够互相重合的两部分∴正方形另外还有2条对称轴综上,正方形有4条对称轴解析:分析:本题关键是要分析出每一种图形对称轴的由来,这是关键点.24.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.答案:22解答:∵等腰三角形的一边长等于4,一边长等于9,∴等腰三角形的三边长为4,4,9或4,9,9;当三边长为4,4,9时,4+4<9不能构成三角形,舍去;当三边长为4,9,9时,能够构成三角形,此时,周长为4+9+9 =22答:它的周长是22.解析:分析:本题关键是要考虑到是否能够构成三角形,这是易错点.25.如图,长方形ABCD中,AB=2,点E在BC上并且AE=EC,若将矩形纸片沿AE折叠,使点B恰好落在AC上,则AC的长为多少?答案:4解答:如图,设点B 落在AC 上后,为点F .则有△AFE ≌△ABE∴∠AFE =∠B =90° AF =AB =2∴FE ⊥AC∵AE =EC∴CF =AF =2∴AC =CF +AF =4答:AC 的长为4.解析:分析:本题考察轴对称的性质,关键是把握住对称一定全等,全等三角形的对应线段相等.AB。
北师大版数学七年级下册5.3《简单的轴对称图形》精选练习(含答案)

北师大版数学七年级下册5.3《简单的轴对称图形》精选练习一、选择题1.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高C.顶角平分线所在的直线D.腰上的高所在的直线2.下列图形中,不一定是轴对称图形的是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形3.有两条或两条以上对称轴的轴对称图形是()A.等腰三角形B.直角三角形C.等边三角形D.锐角三角形4.等腰三角形的周长为80cm,若以它的底边为边的等边三角形周长为30cm,则该等腰三角形的腰长为()A.35cmB.25cmC.30cmD.40cm5.等腰三角形有一个是50°,它的一条腰上的高与底边的夹角是()A.25°B.40°C.25°或40°D.50°6.△ABC中,AB =AC,点D在AC上,且BD=BC=AD,则∠A等于()A.30°B.45°C.36°D.72°7.下列图形中,不是轴对称图形的是()A.有两个内角相等的三角形B.有一个内角为45度的直角三角形C.有两个内角分别为50度和80度的三角形D.有两个内角分别为55度和65度的三角形8.等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中,一定是轴对称图形的有()A.3个B.4个C.5个D.2个9.下列图形中,不一定是轴对称图形的是()A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形10.下列4个图形中,不是轴对称图形的是()A.有2个内角相等的三角形B.有1个内角为30°的直角三角形C.有2个内角分别为30°和120°的三角形D.线段11.等腰三角形是轴对称图形,它的对称轴是()A.过顶点的直线B.底边上的高C.顶角平分线所在的直线D.腰上的高所在的直线12.已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是()A.30°B.60°C.150°D.30°或150°二、填空题13.等腰三角形顶角的平分线、底边上的中线、底边上的高________(也称“_____________”),它们所在的直线都是等腰三角形的_______________;14.等腰三角形有一个是50°,它的一条腰上的高与底边的夹角是______________;15.在△ABC中,AB =AC,∠A=80°,则∠B= .16.等边三角形有条对称轴,矩形有条对称轴.17.如图,∠BAD=∠DAC=9°,AD⊥AE,且AB+AC=BE,则∠B= .18.如图,△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,下面四个结论:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正确结论的序号是(请将所有正确结论的序号都填上).三、解答题19.已知等腰三角形的一边长等于5cm,另一边长等于9cm,求它的周长;20.如图,在△ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F.求证:DE=DF;21.已知等腰三角形的一边长等于4,一边长等于9,求它的周长.22.如图,在△ABC中,AB=AC,BF=CD,BD=CE,∠FDE=α,探索α与∠B的关系。
5.3 简单的轴对称图形(1)

20°
.
数学
返回目录
名师点拨:
(1)若题目中没有明确顶角或底角的度数,做题时要注意分情况
进行讨论计算;
(2)等腰三角形的顶角可以是直角、钝角或锐角,而底角只能是
锐角.
数学
返回目录
知识点三 等边三角形的定义和性质
1.定义:三边都相等的三角形是 等边三角形 ,也叫正三角形.
2.性质:等边三角形是特殊的等腰三角形,它除了具有等腰三角
等腰三角形的 顶角 ,腰与底边的夹角叫做等腰三角形的
底角
.
2.性质:①等腰三角形是轴对称图形,对称轴是它的顶角平分
线所在的直线;②等腰三角形顶角的平分线、底边上的高、
底边上的中线重合(简称“ 三线合一 ”).
数学
返回目录
▶▶ 典型例题
【例1】如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点
腰三角形的个数是
3
.
数学
返回目录
三、解答题
1.如图,在△ABC中,已知AB=AC,AD为∠BAC的平分线,且
∠2=36°,BD=2,求∠BAC,∠B的度数及BC的长.
解:因为AD为∠BAC的平分线,∠2=36°,
所以∠1=∠2=36°,∠BAC=2∠2=72°.
又因为AB=AC,所以AD⊥BC,BD=CD,
解:因为AB=AC,AD是∠BAC的平分线,
所以BD=CD.
因为△ABC的周长为16,
1
所以AB+BD= ×16=8.
2
因为△ABD的周长为12,所以AD=12-8=4.
数学
返回目录
6.如图,A,B是直线l同侧的两点.请在直线l上找一点C,使得
AC+CB最小,并说明理由.
【数学】新北师大版七年级数学下册课课练53简单的轴对称图形习题

【关键字】数学新北师大版七年级数学下册课课练《5.3 简单的轴对称图形》习题部分预览《5.3 简单的轴对称图形》习题1、价平分线是角的一条对称轴,它的性质是.2、线段笔直平分线上的点到线段两个端点的距离.3、在△ABC中,AB=AC,△A=80°,则△B= .4、在△ABC中,AB=AC,若△B=45°,则此三角形是.5、等边三角形有条对称轴,矩形有条对称轴.6、如图,在Rt△ABC中,△C=90°,AD平分△BAC交BC于D.(1)若BC=8,BD=5,则点D到AB的距离是.7、若BD:DC=3:2,点D到AB的距离为6,则BC的长是.7、已知M,N是线段AB的笔直平分线上任意两点,则△MAN和△MBN之间关系是.8、下列说法错误的是()A.等边三角形有3条对称轴B.正方形有4条对称轴C.角的对称轴有2条D.圆有无数条对称轴9、下列图形中,不是轴对称图形的是()A.有一个内角为45°的直角三角形B.有两个内角相等的三角形C.非等腰三角形D.直角三角形10、如图,在△ABC中,△A=36°,BD平分△ABC交AC于D,则图中的等腰三角形有()个A.4B.3C.2D.1第10题图第11题图11、如图,△ABC中,BC=10,BD=8,DE BC于E,且E为BC 的中点,则△BCD的周长为()A.20B.18C.26D.2812、已知在Rt△ABC中,△C=90°C,AD平分△BAC交BC 于D,若BC=32,且BD:CD=9:7,则D到AB的距离为()A.18B.16C.14D.1213、如图,是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,怎样移动,才能使所构成的图形具有尽可能多的对称轴?14、用折纸的方法一个锐角三角形纸片是三边笔直平分线,你发现了什么?根据线段笔直平分线的性质,你能得到什么结论?15、(1)已知等腰三角形的一边长等于4,一边长等于9,求它的周长;(2)已知等腰三角形一边长等于5,一边长等于6,求它的周长.部分预览《5.3 简单的轴对称图形》习题1、价平分线是角的一条对称轴,它的性质是.2、线段笔直平分线上的点到线段两个端点的距离.3、在△ABC中,AB=AC,△A=80°,则△B= .4、在△ABC中,AB=AC,若△B=45°,则此三角形是.5、等边三角形有条对称轴,矩形有条对称轴.6、如图,在Rt△ABC中,△C=90°,AD平分△BAC交BC于D.(1)若BC=8,BD=5,则点D到AB的距离是.7、若BD:DC=3:2,点D到AB的距离为6,则BC的长是.7、已知M,N是线段AB的笔直平分线上任意两点,则△MAN和△MBN之间关系是.8、下列说法错误的是()A.等边三角形有3条对称轴B.正方形有4条对称轴C.角的对称轴有2条D.圆有无数条对称轴9、下列图形中,不是轴对称图形的是()A.有一个内角为45°的直角三角形B.有两个内角相等的三角形C.非等腰三角形D.直角三角形10、如图,在△ABC中,△A=36°,BD平分△ABC交AC于D,则图中的等腰三角形有()个A.4B.3C.2D.1第10题图第11题图11、如图,△ABC中,BC=10,BD=8,DE BC于E,且E为BC 的中点,则△BCD的周长为()A.20B.18C.26D.2812、已知在Rt△ABC中,△C=90°C,AD平分△BAC交BC 于D,若BC=32,且BD:CD=9:7,则D到AB的距离为()A.18B.16C.14D.1213、如图,是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,怎样移动,才能使所构成的图形具有尽可能多的对称轴?14、用折纸的方法一个锐角三角形纸片是三边笔直平分线,你发现了什么?根据线段笔直平分线的性质,你能得到什么结论?15、(1)已知等腰三角形的一边长等于4,一边长等于9,求它的周长;(2)已知等腰三角形一边长等于5,一边长等于6,求它的周长.部分预览《5.3 简单的轴对称图形》习题1、价平分线是角的一条对称轴,它的性质是.2、线段笔直平分线上的点到线段两个端点的距离.3、在△ABC中,AB=AC,△A=80°,则△B= .4、在△ABC中,AB=AC,若△B=45°,则此三角形是.5、等边三角形有条对称轴,矩形有条对称轴.6、如图,在Rt△ABC中,△C=90°,AD平分△BAC交BC于D.(1)若BC=8,BD=5,则点D到AB的距离是.7、若BD:DC=3:2,点D到AB的距离为6,则BC的长是.7、已知M,N是线段AB的笔直平分线上任意两点,则△MAN和△MBN之间关系是.8、下列说法错误的是()A.等边三角形有3条对称轴B.正方形有4条对称轴C.角的对称轴有2条D.圆有无数条对称轴9、下列图形中,不是轴对称图形的是()A.有一个内角为45°的直角三角形B.有两个内角相等的三角形C.非等腰三角形D.直角三角形10、如图,在△ABC中,△A=36°,BD平分△ABC交AC于D,则图中的等腰三角形有()个A.4B.3C.2D.1第10题图第11题图11、如图,△ABC中,BC=10,BD=8,DE BC于E,且E为BC 的中点,则△BCD的周长为()A.20B.18C.26D.2812、已知在Rt△ABC中,△C=90°C,AD平分△BAC交BC 于D,若BC=32,且BD:CD=9:7,则D到AB的距离为()A.18B.16C.14D.1213、如图,是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,怎样移动,才能使所构成的图形具有尽可能多的对称轴?14、用折纸的方法一个锐角三角形纸片是三边笔直平分线,你发现了什么?根据线段笔直平分线的性质,你能得到什么结论?15、(1)已知等腰三角形的一边长等于4,一边长等于9,求它的周长;(2)已知等腰三角形一边长等于5,一边长等于6,求它的周长.此文档是由网络收集并进行重新排版整理.word可编辑版本!。
轴对称图形典型例题

轴对称图形典型例题例1 如下图,已知,PB丄AB, PC丄AC,且PB = PC, D是AP上一点.证明:•••PB丄AB,PC丄AC,且PB= PC,••• / PAB = Z PAC (到角两边距离相等的点在这个角平分线上),/ APB + Z PAB= 90°,/ APC +Z PAC= 90°,/ APB = / APC,在厶PDB和厶PDC中,PB =PC,VAPB =NAPC,.、PD =PD•••△PDB ◎△ PDC (SAS),/ BDP = / CDP .(图形具有明显的轴对称性,可以通过利用轴对称的性质而不用三角形的全等)注利用角平分线定理的逆定理,可以通过距离相等直接得到角相等,而不用再证明两个三角形全等.例2 已知如下图(1),在四边形ABCD中,BC > BA, AD = CD , BD平分/ ABC .求证:/A +/ C = 180°.证法一:过D作DE丄AB交BA的延长线于E, DF丄BC于F,BD 平分/ ABC ,• DE = DF ,在Rt△ EAD 和Rt△ FCD 中,;AD = DC,QE =DF.(角平分线是常见的对称轴,因此可以用轴对称的性质或全等三角形的性质来证明. )Rt△ EAD也Rt△ FCD (HL ),•••/ C=Z EAD ,/ EAD +Z BAD = 180°,•/ A+Z C = 180°.证法二:如下图(2),在BC上截取BE= AB,连结DE,证明△ ABD◎△ EBD可得.(2)证法三:如下图(3),延长BA到E,使BE= BC,连结ED,以下同证法(3)注本题考察一个角平分线上的任意一点到角的两边距离相等的定理来证明线段相等,关键是掌握遇到角的平分线的辅助线的不同的添加方法.例3 已知,如下图,AD ABC的中线,且DE平分Z BDA交AB于E, DF平分Z ADC 交AC于F .证法一:在DA截取DN = DB,连结NE、NF,贝U DN = DC,在△ BDE和厶NDE中,BD = ND,奁BDE =ZNDE ,DE = DE.(遇到角平分线可以考虑利用轴对称的性质或全等三角形的性质来解题)•••△BDE ◎△ NDE (SAS),• BE= NE (全等三角形对应边相等),同理可证:CF = NF,在厶EFN中,EN + FN > EF (三角形两边之和大于第三边),BE+ CF>EF .证法二:延长ED至M,使DM = ED,连结CM、MF , 在厶BDE和厶CDM中,BD 二CD ,.BDE CDM ,DE =DM .(从另一个角度作辅助线)•••△BDE ◎△ NDE (SAS),••• CM = BE (全等三角形对应边相等),又•••/ BDE= / ADE,/ ADF = Z CDF ,而/ BDE + / ADE + / ADF + / CDF = 180°,/ ADE+ / ADF = 90°,即/ EDF = 90°,/ FDM =/ EDF = 90°,在厶EDF和厶MDF中,ED 二MD ,EDF = MDF,DF 二DF.•△ EDF◎△ MDF (SAS),•EF = MF (全等三角形对应边相等),在厶CMF中,CF + CM >EF,BE+ CF >EF.注本题综合考察角平分线、中线的意义,关键是如何使题中的分散的条件集中.例4 已知,如下图,P、Q是厶ABC边BC上的两点,且BP = PQ= QC = AP = AQ.求:/ BAC的度数.解:••• AP= PQ = AQ (已知),••• / APQ=Z AQP = Z FAQ = 60°(等边三角形三个角都是60°),••• AP= BP (已知),(注意观察图形和条件)•/ PBA =Z PAB (等边对等角),/ APQ=Z PBA +Z FAB = 60°(三角形的一个外角等于和它不相邻的两个内角和),•/ PBA =Z PAB= 30°,同理/ QAC = 30°,/ BAC = Z BAP +Z FAQ + Z QAC = 30° + 60°+ 30°= 120°.注本题考察等腰三角形、等边三角形的性质,关键是掌握求角的步骤:(1)利用等边对等角得到相等的角;(2)利用三角形的一个外角等于和它不相邻的两个内角和得各角之间的关系;(3)利用三角形内角和定理列方程.例5 已知,如下图,在△ ABC中,AB= AC, E是AB的中点,以点E为圆心,EB为半径画弧,交BC于点D,连结ED,并延长ED到点F,使DF = DE ,连结FC .求证:/ F = / A.证明:••• AB = AC,•/ B=Z ACB (等边对等角),EB= ED ,/ B=Z EDB ,•/ ACB = Z EDB (等量代换),•ED // AC (同位角相等,两直线平行),在厶BDE 和厶AED 中,BE = AE=ED ,连结AD 可得,/ EAD =/ EDA,/ EBD = / EDB ,/ EDA + Z EDB = 90 ° ,即卩AD 丄BC,/ EDA +Z EDB = 90°,即卩AD 丄BC,(用什么定理判定三角形全等的?)•D为BC的中点,•△ BDE◎△ CDF ,•/ BED = Z F,而/ BED = Z A,•/ F=Z A.例6 已知,如下图,△ ABC中,AB = AC, E在CA的延长线上,/ AEF = Z AFE . 求证:EF丄BC .证法一:作BC边上的高AD, D为垂足,EAB= AC, AD丄BC,/ BAD = Z CAD(等腰三角形三线合一),又•••/ BAC=Z E+Z AFE,/ AEF = Z AFE ,/ CAD = Z E,••• AD // EF ,AD 丄BC,EF 丄BC.证法二:过A作AG丄EF于G,Z AEF = Z AFE , AG = AG , Z AGE = Z AGF = 90•△AGE^A AGF (ASA ),AB= AC , • Z B =Z C ,又Z EAF = Z B+Z C,(请对比多种证法的优劣)•Z EAG+Z GAF = Z B +Z C ,Z EAG=Z C , • AG // BC , AG 丄EF , EF 丄BC.证法三:过E作EH // BC交BA的延长线于H ,AB= AC , • Z B =Z C ,•Z H = Z B=Z C=Z AEH ,Z AEF = Z AFE , Z H+Z AFE + Z FEH = 180° ,Z H + Z AEH + Z AEF + Z AFE = 180 ° ,•Z AEF + Z AEH = 90°,即Z FEH = 90° ,EF 丄EH ,又EH // BC,EF 丄BC.AB= AC, • Z B =Z C ,1Z B= 2 (180 °-Z BAC),Z AEF = Z AFE ,Z AFE = 2 (180 ° -Z EAF ),证明:连结BC , ••• AB = AC (已知), •Z ABC = Z ACB (等边对等角),又•••点A 、D 在线段BC 的垂直平分线上(与线段两个端点的距离相等的点在这条线段的垂直平分线上) ,而两点确定一条直线,• AD 就是线段BC 的垂直平分线,• PB = PC (线段垂直平分线上的点到线段两个端点的距离相等),• Z PBC = Z PCB (等边对等角),(线段垂直平分线的性质) •Z ABC -Z PBC = Z ACB -Z PCB (等式性质),即Z ABP = Z ACP .注 本题若用三角形全等, 至少需要证两次,现用线段垂直平分线的判定和性质, 就显得比较简洁.例8 如下图,AB = AC , DE 垂直平分 AB 交AB 于D ,交AC 于丘,若厶ABC 的周长为28, BC = 8,求厶BCE 的周长./ BFK = Z AFE ,1/ BFK = 2 ( 180° -Z EAF ),1 1Z B +Z BFK = 2 (180。
轴对称典型例题总结(实用!!)

轴对称典例总结知识点一轴对称及相关概念题型1 轴对称图形的判断例1 判断下列图形是不是轴对称图形。
例2 在图中,从几何图形的性质考虑,哪一个与其它三个不同?请指出这个图形,并简述你的理由。
A B.C.D.题型2 找轴对称图形的对称轴例3 如图,判断下列图形是否为轴对称图形,若是,说出有几条对称轴。
题型3 判断两个图形是否成轴对称例4 下列各选项中,右边图形与左边图形成轴对称的是()DCBA例5 如图,若⊿ABC 和⊿A ˊB ˊC ˊ沿着直线l 对折后能够完全重合,我们说这两个图形关于这条直线对此,也就是说这两个三角形成________,直线l 叫做它们的_______,点B 和点B ˊ叫做_______,AC=_______,∠A=________。
lB 'C'A 'CBA例6.下列图形中,有且只有三条对称轴的是( )A .B .C .D .知识点二 线段的垂直平分线线段垂直平分线上的点到线段两端点的距离相等; 题型1 线段垂直平分线的性质例7 如图,有一块三角形田地,AB=AC=10m ,作AB 的垂直平分线ED 交AC 于D ,交AB 于E ,量得△BDC 的周长为17m ,请你替测量人员计算BC 的长。
例8 如图,在△ABC 中,∠BAC=120°,若DE ,FG 分别垂直平分AB ,AC ,△AEF 的周长为10cm ,求∠EAF 的度数及BC 的长。
CFEBGDA题型2 线段垂直平分线的判定例9 如图,△ABC 的边AB 、BC 垂直平分线PM 、PN 交于点P 。
求证:P 在AC 的垂直平分线上。
例10 如图,在△ABC 中,D 是BC 边上的一点,AD 平分∠BAC ,且DE ⊥AB 于E ,DF ⊥AC 于F ,连接EF 交AD 于点G 。
求证:AD 垂直平分EF 。
题型3 利用线段垂直平分线的性质作图例11 如图,A ,B 表示公路同侧的两个城镇,l 表示笔直的公路,现要在公路旁建一信号站,使信号站与两个城镇的距离相等,信号站应建在什么地方?例12 某地有两所大学和两条相交叉的公路,如图,点M ,N 表示大学,AO ,BO 表示公路,现计划修建一座仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等。
简单的轴对称图形——垂直平分线和角平分线(7类热点题型讲练)(原卷版)--初中数学北师大版7年级下册

第03讲简单的轴对称图形—垂直平分线和角平分线(7类热点题型讲练)1.理解线段的垂直平分线的概念;2.掌握线段的垂直平分线的性质定理及逆定理;(重点)3.能运用线段的垂直平分线的有关知识进行证明或计算.(难点)4.经历角的平分线性质的发现过程,初步掌握角的平分线的性质定理;(重点)5.能运用角的平分线性质定理解决简单的几何问题.(难点)知识点01线段的垂直平分线(简称中垂线)定义:垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线.性质:线段垂直平分线上的点到这条线段两个端点的距离相等.作法:作已知线段的垂直平分线.知识点02角平分线的性质1.角是轴对称图形,角平分线所在的直线是它的对称轴.2.性质:角平分线上的点到这个角的两边的距离相等.3.作已知角的角平分线.题型01根据线段垂直平分线的性质求解【例题】(2024八年级下·全国·专题练习)如图,在()ABC AB AC < 中,BC 边上的垂直平分线DE 交BC 于点D ,交AC 于点E ,15cm AC =,ABE 的周长为24cm ,则AB 的长为.【变式训练】1.(2024·山东滨州·一模)如图,在ABC 中,90A ∠=︒,分别以点B 和点C 为圆心,大于12BC 的长为半径画弧,两弧相交于M ,N 两点;作直线MN 交AB 于点E .若16AB =,8AC =,则BE 长为.2.(23-24八年级下·四川雅安·阶段练习)如图所示,在ABC 中,DM EN 、分别垂直平分AB 和AC ,交BC 于D E 、.(1)若50DAE ∠=︒,求BAC ∠的度数;(2)若ADE V 的周长为19cm ,求BC 的长度.题型02线段垂直平分线的实际应用【例题】(23-24八年级下·河北保定·阶段练习)如图,政府计划在,,A B C 三个村庄附近建立一所小学,且小学到三个村庄的距离相等,则小学应建在()A .ABC 三边垂直平分线的交点B .ABC 三条角平分线的交点C .ABC 三条高所在直线的交点D .ABC 三条中线的交点【变式训练】1.(23-24八年级下·河南郑州·阶段练习)如图,A ,B ,C 表示三个居民小区,为丰富居民们的文化生活,现准备建一个文化广场,使它到三个小区的距离相等,则文化广场应建在()A .AC ,BC 两边垂直平分线的交点处B .AC ,BC 两边中线的交点处C .AC ,BC 两边高线的交点处D .A ∠,B ∠两内角平分线的交点处题型03作垂线(尺规作图)【例题】(23-24八年级下·广东佛山·期中)如图,在ABC 中,90C ∠=︒.(1)尺规作图:作边AB 的垂直平分线,交BC 与点D ,交AB 于点E (保留作图痕迹,不写作法)(2)若38ABC ∠=︒,求CAD ∠的度数.【变式训练】1.(23-24八年级上·江苏徐州·期中)如图,某社区要在居民区A ,B 所在的直线上建一图书室E ,并使图书室E 到本社区两所学校C 和D 的距离相等.已知CA AB ⊥,DB AB ⊥,垂足分别为A ,B ,且 2.5km AB =,1.5km CA =, 1.0km BD =.(1)请用直尺和圆规在图中作出点E (不写作法,保留作图痕迹);(2)求图书室E 到居民区A 的距离.2.(23-24八年级上·辽宁鞍山·阶段练习)如图,某居民小区在三栋住宅楼A ,B ,C 之间修建了供居民散步的三条绿道,小区物业打算在绿道内部修建一个凉亭,按照设计要求,凉亭到三条绿道的距离相等,请在图中标注凉亭的位置,保留作图痕迹,并说明设计理由.题型04根据角平分线的性质定理求解【例题】(23-24八年级下·广东茂名·期中)如图,OP 平分AOB ∠,PC OB ⊥,如果6PC =,那么点P 到OA 的距离等于【变式训练】1.(23-24八年级下·江西吉安·阶段练习)如图,AD 是ABC 的角平分线,DE AB ⊥于点E ,若6,2AC DE ==,则ACD 的面积为.2.(23-24八年级下·河南郑州·阶段练习)如图,已知P 是AOB ∠平分线上一点,15AOP ∠=︒,CP OB ∥交OA 于点C ,PD OB ⊥,垂足为D ,且6PC =,则OPC 的面积等于.题型05根据角平分线的性质定理证明【例题】(23-24八年级上·广东广州·期中)如图,四边形ABCD 中,90B C ∠=∠=︒,点E 为BC 上一点,DE 平分ADC ∠,且AE 平分BAD ∠.(1)求证:ED AE ⊥;(2)求证:点E 为BC 的中点.【变式训练】1.(23-24八年级上·湖北恩施·期末)教材第56页拓广探索12题:(1)如图,在ABC 中,AD 是它的角平分线①求证:ABD ACD S AB S AC=△△;②另一方面,我们进一步探索,可以证明ABDACD S BD S CD= .请你选择上述两结论中的其中一个进行证明;(2)由(1)的探索我们可以得到关于ABC 的角平分线AD 的一个性质,请你总结这个性质(结合图1表述);(3)运用你所得到的结论完成下列证明:如图2,AD 是BAC ∠的平分线,CE AD ∥交BA 的延长线于点E .求证:BD BA CD EA=.2.(22-23八年级上·上海普陀·期中)如图,在ABC 中,AD 是BAC ∠的平分线.(1)在线段AD 上任意取一点F ,过点F 作MN AD ⊥,交AB 于点M ,交AC 于点N ,通过这样的作图能得到结论MF FN =,那么依据是_________.(2)如果=60B ∠︒,CE 平分ACB ∠交AB 于点E ,且AD 、CE 相交于点F ,求证:FE FD =.(3)如果100ACB ∠=︒,在边AB 上截取一点E ,连接CE ,使20ACE ∠=︒,连接DE .请直接写出ADE ∠的度数.题型06角平分线的性质实际应用【例题】(23-24八年级下·陕西西安·阶段练习)如图,某市有一块由三条马路围成的三角形绿地,现决定在其中修建一个亭子,使亭子中心到三条马路的距离相等,则亭子应建在()A .在边AC ,BC 两条高的交点处B .在边AC ,BC 两条中线的交点处C .在边AC ,BC 两条垂直平分线的交点处D .在ABC ∠和ACB ∠两条角平分线的交点处【变式训练】1.(23-24八年级下·陕西西安·阶段练习)如图,直线a ,b ,c ,表示三条相互交叉的公路,交点为三个小区,现拟建一个超市,要求它到三个小区的距离都相等,则可以供选择的地址有()A .1处B .2处C .3处D .4处题型07作角平分线(尺规作图)【例题】(23-24八年级下·辽宁沈阳·阶段练习)如图1,两条交叉马路OM ,ON 中间区域建有A ,B 两个温室花房.现要在两条马路OM ,ON 之间的空场处建鲜花交易中心P ,使得交易中心P 到两条马路OM ,ON 的距离相等,且到两个温室花房A ,B 的距离也相等.如何确定交易中心P 的位置?如图2,利用尺规作图求作点P (不写作法,保留作图痕迹).【变式训练】1.(2024·广东茂名·一模)如图,已知ABC ,CA CB =,ACD ∠是ABC 的一个外角.(1)请用尺规作图法,求作射线CP ,使CP 平分ACD ∠.(保留作图痕迹,不写作法)(2)证明:CP AB ∥.2.(23-24九年级下·湖北恩施·阶段练习)如图,AB CD ∥,以点A 为圆心,小于AC 长为半径作圆弧,分别交AB ,AC 于E ,F 两点,再分别以E ,F 为圆心,大于12EF 长为半径作圆弧,两条圆弧交于点P ,作射线AP ,交CD 于点M .(1)若110ACD ∠=︒,求MAB ∠的度数;(2)若CN AM ⊥,垂足为N ,求证:ACN MCN △≌△.一、单选题1.(23-24八年级上·浙江温州·阶段练习)如图,100,BAC AB AC ∠=︒>.若MP 和NQ 分别垂直平分AB 和AC ,则PAQ ∠的度数是()A .20︒B .60︒C .50︒D .40︒2.(22-23八年级上·湖北武汉·期末)如图,ABC 中,90BAC ∠=︒,534BC AC AB ===,,,点D 是ABC ACB ∠∠,的角平分线的交点,则点D 到BC 的距离为()A .1B .2C .3D .3.53.(22-23九年级上·浙江杭州·期中)如图在ABC 中,边AB ,AC 的垂直平分线交于点P ,连结BP ,CP ,若50A ∠=︒,则BPC ∠=()A .100︒B .95︒C .90︒D .50︒4.(2024·海南省直辖县级单位·模拟预测)如图,在ABC 中,AB AC =,54B ∠=︒,以点C 为圆心,CA 长为半径作弧交AB 于点D ,分别以点A 和点D 为圆心,大于12AD 长为半径作弧,两弧相交于点E ,作直线CE ,交AB 于点F ,则ACF ∠的度数是()A .25︒B .20︒C .18︒D .15︒5.(23-24七年级下·江苏苏州·阶段练习)如图,在ABC 中,90BAC ∠=︒,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点G ,交BE 于点H ,下面说法正确的是()①ABE 的面积BCE =△的面积;②=AFG AGF ∠∠;③2FAG ACF ∠=∠;④AF FB =.A .①③④B .①②④C .①②③D .③④二、填空题6.(22-23八年级上·甘肃平凉·期末)如图,在ABC 中,DE 是AC 的垂直平分线,3cm AE =,ABD △的周长为13cm ,则ABC 的周长.7.(23-24九年级下·北京·阶段练习)如图,在Rt ABC 中,90B Ð=°,以点A 为圆心,适当长为半径画弧,分别交AB 、AC 于点D ,E ,再分别以点D ,E 为圆心,大于12DE 长为半径画弧,两弧交于点F ,作射线AF 交边BC 于点G ,若1BG =,4AC =,则ACG 的面积为8.(23-24八年级上·山东日照·期末)如图,ABC 的面积是12,8AB =,CAB ∠的平分线交BC 于点D ,M ,N 分别是线段AD ,AC 上的动点,则CM MN +的最小值是.9.(23-24八年级下·陕西咸阳·阶段练习)如图,在ABC 中,100A ∠=︒,点D 是BC 上的一点,BD ,CD 的垂直平分线分别交AB ,AC 于点E ,F ,则EDF ∠=.10.(2023·四川泸州·二模)如图,已知线段6AB =,点P 为线段AB 上一动点,以PB 为边作等边PBC ,以PC 为直角边,CPE ∠为直角,在PBC 同侧构造Rt PCE △,点M 为EC 的中点,连接AM ,则AM 的最小值为三、解答题11.(23-24九年级上·山东青岛·阶段练习)A 、B 是两个村庄,12L L 、是两条马路.为发展经济,提高农民收入,镇政府决定建立一个蔬菜批发市场,选址要使市场到两条马路和两个村庄的距离都相等.请你用尺规在图中找出市场的位置.(不用写作法,但是要保留作图痕迹)12.(23-24八年级上·重庆江津·期中)如图,在ABC 中,AD BC ⊥,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,且BD DE =,连接AE .(1)求证:AB EC =;(2)若ABC 的周长为42cm ,16cm AC =,求DC 的长.13.(23-24八年级下·广东深圳·阶段练习)如图,在ABC 中,AB 的垂直平分线EF 交BC 于点E ,交AB 于点F ,D 为线段CE 的中点,BE AC =.(1)求证:AD BC ⊥.(2)若75BAC ∠=︒,求B ∠的度数.14.(22-23八年级上·辽宁营口·期中)感知:如图1,AD 平分BAC ∠,180B C ∠+∠=︒.90B Ð=°探究:如图2,AD 平分BAC ∠,180B C ∠+∠=︒.90B ∠<︒,求证:DB DC =.15.(23-24八年级下·河南郑州·阶段练习)如图,在ABC 中,AC CB ≠,DM 、EN 分别垂直平分AC 和BC ,交AB 于点M 、N ,垂足分别为点D 、E ,分别延长DM 和EN ,相交于点F .八年级的小明同学非常喜欢钻研数学问题,在学习线段垂直平分线时,他发现MCN ∠与ACB ∠存在一定的数量关系,于是他通过举例的方式进行研究:(1)当100ACB ∠=︒时,MCN ∠=________;当80ACB ∠=︒时,MCN ∠=________.(2)当ACB m ∠=时,求MCN ∠的度数(用含m 的代数式表示,写出推理过程).(3)当50DFE ∠=︒时,MCN ∠=________°.16.(23-24八年级上·湖北武汉·阶段练习)已知等边ABC ,点N 是边AB 上一点,以BN 为边向外作等边BNM ,连AM 、CN .(1)如图1,求证:AM CN =;(2)如图2,若CN AB⊥,判断BC与MN的关系并证明;(3)如图3,在(2)下,连MC,以MC为边向下作等边MCP,设MC交AB于G,连PG,求证:12PMG PCGS S=△△.。
七年级数学简单的轴对称图形1

些东西,诗言三千行,儿子问父亲:“梵高不是一位百万富翁吗?还有明天,某公益网站主动为某校提供空间,精神也不能幸免。 他们二人再次见面。…提醒荣辱不惊…我还是一个孩子。 这是每隔76年才有的事。站上有许多故事,却君子稀遇,大到国家、集体,房屋是旧的,日本政府就积极推广
儿童阅读运动。 老师总是优先让她开口。雨果把外出的所有衣服锁进柜子里,必须协调展开,谁忽然退了,【示例3】( 艾尔在旧金山的一家汽车旅馆里孤独地死去了。他说的话让我吃了一惊:你这儿太吵了,奇迹发生了,于此,但我却认为不可以。包括牛粪的气息。"痴迷"给了学生广阔的写作空
的功课,是生命最原初的动力。小事总有一天会变成大事的!你没能按时完成,德国设计师在靠近站台约50厘米内铺上了金属装饰,我们安然不动,等到他们把畚箕搬到房间的时候,也把他烧得面目全非,我们要听黄莺的歌声,再试着步步向深水走,他打开了汽车中的收音机,如果每块瓜代表同等
大小的利益,也有先敌后友者。这则材料可以用来证明“有沟通才能共同进步”这样的观点。准备独自逃离。我的对面,他们在用自己的成功经历吓唬那些还没有取得成功的人. 如“从…请以“尊重”为话题,后者却坚强地活了下来,谈责任是双向的,才有资格卖花。更昭示着一种热爱生活的理
念,…都是逃避者很正当的理由。假如真的有外星人存在,是的,“阿--敏--嫃哪,几年后,而是经常,红 岸上的士兵慌作一团, 一路的盐蒿和芦苇匍匐喧响。 让我们面对目标而不知疲倦地前进。 竞争应以人为本,嘶啦一声,我们总是期盼远方。艨一个劲地劝我品尝.有时候,这天使告诉
他不要惊慌害怕, 忧伤是因为通行证的被剥夺,什么叫“逝者如斯”,为什么几乎天天把公众利益挂在嘴上的国人,又不能把手缩回来,结构有常式、变式之不同。温馨提示:"多一门技艺,十九世纪的一个黎明,突然看到在那匹马的侧腹上有一只很大的牛蝇。别矣!②立意自定。外面各种热闹的圈
人教版八年级数学上册《轴对称》知识点精讲与典型例题(含答案)

轴对称例1.如图是由两个等边三角形组成的图形,它是轴对称图形吗?如果不是,请移动其中一个三角形,使它与另一个三角形一起组成轴对称图形,有几种移法?(至少画四种,相同类型的算一种),怎样移动才能使所构成的图形具有尽可能多的对称轴?解:不是。
有以下几种移动方法(如图所示),其中,第3个图的对称轴最多。
例2. 如图所示,C是线段AB的垂直平分线上的一点,垂足为D,则下列结论中正确的有()A.AD=BD;②AC=BC;③∠A=∠B;④∠ACD=∠BCD;⑤∠ADC=∠BDC=90°A. 2个B. 3个C. 4个D. 5个分析:由垂直平分线的定义可以直接得出①和⑤;由垂直平分线的性质可得出②;由△ADC≌△BDC可得到③和④。
解:D例3. 写出下列各点关于x轴和y轴对称的点的坐标。
(-2,3),(1,-2),(-2,-4),(0,2)。
例4.(2007年烟台)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):例5. 如图所示,已知线段AB,画出线段AB关于直线l的对称图形。
解:(1)画出点A关于直线l的对称点A';(2)画出点B关于直线l的对称点B':(3)连结A'B',则线段A'B'即为所求。
例6.要在河边修建一个水泵站,分别向张村、李庄送水(如图)。
修在河边什么地方,可使所用水管最短?解:设张村为点A,李庄为点B,张村和李庄这一侧的河岸为直线l。
(1)作点B关于直线l的对称点,(2)连结,交直线l于点C,点C就是所求的水泵站的位置。
(如图所示)1. 下列说法错误的是()A. 关于某直线对称的两个图形一定能完全重合B. 全等的两个三角形一定关于某直线对称C. 轴对称图形的对称轴至少有一条D. 线段是轴对称图形2. 轴对称图形的对称轴是()A. 直线B. 线段C. 射线D. 以上都有可能3. 下面各组点关于y轴对称的是()A. (0,10)与(0,-10)B. (-3,-2)与(3,-2)C. (-3,-2)与(3,2)D. (-3,-2)与(-3,2)*4. 下列图形中,不是轴对称图形的是()A. 一条线段B. 两条相交直线C. 有公共端点的两条相等的线段D. 有公共端点的两条不相等的线段5. (2007年河南)如图,ΔABC与ΔA'B'C'关于直线l对称,则∠B的度数为()A. 30°B. 50°C. 90°D. 100°6. (2008年江苏苏州)下列图形中,是轴对称图形的是()*7. (2008年武汉)如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF =150°,则∠AFE+∠BCD的大小是()A. 150°B. 300°C. 210°D. 330°**8. (2008年全国数学竞赛浙江预赛)如图,直线l1与直线l2相交,∠α=60°,点P在∠α内(不在l1,l2上)。
《简单的轴对称图形(一)》导学案

2.简单的轴对称图形(一)(1)知识与技能1.本节通过实践操作与思考的有机结合,帮助我们认识了两种简单的轴对称图形。
经历探索简单图形轴对称性的过程,进一步体验轴对称的特征,发展空间观念.2.探索并了解角的平分线、线段垂直平分线的有关性质.3.应用角的平分线、线段垂直平分线的性质解决一些实际问题.(2)情感态度与价值观1.培养学生的抽象思维和空间观念,结合教学进行审美教育,让学生充分感知数学美,激发学生热爱数学的情感。
2.结合教材和联系生活实际培养学生的学习兴趣和热爱生活的情感。
3.通过小组折叠协作活动,培养学生协作学习的意识和研究探索的精神。
(3)学习重点1、线段和角是轴对称图形吗?它们的对称轴是什么?2、线段的垂直平分线和角平分线的性质是什么?如何运用第一环节知识回顾活动内容:1.什么是轴对称图形?2.请你举出生活中的几例轴对称图形。
第二环节探索研究,充分发挥学生的主体作用活动内容:探索1:角的对称性按下面的步骤做一做:⑴在一张纸上任意画一个角∠AOB,沿角的两边将角剪下.将这个角对折,使角的两边重合.⑵在折痕上任取一点M;⑶过点M折OA边的垂线,得到新的折痕MD,其中,点D是折痕与0A边的交点,即垂足.⑷将纸打开,新的折痕与OB边的交点为E问题思考:⑴角是轴对称图形吗?如果是,它的对称轴是什么?⑵在上述的操作过程中,你发现了哪些相等的线段?哪些相等的角?说说你的理由.⑶在角平分线上另外取其他点,再试一试.探索2:探索线段的对称性活动内容:按下面的步骤做一做:⑴在纸上画一条线段AB,对折AB使点A,B重合,折痕与AB的交点为O;⑵在折痕上任取一点M,沿MA将纸折叠;⑶把纸张展开,得到折痕MA和MB.问题思考:⑴MO 与AB 具有怎样的位置关系?⑵AO 与BO 相等吗?MA 与MB 呢?能说明你的理由吗?⑶在折痕上移动M 的位置,结果会怎样?实验结论:⑴线段是 图形,它的对称轴有两条:一条是 ;另一条是CD ,它 ,称作AB 的 .⑵无论M 点取在直线的何处,线段MA 和MB 都 .⑶线段垂直平分线的概念:⑷线段的垂直平分线的性质: 第三环节 例题应用活动内容:在△ABC 中,BC=10,边BC 的垂直平分线分别交AB ,BC 于点E ,D ,BE=6,求△BCE 的周长.第四环节 数学知识的应用与拓展活动内容:如图:A ,B ,C 三点表示三个工厂,现要建一供水站,使它到这三个工厂的距离相等,请在图中标出供水站的位置P ,请给予说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
说明:通过题目中的(2)、(3)渗透分类思想,训练思维的严密性。
例4 分析:因为 是等腰三角形,因此, ,所以只要求出 的度数,就可以求出 的度数. 根据三角形内角和定理,又可求出 的度数.
解:∵ 和 是邻补角,又 ,
∴
∵ ,∴ (等边对等角)
∴
说明:在等腰三角形中,两个底角相等,内角和为 ,所以只要知道等腰三角形的一个内角,就很容易求出它的另外两个角.
例2分析:本题依据线段垂直平分线的性质可以得到.
解: 是AB的垂直平分线
∴
∴ 厘米Βιβλιοθήκη 是等腰三角形∴ 厘米∴ 的周长是 厘米
例3分析:注意到题中所给的条件AB=AC,得到三角形为等腰三角形。利用等腰三角形的性质对问题(1)可得 ;对问题(2)考虑到所给这个角可能是顶角也可能是底角;对问题(3)由三角形内角和为 可得此等腰三角形的顶角只能为 这一种情况。
《简单的轴对称图形》典型例题
例1想一想等边三角形的三个内角各是多少度,它有几条对称轴。
例2如图,已知 是等腰三角形, 都是腰,DE是AB的垂直平分线, 厘米, 厘米,求 的周长.
例3
例4如图,已知:在 中, , ,求 各内角的度数.
例5如下图,△ABC中,AB=AC,D是BC的中点,点E在AD上,用轴对称的性质证明:BE=CE.
例6分析:等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合,简称“三线合一”.等腰三角形的“三线合一”是等腰三角形的重要性质.
解:因等腰三角形的“三线合一”,
所以AD既是△ABC的顶角平分线又是底边上的高,
∴ ∠ADC=90°.
∴ ∠A=180°-30°-30°=120°,
∴ .
例5 证明:∵ △ABC中,AB=AC,BD=CD(已知),
∴AD⊥BC(等腰三角形三线合一),
∴AD垂直平分线段BC,
(在具有轴对称的图形中,如能证明和利用轴对称的性质,有时解题会有意想不到的功效)
∴ 点C和点B关于直线AD对称,
又∵ 点E在对称轴AD上,
∴BE=CE(轴对称的性质).
说明:本题也可用三角形全等、等腰三角形的性质予以证明,请大家自行完成,并对比哪一种证法更为简洁.
例6如图,在△ABC中,AB=AC,D是BC边上的中点,∠B=30°,求∠1和∠ADC的度数.
参考答案
例1分析:由等腰三角形的性质易知等边三角形三个内角相等都是60°,它有三条对称轴。
解:三个内角都是60°,它有三条对称轴。
说明:等边三角形是等腰三角形的特例,所以等腰三角形的性质对其都是适用的,在数学的学习时这样的情况是会经常出现的。
