大连理工矩阵上机作业

大连理工大学矩阵与数值分析上机作业代码

则方程组有解 x = (1,1,⋯ ,1) 。对 n = 10 和 n = 84 ，分别用 Gauss 消去法和列主元消去法解
T
方程组，并比较计算结果。
1.1 程序
（1）高斯消元法 n=10 时， >> [A,b]=CreateMatrix(10) A= 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6
1.3 M 文件
.m 1.3.1 CreateMatrix CreateMatrix.m function [A,b]=CreateMatrix(n) %用于存放习题1的题目信息，并建立构造题目中矩阵的函数 %对矩阵A赋值 A1=6*ones(1,n); A2=ones(1,n-1); A3=8*ones(1,n-1); A=diag(A1)+diag(A2,1)+diag(A3,-1); %对向量b赋值 b=15*ones(n,1); b(1)=7; b(n)=14;
10
，迭代次数上限取默认值
50，使用 Jacobi 法进行迭代。 >> test2 >> b=ones(20,1) >> x0=zeros(20,1) >> [x,n]=JacobiMethod(A,b,x0) x= 0.2766 0.2327 0.2159 0.2223 0.2227 0.2221 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2221 0.2227 0.2223 0.2159 0.2327 0.2766

大连理工大学线性代数实验上机报告材料

大连理工大学线性代数实验上机报告实验一首先随机生成五阶方阵AA=rand(5)A =0.8147 0.0975 0.1576 0.1419 0.6557 0.9058 0.2785 0.9706 0.4218 0.0357 0.1270 0.5469 0.9572 0.9157 0.8491 0.9134 0.9575 0.4854 0.7922 0.9340 0.6324 0.9649 0.8003 0.9595 0.6787>> B=rand(5)随机生成五阶方阵BB =0.7577 0.7060 0.8235 0.4387 0.4898 0.7431 0.0318 0.6948 0.3816 0.4456 0.3922 0.2769 0.3171 0.7655 0.6463 0.6555 0.0462 0.9502 0.7952 0.7094 0.1712 0.0971 0.0344 0.1869 0.7547>> b=rand(1,5)'随机生成列向量bb =0.27600.67970.65510.16260.1190计算A+B>> A+Bans =1.5725 0.8036 0.9811 0.5806 1.1455 1.6489 0.3103 1.6654 0.8033 0.48130.5192 0.8238 1.2743 1.6813 1.49541.5689 1.0037 1.4356 1.5874 1.6434 0.8035 1.0620 0.8347 1.1464 1.4334 计算A-B>> A-Bans =0.0570 -0.6085 -0.6658 -0.2969 0.1660 0.1627 0.2467 0.2758 0.0402 -0.4099 -0.2652 0.2700 0.6401 0.1502 0.2028 0.2579 0.9113 -0.4648 -0.0030 0.2246 0.4612 0.8678 0.7658 0.7726 -0.0760 计算A*B+B*A>> A*B+B*Aans =3.0288 2.3058 3.1439 2.7276 3.10342.9094 2.19673.0040 3.0737 3.25843.3422 2.1423 3.2104 3.5734 3.90494.1446 2.9794 4.3676 4.2354 4.9170 3.1350 1.7787 3.2289 3.1170 3.2815 求Ax=b的解>> x=A\bx =-0.98502.43963.3124-5.65151.7085验证克莱姆法则>> c=A(:,1)c =0.81470.90580.12700.91340.6324>> d=A(:,2)d =0.09750.5469 0.9575 0.9649>> e=A(:,3)e =0.1576 0.9706 0.9572 0.4854 0.8003>> f=A(:,4)f =0.1419 0.4218 0.91570.9595>> g=A(:,5)g =0.65570.03570.84910.93400.6787>> B1=[b';d';e';f';g']'B1 =0.2760 0.0975 0.1576 0.1419 0.6557 0.6797 0.2785 0.9706 0.4218 0.0357 0.6551 0.5469 0.9572 0.9157 0.8491 0.1626 0.9575 0.4854 0.7922 0.9340 0.1190 0.9649 0.8003 0.9595 0.6787>> B2=[c';b';e';f';g']'B2 =0.8147 0.2760 0.1576 0.1419 0.6557 0.9058 0.6797 0.9706 0.4218 0.0357 0.1270 0.6551 0.9572 0.9157 0.8491 0.9134 0.1626 0.4854 0.7922 0.9340 0.6324 0.1190 0.8003 0.9595 0.6787>> B3=[c';d';b';f';g']'B3 =0.8147 0.0975 0.2760 0.1419 0.6557 0.9058 0.2785 0.6797 0.4218 0.0357 0.1270 0.5469 0.6551 0.9157 0.8491 0.9134 0.9575 0.1626 0.7922 0.9340 0.6324 0.9649 0.1190 0.9595 0.6787>> B4=[c';d';e';b';g']'B4 =0.8147 0.0975 0.1576 0.2760 0.6557 0.9058 0.2785 0.9706 0.6797 0.0357 0.1270 0.5469 0.9572 0.6551 0.8491 0.9134 0.9575 0.4854 0.1626 0.9340 0.6324 0.9649 0.8003 0.1190 0.6787>> B5=[c';d';e';f';b']'B5 =0.8147 0.0975 0.1576 0.1419 0.2760 0.9058 0.2785 0.9706 0.4218 0.6797 0.1270 0.5469 0.9572 0.9157 0.6551 0.9134 0.9575 0.4854 0.7922 0.1626 0.6324 0.9649 0.8003 0.9595 0.1190>> x1=det(B1)/det(A)x1 =-0.9850>> x2=det(B2)/det(A) x2 =2.4396>> x3=det(B3)/det(A) x3 =3.3124>> x4=det(B4)/det(A) x4 =-5.6515>> x5=det(B5)/det(A)x5 =1.7085计算A的行列式>> det(A)ans =-0.0250计算B的行列式>> det(B)ans =0.0647求A的逆>> inv(A)ans =3.1375 -0.8078 -1.8788 -4.21945.1680-8.6076 3.5314 2.8907 13.7204 -14.3665 -6.2824 3.7220 3.6132 10.0084 -12.4190 13.6173 -6.8822 -6.3938 -23.5288 27.5825 -2.5292 1.0729 2.4193 5.8870 -7.2671 求B的逆>> inv(B)ans =-0.4430 3.4997 1.3255 -2.6005 -0.4697 1.4047 -1.1626 0.2422 -0.4475 -0.0119 0.7210 -1.8189 -2.0635 2.4434 0.0765 -0.6122 -0.1837 2.0165 0.0375 -1.2564 0.0384 -0.5157 -0.7370 0.5267 1.7407 求A的秩>> rank(A)ans =5求B的秩>> rank(B)ans =5求A*B的行列式>> det(A*B)ans =-0.0016求A*B的逆>> inv(A*B)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360>> rank(A*B)ans =5>> det(A)*det(B)ans =-0.0016验证（1）>> (A*B)'ans =0.9569 1.5566 1.6237 2.2732 2.25520.6922 0.9401 0.4969 0.9371 0.80900.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497()()111,,T T T AB B A AB B A AB BA---==≠>> B'*A'ans =0.9569 1.5566 1.6237 2.2732 2.2552 0.6922 0.9401 0.4969 0.9371 0.8090 0.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497 （2）>> inv(B)*inv(A)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360 （3）>> A*Bans =0.9569 0.6922 0.9461 0.7507 1.13991.5566 0.9401 1.6492 1.5887 1.52121.6237 0.4969 1.6875 1.88402.21492.2732 0.9371 2.3563 1.9421 2.4545 2.2552 0.8090 2.3800 2.1481 2.4497>> B*Aans =2.0719 1.6135 2.1978 1.9769 1.9635 1.3528 1.2566 1.3549 1.4850 1.7372 1.7186 1.6454 1.5229 1.6894 1.6900 1.8714 2.0423 2.0113 2.2932 2.4625 0.8797 0.9697 0.8489 0.9690 0.8317 求矩阵X使得AXB=C首先随机生成五阶方阵C>> C=rand(5)C =0.4984 0.7513 0.9593 0.8407 0.35000.9597 0.2551 0.5472 0.2543 0.19660.3404 0.5060 0.1386 0.8143 0.25110.5853 0.6991 0.1493 0.2435 0.61600.2238 0.8909 0.2575 0.9293 0.4733X=A 的逆*B 的逆>> X=inv(A)*C*inv(B)X =3.8432 -13.8858 2.1418 9.4404 -4.5871-9.3312 41.9602 -7.9101 -28.4683 14.8942-7.8738 35.1218 -5.4107 -22.8861 10.158116.7545 -75.6079 14.6784 49.3951 -24.7450-3.5568 17.0848 -2.9018 -11.2670 5.4559实验二1. 验证：对于一般的方阵A,B,C,D ，首先随机生成方阵A,B,C,D A=rand(5)A BA DB CC D ≠-A =0.8258 0.1067 0.8687 0.4314 0.1361 0.5383 0.9619 0.0844 0.9106 0.8693 0.9961 0.0046 0.3998 0.1818 0.5797 0.0782 0.7749 0.2599 0.2638 0.5499 0.4427 0.8173 0.8001 0.1455 0.1450>> B=rand(5)B =0.8530 0.0760 0.4173 0.4893 0.7803 0.6221 0.2399 0.0497 0.3377 0.3897 0.3510 0.1233 0.9027 0.9001 0.2417 0.5132 0.1839 0.9448 0.3692 0.4039 0.4018 0.2400 0.4909 0.1112 0.0965>> C=rand(5)C =0.1320 0.2348 0.1690 0.5470 0.1835 0.9421 0.3532 0.6491 0.2963 0.3685 0.9561 0.8212 0.7317 0.7447 0.6256 0.5752 0.0154 0.6477 0.1890 0.7802 0.0598 0.0430 0.4509 0.6868 0.0811>> D=rand(5)D =0.9294 0.3063 0.6443 0.9390 0.2077 0.7757 0.5085 0.3786 0.8759 0.3012 0.4868 0.5108 0.8116 0.5502 0.4709 0.4359 0.8176 0.5328 0.6225 0.2305 0.4468 0.7948 0.3507 0.5870 0.8443>> Z=[A,B;C,D]Z =0.8258 0.1067 0.8687 0.4314 0.13610.8530 0.0760 0.4173 0.4893 0.78030.5383 0.9619 0.0844 0.9106 0.86930.6221 0.2399 0.0497 0.3377 0.38970.9961 0.0046 0.3998 0.1818 0.57970.3510 0.1233 0.9027 0.9001 0.24170.0782 0.7749 0.2599 0.2638 0.54990.5132 0.1839 0.9448 0.3692 0.40390.4427 0.8173 0.8001 0.1455 0.14500.4018 0.2400 0.4909 0.1112 0.09650.1320 0.2348 0.1690 0.5470 0.18350.9294 0.3063 0.6443 0.9390 0.20770.9421 0.3532 0.6491 0.2963 0.36850.7757 0.5085 0.3786 0.8759 0.30120.9561 0.8212 0.7317 0.7447 0.62560.4868 0.5108 0.8116 0.5502 0.47090.5752 0.0154 0.6477 0.1890 0.78020.4359 0.8176 0.5328 0.6225 0.23050.0598 0.0430 0.4509 0.6868 0.08110.4468 0.7948 0.3507 0.5870 0.8443求Z的行列式>> det(Z)ans =-0.0295求det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =1.8656e-004随机生成对角矩阵A>> A=diag([rand rand rand rand rand])A =0.1948 0 0 0 0 0 0.2259 0 0 0 0 0 0.1707 0 0 0 0 0 0.2277 0 0 0 0 0 0.4357 随机生成对角矩阵B>> B=diag([rand rand rand rand rand])B =0.3111 0 0 0 0 0 0.9234 0 0 0 0 0 0.4302 0 0 0 0 0 0.1848 0 0 0 0 0 0.9049 随机生成对角矩阵C>> C=diag([rand rand rand rand rand])C =0.9797 0 0 0 0 0 0.4389 0 0 0 0 0 0.1111 0 0 0 0 0 0.2581 0 0 0 0 0 0.4087 随机生成对角矩阵D>> D=diag([rand rand rand rand rand])D =0.5949 0 0 0 00 0.2622 0 0 00 0 0.6028 0 00 0 0 0.7112 00 0 0 0 0.2217>> Z=[A,B;C,D]Z =0.1948 0 0 0 00.3111 0 0 0 00 0.2259 0 0 00 0.9234 0 0 00 0 0.1707 0 00 0 0.4302 0 00 0 0 0.2277 0 0 0 0 0.1848 00 0 0 0 0.4357 0 0 0 0 0.90490.9797 0 0 0 00.5949 0 0 0 00 0.4389 0 0 00 0.2622 0 0 00 0 0.1111 0 00 0 0.6028 0 00 0 0 0.2581 00 0 0 0.7112 00 0 0 0 0.40870 0 0 0 0.2217计算Z的行列式>> det(Z)ans =-1.1243e-004计算det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =-9.3107e-005计算A*D-B*C的行列式>> det(A*D-B*C)ans =-1.1243e-004实验三求A列向量组的一个最大无关组，并把不属于极大无关组的向量利用极大无关组表示.N= 200865083;a=83;b=86;c=50;d=88;e=28;f=63;g=83;h=60;>>A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h, 8,0];>> B=rref(A)B =1.0000 0 0 0 -0.3548 0.46560 1.0000 0 0 -1.4905 -2.00200 0 1.0000 0 0.0473 0.39500 0 0 1.0000 1.79841.3383所以a1,a2,a3,a4是一个极大无关组。

大连理工矩阵上机作业

第一题Lagrange插值函数function y=lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endx0=[1:10];y0=[67.052,68.008,69.803,72.024,73.400,72.063,74.669,74.487,74.065,76 .777];lagrange(x0,y0,17)ans=-1.9516e+12x=[1:0.1:10];x=x';plot(x0,y0,'r');hold onplot(x,y,'k');legend('原函数','拟合函数')拟合图像如下拟合函数出现了龙格现象，运用多项式进行插值拟合时，效果并不好，高次多项式会因为误差的不断累积，导致龙格现象的发生。

第二题function fun =nihe(n)m=[67.052*10^6,68.008*10^6,69.803*10^6,72.024*10^6,73.400*10^6,72.063 *10^6,74.669*10^6,74.487*10^6,74.065*10^6,76.777*10^6];w=[1,2,3,4,5,6,7,8,9,10];d1=0;d2=0;d3=0;y1=polyfit(m,w,1);y2=polyfit(m,w,2);y3=polyfit(m,w,3);y2=poly2sym(s2);y3=poly2sym(s3);y4=poly2sym(s4);f1=subs(y1,17);f2=subs(y2,17);f3=subs(y3,17);for p=1:10;d1=d1+(subs(y1,w(p))-m(p))^2;d2=d2+(subs(y2,w(p))-m(p))^2;d3=d3+(subs(y3,w(p))-m(p))^2;endd1=sqrt(d1);d2=sqrt(d2);d3=sqrt(d3);fun=[f1 f2 f3;d2 d3 d4];return;结果三次函数的均方误差最小，拟合的最好。

大连理工大学优化方法上机作业

大连理工大学优化方法上机作业本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March优化方法上机大作业学院：电子信息与电气工程学部姓名：学号：指导老师：上机大作业（一）%目标函数function f=fun(x)f=100*(x(2)-x(1)^2)^2+(1-x(1))^2;end%目标函数梯度function gf=gfun(x)gf=[-400*x(1)*(x(2)-x(1)^2)-2*(1-x(1));200*(x(2)-x(1)^2)]; End%目标函数Hess矩阵function He=Hess(x)He=[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1), 200;];end%线搜索步长function mk=armijo(xk,dk)beta=0.5; sigma=0.2;m=0; maxm=20;while (m<=maxm)if(fun(xk+beta^m*dk)<=fun(xk)+sigma*beta^m*gfun(xk)'*dk) mk=m; break;endm=m+1;endalpha=beta^mknewxk=xk+alpha*dkfk=fun(xk)newfk=fun(newxk)%最速下降法function [k,x,val]=grad(fun,gfun,x0,epsilon)%功能：梯度法求解无约束优化问题：minf(x)%输入：fun，gfun分别是目标函数及其梯度，x0是初始点，% epsilon为容许误差%输出：k是迭代次数，x，val分别是近似最优点和最优值maxk=5000; %最大迭代次数beta=0.5; sigma=0.4;k=0;while(k<maxk)gk=feval(gfun,x0); %计算梯度dk=-gk; %计算搜索方向if(norm(gk)<epsilon), break;end%检验终止准则m=0;mk=0;while(m<20) %用Armijo搜索步长if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx0=x0+beta^mk*dk;k=k+1;endx=x0;val=feval(fun,x0);>> x0=[0;0];>> [k,x,val]=grad('fun','gfun',x0,1e-4)迭代次数：k =1033x =0.99990.9998val =1.2390e-008%牛顿法x0=[0;0];ep=1e-4;maxk=10;k=0;while(k<maxk)gk=gfun(x0);if(norm(gk)<ep)x=x0miny=fun(x)k0=kbreak;elseH=inv(Hess(x0));x0=x0-H*gk;k=k+1;endendx =1.00001.0000miny =4.9304e-030迭代次数k0 =2%BFGS方法function [k,x,val]=bfgs(fun,gfun,x0,varargin) %功能：梯度法求解无约束优化问题：minf(x)%输入：fun，gfun分别是目标函数及其梯度，x0是初始点，% epsilon为容许误差%输出：k是迭代次数，x，val分别是近似最优点和最优值N=1000;epsilon=1e-4;beta=0.55;sigma=0.4;n=length(x0);Bk=eye(n);k=0;while(k<N)gk=feval(gfun,x0,varargin{:});if(norm(gk)<epsilon), break;enddk=-Bk\gk;m=0;mk=0;while(m<20)newf=feval(fun,x0+beta^m*dk,varargin{:});oldf=feval(fun,x0,varargin{:});if(newf<=oldf+sigma*beta^m*gk'*dk)mk=m;break;endm=m+1;endx=x0+beta^mk*dk;sk=x-x0;yk=feval(gfun,x,varargin{:})-gk;if(yk'*sk>0)Bk=Bk-(Bk*sk*sk'*Bk)/(sk'*Bk*sk)+(yk*yk')/(yk'*sk);endk=k+1;x0=x;endval=feval(fun,x0,varargin{:});>> x0=[0;0];>> [k,x,val]=bfgs('fun','gfun',x0)k =20x =1.00001.0000val =2.2005e-011%共轭梯度法function [k,x,val]=frcg(fun,gfun,x0,epsilon,N)if nargin<5,N=1000;endif nargin<4, epsilon=1e-4;endbeta=0.6;sigma=0.4;n=length(x0);k=0;while(k<N)gk=feval(gfun,x0);itern=k-(n+1)*floor(k/(n+1));itern=itern+1;if(itern==1)dk=-gk;elsebetak=(gk'*gk)/(g0'*g0);dk=-gk+betak*d0; gd=gk'*dk;if(gd>=0),dk=-gk;endendif(norm(gk)<epsilon),break;endm=0;mk=0;while(m<20)if(feval(fun,x0+beta^m*dk)<=feval(fun,x0)+sigma*beta^m*gk'*dk) mk=m;break;endm=m+1;endx=x0+beta^m*dk;g0=gk; d0=dk;x0=x;k=k+1;endval=feval(fun,x);>> x0=[0;0];[k,x,val]=frcg('fun','gfun',x0,1e-4,1000)k =122x =1.00011.0002val =7.2372e-009上机大作业（二）%目标函数function f_x=fun(x)f_x=4*x(1)-x(2)^2-12;%等式约束条件function he=hf(x)he=25-x(1)^2-x(2)^2;end%不等式约束条件function gi_x=gi(x,i)switch icase 1gi_x=10*x(1)-x(1)^2+10*x(2)-x(2)^2-34;case 2gi_x=x(1);case 3gi_x=x(2);otherwiseend%求目标函数的梯度function L_grad=grad(x,lambda,cigma)d_f=[4;2*x(2)];d_g(:,1)=[-2*x(1);-2*x(2)];d_g(:,2)=[10-2*x(1);10-2*x(2)];d_g(:,3)=[1;0];d_g(:,4)=[0;1];L_grad=d_f+(lambda(1)+cigma*hf(x))*d_g(:,1);for i=1:3if lambda(i+1)+cigma*gi(x,i)<0L_grad=L_grad+(lambda(i+1)+cigma*gi(x,i))*d_g(:,i+1);continueendend%增广拉格朗日函数function LA=lag(x,lambda,cee)LA=fun(x)+lambda(1)*hf(x)+0.5*cee*hf(x)^2;for i=1:3LA=LA+1/(2*cee)*(min(0,lambda(i+1)+cee*gi(x,i))^2-lambda(i+1)^2); endfunction xk=BFGS(x0,eps,lambda,cigma)gk=grad(x0,lambda,cigma);res_B=norm(gk);k_B=0;a_=1e-4;rho=0.5;c=1e-4;length_x=length(x0);I=eye(length_x);Hk=I;while res_B>eps&&k_B<=10000dk=-Hk*gk;m=0;while m<=5000if lag(x0+a_*rho^m*dk,lambda,cigma)-lag(x0,lambda,cigma)<=c*a_*rho^m*gk'*dkmk=m;break;endm=m+1;endak=a_*rho^mk;xk=x0+ak*dk;delta=xk-x0;y=grad(xk,lambda,cigma)-gk;Hk=(I-(delta*y')/(delta'*y))*Hk*(I-(y*delta')/(delta'*y))+(delta*delta')/(delta'*y);k_B=k_B+1;x0=xk;gk=y+gk;res_B=norm(gk);end%增广拉格朗日法function val_min=ALM(x0,eps)lambda=zeros(4,1);cigma=5;alpha=10;k=1;res=[abs(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);while res>eps&&k<1000xk=BFGS(x0,eps,lambda,cigma);lambda(1)=lambda(1)+cigma*hf(xk);for i=1:3lambda(i+1)=lambda(i+1)+min(0,lambda(i+1)+gi(x0,1)); endk=k+1;cigma=alpha*cigma;x0=xk;res=[norm(hf(x0)),0,0,0];for i=1:3res(1,i+1)=norm(min(gi(x0,i),-lambda(i+1)/cigma)); endres=max(res);endval_min=fun(xk);fprintf('k=%d\n',k);fprintf('fmin=%.4f\n',val_min);fprintf('x=[%.4f;%.4f]\n',xk(1),xk(2));>> x0=[0;0];>> val_min=ALM(x0,1e-4)k=10fmin=-31.4003x=[1.0984;4.8779]val_min =-31.4003上机大作业（三）A=[1 1;-1 0;0 -1];n=2;b=[1;0;0];G=[0.5 0;0 2];c=[2 4];cvx_solver sdpt3cvx_beginvariable x(n)minimize (x'*G*x-c*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -2.40.40000.6000A=[2 1 1;1 2 3;2 2 1;-1 0 0;0 -1 0;0 0 -1]; n=3;b=[2;5;6;0;0;0];C=[-3 -1 -3];cvx_solver sdpt3cvx_beginvariable x(n)minimize (C*x)subject toA*x<=bcvx_enddisp(x)Status: SolvedOptimal value (cvx_optval): -5.40.20000.00001.600011。

大连理工大学矩阵与数值分析上机作业

s=s+abs(x(i));
end
case2%2-范数
fori=1:n
s=s+x(i)^2;
end
s=sqrt(s);
caseinf%无穷-范数
s=max(abs(x));
end
计算向量x，y的范数
Test1.m
clearall;
clc;
n1=10;n2=100;n3=1000;
x1=1./[1:n1]';x2=1./[1:n2]';x3=1./[1:n3]';
xlabel('x');ylabel('p(x)');
运行结果：
x=2的邻域：
x =
1.6000 1.8000 2.0000 2.2000 2.4000
相应多项式p值：
p =
1.0e-003 *
-0.2621 -0.0005 0 0.0005 0.2621
p(x)在 [1.95,20.5]上的图像
程序：
[L,U]=LUDe.(A);%LU分解
xLU=U\(L\b)
disp('利用PLU分解方程组的解:');
[P,L,U] =PLUDe.(A);%PLU分解
xPLU=U\(L\(P\b))
%求解A的逆矩阵
disp('A的准确逆矩阵:');
InvA=inv(A)
InvAL=zeros(n);%利用LU分解求A的逆矩阵
0 0 0.5000 -0.2500 -0.1250 -0.0625 -0.0625
0 0 0 0.5000 -0.2500 -0.1250 -0.1250
0 0 0 0 0.5000 -0.2500 -0.2500

大连理工大学矩阵分析matlab上机作业

x=zeros(n,1); %为列向量 x 预分配存储空间 y=1:n; %定义行向量 y y=y'; %把行向量 y 改成列向量 for i=1:n
x(i)=1/i; %按要求给向量 x 赋值，其值递减 end normx1=norm(x,1); %求解向量 x 的 1 范数 normx1 normx2=norm(x,2); %求解向量 x 的 2 范数 normx2 normxinf=norm(x,inf); %求解向量 x 的无穷范数 normxinf normy1=norm(y,1); %求解向量 y 的 1 范数 normy1 normy2=norm(y,2); %求解向量 y 的 2 范数 normy2 normyinf=norm(y,inf); %求解向量 y 的无穷范数 normyinf z1=[normx1,normx2,normxinf]; z2=[normy1,normy2,normyinf]; end
for i=2:n
for j=i:n U(i,j)=A(i,j)-L(i,1:i-1)*U(1:i-1,j);
式
%Doolittle 分解计算上三角矩阵的公
L(j,i)=(A(j,i)-L(j,1:i-1)*U(1:i-1,i))/U(i,i); %Doolittle 分解计算下三角矩阵的公式
end
1 1 1 �� x = (1, 2 , 3 , … , ��) ,
�� = (1,2, … , ��)��.
对n = 10，100，1000甚至更大的n计算其范数，你会发现什么结果?你能否修改
你的程序使得计算结果相对精确呢？
1.1 源代码
function [z1,z2]=norm_vector(n) %向量 z1 的值为向量 x 的是三种范数，向量 z2 的值为向量 y 的三种范数，n 为输入参数

大连理工_2012矩阵与数值分析大作业

矩阵与数值分析学生：学号：任课老师：金光日教学班号：（2）班院系：电子信息与电气工程学部《矩阵与数值分析》课程数值实验题目1.给定n 阶方程组A x b =，其中6186186186A ⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭，7151514b ⎛⎫ ⎪⎪ ⎪= ⎪ ⎪⎪⎝⎭则方程组有解(1,1,,1)T x = 。

对10n =和84n =，分别用Gauss 消去法和列主元消去法解方程组，并比较计算结果。

1答：程序1. Gauss 消元法function x=DelGauss(A,b) % Gauss 消去法 [n,m]=size(A); det=1; %存储行列式值 x=zeros(n,1); for k=1:n-1 for i=k+1:n if A(k,k)==0 return endm=A(i,k)/A(k,k); for j=k+1:nA(i,j)=A(i,j)-m*A(k,j); endb(i)=b(i)-m*b(k); enddet=det*A(k,k); %计算行列式enddet=det*A(n,n);for k=n:-1:1 %回代求解for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);end2. 列主元Gauss消去法：function x=detGauss(A,b)% Gauss列主元消去法[n,m]=size(A);nb=length(b);det=1; %存储行列式值x=zeros(n,1);for k=1:n-1amax=0; %选主元for i=k:nif abs(A(i,k))>amaxamax=abs(A(i,k));r=i;endendif amax<1e-10return;endif r>k %交换两行for j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;det=-det;endfor i=k+1:n %进行消元m=A(i,k)/A(k,k);for j=k+1:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);enddet=det*A(k,k);enddet=det*A(n,n);for k=n:-1:1 %回代求解for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);end矩阵A和b的构造clc;clear;n=10;%n=84;A=eye(n)*6+diag(ones(1,n-1)*8,-1)+diag(ones(1,n-1),1); b=[7,15*ones(1,n-2),14]';计算结果：(1)n=10时Gauss消元法>>x=DelGauss(A,b)x =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000列主元Gauss消去法>>x=detGauss(A,b)x =1111111111(2) n=84时Gauss消元法>>x=DelGauss(A,b) x =1.0e+008 *0.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0001 0.0002 -0.0003 0.0007 -0.0013 0.0026 -0.0052 0.0105 -0.0209 0.0419 -0.0836 0.16650.6501-1.25822.3487-4.02635.3684列主元Gauss消去法>>x=detGauss(A,b) x =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.0000 1.0000 1.00001.00001.0000 1.0000结果分析由上述实验结果可知，对于n=10采用Gauss 消去法和Gauss 列主元消去法得到的实验结果是相同的，而对于n=84，Gauss 消去法所得到的结果是错误的，Gauss 列主元消去法得到的结果是正确的。

大工矩阵上机题答案

上机题一．（1）s=0;for j=2:100;s=s+1/(j^2-1); endss =0.7400s=0;for j=100:-1:2;s=s+1/(j^2-1); endss =0.7400（2）s=0;for j=2：10000;s=s+1/(j^2-1); endss =0.7499for j=10000:-1:2;s=s+1/(j^2-1); endss =0.7499（3）s=0;for j=2：1000000;s=s+1/(j^2-1); endss =0.7500s=0;for j=1000000:-1:2; s=s+1/(j^2-1); endss =0.7500二1、Jacobi 迭代法算法：对于线性方程组Ax=b ，如果A 为非奇异方程，则可将A 分解为：A=D-L-U 其中D 为对角阵，其元素为A 的对角元素，L 与U 为A 的下三角阵和上三角阵。

于是Ax=b 化为：111()k k x D L U x D b --+=++，其中1()J B D L U -=+，1f D b -=。

程序：function x=jacobi(A,b,x0)A=[-2 1 0 0;1 -2 1 0;0 1 -2 1;0 0 1 -2];b=[-1 ;0; 0; 0];x0=[0;0 ;0 ;0];D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=D\(L+U);f=D\b;x=B*x0+f;n=1;while norm(x-x0,2)>=1.0e-6x0=x;x=B*x0+f;n=n+1;endfprintf('迭代次数为：')nfprintf('方程组的解为：')计算结果：迭代次数为：n =60方程组的解为：ans =0.80000.60000.40000.2000.Gauss-seidel 迭代法function x=Gaussseidel(A,b,x0)A=[-2 1 0 0;1 -2 1 0;0 1 -2 1;0 0 1 -2];b=[-1 ;0; 0; 0];x0=[0;0 ;0 ;0];D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1);B=(D-L)\U;f=(D-L)\b;x=B*x0+f;n=1;while norm(x-x0,2)>=1.0e-6x0=x;x=B*x0+f;n=n+1;endfprintf('迭代次数')nfprintf('方程组的解为')迭代次数为：n =31方程组的解为：ans =0.80000.60000.40000.20002.用Gauss列主元消去法算法：Gauss列主元消去法是在Gauss消去法中增加选主元的过程，即在第k步（k=1,2,3,…）消元时，首先在第k列主对角元以下（含对角元）元素中挑选绝对值最大的数（即为列主元），并通过初等行变换，使得该数位于主对角线上，然后再继续消元。

大连理工大学-矩阵大作业

（1）从大到小的顺序的计算程序：function y=snd(n)format longy=0;if n<2disp('请输入大于1的数！')elses=0;i=2;while i<=ns=single(s+(1/(i^2-1))); i=i+1;endy=s;end（2）从小到大的顺序的计算程序：function y=snx(n)format longy=0;if n<2disp('请输入大于1的数！')elses=0;i=n;while 1s=single(s+(1/(i^2-1)));i=i-1;if i==1breakendendy=s;end（3）按两种顺序分别计算并指出有效位数（编制程序时用单精度）S的计算结果：①210S的计算结果：②410S的计算结果：③610计算时的有效位数为七位数。

① 秦九昭算法计算程序：function y=qjz(a,x) j=3; i=size(a,2); switch i case 1 y=a(1); case 2y=a(1)*x+a(2); otherwise p=a(1)*x+a(2); while j<=i p=p*x+a(j); j=j+1; end y=p; end② 计算在点23的值。

计算结果如下：当23=x 时()86652=x f 。

①Gauss法计算程序和结果：程序：A(1,:)=[31,-13,0,0,0,-10,0,0,0]; A(2,:)=[-13,35,-9,0,-11,0,0,0,0]; A(3,:)=[0,-9,31,-10,0,0,0,0,0];A(4,:)=[0,0,-10,79,-30,0,0,0,-9]; A(5,:)=[0,0,0,-30,57,-7,0,-5,0]; A(6,:)=[0,0,0,0,-7,47,-30,0,0];A(7,:)=[0,0,0,0,0,-30,41,0,0];A(8,:)=[0,0,0,0,-5,0,0,27,-2];A(9,:)=[0,0,0,-9,0,0,0,-2,29];B=[-15;27;-23;0;-20;12;-7;7;10]; [a,b]=gauss(A,B);j=size(a,2);while j>=1k=j+1;s=b(j);while k<=9s=s-x(k)*a(j,k);k=k+1;endx(j)=s/a(j,j);j=j-1;enddisp(x)function [x,y]=gauss(a,b)num_i=size(a,1);j=1;while j<=(num_i-1)i=j+1;while i<=num_ir=a(i,j)/a(j,j);a(i,:)=a(i,:)-r*a(j,:);b(i,:)=b(i,:)-r*b(j,:);i=i+1;endj=j+1;endx=a;y=b;运行的结果为：()T 289.0-345.0.0=。

大连理工大学线性代数实验上机报告材料

大连理工大学线性代数实验上机报告实验一首先随机生成五阶方阵AA=rand(5)A =0.8147 0.0975 0.1576 0.1419 0.6557 0.9058 0.2785 0.9706 0.4218 0.0357 0.1270 0.5469 0.9572 0.9157 0.8491 0.9134 0.9575 0.4854 0.7922 0.9340 0.6324 0.9649 0.8003 0.9595 0.6787>> B=rand(5)随机生成五阶方阵BB =0.7577 0.7060 0.8235 0.4387 0.4898 0.7431 0.0318 0.6948 0.3816 0.4456 0.3922 0.2769 0.3171 0.7655 0.6463 0.6555 0.0462 0.9502 0.7952 0.7094 0.1712 0.0971 0.0344 0.1869 0.7547>> b=rand(1,5)'随机生成列向量bb =0.27600.67970.65510.16260.1190计算A+B>> A+Bans =1.5725 0.8036 0.9811 0.5806 1.1455 1.6489 0.3103 1.6654 0.8033 0.48130.5192 0.8238 1.2743 1.6813 1.49541.5689 1.0037 1.4356 1.5874 1.6434 0.8035 1.0620 0.8347 1.1464 1.4334 计算A-B>> A-Bans =0.0570 -0.6085 -0.6658 -0.2969 0.1660 0.1627 0.2467 0.2758 0.0402 -0.4099 -0.2652 0.2700 0.6401 0.1502 0.2028 0.2579 0.9113 -0.4648 -0.0030 0.2246 0.4612 0.8678 0.7658 0.7726 -0.0760 计算A*B+B*A>> A*B+B*Aans =3.0288 2.3058 3.1439 2.7276 3.10342.9094 2.19673.0040 3.0737 3.25843.3422 2.1423 3.2104 3.5734 3.90494.1446 2.9794 4.3676 4.2354 4.9170 3.1350 1.7787 3.2289 3.1170 3.2815 求Ax=b的解>> x=A\bx =-0.98502.43963.3124-5.65151.7085验证克莱姆法则>> c=A(:,1)c =0.81470.90580.12700.91340.6324>> d=A(:,2)d =0.09750.5469 0.9575 0.9649>> e=A(:,3)e =0.1576 0.9706 0.9572 0.4854 0.8003>> f=A(:,4)f =0.1419 0.4218 0.91570.9595>> g=A(:,5)g =0.65570.03570.84910.93400.6787>> B1=[b';d';e';f';g']'B1 =0.2760 0.0975 0.1576 0.1419 0.6557 0.6797 0.2785 0.9706 0.4218 0.0357 0.6551 0.5469 0.9572 0.9157 0.8491 0.1626 0.9575 0.4854 0.7922 0.9340 0.1190 0.9649 0.8003 0.9595 0.6787>> B2=[c';b';e';f';g']'B2 =0.8147 0.2760 0.1576 0.1419 0.6557 0.9058 0.6797 0.9706 0.4218 0.0357 0.1270 0.6551 0.9572 0.9157 0.8491 0.9134 0.1626 0.4854 0.7922 0.9340 0.6324 0.1190 0.8003 0.9595 0.6787>> B3=[c';d';b';f';g']'B3 =0.8147 0.0975 0.2760 0.1419 0.6557 0.9058 0.2785 0.6797 0.4218 0.0357 0.1270 0.5469 0.6551 0.9157 0.8491 0.9134 0.9575 0.1626 0.7922 0.9340 0.6324 0.9649 0.1190 0.9595 0.6787>> B4=[c';d';e';b';g']'B4 =0.8147 0.0975 0.1576 0.2760 0.6557 0.9058 0.2785 0.9706 0.6797 0.0357 0.1270 0.5469 0.9572 0.6551 0.8491 0.9134 0.9575 0.4854 0.1626 0.9340 0.6324 0.9649 0.8003 0.1190 0.6787>> B5=[c';d';e';f';b']'B5 =0.8147 0.0975 0.1576 0.1419 0.2760 0.9058 0.2785 0.9706 0.4218 0.6797 0.1270 0.5469 0.9572 0.9157 0.6551 0.9134 0.9575 0.4854 0.7922 0.1626 0.6324 0.9649 0.8003 0.9595 0.1190>> x1=det(B1)/det(A)x1 =-0.9850>> x2=det(B2)/det(A) x2 =2.4396>> x3=det(B3)/det(A) x3 =3.3124>> x4=det(B4)/det(A) x4 =-5.6515>> x5=det(B5)/det(A)x5 =1.7085计算A的行列式>> det(A)ans =-0.0250计算B的行列式>> det(B)ans =0.0647求A的逆>> inv(A)ans =3.1375 -0.8078 -1.8788 -4.21945.1680-8.6076 3.5314 2.8907 13.7204 -14.3665 -6.2824 3.7220 3.6132 10.0084 -12.4190 13.6173 -6.8822 -6.3938 -23.5288 27.5825 -2.5292 1.0729 2.4193 5.8870 -7.2671 求B的逆>> inv(B)ans =-0.4430 3.4997 1.3255 -2.6005 -0.4697 1.4047 -1.1626 0.2422 -0.4475 -0.0119 0.7210 -1.8189 -2.0635 2.4434 0.0765 -0.6122 -0.1837 2.0165 0.0375 -1.2564 0.0384 -0.5157 -0.7370 0.5267 1.7407 求A的秩>> rank(A)ans =5求B的秩>> rank(B)ans =5求A*B的行列式>> det(A*B)ans =-0.0016求A*B的逆>> inv(A*B)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360>> rank(A*B)ans =5>> det(A)*det(B)ans =-0.0016验证（1）>> (A*B)'ans =0.9569 1.5566 1.6237 2.2732 2.25520.6922 0.9401 0.4969 0.9371 0.80900.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497()()111,,T T T AB B A AB B A AB BA---==≠>> B'*A'ans =0.9569 1.5566 1.6237 2.2732 2.2552 0.6922 0.9401 0.4969 0.9371 0.8090 0.9461 1.6492 1.6875 2.3563 2.38000.7507 1.5887 1.8840 1.9421 2.14811.1399 1.52122.2149 2.4545 2.4497 （2）>> inv(B)*inv(A)ans =-74.0649 35.0433 31.2288 121.5740 -137.3442 6.8291 -1.2718 -2.2922 -8.9951 8.6972 63.9620 -31.4202 -29.5061 -105.6918 122.3246 -9.3196 5.7452 4.6259 11.9660 -15.4028 11.9582 -6.3521 -3.3817 -16.7574 18.6360 （3）>> A*Bans =0.9569 0.6922 0.9461 0.7507 1.13991.5566 0.9401 1.6492 1.5887 1.52121.6237 0.4969 1.6875 1.88402.21492.2732 0.9371 2.3563 1.9421 2.4545 2.2552 0.8090 2.3800 2.1481 2.4497>> B*Aans =2.0719 1.6135 2.1978 1.9769 1.9635 1.3528 1.2566 1.3549 1.4850 1.7372 1.7186 1.6454 1.5229 1.6894 1.6900 1.8714 2.0423 2.0113 2.2932 2.4625 0.8797 0.9697 0.8489 0.9690 0.8317 求矩阵X使得AXB=C首先随机生成五阶方阵C>> C=rand(5)C =0.4984 0.7513 0.9593 0.8407 0.35000.9597 0.2551 0.5472 0.2543 0.19660.3404 0.5060 0.1386 0.8143 0.25110.5853 0.6991 0.1493 0.2435 0.61600.2238 0.8909 0.2575 0.9293 0.4733X=A 的逆*B 的逆>> X=inv(A)*C*inv(B)X =3.8432 -13.8858 2.1418 9.4404 -4.5871-9.3312 41.9602 -7.9101 -28.4683 14.8942-7.8738 35.1218 -5.4107 -22.8861 10.158116.7545 -75.6079 14.6784 49.3951 -24.7450-3.5568 17.0848 -2.9018 -11.2670 5.4559实验二1. 验证：对于一般的方阵A,B,C,D ，首先随机生成方阵A,B,C,D A=rand(5)A BA DB CC D ≠-A =0.8258 0.1067 0.8687 0.4314 0.1361 0.5383 0.9619 0.0844 0.9106 0.8693 0.9961 0.0046 0.3998 0.1818 0.5797 0.0782 0.7749 0.2599 0.2638 0.5499 0.4427 0.8173 0.8001 0.1455 0.1450>> B=rand(5)B =0.8530 0.0760 0.4173 0.4893 0.7803 0.6221 0.2399 0.0497 0.3377 0.3897 0.3510 0.1233 0.9027 0.9001 0.2417 0.5132 0.1839 0.9448 0.3692 0.4039 0.4018 0.2400 0.4909 0.1112 0.0965>> C=rand(5)C =0.1320 0.2348 0.1690 0.5470 0.1835 0.9421 0.3532 0.6491 0.2963 0.3685 0.9561 0.8212 0.7317 0.7447 0.6256 0.5752 0.0154 0.6477 0.1890 0.7802 0.0598 0.0430 0.4509 0.6868 0.0811>> D=rand(5)D =0.9294 0.3063 0.6443 0.9390 0.2077 0.7757 0.5085 0.3786 0.8759 0.3012 0.4868 0.5108 0.8116 0.5502 0.4709 0.4359 0.8176 0.5328 0.6225 0.2305 0.4468 0.7948 0.3507 0.5870 0.8443>> Z=[A,B;C,D]Z =0.8258 0.1067 0.8687 0.4314 0.13610.8530 0.0760 0.4173 0.4893 0.78030.5383 0.9619 0.0844 0.9106 0.86930.6221 0.2399 0.0497 0.3377 0.38970.9961 0.0046 0.3998 0.1818 0.57970.3510 0.1233 0.9027 0.9001 0.24170.0782 0.7749 0.2599 0.2638 0.54990.5132 0.1839 0.9448 0.3692 0.40390.4427 0.8173 0.8001 0.1455 0.14500.4018 0.2400 0.4909 0.1112 0.09650.1320 0.2348 0.1690 0.5470 0.18350.9294 0.3063 0.6443 0.9390 0.20770.9421 0.3532 0.6491 0.2963 0.36850.7757 0.5085 0.3786 0.8759 0.30120.9561 0.8212 0.7317 0.7447 0.62560.4868 0.5108 0.8116 0.5502 0.47090.5752 0.0154 0.6477 0.1890 0.78020.4359 0.8176 0.5328 0.6225 0.23050.0598 0.0430 0.4509 0.6868 0.08110.4468 0.7948 0.3507 0.5870 0.8443求Z的行列式>> det(Z)ans =-0.0295求det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =1.8656e-004随机生成对角矩阵A>> A=diag([rand rand rand rand rand])A =0.1948 0 0 0 0 0 0.2259 0 0 0 0 0 0.1707 0 0 0 0 0 0.2277 0 0 0 0 0 0.4357 随机生成对角矩阵B>> B=diag([rand rand rand rand rand])B =0.3111 0 0 0 0 0 0.9234 0 0 0 0 0 0.4302 0 0 0 0 0 0.1848 0 0 0 0 0 0.9049 随机生成对角矩阵C>> C=diag([rand rand rand rand rand])C =0.9797 0 0 0 0 0 0.4389 0 0 0 0 0 0.1111 0 0 0 0 0 0.2581 0 0 0 0 0 0.4087 随机生成对角矩阵D>> D=diag([rand rand rand rand rand])D =0.5949 0 0 0 00 0.2622 0 0 00 0 0.6028 0 00 0 0 0.7112 00 0 0 0 0.2217>> Z=[A,B;C,D]Z =0.1948 0 0 0 00.3111 0 0 0 00 0.2259 0 0 00 0.9234 0 0 00 0 0.1707 0 00 0 0.4302 0 00 0 0 0.2277 0 0 0 0 0.1848 00 0 0 0 0.4357 0 0 0 0 0.90490.9797 0 0 0 00.5949 0 0 0 00 0.4389 0 0 00 0.2622 0 0 00 0 0.1111 0 00 0 0.6028 0 00 0 0 0.2581 00 0 0 0.7112 00 0 0 0 0.40870 0 0 0 0.2217计算Z的行列式>> det(Z)ans =-1.1243e-004计算det(A)*det(D)-det(B)*det(C)>> det(A)*det(D)-det(B)*det(C)ans =-9.3107e-005计算A*D-B*C的行列式>> det(A*D-B*C)ans =-1.1243e-004实验三求A列向量组的一个最大无关组，并把不属于极大无关组的向量利用极大无关组表示.N= 200865083;a=83;b=86;c=50;d=88;e=28;f=63;g=83;h=60;>>A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h, 8,0];>> B=rref(A)B =1.0000 0 0 0 -0.3548 0.46560 1.0000 0 0 -1.4905 -2.00200 0 1.0000 0 0.0473 0.39500 0 0 1.0000 1.79841.3383所以a1,a2,a3,a4是一个极大无关组。

大连理工大学-2015年矩阵上机编程作业

cout<<endl; } } }
} //Ax=b 的解答，A 为上三角矩阵 void SolveOne(double a[9][10],int m,int n){
int j=n-2; double answer[9]; for (int s=m-1;s>=0;s--){
answer[j]=a[s][n-1]/a[s][j]; for(int i=0;i<=s-1;i++){
} } }
} // 发现绝对值最大的元素所在一行和当前的一行做交换 void change(double a[9][10],int m,int n,int nowi,int nowj){
int record=nowi;//记录该和哪一行做交换 bool flag=true; //标志是否需要做交换 double max=a[nowi][nowj]; for(int i=nowi+1;i<m-1;i++){
}
//Gauss 消元解法 //先转化为上三角矩阵 void Gauss(double a[9][10],int m,int n){
double r[9]; //r 为每次的倍数 int k=0; for (int nowi=0,nowj=0;nowi<m-1 && nowj<n-1;nowi++,nowj++){
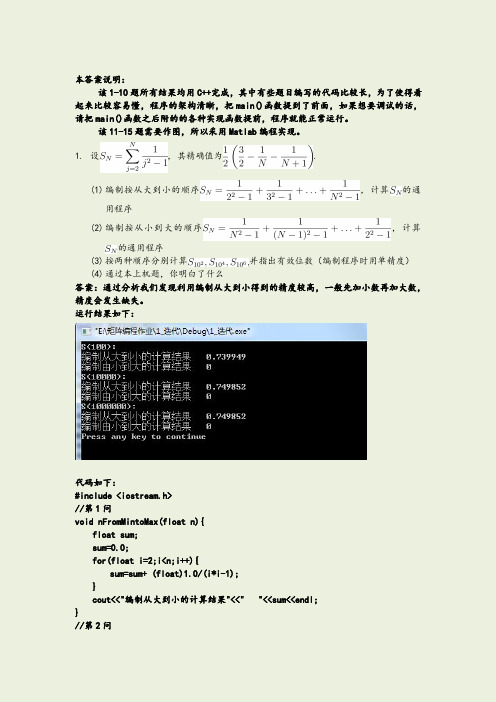
1. 设
, 其精确值为
.
(1) 编制按从大到小的顺序
, 计算的通
用程序 (2) 编制按从小到大的顺序
, 计算
的通用程序
(3) 按两种顺序分别计算
并指出有效位数（编制程序时用单精度）

大连理工大学矩阵与数值分析上机作业13388

大连理工大学矩阵与数值分析上机作业课程名称：矩阵与数值分析研究生姓名：交作业日时间：2016 年12 月20日1.1程序：Clear all;n=input('请输入向量的长度n：')for i=1:n;v(i)=1/i;endY1=norm(v,1)Y2=norm(v,2)Y3=norm(v,inf)1.2结果n=10 Y1 =2.9290Y2 =1.2449Y3 =1n=100 Y1 =5.1874Y2 =1.2787Y3 =1n=1000 Y1 =7.4855Y2 =1.2822Y3 =1N=10000 Y1 =9.7876Y2 =1.2825Y3 =11.3 分析一范数逐渐递增，随着n的增加，范数的增加速度减小；二范数随着n的增加，逐渐趋于定值，无群范数都是1.2.1程序clear all;x(1)=-10^-15;dx=10^-18;L=2*10^3;for i=1:Ly1(i)=log(1+x(i))/x(i); d=1+x(i);if d == 1y2(i)=1;elsey2(i)=log(d)/(d-1);endx(i+1)=x(i)+dx;endx=x(1:length(x)-1);plot(x,y1,'r');hold onplot(x,y2);2.2 结果2.3 分析红色的曲线代表未考虑题中算法时的情况，如果考虑题中的算法则数值大小始终为1，这主要是由于大数加小数的原因。

第3题3.1 程序clear all;A=[1 -18 144 -672 2016 -4032 5376 -4608 2304 -512];x=1.95:0.005:2.05;for i=1:length(x);y1(i)=f(A,x(i));y2(i)=(x(i)-2)^9;endfigure(3);plot(x,y1);hold on;plot(x,y2,'r');F.m文件function y=f(A,x) y=A(1);for i=2:length(A); y=x*y+A(i); end;3.2 结果第4题4.1 程序clear all;n=input('请输入向量的长度n：')A=2*eye(n)-tril(ones(n,n),0);for i=1:nA(i,n)=1;endn=length(A);U=A;e=eye(n);for i=1:n-1[max_data,max_index]=max(abs(U(i:n,i))); e0=eye(n);max_index=max_index+i-1;U=e0*U;e1=eye(n);for j=i+1:ne1(j,i)=-U(j,i)/U(i,i);endU=e1*U;P{i}=e0;%把变换矩阵存到P中L{i}=e1;e=e1*e0*e;endfor k=1:n-2Ldot{k}=L{k};for i=k+1:n-1Ldot{k}=P{i}*Ldot{k}*P{i};endendLdot{n-1}=L{n-1};LL=eye(n);PP=eye(n);for i=1:n-1PP=P{i}*PP;LL=Ldot{i}*LL;endb=ones(n,2);b=e*b; %解方程x=zeros(n,1);x(n)=b(n)/U(n,n);for i=n-1:-1:1x(i)=(b(i)-U(i,:)*x)/U(i,i);endX=U^-1*e^-1*eye(n);%计算逆矩阵AN=X';result2{n-4,1}=AN;result1{n-4,1}=x;fprintf('%d:\n',n)fprintf('%d ',AN);4.2 结果n=51.0625 -0.875 -0.75 -0.5 -0.06250.0625 1.125 -0.75 -0.5 -0.06250.0625 0.125 1.25 -0.5 -0.06250.0625 0.125 0.25 1.5 -0.0625-0.0625 -0.125 -0.25 -0.5 0.0625n=101.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625同样的方法可以算出n=20,n=30时的结果，这里就不罗列了。

大连理工大学概率上机作业

大连理工大学概率上机作业————————————————————————————————作者: ————————————————————————————————日期：ﻩ第一次上机作业1.利用Matlａb自带命令产生100０个均匀随机变量服从Ｕ(０，1）。

>＞unｉfrnｄ(0，1，2０,5０)aｎs＝Ｃoｌｕｍns 1 tｈrouｇh 1０0.81４７0．6５５7０．4387 ０.75130.３517 0.1６22０．106７0.85３00.7８0３0．5４700．9058 0.03570.3８１6 0.25510.8308 0.7９４3 0．９619 0.6221 ０．3897 0.２963０.1270 0.849１０.7６55 0.５06０0．585３0.３1１2 0.０046 0.３5100.241７0.74４70.９134 0.93４00.7952０.6991 0.5４97 ０．52８5 ０.７749 0.51３2 0．４039 0.18900.６3２4 0.６７87 0.1869 0.8909 0.91７2 0.1656 0．８173 0.4０１８０.0965 0.6868０.09750.757７0.48９８0.95９3 0.28５８0．6020 ０．86870．0760０.13２0 0.１8350.2785 ０.743１0.４4５60.５472 0．7５7２0.2６3０0．084４0.23990.９42１0．368５０.５469 0.3９220.64630．138６0.7５37０.65４1 0.３998 ０.1233 0．95６1 ０.６２560．9575 0．6555 ０.7０９4 0．1493 0.3８04 ０.6８９2 0．25990.１83９0.5７５2 0.78０20.９６49 0.1712 0.７５470．257５０.5６7８0．74８2 0．80010.2４00０．05９８0.081１0.1５760.7060 0.27６0 0.８４07 ０.0７59 0.４505 0.４３14 0.4１730.2348 0.929４０.970６0．0３1８０.679７０.２543 0.０5400.083８0．9106 0.０497 0．35３20.７７57０.９572 0．2769 ０.655１0.８１43 0.5308 ０．22９0０.18１8０．９0２7 0.8212 ０．4８６８0.4854 0．0462 0.１６26 ０.2435 0.7792 0.91３3 0.２638 0.94480.01540.４35９0.8003 ０.０971 0.１19０0．92９３0．9340 ０．1524 ０．1455 0．４909 0.０４30 0.4468０.1419 0.8２3５0.49８4 ０．35０0 0.1２9９0.８2５８0.１36１0.4８93 0.1690 0.３０63０.4２18 0.6948０.9597 0.１966０.５６8８０.5383 0.8693 ０.3３７7 0.6491 0.508５0.9157 0.3171０.３4０4 0.2５１1 0．46９4 0.996１0.579７0.9０0１0．7３17 0.51０80.7922 0．９50２0.5853 0.61600.０1190.07８20．54９９０.３692 0.6４77 ０．81760.9５950.0344 ０.2２38 ０.4733 0.３3７1 0.4427０.1450 ０．1１120.4509 0.794８Colｕmns １1 throｕｇh 200.6443 0.31１10．08５5 ０.0377 0.03050.0596 ０．173４0.９51６0.０3２6 0．25180.３7８6 ０.9２3４0.262５0．８8５2 ０.74４1０.68200．39０9 0.920３0.５6120.29040.８116 0.4302 0.8010 ０.9１3３0．500０0．04２4 0.831４0.0527０.８819 0.6171０．５328 0．18480．0292 ０.79620.４7990.07１４0.8034 ０.７379 0.6６9２0.265３0.3５07 0.9049 ０.92８9 0.0987 0.９047０．５21６0.06050.26９10.１９0４0.824４0.9390 0．9７97 0．７303 0.26１９０.609９0.０９6７0．39９3０.４228０．3689 0．982７0.８759 ０.4389 0.4886 ０.３354 0.6177 0.８18１0．5269 0.54790.4607 ０.730２0.55020.11１1 ０.5785 0．67９7 ０.8５94 0．81750．4１680.94２７0.9816 0.３4390.６２２５0.25８1 0.23７30.1366 0.8055 0.７２24 0.６5690.4177 0.1５6４0.58４1０．５870 0.4087 0.458８０．7212 0.5７6７0.1499０．6２80 ０.９83１０．8555 0.1０780．20７70.5949 ０.963１0.106８0.18２９０．６5９6 0.2920 0.3０１5 0.6448 0.９06３0．3012 ０．2622 0．5４680.6５38 ０.２３99０.５186 0.4３1７0.７0１1 0.３763 0.8797０.4709 0.6０2８0．52110.494２0．88６5 0.９７3００.0155 0.６663 0.190９0．817８0.230５0．7112 0.231６0.７79１０.02８70.6490 ０.9841 0．5３91 0．4283 ０.260７0．844３０.2217 ０.488９０.７１50 0．4899 ０.8003 0.1６72 0.6９８１0.４８20 0.59４4０．19４8 0.1174 ０.６241 0．90370．１6790．4５38 0.106２0.666５0．1206 0.02２５0.2２5９0.2９67 0.67９1 0.89０9 0．97８7 0.４３2４0.3724 0.1781 0.５8９５0．425３０.1707 ０．３188 ０.３９55 0.3342 ０.7127 ０.82５3 ０.1981 ０.１280 0．2262 0.31２7０.2277 0．4242 0.3674 0.６987 0.5００5 0.０835 ０.48970.99９1 ０.３846 0.１6150.43５7 0.5０７9 ０.988００.197８0.471１0.1332 ０.3395０.171１0．5830 0.１７88Coluｍnｓ２1thrｏugh 300.4２２９０.７7８8 0.２54８0．17５9 0．６476 0.5８22 ０．4046 0.3477 0．８2１７0.5１４4０．0942 0．42３５0.22４0 ０．7２18 ０．67900.5４070.44８4 ０．1500 ０.42９９0.884３0.598５0．09080.6６７80．473５0.63５8 0．86990．3658 0．5861 ０.88780．58８00.47090.2６65 0.8４４4 0.１527 0.945２0.26480.７63５0.2621 ０．3912 0.1548０.69５9 0.1５3７０.３44５0．34１1０.２089 0.３１８1 ０.６27９0.044５0．7691 0.１999０.６999０．28１0 ０.780５０.６07４0.70930.119２0．77２0 ０.7５49 0．39６8 ０．40７0０.638５0.440１０.6753 0.19170.２３6２0.9398 0.932９0．2428 ０．8085 ０.74870.033６0.5２7１0.０0６7 0.73840．11940.64560.9727 0.442４０．7551 0.8２5６０.０６88 0.４５7４０.6022 0.2４２80.６073 0.4795 0.192００.687８０.3７740.79000.31９6 0.875４０．386８0.9１74 ０.４５０1 0．639３0.13８9０．359２0.2160 0.3185０.53090.5181 ０.9１600.２6９1 ０.4５87０.54４7 0.69６３０.7３63 0.7904 0.53410.6５４4 0.9436 ０.00１2 0．76５5 ０.6619 0.64730.09３8 0.3947 0.９４9３0.090０0.４0７6 0.6377 0.４6２4 0.1887 0．７70３０．5４39 0.52５4 0．6834 0.３2７60．１11７0.8200 0.9５770.4２4３0.287５0.3502 0.７2１0 0.５3030．7040 0．6713 0.13６３0.７18４0.24０７0.46090.0911 0.66２0 0.5225 ０.8611 0.4423 0.4３8６0.67８70．9６8６0.6７61 0.7７0２0.５762 0．41６20.９937 0.４849 0.０196 ０．8３35 0.49520.53１3 0.２89１0.3２25 0．６83４０.８４１９0.２18７０．39３50.33０9 ０.７689 ０．１8970.3251 0.671８0.7847 ０.５466 ０.８32９０．１０58 ０.67１４0．4243 ０.１67３0.495００.1０5６0．6９51０.４7１4 0.4257 ０.２56４０．109７0．７４１3 ０．２7０3 0.８620 0.14７60．61１0 ０．0６８０0.0358０．64４4 ０.６13５0．063６0．520１0．1971 0.9899 0．0５５0Cｏlumｎs 31 thｒｏugh 400．8５０７0．7３8６0.55２３0．１２３９０．737８0.55９0 ０.1781 0.894９0．6３11 ０.6９25０．５60６0.5８６00.62９９０.4904 0．0６3４０.8541 ０.３5９6 0.0715０.0８9９0.55６70.９２96 0.246７0.０320０.8530 0.860４0.3４79 0.０567 0.２425 ０.080９０.3９65０.696７0.６664 ０．6１4７0.873９0.93４４0.4460 0.5２19 ０.05３8 0.777２0.0６1６０．５８２80.０8３50.３624 0.2703 0.9844 0.0542 ０.３358 0．441７0．９０51 0．78020.８1５4 0．62６00.０４９50．2085 0.８589 0.1771０．１７57０.0１330．53380.3３760.87９0 0.６６09 0．４8９6 0.５650 0．7856 0.6６28 0．２08９０.８９7２0．109２0.６0790.988９0.7298 0.19２50．6403 0．51340.３３0８０．90520．19６7 0.8２5８0.7４13０.０0050.89０80.12310.４17０0.17760.8985 ０.67５4 0.09３４0.3３81 0.１048０．8６5４０.98230.２05５0.2060 0.39860.1182 0.4６８5 0．3０74 0．２９40 0.1２79０.６126 0.76９０0．１４6５0.9479０.１３3９0．9884 0.9１2１0.4５61 0.74６3 0.54９50.99０0０.５81４0.1891 0.0８21 ０．030９０.54000.1０４００.１017 0.0103 0.4８520.5277 0.９２８3 ０.0４２7 0．１０57０．9３９1 0.７０69 ０．74５５0.9954 0.０484 0.89０50.４795 0.5801 0．6352 0.142０0.３０1３0.9９95 ０．7363 0.3321 0.６6７９0.7990０.8013 0.０170 0.2819 0．１665 0.295５0.287８0.5619 0.２973 0．6035 0.7343０.2278 0.1209 ０.５386 0.62１00.3３２9 ０.41４5 0.18４20.0620０.526１０.05１30.49８1 0．86２7 0.6952 ０．5７3７0.4671 0．4648 ０.5972 0.２982 ０.7２97０.07２90.9009０.4843 0.４９91 0.0521 0.648２0.7640 ０.2９99 0.0464 0.7073０．088５０.57４70.８44９0.53５８0．9312 0.02５2 ０.81820.134１0.505４０.78１4 0.7984０.８452 0.20940．44５2 0.7287 0.8４22 0.１０0２0.２12６0．76１4０.288０0.9４30Coｌuｍns 41 ｔhｒough 5０0．６8３7 ０.789４0．1123 ０.６733 0．09８６0.9879 0．5９７5 0．７5９3０.809２0.7５190.1３２1 0.367７0.７8４４0.4２9６0.142００.1704 0.33５3 ０.7４０6 0.7486 0.２2870.7２27 ０．2060 0.2916 0.4517 0．１６83 0.2578 ０.２9９2 0．74370.120２０．０6420．110４0.0８67 0.6０350.6０99 0.1９620.3968 ０.4526 ０.１0590.５２50 0．7６730.11７５０.77１９0.9644 0．0594 0.３17５0.0740 0.42２6 ０.68１６０.３２５8 0.6712０.6407 0.2057 0.４3250．3１５8 0.３1640．６841 0.3５9６0.46330.５４64 0．７15２0.3２88 ０.３8８３0.6948 0.7727 0.2176 0.4024 0.5583 0.21２２0.39８9 0.64210.65380.55１8 0.7５810.６９64 0.2５１00.９8２8 0.74250.0985０.4１51 0.41900.74９1 0.2290 0.43２6 0.１２5３0．8929 0.4022 0.42４3 ０．8２360.18０7 0．39080.５８320.６４１9 0.６5550．１３02 0.703２0.６２０7 0．4294 0.17５0 0.25５4 0.81６1０.7400０.48４５０.１0980．0９24 0.５557 0.1544 0．1２49 0.1636 0.02０5 0.317４0.23４8 0.15180．933８0.０078０．1844 0．3813 0.0244 0．66６００.9237 0.８１45０.7350 0.78１9０．18７5 0．４2３１0.２１200．1611 0.２902 ０.８944 0．６５3７0.７89１0.97060.10060．2662 0.655６0.0７7３０.7581０．31７5 ０.5166 0.9３２６0.８5２3０.８669 ０.29410．７978 0．7229 ０.91３８0.８７11 0.６5370.70２7０．1６３5 0.５056０.08620.2３7４0.48760.5312０.7０6７0.３5080.9569 0.1536 0.９２11 0.63570．３664 0.５309 0.769０0.10880.55７8 ０.68550.9３57 0．95３50.７94７0.９509０．３6９2 0.0915 0.39６0 0.6318０.３13４０.2９４1 0.４５79 ０.540９0.577４0.４44０0.68５0 0．405３0.2729０.126５0.1662 ０.530６０.240５0.6797０.4400 ０.06000.5９７9 ０.１04８0.0３72 0.13４3 0．６225 0.832４０.76390.03660．257６0.86672.参考课本综合例题2.5.４和2．5.5中的方法，模拟产生1０00个随机变量，使其服从参数为2的指数分布,进而计算这1000个随机数的均值和方差。

大连理工大学矩阵与数值分析MATLAB上机实验

二、解线性方程组 1．分别 Jacobi 迭代法和 Gauss-Seidel 迭代法求解线性方程组
3 1 0 0 x1 1 1 3 1 0 x2 0 , 0 1 2 1 x3 0 0 0 1 3 x4 0
Gauss 列主元消去法程序:
clc; clear; format long a=[2,4,3,1;8,2,0,0;5,0,4,0;9,0,0,5]; %系数矩阵 b=[12;6;23;16]; [n,m]=size(a); nb=length(b); det=1; for k=1:n-1 amax=0; for i=k:n if abs(a(i,k))>amax amax=abs(a(i,k)); r=i; end end if amax<1e-10 return; end if r>k for j=k:n z=a(k,j); a(k,j)=a(r,j); a(r,j)=z; end z=b(k);
从小到大求和程序计算结果：
N 100 10000 1000000 从小到大求和程序得到的 SN 0.497512437810945 0.499975001249937 0.499999750000134 真实值�� = �� 2�� + 1 0.497512437810945 0.499975001249937 0.499999750000125 计算值有效位数 15 15 13
8
2
1 dx x
复化梯形公式程序
clc; clear; format long syms t m=int(1/t,2,8); %真实值 a=2; b=8; n=300; h=(b-a)/n; sum=0; f=inline('1/x'); for i=1:n-1 sum=sum+f(a+i.*h); end T=h/2*(f(a)+2*sum+f(b))

大连理工大学矩阵与数值分析上机作业13388

共享知识分享快乐大连理工大学矩阵与数值分析上机作业课程名称：矩阵与数值分析研究生姓名：12 交作业日时间：日20 月年2016卑微如蝼蚁、坚强似大象．共享知识分享快乐第1题1.1程序：Clear ;all n=input('请输入向量的长度n：') for i=1:n;v(i)=1/i;endY1=norm(v,1)Y2=norm(v,2)Y3=norm(v,inf)1.2结果n=10 Y1 =2.9290Y2 =1.2449Y3 =1n=100 Y1 =5.1874Y2 =1.2787Y3 =1n=1000 Y1 =7.4855Y2 =1.2822Y3 =1N=10000 Y1 =9.7876Y2 =1.2825Y3 =11.3 分析一范数逐渐递增，随着n的增加，范数的增加速度减小；二范数随着n的增加，逐渐趋于定值，无群范数都是1.卑微如蝼蚁、坚强似大象．共享知识分享快乐第2题2.1程序;clear all x(1)=-10^-15;dx=10^-18;L=2*10^3; i=1:L fory1(i)=log(1+x(i))/x(i); d=1+x(i); d == 1ify2(i)=1;elsey2(i)=log(d)/(d-1);endx(i+1)=x(i)+dx;end x=x(1:length(x)-1););'r'plot(x,y1,on holdplot(x,y2);卑微如蝼蚁、坚强似大象．共享知识分享快乐2.2 结果2.3 分析红色的曲线代表未考虑题中算法时的情况，如果考虑题中的算法则数值大小始终为1，这主要是由于大数加小数的原因。

第3题3.1 程序;clear all A=[1 -18 144 -672 2016 -4032 5376 -4608 2304 -512];x=1.95:0.005:2.05; i=1:length(x);for y1(i)=f(A,x(i)); y2(i)=(x(i)-2)^9;end figure(3);plot(x,y1);;on hold卑微如蝼蚁、坚强似大象．共享知识分享快乐);'r'plot(x,y2,F.m文件y=f(A,x)function y=A(1); i=2:length(A);for y=x*y+A(i);;end3.2 结果第4题卑微如蝼蚁、坚强似大象．共享知识分享快乐4.1 程序;clear all n=input('请输入向量的长度n：')A=2*eye(n)-tril(ones(n,n),0); i=1:n for A(i,n)=1;end n=length(A);U=A; e=eye(n);for i=1:n-1[max_data,max_index]=max(abs(U(i:n,i))); e0=eye(n);max_index=max_index+i-1; U=e0*U; e1=eye(n); j=i+1:n fore1(j,i)=-U(j,i)/U(i,i);endU=e1*U;中把变换矩阵存到P P{i}=e0;% L{i}=e1; e=e1*e0*e;endk=1:n-2for Ldot{k}=L{k}; i=k+1:n-1forLdot{k}=P{i}*Ldot{k}*P{i};endend Ldot{n-1}=L{n-1};LL=eye(n);PP=eye(n); i=1:n-1for PP=P{i}*PP;LL=Ldot{i}*LL;endb=ones(n,2);解方程 %b=e*b;x=zeros(n,1);x(n)=b(n)/U(n,n); i=n-1:-1:1for卑微如蝼蚁、坚强似大象．共享知识分享快乐x(i)=(b(i)-U(i,:)*x)/U(i,i);end计算逆矩阵%X=U^-1*e^-1*eye(n);AN=X'; result2{n-4,1}=AN;result1{n-4,1}=x;,n)'%d:\n'fprintf(fprintf('%d ',AN);4.2 结果n=51.0625 -0.875 -0.75 -0.5 -0.0625-0.0625 0.0625 -0.75 1.125 -0.5-0.0625 0.125 0.0625 1.25 -0.5-0.0625 0.1250.25 0.06251.50.0625-0.5-0.25-0.0625 -0.125n=101.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 -0.0625 1.125 0.0625 -0.75 -0.5 -0.5 0.0625 1.125 -0.75 -0.0625 -0.0625 0.0625 0.125 1.25 1.25 -0.0625 -0.5 0.0625 0.125 -0.5-0.0625 0.250.250.0625 0.1251.5 1.5 -0.0625 0.1250.06250.0625 -0.0625 -0.125 -0.25 0.0625 -0.5 -0.0625 -0.125 -0.25 -0.5 -0.0625 -0.75 1.0625 -0.5 -0.0625 -0.875 -0.5 -0.75 1.0625 -0.875 -0.0625 -0.5 0.0625 1.125 -0.5 0.0625 1.125 -0.75 -0.0625 -0.75 1.25 0.125 0.0625 -0.0625 -0.0625 -0.5 -0.5 0.0625 0.125 1.250.25-0.0625 -0.0625 1.50.1250.0625 0.0625 0.250.1251.5-0.0625 -0.125 -0.25 0.0625-0.5 0.0625 -0.0625 -0.125 -0.25-0.5同样的方法可以算出n=20,n=30时的结果，这里就不罗列了。

大连理工大学优化方法上机大作业

学院：专业：班级：学号：姓名：上机大作业1：1.最速下降法：function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = steepest(x0,eps) gk = grad(x0);res = norm(gk);k = 0;while res > eps && k<=1000dk = -gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;gk = grad(xk);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=steepest(x0,eps)2.牛顿法：function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad2(x)g = zeros(2,2);g(1,1)=2+400*(3*x(1)^2-x(2));g(1,2)=-400*x(1);g(2,1)=-400*x(1);g(2,2)=200;endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = newton(x0,eps)gk = grad(x0);bk = [grad2(x0)]^(-1);res = norm(gk);k = 0;while res > eps && k<=1000dk=-bk*gk;xk=x0+dk;k = k+1;x0 = xk;gk = grad(xk);bk = [grad2(xk)]^(-1);res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x1=newton(x0,eps)--The 1-th iter, the residual is--The 2-th iter, the residual isx1 =法：function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star = bfgs(x0,eps) g0 = grad(x0);gk=g0;res = norm(gk);Hk=eye(2);k = 0;while res > eps && k<=1000dk = -Hk*gk;ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slopeak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;fa0=xk-x0;x0 = xk;go=gk;gk = grad(xk);y0=gk-g0;Hk=((eye(2)-fa0*(y0)')/((fa0)'*(y0)))*((eye(2)-(y0)*(fa0)')/((fa0)'*(y0)))+(fa0*(fa 0)')/((fa0)'*(y0));res = norm(gk);fprintf('--The %d-th iter, the residual is %f\n',k,res);endx_star = xk;End>> clear>> x0=[0,0]';>> eps=1e-4;>> x=bfgs(x0,eps)4.共轭梯度法：function f = fun(x)f = (1-x(1))^2 + 100*(x(2)-x(1)^2)^2; endfunction g = grad(x)g = zeros(2,1);g(1)=2*(x(1)-1)+400*x(1)*(x(1)^2-x(2)); g(2) = 200*(x(2)-x(1)^2);endfunction x_star =CG(x0,eps) gk = grad(x0);res = norm(gk);k = 0;dk = -gk;while res > eps && k<=1000 ak =1; f0 = fun(x0);f1 = fun(x0+ak*dk);slope = dot(gk,dk);while f1 > f0 + *ak*slope ak = ak/4;xk = x0 + ak*dk;f1 = fun(xk);endk = k+1;x0 = xk;g0=gk;gk = grad(xk);res = norm(gk);p=(gk/g0)^2;dk1=dk;dk=-gk+p*dk1;fprintf('--The %d-th iter, the residual is %f\n',k,res); endx_star = xk;end>> clear>> x0=[0,0]';>> eps=1e-4;>> x=CG(x0,eps)上机大作业2：function f= obj(x)f=4*x(1)-x(2)^2-12;endfunction [h,g] =constrains(x) h=x(1)^2+x(2)^2-25;g=zeros(3,1);g(1)=-10*x(1)+x(1)^2-10*x(2)+x(2)^2+34;g(2)=-x(1);g(3)=-x(2);endfunction f=alobj(x) %拉格朗日增广函数%N_equ等式约束个数?%N_inequ不等式约束个数N_equ=1;N_inequ=3;global r_al pena;%全局变量h_equ=0;h_inequ=0;[h,g]=constrains(x);%等式约束部分?for i=1:N_equh_equ=h_equ+h(i)*r_al(i)+(pena/2)*h(i).^2;end%不等式约束部分for i=1:N_inequh_inequ=h_inequ+pena)*(max(0,(r_al(i)+pena*g(i))).^2-r_al(i).^2); end%拉格朗日增广函数值f=obj(x)+h_equ+h_inequ;function f=compare(x)global r_al pena N_equ N_inequ;N_equ=1;N_inequ=3;h_inequ=zeros(3,1);[h,g]=constrains(x);%等式部分for i=1:1h_equ=abs(h(i));end%不等式部分for i=1:3h_inequ=abs(max(g(i),-r_al(i+1)/pena));endh1 = max(h_inequ);f= max(abs(h_equ),h1); %sqrt(h_equ+h_inequ);function [ x,fmin,k] =almain(x_al)%本程序为拉格朗日乘子算法示例算法%函数输入：% x_al:初始迭代点% r_al：初始拉格朗日乘子N-equ:等式约束个数N_inequ:不等式约束个数?%函数输出% X：最优函数点FVAL:最优函数值%============================程序开始================================ global r_al pena ; %参数（全局变量）pena=10; %惩罚系数r_al=[1,1,1,1];c_scale=2; %乘法系数乘数cta=; %下降标准系数e_al=1e-4; %误差控制范围max_itera=25;out_itera=1; %迭代次数%===========================算法迭代开始============================= while out_itera<max_iterax_al0=x_al;r_al0=r_al;%判断函数?compareFlag=compare(x_al0);%无约束的拟牛顿法BFGS[X,fmin]=fminunc(@alobj,x_al0);x_al=X; %得到新迭代点%判断停止条件?if compare(x_al)<e_aldisp('we get the opt point');breakend%c判断函数下降度?if compare(x_al)<cta*compareFlagpena=1*pena; %可以根据需要修改惩罚系数变量elsepena=min(1000,c_scale*pena); %%乘法系数最大1000disp('pena=2*pena');end%%?更新拉格朗日乘子[h,g]=constrains(x_al);for i=1:1%%等式约束部分r_al(i)= r_al0(i)+pena*h(i);endfor i=1:3%%不等式约束部分r_al(i+1)=max(0,(r_al0(i+1)+pena*g(i)));endout_itera=out_itera+1;end%+++++++++++++++++++++++++++迭代结束+++++++++++++++++++++++++++++++++ disp('the iteration number');k=out_itera;disp('the value of constrains'); compare(x_al)disp('the opt point');x=x_al;fmin=obj(X);>> clear>> x_al=[0,0];>> [x,fmin,k]=almain(x_al)上机大作业3： 1、>> clear alln=3; c=[-3,-1,-3]'; A=[2,1,1;1,2,3;2,2,1;-1,0,0;0,-1,0;0,0,-1];b=[2,5,6,0,0,0]';cvx_beginvariable x(n)minimize( c'*x)subject toA*x<=bcvx_endCalling SDPT3 : 6 variables, 3 equality constraints------------------------------------------------------------num. of constraints = 3dim. of linear var = 6*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime -------------------------------------------------------------------0|||+01|+00|+02|+01 +00| 0:0:00| chol 1 11|||||+01|+00 +01| 0:0:01| chol 1 12|||||+00|+00 +01| 0:0:01| chol 1 13|||||+00|+00 +00| 0:0:01| chol 1 14||||||+00 +00| 0:0:01| chol 1 15||||||+00 +00| 0:0:01| chol 1 16||||||+00 +00| 0:0:01| chol 1 17||||||+00 +00| 0:0:01| chol 1 18||||||+00 +00| 0:0:01|stop: max(relative gap, infeasibilities) <------------------------------------------------------------------- number of iterations = 8primal objective value = +00dual objective value = +00gap := trace(XZ) =relative gap =actual relative gap =rel. primal infeas (scaled problem) =rel. dual " " " =rel. primal infeas (unscaled problem) = +00rel. dual " " " = +00norm(X), norm(y), norm(Z) = +00, +00, +00norm(A), norm(b), norm(C) = +00, +00, +00Total CPU time (secs) =CPU time per iteration =termination code = 0DIMACS: +00 +00-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval):2、>> clear alln=2; c=[-2,-4]'; G=[,0;0,1]; A=[1,1;-1,0;0,-1]; b=[1,0,0]'; cvx_beginvariable x(n)minimize( x'*G*x+c'*x)subject toA*x<=bcvx_endCalling SDPT3 : 7 variables, 3 equality constraintsFor improved efficiency, SDPT3 is solving the dual problem.------------------------------------------------------------num. of constraints = 3dim. of socp var = 4, num. of socp blk = 1dim. of linear var = 3*******************************************************************SDPT3: Infeasible path-following algorithms*******************************************************************version predcorr gam expon scale_dataNT 1 1 0it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime -------------------------------------------------------------------0||||+00|+02| +01 +00| 0:0:00| chol 1 11|||||+01| +00 | 0:0:00| chol 1 12|||||+00| +00 | 0:0:00| chol 1 13|||||| | 0:0:00| chol 1 14|||||| | 0:0:00| chol 1 15|||||| | 0:0:00| chol 1 16|||||| | 0:0:00| chol 1 17|||||| | 0:0:00| chol 1 18|||||| | 0:0:00| chol 1 19|||||| | 0:0:00| chol 1 110|||||| | 0:0:00| chol 2 211|||||| | 0:0:00| chol 2 212|||||| | 0:0:00| chol 2 213|||||| | 0:0:00| chol 2 214|||||| | 0:0:00|stop: max(relative gap, infeasibilities) <------------------------------------------------------------------- number of iterations = 14primal objective value =dual objective value =gap := trace(XZ) =relative gap =actual relative gap =rel. primal infeas (scaled problem) =rel. dual " " " =rel. primal infeas (unscaled problem) = +00rel. dual " " " = +00norm(X), norm(y), norm(Z) = +00, +00, +00norm(A), norm(b), norm(C) = +00, +00, +00Total CPU time (secs) =CPU time per iteration =termination code = 0DIMACS: +00 +00-------------------------------------------------------------------------------------------------------------------------------Status: SolvedOptimal value (cvx_optval): -3。