流体力学习题答案.

合集下载

《流体力学》所有做过的习题答案

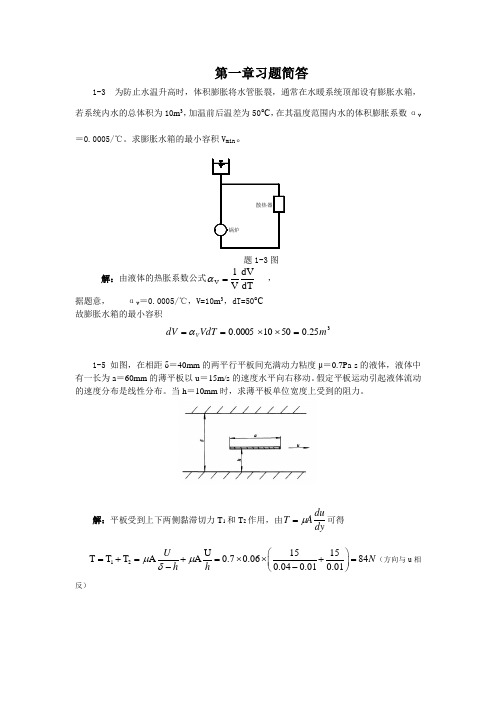
第一章习题简答1-3 为防止水温升高时，体积膨胀将水管胀裂，通常在水暖系统顶部设有膨胀水箱，若系统内水的总体积为10m 3，加温前后温差为50°С，在其温度范围内水的体积膨胀系数αv＝0.0005/℃。

求膨胀水箱的最小容积V min 。

题1-3图解：由液体的热胀系数公式dTdVV 1V =α ，据题意， αv ＝0.0005/℃，V=10m 3，dT=50°С 故膨胀水箱的最小容积325.050100005.0m VdT dV V =⨯⨯==α1-5 如图，在相距δ＝40mm 的两平行平板间充满动力粘度μ＝0.7Pa·s 的液体，液体中有一长为a ＝60mm 的薄平板以u ＝15m/s 的速度水平向右移动。

假定平板运动引起液体流动的速度分布是线性分布。

当h ＝10mm 时，求薄平板单位宽度上受到的阻力。

解：平板受到上下两侧黏滞切力T 1和T 2作用，由dyduAT μ=可得 12U 1515T T T AA 0.70.06840.040.010.01U N h h μμδ⎛⎫=+=+=⨯⨯+= ⎪--⎝⎭（方向与u 相反）1-7 温度为20°С的空气，在直径为2.5cm 的管中流动，距管壁上1mm 处的空气速度为3cm/s 。

求作用于单位长度管壁上的黏滞切力为多少？解：温度为20°С的空气的黏度为18.3×10-6 Pa·s 如图建立坐标系，且设u=ay 2+c 由题意可得方程组⎪⎩⎪⎨⎧+-=+=ca ca 22)001.00125.0(03.00125.00 解得a = -1250，c =0.195 则 u=-1250y 2+0.195则y dy y d dy du 2500)195.01250(2-=+-= Pa dyduAT 561048.4)0125.02500(1025.0103.18--⨯-=⨯-⨯⨯⨯⨯⨯==∴πμ （与课本后的答案不一样。

流体力学习题及答案

第一章绪论1-1 连续介质假设的条件是什么？答：所研究问题中物体的特征尺度L ，远远大于流体分子的平均自由行程l ，即l/L<<1。

1-2 设稀薄气体的分子自由行程是几米的数量级，问下列二种情况连续介质假设是否成立？（1）人造卫星在飞离大气层进入稀薄气体层时；（2）假象地球在这样的稀薄气体中运动时。

答：（1）不成立。

（2）成立。

1-3 粘性流体在静止时有没有切应力？理想流体在运动时有没有切应力？静止流体没有粘性吗？答：（1）由于0=dy dv ，因此0==dydvμτ，没有剪切应力。

（2）对于理想流体，由于粘性系数0=μ，因此0==dydvμτ，没有剪切应力。

（3）粘性是流体的根本属性。

只是在静止流体中，由于流场的速度为0，流体的粘性没有表现出来。

1-4 在水池和风洞中进行船模试验时，需要测定由下式定义的无因次数（雷诺数）νUL=Re ，其中U 为试验速度，L 为船模长度，ν为流体的运动粘性系数。

如果s m U /20=，m L 4=，温度由C ︒10增到C ︒40时，分别计算在水池和风洞中试验时的Re 数。

（C ︒10时水和空气的运动粘性系数为410013.0-⨯和410014.0-⨯，C ︒40时水和空气的运动粘性系数为4100075.0-⨯和410179.0-⨯）。

答：C ︒10时水的Re 为：()()72410154.6/10013.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。

C ︒10时空气的Re 为：()()72410714.5/10014.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。

C ︒40时水的Re 为：()()82410067.1/100075.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。

C ︒40时空气的Re 为：()()62410469.4/10179.04)/(20Re ⨯=⨯⨯==-sm m s m ULν。

《流体力学》试题及答案

《流体力学》试题及答案一、选择题（每题5分，共25分）1. 下列哪个选项不属于流体力学的三大基本方程？A. 连续性方程B. 动量方程C. 能量方程D. 牛顿第二定律答案：D2. 在不可压缩流体中，流速和压力之间的关系可以用下列哪个方程表示？A. 伯努利方程B. 欧拉方程C. 纳维-斯托克斯方程D. 帕斯卡方程答案：A3. 下列哪个现象表明流体具有粘性？A. 流体流动时产生涡旋B. 流体流动时产生湍流C. 流体流动时产生层流D. 流体流动时产生摩擦力答案：D4. 在下列哪种情况下，流体的动能和势能相等？A. 静止流体B. 均匀流动的流体C. 垂直下落的流体D. 水平流动的流体答案：C5. 下列哪个因素不会影响流体的临界雷诺数？A. 流体的粘度B. 流体的密度C. 流体的流速D. 流体的温度答案：D二、填空题（每题5分，共25分）6. 流体力学是研究______在力的作用下运动规律的科学。

答案：流体7. 不可压缩流体的连续性方程可以表示为______。

答案：ρV = 常数8. 在恒定流场中，流体质点的速度矢量对时间的导数称为______。

答案：加速度矢量9. 伯努利方程是______方程在不可压缩流体中的应用。

答案：能量10. 流体的湍流流动特点为______、______和______。

答案：随机性、三维性、非线性三、计算题（每题25分，共50分）11. 一个直径为10cm的管道，流体的流速为2m/s，流体的密度为800kg/m³，求管道中流体的流量。

解：流量Q = ρvA其中，ρ为流体密度，v为流速，A为管道截面积。

A = π(d/2)² = π(0.05)² = 0.00785m²Q = 800kg/m³ 2m/s 0.00785m² = 12.44 kg/s答案：管道中流体的流量为12.44 kg/s。

12. 一个直径为20cm的圆柱形储罐，储罐内充满水，水面高度为1m。

《流体力学》课后习题答案.pdf

得：T1 = t1 + 273 = 50 + 273 = 323K ，T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
，有：
p1
=
mRT1 V1
，
p2
=
mRT2 V2
得： V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l，管段表面积： A = dl
单位长度管壁上粘滞力： = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解： A = 0.8 0.2 = 0.16m2 ，u=1m/s， = 10mm ， = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m，方向水平向左
下表面单位宽度受到的内摩擦力：
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m，方向水平向左
平板单位宽度上受到的阻力：
= 1 + 2 = 21+ 63 = 84N ，方向水平向左。
h1 = 5.6m
2.4 解：如图 1-2 是等压面，3-4 是等压面，5-6 段充的是空气，因此 p6 = p5 ，6-7 是等压面，

流体力学习题库(含答案)

流体力学习题库（含答案）一、单选题（共70题，每题1分，共70分）1、低温泵的气相平衡线的作用是防止泵的( )。

A、憋压B、超温C、汽蚀D、汽缚正确答案：D2、若被输送液体的黏度增大时，离心泵的效率( )。

A、减小B、增大C、不变D、不定正确答案：A3、当地大气压为745mmHg测得一容器内的绝对压强为350mmHg，则真空度为( )A、395mmHgB、350mmHgC、410mmHg正确答案：A4、单位质量的流体所具有的( )称为流体的比容。

A、位能B、动能C、体积D、黏度正确答案：C5、喷射泵是利用流体流动时的( )的原理来工作的。

A、动能转化为静压能B、热能转化为静压能C、静压能转化为动能正确答案：C6、机械密封与填料密封相比( )的功率消耗较大。

A、填料密封B、机械密封C、差不多正确答案：A7、下列不属于离心泵的主要构件是 ( )A、泵轴B、泵壳C、叶轮D、轴封装置正确答案：A8、一台离心泵开动不久，泵入口处的真空度正常，泵出口处的压力表也逐渐降低为零，此时离心泵完全打不出水。

发生故障的原因是( )A、吸入管路堵塞B、忘了灌水C、吸入管路漏气D、压出管路堵塞正确答案：A9、某液体在内径为D0的水平管路中稳定流动，其平均流速为u0，当它以相同的体积流量通过等长的内径为D2（D2=D0/2）的管子时，若流体为层流，则压降ΔP为原来的( )倍。

A、32B、8C、4D、16正确答案：A10、造成离心泵气缚原因是( )A、泵不能抽水B、安装高度太高C、入口管路阻力太大D、泵内流体平均密度太小正确答案：D11、离心泵的轴功率N和流量Q的关系为( )A、Q增大，N增大B、Q增大，N先增大后减小C、Q增大，N减小D、Q增大，N先减小后增大正确答案：A12、在静止的连通的同一种连续流体内，任意一点的压强增大时，其他各点的压强则( )A、减小B、不变C、相应增大D、不一定正确答案：C13、往复泵的流量调节采用( )A、出口支路B、出口阀开度C、入口阀开度D、入口支路正确答案：A14、为了防止( )现象发生，启动离心泵时必须先关闭泵的出口阀A、汽蚀B、电机烧坏C、气缚D、叶轮受损正确答案：B15、某泵在运行的时候发现有汽蚀现象应( )A、停泵向泵内灌液B、降低泵的安装高度C、检查进口管路是否漏液D、检查出口管阻力是否过大正确答案：C16、选离心泵是根据泵的( )A、扬程和轴功率选择B、转速和轴功率选择C、轴功率和流量选择D、扬程和流量选择正确答案：D17、流体运动时，能量损失的根本原因是由于流体存在着 ( )。

流体力学习题答案

ReL
VL
11 10106
1106
0.37L
Re
1/ L
5
0.37 (106 )1/5
0.0233m
23.3mm
式中系数A取P101表中的3300的数值
CDf
（100.06）714/ 5
3300 106
0.00137
FDf
CDf
1 2
V2
A
0.5 0.00137 1000 12 11
Πc
v c
Ma
ΠA
A l2
Π vl
f(ΠF ,Ma, ΠA ,Re) 0
FL CL( Ma,Re, ΠA ) v2l 2 FD CD( Ma,Re, ΠA ) v2l 2
用面积来替换一下，不会影响分析过程
但两式使用的面积有不同，FL中取的面积是与来流平行的面积（水平投影面积）；FD中取的是垂直于来流的迎风面积（迎风的投影面积）。
l' Cll 0.610 6.（0 m）
6-2：
ReL
V L
0.2 2 1.145106
3.4934105
5105
根据层流边界层微分方程的精确解P96
5.0 x U
距平板前缘x=2m处边界层厚度：
5.0 1.145106 2 316.3.98103 m
0.2
ReL
V L
0.2 5 1.145106
1-6：在圆筒的侧面和底面都存在摩擦
• 侧面摩擦应力 • 侧面摩擦力矩
1
du dy
r
T侧
1dh r
d 3h 4
• 底面摩擦应力
2
du dy
r
• 半径r处的微元摩擦力矩

流体力学考试题及答案

流体力学考试题及答案一、选择题（每题2分，共20分）1. 流体力学中，流体的基本假设是什么？A. 流体是不可压缩的B. 流体是完全弹性体C. 流体是完全塑性体D. 流体是连续介质答案：D2. 流体静力学中，压力的分布规律是什么？A. 与深度成正比B. 与深度成反比C. 与深度无关D. 与深度的平方成正比答案：A3. 流体的粘性是由什么决定的？A. 温度B. 压力C. 密度D. 以上都是答案：A4. 伯努利方程描述了什么？A. 流体的静压和动压关系B. 流体的压缩性C. 流体的粘性D. 流体的热力学性质答案：A5. 流体的雷诺数是用来描述什么的？A. 流体的密度B. 流体的粘性C. 流体的惯性力与粘性力的比值D. 流体的压缩性答案：C6. 什么是流体的不可压缩性条件？A. 密度不变B. 温度不变C. 压力不变D. 速度不变答案：A7. 流体的连续性方程描述了什么？A. 流体的动量守恒B. 流体的动能守恒C. 流体的质量守恒D. 流体的热能守恒答案：C8. 流体的湍流与层流的区别是什么？A. 湍流有粘性，层流没有B. 湍流是有序的流动，层流是无序的C. 湍流是无序的流动，层流是有序的D. 湍流和层流都是有序的流动答案：C9. 流体的边界层厚度与什么有关？A. 流体的密度B. 流体的速度C. 流体的粘性D. 流体的压缩性答案：C10. 什么是流体的临界雷诺数？A. 流体开始流动的雷诺数B. 流体从层流转变为湍流的雷诺数C. 流体达到最大速度的雷诺数D. 流体达到最大压力的雷诺数答案：B二、简答题（每题10分，共30分）1. 简述流体力学中的纳维-斯托克斯方程及其物理意义。

答案：纳维-斯托克斯方程是描述流体运动的基本方程，它将流体的动量守恒定律与流体的粘性联系起来。

方程表明，流体的加速度不仅与压力梯度有关，还与粘性力有关。

物理意义上，它描述了流体内部的动量传递过程。

2. 描述流体的粘性对流动的影响。

答案：流体的粘性对流动有显著影响。

流体力学习题及答案

第1章绪论【1.1】按连续介质的概念，流体质点是指：（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

解：流体质点是指体积小到可以看作一个几何点，但它又含有大量的分子，且具有诸如速度、密度及压强等物理量的流体微团。

（d ）【1.2】与牛顿内摩擦定律直接相关的因素是：（a ）切应力和压强；（b ）切应力和剪切变形速度；（c ）切应力和剪切变形；（d ）切应力和流速。

解：牛顿内摩擦定律是d d v y τμ=，而且速度梯度d d v y 是流体微团的剪切变形速度d d t γ，故d d t γτμ=。

（b ）【1.3】流体运动黏度υ的国际单位是：（a ）m2/s ；（b ）N/m2；（c ）kg/m ；（d ）N 〃s/m2。

解：流体的运动黏度υ的国际单位是/s m 2。

（a ）【1.4】理想流体的特征是：（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RTp =ρ。

解：不考虑黏性的流体称为理想流体。

（c ）【1.5】当水的压强增加一个大气压时，水的密度增大约为：（a ）1/20 000；（b ）1/1 000；（c ）1/4 000；（d ）1/2 000。

解：当水的压强增加一个大气压时，其密度增大约95d 1d 0.51011020 000k p ρρ-==⨯⨯⨯=。

（a ）【1.6】从力学的角度分析，一般流体和固体的区别在于流体：（a ）能承受拉力，平衡时不能承受切应力；（b ）不能承受拉力，平衡时能承受切应力；（c ）不能承受拉力，平衡时不能承受切应力；（d ）能承受拉力，平衡时也能承受切应力。

解：流体的特性是既不能承受拉力，同时具有很大的流动性，即平衡时不能承受切应力。

（c ）【1.7】下列流体哪个属牛顿流体：（a ）汽油；（b ）纸浆；（c ）血液；（d ）沥青。

解：满足牛顿内摩擦定律的流体称为牛顿流体。

流体力学习题集答案

流体力学习题集答案《流体力学》习题与答案周立强中南大学机电工程学院液压研究所第1章流体力学的基本概念1-1. 是非题(正确的打“√”，错误的打“?”)1. 理想流体就是不考虑粘滞性的、实际不存在的，理想化的流体。

（√）2. 在连续介质假设的条件下，液体中各种物理量的变化是连续的。

（√ ）3. 粘滞性是引起流体运动能量损失的根本原因。

（√ ）4. 牛顿内摩擦定律适用于所有的流体。

（ ? ）5. 牛顿内摩擦定律只适用于管道中的层流。

（ ? ）6. 有旋运动就是流体作圆周运动。

（ ? ）7. 温度升高时，空气的粘度减小。

（ ? ）8. 流体力学中用欧拉法研究每个质点的轨迹。

（ ? ） 9. 平衡流体不能抵抗剪切力。

（√ ） 10. 静止流体不显示粘性。

（√ ）11. 速度梯度实质上是流体的粘性。

（√ ）12. 流体运动的速度梯度是剪切变形角速度。

（√ ） 13. 恒定流一定是均匀流，层流也一定是均匀流。

（ ? ）14. 牛顿内摩擦定律中，粘度系数m 和v 均与压力和温度有关。

（ ? ） 15. 迹线与流线分别是Lagrange 和Euler 几何描述；它们是对同一事物的不同说法；因此迹线就是流线，流线就是迹线。

（ ? ）16. 如果流体的线变形速度θ=θx +θy +θz =0,则流体为不可压缩流体。

（√ ） 17. 如果流体的角变形速度ω=ωx +ωy +ωz =0,则流体为无旋流动。

（√ ） 18. 流体的表面力不仅与作用的表面积的外力有关，而且还与作用面积的大小、体积和密度有关。

（ ? ）19. 对于平衡流体，其表面力就是压强。

（√ ）20. 边界层就是流体的自由表明和容器壁的接触面。

（ ? ）1-2已知作用在单位质量物体上的体积力分布为：x y z f axf b f cz=?=??=?，物体的密度2lx ry nz ρπ=++，坐标量度单位为m ；其中，0a =，0.1b N kg =，()0.5c N kg m =?；52.0l kg m =，0r =，41.0n kg m =。

流体力学习题答案.

【1-1】500cm 3的某种液体，在天平上称得其质量为0.453kg ，试求其密度和相对密度。

【解】液体的密度3340.4530.90610 kg/m 510m V ρ-===⨯⨯相对密度 330.906100.9061.010w ρδρ⨯===⨯ 【1-2】体积为5m 3的水，在温度不变的条件下，当压强从98000Pa 增加到4.9×105Pa 时，体积减少1L 。

求水的压缩系数和弹性系数。

【解】由压缩系数公式10-1510.001 5.110 Pa 5(4.91098000)p dV V dP β-=-==⨯⨯⨯- 910111.9610 Pa 5.110pE β-===⨯⨯ 【1-3】温度为20℃，流量为60m 3/h 的水流入加热器，如果水的体积膨胀系数βt =0.00055K -1，问加热到80℃后从加热器中流出时的体积流量变为多少？【解】根据膨胀系数1t dVV dtβ=则2113600.00055(8020)6061.98 m /ht Q Q dt Q β=+=⨯⨯-+= 【1-4】用200升汽油桶装相对密度0.70的汽油。

罐装时液面上压强为98000Pa 。

封闭后由于温度变化升高了20℃，此时汽油的蒸汽压力为17640Pa 。

若汽油的膨胀系数为0.0006K -1，弹性系数为13.72×106Pa ，（1）试计算由于压力温度变化所增加的体积，（2）问灌装时汽油的体积最多不应超过桶体积的百分之多少？【解】（1）由1β=-=P p dV Vdp E可得，由于压力改变而减少的体积为6200176400.257L 13.7210⨯∆=-===⨯P p VdP V dV E 由于温度变化而增加的体积，可由1β=tt dV V dT得 0.000620020 2.40L β∆===⨯⨯=t t t V dV VdT（2）因为∆∆t p V V ?，相比之下可以忽略由压力变化引起的体积改变，则由 200L β+=t V V dT 得 1198.8%200110.000620β===++⨯t V dT 【1-5】图中表示浮在油面上的平板，其水平运动速度为u =1m/s ，δ=10mm ，油品的粘度μ=0.9807Pa ·s ，求作用在平板单位面积上的阻力。

流体力学考试题及参考答案

流体力学考试题及参考答案一、单选题（共48题，每题1分，共48分）1.下列流体的作用力不是质量力的是( )。

A、粘性内摩擦力B、电磁力C、惯性力D、重力正确答案：A2.（）管路各段阻力损失相同。

A、分支管系B、并联管系C、串联管系D、短管管系正确答案：B3.沿程水头损失随水流的流程增长而（）。

A、不变B、增大C、减少D、不确定正确答案：B4.伯努利方程中Z+P/ρg表示（）A、单位体积流体具有的机械能B、单位质量流体具有的机械能C、单位重量流体具有的测压管能头D、通过过流断面的流体所具有的总机械能正确答案：C5.下列属于质量力的是（）。

A、剪切力B、压力C、重力D、表面张力正确答案：C6.下列哪些一般当做不可压缩流体（）A、水银B、氮气C、氧气D、空气正确答案：A7.流体的切应力（）。

A、仅仅取决于分子的动量交换B、当流体处于静止状态时，由于内聚力，可以产生C、仅仅取决于内聚力D、当流体处于静止状态时不会产生正确答案：D8.当容器内工质压力大于大气压力时，工质处于（）状态。

A、负压B、临界C、标准D、正压正确答案：D9.某变径管的雷诺数之比Re1：Re2=1:4，则其管径之比d1：d2为（）。

A、02:01B、04:01C、01:04D、01:02正确答案：C10.液体的流动状态用（）来判别。

A、达西公式B、声速C、牛顿内摩擦定律D、雷诺数正确答案：D11.汽轮机轴封压力为30千帕，其绝对压力是（）。

A、71千帕B、171千帕C、30千帕D、130千帕正确答案：D12.动量方程中，ΣF表示作用在控制体内流体上的力是（）A、总表面力B、合外力C、总压力D、总质量力正确答案：B13.在圆管流中，紊流的断面流速分布为（）。

A、均匀规律B、直线变化规律C、抛物线规律D、对数曲线规律正确答案：D14.凝结水泵布置在-1米层，凝汽器压力为-90千帕，其入口绝对压力是（）。

A、90千帕B、10千帕C、1千帕D、21千帕正确答案：D15.变直径管流，细管段直径d1，粗管段直径d2=2d1，两断面雷诺数的关系是（）。

流体力学答案

流体力学习题和解答1. 15℃的空气在直径200mm 的圆管中流动，假定距管壁1mm 处的速度为0.3m/s，试求每米管长上的摩擦阻力。

2. 如图所示，已知动力润滑轴承内轴的直径D＝0.2m，轴承宽度b=0.3m，间隙δ＝0.8mm,间隙内润滑油的动力粘度s Pa 245.0⋅＝μ,消耗的功率P=50.7W,试求轴的转速n 为多少？ [2830 rpm]题2图题5图3. 直径为0.46m 的水平圆盘，在较大的平板上绕其中心以90rpm 的转速旋转。

已知两壁面间的间隙为0.23mm，间隙内油的动力粘度为0.4Pa·s，如果忽略油的离心惯性的影响，试求转动圆盘所需的力矩？4. 两平行平板之间的间隙为2mm，间隙内充满密度为885kg/m 3、运动粘度为0.00159 m 2/s的油，试求当两板相对速度为4m/s 时作用在平板上的摩擦应为多少？5. 如图所示，活塞直径d=152.4mm,缸径D=152.6mm，活塞长L=30.48cm,润滑油的运动粘度41091440-⨯ν.＝m 2/s,密度ρ=920kg/m3。

试求活塞以v＝6m/s 的速度运动时，克服摩擦阻力所消耗的功率。

6. 重500N 的飞轮的回转半径为30cm，转速为600rpm，由于轴承中润滑油的粘性阻滞，飞轮以0.02rad/s2的角减速度放慢，已知轴的直径为2cm，轴套的长度为5cm，它们之间的间隙为0.05mm，求润滑油的动力粘度。

7. 内径8mm 的开口玻璃管，插入20℃的水中，已知水与玻璃的接触角θ＝10o，试求水在玻璃管中上升的高度。

8. 内径8mm 的开口玻璃管，插入20℃的水银中，已知水银与玻璃的接触角约为1400，试求水银液面在管中下降的高度。

[1.36mm]1. 如图所示，用U 形管测压计测量管道A 、B 中的压强差，若A 管中的压强为510744.2⨯Pa ，B 管中的压强为510372.1⨯ Pa ，试确定U 形管中两液面的高度差h 为多少。

流体力学课后习题答案

流体力学-课后习题答案第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。

1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。

1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。

1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。

1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。

1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。

1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。

1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。

1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？解： 10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2 kg ，重量是19.614N 。

1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？解： 44109.807899.3580.5m G g VV ρ====（kg/m 3）答：该油料的密度是899.358 kg/m 3。

1.11 某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。

流体力学课后习题答案.doc

流体力学课后习题答案第一章流体及其主要物理性质1-1. 轻柴油在温度15ºC时相对密度为0.83，求它的密度和重度。

解:4ºC时所以，1-2. 0.83 水 0.83 1000 830kg/m3 0.83 水 0.83 9800 8134N/m3 甘油在温度0ºC时密度为1.26g/cm3，求以国际单位表示的密度和重度。

1.26g/cm3 126kg0/m3 g 126 09.8 1234N8/m31-3. 水的体积弹性系数为1.96×109N/m2，问压强改变多少时，它的体积相对压缩1,,p 1-4. V p V E 0.01E 1.96 107Pa 19.6MPaV容积4m3的水，温度不变，当压强增加105N/m2时容积减少1000cm3，求该水的体积压缩系数βp和体积弹性系数E。

,1000 10,6V,9,1 , 2.5 10Pa 解: p , 5 p10E1-5. 1 p 18 4 10Pa ,92.5 10用200L汽油桶装相对密度为0.70的汽油，罐装时液面上压强为1个大气压，封闭后由于温度变化升高了20ºC，此时汽油的蒸气压为0.18大气压。

若汽油的膨胀系数为0.0006ºC,1，弹性系数为14000kg/cm2。

试计算由于压力及温度变化所增减的体积,问灌桶时每桶最多不超过多少公斤为宜,解:E,E’?g,14000×9.8×10PaΔp,0.18atdV V VdT,dp T pV0 V0 V V TV0 p , , pV0 T T p p4 T所以，dV V VdT,dp TV0dT, pV0dp T p1从初始状态积分到最终状态得:即VV0dV TV0dT, T0Tpp0 pV0dpV,V0 T(T,T0)V0,1(p,p0)V0E0.18 9.8 1040.0006 20 200, 20014000 9.8 1042.4L,2.57 10,3L 2.4L200,2.4 138.32kg 1000M ,V, V, 0.7 1000另解:设灌桶时每桶最多不超过V升，则V,dVt,dVp 200dVt t V dt 0.00061 20VdVp , p V dp ,1 0.18V(1大气压,1Kg/cm2) 14000V,197.6升dVt,2.41升dV p,2.52×10-3升G,0.1976×700,138Kg,1352.4N1-6. 石油相对密度0.9，粘度28cP，求运动粘度为多少m2/s?28 10,33.1 10,5m2/s, 0.31St 31cS,t 0.9 10001-7. 相对密度0.89的石油，温度20ºC时的运动粘度为40cSt，求动力粘度为多少,解:d -42 0.89 ν,40cSt,0.4St,0.4×10m/s水μ,νρ,0.4×10-4×890,3.56×10-2 Pa?s1-8. 图示一平板在油面上作水平运动，已知运动速度u=1m/s，板与固定边界的距离δ=1，油的动力粘度μ,1.147Pa?s，由平板所带动的油层的运动速度呈直线分布，求作用在平板单位面积上的粘性阻力为多少,2解:1-9. du1 1.147 1.147 103N/m2 ,3dy1 10如图所示活塞油缸，其直径D,12cm，活塞直径d,11.96cm，活塞长度L,14cm，油的μ,0.65P，当活塞移动速度为0.5m/s时，试求拉回活塞所需的力F=,解:A,πdL , μ,0.65P,0.065 Pa?s , Δu,0.5m/s , Δy=(D-d)/2 F Adu0.5 0.065 3.14 11.96 10,2 14 10,2 8.55Ndy12,11.96 10,223第二章流体静力学2-1. 如图所示的U形管中装有水银与水，试求:(1)A、C两点的绝对压力及表压各为多少,(2)A、B两点的高度差为多少,解:? pA表,γh水,0.3mH2O,0.03at,0.3×9800Pa,2940PapA绝,pa+ pA表,(10+0.3)mH2O,1.03at,10.3×9800Pa,100940PapC表,γhghhg+ pA表,0.1×13.6mH2O+0.3mH2O,1.66mH2O,0.166at,1.66×9800Pa,16268PapC绝,pa+ pC表,(10+1.66)mH2O,11.66mH2O ,1.166at,11.66×9800Pa,114268Pa ? 30cmH2O,13.6h cmH2O h, 30/13.6cm=2.2cm题2-2 题2-32-2. 水银压力计装置如图。

《流体力学》课后习题详细解答

克服轴承摩擦所消耗的功率为
1-8解:
或，由积分得
1-9解:法一：5atm
10atm
=0.537 x 10-9x (10-5) x98.07 x 103= 0.026%
法二： ,积分得
1-10解：水在玻璃管中上升高度
h =
水银在玻璃管中下降的高度
H= mm
第二章流体静力学
2-1解：已知液体所受质量力的x向分量为–a ,z向分量为-g。液体平衡方程为
重心C位于浮心之上，偏心距
沉箱绕长度方向的对称轴y轴倾斜时稳定性最差。浮面面积A=15m2。浮面关于y
轴的惯性矩和体积排量为
定倾半径
可见， >e,定倾中心高于重心，沉箱是稳定的。
第三章流体运动学
3-1解：质点的运动速度
质点的轨迹方程
3-Байду номын сангаас解：
由和 ,得
故
3-3解：当t=1s时，点A（1,2）处的流速
线速度u = 0r,速度环量
(2)半径r+dr的圆周封闭流线的速度环量为
得
忽略高阶项2 0dr2，得d
（3）设涡量为，它在半径r和r+dr两条圆周封闭流线之间的圆环域上的积分为d 。因为在圆环域上可看作均匀分布，得
将圆环域的面积dA=2 rdr代入该式，得
可解出 =2 + dr/r。忽略无穷小量 dr/r，最后的涡量
沉箱绕长度方向的对称轴y倾斜时稳定性最差。浮面面积A=15m2.浮面关于y轴的惯性矩和体积排量为
定倾半径
可见，，定倾中心低于重心，沉箱是不稳定的。
(2)沉箱的混凝土体积
沉箱的重量
沉箱水平截面面积
设吃水深度为h,取水的密度 =1000kg/m3.浮力F等于重量G。有

流体力学习题及答案

2－15试比较同一水平面上的1、2、3、4、5各点压力的大小，并说明其理由。
2－16多管水银测压计用来测水箱中的表面压力。图中高程的单位为m，当地大气压力为105Pa，试求水面的绝对压力p0。
题2－16图题2－17图
2－17倾斜式微压计中工作液体为酒精(ρ＝800kg/m3)，已测得读数＝50cm，倾角α＝30°，求液面气体压力p1。
1－6海水在海面附近的密度为1025kg/m3，在海面下8km处的压力为81.7MPa，设海水的平均弹性模量为2340MPa，试求该深度处海水的密度。
1－7盛满石油的油槽内部绝对压力为5×105Pa，若从槽中排出石油40kg，槽内压力就降低至l05Pa。已知石油的比重为0.9，体积弹性系数为1．32×109N/m2，求油槽的体积。
2－2容器中空气的绝对压力为pB＝93.2kPa，当地大气压力为pa=98.1kPa试求玻璃管中水银柱上升高度hv。
2－3封闭容器中水面的绝对压力为p1＝105kPa，当地大气压力为pa=98.1kPa，A点在水面下6m，试求：(1)A点的相对压力；(2)测压管中水面与容器中水面的高差。
题2－2图题2－3图
1－16空气中水滴直径为0.3mm时，其内部压力比外部大多少？
1－17在实验室中如果用内径0.6cm和1.2cm的玻璃管作测压管，管中水位由于毛细管现象而引起的上升高度各为多少？
1－18两块竖直的平行玻璃平板相距1mm，求其间水的毛细升高值。
《流体力学》习题（二）
2－1质量为1000kg的油液(S＝0.9)在有势质量力 (N)的作用下处于平衡状态，试求油液内的压力分布规律。
(3)τ＝1秒时的流线方程？
3－4已知速度场为。求τ＝1时，过(0，2)点的流线方程。

流体力学习题答案

6.图示为水泵管路系统，断面2－3分别为水泵进出口断面，水泵扬程的计算公式为：C
7.已知等直径的虹吸管道下游为淹没出流，如图所示，断面的压强水头的绝对值为，（即真空度）则的计算公式为（D）
• 8.设有一恒定分流，如图所示，，根据总流伯努利方程，可列（B ） 9.总流能量方程用于压缩性可忽略的气体时，下述论述中正确者为（B ） • A、及分别为第一断面及第二断面的相对压强； • B、及分别为第一及第二断面的绝对压强； • C、、用相应断面的相对压强或绝对压强，不影响计算结果； • D、上述方程只适用于液体，不适用于气体。 • 10.不可压缩气体总流能量方程中的分别代表（C ） • A、1和2断面上的绝对压强； • B、1断面上的绝对压强及2断面上的相对压强； • C、1和2断面上的相对压强； • D、1断面上的相对压强及2断面上的绝对压强。 • 11.当空气密度大于气体的密度，且气体由位于低处的1断面流向2断面时，气体总流能量方程中的代表（ C） • A、单位重量气体在流动过程中损失的位能； • B、单位重量气体在流动过程中增加的位能； • C、单位体积气体在流动过程中损失的位能； • D、单位体积气体在流动过程中增加的位能。 • 12.不可压缩气体流动时，下述论述中正确的为（D ） • A、总压线、势压线及位压线总是沿程下降的； • B、总压线、势压线及位压线均可能沿程有升有降； • C、总压线及位压线总是沿程下降的，势压线沿程可能有升有降； • D、总压线沿程总是下降的，势压线与位压线沿程可能有升有降。 • 13射流从管道出口垂直下线流入放在磅秤上的一水箱，经水箱侧壁孔口出流而保持水箱水位恒定，水重和箱重共为G，若管道出口流量为Q，出口流速为，水股人射流速为，如图示，则磅秤上的重量读数为（） • A、G B、 C、 D、

(完整版)流体力学练习题及答案

流体力学练习题及答案一、单项选择题1、下列各力中，不属于表面力的是（）。

A ．惯性力B ．粘滞力C ．压力D ．表面张力2、下列关于流体粘性的说法中，不准确的说法是（）。

A ．粘性是实际流体的物性之一B ．构成流体粘性的因素是流体分子间的吸引力C ．流体粘性具有阻碍流体流动的能力D ．流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中，流体质点的加速度包括当地加速度和迁移加速度，迁移加速度反映（）。

A ．由于流体质点运动改变了空间位置而引起的速度变化率B ．流体速度场的不稳定性C ．流体质点在流场某一固定空间位置上的速度变化率D ．流体的膨胀性4、重力场中平衡流体的势函数为（）。

A ．gz -=πB ．gz =πC ．z ρπ-=D ．z ρπ=5、无旋流动是指（）流动。

A ．平行B ．不可压缩流体平面C ．旋涡强度为零的D ．流线是直线的6、流体内摩擦力的量纲[]F 是（）。

A . []1-MLt B . []21--t ML C . []11--t MLD . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ，则流动属于（）。

A ．三向稳定流动B ．二维非稳定流动C ．三维稳定流动D ．二维稳定流动8、动量方程的不适用于( ) 的流场。

A ．理想流体作定常流动in out QV QV F )()(ρρ∑-∑=∑B．粘性流体作定常流动C．不可压缩流体作定常流动D．流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时，以下陈述错误的是：沿流动方向( ) 。

A．流量逐渐减少B．阻力损失量与流经的长度成正比C．压强逐渐下降D．雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失（）。

A．一定不相等B．之和为单位质量流体的总能量损失C．一定相等D．相等与否取决于支管长度是否相等11、边界层的基本特征之一是（）。

《流体力学》课后习题答案

流体力学课后习题答案习题【1】1-1 解：已知：120t =℃，1395p kPa '=，250t =℃ 120273293T K =+=，250273323T K =+= 据p RT ρ=，有：11p RT ρ'=，22p RT ρ'= 得：2211p T p T '='，则2211323395435293T p p kPa T ''=⋅=⨯=1-2 解：受到的质量力有两个，一个是重力，一个是惯性力。

重力方向竖直向下，大小为mg ；惯性力方向和重力加速度方向相反为竖直向上，大小为mg ，其合力为0，受到的单位质量力为01-3 解：已知：V=10m 3，50T ∆=℃，0.0005V α=℃-1根据1V V V Tα∆=⋅∆，得：30.000510500.25m V V V T α∆=⋅⋅∆=⨯⨯=1-4 解：已知：419.806710Pa p '=⨯，52 5.884010Pa p '=⨯，150t =℃，278t =℃ 得：1127350273323T t K =+=+=，2227378273351T t K =+=+= 根据mRT p V =，有：111mRT p V '=，222mRT p V '=G ＝mg自由落体：加速度a ＝g得：421251219.8067103510.185.884010323V p T V p T '⨯=⋅=⨯='⨯，即210.18V V = 体积减小了()10.18100%82%-⨯=1-5 解：已知：40mm δ=，0.7Pa s μ=⋅，a =60mm ，u =15m/s ，h =10mm根据牛顿内摩擦力定律：uT Ayμ∆=∆ 设平板宽度为b ，则平板面积0.06A a b b =⋅= 上表面单位宽度受到的内摩擦力：1100.70.06150210.040.01T A u b N b b h b μτδ-⨯-==⋅=⨯=--/m ，方向水平向左下表面单位宽度受到的内摩擦力：2200.70.061506300.010T A u b N b b h b μτ-⨯-==⋅=⨯=--/m ，方向水平向左平板单位宽度上受到的阻力：12216384N τττ=+=+=，方向水平向左。