工程光学14章例题分析
工程光学课后答案(12 13 15章)

1λ十二 十三 十五第十二章 习题及答案1。
双缝间距为1mm ,离观察屏1m ,用钠灯做光源,它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ,问两种单色光的第10级这条纹之间的间距是多少?解:由杨氏双缝干涉公式,亮条纹时:d Dm λα=(m=0, ±1, ±2···)m=10时,nmx 89.511000105891061=⨯⨯⨯=-,nmx 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆2。
在杨氏实验中,两小孔距离为1mm ,观察屏离小孔的距离为50cm ,当用一片折射率 1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ,试决定试件厚度。
21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆- 3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。
试求注入气室内气体的折射率。
0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ4。
垂直入射的平面波通过折射率为n 的玻璃板,透射光经透镜会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。
(完整版)工程光学习题参考答案第十四章光的偏振和晶体光学

第十四章 光的偏振和晶体光学1. 一束自然光以30度角入射到玻璃-空气界面,玻璃的折射率 1.54n =,试计算(1)反射光的偏振度;(2)玻璃-空气界面的布儒斯特角;(3)以布儒斯特角入射时透射光的偏振度。
解:光由玻璃到空气,354.50sin 1sin ,30,1,54.11212121=⎪⎪⎭⎫ ⎝⎛-====θθθn n n n o①()()()()06305.0tan 1tan ,3528.0sin 1sin 212212-=+-==+--=θθθθθθθθp s r r002222min max min max 8.93=+-=+-=ps ps r r r r I I I I P ②oB n n 3354.11tan tan1121=⎪⎭⎫ ⎝⎛==--θ ③()()4067.0sin 1sin ,0,5790212021=+--===-==θθθθθθθθs p B B r r 时,0298364.018364.011,8364.01=+-===-=P T r T p s s注:若221122,,cos cos p p s s t T t T n n ηηθθη===)(cos ,21222220min 0max θθ-=+-===ps s ps p s p T T t t t t P I T I I T I 或故 2. 自然光以布儒斯特角入射到由10片玻璃片叠成的玻片堆上,试计算透射光的偏振度。
解:每片玻璃两次反射,故10片玻璃透射率()2022010.83640.028s s T r =-==而1p T =,令m m I I in axτ=,则m m m m I I 110.026890.94761I I 10.02689ax in ax in p ττ---====+++3. 选用折射率为2.38的硫化锌和折射率为1.38的氟化镁作镀膜材料,制作用于氟氖激光(632.8nm λ=)的偏振分光镜。
工程光学物理光学11、12、14章答案

1λ第十一章 习题及答案 1。
双缝间距为1mm ,离观察屏1m ,用钠灯做光源,它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ,问两种单色光的第10级这条纹之间的间距是多少? 解:由杨氏双缝干涉公式,亮条纹时:dDm λα=(m=0, ±1, ±2···) m=10时,nm x 89.511000105891061=⨯⨯⨯=-,nm x 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆2。
在杨氏实验中,两小孔距离为1mm ,观察屏离小孔的距离为50cm ,当用一片折射率1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ,试决定试件厚度。
21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆-3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。
试求注入气室内气体的折射率。
0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ4。
垂直入射的平面波通过折射率为n 的玻璃板,透射光经透镜会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。
工程光学Chp14习题答案

tp =
P=
1
2.自然光以 θ B 入射到 10 片玻璃片叠成的玻璃堆上,求透射的偏振度。 解: t s =
2 cosθ 1 sin θ 2 sin(θ 1 + θ 2 )
①
tp =
2 sin θ 2 cosθ 1 ② sin(θ 1 + θ 2 ) cos(θ 1 − θ 2 )
sin θ B = n sin θ 2
图 14-7 例 3 图
方解石晶体(负) 入射光
3
在晶体上表面两分量的透射系数为 t s =
' = 在晶体下表面两分量的透射系数为 t s
2 2 ,tp = no + 1 ne + 1 2 1 +1 no
,
t 'p =
2 1 +1 ne
,
Io A sin θ 2 =( ) = tg 2θ A cosθ Ie
2
I1' p
⎛ A1' p ⎞ ⎟ I = 3.9773 × 10 − 3 I1 p = 1.9886610 − 3 I1 =⎜ ⎜ A1 p ⎟ 1 p ⎝ ⎠
I1' s − I1' p I1' s + I1' p = 0.0602413 ≈ 94% 0.0642187
∴θ p = 32.9977。≈ 33o = θ 1 ∴θ 2 = 57 o
δ = 2π ×
1 π = 4 2
⎡1,0 ⎤ 玻片的琼斯矩阵 G = ⎢ ⎥ ⎣0, i ⎦
5
入射光与 x 轴成 45 E 45o =
o
1 ⎡1⎤ ⎢⎥ 2 ⎣1⎦
⎡1,0 ⎤ 1 ⎡1⎤ 1 ⎡1⎤ = E出 = GE 45o = ⎢ ⎥ ⎥ ⎢ ⎥ 左旋圆偏振光 ⎢ 2 ⎣i ⎦ ⎣0, i ⎦ 2 ⎣1⎦ 1 ⎡1 ⎤ ⎢ ⎥ 2 ⎣− 1⎦ ⎡1,0 ⎤ 1 ⎡1 ⎤ 1 ⎡1 ⎤ E出 = GE−45o = ⎢ ⎥ = ⎥ ⎢ ⎥ ⎢ 2 ⎣− i ⎦ ⎣0, i ⎦ 2 ⎣− 1⎦
工程光学郁道银第二版习题解答

工程光学习题解答 CH11、 生活中有很多光学现象,例如,两个手电筒的发出的光在空气中相遇后又独自的直线转播,平面镜成像,水底的鱼看起来比实际浅等都符合光学基本定律。
2、 根据公式v=c/n 可得:光在水中的传播速度为:v=2.25×108m/s 光在冕牌玻璃中的传播速度为:v=1.987×108m/s 光在火石玻璃中的传播速度为:v=1.82×108m/s 光在加拿大树胶中的传播速度为:v=1.96×108m/s 光在金刚石中的传播速度为:v=1.241×108m/s3、 根据题意可得,可以设x 为屏到孔的距离,根据几何关系有如下式子成立:=+50x x 7060,可以解得x=300mm 4、 见图,本题涉及到全反射现象。
金属片边缘点发出光线照射到玻璃另一面是光密介质传入光疏介质,符合全反射条件,=θ∠ACB,有公式:,15.1sin 90sin =θ32sin =θ, D=2L CD +1=358.77mm图1.1习题45、①光从光密介质射到它与光疏介质的界面上,②入射角等于或大于临界角.这两个条件都是必要条件,两个条件都满足就组成了发生全反射的充要条件。
6、只要证明入射角和出射角相等就可以。
7、见下图,可知,光线通过光学原件后偏角为:δ=αθ-,有1s i n s i n n=∂θ,由于∂,θ都很小,可知,∂=∂=sin ,sin θθ,得δ=αθ-=)1(-∂n图1.2 题78、见课本图1.6所示,数值孔径一般代表光纤传播光的能力。
记为NA 。
根据三角函数关系及其全反射临界条件有:=Im sin 90sin 21n n ,,01Im)90sin(1sin n n I =-解得NA=n 0sin I 1=2221n n -.9、光在冕牌玻璃中的折射率为n=1.51,由全反射临界条件:∂sin 90sin =n,由图可以知道,β=45o -∂,将n=1.51代人,可以解得θ=5o 40'。
物理十四和十五章光学习题解和分析

十四章 几何光学习题与解答14-1.如题图14-1所示,一束平行光线以入射角θ射入折射率为n ,置于空气中的透明圆柱棒的端面.试求光线在圆柱棒内发生全反射时,折射率n 应满足的条件.分析:一次折射,一次反射;利用端面折射角与内侧面入射角互余及全反射条件即可求解。
解:设光线在圆柱棒端面的折射角为γ,在内侧面的入射角为'θ,根据折射定律,有'sin 'cos sin sin 222θθγθn n n n -===光线在界面上发生全反射的条件为1'sin ≥θn∴发生全反射时,n 必须满足θ2sin1+≥n14-2.远处有一物点发出的平行光束,投射到一个空气中的实心玻璃球上.设玻璃的折射率为50.1=n ,球的半径为cm r 4=.求像的位置.分析:利用逐步成像法,对玻璃球的前后两个球面逐一成像,即可求得最后像的位置.用高斯成像公式时,应注意两个球面的顶点位置是不同的.cm r r cm r r 4,421-=-===.解:cm cm r n n f 12)415.15.1(1'11=⨯-=-=cm cm f nf 8)5.112('111-=-=-=cm f p p p f p f 12'',,1''1111111==∞==+或用-∞====-=-1111111111,1,5.1','''p n n n r n n p n p ncm p p 12',415.11'5.111=-=∞--对玻璃球前表面所成的像,对后表面而言是物,所以cm cm r p p 4)812(2'212=-=+=cmcm r nf 8)]4(5.111[11'22=-⨯-=-=cm cm nf f 12)85.1('22-=⨯-=-= cm cm f p f p p p f p f 2)12484('',1''222222222=+⨯=-==+题图14-1或用1',5.1,'''222222222===-=-n n n r n n p n p ncm p p 2',45.1145.1'122=--=-像在球的右侧,离球的右边2cm 处.14-3.如题图14-3所示的一凹球面镜,曲率半径为40cm ,一小物体放在离镜面顶点10cm 处.试作图表示像的位置、虚实和正倒,并计算出像的位置和垂轴放大率.分析:利用凹面镜的半径可确定焦距,以知物距,由球面镜的物像公式和横向放大率公式可求解。
工程光学基础教程习题答案完整

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n =66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
大学物理答案第14章.docx

第十四章波动光学14-1在双缝干涉实验中,若单色光源S到两缝$、S2距离相等,则观察屏上中央明条纹位于图中0处,现将光源S向下移动到图中的S,位置,则()(A)中央明纹向上移动,且条纹间距增大(B)中央明纹向上移动,且条纹间距不变(C)中央明纹向下移动,且条纹间距增大(D)中央明纹向下移动,且条纹间距不变分析与解由S发出的光到达$、S2的光程相同,它们传到屏上中央0处,光程差A=0,形成明纹.当光源由S移到£时,由£到达狭缝$和S2的两朿光产生了光程差.为了保持原中央明纹处的光程差为0,它会向上移到图中O处.使得由空沿S|、S2狭缝传到0’处的光程差仍为0.而屏上各级条纹位置只是向上平移,因此条纹间距不变.故选(B).® 14-1 图14-2如图所示,折射率为血,厚度为0的透明介质薄膜的上方和下方的透明介质的折射率分别为⑴和〃3,且小<叽,灼>"3,若用波长为久的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束的光程差是()(C)2/?2e 一2 (D)2/?2e ———2/7题14-2图分析与解由于® <血,"2 >〃3,因此在上表面的反射光有半波损失,下表面的反2射光没有半波损失,故它们的光程差\ = 附土即 这里久是光在真空中的波长.因此正 确答案为(B ).14-3如图(a )所示,两个直径有微小差别的彼此平行的滚柱之间的距离为L,夹在 两块平面晶体的中间,形成空气劈形膜,当单色光垂直入射时,产生等厚干涉条纹,如果滚 柱之间的距离厶变小,则在厶范围内干涉条纹的( )(A )数目减小,间距变大(B )数目减小,间距不变 (C )数目不变,间距变小 (D )数目增加,间距变小题14-3图分析与解 图⑴)装置形成的劈尖等效图如图(b )所示.图中〃为两滚柱的直径差, b 为两相邻明(或暗)条纹间距.因为d 不变,当厶变小时,3变大,厶,、b 均变小.由图可得sm0 = A n /2h = d /厶‘,因此条纹总数N 二厶f /h = 2d/A tl ,因为d 和久n 不变,所 以N 不变.正确答案为(C )14-4用平行单色光垂直照射在单缝上时,可观察夫琅禾费衍射.若屏上点P 处为第二 级暗纹,则相应的单缝波阵面可分成的半波带数目为( )(A ) 3 个(B ) 4 个 (C ) 分析与解根据单缝衍射公式(暗条纹)k — 1,2,... (明条纹)因此第k 级暗纹对应的单缝处波阵面被分成2k 个半波带,第k 级明纹对应的单缝波阵面 被分成2£+1个半波带.则对应第二级暗纹,单缝处波阵面被分成4个半波带.故选(B )・14-5波长2=550 nm 的单色光垂直入射于光栅常数d =/? + //= 1.0 xlO'4 cm 的光 栅上,可能观察到的光谱线的最大级次为( )(A ) 4 (B ) 3 (C ) 2 (D ) 1分析与解 由光栅方程dsin& = ±Rl (£ = O,l,・・.),可能观察到的最大级次为壘也=述2 max A即只能看到第1级明纹,正确答案为(D ).5个 (D ) 6个±(2八1耳 (b)14-6三个偏振片F\、P?与尸3堆叠在一起,P\与尸3的偏振化方向相互垂直,尸2与Pi的偏振化方向间的夹角为30°,强度为/()的自然光入射于偏振片凡,并依次透过偏振片鬥、E与巴,则通过三个偏振片后的光强为()(A) 3Z0/16 (B) V3 /()/8 (C)3IJ32(D) 0 分析与解自然光透过偏振片后光强为厶=IJ2.由于比和P2的偏振化方向成30。
工程光学 郁道银 第14章作业答案

2ab cos( ud ) sin 琅和费衍射和傅里叶变换的关系,可得夫琅和费衍射(仍假设是 利用透镜在后焦面观察的情形)的强度分布为:
2 1 I ( x, y ) FT E ( x1 , y1 ) f
2
1 2 [2ab cos( ud ) sin c(au ) sin c(bv)] f 2ab 2 dx 2 ax cos sin c f f f
2
2
2 by sin c f
(注:若是不加透镜观察,只需将上式的坐标(x, y)改为(x, y),同时将 f 改为 z 即可;但要注意对应关系)
因此,其在 xy 平面上的复振幅分布为:
ٛ ٛ 2 E ( x, y ) A exp i ( x cos y cos ) = A exp[i 2 105 ( x y / 2)] ٛ
cos
(注:注意单位!空间频率的国际单位是 m-1,常用单位是 mm-1,在复振 幅分布中两个单位均可以用,但要注明。 )
2 1 I ( x, y ) FT E ( x1 , y1 ) f 2
1 2 2 2 [ L sin c( Lu ) sin c(Lv) l sin c(lu ) sin c(lv)] f 1 2 Lx Ly 2 lx ly L sin c sin c l sin c sin c f f f f f
参考解答: (仅供选课学生参考,请勿扩散)
1. 解:根据题目所给的波长和方向余弦,可得 x 和 y 方向上的空间频率分别为:
2/3 105 m 1 4 9 2 / 3 10 10 cos 1/ 3 5 104 m 1 v 4 9 2 / 3 10 10 u
大学物理第十四章波动光学课后习题答案及复习内容

第十四章波动光学一、基本要求1. 掌握光程的概念以及光程差和相位差的关系。
2. 理解获得相干光的方法,能分析确定杨氏双缝干涉条纹及薄膜等厚干涉条纹的位置,了解迈克尔逊干涉仪的工作原理。
3. 了解惠更斯-菲涅耳原理; 掌握用半波带法分析单缝夫琅和费衍射条纹的产生及其明暗纹位置的计算,会分析缝宽及波长对衍射条纹分布的影响。
4. 掌握光栅衍射公式。
会确定光栅衍射谱线的位置。
会分析光栅常数及波长对光栅衍射谱线分布的影响。
5. 了解自然光和线偏振光。
理解布儒斯特定律和马吕斯定律。
理解线偏振光的获得方法和检验方法。
6. 了解双折射现象。
二、基本内容1. 相干光及其获得方法只有两列光波的振动频率相同、振动方向相同、振动相位差恒定时才会发生干涉加强或减弱的现象,满足上述三个条件的两束光称为相干光。
相应的光源称为相干光源。
获得相干光的基本方法有两种:(1)分波振面法(如杨氏双缝干涉、洛埃镜、菲涅耳双面镜和菲涅耳双棱镜等);(2)分振幅法(如薄膜干涉、劈尖干涉、牛顿环干涉和迈克耳逊干涉仪等)。
2. 光程和光程差(1)光程把光在折射率为n的媒质中通过的几何路程r折合成光在真空x中传播的几何路程x,称x为光程。
nr(2)光程差在处处采用了光程概念以后就可以把由相位差决定的干涉加强,减弱等情况用光程差来表示,为计算带来方便。
即当两光源的振动相位相同时,两列光波在相遇点引起的振动的位相差πλδϕ2⨯=∆ (其中λ为真空中波长,δ为两列光波光程差) 3. 半波损失光由光疏媒质(即折射率相对小的媒质)射到光密媒质发生反射时,反射光的相位较之入射光的相位发生了π的突变,这一变化导致了反射光的光程在反射过程中附加了半个波长,通常称为“半波损失”。
4. 杨氏双缝干涉经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况:(1)位相差为0或2π的整数倍,合成振动最强;(2)位相差π的奇数倍,合成振动最弱或为0。
其对应的光程差()⎪⎩⎪⎨⎧-±±=212λλδk k ()()最弱最强 ,2,1,2,1,0==k k 杨氏的双缝干涉明、暗条纹中心位置:dD k x λ±= ),2,1,0( =k 亮条纹 d D k x 2)12(λ-±= ),2,1( =k 暗条纹 相邻明纹或相邻暗纹间距:λd D x =∆ (D 是双缝到屏的距离,d 为双缝间距) 5. 薄膜干涉以21n n <为例,此时反射光要计“半波损失”, 透射光不计“半波损失”。
大学物理第十四章习题解答和评分标准

第十四章光学习题及解答和评分标准1.题号:分值:10分在杨氏双缝干涉实验中,用波长= nm 的纳灯作光源,屏幕距双缝的距离d’=800 nm ,问:(1)当双缝间距1mm 时,两相邻明条纹中心间距是多少(2)假设双缝间距10 mm ,两相邻明条纹中心间距又是多少解答及评分标准:(1) d =1 mm 时mm d d x 47.0'==∆λ (5分)(2) d =10 mm 时mm dd x 047.0'==∆λ (5分) 2.题号:分值:10分洛埃镜干涉如图所示光源波长m 7102.7-⨯=λ,试求镜的右边缘到第一条明纹的距离。
解答及评分标准: λdd x '21⋅=∆ (6分) m m x 57105.4102.722.0302021--⨯=⨯⨯⨯+⨯=∆∴(4分)3.题号:3分值:10分在双缝干涉实验中,用波长=的单色光照射,屏幕距双缝的距离d’=300 mm ,测得中央明纹两恻的两个第五级明纹的间距为, 求两缝间的距离。
解答及评分标准:λd d x '=∆ (4分) mm N x 22.1102.122.12==∆=∆Θ (4分) mm x d d 134.01022.1101.54610300'393=⨯⨯⨯⨯=∆=∴---λ (2分) 4. 题号:分值:10分在双缝干涉实验中,两缝间的距离,用单色光垂直照射双缝, 屏与缝之间的距离为,测得中央明纹两恻的两个第五级暗纹的间距为, 求所用光的波长。
解答及评分标准:λdd x '=∆ (4分) 531.2978.2278.22==∆=∆N x Θ (4分) nm d xd 8.6321020.130.0531.2'3=⨯⨯=∆=∴λ (2分)5.题号:分值:10分单色光照射到相距为的双缝上,双缝与屏幕的垂直距离为1m ,求:(1)从第一级明纹到同侧的第四级明纹间的距离为,求单色光的波长;(2)若入射光的波长为600nm ,求相邻两明纹间的距离。
(完整版)工程光学习题参考答案第十四章光的偏振和晶体光学.doc

工程光学习题解答第十四章 光的偏振和晶体光学1. 一束自然光以 30 度角入射到玻璃 -空气界面, 玻璃的折射率 n 1.54 ,试计算 ( 1)反射光的偏振度;( 2)玻璃 -空气界面的布儒斯特角; ( 3)以布儒斯特角入射时透射光的偏振度。
解:光由玻璃到空气,n 1 1.54,n 2 1,130o , 2 sin 1n 1sin 1 50.354n 2① r ssin 12tan120.06305sin0.3528, r p12tan12I maxI min22Pr sr p93.80 0I maxI min22r sr p② B1n 2tan 1133 otann 11.54③ 1B时, 290B57 0 , r p 0, r ssin 12 0.4067sin 12T s 1 r s 2 0.8364, T p 1P 1 0.8364 9 0 010.8364注:若n 2 cos 2 , T st s 2 ,T pt p2n 1 cos 1ImaxT p I 0, IminT s I 0故Pt p 2t s 2或 T scos 2(12)t p 2 t s 2T p2. 自然光以布儒斯特角入射到由10 片玻璃片叠成的玻片堆上,试计算透射光的偏振度。
10 片玻璃透射率 T s 1 r s20 0.028解:每片玻璃两次反射,故20.836420而 T p 1,令I min ,则p1 IIm ax1Im axm axII m in m in1 0.02689 0.94761 0.026893. 选用折射率为 2.38 的硫化锌和折射率为 1.38 的氟化镁作镀膜材料,制作用于氟氖激光(632.8nm )的偏振分光镜。
试问(1)分光镜的折射率应为多少?(2)膜层的厚度应为多少?解:( 1)n3sin 45 n2 sin 2n1 n3tg 2 (起偏要求)n2n3 452n2 sin 1 n3n3 2 2n2tg 22 n22 1 tg 2n1 n1 1 n1 n2 n22 n2n2 1 n1 2 2 n2 2 n1 2 1.6883n2(2)满足干涉加强 2 2n2 h2 cos 22 ,2 sin 1 n3 30.1065n2 sin 45则 h2 2 76.84 nmcos2n2 2而1 90 2 59.8934 , h12 228.54 nm 2n1 cos 14. 线偏振光垂直入射到一块光轴平行于界面的方解石晶体上,若光矢量的方向与警惕主截面成( 1)30 度( 2)45 度( 3)60 度的夹角,求o光和e光从晶体透射出来后的强度比?解:垂直入射 1 2 3, S 波与 p 波分阶r s 2 r p 2n1 cos 1 n2 cos 2 n1 n2r sn2 cos n1 n2n1 cos 1 2n2 cos 1 n1 cos 2 n2 n1r pn1 cos n2 n1n2 cos 1 2o 光此时对应 s 波r0 1 n0 ,T0 1 r02 4n0 22 21 n0 1 n02e 光此时对应 p 波r en e 1 , T e1 224n en e1 r e21 n e2T 0 sin 224I 0E s T 0 tg 2n 0 1 n e I eE p 2T e cos 2 T en e1 n 0取 n 0 1.6584 , n e 1.4864则Itg 20.9526I e( 1)30 ,I 01 0.9526 0.3175I e3( 2)45 ,I 00.9526I e( 3)60 ,I 03 0.95262.8578I e5. 方解石晶片的厚度 d 0.013mm ,晶片的光轴与表面成60 度角, 当波长632.8nm的氦氖激光垂直入射晶片时(见图14-64),求( 1)晶片内 o 、 e 光线的夹角;( 2) o 光和 e 光的振动方向; ( 3) o 、 e 光通过晶片后的相位差。
大学物理第十四章习题解答和评分标准.doc

(5分)(4分)第十四章光学习题及解答和评分标准1.题号:50341001分值:10分在杨氏双缝干涉实验中,用波长2=589.3 nm 的纳灯作光源,屏幕距双缝的距离/=800 nm,问:⑴当双缝间距1mm 时,两相邻明条纹中心间距是多少?⑵假设双缝间距10 mm, 两相邻明条纹中心间距又是多少?解答及评分标准:d'(1) <7=1 mm 时 Ax = —2 = QAlmm d(2) d=10 mm 时 = — X = 0.047/77/77 d 2.题号:50341002分值:10分洛埃镜干涉如图所示光源波长2 = 7.2x 10" m, 试求镜的右边缘到第一条明纹的距离。
解答及评分标准: •山十役 x7.2xl0f=4.5xl0f (4 分)3. 题号:450342003分值:10分在双缝十■涉实验屮,用波长2=546.Inm 的单色光照射,屏幕距双缝的距离6?'=300 mm, 测得中央明纹两恻的两个第五级明纹的间距为12.2mm,求两缝间的距离。
解答及评分标准:._d'Ax — — A dKN 12.27o~ =1.22mm£2 Ax300x1()7 x 546.1x10-91.22x10 3=0.134mm(4分)(2Ar = 22.78AN22.789=2.531Axd _ 2.531 x 0.30d' ~ 1.20 xlO3=632.8nm(4分)(4分)4.题号:50342004分值:10分在双缝干涉实验中,两缝间的距离0.30mm,用单色光垂直照射双缝,屏与缝之间的距离为1.20m,测得中央明纹两恻的两个第五级暗纹的间距为22.78mm,求所用光的波长。
解答及评分标准:5.题号:50342005分值:10分单色光照射到相距为0.2mm的双缝上,双缝与屏幕的垂直距离为lm,求:(1)从第一级明纹到同侧的第四级明纹间的距离为7.5mm,求单色光的波长;(2)若入射光的波长为600nm,求相邻两明纹间的距离。
工程光学(平面与平面系统)
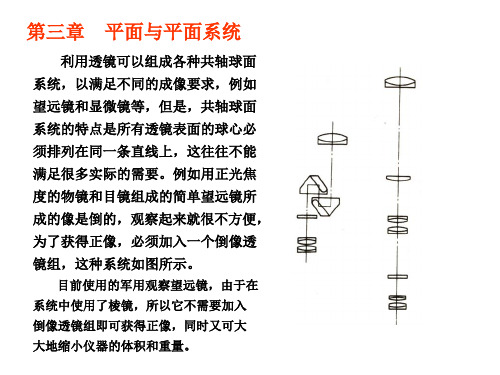
特点:像与物上、下同向,但左右却颠倒,它可通过奇次反射得到。 ② 一致像:物为右手坐标,像也为右手坐标,即物与像是完全一致的,它
可通过偶次反射来得到。
总结:(1)奇数次反射成镜像,偶数次反射成与物一致的像。 (2)当物体旋转时,其像反方向旋转相同的度数。
二、平面镜旋转
重要特性:当入射光方向不变,而平面镜旋转时,反射光线的方向将会改变。 若平面镜转过角α,反射光线将转过2α=θ角。 θ=AOA’’ - AOA’ =2(AON - AON1) ∵ AON - AON1 = α
解:若把折射平面看成是曲率半径为r=∞的折射面,那么,近轴区平面 折射的物象公式可写成
n' l' n' l'
n l n l
n ' n r
0
空气 Ⅱ面 d Ⅰ面 -l1 A2’ A A1’ 乙醇
n2’
n2=n1’ -l’2 n1 -l’1 -l2
设水底有物点A,经水、乙醇交界面(平面Ⅰ) 折射后成像为A’,
x’ o’ y’ z’
镜系统的转像情况。
例2:若将直角棱镜换成屋脊棱镜,则情况由是如何? 例3:如果在系统加上一组透镜系统情况由将如何?
y y x o
z
x
o
z
y’ x’ o’ z’ x’ o’ y’ z’ y’’
x’’
o’’ z’’ y’’’ x’’’ z’’’ o’’’
三、反射棱镜的等效作用与展开
显微镜应向上抬起2.5mm,才可使像清晰。
-l Δl‘ -l
3、应用:将平行玻璃平板简化为一个等效空气平板。
d d l' d / n
举例:1. 一人站在游泳池旁,垂直注视池底物体,试问物体的视见位置要 比实际位置高多少?(水的折射率为4/3) 解:设游泳池水的实际深度为d,有池底物点A发出的光线,经过水平面折 射后,像点A’相对物点A产生了轴向位移。
新编基础物理学第14章习题解答与分析

第14章 波动光学14-1.在双缝干涉实验中,两缝的间距为0.6mm,照亮狭缝S 的光源是汞弧灯加上绿色滤光片.在2.5m 远处的屏幕上出现干涉条纹,测得相邻两明条纹中心的距离为2.27mm .试计算入射光的波长,如果所用仪器只能测量5mm x ∆≥的距离,则对此双缝的间距d 有何要求?分析:由杨氏双缝干涉明纹位置公式求解。
解:在屏幕上取坐标轴Ox ,坐标原点位于关于双缝的对称中心。
屏幕上第k 级明纹中心的距坐标原点距离:λdD kx ±= 可知dD d D k d D k x x x k k λλλ=-+=-=∆+)1(1 代入已知数据,得545nm xd Dλ∆== 对于所用仪器只能测量5mm x ∆≥的距离时0.27mm D d x λ≤=∆14-2.在杨氏双缝实验中,设两缝之间的距离为0.2mm .在距双缝1m 远的屏上观察干涉条纹,若入射光是波长为400nm 至760nm 的白光,问屏上离零级明纹20mm 处,哪些波长的光最大限度地加强?(91nm=10m -)分析:由双缝干涉屏上明纹位置公式,求k 取整数时对应的可见光的波长。
解:已知:d =0.2mm ,D =1m ,x =20mm 依公式λk d D x =∴ 4000n mdxk Dλ== 故k =10 λ1=400nmk =9 λ2=444.4nm k =8 λ3=500nm k =7 λ4=571.4nm k =6 λ5=666.7nm这五种波长的光在所给的观察点最大限度地加强.14-3.如题图14-3所示,在杨氏双缝干涉实验中,若3/1212λ=-=-r r P S P S ,求P 点的强度I 与干涉加强时最大强度Imax 的比值.分析:已知光程差,求出相位差.利用频率相同、振动方向相同的两列波叠加的合振幅公式求出P 点合振幅。
杨氏双缝干涉最大合振幅为2A 。
解:设S 1、S 2分别在P 点引起振动的振幅为A ,干涉加强时,合振幅为2A ,所以2max 4A I ∝ , 因为λ3112=-r r所以S 2到P 点的光束比S 1到P 点的光束相位落后题图14-3()3π23π2π212=⋅=-=∆λλλϕr r P 点合振动振幅的平方为:22223π2cos2A A A A =++ 因为2I A ∝ 所以22m a x 1==44IA I A14-4. 在双缝干涉实验中,波长550nm λ=的单色平行光, 垂直入射到缝间距4210m d -=⨯的双缝上,屏到双缝的距离2m D =.求:(1) 中央明纹两侧的两条第10级明纹中心的间距; (2) 用一厚度为66.610m e -=⨯、折射率为 1.58n =的玻璃片覆盖一缝后,零级明纹将移到原来的第几级明纹处?分析:(1)双缝干涉相邻两条纹的间距为 ∆x =D λ / d ,中央明纹两侧的两条第10级明纹中心的间距为20∆x .(2)不加介质片之前,两相干光均在空气中传播,它们到达屏上任一点P 的光程差由其几何路程差决定,中央明纹对于O 点的光程差0δ=,其余条纹相对O 点对称分布.插入介质片后,两相干光在两介质薄片中的几何路程相等,但光程不等。
大学物理第十四章习题解答和评分标准

大学物理第十四章习题解答和评分标准-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第十四章光学习题及解答和评分标准1.题号:50341001分值:10分 在杨氏双缝干涉实验中,用波长=589.3 nm 的纳灯作光源,屏幕距双缝的距离d’=800 nm ,问:(1)当双缝间距1mm 时,两相邻明条纹中心间距是多少(2)假设双缝间距10 mm ,两相邻明条纹中心间距又是多少?解答及评分标准:(1) d =1 mm 时mm d d x 47.0'==∆λ (5分)(2) d =10 mm 时mm dd x 047.0'==∆λ (5分) 2.题号:50341002分值:10分洛埃镜干涉如图所示光源波长m 7102.7-⨯=λ,试求镜的右边缘到第一条明纹的距离。
解答及评分标准:λdd x '21⋅=∆ (6分) m m x 57105.4102.722.0302021--⨯=⨯⨯⨯+⨯=∆∴(4分) 3.题号:450342003分值:10分在双缝干涉实验中,用波长λ=546.1nm 的单色光照射,屏幕距双缝的距离d’=300 mm ,测得中央明纹两恻的两个第五级明纹的间距为12.2mm, 求两缝间的距离。
解答及评分标准:λdd x '=∆ (4分) mm N x 22.1102.122.12==∆=∆ (4分) mm x d d 134.01022.1101.54610300'393=⨯⨯⨯⨯=∆=∴---λ (2分) 4. 题号:50342004分值:10分在双缝干涉实验中,两缝间的距离0.30mm ,用单色光垂直照射双缝, 屏与缝之间的距离为1.20m ,测得中央明纹两恻的两个第五级暗纹的间距为22.78mm, 求所用光的波长。
解答及评分标准:λdd x '=∆ (4分) 531.2978.2278.22==∆=∆N x (4分) nm d xd 8.6321020.130.0531.2'3=⨯⨯=∆=∴λ (2分)5.题号:50342005分值:10分单色光照射到相距为0.2mm 的双缝上,双缝与屏幕的垂直距离为1m ,求:(1)从第一级明纹到同侧的第四级明纹间的距离为7.5mm ,求单色光的波长;(2)若入射光的波长为600nm ,求相邻两明纹间的距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章1、已知真空中的光速c =3 m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s , 当光在金刚石中,n=2.417时,v=1.24 m/s 。
(例题)2、一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:所以x=300mm即屏到针孔的初始距离为300mm 。
(例题)3、一厚度为200mm 的平行平板玻璃(设n=1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?1mmI 1=90n 1 n 2 200mmLI 2x解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1, n1=1.5,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1 .(例题)5、一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面。
(1)首先考虑光束射入玻璃球第一面时的状态,使用高斯公式:会聚点位于第二面后15mm处。
(2)将第一面镀膜,就相当于凸面镜像位于第一面的右侧,只是延长线的交点,因此是虚像。
还可以用β正负判断:(3)光线经过第一面折射:, 虚像第二面镀膜,则:得到:(4)再经过第一面折射物像相反为虚像。
6、一直径为400mm,折射率为1.5的玻璃球中有两个小气泡,一个位于球心,另一个位于1/2半径处。
沿两气泡连线方向在球两边观察,问看到的气泡在何处?如果在水中观察,看到的气泡又在何处?解:设一个气泡在中心处,另一个在第二面和中心之间。
(1)从第一面向第二面看(2)从第二面向第一面看(3)在水中7、有一平凸透镜r1=100mm,r2=,d=300mm,n=1.5,当物体在时,求高斯像的位置l’。
在第二面上刻一十字丝,问其通过球面的共轭像在何处?当入射高度h=10mm,实际光线的像方截距为多少?与高斯像面的距离为多少?解:8、一球面镜半径r=-100mm,求=0 ,-0.1 ,-0.2 ,-1 ,1 ,5,10,∝时的物距像距。
解:(1)(2)同理,(3)同理,(4)同理,(5)同理,(6)同理,(7)同理,(8)同理,(例题)9、一物体位于半径为r 的凹面镜前什么位置时,可分别得到:放大4倍的实像,放大4倍的虚像、缩小4倍的实像和缩小4倍的虚像?解:(1)放大4倍的实像(2)放大四倍虚像(3)缩小四倍实像(4)缩小四倍虚像第二章(例题)1、已知照相物镜的焦距f’=75mm,被摄景物位于(以F点为坐标原点)x=-∝, -2f, -f, -f/2, 0, f/2, f, 2f, ∝处,试求照相底片应分别放在离物镜的像方焦面多远的地方。
解:(1)x= -∝,xx′=ff′得到:x′=0(2)x′=0.5625(3)x′=0.703(4)x′=0.937(5)x′=1.4(6)x′=2.812、设一系统位于空气中,垂轴放大率,由物面到像面的距离(共轭距离)为7200mm,物镜两焦点间距离为1140mm,求物镜的焦距,并绘制基点位置图。
(例题)3.已知一个透镜把物体放大-3倍投影在屏幕上,当透镜向物体移近18mm时,物体将被放大-4x试求透镜的焦距。
解:4.一个薄透镜对某一物体成实像,放大率为-1x,今以另一个薄透镜紧贴在第一个透镜上,则见像向透镜方向移动20mm,放大率为原先的3/4倍,求两块透镜的焦距为多少?解:5.有一正薄透镜对某一物成倒立的实像,像高为物高的一半,今将物面向透镜移近100mm,则所得像与物同大小,求该正透镜组的焦距。
解:(例题)6.希望得到一个对无限远成像的长焦距物镜,焦距=1200mm,由物镜顶点到像面的距离L=700mm,由系统最后一面到像平面的距离(工作距)为,按最简单结构的薄透镜系统考虑,求系统结构,并画出光路图。
解:7.一短焦距物镜,已知其焦距为35 mm,筒长L=65 mm,工作距,按最简单结构的薄透镜系统考虑,求系统结构。
解:8.已知一透镜求其焦距、光焦度。
解:(例题)9.一薄透镜组焦距为100 mm,和另一焦距为50 mm的薄透镜组合,其组合焦距仍为100 mm,问两薄透镜的相对位置。
解:10.长60 mm,折射率为1.5的玻璃棒,在其两端磨成曲率半径为10 mm的凸球面,试求其焦距。
解:11.一束平行光垂直入射到平凸透镜上,会聚于透镜后480 mm处,如在此透镜凸面上镀银,则平行光会聚于透镜前80 mm处,求透镜折射率和凸面曲率半径。
解:第三章(例题)1.人照镜子时,要想看到自己的全身,问镜子要多长?人离镜子的距离有没有关系?解:镜子的高度为1/2人身高,和前后距离无关。
2.设平行光管物镜L的焦距=1000mm,顶杆与光轴的距离a=10 mm,如果推动顶杆使平面镜倾斜,物镜焦点F的自准直像相对于F产生了y=2 mm的位移,问平面镜的倾角为多少?顶杆的移动量为多少?解:(例题)3.一光学系统由一透镜和平面镜组成,如图3-29所示,平面镜MM与透镜光轴垂直交于D点,透镜前方离平面镜600 mm有一物体AB,经透镜和平面镜后,所成虚像至平面镜的距离为150 mm,且像高为物高的一半,试分析透镜焦距的正负,确定透镜的位置和焦距,并画出光路图。
解:平面镜成β=1的像,且分别在镜子两侧,物像虚实相反。
(例题)4.有一双面镜系统,光线平行于其中一个平面镜入射,经两次反射后,出射光线与另一平面镜平行,问两平面镜的夹角为多少?解:OA M M //32 3211M M N M ⊥∴1''1I I -= 又 2''2I I -=∴α同理:1''1I I -=α 321M M M ∆中 ︒=-+-+180)()(1''12''2I I I I α ︒=∴60α 答:α角等于60︒。
第四章(例题)2.二个薄凸透镜构成的系统,其中,,,位于后,若入射平行光,请判断一下孔径光阑,并求出入瞳的位置及大小。
解:判断孔径光阑:第一个透镜对其前面所成像为本身,第二个透镜对其前面所成像为,其位置:大小为:故第一透镜为孔阑,其直径为4厘米.它同时为入瞳.(例题)2.设照相物镜的焦距等于75mm ,底片尺寸为5555,求该照相物镜的最大视场角等于多少? 解:AOBM 1M 2M 3 N1N 2-I 1 I ''1-I 2I ''2 αααα第五章1、一个100W的钨丝灯,发出总光通量为1400lm,求发光效率为多少?解:2、有一聚光镜,(数值孔径),求进入系统的能量占全部能量的百分比。
解:而一点周围全部空间的立体角为-ωf'3、一个的钨丝灯,已知:,该灯与一聚光镜联用,灯丝中心对聚光镜所张的孔径角,若设灯丝是各向均匀发光,求1)灯泡总的光通量及进入聚光镜的能量;2)求平均发光强度解:4、一个的钨丝灯发出的总的光通量为,设各向发光强度相等,求以灯为中心,半径分别为:时的球面的光照度是多少?解:5、一房间,长、宽、高分别为:,一个发光强度为的灯挂在天花板中心,离地面,1)求灯正下方地板上的光照度;2)在房间角落处地板上的光照度。
解:第六章1.如果一个光学系统的初级子午彗差等于焦宽(),则应等于多少?解:2.如果一个光学系统的初级球差等于焦深(),则应为多少?解:3.设计一双胶合消色差望远物镜,,采用冕牌玻璃K9(,)和火石玻璃F2(,),若正透镜半径,求:正负透镜的焦距及三个球面的曲率半径。
解:第七章(例题)1.一个人近视程度是(屈光度),调节范围是8D,求:(1)其远点距离;(2)其近点距离;(3)配带100度的近视镜,求该镜的焦距;(4)戴上该近视镜后,求看清的远点距离;(5)戴上该近视镜后,求看清的近点距离。
解:远点距离的倒数表示近视程度(例题)2.一放大镜焦距,通光孔径,眼睛距放大镜为50mm,像距离眼睛在明视距离250mm,渐晕系数K=50%,试求:(1)视觉放大率;(2)线视场;(3)物体的位置。
解:3.一显微物镜的垂轴放大倍率,数值孔径NA=0.1,共轭距L=180mm,物镜框是孔径光阑,目镜焦距。
(1)求显微镜的视觉放大率;(2)求出射光瞳直径;(3)求出射光瞳距离(镜目距);(4)斜入射照明时,,求显微镜分辨率;(5)求物镜通光孔径;(6)设物高2y=6mm,渐晕系数K=50%,求目镜的通光孔径。
解:(例题)4.欲分辨0.000725mm的微小物体,使用波长,斜入射照明,问:(1)显微镜的视觉放大率最小应多大?(2)数值孔径应取多少适合?解:此题需与人眼配合考虑5.有一生物显微镜,物镜数值孔径NA=0.5,物体大小2y=0.4mm,照明灯丝面积,灯丝到物面的距离100mm,采用临界照明,求聚光镜焦距和通光孔径。
解:视场光阑决定了物面大小,而物面又决定了照明的大小(例题)6.为看清4km处相隔150mm的两个点(设),若用开普勒望远镜观察,则:(1)求开普勒望远镜的工作放大倍率;(2)若筒长L=100mm,求物镜和目镜的焦距;(3)物镜框是孔径光阑,求出设光瞳距离;(4)为满足工作放大率要求,求物镜的通光孔径;(5)视度调节在(屈光度),求目镜的移动量;(6)若物方视场角,求像方视场角;(7)渐晕系数K=50%,求目镜的通光孔径;解:因为:应与人眼匹配7.用电视摄相机监视天空中的目标,设目标的光亮度为2500,光学系统的透过率为0.6,摄象管靶面要求照度为20lx,求摄影物镜应用多大的光圈。
