PID算法程序—位置式PID控制算法

合集下载

(完整版)PID控制规律及数字PID基本算法

c(t)
Gc (s)
3、比例微分控制
1 u(t)
) Ti s
K p (1 Ti s) Ti s
入了相位滞后，使得系统相对稳定性变差；一阶微分环节的出现，提高了系统的阻尼程度，缓和了控制器零极点对系统稳定性及动态过程的不利影响。
微分控制能反应输入信号的变化趋势，因此在输入信
r(t)

连续PID控制算例
开环传递函数：
G(s)
6
(s 1)(s 2)(s 3)
原系统 PI控制
Matlab/Simulink
PID控制
1.6
1.4
原系统 PI控制
PI控制器：比例系数Kp=3.1815、积分时间常数
1.2
PID控制 Ti=1.345
1
PID控制器：比例系数Kp=4.7787、积分时间常数
系统的快速性及相对稳定性。
PID控制器的时域表达式：
u(t
)

K
p
[e(t
)

1 Ti

e(t)dt
0
Td
de(t ) ] dt
二、连续PID传递函数的离散化
各环节的离散化处理
r(t)

e(t) K p
Td s
c(t)
1/ Ti s
u(t)
r(t)

e(t) c(t)
T
e*(t) K p
为0,0.9,3时系统的阶跃响应。
黄色线对应比例系数为2，微分系数为0时的阶跃响应紫色线对应比例系数为2，微分系数为0.9时的阶跃响应青色线对应比例系数为2，微分系数为3时的阶跃响应
随着微分作用的增强，系统的超调量减小，系统的阻尼程度提高，相对平稳性变好，调整时间缩短，快速性变好

PID控制算法（PID控制原理与程序流程）

PID控制算法（PID控制原理与程序流程）⼀、PID控制原理与程序流程(⼀)过程控制的基本概念过程控制――对⽣产过程的某⼀或某些物理参数进⾏的⾃动控制。

1、模拟控制系统图5-1-1 基本模拟反馈控制回路被控量的值由传感器或变送器来检测，这个值与给定值进⾏⽐较，得到偏差，模拟调节器依⼀定控制规律使操作变量变化，以使偏差趋近于零，其输出通过执⾏器作⽤于过程。

控制规律⽤对应的模拟硬件来实现，控制规律的修改需要更换模拟硬件。

2、微机过程控制系统图5-1-2 微机过程控制系统基本框图以微型计算机作为控制器。

控制规律的实现，是通过软件来完成的。

改变控制规律，只要改变相应的程序即可。

3、数字控制系统DDC图5-1-3 DDC系统构成框图DDC(Direct Digital Congtrol)系统是计算机⽤于过程控制的最典型的⼀种系统。

微型计算机通过过程输⼊通道对⼀个或多个物理量进⾏检测，并根据确定的控制规律(算法)进⾏计算，通过输出通道直接去控制执⾏机构，使各被控量达到预定的要求。

由于计算机的决策直接作⽤于过程，故称为直接数字控制。

DDC系统也是计算机在⼯业应⽤中最普遍的⼀种形式。

(⼆)模拟PID调节器1、模拟PID控制系统组成图5－1－4 模拟PID控制系统原理框图2、模拟PID调节器的微分⽅程和传输函数PID调节器是⼀种线性调节器，它将给定值r(t)与实际输出值c(t)的偏差的⽐例(P)、积分(I)、微分(D)通过线性组合构成控制量，对控制对象进⾏控制。

a、PID调节器的微分⽅程式中b、PID调节器的传输函数a、⽐例环节：即时成⽐例地反应控制系统的偏差信号e(t)，偏差⼀旦产⽣，调节器⽴即产⽣控制作⽤以减⼩偏差。

b、积分环节：主要⽤于消除静差，提⾼系统的⽆差度。

积分作⽤的强弱取决于积分时间常数TI，TI越⼤，积分作⽤越弱，反之则越强。

c、微分环节：能反应偏差信号的变化趋势(变化速率)，并能在偏差信号的值变得太⼤之前，在系统中引⼊⼀个有效的早期修正信号，从⽽加快系统的动作速度，减⼩调节时间。

PID算法程序—位置式PID控制算法

PID算法程序—位置式PID控制算法位置式PID控制算法是一种经典的控制算法，用来实现对于被控对象位置的精确控制。

本文将介绍位置式PID控制算法的原理和实现方式。

位置式PID控制算法的原理是基于被控对象的位置反馈信号，通过比较设定值和实际值之间的差异，进行控制动作的调整。

PID控制算法分为三个部分，即比例（Proportional）、积分（Integral）和微分（Derivative）控制。

比例控制通过比较设定值和实际值的差异，按照一个比例系数进行控制。

比例控制的作用是根据误差的大小来产生一个合适的控制量，使得误差越大，则控制量越大。

比例控制的数学公式为：P=Kp*e，其中P为控制量，Kp为比例系数，e为误差。

积分控制通过对误差进行累计，按照一个积分系数进行控制。

积分控制的作用是根据误差的累积量来产生一个较长期的平均控制量，以消除一些系统方面的偏差。

积分控制的数学公式为：I = Ki * ∫e dt，其中I为控制量，Ki为积分系数，∫e dt为误差的累积量。

微分控制通过对误差的变化率进行控制，按照一个微分系数进行控制。

微分控制的作用是根据误差的变化趋势来产生一个瞬时控制量，以抑制控制过程中的震荡和超调现象。

微分控制的数学公式为：D = Kd * de/dt，其中D为控制量，Kd为微分系数，de/dt为误差的变化率。

位置式PID控制算法的输出为PID控制量，即PID=P+I+D。

PID控制量经过执行机构（如电机）的作用，使被控对象达到设定值。

PID控制算法是一个迭代过程，通过不断调整PID系数，使控制系统的稳态误差趋于零，且响应时间和稳定性都符合要求。

在实际应用中，需要根据被控对象的特性和控制要求，调整PID控制算法的参数。

比例系数Kp决定了响应的敏感度，积分系数Ki决定了控制的稳定性，微分系数Kd决定了控制的平滑性。

通过合理调整这些参数，可以实现对被控对象位置的精确控制。

PID控制算法的实现可以通过编程语言来实现。

STM32实现电机的PID控制

PID控制应该算是非常古老而且应用非常广泛的控制算法了，小到热水壶温度控制，大到控制无人机的飞行姿态和飞行速度等等。

在电机控制中，PID算法用得尤为常见。

一、位置式PID1.计算公式在电机控制中，我们给电机输出的是一个PWM占空比的数值。

话不多说，直接上位置式PID基本公式：控制流程图如下：上图中的目标位置一般我们可以通过按键或者开关等方式编程实现改变目标值，测量位置就是通过stm32 去采集编码器的数据。

目标位置和测量位置之间作差就是目前系统的偏差。

送入PID 控制器进行计算输出，然后再经过电机驱动的功率放大控制电机的转动去减小偏差，最终达到目标位置的过程。

2.C语言实现如何把我们以上的理论分析和控制原理图使用C 语言写出来呢，这是一个有趣且实用的过程。

位置式PID 具体通过C 语言实现的代码如下：int Position_PID (int Encoder,int Target){static float Bias,Pwm,Integral_bias,Last_Bias;Bias=Target- Encoder; //计算偏差Integral_bias+=Bias; //求出偏差的积分//PID基本公式Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);Last_Bias=Bias; //保存上一次偏差return Pwm; //输出}入口参数为编码器的位置测量值和位置控制的目标值，返回值为电机控制PWM(现在再看一下上面的控制框图是不是更加容易明白了)。

第一行是相关内部变量的定义。

第二行是求出位置偏差，由测量值减去目标值。

第三行通过累加求出偏差的积分。

第四行使用位置式PID 控制器求出电机PWM。

第五行保存上一次偏差，便于下次调用。

最后一行是返回。

二、增量式PID1.计算公式速度闭环控制就是根据单位时间获取的脉冲数（这里使用了M 法测速）测量电机的速度信息，并与目标值进行比较，得到控制偏差，然后通过对偏差的比例、积分、微分进行控制，使偏差趋向于零的过程。

单片机PID算法程序精编版

单片机P I D算法程序公司内部编号：（GOOD-TMMT-MMUT-UUPTY-UUYY-DTTI-51单片机P I D算法程序(二)位置式P I D控制算法由51单片机组成的数字控制系统控制中，PID控制器是通过PID控制算法实现的。

51单片机通过AD对信号进行采集，变成数字信号，再在单片机中通过算法实现PID运算，再通过DA把控制量反馈回控制源。

从而实现对系统的伺服控制。

位置式PID控制算法位置式PID控制算法的简化示意图上图的传递函数为：（2-1）在时域的传递函数表达式（2-2）对上式中的微分和积分进行近似（2-3）式中n是离散点的个数。

于是传递函数可以简化为：（2-4）其中u(n)——第k个采样时刻的控制；KP——比例放大系数；Ki——积分放大系数；Kd——微分放大系数；T ——采样周期。

如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

（2-4）表示的控制算法直接按（2-1）所给出的PID控制规律定义进行计算的，所以它给出了全部控制量的大小，因此被称为全量式或位置式PID控制算法。

缺点：1）由于全量输出，所以每次输出均与过去状态有关，计算时要对e(k)(k=0,1,…n)进行累加，工作量大。

2）因为计算机输出的u(n)对应的是执行机构的实际位置，如果计算机出现故障，输出u(n)将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实际生产中是不允许的。

位置式PID控制算法C51程序具体的PID参数必须由具体对象通过实验确定。

由于单片机的处理速度和ram资源的限制，一般不采用浮点数运算，而将所有参数全部用整数，运算到最后再除以一个2的N次方数据（相当于移位），作类似定点数运算，可大大提高运算速度，根据控制精度的不同要求，当精度要求很高时，注意保留移位引起的“余数”，做好余数补偿。

这个程序只是一般常用pid算法的基本架构，没有包含输入输出处理部分。

PID控制实验报告

实验二数字PID 控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。

因此连续PID 控制算法不能直接使用，需要采用离散化方法。

在计算机PID 控制中，使用的是数字PID 控制器。

一、位置式PID 控制算法按模拟PID 控制算法，以一系列的采样时刻点kT 代表连续时间t ，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID 位置式表达式：∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中，D p d I pi T k k T k k ==,，e 为误差信号（即PID 控制器的输入），u 为控制信号（即控制器的输出）。

在仿真过程中，可根据实际情况，对控制器的输出进行限幅。

二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能，符合数字实时控制的真实情况，计算机及DSP 的实时PID 控制都属于这种情况。

1．Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(，式中J=0.0067,B=0.1。

输入信号为)2sin(5.0t π，采用PD 控制，其中5.0,20==d p k k 。

采用ODE45方法求解连续被控对象方程。

因为Bs Js s U s Y s G +==21)()()(，所以u dt dy B dty d J =+22，另y y y y ==2,1，则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ，因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列，第一列为tt时刻对应的y，第二列为tt时刻对应的y导数xk = xx(end,:); % A/D，提取xx中最后一行的值，即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。

位置式PID控制原理

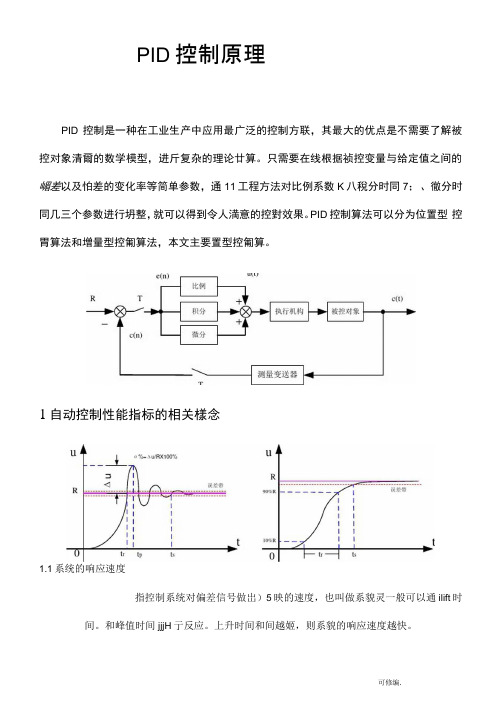
PID控制原理PID控制是一种在工业生产中应用最广泛的控制方联，其最大的优点是不需要了解被控对象清爾的数学模型，进斤复杂的理论廿算。

只需要在线根据祯控变量与给定值之间的嵋差以及怕差的变化率等简单参数，通11工程方法对比例系数K八稅分时同7；、徹分时同几三个参数进行坍整，就可以得到令人満意的控對效果。

PID控制算法可以分为位置型控胃算法和増量型控匍算法，本文主要置型控匍算。

1自动控制性能指标的相关樣念1.1系统的响应速度指控制系统对偏差信号做岀）5映的速度，也叫做系貌灵一般可以通ilift时间。

和峰值时间jjjH亍反应。

上升时间和间越姬，则系貌的响应速度越快。

1.2系统的调节速度系统的快速性主要由调节时间来反映，系缆的调节时间越短，则系统的快速性極好。

系统的快速性与哨应速度是两f不同的Hl念，喑应速度快的系统，其凋节时间不一定短;调节时间短的系统，其哨应速度不一定很高。

1.3系统的稳定性系统的稳定性一般用超圳量"％来反映，超说］量越小，系貌的稳定性越好；起调量強大，系统的稳定性強差。

系统的稳定性与系统的响应速度是一对? IS Ito2PID控制算法式的推导PID控制器的械分方程为:u(t) = K P[e(t) +式中:e⑴一给定值与被控变量的倫差Kp—比例系数刀一枳分时冋常数几一槪分时间常数/一从开始进行期节到输岀当前控制量所经过的时间间用"o—PID调节开始之前瞬间，执行器的输人控制信号，在调节过程中为固定IB对以上各式左右两址分别进行拉普拉祈变換可WPIDSM3的传迪函数为:U(s) _丽—比例0h u P(t) = K P e(t)枳分顶：心(r) = Kp13分顶：心(f) = K£響at对上武进行离散化可得数字武PID控制算式为:u p(n) = K p e(n)“沖)=心?亡e(j)1-0仆(n) = K P¥〔心)-e(“ -1)]式中:e(n)-当前采样时刻给定值与被控变量的偏差T-PID控制采样周期，也就是廿算Jia® e(“)和e(“一l)的时间同禍则位置式PID控翎在当前采样时刻输出至执行器的控制量计算式为:u(n) = Kp<2(”)一心一1)]汁“。

PID算法及参数

PID算法及参数整定知识1.位置表达式位置式表达式是指任一时刻PID控制器输出的调节量的表达式。

PID控制的表达式为式中的y(t)为时刻t控制器输出的控制量，式中的y(0)为被控制量没有偏差时控制器输出的控制量。

由于计算机进入了控制领域。

人们将模拟PID控制规律引入到计算机中来。

由于计算机控制是一种采样控制，它只能根据采样许可的偏差计算控制量，而不能象模拟控制那样连续输出控制量，进行连续控制。

由于这一特点，上面公式中的积分和微分项不能直接使用，必须进行离散化处理。

离散化处理的方法为：以T作为采样周期，k作为采样序号，则离散采样时间kT对应着连续时间 t，用求和的形式代替积分，用增量的形式代替微分，可作如下近似变换：上式中，为了表示方便，将类似于e(kT)简化成e k 形式就可以得到离散的PID表达式：或写成此公式即为位置式的PID表达式。

▪式中：k——采样序号，k=0,1,2,…▪y k ——第k 次采样时刻的计算机输出值▪ e k——第k 次采样时刻输入的偏差值▪e k −1——第k-1 次采样时刻输入的偏差值▪K I ——积分系数。

K I = K P*T/T I▪积分时间T I即为累积多少次/个T）▪K D——微分系数。

K D = K P*T D /T▪如果采样周期取得足够小，则以上近似计算可获得足够精确的结果，离散控制过程与连续控制过程十分接近。

2.增量式表达式利用上面的公式，可得出第k次采样、第k-1次采样时的输出调节量y k、y k-1，用y k-y k-1，即得增量式PID表达式，如下：3.PID参数的工程整定方法参数整定的方法很多，我们只介绍几种工程上最常用的方法。

最实用的是试凑法。

1)临界比例度法这是目前使用较广的一种方法，具体作法如下：先在纯比例作用下（把积分时间放到最大，微分时间放到零），在闭合的调节系统中，从大到小地逐渐地改变调节器的比例度，就会得到一个临界振荡过程，如图8所示。

位置式PID和增量式PID的介绍

位置式PID和增量式PID的介绍1.位置式PIDtypedef struct{float Kp; //⽐例系数Proportionalfloat Ki; //积分系数Integralfloat Kd; //微分系数Derivativefloat Ek; //当前误差float Ek1; //前⼀次误差 e(k-1)float Ek2; //再前⼀次误差 e(k-2)float LocSum; //累计积分位置}PID_LocTypeDef;/************************************************函数名称： PID_Loc功能： PID位置(Location)计算参数： SetValue ------ 设置值(期望值)ActualValue --- 实际值(反馈值)PID ----------- PID数据结构返回值： PIDLoc -------- PID位置作者： strongerHuang*************************************************/float PID_Loc(float SetValue, float ActualValue, PID_LocTypeDef *PID){float PIDLoc; //位置PID->Ek = SetValue - ActualValue;PID->LocSum += PID->Ek; //累计误差PIDLoc = PID->Kp * PID->Ek + (PID->Ki * PID->LocSum) + PID->Kd * (PID->Ek1 - PID->Ek);PID->Ek1 = PID->Ek; return PIDLoc;}2.增量式PIDtypedef struct{float Kp; //⽐例系数Proportionalfloat Ki; //积分系数Integralfloat Kd; //微分系数Derivativefloat Ek; //当前误差float Ek1; //前⼀次误差 e(k-1)float Ek2; //再前⼀次误差 e(k-2)}PID_IncTypeDef;/************************************************函数名称： PID_Inc功能： PID增量(Increment)计算参数： SetValue ------ 设置值(期望值)ActualValue --- 实际值(反馈值)PID ----------- PID数据结构返回值： PIDInc -------- 本次PID增量(+/-)作者： strongerHuang*************************************************/float PID_Inc(float SetValue, float ActualValue, PID_IncTypeDef *PID){float PIDInc; //增量PID->Ek = SetValue - ActualValue;PIDInc = (PID->Kp * PID->Ek) - (PID->Ki * PID->Ek1) + (PID->Kd * PID->Ek2);PID->Ek2 = PID->Ek1;PID->Ek1 = PID->Ek; return PIDInc;}两者的区别：（1）位置式PID控制的输出与整个过去的状态有关，⽤到了误差的累加值;⽽增量式PID的输出只与当前拍和前两拍的误差有关，因此位置式PID控制的累积误差相对更⼤;（2）增量式PID控制输出的是控制量增量，并⽆积分作⽤，因此该⽅法适⽤于执⾏机构带积分部件的对象，如步进电机等，⽽位置式PID适⽤于执⾏机构不带积分部件的对象，如电液伺服阀。

pid算法

在过程控制中，由偏差的比例（P），积分（I）和微分（D）控制的PID控制器（也称为PID调节器）是使用最广泛的自动控制器。

具有原理简单，易于实现，应用范围广，控制参数独立，参数选择简单等优点。

从理论上可以证明，对于过程控制的典型对象“一阶滞后+纯滞后”，对于“二阶滞后+纯滞后”的控制对象，PID控制器是一种最优控制。

控制点目前包含三种比较简单的ＰＩＤ控制算法，分别是：增量式算法，位置式算法，微分先行。

这三种ＰＩＤ算法虽然简单，但各有特点，基本上能满足一般控制的大多数要求。

算法种类：1) PID增量式算法离散化公式：注：各符号含义如下u(t);;;;; 控制器的输出值。

e(t);;;;; 控制器输入与设定值之间的误差。

Kp;;;;;;; 比例系数。

Ti;;;;;;; 积分时间常数。

Td;;;;;;; 微分时间常数。

T;;;;;;;; 调节周期。

对于增量式算法，可以选择的功能有：(1) 滤波的选择可以对输入加一个前置滤波器，使得进入控制算法的给定值不突变，而是有一定惯性延迟的缓变量。

(2) 系统的动态过程加速在增量式算法中，比例项与积分项的符号有以下关系：如果被控量继续偏离给定值，则这两项符号相同，而当被控量向给定值方向变化时，则这两项的符号相反。

由于这一性质，当被控量接近给定值的时候，反号的比例作用阻碍了积分作用，因而避免了积分超调以及随之带来的振荡，这显然是有利于控制的。

但如果被控量远未接近给定值，仅刚开始向给定值变化时，由于比例和积分反向，将会减慢控制过程。

利用这样的算法，可以加快控制的动态过程。

(3) PID增量算法的饱和作用及其抑制在PID增量算法中，由于执行元件本身是机械或物理的积分储存单元，如果给定值发生突变时，由算法的比例部分和微分部分计算出的控制增量可能比较大，如果该值超过了执行元件所允许的最大限度，那么实际上执行的控制增量将时受到限制时的值，多余的部分将丢失，将使系统的动态过程变长，因此，需要采取一定的措施改善这种情况。

位置式PID控制原理

PID 控制原理PID 控制是一种在工业生产中应用最广泛的控制方法，其最大的优点是不需要了解被控对象精确的数学模型，进行复杂的理论计算。

只需要在线根据被控变量与给定值之间的偏差以及偏差的变化率等简单参数，通过工程方法对比例系数P K 、积分时间I T 、微分时间D T 三个参数进行调整，就可以得到令人满意的控制效果。

PID 控制算法可以分为位置型控制算法和增量型控制算法，本文主要讨论位置型控制算。

1 自动控制性能指标的相关概念1.1系统的响应速度指控制系统对偏差信号做出反映的速度，也叫做系统灵敏度。

一般可以通过上升时间r t 和峰值时间p t 进行反应。

上升时间和峰值时间越短，则系统的响应速度越快。

1.2系统的调节速度系统的快速性主要由调节时间来反映，系统的调节时间越短，则系统的快速性越好。

系统的快速性与响应速度是两个不同的概念，响应速度快的系统，其调节时间不一定短；调节时间短的系统，其响应速度不一定很高。

1.3系统的稳定性系统的稳定性一般用超调量% 来反映，超调量越小，系统的稳定性越好；超调量越大，系统的稳定性越差。

系统的稳定性与系统的响应速度是一对矛盾体。

2 PID 控制算法式的推导PID 控制器的微分方程为：式中：)(t e —给定值与被控变量的偏差P K —比例系数I T —积分时间常数D T —微分时间常数t —从开始进行调节到输出当前控制量所经过的时间间隔0u —PID 调节开始之前瞬间，执行器的输入控制信号，在调节过程中为固定值比例项：)()(t e K t u P P =积分项：⎰=t IP I dt t e T K t u 0)(1)( 微分项：dtt de T K t u D P D )()(= 对上式进行离散化可得数字式PID 控制算式为：式中：)(n e —当前采样时刻给定值与被控变量的偏差T —PID 控制采样周期，也就是计算机获取)(n e 和 )1(-n e 的时间间隔则位置式PID 控制在当前采样时刻输出至执行器的控制量计算式为：式中：)(n u —当前采样时刻输出的控制变量0u —PID 调节开始之前瞬间，执行器的输入控制信号3 比例、积分、微分环节的作用3.1 比例环节比例环节是PID 控制器中必不可少的环节。

51单片机PID算法程序(三)增量式PID控制算法解读

图1
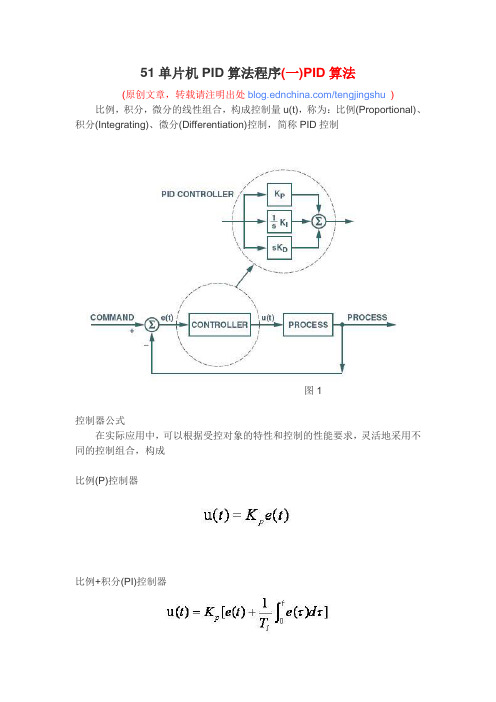
控制器公式
在实际应用中，可以根据受控对象的特性和控制的性能要求，灵活地采用不同的控制组合，构成
比例(P)控制器
比例+积分(PI)控制器
比例+积分+微分(PID)控制器
式中
或ቤተ መጻሕፍቲ ባይዱ
式中
控制系统中的应用
在单回路控制系统中，由于扰动作用使被控参数偏离给定值，从而产生偏差。自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算，并输出统一标准信号，去控制执行机构的动作，以实现对温度、压力、流量、也为及其他工艺参数的自动控制。
T ——采样周期。
如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。
51单片机PID算法程序(一)PID算法
(原创文章，转载请注明出处/tengjingshu)
比例，积分，微分的线性组合，构成控制量u(t)，称为：比例(Proportional)、积分(Integrating)、微分(Differentiation)控制，简称PID控制
（图1，表1）
2）Atmel8-bit AVR Microcontrollers Application Note:AVR221: Discrete PID controller
（图2，图3，图4，图5，表2）
3）使用Ziegler-Nichols方法的自整定控制
/2007-03/200733042815.htm
最好的寻找PID参数的办法是从系统的数学模型出发，从想要的反应来计算参数。很多时候一个详细的数学描述是不存在的，这时候就需要实际地调节PID的参数.
Ziegler-Nichols方法

pid控制算法系列(2)pid控制算法

pid控制算法系列（2）pid控制算法1.PID控制算法的基本思想PID算法是一种具有预见性的控制算法，其核心思想是：1>. PID算法不但考虑控制对象的当前状态值（现在状态），而且还考虑控制对象过去一段时间的状态值（历史状态）和最近一段时间的状态值变化（预期）,由这3方面共同决定当前的输出控制信号；2>.PID控制算法的运算结果是一个数，利用这个数来控制被控对象在多种工作状态（比如加热器的多种功率，阀门的多种开度等）工作，一般输出形式为PWM，基本上满足了按需输出控制信号，根据情况随时改变输出的目的。

2.PID算法分析：设某控制系统：用户设定值为SV(也就是希望通过PID控制算法使被控制对象的状态值保持在SV的附近)。

1>从系统投入运行开始，控制算法每隔一段时间对被控制对象的状态值进行采样。

由此，可得到开机以来由各个采样时间点被控制对象的状态值所形成的数据序列：X1,X2, X3, X4, .... Xk-2,Xk-1,Xk说明：X1：开机以来的第一次采样值Xk: 目前的采样值（最近一次的采样值）2> 从这个采样值序列中提取出三方面信息：①当前采样值Xk与用户设定值SV之间的差值：EkEk =Sv - Xk分析Ek:Ek >0:说明当前状态值未达标Ek=0:说明当前控制状态值正好满足要求Ek<0:说明当前状态值已经超标结论：Ek反应了控制对象当前值与设定值的偏差程度，可以根据Ek的大小对输出信号OUT进行调整：偏差程度大OUT增大，偏差程度小OUT减小。

即输出信号的强弱与当前偏差程度的大小成比例，所以根据Ek的大小来给出控制信号OUT的当前值的算法称为比例控制（Proportion）。

用数学模型可以表示为：POUT=（Kp*Ek）+ Out0Kp:一般称之为比例系数，可以理解为硬件上的放大器（或衰减器），适当选取Kp将当前误差值Ek按一定的增益放大或缩小，以提高控制算法的相应速度。

PID控制规律及数字PID基本算法

PID控制规律及数字PID基本算法
未经许可不得转载内容仅限参考
知识回顾
系统控制的目标
r (t) e(t)
u (t)
校正环节 G c ( s )
c (t)
执行机构
检测单元
c (t) 被控对象 G ( s )
一、连续PID基本控制规律
连续系统校正环节基本控制规律
1、比例控制
r (t)
e (t)
K p u (t)
Kp
c (t)
2、比例积分控制
3、r (比t ) 例微c e( (t分t) )G控cK(s制p)(1KTp1i (s1T)isuT(its)) 微分控制能反应输入信号的变化趋势，因此在输入信
r (t)
号的量值变得太大之前，可为系统引入一个有效的早
e (t)
Kp(1Tds) u ( t )
四、数字PID位置式与增量式算法程序实现
数字PID位置式算例
控制对象 G(s)s387.53253s520010470s
u (k) K p [e (k) T T s i j k0e (j) T de (k) T e s(k 1 )]
设计数字PID控制器，实现系统对正弦信号、
随机信号的跟踪。
rin,yout
k 0
k 0
积分环节的离散化处理
微分环节的离散化处理
1
e(t)dt
Ti 0
T e(kT)
Ti k0
T dde d (tt)
T de(kT)e T [(k 1 )T]
三、数字PID位置式与增量式算法
数字PID位置式
u (k) K p [e (k) T T s i j k0e (j) T de (k) T e s(k 1 )]

位置式PID控制算法的简化示意图

位置式PID控制算法的简化示意图上图的传递函数为：（2-1）在时域的传递函数表达式（2-2）对上式中的微分和积分进行近似（2-3）式中n是离散点的个数。

于是传递函数可以简化为：（2-4）其中u(n)——第k个采样时刻的控制；KP ——比例放大系数；Ki ——积分放大系数；Kd ——微分放大系数；T ——采样周期。

如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

（2-4）表示的控制算法直接按（2-1）所给出的PID控制规律定义进行计算的，所以它给出了全部控制量的大小，因此被称为全量式或位置式PID控制算法。

缺点：1）由于全量输出，所以每次输出均与过去状态有关，计算时要对e(k)(k=0,1,…n)进行累加，工作量大。

位置式PID控制算法C51程序具体的PID参数必须由具体对象通过实验确定。

这个程序只是一般常用pid算法的基本架构，没有包含输入输出处理部分。

=================================================================== ==================================*/#include <reg52.h>#include <string.h> //C语言中memset函数头文件/*================================================================== ==================================PID FunctionThe PID (比例、积分、微分) function is used in mainlycontrol applications. PIDCalc performs one iteration of the PIDalgorithm.While the PID function works, main is just a dummy program showinga typical usage.=================================================================== ==================================*/typedef struct PID {double SetPoint; // 设定目标Desired valuedouble Proportion; // 比例常数Proportional Constdouble Integral; // 积分常数Integral Constdouble Derivative; // 微分常数Derivative Constdouble LastError; // Error[-1]double PrevError; // Error[-2]double SumError; // Sums of Errors} PID;/*================================================================== ==================================PID计算部分=================================================================== ==================================*/double PIDCalc( PID *pp, double NextPoint ){double dError, Error;Error = pp->SetPoint - NextPoint; // 偏差pp->SumError += Error; // 积分dError = Error - pp->LastError; // 当前微分pp->PrevError = pp->LastError;pp->LastError = Error;return (pp->Proportion * Error // 比例项+ pp->Integral * pp->SumError // 积分项+ pp->Derivative * dError // 微分项);}/*================================================================== ==================================Initialize PID Structure PID参数初始化=================================================================== ==================================*/void PIDInit (PID *pp){memset ( pp,0,sizeof(PID));}/*================================================================== ==================================Main Program 主程序=================================================================== ==================================*double sensor (void) // Dummy Sensor Function{return 100.0;}void actuator(double rDelta) // Dummy Actuator Function{}void main(void){PID sPID; // PID Control Structuredouble rOut; // PID Response (Output)double rIn; // PID Feedback (Input)PIDInit ( &sPID ); // Initialize StructuresPID.Proportion = 0.5; // Set PID CoefficientssPID.Integral = 0.5;sPID.Derivative = 0.0;sPID.SetPoint = 100.0; // Set PID Setpointfor (;;) { // Mock Up of PID ProcessingrIn = sensor (); // Read InputrOut = PIDCalc ( &sPID,rIn ); // Perform PID Interation actuator ( rOut ); // Effect Needed Changes}。

PID算法程序—位置式PID控制算法

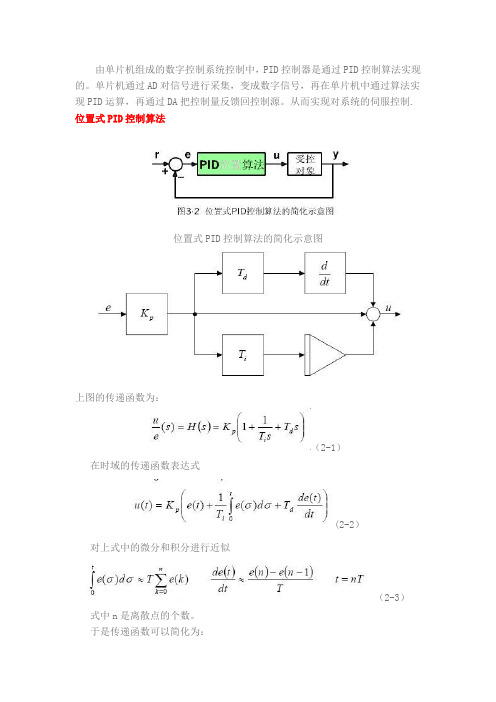
由单片机组成的数字控制系统控制中，PID控制器是通过PID控制算法实现的。

单片机通过AD对信号进行采集，变成数字信号，再在单片机中通过算法实现PID运算，再通过DA把控制量反馈回控制源。

从而实现对系统的伺服控制. 位置式PID控制算法位置式PID控制算法的简化示意图上图的传递函数为：（2-1）在时域的传递函数表达式(2-2）对上式中的微分和积分进行近似（2-3）式中n是离散点的个数。

于是传递函数可以简化为：（2-4）其中u（n)——第k个采样时刻的控制；-—比例放大系数；KP——积分放大系数；KiK——微分放大系数;dT —-采样周期.如果采样周期足够小,则（2—4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

（2-4）表示的控制算法直接按(2-1）所给出的PID控制规律定义进行计算的,所以它给出了全部控制量的大小,因此被称为全量式或位置式PID控制算法。

缺点：1）由于全量输出，所以每次输出均与过去状态有关，计算时要对e（k)（k=0,1，…n）进行累加，工作量大。

2) 因为计算机输出的u(n）对应的是执行机构的实际位置，如果计算机出现故障，输出u（n）将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实际生产中是不允许的。

位置式PID控制算法程序具体的PID参数必须由具体对象通过实验确定。

由于单片机的处理速度和ram资源的限制,一般不采用浮点数运算,而将所有参数全部用整数，可大大提高运算速度。

这个程序只是一般常用pid算法的基本架构，没有包含输入输出处理部分.===================================================================== /＊===================================================================== ==================================================================================================== ================================*/typedef struct PID {double SetPoint；// 设定目标Desired valuedouble Proportion; // 比例常数Proportional Constdouble Integral; // 积分常数Integral Constdouble Derivative；// 微分常数Derivative Constdouble LastError；// Error［-1］double PrevError; // Error［-2］double SumError; // Sums of Errors} PID;/＊===================================================================== ===============================PID计算部分===================================================================== ================================＊/double PIDCalc( PID *pp, double NextPoint ）｛double dError, Error;Error = pp->SetPoint - NextPoint；// 偏差pp—〉SumError += Error；// 积分dError = Error — pp->LastError; // 当前微分pp->PrevError = pp->LastError；pp—〉LastError = Error；return (pp—>Proportion * Error // 比例项+ pp-〉Integral * pp->SumError // 积分项+ pp—>Derivative ＊ dError // 微分项)；｝/＊===================================================================== ===============================Initialize PID Structure PID参数初始化===================================================================== ================================＊/void PIDInit （PID ＊pp)｛memset （ pp,0,sizeof(PID));｝/*=================================================================== =================================Main Program 主程序===================================================================== ================================＊double sensor (void） // Dummy Sensor Function{｝void actuator(double rDelta）// Dummy Actuator Function｛｝void main（void){PID sPID； // PID Control Structuredouble rOut; // PID Response （Output)double rIn; // PID Feedback （Input)PIDInit ( ＆sPID ); // Initialize StructuresPID。

PID控制原理和形式

—交流—
PID控制原理和形式
2024年9月21日
1
3.1概述
—交流—
• 概念：系统偏差旳百分比(Proportional)、积分(Integral)和微分(Derivative)旳综合控制，简称PID控制
• 特点：算法简朴、鲁棒性强和可靠性高
• 发展：气动->电动->电子->数字
2024年9月21日
24
—交流—
控制器百分比作用参数对系统性能旳
影响
P(t) K Pe(t)
1）动态影响
– 百分比系数Kp加大，使系统旳动作敏捷，速度加紧，振荡次数增多，调整时间变长。当 Kp太大时，系统会趋于不稳定。若Kp太小，又会使系统旳响应动作变化缓慢。
2）稳态影响
– 加大百分比系数Kp，在系统稳定旳情况下，能够减小稳态误差，提升控制精度，却不能完全消除稳态误差。
2024年9月21日
15
0
—交流—
（二)百分比调整(P调整)
➢⑴百分比调整器旳调整规律 ➢⑵百分比调整器旳静态偏差 ➢⑶百分比调整器旳特点
2024年9月21日
16
0
—交流—
⑴百分比调整器旳调整规律
输出信号与输入信号成百分比旳调整器称为百分
比调整器，简称P调整器。其调整规律为：
P(t) K Pe(t)
2024年9月21日
29
0
—交流—
（三）百分比积分调整(PI调整)
➢⑴积分调整器旳调整规律 ➢⑵百分比积分调整器旳调整规律 ➢⑶百分比积分调整器旳特点
2024年9月21日
30
0
—交流—
⑴积分调整器旳调整规律
①输出信号与输人信号成积分关系旳调整器称为

51单片机PID算法程序

51单片机PID算法程序(二)位置式PID控制算法由51单片机组成的数字控制系统控制中，PID控制器是通过PID控制算法实现的。

51单片机通过AD对信号进行采集，变成数字信号，再在单片机中通过算法实现PID运算，再通过DA把控制量反馈回控制源。

从而实现对系统的伺服控制。

位置式PID控制算法位置式PID控制算法的简化示意图? 上图的传递函数为：（2-1）?? 在时域的传递函数表达式（2-2）?? 对上式中的微分和积分进行近似（2-3）?? 式中n是离散点的个数。

?? 于是传递函数可以简化为：（2-4）其中u(n)——第k个采样时刻的控制；K P? ——比例放大系数；???K i?? ——积分放大系数；K d?? ——微分放大系数；T?? ——采样周期。

如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

（2-4）表示的控制算法直接按（2-1）所给出的PID控制规律定义进行计算的，所以它给出了全部控制量的大小，因此被称为全量式或位置式PID控制算法。

缺点：1）??????????? 由于全量输出，所以每次输出均与过去状态有关，计算时要对e(k)(k=0,1,…n)进行累加，工作量大。

2）??????????? 因为计算机输出的u(n)对应的是执行机构的实际位置，如果计算机出现故障，输出u(n)将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实际生产中是不允许的。

位置式PID控制算法C51程序具体的PID参数必须由具体对象通过实验确定。

这个程序只是一般常用pid算法的基本架构，没有包含输入输出处理部分。

位置式PID控制原理分享

位置式PID控制原理分享PID 控制原理PID 控制是⼀种在⼯业⽣产中应⽤最⼴泛的控制⽅法，其最⼤的优点是不需要了解被控对象精确的数学模型，进⾏复杂的理论计算。

只需要在线根据被控变量与给定值之间的偏差以及偏差的变化率等简单参数，通过⼯程⽅法对⽐例系数P K 、积分时间I T 、微分时间D T 三个参数进⾏调整，就可以得到令⼈满意的控制效果。

PID 控制算法可以分为位置型控制算法和增量型控制算法，本⽂主要讨论位置型控制算。

1 ⾃动控制性能指标的相关概念1.1系统的响应速度指控制系统对偏差信号做出反映的速度，也叫做系统灵敏度。

⼀般可以通过上升时间r t 和峰值时间p t 进⾏反应。

上升时间和峰值时间越短，则系统的响应速度越快。

1.2系统的调节速度系统的快速性主要由调节时间来反映，系统的调节时间越短，则系统的快速性越好。

系统的快速性与响应速度是两个不同的概念，响应速度快的系统，其调节时间不⼀定短；调节时间短的系统，其响应速度不⼀定很⾼。

1.3系统的稳定性系统的稳定性⼀般⽤超调量%σ来反映，超调量越⼩，系统的稳定性越好；超调量越⼤，系统的稳定性越差。

系统的稳定性与系统的响应速度是⼀对⽭盾体。

2 PID 控制算法式的推导PID 控制器的微分⽅程为：00])()(1)([)(u dt t de T dt t e T t e K t u D tIP +++=?式中：)(t e —给定值与被控变量的偏差P K —⽐例系数I T —积分时间常数 D T —微分时间常数t —从开始进⾏调节到输出当前控制量所经过的时间间隔0u —PID 调节开始之前瞬间，执⾏器的输⼊控制信号，在调节过程中为固定值⽐例项：)()(t e K t u P P =积分项：?=tIPI dt t e T K t u 0)(1)(微分项：dtt de T K t u DP D )()(= 对上式进⾏离散化可得数字式PID 控制算式为：)()(n e K n u P P =∑==ni IPI i e T TK n u 0)()()]1()([)(--=n e n e TT K n u DPD 式中：)(n e —当前采样时刻给定值与被控变量的偏差T —PID 控制采样周期，也就是计算机获取)(n e 和 )1(-n e 的时间间隔则位置式PID 控制在当前采样时刻输出⾄执⾏器的控制量计算式为：00)]1()([)()()(u n e n e T T i e T T n e K n u ni DI P +?--++=∑= 式中：)(n u —当前采样时刻输出的控制变量0u —PID 调节开始之前瞬间，执⾏器的输⼊控制信号3 ⽐例、积分、微分环节的作⽤3.1 ⽐例环节⽐例环节是PID 控制器中必不可少的环节。