图解球体表面积和体积正确计算方法及计算公式
1.3.2 球的体积与表面积

B
练习.若一个球的外切正方体的全面积 等于6,求球的体积。 1
6
A B
O1
C
C
思考练习:左图是一个奖杯的三视图(单位:cm),
画出它的直观图,并计算这个奖杯的表面积
和体积(精确到1cm)。
4 20 8
4
10 16 8
20 2
z’
y’
o'
x'
答、表面积和体积分别是:1193cm2,1067cm3
爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”爱是什么? 一个精灵坐在碧绿的枝叶间沉思。 风儿若有若无。 一只鸟儿飞过来,停在枝上,望着远处将要成熟的稻田。 精灵取出一束黄澄澄的稻谷问道:“你爱这稻谷吗?” “爱。” “为什么?” “它驱赶我的饥饿。” 鸟儿啄完稻谷,轻轻梳理着光润的羽毛。 “现在你爱这稻谷吗?”精灵又取出一束黄澄澄的稻谷。 鸟儿抬头望着远处的一湾泉水回答:“现在我爱那一湾泉水,我有点渴了。” 精灵摘下一片树叶,里面盛了一汪泉水。 鸟儿喝完泉水,准备振翅飞去。 “请再回答我一个问题,”精灵伸出指尖,鸟儿停在上面。 “你要去做什么更重要的事吗?我这里又稻谷也有泉水。” “我要去那片开着风信子的山谷,去看那朵风信子。” “为什么?它能驱赶你的饥饿?” “不能。” “它能滋润你的干渴?” “不能。”
球的体积和表面积公式怎么算

球的体积和表面积公式怎么算
球的体积和表面积怎么算呢?公式又有哪些呢?同学们快来和小编一起看看吧。
下面是由小编为大家整理的“球的体积和表面积公式怎么算”,仅供参考,欢迎大家阅读。
球的体积和表面积公式
球的表面积计算公式: 球的表面积=4πr^2, r为球半径。
一个半圆绕直径所在直线旋转一周所成的空间几何体叫做球体,简称球,半圆的半径即是球的半径。
球体是有且只有一个连续曲面的立体图形,这个连续曲面叫球面。
球的体积V=4/3πR的立方 R为球的半径。
拓展阅读:球体性质
用一个平面去截一个球,截面是圆面。
球的截面有以下性质:
1球心和截面圆心的连线垂直于截面。
2球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R^2-d^2
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆。
在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离。
球的面积公式推导过程
球体表面积公式S(球面)=4πr^2。
运用第一数学归纳法:把一个半径为R的球的上半球横向切成n 份,每份等高,
并且把每份看成一个圆柱,其中半径等于其底面圆半径,
则从下到上第k个圆柱的侧面积S(k)=2πr(k)×h
其中h=R/n,r(k)=√[R^2;-﹙kh^2;]=2πR^2;×√[1/n^2;-(k/n^2)^2;]
则S(1)+S(2)+……+S(n)当n取极限(无穷大)的时候,半球表面积就是2πR^2;
球体乘以2就是整个球的表面积4πR^2。
球的表面积和体积

球
生活中常见的球体:
思考:
一
球的概念是什么?
二
三
球有哪些性质?
如何求球的体积
和表面积?
球的概 念和性 质
一
球的概念
如图所示,半圆以它的直 径为旋转轴,旋转所成的曲面 叫做球面. 球面所围成的几何 体叫做球体,简称球. 半圆的 圆心叫球心,图中点O. 连结球 心和球面上任意一点的线段叫 做球的半径,图中线段R. 连结 球面上两点并且经过球心的线 段叫做球的直径,图中线段AB.
直径.求证: (1) 球的表面积等于 圆柱的侧面积; (2) 球的表面积等于 圆柱全面积的2/3. 证明:(1)设球的半径为 R,则圆柱的底面半径 为R,高S球 4 R , 2 S圆柱面 2 R 2R=4 R .
2
S球 S圆柱面 .
(2)
S圆柱全 4 R 2 R 6 R ,
球的概 念和性 质
二
球的性质
用一个平面(如图中平面 )去截一个球, 截面是圆面,球的截面有下面的性质: ⑴、球心和截面圆心的连线 垂直于截面(如图直线o1o2 垂直于平面 ); o ⑵、球心到截面的距离d R d 与球的半径R及截面的半 r o 径r有下面的关系:
1 2
r R d
2
2
例题 讲解 如图,圆柱的底面直径与高都等于球的 例2、
课堂 小结 熟练掌握球的体积、表面积公式:
4 3 ①V R 3 2 ②S 4 R
A
C RO
B
球的概 念和性 质
一
球的概念
球面被经过球心的平面截得的圆叫做大圆(如 图中红色部分),被不经过球心的截面截得的圆叫 做小圆(如图中绿色部分). Q 球面上两点之间最短连线 的长度,就是经过这两点的 大圆在这两点间的一段劣弧 O 的长度,这个弧长叫做两点 P 的球面距离(如图中 PQ的长 度就是P、Q两点之间的球面 距离 ).
球的表面积与体积PPT课件

5,15,求它的外接球表面积 .
四面体与球的“接切”问题
典型:正四面体ABCD的棱长为a,求 其内切球半径r与外接球半径R.
思考:若正四面体变成正三棱锥,方法 是否有变化?
1、内切球球心到多面体各面的距离均相等,外接球 球心到多面体各顶点的距离均相等 2、正多面体的内切球和外接球的球心重合 3、正棱锥的内切球和外接球球心都在高线上,但不 重合 4、基本方法:构造三角形利用相似比和勾股定理 5、体积分割是求内切球半径的通用做法
R
2R
R
2
延伸阅读:割圆术
早在公元三世纪,我国数学家刘徽 为推导圆的面积公式而发明了“倍 边法割圆术”。
他用加倍的方式不断增加圆内接正
多边形的边数,使其面积与圆的面
积之差更小,即所谓“割之弥细,
所失弥小”。这样重复下去,就达
到了“割之又割,以至于不可再割, 思考:能否也
则与圆合体而无所失矣”。
采取“分割”与
球与正方体的“接切”问题
典型:有三个球,一球切于正方体的各面,一球切 于正方体的各侧棱,一球过正方体的各顶点,求 这三个球的体积之比.
a
r1
a 2
a
r2
2a 2
a
r3
3a 2
a
2a
2a
•画出正确的截面:(1)中截面;(2)对角面 •找准数量关系
球与正方体的“接切”问题
1.一个正方体的顶点都在 球面上,它的棱长 是4cm,求这个球队体积. 2.钢球直径5cm,把钢球放入一个正方 体的 有盖纸盒中,至少要用 多少纸? 3.半球内有一内接正方体 ,正方体的一个面 在半球的底面圆上,若 正方体的一边长为
球的体积与表面积公式

球的体积与表面积公式球体是一种三维几何体,其特点是每一点到中心点的距离都相等。
计算球的体积和表面积是在数学和几何学中的基本问题。
本文将介绍球的体积和表面积的计算公式,并且通过实例演示如何应用这些公式进行计算。
一、球的体积公式球体的体积是指球内部所占据的空间大小,用于描述球体的容积。
球的体积公式如下:V = (4/3)πr³其中,V表示球的体积,π是一个数学常数,近似值为3.14159,r 表示球的半径。
例如,如果已知一个球的半径为5单位长度,我们可以使用体积公式计算该球的体积。
V = (4/3)π(5)³≈ 523.6因此,该球的体积近似为523.6个单位体积。
二、球的表面积公式球体的表面积是指球的外部曲面的总面积,用于描述球的大小。
球的表面积公式如下:A = 4πr²其中,A表示球的表面积,π是一个数学常数,近似值为3.14159,r表示球的半径。
举个例子,如果已知一个球的半径为5单位长度,我们可以使用表面积公式计算该球的表面积。
A = 4π(5)²≈ 314.159因此,该球的表面积近似为314.159个单位面积。
三、应用实例为了更好地理解球的体积和表面积公式的应用,我们举个具体的实例。
假设有一个网球,其半径为3.5单位长度,我们可以通过体积公式计算该网球的体积。
V = (4/3)π(3.5)³≈ 179.592因此,该网球的体积近似为179.592个单位体积。
同时,我们可以通过表面积公式计算该网球的表面积。
A = 4π(3.5)²≈ 153.937因此,该网球的表面积近似为153.937个单位面积。
这个实例向我们展示了如何使用球的体积和表面积公式进行计算。
通过掌握这些公式,我们可以方便地计算不同半径的球体的体积和表面积,为实际问题解决提供了数学工具和便利。
总结:本文介绍了球的体积和表面积的公式,并通过实例演示了如何应用这些公式进行计算。
球的表面积和体积.ppt

A
RO C
B
2. 球的表面积 半径是R的球的表面积是
2. 球的表面积 半径是R的球的表面积是
S=4R2
3. 球的体积 半径是R的球的体积是
3. 球的体积 半径是R的球的体积是
V 4 πR3 . 3
有一种空心钢球, 质量为142g, 测得外径等于5.0cm, 求它的内径 (钢的密度为7.9g/cm3, 精确到0.1cm).
体积公式的应用.
1.3.2 球的体积 和表面积
复习引入
讲授新课
1.球的概念
A
RO C
B
讲授新课
1.球的概念 与定点的距离等于或小于定长的点
的集合,叫做球体,简称球.
Aห้องสมุดไป่ตู้
RO C
B
讲授新课
1.球的概念 与定点的距离等于或小于定长的点
的集合,叫做球体,简称球.
定点叫做球心,
定长叫做球的半径.
A
RO C
B
讲授新课
1.球的概念 与定点的距离等于或小于定长的点
的集合,叫做球体,简称球.
定点叫做球心, 定长叫做球的半径.
与定点距离等 于定长的点的集合 叫做球面.
A
RO C
B
讲授新课
1.球的概念 与定点的距离等于或小于定长的点
的集合,叫做球体,简称球.
定点叫做球心, 定长叫做球的半径.
与定点距离等 于定长的点的集合 叫做球面.
圆柱的底面直径与高都等于球 的直径. (1) 求球的体积与圆柱体积之比; (2) 证明球的表面积等于圆柱的
侧面积.
探究 若正方体的棱长为a,则
⑴正方体的内切球直径= a
⑵正方体的外接球直径= ⑶与正方体所有棱相切的球直径=
圆球的表面积公式和体积公式

圆球的表面积公式和体积公式
圆球的表面积公式和体积公式是指一个圆球的表面积和体积可以用统一的公式来计算,它是几何数学中最重要的几何体之一,广泛应用于生活中。
一般来说,圆球是一种近似球形的物体,它的表面是圆形的,其中只有一个中心点,中心点到表面的距离称为半径r。
根据三角函数的基本性质可知,一个圆的面积和周长都可以用圆的半径r来表示。
因此,圆球的表面积S和体积V可以分别用下面的公式来计算:
圆球的表面积公式:S=4πr²
圆球的体积公式:V=4/3πr³
其中,S表示圆球的表面积,V表示圆球的体积,r表示圆球的半径,π表示圆周率(取值为
3.1415926……)。
同时,我们也可以用另一种方法来计算圆球的表面积S和体积V,即把圆球看作由多个小圆块组成的。
这样,我们可以用如下的公式来计算圆球的表面积S和体积V:圆球的表面积公式:S=2πr(h+r)
圆球的体积公式:V=(4/3)πr³
其中,h表示圆球的高度,r表示圆球的半径,π表示圆周率(取值为3.1415926……)。
此外,圆球的表面积S和体积V也可以通过立体几何的原理来计算。
例如,我们可以把圆球看作由三棱锥和六棱柱组成的,并利用三棱锥和六棱柱的体积公式来计算圆球的表面积S和体积V。
总之,圆球的表面积S和体积V可以用多种方法来计算,从最常见的公式法到更复杂的几何原理法,只要能正确的把握公式和原理,就可以很容易的计算出圆球的表面积S和体积V。
如何求球体的体积和表面积PPT课件

3 半球
定理 半径是 R 的球的体积是
V半球
4 R3
3
第8页/共19页
思考:我们能用同样的方法推导球的
表面积公式吗?
S i
o
第9页/共19页
把球面任意分割为一些“小球面片”,分别
用 S, S, , S, 表示
1
2
3
设以小球面片
S
为底,球心
i
O
为顶点的“小锥体”
i 为第 个小锥体,则球表面积为
答: 空心钢球的内径约为 4.5cm.
第13页/共19页
例2. 一个正方体的顶点在球面上,它的棱长
为4cm,求这个球的体积和表面积。
解:该球的半径为
1 4 2cm 2
V球 =4323=332cm A
C′
o
S球 = 4 221 6 cm
第14页/共19页
例3 地球和火星都可以看作近似球体,地球半径约
2
i
O
V1 SR 1 SR 1 SR .
31 32
3i
1RSS S O
3
1
2
i
S S S S
1
2
i
V 1 RS
O
3
第11页/共19页
V 1 RS
已知球的体积 3
所以
V 4 R3
3
从而
4 R 3 1 RS
3
3
S 4R2
定理
R 半径是 的球的表面积是
S 4R2
第12页/共19页
i 计算第 层“薄圆片“的体积
由勾股定理 ri R2 R ni 1 2, i 1 ,2, ,n
第 i 层“薄圆片”的体积是
球体的表面积和体积的公式

球体的表面积和体积的公式
一、球体的表面积公式。
1. 公式内容。
- 设球的半径为r,球的表面积公式为S = 4π r^2。
2. 公式推导(简单理解)
- 可以把球的表面想象成由很多个小的三角形组成。
当把这些小三角形分得足够小的时候,它们的面积之和就近似等于球的表面积。
- 通过复杂的数学积分等方法可以严格证明得到S = 4π r^2这个公式。
3. 应用示例。
- 例:已知一个球的半径r = 3,求其表面积。
- 解:根据公式S = 4π r^2,将r = 3代入可得S=4π×3^2=4π×9 = 36π。
二、球体的体积公式。
1. 公式内容。
- 设球的半径为r,球的体积公式为V=(4)/(3)π r^3。
2. 公式推导(简单理解)
- 可以使用积分的方法推导。
从球的截面来看,随着高度的变化,截面圆的面积是一个关于高度的函数,对这个函数在球的直径范围内进行积分就可以得到球的体积公式。
- 也可以通过祖暅原理(等幂等积定理),将球与其他已知体积公式的几何体(如圆柱、圆锥等)进行比较推导得出。
3. 应用示例。
- 例:已知球的半径r = 2,求其体积。
- 解:根据公式V=(4)/(3)π r^3,将r = 2代入可得V=(4)/(3)π×2^3=(4)/(3)π×8=(32)/(3)π。
球表面积和体积

球的表面积和体积1.球的表面积公式:S球面=4πR2(R为球半径) 2.球的体积公式:V球=43πR3(R为球半径)球的表面积和体积的计算过球的半径的中点,作一垂直于这条半径的截面,已知此截面的面积为12π cm2,试求此球的表面积.若截面不过球的半径的中点,而是过半径上与球心距离为1的点,且截面与此半径垂直,若此截面的面积为π,试求此球的表面积和体积.球的表面积及体积的应用一个倒立圆锥形容器,它的轴截面是正三角形,在此容器内注入水并且放入一个半径为r的铁球,这时水面恰好和球面相切,问将球从圆锥内取出后,圆锥内水面的高是多少?圆柱形容器的内壁底面半径为5 cm,两个直径为5 cm的玻璃小球都浸没于容器的水中,若取出这两个小球,则容器的水面将下降多少?有关球的切、接问题求棱长为a的正四面体P—ABC的外接球,内切球的体积.有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体各条棱都相切,第三个球过这个正方体的各个顶点,求这三个球的表面积之比.一个球内有相距9 cm的两个平行截面,面积分别为49π cm2和400π cm2,求球的表面积.基础训练1.若球的体积与其表面积数值相等,则球的半径等于()A.12B.1C.2 D.32.用过球心的平面将一个球平均分成两个半球,则两个半球的表面积是原来整球表面积的________倍.3.过球的半径的中点,作一垂直于这条半径的截面,已知此截面的面积为48π cm2,试求此球的表面积和体积.4.正方体的表面积与其外接球表面积的比为()A.3∶π B.2∶πC.1∶2π D.1∶3π5.(2013·温州高一检测)长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )A .25πB .50πC .125πD .都不对4.把3个半径为R 的铁球熔成一个底面半径为R 的圆柱,则圆柱的高为( )A .RB .2RC .3RD .4R6.设三棱柱的侧棱垂直于底面,所有棱的长都为a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2 B.73πa 2C.113πa 2 D .5πa 27.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径是________cm.提高训练.1.一只小球放入一长方体容器内,且与共点的三个面相接触.若小球上一点到这三个面的距离分别为4、5、5,则这只小球的半径是 ( )A .3或8B .8或11C .5或8D .3或112.已知A 、B 、C 是球O 的球面上三点,三棱锥O ABC -的高为22,且ABC ∠=60º ,AB =2, BC =4,则球O 的表面积为( )A . 24π B.32π C. 48π D.192π3.一几何体的三视图如右图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A .4πB .π3C .π2D .π4. 将半径都为1的四个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为 ( )A.3263+B. 2+263C. 4+263D. 43263+5. 某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )A .5πB .12πC .20πD .8π6.【江西省抚州市临川一中2015届高三10月月考】已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的全面积是( )A . 18B .36C . 45D . 547.【浙江省重点中学协作体2015届第一次适应性训练】一几何体的三视图如右图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A . 4πB .π3C .π2D .π8.【山西省大同市2015届高三学情调研测试】设三棱柱的侧棱垂直于底面,所有棱长都为a ,顶点都在一个球面上,则该球的表面积为( )A.2a πB. 237a πC. 2311a πD. 25a π9.【四川省成都实验外国语高2015届高三11月月考】某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的表面积为( )A .3πB .π4C .π2D .π2510. 【全国高考新课标(I )理】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为( )A 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D 、2048π3cm 311. 矩形ABCD 中,4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积是( )A.π12125B.π9125C.π6125D.π3125 12.在半径为R 的球内放入大小相等的4个小球,则小球半径r 的最大值为( )A. (2-1)R B . (6-2)R C. 1 4R D. 1 3R13. 一个平面截一个球得到直径是6的圆面,球心到这个平面的距离是4,则该球的体积是 .14.三棱锥P ABC -的四个顶点均在同一球面上,其中ABC ∆是正三角形,PA ⊥平面ABC ,26PA AB ==,则该球的体积是 .15.一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是16. 四棱锥ABCD P -的五个顶点都在一个球面上,且底面ABCD 是边长为1的正方形,ABCD PA ⊥,2=PA ,则该球的体积为 _ .17. 过球O 表面上一点A 引三条长度相等的弦AB 、AC 、AD ,且两两夹角都为︒60,若球半径为R ,求弦AB 的长度.19. 【改编自浙江高考题】已知球O 的面上四点A 、B 、C 、D ,DA ABC ⊥平面,AB BC ⊥,DA=AB=BC=3,求球O 的体积.20. 【改编自山东高考题】在等腰梯形ABCD 中,AB=2DC=2,0DAB=60∠,E 为AB 的中点,将ADE ∆与BEC ∆分布沿ED 、EC 向上折起,使A B 、重合于点P ,求三棱锥P-DCE 的外接球的体积.21. 一个正四棱锥的底面边长为2,侧棱长为3,五个顶点都在同一个球面上,求此球的表面积.22. 球面上有3个点,其中任意两点的球面距离都等于大圆周长的61,经过3个点的小圆的周长为π4,求这个球的半径.。
1.3.2 球的体积和表面积

题型三 与球相关的“切”“接”问题 【例3-1】 正四棱锥的顶点都在同一球面上,若该棱锥的高为6,底面边 长为4,则该球的表面积为( )
(A) 44 π 3
(B) 484 π 9
(C) 81 π 4
(D)16π
解析:如图,正四棱锥 P-ABCD 中,PE 为四棱锥的高,根据球的 相关知识可知,四棱锥的外接球的球心 O 必在正四棱锥的高线 PE 所在的直线上,因为底面边长为 4,
自我检测(教师备用)
1.一个球的大圆面积为9π ,则它的表面积和体积分别是( C )
(A)9π ,27π
(B)9π ,36π
(C)36π ,36π (D)36π ,48π
2.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( D ) (A)R (B)2R (C)3R (D)4R
3.平面α 截球 O 的球面所得圆的半径为 1,球心 O 到平面α 的距离为 2 ,则此 球的体积为( B )
答案: 6 π ∶2
方法技巧 解决几何体与球相切或相接的策略: (1)要注意球心的位置,一般情况下,由于球的对称性球心在几何体的特 殊位置,比如,几何体的中心或长方体对角线的中点等. (2)解决此类问题的实质就是根据几何体的相关数据求球的直径或半径, 关键是根据“切点”和“接点”,作出轴截面图,把空间问题转化为平 面问题来计算.
3
3
(B) 15 π 3
(D) 4 π + 15 π
3
3
解析:(1)由三视图可知,该几何体由一个球和一个圆锥组合而成,则该器物的 体积 V=V 球+V 圆锥
= 4 π+ 1 ·π× 15 33
= 4 π+ 15 π.
3
球的体积和表面积 课件

பைடு நூலகம்
方法归纳
(1)由三视图计算球或球与其他几何体的组合体的表面积或体 积,最重要的是还原组合体,并弄清组合体的结构特征和三视图中 数据的含义.根据球与球的组合体的结构特征及数据计算其表面积 或体积.此时要特别注意球的三种视图都是直径相同的圆.
(2)计算球与球的组合体的表面积与体积时要恰当地分割与拼 接,避免重叠和交叉.
∴l= r2+h2= 5h,
∴S 圆锥侧=πrl=π×2h× 5h=2 5πh2,S 球=4πR2=4πh2,
∴S圆锥侧=2 S球
4π5hπ2h2=
5 2.
方法归纳
求球的体积与表面积的方法 1.要求球的体积或表面积,必须知道半径 R 或者通过条件能 求出半径 R,然后代入体积或表面积公式求解. 2.半径和球心是球的最关键要素,把握住了这两点,计算球 的表面积或体积的相关题目也就易如反掌了.
所以 S△AOB=12R2. 因为 VO-ABC=VC-AOB,而△AOB 面积为定值, 所以当点 C 到平面 AOB 的距离最大时,VO-ABC 最大, 所以当 C 为与球的大圆面 AOB 垂直的直径的端点时,体积 VO -ABC 最大为13×12R2×R=36, 所以 R=6. 所以球 O 的表面积 S=4πR2=4π×62=144π.故选 C. 【答案】 C
类型二 根据三视图计算球的体积与表面积
[例 2] 若几何体的三视图如图所示,则该几何体的外接球的 表面积为( )
A.34π B.35π C.36π D.17π
【解析】 由几何体的三视图知它是底面为正方形且有一条侧
棱垂直于底面的四棱锥,可把它补成一个长、宽、高分别为 3、3、 4 的长方体,该长方体的外接球即为原四棱锥的外接球,所以 4R2 =32+32+42=18+16=34(其中 R 为外接球的半径),外接球表面积 为 S=4πR2=34π,故选 A.
计算球体的体积和表面积之比

计算球体的体积和表面积之比球体是几何学中的一种特殊几何体,由一组和一个固定点距离相等的点构成,这个固定点就是球心,而点与球心的距离称为半径,用符号r表示。
球体是一个三维的几何体,其体积和表面积是非常重要的性质,可以通过简单的公式进行计算。
一、球体的体积公式球体的体积表示的是球体所包含的三维空间的大小,用公式可以表示为:V = (4/3)πr³其中,V表示球体的体积,π表示圆周率,它约等于3.14159,r表示球体的半径。
二、球体的表面积公式球体的表面积表示的是球体外表面的大小,用公式可以表示为:A = 4πr²其中,A表示球体的表面积,π表示圆周率,r表示球体的半径。
三、体积和表面积之比的计算要计算球体的体积和表面积之比,可以使用上述的公式进行计算,将体积和表面积代入计算。
假设球体的半径r为5单位,那么根据公式计算可得到:V = (4/3)π(5)³ ≈ 523.6A = 4π(5)² ≈ 314.16将计算结果代入比值公式可得:比值= V/A ≈ 523.6 / 314.16 ≈ 1.67所以,球体的体积和表面积之比约为1.67。
结论:通过计算,我们得到了球体的体积和表面积之比为1.67。
这一比值在几何学和物理学中具有一定的意义。
体积和表面积之比的大小取决于球体的半径,当半径增大时,比值也会增大,反之亦然。
这个比值可以用来比较不同球体之间的大小关系,也可以在数学和科学研究中应用。
在实际生活中,球体的体积和表面积之比也可以用来解决一些应用问题,例如在建筑设计、工程计算等领域。
总结:通过本文的介绍,我们了解了如何计算球体的体积和表面积之比,并通过一个实际的例子进行了计算。
体积和表面积是球体的两个重要性质,它们之间的比值可以用来描述球体的大小关系。
了解和掌握这一比值的计算方法对于进一步研究和应用球体的相关问题非常有帮助。
对于读者来说,通过学习本文,可以更深入理解球体的性质和应用,为未来的学习和研究打下坚实的基础。
图解球体表面积和体积正确计算方法及计算公式
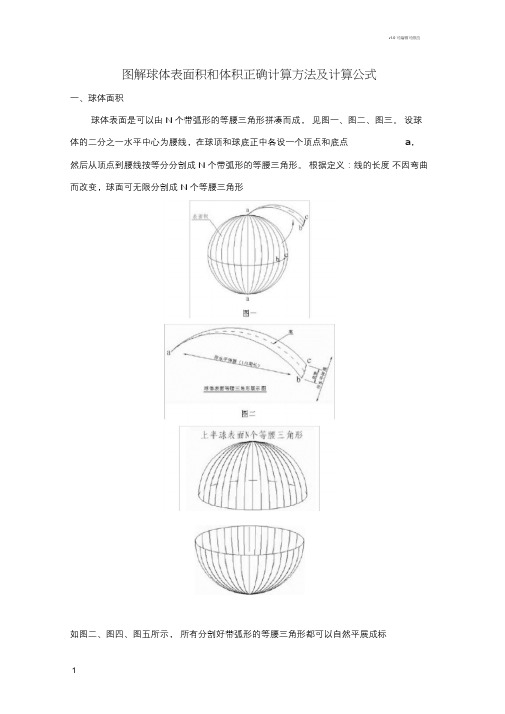
图解球体表面积和体积正确计算方法及计算公式一、球体面积球体表面是可以由N 个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N 个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N 个等腰三角形如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N 个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4 之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4 周长×周长(见图六)例1 :已知球体直径是1 个单位,求球体表面积(用上述最新推导公式S=1/4周长×周长)S =(÷ 4)× = ㎡二、球体体积设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N 个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4 。
则球体体积公式为:V =πR平方×周长的1/4 或:V = D(直径的三次方)×例2:已知球体直径是1 个单位,求球体体积(用上述最新推导公式)V = πR平方×周长的1/4= ××三、公知公式在球体面积、体积计算中出现的错误1、球体面积如何检验球体面积计算的正确,最好的方法就是用计算结果制成N 个等腰三角形的薄膜反贴球体表面。
图解球体表面积和体积正确计算方法及计算公式

图解球体表⾯积和体积正确计算⽅法及计算公式图解球体表⾯积和体积正确计算⽅法及计算公式⼀、球体⾯积球体表⾯是可以由N个带弧形的等腰三⾓形拼凑⽽成,见图⼀、图⼆、图三。
设球体的⼆分之⼀⽔平中⼼为腰线,在球顶和球底正中各设⼀个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三⾓形。
根据定义:线的长度不因弯曲⽽改变,球⾯可⽆限分割成N个等腰三⾓形如图⼆、图四、图五所⽰,所有分割好带弧形的等腰三⾓形都可以⾃然平展成标准的等腰三⾓形,亦可将等腰三⾓形拼凑成⽅形。
在理解上述图例球体表⾯和等腰三⾓形的关系后,我们可以对球体表⾯积的计算有⽐较清晰的判断。
即,球体表⾯可以分割成N个相等的等腰三⾓形,等腰三⾓形亦可拼凑成⽅形,由此推导出球体⾯积可以⽤矩形公式计算。
即S = 长×宽,如果我们设球体1/4之⼀的周长为宽,设球体的周长为长,则球体表⾯积公式为:S=1/4周长×周长(见图六)#例1:已知球体直径是1个单位,求球体表⾯积(⽤上述最新推导公式S=1/4周长×周长)S =(÷4)×= ㎡⼆、球体体积设以球⼼作⼀条垂线或⽔平中⼼线,然后以垂线或⽔平中⼼向外将球体按等分⽆限分割成N个半圆楔形体。
见图七、图⼋。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图⼗。
从图七、图⼋、图九、图⼗看,球体从中⼼按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱⾼正好是球体周长的1/4。
则球体体积公式为:V =πR平⽅×周长的1/4或:V = D(直径的三次⽅)×例2:已知球体直径是1个单位,求球体体积(⽤上述最新推导公式)V =πR平⽅×周长的1/4= ××=三、公知公式在球体⾯积、体积计算中出现的错误1、球体⾯积如何检验球体⾯积计算的正确,最好的⽅法就是⽤计算结果制成N个等腰三⾓形的薄膜反贴球体表⾯。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图解球体表面积和体积正确计算方法及计算公
式
Document number:NOCG-YUNOO-BUYTT-UU986-1986UT
图解球体表面积和体积正确计算方法及计算公式
一、球体面积
球体表面是可以由N个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N个等腰三角形
如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形。
在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4周长×周长(见图六)
例1:已知球体直径是1个单位,求球体表面积(用上述最新推导公式 S=1/4周长×周长)
S =(÷4)× = ㎡
二、球体体积
设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十。
从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4。
则球体体积公式为:V =πR平方×周长的1/4
例2:已知球体直径是1个单位,求球体体积(用上述最新推导公式)V =πR平方×周长的1/4
= ××
三、公知公式在球体面积、体积计算中出现的错误
1、球体面积
如何检验球体面积计算的正确,最好的方法就是用计算结果制成N个等腰三角形的薄膜反贴球体表面。
如薄膜能完整不剩的覆盖球体表面则公式应用和计算正确,如薄膜有剩余或薄膜未能完全覆盖球体表面则公式应用和计算不正确,见图十一。
图十一是用新公式和公知公式分别计算球体直径同是一个单位半球面积的结果对比,新公式计算结果反贴复原后正好能覆盖直径是一个单位半球的球体面积。
计算过程:?
S =(×) = ㎡
公知公式计算结果反贴复原后剩余有㎡的面积。
计算过程:?
S = 1×÷2 = ㎡
2、球体体积
如何检验球体体积计算的正确,最好的方法就是用溢水法进行检验。
根据公知的容积单位:每立方米的水为1000升,每立方厘米的水为1毫升。
因此我们可以将同直径的球体分别用两种不同的公式计算,将计算结果再与用溢水法实际测量的结果进行对比。
在大量的实验中我们的确发现了公知公式的问题,下表是实验中两种公式计算结果与实际测量的数据对比(球体体积):
上表数据对比清楚的表明,用量筒实际测量的结果与新公式计算的结果最为接近,可以证明球体体积新公式是正确可靠的。
