江苏省苏锡常镇四市2020-2021学年高三第三次模拟考试数学试卷含解析《含高考13套》
江苏省苏、锡、常、镇四市高考数学三模试卷解析版

高考数学三模试卷一、填空题(本大题共14小题,共70.0分)1.已知集合A={x|x<1},B={x|0<x<3},则A∩B=______.2.已知复数,其中i是虚数单位,则|z|=______.3.已知双曲线C的方程为,则其离心率为______.4.根据如图所示的伪代码,最后输出的i的值为______.5.某校高一、高二、高三年级的学生人数之比为4:4:3,现按年级用分层抽样的方法抽取若干人,若抽取的高三年级的学生数为15,则抽取的样本容量为______.6.口装中有形状大小完全相同的四个球,球的编号分别为1,2,3,4.若从袋中随机抽取两个球,则取出的两个球的编号之积大于6的概率为______.7.已知等比数列{a n}的前n项和为S n,若a6=2a2,则=______.8.函数的图象关于直线对称,则ω的最小值为______.9.已知正实数a,b满足a+b=1,则的最小值为______.10.已知偶函数f(x)的定义域为R,且在[0,+∞)上为增函数,则不等式f(3x)>f(x2+2)的解集为______.11.过直线l:y=x-2上任意点P作圆C:x2+y2=1的两条切线,切点分别为A,B,当切线最小时,△PAB的面积为______.12.已知点P在曲线C:y=x2上,曲线C在点P处的切线为l,过点P且与直线l垂直的直线与曲线C的另一交点为Q,O为坐标原点,若OP⊥OQ,则点P的纵坐标为______.13.如图,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB为直径在△ABC外作半圆O,P为半圆弧AB上的动点,点Q在斜边BC上,若=,则的最小值为______.14.已知e为自然对数的底数,函数f(x)=e x-ax2的图象恒在直线y=ax上方,则实数a的取值范围为______.二、解答题(本大题共11小题,共150.0分)15.如图,在三棱锥P-ABC中,过点P作PD⊥AB,垂足为D,E,F分别是PD,PC的中点,且平面PAB⊥平面PCD.(1)求证:EF∥平面ABC;(2)求证:CE⊥AB.16.在△ABC中,角A,B,C的对边分别为a,b,c,且.(1)求角A的大小;(2)若cos(B+)=,求cos C的值.17.某工厂拟制造一个如图所示的容积为36π立方米的有盖圆锥形容器.(1)若该容器的底面半径为6米,求该容器的表面积;(2)当容器的高为多少米时,制造该容器的侧面用料最省?18.如图,在平面直角坐标系xOy中,已知椭圆C:=1(a>b>0)的左、右顶点分别为A1(-2,0),A2(2,0),右准线方程为x=4.过点A1的直线交椭圆C于x轴上方的点P,交椭圆C的右准线于点D.直线A2D与椭圆C的另一交点为G,直线OG与直线A1D交于点H.(1)求椭圆C的标准方程;(2)若HG⊥A1D,试求直线A1D的方程;(3)如果,试求λ的取值范围.19.已知函数f(x)=x2+(2-a)x-a ln x,其中a∈R.(1)如果曲线y=f(x)在x=1处的切线斜率为1,求实数a的值;(2)若函数f(x)的极小值不超过,求实数a的最小值;(3)对任意x1∈[1,2],总存在x2∈[4,8],使得f(x1)=f(x2)成立,求实数a的取值范围.20.已知数列{a n}是各项都不为0的无穷数列,对任意的n≥3,n∈N*,a1a2+a2a3+…+a n-1a n=λ(n-1)a1a n恒成立.(1)如果,,成等差数列,求实数λ的值;(2)已知λ=1.①求证:数列是等差数列;②已知数列{a n}中,a1≠a2.数列{b n}是公比为q的等比数列,满足,,(i∈N*).求证:q是整数,且数列{b n}中的任意一项都是数列中的项.21.已知矩阵A=,其逆矩阵A-1=,求A2.22.在平面直角坐标系xOy中,曲线C的参数方程为(θ为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l上两点M,N的极坐标分別为(2,0),(,),求直线l被曲线C截得的弦长.23.已知正数a,b,c满足a+b+c=2,求证:.24.在平面直角坐标系xOy中,已知抛物线C:y2=4x的焦点为F,过F的直线l交抛物线C于A,B两点.(1)求线段AF的中点M的轨迹方程;(2)已知△AOB的面积是△BOF面积的3倍,求直线l的方程.25.已知数列{a n},a1=2,且对任意n∈N*恒成立.(1)求证:a n+1=a n a n-1a n-2…a2a1+1(n∈N*);(2)求证:(n∈N*).答案和解析1.【答案】(0,1)【解析】解:∵A={x|x<1},B={x|0<x<3};∴A∩B=(0,1).故答案为:(0,1).进行交集的运算即可.考查描述法的定义,以及交集的运算.2.【答案】1【解析】解:∵,∴|z|=||=.故答案为:1.直接由商的模等于模的商求解.本题考查复数模的求法,考查数学转化思想方法,是基础题.3.【答案】【解析】解:双曲线C的方程为,可得a=2,b=1,则c==.所以双曲线的离心率为:e=.故答案为:.直接利用双曲线的标准方程,求出a,c,即可求解离心率.本题考查双曲线的简单性质的应用,是基本知识的考查.4.【答案】8【解析】解:模拟程序的运行过程,如下;T=1,i=2,满足T<6;T=2,i=4,满足T<6;T=4,i=6,满足T<6;T=8,i=8,不满足T<6,输出i=8.故答案为:8.模拟程序的运行过程,即可得出程序结束后输出的i值.本题考查了程序运行的应用问题,是基础题.5.【答案】55【解析】解:依题意得抽取的样本容量为:=55.故答案为:55.根据分层抽样得特点知,抽取的样本中,高一,高二,高三的人数之比也为4:4:3可得.本题考查了分层抽样,属基础题.6.【答案】【解析】解:口装中有形状大小完全相同的四个球,球的编号分别为1,2,3,4.从袋中随机抽取两个球,基本事件总数n=,取出的两个球的编号之积大于6包含的基本事件(a,b)有:(2,4),(3,4),共2个,∴取出的两个球的编号之积大于6的概率为p==.故答案为:.从袋中随机抽取两个球,基本事件总数n=,利用列举法取出的两个球的编号之积大于6包含的基本事件(a,b)有2个,由此能取出的两个球的编号之积大于6的概率.本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.7.【答案】【解析】解:因为数列{a n}是等比数列,设其公比为q.所以=q4=2,所以q≠1,所以=====.故填:.设等比数列{a n}的公比是q,所以=q4=2,所以===,将q4=2代入即可.本题考查了等比数列的通项公式,前n项和公式的使用,属于基础题.8.【答案】【解析】解:∵的图象关于直线对称,∴ω-=kπ+π,即ω=2k+,∵ω>0,∴当k=-1时,ω取得最小值为-2+=,故答案为:.根据函数的对称性建立方程关系,求出ω的表达式,进行求解即可.本题主要考查三角函数的对称性的性质,结合条件建立方程关系求出ω的表达式是解决本题的关键.9.【答案】11【解析】解:∵a+b=1∴+=2a+2b++=2++,∵+=(+)(a+b)=1+4++≥5+2=5+4=9,当且仅当=时,即a=,b=时取等号,故+≥2+9=11,故答案为:11.根据基本不等式即可求出最小值.本题主要考查了基本不等式在求解最值中的应用,解题的关键是基本不等式条件的配凑,1的代换的技巧的应用要注意掌握.10.【答案】(-2,-1)∪(1,2)【解析】解:根据题意,函数f(x)为偶函数且其定义域为R,且在[0,+∞)上为增函数,则f(3x)>f(x2+2)⇒f(|3x|)>f(x2+2)⇒|3x|>x2+2,则有或,解可得:-2<x<-1或1<x<2,即不等式的解集为(-2,-1)∪(1,2);故答案为:(-2,-1)∪(1,2).根据题意,结合函数的奇偶性与单调性分析可得,f(3x)>f(x2+2)⇒f(|3x|)>f(x2+2)⇒|3x|>x2+2,由绝对值的定义可得或,解可得x的取值范围,即可得答案.本题考查函数的奇偶性与单调性的综合应用,涉及绝对值不等式的解法,属于基础题.11.【答案】【解析】解:如图,要使切线长最小,则|OP|最小,过O作直线y=x-2的垂线,则垂足为P,可得|OP|=,∴A,B为圆C:x2+y2=1与两坐标轴的交点,则PA=PB=1,∠APB=90°,∴△PAB的面积为.故答案为:.由题意画出图形,可得切线最小时的P点,进一步求得PA=PB=1,∠APB=90°,则答案可求.本题考查直线与圆位置关系的应用,考查数形结合的解题思想方法,是中档题.12.【答案】1【解析】解:由y=可得y′=x,设P(m,),则切线l的斜率为m,故直线PQ的方程为:y-=-(x-m)联立方程组,消去y可得:x2+x-m2-2=0,设Q(n,),则mn=-m2-2,∵OP⊥OQ,∴=0,即mn+=0,∴mn=0(舍)或mn=-4,∴-m2-2=-4,即m2=2.∴P点纵坐标为=1.故答案为:1.设P(m,),求出直线PQ的方程,根据根与系数的关系和=0列方程计算m的值即可得出答案.本题考查了直线与抛物线的位置关系,考查设而不求法的应用,属于中档题.13.【答案】【解析】解:如图,以O为原点建立直角坐标系,可得A(-1,0),B(1,0),C(-1,-2),即有直线BC的方程为y=x-1,可设Q(m,m-1),=,即为(2,0)•(m+1,m-1)=2(m+1)=,解得m=,即Q(,-),设P(cosα,sinα),0≤α≤π,可得=(,-)•(cosα+1,sinα+2)=cosα+-sinα-=(2c osα-sinα)=cos(α+θ),θ∈(0,),当cos(α+θ)=-1即α+θ=π,可得的最小值为-.故答案为:.以O为原点建立直角坐标系,求得A,B,C的坐标,以及直线BC的方程,设出Q的坐标,由数量积的坐标表示,解得Q的坐标,再设P(cosα,sinα),0≤α≤π,由数量积的坐标表示和两角和的余弦公式,余弦函数的值域可得最小值.本题考查向量的数量积的坐标表示,考查三角函数的恒等变换和余弦函数的值域,考查运算能力,属于中档题.14.【答案】(-,0]【解析】解:∵函数f(x)=e x-ax2的图象恒在直线y=ax上方,∴e x-ax2-ax>0对一切实数x恒成立,即e x>ax2+ax对一切实数x恒成立,设g(x)=e x,h(x)=ax2+ax,则①当a>0时,h(x)开口向上,根据h(x)和g(x)的图象易知,a>0时g(x)>h (x)不恒成立,②当a=0时,g(0)=1>h(0)=0,因此g(x)>h(x)恒成立③当a<0时,e x>ax2+ax对一切实数x恒成立,即<对一切实数x恒成立,令F(x)=,则F'(x)==-,令F(x)=0,则x=-1或x=,∴当x<-1或x>时,F'(x)<0,当-1<x<时,F'(x)>0,∴F(x)在(-∞,-1)和(,+∞)上单调递减,在(-1,)上单调递增,又当x>0时,F(x)>0,∴F(x)min=F(-1)=-,∴要使<对一切实数x恒成立,只需<F(x)min=-,∴a>-,又a<0,∴-<a<0,综上,a的取值范围为(-,0].故答案为:(-,0].将函数f(x)=e x-ax2的图象恒在直线y=ax上方转化为e x>ax2+ax对一切实数x恒成立,然后分a>0,a=0,a<0分别求解.本题考查了函数的恒成立问题,对于函数的恒成立问题,一般选用参变量分离法、最值法、数形结合法进行求解,本题这几种方法都有涉及,属于难题.15.【答案】证明:(1)∵E,F分别是PD,PC的中点,∴EF是△PCD的中位线,则有EF∥CD,又EF⊄平面ABC,CD⊂面ABC,∴EF∥平面ABC.解:(2)∵平面PAB⊥平面PCD,平面PAB∩平面PCD=PD,AB⊥PD,AB⊂平面PAB,∴AB⊥平面PCD,又CE⊂平面PCD,则AB⊥CE.【解析】本题考查线面平行、线线垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查空间想象能力与思维能力,考查运算求解能力,是中档题.(1)推导出EF是△PCD的中位线,从而EF∥CD,由此能证明EF∥平面ABC.(2)推导出AB⊥PD,从而AB⊥平面PCD,由此能证明AB⊥CE.16.【答案】(本题满分为12分)解:(1)∵,∴由正弦定理可得:,…2分∴整理可得:sin A+cos A=2,可得:2sin(A+)=2,可得:sin(A+)=1,…4分∵A∈(0,π),A+∈(,),可得:A+=,∴A=.…6分(2)在△ABC中,∵A=,∴B∈(0,),B+∈(,),可得:sin(B+)>0,又∵cos(B+)=,则sin((B+)==,…8分又在△ABC中,A+B+C=π,∴可得:cos C=-cos(A+B)=-cos(B+)=-cos[(B+)+]=-cos(B+)cos+sin(B+)sin=-=.…12分【解析】(1)由正弦定理,三角函数恒等变换的应用化简已知等式可得sin(A+)=1,结合范围A∈(0,π),可得A+=,从而解得A的值.(2)利用同角三角函数基本关系式可求sin(B+)的值,利用三角形内角和定理,两角和的余弦函数公式可求cos C的值.本题主要考查了正弦定理,三角函数恒等变换的应用在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.17.【答案】解:(1)设圆锥形容器的高为h,则容器的体积V=•π•62•h=36π,解得h=3.∴圆锥容器的母线长为=3,∴圆锥容器的表面积为π•62+=(36π+16π)平方米.(2)由V=r2h=36π可得r2=,故圆锥的母线l==,∴容器的侧面积S=πrl=π=π,∵=++≥3=9,当且仅当=即h=6时取等号,∴当h=6时,S取得最小值,即制造该容器的侧面用料最省.【解析】(1)根据体积公式计算容器高,计算母线长,再计算出侧面积和第面积即可;(2)用高h表示出侧面积,利用基本不等式得出侧面积最小时对应的h的值即可.本题考查了圆锥的体积与表面积计算,考查函数最值的计算与基本不等式的应用,属于中档题.18.【答案】解:(1)由椭圆的左、右顶点分别为A1(-2,0),A2(2,0),右准线方程为x=4可得a=2,=4,故c=1,b2=a2-c2=3,故椭圆方程为+=1.(2)设直线A1D:y=k(x+2),①(k>0),则与右准线x=4的交点D(4,6k),又A2(2,0),所以设直线A2D:y=3k(x-2),则,解得G(,),则直线OG的斜率为k OG=,②,∵OG⊥A1D,∴•k=-1,又k>0,解得k=,则直线A1D的方程为y=(x+2).(3)由(2)中②可得,设直线OG:y=x,联立可得,解得H(,),联立,∵解得P(,),∵,∴(x H+2,y H)=λ(x P+2,y P),∴y H=λy P,∴λ==f(k)====,∵f(k)在(0,+∞)为减函数,∴λ∈(,).【解析】(1)由题意可得a=2,=4,故c=1,b2=a2-c2=3,可得椭圆方程,(2)设直线A1D:y=k(x+2),再设直线A2D:y=3k(x-2),求出点G的坐标,根据HG⊥A1D,可求出k的值,即可求出直线方程,(3)分别求出点H,P的坐标,根据向量的运算借助函数的单调性即可求出.本题考查椭圆方程的求法,解题时要认真审题,注意椭圆、直线方程、函数的性质,向量的运算,属于中档题.19.【答案】解:(1)f(x)=x2+(2-a)x-a ln x(x>0),则.∵曲线y=f(x)在x=1处的切线斜率为1,∴f'(1)=2(2-a)=1,∴.(2)当a≤0时,f'(x)>0,∴f(x)在(0,+∞)上单调递增,∴函数f(x)在(0,+∞)上不存在极值;当a>0时,令f'(x)=0,则,∴当时,f'(x)<0;当时,f'(x)<0,∴f(x)在(0,)上单调递减,在(,+∞)上单调递增,∴=≤.∵a>0,∴,令g(a)=(a>0),则,∴g(a)在(0,+∞)上单调递减,又g(2)=0,∴当a≥2时,g(a)≤g(2)=0,∴实数a的最小值为2.(3)记f(x)在[1,2]上的值域为A,在[4,8]上的值域为B,由任意x1∈[1,2],总存在x2∈[4,8],使得f(x1)=f(x2)成立,知A⊆B.当≤1或≥8,即a≤2或a≥16时,f(x)在[1,8]上为单调函数,不合题意;当1<≤2,即2<a≤4时,由(2)知,f(x)在(0,)上单调递减,在(,+∞)上单调递增,∴f()∈A,但f()∉B,不合题意;当2<≤4,即4<a≤8时,A=[f(2),f(1)],B=[f(4),f(8)],由A⊆B,得,即,∴,又4<a≤8,∴;当4<<8,即8<a<16时,由A⊆B,得f(8)≥f(1),∴a≤,∴8<a≤,综上,a的取值范围为.【解析】(1)对f(x)求导后,由导数的几何意义可得f'(1)=2(2-a)=1,从而求出a的值;(2)根据函数f(x)的极小值不超过,对a分类讨论,将问题转化为解关于a的不等式,从而求出a的最小值;(3)设f(x)在[1,2]上的值域为A,在[4,8]上的值域为B,根据任意x1∈[1,2],总存在x2∈[4,8],使得f(x1)=f(x2)成立,知A⊆B,然后分情况求解可得a的范围.本题考查了导数的几何意义,导数在研究函数性质中的应用和集合之间的关系,考查了转化思想,分类讨论思想,考查了逻辑推理能力和运算能力,属难题.20.【答案】解:(1)∵n≥3,且n∈N*时,a1a2+a2a3+…+a n-1a n=λ(n-1)a1a n恒成立,则n=3时,a1a2+a2a3=2λa1a3,∵数列{a n}各项都不为0,同除a1a2a3,得:=,又∵成等差数列,则,比较,得=,∴λ=1.证明:(2)①当λ=1,n=3时,a1a2+a2a3=2a1a3,①整理,得:=,∴=,②当n=4时,a1a2+a2a3+a3a4=3a1a4,③③-①,得:a3a4=3a1a4-2a1a3,∴,∵=,∴,④当n≥3时,a1a2+a2a3+…+a n-1a n=(n-1)a1a n,a1a2+a2a3+…+a n-1a n+a n a n+1=na1a n+1,两式相减,得:a n a n+1=na1a n+1-(n-1)a1a n,∵a n≠0,∴,∴,∴=,∵x==表示首项为q2,公比为q=i-2,(i≥4),共k-3(k≥4)项的等比数列的和,∴x为正整数,∴{b n}中的每一项都是数列{c n},即{}中的项,整理,得,即,(n≥3),⑤由②④⑤得:对任意正整数n≥1恒成立,∴数列{}成等差数列.②设数列{}公差为d,令=c(c≠0),则b1=c1=c,b2=c2=c+d,d=c2-c1=b2-b1=cq-c,当i=2时,b3=c2=b2,∴q=1,b2=b1,∴a1=a2,与已知不符,当i=3时,由b3=c3,cq2=c+2d=c+2c(q-1),得q=1+2(q-1),解得q=1,与已知不符.当i=1时,由=c,得q2=1,由q≠1,得q=-1为整数,数列{b n}为:c,-c,c,…,数列{c n}中,c1=c,c2=-c,公差d=-2c,数列{b n}中每一项都是{c n}中的项,(c=c1,-c=c2),当i≥4时,由b3=c i,cq2=c+(i-1)d=c+(i-1)c(q-1),得q2-(i-1)q+(i-2)=0,得q=1,(舍),q=i-2,(i≥4)为正整数,∵cq=c+d,b3=c i,对任意的正整数k≥4,欲证明b k是数列{c n}中的项,只需=c i+xd=b3+x(cq-c)=cq2+x(cq-c)有正整数解x,等价于:q k-1=q2+x(q-1),x=为正整数,∴q是整数,且数列{b n}中的任意一项都是数列中的项.【解析】(1)n≥3,且n∈N*时,a1a2+a2a3+…+a n-1a n=λ(n-1)a1a n恒成立,n=3时,a1a2+a2a3=2λa1a3,同除a1a2a3,得=,由成等差数列,得,由此能求出λ的值.(2)①当λ=1,n=3时,=,从而=,当n=4时,,从而,当n≥3时,推导出,由此能证明数列{}成等差数列.②设数列{}公差为d,令=c(c≠0),则b1=c1=c,b2=c2=c+d,d=c2-c1=b2-b1=cq-c,推导出cq=c+d,b3=c i,对任意的正整数k≥4,欲证明b k是数列{c n}中的项,只需=c i+xd=b3+x(cq-c)=cq2+x(cq-c)有正整数解x,等价于:q k-1=q2+x(q-1),x=为正整数,由此能证明q是整数,且数列{b n}中的任意一项都是数列中的项.本题考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列的性质基础知识,考查运算求解能力,考查化归与转化思想,是难题.21.【答案】解:由题意,根据公式AA-1=E,可得:•=.即:=.∴,解得:.∴A=.∴A2=•=.【解析】本题先根据公式AA-1=E可将具体矩阵进行代入计算得到a、b、c的值,即可得到矩阵A,则A2即可求出.本题主要考查逆矩阵定义式公式AA-1=E,然后代入矩阵求参数的值,以及矩阵的乘法运算.22.【答案】解:由x=ρcosθ,y=ρsinθ,得,M(2,0),N(3,),则直线l:y=(x-2),曲线C:(x-2)2+(y+)2=4,圆心C(2,-),半径r=2,则圆心到直线l的距离为d==,则直线l被曲线C截得的弦长为2=.【解析】将直线和圆化成直角坐标方程后,利用圆中的勾股定理列式可得弦长.本题考查了简单曲线的极坐标方程,属中档题.23.【答案】证明:∵a,b,c都是正数,且a+b+c=2,∴2a+2b+2c=4,∴4(++)=[(b+c)+(c+a)+(a+b)](++)≥(+•+•)2=(a+b+c)2=4,∴++≥1.【解析】不等式两边同乘(2a+2b+2c),利用柯西不等式证明.本题考查了不等式的证明,柯西不等式的应用,属于中档题.24.【答案】解:(1)抛物线的焦点为F(1,0),设M(x,y),则A(2x-1,2y),把A(2x-1,2y)代入y2=4x可得4y2=8x-4,即y2=2x-1.(2)设直线l的方程为x=my+1,代入y2=4x可得y2-4my-4=0,设A(x1,y),B(x2,y2),则y1y2=-4,①若A在第一象限,B在第四象限,则y1>0,y2<0,则S AOB=•OF•(y1-y2),S△BOF=•OF•(-y2),∵S△AOB=3S△BOF,∴y1-y2=-3y2,∴y1=-2y2,又y1y2=-4,∴y1=2,y2=-.故x1=2,x2=,把A(2,2)代入x=my+1可得m==,∴直线l的方程为x-y-1=0,即4x-y-4=0.②若A在第四象限,B在第一象限,则y1<0,y2>0,S AOB=•OF•(y2-y1),S△BOF=•OF•y2,∵S△AOB=3S△BOF,∴y2-y1=3y2,∴y1=-2y2,又y1y2=-4,∴y1=-2,y2=.故x1=2,x2=,把A(2,-2)代入x=my+1可得m=-=-,∴直线l的方程为x+y-1=0,即4x+y-4=0.综上,直线l的方程为:4x-y-4=0或4x+y-4=0.【解析】(1)设M(x,y),表示出A点坐标,代入抛物线方程化简即可;(2)设A(x1,y),B(x2,y2),直线l的方程为x=my+1,联立方程组可得则y1y2=-4,三角形的面积比得出y1=-2y2,讨论A,B所在象限得出A的坐标,进而可得出直线l的方程.本题考查了轨迹方程的求解,直线与抛物线的位置关系,属于中档题.25.【答案】证明:(1)∵a1=2,且对任意n∈N*恒成立,∴当n=1时,a2=3=1+a1成立,假设当n=k时成立,即a k+1=a k a k-1a k-2…a2a1+1,当n=k+1时,a k+2=a k+1(a k+1-1)+1=(a k a k-1a k-2…a2a1)a k+1+1=a k+1a k a k-1…a2a1+1,则当n=k+1时,命题成立,综上可得,a n+1=a n a n-1a n-2…a2a1+1;(2)要证:,由(1)a n+1=a n a n-1a n-2…a2a1+1,只要证∴a n a n-1a n-2…a2a1>n n,下面用数学归纳法证明:当n=1,2,3时,a1=2,a2=3,a3=7,则2>1,2×3>22,2×3×7>33假设当n=k(k≥3)时结论成立,即a k a k-1a k-2…a2a1>k k,则当n=k+1时a k+1a k a k-1…a2a1+1=(a k a k-1…a2a1+1)a k a k-1…a2a1>(a k a k-1…a2a1)2>k2k设f(x)=2x lnx-(x+1)ln(x+1),x≥3,则=ln(x-1)+1≥ln2+1>0∴f(x)单调递增,则f(x)≥f(3)=2(3ln3-2ln4)=2ln>0则2k lnk>(k+1)ln(k+1),∴ln k2k>ln(k+1)k+1,即k2k>(k+1)k+1,∴a k+1a k a k-1…a2a1>(k+1)k+1,则当n=k+1时,命题成立综上可得,a n a n-1a n-2…a2a1>n n,∴,【解析】(1)结合题意可用数学归纳法证明命题成立;(2)要证:,由(1)a n+1=a n a n-1a n-2…a2a1+1,只要证∴a n a n-1a n-2…a2a1>n n,可用数学归纳法证明.本题主要考查了利用数学归纳法证明与数列有关的等式及不等式,试题具有一定的综合性。
江苏 苏锡常镇三模数学试题

2020-2021学年度苏锡常镇四市高三教学情况调研数 学一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若a ∈R ,则“a =2”是“复数z =2-a i 的模为22”(i 为虚数单位)的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .不充分也不必要条件 2.若集合A ={x ︱y =2-x },B ={y ︱y =2x},则A ∩B = ( )A .(-∞,2]B .[2,+∞)C .(0,2]D .[0,2] 3.从标有1,2,3,4,5,6的6张卡片中,不放回地随机抽取两次,每次抽取张.“在第一次抽到标号是4的条件下,第二次抽到的标号是奇数”的概率为 ( ) A .35 B .12 C .110 D .1124.已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的右焦点为F 2,左顶点为A 1,若E 上的点P 满足PF 2⊥x 轴,sin ∠PA 1F 2=35,则E 的离心率为 ( )A .12B .25C .14D .155.已知a =sin1,b =cos1,则下列不等式正确的是 ( )A .log a b <a b <b aB .log a b <b a <a bC .a b <b a <log a bD .b a <a b <log a b 6.已知3sin(α-π6)=sin(α+π6),则cos2α=( ) A .17 B .-17 C .1113 D .-11137.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,它由四个全等的直角三角形和一个正方形所构成(如图),后人称其为“赵爽弦图”.在 直角三角形CGD 中,已知GC =4,GD =3,在线段EF 上任取一点P ,线段BC 上任取一点Q ,则→AP ·→AQ 的最大值为 ( ) A .25B .27C .29D .31 8.已知函数f (x )=x 2-2x 23x +1+1,若存在m ∈(1,4),使得不等式f (4-ma )+f (m 2+3m )>2成立,则实数a 的取值范围是 ( )A .(-∞,7)B .(-∞,7]C .(-∞,8)D .(-∞,8]二.选择题:本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分.9.某中学为了研究高三年级学生的身高和性别的相关性问题,从高三年级800名学生中随机抽取200名学生测量身高,测量数据的列联表如下:AB CDEF HG下列说法正确的有 ( ) A .从列联表可以判断该样本是由分层抽样而得B .从列联表可以看出该中学高三学生身高最高的是男生C .有99.9%的把握认为该中学高三学生的身高与性别有关联D .若该样本中男生身高h (单位:cm)服从正态分布N (175,25),则该样本中身高在区 间(175,80]内的男生超过30人附1:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),(其中n =a +b +c +d ).参考数据: P (K 2≥3.841)=0.050;P (K 2≥6.635)=0.010;P (K 2≥10.828)=0.001.附2:若X ~N (μ,σ2),则P (|X -μ|≤σ)≈0.683.10.在数学发展史上,曾经定义过下列两种函数:1-cos θ称为角的正矢,记作versin θ;1-sin称为角θ的余矢,记作coversin θ.则 ( )A .versin2021π6=32B .函数f (θ)=versin θ·coversin θ最值为3+222C .存在一个θ,使得函数f (θ)=versin θ-coversin θ的值为32D .将函数f (θ)=coversin θ的图象向左平移π2个单位后,可得到函数g (θ)=versin θ的图象11.已知正四棱柱ABCD -A 1B 1C 1D 1的底面边长为1,侧棱长为2,点M 为侧棱CC 1上的动点,AM ⊥平面α.下列说法正确的有 ( ) A .异面直线AM 与B 1C 可能垂直 B .直线BC 与平面α不可能垂直C .AB 与平面α所成角的正弦值的范围为(0,22] D .若M ∈α且CM =MC 1,则平面α截正四棱柱所得截面多边形的周长为3 212.已知函数f (x )的定义城为R ,且在R 上可导,其导函数记为f ′(x ),下列命题正确的有( )A .若f (x )是奇函数,则f ′(x )是偶函数B .若f ′(x )是偶函数,则f (x )是奇函数C .若f (x )是周期函数,则f ′(x )也是周期函数D .若f ′(x )是周期函数,则f (x )也是周期函数三.填空题:本题共4小题,每小题5分,共20分.请将答案填写在答题卡相应的位置上.13.抛物线y 2=2px (p >0)的焦点为F ,点A (0,2),线段FA 的中点B 在抛物线上,则p =_______. 14.已知等差数列{a n }的首项为a ,公差为b (其中a ,b ∈N*),且a 2<ab <a 3,写出一个满足条件的数列{a n }的通项公式:_______. 15.已知平面向量a ,b ,c 满足|b |=|c |=1,|b -c |=3,2a ·b =a ·c =1,则b 与c 的夹角为_______;|a |等于_______.(第一空2分,第二空3分)16.一个组合体由上下两部分组成,上部是一个半球,下部是一个圆柱,半球的底面与圆柱的上底面重合.若该组合体的体积为定值V,则当圆柱底面半径r=____时,该组合体的表面积最小.四.解答题:本题共6小题,共70分.解答应写出文字说明.证明过程或演算步骤17.(10分)在△ABC中,a,b,c分别为内角A,B,C的对边,且a-b=a cos B-b cos A.(1) 求证:a=b;(2) 若c=4,cos C=35,求△ABC的面积18.(12分)在①na n+1-(n+1)a n=n2+n,②3S n=(n+2)a n,③T n+1=(n+2)a n T nn这三个条件中任选一个补充在下面问题中,并解答下列题目.设首项为2的数列{a n}的前n项和为S n,前n项积为T n,且_______.(1) 求数列{a n}的通项公式;(2) 设b n=(-1)n a n,求数列{b n}的前n项和.19.(12分)如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,平面ABC⊥平面AA1B1B,A1A =A1B,∠A1AB=60°,O为AB的中点,M为A1C1的中点.(1) 求证:OM∥平面BB1C1C;(2) 求二面角C1-BA1-C的正弦值.20.(12分)在平面直角坐标系xOy中,已知动点M到定点F(-2,0)的距离与到定直线l:x=-32的距离之ABCO1A1B1CM比为定值233.(1) 求动点M 的轨迹E 的方程;(2) 过点F 作互相垂直的两条直线l 1,l 2,其中l 1交动点M 的轨迹E 于M ,N 两点,l 2交圆D :(x -4)2+y 2=9于P ,Q 两点,点R 是线段PQ 的中点,求△RMN 面积的最小值.21.(12分)某校高二学生社团打算在开学初组织部分同学打扫校园.该社团通知高二同学自愿报名,由于报名的人数多达50人,于是该社团采用了在报名同学中用抽签的方式来确定打扫校园的人员名单.抽签方式如下:将50名同学编号,通过计算机从这50个编号中随机抽取30个编号,然后再次通过计算机从这50个编号中随机抽取30个编号,两次都被抽取到的同学打扫校园. (1) 设该校高二年级报名打扫校园的甲同学的编号被抽取到的次数为Y ,求Y 的数学期望. (2) 设两次都被抽取到的人数为变量X ,则X 的可能取值是哪些?其中X 取到哪一个值的可能性最大?请说明理由.22.(12分)已知函数f (x )=axex(e 为自然对数的底数).(1) 若函数g (x )=x -f (x )在(0,+0)上为增函数,求实数a 的取值范围; (2) 证明:对任意实数a ,函数h (x )=f (x )-ln x 有且只有一个零点.。
2020-2021学年江苏省高考三模(最后一卷)数学试卷及答案解析

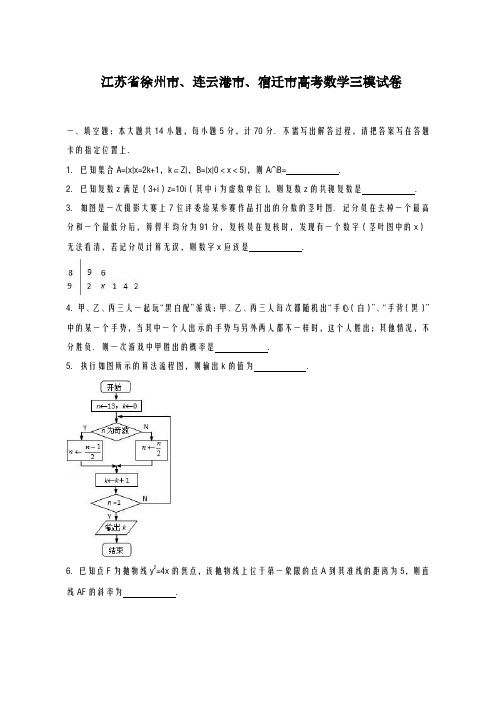
高三数学第三次模拟考试试卷数 学注意事项:1.本试卷共4页,包括填空题(第1题~第14题)、解答题(第15题~第20题)两部分.本试卷满分160分,考试时间120分钟.2.答题前,请您务必将自己的姓名、考试号用0.5毫米黑色字迹的签字笔填写在试卷的指定位置.3.答题时,必须用书写黑色字迹的0.5毫米签字笔写在试卷的指定位置,在其它位置作答一律无效.4.如有作图需要,可用2B 铅笔作答,并请加黑加粗,描写清楚.一、填空题:本大题共14小题,每小题5分,共70分.不需要写出解答过程,请把答案直接填在答题卡相应位置上......... 1.已知集合{1,3}A =,{1,2,}B m =,若A B ⊆,则实数m = ▲ 2.已知复数512iz =+(i 是虚数单位),则复数z 的模为 ▲ . 3.为了镇江市中学生运动会,现要在学生人数比例为5:3:2的A 、B 、C 三所学校中,用分层抽样方法抽取n 名志愿者,若在A 学校恰好抽出了6名志愿者, 那么n = ▲ .4. 在一个袋子中装有分别标注数字1,2,3,4的四个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为5的概率是 ▲ . 5.已知F 为双曲线C :2224(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为 ▲ .6. 运行右图所示程序框图,若输入值x [2,2],则输出值y 的取值范围是 ▲ .7. 已知,x y 满足约束条件0,2,0,x y x y y -≥⎧⎪+≤⎨⎪≥⎩若z ax y =+的最大值为4,则a 的值为 ▲ .8. 设,a b 为不重合的两条直线,,αβ为不重合的两个平面,给 出下列命题:(1)若a ∥α且b ∥α,则a ∥b ;(2)若a α⊥且a β⊥,则α∥β; (3)若α⊥β,则一定存在平面γ,使得,γαγβ⊥⊥; (4)若α⊥β,则一定存在直线l ,使得,//l l αβ⊥. 上面命题中,所有真命题...的序号是 ▲ .9. 等差数列{}n a 的公差为d ,关于x 的不等式22d x +12d a x ⎛⎫- ⎪⎝⎭+c ≥0的解集为[0,20],则使数列{}n a 的前n 项和n S 最大的正整数n 的值是 ▲ . 10. 设α为锐角,若53)6πcos(=+α,则sin 212απ⎛⎫+ ⎪⎝⎭的值为 ▲ .11. 在ABC ∆中,6=AB ,2=AC ,3π2=∠BAC ,若AC y AB x AM +=,且13=+y x ,的最小值为 ▲ .12. 在平面直角坐标系xOy 中,圆O 的方程为221x y +=,()2,0A -,对圆O 上的任意一点P ,存在一定点()(),02B b b ≠-和常数λ,都有PB PA λ=成立,则b λ+的值为 ▲ .13. 已知函数R 2)(2∈+=x x x x f ,,若方程01)(=--x a x f 恰有4个互异的小于1的实数根,则实数a 的取值范围为 ▲ .14. 若实数y x ,满足1222112sin cos =x x e y y--++,则x y 2tan 2的值为 ▲ . 二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答,解答时应写出必要的文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,角,,A B C 的对边分别为,,a b c ,且()(sin sin )()sin a c A C b B -+=-. (1)求角A ;(2)若22()cos ()sin ()f x x A x A =+--,求()f x 的单调递增区间.16.(本小题满分14分)如图,在三棱锥P ABC -中,PA PC =,AC AB ⊥,M 为BC 的中点,N 为AC 上一点,且MN ∥平面PAB .求证:(1)直线AB ∥平面PMN ; (2)平面ABC ⊥平面PMN .17.(本小题满分14分)某学校有长度为14米的旧墙一面,现准备利用这面旧墙建造平面图形为矩形,面积为126 m 2的活动室,工程条件是:①建1 m 新墙的费用为a 元;② 修1 m 旧墙的费用是4a 元;③ 拆去1 m 旧墙所得的材料,建1 m 新墙的费用为2a元,经过讨论有两种方案:(1)问如何利用旧墙的一段x 米)14(<x 为矩形厂房的一面边长;(2)矩形活动室的一面墙的边长14x …. 利用旧墙,即x 为多少时建墙的费用最省?(1)(2)两种方案,哪种方案最好?18.(本小题满分16分)在平面直角坐标系xOy 中,已知斜率为1-的直线l 与椭圆22221(0)y x a b a b +=>>相交于A ,B 两点,且AB 的中点为(2,1)M .(1)求椭圆的离心率;(2)设椭圆的右焦点为F ,且5AF BF ⋅=,求椭圆的方程.19.(本小题满分16分)已知正项数列{}n a 满足*112(1)(N )n n a a a S n +-=-∈,其中n S 为数列{}n a 的前n 项和, 2a t =.(1)求数列{}n a 的通项公式; (2)求证:1()2n n n a a S +…,并指出等号成立的条件.20.(本小题满分16分)已知函数()ln f x x =,2()g x kx ax =-,其中,k a 为实数. (1)若1,0k a ==,求方程()()0f x g x +=的零点个数;(2)若0a =,实数k 使得()()f x g x <恒成立,求k 的取值范围; (3)若1k =,试讨论函数()()()h x g x f x =-的单调性.高三教学情况调研(三)数 学 Ⅱ 试 题注意事项:1.本试卷只有解答题,供理工方向考生使用.本试卷第21题有4个小题供选做,每位考生在4个选做题中选答2题,如多答,则按选做题中的前2题计分.第22,23题为必答题.每小题10分,共40分.考试用时30分钟.2.答题前,请您务必将自己的姓名、考试号用0.5毫米黑色字迹的签字笔填写在试卷的指定位置.3.答题时,必须用0.5毫米黑色字迹的签字笔填写在试卷的指定位置,在其它位置作答一律无效.4.如有作图需要,可用2B 铅笔作答,并请加黑加粗,描写清楚.5.请保持答题卡卡面清洁,不要折叠、破损.一律不准使用胶带纸、修正液、可擦洗的圆珠笔.21.【选做题】本题包括A ,B ,C ,D 四小题,每小题10分. 请选定其中两题......,并.在相应的....答题区域....内作答...,若多做,则按作答的前两题评分.解答时应写出必要的文字说明、证明过程或演算步骤. A .(选修4-1:几何证明选讲)如图,A,B,C是圆O上不共线的三点,OD AB⊥于D,BC和AC分别交DO的延长线于P和Q,求证:OBP CQP∠=∠.B.(选修4—2:矩阵与变换)已知矩阵1221A⎡⎤=⎢⎥-⎣⎦,31B⎡⎤=⎢⎥⎣⎦满足AX B=,求矩阵X.C.(选修4—4:坐标系与参数方程)将参数方程(22)cos,(22)sin,t tt txyθθ--⎧=+⎪⎨=-⎪⎩(θ为参数,t为常数)化为普通方程.D.(选修4—5:不等式选讲)QPDCBAO已知,,x y z 均为正数.求证:111yx z yz zx xy x y z≥++++.【必做题】第22,23题,每小题10分,计20分. 请把答案写在答题纸的指定区域内,解答时应写出文字说明、证明过程或演算步骤. 22.(本小题满分10分)某考生从6道预选题一次性随机的抽取3道题作答,其中4道填空题,2道解答题. (1)求该考生至少抽到1道解答题的概率;(2)若所取的3道题中有2道填空题,1道解答题.已知该生答对每道填空题的概率均为23,答对每道解答题的概率均为12,且各题答对与否相互独立.用X 表示该考生答对题的个数,求X 的分布列和数学期望.23.(本小题满分10分)设整数9n ≥,在集合{1,2,3,,}n L 中任取三个不同元素,,a b c ()a b c >>,记()f n 为满足a b c ++能被3整除的取法种数.(1) 直接写出(9)f 的值; (2) 求()f n 表达式.数学参考答案一、填空题.1. 3 2.3.30 4.315. 26.[-1,6] 7. 2 8.(2)(3)(4)9.10 10.50231 11.112.3213.)(32-4,0 14.21二、解答题:本大题共6小题,共计90分.15. 解:(1)由B c b C A c a sin )3()sin )(sin (-=+-, 及CcB b A a sin sin sin ==,(不交代定理扣1分) 得b c b c a c a )3())((-=+-即 bc c b a 3222-+= ... ... 3分由余弦定理,(不交代定理扣1分)得: 21cos =A , .. ... 5分 由0<A<π, 则6π=A . ... (7)分 (2)2)32cos(12)32cos(1)6(sin )6(cos )(sin )(cos )(2222ππππ---++=--+=--+=x x x x A x A x x f ... ...10分x 2cos 21=... ...12分 2222,,2k x k k Z k x k k Zππππππππ+≤≤+∈+≤≤+∈令得:(不交代k Z ∈合计扣1分)()[,],2f x k k k Z ππππ++∈则的单调增区间为 ... ...14分16. 证明:(1)因为MN ∥平面PAB ,MN ⊂平面ABC ,平面PAB I 平面ABC AB =,所以MN ∥AB . ········3分因为MN ⊂平面PMN ,AB ⊄平面PMN ,所以AB ∥平面PMN . ·········6分(2)因为M 为BC 的中点,MN ∥AB ,所以N 为AC 的中点. ·········8分又因为PA PC =,所以PN AC ⊥, ·······10分又MN AC ⊥.MN PN ⊂,平面PMN ,MN PN N =I ,所以AC ⊥平面PMN . ·······12分因为AC ⊂平面ABC ,所以平面ABC ⊥平面PMN . ········14分17. 解:设利用旧墙的一面边长x 米,则矩形另一边长为126x 米. ········1分 (1) 当14x <时,总费用25236()(14)(214)7(1)35424a a x f x x x a x a a x x =+-++-=+-≥, 当且仅当12x =时取最小值35a . …… 7分(2) 当14x ≥时,总费用25212649()14(214)2()44a f x a x a x x x =⨯++-=+-,……10分则2126()2(1)0f x a x '=->,故()f x 在[14,)+∞上单调递增, 所以,当14x =时取最小值35.5a . ......13分 答:第(1)种方案最省,即当14x =米时,总费用最省,为35a 元. (14)分18. 解:(1)由题意可知,l 的方程为y=-x+3 ... ... 2分代入12222=+by a x ,得096)(2222222=-+-+b a a x a x a b设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2226a b a +,x 1x 2=222229a b b a a +- ① ... ... 5分由AB 中点为M (2,1)故 2226ab a +=4,即222b a = 故22122=-=ab e ② ... (8)分(2)由①②知椭圆方程为:122222=+by b xx 1+x 2=4,x 1x 2=2326b -因为121212221212222,()()()1243354353AFe AF a ex a x cBF a ex AF BF a ex a ex a ae x x e x x b b b b b ==--=-⋅=--=-++=-+-=-+=则同理:则因此: ... ...10分即:061252=--b b)(52,3舍或-==b b ... ... 14分则18222==b a因此椭圆方程为:191822=+y x ... (16)分19. 解:(1)令1n =,得2121(1)a a a a -=-,即221a a a =⋅, 因0n a >,则11a =,得221a a t a ==, ……2分当2n ≥时 112(1)n n a a a S +-=-, 121(1)n n a a a S --=- 两式相减得:12(1)n n n a a a a +-=- 即12n n a a a +=,因0n a >则12n na a t a +==……5分 综上:1(*)n na t n N a +=∈……6分 从而,{}n a 是以1为首项,t 为公比的等比数列故1n n a t -=. ……7分(2)令111()(1)()1,022n n n n n n a a n t f t S t t t --++=-=++⋅⋅⋅+->当1t =时,(1)0n f =,即1()2n n n a a S +=……9分 当1t ≠时,22(1)'()12(1)2n n n n n t f t t n t---=++⋅⋅⋅+--, 若(0,1)t ∈,22(1)'()[12(1)]02n n n n n t f t n t--->++⋅⋅⋅+--=若(1,)t ∈+∞,22(1)'()[12(1)]02n n n n n t f t n t---<++⋅⋅⋅+--=即'()n f t 在(0,1)t ∈时单调递增,当(1,)t ∈+∞时单调递减, ……14分则()(1)0n n f t f <=,即1()2n n n a a S +<, ……15分故1()2n n n a a S +≤,当且仅当1t =时取“”. ……16分20. 解:(1)1,0k a ==,则2()()ln f x g x x x +=+, 记2()ln F x x x =+,因为()F x 在(0,)+∞上单调递增, ……1分221111()ln 10F e e e e=+=-+<, ……2分 (1)10F =>……3分所以()0F x =仅有一个零点01(,1)x e∈,即方程()()0f x g x +=的零点个数为1. ……4分(2)由0a =,实数k 使得()()f x g x <恒成立, 可得:2ln x k x ≥在0x >时恒成立,则max 2ln ()xk x>, ……5分记2ln (),(0)xG x x x =>, 312ln '()xG x x-=……6分当'()0x G x ∈>,()G x 在上单调递增,当),'()0x G x ∈+∞<,()G x 在)+∞上单调递减,则x ()G x 取得最大值12e, 故k 的取值范围是1(,)2e+∞. ……8分(3)21,()ln ,(0)k h x x ax x x ==--> 若0a …,则2()ln h x x ax x =--,故2121()2x ax h x x a x x --'=--=令()0h x '=,得x =(负值舍去)记b =于是,()h x 在区间(0,)b 上单调递减,在区间(,)b +∞上单调递增; ……10分若0a >,则22ln ,()ln ,0x ax x x ah x x ax x x a ⎧--⎪=⎨-+-<<⎪⎩≥,先讨论2()ln ()h x x ax x x a =--≥的单调性,由2121()2x ax h x x a x x --'=--=令()0h x '=,得0x => 当b a >,即1a <时,()h x 在区间(,)a b 上单调递减,在区间(,)b +∞上单调递增;当b a …,即1a ≥时,()h x 在区间(,)a +∞上单调递增; ……12分再讨论2()ln (0)h x x ax x x a =-+-<<的单调性,注意到2121()2x ax h x x a x x-+-'=-+-=当280a ∆=-…时,即0a <…时,()0h x '≤()h x 在区间(0,)a 上单调递减.当280a ∆=->时,即a >()0h x '=得x a =<,则()h x 在区间)a 上单调递减,在区间上单调递增; (15)分综上,当1a <时,()h x 在区间上单调递减,在区间)+∞上单调递增;当1a 剟()h x 在区间(0,)a 上单调递减,在区间(,)a +∞上单调递增;当a >时,则()h x 在区间)a 上单调递减,在区间上单调递增. ……16分数 学 Ⅱ 试 题A .(选修4-1:几何证明选讲)证:连接OA ,因为OD AB ⊥,OA OB =,所以12BOD AOD AOB ∠=∠=∠, 又12ACB AOB ∠=∠,所以ACB DOB ∠=∠,………5分 又因为180BOP DOP ∠=-∠o ,180QCP ACB ∠=-∠o, 所以BOP QCP ∠=∠,所以B ,O ,C ,Q 四点共圆,所以OBP CQP ∠=∠. ………10分 B .(选修4—2:矩阵与变换)解:设a X b ⎡⎤=⎢⎥⎣⎦,由123211a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦得23,21,a b a b +=⎧⎨-=⎩………6分解得1,1,a b =⎧⎨=⎩此时11X ⎡⎤=⎢⎥⎣⎦.………10分C .(选修4—4:坐标系与参数方程)解:当t0时,y0,x 2cos θ,即y0,且22x -≤≤; ………2分当t ≠0时,cos 22t t x θ-=+,sin 22t ty θ-=-, ………6分所以22221(22)(22)t t t t x y --+=+-. ………10分D.(选修4—5:不等式选讲)证明:因为x ,y ,z 都是为正数,所以12()x y x y yz zx z y x z+=+≥.………5分 同理可得22y z z x zx xy x xy yz y++≥,≥,将上述三个不等式两边分别相加,并除以2,得111x y z yz zx xy x y z++++≥.………10分 【必做题】第22,23题,每小题10分,计20分. 请把答案写在答题纸的指定区域内,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)解(1)记该考生至少抽到1道解答题为事件A , 则()343614()11155C P A P A C =-=-=-=. ………4分 (2)X 所有的可能取值为0,1,2,3.2211(0)(1)(1)3218P X ==-⋅-=; 122221215(1)(1)(1)(1)3323218P X C ==⋅⋅-⋅-+-⋅=; 12222121105(2)(1)()(1)33232189P X C ==⋅⋅-⋅+⋅-==; 22121(3)()32189P X ==⋅==. 所以X 的分布列为:………8分所以155131()0123.18189918E X =⨯+⨯+⨯+⨯=………10分 23.(本小题满分10分)解 (1) (9)12=f . ………2分(2)①当*3(3,)N n k k k =∈≥时,记3n k =,集合为{1,2,3,,31,3}k k -L . 将其分成三个集合:{1,4,,32}A k =-L ,{2,5,,31}B k =-L ,{3,6,,3}C k =L .要使得a b c ++能被3整除,,,a b c 可以从A 取三个或从B 取三个或从C 取三个或从C 取一个,从A 中取一个,从B 中取一个(此数与A 中取的那个数之和能被3整除).故有323112(1)(2)3183254k k kk k k n n n C C C k ---++=+=g 种取法;………5分 ②当*31(3,)N n k k k =+∈≥时,记13n k -=,集合为{1,2,3,,3,31}k k +L . 将其分成三个集合:{1,4,,32,31}A k k =-+L ,{2,5,,31}B k =-L ,{3,6,,3}C k =L . 要使得a b c ++能被3整除,,,a b c 可以从A 取三个或从B 取三个或从C 取三个或从C 取一个,从B 中取一个,从A 中取一个(此数与B 中取的那个数之和能被3整除).故有2323311221(1)(2)(1)(1)(1)31210236254k k k kk k k k k k k k n n n C C C C k k +--+---+-++=++=+=g 种取法; ……7分 ③当*32(3,)N n k k k =+∈≥时,记23n k -=,集合为{1,2,3,,31,32}k k ++L . 将其分成三个集合:{1,4,,32,31}A k k =-+L ,{2,5,,31,32}B k k =-+L ,{3,6,,3}C k =L .要使得a b c ++能被3整除,,,a b c 可以从A 取三个或从B 取三个或从C 取三个或从C 取一个,从B 中取一个,从A 中取一个(此数与B 中取的那个数之和能被3整除).故有232331111(1)(2)(1)(1)(1)318322(1)(1)63254k k k k k k k k k k k k n n n C C C C k k k k ++--+---++++=+++=++=g 种取法;………9分 综上所述,32*32*32*318,3(3,),5431210(),31(3,),5431832,32(3,).54N N N n n n n k k k n n n f n n k k k n n n n k k k ⎧-+=∈⎪⎪⎪-+-==+∈⎨⎪⎪-++=+∈⎪⎩≥≥≥………10分。
江苏省无锡市2021届新高考数学三模试卷含解析

江苏省无锡市2021届新高考数学三模试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设等比数列{}n a 的前n 项和为n S ,则“10a <”是“20210S <”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】C 【解析】 【分析】根据等比数列的前n 项和公式,判断出正确选项. 【详解】由于数列{}n a 是等比数列,所以20212021111q S a q -=⋅-,由于2021101q q ->-,所以 1202100a S <⇔<,故“10a <”是“20210S <”的充分必要条件.故选:C 【点睛】本小题主要考查充分、必要条件的判断,考查等比数列前n 项和公式,属于基础题.2.在ABC 中,D 为BC 边上的中点,且||1,|2,120AB AC BAC ==∠=︒,则||=AD ( )A B .12C .34D 【答案】A 【解析】 【分析】由D 为BC 边上的中点,表示出()12AD AB AC =+,然后用向量模的计算公式求模. 【详解】解:D 为BC 边上的中点,()12AD AB AC =+,()()()()22222112412411221212043=AD AB AC AB AC AB AC AB AC COS =+=+=++⋅=++⨯⨯⨯。
故选:A 【点睛】在三角形中,考查中点向量公式和向量模的求法,是基础题.3.设a ,b ,c 分别是ABC ∆中A ∠,B ,C ∠所对边的边长,则直线sin 0A x ay c ⋅--=与sin sin 0bx B y C +⋅+=的位置关系是( )A .平行B .重合C .垂直D .相交但不垂直【答案】C 【解析】试题分析:由已知直线sin 0A x ay c ⋅--=的斜率为,直线sin sin 0bx B y C +⋅+=的斜率为,又由正弦定理得,故,两直线垂直考点:直线与直线的位置关系4.若x ,y 满足约束条件103020x y x y x +-≤⎧⎪-+≤⎨⎪+≥⎩,则22x y +的最大值是( )A .92B 32C .13D 13【答案】C 【解析】 【分析】由已知画出可行域,利用目标函数的几何意义求最大值. 【详解】 解:22xy +表示可行域内的点(,)x y 到坐标原点的距离的平方,画出不等式组表示的可行域,如图,由1020x y x +-=⎧⎨+=⎩解得32y x =⎧⎨=-⎩即()2,3A -点()2,3A -到坐标原点(0,0)的距离最大,即2222()(2)313max x y +=-+=. 故选:C . 【点睛】本题考查线性规划问题,考查数形结合的数学思想以及运算求解能力,属于基础题. 5.复数12i2i+=-( ). A .i B .1i +C .i -D .1i -【答案】A 【解析】试题分析:12(12)(2)2422(2)(2)5i i i i i i i i i +++++-===--+,故选A. 【考点】复数运算【名师点睛】复数代数形式的四则运算的法则是进行复数运算的理论依据,加减运算类似于多项式的合并同类项,乘法法则类似于多项式的乘法法则,除法运算则先将除式写成分式的形式,再将分母实数化. 6.已知||23z z i =-(i 为虚数单位,z 为z 的共轭复数),则复数z 在复平面内对应的点在( ). A .第一象限 B .第二象限C .第三象限D .第四象限【答案】D 【解析】 【分析】设i,(,)z a b a b R =+∈,由||23z z i =-,得222i=(2)i=3a b z a b +--+,利用复数相等建立方程组即可. 【详解】设i,(,)z a b a b R =+∈,则222i=(2)i=3a bz a b +--+,所以22320a b a b ⎧+⎪=⎨⎪+=⎩,解得2a b ⎧=⎪⎨⎪=-⎩2i 2z =-,复数z在复平面内对应的点为(2)2-,在第四象限. 故选:D. 【点睛】本题考查复数的几何意义,涉及到共轭复数的定义、复数的模等知识,考查学生的基本计算能力,是一道容易题.7.已知a ,b ,c 分别为ABC ∆内角A ,B ,C 的对边,1a =,4sin 3cos c A C =,ABC ∆的面积为32,则c =( ) A.B .4C .5D.【答案】D 【解析】 【分析】由正弦定理可知4sin 4sin 3cos c A a C C ==,从而可求出34sin ,cos 55C C ==.通过13sin 22ABC S ab C ∆==可求出5b =,结合余弦定理即可求出c 的值.【详解】 解:4sin 3cos c A C =,即4sin 3cos c A a C =4sin sin 3sin cos A C A C ∴=,即4sin 3cos C C =.22sin cos 1C C += ,则34sin ,cos 55C C ==. 1133sin 12252ABC S ab C b ∆∴==⨯⨯⨯=,解得5b =.222242cos 15215185c a b ab C ∴=+-=+-⨯⨯⨯=,c ∴=故选:D. 【点睛】本题考查了正弦定理,考查了余弦定理,考查了三角形的面积公式,考查同角三角函数的基本关系.本题的关键是通过正弦定理结合已知条件,得到角C 的正弦值余弦值. 8.已知平面向量,a b ,满足1,13a b ==,且2a b a b +=+,则a 与b 的夹角为( ) A .6π B .3π C .23π D .56π【答案】C 【解析】 【分析】根据2a b a b +=+, 两边平方222a b a b +=+,化简得()223ab a =-,再利用数量积定义得到()22cos ,3a b a b a =-求解.【详解】因为平面向量,a b ,满足1,13a b ==,且2a b a b +=+, 所以222a b a b +=+, 所以()223ab a =-,所以 ()22cos ,3a b a b a =-,所以1cos ,2a b =-, 所以a 与b 的夹角为23π.故选:C 【点睛】本题主要考查平面向量的模,向量的夹角和数量积运算,属于基础题. 9.在ABC ∆中,“tan tan 1B C >”是“ABC ∆为钝角三角形”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既不充分也不必要条件【答案】C 【解析】分析:从两个方向去判断,先看tan tan 1A B >能推出三角形的形状是锐角三角形,而非钝角三角形,从而得到充分性不成立,再看当三角形是钝角三角形时,也推不出tan tan 1A B >成立,从而必要性也不满足,从而选出正确的结果.详解:由题意可得,在ABC ∆中,因为tan tan 1A B >, 所以sin sin 1cos cos A BA B>,因为0,0A B ππ<<<<,所以sin sin 0A B >,cos cos 0A B >,结合三角形内角的条件,故A,B 同为锐角,因为sin sin cos cos A B A B >, 所以cos cos sin sin 0A B A B -<,即cos()0A B +<,所以2A B ππ<+<,因此02C <<π,所以ABC ∆是锐角三角形,不是钝角三角形,所以充分性不满足,反之,若ABC ∆是钝角三角形,也推不出“tan tan 1B C >,故必要性不成立, 所以为既不充分也不必要条件,故选D.点睛:该题考查的是有关充分必要条件的判断问题,在解题的过程中,需要用到不等式的等价转化,余弦的和角公式,诱导公式等,需要明确对应此类问题的解题步骤,以及三角形形状对应的特征.10.已知正项数列{}{},n n a b 满足:1110n n nn n n a a b b a b ++=+⎧⎨=+⎩,设n n n a c b =,当34c c +最小时,5c 的值为( )A .2B .145C .3D .4【答案】B 【解析】 【分析】由1110n n nn n n a a b b a b ++=+⎧⎨=+⎩得11911n nn na ab b ++=++,即1911n nc c +=++,所以得3433911c c c c +=+++,利用基本不等式求出最小值,得到32c =,再由递推公式求出5c . 【详解】由1110n n n n n n a a b b a b ++=+⎧⎨=+⎩得1110109111nn n n n n n n n nn na a ab b a a b a b b b ++++===++++,即1911n n c c +=++, 34339161c c c c ∴+=++≥+,当且仅当32c =时取得最小值, 此时45349914141115,c c c c =+==+=++. 故选:B 【点睛】本题主要考查了数列中的最值问题,递推公式的应用,基本不等式求最值,考查了学生的运算求解能力. 11.函数()()()sin 0,02g x A x A ωϕϕπ=+><<的部分图象如图所示,已知()506g g π⎛⎫== ⎪⎝⎭,函数()y f x =的图象可由()y g x =图象向右平移3π个单位长度而得到,则函数()f x 的解析式为( )A .()2sin 2f x x =B .()2sin 23f x x π⎛⎫=+⎪⎝⎭ C .()2sin f x x =- D .()2sin 23f x x π⎛⎫=-⎪⎝⎭【答案】A 【解析】 【分析】由图根据三角函数图像的对称性可得522662T πππ=-⨯=,利用周期公式可得ω,再根据图像过(,0,36π⎛⎫⎪⎝⎭,即可求出,A ϕ,再利用三角函数的平移变换即可求解. 【详解】 由图像可知522662T πππ=-⨯=,即T π=, 所以2T πω=,解得2ω=,又sin 2066g A ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,所以()3k k ϕπ+=π∈Z ,由02ϕπ<<, 所以23ϕπ=或53π,又()03g =所以sin 3A ϕ=,()0A >, 所以23ϕπ=,2A =, 即()22sin 23g x x π⎛⎫=+ ⎪⎝⎭,因为函数()y f x =的图象由()y g x =图象向右平移3π个单位长度而得到,所以()22sin 22sin 233y f x x x ππ⎡⎤⎛⎫==-+= ⎪⎢⎥⎝⎭⎣⎦. 故选:A 【点睛】本题考查了由图像求三角函数的解析式、三角函数图像的平移伸缩变换,需掌握三角形函数的平移伸缩变换原则,属于基础题.12.定义在R 上的函数()()f x x g x =+,()22(2)g x x g x =--+--,若()f x 在区间[)1,-+∞上为增函数,且存在20t -<<,使得(0)()0f f t ⋅<.则下列不等式不一定成立的是( ) A .()2112f t t f ⎛⎫++>⎪⎝⎭B .(2)0()f f t ->>C .(2)(1)f t f t +>+D .(1)()f t f t +>【答案】D 【解析】 【分析】根据题意判断出函数的单调性,从而根据单调性对选项逐个判断即可. 【详解】由条件可得(2)2(2)2()22()()f x x g x x g x x g x x f x --=--+--=--+++=+=∴函数()f x 关于直线1x =-对称;()f x 在[1-,)+∞上单调递增,且在20t -<<时使得(0)()0f f t <;又(2)(0)f f -=()0f t ∴<,(2)(0)0f f -=>,所以选项B 成立;223112()0224t t t ++-=++>,21t t ∴++比12离对称轴远, ∴可得21(1)()2f t t f ++>,∴选项A 成立;22(3)(2)250t t t +-+=+>,|3||2|t t ∴+>+,∴可知2t +比1t +离对称轴远 (2)(1)f t f t ∴+>+,选项C 成立;20t -<<,22(2)(1)23t t t ∴+-+=+符号不定,|2|t ∴+,|1|t +无法比较大小, (1)()f t f t ∴+>不一定成立.故选:D . 【点睛】本题考查了函数的基本性质及其应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.二、填空题:本题共4小题,每小题5分,共20分。
2020-2021学年江苏省高考数学三模试卷及答案解析

江苏省高考数学三模试卷、填空题(每题5分,满分70分,江答案填在答题纸上)已知集合A={-1, 1, 2}, B={0, 1, 2, 7},则集合AU B 中元素的个数为6.已知一组数据3, 6, 9, 8, 4,则该组数据的方差是2. 设 a, bC R, =a+bi (i 为虚数单位),则b 的值为3. 2在平面直角坐标系xOy 中,双曲线三-- 4=1的离心率是4. 现有三张识字卡片,分别写有 中“、国“、梦”这三个字.将这三张卡片随机排 序,则能组成 中国梦”的概率是5. 如图是一个算法的流程图,则输出的 k 的值为7.已知实数x, ,则匕的取值范围是 Ju,……一、 ....................................................... 卬8.右函数 f (x) =2sin (2x+(|)) (0< i><^2 )的图象过点(0,5),则函数f (x )在[0,可上的单调减区间是9 .在公比为q 且各项均为正数的等比数列{&}中,S n 为{a }的前n 项和.若a i 85=82+2,则q 的值为10 .如图,在正三棱柱 ABC- A 1B 1G 中,已知AB=AA=3,点P 在棱CG 上,则三棱锥11 .如图,已知正方形ABCD 的边长为2, BC 平行于x 轴,顶点A, B 和C 分别在函 数y i =3log a x, y 2=2log a x 和y 3=log a x (a> 1)的图象上,则实数 a 的值为.12 .已知对于任意的 xC (- 8, 1)u (5, +8),都有 x 2 2 (a-2) x+a> 0,则 实数a 的取值范围是. 13 .在平面直角坐标系xOy 中,圆C: (x+2) 2+ (y-m) 2=3,若圆C 存在以G 为中 点的弦AB,且AB=2GQ 则实数m 的取值范围是. 14 .已知△ ABC 三个内角A, B, C 的对应边分别为 % b, c,且C=— , c=2.当R .总 J取得最大值时,上的值为 a-----且P-ABA 的体积为¥ L二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)d R I15.如图,在△ABC中,已知点D 在边AB上,AD=3DB cosA『,cosZACB=v,5 13 BC=13(1)求cosB的值;(2)求CD的长.16.如图,在四棱锥P-ABCD中,底面ABCD是矩形,点E在棱PC上(异于点P,C),平面ABE与棱PD交于点F.(1)求证:AB// EF;(2)若平面PADXT面ABCD求证:AE±EE17.如图,在平面直角坐标系xOy中,已知椭圆C: 哼=1的左、右顶点分别为A, B,过右焦点F的直线l与椭圆C交于P, Q两点(点P在x轴上方).(1)若QF=2FP求直线l的方程;(2)设直线AP, BQ的斜率分别为ki, k2,是否存在常数入,使得k尸入电?若存在,求出入的值;若不存在,请说明理由.18.某景区修建一栋复古建筑,其窗户设计如图所示.圆O的圆心与矩形ABCD对角线的交点重合,且圆与矩形上下两边相切(E为上切点),与左右两边相交(F, G为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为1m且票》上,设/EOF=9,透光区域的面积为S.(1)求S关于8的函数关系式,并求出定义域;(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边AB的长度.19.已知两个无穷数列{a}和{b n}的前n项和分别为T n, a i=1, 4=4,对任意的nCN*,者B有3S n+i=2S+S+2+a.(1)求数列{a n}的通项公式;(2)若{b n}为等差数列,对任意的nC N ,都有S n>T.证明:a>b n;*(3)右{b n}为等比数列,b i=ai, b2=a,求满足匕丁” =a (kC N )的n值.20.已知函数f (x) =—+xlnx (m>0), g (x) =lnx-2.(1)当m=1时,求函数f (x)的单调区问;(2)设函数h (x) =f (x) - xg (x) -V2, x>0.若函数y=h (h (x))的最小值是,求m的值;(3)若函数f (x), g (x)的定义域都是[1, e],对于函数f (x)的图象上的任意一点A,在函数g (x)的图象上都存在一点B,使得OALOB,其中e是自然对数的底数,O为坐标原点,求m的取值范围.【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答,若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选彳4-1 :几何证明选讲21.如图,圆。
江苏省苏锡常镇四市2020届高三数学第三次模拟考试试题

江苏省苏锡常镇四市2020届高三数学第三次模拟考试试题(满分160分,考试时间120分钟)2020.5一、 填空题:本大题共14小题,每小题5分,共70分.1. 已知集合A ={x|x<1},B ={x|0<x<3},则A∩B=________.2. 已知复数z =3+4i5i ,其中i 是虚数单位,则|z|=________.3. 已知双曲线C 的方程为x 24-y 2=1,则其离心率为________.4. 根据如图所示的伪代码,最后输出i 的值为________. T←1 i ←2While T<6 T←2T i←i+2 End While Print i (第4题)5. 某校高一、高二、高三年级的学生人数之比为4∶4∶3,现按年级用分层抽样的方法抽取若干人,若抽取的高三年级的学生人数为15,则抽取的样本容量为________.6. 口装中有形状、大小完全相同的四个球,球的编号分别为1,2,3,4.若从袋中随机抽取两个球,则取出的两个球的编号之积大于6的概率为________.7. 已知等比数列{a n }的前n 项和为S n .若a 6=2a 2,则S 12S 8=________.8. 若函数f(x)=cos (ωx-π3)(ω>0)的图象关于直线x =π2对称,则ω的最小值为________.9. 已知正实数a ,b 满足a +b =1,则2a 2+1a -2b 2+4b的最小值为________.10. 已知偶函数f(x)的定义域为R ,且在[0,+∞)上为增函数,则不等式f(3x)>f(x 2+2)的解集为____________.11. 过直线l :y =x -2上任意一点P 作圆C :x 2+y 2=1的两条切线,切点分别为A ,B ,当切线长最小时,△PAB 的面积为________.12. 已知点P 在曲线C :y =12x 2上,曲线C 在点P 处的切线为l ,过点P 且与直线l 垂直的直线与曲线C 的另一交点为Q ,O 为坐标原点.若OP⊥OQ,则点P 的纵坐标为________.13. 如图,在等腰直角三角形ABC 中,∠CAB =90°,AB =2,以AB 为直径在△ABC 外作半圆O ,P 为半圆弧AB 上的动点,点Q 在斜边BC 上.若AB →·AQ →=83,则AQ →·CP →的最小值为________.14. 已知e 为自然对数的底数,函数f(x)=e x -ax 2的图象恒在直线y =32ax 上方,则实数a 的取值范围是________.二、 解答题:本大题共6小题,共90分. 解答时应写出必要的文字说明、证明过程或演算步骤.15. (本小题满分14分)如图,在三棱锥PABC 中,过点P 作PD⊥AB,垂足为D ,点E ,F 分别是PD ,PC 的中点,且平面PAB⊥平面PCD.求证:(1) EF∥平面ABC ; (2) CE⊥AB.16. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且3a c =2-cos A sin C. (1) 求角A 的大小;(2) 若cos(B +π6)=14,求cos C 的值.某工厂拟制造一个如图所示的容积为36π立方米的有盖圆锥形容器.(1) 若该容器的底面半径为6米,求该容器的表面积;(2) 当容器的高为多少米时,制造该容器的侧面用料最省?如图,在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y2b 2=1(a >b >0)的左、右顶点分别为A 1(-2,0),A 2(2,0),右准线方程为x =4.过点A 1的直线交椭圆C 于x 轴上方的点P ,交椭圆C 的右准线于点D.直线A 2D 与椭圆C 的另一交点为G ,直线OG 与直线A 1D 交于点H.(1) 求椭圆C 的标准方程;(2) 若HG⊥A 1D ,试求直线A 1D 的方程;(3) 如果A 1H →=λA 1P →,试求λ的取值范围.已知函数f(x)=x 2+(2-a)x -aln x ,其中a∈R .(1) 如果曲线y =f(x)在x =1处的切线斜率为1,求实数a 的值; (2) 若函数f(x)的极小值不超过a2,求实数a 的最小值;(3) 对任意x 1∈[1,2],总存在x 2∈[4,8],使得f(x 1)=f(x 2)成立,求实数a 的取值范围.已知数列{a n}是各项都不为0的无穷数列,对任意的n≥3,n∈N,a1a2+a2a3+…+a n-1a n =λ(n-1)a1a n恒成立.(1) 如果1a1,1a2,1a3成等差数列,求实数λ的值;(2) 已知λ=1.①求证:数列{1a n}是等差数列;②已知数列{a n}中,a1≠a2.数列{b n}是公比为q的等比数列,满足b1=1a1,b2=1a2,b3=1a i(i∈N).求证:q是整数,且数列{b n}中的任意一项都是数列{1a n}中的项.2020届高三模拟考试试卷数学附加题(满分40分,考试时间30分钟)21. 【选做题】 在A ,B ,C 三小题中只能选做两题,每小题10分,共20分.若多做,则按作答的前两题计分.解答时应写出必要的文字说明、证明过程或演算步骤.A. (选修42:矩阵与变换)已知矩阵A =⎣⎢⎡⎦⎥⎤210a ,其逆矩阵A -1=⎣⎢⎡⎦⎥⎤b c 01,求A 2.B. (选修44:坐标系与参数方程)在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎨⎧x =2+2cos θ,y =-3+2sin θ(θ为参数).以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,直线l 上两点M ,N 的极坐标分別为(2,0),(23,π6),求直线l 被曲线C 截得的弦长.C. (选修45:不等式选讲)已知正数a ,b ,c 满足a +b +c =2,求证:a 2b +c +b 2c +a +c2a +b ≥1.【必做题】第22,23题,每小题10分,共20分.解答时应写出必要的文字说明、证明过程或演算步骤.22. 在平面直角坐标系xOy中,已知抛物线C:y2=4x的焦点为F,过F的直线l交抛物线C于A,B两点.(1) 求线段AF的中点M的轨迹方程;(2) 已知△AOB的面积是△BOF面积的3倍,求直线l的方程.23. 已知数列{a n}中,a1=2,且a n+1=a2n-a n+1对任意n∈N恒成立.求证:(1) a n+1=a n a n-1a n-2…a2a1+1(n∈N);(2) a n+1>n n+1(n∈N).2020届高三模拟考试试卷(苏锡常镇)数学参考答案及评分标准1. (0,1)2. 13. 524. 85. 556. 137. 738. 239. 11 10. (-2,-1)∪(1,2) 11. 1212. 1 13. -25314. (-2e -1,0]15. 证明:在三棱锥PABC 中:(1) 因为点E ,F 分别是PD ,PC 的中点,所以EF 为△PCD 的中位线,(2分) 则有EF∥CD.(3分) 又EF平面ABC ,CD平面ABC ,所以EF∥平面ABC.(7分)(2) 因为平面PAB⊥平面PCD ,平面PAB∩平面PCD =PD ,AB ⊥PD ,AB 平面PAB ,所以AB⊥平面PCD.(11分) 又CE平面PCD ,所以AB⊥CE.(14分)16. 解:(1) 由正弦定理a sin A =b sin B =c sin C ,且3a c =2-cos Asin C,(1分) 得3sin A sin C =2-cos Asin C,(2分)则有3sin A =2-cos A ,即3sin A +cos A =2,2sin(A +π6)=2, 故sin(A +π6)=1.(4分)因为A∈(0,π),则A +π6∈(π6,7π6),所以A +π6=π2,即A =π3.(6分)(2) 在△ABC 中,因为A =π3,则B∈(0,2π3),B +π6∈(π6,5π6),所以sin(B +π6)>0.因为cos(B +π6)=14,所以sin(B +π6)=1-cos 2(B +π6)=154.(8分)在△ABC 中,A +B +C =π,(9分)所以cos C =cos(π-A -B)=-cos(A +B)=-cos(B +π3)(10分)=-cos[(B +π6)+π6]=-cos(B +π6)cos π6+sin(B +π6)sin π6=-32×14+12×154=15-38.(14分) 17. 解:设圆锥形容器的底面半径为r 米,高为h 米,母线为l 米,侧面积为S 平方米,容积为V 立方米,则V =36π.(1) 由r =6,得V =13πr 2h =36π,得h =3,(1分)所以S =πrl =πr r 2+h 2=6π62+32=185π.(2分)又底面积为πr 2=36π(平方米),(3分)故该容器的表面积为(185π+36π)=18(2+5)π(平方米).(4分) 答:该容器的表面积为18(2+5)π平方米.(5分)(2) 因为V =13πr 2h =36π,得r 2=3×36ππh =108h ,其中h>0,所以S =πrl =πr r 2+h 2=πr 4+r 2h 2=π1082h 2+108hh 2=π1082h2+108h =π108108h2+h.(8分) 记f(h)=108h 2+h ,令f′(h)=-216h 3+1=h 3-216h3=0,得h =6.(10分) 当h∈(0,6)时,f ′(h)<0,f(h)在(0,6)上单调递减;当h∈(6,+∞)时,f ′(h)>0,f(h)在(6,+∞)上单调递增.(12分) 所以,当h =6时,f(h)最小,此时S 最小.(13分)答:当容器的高为6米时,制造容器的侧面用料最省.(14分)18. 解:(1) 由椭圆C 的左、右顶点分别为A 1(-2,0),A 2(2,0),右准线方程为x =4,得a =2,a 2c =4,故c =1,b 2=a 2-c 2=3.(2分)所以椭圆C 的方程为x 24+y23=1 ①.(3分)(2) 设直线A 1D :y =k(x +2)(k>0) ②,则与右准线x =4的交点D(4,6k). 又A 2(2,0),所以设直线A 2D :y =3k(x -2),联立①,得 ⎩⎪⎨⎪⎧x 24+y 23=1,y =3k (x -2),解得G(24k 2-21+12k 2,-12k1+12k2),(5分)则直线OG 的斜率为k OG =-6k12k 2-1 ③.因为OG⊥A 1D ,故-6k 12k 2-1·k =-1.又k>0,解得k =66,(7分)则直线A 1D 的方程为y =66(x +2).(8分) (3) 由(2)中③可设直线OG :y =-6k12k 2-1x ,联立②,得⎩⎪⎨⎪⎧y =-6k 12k 2-1x ,y =k (x +2),解得H(-24k 2+212k 2+5,12k 12k 2+5).(10分) 联立①②,得⎩⎪⎨⎪⎧x 24+y 23=1,y =k (x +2),解得P(6-8k 23+4k 2,12k3+4k2).(12分)因为AH →=λAP →,所以(x H +2,y H )=λ(x P +2,y P ),则y H =λy P ,λ=y H y P =f(k)=12k 12k 2+512k 3+4k 2=3+4k 212k 2+5=112k 2+9-43+4k 2=13-43+4k 2.(14分) 因为f(k)在(0,+∞)上为减函数,(15分) 所以λ∈(13,35).(16分)19. 解:因为f(x)=x 2+(2-a)x -aln x ,所以f′(x)=(x +1)(2x -a )x 2.(1分) (1) 因为曲线y =f(x)在x =1处的切线斜率为1, 所以f′(1)=2(2-a)=1,解得a =32.(2分)(2) ① 当a≤0时,f ′(x)>0在(0,+∞)上恒成立,即f(x)在(0,+∞)上单调递增, 故函数f(x)不存在极值.(3分) ②当a>0时,令f′(x)=0,得x =a2.x (0,a 2)a 2 (a2,+∞) f′(x) -0 +f(x)极小值(5分)则f(x)min =f(a 2)=a -a 24-aln a 2≤a 2.因为a>0,则12-a 4-ln a2≤0.令g(a)=12-a 4-ln a 2=12+ln 2-a 4-ln a ,则g′(a)=-14-1a<0,则g(a)在(0,+∞)上单调递减.(7分)又g(2)=0,所以g(a)≤g(2)=0,则a≥2,则实数a 的最小值为2.(8分) (3) 记f(x)在[1,2]上的值域为A ,在[4,8]上的值域为B ,“任意x 1∈[1,2],总存在x 2∈[4,8],使得f(x 1)=f(x 2)成立”等价于“A B ”. ①当a 2≤1或a2≥8,即a≤2或a≥16时,由(2)知f(x)在[1,8]上为单调函数,不合题意;(9分)②当1<a 2≤2,即2<a≤4时,由(2)知f(x)在(0,a 2)上单调递减,在(a2,+∞)上单调递增,故f(a 2)∈A ,但f(a2)B ,不合题意;(10分)③当2<a2≤4,即4<a≤8时,A =[f(2),f(1)],B =[f(4),f(8)],由A B ,得⎩⎪⎨⎪⎧f (2)≥f(4),f (1)≤f(8),则⎩⎪⎨⎪⎧8-2a -aln 2≥24-4a -2aln 2,3-a≤80-8a -3aln 2,解得⎩⎪⎨⎪⎧a ≥162+ln 2,a ≤777+3ln 2.(11分)因为0<ln 2<1,则2<2+ln 2<3,即4<163<162+ln 2<8.因为e>2.7,计算得e 3>24,则e 72>e 3>24,即72>ln 24=4ln 2,即7>8ln 2,也即21>24ln 2,则777+3ln 2-8=21-24ln 27+3ln 2>0,即777+3ln 2>8.所以162+ln 2≤a ≤8.(13分)④当4<a2<8,即8<a<16,由A B ,得f(8)≥f(1),得a ≤777+3ln 2<777=11<16,则8<a≤777+3ln 2.(15分) 综上,162+ln 2≤a ≤777+3ln 2.(16分)20. (1) 解:因为n≥3且n∈N *时,a 1a 2+a 2a 3+…+a n -1a n =λ(n-1)a 1a n 恒成立,所以n =3时,a 1a 2+a 2a 3=2λa 1a 3 (*). 因为数列{a n }各项都不为0,所以(*)式两边同除以a 1a 2a 3,得2λa 2=1a 1+1a 3.(1分)因为1a 1,1a 2,1a 3成等差数列,则2a 2=1a 1+1a 3.(2分)比较得2λa 2=2a 2,所以λ=1.(3分)(2) 证明:① 当λ=1,n =3时,a 1a 2+a 2a 3=2a 1a 3 (i),整理,得1a 1+1a 3=2a 2,则1a 2-1a 1=1a 3-1a 2(ii).(4分) 当n =4时,a 1a 2+a 2a 3+a 3a 4=3a 1a 4 (iii). (iii)-(i),得a 3a 4=3a 1a 4-2a 1a 3,得1a 1=3a 3-2a 4.又1a 1+1a 3=2a 2,所以1a 4-1a 3=1a 3-1a 2 (iv).(5分) 当n≥3时,a 1a 2+a 2a 3+…+a n -1a n =(n -1)a 1a n , a 1a 2+a 2a 3+…+a n -1a n +a n a n +1=na 1a n +1, 两式相减,得a n a n +1=na 1a n +1-(n -1)a 1a n .因为a n ≠0,所以1a 1=n a n -n -1a n +1,(6分)所以1a 1=n +1a n +1-n a n +2,所以n a n -n -1a n +1=n +1a n +1-n a n +2,整理,得1a n +1a n +2=2a n +1,即1a n +2-1a n +1=1a n +1-1a n(n≥3) (v).(7分)由(ii)(iv)(v),得1a n +2-1a n +1=1a n +1-1a n 对任意的正整数n≥1恒成立,(8分)所以数列{1a n}成等差数列.(9分)②设数列{1a n }的公差为d ,令c n =1a n ,c 1=1a 1=c(c≠0),则b 1=c 1=c ,b 2=c 2=c +d ,d =c 2-c 1=b 2-b 1=cq -c.当i =2时,b 3=c 2=b 2,从而q =1,b 2=b 1,得a 1=a 2,与已知不符.(10分)当i =3时,由b 3=c 3,cq 2=c +2d =c +2c(q -1),得q 2=1+2(q -1), 得q =1,与已知不符.(11分)当i =1时,由b 3=c 1,cq 2=c ,得q 2=1,则q =-1(上面已证q≠1)为整数. 数列{b n }为c ,-c ,c ,…;在数列{c n }中,c 1=c ,c 2=-c ,公差d =-2c. 数列{b n }每一项都是{c n }中的项(c =c 1,-c =c 2).(12分)当i≥4时,由b 3=c i ,cq 2=c +(i -1)d =c +(i -1)c(q -1),得q 2-(i -1)q +(i -2)=0,得q =1(舍去),q =i -2(i≥4)为整数.(14分) 因为cq =c +d ,b 3=c i ,对任意的正整数k≥4,欲证明b k 是数列{c n }中的项,只需b k =cq k -1=c i +xd =b 3+x(cq -c)=cq 2+x(cq -c)有正整数解x.等价于qk -1=q 2+x(q -1),x =qk -1-q2q -1为正整数. 因为x =qk -1-q 2q -1=q 2(q k -3-1)q -1表示首项为q 2,公比为q =i -2(i≥4), 共k -3(k≥4)项的等比数列的和,所以x 为正整数. 因此,{b n }中的每一项都是数列{c n }也即{1a n }中的项.(16分)2020届高三模拟考试试卷(苏锡常镇) 数学附加题参考答案及评分标准21. A. 解: 因为AA -1=⎣⎢⎡⎦⎥⎤1001,则有⎣⎢⎡⎦⎥⎤210a ⎣⎢⎡⎦⎥⎤b c 01=⎣⎢⎡⎦⎥⎤1001,(2分) 即a =1,b =12,c =-12,则A =⎣⎢⎡⎦⎥⎤2101,(5分)则A 2=⎣⎢⎡⎦⎥⎤2101⎣⎢⎡⎦⎥⎤2101=⎣⎢⎡⎦⎥⎤4301.(10分)B. 解:由x =ρcos θ,y =ρsin θ,得M(2,0,)N(3,3), 则直线l :y =3(x -2),(2分)曲线C :(x -2)2+(y +3)2=4,圆心为(2,-3),半径r =2, 则圆心到直线l 的距离d =|0-3|2=32,(6分)则直线l 被曲线C 截得的弦长为2r 2-d 2=13.(10分)C. 证明:因为a>0,b>0,c>0,a +b +c =2,由柯西不等式,得 [(b +c)+(c +a)+(a +b)](a 2b +c +b 2c +a +c2a +b )=[(b +c)2+(c +a)2+(a +b)2][(a b +c )2+(b c +a)2+(c a +b)2]=(b +cab +c +c +abc +a +a +bca +b)2(5分) =(a +b +c)2=22,(8分)则a 2b +c +b 2c +a +c 2a +b ≥22(b +c )+(c +a )+(a +b )=44=1. 所以a 2b +c +b 2c +a +c 2a +b≥1.(10分)22. 解:因为抛物线方程为y 2=4x ,所以F(1,0).(1分) (1) 设M(x ,y),A(x 0,y 0).因为点M 为线段AF 的中点,则x =x 0+12,y =y 02,(2分)则x 0=2x -1,y 0=2y ,代入抛物线方程,得y 2=2x -1,即点M 的轨迹方程为y 2=2x -1.(4分)(2) 设A(x 1,y 1),B(x 2,y 2),不妨设y 1>0,y 2<0, 设△AOB 和△BOF 的面积分别为S 1,S 2.因为△AOB 的面积是△BOF 面积的3倍,即S 1+S 2=3S 2,所以S 1=2S 2. 因为S 1=12OF ·y 1,S 2=12OF ·|y 2|=-12OF ·y 2,则y 1=-2y 2 ①.(6分)设直线AB :x =ty +1(t>0) ②,与y 2=4x 联立,消去x ,得y 2-4ty -4=0, y 1,2=2t±2t 2+1,y 1+y 2=4t ③,y 1y 2=-4 ④.(8分)由①③④可得t =122,代入②,得直线l :y =22(x -1);同理当y 1<0,y 2>0时,得直线l :y =-22(x -1). 综上,直线l 的方程为y =±22(x -1).(10分)23. 证明:(1) 当n =1时,a 2=a 1(a 1-1)+1=3=a 1+1成立. 假设n =k 时,结论成立,即a k +1=a k a k -1…a 2a 1+1.当n =k +1时,a k +2=a k +1(a k +1-1)+1=a k +1(a k a k -1…a 2a 1+1-1)+1 =a k +1a k a k -1…a 2a 1+1.则当n =k +1时,命题成立.综上,a n +1=a n a n -1a n -2…a 2a 1+1.(4分)(2) 要证a n +1>n n+1,由(1)a n +1=a n a n -1a n -2…a 2a 1+1,只需证a n a n -1a n -2…a 2a 1>n n.下用数学归纳法证明:当n =1,2,3时,a 1=2,a 2=3,a 3=7,则2>1,2×3>22,2×3×7>33.假设n =k(k≥3)时,结论成立,即a k a k -1a k -2…a 2a 1>k k,(6分) 则n =k +1时,a k +1a k …a 2a 1=(a k a k -1…a 2a 1+1)a k a k -1…a 2a 1>(a k a k -1a k -2…a 2a 1)2>k 2k.(7分)设f(x)=2xln x -(x +1)ln(x +1)(x≥3),则f′(x)=ln x 2x +1+1>ln x 2-1x +1+1=ln(x -1)+1≥ln 2+1>0,所以f(x)为增函数,则f(x)≥f(3)=2(3ln 3-2ln 4)=2ln 2716>0,则2kln k>(k +1)ln(k +1),ln k 2k>ln(k +1)(k +1),即k 2k>(k +1)(k +1).即a k +1a k …a 2a 1>(k +1)k +1,则n =k +1时,命题成立.(9分)综上,a n a n -1a n -2…a 2a 1>n n ,所以a n +1>n n+1.(10分)。
2021年江苏省苏州市高考数学三模试卷(含答案解析)

2021年江苏省苏州市高考数学三模试卷一、单选题(本大题共8小题,共40.0分)1.已知U为全集,非空集合A,B满足,则()A. A⊆BB. B⊆AC. D.2.设随机变量ξ服从正态分布N(1,4),则P(ξ<3)的值为()(参考数据:P(u−σ<ξ<u+σ)=0.6526,P(u−2σ<ξ<u+2σ)=0.9544)A. 0.1737B. 0.3474C. 0.6837D. 0.82633.欧拉公式e iθ=cosθ+isinθ(其中i为虚数单位)是把复指数函数与三角函数联系起来的一个公式,其中e是自然对数的底,i是虚数单位.它将指数函数的定义域扩大到复数,建立了三角函数和指数函数的关系,它不仅出现在数学分析里,而且在复变函数论里也占有非常重要的地位,更被誉为“数学中的天桥”.当θ=π时,恒等式e iπ+1=0更是被数学家们称为“上帝创造的公式”.根据上述材料可知|e iθ−e iπ|的最大值为()A. 1B. 2C. √2D. 44.为了更好地管理班级,班主任决定选若干名学生担任班主任助理,于是征求语、数、英三科任课教师的意见.语文老师:如果不选小李,那么不选小宋;数学老师:如果不选小宋,那么选小李;英语老师:小宋和小李两人中至少选一个并且至多选一个.若班主任同时采纳了三人的建议,则作出的选择是()A. 选小宋,不选小李B. 选小李,不选小宋C. 两人都选D. 两人都不选5.已知(x+1)6=a0+a1(x−1)+⋯+a6(x−1)6,则a3=()A. 15B. 20C. 60D. 1606.函数f(x)=2x+2−x的图象大致为()ln(√x2+1−x)A. B.C.D.7. 如图为陕西博物馆收藏的国宝——唐⋅金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代金银细作的典范之作.该杯的主体部分可以近似看作是双曲线C :x 2a2−y 2b 2=1(a >0,b >0)的右支与y 轴及平行于x 轴的两条直线围成的曲边四边形ABMN 绕y 轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为10√33,下底座外直径为2√393,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周长为( )A. 2√2πB. 3πC. 2√3πD. 4π8.若函数g(x)在区间D 上,对∀a ,b ,c ∈D ,g(a),g(b),g(c)为一个三角形的三边长,则称函数g(x)为“稳定函数”.已知函数f(x)=lnx x+m 在区间[1e 2,e 2]上是“稳定函数”,则实数m 的取值范围为( )A. (2e +1e ,+∞)B. (2e 2+1e ,+∞)C. (4e +1e ,+∞)D. (4e 2+1e ,+∞)二、多选题(本大题共4小题,共20.0分) 9.已知△ABC 是边长为2的正三角形,该三角形重心为点G ,点P 为△ABC 所在平面内任一点,下列等式一定成立的是( ) A. |AB⃗⃗⃗⃗⃗ +AC ⃗⃗⃗⃗⃗ |=2 B. AB⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =2 C. PA ⃗⃗⃗⃗⃗ +PB ⃗⃗⃗⃗⃗ +PC ⃗⃗⃗⃗⃗ =3PG ⃗⃗⃗⃗⃗D. |AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ |=|AB ⃗⃗⃗⃗⃗ +CB⃗⃗⃗⃗⃗ | 10. 若实数x ,y 满足x >y >0,则( )A. 1y >1xB. ln(x −y)>lnyC. x +y <√2(x 2+y 2)D. x −y <e x −e y11.定义:若存在非零常数k,T,使得函数f(x)满足f(x+T)=f(x)+k对定义域内的任意实数x恒成立,则称函数f(x)为“k距周期函数”,其中T称为函数的“类周期”,则()A. 一次函数均为“k距周期函数”B. 存在某些二次函数为“k距周期函数”C. 若“1距周期函数”f(x)的“类周期”为1,且f(1)=1,则f(x)=xD. 若g(x)是周期为2函数,且函数f(x)=x+g(x)在[0,2]上的值域为[0,1],则函数f(x)=x+g(x)在区间(2n,2n+2]上的值域为(2n,2n+1]12.斐波那契,公元13世纪意大利数学家.他在自己的著作《算盘书》中记载着这样一个数列:1,1,2,3,5,8,13,21,34,⋯,其中从第三个数起,每一个数都等于它前面两个数的和,这就是著名的斐波那契数列.斐波那契数列与代数和几何都有着不可分割的联系.现有一段长为a米的铁丝,需要截成n(n>2)段,每段的长度不小于1m,且其中任意三段都不能构成三角形,若n的最大值为10,则a的值可能是()A. 100B. 143C. 200D. 256三、填空题(本大题共4小题,共20.0分)13.写出一个长轴长等于离心率8倍的椭圆标准方程为.14.已知等差数列{a n}的前n项和为{S n},公差为d,若S2n=2S n+n2,则d=.15.如图,三根绳子上共挂有6只气球,绳子上的球数依次为1,2,3,每枪只能打破一只气球,而且规定只有打破下面的气球才能打上面的气球,则将这些气球都打破的不同打法数是.16.如图,一个酒杯的内壁的轴截面是抛物线的一部分,杯口宽4√2cm,杯深8cm,称为抛物线酒杯.①在杯口放一个表面积为36πcm2的玻璃球,则球面上的点到杯底的最小距离为cm;②在杯内放入一个小的玻璃球,要使球触及酒杯底部,则玻璃球的半径的取值范围为(单位:cm).四、解答题(本大题共6小题,共70.0分)17.△ABC的内角A,B,C的对边分别为a,b,c,已知1a +1b=kc(k>0).(1)若k=2√2,C=π2,求A的值;(2)若k=2,当角C最大时,判断△ABC的形状.18.①S n+1=2S n+2,②a n+1−a n=2n,③S n=a n+1−2,在这三个条件中任选一个,补充在下面的问题中,并解答.已知数列{a n}的前n项和为S n,首项为2,且满足_______.(1)求数列{a n}的通项公式;(2)在a n与a n+1之间插入n个数,使这n+2个数组成一个公差为d n的等差数列,求证:d n>n2.19.在平面直角坐标系xOy中,已知双曲线C:x2a2−y2b2=1(a,b>0)的左、右顶点分别为A,B,其图象经过点(√3,1),渐近线方程为y=±x.(1)求双曲线C的方程;(2)设点E,F是双曲线C上位于第一象限的任意两点,求证:∠EAF=∠EBF.20.如图,在多面体ABCDE中,平面ACDE⊥平面ABC,四边形ACDE为直角梯形,CD//AE,AC⊥AE,∠ABC=60°,CD=1,AE=AC=2,F为BE的中点.(1)当BC的长为多少时,DF⊥平面ABE.(2)求平面ABE与平面BCD所成的锐二面角的大小.21.为落实十三五规划节能减排的国家政策,某职能部门对市场上两种设备的使用寿命进行调查统计,随机抽取A型和B型设备各100台,得到如图频率分布直方图:(1)将使用寿命超过2500小时和不超过2500小时的台数填入下面的列联表:超过2500小时不超过2500小时总计A型B型总计根据上面的列联表,能否有99%的把握认为使用寿命是否超过2500小时与型号有关?(2)用分层抽样的方法从不超过2500小时A型和B型设备中抽取8台,再从这8台设备中随机抽取3台,其中A型设备为X台,求X的分布列和数学期望;(3)已知用频率估计概率,现有一项工作需要10台同型号设备同时工作2500小时才能完成,工作期间设备损坏立即更换同型号设备(更换设备时间忽略不计),A型和B型设备每台的价格分别为1万元和0.6万元,A型和B型设备每台每小时耗电分别为2度和6度,电价为0.75元/度.只考虑设备的成本和电费,你认为应选择哪种型号的设备,请说明理由.,n=a+b+c+d.参考公式:χ2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)参考数据:P(χ2≥k0)0.0500.0100.001 k0 3.841 6.63510.82822.已知函数f(x)=e x sinx−kx(k∈R)(其中e为自然对数的底数).(1)若对任意x∈[0,π2],f(x)≥0成立,求实数k的取值范围;(2)设x1,x2∈(0,π2),且x1+x2=1,求证:sinx1x2+sinx2x1>√e.参考答案及解析1.答案:A解析:本题考查集合的交并补混合运算,集合包含关系等基础知识,考查运算求解能力等数学核心素养,是基础题.利用并集、交集、补集的定义直接求解.解:∵U为全集,非空集合A,B满足,∴A⊆B.故选:A.2.答案:D解析:本题考查了正态分布的性质的运用,解题的关键是掌握正态分布的对称性,属于基础题.利用正态分布的对称性求解即可.解:因为随机变量ξ服从正态分布N(1,4),所以u=1,σ=2,由正态分布的对称性可得:P(ξ<3)=P(ξ⩽−1)+12P(1−2<ξ<1+2)=0.5+12P(1−2<ξ<1+2)=0.5+12×0.6526=0.8263.故选:D.3.答案:B解析:本题考查了复数的三角形式、欧拉公式的应用、倍角公式、同角三角函数基本关系式等知识,考查了推理能力与计算能力,属于基础题.利用欧拉公式化简e iθ−e iπ,再利用复数模的计算公式、倍角公式、同角三角函数基本关系式即可得出结论.解:e iθ−e iπ=cosθ+isinθ+1,|≤2,所以|e iθ−e iπ|=√(cosθ+1)2+sin2θ=√2+2cosθ=2|cosθ2可得|e iθ−e iπ|的最大值为2.故选:B.4.答案:B解析:本题考查了简单的合情推理的应用,考查了推理论证能力、应用意识以及创新意识,考查逻辑推理的核心素养,属于基础题.分别针对三位老师的话进行分析,即可得到答案.解:由英语老师的话可知,两人中选且只选一人,由语文老师的话可知,要么选小李(小宋可选可不选),要么两人都不选,由数学老师的话可知,要么选小宋(小李可选可不选),要么不选小宋选小李,综上所述,班主任作出的选择应该是选小李,不选小宋.故选:B.5.答案:D解析:本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于中档题.根据[2+(x−1)]6=a0+a1(x−1)+⋯+a6(x−1)6,利用展开式的通项公式,即可求得a3的值.解:(x+1)6=[2+(x−1)]6=a0+a1(x−1)+⋯+a6(x−1)6,则a3=C63⋅23=160,故选:D.6.答案:B解析:本题主要考查函数图象的识别和判断,利用函数的奇偶性和对称性,以及函数值的符号,利用排除法是解决本题的关键,是基础题.判断函数的奇偶性和对称性,利用f(1)的符号进行判断即可.解:函数的定义域为{x|x≠0},。
2020-2021学年江苏省三市联考高考数学三模试卷及答案解析
江苏省徐州市、连云港市、宿迁市高考数学三模试卷一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题卡的指定位置上.1.已知集合A={x|x=2k+1,k∈Z},B={x|0<x<5},则A∩B= .2.已知复数z满足(3+i)z=10i(其中i为虚数单位),则复数z的共轭复数是.3.如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是.4.甲、乙、丙三人一起玩“黑白配”游戏:甲、乙、丙三人每次都随机出“手心(白)”、“手背(黑)”中的某一个手势,当其中一个人出示的手势与另外两人都不一样时,这个人胜出;其他情况,不分胜负.则一次游戏中甲胜出的概率是.5.执行如图所示的算法流程图,则输出k的值为.6.已知点F为抛物线y2=4x的焦点,该抛物线上位于第一象限的点A到其准线的距离为5,则直线AF的斜率为.7.已知公差为d的等差数列{a n}的前n项和为S n,若=3,则= .8.已知圆锥的母线长为10cm,侧面积为60πcm2,则此圆锥的体积为cm3.9.若实数x,y满足约束条件,则|3x﹣4y﹣10|的最大值为.10.已知函数f(x)=sinx(x∈[0,π])和函数g(x)=tanx的图象交于A,B,C三点,则△ABC 的面积为.11.若点P,Q分别是曲线y=与直线4x+y=0上的动点,则线段PQ长的最小值为.12.已知,,是同一平面内的三个向量,其中,是相互垂直的单位向量,且()•(﹣)=1,||的最大值为.13.已知对满足x+y+4=2xy的任意正实数x,y,都有x2+2xy+y2﹣ax﹣ay+1≥0,则实数a的取值范围为.14.已知经过点P(1,)的两个圆C1,C2都与直线l1:y=x,l2:y=2x相切,则这两圆的圆心距C1C2等于.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内.15.如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2,∠CAD=,tan∠ADC=﹣2,求:(1)CD的长;(2)△BCD的面积.16.如图,在直三棱柱ABC﹣A1B1C1中,已知AB=AC,M,N,P分别为BC,CC1,BB1的中点.求证:(1)平面AMP⊥平面BB1C1C;(2)A1N∥平面AMP.17.在平面直角坐标系xOy中,已知点P(1,)在椭圆C:=1(a>b>0)上,P到椭圆C的两个焦点的距离之和为4.(1)求椭圆C的方程;(2)若点M,N是椭圆C上的两点,且四边形POMN是平行四边形,求点M,N的坐标.18.经市场调查,某商品每吨的价格为x(1<x<14)百元时,该商品的月供给量为y1万吨,y1=ax+a2﹣a(a>0);月需求量为y2万吨,y2=﹣x2﹣x+1.当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量.该商品的月销售额等于月销售量与价格的乘积.(1)若a=,问商品的价格为多少时,该商品的月销售额最大?(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6百元,求实数a的取值范围.19.已知函数f(x)=,g(x)=ax﹣2lnx﹣a (a∈R,e为自然对数的底数).(1)求f(x)的极值;(2)在区间(0,e]上,对于任意的x0,总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0),求a的取值范围.20.在数列{a n}中,已知a1=1,a2=2,a n+2=(k∈N*).(1)求数列{a n}的通项公式;(2)求满足2a n+1=a n+a n+2的正整数n的值;(3)设数列{a n}的前n项和为S n,问是否存在正整数m,n,使得S2n=mS2n﹣1?若存在,求出所有的正整数对(m,n);若不存在,请说明理由.三.[选做题]本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.如图,AB是圆O的直径,弦BD,CA的延长线相交于点E,过E作BA的延长线的垂线,垂足为F.求证:AB2=BE•BD﹣AE•AC.B.[选修4-2:矩阵与变换](本小题满分0分)22.已知矩阵A=,向量=,计算A5.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的极坐标方程为,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C的参数方程为(α为参数),求直线l与曲线C 的交点P的直角坐标.D.[选修4-5:不等式选讲](本小题满分0分)24.已知a、b∈R,a>b>e(其中e是自然对数的底数),求证:b a>a b.(提示:可考虑用分析法找思路)四.[必做题]第22、23题,每小题0分,计20分.请把答案写在答题卡的指定区域内.25.已知甲箱中装有3个红球、3个黑球,乙箱中装有2个红球、2个黑球,这些球除颜色外完全相同.某商场举行有奖促销活动,设奖规则如下:每次分别从以上两个箱中各随机摸出2个球,共4个球.若摸出4个球都是红球,则获得一等奖;摸出的球中有3个红球,则获得二等奖;摸出的球中有2个红球,则获得三等奖;其他情况不获奖.每次摸球结束后将球放回原箱中.(1)求在1次摸奖中,获得二等奖的概率;(2)若连续摸奖2次,求获奖次数X的分布列及数学期望E(X).26.在集合A={1,2,3,4,…,2n}中,任取m(m≤n,m,n∈N*)个元素构成集合A m.若A m 的所有元素之和为偶数,则称A m为A的偶子集,其个数记为f(m);若A m的所有元素之和为奇数,则称A m为A的奇子集,其个数记为g(m).令F(m)=f(m)﹣g(m).(1)当n=2时,求F(1),F(2),F(3)的值;(2)求F(m).参考答案与试题解析一、填空题:本大题共14小题,每小题5分,计70分.不需写出解答过程,请把答案写在答题卡的指定位置上.1.已知集合A={x|x=2k+1,k∈Z},B={x|0<x<5},则A∩B= {1,3} .【考点】交集及其运算.【分析】由A与B,求出两集合的交集即可.【解答】解:∵A={x|x=2k+1,k∈Z},B={x|0<x<5},∴A∩B={1,3},故答案为:{1,3}.2.已知复数z满足(3+i)z=10i(其中i为虚数单位),则复数z的共轭复数是1﹣3i .【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则、共轭复数的定义即可得出.【解答】解:∵(3+i)z=10i,∴(3﹣i)(3+i)z=10i(3﹣i),∴10z=10(3i+1),化为:z=1+3i,则复数z的共轭复数是1﹣3i.故答案为:1﹣3i.3.如图是一次摄影大赛上7位评委给某参赛作品打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后,算得平均分为91分,复核员在复核时,发现有一个数字(茎叶图中的x)无法看清,若记分员计算无误,则数字x应该是 1 .【考点】茎叶图.【分析】根据讨论x>4时,求出平均分不是91分,显然x≤4,表示出平均分,得到关于x的方程,解出即可.【解答】解:若x>4,去掉一个最高分(90+x)和一个最低分86后,平均分为(89+91+92+92+94)=91.6分,不合题意,故x≤4,最高分是94,去掉一个最高分94和一个最低分86后,故平均分是(89+92+90+x+91+92)=91,解得x=1,故答案为:1.4.甲、乙、丙三人一起玩“黑白配”游戏:甲、乙、丙三人每次都随机出“手心(白)”、“手背(黑)”中的某一个手势,当其中一个人出示的手势与另外两人都不一样时,这个人胜出;其他情况,不分胜负.则一次游戏中甲胜出的概率是.【考点】列举法计算基本事件数及事件发生的概率.【分析】根据题意,分析可得甲、乙、丙出的方法种数都有2种,由分步计数原理可得三人进行游戏的全部情况数目,进而可得甲胜出的情况数目,由等可能事件的概率,计算可得答案.【解答】解:一次游戏中,甲、乙、丙出的方法种数都有2种,所以总共有23=8种方案,而甲胜出的情况有:“甲黑乙白丙白”,“甲白乙黑丙黑”,共2种,所以甲胜出的概率为=,故答案为:.5.执行如图所示的算法流程图,则输出k的值为 3 .【考点】程序框图.【分析】根据框图的流程模拟运行程序,直到满足条件n=1,跳出循环,确定输出k的值.【解答】解:n=13是奇数,n==6>1,不符,此时k=1,n=6是偶数,n=3>1,不符,此时k=2,n=3是奇数,n=1=1,符合,此时k=3,故答案为:3.6.已知点F为抛物线y2=4x的焦点,该抛物线上位于第一象限的点A到其准线的距离为5,则直线AF的斜率为.【考点】抛物线的简单性质.【分析】求出抛物线的焦点坐标,设出A,利用抛物线上位于第一象限的点A到其准线的距离为5,求出A的横坐标,然后求解斜率.【解答】解:由题可知焦点F(1,0),准线为x=﹣1设点A(x A,y A),∵抛物线上位于第一象限的点A到其准线的距离为5,∴x A+=5,∴x A=4,∴y A=4,∴点A(4,4),∴直线AF的斜率为=,故答案为:.7.已知公差为d的等差数列{a n}的前n项和为S n,若=3,则= .【考点】等差数列的前n项和.【分析】设出等差数列的首项,由=3得到首项和公差的关系,代入等差数列的通项公式可得.【解答】解:设等差数列{a n}的首项为a1,则,由=3,得,即d=4a1,∴=.故答案为:.8.已知圆锥的母线长为10cm,侧面积为60πcm2,则此圆锥的体积为96πcm3.【考点】旋转体(圆柱、圆锥、圆台).【分析】根据侧面积计算圆锥的底面半径,根据勾股定理得出圆锥的高,代入圆锥的体积公式计算体积.【解答】解:设圆锥的底面半径为r,则S侧=π×r×10=60π,解得r=6.∴圆缀的高h==8,∴圆锥的体积V===96π.故答案为:96π.9.若实数x,y满足约束条件,则|3x﹣4y﹣10|的最大值为.【考点】简单线性规划.【分析】由题意作平面区域,而根据点到直线的距离公式可知转化为求阴影内的点到直线l的距离最大,从而解得.【解答】解:由题意作平面区域如下,,直线l的方程为3x﹣4y﹣10=0,点A到直线l的距离最大,由解得,A(,),故点A到直线l的距离d==,故|3x﹣4y﹣10|的最大值为×5=;故答案为:.10.已知函数f(x)=sinx(x∈[0,π])和函数g(x)=tanx的图象交于A,B,C三点,则△ABC 的面积为π.【考点】正切函数的图象;正弦函数的图象.【分析】根据题意,令sinx=tanx,结合x∈[0,π]求出x的值,得出三个点A、B、C的坐标,即可计算△ABC的面积.【解答】解:根据题意,令sinx=tanx,即sinx(1﹣)=0,解得sinx=0或1﹣=0,即sinx=0或cosx=;又x∈[0,π],所以x=0或x=π或x=;所以点A(0,0),B(π,0),C(,);所以△ABC的面积为S=|AB|h=×π×=π.故答案为:π.11.若点P,Q分别是曲线y=与直线4x+y=0上的动点,则线段PQ长的最小值为.【考点】两点间距离公式的应用.【分析】求出原函数的导函数,得到与直线4x+y=0平行的曲线的切线方程,由平行线间的距离公式求得线段PQ长的最小值.【解答】解:由y==1+,得y′=,由,得x2=1,∴x=±1.当x=1时,y=5,则与4x+y=0且与曲线y=相切的直线方程为y﹣5=﹣4(x﹣1),即4x+y﹣9=0.此时两平行线间的距离为;当x=﹣1时,y=﹣3,则与4x+y=0且与曲线y=相切的直线方程为y+3=﹣4(x+1),即4x+y+7=0.此时两平行线间的距离为.∴曲线y=与直线4x+y=0上两动点PQ距离的最小值为.故答案为:.12.已知,,是同一平面内的三个向量,其中,是相互垂直的单位向量,且()•(﹣)=1,||的最大值为1+.【考点】平面向量数量积的运算.【分析】不妨设=(1,0),=(0,1),设=(x,y),根据向量的坐标运算和数量积运算得到(x﹣)2+(y﹣)2=2,结合图形即可求出最大值.【解答】解:∵,是相互垂直的单位向量,不妨设=(1,0),=(0,1),设=(x,y),∴=(1﹣x,﹣y),﹣=(﹣x,﹣y),∵()•(﹣)=1,∴﹣(1﹣x)x﹣y(﹣y)=1,∴x2﹣x+y2﹣y=1,∴(x﹣)2+(y﹣)2=2,∴向量的轨迹为以(,)为圆心,以为半径的圆,∴圆心到原点的距离为1,∴||的最大值为1+故答案为:1+13.已知对满足x+y+4=2xy的任意正实数x,y,都有x2+2xy+y2﹣ax﹣ay+1≥0,则实数a的取值范围为(﹣∞,] .【考点】基本不等式.【分析】依题意,由正实数x,y满足x+y+4=2xy,可求得x+y≥4,由x2+2xy+y2﹣ax﹣ay+1≥0恒成立可求得a≤x+y+恒成立,利用双钩函数的性质即可求得实数a的取值范围.【解答】解:因为正实数x,y满足x+y+4=2xy,而4xy≤(x+y)2,代入原式得(x+y)2﹣2(x+y)﹣8≥0,解得(x+y)≥4或(x+y)≤﹣2(舍去)由x2+2xy+y2﹣ax﹣ay+1≥0可得a(x+y)≤(x+y)2+1,即a≤x+y+令t=x+y∈[4,+∞),则问题转化为a≤t+,因为函数y=t+在[4,+∞)递增,所以y min=4+=,所以a≤故答案为:(﹣∞,].14.已知经过点P(1,)的两个圆C1,C2都与直线l1:y=x,l2:y=2x相切,则这两圆的圆心距C1C2等于.【考点】直线与圆的位置关系.【分析】设圆心坐标为(x,y),由于圆与直线l1:y=x,l2:y=2x都相切,根据点到直线的距离公式得圆心只能在直线y=x上,设C1(a,a),C2(b,b),推导出a,b是方程(1﹣x)2+()2=的两根,由此能求出.这两圆的圆心距CC2.1【解答】解:设圆心坐标为(x,y),由于圆与直线l1:y=x,l2:y=2x都相切,根据点到直线的距离公式得:,解得y=x,∴圆心只能在直线y=x上,设C1(a,a),C2(b,b),则圆C1的方程为(x﹣a)2+(y﹣a)2=,圆C2的方程为(x﹣b)2+(y﹣b)2=,将(1,)代入,得:,∴a,b是方程(1﹣x)2+()2=,即=0的两根,∴,ab=,∴|C1C2|==•=•=.故答案为:.二、解答题:本大题共6小题,计90分.解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内.15.如图,在梯形ABCD中,已知AD∥BC,AD=1,BD=2,∠CAD=,tan∠ADC=﹣2,求:(1)CD的长;(2)△BCD的面积.【考点】解三角形的实际应用.【分析】(1)根据tan∠ADC=﹣2计算sin∠ADC,得出sin∠ACD,在△ACD中使用正弦定理求出CD;(2)根据∠ADC+∠BCD=180°求出sin∠BCD,cos∠BCD,在△BCD中使用余弦定理解出BC,则=.S△BCD【解答】解:(1)∵tan∠ADC=﹣2,∴sin∠ADC=,cos∠ADC=﹣.∴sin∠ACD=sin(∠CAD+∠ADC)=sin∠CADcos∠ADC+cos∠CADsin∠ADC==.在△ACD中,由正弦定理得,即,解得CD=.(2)∵AD∥BC,∴∠ADC+∠BCD=180°,∴sin∠BCD=sin∠ADC=,cos∠BCD=﹣cos∠ADC=.在△BCD中,由余弦定理得BD2=CD2+BC2﹣2BC•CDcos∠BCD,即40=5+BC2﹣2BC,解得BC=7或BC=﹣5(舍).=BC•CDsin∠BCD==7.∴S△BCD16.如图,在直三棱柱ABC﹣A1B1C1中,已知AB=AC,M,N,P分别为BC,CC1,BB1的中点.求证:(1)平面AMP⊥平面BB1C1C;(2)A1N∥平面AMP.【考点】直线与平面平行的判定;平面与平面垂直的判定.【分析】(1)由已知条件推导出AM⊥BC,AM⊥BB1,从而AM⊥平面BB1C1C,由此能证明平面AMP⊥平面BB1C1C.(2)取B1C1中点E,连结A1E、NE、B1C,推导出平面A1NE∥平面APM,由此能证明A1N∥平面AMP.【解答】证明:(1)∵在直三棱柱ABC﹣A1B1C1中,AB=AC,M是BB1的中点,∴AM⊥BC,AM⊥BB1,∵BC∩BB1=B,∴AM⊥平面BB1C1C,∵AM⊂平面AMP,∴平面AMP⊥平面BB1C1C.(2)取B1C1中点E,连结A1E、NE、B1C,∵M,N,P分别为BC,CC1,BB1的中点,∴NE∥BC1∥PM,A1E∥AM,∵PM∩AM=M,A1E∩NE=E,PM、AM⊂平面APM,A1E、NE⊂平面A1EN,∴平面A1NE∥平面APM,∵A1N⊂平面A1NE,∴A1N∥平面AMP.17.在平面直角坐标系xOy中,已知点P(1,)在椭圆C:=1(a>b>0)上,P到椭圆C的两个焦点的距离之和为4.(1)求椭圆C的方程;(2)若点M,N是椭圆C上的两点,且四边形POMN是平行四边形,求点M,N的坐标.【考点】椭圆的简单性质.【分析】(1)由点P(1,)在椭圆上,P到椭圆C的两个焦点的距离之和为4,列出方程组求出a,b,由此能求出椭圆C的方程.(2)由题意设直线AB:y=,A(x1,y1),B(x2,y2),联立,消去y,得:3x2+3mx+m2﹣3=0,由此利用韦达定理、弦长公式、平行四边形性质,结合已知条件能求出M、N的坐标.【解答】解:(1)∵点P(1,)在椭圆C:=1(a>b>0)上,P到椭圆C的两个焦点的距离之和为4,∴,解得a=2,b=,∴椭圆C的方程为.(2)由题意设直线MN:y=,M(x1,y1),N(x2,y2),联立,消去y,得:3x2+3mx+m2﹣3=0,△>0,,∵四边形POMN是平行四边形,∴|MN|==,解得m=±3,当m=3时,解方程:3x2+9x+6=0,得M(﹣1,),N(﹣2,0);当m=﹣3时,解方程:3x2﹣9x+6=0,得M(1,),N(2,6).18.经市场调查,某商品每吨的价格为x(1<x<14)百元时,该商品的月供给量为y1万吨,y1=ax+ a2﹣a(a>0);月需求量为y2万吨,y2=﹣x2﹣x+1.当该商品的需求量大于供给量时,销售量等于供给量;当该商品的需求量不大于供给量时,销售量等于需求量.该商品的月销售额等于月销售量与价格的乘积.(1)若a=,问商品的价格为多少时,该商品的月销售额最大?(2)记需求量与供给量相等时的价格为均衡价格,若该商品的均衡价格不低于每吨6百元,求实数a的取值范围.【考点】函数模型的选择与应用.【分析】(1)利用商品的月销售额等于月销售量与价格的乘积,分类讨论,即可求解商品的价格为多少时,该商品的月销售额最大?(2)设f(x)=y1﹣y2=ax+a2﹣a﹣(﹣x2﹣x+1)=x2+(+a)x+a2﹣a﹣1,因为a>0,所以f(x)在区间(1,14)上是增函数,若该商品的均衡价格不低于6百元,即函数f(x)在区间[6,14)上有零点,即可得出结论.【解答】解:(1)若a=,y1=x﹣,y2>y1,即﹣x2﹣x+1>x﹣,∵1<x<14,∴1<x<6,月销售量为y1=x﹣,商品的月销售额等于(x﹣)x,在(1,6)上单调递增,(x﹣)x<;y2≤y1,即﹣x2﹣x+1≤x﹣,∵1<x<14,∴6≤x<14,月销售量为y2=﹣x2﹣x+1,商品的月销售额等于y=(﹣x2﹣x+1)x,y′=﹣(x﹣8)(3x+28),∴函数在(6,8)上单调递增,(8,14)上单调递减,x=8时,取得最大值>,∴商品的价格为8元时,该商品的月销售额最大;(2)设f(x)=y1﹣y2=ax+a2﹣a﹣(﹣x2﹣x+1)=x2+(+a)x+a2﹣a﹣1因为a>0,所以f(x)在区间(1,14)上是增函数,若该商品的均衡价格不低于6百元,即函数f(x)在区间[6,14)上有零点,所以f(6)≤0,f(14)>0,所以0<a≤.19.已知函数f(x)=,g(x)=ax﹣2lnx﹣a (a∈R,e为自然对数的底数).(1)求f(x)的极值;(2)在区间(0,e]上,对于任意的x0,总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0),求a的取值范围.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(1)求出f(x)的导数,得到函数的单调区间,从而求出函数的极值即可;(2)求出当x∈(0,e]时,函数f(x)的值域,通过讨论a的范围结合g(x)的单调性,求出a的具体范围即可.【解答】解:(1)因为f(x)=,所以f′(x)=,…令f′(x)=0,得x=1.…当x∈(﹣∞,1)时,f′(x)>0,f(x)是增函数;当x∈(1,+∞)时,f′(x)<0,f(x)是减函数.所以f(x)在x=1时取得极大值f(1)=1,无极小值.…(2)由(1)知,当x∈(0,1)时,f(x)单调递增;当x∈(1,e]时,f(x)单调递减.又因为f(0)=0,f(1)=1,f(e)=e•e1﹣e>0,所以当x∈(0,e]时,函数f(x)的值域为(0,1].…当a=0时,g(x)=﹣2lnx在(0,e]上单调,不合题意;…当a≠0时,g′(x)=,x∈(0,e],故必须满足0<<e,所以a>.…此时,当x 变化时,g′(x),g(x)的变化情况如下:x (0,)(,e]g′(x)﹣0 +g(x)单调减最小值单调增所以x→0,g(x)→+∞,g()=2﹣a﹣2ln,g(e)=a(e﹣1)﹣2,所以对任意给定的x0∈(0,e],在区间(0,e]上总存在两个不同的x1,x2使得g(x1)=g(x2)=f(x0),当且仅当a满足下列条件,即,…令m(a)=2﹣a﹣2ln,a∈(,+∞),m′(a)=﹣,由m′(a)=0,得a=2.当a∈(2,+∞)时,m′(a)<0,函数m(a)单调递减;当a∈(,2)时,m′(a)>0,函数m(a)单调递增.所以,对任意a∈(,+∞)有m(a)≤m(2)=0,即2﹣a﹣2ln≤0对任意a∈(,+∞)恒成立.由a(e﹣1)﹣2≥1,解得a≥,综上所述,当a∈[,+∞)时,对于任意给定的x0(0,e],在区间(0,e]上总存在两个不同的x1,x2,使得g(x1)=g(x2)=f(x0).…20.在数列{a n}中,已知a1=1,a2=2,a n+2=(k∈N*).(1)求数列{a n}的通项公式;(2)求满足2a n+1=a n+a n+2的正整数n的值;(3)设数列{a n}的前n项和为S n,问是否存在正整数m,n,使得S2n=mS2n﹣1?若存在,求出所有的正整数对(m,n);若不存在,请说明理由.【考点】数列的求和;数列递推式.【分析】(1)由题意可得数列{a n}的奇数项是以1为首项,公差为2的等差数列;偶数项是以2为首项,公比为3的等比数列.分别利用等差数列与等比数列的通项公式即可得出.(2)①当n为奇数时,由2a n+1=a n+a n+2可得:=n+n+2,化为:=n+1,令f(x)=2×﹣x﹣1(x≥1),利用导数研究函数的单调性即可得出.②当n为偶数时,由2a n+1=a n+a n+2可得:2(n+1)=2+2×,化为:n+1=+,即可判断出不成立.(3)S2n=(a1+a3+…+a2n﹣1)+(a2+a4+…+a2n)=3n+n2﹣1,n∈N*.S2n﹣1=S2n﹣a2n=3n﹣1+n2﹣1.假设存在正整数m,n,使得S2n=mS2n﹣1,化为3n﹣1(3﹣m)=(m﹣1)(n2﹣1),可得1,2,3.分类讨论即可得出.【解答】解:(1)由a1=1,a2=2,a n+2=(k∈N*).可得数列{a n}的奇数项是以1为首项,公差为2的等差数列;偶数项是以2为首项,公比为3的等比数列.∴对任意正整数k,a2k﹣1=1+2(k﹣1)=2k﹣1;a2k=2×3k﹣1.∴数列{a n}的通项公式a n=,k∈N*.(2)①当n为奇数时,由2a n+1=a n+a n+2可得:=n+n+2,化为:=n+1,令f(x)=2×﹣x﹣1(x≥1),由f′(x)=××ln﹣1≥﹣1=ln3﹣1>0,可知f(x)在[1,+∞)上是增函数,∴f(x)≥f(1)=0,∴当且仅当n=1时,满足=n+1,即2a2=a1+a3.=a n+a n+2可得:2(n+1)=2+2×,②当n为偶数时,由2an+1化为:n+1=+,上式左边为奇数,右边为偶数,因此不成立.综上,满足2a n+1=a n+a n+2的正整数n的值只有1.(3)S2n=(a1+a3+…+a2n﹣1)+(a2+a4+…+a2n)=+=3n+n2﹣1,n∈N*.S2n﹣1=S2n﹣a2n=3n﹣1+n2﹣1.假设存在正整数m,n,使得S2n=mS2n﹣1,则3n+n2﹣1=m(3n﹣1+n2﹣1),∴3n﹣1(3﹣m)=(m﹣1)(n2﹣1),(*)从而3﹣m≥0,∴m≤3,又m∈N*,∴m=1,2,3.①当m=1时,(*)式左边大于0,右边等于0,不成立.②当m=3时,(*)式左边等于0,∴2(n2﹣1)=0,解得n=1,∴S2=3S1.③当m=2时,(*)式可化为3n﹣1=(n+1)(n﹣1),则存在k1,k2∈N*,k1<k2,使得n﹣1=,n+1=,且k1+k2=n﹣1,从而==2,∴﹣=2,=1,∴k1=0,k2﹣k1=1,于是n=2,S4=2S3.综上可知,符合条件的正整数对(m,n)只有两对:(2,2),(3,1).三.[选做题]本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.解答时应写出文字说明、证明过程或演算步骤.A.[选修4-1:几何证明选讲](本小题满分10分)21.如图,AB是圆O的直径,弦BD,CA的延长线相交于点E,过E作BA的延长线的垂线,垂足为F.求证:AB2=BE•BD﹣AE•AC.【考点】与圆有关的比例线段.【分析】连接AD,利用AB为圆的直径结合EF与AB的垂直关系,通过证明A,D,E,F四点共圆知,BD•BE=BA•BF,再利用△ABC∽△AEF得到比例式,最后利用线段间的关系即求得AB2=BE•BD ﹣AE•AC.【解答】证明:连接AD,因为AB为圆的直径,所以∠ADB=90°,又EF⊥AB,∠AFE=90°,则A,D,E,F四点共圆,∴BD•BE=BA•BF,又△ABC∽△AEF,∴,即AB•AF=AE•AC∴BE•BD﹣AE•AC=BA•BF﹣AB•AF=AB•(BF﹣AF)=AB2.B.[选修4-2:矩阵与变换](本小题满分0分)22.已知矩阵A=,向量=,计算A5.【考点】特征向量的意义.【分析】令f(λ)==λ2﹣5λ+6=0,解得λ=2或3.分别对应的一个特征向量为;.设=m++n.解得m,n,即可得出.【解答】解:∵f(λ)==λ2﹣5λ+6,由f(λ)=0,解得λ=2或3.当λ=2时,对应的一个特征向量为α1=;当λ=3时,对应的一个特征向量为α2=.设=m++n.解得.∴A5=2×25+1×35=.C.[选修4-4:坐标系与参数方程](本小题满分0分)23.在极坐标系中,直线l的极坐标方程为,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,曲线C的参数方程为(α为参数),求直线l与曲线C 的交点P的直角坐标.【考点】简单曲线的极坐标方程.【分析】先利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换将极坐标方程化成直角坐标方程.再利用消去参数的方法化参数方程为直角坐标方程,通过直角坐标方程求出交点即可.【解答】解:因为直线l的极坐标方程为所以直线l的普通方程为,又因为曲线C的参数方程为(α为参数)所以曲线C的直角坐标方程为,联立解方程组得或,根据x的范围应舍去,故P点的直角坐标为(0,0).D.[选修4-5:不等式选讲](本小题满分0分)24.已知a、b∈R,a>b>e(其中e是自然对数的底数),求证:b a>a b.(提示:可考虑用分析法找思路)【考点】分析法和综合法.【分析】直接利用分析法的证明步骤,结合函数的单调性证明即可.【解答】证明:∵b a>0,a b>0,∴要证:b a>a b只要证:alnb>blna只要证.(∵a>b>e)取函数,∵∴当x>e时,,∴函数在上是单调递减.∴当a>b>e时,有,即.得证.四.[必做题]第22、23题,每小题0分,计20分.请把答案写在答题卡的指定区域内.25.已知甲箱中装有3个红球、3个黑球,乙箱中装有2个红球、2个黑球,这些球除颜色外完全相同.某商场举行有奖促销活动,设奖规则如下:每次分别从以上两个箱中各随机摸出2个球,共4个球.若摸出4个球都是红球,则获得一等奖;摸出的球中有3个红球,则获得二等奖;摸出的球中有2个红球,则获得三等奖;其他情况不获奖.每次摸球结束后将球放回原箱中.(1)求在1次摸奖中,获得二等奖的概率;(2)若连续摸奖2次,求获奖次数X的分布列及数学期望E(X).【考点】离散型随机变量的期望与方差;离散型随机变量及其分布列.【分析】(1)设“在1次摸奖中,获得二等奖”为事件A,利用互斥事件概率计算公式能求出在1次摸奖中,获得二等奖的概率.(2)设“在1次摸奖中,获奖”为事件B,先求出P(B),由题意可知X的所有可能取值为0,1,2.分别求出相应的概率,由此能求出X的分布列和E(X).【解答】解:(1)设“在1次摸奖中,获得二等奖”为事件A,则P(A)==.…(2)设“在1次摸奖中,获奖”为事件B,则获得一等奖的概率为=,获得三等奖的概率为P3==,所以P(B)==.…由题意可知X的所有可能取值为0,1,2.P(X=0)=(1﹣)2=,P(X=1)==,P(X=2)=()2=.所以X的分布列是X 0 1 2P所以E(X)=0×+2×=.…26.在集合A={1,2,3,4,…,2n}中,任取m(m≤n,m,n∈N*)个元素构成集合A m.若A m 的所有元素之和为偶数,则称A m为A的偶子集,其个数记为f(m);若A m的所有元素之和为奇数,则称A m为A的奇子集,其个数记为g(m).令F(m)=f(m)﹣g(m).(1)当n=2时,求F(1),F(2),F(3)的值;(2)求F(m).【考点】子集与真子集;元素与集合关系的判断.【分析】(1)根据已知条件利用列举法能F(1),F(2),F(3);(2)分m为奇数和m为偶数两种情况,再根据二项式定理和排列组合的知识即可求出答案.【解答】解:(1)当n=2时,集合为{1,2,3,4},当m=1时,偶子集有{2},{4},奇子集有{1},{3},f(1)=2,g(1)=2,F(1)=0;当m=2时,偶子集有{2,4},{1,3},奇子集有{1,2},{1,4},{2,4},{3,4},f(2)=2,g(2)=4,F(2)=﹣2;当m=3时,偶子集有{1,2,3},{1,3,4},奇子集有{1,2,4},{2,3,4},f(3)=2,g(3)=2,F(3)=0;(2)当m为奇数时,偶子集的个数f(m)=C n0C n m+C n2C n m﹣2+C n4C n m﹣4+…+C n m﹣1C n1,奇子集的个数g(m)=C n1C n m﹣1+C n3C n m﹣3+…+C n m C n0,所以f(m)=g(m),F(m)=f(m)﹣g(m)=0.当m为偶数时,偶子集的个数f(m)=C n0C n m+C n2C n m﹣2+C n4C n m﹣4+…+C n m C n0,奇子集的个数g(m)=C n1C n m﹣1+C n3C n m﹣3+…+C n m﹣1C n1,所以F(m)=f(m)﹣g(m)=C n0C n m﹣C n1C n m﹣1+C n2C n m﹣2﹣C n3C n m﹣3+…﹣C n m﹣1C n1+C n m C n0,一方面,(1+x)m(1﹣x)m=(C m0+C m1x+C m2x2+…+C m m x m)[C m0﹣C m1x+C m2x2+…+(﹣1)m C m m x m]所以,(1+x)m(1﹣x)m中x m的系数为C m0C m m﹣C m1C m m﹣1+C m2C m m﹣2﹣C m3C m m﹣3+…﹣C m m﹣1C m1+C m m C m0,另一方面,(1+x)m(1﹣x)m=(1﹣x2)m,(1﹣x2)m中x m的系数为(﹣1),故f(m)=(﹣1),综上,F(m)=。
江苏省2020版高考数学三模试卷(理科)(II)卷

江苏省2020版高考数学三模试卷(理科)(II)卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2018·河北模拟) 已知复数满足(为虚数单位),则复数的共轭复数在复平面内对应的点在()A . 第一象限B . 第二象限C . 第三象限D . 第四象限2. (2分) (2017高一上·高州月考) 方程组的解集是()A .B .C .D .3. (2分)抛物线的焦点坐标是()A .B .C .D .4. (2分)(2018·石家庄模拟) 程序框图如图所示,该程序运行的结果为,则判断框中可填写的关于的条件是()A .B .C .D .5. (2分) (2020高三上·渭南期末) 设数列{an}是正项等比数列,Sn为其前n项和,已知a2a4=1,S3=7,则公比q=()A .B . 3C .D . 26. (2分)若实数x、y满足,则z=x+y的最大值是()A .B .C .D . 17. (2分)一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的体积为()A .B .C .D .8. (2分)某学生解选择题出错的概率为0.1,该生解三道选择题至少有一道出错的概率是()A .B .C .D .9. (2分)设函数,则下列关于函数的说法中正确的是()A . 是偶函数B . 最小正周期为πC . 图象关于点对称D . 在区间上是增函数10. (2分) (2019高二下·舒兰月考) 将正整数排列如下:12 3 45 6 7 8 910 11 12 13 14 15 16… …则图中数2019出现在()A . 第44行第83列B . 第44行84列C . 第45行83列D . 第45行84列11. (2分)如图,在等腰直角三角形ABC中,AB=AC=, D,E是线段BC上的点,且DE=BC,则的取值范围是()A . [,]B . [,]C . [,]D . [,+)12. (2分) (2016高一上·临川期中) 已知函数,那么f[f()]的值为()A . 9B .C . ﹣9D . ﹣二、填空题 (共4题;共4分)13. (1分) (2019高二上·靖安月考) 已知等差数列的前n项和为,,,则的前n项和为________.14. (1分)(2017·海淀模拟) 已知曲线C1:y=ex与曲线C2:y=(x+a)2 .若两个曲线在交点处有相同的切线,则实数a的值为________.15. (1分)将直线绕原点按顺时针方向旋转30°,所得直线与圆(x﹣2)2+y2=3的位置关系是________.16. (1分) (2019高二上·洛阳月考) 已知双曲线的一条渐近线方程为,左焦点为,当点在双曲线右支上,点在圆上运动时,则的最小值为________.三、解答题 (共7题;共65分)17. (5分)已知向量=(2sinx,﹣cosx),=(cosx,2cosx),f(x)=•+1(I)求函数f(x)的最小正周期,并求当时f(x)的取值范围;(Ⅱ)将函数f(x)的图象向左平移个单位,得到函数g(x)的图象.在△ABC中,角A,B,C的对边分别为a,b,c,若g=1,a=2,b+c=4,求△ABC的面积.18. (5分) (2016高二上·枣阳期中) 某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有A,B,C三家社区医院,并且他们的选择是相互独立的.(Ⅰ)求甲、乙两人都选择A社区医院的概率;(Ⅱ)求甲、乙两人不选择同一家社区医院的概率;(Ⅲ)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.19. (10分)四棱锥P﹣ABCD中,点P在平面ABCD内的射影H在棱AD上,PA⊥PD,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2.(1)求证:平面PAB⊥平面PAD;(2)若直线AC与PD所成角为60°,求二面角A﹣PC﹣D的余弦值.20. (10分)(2017·新乡模拟) 设椭圆C: + =1(a>b>0)的左、右焦点分别为F1、F2 ,上顶点为A,过A与AF2垂直的直线交x轴负半轴于Q点,且F1恰好是线段QF2的中点.(1)若过A、Q、F2三点的圆恰好与直线3x﹣4y﹣7=0相切,求椭圆C的方程;(2)在(1)的条件下,B是椭圆C的左顶点,过点R(,0)作与x轴不重合的直线l交椭圆C于E、F 两点,直线BE、BF分别交直线x= 于M、N两点,若直线MR、NR的斜率分别为k1 , k2 ,试问:k1k2是否为定值?若是,求出该定值;若不是,请说明理由.21. (15分) (2017高三下·黑龙江开学考) 定义在R上的函数f(x)满足,.(1)求函数f(x)的解析式;(2)求函数g(x)的单调区间;(3)如果s、t、r满足|s﹣r|≤|t﹣r|,那么称s比t更靠近r.当a≥2且x≥1时,试比较和ex﹣1+a 哪个更靠近lnx,并说明理由.22. (10分)选修4﹣4:坐标系与参数方程在平面直角坐标系xOy中,已知曲线(α为参数),直线l:x﹣y﹣6=0.(1)在曲线C上求一点P,使点P到直线l的距离最大,并求出此最大值;(2)过点M(﹣1,0)且与直线l平行的直线l1交C于点A,B两点,求点M到A,B两点的距离之积.23. (10分)(2019·泸州模拟) 已知函数,,其中,.(1)若函数的图象关于直线对称,且,求不等式的解集;(2)若函数的最小值为2,求的最小值及其相应的和的值.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共65分) 17-1、18-1、19-1、19-2、20-1、20-2、21-1、21-2、21-3、22-1、22-2、23-1、23-2、。
江苏省“五校联考”2021-2022学年高三第三次模拟考试数学试卷含解析

2021-2022高考数学模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数y=sin x+x在x∈[-2π,2π]上的大致图象是()A.B.C.D.2.若函数y=2sin (2x+ϕ)ϕ<对称轴的方程可以为() A.x=-⎛⎝π⎫2⎭⎪的图象经过点⎛π⎫,0⎪,则函数f(x)=sin(2x-ϕ)+cos(2x-ϕ)图象的一条12⎝⎭π24B.x=37π24C.x=17π24D.x=-13π243.在等差数列{an}中,a2=-5,a5+a6+a7=9,若bn=A.-3 C.1B.-D.33(n∈N*),则数列{bn}的最大值是()an134.已知a,b∈R,3+ai=b-(2a-1)i,则|3a+bi|=()A.10B.232C.3D.45.设函数f (x)=2cos x+23sin x cos x+m,当x∈⎢0,A.⎡π⎤⎡17⎤f x∈,⎥,则m=()()时,⎢⎥⎣22⎦⎣2⎦D.12B.32C.1726.已知ω>13,函数f (x )=sin ⎛⎝2ωx -π⎫3⎪⎭在区间(π,2π)内没有最值,给出下列四个结论:①f (x )在(π,2π)上单调递增;②ω∈⎢⎡511⎣12,⎤24⎥⎦③f (x )在[0,π]上没有零点;④f (x )在[0,π]上只有一个零点.其中所有正确结论的编号是()A .②④B .①③C .②③D .①②④7.已知直线l :x +m 2y =0与直线n :x +y +m =0则“l //n ”是“m =1”的()A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件8.直线经过椭圆的左焦点,交椭圆于两点,交轴于点,若,则该椭圆的离心率是()A .B .C .D .9.已知定义在R 上的奇函数f (x ),其导函数为f '(x ),当x ≥0时,恒有x3f '(x )+f (x )>0.则不等式x 3f (x )-(1+2x )3f (1+2x )<0的解集为().A .{x |-3<x <-1}B .{x |-1<x <-13}C .{x |x <-3或x >-1}D .{x |x <-1或x >-13}610.(x 3-1)⎛ ⎝x +2⎫x ⎪的展开式中的常数项为()⎭A .-60B .240C .-80D .18011.在复平面内,复数z =i 对应的点为Z ,将向量OZ 绕原点O 按逆时针方向旋转π6,所得向量对应的复数是(A .-132+32i B .-312+2i C .-12-32i D .-2-12i )12.如图,在平行四边形ABCD 中,对角线AC 与BD 交于点O ,且AE =2EO ,则ED =()12AD -AB3321C .AD -AB33A .21AD +AB3312D .AD +AB33B .二、填空题:本题共4小题,每小题5分,共20分。
江苏省常州市2021届新高考第三次模拟数学试题含解析

江苏省常州市2021届新高考第三次模拟数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,下图是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级,一级空气质量最好,一级和二级都是质量合格天气,下面叙述不正确的是( )A .1月至8月空气合格天数超过20天的月份有5个B .第二季度与第一季度相比,空气达标天数的比重下降了C .8月是空气质量最好的一个月D .6月份的空气质量最差. 【答案】D 【解析】由图表可知5月空气质量合格天气只有13天,5月份的空气质量最差.故本题答案选D . 2.若复数z 满足3(1)1z z i +=,复数z 的共轭复数是z ,则z z +=( ) A .1 B .0C .1-D .132-+ 【答案】C 【解析】 【分析】根据复数代数形式的运算法则求出z ,再根据共轭复数的概念求解即可. 【详解】解:∵331z i zi -=, ∴3132213i z i i==-+-,则1322z =--,∴1z z +=-, 故选:C . 【点睛】本题主要考查复数代数形式的运算法则,考查共轭复数的概念,属于基础题.3.已知()()()[)3log 1,1,84,8,6x x f x x x ⎧+∈-⎪=⎨∈+∞⎪-⎩ 若()()120f m f x ⎡⎤--≤⎣⎦在定义域上恒成立,则m 的取值范围是( ) A .()0,∞+ B .[)1,2C .[)1,+∞D .()0,1【答案】C 【解析】 【分析】先解不等式()2f x ≤,可得出89x ≥-,求出函数()y f x =的值域,由题意可知,不等式()()819m f x -≥-在定义域上恒成立,可得出关于m 的不等式,即可解得实数m 的取值范围. 【详解】()()()[)3log 1,1,84,8,6x x f x x x ⎧+∈-⎪=⎨∈+∞⎪-⎩Q ,先解不等式()2f x ≤.①当18x -<<时,由()()3log 12f x x =+≤,得()32log 12x -≤+≤,解得889x -≤≤,此时889x -≤<; ②当8x ≥时,由()426f x x =≤-,得8x ≥. 所以,不等式()2f x ≤的解集为89x x ⎧⎫≥-⎨⎬⎩⎭.下面来求函数()y f x =的值域.当18x -<<时,019x <+<,则()3log 12x +<,此时()()3log 10f x x =+≥; 当8x ≥时,62x -≥,此时()(]40,26f x x =∈-. 综上所述,函数()y f x =的值域为[)0,+∞, 由于()()120f m f x ⎡⎤--≤⎣⎦在定义域上恒成立,则不等式()()819m f x -≥-在定义域上恒成立,所以,10m -≥,解得m 1≥.因此,实数m 的取值范围是[)1,+∞. 故选:C. 【点睛】本题考查利用函数不等式恒成立求参数,同时也考查了分段函数基本性质的应用,考查分类讨论思想的应用,属于中等题.4.已知数列{}n a 中,121,2a a ==,且当n 为奇数时,22n n a a +-=;当n 为偶数时,()2131n n a a ++=+.则此数列的前20项的和为( )A .1133902-+B .11331002-+C .1233902-+D .12331002-+【答案】A 【解析】 【分析】根据分组求和法,利用等差数列的前n 项和公式求出前20项的奇数项的和,利用等比数列的前n 项和公式求出前20项的偶数项的和,进而可求解. 【详解】当n 为奇数时,22n n a a +-=,则数列奇数项是以1为首项,以2为公差的等差数列, 当n 为偶数时,()2131n n a a ++=+,则数列中每个偶数项加1是以3为首项,以3为公比的等比数列. 所以201232013192420S a a a a a a a a a a =++++=+++++++L L L()()()24201091012111102a a a ⨯=⨯+⨯++++++-L ()1101313100101333902-=+--+=-.故选:A 【点睛】本题考查了数列分组求和、等差数列的前n 项和公式、等比数列的前n 项和公式,需熟记公式,属于基础题.5.德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家、天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n =,则输出的结果是( )A .11114(1)35717P =-+-+⋅⋅⋅+ B .11114(1)35719P =-+-+⋅⋅⋅- C .11114(1)35721P =-+-+⋅⋅⋅+D .11114(1)35721P =-+-+⋅⋅⋅-【答案】B 【解析】 【分析】执行给定的程序框图,输入10n =,逐次循环,找到计算的规律,即可求解. 【详解】由题意,执行给定的程序框图,输入10n =,可得: 第1次循环:1,2S i ==;第2次循环:11,33S i =-=;第3次循环:111,435S i =-+=;L L第10次循环:11111,1135719S i =-+-+-=L , 此时满足判定条件,输出结果111144(1)35719P S ==-+-+⋅⋅⋅-,故选:B. 【点睛】本题主要考查了循环结构的程序框图的计算与输出,其中解答中认真审题,逐次计算,得到程序框图的计算功能是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.6.数学中有许多形状优美、寓意美好的曲线,例如:四叶草曲线就是其中一种,其方程为()32222x yx y +=.给出下列四个结论: ①曲线C 有四条对称轴;②曲线C 上的点到原点的最大距离为14; ③曲线C 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为18; ④四叶草面积小于4π. 其中,所有正确结论的序号是( )A .①②B .①③C .①③④D .①②④【答案】C 【解析】 【分析】①利用,x y 之间的代换判断出对称轴的条数;②利用基本不等式求解出到原点的距离最大值;③将面积转化为,x y 的关系式,然后根据基本不等式求解出最大值;④根据,x y 满足的不等式判断出四叶草与对应圆的关系,从而判断出面积是否小于4π. 【详解】①:当x 变为x -时, ()32222x y x y +=不变,所以四叶草图象关于y 轴对称;当y 变为y -时,()32222x y x y +=不变,所以四叶草图象关于x 轴对称;当y 变为x 时,()32222x yx y +=不变,所以四叶草图象关于y x =轴对称; 当y 变为x -时,()32222x yx y +=不变,所以四叶草图象关于y x =-轴对称;综上可知:有四条对称轴,故正确; ②:因为()32222x y x y +=,所以()222322222x y x yx y ⎛⎫++=≤ ⎪⎝⎭,所以2214x y +≤2212x y +≤,取等号时2218x y ==,所以最大距离为12,故错误; ③:设任意一点(),P x y ,所以围成的矩形面积为xy , 因为()32222x y x y +=,所以()()3322222x y x y xy =+≥,所以18xy ≤,取等号时x y ==,所以围成矩形面积的最大值为18,故正确;④:由②可知2214x y +≤,所以四叶草包含在圆2214x y +=的内部,因为圆的面积为:144S ππ=⋅=,所以四叶草的面积小于4π,故正确. 故选:C. 【点睛】本题考查曲线与方程的综合运用,其中涉及到曲线的对称性分析以及基本不等式的运用,难度较难.分析方程所表示曲线的对称性,可通过替换方程中,x y 去分析证明. 7.已知函数321()(0)3f x ax x a =+>.若存在实数0(1,0)x ∈-,且012x ≠-,使得01()()2f x f =-,则实数a 的取值范围为( ) A .2(,5)3B .2(,3)(3,5)3⋃ C .18(,6)7D .18(,4)(4,6)7⋃ 【答案】D 【解析】 【分析】首先对函数求导,利用导数的符号分析函数的单调性和函数的极值,根据题意,列出参数所满足的不等关系,求得结果. 【详解】()22f x ax x '=+,令()0f x '=,得10x =,22x a=-.其单调性及极值情况如下:若存在0111,,022x ⎛⎫⎛⎫∈--⋃- ⎪ ⎪⎝⎭⎝⎭,使得()012f x f ⎛⎫=- ⎪⎝⎭,则()21221112a a f f⎧-<-⎪⎪⎪->-⎨⎪⎪⎛⎫-<-⎪ ⎪⎝⎭⎩(如图1)或3122a a -<-<-(如图2).(图1)(图2) 于是可得()18,44,67a ⎛⎫∈⋃ ⎪⎝⎭, 故选:D. 【点睛】该题考查的是有关根据函数值的关系求参数的取值范围的问题,涉及到的知识点有利用导数研究函数的单调性与极值,画出图象数形结合,属于较难题目.8.设数列{}n a 是等差数列,1356a a a ++=,76a =.则这个数列的前7项和等于( ) A .12 B .21C .24D .36【答案】B 【解析】 【分析】根据等差数列的性质可得3a ,由等差数列求和公式可得结果. 【详解】因为数列{}n a 是等差数列,1356a a a ++=, 所以336a =,即32a =, 又76a =,所以73173a a d -==-,1320a a d =-=, 故1777()212a a S +== 故选:B 【点睛】本题主要考查了等差数列的通项公式,性质,等差数列的和,属于中档题.9.已知双曲线C :()222210,0x y a b a b -=>>的焦距为2c ,焦点到双曲线C 的渐近线的距离为2c ,则双曲线的渐近线方程为()A .y =B .y =C .y x =±D .2y x =±【答案】A 【解析】 【分析】利用双曲线C :()222210,0x y a b a b -=>>,求出a ,b 的关系式,然后求解双曲线的渐近线方程. 【详解】双曲线C :()222210,0x y a b a b -=>>的焦点(),0c 到渐近线0bx ay +=的距离为2c ,可得:2c =,可得2b c =,ba =C 的渐近线方程为y =.故选A . 【点睛】本题考查双曲线的简单性质的应用,构建出,a b 的关系是解题的关键,考查计算能力,属于中档题. 10.已知集合1|2A x x ⎧⎫=<-⎨⎬⎩⎭,{|10}B x x =-<<则A B =I ( )A .{|0}x x <B .1|2x x 禳镲镲<-睚镲镲铪C .1|12x x ⎧⎫-<<-⎨⎬⎩⎭D .{|1}x x >-【答案】C 【解析】 【分析】由题意和交集的运算直接求出A B I . 【详解】∵ 集合1|2A x x ⎧⎫=<-⎨⎬⎩⎭,{|10}B x x =-<<∴A B =I 1|12x x ⎧⎫-<<-⎨⎬⎩⎭. 故选:C. 【点睛】本题考查了集合的交集运算.集合进行交并补运算时,常借助数轴求解.注意端点处是实心圆还是空心圆.11.设,a b r r 为非零向量,则“a b a b +=+r r r r ”是“a r 与b r共线”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】A 【解析】 【分析】根据向量共线的性质依次判断充分性和必要性得到答案. 【详解】若a b a b +=+r r r r ,则a r 与b r 共线,且方向相同,充分性; 当a r 与b r共线,方向相反时,a b a b ≠++r r r r ,故不必要.故选:A . 【点睛】本题考查了向量共线,充分不必要条件,意在考查学生的推断能力.12.已知抛物线2:4(0)C y px p =>的焦点为F ,过焦点的直线与抛物线分别交于A 、B 两点,与y 轴的正半轴交于点S ,与准线l 交于点T ,且||2||FA AS =,则||||FB TS =( ) A .25B .2C .72D .3【答案】B 【解析】 【分析】过点A 作准线的垂线,垂足为M ,与y 轴交于点N ,由2FA AS =和抛物线的定义可求得TS ,利用抛物线的性质1122AF BF p+=可构造方程求得BF ,进而求得结果. 【详解】过点A 作准线的垂线,垂足为M ,AM 与y 轴交于点N ,由抛物线解析式知:(),0F p ,准线方程为x p =-.2FA AS =Q ,13SASF ∴=,133p AN OF ∴==,43AM p ∴=, 由抛物线定义知:43AF AM p ==,1223AS AF p ∴==,2SF p ∴=, 2TS SF p ∴==.由抛物线性质11212AF BF p p +==得:3114p BF p+=,解得:4BF p =, 422FB p TS p∴==. 故选:B . 【点睛】本题考查抛物线定义与几何性质的应用,关键是熟练掌握抛物线的定义和焦半径所满足的等式. 二、填空题:本题共4小题,每小题5分,共20分。
苏锡常镇2020届高三年级第三次模拟考试数学试卷

苏锡常镇2020届高三年级第三次模拟考试数学试卷(满分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合A ={1,2},B ={-1,a},若A ∪B ={-1,a ,2},则a =________.2. 若复数z 满足(1-i)z =1+i ,其中i 是虚数单位,则z 的实部为________.3. 某校100名学生参加知识竞赛的成绩均在[50,100]内,将学生成绩分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图,则成绩在[80,90)内的学生人数是________.(第3题) (第4题) (第9题) 4. 一个算法的伪代码如图所示,执行此算法,最后输出的y 的值为________.5. 某班推选一名学生管理班级防疫用品,已知每个学生当选是等可能的.若“选到女生”的概率是“选到男生”的概率的12,则这个班级的男生人数与女生人数的比值为________.6. 函数f(x)=2-x +lnx 的定义域为________.7. 在平面直角坐标系xOy 中,抛物线y 2=4x的焦点是双曲线x 2a 2-y 24a=1的顶点,则a =________.8. 已知等比数列{a n }的前n 项和为S n ,S 4=5S 2,a 2=2,则a 4=________.9. 已知正方体ABCD-A 1B 1C 1D 1的棱长为6,M 是对角线A 1C 上靠近点A 1的三等分点,则三棱锥C-MBD 的体积为________.10. 已知定义在R 上的奇函数f(x)的周期为2,且当x ∈[0,1]时,f(x)=⎩⎨⎧2x+a , 0≤x ≤12,bx -1x +1, 12<x ≤1,则a+b =________.11. 已知锐角α满足sin2α-2cos2α=-1,则tan ⎝⎛⎭⎫α+π4=________. 12. 如图,在△ABC 中,∠ABC =π2,AB =1,BC =3,以AC 为一边在△ABC 的另一侧作正三角形ACD ,则BD →·AC →=________.13. 在平面直角坐标系xOy 中,AB 是圆O :x 2+y 2=1的直径,且点A 在第一象限.圆O 1:(x -a)2+y 2=r 2(a >0)与圆O 外离,线段AO 1与圆O 1交于点M ,线段BM 与圆O 交于点N ,且OM →+O 1N →=0,则a 的取值范围为________. 14. 已知a ,b ∈R ,a +b =t(t 为常数),且直线y =ax +b 与曲线y =xe x (e 是自然对数的底数,e ≈2.718 28…)相切.若满足条件的有序实数对(a ,b)唯一存在,则实数t 的取值范围为________.二、 解答题:本大题共6小题,共计90分.解答时应写出文字说明,证明过程或演算步骤. 15. (本小题满分14分)已知在△ABC 中,a ,b ,c 分别为角 A ,B ,C 的对边,且bsin2A =asinB. (1) 求A 的值;(2) 求cos ⎝⎛⎭⎫B +π6+sin ⎝⎛⎭⎫C +π3的最大值.16. (本小题满分14分)已知在四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 是菱形,且平面A 1ADD 1⊥平面ABCD ,DA 1=DD 1,E ,F 分别为线段A 1D 1,BC 的中点.求证: (1) EF ∥平面CC 1D 1D ; (2) AC ⊥平面EBD.17. (本小题满分14分)在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,右焦点到右准线的距离为3.(1) 求椭圆C 的标准方程;(2) 过点P(0,1)的直线l 与椭圆C 交于A ,B 两点.已知在椭圆C 上存在点Q ,使得四边形OAQB 是平行四边形,求点Q 的坐标.18. (本小题满分16分)某地开发一片荒地,如图,荒地的边界是以C 为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE ,OF ,分别与荒地的边界有且仅有一个接触点A ,B.现规划修建一条新路(由线段MP ,PQ ︵,线段QN 三段组成),其中点M ,N 分别在OE ,OF 上,且使得MP ,QN 所在直线分别与荒地的边界有且仅有一个接触点P ,Q ,PQ ︵所对的圆心角为π6. 记∠PCA =2θ(道路宽度均忽略不计).(1) 若θ=5π12,求QN 的长度;(2) 求新路总长度的最小值.19. (本小题满分16分)已知各项均为正数的数列{a n }的前n 项和为S n ,a 1=2,且对任意n ∈N *,a n S n +1-a n +1S n =2a n +1-2a n 恒成立.(1) 求证:数列⎩⎨⎧⎭⎬⎫S n +2a n 是等差数列,并求数列{a n }的通项公式; (2) 设b n =a n +4n -3,已知b 2,b i ,b j (2<i <j)成等差数列,求正整数i ,j 的值.20. (本小题满分16分)已知函数f(x)=(m -1)x +lnx ,g(x)=(m -2)x 2+(n +3)x -2,m ,n ∈R . (1) 当m =0时,求函数f(x)的极值;(2) 当n =0时,函数F(x)=g(x)-f(x)在(0,+∞)上为单调函数,求m 的取值范围;(3) 当n >0时,判断是否存在正数m ,使得函数f(x)与g(x)有相同的零点,并说明理由.数学附加题(本部分满分40分,考试时间30分钟)21. 【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A. [选修4-2:矩阵与变换](本小题满分10分) 已知点M(2,1)在矩阵A =⎣⎢⎡⎦⎥⎤1a b2对应的变换作用下得到点N(5,6),求矩阵A 的特征值.B. [选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cosα,y =sinα(α为参数).以原点O 为极点,x轴的非负半轴为极轴建立极坐标系,直线l 的极坐标方程为ρsin ⎝⎛⎭⎫θ+π4=10. (1) 求曲线C 的普通方程和直线l 的直角坐标方程;(2) P 是曲线C 上的动点,求点P 到直线l 的距离的最小值.C. [选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 是正数,求证:对任意x ∈R ,不等式||x -2-||x +1≤b a +c b +ac 恒成立.【必做题】第22题、第23题,每题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤.22. (本小题满分10分)如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AB =2,AD =AP =3,M 是棱PD 的中点.(1) 求二面角M-AC-D 的余弦值;(2) N 是棱PC 上的点,已知直线MN 与平面ABCD 所成角的正弦值为32222,求PNPC的值.23. (本小题满分10分)已知在数列{a n }中,a 1=6,a n +1=13a 2n -a n +3( n ∈N *).(1) 分别比较下列每组中两个数的大小: ①a 2和6×32;②a 3和6×⎝⎛⎭⎫323;(2) 当n ≥3时,证明:∑ni =2⎝⎛⎭⎫a i 62i >2⎝⎛⎭⎫32n-3. 数学参考答案 1. 1 2. 0 3. 30 4. -1 5. 2 6. (0,2] 7. 1 8. 2或8 9. 24 10. 0 11. 2 12. 4 13. (22,4) 14. {e}∪(-∞,-5e -2) 15. (1) 因为bsin 2A =asin B , 所以2bsin Acos A =asin B , 所以由正弦定理a sin A =bsin B ,得2bacos A =ab.(3分)因为ab ≠0,所以cos A =ab 2ab =12.又因为A ∈(0,π),所以A =π3.(6分)(2) 由(1)得A =π3,又A +B +C =π,所以C =2π3-B ,B ∈⎝⎛⎭⎫0,2π3,所以cos ⎝⎛⎭⎫B +π6+sin(C +π3)=cos Bcos π6-sin Bsin π6+sin(π-B)=12sin B +32cos B =sin ⎝⎛⎭⎫B +π3.(11分) 因为0<B<2π3,所以π3<B +π3<π,所以当B +π3=π2,即B =π6时,sin ⎝⎛⎭⎫B +π3取最大值1, 所以cos ⎝⎛⎭⎫B +π6+sin ⎝⎛⎭⎫C +π3的最大值为1.(14分) 16. (1) 连结CD 1,由题意得四边形A 1B 1C 1D 1,BB 1C 1C 是平行四边形,所以A 1D 1∥ B 1C 1,BC ∥B 1C 1,且A 1D 1=B 1C 1,BC =B 1C 1. 又因为E ,F 分别为线段A 1D 1,BC 的中点, 所以ED 1∥FC ,ED 1=FC ,所以四边形ED 1CF 是平行四边形,(3分) 所以EF ∥CD 1.又因为EF ⊄平面CC 1D 1D ,CD 1⊂平面CC 1D 1D , 所以EF ∥平面CC 1D 1D.(6分)(2) 在四棱柱ABCD-A 1B 1C 1D 1中,四边形AA 1D 1D 是平行四边形,所以AD ∥A 1D 1. 在△DA 1D 1中,DA 1=DD 1,E 为线段A 1D 1的中点,所以DE ⊥A 1D 1. 又因为AD ∥A 1D 1,所以DE ⊥AD.(8分)又因为平面A 1ADD 1⊥平面ABCD ,平面A 1ADD 1∩平面ABCD =AD ,DE ⊂平面A 1ADD 1, 所以DE ⊥平面ABCD.又AC ⊂平面ABCD ,所以DE ⊥AC.(11分) 因为底面ABCD 是菱形,所以BD ⊥AC. 又因为BD ∩DE =D ,BD ,DE ⊂平面EBD , 所以AC ⊥平面EBD.(14分)17. (1) 由椭圆C :x 2a 2+y 2b 2=1的离心率为12,右焦点与右准线的距离为3,得c a =12,a 2c -c =3,解得c =1,a =2, 所以b 2=a 2-c 2=3,(4分)所以椭圆C 的标准方程为x 24+y 23=1.(5分)(2) 设A(x 1,y 1),B(x 2,y 2),当四边形OAQB 是平行四边形时,则OQ →=OA →+OB →. 当直线l 的斜率不存在时,直线l 过原点O ,此时O ,A ,B 三点共线,不符合题意;(7分)当直线l 的斜率存在时,设直线l 的方程为y =kx +1,与椭圆方程联立有⎩⎪⎨⎪⎧y =kx +1,x 24+y 23=1,所以x 24+(kx +1)23=1,即(3+4k 2)x 2+8k 2x -8=0,所以Δ>0,x 1+x 2=-8k3+4k 2,所以y 1+y 2=63+4k 2.(10分) 将点Q(x 1+x 2,y 1+y 2)的坐标代入椭圆方程得⎝⎛⎭⎫-8k 3+4k 224+⎝⎛⎭⎫63+4k 223=1,化简得k 2=14,所以k =±12,符合题意,(13分)所以点Q 的坐标是⎝⎛⎭⎫±1,32.(14分) 18. (1) 因为PQ ︵所对的圆心角为π6,θ=5π12,所以∠PCQ =π6,∠PCA =2θ=5π6.又因为∠BCA =π2,所以∠BCQ =2π-5π6-π2-π6=π2,所以在四边形BCQN 中,∠BCQ =∠CBN =∠CQN =π2,所以四边形BCQN 是矩形,所以QN =CB =1, 故QN 的长为1千米 .(4分)(2) PM =tan ∠PCA 2=tan θ,∠BCQ =4π3-2θ,NQ =tan ∠BCQ 2=tan ⎝⎛⎭⎫2π3-θ,PQ ︵的长为π6,(6分) 所以PM +NQ =tan θ+tan ⎝⎛⎭⎫2π3-θ=tan θ+tan2π3-tan θ1+tan 2π3tan θ=tan θ+-3-tan θ1-3tan θ, 即PM +NQ =tan θ+3+tan θ3tan θ-1=tan θ+1+33tan θtan θ-33,(9分)其中θ∈⎝⎛⎭⎫π6,π2,tan θ∈⎝⎛⎭⎫33,+∞,tan θ-33∈(0,+∞),(11分)所以PM +NQ =⎝⎛⎭⎫tan θ-33+43tan θ-33+233≥2⎝⎛⎭⎫tan θ-33·43tan θ-33+233=23,(14分)当且仅当tan θ-33=43tan θ-33,又θ∈⎝⎛⎭⎫π6,π2,即θ=π3时取等号,(15分) 所以当∠PCA =2π3时,新路总长度的最小值为⎝⎛⎭⎫23+π6千米.(16分) 19. (1)S 1+2a 1=2+22=2, 因为a n S n +1-a n +1S n =2a n +1-2a n ,所以a n S n +1+2a n =a n +1S n +2a n +1. 又因为a n >0,两边除以a n a n +1得S n +1+2a n +1=S n +2a n ,所以S n +1+2a n +1-S n +2a n =0,n ∈N *,所以数列⎩⎨⎧⎭⎬⎫S n +2a n 是首项为2,公差为0的等差数列,所以S n +2a n =2,(3分)则S n +2=2a n ,S n +1+2=2a n +1,两式作差得a n +1=S n +1-S n =2a n +1-2a n , 所以a n +1=2a n .又因为a n >0,所以a n +1a n=2,n ∈N *,所以数列{a n }是首项为2,公比为2的等比数列,所以a n =2n .(7分)(2) b n =2n +4n -3,由b 2,b i ,b j 成等差数列得2b i =b 2+b j ,即2(2i +4i -3)=9+2j +4j -3,整理得2i -1+2i =2j -2+j +3(2<i<j),(*)若j =i +1,则2i -1+2i =2i -1+i +1+3, 所以i =4,j =5.(10分)若j ≥i +2,则(2j -2+j +3)-(2i -1+2i)≥2i +i +5-2i -1-2i =2i -1-i +5.(12分) 设c n =2n -1-n +5(n>2),c n +1-c n =(2n -n +4)-(2n -1-n +5)=2n -1-1>0,则c n +1>c n (n>2),所以当n>2时,数列{c n }单调递增,其中c 3=6>0,所以c n >0, 即2j -2+j +3>2i -1+2i ,所以(*)式不成立.(15分) 综上可得,i =4,j =5.(16分)20. (1) 当m =0时,f(x)=-x +lnx ,令f′(x)=-1+1x=0,得x =1,列表如下:所以当x =1时,函数f(x)的极大值为f(1)=-1,函数f(x)无极小值.(3分) (2) 当n =0时,F(x)=(m -2)x 2+(4-m)x -lnx -2,x ∈(0,+∞), 则F′(x)=2(m -2)x +(4-m)-1x=2(m -2)x 2+(4-m )x -1x=(2x -1)[(m -2)x +1]x.当m -2≥0时,即m ≥2,令F′(x)>0,则x>12,所以函数F(x)在⎝⎛⎭⎫0,12上单调递减,在⎝⎛⎭⎫12,+∞上单调递增,不符合题意; (5分)当m<2时,令F ′(x)=0,则x =12或x =12-m .若12-m <12,令F′(x)>0,则12-m<x<12,所以函数F(x)在⎝⎛⎭⎫0,12-m 上单调递减,在⎝⎛⎭⎫12-m ,12上单调递增,在⎝⎛⎭⎫12,+∞上单调递减,不符合题意; 若12-m >12,令F′(x)>0,则12<x<12-m,所以函数F(x)在⎝⎛⎭⎫0,12上单调递减,在⎝⎛⎭⎫12,12-m 上单调递增,在⎝⎛⎭⎫12-m ,+∞上单调递减,不符合题意;若12-m =12,即m =0,此时F′(x)=-(2x -1)2x ≤0恒成立,所以函数F(x)在(0,+∞)上单调递减,符合题意. (8分) 综上可得,m =0.(9分)(3) 对于任意的n>0,构造函数h(x)=x +lnx +2x -(3+n)(x>0),则h′(x)=1+1x -2x 2=x 2+x -2x 2=(x +2)(x -1)x 2.令h′(x)=0,则x =1,当0<x<1时,h′(x)<0,当x>1时,h′(x)>0,所以函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增, 所以当x =1时,h(x)取得极小值h(1).因为h(1)=-n<0,h(n +3)=ln(n +3)+2n +3>0,且h(x)在[1,n +3]上的图象是一条连续不间断的曲线,所以存在x 0∈(1,n +3),使得h(x 0)=0,即x 0+lnx 0+2x 0-(3+n)=0,两边同时乘x 0,可得x 20+x 0lnx 0+2-(3+n)x 0=0.①(12分) 取m =1-lnx 0x 0,构造函数k(x)=1-lnx x ,x>0,则k′(x)=lnx -1x 2. 令k′(x)=0,得x =e ,则函数k(x)在(0,e)上单调递增,在(e ,+∞)上单调递减, 所以当x =e 时,k(x)取最小值1-1e>0,所以m =1-lnx 0x 0>0,两边同时乘x 0,可得mx 0=x 0-lnx 0,化简得(m -1)x 0+lnx 0=0,即x 0也是f(x)的零点; 两边同时乘x 0,可得(m -1)x 20+x 0lnx 0=0.② (14分)由②-①,得(m -2)x 20+(n +3)x 0-2=0,所以x 0也是g(x)的一个零点, 所以当n>0时,存在正数m ,使得函数f(x)与g(x)有相同的零点.(16分) 21. A. 因为点M(2,1)在矩阵A =⎣⎢⎡⎦⎥⎤1a b 2对应的变换作用下得到点N(5,6),所以⎣⎢⎡⎦⎥⎤1a b 2 ⎣⎢⎡⎦⎥⎤21=⎣⎢⎡⎦⎥⎤56,则⎩⎪⎨⎪⎧2+a =5,2b +2=6, 解得⎩⎪⎨⎪⎧a =3,b =2,所以A =⎣⎢⎡⎦⎥⎤1322.(5分)f(λ)=⎪⎪⎪⎪⎪⎪λ-1-3-2λ-2=(λ-1)(λ-2)-6,令f(λ)=0,得λ2-3λ-4=0,即(λ-4)(λ+1)=0,解得λ1=4,λ2=-1, 所以矩阵A 的特征值为4和-1.(10分)B. (1) 由题意,曲线C 的普通方程为x 24+y 2=1,直线l 的直角坐标方程为x +y -25=0.(4分)(2) 设P(2cosα,sinα),则点P 到直线l 的距离d =|2cosα+sinα-25|2=|5sin (α+θ)-25|2=25-5sin (α+θ)2,(8分)所以当sin(α+θ)=1时,d min =102, 所以点P 到直线l 的距离的最小值为102.(10分) C. 对于正数a ,b ,c ,由均值不等式得b a +c b +ac ≥33b a ×c b ×a c=3,当且仅当a =b =c 时取等号.(4分)任意x ∈R ,由绝对值不等式得|x -2|-|x +1|≤||x -2|-|x +1||≤|(x -2)-(x +1)|=3, 当且仅当x ≤-1时取等号,(8分)所以对任意x ∈R ,都有不等式|x -2|-|x +1|≤b a +c b +ac成立.(10分)22. (1) 以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系Axyz ,则各点的坐标为A(0,0,0),B(2,0,0),C(2,3,0),D(0,3,0),P(0,0,3),M ⎝⎛⎭⎫0,32,32,AP →=(0,0,3),AC →=(2,3,0),AM →=⎝⎛⎭⎫0,32,32. 因为PA ⊥平面ABCD ,所以平面ACD 的一个法向量为AP →=(0,0,3).(1分) 设平面MAC 的法向量为n =(x ,y ,z), 所以⎩⎪⎨⎪⎧n ·AC →=0,n ·AM →=0,即⎩⎪⎨⎪⎧2x +3y =0,32y +32z =0,取n =(3,-2,2),(3分)所以cos 〈AP →,n 〉=AP →·n |AP →||n |=63×9+4+4=21717,所以由图可得二面角MACD 的余弦值为21717.(5分)(2) 设PN →=λPC →(λ∈(0,1)),其中PC →=(2,3,-3),所以MN →=MP →+PN →=⎝⎛⎭⎫0,-32,32+(2λ,3λ,-3λ)=⎝⎛⎭⎫2λ,3λ-32,-3λ+32. 因为平面ABCD 的一个法向量为AP →=(0,0,3), 所以cos 〈AP →,MN →〉=AP →·MN →|AP →||MN →|=3⎝⎛⎭⎫-3λ+323(2λ)2+⎝⎛⎭⎫3λ-322+⎝⎛⎭⎫-3λ+322=-3λ+3222λ2-18λ+92.(8分)因为直线MN 与平面ABCD 所成角的正弦值为32222,所以⎪⎪⎪⎪⎪⎪-3λ+3222λ2-18λ+92=32222,所以⎝⎛⎭⎫-3λ+32222λ2-18λ+92=922,化简得4λ=1,即λ=14,所以PN PC =14.(10分)23. (1) ①因为a 2=9,6×32=9,所以a 2=6×32.②因为a 3=21,6×⎝⎛⎭⎫323=814, 所以a 3>6×⎝⎛⎭⎫323.(3分) (2) 先用数学归纳法证明:当n ≥3时,a n >6×⎝⎛⎭⎫32n (n -1)2.(4分) ①当n =3时,a 3>6×⎝⎛⎭⎫323;②假设当n =k(k ≥3,k ∈N *)时,结论成立, 即a k >6×⎝⎛⎭⎫32k (k -1)2.当n =k +1时,a k +1=13a 2k -a k +3>13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)22-6×⎝⎛⎭⎫32k (k -1)2+3>13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)22-6×⎝⎛⎭⎫32k (k -1)2,其中a k +16×⎝⎛⎭⎫32(k +1)k 2> 13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)226×⎝⎛⎭⎫32(k +1)k 2-6×⎝⎛⎭⎫32k (k -1)26×⎝⎛⎭⎫32(k +1)k 2=2×⎝⎛⎭⎫32k (k -3)2-⎝⎛⎭⎫32-k >1, 所以a k +1>6×⎝⎛⎭⎫32(k +1)k2,所以当n =k +1时,结论也成立. 综上可得,当n ≥3时,a n >6×⎝⎛⎭⎫32n (n -1)2.(8分)所以当n ≥3时,⎝⎛⎭⎫a n 62n >⎝⎛⎭⎫32n -1,则∑ni =2(a i 6)2i >(a 26)22+(32)2+(32)3+…+(32)n -1=32+⎝⎛⎭⎫322+⎝⎛⎭⎫323+…+⎝⎛⎭⎫32n -1=32×1-⎝⎛⎭⎫32n -11-32=2⎝⎛⎭⎫32n-3, 所以当n ≥3时,∑ni =2⎝⎛⎭⎫a i 62i >2⎝⎛⎭⎫32n-3.(10分)。
苏锡常镇2020届高三年级第三次模拟考试数学试卷

苏锡常镇2020届高三年级第三次模拟考试数学试卷(满分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,共计70分.1. 已知集合A ={1,2},B ={-1,a},若A ∪B ={-1,a ,2},则a =________.2. 若复数z 满足(1-i)z =1+i ,其中i 是虚数单位,则z 的实部为________.3. 某校100名学生参加知识竞赛的成绩均在[50,100]内,将学生成绩分成[50,60),[60,70),[70,80),[80,90),[90,100]五组,得到如图所示的频率分布直方图,则成绩在[80,90)内的学生人数是________.(第3题) (第4题) (第9题) 4. 一个算法的伪代码如图所示,执行此算法,最后输出的y 的值为________.5. 某班推选一名学生管理班级防疫用品,已知每个学生当选是等可能的.若“选到女生”的概率是“选到男生”的概率的12,则这个班级的男生人数与女生人数的比值为________.6. 函数f(x)=2-x +lnx 的定义域为________.7. 在平面直角坐标系xOy 中,抛物线y 2=4x的焦点是双曲线x 2a 2-y 24a=1的顶点,则a =________.8. 已知等比数列{a n }的前n 项和为S n ,S 4=5S 2,a 2=2,则a 4=________. 9. 已知正方体ABCD-A 1B 1C 1D 1的棱长为6,M 是对角线A 1C 上靠近点A 1的三等分点,则三棱锥C-MBD 的体积为________.10. 已知定义在R 上的奇函数f(x)的周期为2,且当x ∈[0,1]时,f(x)=⎩⎨⎧2x+a , 0≤x ≤12,bx -1x +1, 12<x ≤1,则a +b =________.11. 已知锐角α满足sin2α-2cos2α=-1,则tan ⎝⎛⎭⎫α+π4=________. 12. 如图,在△ABC 中,∠ABC =π2,AB =1,BC =3,以AC 为一边在△ABC 的另一侧作正三角形ACD ,则BD →·AC →=________.13. 在平面直角坐标系xOy 中,AB 是圆O :x 2+y 2=1的直径,且点A 在第一象限.圆O 1:(x -a)2+y 2=r 2(a >0)与圆O 外离,线段AO 1与圆O 1交于点M ,线段BM 与圆O 交于点N ,且OM →+O 1N →=0,则a 的取值范围为________.14. 已知a ,b ∈R ,a +b =t(t 为常数),且直线y =ax +b 与曲线y =xe x (e 是自然对数的底数,e ≈2.718 28…)相切.若满足条件的有序实数对(a ,b)唯一存在,则实数t 的取值范围为________.二、 解答题:本大题共6小题,共计90分.解答时应写出文字说明,证明过程或演算步骤. 15. (本小题满分14分)已知在△ABC 中,a ,b ,c 分别为角 A ,B ,C 的对边,且bsin2A =asinB.(1) 求A 的值;(2) 求cos ⎝⎛⎭⎫B +π6+sin ⎝⎛⎭⎫C +π3的最大值.16. (本小题满分14分)已知在四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 是菱形,且平面A 1ADD 1⊥平面ABCD ,DA 1=DD 1,E ,F 分别为线段A 1D 1,BC 的中点.求证: (1) EF ∥平面CC 1D 1D ; (2) AC ⊥平面EBD.17. (本小题满分14分)在平面直角坐标系xOy 中,椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,右焦点到右准线的距离为3.(1) 求椭圆C 的标准方程;(2) 过点P(0,1)的直线l 与椭圆C 交于A ,B 两点.已知在椭圆C 上存在点Q ,使得四边形OAQB 是平行四边形,求点Q 的坐标.18. (本小题满分16分)某地开发一片荒地,如图,荒地的边界是以C 为圆心,半径为1千米的圆周.已有两条互相垂直的道路OE ,OF ,分别与荒地的边界有且仅有一个接触点A ,B.现规划修建一条新路(由线段MP ,PQ ︵,线段QN 三段组成),其中点M ,N 分别在OE ,OF 上,且使得MP ,QN 所在直线分别与荒地的边界有且仅有一个接触点P ,Q ,PQ ︵所对的圆心角为π6. 记∠PCA=2θ(道路宽度均忽略不计).(1) 若θ=5π12,求QN 的长度;(2) 求新路总长度的最小值.19. (本小题满分16分)已知各项均为正数的数列{a n }的前n 项和为S n ,a 1=2,且对任意n ∈N *,a n S n +1-a n +1S n =2a n +1-2a n 恒成立.(1) 求证:数列⎩⎨⎧⎭⎬⎫S n +2a n 是等差数列,并求数列{a n }的通项公式; (2) 设b n =a n +4n -3,已知b 2,b i ,b j (2<i <j)成等差数列,求正整数i ,j 的值.20. (本小题满分16分)已知函数f(x)=(m -1)x +lnx ,g(x)=(m -2)x 2+(n +3)x -2,m ,n ∈R . (1) 当m =0时,求函数f(x)的极值;(2) 当n =0时,函数F(x)=g(x)-f(x)在(0,+∞)上为单调函数,求m 的取值范围; (3) 当n >0时,判断是否存在正数m ,使得函数f(x)与g(x)有相同的零点,并说明理由.数学附加题(本部分满分40分,考试时间30分钟)21. 【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A. [选修4-2:矩阵与变换](本小题满分10分) 已知点M(2,1)在矩阵A =⎣⎢⎡⎦⎥⎤1 a b 2对应的变换作用下得到点N(5,6),求矩阵A 的特征值.B. [选修4-4:坐标系与参数方程](本小题满分10分)在平面直角坐标系xOy 中,曲线C 的参数方程为⎩⎪⎨⎪⎧x =2cosα,y =sinα(α为参数).以原点O 为极点,x 轴的非负半轴为极轴建立极坐标系,直线l 的极坐标方程为ρsin ⎝⎛⎭⎫θ+π4=10. (1) 求曲线C 的普通方程和直线l 的直角坐标方程;(2) P 是曲线C 上的动点,求点P 到直线l 的距离的最小值.C. [选修4-5:不等式选讲](本小题满分10分)已知a ,b ,c 是正数,求证:对任意x ∈R ,不等式||x -2-||x +1≤b a +c b +ac 恒成立.【必做题】第22题、第23题,每题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤. 22. (本小题满分10分)如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,PA ⊥平面ABCD ,AB =2,AD =AP =3,M 是棱PD 的中点.(1) 求二面角M-AC-D 的余弦值;(2) N 是棱PC 上的点,已知直线MN 与平面ABCD 所成角的正弦值为32222,求PNPC的值.23. (本小题满分10分)已知在数列{a n }中,a 1=6,a n +1=13a 2n -a n +3( n ∈N *).(1) 分别比较下列每组中两个数的大小: ①a 2和6×32;②a 3和6×⎝⎛⎭⎫323;(2) 当n ≥3时,证明:∑ni =2⎝⎛⎭⎫a i 62i >2⎝⎛⎭⎫32n-3. 数学参考答案 1. 1 2. 0 3. 30 4. -1 5. 2 6. (0,2] 7. 1 8. 2或8 9. 24 10. 0 11. 2 12. 4 13. (22,4) 14. {e}∪(-∞,-5e -2) 15. (1) 因为bsin 2A =asin B , 所以2bsin Acos A =asin B , 所以由正弦定理a sin A =bsin B,得2bacos A =ab.(3分)因为ab ≠0,所以cos A =ab 2ab =12.又因为A ∈(0,π),所以A =π3.(6分)(2) 由(1)得A =π3,又A +B +C =π,所以C =2π3-B ,B ∈⎝⎛⎭⎫0,2π3,所以cos ⎝⎛⎭⎫B +π6+sin(C +π3)=cos Bcos π6-sin Bsin π6+sin(π-B)=12sin B +32cos B =sin ⎝⎛⎭⎫B +π3.(11分) 因为0<B<2π3,所以π3<B +π3<π,所以当B +π3=π2,即B =π6时,sin ⎝⎛⎭⎫B +π3取最大值1, 所以cos ⎝⎛⎭⎫B +π6+sin ⎝⎛⎭⎫C +π3的最大值为1.(14分) 16. (1) 连结CD 1,由题意得四边形A 1B 1C 1D 1,BB 1C 1C 是平行四边形,所以A 1D 1∥ B 1C 1,BC ∥B 1C 1,且A 1D 1=B 1C 1,BC =B 1C 1. 又因为E ,F 分别为线段A 1D 1,BC 的中点, 所以ED 1∥FC ,ED 1=FC ,所以四边形ED 1CF 是平行四边形,(3分) 所以EF ∥CD 1.又因为EF ⊄平面CC 1D 1D ,CD 1⊂平面CC 1D 1D , 所以EF ∥平面CC 1D 1D.(6分)(2) 在四棱柱ABCD-A 1B 1C 1D 1中,四边形AA 1D 1D 是平行四边形,所以AD ∥A 1D 1. 在△DA 1D 1中,DA 1=DD 1,E 为线段A 1D 1的中点,所以DE ⊥A 1D 1. 又因为AD ∥A 1D 1,所以DE ⊥AD.(8分)又因为平面A 1ADD 1⊥平面ABCD ,平面A 1ADD 1∩平面ABCD =AD ,DE ⊂平面A 1ADD 1, 所以DE ⊥平面ABCD.又AC ⊂平面ABCD ,所以DE ⊥AC.(11分) 因为底面ABCD 是菱形,所以BD ⊥AC. 又因为BD ∩DE =D ,BD ,DE ⊂平面EBD , 所以AC ⊥平面EBD.(14分)17. (1) 由椭圆C :x 2a 2+y 2b 2=1的离心率为12,右焦点与右准线的距离为3,得c a =12,a 2c-c =3,解得c =1,a =2,所以b 2=a 2-c 2=3,(4分)所以椭圆C 的标准方程为x 24+y 23=1.(5分)(2) 设A(x 1,y 1),B(x 2,y 2),当四边形OAQB 是平行四边形时,则OQ →=OA →+OB →. 当直线l 的斜率不存在时,直线l 过原点O ,此时O ,A ,B 三点共线,不符合题意;(7分)当直线l 的斜率存在时,设直线l 的方程为y =kx +1,与椭圆方程联立有⎩⎪⎨⎪⎧y =kx +1,x 24+y 23=1,所以x 24+(kx +1)23=1,即(3+4k 2)x 2+8k 2x -8=0,所以Δ>0,x 1+x 2=-8k3+4k 2,所以y 1+y 2=63+4k 2.(10分) 将点Q(x 1+x 2,y 1+y 2)的坐标代入椭圆方程得⎝⎛⎭⎫-8k 3+4k 224+⎝⎛⎭⎫63+4k 223=1,化简得k 2=14,所以k =±12,符合题意,(13分)所以点Q 的坐标是⎝⎛⎭⎫±1,32.(14分) 18. (1) 因为PQ ︵所对的圆心角为π6,θ=5π12,所以∠PCQ =π6,∠PCA =2θ=5π6.又因为∠BCA =π2,所以∠BCQ =2π-5π6-π2-π6=π2,所以在四边形BCQN 中,∠BCQ =∠CBN =∠CQN =π2,所以四边形BCQN 是矩形,所以QN =CB =1, 故QN 的长为1千米 .(4分)(2) PM =tan ∠PCA 2=tan θ,∠BCQ =4π3-2θ,NQ =tan ∠BCQ 2=tan ⎝⎛⎭⎫2π3-θ,PQ ︵的长为π6,(6分)所以PM +NQ =tan θ+tan ⎝⎛⎭⎫2π3-θ=tan θ+tan2π3-tan θ1+tan 2π3tan θ=tan θ+-3-tan θ1-3tan θ, 即PM +NQ =tan θ+3+tan θ3tan θ-1=tan θ+1+33tan θtan θ-33,(9分)其中θ∈⎝⎛⎭⎫π6,π2,tan θ∈⎝⎛⎭⎫33,+∞,tan θ-33∈(0,+∞),(11分) 所以PM +NQ =⎝⎛⎭⎫tan θ-33+43tan θ-33+233≥2⎝⎛⎭⎫tan θ-33·43tan θ-33+233=23,(14分)当且仅当tan θ-33=43tan θ-33,又θ∈⎝⎛⎭⎫π6,π2,即θ=π3时取等号,(15分) 所以当∠PCA =2π3时,新路总长度的最小值为⎝⎛⎭⎫23+π6千米.(16分) 19. (1)S 1+2a 1=2+22=2, 因为a n S n +1-a n +1S n =2a n +1-2a n ,所以a n S n +1+2a n =a n +1S n +2a n +1. 又因为a n >0,两边除以a n a n +1得S n +1+2a n +1=S n +2a n ,所以S n +1+2a n +1-S n +2a n =0,n ∈N *,所以数列⎩⎨⎧⎭⎬⎫S n +2a n 是首项为2,公差为0的等差数列,所以S n +2a n =2,(3分)则S n +2=2a n ,S n +1+2=2a n +1,两式作差得a n +1=S n +1-S n =2a n +1-2a n , 所以a n +1=2a n .又因为a n >0,所以a n +1a n=2,n ∈N *,所以数列{a n }是首项为2,公比为2的等比数列,所以a n =2n .(7分)(2) b n =2n +4n -3,由b 2,b i ,b j 成等差数列得2b i =b 2+b j ,即2(2i +4i -3)=9+2j +4j -3,整理得2i -1+2i =2j -2+j +3(2<i<j),(*)若j =i +1,则2i -1+2i =2i -1+i +1+3, 所以i =4,j =5.(10分)若j ≥i +2,则(2j -2+j +3)-(2i -1+2i)≥2i +i +5-2i -1-2i =2i -1-i +5.(12分)设c n =2n -1-n +5(n>2),c n +1-c n =(2n -n +4)-(2n -1-n +5)=2n -1-1>0,则c n +1>c n (n>2),所以当n>2时,数列{c n }单调递增,其中c 3=6>0,所以c n >0, 即2j -2+j +3>2i -1+2i ,所以(*)式不成立.(15分) 综上可得,i =4,j =5.(16分)20. (1) 当m =0时,f(x)=-x +lnx ,令f′(x)=-1+1x=0,得x =1,列表如下:所以当x =1时,函数f(x)的极大值为f(1)=-1,函数f(x)无极小值.(3分) (2) 当n =0时,F(x)=(m -2)x 2+(4-m)x -lnx -2,x ∈(0,+∞), 则F′(x)=2(m -2)x +(4-m)-1x=2(m -2)x 2+(4-m )x -1x=(2x -1)[(m -2)x +1]x.当m -2≥0时,即m ≥2,令F′(x)>0,则x>12,所以函数F(x)在⎝⎛⎭⎫0,12上单调递减,在⎝⎛⎭⎫12,+∞上单调递增,不符合题意; (5分)当m<2时,令F ′(x)=0,则x =12或x =12-m .若12-m <12,令F′(x)>0,则12-m<x<12,所以函数F(x)在⎝⎛⎭⎫0,12-m 上单调递减,在⎝⎛⎭⎫12-m ,12上单调递增,在⎝⎛⎭⎫12,+∞上单调递减,不符合题意;若12-m >12,令F′(x)>0,则12<x<12-m,所以函数F(x)在⎝⎛⎭⎫0,12上单调递减,在⎝⎛⎭⎫12,12-m 上单调递增,在⎝⎛⎭⎫12-m ,+∞上单调递减,不符合题意;若12-m =12,即m =0,此时F′(x)=-(2x -1)2x ≤0恒成立,所以函数F(x)在(0,+∞)上单调递减,符合题意. (8分) 综上可得,m =0.(9分)(3) 对于任意的n>0,构造函数h(x)=x +lnx +2x-(3+n)(x>0),则h′(x)=1+1x -2x 2=x 2+x -2x 2=(x +2)(x -1)x 2.令h′(x)=0,则x =1,当0<x<1时,h′(x)<0,当x>1时,h′(x)>0,所以函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增, 所以当x =1时,h(x)取得极小值h(1).因为h(1)=-n<0,h(n +3)=ln(n +3)+2n +3>0,且h(x)在[1,n +3]上的图象是一条连续不间断的曲线,所以存在x 0∈(1,n +3),使得h(x 0)=0,即x 0+lnx 0+2x 0-(3+n)=0,两边同时乘x 0,可得x 20+x 0lnx 0+2-(3+n)x 0=0.①(12分) 取m =1-lnx 0x 0,构造函数k(x)=1-lnx x ,x>0,则k′(x)=lnx -1x 2. 令k′(x)=0,得x =e ,则函数k(x)在(0,e)上单调递增,在(e ,+∞)上单调递减, 所以当x =e 时,k(x)取最小值1-1e>0,所以m =1-lnx 0x 0>0,两边同时乘x 0,可得mx 0=x 0-lnx 0,化简得(m -1)x 0+lnx 0=0,即x 0也是f(x)的零点; 两边同时乘x 0,可得(m -1)x 20+x 0lnx 0=0.② (14分)由②-①,得(m -2)x 20+(n +3)x 0-2=0,所以x 0也是g(x)的一个零点, 所以当n>0时,存在正数m ,使得函数f(x)与g(x)有相同的零点.(16分) 21. A. 因为点M(2,1)在矩阵A =⎣⎢⎡⎦⎥⎤1a b 2对应的变换作用下得到点N(5,6),所以⎣⎢⎡⎦⎥⎤1a b 2⎣⎢⎡⎦⎥⎤21=⎣⎢⎡⎦⎥⎤56,则⎩⎪⎨⎪⎧2+a =5,2b +2=6, 解得⎩⎪⎨⎪⎧a =3,b =2,所以A =⎣⎢⎡⎦⎥⎤1322.(5分) f(λ)=⎪⎪⎪⎪⎪⎪λ-1-3-2λ-2=(λ-1)(λ-2)-6,令f(λ)=0,得λ2-3λ-4=0,即(λ-4)(λ+1)=0,解得λ1=4,λ2=-1, 所以矩阵A 的特征值为4和-1.(10分)B. (1) 由题意,曲线C 的普通方程为x 24+y 2=1,直线l 的直角坐标方程为x +y -25=0.(4分)(2) 设P(2cosα,sinα),则点P 到直线l 的距离d =|2cosα+sinα-25|2=|5sin (α+θ)-25|2=25-5sin (α+θ)2,(8分)所以当sin(α+θ)=1时,d min =102, 所以点P 到直线l 的距离的最小值为102.(10分) C. 对于正数a ,b ,c ,由均值不等式得b a +c b +ac ≥33b a ×c b ×a c =3,当且仅当a =b =c 时取等号.(4分)任意x ∈R ,由绝对值不等式得|x -2|-|x +1|≤||x -2|-|x +1||≤|(x -2)-(x +1)|=3, 当且仅当x ≤-1时取等号,(8分)所以对任意x ∈R ,都有不等式|x -2|-|x +1|≤b a +c b +ac成立.(10分)22. (1) 以{AB →,AD →,AP →}为正交基底建立如图所示的空间直角坐标系Axyz ,则各点的坐标为A(0,0,0),B(2,0,0),C(2,3,0),D(0,3,0),P(0,0,3),M ⎝⎛⎭⎫0,32,32,AP →=(0,0,3),AC →=(2,3,0),AM →=⎝⎛⎭⎫0,32,32. 因为PA ⊥平面ABCD ,所以平面ACD 的一个法向量为AP →=(0,0,3).(1分) 设平面MAC 的法向量为n =(x ,y ,z), 所以⎩⎪⎨⎪⎧n ·AC →=0,n ·AM →=0,即⎩⎪⎨⎪⎧2x +3y =0,32y +32z =0,取n =(3,-2,2),(3分)所以cos 〈AP →,n 〉=AP →·n |AP →||n |=63×9+4+4=21717,所以由图可得二面角MACD 的余弦值为21717.(5分)(2) 设PN →=λPC →(λ∈(0,1)),其中PC →=(2,3,-3),所以MN →=MP →+PN →=⎝⎛⎭⎫0,-32,32+(2λ,3λ,-3λ)=⎝⎛⎭⎫2λ,3λ-32,-3λ+32.因为平面ABCD 的一个法向量为AP →=(0,0,3), 所以cos 〈AP →,MN →〉=AP →·MN →|AP →||MN →|=3⎝⎛⎭⎫-3λ+323(2λ)2+⎝⎛⎭⎫3λ-322+⎝⎛⎭⎫-3λ+322=-3λ+3222λ2-18λ+92.(8分)因为直线MN 与平面ABCD 所成角的正弦值为32222,所以⎪⎪⎪⎪⎪⎪-3λ+3222λ2-18λ+92=32222,所以⎝⎛⎭⎫-3λ+32222λ2-18λ+92=922,化简得4λ=1,即λ=14,所以PN PC =14.(10分)23. (1) ①因为a 2=9,6×32=9,所以a 2=6×32.②因为a 3=21,6×⎝⎛⎭⎫323=814, 所以a 3>6×⎝⎛⎭⎫323.(3分) (2) 先用数学归纳法证明: 当n ≥3时,a n >6×⎝⎛⎭⎫32n (n -1)2.(4分)①当n =3时,a 3>6×⎝⎛⎭⎫323;②假设当n =k(k ≥3,k ∈N *)时,结论成立, 即a k >6×⎝⎛⎭⎫32k (k -1)2.当n =k +1时,a k +1=13a 2k -a k +3>13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)22-6×⎝⎛⎭⎫32k (k -1)2+3>13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)22-6×⎝⎛⎭⎫32k (k -1)2,其中a k +16×⎝⎛⎭⎫32(k +1)k 2> 13×⎣⎡⎦⎤6×⎝⎛⎭⎫32k (k -1)226×⎝⎛⎭⎫32(k +1)k 2-6×⎝⎛⎭⎫32k (k -1)26×⎝⎛⎭⎫32(k +1)k 2=2×⎝⎛⎭⎫32k (k -3)2-⎝⎛⎭⎫32-k >1, 所以a k +1>6×⎝⎛⎭⎫32(k +1)k2,所以当n =k +1时,结论也成立.综上可得,当n ≥3时,a n >6×⎝⎛⎭⎫32n (n -1)2.(8分)所以当n ≥3时,⎝⎛⎭⎫a n 62n >⎝⎛⎭⎫32n -1,则∑ni =2(a i 6)2i >(a 26)22+(32)2+(32)3+…+(32)n -1=32+⎝⎛⎭⎫322+⎝⎛⎭⎫323+…+⎝⎛⎭⎫32n -1=32×1-⎝⎛⎭⎫32n -11-32=2⎝⎛⎭⎫32n-3,所以当n ≥3时,∑ni =2⎝⎛⎭⎫a i 62i >2⎝⎛⎭⎫32n-3.(10分)。
2020年江苏省苏锡常镇四市高考数学模拟试卷(一)(3月份)

2020年江苏省苏锡常镇四市高考数学模拟试卷(一)(3月份)一、填空题:本大题共14小题,每小题5分,共计70分•不需要写出解答过程,请把答案直接填写在答题卡相应位置上.1. (5分)已知i为虚数单位,复数z —,则|z| _________ .1 i2. _____________ (5分)已知集合A {x|0剟X 1} , B {x|a 1剟X 3},若A| B中有且只有一个元素,则实数a的值为.3. ______________________________________________________________ (5分)已知一组数据 1.6, 1.8, 2, 2.2, 2.4,则该组数据的方差是__________________________ .2 24. (5分)在平面直角坐标系xOy中,已知双曲线笃—1(a 0)的一条渐近线方程为a 4y 2x,贝U a .35. (5分)甲乙两人下棋比赛,两人下成和棋的概率是1,乙获胜的概率是1,则乙不输的2 3概率是_____ .6. (5分)如图是一个算法的流程图,则输出的x的值为兰/」-7. (5分)“直线11: ax y 1 0与直线L :4x ay 3 0平行”是“ a 2 ”的_________ 条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”)& (5分)已知等差数列{a n}的前n项和为S , a1 9 ,会 ' 4,则a n ____________ .9 59. (5分)已知点M是曲线y 2lnx x2 3x上一动点,当曲线在M处的切线斜率取得最小值时,该切线的方程为_____ .10. (5 分)已知3cos2 ____________________ 4sin(—), (—,),贝U sin24 411. (5分)如图,在矩形ABCD中,E为边AD的中点,AB 1 , BC 2,分别以A、D为圆心,1为半径作圆弧E B、?C(E在线段AD 上).由两圆弧?B、?C及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为_________uur uuir uuu12. (5分)在ABC中,(AB AC) BC( 1),若角A的最大值为一,则实数的值是6 —13. (5分)若函数f(x) a x(a 0且a 1)在定义域[m , n]上的值域是[m2, n2](1 m n),则a的取值范围是14. (5分)如图,在ABC中,AB 4 , D是AB的中点,E在边AC上,AE 2EC , CD、解答题:本大题共6小题,共计90分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤.15(14分)在ABC中,角A ,B ,C所对的边分别为a ,b ,c,且满足bcosA . 3asinB 0 .(1 )求A ;(2)已知a 2 3 , B —,求ABC的面积.316. (14分)如图,在四棱锥P ABCD中,四边形ABCD为平行四边形,BD DC , PCD 为正三角形,平面PCD 平面ABCD , E为PC的中点.(1)证明:AP//平面EBD ;(2)证明:BE PC .17. (14分)某地为改善旅游环境进行景点改造•如图,将两条平行观光道 h 和12通过一段抛物线形状的栈道 AB 连通(道路不计宽度),h 和12所在直线的距离为 0.5(百米),对岸堤 岸线13平行于观光道且与12相距1.5 (百米)(其中A 为抛物线的顶点,抛物线的对称轴垂直 于13,且交13于M ),在堤岸线13上的E ,F 两处建造建筑物,其中 E ,F 到M 的距离为1 (百米),且F 恰在B 的正对岸(即BF 13).(1 )在图②中建立适当的平面直角坐标系,并求栈道AB 的方程;(2)游客(视为点P )在栈道AB 的何处时,观测EF 的视角(2 218. (16分)如图,在平面直角坐标系xoy 中,已知椭圆C:务与1(a b 0)的离心率为a b1,且经过点(1,j ) , A , B 分别为椭圆C 的左、右顶点,过左焦点 F 的直线I 交椭圆C 于 D , E 两点(其中D 在x 轴上方). (1) 求椭圆C 的标准方程;(2)若 AEF 与 BDF 的面积比为1:7,求直线I 的方程.-----------1/EPF )最大?请在(1)的坐u标系中,写出观测点 P 的坐标.圏①圈②(1)求曲线C 的普通方程;(2)求曲线I 和曲线C 的公共点的极坐标.[选修4-5:不等式选讲]的值.元可以抽奖一次,满 400元可以抽奖两次,依此类推) 袋中装有编号分别为1, 2, 3, 4, 5的5个完全相同的小球,顾客每次从口袋中摸出一个小 球,共摸三次,每次摸出的小球均不放回口袋, 若摸得的小球编号一次比一次大 (如1 , 2, 5),则获得一等奖,奖金 40元;若摸得的小球编号一次比一次小(如 5, 3, 1),则获得二19. (16 分) (1)若函数 2 3 2 2已知函数 f (x) x mx m x(m R)的导函数 f (x).3f (x)存在极值,求m 的取值范围;g(x ) f (x )(2)设函数 h (x ) f (e x ) f (lnx)(其中e 为自然对数的底数),对任意m R ,若关于x 的 不等式h(x)- • m 2 k 2在(0,)上恒成立,求正整数 k 的取值集合.20. (16 分) 已知数列a n,n为奇数,n N*b n ,n 为偶数,(1 )若 a n n , b n 2n ,求数列{C n }的前2n 项和T 2n ;(2)若数列 {a n }为等差数列,且对任意 n N* , C n 1C n 恒成立.①当数列{b n }为等差数列,求证:数列{a n } , {b n }的公差相等; ②数列{b n }能否为等比数列?若能,请写出所有满足条件的数列 {b n };若不能,请说明理由. 数学n (附加题)[选修4-2 ;矩阵与变换1 321. (10分)已知矩阵 A2 13,且二阶矩阵M 满足AM 求M 的特征值及属于各特征值的一个特征向量. [选修4-4;坐标系与参数方程]2 cos22.( 10 分)在平面直角坐标系 xOy 中,曲线I 的参数方程为以原点O 为极点,x 轴非负半轴为极轴建立极坐标系,曲线( 2C 的极坐标方程为3 2.3cos 2为参数),4sin23.已知正数x , y , z 满足x y z t(t 为常数), 2y_ 9 2z 的最小值为,求实数t24. (10分)某商店举行促销反馈活动,顾客购物每满 200 元,有一次抽奖机会(即满 200.抽奖的规则如下:在一个不透明口。
2020届苏锡常镇三模考试数学卷

2020届苏锡常镇三模考试数学卷江苏镇江韩雨一、填空题:本大题共14小题,每小题5分,共计70分。
不需要写出解答过程,请把答案直接填在答题卡相应位置上。
1.已知集合A =1,2 ,B =-1,a 2 ,若A ∩B =a ,则实数a =_______.2.若复数z 满足(1-3i )z =3+i ,其中i 是虚数单位,z =________.3.已知α,β是某个平行四边形的两个内角,命题P :α=β;命题Q :sin α=sin β,则命题P 是命题Q 的______条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分也不必要”中选择一个合适的填空)。
4.为了研究疫情病毒和人的血型间的关系,在被感染的600人中,O 型血有200人,A 型血有150人,B 型血有150人,AB 型血有100人。
在这600人中,为抽取一个容量为60人的样本,则应从O 型血中抽取的人数为______.5.已知直线l 1:x -2y +3=0,l 2:2x +ky +k =0,且l 1∥l 2,则直线l 1,l 2间的距离为______.6.一周后的6月25日为端午节,国家规定调休放假3天,甲、乙、丙三人端午节值班,每人值班一天,每天一人值班,则甲在乙前面值班的概率为_______.7.中国古诗词中,有一道“八子分绵”的数学名题:“九百九十六斤绵,赠分八子作盘缠,次第每人多十七,要将第八数来言”。
意思是把996斤绵分给8个儿子作盘缠,按照年龄从大到小的顺序依次排列分绵,每个弟弟都比前面的哥哥多17斤绵,那么第8个儿子分到的绵的斤数为______.8.已知抛物线y 2=4x 的准线是双曲线x 2a 2 -y 22 =1(a >0)的左准线,则a =______.9.《算数书》竹简于20世纪80年代在湖北省江陵县张家山出土,这是我们现存最早的成系统的数学典籍.其中记载有求“囷盖”术:“冒如其周,令相乘也,又以高乘之,三十六成一”,该术相当于给出了由圆锥的底面周长L 与高h ,计算其体积V 的近似公式:V =136L 2h .它实际上将圆锥体积公式中的圆周率π取近似值 .10.已知圆C 1:(x −a )2+(y +2)2=4与圆C 2:(x +b )2+(y +1)2=1外切,则ab 的最大值为 .11.《九章算术》是我国古代著名数学经典,其对勾股定理的论述比西方早一千多年.其中有这样一个问题:“今有勾五步,股十二步,问勾中容方几何?”其意为:今有直角三角形ABC ,勾(短直角边)BC 长5步,股(长直角边)AB 长12步,问该直角三角形能容纳的正方形DEBF 边长为多少?在如图所示中,求得正方形DEBF 的边长后,可求得tan ∠ACE = .12.已知在ΔOAB 中,OA =2 ,OB =2,∠AOB =135∘,P 为平面OAB 上一点,且OP =OA +λOB (λ∈R ),当OP 最小时,向量OP 与OB 的夹角为 .13.已知函数f (x )=e x ,x ≤1,−x 2+4x −3 ,1<x <3, 若函数g (x )=f (x )−k x +2 有三个零点,则实数k 的取值范围是 .14.在锐角ΔABC 中,角A ,B ,C 的对边分别为a ,b ,c 若(b −sin C )cos A =sin A cos C ,且a =2,则tan A tan B tan C的最大值为 .二、解答题:本大题共6小题,共计90分.15.如图,在直三棱柱ABC −A 1B 1C 1中,D 为AC 中点,AB =BC ,A 1D ⊥AC 1.求证:(1)B 1C ∥平面A 1BD ;(2)平面A 1BD ⊥平面AB 1C 1.16.在ΔABC 中,三角A ,B ,C 的对边分别为a ,b ,c ,且cos A =5 5,sin B =5 cos C (1)求tan C 的值;(2)若a =22 ,求ΔABC 的面积.17、在平而直角坐标系xOy 中,椭圆C :x 2a 2 +y 2b 2 =1a >b >0 左、右焦点分别为F 1,F 2,离心率为2 2,两准线间距离为8,圆O 的直径为F 1F 2,直线l 与圆O 相切于第四象限点T ,与y 轴交于M 点,与椭圆C 交于点N (N 点在T 点上方),且OM =ON .(1)求椭圆C 的标准方程:(2)求直线l 的方程:(3)求直线l 上满足到F 1,F 2距离之和为42 的所有点的坐标.18、镇江市长江路江边春江潮广场要设计一尊鼎型塑像(如图1),塑像总高度为12米,塑像由两部分组成,上半部分由四根垂直于水平地面的等高垂直立柱组成(立柱上凸起部分忽略不计),下半部分由正四棱台的上底面四根水平横柱和正四棱台的四根侧棱斜柱组成,如图2所示.设计要求正棱台的水平横柱长度为4米,下底面边长为8米,设斜柱与地面的所成的角为θ.(1)用θ表示塑像上半部分立柱的高度,并求sin θ的取值范围?(2)若该塑像上半部分立柱的造价为3 千元/米(立柱上凸起部分忽略不计),下半部分横柱和斜柱的造价都为2千元/米,问当θ为何值时,塑像总造价最低?19.各项为正数的数列a n 如果满足:存在实数k ≥1,对任意正整数n ,1k≤a n +1a n ≤k 恒成立,且存在正整数n ,使得a n +1a n =k 或a n +1a n =1k成立,则称数列a n 为“紧密数列”,k 称为“紧密数列”a n 的“紧密度”.已知数列a n 的各项为正数,前n 项和为S n ,且对任意正整数n ,S n =a n 2+Ba n +C (A ,B ,C 为常数)恒成立(1)当A =14 ,B =12 ,C =14时,①求数列a n 的通项公式;②证明数列a n 是“紧密度”为3的“紧密数列”;(2)当A =0时,已知数列a n 和数列S n 都为“紧密数列”,“紧密度”分别为k 1,k 2,且k 1,k 2∈1,2 ,求实数B 的取值范围.20、已知函数f x =e x -ax ,a ∈R ,其中e 是自然对数的底数.(1)当a =1时,求曲线y = f x 在x =1处的切线方程;(2)如果对任意x ∈R ,不等式f x ≥0恒成立,求实数a 的取值范围;(3)讨论函数g x = f x -e -x 的零点个数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省苏锡常镇四市2020-2021学年高三第三次模拟考试数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数()sin 2cos 2f x x a x =+的图象的一条对称轴为12x π=,将函数()f x 的图象向右平行移动4π个单位长度后得到函数()g x 图象,则函数()g x 的解析式为( ) A .()2sin(2)12g x x π=- B .()2sin(2)12g x x π=+C .()2sin(2)6g x x π=-D .()2sin(2)6g x x π=+2.设等差数列{}n a 的前n 项和为n S ,若5632a a a +=+,则7S =( ) A .28B .14C .7D .23.已知实数,x y 满足,10,1,x y x y y ≥⎧⎪+-≤⎨⎪≥-⎩则2z x y =+的最大值为( )A .2B .32C .1D .04.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”意思为有一个人要走378里路,第一天健步行走,从第二天起脚痛,每天走的路程为前一天的一半,走了六天恰好到达目的地,请问第二天比第四天多走了( ) A .96里B .72里C .48里D .24里5.0y m -+=过双曲线C :22221(0,0)x y a b a b-=>>的左焦点F ,且与双曲线C 在第二象限交于点A ,若||||FA FO =(O 为坐标原点),则双曲线C 的离心率为 A .2B.1CD16.已知条件:1p a =-,条件:q 直线10x ay -+=与直线210x a y +-=平行,则p 是q 的( )让3个学生“向后转”,若4个学生全部转到面朝正北方向,则至少需要“向后转”的次数是( ) A .3 B .4C .5D .68.设1tan 2α=,4cos()((0,))5πββπ+=-∈,则tan 2()αβ-的值为( )A .724-B .524-C .524D .7249.已知点(m,8)在幂函数()(1)n f x m x =-的图象上,设,(ln ),()m a f b f c f n n π⎛⎫=== ⎪⎝⎭,则( ) A .b <a <cB .a <b <cC .b <c <aD .a <c <b10.设,,a b c ∈R 且a b >,则下列不等式成立的是( ) A .c a c b -<-B .22ac bc >C .11a b< D .1b a< 11.已知a b ,满足23a =,3b =,6a b ⋅=-,则a 在b 上的投影为( ) A .2-B .1-C .3-D .212.定义在R 上的偶函数()f x 满足()()11f x f x +=-()()0≠f x ,且在区间()20172018,上单调递减,已知,αβ是锐角三角形的两个内角,则()()sin cos f f βα,的大小关系是( ) A .()()sin cos βα<f f B .()()sin cos βα>f f C .()()sin =cos βαf fD .以上情况均有可能二、填空题:本题共4小题,每小题5分,共20分。
13.设全集U =R ,{|31,}A x x x Z =-<≤∈,{}2|20,B x x x x R =--≥∈,则UAB =______.14.若6260126(21)(1)(1)(1)x a a x a x a x +=+++++⋅⋅⋅++,则012345623456a a a a a a a ++++++=________.15.已知点F 是抛物线22y x =的焦点,M ,N 是该抛物线上的两点,若17||||4MF NF +=,则线段MN 中点的纵坐标为__________.16.函数()ln(1)=-+f x x ____________.(写成区间的形式) 三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
17.(12分)本小题满分14分)已知曲线C 的极坐标方程为4sin ρθ=,以极点为原点,极轴为x 轴的非负半轴建立平面直角坐标系,直线l的参数方程为1,21x t y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),求直线l 被曲线C 截得的线段的长度18.(12分)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知125()a c b ac +=. (1)若a ,b ,c 成等差数列,求cos B 的值;(2)是否存在ABC 满足B 为直角?若存在,求sin A 的值;若不存在,请说明理由.19.(12分)已知数列{}n a 为公差为d 的等差数列,0d >,44a =,且1a ,3a ,9a 依次成等比数列,2n a n b =. (1)求数列{}n b 的前n 项和n S ; (2)若12nn n n b c S S +=⋅,求数列{}n c 的前n 项和为n T .20.(12分)ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC ∆的面积为24sin aA. (1)求sin sin B C ;(2)若10cos cos 1B C =-,a =ABC ∆的周长.21.(12分)已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为1F ,过点1F 且与x 轴垂直的直线被椭圆截得,且1F 与短轴两端点的连线相互垂直. (1)求椭圆C 的方程;(2)若圆222:O x y a +=上存在两点M ,N ,椭圆C 上存在两个点,P Q 满足:1,,M N F 三点共线,1,,P Q F 三点共线,且0PQ MN ⋅=,求四边形PMQN 面积的取值范围.22.(10分)设函数()1f x x x=-,()ln g x t x =,其中()0,1x ∈,t 为正实数. (1)若()f x 的图象总在函数()g x 的图象的下方,求实数t 的取值范围;(2)设()()()221ln 1e 11x H x x x x x ⎛⎫=-++--⎪⎝⎭,证明:对任意()0,1x ∈,都有()0H x >.要求的。
1、C 【解析】 【分析】根据辅助角公式化简三角函数式,结合12x π=为函数()f x 的一条对称轴可求得a ,代入辅助角公式得()f x 的解析式.根据三角函数图像平移变换,即可求得函数()g x 的解析式.【详解】函数()sin 2cos 2f x x a x =+,由辅助角公式化简可得()()2,tan f x x a θθ=+=, 因为12x π=为函数()sin 2cos 2f x x a x =+图象的一条对称轴,代入可得sin 2cos 21212a ππ⎛⎫⎛⎫⨯+⨯= ⎪ ⎪⎝⎭⎝⎭即12=(20a -=,即a =所以()sin 22f x x x =+2sin 23x π⎛⎫=+ ⎪⎝⎭将函数()f x 的图象向右平行移动4π个单位长度可得()g x , 则()2sin 22sin 2436g x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, 故选:C. 【点睛】本题考查了辅助角化简三角函数式的应用,三角函数对称轴的应用,三角函数图像平移变换的应用,属于中档题. 2、B 【解析】 【分析】根据等差数列的性质a a a a +=+并结合已知可求出a ,再利用等差数列性质可得【详解】因为6345a a a a +=+,所以5452a a a +=+,所以42a =, 所以17747()7142a a S a +===, 故选:B 【点睛】本题主要考查等差数列的性质及前n 项和公式,属于基础题. 3、B 【解析】 【分析】作出可行域,平移目标直线即可求解. 【详解】 解:作出可行域:由2z x y =+得,1122y x z =-+ 由图形知,1122y x z =-+经过点时,其截距最大,此z 时最大10y x x y =⎧⎨+-=⎩得1212x y ⎧=⎪⎪⎨⎪=⎪⎩,11,22C ⎛⎫ ⎪⎝⎭ 当1212x y ⎧=⎪⎪⎨⎪=⎪⎩时,max 1232222z =+⨯=故选:B 【点睛】考查线性规划,是基础题. 4、B人每天走的路程构成公比为12的等比数列,设此人第一天走的路程为1a ,计算1192a =,代入得到答案. 【详解】由题意可知此人每天走的路程构成公比为12的等比数列,设此人第一天走的路程为1a , 则61112378112a ⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=-,解得1192a =,从而可得3241119296,1922422a a ⎛⎫=⨯==⨯= ⎪⎝⎭,故24962472a a -=-=.故选:B . 【点睛】本题考查了等比数列的应用,意在考查学生的计算能力和应用能力. 5、B 【解析】 【分析】 【详解】0y m -+=的倾斜角为π3,易得||||FA FO c ==.设双曲线C 的右焦点为E ,可得AFE △中,90FAE ∠=,则||AE =,所以双曲线C的离心率为1e =.故选B .6、C 【解析】 【分析】先根据直线10x ay -+=与直线210x a y +-=平行确定a 的值,进而即可确定结果.【详解】因为直线10x ay -+=与直线210x a y +-=平行,所以20a a +=,解得0a =或1a =-;即0q a =:或1a =-; 所以由p 能推出q ;q 不能推出p ; 即p 是q 的充分不必要条件. 故选C 【点睛】本题主要考查充分条件和必要条件的判定,熟记概念即可,属于基础题型.【分析】通过列举法,列举出同学的朝向,然后即可求出需要向后转的次数. 【详解】“正面朝南”“正面朝北”分别用“∧”“∨”表示, 利用列举法,可得下表,可知需要的次数为4次. 故选:B. 【点睛】本题考查的是求最小推理次数,一般这类题型构造较为巧妙,可通过列举的方法直观感受,属于基础题. 8、D 【解析】 【分析】利用倍角公式求得tan2α的值,利用诱导公式求得cos β的值,利用同角三角函数关系式求得sin β的值,进而求得tan β的值,最后利用正切差角公式求得结果. 【详解】1tan 2α=,22tan 4tan21tan 3ααα==-,()4cos cos 5πββ+=-=-,()(0,βπ∈,4cos 5β∴=,3sin 5β=,3tan 4β=,()43tan2tan 734tan 2431tan2tan 24134αβαβαβ---===++⨯,故选:D. 【点睛】该题考查的是有关三角函数求值问题,涉及到的知识点有诱导公式,正切倍角公式,同角三角函数关系式,正切差角公式,属于基础题目. 9、B 【解析】(x )的单调性,即可得到a ,b ,c 的大小关系. 【详解】由幂函数的定义可知,m ﹣1=1,∴m =2, ∴点(2,8)在幂函数f (x )=x n 上, ∴2n =8,∴n =3,∴幂函数解析式为f (x )=x 3,在R 上单调递增,∵23m n =,1<lnπ<3,n =3, ∴mln n nπ<<, ∴a <b <c , 故选:B. 【点睛】本题主要考查了幂函数的性质,以及利用函数的单调性比较函数值大小,属于中档题. 10、A 【解析】A 项,由a b >得到a b -<-,则c a c b -<-,故A 项正确;B 项,当0c 时,该不等式不成立,故B 项错误;C 项,当1a =,2b =-时,112>-,即不等式11a b<不成立,故C 项错误;D项,当1a =-,2b =-时,21ba =>,即不等式1b a<不成立,故D 项错误. 综上所述,故选A . 11、A 【解析】 【分析】根据向量投影的定义,即可求解. 【详解】a 在b 上的投影为6cos 23a b a bθ⋅-===-. 故选:A 【点睛】本题考查向量的投影,属于基础题. 12、B由已知可求得函数的周期,根据周期及偶函数的对称性可求()f x 在(0,1)上的单调性,结合三角函数的性质即可比较. 【详解】 由1(1)()f x f x +=-可得1(2)[(1)1]()(1)f x f x f x f x +=++=-=+,即函数的周期2T =, 因为在区间(2017,2018)上单调递减,故函数在区间(1,0)-上单调递减, 根据偶函数的对称性可知,()f x 在(0,1)上单调递增, 因为α,β是锐角三角形的两个内角, 所以1,(0,)2αβπ∈且12αβπ+>即12απβ>-, 所以1cos cos()2απβ<-即0cos sin 1αβ<<<,(cos )(sin )f f αβ<.故选:B . 【点睛】本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.二、填空题:本题共4小题,每小题5分,共20分。
