编译原理_第3章_第1节_词法分析、DFA、NFA和其转换
编译原理第三章_有穷自动机

例 过河问题 分析(续)
初始状态:MWGC-φ;终止状态:φ-MWGC。 g
MWGC-φ
WC-MG
问题:
6
例 过河问题 状态转换图
起始 g
MWGC-φ g
g φ-MWGC
g
7
WC-MG
m
m MWC-G
w
w
c
C-MWG
c W-MGC
g
g
MGC-W c
MG-WC
w
m
c G-MWC
m
gg MWG-C
+dd. ddd;
输入符号串
数字 数字
SB
.
数字
+
A
H
-.
数字
.G
接收:若扫描完输入串, 且在一个终止状态上结 束。
数字 阻塞:若扫描结束但未 停止在终止状态上;或 者为能扫描完输入串 (如遇不合法符号)。
不完全描述:某些状态 对于某些输入符号不存 在转换。
练习:+34.567 .123 3.4.5
w
有穷自动机(FA)
数字系统:可以从一个状态移动到另一个状态;每次 状态转换,都上由当前状态及一组输入符号确定的;可以 输出某些离散的值集。
FA:一个状态集合;状态间的转换规则;通过读头来 扫描的一个输入符号串。
读头:从左到右扫描符号串。移动(扫描)是由状态 转换规则来决定的。
8
读头
一个FA的例子
(3)运行: 串f(,Q,且t1tt21)∈= Σf(,f(Qt1,t2t1∈), Σt2*),其中Q∈K, t1t2为输入字符
17
例3
题:试证abba可为例1的DFA M所识别(所接受)。
编译原理词法NFADFA的确定化和化简

编译原理词法NFADFA的确定化和化简编译原理中的词法分析主要包括以下步骤:词法分析器将输入的源程序文本转化为一个个单词(token),即词法单元。
在词法分析过程中,使用的主要工具是有限自动机(NFA)和确定的有限自动机(DFA)。
NFA(DFA)的确定化是指将一个非确定的有限自动机转化为一个确定的有限自动机。
非确定有限自动机具有多个可能的转换路径,而确定有限自动机每个状态只能有一个转换路径。
确定化的目的是简化自动机的状态图,减少转换的复杂性,便于理解和实现。
确定化的过程一般包括以下步骤:1)初始化:将NFA的起始状态作为DFA的起始状态,并为其创建一个新的DFA状态。
2)闭包运算:对于DFA中的每个状态,根据NFA的ε-转换,计算其ε-闭包(即能够通过ε-转换到达的状态集合)。
3)转换运算:对于DFA中的每个状态和每个输入符号,根据NFA的转换函数,计算DFA中该输入下的状态转移集合。
4)如果新生成的DFA状态集合不在已有的DFA状态集合中,则将其加入到DFA状态集合中,并进行闭包和转换运算;如果已存在,则继续下一个输入符号的转换运算。
5)重复步骤4,直到不再生成新的DFA状态集合。
化简是指对于一个确定的有限自动机(DFA),将其中无用的状态进行合并,得到一个更加简洁的自动机。
化简的目的是减少状态数目,提高运行效率和存储效率。
化简的过程一般包括以下步骤:1)初始化:将DFA状态分为两个集合,一个是终止状态集合,一个是非终止状态集合。
2)将所有的等价状态划分到同一个等价类中。
3)不断迭代以下步骤,直到不能再划分等价类为止:a)对于每对不同的状态p和q,若存在一个输入符号a,通过转移函数计算得到的状态分别位于不同的等价类中,则将该状态划分到不同的等价类中。
b)对于每个等价类中的状态集合,将其进一步划分为更小的等价类。
最终,得到的化简DFA状态图比原始DFA状态图要小,且功能等价。
nfa转换为dfa编译原理 c++

nfa转换为dfa编译原理 c++有限自动机(NFA)和确定有限自动机(DFA)是计算机科学中有限状态自动机的两种形式。
NFA可以接受多个转移状态,而DFA则只能有一个转移状态。
NFA到DFA的转换是一个重要的编译原理问题。
以下是NFA转换为DFA的步骤:1. 确定NFA的开始状态和接受状态。
2. 对于每个输入符号,确定NFA的转换规则和转换后的状态。
3. 重复第二步,直到我们不能获得新的状态。
4. 标记DFA中的状态,即从NFA的多个状态中派生出的状态。
5. 为DFA添加开始状态和接受状态。
开始状态是NFA的开始状态的ε闭包。
6. 对于每个输入符号,使用NFA的转移规则来定义DFA中的转移。
7. 扫描DFA的状态表,并删除不可到达的状态。
下面是在C++中实现的NFA到DFA转换过程的伪代码://定义状态类class State{public:string name;unordered_map<char, set<string>> transitions;bool is_final_state;};//定义NFA类class NFA{public:State start_state;set<State> final_states;unordered_set<State> all_states;};//定义DFA类class DFA{public:State start_state;set<State> final_states;unordered_set<State> all_states;};//NFA转换为DFADFA ConvertToDFA(NFA nfa){//创建DFA对象DFA dfa;//确定开始状态dfa.start_state = nfa.start_state;//确定接受状态dfa.final_states = nfa.final_states;//添加开始状态到DFA的所有状态dfa.all_states.insert(dfa.start_state);while (有新的状态可以加入DFA){//从DFA中选择一个未标记的状态State current_state = 选择一个未标记的状态;for (每个输入符号a){//根据当前状态的a过渡创建新状态State new_state = 创建新状态;//从当前状态开始,获得状态a的ε闭包set<State> epsilon_closure = current_state.获取状态a的ε闭包;//通过NFA的规则从当前状态和ε闭包中跳转到新状态set<State> transition_states = 通过NFA规则从当前状态和ε闭包中跳转到新状态;//确定新状态是否应该成为DFA的接受状态bool is_final_state = 确定新状态应该成为DFA的接受状态;//设置新状态的属性new_ = 新状态的名称;new_state.transitions = 转移函数;new_state.is_final_state = is_final_state;//将状态添加到DFA中dfa.all_states.insert(new_state);}}return dfa;}这是将NFA转换为DFA的基本伪代码。
[编译原理代码][NFA转DFA并最小化DFA并使用DFA进行词法分析]
![[编译原理代码][NFA转DFA并最小化DFA并使用DFA进行词法分析]](https://img.taocdn.com/s3/m/4706449103d276a20029bd64783e0912a2167c14.png)
[编译原理代码][NFA转DFA并最⼩化DFA并使⽤DFA进⾏词法分析]#include <iostream>#include <vector>#include <cstring>#include "stack"#include "algorithm"using namespace std;int NFAStatusNum,AlphabetNum,StatusEdgeNum,AcceptStatusNum;char alphabet[1000];int accept[1000];int StartStatus;int isDFAok=1;int isDFA[1000][1000];/** NFA状态图的邻接表*/vector<vector<int>> Dstates;int Dstatesvisit[1000];int Dtran[1000][1000];vector<int> Dtranstart;vector<int> Dtranend;int isDtranstart[1000];int isDtranend[1000];class Edge{public:int to,w,next;} ;Edge edge[10000];int edgetot=0;int Graph[1000];void link(int u,int v,int w){edge[++edgetot].to=v;edge[edgetot].w=w;edge[edgetot].next=Graph[u];Graph[u]=edgetot;}void input(){int u,v,w;memset(Dtran,-1,sizeof(Dtran));scanf("%d %d %d %d\n",&NFAStatusNum,&AlphabetNum,&StatusEdgeNum,&AcceptStatusNum);for(int i=1;i<=AlphabetNum;i++){ //读⼊字母表scanf("%c",&alphabet[i]);}for(int i=1;i<=AcceptStatusNum;i++){scanf("%d",&accept[i]);}//开始状态序号scanf("%d",&StartStatus);for(int i=0;i<StatusEdgeNum;i++){scanf("%d%d%d\n",&u,&v,&w);link(u,v,w);if(isDFA[u][v]==0){isDFA[u][v]=1;}else{isDFAok=0;}if(w==0){isDFAok=0;}}//读⼊测试字符串}void e_clouser(vector<int> &T,vector<int> &ans){int visit[1000];memset(visit,0,sizeof(visit));stack<int> Stack;//T all push in Stack and copy to ansfor (int i=0;i < T.size();++i){Stack.push(T[i]);ans.push_back(T[i]);visit[T[i]]=1;while(Stack.empty()!=1){int t = Stack.top(); Stack.pop();for(int p=Graph[t];p!=0;p=edge[p].next){if(edge[p].w==0){if(visit[edge[p].to]==0){visit[edge[p].to]=1;Stack.push(edge[p].to);ans.push_back(edge[p].to);}}}}sort(ans.begin(),ans.end());}void move(vector<int> &T,int a,vector<int> &ans){ int visit[1000];memset(visit,0,sizeof(visit));for(int i=0;i<T.size();i++) {int t=T[i];for (int p = Graph[t]; p != 0; p = edge[p].next) { if (edge[p].w == a) {if (visit[edge[p].to] == 0) {visit[edge[p].to] = 1;ans.push_back(edge[p].to);}}}}}bool notin(vector<int> &a,int &U){for(int i=0;i<Dstates.size();i++){int ok=1;if(Dstates[i].size()==a.size()){for(int j=0;j<a.size();j++){if(Dstates[i][j]!=a[j]){ok=0;break;}}if(ok==1) {U=i;return false;}}}U=Dstates.size();return true;}void nfatodfa(){vector<int> s,t;s.push_back(StartStatus);e_clouser(s,t);Dstates.push_back(t);stack<int> Stack;Stack.push(Dstates.size()-1);while(Stack.empty()!=1){int T=Stack.top();Stack.pop();int U;for(int i=1;i<=AlphabetNum;i++){vector<int> ans,ans2;move(Dstates[T],i,ans2);e_clouser(ans2,ans);if(notin(ans,U)){Dstates.push_back(ans);Stack.push(Dstates.size()-1);}Dtran[T][i]=U;}}}void getDtranStartEnd(){for(int i=0;i<Dstates.size();i++){int ok=1;for(int j=0;j<Dstates[i].size();j++){if(Dstates[i][j]==StartStatus){Dtranstart.push_back(i);isDtranstart[i]=1;}for(int k=1;k<=AcceptStatusNum;k++){if(Dstates[i][j]==accept[k]){ok=0;Dtranend.push_back(i);isDtranend[i]=1;}}}}}}vector<vector<int>> newDstates;int newDstatesvisit[1000];int newDtran[1000][1000];int set[1000];vector<int> newDtranstart;vector<int> newDtranend;int isnewDtranstart[1000];int isnewDtranend[1000];void simple(){int visit[1000];memset(visit,0,sizeof(visit));vector<int> a,b;//接受结点加⼊afor(int i=0;i<Dtranend.size();i++){a.push_back(Dtranend[i]);visit[Dtranend[i]]=1;set[Dtranend[i]]=0;}//剩余结点加⼊bfor(int i=0;i<Dstates.size();i++){if(visit[i]==0){b.push_back(i);set[i]=1;}}newDstates.push_back(a);newDstates.push_back(b);while(1){int ok=0;for(int i=0;i<newDstates.size();i++){for (int k = 1; k <= AlphabetNum; k++) {for(int j=1;j<newDstates[i].size();j++) {int pp= Dtran[newDstates[i][0]][k];int u = newDstates[i][j], v = Dtran[u][k];if (set[v] != set[pp] ) {//将u剥离newDstates[i].erase(newDstates[i].begin() + j); vector<int> temp;temp.push_back(u);set[u] = newDstates.size();newDstates.push_back(temp);ok = 1;break;}if (ok == 1) break;}if(ok==1) break;}if(ok==1) break;}if(ok==0) break;}//isnewDtranstart,isnewDtranend,newDtranfor(int i=0;i<Dstates.size();i++) {for (int j = 1; j <= AlphabetNum; j++) {newDtran[set[i]][j]=set[Dtran[i][j]];}if(isDtranend[i]==1)isnewDtranend[set[i]]=1;if(isDtranstart[i]==1)isnewDtranstart[set[i]]=1;}//isnewDtranstart,isnewDtranend}bool dfa(char *S){int status=0;for(int i=0;i<newDstates.size();i++){if(isnewDtranstart[i]==1){status=i;}}for(int i=0;i<strlen(S);i++) {//这⾥我偷懒了,懒得弄个map存映射,直接对这个例⼦进⾏操作,就是 S[i]-'a'+1; int p=S[i]-'a'+1;status=newDtran[status][p];}if(isnewDtranend[status]==1) return true;else return false;}int main() {freopen("E:\\NFATODFA\\a.in","r",stdin);input();if(isDFAok==0){printf("This is NFA\n");nfatodfa();}else{printf("This is DNA\n");}//打印DFAprintf("\nPrint DFA's Dtran:\n");printf(" DFAstatu a b");getDtranStartEnd();for(int i=0;i<Dstates.size();i++){printf("\n");if(isDtranstart[i]==1)printf("start ");else if(isDtranend[i]==1)printf("end ");else printf(" ");printf("%5c ",i+'A');for(int j=1;j<=AlphabetNum;j++)printf("%5c ",Dtran[i][j]+'A');}printf("\nPrint simple DFA's Dtran:\n");simple();printf(" DFAstatu a b");for(int i=0;i<newDstates.size();i++){printf("\n");if(isnewDtranstart[i]==1)printf("start ");else if(isnewDtranend[i]==1)printf("end ");else printf(" ");printf("%5c ",i+'A');for(int j=1;j<=AlphabetNum;j++)printf("%5c ",newDtran[i][j]+'A');}printf("\n");char S[1000];while(scanf("%s\n",S)!=EOF){if(dfa(S)){printf("%s belongs to the DFA\n",S);}elseprintf("%s don't belong to the DFA\n",S);}return 0;}。
编译原理第三版 第三章 词法分析

超前搜索
例:FORTRAN语言中关键字的识别: DO99K=1,10 识别DO为关键字要搜 DO99K=1.10 索到“,” FORTRAN语言中常数的识别:
5.EQ.M, 5.E08
识别5为常数要搜索到Q
2、状态转换图
大多数程序设计语言中单词符号的词法规则可 以用正规文法描述。如: <标识符>→ 字母|<标识符>字母|<标识符>数字 <整数>→数字|<整数>数字 <运算符>→+|-|×|÷„ <界符>→; |, |( | )|„
#
3.3 正规表达式与有限自动机
目的: 形式化地描述词法规则和词法分析程序 词法分析程序的自动生成 主要内容 正规式与正规集 确定有限自动机 (DFA) 非确定有限自动机(NFA) 正规式与有限自动机的等价性 确定有限自动机的化简
正规文法
多数程序设计语言单词的语法都能用正规文法 (3型文法)描述 正规文法回顾 文法的任一产生式α→β的形式都为
单词符号的种类
(3) 常数 常数的类型一般有整型、实型、布 尔型、字符型等。
(4) 运算符 如 +,-,*,/等,对具体语言个 数是确定的。 (5) 界符 如 , ;()等,对具体语言个数是 确定的。
单词符号的表示形式
词法分析器所输出的单词符号常常表示成如下的 二元式:<单词种别,单词符号的属性值> 单词种别:由语法分析阶段使用的抽象符号。如: 用整数编码。 最简单的编码方案为一类一码,种别编码可设为: 1,2,3,4,5。 另一种编码方案(如本教材中): 标识符:列为一种,用一个整数编码表示; 常数:按类型分种编码; 关键字、运算符、界符:采用一字一种编码。
《编译原理实践及应用》第3章词法分析—DFA与NFA

其中 Κ ={ S 0 ,S1 ,S 2 } Σ ={a,b}
Ѕ={ S 0 , S1 } ( S0 ,a)={ S1 }
F={ S 2 }
( S 0 ,b)={ S 0 ,S 2 }
( S1 ,a)= Φ
(S1 ,b)={S 2 }
( S 2 ,a)= Φ
(S 2 ,b)={S1 }
②以每个非终结符号做其它状态
③对于形如Q→q的规则,
q
S
Q
对于形如Q→Rq的规则,
Rq Q
④以文法开始符号为终止状态。
例3-1: 文法G[Z]: Z→Za|Aa|Bb
aA
a
A→Ba|a B→Ab|b
Sb a
Za
b
Bb
2.应用状态转换图识别句子
识别句子:从开始状态到终止状态经过的边上的符号序列。 识别句子的步骤: ①从开始状态出发,以欲识别符号串的最左字符开始,寻找标
Z→Cb C→b|Bb B→Ab A→a|Ba
有限自动机(FA)
FA可看作一个机器模型,由一个带读头的有限控制器和 一条字符输入带组成。
#
a b a ba
…
输入带
控制器
工作原理:读头从左到右扫描输入带,读到一个字符,状态改
变,同时读头右移一个字符,…,直到读头读到
“#”,状态进入终止状态。
控制器中包括有限个状态,读入一个字符形成状态转换。
( S1 ,a)= S0 ( S1 ,c)= S3 ( S 2 ,b)= S1
( S3 ,b)= S3
a
b
S2 a
S0 a S1
ba
C
S3 b
定义: 所接收的语言(正则集)
L( AD)={β | S β S, S∈ F },
编译原理chapter3 词法分析
一 设计一个奇偶校验器
DFA是由集合,序列和函数定义的数学模型, 它对于 上的w,判定是可接受的还是不可 接受的。例如,设计一个DFA m ,奇偶校验 器,首先,w是由0,1组成的字符串,因此, 1. ={0 ,1}且w在一条输入带上。
0 1 0 1 1$
读头
精品文档
11
2. 状态集:它记忆已读入w子串的状态,m是 奇偶校验器,它应该记住,初始序列是奇数 个1还是偶数个1。因此,m有even和odd两个 状态. 3 .even为开始状态。
词法分析器
‘while’,‘i’,‘<>’,‘j’, ‘do’, ‘if’,‘i’,‘>’,‘j’,‘then’, 'i', ':=’ , 'i', ’-’ , 'j', 'else', 'j', ':=', 'j', '-', ‘i'
精品文档
4
词类和属性
computator n. Calcculating machine.
3.1.1 词法分析程序的功能 源程序 单词词序法列分析器
3.1.2 单词的词类和属性 (词类符号,单词的属性值)
3.1.3 词法分析程序作为一个独立子程序 (1)语法分析程序的子程序; (2)组 织成一遍扫描。
精品文档
3
While i<>j do if i>j then i:=i-j else j:=j-I
三 一个DFA有三种表示:
(1)象上面,用转换函数;
精品文档
14
转移矩阵
状态转换图
a
b
0
1
2
a
编译原理NFA的确定化优秀文档

(2)M的输入字母表∑M 和N′是相同的, 即∑M = ∑
(3)转换函数δM δM([S1 S2... Sj], a)
=ε-closure(move([S1, S2,... Sj],a))
即集合[S1 S2... Sj]的a弧转换
(4)M的初态 S0M = ε-closure(S0), 从N的初态S0出发, 经过任意条ε弧所能 到达的状态所组成的集合
(5)M的终态集合FM FM ={[Sj Sk... Se], 其中[Sj Sk... Se]∈SM 且 {Sj , Sk,,.Байду номын сангаас. Se}∩F≠φ },
即构造的子集族中凡是含有原NFA终态 的子集都是DFA的终态。
= {5, 4, 3, 6, 2, 7, 8}
而能到达的任何状态q′都属于 {
标记T;
(4)M的初态 S0M = ε-closure(S0),
有穷自动机等价的定义
ε_CLOSURE(I); 使状态转换图中的每条箭弧上的标记
= {5, 4, 3, 6, 2, 7, 8}
或为ε, 或为∑中的单个字母.
3 非确定有限自动机
补充例: NFA的确定化 – 子集法
确定化后的DFA也以状态转换图(矩阵)给出。
即: 把从S0出发经过一条标记为a的弧所能到达的状态(其前其后可经过若干条ε矢线)所组成的集合作为下一个状态置于SM中.
I={1, 5}, ε-closure(I)={1, 2, 5, 6}
补充例 :
I={1}, ε-closure(I)={1, 2} I={5}, ε-closure(I)={5, 6, 2} I={1, 5}, ε-closure(I)={1, 2, 5, 6}
编译原理

13
3.9直接从正则式到DFA
构造算法
实例 例3.37
得到的DFA状态比通过NFA得到的DFA状态少!
14
3.10 DFA最简化(3.9.6-3.9.7)
DFA最简化原理
最简DFA唯一性:每一个正则式可以由一个状态数最少
的DFA识别,且这个DFA唯一。 可行性:DFA存在不可区别状态,可以合并。 化简条件:确保DFA是全函数
8
3.9直接从正则式到DFA
构造原理
转换表:聚焦重要状态之间的转移 开始状态:可能出现在给定正则表达式描述的语言中任
何一个串第一个符号位置的所有重要状态。 接受状态:和结尾#相关的位置
9
3.9直接从正则式到DFA
构造算法
定义四个函数:nullable、firstpos、lastpos、
C b a B a b
开始
A
a
b
a
D
19
例 题 1
叙述下面的正则式描述的语言,并画出接受该语言 的最简DFA的状态转换图 (1|01)* 0*
描述的语言:所有不含子串001的0和1的串
1 0
1
.
start 1 刚读过的不是0 0 2 连续读过一个0 0 3 连续读过 不少于两个0
20
例 题 2
编译原理
第三章 词法分析
1
计算机科学与技术学院
3.8词法分析器生成工具的设计
词法分析器模型 图3.49
词法分析器工作方式
DFA模拟器 图3.27
NFA模拟器 图3.27
DFA转换表
NFA转换表
编译原理NFA转DFA

编译原理实验报告实验名称不确定有限状态自动机的确定化实验时间院系计算机科学与技术学院班级学号姓名1.试验目的输入:非确定有限(穷)状态自动机。
输出:确定化的有限(穷)状态自动机2.实验原理一个确定的有限自动机(DFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:(1)K是一个有穷非空集,集合中的每个元素称为一个状态;(2)∑是一个有穷字母表,∑中的每个元素称为一个输入符号;(3)F是一个从K×∑→K的单值转换函数,即F(R,a)=Q,(R,Q∈K)表示当前状态为R,如果输入字符a,则转到状态Q,状态Q称为状态R的后继状态;(4)S∈K,是惟一的初态;(5)Z⊆K,是一个终态集。
由定义可见,确定有限自动机只有惟一的一个初态,但可以有多个终态,每个状态对字母表中的任一输入符号,最多只有一个后继状态。
对于DFA M,若存在一条从某个初态结点到某一个终态结点的通路,则称这条通路上的所有弧的标记符连接形成的字符串可为DFA M所接受。
若M的初态结点同时又是终态结点,则称ε可为M所接受(或识别),DFA M所能接受的全部字符串(字)组成的集合记作L(M)。
一个不确定有限自动机(NFA)M可以定义为一个五元组,M=(K,∑,F,S,Z),其中:(1)k是一个有穷非空集,集合中的每个元素称为一个状态;(2)∑是一个有穷字母表,∑中的每个元素称为一个输入符号;(3)F是一个从K×∑→K的子集的转换函数;(4)S⊆K,是一个非空的初态集;(5)Z⊆K,是一个终态集。
由定义可见,不确定有限自动机NFA与确定有限自动机DFA的主要区别是:(1)NFA的初始状态S为一个状态集,即允许有多个初始状态;(2)NFA中允许状态在某输出边上有相同的符号,即对同一个输入符号可以有多个后继状态。
即DFA中的F是单值函数,而NFA中的F是多值函数。
因此,可以将确定有限自动机DFA看作是不确定有限自动机NFA的特例。
编译原理-第3章 词法分析--习题答案

第3章词法分析习题答案1.判断下面的陈述是否正确。
(1)有穷自动机接受的语言是正规语言。
(√)(2)若r1和r2是Σ上的正规式,则r1|r2也是Σ上的正规式。
(√)(3)设M是一个NFA,并且L(M)={x,y,z},则M的状态数至少为4个。
(× )(4)设Σ={a,b},则Σ上所有以b为首的符号串构成的正规集的正规式为b*(a|b)*。
(× )(5)对任何一个NFA M,都存在一个DFA M',使得L(M')=L(M)。
(√)(6)对一个右线性文法G,必存在一个左线性文法G',使得L(G)=L(G'),反之亦然。
(√) (7)一个DFA,可以通过多条路识别一个符号串。
(× )(8)一个NFA,可以通过多条路识别一个符号串。
(√)(9)如果一个有穷自动机可以接受空符号串,则它的状态图一定含有 边。
(× )(10)DFA具有翻译单词的能力。
(× )2.指与出正规式匹配的串.(1)(ab|b)*c 与后面的那些串匹配?ababbc abab c babc aaabc(2)ab*c*(a|b)c 与后面的那些串匹配? acac acbbc abbcac abc acc(3)(a|b)a*(ba)* 与后面的那些串匹配? ba bba aa baa ababa答案(1) ababbc c babc(2) acac abbcac abc(3) ba bba aa baa ababa3. 为下边所描述的串写正规式,字母表是{0, 1}.(1)以01 结尾的所有串(2)只包含一个0的所有串(3) 包含偶数个1但不含0的所有串(4)包含偶数个1且含任意数目0的所有串(5)包含01子串的所有串(6)不包含01子串的所有串答案注意 正规式不唯一(1)(0|1)*01(2)1*01*(3)(11)*(4)(0*10*10*)*(5)(0|1)*01(0|1)*(6)1*0*4.请描述下面正规式定义的串. 字母表{x, y}.(1) x(x|y)*x(2)x*(yx)*x*(3) (x|y)*(xx|yy) (x|y)*答案(1)必须以 x 开头和x结尾的串(2)每个 y 至少有一个 x 跟在后边的串 (3)所有含两个相继的x或两个相继的y的串5.处于/* 和 */之间的串构成注解,注解中间没有*/。
编译原理NFA转化为DFA的转换算法及实现

编译原理NFA转化为DFA的转换算法及实现编译原理是研究计算机程序语言的一门学科,其中一项重要的内容就是自动机理论,包括NFA(非确定性有限自动机)和DFA(确定性有限自动机)的转换。
NFA到DFA转换算法的实现分为几个关键步骤,下面将逐一进行介绍。
首先,我们需要了解NFA和DFA的基本概念。
NFA是一种具有状态、输入字母表和状态转移函数的自动机模型,允许多个状态同时转移到其他状态。
而DFA则是一种状态转移函数确定的自动机模型,每个输入字符只能引发一条状态转移。
接下来,我们将介绍NFA到DFA的转换算法。
1. 子集构造法(Subset Construction)子集构造法是将NFA转化为DFA的一种常用算法。
该算法的基本思想是,将NFA的每个状态集表示为DFA的状态。
转换过程如下:-创建DFA的初始状态集,初始状态集即为NFA的初始状态的ε闭包。
-逐个处理DFA的状态集,对于每个状态集,针对输入字符进行转移,计算新的状态集的ε闭包。
-若新的状态集已存在于DFA中,则不需要再次处理,若不存在,则将其加入到DFA中。
-迭代上述步骤,直至没有新的状态集加入。
2. ε闭包(ε-closure)ε闭包是指在NFA中的一些状态集S中,能够通过连续零个或多个ε转移到达的状态集合。
在转换过程中,需要计算新的状态集的ε闭包,来确定DFA的状态集。
具体步骤如下:-初始化ε闭包为输入的状态集S。
-对于S中的每个状态,获取其所有的ε转移目标状态,并将其添加到ε闭包中。
-重复上述步骤,直到ε闭包不再发生变化为止。
3. 状态转移(Transition)在NFA中,状态可以同时转移到多个状态。
而在DFA中,每个状态只能转移到一个状态。
因此,在转换过程中,需要确定每个状态在一些输入字符下的转移目标。
-对于每个状态集S、输入字符a,计算S在输入字符a下的转移目标状态集,即计算S中每个状态通过输入字符a能够到达的状态集。
-根据计算的转移目标状态集,将其作为DFA中S状态在输入字符a下的转移目标。
编译原理nfa-dfa
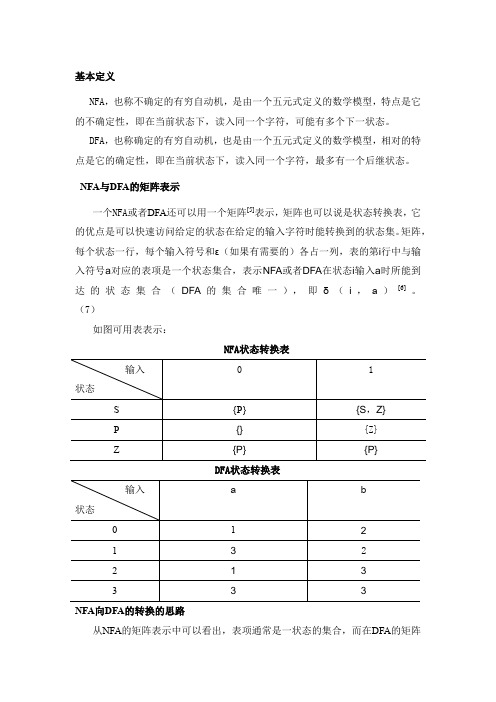
基本定义NFA,也称不确定的有穷自动机,是由一个五元式定义的数学模型,特点是它的不确定性,即在当前状态下,读入同一个字符,可能有多个下一状态。
DFA,也称确定的有穷自动机,也是由一个五元式定义的数学模型,相对的特点是它的确定性,即在当前状态下,读入同一个字符,最多有一个后继状态。
NFA与DFA的矩阵表示一个NFA或者DFA还可以用一个矩阵[5]表示,矩阵也可以说是状态转换表,它的优点是可以快速访问给定的状态在给定的输入字符时能转换到的状态集。
矩阵,每个状态一行,每个输入符号和ε(如果有需要的)各占一列,表的第i行中与输入符号a对应的表项是一个状态集合,表示NFA或者DFA在状态i输入a时所能到达的状态集合(DFA的集合唯一),即δ(i,a)[6]。
(7)如图可用表表示:NFA状态转换表DFA状态转换表NFA向DFA的转换的思路从NFA的矩阵表示中可以看出,表项通常是一状态的集合,而在DFA的矩阵表示中,表项是一个状态,NFA到相应的DFA的构造的基本思路是:DFA的每一个状态对应NFA的一组状态DFA使用它的状态记录在NFA读入一个输入符号后可能达到的所有状态[4]。
NFA和DFA之间的联系在非确定的有限自动机NFA中,由于某些状态的转移需从若干个可能的后续状态中进行选择,故一个NFA对符号串的识别就必然是一个试探的过程。
这种不确定性给识别过程带来的反复,无疑会影响到FA的工作效率。
而DFA则是确定的,将NFA转化为DFA将大大提高工作效率,因此将NFA转化为DFA是有其一定必要的。
子集构造法已证明:非确定的有限自动机与确定的有限自动机从功能上来说是等价的,也就是说,我们能够从:NFA M使得L(M)=L(M’)为了使得NFA确定化,我们首先给出两个定义:定义1:集合I的ε-闭包:令I是一个状态集的子集,定义ε-closure(I)为:1)若s∈I,则s∈ε-closure(I);2)若s∈I,则从s出发经过任意条ε弧能够到达的任何状态都属于ε-closure(I)。
编译原理第二版第3章词法分析

1. ε和φ都是∑上的正规式,它所表示的正规集分
别为{ε}和Ф; 2. 任何a∈∑,a是∑上的正规式,它所表示的正 规集为{a}; 3. 假定e1和e2都是∑上的正规式,他们所表示的 正规集分别为L(e1)和L(e2),那么,以下也 都是正规式和他们所表示的正规集;
一、正规式与正规集的递归定义
3.2 单词符号及输出单词的形式
单词自身值
对常数,基本字,运算符,界符就是他们本 身的值 对标识符,将标识符的名字登记在符号表中, ‚自身值‛是指向该标识符所在符号表中位 置的指针。
假定基本字、运算符和界符都是一符一种 例:if(a>1) b=100; 词法分析后输出的单词序列是: (2, ) if (29, ) ( (10,‘a’) a (23, ) > (11,‘1’) 1 (30, ) ) (10,’b’) b (17, ) = (11,‘100’) 100 (26, ) ;
4. 仅由有限次使用上述三步定义的表达式才是∑上的 正规式,仅由这些正规式所表示的字集才是∑上 的正规集。
重点回顾
四、将正规文法转换成正规式 求非终结符的正规式 将正规文法中的每个非终结符表示成关 于它的一个正规式方程,获得一个联立 方程组 用代入法解正规式方程组 最后只剩下一个开始符号定义的正规式, 其中不含非终结符
3.3 语言单词符号的两种定义方式
作用: 描述单词的构成规则,基于这类描 述工具建立词法分析技术,进而实现词法 分析程序的自动构造。 工具有: 正规文法 正规式(Regular Expression)
多数程序设计语言的单词符号都能用正 规文法或正规式来定义。
3.3.1 正规文法
多数程序设计语言单词的语法都能用正 规文法(3型文法)描述 正规文法回顾 文法的任一产生式α →β 的形式都为 A→aB或A→a,其中A ,B∈VN ,a∈VT A→Ba或A→a,其中A ,B∈VN ,a∈ VT 正规文法描述的是VT*上的正规集
DFA与NFA

词法分析(1)---词法分析的有关概念以及转换图词法分析是编译的第一个阶段,前面简介中也谈到过词法分析器的任务就是:字符流------>词法记号流这里词法分析和语法分析会交错进行,也就是说,词法分析器不会读取所有的词法记号再使用语法分析器来处理,通常情况下,每取一个词法记号,就送入语法分析器进行分析,图解:词法分析器是编译器中与源程序直接接触的部分,因此词法分析器可以做诸如1). 去掉注释,自动生成文档(c#中的///注释)2). 提供错误位置(可以通过记录行号来提供),当字符流变成词法记号流以后,就没有了行的概念3). 完成预处理,比如宏定义1. 词法记号,词法单元(lexeme),模式模式是一种规则每个词法单元都有一个特定记号比如 int a=3,这里 int,a,=,3都是词法单元,每个词法单元都属于某个词法记号,比如3就是"num"这个词法记号的一个词法单元,而模式规定了什么样的字符串的词法记号是什么样的(模式是一种规则)某一特定模式规定了某个词法记号下的一类词法单元,比如:模式:用字母开头的包含字母和数字的串上面模式的词法记号:id(所有符合上面模式的字符串的记号都是id)词法单元:a123 或者 aabc 等词法记号举例(简称为记号):1) 每个的关键字都有属于自己的一个记号,比如关键字for,它可以使用记号f or;关键字int,可以使用记号int2) 所有的关系运算符只有一个记号,比如 >=,<=都用记号relation3) 所有的标识符只有一个记号,比如a123,aab使用记号id4) 所有的常数只有一个记号,比如123,22,32.3,23E10使用记号num5) 所有的字符串只有一个记号,比如"123","ab1"使用记号literal在实际的编译器设计中,词法记号,一般用一个整形数字表示词法记号的属性:我们喜欢用<词法记号, 属性>这个二元组来描述一个词法单元,比如,对于源代码:position := initial + rate * 60对于词法单元 +,我们可以使用 <add_op, '+'> 来表示。
编译原理第3章课后习题答案

Dtran[I,b] =ε-closure(move(I,b))= ε-closure({5, 16})=G DFA D 的转换表 Dtran NFA 状态 {0,1,2,4,7} {1,2,3,4,6,7,8} {1,2,4,5,6,7} {1,2,4,5,6,7,9} {1,2,4,5,6,7,10,11,12,13,15} {1,2,3,4,6,7,8,12,13,14,15,17,18} {1,2,4,5,6,7, 12,13,15,16,17,18} {1,2,4,5,6,7, 9,12,13,15,16,17,18} {1,2,4,5,6,7, 10,11,12,13,15,16,17,18} 可得 DFA 的如下状态转换图: DFA 状态 A B C D E F G H I a B B B B F F F F F b C D C E G H G I G
3.3.1 给出 3.2.2 中正则表达式所描述的语言的状态转换图。
(1)a( a|b )*a 的状态转换图如下:
(2)
ε
ε a
b
(3)
a
start 0
a a a
1 2
4
b a b
5
b b
3
6
7
(4)a*ba*ba*ba*
a b
a b
a b
a
3.6.3 使用算法 3.25 和 3.20 将下列正则表达式转换成 DFA: (1)
注:consonant 为除五元音外的小写字母,记号 ctnvowels 对应的定义即为题目要求的正则
定义。
(2) 所有由按字典顺序递增序排列的小写字组成的串。 a*b*……z* (3)注释,即/*和*/之间的串,且串中没有不在双引号( “)中的*/。 head——>/* tail ——>*/ * * incomment->(~(*/)|“. ”) comment->head incomment tail (9)所有由 a 和 b 组成且不含有子串 abb 的串。 * * A->b (a︱ab)
编译原理第3章第1节词法分析、DFA、NFA及其转换
单词经常表示为二元组:(单词类别,单词值) 对某些单词来说,不仅需要它们的值,还需要一些其它信息,
这些都记录在符号表中,所以相应表示为:(标识符,指向该标 识符所在符号表中位置的指针)
(单词类别,单词的属性)
区分单词所属的类 (整数编码)
单词的值
3.1.1 单词符号的表示
单词的表示:举例
(1)剔除无用的空白符、跳格符、回车符、换行符。 ‘ ‘, ‘\t’, ‘\r’, ‘\n’
(2)剔除注释:/*…………*/, //
(3)合并空白符。
3.1.2 词法分析器的结构
预处理程序
例:
int max(int x, int y) // 求x,y的最大值 {
int z; z = (x > y ? x : y); return z; }
语法分析器
使整个编译程序的结构更简洁、清晰和条理化; 编译程序效率更高; 增强编译程序的可移植性。
符号表
3.1.2 词法分析器的结构
扫描缓冲区
1.预处理程序:取消注解,剔除无用的空白、 跳格、回车、换行等 2.输入缓冲区:源程序输入缓冲区
3.1.2 词法分析器的结构
预处理程序
主要是为方便单词的识别工作:
仅由有限次使用上述三步骤得到的表达式才是正规式,仅由这些正 规式所表示的字集才是∑上的正规集。
例3.1 令∑={a,b}
ba*
∑上所有以b为首,后跟任意多个a的字符串;
a(a|b)* ∑上所有以a为首的字符串;
(a|b)*(aa|bb)(a|b)* ∑上含两个连续a或两个连续b的字符串。
第三章 词法分析
源程序
词法分析
语法分析
编译实验三NFA转换成DFA和DFA化简要点

编译实验三NFA转换成DFA和DFA化简要点NFA转换成DFA是正则表达式、有限自动机以及编译原理等课程的重要内容之一、本文将从NFA的定义、转换方法和DFA化简方法这三个方面进行详细讲解。
一、NFA的定义有限自动机(NFA)是一种图形化工具,用于描述正则表达式的结构和过程。
它由状态集合、输入字母表、状态转换函数和初始状态、接受状态组成。
1. 状态集合:NFA的状态集合是有限的,用Q表示,可以表示为{q1, q2, ..., qn}。
2. 输入字母表:NFA的输入字母表是有限的,用Σ表示,可以表示为{a1, a2, ..., am}。
3.状态转换函数:NFA的状态转换函数是从状态集合到状态集合的映射,用δ表示,可以表示为δ:Q×Σ→2^Q,即对于状态q和输入a,转换函数δ(q,a)表示从状态q经过输入a可能到达的一组状态。
4.初始状态:NFA的初始状态是一个状态,用q0表示,它属于状态集合Q。
5.接受状态:NFA的接受状态是一组状态,用F表示,属于状态集合Q。
二、NFA转换成DFA的方法将NFA转换成DFA是为了更方便地处理和理解正则表达式。
下面介绍两种常用的NFA转DFA的方法:子集法和马勒机法。
1.子集法:子集法是NFA转DFA的一种常用方法。
具体步骤如下:(1)根据NFA的接受状态构造DFA的接受状态。
(2)以NFA的初始状态为起点,利用状态转换函数生成新的状态。
(3)重复第二步,直到没有新状态为止。
2.马勒机法:马勒机法是NFA转DFA的另一种常用方法。
具体步骤如下:(1)将NFA的状态集合拆分成两组,一组是NFA接受状态的集合,另一组是其余状态的集合。
(2)建立一个新的DFA状态对应于每一组。
(3)将NFA状态转换函数进行转换,使得DFA状态和输入字母的组合对应一个新的DFA状态。
三、DFA化简方法对于转换完成的DFA,为了提高运行效率和降低资源消耗,一般需要进行化简,即将等价的状态合并为一个。
词法分析NFA到DFA

#include<iostream>#include<stack>#include<sstream>#include<vector>#include<queue>#include<set>using namespace std;class NFA_Node;class Trans{public:char incept;NFA_Node* des;Trans(char incept,NFA_Node* des){this->incept=incept;this->des=des;}};class NFA_Node{public:int stateID;vector<Trans*> t;bool visit;NFA_Node(int stateID){visit=false;this->stateID=stateID;}void AddTrans(Trans* tt){t.push_back(tt);}};class NFA{public:NFA_Node* start;NFA_Node* end;NFA(){}NFA(int SID,char c){NFA_Node* s1=new NFA_Node(SID);NFA_Node* s2=new NFA_Node(SID+1);Trans* tt=new Trans(c,s2);s1->AddTrans(tt);start=s1;end=s2;}};class Converter{public:int S_ID;Converter(string str){pretreat(str);Houzhui(this->lamb);S_ID=1;}Converter(){S_ID=1;}void show(){cout<<this->lamb<<endl;}NFA ToNFA(){//stNFA.Clear();//Operator_Stack.Clear();NFA tempb,tempb1,tempb2;char tempc1;for(int i=0;i<lamb.size();i++){tempc1 = lamb[i];if (isOperator(tempc1)){switch (tempc1){case '|':tempb1 = stNFA.top();stNFA.pop();tempb2 = stNFA.top();stNFA.pop();tempb1=Union(tempb2,tempb1);stNFA.push(tempb1);break;case '&':tempb1 = stNFA.top();stNFA.pop();tempb2 = stNFA.top();stNFA.pop();tempb2=Connect(tempb1,tempb2);stNFA.push(tempb2);break;case '*':tempb1 = stNFA.top();stNFA.pop();tempb1=Closure(tempb1);stNFA.push(tempb1);break;}}else{tempb = NFA(S_ID,tempc1);S_ID+=2;stNFA.push(tempb);}}tempb = stNFA.top();stNFA.pop();return tempb;}private:stack<NFA> stNFA;stack<char> Operator_Stack;string lamb;bool isOperator(char c){switch (c){case '|':case '&':case '(':case ')':case '!':case '*': return true;default: return false;}}int getOperatorNumber(char t1){switch (t1){case '$': return 0;case '!': return 1;case ')': return 2;case '|': return 3;case '&': return 4;case '*': return 5;case '(': return 6;default: return 7;}}bool Operator_Less_Than(char t1, char t2){int temp1 = getOperatorNumber(t1);int temp2 = getOperatorNumber(t2);if (temp1 <= temp2)return true;return false;}void pretreat(string str)//穿进去原始正则表达式使ab变成a&b {int i=0;char c,pc;pc=str[i];c=str[++i];while(str[i]!='\0'){if(((pc==')'&&c=='('))||(!isOperator(pc)&&!isOperator(c))||(!isOperator(pc)&&c=='(')||(pc==' )'&&!isOperator(c))||(pc=='*'&&!isOperator(c))||(pc=='*'&&c=='('))//四种情况需要加&str.insert(i,"&");pc=str[i++];c=str[i];}str+="!";this->lamb=str;}void Houzhui(string lamb){string l="";Operator_Stack.push('$');char tempc,tempc2;for(int i=0;i<lamb.size();i++){tempc = lamb[i];if (isOperator(tempc)){switch (tempc){case '(': Operator_Stack.push(tempc); break;case ')':while (Operator_Stack.top() != '('){tempc2 = Operator_Stack.top();Operator_Stack.pop();l += tempc2;}Operator_Stack.pop();break;default :tempc2 = Operator_Stack.top();while (tempc2!='('&&Operator_Less_Than(tempc,tempc2)){tempc2 = Operator_Stack.top();Operator_Stack.pop();l += tempc2;tempc2 = Operator_Stack.top();}Operator_Stack.push(tempc);break;}}elsel += tempc;}this->lamb=l;}NFA& Connect(NFA G1, NFA G2) //把G1连在G2后面{Trans* t=new Trans('@',G1.start);G2.end->AddTrans(t) ;G2.end = G1.end;return G2;}NFA& Union(NFA G1, NFA G2) //G1|G2{NFA_Node* n1=new NFA_Node(S_ID++);Trans* t1=new Trans('@',G1.start);Trans* t2=new Trans('@',G2.start);n1->AddTrans(t1);n1->AddTrans(t2);NFA_Node* n2=new NFA_Node(S_ID++);Trans* t3=new Trans('@',n2);Trans* t4=new Trans('@',n2);G1.end->AddTrans(t3);G2.end->AddTrans(t4);NFA* G=new NFA();G->start=n1;G->end=n2;return *G;}NFA& Closure(NFA G2) //G2*{Trans* t=new Trans('#',G2.start);//#表示是重复的空输入G2.end->AddTrans(t);NFA_Node* n1=new NFA_Node(S_ID++);Trans* t1=new Trans('@',n1);G2.end->AddTrans(t1);NFA_Node* n2=new NFA_Node(S_ID++);Trans* t2=new Trans('@',G2.start);n2->AddTrans(t2);Trans* t3=new Trans('@',n1);n2->AddTrans(t3);NFA* G=new NFA();G->start=n2;G->end=n1;return *G;}};void Display(NFA &G,set<char> &S,vector<NFA_Node*> &V){cout<<"正则表达式转NFA"<<endl;queue<NFA_Node*> MyQueue;MyQueue.push(G.start);cout<<"开始状态"<<G.start->stateID<<endl;char tt;while(!MyQueue.empty()){NFA_Node* tmp=MyQueue.front();MyQueue.pop();V.push_back(tmp);tmp->visit=true;if(tmp->t.size()>0)cout<<"从状态"<<tmp->stateID<<"出发"<<endl;if(tmp->t.size()>0)for(int i =0;i<tmp->t.size();i++){tt=tmp->t[i]->incept;if(tt!='@'&&tt!='#')S.insert(tt);if(tt=='@'){cout<<tmp->stateID<<"---"<<"epsilon"<<"--->"<<tmp->t[i]->des->stateID;if(tmp->t[i]->des->t.size()==0) cout<<"接收状态";cout<<endl;if(tmp->t[i]->des->visit==false){MyQueue.push(tmp->t[i]->des);tmp->t[i]->des->visit=true;}}else if(tt=='#'){cout<<tmp->stateID<<"---"<<"epsilon回到"<<"--->"<<tmp->t[i]->des->stateID<<endl;}else{cout<<tmp->stateID<<"---"<<tt<<"--->"<<tmp->t[i]->des->stateID;if(tmp->t[i]->des->t.size()==0) cout<<"接收状态";cout<<endl;if(tmp->t[i]->des->visit==false){MyQueue.push(tmp->t[i]->des);tmp->t[i]->des->visit=true;}}}}cout<<"接收状态"<<G.end->stateID<<endl;}class DFA_Edge;class DFA_Node{public:int stateID;vector<DFA_Edge*> t;vector<int> ori;bool flag;DFA_Node(int s){flag=false;stateID=s;}};class DFA_Edge{public:char incept;DFA_Node* des;bool visit;DFA_Edge(char a,DFA_Node* &b){incept=a;des=b;visit=false;}};const int MAX=100;class NFA_To_DFA{public:int MaxStatus;int T[MAX][MAX];int visit[MAX];vector<NFA_Node*> tmp;set<char> Alpha;vector<NFA_Node*> nfa;NFA_Node* start;vector<DFA_Node*> dfa;int cando;//存NFA的接收状态NFA_To_DFA(int max,NFA_Node* &S,int cando){this->MaxStatus=max;this->start=S;this->cando=cando;Init();for(int i=0;i<=MAX;i++)for(int j=0;j<=MAX;j++)T[i][j]=0;}void Init(){for(int i=0;i<=this->MaxStatus;i++){this->visit[i]=0;}this->tmp.clear();}NFA_Node*& find(int st){for(int i=0;i<nfa.size();i++)if(nfa[i]->stateID==st) return nfa[i];}DFA_Node*& finddfa(int st){for(int i=0;i<dfa.size();i++)if(dfa[i]->stateID==st) return dfa[i];}void findclosure(NFA_Node* p){visit[p->stateID]=1;visit[0]++;if(p->t.size()==0) return;for(int i=0;i<p->t.size();i++){if(!visit[p->t[i]->des->stateID]&&(p->t[i]->incept=='#'||p->t[i]->incept=='@')) findclosure(p->t[i]->des);}}void closure(){for(int i=0;i<tmp.size();i++){findclosure(tmp[i]);}}int AddStatus()//T[0][0]当前状态集合数初始为0{if(visit[0]==0)//表示没有状态return -2;for(int i=1;i<=T[0][0];i++){if(visit[0]!=T[i][0])//此集合状态数不一样则跳过continue;int j=1;for(;j<=MaxStatus;j++)if(visit[j]!=T[i][j])//有一个状态不一样则跳过break;if(j==(MaxStatus+1)) //说明矩阵T中已有此集合,并返回位置return i;}T[0][0]++;for(int i=0;i<=MaxStatus;i++)T[T[0][0]][i]=visit[i];// cout<<T[T[0][0]][0];return -1;}//返回-1表示插入了新状态集合void moveto(int st,char c){// if(st==2) cout<<T[st][0]<<endl;for(int i=1;i<=MaxStatus;i++){if(T[st][i]){NFA_Node* p=find(i);if(p->t.size()>0)for(int j=0;j<p->t.size();j++)if(p->t[j]->incept==c){tmp.push_back(p->t[j]->des);}//cout<<c<<" "; cout<<p->t[j]->des->stateID<<endl;}}}}void Convert(){int i,j;findclosure(start);AddStatus();DFA_Node* s1=new DFA_Node(1);if(visit[cando]) s1->flag=true;for(i=1;i<=MaxStatus;i++)if(visit[i]) s1->ori.push_back(i);dfa.push_back(s1);Init();//cout<<Alpha.size();for(i=1;i<=T[0][0];i++)//i目前的状态集合号{for(set<char>::iterator t1=Alpha.begin();t1!=Alpha.end();t1++){moveto(i,*t1);closure();if((j=AddStatus())>=0)//没有新状态产生{DFA_Edge* e1=new DFA_Edge(*t1,finddfa(j));finddfa(i)->t.push_back(e1);}else if(j==-1)//产生了新状态{DFA_Node* d1=new DFA_Node(T[0][0]);if(visit[cando]) d1->flag=true;//是否是接收状态for(int tt=1;tt<=MaxStatus;tt++)if(visit[tt]) d1->ori.push_back(tt);//把原状态加进去dfa.push_back(d1);DFA_Edge* e1=new DFA_Edge(*t1,finddfa(T[0][0]));finddfa(i)->t.push_back(e1);// cout<<T[0][0]<<endl;}Init();}}}void show(DFA_Node* p){if(p->ori.size()==0) return;cout<<"(原状态";for(int i=0;i<p->ori.size();i++)cout<<p->ori[i];cout<<")";}void Display(){cout<<"NFA转DFA"<<endl;for(int i=0;i<dfa.size();i++)dfs(dfa[i]);}void dfs(DFA_Node* &p){if(p->t.size()>0)for(int i=0;i<p->t.size();i++)if(p->t[i]->visit==false){cout<<p->stateID;if(p->flag) cout<<"(接收状态)";show(p);cout<<"---"<<p->t[i]->incept<<"--->"<<p->t[i]->des->stateID;show(p->t[i]->des);if(p->t[i]->des->flag) cout<<"(接收状态)";cout<<endl;p->t[i]->visit=true;dfs(p->t[i]->des);}}};int main(){string str;char s[100];while(gets(s)){str=s;Converter cnt(str);// cnt.show();NFA result=cnt.ToNFA();NFA_To_DFA ntd(cnt.S_ID-1,result.start,result.end->stateID);// cout<<result.start->stateID;// cout<<result.start->t.size();Display(result,ntd.Alpha,ntd.nfa);ntd.Convert();ntd.Display();}while(1); }。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.1 单词符号的表示
单词的分类
单词分类的原则
❖ 保留字(关键字):可以看作一类,也可以一字一类; ❖ 算符和界符:可以一符一类,算符还可以把有一定共性算
符分为一类; ❖ 常数:可以按照数据类型分类; ❖ 标识符:统一归为一类。
3.1.1 单词符号的表示
语法分析器
使整个编译程序的结构更简洁、清晰和条理化; 编译程序效率更高; 增强编译程序的可移植性。
符号表
3.1.2 词法分析器的结构
扫描缓冲区
1.预处理程序:取消注解,剔除无用的空白、 跳格、回车、换行等 2.输入缓冲区:源程序输入缓冲区
3.1.2 词法分析器的结构
预处理程序
❖主要是为方便单词的识别工作:
int
3056
int
3060
3.1.2 词法分析器的结构
词法分析器与语法分析器的联系
(1)词法分析作为单独的一遍
字符
字符串形式的源程序
词法分析器
单词串形式的源程序
3.1.2 词法分析器的结构
词法分析器与语法分析器的联系
(2)词法分析作为子程序
输入串
词法分析器
返
取
回
下
下
一
一
单
单
词
词
将词法分析器分离的考虑
例3.1 令∑={a,b}
正规式 a a|b ab (a|b)(a|b) a* (a|b) * (a|b) *(aa|bb) (a|b) *
缓冲区长度:256
缓冲区长度:256
标识符起 搜索指 点(252) 示器
小结
❖词法分析器的任务; ❖单词符号的分类; ❖单词符号的表示; ❖词法分析预处理; ❖词法分析器的工作方式; ❖扫描缓冲区的双缓冲策略。
3.2.1 正规式与正规集
正规式和正规表达式
正规式(正规表达式):用以描述单词符号的工 具,是说明单词的模式的一种重要的表示法, 是定 义正规集的工具。
仅由有限次使用上述三步骤得到的表达式才是正规式,仅由这些正规式 所表示的字集才是∑上的正规集。
例3.1 令∑={a,b}
ba*
∑上所有以b为首,后跟任意多个a的字符串;
a(a|b)* ∑上所有以a为首的字符串;
(a|b)*(aa|bb)(a|b)* ∑上含两个连续a或两个连续b的字符串。
3.2.1 正规式与正规集
(1)剔除无用的空白符、跳格符、回车符、换行符。 ‘ ‘, ‘\t’, ‘\r’, ‘\n’
(2)剔除注释:/*…………*/, //
(3)合并空白符。
3.1.2 词法分析器的结构
预处理程序
例:
int max(int x, int y) // 求x,y的最大值 {
int z; z = (x > y ? x : y); return z; }
预处理后: int max(int x,int y) {int z; z=(x>y ? x : y); return z;}
3.1.2 词法分析器的结构
缓冲区的设计
扫描缓冲区:从输入缓冲区输入固定长度的字符串到另一个缓冲区(扫 描缓冲区),词法分析可以直接在此缓冲区中进行符号识别。扫描缓冲 区的结构:
例:while (i >=j) i--; 输出:
编号 类别
(3, “while”)
1
标识符
(5, “(“)
2
常数
(1, 指向i的符号表入口)
3
保留字
(4, “>=“)
4
算符
(1, 指向j的符号表入口)
5
界符
(5, “)”)
(1, 指向i的符号表入口)
(4, “--”)
(5, “;”)
数据类型 存储地址
单词的表示
单词经常表示为二元组:(单词类别,单词值) 对某些单词来说,不仅需要它们的值,还需要一些其它信息,
这些都记录在符号表中,所以相应表示为:(标识符,指向该标 识符所在符号表中位置的指针)
(单词类别,单词的属性)
区分单词所属的类 (整数编码)
单词的值
3.1.1 单词符号的表示
单词的表示:举例
起点指针:用来指示正在扫描的单词的起点; 搜索指针:用于向前搜索,寻找单词的结束; 缓冲区结构
假设标识符和常数的最大长度为256
缓冲区长度:512
标识符起 搜索指 点(500) 示器
3.1.2 词法分析器的结构
缓冲区的设计
:设置左右两个缓冲区,当左缓冲区读完后,新读入的字符存 入右缓冲区;反之,存放在左缓冲区;Βιβλιοθήκη 3.1.1 单词符号的表示
单词的分类
单词的分类,如:while (i < 10) i++;
❖ 基本字:也称关键字,如C语言中的int, void, if, while等; ❖ 标识符:用来表示各种名字,如变量名、常量名、函数名等; ❖ 常数:如25, 3.1415926, ‘a’, “hello”, TRUE等; ❖ 算符:如+, =, ~等; ❖ 界符:如逗号,分号,括号等。 ❖ 基本字、运算符和界符一般确定; ❖ 标识符和常数的数量一般不加限制。 注: (1)程序设计语言单词的分类纯属技术性问题,可以有不同的方法
第三章 词法分析
源程序
词法分析
语法分析
表
格
语义分析
管
理
中间代码生成
错 误 检 测
代码优化
目标代码生成 目标程序
第三章 词法分析
主要内容
1.介绍词法分析的过程 2.讨论词法分析器的设计与实现 3.介绍实现词法分析器的主要工具:状态转换图
3.1 词法分析器的任务
❖ 人们理解一篇文章(或程序)起码是先在单词级别上思考。
一个正规式对应一个正规集
3.2.1 正规式与正规集
正规式和正规表达式
对字母表∑:
(1) ε和Φ都是∑上的正规式,它们所表示的正规集分别为{ε}和Φ;
(2) a∈∑,a是∑上的一个正规式,它所表示的正规集为{a};
(3) 假定U和V都是∑上的正规式,它们所表示的正规集分别记为L(U)和L(V), 那么(U|V)、(UV)和(U)*也是正规式,它们所对应的正规集分别为 L(U)∪L(V)、L(U)L(V)和(L(U))*。
❖ 编译程序要分析和翻译源程序,也先要区分一个一个的单词。
❖ 词法分析程序的任务是:从左到右逐个字符对源程序扫描,产生一 个单词序列,把作为字符串的源程序改造为单词符号串的中间程序。
❖ 词法分析程序又称词法分析器或扫描器。
除了识别单词的基本任务外,词法分析还可以完成以下任务: (1)组织源程序的输入 (2)删除注释、空格及无用符号(如回车等) (3)行、列计数 (4)列表打印源程序 (5)发现并定位词法错误 (6)建立、查填符号表
