信息论与编码理论-信道编码-线性分组码1
合集下载
信息论与编码(第三版) 第6章 信道编码理论
信号无失真传 输条件：通频 带内系统增益 为常数；相位 为线性(群延时
相等)
❖ 信号差错的指标通常用概率大小表征，符号差错概率 也称为误码元率，是指信号差错的概率；
❖ 误比特率则是表示信息差错概率的一种方法 ；
❖ 对于M进制码元，差图样E为
E (C R)(mod M )
❖ 二进制码而言 E CR
2需要反馈信道， 占用额外频率资源
二、前向纠错方式（FEC）
检测 结果
发送端
信道
接收端
发送
纠错码
接收码字
根据编译 码规则
Y 错误
N
译码 规则 纠错
纠错能力足够好，能够纠 正信道引入的数据错误
输出信息
优点 不足
1.不需要反馈信道，能够实现一对多的同 步广播通信 2.译码实时性好，控制电路比ARQ也简 单 由于假设纠错码的纠错能力足够纠正信息序 列传输中的错误，也就是纠错码与信道的干 扰是相匹配的，所以对信道的适应性较差
❖ 差错图样中的1就是符号差错，同时也是比特差错，而差错 的个数就是汉明距离。
C (1010)
R (0011)
E C R (1001)
一、功能
纠错码的分类
检测码
纠错码
只检测信息传输是否出现错 误，本身没有纠错的能力
不仅能够检测信 息传输中的错误，
并且能够自动纠
循环冗余校验码、 奇偶校验码等
信号传输过程中出现大的 信号波形畸变，导致信号 检错时发生错误，进而出 现 码元错误
叠加强的干扰 或者噪声
信号传输过程 中出现线性或 者非线性失真
线性失真
信号传输过程中不同的频率 分量增益不同，或者由于非
线性相位引起的延时不同
相等)
❖ 信号差错的指标通常用概率大小表征，符号差错概率 也称为误码元率，是指信号差错的概率；
❖ 误比特率则是表示信息差错概率的一种方法 ；
❖ 对于M进制码元，差图样E为
E (C R)(mod M )
❖ 二进制码而言 E CR
2需要反馈信道， 占用额外频率资源
二、前向纠错方式（FEC）
检测 结果
发送端
信道
接收端
发送
纠错码
接收码字
根据编译 码规则
Y 错误
N
译码 规则 纠错
纠错能力足够好，能够纠 正信道引入的数据错误
输出信息
优点 不足
1.不需要反馈信道，能够实现一对多的同 步广播通信 2.译码实时性好，控制电路比ARQ也简 单 由于假设纠错码的纠错能力足够纠正信息序 列传输中的错误，也就是纠错码与信道的干 扰是相匹配的，所以对信道的适应性较差
❖ 差错图样中的1就是符号差错，同时也是比特差错，而差错 的个数就是汉明距离。
C (1010)
R (0011)
E C R (1001)
一、功能
纠错码的分类
检测码
纠错码
只检测信息传输是否出现错 误，本身没有纠错的能力
不仅能够检测信 息传输中的错误，
并且能够自动纠
循环冗余校验码、 奇偶校验码等
信号传输过程中出现大的 信号波形畸变，导致信号 检错时发生错误，进而出 现 码元错误
叠加强的干扰 或者噪声
信号传输过程 中出现线性或 者非线性失真
线性失真
信号传输过程中不同的频率 分量增益不同，或者由于非
线性相位引起的延时不同
信息论与编码_第7章线性分组码
1 1 1 0 1 1 [000]. 0 0 1 0 0 1
17
线性分组码的校验矩阵
例7-2（续2）：求对偶码C
1 1 0 1 0 0 对偶码的生成矩阵=校验矩阵H 1 1 1 0 1 0 . 1 0 1 0 0 1
c mH , c1 m1 m2 m3 c m m 1 2 2 c3 m2 m3 c4 m1 c5 m2 c6 m3
例7-3 设一个（6,3）线性分组码C的校验矩阵为
1 1 0 1 0 0 H 1 1 1 0 1 0 0 0 1 0 0 1
任何1列线性无关， 第1、2列线性相关， C的最小汉明距离 =2
23
线性分组码
线性分组码概念 线性分组码的生成矩阵 线性分组码的校验矩阵 线性分组码的最小汉明重量 线性分组码的译码 完备码 汉明码
21
线性分组码的最小汉明重量
定理7-4 线性分组码C的最小汉明距离等于该码中非零 码字的最小 汉明重量 。 例7-2（续3） 全体码字为：
码字 000000 011101 110001 101100 111010 100111 001011 010110
C的最小汉明距离=3， 可以纠1个错，检2个错
对偶码C 000 000 101 001 111 010 010 011 110 100 011 101 001 110 100 111
18
线性分组码的校验矩阵
课堂练习：已知(5, 3)线性分组码的生成矩阵为G
1 0 1 1 0 G 0 1 0 1 1 1 1 0 1 0
信息元
000 001 010 011 100 101 110 111
陈运-信息论与编码-第六章 信道编码
i 1, 2, , n
a x an 1 x n 1 an 2 x n 2 a1 x a0 ai 0,1 1 a x an 2 x n 1 an 3 x n 2 a1 x 2 a0 x an i a x an 1i x n 1 an 2i x n 2 a1 x i 1 a0 x i an 1 x i 1 an i
T T T
S可以指示差错的存在
25
6.4 线性分组码
s [ s0 s1 s2 ]T Hz T z0 z 1 0 z2 z 0 3 1 z4 z5 z 6
26
1 0 1
1 1 1
1 1 0
0 1 1
1 0 0
0 1 0
6.4 线性分组码
伴随式 错误 s0 s1 s2 位置 z0 101
111 110 011 z1 z2 z3 错误图样 1000000 0100000
s1 z0 z1 z2 z4 s2 z1 z2 z3 z5 s3 z0 z1 z3 z6
第 6 章 信道编码
6.1 概述
• 作用
提高信息传输时的抗干扰能力
• 目的
增加信息传输的可靠性
• 手段
增加信息冗余度
• 名称
信道码、数据传输码、差错控制码
2
6.1 概述
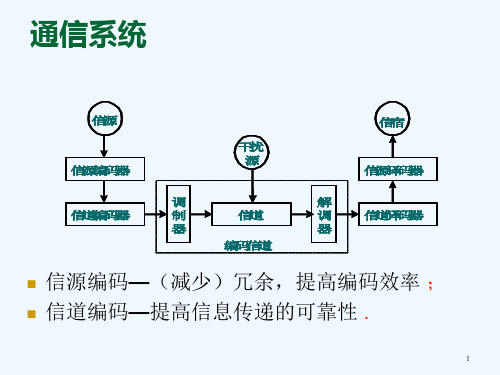
• 信道编码器在通信系统中的位置
信源
信源编码
加密
信道编码
信宿
信源译码
解密
信道译码
3
6.1 概述
• 分类
分 组 码 树 码 线 性 码 非 线 性 码 检 错 码 纠 错 码 抗 随 机 差 错 码 抗 突 发 差 错 码 代 几 组 数 何 合 码 码 码
信息论与编码(曹雪虹第三版)第一、二章
信道的分类
根据传输介质的不同，信道可分为有线信道和无线信道两大类。有线信道包括 双绞线、同轴电缆、光纤等；无线信道包括微波、卫星、移动通信等。
信道容量的定义与计算
信道容量的定义
信道容量是指在给定条件下，信道能 够传输的最大信息量，通常用比特率 (bit rate)来衡量。
信道容量的计算
信道容量的计算涉及到信道的带宽、 信噪比、调制方式等多个因素。在加 性高斯白噪声(AWGN)信道下，香农 公式给出了信道容量的理论上限。
信道编码分类
根据编码方式的不同，信道编码可分为线性分组码和卷积码 两大类。
线性分组码
线性分组码定义
线性分组码是一种将信息 序列划分为等长的组，然 后对每个组独立进行编码 的信道编码方式。
线性分组码特点
编码和解码过程相对简单 ，适用于各种信道条件， 且易于实现硬件化。
常见的线性分组码
汉明码、BCH码、RS码等 。
将信源消息通过某种数学变换转换到另一个域中，然后对变换 系数进行编码。
将连续的信源消息映射为离散的数字值，然后对数字值进行编 码。这种方法会导致量化噪声，是一种有损的编码方式。
信道编码的定义与分类
信道编码定义
信道编码是为了提高信息传输的可靠性、增加通信系统的抗 干扰能力而在发送端对原始信息进行的一种变换。
信息熵总是非负的，因 为自信息量总是非负的 。
当随机变量为确定值时 ，其信息熵为0。
对于独立随机变量，其 联合信息熵等于各自信 息熵之和。
当随机变量服从均匀分 布时，其信息熵达到最 大值。
03
信道与信道容量
信道的定义与分类
信道的定义
信道是信息传输的媒介，它提供了信号传输的通路，是通信系统中的重要组成 部分。
根据传输介质的不同，信道可分为有线信道和无线信道两大类。有线信道包括 双绞线、同轴电缆、光纤等；无线信道包括微波、卫星、移动通信等。
信道容量的定义与计算
信道容量的定义
信道容量是指在给定条件下，信道能 够传输的最大信息量，通常用比特率 (bit rate)来衡量。
信道容量的计算
信道容量的计算涉及到信道的带宽、 信噪比、调制方式等多个因素。在加 性高斯白噪声(AWGN)信道下，香农 公式给出了信道容量的理论上限。
信道编码分类
根据编码方式的不同，信道编码可分为线性分组码和卷积码 两大类。
线性分组码
线性分组码定义
线性分组码是一种将信息 序列划分为等长的组，然 后对每个组独立进行编码 的信道编码方式。
线性分组码特点
编码和解码过程相对简单 ，适用于各种信道条件， 且易于实现硬件化。
常见的线性分组码
汉明码、BCH码、RS码等 。
将信源消息通过某种数学变换转换到另一个域中，然后对变换 系数进行编码。
将连续的信源消息映射为离散的数字值，然后对数字值进行编 码。这种方法会导致量化噪声，是一种有损的编码方式。
信道编码的定义与分类
信道编码定义
信道编码是为了提高信息传输的可靠性、增加通信系统的抗 干扰能力而在发送端对原始信息进行的一种变换。
信息熵总是非负的，因 为自信息量总是非负的 。
当随机变量为确定值时 ，其信息熵为0。
对于独立随机变量，其 联合信息熵等于各自信 息熵之和。
当随机变量服从均匀分 布时，其信息熵达到最 大值。
03
信道与信道容量
信道的定义与分类
信道的定义
信道是信息传输的媒介，它提供了信号传输的通路，是通信系统中的重要组成 部分。
信道编码理论
➢ Proof . [hint: 必要性：采用反证法；充分性：将H中某 些d列线性相关的列的系数作为码字中对应的非0分量]
推论: [n, k, d]线性分组码的最大可能的最小汉明 距离为n-k+1。
➢ Proof: 由于校验矩阵H的n-k行是线性无关的，也就是说 H的行秩为n-k，从而可推出H的列秩最大是n-k，即H最 多有任意n-k列线性无关，由定理得到n-k≥d-1,有d≤nk+1。
k个信息位
nk个校验位
n-k个校验位可用k个已知的信息位表示出来：
cnk1 hnk1,n1 cn1 hnk1,n2 cn2 hnk1,nk cnk
cnk2 hnk2,n1 cn1 hnk2,n2 cn2 hnk2,nk cnk
c0 h0,n1 cn1 h0,n2 cn2 h0,nk cnk
12
缩短码
例子：
➢ 表1的[7, 3, 4]码：0000000，0011101，0100111， 0111010，1001110，1010011，1101001，1110100
11
对偶码，系统码与缩短码
对偶码
➢ 设[n, k, d]线性分组码C的生成矩阵为G，校验矩阵为H， 以H作为生成矩阵，G为对应的校验矩阵，可构造另一 个[n, n-k, d’]线性分组码C1，我们称C1为C的对偶码。
系统码
G IkP
缩短码
H PT Ink
➢ 从[n, k, d]线性分组码的所有码字中，把前面i位全为零 的码字挑选出来构成一个新的子集，该子集即为[n, k, d] 的缩短码。传输时，仅传输后面的n-i位码元，记为[n-i, k-i, d]码，其纠错能力至少与原[n, k, d]码相同。
7
码1 0 0 cn1 0
推论: [n, k, d]线性分组码的最大可能的最小汉明 距离为n-k+1。
➢ Proof: 由于校验矩阵H的n-k行是线性无关的，也就是说 H的行秩为n-k，从而可推出H的列秩最大是n-k，即H最 多有任意n-k列线性无关，由定理得到n-k≥d-1,有d≤nk+1。
k个信息位
nk个校验位
n-k个校验位可用k个已知的信息位表示出来：
cnk1 hnk1,n1 cn1 hnk1,n2 cn2 hnk1,nk cnk
cnk2 hnk2,n1 cn1 hnk2,n2 cn2 hnk2,nk cnk
c0 h0,n1 cn1 h0,n2 cn2 h0,nk cnk
12
缩短码
例子：
➢ 表1的[7, 3, 4]码：0000000，0011101，0100111， 0111010，1001110，1010011，1101001，1110100
11
对偶码，系统码与缩短码
对偶码
➢ 设[n, k, d]线性分组码C的生成矩阵为G，校验矩阵为H， 以H作为生成矩阵，G为对应的校验矩阵，可构造另一 个[n, n-k, d’]线性分组码C1，我们称C1为C的对偶码。
系统码
G IkP
缩短码
H PT Ink
➢ 从[n, k, d]线性分组码的所有码字中，把前面i位全为零 的码字挑选出来构成一个新的子集，该子集即为[n, k, d] 的缩短码。传输时，仅传输后面的n-i位码元，记为[n-i, k-i, d]码，其纠错能力至少与原[n, k, d]码相同。
7
码1 0 0 cn1 0
信息论与编码理论基础(第六章)
可逆行变换变为H '， H '是同一个线性分组码的另一个校验矩阵。
（2）固定一个校验矩阵H。则一个N维向量u是一个码字，当且仅当： uHT=全0的N-L维行向量。
（3）设一个D元(N, L)线性分组码的生成矩阵G，校验矩阵H。则H 是一个D元(N, N-L)线性分组码的生成矩阵，G是此码的一个校验 矩阵。称这两个码互为对偶码。
2021/6/19
3
§6.1 分组码的概念
预备知识1：有限域 设D是一个素数。于是字母表{0, 1, …, D-1}中的所有字母关
于(modD)加法、(modD)乘法构成了一个封闭的代数结构， 称作有限域，又称作Galois域，记作GF(D)： GF(D)=({0, 1, …, D-1}, (modD)加法, (modD)乘法)。 即
2021/6/19
17
§6.2 线性分组码
例 此二元(7, 4)码是线性分组码，生成矩阵G是由信息向量 (1000)、(0100)、(0010)、(0001)的码字组成的4行
1 1 0 1 0 0 0 G0 1 1 0 1 0 0
1 1 1 0 0 1 0 1 0 1 0 0 0 1
该码是系统码。
1 1
0 0
1 0
0，则可取 H 1
1 0
0 1
1 0
1 1
10。
1 0 1 0 0
其中(x1, x2, …, xL)是信息向量，(u1, u2, …, uN)是对应的码字。 （1）称此码为D元(N, L)线性分组码。 （2）称矩阵G为此码的生成矩阵。
2021/6/19
12
§6.2 线性分组码
线性分组码的代数结构 命题1 不同的信息向量对应不同的码字。
（2）固定一个校验矩阵H。则一个N维向量u是一个码字，当且仅当： uHT=全0的N-L维行向量。
（3）设一个D元(N, L)线性分组码的生成矩阵G，校验矩阵H。则H 是一个D元(N, N-L)线性分组码的生成矩阵，G是此码的一个校验 矩阵。称这两个码互为对偶码。
2021/6/19
3
§6.1 分组码的概念
预备知识1：有限域 设D是一个素数。于是字母表{0, 1, …, D-1}中的所有字母关
于(modD)加法、(modD)乘法构成了一个封闭的代数结构， 称作有限域，又称作Galois域，记作GF(D)： GF(D)=({0, 1, …, D-1}, (modD)加法, (modD)乘法)。 即
2021/6/19
17
§6.2 线性分组码
例 此二元(7, 4)码是线性分组码，生成矩阵G是由信息向量 (1000)、(0100)、(0010)、(0001)的码字组成的4行
1 1 0 1 0 0 0 G0 1 1 0 1 0 0
1 1 1 0 0 1 0 1 0 1 0 0 0 1
该码是系统码。
1 1
0 0
1 0
0，则可取 H 1
1 0
0 1
1 0
1 1
10。
1 0 1 0 0
其中(x1, x2, …, xL)是信息向量，(u1, u2, …, uN)是对应的码字。 （1）称此码为D元(N, L)线性分组码。 （2）称矩阵G为此码的生成矩阵。
2021/6/19
12
§6.2 线性分组码
线性分组码的代数结构 命题1 不同的信息向量对应不同的码字。
信息论基础——线性分组码
即校验位是由信息位线性组合得到.
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见，码字的三个校验元都由其前两位线 性组合得到，即可由的线性方程组求得；
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离： 指（n,k）分组码中两个码字xn 、 yn对应位取 值不同的个数；记为d（xn ， yn）.
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例： x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离： 称（n,k）分组码中任两个码字汉明距离的最小 值，为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1： 下面是某个（n，k）线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值；
17
线性分组码的基本概念
信息位 00 01 10 11 x2 x0 x1 00000 x3 x0 x x x 01101 0 1 4 码字 10111 11010
信息位k=2 码字数M=4
可见，码字的三个校验元都由其前两位线 性组合得到，即可由的线性方程组求得；
18
线性分组码的基本概念
f1 : GF (2) 2 GF (2)5
信息位 00 01 10 11 码字 00000 01101 10111 11010
1 ( 0 1 ) 1 ( 1 0 ) 1 1
f( 1 1 ) 1 1 0 1 0
1 ( 0 1 1 0 1 )1 ( 1 0 1 1 1 ) 1 1 0 1 0
30
线性分组码的基本概念
汉明距离： 指（n,k）分组码中两个码字xn 、 yn对应位取 值不同的个数；记为d（xn ， yn）.
5 5 ( 1 0 1 0 1 ) , y ( 0 1 1 1 1 ) 例： x
d(x ,y ) 3
5 5
31
线性分组码的基本概念
线性分组码的最小距离： 称（n,k）分组码中任两个码字汉明距离的最小 值，为该分组码的最小距离d.
f ( 1 ( 0 1 ) 1 ( 1 0 ) ) 1 ( 0 1 1 0 1 ) 1 ( 1 0 1 1 1 ) 线性编码
19
线性分组码的基本概念
例题1： 下面是某个（n，k）线性二元码的全部码字
x16=000000 x26=100011 x36=010101 x46=001111 x56=110110 x66=101100 x76=011010 x86=111001 求n、k的值；
信息论与编码_第7章线性分组码
例7-3 设一个（6,3）线性分组码C的校验矩阵为
1 1 0 1 0 0 H 1 1 1 0 1 0 0 0 1 0 0 1
任何1列线性无关， 第1、2列线性相关， C的最小汉明距离 =2
23
线性分组码
线性分组码概念 线性分组码的生成矩阵 线性分组码的校验矩阵 线性分组码的最小汉明重量 线性分组码的译码 完备码 汉明码
22
线性分组码的最小汉明重量
定理7-5 线性分组码C的最小汉明距离是d当且仅当它的校 验矩阵H的任意d1列线性无关，而存在d列线性相关。 例7-2（续4） 校验矩阵为
1 1 0 1 0 0 H 1 1 1 0 1 0 1 0 1 0 0 1
任何2列线性无关， 第2、4、5列线性相 关，C的最小汉明 距离=3
13
对偶码
线性分组码的校验矩阵
线性码C k维线性子空间C{0,1}n
对偶空间V={a=(a0,a1,…,an1){0,1}n， c=(c0,c1,…,cn1)C, ac }{0,1}n 是nk维子空间
C确定一个（n, nk）线性分组码，称为码C的 对偶码C，其生成矩阵记为H
d m1 1 0 0 1 1 1 m2 0 1 0 1 1 0 m3 0 0 1 0 1 1.
11
线性分组码的生成矩阵
例7-2（续1）：求系统生成矩阵Gs及全部码字
信息元
码f 000000 011101 110001 101100 111010 100111 001011 010110
1 1 1 0 1 1 [000]. 0 0 1 0 0 1
17
线性分组码的校验矩阵
例7-2（续2）：求对偶码C
第9章 1信道编码-线性分组码
主要内容
n n
信道编码的基本概念和分类 两种主要的信道编码
n n
分组码 卷积码
n n
其他类型编码和编码界限(了解) 工程应用(了解)
北京邮电大学 无线通信中心
2
主要内容
n n
信道编码的基本概念 线性分组码
n n
循环码 BCH码
n n
卷积码 其他编码类型
n
纠正突发错误码、交织码、级联码、Turbo 码、高效率信道编码TCM
北京邮电大学 无线通信中心 8
9.1 信道编码的基本概念
n
信道编码分类（按纠正错误类型分类）
n
n
n
纠独立随机差错码：分组码和卷积码中的大 部分种类 纠突发差错码：分组码和卷积码中的几类、 交织码 纠混合差错码：级联码
北京邮电大学 无线通信中心
9
9.1 信道编码的基本概念
n
信道编码分类（按约束关系分类）
n
信道分类（按差错出现类型）
n
突发差错信道
n n
n
差错成串出现（记忆性） 原因：信道传输特性不理想（衰落和码间干扰）， 有大的脉冲干扰 例如：短波信道、移动通信信道、散射信道、明 线和电缆信道、磁介质存储
n
混合信道
注意：出错类型是统计意义上的，并不表示错误一定发生
北京邮电大学 无线通信中心 6
9.1 信道编码的基本概念
n n
需要反馈信道 实时性和译码复杂度是FEC和ARQ两种方式 的折衷
北京邮电大学 无线通信中心
17
9.1信道编码的基本概念
n
n
信道编码是数字通信中用来提高传输可 靠性的一种重要技术 常用信道编码
n n n
重复码 偶校验码 线性分组码
n n
信道编码的基本概念和分类 两种主要的信道编码
n n
分组码 卷积码
n n
其他类型编码和编码界限(了解) 工程应用(了解)
北京邮电大学 无线通信中心
2
主要内容
n n
信道编码的基本概念 线性分组码
n n
循环码 BCH码
n n
卷积码 其他编码类型
n
纠正突发错误码、交织码、级联码、Turbo 码、高效率信道编码TCM
北京邮电大学 无线通信中心 8
9.1 信道编码的基本概念
n
信道编码分类（按纠正错误类型分类）
n
n
n
纠独立随机差错码：分组码和卷积码中的大 部分种类 纠突发差错码：分组码和卷积码中的几类、 交织码 纠混合差错码：级联码
北京邮电大学 无线通信中心
9
9.1 信道编码的基本概念
n
信道编码分类（按约束关系分类）
n
信道分类（按差错出现类型）
n
突发差错信道
n n
n
差错成串出现（记忆性） 原因：信道传输特性不理想（衰落和码间干扰）， 有大的脉冲干扰 例如：短波信道、移动通信信道、散射信道、明 线和电缆信道、磁介质存储
n
混合信道
注意：出错类型是统计意义上的，并不表示错误一定发生
北京邮电大学 无线通信中心 6
9.1 信道编码的基本概念
n n
需要反馈信道 实时性和译码复杂度是FEC和ARQ两种方式 的折衷
北京邮电大学 无线通信中心
17
9.1信道编码的基本概念
n
n
信道编码是数字通信中用来提高传输可 靠性的一种重要技术 常用信道编码
n n n
重复码 偶校验码 线性分组码
信息论与编码第六章3
信息论与编码-线性分组码
上次课小结： • 信道编码定理：
Pe eNE (R)
• 差错控制的途径 增加码长、增加带宽、提高信噪比、噪声均
化 • 码距与检错纠错的关系
ec dmin 1 / 2 ed dmin 1
信息论与编码-线性分组码
• 最优译码与最大似然译码
最优译码：
Cˆi
max
i1,2, ,2k
系统码的前k位为信息位，后n-k位为校验位。
信息论与编码-线性分组码
校验矩阵H除了可以用来检验码字外，还与码的最 小距离（也就和码的检错纠错能力）有关。
因为
h11 H h(hn21k)1
h12 h22 h(nk)2
h1n
h2n h(nk )n
(h1 , h 2 ,
,hn
)
其中，h1,h2, ,hn 是H矩阵的列向量。
h
T j
项，而右边为零。
也就是说， dmin个
h
T j
是线性相关的。
而
信息论与编码-线性分组码
dmin 1
个
h
T j
一定是线性无关的（反证法：如
果 dmin 1
个
h
T j
列矢量是线性相关的，则可以把
其对应的系数当成码字，而该码字的重量
为 dmin
盾）。
1
，这与码字的最小重量为
d min
相矛
由于H是 (n k) n 的矩阵，其秩最大为n-k，也就是 说，最多有n-k个列矢量线性无关。所以
p1(nk )
p2(n
k
)
pk (nk )
这样生成的（n，k）码是系统码。
信息论与编码-线性分组码
上次课小结： • 信道编码定理：
Pe eNE (R)
• 差错控制的途径 增加码长、增加带宽、提高信噪比、噪声均
化 • 码距与检错纠错的关系
ec dmin 1 / 2 ed dmin 1
信息论与编码-线性分组码
• 最优译码与最大似然译码
最优译码：
Cˆi
max
i1,2, ,2k
系统码的前k位为信息位，后n-k位为校验位。
信息论与编码-线性分组码
校验矩阵H除了可以用来检验码字外，还与码的最 小距离（也就和码的检错纠错能力）有关。
因为
h11 H h(hn21k)1
h12 h22 h(nk)2
h1n
h2n h(nk )n
(h1 , h 2 ,
,hn
)
其中，h1,h2, ,hn 是H矩阵的列向量。
h
T j
项，而右边为零。
也就是说， dmin个
h
T j
是线性相关的。
而
信息论与编码-线性分组码
dmin 1
个
h
T j
一定是线性无关的（反证法：如
果 dmin 1
个
h
T j
列矢量是线性相关的，则可以把
其对应的系数当成码字，而该码字的重量
为 dmin
盾）。
1
，这与码字的最小重量为
d min
相矛
由于H是 (n k) n 的矩阵，其秩最大为n-k，也就是 说，最多有n-k个列矢量线性无关。所以
p1(nk )
p2(n
k
)
pk (nk )
这样生成的（n，k）码是系统码。
信息论与编码-线性分组码
信息论与编码-第7章-第13讲-信道编码-线性分组码1
16
2013/8/20
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性系统分组码 通过行初等变换，将 G 化为前 k 列是单位子阵的标准 形式
6.2 线 性 分 组 码
2013/8/20
17
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性系统分组码：用标准生成矩阵 Gk×n 编成的码字，前面 k 位为信息数字，后面 r=n－k 位为校验字，这种信息数字在前 校验数字在后的线性分组码称为线性系统分组码。
2013/8/20
13
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性码的封闭性：线性码任意两个码字之和仍是一个码字。 定理6.2.1：设二元线性分组码 CI (CI表示码字集合) 是由监督矩阵 H所定义的，若 U 和 V 为其中的任意两个码字，则 U+V 也是 CI中的一个码字。 [证明]：由于 U 和 V 是码 CI 中的两个码字，故有 HUT=0T，HVT=0T 那么 H(U+V)T=H(UT+VT)=HUT+HVT=0T 即 U+V 满足监督方程，所以 U+V 一定是一个码字。 一个长为 n 的二元序列可以看作是GF(2)(二元域)上的 n 维线 性空间中的一点。长为 n 的所有 2n 个矢量集合构成了GF(2) 上的 n 维线性空间Vn。把线性码放入线性空间中进行研究， 将使许多问题简化而比较容易解决。 (n,k) 线性码是 n 维线性空间Vn中的一个 k 维子空间 Vk。
14
(1) 线性码的封闭性
6.2 线 性 分 组 码
2013/8/20
第六章 信道编码
2013/8/20
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性系统分组码 通过行初等变换，将 G 化为前 k 列是单位子阵的标准 形式
6.2 线 性 分 组 码
2013/8/20
17
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性系统分组码：用标准生成矩阵 Gk×n 编成的码字，前面 k 位为信息数字，后面 r=n－k 位为校验字，这种信息数字在前 校验数字在后的线性分组码称为线性系统分组码。
2013/8/20
13
第六章 信道编码
6.2.3 线性分组码的生成矩阵
线性码的封闭性：线性码任意两个码字之和仍是一个码字。 定理6.2.1：设二元线性分组码 CI (CI表示码字集合) 是由监督矩阵 H所定义的，若 U 和 V 为其中的任意两个码字，则 U+V 也是 CI中的一个码字。 [证明]：由于 U 和 V 是码 CI 中的两个码字，故有 HUT=0T，HVT=0T 那么 H(U+V)T=H(UT+VT)=HUT+HVT=0T 即 U+V 满足监督方程，所以 U+V 一定是一个码字。 一个长为 n 的二元序列可以看作是GF(2)(二元域)上的 n 维线 性空间中的一点。长为 n 的所有 2n 个矢量集合构成了GF(2) 上的 n 维线性空间Vn。把线性码放入线性空间中进行研究， 将使许多问题简化而比较容易解决。 (n,k) 线性码是 n 维线性空间Vn中的一个 k 维子空间 Vk。
14
(1) 线性码的封闭性
6.2 线 性 分 组 码
2013/8/20
第六章 信道编码
信息论与编码第7章信道编码技术
阿 贝
3.加法运算满足交换律
abba
尔 群
4.集合F包含一个称为0的元素，满足a0a
(加法恒等元）
5. 每个元素都有一个负元素，如果b是一个元
素，其负元素记作－b，两个元素减法运算
定义为 a (b)
(加法逆元）
7.1 线性分组码
有限域的乘法
乘法运算是闭合的 a,bF abF
乘法运算满足结合律 a ,b ,c F a (b c ) (a b )c
输入信息
xm4 xm3 xm2 xm1
cm7 cm6 cm5
输出码字
使用移位寄存器实现方法
校验矩阵 H
1、线性码(n,k)都存在对偶码（零空间上的码 字）;
2、对偶码共有2n-k个码矢量;
3、对偶码是(n,n-k)的线性分组码，生成矩阵 用H表示 ；
4、每个码字都是从零空间中选取，所以有
CmHT 0
对于二元分组码（n,k)：
矢量空间是由2k个二元值的n重构成的 ;
线性码（n,k）是2k个n重的集合，所有码字 构成二元域子空间 Sc;
Sc中共有2k个码字， Sc的基底有k个，这就 是说需要k个线性独立的码字去构造2k种线 性组合，从而产生整个码。
Sc的零空间是另一种线性码，它是由码长为n， 信息比特数为n-k的2n-k个码字所组成。
1 0 0 0 1 0 1
GIk
|
P
0 0
1 0
0 1
0 0
1 1
1 1
1 0
0 0 0 1 0 1 1
1 1 1 0 1 0 0 H 0 1 1 1 0 1 0
1 1 0 1 0 0 1
设码字 C m (x m 1 x m 2 x m 3 x m 4 c m 5 c m 6 c m 7 ) 由 CmHT 0 可以得到三个校验方程
(完整word版)线性分组码信道编码
数字通信课程报告题目：数字通信中的线性分组码讲课老师：学生姓名：所属院系:专业：学号：1设计目的和要求0 1 1 1 0 1 1 1 0数字信号在传输中往往由于各种原因，使得在传送的数据流中产生误码，从而使接收端产生图像跳跃，不连续，出现马赛克等现象.通过信道编码可实现对数据流进行相应的处理，使系统具有一定的纠错能力和抗干扰能力，可极大地避免码流传送中误码的发生。
通过线性分组码实现信道编码,提高系统的可靠性。
2 设计原理要设计一个（6，3)线性分组码的编译码程序，最基本的是要具备对输入的信息码进行编码，让它具有抗干扰的能力。
同时，还要让它具有对接收到的整个码组中提取信息码组的功能。
但是,在实际的通信系统中，由于信道传输特性不理想以及加性噪声的影响，接收到的信息中不可避免地会发生错误，影响通信系统的传输可靠性，因而,本设计还要让该程序具有纠正错误的能力,当接收到的码组中有一位码，发生错误时可以检测到这一位错码，并且可以纠正这一位错码,并且让系统从纠正后的码组中提取正确的信息码组. 针对给定的矩阵Q=完成如下的工作：1 完成对任意信息序列的编码2 根据生成矩阵,形成监督矩阵;3 根据得到的监督矩阵，得到伴随式，并根据它进行译码；4 验证工作的正确性.2。
1 线性分组码的编码2.1.1 生成矩阵线性分组码（n ，k ）中许用码字(组)为2k 个。
定义线性分组码的加法为模二加法，乘法为二进制乘法。
即1+1=0、1+0=1、0+1=1、0+0=0；1×1=1、1×0=0、0×0=0、0×1=0.且码字与码字的运算在各个相应比特位上符合上述二进制加法运算规则。
线性分组码具有如下性质（n,k）的性质：1、封闭性。
任意两个码组的和还是许用的码组。
2、码的最小距离等于非零码的最小码重。
对于码组长度为n、信息码元为k位、监督码元为r＝n－k位的分组码，常记作(n，k）码，如果满足2r－1≥n，则有可能构造出纠正一位或一位以上错误的线性码。
信息论与编码(第三版) 第6章 信道编码理论
6.3.1两种译码规则
最大概率译码(MAP) 错误译码的概率最小，也称最小错误概率译码
最大似然译码(MLD)
MAP的简化形式
单个符号传输情况(二元信道)
信道
输入X
0 1 pe
信道 输出Y
0
根据接收符号y来估计 发送符号x是0还是1
计算后验概率p(xi|y)
估值准则
x$ max P(xi | y)
结果是译码错误最 小，所以也称最小
不同的编码规则产生不同的码字， 称被选中的2k个n重为许用码组
其余的2 n-2k个n重为禁用码组
编码不会出现，许用 码字经过信道后，可 能会出现，一旦出现， 数据传输出错（检测 的依据）
分组码的码率为 R k / n
是衡量分组码编码有效性的基本 参数，表示了信息位在码字中所 占的比例。
在纠错能力相同情况下，码率 越大效率越高，有利于提高信息 传输的效率。
差错控制方式
重传反馈方式 (ARQ)
前向纠错方式 (FEC)
混合纠错方式 (HEC)
❖ 一、重传反馈方式（ARQ）
信源
检错码 编码器
存储器
前向信道 噪声源
检错码 解码器
信宿
判决检测器 控制器
反馈信道
反馈 控制器
工作方式描述
发送端 发送检测码
前向 接收端
信道
接收码字
发送 后续 数据
Y N
重新发送
出错
编码规则
发送端所采用的编码算法及其 对应的码集合是已知的
接收到的码 字序列
信道模型及 先验概率为信道转移矩阵和发
参数
送符号的统计规律
确定译码规 则，对接收
最合理规则是译码错误概率最小
信道编码_第2章
1 1 H 1 0
0 1 1 1
1 1 0 1
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
它是一个(n -k )×n 阶矩阵。 由此H矩阵可
以很快地建立码的线性方程组：
h1,n 2 h1,0 h1,n 1 h h h 2 ,n 1 2 ,n 2 2,0 H hn k ,n 1 hn k ,n 2 hn k ,0
(2.3.5)
n维n重空间R
k维k重 信息组 空间m
k维n重 码空间C
G
n-k维n重 对偶空间D
H
码空间与映射
4-k ， d］码的生成矩阵
G， 而把［n ， k ， d］码的G看成是它的校验
矩阵H， 则我们称由G生成的［n ， k ， d］码 C与由H生成的［n ， n -k ， d］码C⊥互为对 偶码。 相应地， 称Vn ， k与Vn 偶空间。
可由以下线性方程组求得：
1·c3=1·c6+0·c5+1·c4
1·c2=1·c6+1·c5+1·c4
1·c1=1·c6+1·c5+0·c4
1· c0 =0· c6+1· c5+1· c4
c6+0 +c4+c3+0 +0 + 0 =0 c6+c5+c4+0 +c2+0 +0 =0 c6+c5+0 +0 +0 +c1+0 =0 0 +c5+c4+0 +0 +0 +c0=0
信息论与编码15-线性分组码
(若矩阵的秩为r，则矩阵列向量中线性无关的最大个数为r)
6
6.2.2 线性分组码的译码
m 编码器 c + r 译码器 y
e
译
码纠检错错译译码码：译 译y 码 码(失 成r ,
s) s :差
功：y cˆ 败：y (r, s)
错
标
志
定义：(n,k)线性分组码的伴随式是一个r(r =n-k)维向量s
H的线性不相关行数为r (r=n-k)，
h 0, 0
称H为(n,k)线性分组码的一致校验矩阵
H
h 1, 0
h r1, 0
h 0, 1 h 1, 1
hr1, 1
h 0, n1
h 1,
n1
6.2.1 线性分组码的描述
定理：任意满足下式的n维向量α都是一个(n,k)线性分组码的码字。
s
rH T
（s0 ,s1 ,
,sr
）
-1
r ce
s
rH T
eH T
s
传输中一定有差错发生
无 差 错 发 生
s e c 不可检测错误图样 7
6.2.2 线性分组码的译码
结论：1. 伴随式s 仅与e 有关，而与码字c 无关。
2. s 是错误的判别式。
例：
定理：二元(n,k)线性分组码有 2(rr =n-k)种的伴随式，如果一个伴随式s
§6.1 信道编码的概念
◆ 信道编码的基本思想:
按一定的规则，在待传输的信息序列中人为地增加一些多余的码 元
（冗余位），使之具有相关特性，在接收端利用相关性进行检测或
纠
错，以保证传输过程的可靠性。
◆ 2k个码字集合——(n,k)线性分组码
6
6.2.2 线性分组码的译码
m 编码器 c + r 译码器 y
e
译
码纠检错错译译码码：译 译y 码 码(失 成r ,
s) s :差
功：y cˆ 败：y (r, s)
错
标
志
定义：(n,k)线性分组码的伴随式是一个r(r =n-k)维向量s
H的线性不相关行数为r (r=n-k)，
h 0, 0
称H为(n,k)线性分组码的一致校验矩阵
H
h 1, 0
h r1, 0
h 0, 1 h 1, 1
hr1, 1
h 0, n1
h 1,
n1
6.2.1 线性分组码的描述
定理：任意满足下式的n维向量α都是一个(n,k)线性分组码的码字。
s
rH T
（s0 ,s1 ,
,sr
）
-1
r ce
s
rH T
eH T
s
传输中一定有差错发生
无 差 错 发 生
s e c 不可检测错误图样 7
6.2.2 线性分组码的译码
结论：1. 伴随式s 仅与e 有关，而与码字c 无关。
2. s 是错误的判别式。
例：
定理：二元(n,k)线性分组码有 2(rr =n-k)种的伴随式，如果一个伴随式s
§6.1 信道编码的概念
◆ 信道编码的基本思想:
按一定的规则，在待传输的信息序列中人为地增加一些多余的码 元
（冗余位），使之具有相关特性，在接收端利用相关性进行检测或
纠
错，以保证传输过程的可靠性。
◆ 2k个码字集合——(n,k)线性分组码
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
码矢：一个 n 重的码字可以用矢量来表示
C=(Cn－1,Cn－2,…,C1,C0 )
所以码字又称为码矢。
(n,k) 线性码：信息位长为 k，码长为 n 的线性码。
编码效率/编码速率/码率/传信率：R=k /n。它说明了信道的利
用效率，R是衡量码性能的一个重要参数。
2020/4/9
4
第六章 信道编码
(6.2.6)
2020/4/9
10
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
令上式的系数矩阵为 H，码字行阵列为 C
h11 h12 h1n
H rn
h21
h22
h2
n
hr1
hr 2
hrn
(6.2.7)
C1n Cn1 Cn2 C0
式 (6.2.6)可写成
H rn
由于一致监督方程是线性的，即监督元和新信源之间是 线性运算关系，所以由线性监督方程所确定的分组码是 线性分组码。
2020/4/9
6
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
(2) 举例
信息码组 (101)，即C6=1, C5=0, C4=1
代入 (6.2.1) 得： C3=0, C2=0, C1=1, C0=1
第六章 信道编码
Enthusiasm takes you further
2020/4/9
1
第六章 信道编码
6.2 线性分组码
6.2.1 一般概念 6.2.2 一致监督方程和一致监督矩阵 6.2.3 线性分组码的生成矩阵 6.2.4 线性分组码的编码 6.2.5 线性分组码的最小距离、检错和纠错能力 6.2.6 线性分组码的译码 6.2.7 线性分组码的性能 6.2.8 汉明码 6.2.9 由已知码构造新码的方法 6.2.10 线性分组码的码限
C
T n1
0T r 1
或
C1n
H
T n
r
0 1r
(6.2.8)
称H为(n, k )线性分组码的一致监督 矩阵，简称监督矩阵。
2020/4/9
11
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
(4) 一致监督矩阵特性
对H 各行实行初等变换，将后面 r 列化为单位子阵，于是得到下
面矩阵，行变换所得方程组与原方程组同解。
C6 0C4 C3 000 0
CC66
C5 C5
C4 0C2 00 000C1 0 0
0
100 101 110
1001110 1010011 1101001
0C5 C4 000C0 0
111 1110100
2020/4/9
7
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
(3) 一致监督矩阵
由信息码组 (101) 编出的码字为
(1010011)。其它7个码字如表6.2.1。
表 6.2.1 (7,3)分组码编码表
信息组 对应码字
C3 C6 C4
CC12
C6 C6
C5 C5
C4
(6.2.1)
000 001
0000000 0011101
C0 C5 C4
010 0100111
011 0111010
6.2.2 一致监督方程和一致监督矩阵
系数矩阵 H 的后四列组成一个 (4×4) 阶单位子阵，用 I4 表示，H 的其余部分用 P 表示
1 0 1
P43
1 1ቤተ መጻሕፍቲ ባይዱ
1 1
1 0
0 1 1
1 0 0 0
I4
0 0
1 0
0 1
0 0
0 0 0 1
所以
H P I (7,3)
43 4
(6.2.5)
2020/4/9
6.2.2 一致监督方程和一致监督矩阵
(1) 一致监督方程
编码就是给已知信息码组按预定规则添加监督码元，以构成码字。
在 k 个信息码元之后附加 r(r=n－k) 个监督码元，使每个监督元是 其中某些信息元的模2和。
举例：k=3, r=4，构成 (7,3) 线性分组码。设码字为
(C6,C5,C4,C3,C2,C1,C0) C6,C5,C4为信息元，C3,C2,C1,C0为监督元，每个码元取“0”或“1” 监督元可按下面方程组计算
p11 p12 p1k 1 0 0
Hrnp 21
C3 C6 C4
CC12
C6 C6
C5 C5
C4
C0 C5 C4
(6.2.1)
2020/4/9
5
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
一致监督方程/一致校验方程：确定由信息元得到监督元规
则的一组方程称为监督方程/校验方程。由于所有码字都按同一规 则确定，又称为一致监督方程/一致校验方程。
为了运算方便，将式 (6.2.1)监督方程写成 矩阵形式，得
式(6.2.2)可写成
H CT=0T或 C HT=0 CT、HT、0T分别表 示C、H、0的转置
矩阵。
C 6
1
1
1
0
0 1 1 1
1 1 0 1
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
C C C C C
2020/4/9
2
第六章 信道编码
6.2.1 一般概念
线性分组码的编码：线性分组码的编码过程分为两步：
把信息序列按一定长度分成若干信息码组，每组由 k 位组成；
编码器按照预定的线性规则(可由线性方程组规定)，把信息码 组变换成 n 重 (n>k) 码字，其中 (n－k) 个附加码元是由信息码 元的线性运算产生的。
9
第六章 信道编码
6.2.2 一致监督方程和一致监督矩阵
推广到一般情况：对 (n,k) 线性分组码，每个码字中的 r(r=n－k) 个监督元与信息元之间的关系可由下面的线性 方程组确定
h11Cn1h12Cn2h1nC0 0 h21Cn1h22Cn2 h2nC0 0 hr1Cn1hr2Cn2hrnC0 0
信息码组长 k 位，有 2k 个不同的信息码组，则有 2k 个 码字与它们一一对应。
2020/4/9
3
第六章 信道编码
6.2.1 一般概念
名词解释
线性分组码：通过预定的线性运算将长为 k 位的信息码组变换 成 n 重的码字 (n>k)。由 2k 个信息码组所编成的 2k个码字集合 ，称为线性分组码。
5 4 3 2 1
0
0
0
0
C 0
(6 .2 .2 )
令 C C 6 C 5 C 4 C 3 C 2 C 1 C 0 0 0 0 0 0
1 0 1 1 0 0 0
H
1
1
1
0
1
0
0
1 1 0 0 0 1 0
0
1
1
0
0
0
1
(6 .2 .3)
2020/4/9
8
第六章 信道编码