王育民信息论与编码理论第四章答案2

信息论与编码理论习题答案

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载信息论与编码理论习题答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第二章信息量和熵2.2 八元编码系统，码长为3，第一个符号用于同步，每秒1000个码字，求它的信息速率。

解：同步信息均相同，不含信息，因此每个码字的信息量为 2=23=6 bit因此，信息速率为 61000=6000 bit/s2.3 掷一对无偏骰子，告诉你得到的总的点数为：(a) 7; (b) 12。

问各得到多少信息量。

解：(1) 可能的组合为 {1，6},{2，5},{3，4},{4，3},{5，2},{6，1} ==得到的信息量 ===2.585 bit(2) 可能的唯一，为 {6，6}=得到的信息量===5.17 bit2.4 经过充分洗牌后的一副扑克（52张），问：(a) 任何一种特定的排列所给出的信息量是多少？(b) 若从中抽取13张牌，所给出的点数都不相同时得到多少信息量？解：(a) =信息量===225.58 bit(b)==信息量==13.208 bit2.9 随机掷3颗骰子，X表示第一颗骰子的结果，Y表示第一和第二颗骰子的点数之和，Z表示3颗骰子的点数之和，试求、、、、。

解：令第一第二第三颗骰子的结果分别为，，，相互独立，则，，==6=2.585 bit===2(36+18+12+9+)+6=3.2744 bit=-=-[-]而=，所以= 2-=1.8955 bit或=-=+-而= ，所以=2-=1.8955 bit===2.585 bit=+=1.8955+2.585=4.4805 bit2.10 设一个系统传送10个数字，0，1，…，9。

奇数在传送过程中以0.5的概率错成另外一个奇数，其余正确接收，求收到一个数字平均得到的信息量。

信息论与编码第四章习题参考答案

4.1某离散无记忆信源概率空间为分别使用长度为10和100的序列进行等长无失真编码，分别计算最短平均码长和编码效率。

解：信源的熵为881.03.03.07.07.0)(H =--=lb lb X 比特/符号当N=10时，序列码长应当满足 81.81881.0102)(L 1=⨯=>lb X NH 比特/序列考虑到序列码长应该为整数，取L1=9比特/符号，平均每个符号的码长为9.0NL L 11==比特/符号所以编码效率为%9.97L )(H 11==X η 当N=100时，序列码长为1.881881.01002)(L 1=⨯=>lb X NH 比特/100符号取L1=89比特/符号，平均每个符号的码长为89.0NL L 22==比特/符号编码效率为%99L )(H 22==X η 4.2设离散无记忆信源为如果要求编码效率为，允许错误概率为，求编码序列的长度。

解：信源的熵为722.02.02.08.08.0)(H =--=lb lb X 比特/符号自信息量方差为64.0722.0-）2.0（2.0）8.0（8.0D 222=+=lb lb采用二进制码进行等长编码，序列长度应当满足72221062.1)1)((D N ⨯=-≥δηηX H4.3设离散无记忆信源的概率空间为要求编码效率为(1) 如果采用序列等长编码，而允许译码错误概率为，求编码序列的长度。

(2) 如果采用序列变长编码，求编码序列的长度，并且与(1)比较，说明为什么会有这样的结果。

解1）信源的熵为811.025.025.075.075.0)(H =--=lb lb X 比特/符号自信息量方差为471.0811.0-）25.0（25.0）75.0（75.0D 222=+=lb lb采用二进制编码，序列长度为62221029.1)1)((D N ⨯=-≥δηηX H2）对信源进行二次扩展，并采用下列编码方式构成唯一可译码平均码长为6875.13161316321631169L =⨯+⨯+⨯+⨯=比特/2符号每个符号码长为84375.026875.12L L ===比特/符号编码效率为%95%1.9684375.0811.0L H(X)=>===δη 由于变长编码能够更好利用不同序列的概率分布进行编码，概率越大，序列的码长越短，概率越小，序列的码长越长，所以相对等长编码而言，变长编码的平均码长很短。

《信息论与编码》习题解答-第四章(新)

《信息论与编码》习题解答第四章信息率失真函数-习题答案4.1解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率⎥⎦⎤⎢⎣⎡--=εεεε11)|(i j a b p 平均失真：εεεεε=⨯-⨯+⨯⨯+⨯⨯+⨯-⨯==∑∑==0)1(2/112/112/10)1(2/1),()|()(2121j i i j i j i b a d a b p a p D4.2解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0210d ， 0min =D ,∑=⨯+⨯=⨯+⨯===ij i i j j y x d x p D D )102/122/1(2/112/102/1),()(min min max 舍去当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=1001P当2/1max =D ，0)(max =D R因为取的是第二列的max D 值，所以输出符号概率:,1)(,0)(21==b p b p ,,2221b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=1010P 4.3解：0min =D0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 当0min =D ，bit X H R D R 24log )()0()(min ==== 因为没有失真，此时的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P 当4/3max =D ，0)(max =D R因为任何一列的max D 值均为3/4，所以取输出符号概率:0)(,0)(,0)(,1)(4321====b p b p b p b p ，即14131211,,,b a b a b a b a →→→→因此编码器的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P 4.4解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=4/1014/110d ， 0min =D∑=⨯+⨯===ij i i j j y x d x p D D )2/12(4/1)4/12/14/12/1min(),()(min min max 个均为其它当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=010001P 当4/1max =D ，0)(max =D R因为取的是第三列的max D 值为1/4，所以取输出符号概率:1)(,0)(,0)(321===b p b p b p ，即3231,b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=100100P 4.5解：(1)依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率为：⎥⎦⎤⎢⎣⎡-=q q P 101 )1(0)1()1(1)1(1001),()|()(11p q q p q p p p y x d x y p x p D n i mj j i i j i -⨯=⨯-⨯-+⨯⨯-+⨯⨯+⨯⨯==∑∑==(2) 0min =D因为)(D R 是D 的递减函数，所以)1log()1(log )()()())(m ax (min min p p p p D H p H D R D R ----=-==当0=q 时可达到))(max(D R ，此时0=D(3) ∑-=⨯+⨯===iji i j j ，p p p p y x d x p D D )1(10),()(min min max 舍去更大另一个因为)(D R 是D 的递减函数，所以0)()()())(m in(max max =-==D H p H D R D R当1=q 时可达到))(min(D R ，此时p D -=1(图略，见课堂展示)4.6解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡∞∞=1010d ，信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/12/110)(u p u 0min =D ，∑⨯+⨯⨯+∞⨯∞⨯+⨯===iji i j j y x d x p D D )12/112/1,02/12/1,2/102/1min(),()(min min max )(1]1,,m in[舍去另二个，∞=∞∞=10≤≤D因为二元等概信源率失真函数：⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中1,2==a n ，所以率失真函数为：D D R -=1)(4.7解：失真矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110d ，按照P81页方法求解。

王育民信息论与编码理论第四章答案2

4.5若将N 个相同的BSC 级联如题图4.5所示，各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11。

令Q t =P{X t =0}，t=0,1,…,N,且Q 0为已知。

题图 4.5(a)求Q t 的表达式。

(b)证明N →∞时有Q N →1/2，且与Q 0取值无关，从而证明N →∞级联信道的信道容量C N →0，P>0。

解：(a)对于满足X N 为马氏链的串联信道，他们总的信道转移概率矩阵为各个串联信道矩阵的乘积，即P(X N |X 0)= P(X 1|X 0) P(X 2|X 1)……P(X N |X N-1)由已知得，但各信道的转移概率矩阵为⎥⎦⎤⎢⎣⎡--p p p p 11 则两个信道级联的转移概率矩阵为： P 2=⎥⎦⎤⎢⎣⎡--p p p p 11⎥⎦⎤⎢⎣⎡--p p p p 11=()()()()⎥⎦⎤⎢⎣⎡-+---+2222112p 12p 1p p p p p p 三个信道级联的转移概率矩阵为： P 3=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+33331221211221211221211-2p 2121p p p 四个信道级联的转移概率矩阵为： P 4=()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+44441221211221211221211-2p 2121p p p 以此类推：可得N 个信道级联的转移概率矩阵为：P N =()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+----+N N N N p p p 1221211221211221211-2p 2121 则Q t =P{X t =0}=()()()()()000121221211122121122121Q p p Q p Q p t t t t -+--=-⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡-+即Q t 的表达式为：Q t =()()012122121Q p p t t -+-- t=0,1,……,N (b) 由(a)可得到：Q N =()()012122121Q p p t t -+-- 由0<p<1，则0<2p<2，-1<2p-1<1，即|2p-1|<1 则21lim =∞→N N Q ，与Q 0取值无关。

信息论第四章习题解答

四解 (1) 要能纠一位错，监督位数 r 必须满足 2r ? n ? 1,
章
由 n = 6 ? r 可求得满足该条件的最小的 r 为 r = 4 .
抗
故需构造 (10, 6 ) 码。
干
(2) 可以构造出多种 (10, 6 ) 码，下面仅给出其中的一种。
扰
111100 1000
二元
监督阵 [H ] =
二
元编
当
d
为偶数时，可以纠正
??? d
2
2 ?? 位错误， ?
码
且发现 ?? d - 2 ?? ? 1 位错误。
?2?
4
习题解答
第 4.4 试计算 ( 8, 7 ) 奇偶校验码的漏检概率和编码效率，
四
已知码元的错误概率为 Pe = 10- 4 .
章解 (1) 奇偶校验码不能发现偶数位错误，其漏检概率为：
码
(5) 系统码和非系统码 (略)。
(P 175)
19
习题解答
第 4.13 已知 (7, 4) 循环码的生成多项式为 g( x) = x3 ? x2 ? 1,
四
当收到一循环码字为 0010011 时，根据校验子判断有
章
无错误？哪一位错了？
抗解 (1) 求校验子干扰二元编码
c0 位错 c1 位错 c2 位错 c3 位错 c4 位错 c5 位错 c6 位错
00000，11101，11110，11000，10100。
编
码
2
习题解答
第 4.2 求 000000、110110、011101、101010 四码字的汉明距离，
四
并据此拟出校正错误用的译码表。

信息论与编码技术第四章课后习题答案

解：（1） D =
∑ P(u,υ )d (u,υ ) = (1 − p)q
UV
（2）根据题4.5，可知R(D)的最大值为H(p),此时q=0,平均失真D=0; （3）R(D)的最大值为0,此时q=1,平均失真D=（1-p）; 4.7 设连续信源 X ，其概率密度分布为
p ( x) =
a − a | x| e 2
达到
D
min
的信道为
⎡1 ⎡1 0 ⎤ ⎡1 0 ⎤ ⎢ ⎥ ⎢ ⎥ ⎢1 [ P (υ j | u i )] = ⎢ ⎢ 0 1 ⎥ , ⎢1 0 ⎥ 或 ⎢ 2 ⎢ ⎣0 1 ⎥ ⎦ ⎢ ⎣0 1⎥ ⎦ ⎢0 ⎣
4.2 已知二元信源 ⎢
0⎤ 1⎥ ⎥ 2⎥ 1⎥ ⎦
1 ⎤ ⎡ X ⎤ ⎡ 0, ⎡0 1⎤ =⎢ =⎢ 以及失真矩阵 ⎡ dij ⎤ ⎥ ⎥ ⎥ ，试求： ⎣ ⎦ ⎣ p ( x ) ⎦ ⎣ p, 1 − p ⎦ ⎣1 0 ⎦
g (θ ) 的傅立叶变换
G s(w) = ∫
+∞ −∞
g
s
(θ )e
− jwθ
dθ =
s
2
s
2 2
+w
, (3)
得: Q( w) = P ( w) + w2 P( w), (4)
2
s
求式（4）的傅立叶反变换，又根据式（2）得
p( y ) = p( x = y) − D 所以 p( y ) =
2
p ( x = y), (5)
⎡0 ⎢1 定义为 D = ⎢ ⎢1 ⎢ ⎣1
解：
1 0 1 1
1 1 0 1
1⎤ 1⎥ ⎥ ，求 Dmax , Dmin 及信源的 R ( D ) 函数，并作出率失真函数曲线(取4到5个点)。 1⎥ ⎥ 0⎦

《信息论与编码理论》(王育民李晖梁传甲)课后习题问题详解高等教育出版社

信息论与编码理论习题解第二章-信息量和熵2.1解: 平均每个符号长为:1544.0312.032=⨯+⨯秒每个符号的熵为9183.03log 3123log 32=⨯+⨯比特/符号所以信息速率为444.34159183.0=⨯比特/秒2.2 解: 同步信号均相同不含信息,其余认为等概,每个码字的信息量为 3*2=6 比特；所以信息速率为600010006=⨯比特/秒2.3 解:(a)一对骰子总点数为7的概率是366 所以得到的信息量为 585.2)366(log 2= 比特 (b) 一对骰子总点数为12的概率是361 所以得到的信息量为 17.5361log 2= 比特 2.4 解: (a)任一特定排列的概率为!521,所以给出的信息量为 58.225!521log 2=- 比特 (b) 从中任取13张牌,所给出的点数都不相同的概率为13521313521344!13C A =⨯所以得到的信息量为 21.134log 1313522=C 比特.2.5 解:易证每次出现i 点的概率为21i,所以比特比特比特比特比特比特比特398.221log 21)(807.1)6(070.2)5(392.2)4(807.2)3(392.3)2(392.4)1(6,5,4,3,2,1,21log )(2612=-==============-==∑=i i X H x I x I x I x I x I x I i ii x I i2.6 解: 可能有的排列总数为27720!5!4!3!12= 没有两棵梧桐树相邻的排列数可如下图求得， Y X Y X Y X Y X Y X Y X Y X Y图中X 表示白杨或白桦，它有⎪⎪⎭⎫⎝⎛37种排法，Y 表示梧桐树可以栽种的位置，它有⎪⎪⎭⎫⎝⎛58种排法，所以共有⎪⎪⎭⎫ ⎝⎛58*⎪⎪⎭⎫⎝⎛37=1960种排法保证没有两棵梧桐树相邻，因此若告诉你没有两棵梧桐树相邻时，得到关于树排列的信息为1960log 27720log 22-=3.822 比特 2.7 解: X=0表示未录取，X=1表示录取； Y=0表示本市，Y=1表示外地；Z=0表示学过英语，Z=1表示未学过英语，由此得比特比特比特)01(log )01()0()00(log )00()0()(8113.04log 4134log 43)()(02698.04110435log 104354310469log 10469)1()01(log )01()0()00(log )00()0;(104352513/41)522121()0(/)1())11()1,10()10()1,00(()01(104692513/43)104109101()0(/)0())01()0,10()00()0,00(()00()(4512.04185log 854383log 83)1()01(log )01()0()00(log )00()0;(8551/4121)0(/)1()10()01(8351/43101)0(/)0()00()00()(,251225131)1(,2513100405451)10()1()00()0()0(,54511)1(,51101432141)10()1()00()0()0(,41)1(,43)0(222222222222+=====+=======+==+======+========⨯⨯+========+=========⨯⨯+========+=========+======+========⨯=========⨯=========-===⨯+====+======-===⨯+⨯====+=========x y p x y p x p x y p x y p x p X Y H X H c x p z x p z x p x p z x p z x p z X I z p x p x y p x y z p x y p x y z p z x p z p x p x y p x y z p x y p x y z p z x p b x p y x p y x p x p y x p y x p y X I y p x p x y p y x p y p x p x y p y x p a z p y z p y p y z p y p z p y p x y p x p x y p x p y p x p x p2.8 解:令{}{}R F T Y B A X ,,,,==，则比特得令同理03645.0)()(5.0,02.03.0)2.05.0(log 2.0)()2.05.0(log )2.05.0()2.03.0(log )2.03.0(5.0log 5.03.0log 3.0)5log )1(2.02log )1(5.0log )1(3.05log 2.0log 3.02log 5.0(2.0log 2.0)2.05.0(log )2.05.0()2.03.0(log )2.03.0()()();()(2.0)(,2.05.0)(2.03.0)1(3.05.0)()()()()(5.0max 2'2222223102231022222==∴==+-=---++-+=-+-+-+++-----++-=-===-=+=-⨯+=+==p p I p I p pp p I p p p p p p p p p p p p p p X Y H Y H Y X I p I R P p F P pp p B P B T P A P A T P T P2.9 & 2.12解:令X=X 1,Y=X 1+X 2,Z=X 1+X 2+X 3, H(X 1)=H(X 2)=H(X 3)= 6log 2 比特 H(X)= H(X 1) = 6log 2 =2.585比特 H(Y)= H(X 2+X 3)=6log 61)536log 365436log 364336log 363236log 36236log 361(2222222+++++ = 3.2744比特 H(Z)= H(X 1+X 2+X 3)=)27216log 2162725216log 2162521216log 2162115216log 2161510216log 216106216log 21663216log 2163216log 2161(222222222++++++= 3.5993比特所以H(Z/Y)= H(X 3)= 2.585 比特 H(Z/X) = H(X 2+X 3)= 3.2744比特 H(X/Y)=H(X)-H(Y)+H(Y/X) = 2.585-3.2744+2.585 =1.8955比特H(Z/XY)=H(Z/Y)= 2.585比特 H(XZ/Y)=H(X/Y)+H(Z/XY) =1.8955+2.585 =4.4805比特 I(Y;Z)=H(Z)-H(Z/Y) =H(Z)- H(X 3)= 3.5993-2.585 =1.0143比特 I(X;Z)=H(Z)-H(Z/X)=3.5993- 3.2744 =0.3249比特 I(XY ;Z)=H(Z)-H(Z/XY) =H(Z)-H(Z/Y)=1.0143比特 I(Y;Z/X)=H(Z/X)-H(Z/XY) = H(X 2+X 3)-H(X 3) =3.2744-2.585 =0.6894比特 I(X;Z/Y)=H(Z/Y)-H(Z/XY) =H(Z/Y)-H(Z/Y) =02.10 解:设系统输出10个数字X 等概,接收数字为Y,显然101)(101)()()(919===∑∑==i j p i j p i Q j w i iH(Y)=log10比特奇奇奇奇偶18log 81101452log 211015)(log)()()(log )()(0)(log ),()(log ),()(22,2222=⨯⨯⨯⨯+⨯⨯⨯=--=--=∑∑∑∑∑∑∑≠====x y p x y p x p x x p x x p x p x y p y x p x y p y x p X Y H x y x i y x y x所以I(X;Y)= 3219.2110log 2=-比特2.11 解:（a ）接收前一个数字为0的概率 2180)0()()0(==∑=i i i u p u q wbits p pw u p u I )1(log 11log )0()0(log )0;(2212121-+=-==（b ）同理 418)00()()00(==∑=ii iu p u q wbits p p w u p u I )1(log 22)1(log )00()00(log )00;(24122121-+=-== （c ）同理 818)000()()000(==∑=ii iu p u q wbits p p w u p u I )1(log 33)1(log )000()000(log )000;(28132121-+=-== （d ）同理 ))1(6)1(()0000()()0000(4226818p p p p u p u q w ii i+-+-==∑=bitsp p p p p p p p p p w u p u I 42264242268142121)1(6)1()1(8log ))1(6)1(()1(log )0000()0000(log )0000;(+-+--=+-+--==2.12 解:见2.9 2.13 解: (b))/()/()/(1log)()/(1log)()/()/(1log)()/(1log)()/(XY Z H X Y H xy z p xyz p x y p xyz p xy z p x y p xyz p x yz p xyz p X YZ H x y z xyzxyzxyz+=+===∑∑∑∑∑∑∑∑∑∑∑∑(c))/()/(1log)/()()/(1log)/()()/(X Z H x z p xy z p xy p xy z p xy z p xy p XY Z H xyzxyz=≤=∑∑∑∑∑∑（由第二基本不等式）或)1)/()/((log )/()()/()/(log)/()()/(1log)/()()/(1log)/()()/()/(=-⨯≤=-=-∑∑∑∑∑∑∑∑∑∑∑∑xy z p x z p e xy z p xy p xy z p x z p xy z p xy p x z p xy z p xy p xy z p xy z p xy p X Z H XY Z H xyzxyzxyzxyz（由第一基本不等式）所以)/()/(X Z H XY Z H ≤(a))/()/()/()/()/(X YZ H XY Z H X Y H X Z H X Y H =+≥+等号成立的条件为)/()/(x z p xy z p =,对所有Z z Y y X x ∈∈∈,,,即在给定X 条件下Y 与Z 相互独立。

《信息论与编码》习题解答第四章(新)new

《信息论与编码》习题解答第四章信息率失真函数-习题答案4.1解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率⎥⎦⎤⎢⎣⎡--=εεεε11)|(i j a b p 平均失真：εεεεε=⨯-⨯+⨯⨯+⨯⨯+⨯-⨯==∑∑==0)1(2/112/112/10)1(2/1),()|()(2121j i i j i j i b a d a b p a p D4.2解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0210d ， 0min =D ,∑=⨯+⨯=⨯+⨯===ij i i j j y x d x p D D )102/122/1(2/112/102/1),()(min min max 舍去当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=1001P当2/1max =D ，0)(max =D R因为取的是第二列的max D 值，所以输出符号概率:,1)(,0)(21==b p b p ,,2221b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=1010P 4.3解：0min =D0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 当0min =D ，bit X H R D R 24log )()0()(min ==== 因为没有失真，此时的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P 当4/3max =D ，0)(max =D R因为任何一列的max D 值均为3/4，所以取输出符号概率:0)(,0)(,0)(,1)(4321====b p b p b p b p ，即14131211,,,b a b a b a b a →→→→因此编码器的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P 4.4解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=4/1014/110d ， 0min =D∑=⨯+⨯===ij i i j j y x d x p D D )2/12(4/1)4/12/14/12/1min(),()(min min max 个均为其它当0min =D ，bit X H R D R 12log )()0()(min ====因为没有失真，此时的转移概率为⎥⎦⎤⎢⎣⎡=010001P 当4/1max =D ，0)(max =D R因为取的是第三列的max D 值为1/4，所以取输出符号概率:1)(,0)(,0)(321===b p b p b p ，即3231,b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=100100P 4.5解：(1)依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡=0110d ，转移概率为：⎥⎦⎤⎢⎣⎡-=q q P 101 )1(0)1()1(1)1(1001),()|()(11p q q p q p p p y x d x y p x p D n i mj j i i j i -⨯=⨯-⨯-+⨯⨯-+⨯⨯+⨯⨯==∑∑==(2) 0min =D因为)(D R 是D 的递减函数，所以)1log()1(log )()()())(m ax (min min p p p p D H p H D R D R ----=-==当0=q 时可达到))(max(D R ，此时0=D(3) ∑-=⨯+⨯===iji i j j ，p p p p y x d x p D D )1(10),()(min min max 舍去更大另一个因为)(D R 是D 的递减函数，所以0)()()())(m in(max max =-==D H p H D R D R当1=q 时可达到))(min(D R ，此时p D -=1(图略，见课堂展示)4.6解：依题意可知：失真矩阵：⎥⎦⎤⎢⎣⎡∞∞=1010d ，信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/12/110)(u p u 0min =D ，∑⨯+⨯⨯+∞⨯∞⨯+⨯===iji i j j y x d x p D D )12/112/1,02/12/1,2/102/1min(),()(min min max )(1]1,,m in[舍去另二个，∞=∞∞=10≤≤D因为二元等概信源率失真函数：⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中1,2==a n ，所以率失真函数为：D D R -=1)(4.7解：失真矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110d ，按照P81页方法求解。

信息论与编码第四章课后习题答案

∫ =
− log λe−λx
∞ 0
+ log e
ln e−λx de−λx
∫ =
− log
λ
+
log
et
ln
t
0 1
−
log
e
dt
= −log λ + log e
= log e λ
（2）
h( X )
= −∫ p(x)log p(x)dx
∫ = − ∞ 1 λe−λ x log 1 λe−λ x dx
−∞ 2
2
∫ = − ∞ λe−λx log 1 λe−λxdx
0
2
∫ ∫ = − ∞ λe−λx log 1 dx − ∞ λe−λx log λe−λxdx
0
2
0
= log 2 + log e λ
= log 2e λ
注：（2）题直接借用了（1）的结论。
【4.3】设有一连续随机变量，其概率密度函数为：
sin
x
=
1 2
log
e∫
ln(1
+
sin
x)d
sin
x
+
1 2
log
e∫
ln(1
−
sin
x)d
sin
x
∫ ∫ ln(1+ sin x)d sin x
π
= (1 + sin
x) ln(1+ sin
x)
2 −π
−
2
1 + sin x d sin x 1 + sin x
= 2ln 2 − 2
∫ ln(1− sin x)d sin x

信息论与编码原理-第4、5章课后习题-20140604-23点-自己整理

（4）编码效率
H (S ) R L 0.839 Rmax log r
s2 s3 s4 s5 s6 4.3 某信源概率空间为 S s1 P(s) 0.3 0.25 0.2 0.15 0.06 0.04 进行二元编码，5种不同的编码方案如表4.20所示。
5.1 设二进制对称信道的传递矩阵为
0.8 0.2 0.2 0.8
（1）若信道输入符号 P（0） 3/ 4, P(1) 1/ 4 ，求 H ( X ) 、 H ( X | Y )、
H (Y | X ) 和 I ( X ; Y ) 。
（2）求该信道的信道容量及达到信道容量的最佳输入概率分布。（3）如果信道输入符号 P（0） 3/ 4, P(1) 1/ 4 时，计算信道剩余度。
5.4 设某信道的转移矩阵为
p 1 p q q P p q 1 p q
求其信道容量。
1 p q1 p q
p 1 p q P1 p 1 p q q P2 q
（1） H ( x) H ( 3 4 , 1 4) 0.811 bit/符号
X Y 的联合分布概率为：
X
Y
0 1
0 3 5 1 20
1
3 20 1 5
H ( XY ) H ( 3 , 3 , 1 , 1 ) 1.533 bit/符号 5 20 20 5
H (Y ) H (13 20 ,7 ) 0.934 bit/符号 20
5.3 设某对称离散信道的信道矩阵为
0 0.5 0.5 0 0 0 0.5 0.5 P 0.5 0 0 0.5 0 0.5 0.5 0 （1）求其信道容量。

信息论与编码第4章习题解答

《信息论与编码》第四章习题解答4.1 计算如下所示离散无记忆信道的容量：习题4.1图［解］　（a ）信道概率转移矩阵为−−−−=δεδεεδδε11P ，信道是准对称信道，因此在输入为等概分布时达到信道容量，即5.0)1()0(====X P X P 时达到信道容量。

这时δ5.05.0)0(−==Y P δ==)1(Y Pδ5.05.0)2(−==Y P相应的信道容量为);1();0(Y X I Y X I C ====∑==2)()0|(log)0|(j j p j p j p 0111-ε1-δε δ 00 121-ε-δ εδδ 1-ε-δ1ε0 221 0.5 δ 110.250.25 0.50.50 2 21-ε ε ε 1-ε1ε 11-ε 0 0 223/41/4 111/3 1/31/3 1/43/40 2 311/3 211/31/3 1/31/31/3 1/3 1/31/3 (c)(a)(b) (e)(f)(d)δεεδδδδδεδε5.05.0log log 5.05.01log)1(−++−−−−−=)5.05.0log()1(log )1log()1(δδεεδεδε−−−+−−−−= （b ）信道概率转移矩阵为=5.05.0025.025.05.0001P当5.0)2()0(====X P X P ，0)(=X P 时，5.0)0(==Y P ，25.0)1(==Y P ，25.0)2(==Y P1)()0|(log )0|();0(2===∑=j j p j p j p Y X I bit∑===2)()2|(log)2|();2(j j p j p j p Y X I 125.05.0log 5.025.05.0log 5.0=+= bit10);1(≤==Y X I ；所以满足定理4.2.2条件，由达到信道容量充要条件可知，信道容量C =1 bit/次（c ）信道转移概率矩阵为−−−=εεεεεε101001P ，信道是对称信道，当输入为均匀分布时，即31)2()1()0(======X P X P X P 时，达到信道容量。

信息论与编码第四章课后习题答案

π 2 π − 2
−∫
1 − sin x d sin x 1 − sin x
因此有
h( X ) = −2 A log A −
A log e(2 ln 2 − 2 + 2 ln 2 − 2) 2Байду номын сангаас= −2 A log A + 2 A log e − 2 A log e ln 2 = −2 A log A + 2 A log e − 2 A 1 ，因此 2
试计算 h( X ) ， h(Y ) ， h( XY ) 和 I ( X ; Y ) 。解： p( x) = ∫ p ( x, y )dy 1 =∫ dy (a 2 − a1 )(b2 − b1 ) = 1 a2 − a1
同理， p( y ) = 因此
1 。 b2 − b1
h( X ) = − ∫ p ( x ) log p ( x)dx = log(a 2 − a1 ) h(Y ) = − ∫ p( y ) log p( y )dy = log(b2 − b1 ) h( XY ) = − ∫ p ( x, y ) log p ( x, y )dxdy = log( a2 − a1 ) + log(b2 − b1 ) I ( X ; Y ) = h( X ) + h(Y ) − h( XY ) = 0 【4.7】在连续信源中，根据差熵、条件差熵和联合差熵的定义，证明（1） h( X | Y ) ≤ h( X ) ，当且仅当 X 和 Y 统计独立时等号成立；（2）h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) ，当且仅当 X 1 X 2 L X N 彼此统计独立时等式成立。证明：（1） h( XY ) = − ∫ p( y )dy ∫ p( x | y ) log p ( x | y )dx ≤ − ∫ p ( y )dy ∫ p( x | y ) log p ( x )dx = − ∫ p( x, y ) log p ( x )dxdy = h( X ) 等号成立当且仅当 p( x | y ) = p ( x ) ，即 p( x, y ) = p( x ) p ( y ) ，因此仅当 X 和 Y 统计独立时等号成立。（2）根据条件概率密度的相关公式，有 h( X 1 X 2 X N ) = h( X 1 ) + h( X 2 | X 1 ) + h( X 3 | X 1 X 2 ) + L + h( X N | X 1 X 2 X N −1 ) 根据（1）的结论，条件差熵小于差熵，因此有 h( X 1 X 2 L X N ) ≤ h( X 1 ) + h( X 2 ) + L + h( X N ) 等号成立当且仅当

第4章习题解答

信息论与编码习题详解第四章4。

1 某集源按 P（0)=3/4，P(1）=1/4 的概率产生统计独立的二元序列.(1)试求 N0，使当 N>N 0时有： P｛｜ I(a i)/N－H(S）｜≥ 0.05}≤ 0.01其中 H（ S)是信源的熵。

(2)试求当 N= N0时典型序列集 Gε N 中含有的信源序列个数.解：(1) H(S)= —∑ Pi ㏒ Pi= -3/4 ㏒ (3/4) —1/4 ㏒ (1/4 ）=0.811比特/符号依照契比雪夫不等式，对于任意ε＞0，当 N＞ N0 时，P ｛∣ I( αi)/N – H(S ）∣≥ε｝≤ D[I(Si ）］/N ε2现有ε =0.05, 欲证原式，只要D［ I(Si ）]/N ε2≤ 0。

01依照信源， D［ I （ Si)]= ∑P（ Si ）［㏒ P(Si) ］2– H 2（ S)=3/4 （㏒ 3/4) 2+1/4 （㏒ 1/4) 2— (0 。

811) 2=0 。

4712 2∴ N0= D[I(Si)]/0。

01ε =0.471/0 。

01×（ 0.05) =18840(2)序列 GεN是所有 N 长的ε典型序列会集，（1-δ）2N［H（ S）—ε ] ≤‖GεN‖≤2N[H（ S） - ε]0.99 × 214342。

5≤‖ GεN‖≤ 216226。

54。

2 设无记忆二元信源，其概率为P1=0.005, P0=0。

995.信源输出 N＝ 100 的二元序列 .在长为 N＝100 的信源序列中只对含有 3 个或小于 3 个“1的”各信源序列组成一一对应的一组等长码。

（1）求码字所需的最小长度。

（2）计算式（ 4.27a）中的ε。

(3）考虑没有恩赐编码的信源序列出现的概率，该等长码引起的错误概率PE 是多少？若从契比雪夫不等式（ 4。

22）考虑， PE 应是多少？试加以比较。

解：（ 1）无记忆二元信源S 0, 1P s i 0.995 0.005N=100 的扩展信源S NN N N N1 0，2 0，，2 N 1 11 10, 2 N 11 1P i 0 01N N－1 ，，N 1 N0.995 , 0.995 0.995 0.005 , 0.0050.005现只对含有 3 个或小于 3 个“ 1”的各信源序列组成一一对应的一组二元等长码。

第四章习题答案

第4章习题4-1 对信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s P S 7654321进行二元编码，编码方案为（1）计算平均码长L ；（2）编码后信息传输率R ；（3）编码信息率R '；（4）编码效率η。

解：（1）()14.3Ls p L iq1i i=⋅=∑=（码元/信源符号）（2）()61.2S H =（比特/信源符号）()831.014.361.2L S ===H R （bit/码元）（3）logr L R ='=3.14（ bit/信源符号）（4）831.0R Rmax==η 或者()831.0RS H ='=η 4-2 设离散无记忆信源的概率空间为⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡4143s s S 21P ，若对信源采取等长二元编码，要求编码效率96.0=η，允许译码错误概率510-≤δ，试计算需要的信源序列长度N 为多少？解：信源熵为()811034log 434log 41S .Η=+=（bit/符号）自信息量的方差()()()[]22i q1i i 2S H logp p S -=∑=σ4715.0811.041log 4143log 43222=-⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛= 因为编码效率96.0=η，由()()ε+=S S H H η可得()3379.0811.096.004.0S H 1=⨯=-=ηηε 可得()752221013.4103379.04715.0S N ⨯=⨯=≥-δεσ 所以，信源序列长度达到71013.4⨯以上，才能实现给定的要求，因此等长编码没有实际的意义，一般统计编码都是采用不等长编码。

4-6设离散无记忆信源的概率空间为⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡1.09.0s s S 21P ，对信源进行N 次扩展，采用霍夫曼编码。

当N=1，2，∞时的平均码长和编码效率为多少？解：（1）N=1时，将1s 编成0，2s 编成1，则1L 1=又因为信源熵()469.0))logp(s p(s S H q1i i i =-=∑=bit/符号所以()469.0L S H 11==η （2）N=2时，编码过程如下2S概率霍夫曼编码11s s 0.81121s s 0.09 01 12s s 0.09 000 22s s 0.01001所以()=+⨯+⨯+⨯=0.090.0130.0920.811L 2则645.02L 2= 所以()==0.645X H 2η （3）N=∞时，由香农第一定理可知，必然存在唯一可译码，使()S H N L limr NN =∞→而霍夫曼编码为最佳码，即平均码长最短的码，故()()469.0S H S H N L limr NN ===∞→即1lim N N =∞→η4-7已知信源共7个符号消息，其概率空间为()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.010.015.017.018.019.02.0s s s s s s s x P S 7654321试进行香农编码。

信息论与编码第4章习题解答

P[ Z N
= 1|
X
= 0] =
P
Z
'
N
>
1 2
|
X
= 0
=
PZ 'N
−p
>
1 2
−
p|
X
=
0
≤
P|
Z
' N
−
p
|>
1 2
−
p|
X
=
0
≤
σ2 Z 'N |X =0

1 2
−
p 2
= p(1 − p) N (1 − p)2 2
当 p < 1 ，以及 N 充分大时 2
求该级联信道的容量 C N
，并证明
lim
N →∞
C
N
=0
X0
BSC X1
BSC X2 ……
BSC XN
习题 4.4（1）图级联信道
（2）并联输入信道，把输入 X 并联接到各信道，输出是矢量，当 N → ∞ 时并联输
入信道容量趋于 1。
X
BSC Y1
BSC Y2
BSC YN
习题 4.4（2）图并联输入信道
所以
C = 6 ⋅ 1 log 1/ 3 + 3 ⋅ 1 log 1/ 3 9 2/9 9 1/3
= 2 log 3 bit/次 32
（f）信道转移概率矩阵
P
=
1
− δ
ε
1
ε −
δ

利用方程求逆方法计算信道容量。设
p( X = 0) = q ， p( X = 1) = 1 − q ， 0 < q < 1

信息论与编码理论-第4章无失真信源编码-习题解答-20071202

信息论与编码理论-第4章无失真信源编码-习题解答-20071202信息论与编码理论第4章无失真信源编码习题及其参考答案4-1 有一信源，它有六个可能的输出，其概率分布如下表所示，表中给出了对应的码A、B、C、D、E和F（1）求这些码中哪些是唯一可译码；（2）求哪些码是及时码；（3）对所有唯一可译码求出其平均码长。

?X??s14-2 设信源????p(s)P(X)???1s6?p(s2)?p(s6)???s2?p(s)?1。

对此次能源进行m元唯一ii?16可译编码，其对应的码长为（l1,l2,…,l6）=(1,1,2,3,2,3)，求m值的最好下限。

（提示：用kraft不等式）?s?X??14-3设信源为??1??p(X)???2?（1）信源的符号熵；（2）这种码的编码效率；s214s3s411816s5132s6s7s8?，编成这样的码：（000，001，111???64128128?010，011，100，101，110，111）。

求（3）相应的仙农码和费诺码。

4-4求概率分布为(,11122信)源的二元霍夫曼编码。

讨论此码对于概率分布为355151511111(,,,,)的信源也是最佳二元码。

555554-5有两个信源X和Y如下：1信息论与编码理论s2s3s4s5s6s7??X??s1??p(X)??0.200.190.180.170.150.100.01?????s2s3s4s5s6s7s8s9??Y??s1??p(Y)??0.490.140.140.070.070.040.020.02 0.01?????（1）用二元霍夫曼编码、仙农编码以及费诺编码对信源X和Y进行编码，并计算其平均码长和编码效率；（2）从X，Y两种不同信源来比较三种编码方法的优缺点。

4-6设二元霍夫曼码为（00，01，10，11）和（0，10，110，111），求出可以编得这样霍夫曼码的信源的所有概率分布。

4-7设信源为?码。

信息论编码第四章答案

解：
唯一可译码是Ａ，Ｂ，Ｃ，Ｅ唯可译码是Ａ，Ｂ，Ｃ，Ｅ,非延长码为A，C，E Ａ的平均码长：n = p( si )ni
i =1 6
= 3(1 / 2 + 1 / 4 + 1 / 16 + 1 / 16 + 1 / 16 + 1 / 16)
= 3码符号 / 信源符号
编码效率：
η=
H (s) 2 = * 100% = 66.67% n log r 3
2. 有一个信源X如下：
x2 x3 x4 x5 x6 X x1 p ( x) = 0.32 0.22 0.18 0.16 0.08 0.04
(1)、求信源熵; (2)、用Shannon编码法编成二进制变长码，并计算其编码效率； (3)、用用Fano编码法编成二进制变长码，并计算其编码效率；编码法编成二进制变长码并计算其编码效率 (4)、用Huffman码编码成二进制变长码，并计算其编码效率； (5)、用Huffman码编码成三进制变长码，并计算其编码效率； (6)、比较三种编码方法的优缺点。
H ( X ) 2.3522 = × 100% = 98% n log l r 2.4 log l 2
三进制Huffman编码 ? 首先, 判断q − (r − 1)α = r 6 − (3 − 1) × 2 = 2 < 3
选择m = r − [q − (r − 1)α ] = 3 − 2 = 1个虚假符号
0.40 0.60 0 0.37 0 0.40 1 0 0.23 1 1
L = P( si )li = 2.63
i =1
二元符号／灰度级
通过哈夫曼最佳二元编码后，每个像素平均需要用 2.63个二元符号，则此图象平均共需要用263个二元符号来表示。因此，需2.63秒才能传送完这幅图象。 (3)在(2)题中计算时没有考虑图象的像素之间的依赖关系，但实际此图象的像素之间是有依赖的。例如，若考虑像素前后之间灰度的依赖关系，就有灰度“1”后面只可能出现灰度“1”或 “2”；灰度“2”后只可能出现“2” 或“3” ，等等。这时，此图象灰度值信源Ｓ可以看成一阶马尔可夫信源。还可以进一步看成为m 阶马尔可夫信源。因此，在考虑了这些依赖关系后，像素的灰度值信源Ｓ的实际信息熵 H ∞ < H ( S ) 。根据香农第一理，总可以找到一种编码，使每个灰度级的平均码长L → H ∞ (极限熵)。所以，这幅图象还可以进一步压缩，平均每个像素(灰度)所需要的二元码符号数 L < H ( S ) 。

信息论与编码理论-第4章无失真信源编码-习题解答-20071202

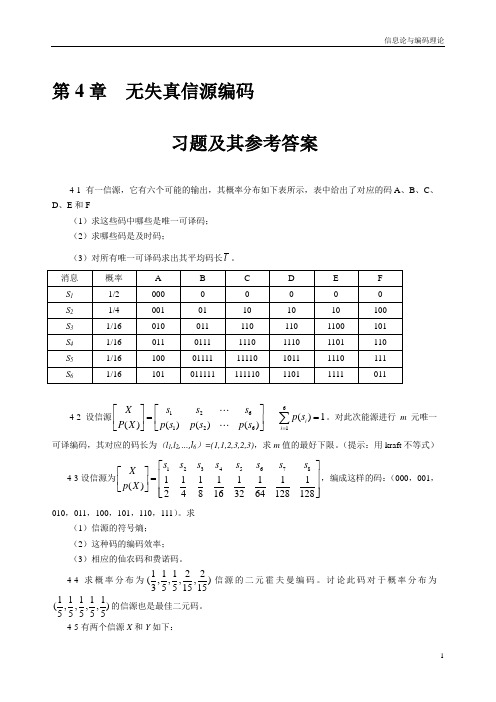
第4章无失真信源编码习题及其参考答案4-1 有一信源，它有六个可能的输出，其概率分布如下表所示，表中给出了对应的码A、B、C、D、E和F（1）求这些码中哪些是唯一可译码；（2）求哪些码是及时码；（3）对所有唯一可译码求出其平均码长l。

4-2 设信源61261126()1()()()()iis s sXp sp s p s p sP X=⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∑。

对此次能源进行m元唯一可译编码，其对应的码长为（l1,l2,…,l6）=(1,1,2,3,2,3)，求m值的最好下限。

（提示：用kraft不等式）4-3设信源为1234567811111111()248163264128128s s s s s s s sXp X⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦，编成这样的码：（000，001，010，011，100，101，110，111）。

求（1）信源的符号熵；（2）这种码的编码效率；（3）相应的仙农码和费诺码。

4-4求概率分布为11122(,,,,)3551515信源的二元霍夫曼编码。

讨论此码对于概率分布为11111(,,,,)55555的信源也是最佳二元码。

4-5有两个信源X和Y如下：121234567()0.200.190.180.170.150.100.01X s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦123456789()0.490.140.140.070.070.040.020.020.01Y s s s s s s s s s p Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦（1）用二元霍夫曼编码、仙农编码以及费诺编码对信源X 和Y 进行编码，并计算其平均码长和编码效率；（2）从X ，Y 两种不同信源来比较三种编码方法的优缺点。

4-6设二元霍夫曼码为（00，01，10，11）和（0，10，110，111），求出可以编得这样霍夫曼码的信源的所有概率分布。

4-7设信源为12345678()0.40.20.10.10.050.050.050.05X s s s s s s s s p X ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，求其三元霍夫曼编码。

《信息论与编码理论》(王育民李晖梁传甲)课后习题答案高等教育出版社

信息论与编码理论习题解第二章 -信息量和熵2.1 解: 平均每个符号长为 :20.2 10.4 4 秒3315每个符号的熵为 2log31 log 3 0.9183 比特 /符号 32 3所以信息速率为 0.9183 15 3.444 比特 /秒42.2 解: 同步信号均相同不含信息,其余认为等概 ,每个码字的信息量为 3*2=6 比特；所以信息速率为 6 10006000 比特 /秒2.3 解:(a) 一对骰子总点数为 7 的概率是 636所以得到的信息量为log 2( 6) 2.585 比特36(b)一对骰子总点数为 12 的概率是 136所以得到的信息量为log 21 比特5.17362.4 解: (a)任一特定排列的概率为1,所以给出的信息量为52!1log252 !225.58比特(b) 从中任取 13 张牌 ,所给出的点数都不相同的概率为13! 413413A 5213C 135213所以得到的信息量为 log 2C 5213.21 比特 .4132.5 解:易证每次出现 i 点的概率为i,所以21I (x i )log 2i, i 1,2,3,4,5,6 21I (x1) 4.392 比特I (x2) 3.392 比特I (x3) 2.807 比特I (x4) 2.392比特I (x5) 2.070 比特I (x6) 1.807 比特6i log2i比特H(X)212.398i 1212.6 解: 可能有的排列总数为12!277203! 4! 5!没有两棵梧桐树相邻的排列数可如下图求得，Y X Y X Y X Y X Y X Y X Y X Y图中 X 表示白杨或白桦，它有73种排法， Y 表示梧桐树可以栽种的位置，它有8种排法，所以共有8 *7=1960种排法保证没有553两棵梧桐树相邻，因此若告诉你没有两棵梧桐树相邻时，得到关于树排列的信息为 log2 27720log 2 1960 =3.822比特2.7 解: X=0 表示未录取， X=1 表示录取；Y=0 表示本市， Y=1 表示外地；Z=0 表示学过英语， Z=1 表示未学过英语，由此得p( x0) 3 ,p(x1)4 p( y0)p( x 0) p( y 1 1 3 142 410 p( y 1)1 1 4 ,5 5p( z 0)p( y 0) p(z 14405 5 100 p( z 1)1 13 12 ,25 25(a) p( x0 y 0) p( yp( x1 y 0) p( y1 , 40 x 0)p( x 1) p( y 0 x 1)1 , 50 y 0) p( y 1) p( z 0 y 1)13 , 250 x 0) p( x 0) / p( y0)13 1310/5 84 0 x 1) p( x 1) / p( y0) 1 1 / 152 4 58I ( X ; y 0)p(x0 y p(x 0 y 0) p( x 1 y 0)0) log 2p(x 1 y 0) log 2p( x 0)p( x 1)3 log 2 35log 2 58 8 8 3 8 14 40.4512比特(b) p( x0 z 0)( p( z 0 y 0, x 0) p( y 0 x 0) p( z 0 y 1, x 0) p( y 1x 0)) p(x0) / p( z 0)(19 4 ) 3/1369 10 10 10 4 25 104p( x 1z 0)( p( z 0 y 0, x 1) p( y 0 x 1) p(z 0 y1, x 1) p( y 1 x 1)) p( x1) / p(z 0)(11 2) 1/13 3522 5 4 25104I ( X ; z 0)p( x 0 zp( x 0 z 0)p( x p(x 1 z 0)0) log 21z 0) log 21)p( x 0)p( x6969log 2104104343510435log 21041 40.02698 比特(c) H ( X )3 log 24 1 log 2 40.8113 比特4 3 4H(Y X)p( x 0) p( y 0 x 0) log 2 p( y 0 x 0) p( x 0) p( y 1 x 0) log 2 p( y 1x 0)p( x 1) p( y 0 x1) log 2 p( y 0 x 1)p( x 1) p( y 1 x1) log 2 p( y 1 x1)3 1log 2 10 3 9log 2 10 1 1 log 2 2 11log 2 2 410410 9 4 2 4 20.6017比特2.8 解:令X A,B,Y T,F,R ，则P(T)P(T A)P(A)P(T B)P(B)0.5 p0.3(1p)0.3 0.2 p同理P(F )0.50.2 p,P(R)0.2I ( p) I ( X ; Y)H (Y)H(Y X)(0.30.2p) log2 (0.30.2 p)(0.50.2p) log2 (0.50.2 p)0.2log 2 0.2(0.5 p log2 20.3 plog 21030.2 p log2 50.3(1p) log2103 0.5(1 p) log2 20.2(1p) log2 5)0.3log 2 0.30.5log 2 0.5(0.30.2p) log2 (0.30.2 p)(0.50.2 p) log2 (0.5 0.2 p)令I '( p)0.2 log2(0.50.2 p)0,得p0.50.30.2 pI ( p)max I ( p) p0 .50.03645比特2.9 & 2.12解:令 X=X 1,Y=X 1+X 2,Z=X 1+X 2+X 3, H(X 1)=H(X 2)=H(X 3)= log26比特H(X)= H(X 1) = log26=2.585 比特H(Y)= H(X 2+X 3)=2( 1log 2 362log 2363log 2364log 2365log 236 )1log 2 6363623633643656 = 3.2744 比特H(Z)= H(X 1+X 2+X 3)=2( 1 log 2 216 3 log 2 216 6log 2 216 10 log 2 216 15 log 2 216216 216 3 216 6 216 10 216 15 21 216 25 216 27 216 )log 2 21 log 2 log 2 27216 216 25 216= 3.5993 比特所以H(Z/Y)= H(X 3)= 2.585 比特H(Z/X) = H(X 2+X 3)= 3.2744 比特H(X/Y)=H(X)-H(Y)+H(Y/X)= 2.585-3.2744+2.585 =1.8955 比特H(Z/XY)=H(Z/Y)= 2.585 比特 H(XZ/Y)=H(X/Y)+H(Z/XY)=1.8955+2.585=4.4805 比特I(Y;Z)=H(Z)-H(Z/Y)=H(Z)- H(X 3)= 3.5993-2.585 =1.0143 比特I(X;Z)=H(Z)-H(Z/X)=3.5993- 3.2744=0.3249 比特I(XY ;Z)=H(Z)-H(Z/XY)=H(Z)-H(Z/Y)=1.0143 比特I(Y;Z/X)=H(Z/X)-H(Z/XY)=H(X 2+X 3)-H(X3) =3.2744-2.585=0.6894 比特I(X;Z/Y)=H(Z/Y)-H(Z/XY)=H(Z/Y)-H(Z/Y)=02.10 解:设系统输出10 个数字 X 等概 ,接收数字为 Y,9191显然 w( j )Q(i ) p( j i )p( j i )i010 i 110H(Y)=log10H(YX)p( x, y) log 2 p( y x)p( x, y) log2 p( y x)y x 偶y x 奇0p( x) p( x x) log 2 p( x x)p(x) p( y x) log 2 p( y x) i奇y x,奇 x奇511log2 2 5 411log2 81021081比特所以I(X;Y)=log 2 10 1 2.3219比特2.11 解:（a）接收前一个数字为0 的概率81w( 0)q(u i ) p( 0 u i )2i 0I (u1 ;0)log2p(0 u1)1p(1 p) bitslog 21 1 log 2w(0)28（b ）同理w(00)q(u ) p(00 u ) 41iI (u 1;00)p(00u 1)log 2 (1p)22 2 log 2 (1 p) bitslog 2 w(00)14（c ）同理 w(000)8q(u i ) p(000 u i )81i 0I (u 1;000) log 2 p(000u 1 ) log 2 (1 p)33 3log 2 (1p)bitsw(000)18（d ）同理 w(0000 )8q(u i ) p(0000 u i )81((1p)66 p 2 (1 p)2p 4 )i 0p(0000u 1 )(1 p)4I (u 1;0000)log 2w(0000)log 281((1 p)6 6 p 2 (1p) 2p 4 )log 2 8(1 p) 4bits(1 p) 6 6 p 2 (1 p) 2p 42.12 解:见 2.92.13 解:(b)H(YZ/ X)xyzxyzxyzH(Y/ X)1p( xyz)logp( yz / x)1p( xyz) logp( y / x) p(z / xy)11p( xyz) logp(xyz)logp( y / x)x yzp( z / xy)H(Z/ XY)(c)H (Z / XY )p(xy)p( z / xy) log1xyzp(xy)xyzH(Z / X)p(z / xy)1p( z/ xy) log （由第二基本不等式） p(z / x)或H(Z/XY)H(Z/X)p(xy)1p( z / xy) logxyzp(z / xy)p( xy)p( z/ xy) log1p( z / x)xyzp( xy)p( z/ xy) logp(z / x)（由第一基xyzp( z / xy )p( xy)p(z / xy) log e( p(z / x)1)xyzp(z / xy)本不等式）所以H(Z/XY) H(Z/X)(a)H(Y/ X) H(Z / X)H(Y/ X) H(Z/XY) H(YZ/X)等号成立的条件为 p(z / xy) p( z / x) ,对所有 xX , y Y, z Z ,即在给定 X条件下 Y 与 Z 相互独立。