圆各种定理详细图解

平面几何中的圆及其相关定理

平面几何中的圆及其相关定理圆是平面上最基本的几何形状之一，它具有许多特殊的性质和定理。

本文将介绍圆的定义、圆心角定理、弧长定理以及切线定理等相关内容。

一、圆的定义圆是平面上所有到一个固定点距离相等的点的集合。

这个点被称为圆心，到圆心的距离称为半径。

圆的符号通常用字母"〇"来表示。

二、圆心角定理圆心角是以圆心为顶点的角。

圆心角定理指出，在同一个圆中，不论圆心角所对的弧长长短如何，其对应的圆心角大小都相等。

也就是说，对于同一圆上的两个弧所对应的圆心角相等。

三、弧长定理弧是由圆上的两个点所确定的一段弧线。

弧长是弧所对的圆心角的一部分，它等于整个圆的周长乘以圆心角所占的比例。

弧长定理可以表示为：弧长 = (圆的周长 / 360°) ×圆心角的度数。

四、切线定理在圆上，从切点引出的切线与半径垂直。

根据切线定理，切线与半径的垂直关系可以推导出许多重要的定理和性质。

切线定理的一个重要应用是圆的切线与半径之间的关系。

如果从圆的外部点引出两条切线，并连接切点和该点，那么连接两个切点所得的线段垂直于两个切线的连线，并且等于两个切线的长度之和。

五、圆的相交定理当两个圆相交时，有以下几种可能的情况：内切、外切、相交和包含。

内切是指两个圆的内部都有公共的一部分；外切是指两个圆的外部都有公共的一部分；相交是指两个圆的内部和外部都有公共的一部分；包含是指一个圆的内部包含了另一个圆。

根据圆的相交定理，当两个圆相交时，连接两个圆的圆心与两个切点，可以得到一条直线。

此直线称为两个圆的公共弦，对于内切和外切的情况，公共弦也是切线。

六、圆内接四边形定理圆内接四边形是指一个四边形的四个顶点都在同一个圆上。

根据圆内接四边形定理，一个四边形是圆内接四边形的充分必要条件是对角线互相垂直，即两对对角线的交点构成的四个角互为直角。

结论通过对平面几何中的圆及其相关定理的介绍，我们了解到圆与圆心角的关系、弧长定理、切线定理、圆的相交情况以及圆内接四边形的定理。

圆的几个定理

圆的几个定理
圆的定理是数学中关于圆的性质和关系的重要定理，下面将从不同角度介绍几个与圆相关的定理。

一、切线定理
圆的切线是指与圆相切于一点的直线。

切线定理是指通过圆外一点可以作唯一的一条切线。

这个定理可以用来解决很多实际问题，比如求解一个物体沿圆形路径的最短路线等。

二、切割圆定理
切割圆定理是指将一个圆分成两个或多个部分的直线或弧线，那么这些部分的面积之和等于整个圆的面积。

这个定理可以应用于计算圆的面积，以及解决一些与圆相关的几何问题。

三、圆的内切定理
圆的内切定理是指一个圆可以内切于一个三角形的三条边，而且这个圆的圆心与三角形的三条边的交点共线。

这个定理可以用来确定三角形的内切圆的圆心和半径，以及解决一些与内切圆相关的几何问题。

四、圆的外切定理
圆的外切定理是指一个圆可以外切于一个三角形的三条边，而且这个圆的圆心与三角形的三条边的交点共线。

这个定理可以用来确定三角形的外切圆的圆心和半径，以及解决一些与外切圆相关的几何
问题。

五、圆的相似定理
圆的相似定理是指两个圆的半径成正比时，这两个圆是相似的。

这个定理可以用来解决一些与相似圆相关的几何问题，比如求解相似圆的半径比、面积比等。

以上是关于圆的几个定理的介绍。

希望通过这些定理的应用，能够帮助读者更好地理解和应用圆的性质和关系，解决实际问题。

与圆有关的几何定理课件

在物理学中，圆定理也被广泛应用，如机械运动、光学、电磁学等。
05
圆的拓展知识
圆与正多边形的联系
01
正多边形内切于圆
正多边形的各顶点均位于同一个圆上，且各边中点也位于该圆上。
02 03
正多边形外接于圆
正多边形的各边的垂直平分线均交于一点，该点称为正多边形的中心，而以该点为圆心、半径等于正多边形边长的一半的圆称为正多边形的外接圆。
切线长定理
总结词
切线长定理是关于圆的切线的性质和关系的定理。
详细描述
切线长定理表明，如果一条直线与圆相切于两点，则这两点处的切线长度相等。此外，切线长定理还表明，两个切点之间的连线段垂直于经过这两点的切线。
圆周角定理
总结词
圆周角定理是关于圆周角和圆心角之间关系的定理。
详细描述
圆周角定理表明，在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。这个定理在证明圆的性质和解决与圆有关的问题时非常有用。
圆心到圆上任一点的距离相等
总结词
圆心到圆上任一点的距离都等于半径。
详细描述
在几何学中，圆心到圆上任一点的距离都等于半径，这是圆的基本性质之一。这个性质说明了圆是一个等距曲线，即所有到圆心的距离相等的点都在圆上。
圆心到圆上任一点的连线段为圆的半径
总结词
圆心到圆上任一点的连线段是圆的半径。
详细描述
在几何学中，通过圆心并与圆相交的线段被称为圆的半径。这个性质说明了半径是从圆心出发，通过圆上任意一点的线段。
02
圆的定理
垂径定理
总结词
垂径定理是圆几何中的基本定理之一，它描述了通过圆心的直径将圆分成两个相等的部分。

初三《圆》知识点及定理

高图教育数学教研组卢老师专用《圆》知识点及定理一、圆的概念集合形式的概念： 1 、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充） 2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；四、圆与圆的位置关系外离（图 1）无交点d R r ；外切（图 2）有一个交点d R r ；相交（图 3）有两个交点R r d R r ；内切（图 4）有一个交点d R r ；内含（图 5）无交点d R r ；d dR r R r图 1图 23、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

dR r图3d rRdR图4r二、点与圆的位置关系1、点在圆内d r点 C 在圆内；2、点在圆上d r点 B 在圆上；A d3、点在圆外d r点 A 在圆外；r OBd三、直线与圆的位置关系C1、直线与圆相离d r无交点；2、直线与圆相切d r有一个交点；3、直线与圆相交d r有两个交点；rd d=r r d图 5五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论 1：（ 1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共 4 个定理，简称 2 推 3 定理：此定理中共 5 个结论中，只要知道其中 2 个即可推出其它 3 个结论，即：①AB是直径②AB CD③CE DE④ 弧BC弧BD⑤ 弧AC弧 AD中任意 2 个条件推出其他 3 个结论。

数学圆知识点总结图文

数学圆知识点总结图文圆是平面上到定点的距离不大于定长的点的集合，其中定点称为圆心，定长称为半径。

圆的直径是由圆心穿过圆上一点并且与圆相交的线段的两端点组成，直径的长度等于半径长度的两倍。

圆的性质：1. 圆的周长公式：C=2πr，其中 r 为圆的半径，C 为圆周的长度。

2. 圆的面积公式：A=πr²，其中 r 为圆的半径，A 为圆的面积。

3. 弧长与扇形面积：圆的周长也称为圆的弧长，根据圆的性质，圆的周长与圆的面积之间存在一定的比例关系：一个圆的圆心角所对的弧所对应的圆是圆的周长的多少分之多少，所以圆的弧长也可以用来求圆的扇形面积。

4. 弧度制：圆的周长等于2πr，我们可以用圆的半径作为角度的一个单位，定义一个完整圆的周长等于圆周的角度为 360°，所以我们定义一个弧度＝半径的长度。

5. 切线和切点：在圆上的一点上可以作至多两个切线，同时，在同一个圆上，两个切点构成一对对称轴。

6. 直径和半径的关系：直径的长度等于半径的长度的两倍。

7. 弦和弦长：圆上的弦是圆上两个点之间的线段，而这段线段的长度就是弦长。

8. 内接四边形：内切于圆的四边形称为内接四边形，在内接四边形中，相邻两条边的和等于另外两条边的和，也就是说，相邻两条边相等。

9. 弧与圆心角：一个圆的周长也可以称为圆的弧长，一条切线与半径所夹的角就是等于它所对应的圆弧的角，这个角称为圆心角。

10. 圆锥曲线：圆锥曲线是一种经常被用来描述物理定律的曲线，其中圆是最简单的一种。

圆的定义可以被一组关于圆心和半径的方程来描述，其中的点被定义为满足这组方程的点。

11. 圆锥截线：直线直接经过球面内部一点并且与球面相交的弧的两端点构成，这个线段就称为圆锥截线，一个圆锥截线具有和球面具有相同圆心和半径。

12. 弧度与角度：弧度是圆周上的弧与圆心所夹得的角。

13. 切线和切点：在圆上的一点上可以作至多两个切线，同时，在同一个圆上，两个切点构成一对对称轴。

各种圆定理总结（包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆）

各种圆定理总结（包括托勒密定理、塞⽡定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆）托勒密定理⼀些圆定理.doc定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对⾓线的乘积。

原⽂：圆的内接四边形中，两对⾓线所包矩形的⾯积等于⼀组对边所包矩形的⾯积与另⼀组对边所包矩形的⾯积之和。

从这个定理可以推出正弦、余弦的和差公式及⼀系列的三⾓恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出⼀般⼏何教科书中的“托勒密定理”，实出⾃依巴⾕(Hipparchus)之⼿，托勒密只是从他的书中摘出。

证明⼀、（以下是推论的证明，托勒密定理可视作特殊情况。

）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)⽽∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC⼜因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成⽴，即“托勒密定理”）所以命题得证复数证明⽤a、b、c、d分别表⽰四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

⾸先注意到复数恒等式：(a ? b)(c? d) + (a? d)(b? c) = (a? c)(b? d) ，两边取模，运⽤三⾓不等式得。

等号成⽴的条件是(a-b)(c-d)与(a-d)(b-c)的辐⾓相等，这与A、B、C、D四点共圆等价。

四点不限于同⼀平⾯。

平⾯上，托勒密不等式是三⾓不等式的反演形式。

⼆、设ABCD是圆内接四边形。

在弦BC上，圆周⾓∠BAC = ∠BDC，⽽在AB上，∠ADB = ∠ACB。

圆的各种定理

圆的各种定理一、垂径定理1. 定理内容- 垂直于弦的直径平分弦且平分这条弦所对的两条弧。

- 用符号语言表示：设圆O中，直径CD⊥弦AB于点E，则AE = BE，widehat{AD}=widehat{BD}，widehat{AC}=widehat{BC}。

2. 推论- 平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

- 弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

- 平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

二、弧、弦、圆心角定理1. 定理内容- 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

- 符号语言：在⊙ O中，若∠ AOB=∠ COD，则widehat{AB}=widehat{CD}，AB = CD。

2. 推论- 在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等。

- 在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的优弧和劣弧分别相等。

三、圆周角定理1. 定理内容- 一条弧所对的圆周角等于它所对的圆心角的一半。

- 符号语言：在⊙ O中，∠ BAC是widehat{BC}所对的圆周角，∠ BOC是widehat{BC}所对的圆心角，则∠ BAC=(1)/(2)∠ BOC。

2. 推论- 同弧或等弧所对的圆周角相等。

- 半圆（或直径）所对的圆周角是直角，90^∘的圆周角所对的弦是直径。

- 圆内接四边形的对角互补。

即四边形ABCD内接于⊙ O，则∠ A+∠ C = 180^∘，∠ B+∠ D=180^∘。

四、切线的性质定理1. 定理内容- 圆的切线垂直于经过切点的半径。

- 符号语言：直线l是⊙ O的切线，切点为A，则OA⊥ l。

五、切线的判定定理1. 定理内容- 经过半径的外端并且垂直于这条半径的直线是圆的切线。

- 符号语言：点A在⊙ O上，OA是半径，直线l⊥ OA于点A，则直线l是⊙O的切线。

六、切线长定理1. 定理内容- 从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

圆的有关定理暨图示.

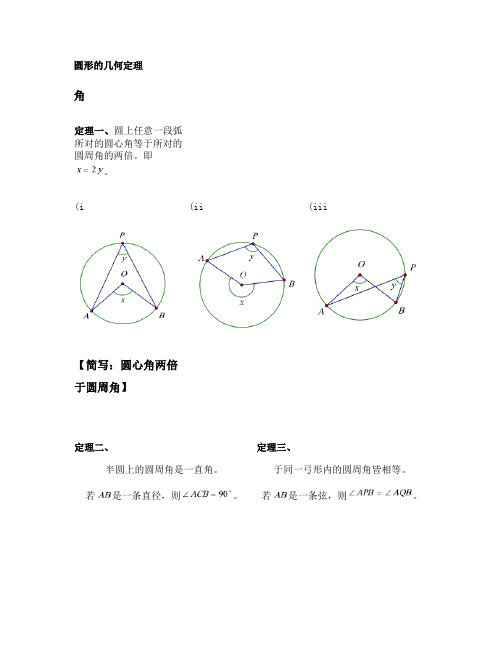
圆形的几何定理角定理一、圆上任意一段弧所对的圆心角等于所对的圆周角的两倍。

即。

(i(ii(iii【简写：圆心角两倍于圆周角】定理二、半圆上的圆周角是一直角。

若是一条直径，则。

定理三、于同一弓形内的圆周角皆相等。

若是一条弦，则。

【简写：半圆上的圆周角】【简写：同弓形内的圆周角】定理四、圆内接四边形的两个对角互补。

即。

及。

【简写：圆内接四边形对角】定理五、圆内接四边形任何一个外角与其内对角相等。

即。

【简写：圆内接四边形外角】弦定理六由圆心画一垂直线至任何一条弦会平分定理七由圆心画一条直线至弦的中点，则该直线必与该弦互相垂直。

即若，该弦。

即若，则。

【简写：圆心至弦的垂线平分弦】则。

【简写：圆心至弦中点的联机垂直弦】定理八若某圆内的两条弦相等，则该两条弦与圆心的距离相等。

即若，则。

【简写：等弦与圆心等距】定理九若两条弦与圆心等距，则该两条弦的长度相等。

即若，则。

【简写：与圆心等距的弦等长】弧定理十、相等的圆心角所对的弧及弦相等。

即若，则、。

【简写：等角对等弦】、【简写：等角对等弧】定理十一、相等的弧所对的圆心角及弦相等。

即若，则、。

【简写：等弧对等角】、【简写：等弧对等弦】定理十二、相等的弦所对的圆心角及弧长相等。

即若，则、。

【简写：等弦对等角】、【简写：等弦对等弧】定理十三、弧长与所对的圆心角(圆周角成比例。

即。

【简写：弧长与圆心角成比例】【简写：弧长与圆周角成比例】切线定理十四、为圆心，为圆周上的点，为直线。

若为圆在点的切线，则。

定理十五、为圆心，为圆周上的点，为直线。

若，则为圆在点的切线。

【简写：切线半径】【简写：切线半径的逆定理】定理十六、若从圆外的一点分别作两条与圆切于和的切线和，而为圆心，则(a(b(c【简写：切线性质】定理十七、若为圆在点上的切线而为弦，则则【简写：交错弓形的圆周角】定理一、【圆心角两倍于圆周角】定理二、【半圆上的圆周角】定理三、【同弓形内的圆周角】定理四、【圆内接四边形对角】定理五、【圆内接四边形外角】定理六、【圆心至弦的垂线平分弦】定理七、【圆心至弦中点的联机垂直弦】定理八、【等弦与圆心等距】定理九、【与圆心等距的弦等长】定理十、【等角对等弦】定理十一、【等弧对等角】定理十二、【等弦对等弧】定理十三、【弧长与圆心角成比例】定理十四、【切线半径】定理十五、【切线半径的逆定理】定理十六、【切线性质】定理十七、【交错弓形的圆周角】。

初三数学圆的性质定理

初三数学圆的性质定理1、圆的对称性：圆是轴对称图形，任一条直径所在的直线都是它的对称轴.2、垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.3、垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.4、垂径定理的应用：①用直尺和圆规平分一条弧.作法是过圆心作弧所对弦的垂线，理由是垂径定理；②在利用垂径定理计算或证明时，我们通常将其化为一个直角三角形的边和角，这个特殊直角三角形的三边分别是半径、弦的一半和圆心到弦的垂线段.例1、如图，已知以点O为公共圆心的两个同心圆，大圆的弦AD交小圆于B、C.(1)求证：AB=CD(2)如果AD=6cm，BC=4cm，求圆环的面积.1.圆周角定义：顶点在圆周上，并且两边都和圆相交的角叫做圆周角.2.圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.3.推论：①同圆或等圆中，相等的圆周角所对的弧一定相等.②半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径.③如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形.4．圆的内接四边形：①定义：如果一个多边形的所有顶点都在同一圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.②圆内接四边形的性质：圆内接四边形的对角互补.例2、如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交BC于D.若BC=8，ED=2，求⊙O的半径.1、如图，已知AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP∶PB=1∶5，那么⊙O的半径是（）2、圆的半径为13cm，两弦AB∥CD，AB=24cm，CD=10cm，则两弦AB、CD的距离是（）A．7cm B．17cm C．12cm D．7cm或17cm3、如下图所示，AB是⊙O的一条固定直径，它把⊙O分成上、下两个半圆，自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆（不包括A、B两点）移动时，点P（）A．到CD的距离保持不变B．位置不变C．平分D．随点C的移动而移动4、如上中图，BD是⊙O的直径，弦AC、BD相交于点E，则下列结论不成立的是（）A．∠ABD=∠ACD B．C．∠BAE=∠BDC D．∠ABD=∠BDC5、如上右图，⊙O的直径CD过弦EF的中点G，∠EOD=40°，则∠DCF等于（）A．80°B．50°C．40°D．20°6、如下图，A、B、C是⊙O上三点，∠ACB=40°，则∠ABO等于__________度．7、如上左二图，△ABC的顶点都在⊙O上，∠C=30°，AB=2cm，则⊙O的半径为__________cm．8、如上左三图，在平面直角坐标系中，P是经过O（0，0），A（0，2），B（2，0）的圆上的一个动点（P与O、A 、B不重合），则∠OAB=__________，∠OPB=__________．9、如右上图，△ABC内接于⊙O，∠B=∠OAC，OA=8cm，则AC=__________cm．10、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则BC=__________．11、如图，⊙O中的弦AB、CD互相垂直于E，AE=5cm，BE=13cm，O到AB的距离为．求⊙O的半径及O到CD的距离．12、如图，某地有一座圆弧形的拱桥，桥下水面宽为7.2m，拱顶高出水面2.4m，现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．13、如图，AB为⊙O的直径，BD是⊙O的弦，延长到C，使BD＝DC，连接AC交⊙O于点F，点F不与点A重合．（1）AB与AC的大小有什么关系？为什么？（2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．一、确定圆的条件(1)因为作圆实质上是确定圆心和半径，要经过已知点A作圆，只要圆心确定下来，半径就随之确定了下来．所以以点A以外的任意一点为圆心，以这一点与点A所连的线段为半径就可以作一个圆．由于圆心是任意的．因此这样的圆有无数个．如图(1)．(2)已知点A、B都在圆上，它们到圆心的距离都等于半径．因此圆心到A、B的距离相等．根据前面提到过的线段的垂直平分线的性质可知，线段的垂直平分线上的点到线段两端点的距离相等，则圆心应在线段AB的垂直平分线上．在AB的垂直平分线上任意取一点，都能满足到A、B两点的距离相等，所以在AB的垂直平分线上任取一点都可以作为圆心，这点到A的距离即为半径，圆就确定下来了．由于线段AB的垂直平分线上有无数点，因此有无数个圆心，作出的圆有无数个．如图(2)．(3)要作一个圆经过A、B、C三点，就是要确定一个点作为圆心，使它到三点的距离相等．因为到A、B两点距离相等的点的集合是线段AB的垂直平分线，到B、C两点距离相等的点的集合是线段BC的垂直平分线，这两条垂直平分线的交点满足到A、B、C三点的距离相等，就是所作圆的圆心．因为两条直线的交点只有一个，所以只有一个圆心，即只能作出一个满足条件的圆．过不在同一条直线上的三点确定一个圆2、经过三角形三个顶点的圆，叫做三角形的外接圆，外接圆的圆心是三角形三边垂直平分线的交点，叫做三角形的外心，这个三角形叫做这个圆的内接三角形．因为画圆的关键是确定圆心和半径，所以作三角形的外接圆时，只要找三边垂直平分线的交点，这就是圆心，以这点到三角形任一顶点间的距离为半径就可作出三角形的外接圆．3、利用尺规过不在同一条直线上的三个点作圆的方法作法图示1．连结AB、BC2．分别作AB、BC的垂直平分线DE和FG，DE和FG相交于点O3．以O为圆心，OA为半径作圆⊙O就是所要求作的圆例1、已知锐角三角形、直角三角形、钝角三角形，分别作出它们的外接圆，它们外心的位置有怎样的特点？（1）（2）（3）例3、如图，点A、B、C表示三个村庄，现要建一座深水井泵站，向三个村庄分别送水，为使三条输水管线长度相同，水泵站应建在何处？请画出图，并说明理由．1、下列关于外心的说法正确的是（）A．外心是三个角的平分线的交点 B．外心是三条高的交点C．外心是三条中线的交点 D．外心是三边的垂直平分线的交点2、下列条件中不能确定一个圆的是（）A．圆心和半径B．直径 C．三角形的三个顶点D．平面上的三个已知点3、三角形的外心具有的性质是（）A．到三边的距离相等B．到三个顶点的距离相等 C．外心在三角形外D．外心在三角形内4、等腰三角形底边上的中线所在的直线与一腰的垂直平分线的交点是（）A．重心B．垂心 C．外心D．无法确定5、如图所示，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（）A．点P B．点Q C．点R D．点M6、如图，是△ABC的外接圆，∠BAC=30°，BC=2 cm ，则△OBC的面积是_______.7、直角三角形的两边长分别为16和12，则此三角形的外接圆半径是_______．8、如图，有一个圆形的盖水桶的铁片，部分边沿由于水生锈残缺了一些，很不美观，为了废物利用，将铁片剪去一些使其成为圆形的，应找到圆心，并找到合理的半径，在铁片上画出圆，沿圆剪下即可，问应怎么样找到圆心和半径？。

初中《圆》知识点及定理

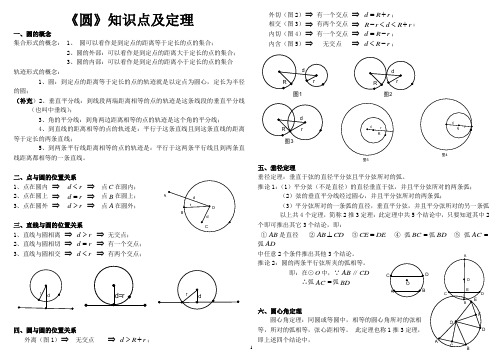
《圆》知识点及定理一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合；2、圆的外部：可以看作是到定点的距离大于定长的点的集合；3、圆的内部：可以看作是到定点的距离小于定长的点的集合轨迹形式的概念：1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线。

二、点与圆的位置关系1、点在圆内⇒d r<⇒点C在圆内；2、点在圆上⇒d r=⇒点B在圆上；3、点在圆外⇒d r>⇒点A在圆外；三、直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；四、圆与圆的位置关系外离（图1）⇒无交点⇒d R r>+；外切（图2）⇒有一个交点⇒d R r=+；相交（图3）⇒有两个交点⇒R r d R r-<<+；内切（图4）⇒有一个交点⇒d R r=-；内含（图5）⇒无交点⇒d R r<-；五、垂径定理垂径定理：垂直于弦的直径平分弦且平分弦所对的弧。

推论1：（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论，即：①AB是直径②AB CD⊥③CE DE=④弧BC=弧BD⑤弧AC=弧AD中任意2个条件推出其他3个结论。

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆).

托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

证明一、（以下是推论的证明，托勒密定理可视作特殊情况。

）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、AD、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

首先注意到复数恒等式：(a − b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ，两边取模，运用三角不等式得。

等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

四点不限于同一平面。

平面上，托勒密不等式是三角不等式的反演形式。

二、设ABCD是圆内接四边形。

在弦BC上，圆周角∠BAC = ∠BDC，而在AB上，∠ADB = ∠ACB。

在AC上取一点K，使得∠ABK = ∠CBD；因为∠ABK + ∠CBK =∠ABC = ∠CBD + ∠ABD，所以∠CBK = ∠ABD。

关于圆的定理

1 圆心角定理：在同圆或等圆中，相等的圆心角所对弧相等，所对的弦相等，所对的弦的弦心距相等。

2 圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

3 垂径定理：垂直弦的直径平分该弦，并且平分这条弦所对的两条弧。

4 切线之判定定理：经过半径的外端并且垂直于该半径的直线是圆的切线。

5 切线长定理：从圆外一点引圆的两条切线，他们的切线长相等，这一点与圆心的连线平分这两条切线的夹角。

6 公切线长定理：如果两圆有两条外公切线或两条内公切线，那么这两条外公切线长相等，两条内公切线长也相等。

如果他们相交，那么交点一定在两圆的连心线上。

7 相交弦定理：圆内两条弦相交，被交点分成的两条线段长的乘积相等。

8 切割线定理：从圆外一点向圆引一条切线和一条割线，则切线长是这点到割线与圆的两个交点的两条线段长的比例中项。

9 割线长定理：从圆外一点向圆引两条割线，这一条到每条割线与圆的交点的两条线段长的积相等。

10 圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

11 西姆松定理说明：有三角形ABC，平面上有一点P。

P在三角形三边上的投影（即由P到边上的垂足）共线（此线称为西姆松线, Simson line）当且仅当P在三角形的外接圆上。

初中数学关于【圆】的七大定理

【圆】七大定理汇总一、垂径定理垂径定理通俗的表达是：垂直于弦的直径平分弦且平分这条弦所对的两条弧。

数学表达为：如右图，直径DC垂直于弦AB，则AE=EB，劣弧AD等于劣弧BD，等弧CAD=优弧CBD。

垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。

一条直线，在下列5条中只要具备其中任意两条作为条件，就可以推出其他三条结论，称为“知二推三”。

1.平分弦所对的优弧；2.平分弦所对的劣弧；3.平分弦（不是直径）；4.垂直于弦；5.经过圆心二、韦达定理韦达定理为解析几何中的一个定理，说明了一元n次方程中根和系数之间的关系。

以一元二次方程两根之间的关系为例，方程aX²+bX+c=0中，两根X1、X2满足X1+X2=-b/a和X1×X2=c/a两个关系。

三、托勒密定理在数学中，托勒密定理是欧几里得几何学中的一个关于四边形的定理。

托勒密定理指出凸四边形两组对边乘积之和不小于两条对角线的乘积，等号当且仅当四边形为圆内接四边形，或退化为直线取得（这时也称为欧拉定理）。

狭义的托勒密定理也可以叙述为：圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。

它的逆定理也是成立的：若一个凸四边形两对对边乘积的和等于两条对角线的乘积，则这个凸四边形内接于一圆。

四、射影定理射影定理是指在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，直角边是这条直角边在斜边的射影和斜边的比例中项，直角三角形射影定理，又称“欧几里德定理”。

定理内容是：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项，每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。

五、相交弦定理相交弦定理，是指圆内的两条相交弦，被交点分成的两条线段长的积相等。

概念定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。

（经过圆内一点引两条弦，各弦被这点所分成的两段的积相等）六、切割线定理圆幂定理的一种，具体如下：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

圆有关定理

3.已知：如图1直线MN与⊙O相切于C，AB为直径，∠CAB＝40°，则∠MCA的度数（）
图1
A. 50°B. 40°C. 60°D. 55°
4.圆内两弦相交，一弦长8cm且被交点平分，另一弦被交点分为1：4，则另一弦长为（）
A. 8cm B. 10cm C. 12cm D. 16cm
5.在△ABC中，D是BC边上的点，AD= cm，BD＝3cm，DC＝4cm，如果E是AD的延长线与△ABC的外接圆的交点，那么DE长等于（）
当∠DEF＝45°时，求证:点G为线段EF的中点；
图8
【模拟试题】（答题时间：40分钟）
一、选择题
1.已知：PA、PB切⊙O于点A、B，连结AB，若AB＝8，弦AB的弦心距3，则PA＝（）
A.20/3B.25/3C. 5 D. 8
2.下列图形一定有内切圆的是（）
A.平行四边形B.矩形
C.菱形D.梯形
5.弄清和圆有关的角：圆周角，圆心角，弦切角，圆内角，圆外角。
6.遇到圆的切线，可联想“角”弦切角，“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段
定理
图形
已知
结论
证法
相交弦定理
⊙O中，AB、CD为弦，交于P.
PA·PB＝PC·PD
连结AC、BD，C=B,A=D,所以△APC∽△DPB
相交弦定理的推论
⊙O中，AB为直径，CD⊥AB于P.
PC2＝PA·PB
用相交弦定理.
切割线定理
⊙O中，PT切⊙O于T，割线PB交⊙O于A
PT2＝PA·PB
连结TA、TB，则∠PTA=∠B（弦切角等于同弧圆周角）所以△PTA∽△PBT，所以
PT2＝PA·PB
切割线定理推论

关于圆的定理

圆幂定理圆幂的定义:一点P 对半径R 的圆O 的幂定义如下：22OP R - 所以圆内的点的幂为负数，圆外的点的幂为正数，圆上的点的幂为零。

圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)及他们推论的统称。

相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。

如图，AB 、CD 为圆O 的两条任意弦。

相交于点P ，连接AD 、BC ，则∠D=∠B ， ∠A=∠C 。

所以△APD ∽△BPC 。

所以A P P D A PB P PC PD P CB P=⇒⋅=⋅切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆焦点的两条线段长的比例中项。

如图，PT 为圆切线，PAB 为割线。

连接TA ，TB ，则∠PTA=∠B （弦切角等于同弧圆周角）所以△PTA ∽△PBT ，所以2P T P A P TP A P B P BP T=⇒=⋅割线定理：从圆外一点P 引两条割线与圆分别交于A.B.C.D 则有 PA·PB=PC·PD 。

这个证明就比较简单了。

可以过P 做圆的切线，也可以连接CB 和AD 。

证相似。

存在：P A P B P C P D ⋅=⋅进一步升华（推论）：过任意在圆O 外的一点P 引一条直线L1与一条过圆心的直线L2，L1与圆交于A 、B （可重合，即切线），L2与圆交于C 、D 。

则PA·PB=PC·PD 。

若圆半径为r ，则2222()()||PC PD PO R PO R PO R PO R ⋅=-⋅+=-=-（一定要加绝对值，原因见下）为定值。

这个值称为点P 到圆O 的幂。

（事实上所有的过P 点与圆相交的直线都满足这个值）若点P 在圆内，类似可得定值为2222||R PO PO R -=-故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝对值。

（这就是“圆幂”的由来）切线判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。

圆中知识结构图

关于《圆》的知识结构整理一.主要定理及其作用：1.圆心角，弧，弦，弦心距之间的关系定理：在同圆或等圆中，如果①两个圆心角②两条弧，③两条弦④两条弦心距中，有一组量相等, 那么它们所对应的其余各组量都分别相等：（等弧一等角-一等弦……）用的最多的依据：①在同圆或等圆中，如果两个圆心角相等,那么它们所对的两条弧相等②等弧所对的圆心角相等：③在同圆或等圆中，如果两条弦相等,那么它们所对的两条弧相等④等弧所对的两条弦相等2.垂径定理：如果一条直线①过圆心；②垂直于弦：③平分弦：④平分劣弧：⑤平分优弧•只要具备其中两个条件，就可推岀其余三个结论. （直角三角形一等弧……）用的最多的依据：①垂直于弦的直径平分弦，并且平分弦所的两条弧②平分弦（非直径）的直径垂直于这条弦，并且平分这条弦所对的两条弧.③一条弦的垂直平分线I I经过圆心，并且平分这条弦所对的两条弧④平分弧的直径过圆心的直线垂直平分这条弧所对的弦.3.圆周角定理：（1）直径所对的圆周角是直角：（2） 90°的圆周角所对的弦是直径。

（3）—条弧所对的圆周角等于它所对的圆心角的一半：（4）同弧所对的圆周角相等：（5）等弧所对的圆周角相等：（6）在同圆或等圆中，相等的圆周角所对的弧相等：（等弧——等角——直角三角形）4.切线的性质定理：圆的切线垂直于经过切点的半径（直径）。

（垂直关系）5.切线的判定定理：经过半径的外端，并且垂直于这条半径的直线是圆的切线O6.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

（等弦一-等弧一-等角）7.相切和相交两圆的性质定理：如果两圆相切，连心线必过切点。

如果两圆相交，连心线垂直平分公共弦二.主要辅助线及其作用：1.作弦心距：弦的中点.弧的中点。

2.过某一点作弦：构造相等的圆周角。

3.作直径：构造直角三角形和同弧所对的圆周角。

4.连结过切点的半径：“题中若有圆切线圆心切点连一连”。

与圆有关的几个定理

A F
E
B
O
D
C
难点概念：三角形的外接圆和内切圆：
A
A
O
I
C
B
C
B
实质
性质
三角形的三角形三边垂直到三角形各顶
外心
平分线的交点点的距离相等
三角形的三角形三内角角到三角形各边
内心
平分线的交点的距离相等
特别的:
等边三角形的外心与内心重合. 内切圆半径与外接圆半径的比是1:2.
A
O
B
D
C
同如图，从⊙O外一点P作⊙O的两条切线，分别步切⊙O于A 、B，在AB上任取一点C作⊙O的切线自分别交PA 、PB于D 、E 测
M└
若 ① CD是直径
●O
② CD⊥AB
可推得
③AM=BM,
④A⌒C=B⌒C, ⑤A⌒D=B⌒D.
D
基本模型“垂径定理、直角三角形”
(2）垂径定理以及推论
C
(1)直径 (过圆心的线)；(2)垂直弦； A M└
B
(3) 平分弦；
(4)平分劣弧；
●O
(5)平分优弧.
知二得三
D
注意: “ 直径平分弦则垂直弦.” 这句话对吗?
A．35°
B.70°
C．110° D.140°
二、点和圆的位置关系
.o .p r
Op＜r Op=r Op＞r
.p .o
.o
.p
点p在⊙o内点p在⊙o上点p在⊙o外
三.直线与圆的位置关系
r ●O ┐d
相交
r ●O
d ┐ 相切
1、直线和圆相交
d < r;
2、直线和圆相切 3、直线和圆相离

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)-标准化文件发布号：（9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII托勒密定理定理图定理的内容托勒密(Ptolemy)定理指出，圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。

原文：圆的内接四边形中，两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。

从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式，托勒密定理实质上是关于共圆性的基本性质．定理的提出一般几何教科书中的“托勒密定理”，实出自依巴谷(Hipparchus)之手，托勒密只是从他的书中摘出。

证明一、（以下是推论的证明，托勒密定理可视作特殊情况。

）在任意四边形ABCD中，作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD因为△ABE∽△ACD所以 BE/CD=AB/AC,即BE·AC=AB·CD (1)而∠BAC=∠DAE，，∠ACB=∠ADE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD（仅在四边形ABCD是某圆的内接四边形时，等号成立，即“托勒密定理”）所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数，则AB、CD、A D、BC、AC、BD的长度分别是：(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。

首先注意到复数恒等式： (a− b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ，两边取模，运用三角不等式得。

等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等，这与A、B、C、D四点共圆等价。

四点不限于同一平面。

圆各种定理详细图解

平面几何中的圆及其相关定理

圆的几个定理

与圆有关的几何定理课件

初三《圆》知识点及定理

数学圆知识点总结图文

各种圆定理总结（包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆）

圆的各种定理

圆的有关定理暨图示.

初三数学 圆的性质定理

初中《圆》知识点及定理

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆).

关于圆的定理

初中数学关于【圆】的七大定理

圆有关定理

关于圆的定理

圆中知识结构图

与圆有关的几个定理

各种圆定理总结(包括托勒密定理、塞瓦定理、西姆松定理、梅涅劳斯定理、圆幂定理和四点共圆)

初三数学圆的性质定理