苏教版八年级下册数学压轴题(非常好的题目)

合集下载

苏教版八年级下册数学压轴题(非常好的题目)之欧阳学创编

压轴题精选时间：2021.03.03创作：欧阳学1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒． ⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直y x O P Q AB角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳育创编

压轴题精选时间：2021.02.04创作：欧阳育1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AO B 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB，则∠MOB=31∠AOB．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使y x OP Q A B点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳体创编

压轴题精选时间：2021.02.03创作：欧阳体1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使y xOPQ A B点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

江苏八年级下期末真题精选(压轴60题19个考点专练)～【满分全攻略】2022～2023

江苏八年级下期末真题精选（压轴A．6B．3（2020•重庆）4．如图，在平面直角坐标系中，是x轴上一点，连接AE．若ADA．6B．12（2022春•泰州期末）5．如图，A（a，b）、B（－a，－b A、B作y轴的平行线，与反比例函数（2022春•高邮市期末）8．如图，在平面直角坐标系中，的图像经过OA 的中点C 和点9．如图，在平面直角坐标系中，边，在第一象限内作矩形点O 重合，折痕为MN ，点()0ky k =≠的图像恰好过A．27 4五．反比例函数与一次函数的交点问题（共（2021•武威二模）11．已知反比例函数y(1)求这两个函数的关系式；a___________(1)直接写出=(2)结合图象直接写出关于x的不等式C n在反比例函数y(3)点(),2（2022春•安居区期末）(1)求该反比例函数和一次函数的表达式；的面积；(2)连接AO，求AOB(3)直接写出关于x的不等式mx （2014•巴中）15．如图，在平面直角坐标系（1）求反比例函数和直线EF（2）求△OEF的面积；（3）请结合图象直接写出不等式（2018春•秦淮区期末）16．如图，在直角坐标系中，函数(1)点A 、B 的坐标分别是、；(2)在同一平面直角坐标系中，画出函数34y x=-的图象；(3)垂直于y 轴的直线l 与函数1y 、2y 、3y 的图象分别交于点3(N x ，3)y ，若123x x x <<，结合函数的图象，直接写出六．反比例函数的应用（共5小题）（2022•青秀区校级一模）17．学校的自动饮水机，开机加热时每分钟上升10开始下降，此时水温y ℃与通电时间x （min ）成反比例关系．当水温降至机再自动加热，若水温在20︒时接通电源，水温y 则下列说法中正确的是（）A ．水温从20︒升高到100B ．水温下降过程中，y 与C ．早晨8点接通电源从20D ．在单次加热—降温的过程中，水温不低于100℃，停止加热，水温开始下降，此时水温()℃与开机后用时()min 成反比例关系．直至水温降至30℃，饮水机关机．饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时，接通电源后，水温()y ℃和时间()min 的关系如图，为了在上午第一节下课时()8:45能喝到不超过50℃的水，则接通电源的时间可以是当天上午的（）A ．7:20B ．7:30C ．7:45D ．8:00（2022春•海州区校级期末）19．某车队要把4000吨货物运到灾区，已知每天的运输量不变．(1)从运输开始，每天运输的货物吨数n （吨）与运输时间t （天）之间有怎样的函数表达式？(2)因灾区道路受阻，实际每天比原计划少运20%，推迟2天完成任务，求原计划完成任务的天数．（2021•蒸湘区校级一模）20．某医药研究所研制了一种新药，在试验药效时发现：成人按规定剂量服用后，检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克，第100分钟达到最高，接着开始衰退．血液中含药量y （微克）与时间x （分钟）的函数关系如图，并发现衰退时y 与x 成反比例函数关系．(1)=a _____________；(2)当5100≤≤x 时，y 与x 之间的函数关系式为_____________；当100x >时，y 与x 之间的函数关系式为_____________；(3)如果每毫升血液中含药量不低于10微克时是有效的，求出一次服药后的有效时间多(1)求k的值；(2)恒温系统在一天内保持大棚内温度不低于七．三角形中位线定理（共（2019•铁西区二模）22．如图，△ABC中，∠A=60° ，AC（2015•呼伦贝尔）26．如图，在平行四边形ABCD （1）求证：△ADE≌△CBF；（2）若∠ADB是直角，则四边形一十．平行四边形的判定与性质（共2022春•南京期末）．在ABCD 中，6cm AB =（2011•北京）30．在▱ABCD 中，∠一十一．菱形的性质（共（2021春•滨湖区期末）32．如图，已知菱形ABCD=，连接动点，且PC CQA．45B．（2022•新市区校级三模）33．已知如图，在菱形ABCD(1)求证：四边形AODE是矩形；(2)若AB＝6，∠BCD＝120°，求四边形一十二．菱形的判定与性质（共（2023•郧西县模拟）34．在Rt△ABC中，∠BAC＝90°，A ．逐渐增大C ．不变（2022春•靖江市校级期末）36．如图，线段AB 的长为10，点（2018•邵阳模拟）38．如图，矩形ABCD 中，点边于点,E F AF AE =、．(1)求证：四边形AFCE 是菱形；(2)若8,6BC AB ==，求EF 的长．（2021春•淮安区期末）39．如图所示，在矩形ABCD 中，AB =4cm ，BC =8cm ，AC 的垂直平分线EF 分别交BC ，AD 于点E ，F ，垂足为O ，连接AE ，CF ．（1）求证：四边形AFCE 为菱形；（2）求AF 的长．（2019•无锡模拟）40．已知：如图，在平行四边形ABCD 和矩形ABEF 中，AC 与DF 相交于点G .(1) 试说明DF ＝CE ；(2) 若AC ＝BF ＝DF ，求∠ACE 的度数．（2011•福州）41．已知，矩形ABCD 中，AB =4cm ，BC =8cm ，AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ，垂足为O ．（1）如图1，连接AF 、CE ．求证四边形AFCE 为菱形，并求AF 的长；（2）如图2，动点P 、Q 分别从A 、C 两点同时出发，沿△AFB 和△CDE 各边匀速运动一周．即点P 自A →F →B →A 停止，点Q 自C →D →E →C 停止．在运动过程中，①已知点P 的速度为每秒5cm ，点Q 的速度为每秒4cm ，运动时间为t 秒，当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时，求t 的值．②若点P 、Q 的运动路程分别为a 、b （单位：cm ，ab ≠0），已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形，求a 与b 满足的数量关系式．（2022春•工业园区期末）42．已知，如图，在长方形ABCD 中，46AB AD ==，．延长BC 到点E ，使3CE =，连接DE ．(1)动点P 从点B 出发，以每秒1个单位的速度沿BC CD DA --向终点A 运动，设点P 运动的时间为t 秒，求当t 为何值时，ABP 和DCE △全等？(2)若动点P 从点B 出发，以每秒1个单位的速度仅沿着BE 向终点E 运动，连接DP ．设点P 运动的时间为t 秒，是否存在t ，使PDE △为等腰三角形？若存在，请求出t 的值；否则，说明理由．（2012•云南）43．如图，在矩形ABCD 中，对角线BD 的垂直平分线MN 与AD 相交于点M ，与BD 相交于点O ，与BC 相交于点N ，连接BM 、DN ．(1)求证：四边形BMDN 是菱形；(2)若4AB =，8AD =，求MD 的长．一十四．正方形的性质（共5小题）（2012•黔东南州）44．点P 是正方形ABCD 边AB 上一点(不与A 、B 重合),连接PD 并将线段PD 绕点P 顺时针旋转90°,得线段PE,连接BE,则∠CBE 等于（）（2022春•仪征市期末）46．在正方形ABCD中，点(1)当α＝20°时，求∠DAE的度数；(2)判断△AEG的形状，并说明理由；(3)当GF＝1时，求CE的长．一十五．正方形的判定（共（2022春•隆安县期末）(1)求证：BC＝BE；(2)连接CF，若∠ADF＝∠BCF（1）证明四边形EGFH是平行四边形；形EGFH是正方形.一十六．正方形的判定与性质（共（2022春•仪征市期末）51．我们知道菱形与正方形的形状有差异，“接近度”．A ．424-（2022•南京模拟）53．在矩形ABCD 中，点A 顺时针旋转90°得到A ．25B ．（2022•常熟市模拟）54．如图，在Rt ABC △中，动点，A B C ABC ''△△≌，将（2022•平邑县一模）56．在正方形ABCD 中，点E 在射线BC 上（不与点B 、C 重合），连接DB ，DE ，将DE 绕点E 逆时针旋转90 得到EF ，连接BF ．(1)如图1，点E 在BC 边上．①依题意补全图1；②若=6AB ，=2EC 求BF 的长；(2)如图2，点E 在BC 边的延长线上，用等式表示线段BD ，BE ，BF 之间的数量关系．（2016春•工业园区期末）57．如图，在△ABC 中，∠BAC ＝50°，将△ABC 绕点A 按逆时针方向旋转后得△AB 1C 1．当B 1B ∥AC 时，求∠BAC 1的度数．（2021•厦门二模）58．在正方形ABCD 中，将边AD 绕点A 逆时针旋转()090a a ︒<<︒得到线段AE ，AE 与CD 延长线相交于点F ，过B 作//BG AF 交CF 于点G ，连接BE ．（1）如图1，求证：2BGC AEB ∠=∠；（2）当（4590a ︒<<︒）时，依题意补全图2，用等式表示线段AH EF DG ，，之间的数量关系，并证明．一十八．作图－旋转变换（共1小题）（2022春•盱眙县期末）59．如图，在平面直角坐标系中，已知ABC 的三个顶点的坐标分别为()()()5,1,2,2,1,4A B C ---，请按下列要求画图：(1)将ABC 先向右平移4个单位长度、再向下平移1个单位长度，得到111A B C △，画出111A B C △；(2)222A B C △与ABC 关于原点O 成中心对称，画出222A B C △．一十九．条形统计图（共1小题）（2022春•盱眙县期末）60．我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A （体操）、B （乒乓球）、C （毽球）、D （跳绳）四项活动．为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图．请根据统计图回答下列问题：（1）这次被调查的学生共有_____人；（2）请将统计图2补充完整；（3）统计图1中B项目对应的扇形的圆心角是_____度；（4）已知该校共有学生1000人，根据调查结果估计该校喜欢体操的学生有_____人．∵△AOB 和△ACD 均为正三角形，∴60AOB CAD ∠=∠=︒，∴AD ∥OB ，∴ABP AOP S S = ，∵四边形ABCD为矩形，O为对角线，∴AO=OD，∴∠ODA=∠OAD，又∵AD为∠DAE的平分线，∴∠OAD=∠EAD，∴∠EAD=∠ODA，∵AD AC =，∴,ABD ABC EAD EACS S S S == ∴23BED BEC S S ∆∆==∵AB AC AD AC ==，，∴AD AB =，∵AB y ∥轴，∴AD x ⊥轴．∵反比例函数()0k y x x=<∴设k B x x ⎛⎫ ⎪⎝⎭，，令0x =，则077y =-=-，()0,7H ∴- 直线AB 的解析式为y x =-∴设直线CG 的表达式为y =将点()3,2C -代入y x t =+；（3）解：由图象可知，若123x x x <<，垂直于y 轴的直线l 在x 轴与直线=2y -之间，∴饮水机的一个循环周期为1003分钟，每一个循环内，在水温不超过50℃．∵7:20至8:45之间有85分钟，100 85-段内，A选项不符合题意；100设AD 的解析式为：y mx n =+，把()0,10D 、()2,20A 代入y mx =∵在▱ABCD中，AE=4，∴22=-= EC AC AE∵在▱ABCD中，AE=4，AB＝∴222016=-=-EC AC AE∴BC=BE-EC=3-2=1，的周长=2（AB+BC∴ABCD故答案为：20或12．考点：平行四边形的性质；坐标与图形性质．26．（1）证明见解析；（2）若。

苏教版八年级下册数学压轴题(非常好的题目)之令狐文艳创作

压轴题精选令狐文艳1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒． ⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点Ny xO P Q AB处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题非常好的题目精修订

苏教版八年级下册数学压轴题非常好的题目 GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-压轴题精选1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个着名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数xy 1的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(bb R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；yxOPQAB（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳道创编

压轴题精选时间：2021.03.06创作：欧阳道1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒． ⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面y x O P Q A B直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳家百创编

压轴题精选欧阳家百（2021.03.07）1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒． ⑴求直线AB 的解析式； ⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(bb R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E 坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．y xO P QA B（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳与创编

压轴题精选时间：2021.03.08创作：欧阳与1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两y O P Q A B直线相交于点Q．请说明Q点在直线OM上，并据此1∠AOB．证明∠MOB=33、（14分）如图，在平面直角坐标系xOy中，矩形OEFG的顶点E坐标为(4，0)，顶点G坐标为(0，2)．将矩形OEFG绕点O逆时针旋转，使点F落在轴的点N处，得到矩形OMNP，OM与GF交于点A．（1）判断△OGA和△OMN是否相似，并说明理由；（2）求过点A的反比例函数解析式；（3）设（2）中的反比例函数图象交EF于点B，求直线AB的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG的对称中心，并说明理由．4、如图，在平面直角坐标系xOy中，一次函数y kx b=+的图象经过点()0,2B，且与x轴的正半轴相交于点A，点P、点Q在线段AB上，点M、N在线段AO上，且OPM与QMN是相似比为3∶1的两个等腰直角三角形，90∠=∠=。

苏教版初二下数学压轴题

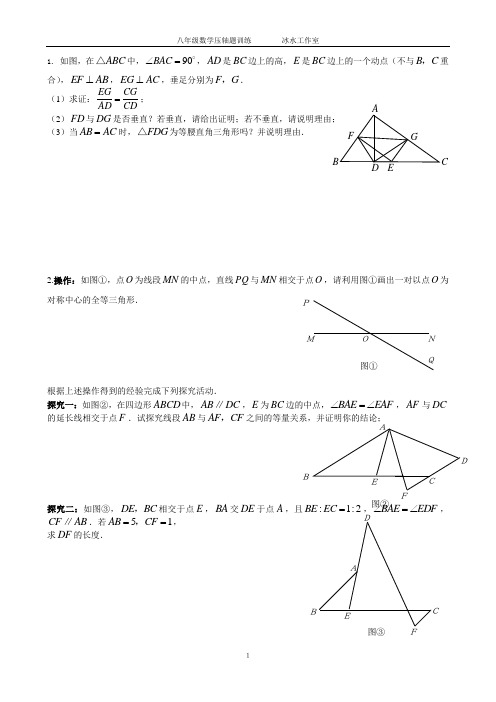
１1. 如图，在ABC △中，90BAC ∠=，AD 是BC 边上的高，E 是BC 边上的一个动点（不与B C ，重合），EF AB ⊥，EG AC ⊥，垂足分别为F G ，．（1）求证：EG CGAD CD=；（2）FD 与DG 是否垂直？若垂直，请给出证明；若不垂直，请说明理由；（3）当AB AC =时，FDG △为等腰直角三角形吗？并说明理由．2.操作：如图①，点O 为线段MN 的中点，直线PQ 与MN 相交于点O ，请利用图①画出一对以点O 为对称中心的全等三角形．根据上述操作得到的经验完成下列探究活动．探究一：如图②，在四边形ABCD 中，AB DC ∥，E 为BC 边的中点，BAE EAF ∠=∠，AF 与DC 的延长线相交于点F ．试探究线段AB 与AF CF ，之间的等量关系，并证明你的结论；探究二：如图③，DE BC ，相交于点E ，BA 交DE 于点A ，且:1:2BE EC =，BAE EDF ∠=∠，CF AB ∥．若51AB CF ==，，求DF 的长度．FAGCEBＰＯＭＮＱ图① ＡＢＥＦＣＤ图②ＤＡＢＥＦＣ图③２3.如图，在平面直角坐标系中，O 是坐标原点，点A 的坐标为()40-，，点B 的坐标为()()00.b b >，P 是直线AB 上的一个动点，作PC x ⊥轴，垂足为.C 记点P 关于y 轴的对称点P ′（点P ′不在y 轴上），连结PP P A P C ''′，，．设点P 的横坐标为.a （1）当3b =时，①求直线AB 的解析式；②若点P ′的坐标是()1m -，，求m 的值；（2）若点P 在第一象限，记直线AB 与P C ′的交点为.D 当13P D DC =′∶∶时，求a 的值；（3）是否同时存在a b ，，使P CA △′为等腰直角三角形？若存在，请求出所有满足要求的a b ，的值；若不存在，请说明理由.4.如图，在等腰梯形ABCD 中，AD BC ∥，5AB DC ==，6AD =，12BC =．动点P 从D 点出发沿DC 以每秒1个单位的速度向终点C 运动，动点Q 从C 点出发沿CB 以每秒2个单位的速度向B 点运动．两点同时出发，当P 点到达C 点时，Q 点随之停止运动．（1）梯形ABCD 的面积等于；（2）当PQ AB ∥时，P 点离开D 点的时间等于秒；（3）当P Q C ，，三点构成直角三角形时，P 点离开D 点多少时间？C B３5、如图1，在平面直角坐标系中，等腰Rt △AOB 的斜边OB 在x 轴上，直线y=3x- 4经过等腰Rt △AOB 的直角顶点A ，交y 轴于C 点，双曲线ky x=也经过A 点。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳家百创编

压轴题精选欧阳家百（2021.03.07）1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒． ⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？ 2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋转，使点F 落在轴的点N 处，得y xO PQA B到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳育创编

压轴题精选时间：2021.02.04创作：欧阳育1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？ 2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋y xO P QA B转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳体创编

压轴题精选时间：2021.02.03创作：欧阳体1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q 移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？ 2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数x y 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(b b R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶点E坐标为(4，0)，顶点G 坐标为(0，2)．将矩形OEFG 绕点O 逆时针旋y xO P QA B转，使点F 落在轴的点N 处，得到矩形OMNP ，OM 与GF 交于点A ．（1）判断△OGA 和△OMN 是否相似，并说明理由；（2）求过点A 的反比例函数解析式；（3）设（2）中的反比例函数图象交EF 于点B ，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG 的对称中心，并说明理由．4、如图，在平面直角坐标系xOy 中，一次函数y kx b =+的图象经过点()0,2B ，且与x轴的正半轴相交于点A ，点P 、点Q 在线段AB 上，点M 、N 在线段AO 上，且OPM 与QMN 是相似比为3∶1的两个等腰直角三角形，90OPM MQN ∠=∠=。

二次根式全章五类必考压轴题—2023-2024学年八年级数学下册(苏科版)(解析版)

二次根式全章五类必考压轴题题型一：二次根式的双重非负性的运用题型二：二次根式的规律探究题型三：复合二次根式的化简题型四：二次根式运算与求值技巧题型五：分母有理化题型一：二次根式的双重非负性的运用1．实数a 和b 在数轴上的位置如图所示，化简a b − ）A ．2aB ．2b −C ．2a −D ．2b 【答案】B101b a <−<<<a b +和绝对值的性质，即可得到答案．解题的关键是掌握所学的知识，正确得到101b a <−<<<．【详解】解：根据题意，则101b a <−<<<，∴0a b −>，0a b +<，∴a b −=a b a b−++ =a b a b −−−=2b −；故选：B ．2．已知三角形的三边长3,7,a 10a −的值为（）A ．7B ．7−C ．132a −D ．213a −【答案】A 【分析】本题主要考查了三角形和非负数．熟练掌握三角形三边关系，二次根式性质和绝对值性质，是解决问题的关键．根据三角形三边关系，得到410a <<，得到30a −>，100a −<，根据二次根式性质和绝对值性质即得．【详解】∵三角形的三条边长分别为3、7、a ，∴7373a −<<+，即410a <<，∴40a −>，100a −<，∴30a −>，()103103107a a a a a −=−−−=−−+=．故选：A ．3．已知a 、b 为有理数，且满足a +=a b −等于（）A ．2−B ．4−C ．2D ．4 【答案】D【分析】本题考查了二次根式的性质与化简，解题的关键是把33a 、b 的值，即可计算a b −的值．【详解】解：3==又∵a +=∴3a +=∴3a =，1b =-，∴()31314a b −=−−=+=，故选：D ．4．若(20m =，则n m的值是．【答案】【分析】本题考查了非负数的性质，分母有理化，根据非负数之和为零，则每个非负数都是零可得1m n ==−，进而代入代数式，即可求解．【详解】解：∵(20m =，∴1m n ==−=−，∴n m ==，故答案为：．5．已知x y ，是有理数，且6y =++化简的结果为．【答案】【分析】本题考查了二次根式有意义的条件、利用二次根式的性质进行化简，先由二次根式有意义的条件得出2x =，从而得出6y =【详解】解：由题意得：20x −≥，20x −≥，解得：2x =，将2x =代入6y =++得6y =，===故答案为：68b =+ ．【答案】5【分析】根据二次根式的性质得到170a −≥，170a −≥，求出17a =，8b =−，代入计算可得．【详解】解：由题可得170a −≥，170a −≥，解得17a =，∴08b =+，∴8b =−，5=，故答案为：5．【点睛】此题考查了二次根式有意义的条件，二次根式的化简求值，正确理解二次根式有意义的条件是解题的关键．7成立的条件是．【答案】x=2【分析】根据二次根式的意义，被开方数要大于等于零，去求x 的范围．【详解】根据二次根式有意义的条件，，∴x 必须满足的条件是20x −≥且20x −≤，则2x =．故答案是：2x =．【点睛】本题考查二次根式的意义，解题的关键是掌握二次根式有意义的条件．80=的根是．【答案】6x =【分析】根据二次根式有意义的条件得60x −≥或60x −≥，可得答案．【详解】解：根据二次根式有意义的条件得60x −≥或60x −≥，得：6x =，故答案为：6x =．【点睛】本题考查了二次根式有意义的条件，掌握其非负数的性质是解决此题的关键．题型二：二次根式的规律探究9．如图，在平面直角坐标系中，等腰直角三角形1OAA 的直角边OA 在x 轴上，点1A 的坐标为()1,1，以点1A 为直角顶点，1OA 为一直角边作等腰直角三角形12OA A ，再以点2A 为直角顶点，2OA 为直角边作等腰直角三角形23,OA A ⋅⋅⋅⋅⋅⋅，依此规律，则点2024A 的坐标为（）A ．()101110112,2−B ．()10112,0C ．()101210122,2−D ．()10122,0 【答案】D【分析】本题是平面直角坐标系下的规律探究题，除了研究动点变化的相关数据规律，还应该注意各个象限内点的坐标符号．点A 坐标变化规律要分别从旋转次数与点A 所在象限或坐标轴、点A 到原点的距离与旋转次数的对应关系寻找，再求解．【详解】解：由已知，点A 每次旋转转动45°，则转动一周需转动8次，每次转动点A 到原∵20248253÷=，∴点2024A 的在x 轴的正半轴上，则2024101220242OA ==， ∴()101220242,0A ，故选：D ．10．2222222x ⋅⋅⋅⋅⋅⋅，，，第n 个单项式是（）A 2B C 2 D ．2n x 【答案】A【分析】本题主要考查了数字变化规律．观察已知式子，总结规律即可得第n 个单项式是2．2，22x 2，22，2⋯⋯，总结规律得第n 2．故选：A ．11．如图，12OA A △为等腰直角三角形，11OA =，以斜边2OA 为直角边作等腰23Rt OA A △，再以3OA 为直角边作等腰34Rt OA A △，…，按此规律作下去便得到了一个海螺图案，则n OA 的长度为．（用含n 的式子表示）【答案】1n −【分析】本题主要考查等腰直角三角形的性质，熟练掌握等腰直角三角形的性质是解题的关键；由题意易得2OA =32OA =，4OA = 【详解】解：∵12OA A △为等腰直角三角形，11OA =，∴121OA ==，同理可得：2322OA ===，343OA ===，……；综上所述：1n n OA −=；故答案为1n −．题型三：复合二次根式的化简12．先阅读下列解答过程，然后作答：a ，b 使a b m +=，ab n =，这样22m +==)a b =>，例7m =，12n =；由于437+=，4312⨯=，即227+==2===根据上述例题的方法化简：；【答案】【分析】本题考查二次根式根号内含有根号的式子化简，二次根式的性质及完全平方公式，（1）根据解答过程即可得解，（2（3二次根式根号内含有根号的式子化简主要是根据完全平方公式的特点将该式子转化为平方的形式．【详解】（1=；（2==（3==13．先阅读下列的解答过程，然后再解答：a b 、，使,a b m ab n +==，使得22m +==)a b =>7m =，12n =由于，4312⨯=437+=即227+==2\=(1)______=______；(2)【答案】3【分析】本题考查了二次根式的化简求值，涉及了配方法的运用和完全平方式的运用以及二次根式性质的运用．（1a ，b 值为3和2后，即可得出结论；确定a ，b 值为8和9后，即可得出结论（2a 的形式化简，求解．即可．【详解】（1===3=，3；（2===．14．阅读下面这道例题的解法，并回答问题．11====依据上述计算，填空：，；(2)199+− 【答案】(1)23(2)9【分析】本题主要考查了化简复合二次根式：（1）根据例题的方法，凑完全平方公式，然后根据二次根式的性质化简即可求解；（2）根据例题的方法，凑完全平方公式，然后根据二次根式的性质化简即可求解．【详解】（1=2==3=；故答案为：23；（2199+−(100+1100+−1101=−9=．15．像这样的根式叫做复合二次根式．有一些复合二次根式可以借助构造完全平方式进行化简，如：1===，再如：=法探索并解决下列问题：(1)化简：(2)化简：(3)若()2a m +=，且a ，m ，n 为正整数，求a 的值．【答案】(3)14或46【分析】此题考查化简二次根式，活用完全平方公式，把数分解成完全平方式，进一步利用公式因式分解化简，注意在整数分解时参考后面的二次根号里面的数值．（1）利用题中复合二次根式借助构造完全平方式的新方法求解；（2）利用题中复合二次根式借助构造完全平方式的新方法求解；（3）利用完全平方公式，结合整除的意义求解．【详解】（1=（2）==（3）∵2252a m n +=++∴225a m n =+，62mn =，∴3mn =又∵a m 、、n 为正整数， ∴1,3m n ==，或者3,1m n ==， ∴当1,3m n ==时，46a =；当3,1m n ==时，14a =． ∴a 的值为：14或46．16．【规律探究题】观察下列运算：①由)111=1=；②由1== …… 问题：=______=______； (2)利用（1）中发现的规律计算：)12024+．【答案】n 为正整数） (2)2024【分析】本题考查了二次根式的混合运算，分母有理化和平方差公式等知识点，能根据已知算式得出规律是解此题的关键．（1）根据已知算式得出规律即可；（2）根据（1）中得出的规律进行变形，再根据二次根式的加法法则进行计算，最后根据平方差公式求出答案即可．【详解】（1==−（n 为正整数）（2）原式)120241=+)11202512024==−=17．观察下列等式：第11112⎛⎫=+− ⎪⎝⎭；第211123⎛⎫+− ⎪⎝⎭；第311134⎛⎫+− ⎪⎝⎭， ……按照以上规律，解决下列问题． (1)写出第4个等式：______．(2)写出你猜想的第n 个等式（用含n 的等式表示）． (3)请用（2）中发现的规律计算：12024++【答案】11145⎛⎫+− ⎪⎝⎭1111n n ⎛⎫+− ⎪+⎝⎭(3)202420242025【分析】本题考查了二次根式的规律探究，分式的规律探究．根据题意推导一般性规律是解题的关键．（1）由题意可得，第411145⎛⎫+− ⎪⎝⎭；（2）由题意知，第n 1111n n ⎛⎫=+− ⎪+⎝⎭；（3）根据12024++1111111202412233420242025⎛⎫=+−+−+−++− ⎪⎝⎭，计算求解即可．【详解】（1）解：由题意可得，第411145⎛⎫=+− ⎪⎝⎭，11145⎛⎫=+− ⎪⎝⎭；（2）解：由题意知，第n 1111n n ⎛⎫=+− ⎪+⎝⎭；（312024++1111111111112233420242025⎛⎫⎛⎫⎛⎫⎛⎫=+−++−++−++− ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1111111202412233420242025⎛⎫=+−+−+−++− ⎪⎝⎭ 1202412025=+−202420242025=，52024202142220=++．18．观察下列算式的特征及运算结果，探索规律：2=3=4=5．(1)观察算式规律，计算、= ；= ；(2)用含正整数 n 的代数式表示上述算式的规律；(3)计算：2020− 【答案】(1)6,37()11n n +≥()2n n =≥(3)1013【分析】本题考查二次根式运算中的规律探究：（1）根据题干给定的等式，进行作答即可；（2）根据题干给定的等式，确定相应的规律作答即可；（3）先根据规律化简各式，再进行计算即可．【详解】（16=37=；故答案为：6,37；（2）由题意，()11n n =+≥()2n n =≥；（32020−3579201920212023=−+−++−+()()2222023=−+−++−+()20191220234+=−⨯+10102023=−+ 1013=．题型四：二次根式运算与求值技巧19．（1（2）2(1(2−−【答案】（1（2）12−【分析】（1）利用二次根式的乘除法运算法则进行计算，再合并即可求解；（2）利用完全平方公式、平方差公式展开，再合并即可求解；本题考查了二次根式的混合运算，掌握二次根式的性质和运算法则是解题的关键．【详解】解：（1）原式===（2）原式()11243=−−−131=−，12=−20．计算：(1)+(2)()21+【答案】(1)(2)8−【分析】本题主要考查了二次根式的混合计算：（1）先化简二次根式，再计算二次根式加减法即可；（2）先利用平方差公式和完全平方公式去括号，然后计算二次根式加减法即可．【详解】（1）解：+=((=+=（2）解：()21+()()2381=−+−19=−+−8=−21．计算：(1)(；【答案】(1)63【分析】本题主要考查了二次根式的混合运算、平方差公式的知识点，灵活运用二次根式的混合运算法则成为解题的关键．（1）先根据平方差公式计算，然后再运用二次根式的混合运算法则计算即可；（2）直接运用二次根式的混合运算法则计算即可．【详解】（1）解：((22=−126=−6=．（2=3=−3=．22．计算：(1)÷(2))22【答案】(1)7 2(2)1【分析】本题主要考查了二次根式的混合运算，熟练掌握运算法则、正确计算是解题的关键．（1）先计算小括号内的二次根式乘法，再化简二次根式并合并同类二次根式，最后计算二次根式除法即可；（2）先计算二次根式乘法，再加减计算即可．【详解】（1）解：÷=÷(=÷=72=；（2）解：)22222-+=34=−12=−+1=．23．计算下列各小题．(2)()21+．【答案】(1)12(2)24−【分析】（1）关键二次根式乘除的混合运算计算即可；（2）根据二次根式混合运算计算即可．本题考查了二次根式的混合运算，熟练掌握运算法则是解题的关键．【详解】（112=．（2））()21+22241=−+−2324124=−+−=− 24．计算：(2)(222−【答案】(1)3(2)6+【分析】本题考查了二次根式的混合计算，熟练掌握二次根式的性质，二次根式的乘法和除法法则、乘法公式是解决问题的关键．（1）直接利用二次根式的加减乘除运算法则进行计算；（2）先计算完全平方式及平方差公式，最后再计算加减法即可．【详解】（1）解：原式=3=−3=（2）原式()3245=++−51=+6=+25．计算：(2)⎛÷⎝；(3))(23−．【答案】(1)8(2)73(3)1−【分析】题目主要考查二次根式的混合运算，熟练掌握运算法则是解题关键．（1）将二次根式化简，然后计算乘除法即可；（2）先将二次根式化简，接着计算小括号里面的，然后再算除法即可；（3）利用完全平方公式和平方差公式进行计算，然后计算加减法即可．【详解】（1===；（2）解：⎛÷⎝⎛=÷⎝73=；（3）解：)(23−()59207=−−−5913=−−1=−26．先化简，再求值：()()()()232x y x y y x y x y −+++−−，其中2x =2y = 【答案】5xy ，5【分析】本题考查整式的混合运算，二次根式的混合运算，根据平方差公式，单项式乘多项式及完全平方公式将原式化简，再将x 、y 的值代入，利用平方差公式计算可得结论．掌握相应的运算法则和公式是解题的关键．【详解】解：()()()()232x y x y y x y x y −+++−−()22222322x y xy y x xy y =−++−−+22222322x y xy y x xy y =−++−+− 5xy =，当2x =2y =原式(()5225435=⨯+=⨯−=．27．已知x y = (1)代数式xy 的值； (2)代数式22x y xy +的值．【答案】(1)1(2)【分析】（1）利用平方差公式即可得答案；（2）由于x y +=1xy =方便运算，故可考虑将代数式化为含()x y +和xy 的项，再整体代入()x y +和xy 的值，进行代数式的求值运算．【详解】（1）xy = 32=− 1=；（2）由已知：x y + =+ =，xy = 32=− 1=，故：原式()xy x y =+=【点睛】本题考查二次根式的化简求值，由于直接代入计算复杂容易出错，因此可考虑整体代入，本题考查了整体代入的思想．28．已知22a b ==(1)22a b +；(2)22a b ab +【答案】(1)12(2)6【分析】（1）根据已知条件式得出4,2a b ab +==，然后根据完全平方公式变形求值即可求解；（2）将2ab =，代入进行计算即可求解．【详解】（1）解：∵22a b ==，∴224a b +==，(22422ab ==−=，∴()2222242212a b a a b b =+−=−=+⨯；（2）解：∵2ab =，∴22a b ab +222=+6=【点睛】本题考查了二次根式的混合运算，熟练掌握完全平方公式与二次根式的运算法则是解题的关键．29．先化简，再求值：2312111a a a a a ++⎛⎫−÷ ⎪++−⎝⎭，其中1a ．【答案】1a −【分析】本题主要考查分式的混合运算以及二次根式的化简求值，先通分算括号内的，把除法化为乘法，化简后将a 的值代入计算即可．【详解】解：2312111a a a a a ++⎛⎫−÷ ⎪++−⎝⎭ ()()22111a a a a a ++=÷++−()()11212a a a a a +−+=⋅++ 1a =−．当1a 时，原式11=−30．先化简，再求值：221121x x x x x −−+++，其中1x =．【答案】11x +，【分析】本题考查的是分式的化简求值，熟知分式混合运算的法则是解题的关键．先根据分1x 代入进行计算即可．【详解】解：221121x x x x x −−+++ ()()()21111x x x x x +−=−++111x x x x −=−++x x 1x 1−+=+11x =+，当1x =1=．31．已知22x y ==(1)22xy +； (2)x y y x−．【答案】(1)14(2)【分析】（1）先将22x y +变形为2()2x y xy +−，再将x ，y 的值代入，利用二次根式运算法则计算即可，（2）先将x y y x −整理为()()x y x y xy +−，再将x ，y 的值代入，利用二次根式运算法则计算即可，本题考查了二次根式的运算及平方差公式的运用，解题的关键是先将待求式子进行化简，并熟练掌握二次根式的运算法则．【详解】（1）解：∵22x y ==∴222()2x y x y xy +=+−(2(22222=−162=−14=，（2）解：∵22x y == ∴()()22x y x y x y x y y x xy xy +−−−=====题型五：分母有理化32．阅读下列简化过程：1；==== 解答下列问题：(1)(2)2021++ (3)设ab ，c a ，b ，c 的大小关系．【答案】1−(3)a ＜b ＜c【分析】此题考查代数式计算规律探究，分母有理化计算，根据例题掌握计算的规律并解决问题是解题的关键．（1）根据已知可得：两个连续正整数算术平方根的和的倒数，等于分子分母都乘以这两个连续正整数算术平方根的差，化简得这两个连续正整数算术平方根的差；（2）利用分母有理化分别化简，再合并同类二次根式得解；（3）将a 、b 、c 分别化简，比较结果即可．【详解】（1）解：原式==；（2）解：原式12022=+1；（3）解：a ==2b ==2c ==，22，33．阅读材料，回答下列问题：两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，我们就说这两个代数式互(0)a a =>，1)1=11互为有理化因式．（1______．这样，化简一个分母含有二次根式的式子时，采用分子、分母同乘以分母的有理化因式的方法就可以了，例如：==，1=，==2==…，（2）用上述方法判断：若a 2b =a ，b 的关系是______．（3）计算：1)2024+．【答案】（1（2）a b =−；（3）2023【分析】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可，二次根式的分母有理化是解题的关键．（1）根据有理化因式求解；（2）利用分母有理化把a 进行化简可得到a 与b 的关系；（3）先分母有理化，然后利用平方差公式计算．【详解】解：（1（2）a 与b 互为相反数．理由如下：(2a =−，a b ∴=−，故答案为：a b =−；（3）1)11)=1)=20241=−2023=．34.【阅读理解】爱思考的小名在解决问题：已知a =，求2281a a −+的值．他是这样分析与解答的：122a ==+2a −= ()223a ∴−=，即2443a a −+=．241a a ∴−=−．()()222812412111a a a a ∴−+=−+=⨯−+=−．请你根据小名的分析过程，解决如下问题：(1)=______； (2)=______； (3)若a =23121a a −−的值．【答案】1(2)1(3)2【分析】本题考查了二次根式的混合运算，求代数式的值，熟练掌握二次根式的分母有理化（1）仿照题的方法化简即可；（2）把每项按照题中方法化简，再相加减即可；（3）仿照题中方法求代数式值的方法求解即可．【详解】（11=，1；（2=(2024=+12024+11=，故答案为：1；（3）解：∵2a ===，∴2a −=∴2(2)5a −=，即241a a −=， ∴2231213(4)13112a a a a −−=−−=⨯−=．35．阅读下面的材料，解决问题：1==；==2==(1)= ；= ； (2)...+ (3)...【答案】(2)9(3)12−【分析】本题考查了二次根式的混合运算，熟练掌握二次根式的运算法则是解答本题的关键．（1）根据题干提供的方法化简即可；（2）先根据题干提供的方法化简，再合并同类二次根式；（3）先根据题干提供的方法化简，再合并同类二次根式．【详解】（1==；==．（2......=+1...1=−110=−+9=（3......=+ 11...2=(112=−12=− 36)4141151⨯⨯==−以上这种化简的步骤叫做分母有理化．回答问题：(1)(2)（m 为正整数）．【答案】(2)2．【分析】此题主要考查了分母有理化，第二题是个难点，需要总结规律，再计算．（1（2）各项进行分母有理化，再合并同类项即可．【详解】（14462=−⋅⋅⋅+（242424⋅⋅⋅4()=+++⋅⋅⋅+222222=2。

苏教版八年级下册数学压轴题(非常好的题目)之欧阳历创编

压轴题精选时间：2021.02.09创作人：欧阳历1、如图，在平面直角坐标系内，已知点A （0，6）、点B （8，0），动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 移动，同时动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点A 移动，设点P 、Q移动的时间为t 秒．⑴求直线AB 的解析式；⑵当t 为何值时，△APQ 与△AOB 相似？ 2、“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”．下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法（如图）：将给定的锐角∠AOB 置于直角坐标系中，边OB 在x 轴上、边OA 与函数xy 1 的图象交于点P ，以P 为圆心、以2OP 为半径作弧交图象于点R ．分别过点P 和R 作x 轴和y 轴的平行线，两直线相交于点M ，连接OM 得到∠MOB ，则∠MOB=31∠AOB ．要明白帕普斯的方法，请研究以下问题：（1）设)1,(a a P 、)1,(bb R ，求直线OM 对应的函数表达式（用含b a ,的代数式表示）．（2）分别过点P 和R 作y 轴和x 轴的平行线，两直线相交于点Q ．请说明Q 点在直线OM 上，并据此证明∠MOB=31∠AOB ．3、（14分）如图，在平面直角坐标系xOy 中，矩形OEFG 的顶y xO P QA B点E坐标为(4，0)，顶点G坐标为(0，2)．将矩形OEFG绕点O逆时针旋转，使点F落在轴的点N处，得到矩形OMNP，OM与GF交于点A．（1）判断△OGA和△OMN是否相似，并说明理由；（2）求过点A的反比例函数解析式；（3）设（2）中的反比例函数图象交EF于点B，求直线AB 的解析式；（4）请探索：求出的反比例函数的图象，是否经过矩形OEFG的对称中心，并说明理由．4、如图，在平面直角坐标系xOy中，一次函数y kx b=+的图象经过点()0,2B，且与x轴的正半轴相交于点A，点P、点Q在线段AB上，点M、N在线段AO上，且OPM与QMN是相似比为3∶1的两个等腰直角三角形，90∠=∠=。

苏教版初二八下期中复习平行四边形压轴题含答案(非常好)

教学主题平行四边形压轴题教学目标重要知识点1.2.3.易错点教学过程一．选择题（共15小题）1．（2012•玉环县校级模拟）如图，菱形ABCD中，AB=3，DF=1，∠DAB=60°，∠EFG=15°，FG⊥BC，则AE=（）A．B．C．D．考点：菱形的性质；解直角三角形．专题：压轴题．分析：首先过FH⊥AB，垂足为H．由四边形ABCD是菱形，可得AD=AB=3，即可求得AF的长，又由∠DAB=60°，即可求得AH与FH的长，然后由∠EFG=15°，证得△FHE是等腰直角三角形，继而求得答案．解答：解：过FH⊥AB，垂足为H．∵四边形ABCD是菱形，∴AD=AB=3，∵DF=1，∴AF=AD﹣FD=2，∵∠DAB=60°，∴∠AFH=30°，∴AH=1，FH=，又∵∠EFG=15°，∴∠EFH=∠AFG﹣∠AFH﹣∠EFG=90°﹣30°﹣15°=45°，∴△FHE是等腰直角三角形，∴HE=FH=，∴AE=AH+HE=1+．故选D．点评：此题考查了菱形的性质、直角三角形的性质、勾股定理以及等腰直角三角形的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．2．（2015•泰安模拟）如图，已知直角梯形ABCD中，AD∥BC，∠BCD=90°，BC=CD=2AD，E、F分别是BC、CD边的中点，连接BF、DE交于点P，连接CP并延长交AB于点Q，连接AF，则下列结论：①CP平分∠BCD；②四边形ABED为平行四边形；③CQ将直角梯形ABCD分为面积相等的两部分；④△ABF为等腰三角形，其中不正确的有（）A．1个B．2个C．3个D．0个考点：直角梯形；全等三角形的判定与性质；等腰三角形的判定；平行四边形的判定．专题：证明题；压轴题．分析：解答：解：∵BC=CD=2AD，E、F分别是BC、CD边的中点，∴CF=CE，BE=DF，在△BCF和△DCE中，∵，∴△BCF≌△DCE（SAS），∴∠FBC=∠EDC，BF=ED，在△BPE和△DPF中，∵，∴△BPE≌△DPF（AAS），∴BP=DP，在△BPC和△DPC中，∵，∴△BPC≌△DPC（SSS），∴∠BCP=∠DCP，即CP平分∠BCD，故选项①正确；又∵AD=BE且AD∥BE，∴四边形ABED为平行四边形，故选项②正确；显然S△BPC=S△DPC，但是S△BPQ≠S四边形ADPQ，∴S△BPC+S△BPQ≠S△DPC+S四边形ADPQ，即CQ不能将直角梯形ABCD分为面积相等的两部分，故选项③不正确；∵BF=ED，AB=ED，∴AB=BF，即△ABF为等腰三角形，故④正确；综上，不正确的选项为③，其个数有1个．故选A．点评：本题考查了等腰三角形的判定，平行四边形的判定与性质，以及全等三角形的判定与性质，熟记以上图形的性质，并能灵活运用其性质，是解答本题的关键，本题综合性较好．5．（2014•江阴市二模）在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、FA⊥AE 交DP于点F，连接BF，FC．下列结论：①△ABE≌△ADF；②FB=AB；③CF⊥DP；④FC=EF其中正确的是（）A．①②④B．①③④C．①②③D．①②③④考点：正方形的性质；三角形内角和定理；全等三角形的判定与性质；直角三角形斜边上的中线；等腰直角三角形．专题：压轴题．分析：解答：解：∵正方形ABCD，BE⊥ED，EA⊥FA，∴AB=AD=CD=BC，∠BAD=∠EAF=90°=∠BEF，∵∠APD=∠EPB，∴∠EAB=∠DAF，∠EBA=∠ADP，∵AB=AD，∴△ABE≌△ADF，∴①正确；∴AE=AF，BE=DF，∴∠AEF=∠AFE=45°，取EF的中点M，连接AM，∴AM⊥EF，AM=EM=FM，∴BE∥AM，∵AP=BP，∴AM=BE=DF，∴∠EMB=∠EBM=45°，∴∠AMB=90°+45°=135°=∠FMB，∵BM=BM，AM=MF，∴△ABM≌△FBM，∴AB=BF，∴②正确；∴∠BAM=∠BFM，∵∠BEF=90°，AM⊥EF，∴∠BAM+∠APM=90°，∠EBF+∠EFB=90°，∴∠APF=∠EBF，∵AB∥CD，∴∠APD=∠FDC，∴∠EBF=∠FDC，∵BE=DF，BF=CD，∴△BEF≌△DFC，∴CF=EF，∠DFC=∠FEB=90°，∴③正确；④正确；故选D．点评：本题主要考查对正方形的性质，等腰直角三角形，直角三角形斜边上的中线性质，全等三角形的性质和判定，三角形的内角和定理等知识点的理解和掌握，综合运用这些性质进行推理是解此题的关键．6．（2014•武汉模拟）如图，正方形ABCD的三边中点E、F、G．连ED交AF于M，GC交DE于N，下列结论：①GM⊥CM；②CD=CM；③四边形MFCG为等腰梯形；④∠CMD=∠AGM．其中正确的有（）A．①②③B．①②④C．①③④D．①②③④考点：正方形的性质；全等三角形的判定与性质；等腰梯形的判定．专题：压轴题．分析：要证以上问题，需证CN是DN是垂直平分线，即证N点是DM中点，利用中位线定理即可解答：解：∵由已知，AG∥FC且AG=FC，故四边形AGCF为平行四边形，∴∠GAF=∠FCG又AE=BF，AD=AB，且∠DAE=∠ABF，可知∠ADE=∠BAF∴DE⊥AF，DE⊥CG．又∵G点为中点，∴GN为△ADM的中位线，即CG为DM的垂直平分线，可证CD=CM，∴∠CDG=∠CMG，即GM⊥CM．又∠MGN=∠DGC=∠DAF（外角等于内对角），∴∠FCG=∠MGC．故选A．点评：在正方形中对中点问题的把握和运用，灵活运用几何图形知识．7．（2013•绍兴模拟）如图，△ABC纸片中，AB=BC＞AC，点D是AB边的中点，点E在边AC上，将纸片沿DE折叠，使点A落在BC边上的点F处．则下列结论成立的个数有（）①△BDF是等腰直角三角形；②∠DFE=∠CFE；③DE是△ABC的中位线；④BF+CE=DF+DE．A．1个B．2个C．3个D．4个考点：三角形中位线定理；翻折变换（折叠问题）．专题：压轴题；操作型．分析：根据题意可知△DFE是△DAE对折的图形，所以全等，故AD=DF，而AD=BD，所以BD=DF，但是∠B不一定等于45°，所以△BDF不一定是等腰直角三角形，①不成立；结合①中的结论，BD=DF，而∠ADE=∠FDE，∠ADF=∠DBF+∠DFB，可证∠BFD=∠EDF，故DE∥BC，即DE是△ABC的中位线，③成立；若③成立，利用△ADE≌△FDE，DE∥BC，∠AEF=∠EFC+∠ECF，可证∠DFE=∠CFE，②成立；根据折叠以及中位线定理得右边=AB，要和左边相等，则需CE=CF，则△CEF应是等边三角形，显然不一定，故④不成立．解答：解：①根据折叠知AD=DF，所以BD=DF，即一定是等腰三角形．因为∠B不一定等于45°，所以①错误；②连接AF，交DE于G，根据折叠知DE垂直平分AF，又点D是AB边的中点，在△ABF中，根据三角形的中位线定理，得DG∥BF．进一步得E是AC的中点．由折叠知AE=EF，则EF=EC，得∠C=∠CFE．又∠DFE=∠A=∠C，所以∠DFE=∠CFE，正确；③在②中已证明正确；④根据折叠以及中位线定理得右边=AB，要和左边相等，则需CE=CF，则△CEF应是等边三角形，显然不一定，错误．故选B．点评：本题结合翻折变换，考查了三角形中位线定理，正确利用折叠所得对应线段之间的关系以及三角形的中位线定理是解题的关键．8．（2013•惠山区校级一模）如图，已知在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：①△APD≌△AEB﹔②点B到直线AE的距离为﹔③EB⊥ED﹔④S△APD+S△APB=0.5+．其中正确结论的序号是（）A．①③④B．①②③C．②③④D．①②④考点：正方形的性质；全等三角形的判定与性质．专题：压轴题．分析：根据正方形的性质可得AB=AD，再根据同角的余角相等求出∠BAE=∠DAP，然后利用“边角边”证明△APD和△AEB全等，从而判定①正确，根据全等三角形对应角相等可得∠AEB=∠APD=135°，然后求出∠BEP=90°，判定③正确，根据等腰直角三角形的性质求出PE，再利用勾股定理列式求出BE的长，然后根据S△APD+S△APB=S△APE+S△BPE列式计算即可判断出④正确；过点B作BF⊥AE交AE的延长线于F，先求出∠BEF=45°，从而判断出△BEF是等腰直角三角形，再根据等腰直角三角形的性质求出BF的长为，判断出②错误．解答：解：在正方形ABCD中，AB=AD，∵AP⊥AE，∴∠BAE+∠BAP=90°，又∵∠DAP+∠BAP=∠BAD=90°，∴∠BAE=∠DAP，在△APD和△AEB中，，∴△APD≌△AEB（SAS），故①正确；∵AE=AP，AP⊥AE，∴△AEP是等腰直角三角形，∴∠AEP=∠APE=45°，∴∠AEB=∠APD=180°﹣45°=135°，∴∠BEP=135°﹣45°=90°，∴EB⊥ED，故③正确；∵AE=AP=1，∴PE=AE=，在Rt△PBE中，BE===2，∴S△APD+S△APB=S△APE+S△BPE，=×1×1+××2，=0.5+，故④正确；过点B作BF⊥AE交AE的延长线于F，∵∠BEF=180°﹣135°=45°，∴△BEF是等腰直角三角形，∴BF=×2=，即点B到直线AE的距离为，故②错误，综上所述，正确的结论有①③④．故选A．点评：本题考查了正方形的性质，全等三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理的应用，综合性较强，难度较大，熟记性质并仔细分析图形，理清图中三角形与角的关系是解题的关键．9．（2013•江苏模拟）在正方形ABCD外取一点E，连接AE、BE、DE，过A作AE的垂线交ED于点P，若AE=AP=1，PB=，下列结论：①△APD≌△AEB；②点B到直线AE的距离为；③S正方形ABCD=4+；其中正确的是（）A．①②③B．只有①③C．只有①D．只有③考点：正方形的性质；全等三角形的判定与性质；等腰直角三角形．专题：计算题；压轴题．分析：首先利用已知条件根据边角边可以证明△APD≌△AEB，故选项①正确；由①可得∠BEP=90°，故BE不垂直于AE过点B作BM⊥AE延长线于M，由①得∠AEB=135°所以∠EMB=45°，所以△EMB是等腰Rt△，求出B到直线AE距离为BF，即可对于②作出判断；根据三角形的面积公式得到S△BPD=PD×BE=，所以S△ABD=S△APD+S△APB+S△BPD=2+，由此即可对③判定．解答：解：∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD，∴∠BAP+∠PAD=90°，∵EA⊥AP，∴∠EAB+∠BAP=90°，∴∠PAD=∠EAB，∵在△APD和△AEB中，，∴△APD≌△AEB（SAS），故①正确；∵△AEP为等腰直角三角形，∴∠AEP=∠APE=45°，∴∠APD=∠AEB=135°，∴∠BEP=90°，过B作BF⊥AE，交AE的延长线于F，则BF的长是点B到直线AE的距离，在△AEP中，AE=AP=1，根据勾股定理得：PE=，在△BEP中，PB=，PE=，由勾股定理得：BE=，∵∠PAE=∠PEB=∠EFB=90°，AE=AP，∴∠AEP=45°，∴∠BEF=180°﹣45°﹣90°=45°，∴∠EBF=45°，∴EF=BF，在△EFB中，由勾股定理得：EF=BF=，故②是错误的；由△APD≌△AEB，∴PD=BE=，∵S△BPD=PD×BE=，∴S△ABD=S△APD+S△APB+S△BPD=2+，∴S正方形ABCD=2S△ABD=4+．故选项③正确，则正确的序号有：①③．故选B．点评：此题分别考查了正方形的性质、全等三角形的性质与判定、三角形的面积及勾股定理，综合性比较强，解题时要求熟练掌握相关的基础知识才能很好解决问题．10．（2013•武汉模拟）如图，正方形ABCD的对角线相交于O点，BE平分∠ABO交AO于E点，CF⊥BE于F点，交BO于G点，连结EG、OF．则∠OFG的度数是（）A．60°B．45°C．30°D．75°考点：正方形的性质；等腰三角形的判定与性质；直角三角形斜边上的中线．专题：压轴题．分析：根据正方形的对角线平分一组对角可得∠ABO=∠CBO=∠BCO=45°，再根据角平分线的定义求出∠OBE=22.5°，然后求出∠CBE=67.5°，再求出∠CEB=67.5°，从而得到∠CBE=∠CEB，根据等腰三角形三线合一的性质可得BF=EF，再根据直角三角形斜边上的中线等于斜边的一半可得OF=BF，然后利用等边对等角求出∠BOF=∠OBE，最后在△BOF中，利用三角形的内角和定理列式计算即可得解．解答：解：在正方形ABCD中，∠ABO=∠CBO=∠BCO=45°，∵BE平分∠ABO，∴∠OBE=22.5°，∴∠CBE=180°﹣45°﹣67.5°=67.5°，∴∠CBE=∠CEB，∵CF⊥BE，∴BF=EF，又∵∠AOB=90°，∴OF=BF，∴∠BOF=∠OBE=22.5°，在△BOF中，∠OFG+22.5°+22.5°+90°=180°，∴∠OFG=45°．故选B．点评：本题考查了正方形的对角线平分一组对角的性质，等腰三角形的判定与等腰三角形三线合一的性质，直角三角形斜边上的中线等于斜边的一半的性质，熟记各性质并准确识图求出∠BOF的度数是解题的关键．11．（2012•武汉）在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=5，BC=6，则CE+CF的值为（）A．11+B．11﹣C．11+或11﹣D．11+或1+考点：平行四边形的性质；勾股定理．专题：计算题；压轴题；分类讨论．分析：根据平行四边形面积求出AE和AF，有两种情况，求出BE、DF的值，求出CE和CF的值，相加即可得出答案．解答：解：∵四边形ABCD是平行四边形，∴AB=CD=5，BC=AD=6，①如图：过点A作AE⊥BC垂足为E，过点A作AF⊥DC垂足为F，由平行四边形面积公式得：BC×AE=CD×AF=15，求出AE=，AF=3，在Rt△ABE和Rt△ADF中，由勾股定理得：AB2=AE2+BE2，把AB=5，AE=代入求出BE=，同理DF=3＞5，即F在DC的延长线上（如上图），∴CE=6﹣，CF=3﹣5，即CE+CF=1+，②如图：过点A作AF⊥DC垂足为F，过点A作AE⊥BC垂足为E，∵AB=5，AE=，在△ABE中，由勾股定理得：BE=，同理DF=3，由①知：CE=6+，CF=5+3，∴CE+CF=11+．故选D．点评：本题考查了平行四边形性质，勾股定理的应用，主要培养学生的理解能力和计算能力，注意：要分类讨论啊．12．（2012•河南模拟）如图，DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，则S△CEF：S△DGF等于（）A．2：1 B．3：1 C．4：1 D．5：1考点：三角形中位线定理；全等三角形的判定与性质．专题：压轴题．分析：取CG的中点H，连接EH，根据三角形的中位线定理可得EH∥AD，再根据两直线平行，内错角相等可得∠GDF=∠HEF，然后利用“角边角”证明△DFG和△EFH全等，根据全等三角形对应边相等可得FG=FH，全等三角形的面积相等可得S△EFH=S△DGF，再求出FC=3FH，再根据等高的三角形的面积比等于底边的比求出两三角形的面积的比，从而得解．解答：解：如图，取CG的中点H，连接EH，∵E是AC的中点，∴EH是△ACG的中位线，∴EH∥AD，∴∠GDF=∠HEF，∵F是DE的中点，∴DF=EF，在△DFG和△EFH中，，∴△DFG≌△EFH（ASA），∴FG=FH，S△EFH=S△DGF，又∵FC=FH+HC=FH+GH=FH+FG+FH=3FH，∴S△EFC=3S△EFH，∴S△EFC=3S△DGF，因此，S△CEF：S△DGF=3：1．故选B．点评：本题考查了三角形的中位线定理，全等三角形的判定与性质，作辅助线，利用三角形的中位线进行解题是解题的关键．13．（2012•杭州模拟）如图，①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH（不重叠无缝隙）．若①②③④四个平行四边形面积的和为28cm2，四边形ABCD面积是18cm2，则①②③④四个平行四边形周长的总和为（）A．72cm B．64cm C．56cm D．48cm考点：平行四边形的性质；菱形的性质．专题：压轴题．分析：求出⑤平行四边形的面积，求出菱形EFGH的面积，过E作EM⊥GH于M，设EH=HG=FG=EF=xcm，求出x的值，结合图形即可求出答案．解答：解：∵①②③④四个平行四边形面积的和为28cm2，四边形ABCD面积是18cm2，∴平行四边形⑤的面积是18﹣×28=4（cm2），∴菱形EFGH的面积是4+28=32cm2，过E作EM⊥GH于M，设EH=HG=FG=EF=xcm，∵∠H=30°，∴EM=x，即x•x=32，x=8，∴EH=HG=FG=EF=8cm，∴①②③④四个平行四边形的周长的和正好是8×8=64，故选B．点评：本题考查了含30度角的直角三角形性质，平行四边形性质，菱形性质等知识点，能根据图形得出①②③④四个平行四边形的周长的和正好是8个EF是解此题的关键，注意：菱形的对边相等，平行四边形的对边相等．14．（2012•淄博模拟）则在▱ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG、BG，∠BDG的大小是（）A．30°B．45°C．60°D．75°考点：平行四边形的性质；全等三角形的判定与性质．专题：压轴题．分析：分别连接GB、GC，求证四边形CEGF是平行四边形，再求证△ECG是等边三角形．由AD∥BC及AF平分∠BAD可得∠BAE=∠AEB，则可证得△BEG≌△DCG，然后即可求得答案．解答：解：延长AB、FG交于H，连接HD．∵AD∥GF，AB∥DF，∴四边形AHFD为平行四边形，∵∠ABC=120°，AF平分∠BAD，∴∠DAF=30°，∠ADC=120°，∠DFA=30°，∴△DAF为等腰三角形，∴AD=DF，∴平行四边形AHFD为菱形，∴△ADH，△DHF为全等的等边三角形，∴DH=DF，∠BHD=∠GFD=60°，∵FG=CE，CE=CF，CF=BH，∴BH=GF，在△BHD和△GFD中，，∴△BHD≌△GFD（SAS），∴∠BDH=∠GDF，∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°．故选C．点评：此题主要考查平行四边形的性质，全等三角形的判定与性质，等边三角形的判定与性质，菱形的判定与性质等知识点．此题难度较大，注意掌握辅助线的作法，注意数形结合思想的应用．15．（2012•碑林区校级模拟）如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD 于点P，则∠FPC=（）A．35°B．45°C．50°D．55°考点：菱形的性质．专题：压轴题．分析：延长EF交DC的延长线于H点．证明△BEF≌△CHF，得EF=FH．在Rt△PEH中，利用直角三角形斜边上的中线等于斜边的一半，得∠FPC=∠FHP=∠BEF．在等腰△BEF中易求∠BEF的度数．解答：解：延长EF交DC的延长线于H点．∵在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，∴∠B=80°，BE=BF．∴∠BEF=（180°﹣80°）÷2=50°．∵AB∥DC，∴∠FHC=∠BEF=50°．又∵BF=FC，∠B=∠FCH，∴△BEF≌△CHF．∴EF=FH．∵EP⊥DC，∴∠EPH=90°．∴FP=FH，则∠FPC=∠FHP=∠BEF=50°．故选C．点评：此题考查了菱形的性质、全等三角形的判定方法、直角三角形斜边上的中线等于斜边的一半等知识点，综合性较强．如何作出辅助线是难点．。

苏教版八年级数学下复习反比例函数的四边形压轴题

反比例函数和四边形压轴题精选【精讲精练】例1.如图，已知正比例函数y=2x和反比例函数的图象交于点A（m，-2）．（1）求反比例函数的解析式；（2）观察图象，直接写出正比例函数值大于反比例函数值时自变量x的取值范围；（3）若双曲线上点C（2，n）沿OA5B，判断四边形OABC的形状并证明你的结论．例2.如图，把一块等腰直角三角板ABC放在平面直角坐标系的第二象限内，若∠A=90°，AB=AC，且A、B两点的坐标分别为（-4，0）、（0，2）．（1）求点C的坐标；（2）将△ABC沿x轴的正方向平移m个单位长度至第一象限内的△DEF位置，若B、C两点的对应点E、F都在反比例函数kyx=的图象上，求m、k的值和直线EF的解析式；（3）在（2）的条件下，直线EF交y轴于点G，问是否存在x轴上的点M和反比例函数图象上的点P，使得四边形PGMF是平行四边形？若存在，求出点M和点P的坐标；若不存在，请说明理由．例3.如图1，直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=8，BC=6，点M从点D出发，以每秒2个单位长度的速度向点A运动，同时，点N从点B出发，以每秒1个单位长度的速度向点C运动．其中一个动点到达终点时，另一个动点也随之停止运动．过点N作NP⊥AD 于点P，连接AC交NP于点Q，连接MQ．设运动时间为t秒．（1）AM= ，AP= ．（用含t的代数式表示）（2）当四边形ANCP为平行四边形时，求t的值（3）如图2，将△AQM沿AD翻折，得△AKM，是否存在某时刻t，①使四边形AQMK为为菱形，若存在，求出t的值；若不存在，请说明理由②使四边形AQMK为正方形，则AC= ．例4.如图1，在平面直角坐标系中，等腰Rt△AOB的斜边OB在x轴上，直线y=3x-4经过等腰Rt△AOB的直角顶点A，交y轴于C点，双曲线kyx=（x＞0）也恰好经过点A．（1）求k的值；（2）如图2，过O点作OD⊥AC于D点，求22CD AD-的值；（3）如图3，点P为x轴上一动点．在（1）中的双曲线上是否存在一点Q，使得△PAQ是以点A为直角顶点的等腰三角形．若存在，求出点P、点Q的坐标，若不存在，请说明理由．例5.如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t＞0）秒．（1）求线段AC的长度；（2）当点Q从B点向A点运动时（未到达A点），求△APQ的面积S关于t的函数关系式，并写出t的取值范围；（3）伴随着P，Q两点的运动，线段PQ的垂直平分线为l：①当l经过点A时，射线QP交AD于点E，求AE的长；②当l经过点B时，求t的值．例6.如图1，已知点A（a，0），B（0，b），且a、b满足()2130a a b++++=，?ABCD的边AD与y轴交于点E，且E为AD中点，双曲线kyx=经过C、D两点．（1）求k的值；（2）点P在双曲线kyx=上，点Q在y轴上，若以点A、B、P、Q为顶点的四边形是平行四边形，试求满足要求的所有点P、Q的坐标；（3）以线段AB为对角线作正方形AFBH（如图3），点T是边AF上一动点，M是HT的中点，MN⊥HT，交AB于N，当T在AF上运动时，MNHT的值是否发生改变？若改变，求出其变化范围；若不改变，请求出其值，并给出你的证明．例7.将一副三角尺（在Rt△ABC中，∠ACB=90°，∠B=60°；在Rt△DEF中，∠EDF=90°，∠E=45°）如图①摆放，点D为AB的中点，DE交AC于点P，DF经过点C．（1）求∠ADE的度数；（2）如图②，将△DEF绕点D顺时针方向旋转角α（0°＜α＜60°），此时的等腰直角三角尺记为△DE′F′，DE′交AC于点M，DF′交BC于点N，试判断的值是否随着α的变化而变化？如果不变，请求出的值；反之，请说明理由．例8 .从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中有一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。