分式加减法专项练习60题

合集下载

分式加减法专项练习60题含答案

分式加减法专项练习60题（有答案）1．2．a（a﹣1）+3．4．．5. +．6．．7．=_________．8．．6yue289．．10．．11．．12．13．14．．15．16．（1）；（2）17．18．1+ 19．﹣+20．21．+．22．23．．24．，25．26．++．27．+﹣．28．29．（式中a，b，c两两不相等）：30．31．（1）；（2）…．32．+﹣33．化简分式：．34．．35．计算：﹣．36．计算：．37．计算：．38．．39．计算化简：．40．计算：+++．41．计算．42．计算：．43．化简：．44．．45．计算：．zuoguo46．．55．化简：．47．化简：．48．．49．．50．计算：﹣．51．计算：．52．计算：1﹣•．53．计算：．54．化简56．先观察下列等式，然后用你发现的规律解答下列问题：由，，…（1）计算++++++=_________（n为正整数）；（2）化简：+…+．57．化简：﹣．60．求和．58．请你阅读下列计算过程，再回答所提出的问题：题目计算：解：原式=（A）=（B）=a﹣3﹣6（C）=a﹣9（D）（1）上述计算过程中，从哪一步开始出现错误：_________．（2）从B到C是否正确，若不正确，错误的原因是_________．（3）请你把正确解答过程写下来．59．观察下面的变形规律：=1﹣；=﹣；=﹣；…解答下面的问题：（1）若n为正整数，请你猜想=_________；（2）证明你猜想的结论；（3）求和：+++…+．参考答案：1．原式===1+1=2．2．原式=a2﹣a+=a2﹣a+a=a2．3．==．4．原式===．5．原式=+==．6．原式===．7．==．8．原式===a﹣1．9．原式==．10．+=+=+==1．11．原式=﹣==．12.原式=﹣=﹣=．13．原式=+===14．原式=+==．15．=﹣=﹣==﹣1．16．（1）原式=；（2）原式=17．====．18．原式=1﹣====．19．原式=﹣•==．20．===0．21．原式=+==．22．原式=﹣==．23．原式=====1．24．原式====；x的取值范围是x≠﹣2且x≠1的实数．25．原式==．26．====027．原式=﹣﹣==28．=．29．原式=++=+++++=0．30．原式=+﹣==．31．（1），=，=；（2）+…+=﹣+﹣+…+﹣=﹣=．32．==﹣2 33．=（2a+1）+﹣（a﹣3）﹣﹣（3a+2）++（2a﹣2）﹣=[（2a+1）﹣（a﹣3）﹣（3a+2）+（2a﹣2）]+（﹣+﹣）=﹣+﹣=﹣=．34．原式=﹣=﹣===35．原式====﹣36．原式====37．原式==38．原式=+﹣==39．原式=++=+﹣==== 40．原式=+++=++ =++=+=+=．41．设2x2+3x=y，则原式=﹣+===．42．原式=﹣a+2=a+1﹣a+2=3．43. 原式====．44．原式===，===45.=﹣===46．=== ==47．原式=，=﹣+，=+﹣﹣++，=048．原式=2a﹣a﹣1+a+1=2a．49．原式====．50．原式====．51．原式===．52．原式=1﹣×=1﹣==﹣．53．原式=+﹣====54．原式=++=+++++=﹣+﹣+﹣=0+0+0=055．原式===156．（1）原式=1﹣+﹣+…+﹣=1﹣=；（2）原式=﹣+…+﹣=﹣=57．原式=﹣=﹣=158．（1）A（2）不正确，不能去分母（3）原式===59．（1）=﹣；（2）﹣=﹣==；（3）+++…+=1﹣+﹣+﹣+…+﹣=1﹣=60．原式=++++…+﹣=+++…+﹣=+﹣=﹣=．。

初二数学分式的加减练习题

初二数学分式的加减练习题在初二数学学习中，分式是一个重要的知识点。

理解和掌握分式的加减运算是非常关键的，本文将提供一些初二数学分式的加减练习题，帮助同学们加深对该知识点的理解。

1. 计算下列分式的和或差：a) $\frac{1}{3}+\frac{2}{3}$b) $\frac{5}{6}-\frac{3}{6}$c) $\frac{2}{5}+\frac{1}{10}$d) $\frac{3}{4}-\frac{1}{8}$2. 计算下列分式的和或差：a) $\frac{1}{2}+\frac{3}{4}$b) $\frac{5}{6}-\frac{1}{3}$c) $\frac{7}{8}+\frac{3}{16}$d) $\frac{2}{5}-\frac{3}{10}$3. 计算下列分式的和或差：a) $\frac{1}{2}+\frac{3}{5}$b) $\frac{7}{8}-\frac{1}{2}$c) $\frac{2}{3}+\frac{4}{9}$d) $\frac{3}{4}-\frac{1}{6}$4. 计算下列分式的和或差：a) $\frac{2}{3}+\frac{1}{4}$b) $\frac{5}{6}-\frac{2}{5}$c) $\frac{8}{9}-\frac{2}{3}$d) $\frac{7}{8}+\frac{3}{16}$5. 计算下列分式的和或差：a) $\frac{4}{5}+\frac{2}{3}$b) $\frac{1}{2}-\frac{1}{4}$c) $\frac{5}{6}+\frac{1}{3}$d) $\frac{7}{8}-\frac{1}{8}$以上就是初二数学分式的加减练习题。

同学们可以按照题目给定的分式进行加减运算，通过练习来巩固对分数的理解和掌握。

如果有疑问，可以向老师请教，或者在学习中与同学一起讨论解题思路。

分数的加减运算需要注意分母相同与分母不同的情况，逐步学习和练习，同学们会越来越熟练掌握这一知识点。

分式加减法专项练习60题(有答案)

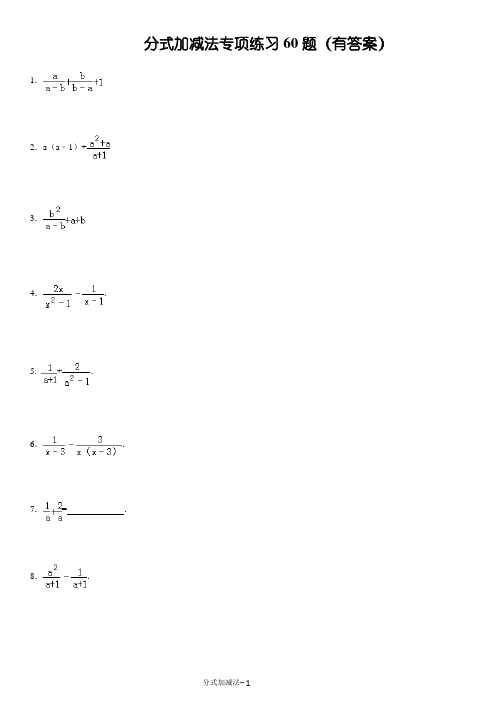
分式加减法专项练习60题（有答案）1．2．a（a﹣1）+3．4．．5. +．6．．7．=_________．8．．9．．10．．11．．12．13．14．．15．16．（1）；（2）．17．18．1+19．﹣+ 20．21．+．22．23．．24．，25．26．++．27．+﹣．28．29．（式中a，b，c两两不相等）：30．31．（1）；（2）…．32．+﹣33．化简分式：．34．．35．计算：﹣．36．计算：．37．计算：．38．．39．计算化简：．40．计算：+++．41．计算．42．计算：．43．化简：．44．．45．计算：．46．．47．化简：．48．．49．．50．计算：﹣．51．计算：．52．计算：1﹣•．53．计算：．54．化简．55．化简：．56．先观察下列等式，然后用你发现的规律解答下列问题：由，，…（1）计算++++++=_________（n为正整数）；（2）化简：+…+．57．化简：﹣．58．请你阅读下列计算过程，再回答所提出的问题：题目计算：解：原式=（A）=（B）=a﹣3﹣6（C）=a﹣9（D）（1）上述计算过程中，从哪一步开始出现错误：_________．（2）从B到C是否正确，若不正确，错误的原因是_________．（3）请你把正确解答过程写下来．59．观察下面的变形规律：=1﹣；=﹣；=﹣；…解答下面的问题：（1）若n为正整数，请你猜想=_________；（2）证明你猜想的结论；（3）求和：+++…+．60．求和．参考答案：1．原式===1+1=2．2．原式=a2﹣a+=a2﹣a+a=a2．3．==．4．原式===．5．原式=+==．6．原式===．7．==．8．原式===a﹣1．9．原式==．10．+=+=+==1．11．原式=﹣==．12.原式=﹣=﹣=．13．原式=+===14．原式=+==．15．=﹣=﹣==﹣1．16．（1）原式=；（2）原式=17．====．18．原式=1﹣====．19．原式=﹣•==．20．===0．21．原式=+==．22．原式=﹣==．23．原式=====1．24．原式====；x的取值范围是x≠﹣2且x≠1的实数．25．原式==．26．====027．原式=﹣﹣==28．=．29．原式=++=+++++=0．30．原式=+﹣==．31．（1），=，=；（2）+…+=﹣+﹣+…+﹣=﹣=．32．==﹣2 33．=（2a+1）+﹣（a﹣3）﹣﹣（3a+2）++（2a﹣2）﹣=[（2a+1）﹣（a﹣3）﹣（3a+2）+（2a﹣2）]+（﹣+﹣）=﹣+﹣=﹣=．34．原式=﹣=﹣===35．原式====﹣36．原式====37．原式==38．原式=+﹣==39．原式=++=+﹣==== 40．原式=+++=++ =++=+=+=．41．设2x2+3x=y，则原式=﹣+===．42．原式=﹣a+2=a+1﹣a+2=3．43. 原式====．44．原式===，===45.=﹣===46．=== ==47．原式=，=﹣+，=+﹣﹣++，=048．原式=2a﹣a﹣1+a+1=2a．49．原式====．50．原式====．51．原式===．52．原式=1﹣×=1﹣==﹣．53．原式=+﹣====54．原式=++=+++++=﹣+﹣+﹣=0+0+0=055．原式===156．（1）原式=1﹣+﹣+…+﹣=1﹣=；（2）原式=﹣+…+﹣=﹣=57．原式=﹣=﹣=158．（1）A（2）不正确，不能去分母（3）原式===59．（1）=﹣；（2）﹣=﹣==；（3）+++…+=1﹣+﹣+﹣+…+﹣=1﹣=60．原式=++++…+﹣=+++…+﹣=+﹣=﹣=．。

分式的加减法速算练习题(打印版)

分式的加减法速算练习题（打印版）### 分式的加减法速算练习题#### 一、基础练习题1. 计算以下分式的和：\[\frac{1}{2} + \frac{3}{4}\]2. 计算以下分式的差：\[\frac{5}{6} - \frac{1}{3}\]3. 计算以下分式的和：\[\frac{3}{8} + \frac{5}{12}\]4. 计算以下分式的差：\[\frac{7}{9} - \frac{2}{9}\]#### 二、进阶练习题1. 计算以下分式的和：\[\frac{2}{5} + \frac{1}{10} + \frac{3}{20}\]2. 计算以下分式的差：\[\frac{4}{7} - \frac{2}{21} - \frac{1}{3}\]3. 计算以下分式的和：\[\frac{3}{7} + \frac{5}{14} + \frac{1}{2}\]4. 计算以下分式的差：\[\frac{8}{15} - \frac{1}{5} + \frac{3}{10}\]#### 三、挑战练习题1. 计算以下分式的和：\[\frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} \]2. 计算以下分式的差：\[\frac{5}{11} - \frac{3}{22} + \frac{1}{66}\]3. 计算以下分式的和：\[\frac{2}{3} + \frac{1}{6} - \frac{1}{9} + \frac{1}{18}\]4. 计算以下分式的差：\[\frac{7}{12} - \frac{1}{4} + \frac{1}{6} - \frac{1}{3}\]#### 答案解析1. $\frac{1}{2} + \frac{3}{4} = \frac{2}{4} + \frac{3}{4} =\frac{5}{4}$2. $\frac{5}{6} - \frac{1}{3} = \frac{5}{6} - \frac{2}{6} =\frac{3}{6} = \frac{1}{2}$3. $\frac{3}{8} + \frac{5}{12} = \frac{9}{24} + \frac{10}{24} = \frac{19}{24}$4. $\frac{7}{9} - \frac{2}{9} = \frac{5}{9}$5. $\frac{2}{5} + \frac{1}{10} + \frac{3}{20} = \frac{8}{20} + \frac{2}{20} + \frac{3}{20} = \frac{13}{20}$6. $\frac{4}{7} - \frac{2}{21} - \frac{1}{3} = \frac{12}{21} - \frac{2}{21} - \frac{7}{21} = \frac{3}{21} = \frac{1}{7}$7. $\frac{3}{7} + \frac{5}{14} + \frac{1}{2} = \frac{6}{14}+ \frac{5}{14} + \frac{7}{14} = \frac{18}{14} = \frac{9}{7}$8. $\frac{8}{15} - \frac{1}{5} + \frac{3}{10} = \frac{16}{30} - \frac{6}{30} + \frac{9}{30} = \frac{19}{30}$9. $\frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81}= \frac{27}{81} + \frac{18}{81} + \frac{12}{81} + \frac{8}{81} = \frac{65}{81}$10. \(\frac{5}{11} - \frac{3}{22。

(05)分式加减法专项练习60题(有答案)ok

分式加减法专项练习60题（有答案）6yue281 12a41|a 2-l[13 nx-：3 x ( X-3)5.6.2 a ..] a+1.i '.8.1 ID - 5 in2 _ in 2ID 2 _ 214.9.10. ab b：I.7'-'-.11.2m _ 1 m 2 -4 时2x 2 2x .K 2+X -2 /-4X £+4X +412.a - 1a 2+a- 2a+l¥-115.13.16 .(1)x+x | - 9X2+6I+917 .n m ^2_2L珂0jm_ 2n n, - 4im+4n*18.1+a2+ab+ b 2?-b319 .b2ab+ b2 - 2ab+ b2'a2 - b22a * b ~ e , 2b ~ c - a _ 2e - a - b~2I 5' oa - ab - ac+bc b - ab - bc+ac c - ac - bc+ab23.ir^+2ni+l V 7?(i-l)(K +2)-1 ,r 12.L2IE 2 - 9 TS；_ IT 26.25.27.2y+z —■+28 卅9b _ a+3b.：.- --29.（式中a , b , c 两两不相等）231. (1) ^― ■出;x+y2曰'+3*2 _ 己2 _ 廿 _ 5 _ 3 a? _ 4邑- § 2护 - 3时5 a+1af2 a - 2 + a - 3:, 1 … K (xfl) T (计1)(計刃 (x+2005) (x+2006)(2) b 2a+c b-ca 一 b+c|b ' a _ c b -耳-百 32.33.化简分式:34. 72x y+xy35 .计算:2x+2y36. 计算: 37•计算:3K - 4y40. 38. 39.计算化简：一X2+3X +2 X 2+K -2 1- T 21124 1-X|i+d1+/计算:41 . 1 2 12X 2+31-1 2 K 2+3X +1 2X 2+3I ^3计算45•计算：f「二47.化简：2a_ b-c _ 2b _c _a , 2c _a ~ b (a-b) ta_c) * (b_c) Cb - a)亠(G_(G_b)42•计算: 7s +2a+l a+148. ：：-■-a- 1 49.a2-l51 •计算:2JS' y _z 2y _ _2 2z _K_y~~5 "I o "I- Ky- xz+yz y^- xy - yz+xz z^-KZ- yz+sy54.化简(2)化简:1 + + + +■ ++=1X^ 2X3 3X4 4X5 5X6|6X7 7X8 _—□__________ 1______ .L[(n为正整数)；+・・+1(x+2QQ8) C K+2009)50.计算:56.先观察下列等式，然后用你发现的规律解答下列问题：由 __ _!—丄_J_一_!_! _J__1X2 2 1 2 2X3 6 2 3 3Xq 12 3 4 (1)计算(K+2) (X+3)(x+1)(x+1) (x+2)解答下面的问题：(1 )若n 为正整数，请你猜想一.1.= _|n Cn+1)(2) 证明你猜想的结论；(3) ------------------------------------------------------------- 求和：一=—+—=—+—=—+ •- +=1X2 2X3 3X4 2011X2012解：原式= ----- ------------ ' (A )a+3(a+3)(a - 3)= a-3_6(a+3)_3)((a - 3)58•请你阅读下列计算过程，再回答所提岀的问题：题目计算:(B)=a — 3- 6 (C ) =a - 9 ( D )(1 )上述计算过程中，从哪一步开始岀现错误： _ _ •(2)从B 到C 是否正确，若不正确，错误的原因是 __________________ (3 )请你把正确解答过程写下来.59 •观察下面的变形规律:=11X21::;L1 1 1 |1 12|3|；3X4 3 4；参考答案:1 原式=• .' . -1 - I =1 + 1=2 .a _ ba _b a _ ba 2 - abb a (a b) n = • a + b a+b|Pt/a+b(a+b) (a _b)a+b a +h| a+ba+b|m _ 2 2m (mH)4. 5. 6. 2x1x 11(xH) (K--1) x-1 (計 1) (x-1) x+1-+a+1 (aH )2冷-1)a- 1+2 _ (aH)〔耳 T) 1 1 1-1 X3x _ 3 1 1x (x _3) x (x-3)"x Cs _ 3) x1 . 2_l+2_3 a da a T a14.十「、2自(已+1)222 .原式=a — a+ =a - a+a=a .nfl3.原式=原式= 原式=7. 10.(ID - 1 ) (ID - 2)2m (ID - 1) (nrl-1)a _ 1_ 3.^+0| a-1 |a (a+1) | 1 |a 1 _ a □ -l =a-la 2 - 2a+l a 2 - T'(a -D 旷(a -1) (a+1)〜1 一-11 _ 4 _ - a+2 _41□ _ 2 (at2) Ca _ 2) (af2)冷-2)(a+2) (a _ 2)(寸2〕_ 2)16.17.18. 19. 20.21 .22.23.24.25. 26.27.28. 29.D 2,1血G+l ) 2(x+1)(x-1)(xH) (K-1)(xH) C K -1)K-l 原式 2xy y (旳)= ¥ a - y) y (K _ y) (K +Y ) (K _ y) Cx+y)（富一 y ）〔盂+y ）(nrFl ) 22 itd-1 2 | irr^L - 2 ra _1 A (1□- 1) (nrbl) m - 1 m _ 1 m _ 1 m _ 1 m _ 1x (x+2)5 _(X- n (X42) _x 2+2x-3 - X 2-X +2 (K- 1) (x+2)(K-1；(x+2)〔耳「1）（計2）_ （i-l ）（计2）原式原式原式；x 的取值范围是x a 2且x 的实数.K - 12m -n nr^n m n _ ID n ~ IT ] 原式-- ・ 1 _ 12 -2 (m+3)皿2 _ 9 _ in 「nr+3 (ml-3) (ID - 3i 丁 (nrl-3) Cm - 3)12-2 (昭引 +2 57)L2-2u- -&+2m - 61 J -■ i :(nrf 3) ■i 02 Cm - 3) +(nH-3)~_ 3)2y+xy2x2y+z - y - 2iy x",(xfy) (K _y)1 x+ya 2= 1(ad-2) Ca _2)nt - n (m - 2n ) in - 2n (mi-n) (m 一 n)a 2+ab+ b 2m _ 2n _rrH ■口 - ( m _ 2n) jirl-n _ irrl^2n _irr^nrn^n m+n— b 24_ 1 _ b_1 -b(a -b) 2| b ( a+b)'□-b(旦-b) ~a+l+a 1 2a 0 且一 1 8+1 /-I(a - 1) (a+1) (a+1) fa _ 1)a+9b a +3t 廿9b =~ (a-K3b) ■仙 23ab3ab - 3ab 3ab a原式=1 -=0.(a~b) ( a^+ab+ b 2)原式=原式34.…氏+F )'原式x - y x+y-莖+y 2y 2xy xy xy x36. / - 2xy+ y 2 - 2Z 3 - 2y 2z+y2 (x+y) (K -y) =b 【葢-y)J s+2y y -1yi+2y - y+1 - yx+1 | 1 |_l-x 2 1-S 2l-,21 1*1 - ：, 1 -.37. 原式2-y 238. 原式三買丄玄-丄?x 2 (x _ 1)(2)「| J +••+^亠亠 + 亠——+ ••+ -s (xfl) (K +1) (X +2) (X +2005) (r+2006)同莎直+1 越 x+200EL =. 200& 丈我006=x (x+200G)” b2a^c b - c b 2a+c - b-+c - b 2a - M2c 2a - 2b+2<na " t+cb _ a _ cb _ a _ ca" b+cb _ a _ Gb _ a _G b _ a - G b 一且一 E2a 2+3a+2 __ 3a 2_4a~^ 2 a 2 _ Sa+Sarbla+2 a _ 2 + a - 3=(2a+1)-( a - 3)--( 3a+2) +—'a+1a+2a-=[(2a+1)-( a - 3)-( 3a+2) + ( 2a - 2) ]+ (-—r ■丁arl a+Z a _ J 耳一/ 丄-一：-• = . •. -a+1 a+2 □ _ 2 a _ 3 (aH 〕(a+2)(a _ 2) (a _ 3)-盼4(a-bl)( a+2) (a - 2)(a _ 3)x+2006-40x+40 (x-2) (K -4)31. (1)x+ysy (x - y)35.原式22 - K - 3yJy+ x 2C K - 1)(y+1)(y+3) -2 (y 1? (y+3) + (y■-1D (y+1) rs(y-1) Cy+1)Cy+3) =(厂⑴(y+D (y+3)8(2x ?+3i- 1)(2 x 2+3X +1 )(2 x 2+3x+3)'2c - a - k>4 (1+/) 4 (1+ J)—丄8 (1-』)(Hx 4) (1-/) (1+/)1-x 8 2 41 .设2x +3x=y ，则原式=X J y 2 2 _ * y _xK ( K ~ y) y(y _z) K ( K ~ y) y (K_ y) xy (K _ y) xy (K _y)_ 2 . y K -（旳）Cx -y)s+y xy -y)xy (h -y)XV44.原式 2y 严2 y2X1 y 2-x 2(y+莖)Cy x) /-/y-xx (K - y)K (x - y) x U - y) x (s - y) 45.2KVx _ xE M 什貨(x - y) +x (x+y) 992zy+ z - XV+ 92sy+2 x 凤2 -x+y ^-y _ ］宀/ I'_2 _ 2K y(x _y) (x+y)46. 2工（旳）n （旳）「2工m 一y39.原式=JS ( 1 - 1 )X (x+1) 2 (x+2)(K +2) (X +1 } (x _ 1)( K +2) C X H) (s-1) | | (K +2) C K H)(; cl)K ?K + K2+X 2x - 4=2x 2 2x 4J 2 ( 英-2〕(x+1)2K - 4 （計刃（?-n 丨丘+对a+D G — i ） (xf2) (x+1) (x-1)X2+K - 240.原式=14■覽(1 - x)~(1 十辺2 (1+ x 2) 2 (1- J)丄+ 4 =44 I(1 -4 (H x £)(1-?) (1+?)1十 J 1- J 1+J+ -+ ■-1+x 2 1+J42 .原式=■-+ 乩一x - x+y 1K +X (s+y)(盖—y)(s+y) (x-y) (x+y) (K - y)K _ y47 .原式=.一： - 1〔一，，++(x+2) &十 1)(1 十小(1 -X ) (2 (x-1)2+4(1-X )(1+G(1-X )(1卄)43.原式-a+2=a+1 - a+2=3.48.49.50.(a-k>) + (且-c)—(h* - c? + (b - s) +(c-a) +〔匚-b)(a- b) (a~ c)(b-c) (a-b) 〔£-辺)(c - b)+++]—,=0a+ (3a+l) ・(2a+3) a+3a4-l -•岛・3 2 (a- 1? .2 I宀1a-1a+1'=1 3x+5=h 1 ③+5)-2：計孑(X-HS) ( K _ 1 )(K+3)(K-D(K+3)G-1)原式原式原式=2a - a _1+a+仁2a.4 x- 81 3 x+612= 7 x- 14(x+2 ) ( x-2 )(x+2 ) ( x-2 )(x+2 ) ( x -2 )](也)(K-2 )51.原式乂且（# 3）52.原式=1 -2a+12a+b 2b^2a- (2a+b) 2b+2a 2a b=1..--2ab2ab Znb 2ab=1 -(曲)Ca_ 1)a+3a+153. 原式-I- , 1-L2ab 2ab1 1r 1 亠1-L 1 4.1 1x _ z z _ y y _s 1y _ m 12 _y i Z _I X _z55.原式X2-1+2(好1) (x+L ) 2= 4+1 )戈=_（田）2=1M -—+ •-+3118 =1 -+ - - + 1L56. (1)原式=1 -12=』；11= 2009灶2009K (計20Q9)=157 .原式=■K (x+2) 2 XK-2'_X- 2K+2008 K+200^y- 一a-3 ’£寸畀(arf3) G - 3)(a+3)(且- 3)丁(af3) Ca_ 3)a - 3+6 十1(时3) (a-3) (a+3) ( □ _3) a.-3(x+2) (x _2)58. (1) A (2)不正确，不能去分母(3)原式=1 ]11n (汩1)=n n+1；59. (1)-=.n+1 n .n+1 - n 1n+1 n (n+1)n (n+1) n (nil) b 5+i)(2) 2岛说九X4=14墙4 i弓-—+ ••+2011X20121feOll2012 =20122011 2012—=1.=2 +」+4+ ••+ 「1 ] 1 - X 1-x 2l+i 21出1+4|1-』60•原式叮・+.「.。

分式的加减练习题

分式的加减习题精选（一）一、判断题··二、选择题三、填空题9．10．11．12．四、计算题13．14．15．16．分式的加减习题精选（二）1．1+--b b a等于（）Ａ．b b b a -+-2 Ｂ．b b b a ++-2 Ｃ．b b b a +--2 Ｄ．b b b a ---2 2．⎪⎪⎭⎫⎝⎛-÷y x x 11等于（）Ａ．y x y x -2 Ｂ．x y y x -2Ｃ．xy x -2 Ｄ．2x xy -3．m n m n m n -+-22等于（）Ａ．ｍ＋ｎＢ．ｍ－ｎＣ．－ｍ＋ｎＤ．－ｍ－ｎ4．计算)6(246612--+--a a a a a ，其结果等于（）Ａ．)6(210--a a Ｂ．)6(210--a a Ｃ．a a 24- Ｄ．a a 24+5．如果x y <<-1，那么2211++-++x y x y 的值（）Ａ．大于零Ｂ．等于零Ｃ．小于零Ｄ．以上都有可能6．计算：1213223-+----x x x x x 7．计算：22229631y xy x y x y x y x +--÷---8．计算： 1596234122--÷⎪⎪⎭⎫ ⎝⎛+---+-+y y y y y y y y9．计算： ⎪⎭⎫⎝⎛-++÷⎥⎦⎤⎢⎣⎡--+1111)1(1)1(122x x x x 10．计算：2343223811113a a a a a a a a +++÷⎪⎭⎫ ⎝⎛+-+--+11．已知⎩⎨⎧=-=+42112y x y x ，求分式⎪⎪⎭⎫ ⎝⎛--++-++÷+-2222332222y x yx y x y xy x y xy x x 的值．12．计算：x x x x -----52335175 13．计算：y x z zy z x y z x z y x y x -++---+++-+14．计算： 1123-+-+x x x x15．已知0132=++x x ，求441x x +的值．16．已知x x xx x -=+--2222313，求x x x x x x x x -÷⎪⎭⎫ ⎝⎛+----+44412222的值. 分式的加减习题精选（三）一、选择题：1．分式的值为（）A ．B ．C ．D ．2．分式、、的最简公分母是（） A ．B ．C ．D ．3．分式的值为（）A ．B ．C ．D ．以上都不对4．把分式、、通分后，各分式的分子之和为（）A ．B ．C ．D ．5．若的值为，则的值为（）A．B．C．D．6．已知为整数，且为整数，则符合条件的有（）A．2个B．3个C．4个D．5个二、填空题：1．式子的最简公分母是___________。

分式加减法专项练习60题ok

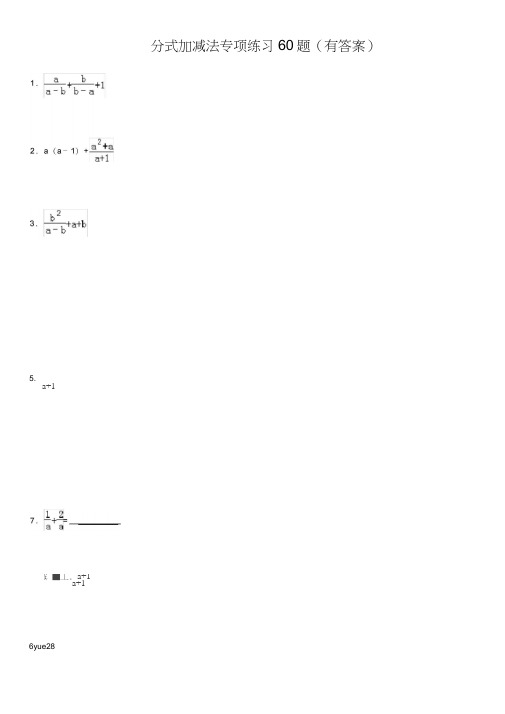
分式加减法专项练习60题（有答案）5.a+1£ ■丄. a+1a+16yue289.10.且‘ - ab b ,-/烏状11 .2mm2 - 4x2 2x .X2+X-2/ -4 K£+4T+412.16.(1)21 .17. 12 _ 2 ； ID 2- 9 皿_3'(2)+X 2~9X 2+3I x 2f6x+91 _ 4a-2 a 2 _4n _ rri2_2l111nm _ 2n- 4mn+4ii"18. 1 + a 2-hab+ b 2b 21ab+b ，a 3-b 3b 2 - 2ab+ b 2+a 2-b 219. 20 .M 11 .4垃K +L+ x 2-l32a ' b - c2b _ c _ a 2c ~ a - b~2 "I 2 2a ~ ab~ ac+bcb - ab - bc+ac 匚一吕c 一 bc+ab9ID +2nri-l2Hi IT - 123. 24.12 + 23 ir| 26 .+亠n^32y+iy2丈+y 2-x 227. 28. aH-9ba+3b 3ab25.29.（式中a , b , c 两两不相等）5 7K- 10------------ 十---------------- -- ---------------x2+x - 6 X2- x _ 12 s 2 _ 6x+8231 . (1) ^―・旳;xfy33 .化简分式:2a2+3a+2 _ a2- a-S _ 3a2 _ 4a- 5( 2a2_ Sa+5 afl a+2 a_ 2「a-3:, 1 … -K (xfl) T (计1)(計刃(x+2005) (x+2006) b2a+c厅 - b+c +b _ 己_ €32.39 •计算化简：—X 2+3X +2 I H-X -2 1- x241•计算..-_2I 2+3I -12/十 3计1Z X 2+3X +336. x^+2sy+ y K 2- 2sy+y 22 , 2 X y+xyy 2y-Ky 234. 35 .计算:2x+2y计算:37 .计算:40. 1 + 1 | I 2 +41-x 1+r1+s 21+J38.计算:47 .化简：2a _ b _c , 2b _c ~ a , 2c _a -b (a-b) (a-G)" (b _c) (b _a) "(G_a) (c _b)42 •计算: 9a+1(3-2) •43 .化简:2y寸44.45 .计算:zuoguo46.55 .化简:"9x z+2z+L2- 1 . 248.■i- 149.0 3a+l 绝+31 3莖+5 1 1 150 .计算:时3 x 2+3£-l 351 •计算:52 .计算：1 -53 .计算: 54 .化简 2^~ y - z 2y _ x _ z 2z ~ x _ ,y ~" 5 ~o - xy- xz4yz y £- xy - yz+xz z £ - xz - yz+sy56 •先观察下列等式，然后用你发现的规律解答下列问(1)计算1J-1 -L 11」 .1丄丄 ,11X212X3I3X4 4X5 5X6 6XT2L ： -1 1 1 _ 1 3X4_12_3 4(n 为正整数)；(2)化简:- ----------------- X --------------------------- -------- -------- X --- -- ---------- ------------------------(K +1)(x+1) (t+2)(z+2) (x+3)+・・+ (K +2008)(計 3TO9)2 57. 化简:58•请你阅读下列计算过程，再回答所提岀的问题：题目计算:K 16*:原式=—--- ------- -- (A) ( ar+LJ ) (a-3)a - 36 n(a+3) (a - 3)(a+3) (a _ 3)=a — 3 - 6 (C ) =a — 9 ( D )(1 )上述计算过程中，从哪一步开始岀现错误： ________________ . (2)从B 到C 是否正确，若不正确，错误的原因是 __________________ (3 )请你把正确解答过程写下来.解答下面的问题:(2)证明你猜想的结论;460 .求和(1 )若n 为正整数，请你猜想n Cn+1)11 1 ■ . . . 111X2 + 1T2X3 3X4+…+2011X2012(3)求和:59.观察下面的变形规律:11X2 115. =-1.a — 1 _ a^+aa- 1 a (a+1) J 1a1 a - 2a+1/ - 1 (a-1 ) 2 (a - 1) (aH) 'a-1a-la-1参考答案:原式=^^ —」_扌1=^^+1=1+1=2 a _ b a _ b a _b-+2r a-1+2 J 1 1a+1(a+1)冷-1)(a+1} (a - 1} a _ 13 "1 L ^-3111x (x _ 3)x J7)K (x - 3) H'1+23 计 a a 3a|a 2-l.(al-1) (a 1)a+1a+12xy葢(,^-y)2xy+ x 2 _ _ K (x+y) _ y(沈+y) (x~ y)(計y) (y _y)(K _ y) (x+y 〕 ( x - y) ( s+y) x _ y10.a 2 - ab2mIT - 2m+2 I 1 ](nrl-2) Cm - 2)(nrl-2) (m _ 2) (nri-2) Cm" 2)TW~Zx (x 2)3・1) (^2)Xx - 1(K _ 2) (x+2)（我）2x+I :-■ ：■=> :：'2 (in+1)ID Cm - 5)in 一 3nd-2 (ID - 1) (m - 2)2m (in - 1) (iir+1)2m (in _ 1)Ml) 2m (m 「1)(nH-1)2. 2 2 2原式=a - a+=a - a+a=a .ar+15. 原式=原式=7.原式==a -1 .原式=+丄= +亠 +丄亠=1 .且（且-b ） 2 a+t> (乩+b 〕(a _ b) a+b a+b a4b a+l>11 .原式12.原式13 .原式14 .原式=1 1+a'1 ________ 4 _______ W ________ 4 _______ = 曲 a -2 (a+2) (a _ 2) (a+2) (□ - 2) (a+2) (□ _ 2) (a+2)( _______ 自-2 =「1 (n+2) (a - 2) a+2 m _ n - ■2n) 2 m - 2n irr^n- —1 —■ — (in - 2n) m4-n in+2n m _2n (irr^n) Cm _n) m+n nrin m+n原式=1 - b 2 c (a+b) (a - b) _ 1 Ca b) 2 b (arhb) a _ b<+日b+b ， (a- b) ( a?+eib+ b 2) =0 .i ia+l+a 1 - 2a 1 0且一1 a+l a 2 -](a -1) (a+l)(a+l) (a~ 1) 原式= 原式 + Cx+1 ) 2K - 1 ) 2 (XH ) 〔55-1) 原式 y (x+y)y Cx ~ y) y(K - y)(旳)(K ~ y) (x+y) x+y2 _ irH -! _ 2 nM-L - 2 m _ 1(孟+D GT) (x+1) (K-1) (K ~ y) (sc+y) m _ 1 ni _ 1 m _ 1 ni 一 1 原式= X (x+2) _ s (x - 1) (x+2) 才+2x - 3-(K-1) (x+2) (K-1) (K +2) 0-1) (H2) (x-n V 1 1 x ^- 2且x 力的实数.；x 口的取值范围是（K -1）（x+2） |x+2 原式=2ID _ n _ nr+n mn _ m n _ ir12,2 , 2 | | 12 ,- -2 CiH-3； 2 缶-3) 原式 (nrtS) (IP 7) n+3 (ITJ 4-3) (m _ 3) (nri-3) (m _ 3) m 2 -9 3-m (nrHl)」 (io - 1) (nr+1) m 一 x 2 - x+2 (x+2)12-2 (nH-3) +2 Cm- 3) 1 12 - 2nt - 64缶-6 (nrF3) Cm 3) （卅孑）（m~ 3j原式= ¥-泳2y+x y 2xy _ x- x 2-y 2(s+y) (K _ y)計ya+9b a+3b a+9b * -(a+3b) 6b 2 3ab 3ab = 3ab 3ab ax 2-y 2+ ta _ c)(b>- c) + ( b - a) (c _ a) + Cc _ t>) '■ i1+H ■ b - 〔£ - 卫)(G - b)原式=4a - 2)3n nr+n _ = L-b16.17.18.19.20. 21 . 22. 23. 24.25.26.27.28.29.2a 2+3a+2 . J -耳 -5. 3a.' —4可-52a 2 _ Sa+Sa+1 a+2 a _ 2" a - 3=■+■+'+□ _ G a _ b b _ □1+ + b _ 4 G _I? r i c _ □=0 .= '>；T (rl-3) C K - 2) 2x- 5 ]r 7x-io (x+3) C K -4) ]P (K -2) (K -4) 5K (s 4) + (2x - 5) (i-2)-(i 10) G+3) = -40/4Q(rl-3) Cs _ 2) (K -4)(K +3) (X -2) (X -4)30 .原式] z+2006=1 1 =2006 n 』疋+200E K (x+20Q6)'b b 2a^cb - Qb 2a+< 一 l?+c -b 2a _ b-+2c 2a - 2L+2<n ~ b+c b _ a _c b _ a _b+u b ~ a~ c b 一a - cb _ a _c b 一石一亏33.34. 36. 37. 38. =(2a+1 ) +a+1 -(a - 3)a42-(3a+2)---+ --:=1a+1 a+ 2 □ 2 □ _ 3 (a+1)(寸2) -8a+^(afl)( a+2) (a _ 2j(a-3)1 Q~ 2]+ ( + (2a - 2)----------------1 ------- a41 a+2 a - 21a _ 3‘•)己一 d(x-y)[ _M _ yx+y - x+y2xy (x _yJiyxyXK2- 2xy+ y 2-2K 2-2y 22 &+y) (、耳 _ y)i+2y _ y 1 _ y x-F2y - y+1 - yi+l1 1- / 1- i 21- i 2'=1-z 21-?1 - X原式=叙 t^-1) | |6/ + —X 2 Cx - 1) X 2 ( K' - 1 )3x (K- 1) +6 s 2-(廿5)Cx - 1)g 异- T 工+5 X 2(K - ID/(K - 1)31 . (1)1+ ••+K +200532.=-2(孟+]〉" (孟+1) ―(x+2) 1(K +2005) (X-F2006)=[(2a+1 )-( a - 3)-( 3a+2) + (2a - 2) (a - 2) (a - 3)原式=U+y ) 2Jty (x+y)35.Z (K-y)原式=7s+2y 3y(K +5)(愛・1)原式=47.(什 1) Cy+3) -2 (y-n (y+3) + (y-13 (y+1) 18(y-1) Cy+l) (yf3) (y-1) (y+1)(y+3)8(2j+3x-l)(2X 2+3X +1) (2X 2+3I +3)|• ■ j1；- :. ■-•• 'I ，> -‘： + ■' + :(K +刃(s+1) (s+2) (x _ 1) | | (1+x) (1-翼)X ( X 1) 直 Cx+D 2 (x+2)(x+2)(計1) (x _ 1} (x+2) Cx+1) 0-1) (xf2) G+l) GT)39.K + K^+x 2x 4= 2 宀4_ I 2 (K -2) (M +,1 ) 1 =2M - 4〔計刀〔*-1）■ l ■ 1 1 ■ 1 ::.- (x+2) CH-1) (X -1) x Z +x-2+=2y , H 2 r2 K— (y+丈) （V - X ） 9 + - x 2-xy y —*K (x - y)x (x - y)K (K _ x (x -y)45. 2zy z _ x (s - y) 4*s C«+yD 9 b 9 2xy+ x" - xy+ 92xy+2 x 冥2 — / x+y s-y __2 _ 2 ' 工 y(x _y) (x+y)46. I+K丄1 ■XI £ + 4 =2 ]d-x)(i 十工)(i-x ；)〔1+“if x 21+/ (1 - x) (Bi)2 C1+ x 2) ,2 (1- x 2) -L4 =4 Cf-?) (1+x 2) C) (i+显)I1+/1-S 4|4 (H J)4 (1十 J j-J_呂(1- x 4) (1+/)Cl - /) (1+/)l-x S42 .原式=(◎+1 )'aPl-a+2=a+1 - a+2=3 .43.原式=x - y+2yK -yK+y T <s+y) 1 d ~y)（旳）（v $yK ( K _y? y(y - 工) & (s~ yJ/ - 2 1 - y K =-(x+y? (K - y)xy (x - y)xy ( K -y)(x+y) C K _y)1瓦一y2sy (x _ y) uy (s ~y)'2z 3y) 2x (x - y) (x+y) _K _ y心一 2a_t ，_c40 .原式=41 .设 2x 2+3x=y ，则原式=1 y+32y 44 .原式 y (x _y)( 2) — == + - - + + , =048 .原式=2a — a — 1+a+仁2a . 49 ．原式 ===50 ．原式 =51 ．原式53. 原式 =+ — =54. 原式 =++ + + + +55 ．原式 = = =157．原式 = — = — =158 ．( 1 ) A ( 2)不正确，不能去分母 ( 3)原式 =59 ．( 1 )(3)+++ •• +52 .原式=1 — X=1 —=0+0+0=056 . (1)原式=1 —+ — +•• + =1 —=1原式= -------- + +1 - K 1+1C2 + 4+ —+2n1+s2 1 + J1+3】=・—|1F+1+x4+2n__ L1 _x单纯的课本内容，并不能满足学生的需要，通过补充，达到内容的完善教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。

带未知数分式加减法练习题(打印版)

带未知数分式加减法练习题（打印版）一、选择题1. 已知 $\frac{1}{x} + \frac{1}{y} = \frac{3}{2}$，求$\frac{1}{x} - \frac{1}{y}$ 的值。

A. $\frac{1}{2}$B. $\frac{1}{6}$C. $\frac{1}{3}$D. $\frac{1}{4}$2. 如果 $\frac{a}{b} + \frac{c}{d} = 1$，那么 $\frac{a}{b} - \frac{c}{d}$ 等于多少？A. $\frac{1}{2}$B. $\frac{1}{3}$C. $\frac{1}{4}$D. $\frac{1}{5}$3. 计算 $\frac{2}{x} + \frac{3}{y} - \frac{5}{z}$ 的值，当$x = 1$，$y = 2$，$z = 3$ 时。

A. $\frac{1}{2}$B. $\frac{1}{3}$C. $\frac{1}{4}$D. $\frac{1}{5}$二、填空题1. 计算 $\frac{m}{n} + \frac{p}{q} = \frac{7}{12}$，当 $m = 2$，$n = 3$，$p = 4$ 时，$q$ 的值是 ________。

2. 如果 $\frac{x}{y} - \frac{z}{w} = \frac{1}{3}$，且 $x = 4$，$y = 5$，$z = 3$，求 $w$ 的值。

三、解答题1. 已知 $\frac{a}{b} + \frac{c}{d} = \frac{5}{6}$，求$\frac{a}{b} + \frac{c}{d} - \frac{a}{c} - \frac{b}{d}$ 的值。

2. 计算 $\frac{2x}{3y} + \frac{3x}{2y} - \frac{5x}{6y}$，当$x = 2$，$y = 3$。

分式分数加减法练习题(打印版)

分式分数加减法练习题（打印版）# 分式分数加减法练习题## 一、基础练习题1. 计算下列分式的和：\[\frac{1}{2} + \frac{3}{4}\]2. 计算下列分式的差：\[\frac{5}{6} - \frac{2}{3}\]3. 计算下列分式的和：\[\frac{2}{3} + \frac{1}{6}\]4. 计算下列分式的差：\[\frac{7}{8} - \frac{5}{12}\]5. 计算下列分式的和：\[\frac{3}{5} + \frac{4}{15}\]6. 计算下列分式的差：\[\frac{11}{12} - \frac{1}{4} \]## 二、进阶练习题7. 计算下列分式的和，并约分： \[\frac{4}{9} + \frac{5}{12} \]8. 计算下列分式的差，并约分： \[\frac{8}{15} - \frac{3}{10} \]9. 计算下列分式的和，并约分： \[\frac{7}{12} + \frac{5}{18} \]10. 计算下列分式的差，并约分： \[\frac{9}{14} - \frac{2}{7} \]11. 计算下列分式的和，并约分： \[\frac{2}{5} + \frac{3}{10}\]12. 计算下列分式的差，并约分：\[\frac{13}{18} - \frac{5}{9}\]## 三、综合应用题13. 某工厂生产一批零件，第一天生产了总数的 $\frac{3}{8}$，第二天生产了总数的 $\frac{1}{4}$，求两天共生产了总数的几分之几。

14. 一个班级有40名学生，其中 $\frac{1}{5}$ 参加了数学竞赛，$\frac{1}{8}$ 参加了科学竞赛。

求参加竞赛的学生总数。

15. 一个水池的容量为 $\frac{3}{4}$ 立方米，第一天用去了$\frac{1}{6}$ 的容量，第二天用去了 $\frac{1}{12}$ 的容量。

分式的加减法练习题

分式加减法（一）一．填空题1.若代数式1324x x x x ++÷++有意义,则x 的取值范围是__________. 2.化简131224a a a -⎛⎫-÷ ⎪--⎝⎭ 的结果是___________. 3.若222222M xy y x y x y x y x y--=+--+ ,则M=___________. 4.公路全长s 千米,骑车t 小时可到达,要提前40分钟到达,每小时应多走____千米.5.某班a 名同学参加植树活动，其中男生b 名(b<a)．若只由男生完成，每人需植树15棵；若只由女生完成，则每人需植树棵．6.已知y x 11-=3，则分式y xy x y xy x ---+2232= 。

7.化简13+a a －1+a a= ，8.若50m x y y x -=--，则m =9.若113x y -=，则232x xy y x xy y +---= 10. ________6,4的最简公分母是x a a 11. ________25,43,322422的最简公分母是c a b c b a b a c - 12. ________21,442的最简公分母是--m m 13. ________221,)(2,432的最简公分母是y x y x x xy -- 14. ________341,651,231222的最简公分母是+-+-+-x x x x x x7.若113x y -=，则232x xy y x xy y +---= __________________二．选择题1.下列等式中不成立的是（）A 、y x y x --22=x －yB 、y x yx y xy x -=-+-222 C 、yx y xy x xy -=-2 D 、xy x y y x x y 22-=- 2.下列各式中，从左到右的变形正确的是( )A 、y x y x y x y x ---=--+-B 、yx y x y x y x +-=--+- C 、y x y x y x y x -+=--+- D 、yx y x y x y x +--=--+- 3.如果从一卷粗细均匀的电线上截取1米长的电线, 称得它的质量为a 克，再称得剩余电线的质量为b 克, 那么原来这卷电线的总长度是( )A ．b+1a 米B ．（b a +1）米C ．（a+b a +1）米D ．（a b +1）米4.已知a ，b 为实数，且ab=1，设M=11+++b b a a ，N=1111+++b a ，则M ，N 的大小关系是（） A 、M>N B 、M=N C 、M<N D 、不确定5.下列分式的运算中，其中结果正确的是（）A 、a 1+b a b +=21B 、323)(a a a =C 、b a b a ++22=a+bD 、319632-=+--a a a a 6.下列各式从左到右的变形正确的是（）A.122122x y x y x y x y --=++ B .0.220.22a b a b a b a b ++=++ C.11x x x y x y +--=-- D.a b a b a b a b+-=-+ 7.若有m 人a 天完成某项工程，则（m+n ）个同样工作效率的人完成这项工程需要的天数是（） BA 、a+mB 、n m ma + C 、n m a + D 、man m + 8.已知两个分式：244A x =-，1122B x x =++-，其中2x ≠±，则A 与B 的关系是（） A.相等 B.互为倒数 C.互为相反数 D.A 大于B三、计算题:1.化简（x x x x x 2)2422+÷-+-2.化简：÷--23x x （25-x -x-2），3.化简：ab b a ab b a b a 21(222222++÷-- ），4.化简：22193m m m -=-+． 5.(m 1＋n 1)÷n n m ＋ 6. 24111a a a a++-- 7.)11(122xx x x +⋅+- 8.化简x －1x ÷(x －1x ). 9.xx x x x x x 112122÷⎪⎭⎫ ⎝⎛+---+ 10.2221412211a a a a a a --÷+-+- 11.222299369x x x x x x x +-++++; 12.23111x x x x -⎛⎫÷+- ⎪--⎝⎭ 13.2a a b a b --- 14.2222a a a a +-+-+ 15.233a a a ---16.22111x x x -+- 17．18．19．20．21．1213223-+----x x x x x 2222229631y xy x y x y x y x +--÷---23. 1596234122--÷⎪⎪⎭⎫ ⎝⎛+---+-+y y y y y y y y24. ⎪⎭⎫ ⎝⎛-++÷⎥⎦⎤⎢⎣⎡--+1111)1(1)1(122x x x x 25. 2343223811113a a a a a a a a +++÷⎪⎭⎫ ⎝⎛+-+--+26. 已知⎩⎨⎧=-=+42112y x y x ，求分式⎪⎪⎭⎫ ⎝⎛--++-++÷+-2222332222y x y x y x y xy x y xy x x 的值．27.x x x x -----52335175 28.1123-+-+x x x x 29.y x z z y z x y z x z y x y x -++---+++-+ 30. 已知0132=++x x ，求441x x +的值．31. 已知x x xx x -=+--2222313，求x x x x x x x x -÷⎪⎭⎫ ⎝⎛+----+44412222的值. 32. 33.34． 35．36． 37．38．39． 35．先化简，再求值：(1). 请你先化简，再选取一个你喜欢的数代入并求值:11)1(212--+-+a a a a . (2). 14422-+-x x x ÷（13+x -1），其中x =-2⑶. 2132·446222--+-+-+x x x x x x x ，其中2-=x(4). 先化简再求值：()x x x x x x x x x x -+⋅+++÷--=-11442412222，其中。

分式加减法之找最简公分母专项练习30题(有答案)ok

找最简公分母专项练习30题（有答案）1．分式，，的最简公分母是（）A．（a2﹣2ab+b2）（a2﹣b2）（a2+2ab+b2）B．（a+b）2（a﹣b）2C．（a+b）2（a﹣b）2（a2﹣b2）D．a4﹣b42．分式、、的最简公分母是（）A．15abx B．15abx3C．30abx D．30abx33．分式的最简公分母是（）A．（a2﹣b2）（a+b）（a﹣b）B．（a2﹣b2）（a+b）C．（a2﹣b2）（b﹣a）D． a2﹣b2 4．分式和的最简公分母为（）A．12x2yz B．12xyz C．24x2yz D．24xyz5．下列各题中，所求最简公分母正确的是（）A．与的最简公分母为6x2B．与的最简公分母为3ab2cC．与的最简公分母为ab（x﹣y）（y﹣x）D．与的简公分母为ab（m2﹣n2）6．与的最简公分母为（）A．（x2﹣y2）（x2+xy）B． x（x﹣y）（x+y）C． x（x﹣y）（x+y）2D．（x﹣y）（x+y）7．分式﹣的最简公分母为（）A． 4（m﹣n）（n﹣m）B．C． 4x2（m﹣n）2D． 4（m﹣n）x2 x28．下列各题中，所求的最简公分母错误的是（）A．与最简公分母是6x2B．与的最简公分母是3a2b3cC．与的最简公分母是m2﹣n2D．与的最简公分母是ab（x﹣y）（y﹣x）9．分式的最简公分母是（）A．24a2b2c2B．24a6b4c3C．24a3b2c3D．24a2b3c310．分式的最简公分母是（）A．（x2﹣y2）（x﹣y）B．（x2﹣y2）（x+y）（x﹣y）C. 2（x+y）（x﹣y） D．x2﹣y2 11．分式的最简公分母是（）A．（a2+1）2B．（a+1）（a﹣1）（a2+1）C．（a+1）2（a﹣1）2D．（a﹣1）4 12．分式的最简公分母是（）A．B．C．（x﹣y）2（x+y）2D．（x﹣y）2（y2﹣x2）（x+y）2 13．分式、、的最简公分母是（）A．（x2+1）（x﹣1）B．（x2﹣1）（x2+1）C．（x﹣1）2（x2+1）D．（x﹣1）214．分式，，的最简公分母为_________；15．分式，，的最简公分母是_________．16．分式，，的最简公分母是_________．17．请写出最简公分母是6a（a+1）的两个分式：_________．18．与的最简公分母为_________；化简：=_________．19．分式的最简公分母是_________．20．分式与的最简公分母是_________．21．分式的最简公分母是_________．22．分式与的最简公分母是_________．23．当x=_________时，分式的值为0；分式，，的最简公分母是_________．24．分式与的最简公分母是_________．25．分式，，的最简公分母是_________．26．分式，﹣，的最简公分母是_________．27．，，的最简公分母是_________．28．分式，，的最简公分母是_________．29．分式的最简公分母是_________．30．写出两个分式，使得它们的最简公分母为6a2b，且其中一个分式的分母不含字母a．参考答案：1．∵a2﹣2ab+b2=（a﹣b）2，a2﹣b2=（a+b）（a﹣b），a2+2ab+b2=（a+b）2，∴这三个分式的最简公分母是（a+b）2（a﹣b）2．故选B．2．因为各分母都是单项式，所以最简公分母就是各系数的最小公倍数，相同字母的最高次幂，所有不同字母都写在积里．因此，所求分式的最简公分母为30abx3．故选D．3．分母是a+b，分母分解后是（a+b）（a﹣b），分母可变形为﹣（a﹣b），所以最简公分母是的分母，即a2﹣b2．故选D4．﹣的分母为6x2y，的分母为4xyz，∵6，4的最小公倍数是12，∴分式的最简公分母为12x2yz．故选A．5．A、两分母分别是3x和6x2，故最简公分母是6x2；B、两分母分别是3a2b3和3a2b3c，故最简公分母是3a2b3c，而不是3ab2c；C、两分母分别是a（x﹣y）和b（y﹣x），故最简公分母是ab（x﹣y），而不是ab（x﹣y）（y﹣x）；D、两分母分别是m+n和m﹣n，故最简公分母是m2﹣n2，而不是ab（m2﹣n2）．故选A．6．分母为x2﹣y2=（x﹣y）（x+y），的分母为x2+xy=x（x+y），即最简公分母是x（x﹣y）（x+y），故选B．7．把n﹣m变形为﹣（m﹣n），可得这三个分式的最简公分母是4（m﹣n）x2，故选D．8．D中与中字母最高次幂的积为一次，所以最简公分母是ab（x﹣y）；故选D．9．3，2，8的最小公倍数为24，a2b，ab2，a3bc3的最小公倍数为a3b2c3，∴分式的最简公分母为24a3b2c3，故选C．10．分式的分母为x+y，分母分解因式为（x+y）（x﹣y），分母可以变形为﹣2（x﹣y），取各分母系数的最小公倍数2；把x+y、x﹣y作为最简公分母的因式，得到的因式的积就是最简公分母，即2（x+y）（x﹣y）．故选C．11．的分母为a2﹣2a+1=（a﹣1）2，的分母为a2﹣1=（a+1）（a﹣1），的分母为a2+2a+1=（a+1）2，则最简公分母是（a+1）2（a﹣1）2．故选C12．把的分母因式分解得：，则分式的最简公分母是（x﹣y）2（x+y）2，故选C．13．将第二个分式的分母可分解为（x﹣1）2，所以最简公分母是（x﹣1）2（x2+1）．故选C．14．三个分式的分母分别为3x，（x﹣1），（x2﹣1），所以分式的最简公分母为3x（x+1）（x﹣1）或3x（x2﹣1）15．分式，，的分母分别是x（x﹣1）、（x+1）（x﹣1）、（x﹣1）2，故最简公分母是x（x+1）（x﹣1）2．故答案为x（x+1）（x﹣1）2．16．分式，，的最简公分母是12x3y2z．故答案为：12x3y2z．17．根据题意得，两个分式可以是：，（答案不唯一），故答案为：，（答案不唯一）．18．与的最简公分母为6a2bc2；原式==．故答案为6a2bc2；19．∵x2+x=x（x+2），x2+2x+1=（x+1）2，∴各项的最简公分母为：x（x+1）2．故答案为：x（x+1）2．20．∵分式与的分母不同的因式有x﹣1，x+1，∴最简公分母是（x﹣1）（x+1）或x2﹣1，故答案为：（x﹣1）（x+1）或x2﹣1．21．∵x2﹣9=（x+3）（x﹣3）6﹣2x=2（3﹣x）∴各项的最简公分母为：2（x+3）（x﹣3）故答案为2（x+3）（x﹣3）22．∵m2﹣4=（m+2）（m﹣2），2m﹣4=2（m﹣2），∴两分式的最简公分母是：2（m+2）（m﹣2）．故答案为：2（m+2）（m﹣2）．23. ∵分式的值为0，∴分子x2﹣1=0，解得x=1或x=﹣1，分母x+1≠0，即x≠﹣1，则x=1；把变形为，变形为，∴三分式的分母分别为x，（x+2）（x﹣2），x﹣2，其系数都为1，所以最简公分母的系数为1，x与x+2为单独出现的式子，x﹣2取最高次幂1次，则三分式的最简公分母是x（x+2）（x﹣2）．故答案为：1；x（x+2）（x﹣2）24．分式与的最简公分母是x（x+y）（x﹣y），故答案为：x（x+y）（x﹣y）25．∵分式，，的分母分别为：ax，﹣3bx，5cx3，∴各分母的系数1，﹣3，5的最小公倍数为﹣15，a，b，c为单独出现的字母，x的最高次幂为3次，则三分式的最简公分母为：﹣15abcx3．故答案为：﹣15abcx326．分式，﹣，的分母分别是a2b、c2，2ac2、3b2c，故最简公分母为6a2b2c2．故答案为6a2b2c2．27．x2﹣1=（x+1）（x﹣1）；x2﹣x=x（x﹣1）．则最简公分母是：x（x+1）（x﹣1）．故答案是：x（x+1）（x﹣1）28．∵x2﹣2x+1=（x﹣1）2，∴分式，，的最简公分母是x（x﹣1）2．故答案为x（x﹣1）2．29．∵=，，=，∴以上分式点额最简公分母是（x+2）（x﹣2）（x+3）2，故答案为：（x+2）（x﹣2）（x+3）2．30．根据题意，两个分式可以为：和．本题答案不唯一．。

(完整word版)(05)分式加减法专项练习60题(有答案)ok

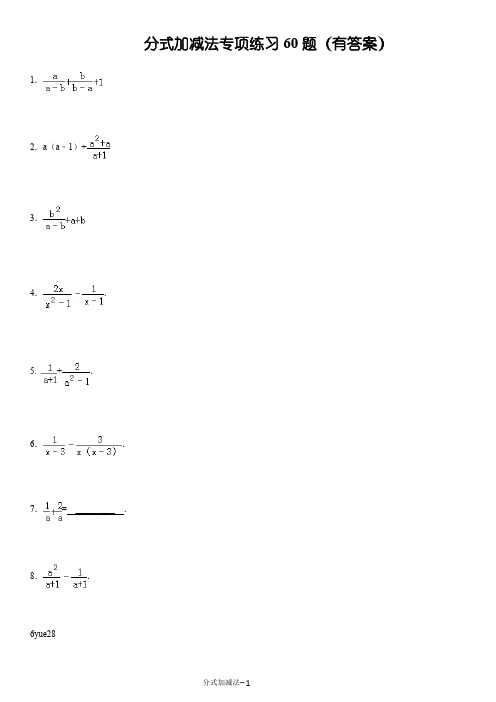
分式加减法专项练习60题（有答案）1．2．a（a﹣1）+3．4．．5. +．6．．7．=_________．8．．6yue289．．10．．11．．12．13．14．．15．16．（1）；（2）17．18．1+ 19．﹣+20．21．+．22．23．．24．，25．26．++．27．+﹣．28．29．（式中a，b，c两两不相等）：30．31．（1）；（2）…．32．+﹣33．化简分式：．34．．35．计算：﹣．36．计算：．37．计算：．38．．39．计算化简：．40．计算：+++．41．计算．42．计算：．43．化简：．44．．45．计算：．zuoguo46．．55．化简：．47．化简：．48．．49．．50．计算：﹣．51．计算：．52．计算：1﹣•．53．计算：．54．化简56．先观察下列等式，然后用你发现的规律解答下列问题：由，，…（1）计算++++++=_________（n为正整数）；（2）化简：+…+．57．化简：﹣．60．求和．58．请你阅读下列计算过程，再回答所提出的问题：题目计算：解：原式=（A）=（B）=a﹣3﹣6（C）=a﹣9（D）（1）上述计算过程中，从哪一步开始出现错误：_________．（2）从B到C是否正确，若不正确，错误的原因是_________．（3）请你把正确解答过程写下来．59．观察下面的变形规律：=1﹣；=﹣；=﹣；…解答下面的问题：（1）若n为正整数，请你猜想=_________；（2）证明你猜想的结论；（3）求和：+++…+．参考答案：1．原式===1+1=2．2．原式=a2﹣a+=a2﹣a+a=a2．3．==．4．原式===．5．原式=+==．6．原式===．7．==．8．原式===a﹣1．9．原式==．10．+=+=+==1．11．原式=﹣==．12.原式=﹣=﹣=．13．原式=+===14．原式=+==．15．=﹣=﹣==﹣1．16．（1）原式=；（2）原式=17．====．18．原式=1﹣====．19．原式=﹣•==．20．===0．21．原式=+==．22．原式=﹣==．23．原式=====1．24．原式====；x的取值范围是x≠﹣2且x≠1的实数．25．原式==．26．====027．原式=﹣﹣==28．=．29．原式=++=+++++=0．30．原式=+﹣==．31．（1），=，=；（2）+…+=﹣+﹣+…+﹣=﹣=．32．==﹣2 33．=（2a+1）+﹣（a﹣3）﹣﹣（3a+2）++（2a﹣2）﹣=[（2a+1）﹣（a﹣3）﹣（3a+2）+（2a﹣2）]+（﹣+﹣）=﹣+﹣=﹣=．34．原式=﹣=﹣===35．原式====﹣36．原式====37．原式==38．原式=+﹣==39．原式=++=+﹣====40．原式=+++=++ =++=+=+=．41．设2x2+3x=y，则原式=﹣+===．42．原式=﹣a+2=a+1﹣a+2=3．43. 原式====．44．原式===，===45.=﹣===46．=== ==47．原式=，=﹣+，=+﹣﹣++，=048．原式=2a﹣a﹣1+a+1=2a．49．原式====．50．原式====．51．原式===．52．原式=1﹣×=1﹣==﹣．53．原式=+﹣====54．原式=++=+++++=﹣+﹣+﹣=0+0+0=055．原式===156．（1）原式=1﹣+﹣+…+﹣=1﹣=；（2）原式=﹣+…+﹣=﹣=57．原式=﹣=﹣=158．（1）A（2）不正确，不能去分母（3）原式===59．（1）=﹣；（2）﹣=﹣==；（3）+++…+=1﹣+﹣+﹣+…+﹣=1﹣=60．原式=++++…+﹣=+++…+﹣=+﹣=﹣=．。

100题分数加减法(有答案)

100题分数加减法(有答案)100题分数加减法(有答案)1. 1/2 + 1/3 = 5/62. 3/4 - 1/5 = 11/203. 2/3 + 4/5 = 22/154. 7/10 - 1/3 = 17/305. 2/5 + 3/8 = 31/406. 4/7 - 2/9 = 22/637. 3/8 + 1/6 = 11/248. 5/6 - 1/4 = 1/39. 2/5 + 7/12 = 29/3010. 1/3 - 1/9 = 2/9在这个分数加减法练习中，我们将解决一系列的分数加减法题目。

下面是一百道题目，每一道题都附有答案供您核对。

11. 3/4 + 2/3 = 17/1212. 5/7 - 1/6 = 29/4213. 1/2 + 3/4 = 5/414. 2/5 - 1/3 = 1/1515. 3/8 + 2/5 = 31/4017. 1/4 + 1/6 = 5/1218. 4/5 - 2/9 = 26/4519. 1/3 + 1/8 = 11/2420. 5/6 - 1/4 = 1/321. 1/2 + 1/3 = 5/622. 3/4 - 1/5 = 11/2023. 2/3 + 4/5 = 22/1524. 7/10 - 1/3 = 17/3025. 2/5 + 3/8 = 31/4026. 4/7 - 2/9 = 22/6327. 3/8 + 1/6 = 11/2428. 5/6 - 1/4 = 1/329. 2/5 + 7/12 = 29/3030. 1/3 - 1/9 = 2/9在这一组题目中，我们需要计算分数的加法和减法。

分数加减法是数学中的基础概念之一，通过练习可以提高我们的计算能力。

31. 3/4 + 2/3 = 17/1232. 5/7 - 1/6 = 29/4234. 2/5 - 1/3 = 1/1535. 3/8 + 2/5 = 31/4036. 6/7 - 3/4 = 9/2837. 1/4 + 1/6 = 5/1238. 4/5 - 2/9 = 26/4539. 1/3 + 1/8 = 11/2440. 5/6 - 1/4 = 1/3在这一组题目中，我们再次进行分数的加法和减法练习。

分式加减法混合运算测试题及答案

B 、x2-2xy+ y2=x- y分式加减乘除混合运算测试题（总分100分,时间100分钟）班级___________ 姓名________________ 得分_________________________一.填空题（每题3分，共2 4分）x + \ X + 31•若代数式——有意义，则X的取值范围是____________________ ・x+2 x+4（ 1 A 3_a2•化简1 -------- 一——的结果是___________________ ・< a — 2 丿 2" — 4M 2xy - y2 x -y …3.若一 =一 +—-，则M二 ________________________ ■牙・_）厂x + y4.公路全长s千米，骑车t小时可到达,要提前40分钟到达，每小时应多建—千米.5 .某班a名同学参加植树活动，其中男生b^（b<a）.若只由男生完成，每人需植树1 5棵：若只由女生完成,则每人需植树______________ 棵.6.化简--------- 二_____________ .7.若--------- =0,贝I]m = _________a+1 a+1 x-y y-x8.若1-1 = 3,贝严3gy= ______________________x y x-xy- y二选择题（每题3分，共24分）1 •下列等式中不成立的是（x 2 -xy x- y D 、x y xyB 、 2•下列各式中，从左到右的变形正确的是（-x + V -% - VA 、 ----- = --------_ x _ y x-yC、D 、 A. \ F(b+1,B.(£+1)C ・（错误!+ 1 ）米A. x-B三.计B. x+\ 。

-x+y_x+y_牙 + y _ x-y_ x _ y x _ y_ x _ y x + y3.如果从一卷粗细均匀的电线上截取1米长的电线，称得它的质量为d 克，再称得剩余电线的质量为〃克，那么原来这卷电线的总长度是（）D.(错误!+1 )米 N 的大小关系是（ )A 、M>NB 、M=NC . M<ND 、不确定5.下列分式的运算中，其中结果正确的是（）A 1+ 12B c (r+b 2 =a +b D 、a ba + bau + ba-31a 1-6a+ 9a-36.下列各式从左到右的变形正确的是（）1 x__y A -1 亍+y 2x-y x + 2y c 0.2a+ b 2a+ bB. ----------- = ----------6/4-0.27? a + 2bc._7x —y x-1x-y,、a + b a-b 。