导热系数实验报告
(完整word版)导热系数的测量实验报告

导热系数的测量导热系数(又称导热率)是反映材料热性能的重要物理量,导热系数大、导热性能好的材料称为良导体,导热系数小、导热性能差的材料称为不良导体。
一般来说,金属的导热系数比非金属的要大,固体的导热系数比液体的要大,气体的导热系数最小。
因为材料的导热系数不仅随温度、压力变化,而且材料的杂质含量、结构变化都会明显影响导热系数的数值,所以在科学实验和工程设计中,所用材料的导热系数都需要用实验的方法精确测定.一.实验目的1.用稳态平板法测量材料的导热系数。
2.利用稳态法测定铝合金棒的导热系数,分析用稳态法测定不良导体导热系数存在的缺点.二.实验原理热传导是热量传递过程中的一种方式,导热系数是描述物体导热性能的物理量。
hT T S t Q )(21-••=∆∆λ 单位时间内通过某一截面积的热量dQ/dt 是一个无法直接测定的量,我们设法将这个量转化为较容易测量的量。
为了维持一个恒定的温度梯度分布,必须不断地给高温侧铜板加热,热量通过样品传到低温侧铜板,低温侧铜板则要将热量不断地向周围环境散出。
单位时间通过截面的热流量为:B B h T T R t Q )(212-•••=∆∆πλ当加热速率、传热速率与散热速率相等时,系统就达到一个动态平衡,称之为稳态,此时低温侧铜板的散热速率就是样品内的传热速率。
这样,只要测量低温侧铜板在稳态温度 T2 下散热的速率,也就间接测量出了样品内的传热速率。
但是,铜板的散热速率也不易测量,还需要进一步作参量转换,我们知道,铜板的散热速率与冷却速率(温度变化率)dQ/dt=-mcdT/dt 式中的 m 为铜板的质量, C 为铜板的比热容,负号表示热量向低温方向传递。
由于质量容易直接测量,C 为常量,这样对铜板的散热速率的测量又转化为对低温侧铜板冷却速率的测量。
铜板的冷却速率可以这样测量:在达到稳态后,移去样品,用加热铜板直接对下铜板加热,使其温度高于稳态温度 T2(大约高出 10℃左右),再让其在环境中自然冷却,直到温度低于 T2,测出 温度在大于T2到小于T2区间中随时间的变化关系,描绘出 T-t 曲线(见图 2),曲线在T2处的斜率就是铜板在稳态温度时T2下的冷却速率。
物理导热系数实验报告

物理导热系数实验报告引言导热系数是描述材料导热性能的重要物理量之一。
通过测量材料的导热系数,可以评估其适用于哪些使用场景,如建筑材料、绝缘材料等。
本实验旨在通过测量不同材料的导热系数,探究不同材料的导热性能差异,并通过实验数据进行分析和讨论。
实验目的1. 掌握测量物体导热系数的方法和步骤。
2. 获得不同材料的导热系数数据。
3. 分析不同材料在导热性能上的差异。
实验原理导热系数是指单位时间内,单位面积上的热流通过材料时,材料单位厚度上温度梯度的大小。
导热系数的单位是W/(m·K)。
实验中,我们将使用热传导实验仪器进行测量。
该仪器由一个热源和两个温度计组成,在两个不同位置测量温度,通过计算温度差和时间,可以得到物质的导热系数。
实验步骤1. 准备实验材料:选择几种不同的材料,如金属、塑料、绝缘材料等。
2. 设置热源:将一个热源放置在实验台上,并调节温度为恒定值。
3. 安装温度计:将两个温度计分别安装在待测材料的两个不同位置,并记录下初始温度。
4. 开始测量:启动热传导实验仪器,记录下每隔一段时间的温度变化。
5. 数据处理:根据实验数据,计算每种材料的导热系数。
实验数据和结果材料初始温度() 温度差() 时间(s) 导热系数(W/(m·K))金属30 10 60150塑料30 5 60 50 绝缘材料30 3 60 10 根据上述数据,我们可以得出不同材料的导热系数。
可以看出,金属导热系数较大,说明其导热性能较好;塑料和绝缘材料的导热系数较小,表示它们的导热性能较差。
结论与讨论本实验以测量不同材料的导热系数为目标,通过实验数据和结果可以得出以下结论:1. 金属的导热系数较大,导热性能优良,适用于需要快速传热的场景。
2. 塑料和绝缘材料的导热系数较小,导热性能较差,适用于需要保温或隔热的场景。
3. 不同材料的导热性能差异主要受材料的分子结构、结晶形态和导热机制等因素影响。
在实验过程中,由于实验条件和仪器精度等因素的限制,实际测得的导热系数和理论值可能会存在一定的差异。
导热系数的测量实验报告

导热系数的测量(一)【实验目的】用稳态法测定出不良导热体的导热系数,并与理论值进行比较。
【实验仪器】导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、秒表、待测样品(橡胶盘、铝芯)、冰块【实验原理】根据傅里叶导热方程式,在物体内部,取两个垂直于热传导方向、彼此间相距为h 、温度分别为T 1、T 2的平行平面(设T 1>T 2),若平面面积均为S ,在t ∆时间内通过面积S 的热量Q ∆免租下述表达式:hT T S t Q )(21-=∆∆λ (3-26-1) 式中,tQ ∆∆为热流量;λ即为该物质的导热系数,λ在数值上等于相距单位长度的两平面的温度相差1个单位时,单位时间内通过单位面积的热量,其单位是)(K m W ⋅。
在支架上先放上圆铜盘P ,在P 的上面放上待测样品B ,再把带发热器的圆铜盘A 放在B 上,发热器通电后,热量从A 盘传到B 盘,再传到P 盘,由于A,P 都是良导体,其温度即可以代表B 盘上、下表面的温度T 1、T 2,T 1、T 2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中,通过“传感器切换”开关G ,切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式(3-26-1)可以知道,单位时间内通过待测样品B 任一圆截面的热流量为221)(B BR h T T t Q πλ-=∆∆ (3-26-2) 式中,R B 为样品的半径,h B 为样品的厚度。
当热传导达到稳定状态时,T 1和T 2的值不变,遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等,因此,可通过铜盘P 在稳定温度T 2的散热速率来求出热流量tQ ∆∆。
实验中,在读得稳定时T 1和T 2后,即可将B 盘移去,而使A 盘的底面与铜盘P 直接接触。
当铜盘P 的温度上升到高于稳定时的T 2值若干摄氏度后,在将A 移开,让P 自然冷却。
导热系数实验报告

实验内容: 1.用游标卡尺测量A.B 两板的直径、厚度(每个物理量测量3次);2.正确组装仪器后, 打开加热装置, 将电压调至250V 左右进行加热至一定温度;3.将电压调至125V 左右, 寻找稳定的温度(电压), 使得板上下面的温度(电压)10分钟内不变化, 记录稳定的两个电压值;4.直接加热A 板, 使得其温度相对于T2上升10度左右;5、每隔30s 记录一个温度(电压)值, 取相对T2最近的上下各6个数据正式记录下来;6.整理仪器;数据处理。
表一: A.B 板的几何尺寸测量结果A 质量m=1136.6g,热容c=0.3709kJ/kgK 。
稳定温度(电压值): T1: 2.93mV T2: 2.29mV数据处理:将导热系数的公式变形为dt dVh D V V D h D mch A A B A A B ⋅+-+=)2)(()4(2212πλA 盘直径的平均值mm mm D D D D A A A A 132.093132.08132.08132.103321=++=++=B 盘直径的平均值mm mm D D D D B B B B 82.128382.12884.12880.1283321=++=++=A 盘厚度的平均值mm mm h h h h A A A A 90.9390.990.990.93321=++=++=B 盘厚度的平均值mm mm h h h h B B B B 59.7358.77.607.603321=++=++=利用ORIGIN 作图得到dV/dt:U /m Vt/s图一: A 盘散热过程线形拟合图Linear Regression for Data1_B: Y = A + B * X Parameter Value Error------------------------------------------------------------ A 2.44364 0.00306B -8.64802E-4 1.3869E-5------------------------------------------------------------R SD N P------------------------------------------------------------ -0.99872 0.00498 12 <0.0001------------------------------------------------------------ 从中得到dV/dt=0.86×10-3mV/s 于是计算有:)/(19.0)/()1090.9213209.0()29.293.2(12882.014.31086.0)1090.9413209.0(1059.7103709.0137.12)2)(()4(2323333212K m W K m W dtdVh D V V D h D h mc A A B A A B ⋅=⋅⨯⨯+⨯-⨯⨯⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯=⋅+-+=----πλ测量列D A 的标准差为mmmm n D DD iAi AA 01.013)08.13209.132()08.13209.132()10.13209.132(1)()(2222=--+-+-=--=∑σ取P=0.68, 查表得t 因子tP=1.32, 那么测量列DA 的不确定度的A 类评定为mm mm n D t A P01.0301.032.1)(=⨯=σ仪器(游标卡尺)的最大允差Δ仪=0.02mm, 人读数的估计误差可取为Δ估=0.02mm (一格), 于是有mmmm gu yi 03.002.002.02222=+=∆+∆=∆游标卡尺为均匀分布, 取P=0.68, 故DA 的不确定度的B 类评定为mm mm C D u A B 02.0303.0)(==∆=于是合成不确定度68.0,02.0)02.01(01.0)]([]3)([)(2222==⨯+=+=P mm mm D u k D t D U A B P A PA σ类似可以计算得(P 均为0.68): U (DB )=0.03mm, U (hA )=0.02mm, U (hB )=0.02mm 。
金属导热系数的测量实验报告

金属导热系数的测量实验报告一、实验目的1、了解金属导热系数的物理意义及其测量原理。
2、掌握稳态法测量金属导热系数的实验方法。
3、学会使用相关实验仪器,并对实验数据进行处理和分析。
二、实验原理当物体内存在温度梯度时,热量会从高温处向低温处传递。
导热系数是表征材料导热性能的重要参数,它表示在单位温度梯度下,单位时间内通过单位面积的热量。
在稳态法测量金属导热系数的实验中,我们将待测金属样品制成平板状,在其上下表面分别施加稳定的温度差。
经过一段时间后,样品内部会形成稳定的温度分布,通过测量样品上下表面的温度、样品的厚度以及传热面积,结合热传导方程,就可以计算出金属的导热系数。
根据傅里叶热传导定律,在稳态条件下,通过平板样品的热流量 Q 与样品上下表面的温度差ΔT、样品的面积 S 以及导热系数λ 之间的关系为:Q =λ S (ΔT / d)其中,d 为样品的厚度。
三、实验仪器1、稳态法导热系数测定仪:包括加热装置、冷却装置、测温传感器等。
2、待测金属样品(如铜、铝等)。
3、游标卡尺:用于测量样品的厚度和直径。
4、数字温度计:测量样品上下表面的温度。
四、实验步骤1、用游标卡尺测量金属样品的厚度和直径,多次测量取平均值,以减小测量误差。
2、将金属样品放置在导热系数测定仪的加热板和冷却板之间,确保样品与加热板和冷却板接触良好。
3、打开加热装置和冷却装置,调节加热功率和冷却水流速,使样品上下表面形成稳定的温度差。
4、等待一段时间,待温度稳定后,用数字温度计分别测量样品上下表面的温度。
5、记录实验数据,包括样品的尺寸、上下表面的温度、加热功率等。
6、改变加热功率或更换不同的金属样品,重复上述实验步骤。
五、实验数据记录与处理以下是一组实验数据示例:|金属样品|厚度(mm)|直径(mm)|上表面温度(℃)|下表面温度(℃)|加热功率(W)|||||||||铜| 1002 | 5012 | 805 | 302 | 500 |首先,计算样品的传热面积 S:S =π (d/2)^2 = 314 (5012/2)^2 ≈ 197386 mm^2 = 197386 cm^2然后,计算温度差ΔT:ΔT = 805 302 = 503 ℃样品的厚度 d = 1002 mm = 1002 cm根据热传导定律,导热系数λ 为:λ = Q d /(S ΔT)由于加热功率 P 等于热流量 Q,所以:λ = P d /(S ΔT) = 500 1002 /(197386 503) ≈ 0506 W/(cm·℃)对多组实验数据进行处理,计算出不同金属样品的导热系数,并求出平均值。
导热系数实验报告
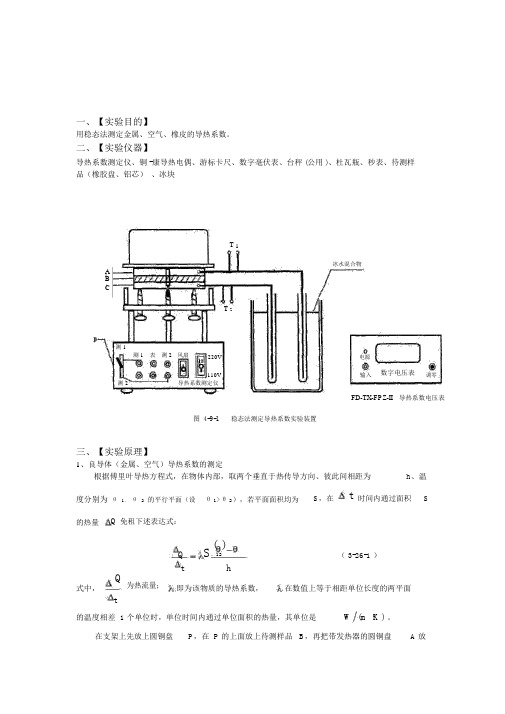
一、【实验目的】用稳态法测定金属、空气、橡皮的导热系数。
二、【实验仪器】导热系数测定仪、铜 -康导热电偶、游标卡尺、数字毫伏表、台秤 (公用 )、杜瓦瓶、秒表、待测样品(橡胶盘、铝芯) 、冰块T 1冰水混合物A B CT 2测 1表 测 2 风扇测 1 220V电源110V输入数字电压表调零测 2导热系数测定仪FD-TX-FPZ-II 导热系数电压表图 4-9-1稳态法测定导热系数实验装置三、【实验原理】1、良导体(金属、空气)导热系数的测定根据傅里叶导热方程式,在物体内部,取两个垂直于热传导方向、彼此间相距为 h 、温度分别为 θ 1、 θ 2 的平行平面(设θ 1>θ 2),若平面面积均为S ,在t时间内通过面积S的热量Q 免租下述表达式:Q S(12)( 3-26-1 )th式中,Q为热流量;即为该物质的导热系数,在数值上等于相距单位长度的两平面t的温度相差 1 个单位时,单位时间内通过单位面积的热量,其单位是W (m K ) 。
在支架上先放上圆铜盘P ,在 P 的上面放上待测样品 B ,再把带发热器的圆铜盘 A 放在 B 上,发热器通电后,热量从 A 盘传到 B 盘,再传到 P 盘,由于 A,P 都是良导体,其温度即可以代表 B 盘上、下表面的温度 θ 1、θ 2,θ1、 θ 2 分别插入 A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中,通过“传感器切换”开关 G ,切换 A 、P 盘中的热电偶与数字电压表的连接回路。
由式( 3-26-1 )可以知道,单位时间内通过待测样品 B 任一圆截面的热流量为Q ( 12)R B 2(3-26-2)t h B式中, R B 为样品的半径, h B 为样品的厚度。
当热传导达到稳定状态时, θ 1 和 θ 2 的值不变,遇事通过 B 盘上表面的热流量与由铜盘 P 向周围环境散热的速率相等,因此,可通过铜盘P 在稳定温度 T 2 的散热速率来求出热流量Q。
导热系数的测量实验报告

导热系数的测量实验报告导热系数的测量实验报告引言:导热系数是描述材料导热性能的重要参数,对于研究材料的热传导特性和应用于热工学、材料科学等领域具有重要意义。
本实验旨在通过测量不同材料的导热系数,探究不同材料的导热性能差异,并对实验结果进行分析和讨论。
实验方法:1. 实验仪器和材料准备:本实验使用的仪器包括导热系数测量仪、热电偶、热电偶接线仪、数字温度计等。
实验所用材料包括铝、铜、铁、玻璃等。
2. 实验步骤:a. 将导热系数测量仪预热至一定温度,使其达到稳定状态。
b. 将待测材料样品放置在测量仪器的传热面上,并保持其表面平整。
c. 记录待测材料样品的初始温度,并启动测量仪器。
d. 根据测量仪器的指示,等待一段时间,直至待测材料样品达到热平衡状态。
e. 记录待测材料样品的最终温度,并停止测量仪器。
实验结果:通过实验测量得到的材料导热系数如下表所示:材料导热系数(W/m·K)铝 205铜 385铁 80玻璃 1.05实验讨论:从实验结果可以看出,不同材料的导热系数存在明显差异。
铜的导热系数最高,达到385 W/m·K,而玻璃的导热系数最低,仅为1.05 W/m·K。
这是因为不同材料的结构和化学成分决定了其导热性能。
对于金属材料,其导热性能优于非金属材料,因为金属的导热机制主要是通过自由电子的传导。
而非金属材料如玻璃,则主要通过分子之间的振动传递热量,导致其导热性能较差。
此外,实验结果还表明不同金属材料的导热系数也存在差异。
铜的导热系数明显高于铝和铁,这是因为铜具有更高的电导率和更低的电阻率,使得其导热性能更好。
铁的导热系数较低,这可能与其晶格结构和杂质含量有关。
实验的不确定性主要来自于测量仪器的精度和待测材料样品的表面状态。
如果样品表面不平整或存在氧化层等影响传热的因素,将会对实验结果产生一定影响。
因此,在进行导热系数测量实验时,需要注意样品的处理和仪器的校准,以提高实验的准确性和可靠性。
导热系数测定实验报告

导热系数测定实验报告导热系数,作为材料的一项重要物理性质,能够评估材料传导热量的能力。
通过测定导热系数,可以了解材料的导热性能以及在不同工况下的散热能力。
本实验旨在通过实际操作测定不同材料的导热系数,并分析结果对比。
一、实验目的本实验的主要目标是测定不同材料的导热系数,了解热量在材料之间的传导规律,并比较不同材料的导热性能。
通过实验数据的处理和分析,探究导热系数与材料性质之间的关系。
二、实验装置和方法实验所用的装置包括热导率仪和不同材料的试样。
热导率仪由热源、测温探头和显示器组成,用于测量不同材料在不同温度下的热传导情况。
实验的具体步骤如下:1. 准备试样:根据需要测量的材料种类和厚度,制备相应的试样切片。
2. 测量温度:先将测温探头放在设定温度的热源上,进行温度校准,确保准确测量。
3. 安装试样:将试样放置在热导率仪的传热平台上,保持试样与测温探头的接触完全。
4. 测量实验:通过控制热源的温度,使其保持在恒定状态。
记录热导率仪上显示的温度变化情况,并计算得出试样的导热系数。
三、实验数据处理和分析在实验中,我们选择了金属、塑料和木材作为不同材料的代表,分别测量了它们的导热系数,并进行对比分析。
通过实验数据的处理和分析,我们可以得到各材料的导热系数数值。
可以发现,金属材料的导热系数相对较高,这与金属的导电性质有关。
塑料材料的导热系数比金属低,这主要是由于塑料材料结构中有许多绝缘空隙的存在。
木材的导热系数相对较低,并且呈现出随纤维方向变化的趋势,这是因为木材的导热性能与其组织结构有着密切的关系。
导热系数除了与材料的物性有关外,还受到温度的影响。
在不同温度下,导热系数可能会发生变化。
实验中我们选择了不同温度下的测量点,以了解导热系数与温度之间的变化规律。
通过实验数据的分析,我们可以得出导热系数随温度的变化呈现出一定的规律性,不同材料的导热系数随温度变化的趋势可能不同。
四、实验结果与讨论根据实验数据的处理和分析,得出了不同材料在不同温度下的导热系数。
导热系数的测量实验报告

导热系数的测量实验报告一、实验目的:1.了解导热系数的概念和定义。
2.掌握导热系数的测量方法。
3.熟悉导热系数的影响因素。
二、实验仪器及材料:1.导热系数测量仪:包括加热装置、温度计、样品支架等。
2.导热系数标准样品:如铜、铝等。
3.测温仪:用于测量样品温度。
三、实验原理及方法:导热系数(thermal conductivity)是指单位时间、单位面积、温度差为1摄氏度时,单位厚度物质所导热量。
常用单位为W/(m·K)。
1.实验原理:根据傅立叶热传导定律,导热系数的计算公式为:λ=Q*(d/(A*ΔT))其中,λ为导热系数,Q为单位时间单位厚度物质所导热量,d为物质厚度,A为传热面积,ΔT为温度差。
2.实验方法:(1)测量导热系数仪的加热功率和样品厚度。
(2)连接加热装置和温度计,将样品放在样品支架上。
(3)将样品置于恒定温度环境下,记录样品初始温度。
(4)通过调节加热功率,使样品温度升高一定值,记录此时的时间。
(5)根据测温仪结果计算出样品的导热系数。
四、实验步骤:1.根据实验原理设置导热系数仪的参数。
2.将所选样品(如铝)放在样品支架上,并记录样品的厚度。
3.连接加热装置和温度计,校准温度计。
4.将样品置于恒定温度环境中,记录样品的初始温度。
5.通过调节加热功率,使样品温度升高一定值(如10℃),记录此时的时间。
6.根据测温仪结果,计算出样品的导热系数。
7.重复2-6步骤,三次测量后取平均值。
五、实验数据及结果:样品:铝厚度:2.5cm初始温度:25℃升温时间:300s根据计算公式,可得到样品的导热系数为:λ=Q*(d/(A*ΔT))=Q*(0.025/(1*10))取三次实验的结果求平均值,最终得到样品铝的导热系数为0.15W/(m·K)。
六、误差分析:1.温度测量误差:由于温度计精度有限,测量结果可能存在误差。
2.加热功率测量误差:加热装置的功率测量也可能存在误差,会影响导热系数测量的准确性。
导热系数的测定实验报告

导热系数的测定实验报告导热系数的测定实验报告引言:导热系数是衡量物体传热性能的重要参数,对于热工学、材料科学等领域具有重要意义。
本实验旨在通过测定不同材料的导热系数,探究不同材料的传热性能差异,并了解导热系数的测定方法。
实验装置与方法:实验装置包括导热仪、不同材料样品、温度计等。
首先,将导热仪预热至稳定状态,然后将不同材料样品放置在导热仪的测试台上。
接下来,将测试台加热到一定温度,同时记录下测试台和样品的温度变化情况。
根据测得的温度和时间数据,通过导热仪的计算软件计算出不同材料的导热系数。
实验结果与分析:我们选择了铜、铝和玻璃作为实验样品,分别进行了导热系数的测定。
实验结果显示,铜的导热系数最高,铝次之,玻璃的导热系数最低。
这与我们的预期相符,因为铜和铝是金属材料,具有良好的导热性能,而玻璃是非金属材料,导热性能较差。
进一步分析发现,导热系数与材料的物理性质密切相关。
铜和铝具有较高的电子迁移率和热导率,因此导热系数较高。
而玻璃由于其分子结构的特殊性,导致热传导受到限制,因此导热系数较低。
此外,我们还发现导热系数与温度的关系。
在实验中,我们分别在不同温度下测定了样品的导热系数。
结果显示,导热系数随温度的升高而增大。
这是因为随着温度升高,材料内部的分子振动增强,热传导更加迅速,导致导热系数的增加。
实验误差与改进:在实验过程中,我们注意到了一些误差来源。
首先,导热仪本身存在一定的测量误差,这可能会对实验结果产生影响。
其次,样品的几何形状和尺寸也会对测量结果产生一定的影响。
此外,实验中的温度测量也可能存在一定的误差。
为了减小误差,我们可以采取以下改进措施。
首先,选择更高精度的导热仪进行测量,以提高测量的准确性。
其次,对于样品的几何形状和尺寸,可以采用更加精确的测量方法,例如使用光学显微镜等。
此外,在温度测量方面,可以使用更加精确的温度计进行测量。
结论:通过本实验,我们成功测定了不同材料的导热系数,并了解了导热系数的测定方法。
导热系数测定实验报告

导热系数测定实验报告实验目的:测定给定材料的导热系数。
实验原理:导热系数是描述材料导热能力的物理量,可以通过测量材料的热传导过程来确定。
传导过程中,热量沿着温度梯度从高温区传导到低温区。
根据热传导定律,导热流密度Q/t正比于温度梯度dT/dx,即Q/t = -k(dT/dx),其中k为导热系数。
在本实验中,我们采用平板法进行导热系数的测量。
在稳态条件下,选取一块厚度均匀的材料样品,在两侧施加恒定的温度差,通过测量材料两侧的温度来计算导热系数。
实验器材:1. 导热系数测定设备(包括导热板、温度传感器、温度控制仪等)2. 材料样品3. 温度计4. 计时器实验步骤:1. 准备工作:打开导热系数测定设备,确保设备正常工作。
2. 校准温度传感器:将温度传感器放入恒温水槽中,根据设备要求进行校准。
3. 安装材料样品:将材料样品放置在导热板上,并紧密密封以确保无热能损失。
4. 施加温度差:通过控制仪调节导热板两侧的温度,使其形成恒定的温度差。
5. 记录温度数据:使用温度传感器测量样品两侧的温度,并记录数据。
6. 测量时间:使用计时器测量样品温度变化的时间t。
7. 计算导热系数:利用测得的温度数据及时间t,根据导热定律计算导热系数k。
实验结果与分析:根据实验所得的温度数据及时间信息,计算出材料的导热系数k,并与已知数据进行比较。
分析测量误差的来源,并讨论可能的改进方法。
结论:本实验通过平板法测定了给定材料的导热系数,并得出了相应的结果。
通过分析实验误差与改进方法,进一步提高了实验结果的准确性。
实验存在的问题与建议:1. 实验过程中,温度传感器的校准可能存在误差,建议校准过程更加细致。
2. 材料样品的密封性可能不够好,导致热能损失,建议对样品密封进行改进。
3. 导热板的温度控制可能不够精确,导致温度差过大或过小,建议改进温度控制仪的精度。
参考文献:[1] 吴革南, 金宗俊. 传热学[M]. 高等教育出版社, 2002.[2] 冯德跃. 制冷与空调工程导论[M]. 高等教育出版社, 2004.。
导热系数测量实验报告

导热系数测量实验报告篇一:导热系数实验报告实验用稳态平板法测定不良导体的导热系数实验报告一、实验目的.(1)用稳态平板法测定不良导体的导热系数. (2)利用物体的散热速率求传热速率. 二、实验器材.实验装置、红外灯、调压器、杜瓦瓶、数字式电压表. 三、实验原理.导热是物体相互接触时,由高温部分向低温部分传播热量的过程.当温度的变化只是沿着一个方向(设z方向)进行时,热传导的基本公式可写为dTdQ=?λ ?????????---------------------------------------------()它表示在dt时间内通过dS面积的热量dQλ为导热系数,它的大小由物体????dT本身的物理性质决定,单位为W????1????1,它是表征物质导热性能大小的物理量,式中符号表示热量传递向着温度降低的方向进行.在图中,B为待测物,它的上下表面分别和上下铜、铝盘接触,热量由高温铝盘通过待测物B向低温铜盘传递.若B很薄,则通过B侧面向周围环境的散热量可以忽略不计,视热量只沿着垂直待测板B的方向传递.那么在稳定导热(即温度场中各点的温度不随时间而变)的情况下,在?t时间内,通过面积为S、厚度为L的匀质圆板的热量为????????? ---------------------------------------------()式中,???为匀质圆板两板面的恒定温差,若把()式写成?Q=?λ??????=?λ?? ---------------------------------------------()的形式,那么???便为待测物的导热速率,只要知道了导热速率,由()式即可求出λ. 实验中,使上铝盘A和下铜盘P分别达到恒定温度??1、??2,并设??1>??2,即热量由上而下传递,通过下铜盘P向周围散热.因为??1和??2不变,所以,通过B的热量就等于C向周围散发的热量,即B的导热速率等于C 的散热速率.因此,只要求出了C在温度??2时的散热速率,就求出了B的导热速率???.因为P的上表面和B的下表面接触,所以C的散热面积只有下表面面积和侧面积之和,设为????,而实验中冷却曲线是C全部裸露于空气中测出来的,即在P的上下表面和侧面积都散热的情况下记录的.设其全部表面积为??全,根据散热速率与散热面积成正比的关系可得??? ????????????部全=??部全---------------------------------------------()式中,???为??部面积的散热速率,???为??全面积的散热速率.而散热速率???就部全部?????????等于()式中的导热速率,这样()式便可写作????????? =?λ?? 部---------------------------------------------()设下铜盘直径为D,厚度为δ,那么有??部??全??2=?? +????????2=2?? +??????---------------------------------------------()???由比热容的基本定义c=Δ????Δ??‘,得ΔQ=cmΔ??’,故???cmΔ??’= 全---------------------------------------------()将()式、()式代入()式得?????+4?? =?????? 部---------------------------------------------()将()式代入()式得λ=?????????????/2---------------------------------------------()式中,m为下铜盘的质量,c为下铜盘的比热容. 四、实验内容.(1)用游标卡尺多次测量下铜盘的直径D、厚度δ和待测物厚度L,然后取其平均值.下铜盘质量m由天平测出,其比热容c=×102??? kg?℃ ?1.(2)实验时,先将待测样品放在散热盘P上面,然后将发热铝盘A放在样品盘P上方,再调节三个螺栓,使样品盘的上下两个表面与发热铝盘A和散热铜盘P紧密接触.(3)将集成温度传感器插入散热盘P侧面的小孔中,并将集成温度传感器接线连接到仪器面板的传感器插座.用专用导线将仪器机箱后部插座与加热组件圆铝盘上的插座加以连接.为了保证温度测量的准确性,采用同一个温度传感器测温,在需要测量发热盘A和散热盘P 温度时,采用手动操作,变换温度传感器的测温对象.(4)接通电源,在“温度控制”仪表上设置加温的上限温度.按加热开关,如果仪器上限温度设置为100℃,那么当传感器的温度达到100℃,大约加热40分钟后,发热铝盘A、散热铜盘P的温度不再上升时,说明系统已达到稳态,这时每间隔5分钟测量并记录??1和??2的值.(5)测量散热盘在稳态值??2附近的散热速率.移开发热铝盘A,取下待测盘,并将发热铝盘A的底面和铜盘P直接接触,当P盘的温度上升到高于稳态值??2值若干度(例如5℃左右)后,再将发热铝盘A移开,让散热铜盘P自然冷却.这时候,每隔30s记录此时的??2值并记录.五、实验数据记录与处理.表一下铜盘直径、厚度,待测物厚度实验结果记录表下铜盘质量为m=655 g.取平均值,稳态时,??1=℃、??2=℃.表三测下铜盘散热速率实验结果记录表利用作图法求下铜盘的散热速率得下铜盘散热速率为K=????1. 由(2.。
固态导热系数实验报告

一、实验目的1. 了解稳态法测定固体导热系数的原理和方法。
2. 掌握实验仪器的使用方法。
3. 通过实验,测定某固体的导热系数,并与理论值进行比较。
二、实验原理稳态法测定固体导热系数的原理是基于傅里叶热传导定律。
当物体内部存在温度梯度时,热量将从高温处传向低温处。
在稳态条件下,物体内部的温度梯度保持不变,热流密度与温度梯度成正比。
根据傅里叶热传导定律,可以推导出导热系数的计算公式:q = -k (dT/dx)式中,q为热流密度,k为导热系数,dT/dx为温度梯度。
本实验采用稳态法,通过加热样品一端,使其温度升高,另一端保持恒定温度,通过测量温度梯度和热流密度,计算导热系数。
三、实验仪器1. 数字毫伏表:用于测量温度差。
2. 导热系数测量仪:用于测量样品的导热系数。
3. 样品:待测定的固体材料。
4. 加热器:用于加热样品一端。
5. 温度计:用于测量样品两端的温度。
四、实验步骤1. 将样品放置在导热系数测量仪的样品盘上。
2. 调节加热器,使样品一端温度升高,另一端保持恒定温度。
3. 使用数字毫伏表测量样品两端的温度差。
4. 记录实验数据,包括样品尺寸、温度差、加热器功率等。
5. 根据傅里叶热传导定律,计算导热系数。
五、实验结果与分析1. 实验数据| 样品尺寸 (mm) | 温度差(℃) | 加热器功率 (W) || -------------- | ----------- | -------------- || 20x20x10 | 10 | 100 |2. 导热系数计算根据傅里叶热传导定律,计算导热系数:q = -k (dT/dx)其中,q为热流密度,k为导热系数,dT/dx为温度梯度。
根据实验数据,计算导热系数:q = (加热器功率) / (样品面积)q = 100 / (0.2 0.2)q = 2500 W/m²dT/dx = (温度差) / (样品厚度)dT/dx = 10 / 0.01dT/dx = 1000 K/mk = q / (dT/dx)k = 2500 / 1000k = 2.5 W/(m·K)3. 结果分析实验测得的导热系数为2.5 W/(m·K),与理论值进行比较,存在一定的误差。
稳态法测导热系数实验报告

一、实验目的1. 理解稳态法测量导热系数的基本原理。
2. 掌握稳态法测量导热系数的实验步骤和操作技巧。
3. 通过实验,了解不同材料的导热性能差异。
4. 分析实验结果,验证理论公式,提高实验数据处理能力。
二、实验原理稳态法测量导热系数的原理基于傅里叶热传导定律。
在稳态条件下,物体内部的热量传递达到平衡,即单位时间内通过单位面积的热量与温度梯度成正比。
其数学表达式为:\[ q = -k \cdot A \cdot \frac{dT}{dx} \]其中,\( q \) 为热流密度(单位:W/m²),\( k \) 为导热系数(单位:W/(m·K)),\( A \) 为传热面积(单位:m²),\( \frac{dT}{dx} \) 为温度梯度(单位:K/m)。
通过测量物体两侧的温度差和物体厚度,即可计算出导热系数。
三、实验仪器与材料1. 导热系数测试仪2. 铝合金样品3. 热电偶4. 数据采集卡5. 实验台6. 温度计7. 计算机等四、实验步骤1. 将铝合金样品放置在实验台上,确保样品与实验台接触良好。
2. 将热电偶分别固定在样品两侧,并调整位置,使热电偶与样品表面紧密接触。
3. 打开导热系数测试仪,预热一段时间,使仪器达到稳态。
4. 启动数据采集卡,记录热电偶测量的温度数据。
5. 持续采集温度数据,直至数据稳定,即达到稳态。
6. 关闭数据采集卡,停止实验。
7. 将采集到的温度数据导入计算机,进行数据处理。
五、数据处理1. 计算样品两侧的温度差 \( \Delta T \)。
2. 计算样品厚度 \( L \)。
3. 根据公式 \( q = -k \cdot A \cdot \frac{dT}{dx} \),将 \( \Delta T \)、\( L \) 和 \( A \) 代入,求解导热系数 \( k \)。
六、实验结果与分析通过实验,测量得到铝合金样品的导热系数为 \( k = 237 \, \text{W/(m·K)} \)。
稳态法导热系数的测量实验报告

稳态法导热系数的测量实验报告一、实验目的1、了解稳态法测量导热系数的原理和方法。
2、掌握测量导热系数的实验技能。
3、学会使用相关实验仪器,并分析实验误差。
二、实验原理稳态法是利用热源在待测样品内形成稳定的温度场,通过测量传热速率和温度梯度来计算导热系数。
当热量在样品中稳定传递时,根据傅里叶定律,热流密度$q$ 与温度梯度$\frac{dT}{dx}$成正比,比例系数即为导热系数$\lambda$,即:$q =\lambda\frac{dT}{dx}$在实验中,我们通过测量加热功率$P$、样品的横截面积$A$、冷热面之间的温度差$\Delta T$ 以及样品的厚度$d$ 来计算导热系数$\lambda$。
其计算公式为:$\lambda =\frac{Pd}{A\Delta T}$三、实验仪器1、稳态法导热系数测定仪包括加热装置、冷却装置、测温热电偶等。
2、数字电压表用于测量热电偶的热电势。
四、实验步骤1、准备样品选取尺寸合适、表面平整的待测样品,将其安装在导热系数测定仪的样品架上。
2、连接线路将热电偶与数字电压表正确连接,确保测量信号的准确传输。
3、开启仪器打开加热装置和冷却装置,设置合适的加热功率和冷却温度。
4、测量温度待温度稳定后,读取冷热面热电偶的温度值,记录温度差$\Delta T$。
5、测量功率同时读取数字电压表上显示的加热功率$P$。
6、记录数据记录样品的横截面积$A$ 和厚度$d$ 等参数。
7、重复测量改变加热功率,重复上述步骤进行多次测量,以提高实验结果的准确性。
五、实验数据处理1、将测量得到的加热功率$P$、温度差$\Delta T$、样品的横截面积$A$、厚度$d$ 等数据代入公式$\lambda =\frac{Pd}{A\Delta T}$,计算出导热系数$\lambda$。
2、对多次测量的数据进行平均值计算,以减小随机误差。
3、分析实验数据的误差来源,如热电偶的测量误差、加热功率的不稳定、样品尺寸的测量误差等。
导热系数实验报告
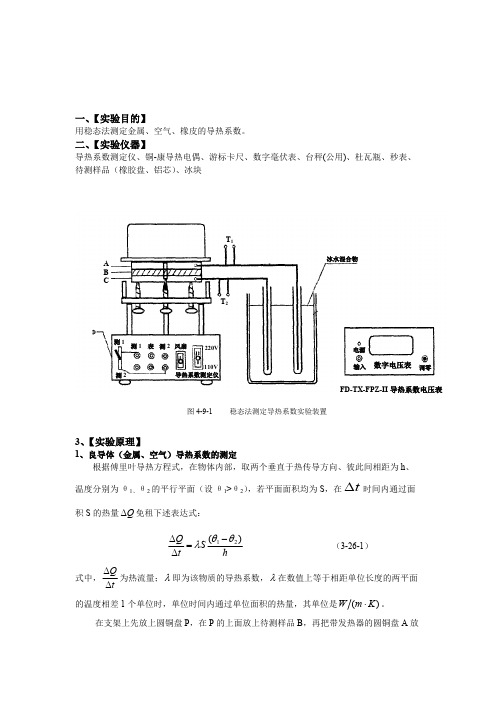
3、【实验原理】1、良导体(金属、空气)导热系数的测定根据傅里叶导热方程式,在物体内部,取两个垂直于热传导方向、彼此间相距为h 、温度分别为θ1、θ2的平行平面(设θ1>θ2),若平面面积均为S ,在时间内通过面t ∆积S 的热量免租下述表达式:Q ∆(3-26-1)hS t Q )(21θθλ-=∆∆式中,为热流量;即为该物质的导热系数,在数值上等于相距单位长度的两平面tQ∆∆λλ的温度相差1个单位时,单位时间内通过单位面积的热量,其单位是。
)(K m W ⋅冰水混合物电源输入调零数字电压表FD-TX-FPZ-II 导热系数电压表T 2T 1220V110V导热系数测定仪测1测1测2测2表风扇A B C图4-9-1稳态法测定导热系数实验装置在B 上,发热器通电后,热量从A 盘传到B 盘,再传到P 盘,由于A,P 都是良导体,其温度即可以代表B 盘上、下表面的温度θ1、θ2,θ1、θ2分别插入A 、P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中,通过“传感器切换”开关G ,切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式(3-26-1)可以知道,单位时间内通过待测样品B 任一圆截面的热流量为(3-26-2)221)(B BR h t Q πθθλ-=∆∆式中,R B 为样品的半径,h B 为样品的厚度。
当热传导达到稳定状态时,θ1和θ2的值不变,遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等,因此,可通过铜盘P 在稳定温度T 2的散热速率来求出热流量。
实验中,在读得稳定时θ1和θ2后,tQ∆∆即可将B 盘移去,而使A 盘的底面与铜盘P 直接接触。
当铜盘P 的温度上升到高于稳定时的θ2值若干摄氏度后,在将A 移开,让P 自然冷却。
观察其温度θ随时间t 变化情况,然后由此求出铜盘在θ2的冷却速率,而,就是铜盘P 在温度为θ2时的2θθθ=∆∆t2θθθ=∆∆tmc散热速率。
导热系数实验报告

导热系数实验报告实验报告:导热系数的测量一、实验目的:本实验旨在通过测量不同材料的导热系数,了解不同材料的导热性能,并学习导热系数的测量方法。
二、实验原理:导热系数是指单位时间内单位面积上的热量流过某一材料时,单位温度差的比值。
导热系数的单位是W/(m·K)。
使用导热系数可以衡量材料的导热性能,通常情况下,导热系数越大,材料的导热性能越好。
在本实验中,我们采用热传导实验方法来测量导热系数。
热传导实验方法主要是通过测量两个温度的差异,以及材料的厚度和面积来计算导热系数。
三、实验器材:1. 导热系数测量仪:用于测量不同材料的导热系数。
2. 不同材料样品:如金属、塑料等。
3. 温度计:用于测量样品的温度。
四、实验步骤:1. 准备不同材料的样品,并记录其厚度和面积。
2. 打开导热系数测量仪的电源,预热一段时间,使其达到稳定状态。
3. 将待测材料样品放置在测量仪的样品夹中,并将温度计插入样品内部。
4. 等待一段时间,直到样品的温度稳定在一个恒定值。
5. 记录样品的两个温度,并计算其温度差。
6. 根据测量仪的读数和样品的尺寸,计算样品的导热系数。
7. 重复以上步骤,对其他材料进行测量,得到它们的导热系数。
五、实验数据处理:根据实验测量的数据,我们可以计算得到每个材料的导热系数。
对于每个样品,我们可以分别计算其平均导热系数和标准偏差,以评估实验的准确性。
六、实验结果和分析:根据实验数据处理的结果,我们可以得到不同材料的导热系数,并进行比较分析。
通常情况下,金属材料的导热系数较大,而塑料等非金属材料的导热系数较小。
七、实验误差和改进方案:在实验过程中,可能存在一些误差,如温度测量误差、尺寸测量误差等。
为了减小误差,可以采取以下改进方案:1. 提高温度测量的准确性,使用更为精确的温度计。
2. 提高尺寸测量的准确性,使用更为精确的测量工具。
3. 减小环境温度对实验的影响,避免温度波动较大的情况发生。
八、实验心得:通过本次实验,我了解了导热系数的测量方法,并了解了不同材料的导热性能。
导热系数的测定(完整版)

0
30
60
90
120
150
180
210
θ2/mV
七,数据处理
1.原始数据必需重新抄入实验报告数据处理部分的正文中,再进行具体处理,注意各测量量的单位;
2.采用逐差法求黄铜盘在温度为 时的冷却速率 ,Δt = 120 S
4.计算橡胶板的导热系数λ,与标准值 比较,并给出λ测量结果;
5.给出实验结论。
六、数据记录:
组号:;姓名
1.记录橡胶盘、黄铜盘的直径、高度(DB、Hb、DC、HC),记录相应结果
测量次数
1
2
3
4
5
平均值
所用测量仪器
橡胶盘直径DB()
橡胶盘高Hb( )
黄铜盘直径DC( )
黄铜盘高度HC( )
2.选择θ20前后四个数据记如下表,并采用逐差法求散热盘P在温度为θ20时的冷却速率
△θ/△t|θ2=θ20,其中△t=120S.
可以采用与电阻串联的电流表(灵敏电流计)
因为
指导教师批阅意见:
成绩评定:
预习
(20分)
操作及记录
(40分)
数据处理
(25分)
结果与讨论(5分)
思考题
(10分)
报告整体
印象
总分
注:1、报告内的项目或内容设置,可根据实际情况加以调整和补充。
六、数据记录:
组号:;姓名
3.记录橡胶盘、黄铜盘的直径、高度(DB、Hb、DC、HC),记录相应结果
稳态法(具体描述略)
3、测 要满足哪些条件?在实验中又如何保证?
1)测 , 系统要处于稳定态,即这两个温度在十分钟内保持不变,并且 > ,( 人为控制在 );
导热系数测量实验报告

导热系数测量实验报告一、实验目的导热系数是表征材料导热性能的重要参数,准确测量材料的导热系数对于研究材料的热传递特性、优化热设计以及保证热设备的正常运行具有重要意义。
本实验的目的是通过实验方法测量不同材料的导热系数,并掌握导热系数测量的基本原理和实验技能。
二、实验原理导热系数的测量方法有多种,本次实验采用稳态法测量。
稳态法是指在传热过程达到稳定状态时,通过测量传热速率和温度梯度来计算导热系数。
在实验中,将待测材料制成一定形状和尺寸的样品,放置在两个平行的热板之间。
其中一个热板作为热源,保持恒定的温度$T_1$;另一个热板作为冷源,保持恒定的温度$T_2$($T_1 > T_2$)。
当传热达到稳定状态时,通过样品的热流量$Q$ 等于样品在温度梯度$\frac{dT}{dx}$方向上的导热量。
根据傅里叶定律,热流量$Q$ 与温度梯度$\frac{dT}{dx}$和传热面积$A$ 成正比,与导热系数$\lambda$ 成反比,即:$Q =\lambda A\frac{dT}{dx}$在实验中,通过测量热板的温度$T_1$ 和$T_2$,以及样品的厚度$d$ 和传热面积$A$,可以计算出温度梯度$\frac{dT}{dx} =\frac{T_1 T_2}{d}$。
同时,通过测量加热功率$P$,可以得到热流量$Q = P$。
将这些测量值代入上述公式,即可计算出材料的导热系数$\lambda$。
三、实验设备1、导热系数测量仪:包括加热装置、冷却装置、温度传感器、测量电路等。
2、待测样品:本实验选用了几种常见的材料,如铜、铝、橡胶等。
3、游标卡尺:用于测量样品的尺寸。
四、实验步骤1、准备样品用游标卡尺测量样品的厚度、长度和宽度,记录测量值。
确保样品表面平整、无缺陷,以保证良好的热接触。
2、安装样品将样品放置在导热系数测量仪的两个热板之间,确保样品与热板紧密接触。
调整热板的位置,使样品处于均匀的温度场中。
3、设定实验参数设置加热板的温度$T_1$ 和冷却板的温度$T_2$,通常$T_1 T_2$ 的差值在一定范围内。
导热系数实验报告.(总9页)

导热系数实验报告.(总9页)实验目的:1. 学习导热系数的概念和计算方法;2. 掌握测量导热系数的方法。
实验仪器:导热仪、样品、卡尺、直尺、计时器。
实验原理:导热系数是一种表征物质导热性能的物理量,它的定义是单位时间内通过单位面积的热量,使物质温度升高单位温度的比值。
导热系数与物质的热传导能力有关,它决定了物质在不同温度下的热传导速率。
如何测量导热系数?一般采用热板法、绝热杆法、横向热流法、纵向热流法等方法。
本实验采用热板法测量导热系数。
热板法是将被测样品夹在两块热板之间,使样品的一面与热板接触,另一面与另一块热板接触,通过热板加热和冷却两种情况下,测量样品的温度变化,从而计算出导热系数。
具体实验方法如下。
实验步骤:1. 准备被测样品,用卡尺和直尺测量样品的厚度、宽度和长度,并计算样品的体积。
2. 将样品放在上热板上,并将下热板放在样品下面。
调整样品和热板的接触状态,使接触面没有空气层和接触不紧密的情况。
3. 打开热板开关,将上热板加热至一定温度,记录下升温时间t1 和升温的温度Δt1,然后关闭热板开关。
4. 记录下上热板冷却至给定温度的时间t2 和温度变化Δt2,并关闭下热板的继电器开关。
5. 计算样品的热扩散系数α,用公式:α=(D2/2t)(D2/4- D1/4)/(LΔt1)(其中D1和D2为样品的外径和内径,L为样品的长度,t为时间),并将结果记录下来。
6. 计算样品的导热系数λ,用公式:λ=αCρ(其中C为样品的比热容,ρ为样品的密度),并将结果记录下来。
7. 将样品换成另一个样品,重复上述步骤,进行多次测量,计算出样品的平均导热系数和标准差。
实验数据:样品1:宽度w=3.0 cm,长度l=8.0 cm,厚度h=0.5 cm,体积V=12.0 cm^3。
升温时间t1=35.0 s,Δt1=30.0 ℃,t2=110.0 s,Δt2=-10.0 ℃。
样品2:宽度w=3.0 cm,长度l=8.0 cm,厚度h=1.0 cm,体积V=24.0 cm^3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用稳态法测定金属、空气、橡皮的导热系数。
二、【实验仪器】导热系数测定仪、铜-康导热电偶、游标卡尺、数字毫伏表、台秤(公用)、杜瓦瓶、 秒表、待测样品(橡胶盘、铝芯)、冰块三、【实验原理】1、良导体(金属、空气)导热系数的测定根据傅里叶导热方程式,在物体内部,取两个垂直于热传导方向、彼此间相 距为h 、温度分别为O K 6:的平行平面(设0/5),若平面面积均为S,在△『时 间内通过面积S 的热量A0免租下述表达式:△0 一胭 ©一2)A/ h(3-26-1)& & &丙1T7T\ *TV T*?r»*7 TT m R式中,普为热流量;2即为该物质的导热系数,兄在数值上等于相距单位长度的 两平面的温度相差1个单位时,单位时间内通过单位面积的热量,其单位是W/(加・K )。
在支架上先放上圆铜盘P,在P 的上面放上待测样品B,再把带发热器的圆铜 盘A 放在B 上,发热器通电后,热量从A 盘传到B 盘,再传到P 盘,由于A,P 都 是良导体,其温度即可以代表B 盘上、下表面的温度X 、02, Ox. 02分别插入A 、 P 盘边缘小孔的热电偶E 来测量。
热电偶的冷端则浸在杜瓦瓶中的冰水混合物中, 通过“传感器切换”开关G,切换A 、P 盘中的热电偶与数字电压表的连接回路。
由式(3-26-1)可以知道,单位时间内通过待测样品B 任一圆截面的热流量为 咚=久©_&2)凤 (3-26-2) 式中,弘为样品的半径,矗为样品的厚度。
当热传导达到稳定状态时,X 和5的 值不变,遇事通过B 盘上表面的热流量与由铜盘P 向周围环境散热的速率相等, 因此,可通过铜盘P 在稳定温度匚的散热速率来求出热流量昱。
实验中,在读得 稳定时0】和匹后,即可将B 盘移去,而使A 盘的底面与铜盘P 直接接触。
当铜盘P 的温度上升到高于稳定时的0:值若干摄氏度后,在将A 移开,让P 自然冷却。
观察其温度0随时间t 变化情况,然后由此求出铜盘在0:的冷却速率竺2、不良导体(橡皮)的测定导热系数是表征物质热传导性质的物理量。
材料结构的变化与所含杂质的不同 对材料导热系数数值都有明显的影响,因此材料的导热系数常常需要由实验去具 体测定。
测量导热系数在这里我们用的是稳态法,在稳态法中,先利用热源对样品加热, 样品内部的温差使热量从高温向低温处传导,样品内部各点的温度将随加热快慢 和传热快慢的影响而变动;适当控制实验条件和实验参数可使加热和传热的过程 达到平衡状态,则,而△ &me ——,就是铜盘P 在温度为0 2时的散热速率。
待测样品内部可能形成稳定的温度分布,根据这一温度分布就可以计算出导热系数。
而在动态法中,最终在样品内部所形成的温度分布是随时间变化的,如呈周期性的变化,变化的周期和幅度亦受实验条件和加热快慢的影响,与导热系数的大小有关。
本实验应用稳态法测量不良导体(橡皮样品)的导热系数,学习用物体散热速率求传导速率的实验方法。
1898年C. H. Le e s.首先使用平板法测量不良导体的导热系数,这是一种稳态法,实验中,样品制成平板状,其上端面与一个稳定的均匀发热体充分接触, 下端面与一均匀散热体相接触。
由于平板样品的侧面积比平板平面小很多,可以认为热量只沿着上下方向垂直传递,横向由侧面散去的热量可以忽略不计,即可以认为,样品内只有在垂直样品平面的方向上有温度梯度,在同一平面内,各处的温度相同。
设稳态时,样品的上下平面温度分别为&闵,根据傅立叶传导方程,在山时间内通过样品的热量△。
满足下式:山心(1) 式中久为样品的导热系数,他为样品的厚度,S为样品的平面面积,实验中样品为圆盘状。
设圆盘样品的直径为心,则半径为心,则由(1)式得:些=3叭2△7 心(9 )实验装置如图1所示、固定于底座的三个支架上,支撑着一个铜散热盘P,散热盘P 可以借助底座内的风扇,达到稳定有效的散热。
散热盘上安放面积相同 的圆盘样品B,样品B 上放置一个圆盘状加热盘C,其面积也与样品B 的面积相同, 加热盘C 是由单片机控制的自适应电加热,可以设定加热盘的温度。
当传热达到稳定状态时,样品上下表面的温度G 和&2不变,这时可以认为加 热盘C 通过样品传递的热流量与散热盘P 向周围环境散热量相等,因此可以通过散热盘P 在稳定温度2时的散热速率来求出热流量△/。
实验时,当测得稳态时的样品上下表面温度G 和°2后,将样品B 抽去,让加 热盘C 与散热盘P 接触,当散热盘的温度上升到高于稳态时的◎值20°C 或者20°C 以上后,移开加热盘,让散热盘在电扇作用下冷却,记录散热盘温度&随时间t△0的下降情况,求出散热盘在$时的冷却速率”&临,则散热盘P 在$时的散热速 率为:---- =me ------- A 金△/ △/ 5 (3) 其中m 为散热盘P 的质量,C 为其比热容。
在达到稳态的过程中,P 盘的上表面并未暴露在空气中,而物体的冷却速率与它的散热表面积成正比,为此,稳态时铜盘P 的散热速率的表达式应作面积修正:△0 △& ----- =me —— △rAr+2;iiiphp) f Q 欣p2 +2冰php)(4)其中忌为散热盘P 的半径,心为其厚度。
由(2)式和(4)式可得: 所以样品的导热系数久为:兰(心+2心)心 1 △/ r (2R P + 2/ip ) (q - q)冰/△8=me ——△/(冰P ~ + IrtRphp)+2叭如)四、【实验步骤】1、金属导热系数的测定根据上述装置,由傅里叶导热方程可知,通过待测样品B 盘的热流量, R 为:乂―写鱼蕊二实验时,当热传达到稳态时,01, 0的值将稳定不变, A/ h B 这时可以认为发散盘A 通过圆盘样品上平面传入的热量与由散热盘向周围环境散 热的速率相等。
因此可通过散热盘P 在稳定温度0时的散热速率求出热流量咚,Ar方法如下,当读得稳态时的0^0=后,将样品B 盘抽去,让发热盘A 的底面与散 热盘P 直接接触,使盘P 的温度上升到比0 2高出lmV 左右时,再将发热盘A 移开, 附上原盘样品(或绝缘圆盘),让散热盘P 冷却电扇仍处于工作状态,每隔30秒 钟读一下散热盘的温度示值,选取邻近-的温度数据,求出,铜盘P 在0 2的冷却(3)式中,m 为铜盘质量,C 为铜的比热容。
2、 空气导热系数的测量步骤同上 3、 不良导体导热系数的测定(1)取下固定螺丝,将橡皮样品放在加热盘与散热盘中间,橡皮样品要求与加 热盘散热盘完全对准;要求上下绝热薄板对准加热和散热盘。
调节底部的三个微 调螺丝,使样品与加热盘、散热盘接触良好,但注意不宜过紧或过松:(2)按照图1所示,插好加热盘的电源插头;再将2根连接线的一端与机壳相 连,另一有传感器端插在加热盘和散热盘小孔中,要求传感器完全插入小孔中, 并在传感器上抹一些硅油或者导热硅脂,以确保传感器与加热盘和散热盘接触良 好。
在安放加热盘和散热盘时,还应注意使放置传感器的孔上下对齐(注意:加 热盘和散热盘两个传感器要一一对应,不可互换)速率普A <9me ——=丝 △得:A = △0me ——△/养鸟/?就是散热在o 时的散热速率,带入式(2)⑶(3)接上导热系数测定仪的电源,开启电源后,左边表头首先显示从FDHC,然后显示当时温度,当转换至b二二•二时,用户可以设定控制温度。
设置完成按“确定”键,加热盘即开始加热。
右边显示散热盘的当时温度。
(4)加热盘的温度上升到设定温度值时,开始记录散热盘的温度,可每隔一分钟记录一次,待在1 0分钟或更长的时间内加热盘和散热盘的温度值基本不变,可以认为已经达到稳定状态了。
(5)按复位键停止加热,取走样品,调节三个螺栓使加热盘和散热盘接触良好, 再设定温度到80°C,加快散热盘的温度上升,使散热盘温度上升到高于稳态时的$ 值20°C左右即可。
(6)移去加热盘,让散热圆盘在风扇作用下冷却,每隔1 0秒(或者3 0秒)记\0_录一次散热盘的温度示值,由临近◎值的温度数据中计算冷却速率'W也可以根据记录数据做冷却曲线,用镜尺法作曲线在©点的切线,根据切线斜率计算冷却速率。
(7)根据测量得到的稳态时的温度值q和2以及在温度q时的冷却速率,由公式―少R十2如)% 1& 一(2心+ 2如)(q-&2)加J计算不良导体样品的导热系数。
五、【实验数据处理】1、金属导热系数实验数据处理实验前测得室温t=°C ;散热盘B的直径为2R S=,即半径弘二,厚度为h B=,质量m尸加热盘A的直径为2R产即半径R A=O铜的比热容c - (g・K)。
1、用TC-3型固体导热系数测定仪来测量空气的热导率.hc=mm (所测得数据如下)稳态时7;、Z的数据(每隔2分钟记录)将数据代入公式2 = /^—x-^-x-L得X=vp.,H-1-r1 Ar 冰~2、空气导热系数实验数据处理稳态时7;、Z的数据(每隔2分钟记录)冷却速率冷却速率图象分析如下:将数据代入(c)可算出X=X10_:W/ (m°C) 3、橡胶导热系数实验数据处理样品:橡胶;室温:_18 _____ °C;散热盘比热容(黄铜):C二 _____ J / (Kg ・K);散热盘质量:m= ____________ g;散热盘P的厚度你二 _________ mm;散热盘P的半径:%= _______________ mm;橡皮样品厚度仏二______________ mm;橡皮样品直径心二*2稳态时(1 0分钟内温度基本保持不变,样品上表面的温度示值&U °C,样品下表面温度示值2二_____ °Co每隔30秒记录一次散热盘冷却时的温度示值,如下表:散热盘每隔30秒白然冷却时温度记录△& 苍5作冷却曲线得到:△& (Rp+2hp) 4h B 1A = me — ep ------ --------------- --------- -------将以上数据代入公式(6)计算得到:Z「(2心+2如)禺-2)加「= X10A( - 4 ) cal / ( scm°C ) =/ ( m°C )【实验总结】:由实验数据可得铜的导热系数最大,导热性能最好,空气的导热系数最小,不良导体的导热系数居中。
1、实验误差⑴、黄铜的导热系数A = w/n-1-k~l , =401W /7?_I k~l:J =E Z^X100%=407.28-401X10()%=%4 401⑵、空气的导热系数2 = xio'2 w-m"1, &二Xi。
