surfer 3 插值方法
surfer软件的使用方法

surfer软件的使用方法【转】goldensurfer8.0初学者教程2021年12月13日星期日15:22戈德恩瑟费尔。
0初学者教程一、简介戈德弗特斯沃兹。
0(以下简称surfer)是三维图形(等高)线,imagemap,3dsurface)的软件,该软件简单易学,可以在几分钟内学会主要内容,且其自带的英文帮助(help菜单)对如何使用surfer解释的很详细,其中的tutorial教程更是清晰的介绍了surfer的简单应用,应该说surfer软件自带的帮助文件是相当完美且容易阅读的,只要学过英语的人都可以很快上手。
Surfer是一款具有插值功能的绘图软件,因此即使数据间距不等,也可以使用它进行绘图。
然而,根据作者的经验,最好不要使用surfer的插值功能,尤其是在需要精确确定等高线时。
由于surfer是一款美国软件,它不支持中文,这可以算是一个小小的遗憾。
surfer的主要功能是绘制等高线图(contourmap),此外它还可以绘制postmap,classedpostmap,vectormap,imagemap,wireframemap,3dsurfacemap,等形式的图形。
其功能是比较强的,但没有各种投影变化是它的一大缺点。
尤其是在等高线领域,这不能不说是它的应用受到限制的地方。
由于surfer软件没有中文说明书,对一些初学者来说可能会存在上手较难的问题,鉴于此种需求,编写了这一初学者参考手册,希望对大家有所帮助。
二、等高线的绘制Surfer的主要功能是绘制等高线图,但我们不能直接用数据文件绘制等高线。
Surfer 要求等高线图的数据有特殊的格式要求,即首先将数据文件转换为Surfer认可的GRD文件格式,绘制等高线(当然,你可以直接生成surfer接受的ASCII码的GRD文件格式,这样你就可以直接绘制。
这个方法将在后面介绍。
首先,我们将介绍常见的绘制方法)。
假设有三列数据,即x、y和Z,其中Z是点(x,y)的值,有一个文件test Dat(数据见附件),其中第一列是x坐标,第二列是y坐标,第三列是(x,y)上的值Z。
Surfer软件插值方法

Surfer软件插值方法1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。
克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。
3、最小曲率法最小曲率法广泛用于地球科学。
用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。
最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。
使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。
4、多元回归法多元回归被用来确定你的数据的大规模的趋势和图案。
你可以用几个选项来确定你需要的趋势面类型。
多元回归实际上不是插值器,因为它并不试图预测未知的Z 值。
它实际上是一个趋势面分析作图程序。
Surfer插值方法介绍 中英混合版

一篇英文文章,用百度翻译翻译的还有一篇中文文章供参考满满的诚意,求赏金ABSTRACTSURFER is a contouring and 3D surface mapping program, which quickly and easily transforms random surveying data, using interpolation, into continuous curved face contours. In particular, the new version, SURFER 8.0, provides over twelve interpolation methods, each having specific functions and related parameters. In this study, the 5 meter DTM was used as test data to compare the various interpolation results; the accuracy of these results was then discussed and evaluated.摘要冲浪是一个轮廓和三维表面的绘制程序,并迅速和容易地变换随机测量数据,使用插值,成连续的曲面轮廓。
特别是,新版本,上网8,提供超过十二的插值方法,每一个具有特定功能和相关参数。
在这项研究中,5米DTM作为测试数据,比较不同的插值结果;讨论和评价,然后这些结果的准确性。
1. INTRODUCTIONHow to adequately use exist numerous wide-distributed height points has been an important topic in the field of spatial information. Normally, contouring is the way to accurately describe the terrain relief by means of Scenography, Shading, Hachure and Layer Tinting in a way which is best fit to the habit of human vision.Presently, discretely collected height points have to be interpolated to form curved faces, the selection of spatial interpolation methods decide the quality, accuracy and follow-up analysis applications. Interpolation methods are used here to calculated the unknown heights of interested points by referring to the elevation information of neighboring points. There are a great many commercial interpolation software, however, most of them are tiny and designed to solve specific problems with limited versatility. The SURFER is a software developed by US GOLDEN company, and the newest version 8.0 contains up to 12 interpolation methods to been free chosen for various needs. Users are suggested to first have the basic understanding of every interpolation methods before he or she can effectively select parameters in every interpolation methods. In the following paper, we will introduce every interpolation method in SURFER.1。
surfer插值
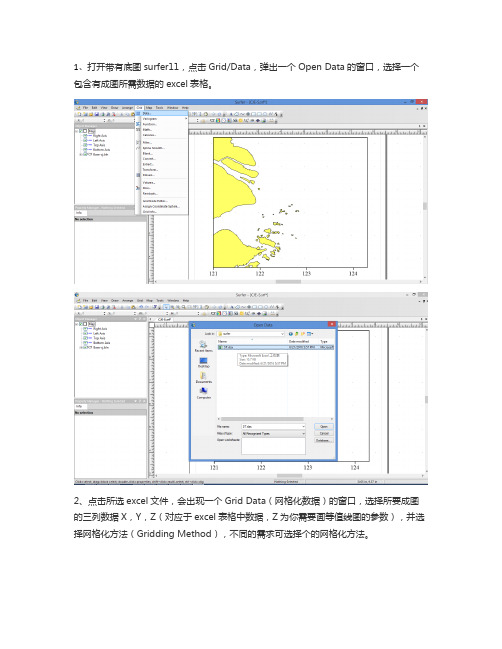
1、打开带有底图surfer11,点击Grid/Data,弹出一个Open Data的窗口,选择一个包含有成图所需数据的excel表格。
2、点击所选excel文件,会出现一个Grid Data(网格化数据)的窗口,选择所要成图的三列数据X,Y,Z(对应于excel表格中数据,Z为你需要画等值线图的参数),并选择网格化方法(Gridding Method),不同的需求可选择个的网格化方法。
3、选择存路径等,最后点击OK,就会输出一个grd文件并关闭Gridding Report, 得到插值的网格化grd.文件。
4、选择菜单栏Map/New/Contour Map,或者右击左边菜单栏里的Map/Add/Contour Layer,
5、找到上面的grd文件所在位置,点击打开,就得到所要的平面等值线图(未上色)。
如果等值线不够平滑,可以点击Contours...,在左下属性管理(Property Manager)选择General/Smoothing,进行None,Low,Medium,High四种不同程度地平滑
6、然后就是为等值线图上色;点击Contours...,在左下属性管理(Property Manager)选择Levels/Filled Contours/Fill Colors,勾选Fill Contours和Color Scale。
Surfer插值方法介绍 中英混合版

一篇英文文章,用百度翻译翻译的还有一篇中文文章供参考满满的诚意,求赏金ABSTRACTSURFER is a contouring and 3D surface mapping program, which quickly and easily transforms random surveying data, using interpolation, into continuous curved face contours. In particular, the new version, SURFER 8.0, provides over twelve interpolation methods, each having specific functions and related parameters. In this study, the 5 meter DTM was used as test data to compare the various interpolation results; the accuracy of these results was then discussed and evaluated.摘要冲浪是一个轮廓和三维表面的绘制程序,并迅速和容易地变换随机测量数据,使用插值,成连续的曲面轮廓。
特别是,新版本,上网8,提供超过十二的插值方法,每一个具有特定功能和相关参数。
在这项研究中,5米DTM作为测试数据,比较不同的插值结果;讨论和评价,然后这些结果的准确性。
1. INTRODUCTIONHow to adequately use exist numerous wide-distributed height points has been an important topic in the field of spatial information. Normally, contouring is the way to accurately describe the terrain relief by means of Scenography, Shading, Hachure and Layer Tinting in a way which is best fit to the habit of human vision.Presently, discretely collected height points have to be interpolated to form curved faces, the selection of spatial interpolation methods decide the quality, accuracy and follow-up analysis applications. Interpolation methods are used here to calculated the unknown heights of interested points by referring to the elevation information of neighboring points. There are a great many commercial interpolation software, however, most of them are tiny and designed to solve specific problems with limited versatility. The SURFER is a software developed by US GOLDEN company, and the newest version 8.0 contains up to 12 interpolation methods to been free chosen for various needs. Users are suggested to first have the basic understanding of every interpolation methods before he or she can effectively select parameters in every interpolation methods. In the following paper, we will introduce every interpolation method in SURFER.1。
surfer 3 插值方法

Shepard‘s法与距离反比法插值法相似,但没 有产生等值线“牛眼”效应的缺点。 线性内插三角形法对于中等数量的数据点, 网格化很快。一个优点是,当有足够的数据 点时,三角形法可以反映出数据文件所内含 的不连续性。例如断层线。
径向基本函数法 (Radial Basis Functions) )
径向基本函数法是一种准确插值的方法。其 中的多重二次曲面法被许多人认为是最好的 方法。在插值生成一个网格结点时,这些函 数确定了使用数据点的最优权重组。 径向基本函数法的函数类型包括:
反比多重二次曲面法; 多重对数; 多重二次曲面法; 自然三次样条和薄板样条。
距离反比法最快,但是围绕数据点,有产生“牛眼” 效应的趋势。 大部分情况下,具有线性变异图的Kriging法是十分 有效的,应首先予以推荐。其次是很接近的经向基 本函数法中的多重二次曲面法。这两种方法都能产 生较好地代表原始数据的网格。但对于大量数据的 网格化,Kriging法比较慢。
最小曲率法构成平滑的曲面,且多情况下, 网格化速度也快。 多项式回归是一种趋势面分析,反映整体趋 势。对于任何数量的数据点,网格化的速度 都非常快,但构成的网格缺少数据的局部细 节。 径向基本函数法十分灵活,与Kriging法产生 的网格十分类似。
径向基本函数法类似Kriging法中的变异图。 在大多数情况下,多重二次曲面函数是最合 乎要求的。 R2参数是一个决定锐化或平滑的参数。 R2值愈大,山顶愈圆滑,等值线愈平滑。R2 合理的实验值是在一个平均样本间距和半个 平均样本间距之间。
最近临点法( 最近临点法(Nearest Neighbor) )
距离反比法 (Inverse Distance to a Power)
一种加权平均插值的网格化方法。 在计算一个网格结点的Z值时,一定范围内,所有 数据点的权重的和为1,权重与某数据点到该结点 距离成反比,愈靠近该结点的原始数据点,其权重 愈大。 如果网格结点正好位于某原始数据点,该结点的Z 值就等于此原始数据点的Z值,即此原始数据点对 于该结点的权重为1,而其它数据点对于该结点的 权重为0。 距离反比法是一种准确插值方法。
surfer教程

surfer教程Golden Software Surfer(以下简称Surfer)是一款画三维图(等高线,image map, 3d surface)的软件,该软件简单易学,可以在几分钟内学会主要内容. Surfer软件不难,自带的英文帮助(help 菜单)把如何使用解释的很详细。
Surfer是具有插值功能的绘图软件,因此,即使你的数据是不等间距的,依然可以用它作图。
但依据本人的经验,最好不使用Surfer自带的插值功能,尤其是要精确确定等高线时(方法请见下面的介绍)。
Note:surfer8.0不支持中文.Surfer的最主要的功能是绘制等高线图,简介如下:假设你由三列数据分别为X,Y,Z,其中Z为点(x,y)处的值。
存为文件test.dat(数据见后)第一列是X坐标,第二列是Y坐标,第三列是(x,y)上的值Z.则画等高线的步骤如下:Note:并不是直接打开test.dat数据就可以画等高线,首先要将数据文件转换成Surfer认识的grd文件格式,才能画出等高线。
步骤一:把数据文件转换成grd文件1.打开Surfer软件,打开菜单“Grid | Data..." ,在open对话框中选择文件test.dat2. 这会打开”Grid Data“对话框。
在“Data Columns”中选择要进行GRID的列数据(这里我们不用选择,因只有3列数据且它们的排列顺利已经是XYZ了,如果是多列数据,则可以在下拉菜单中选择所需要的列数据)。
在“Griding Method"中选择一种插值方法(如果你需要比原始数据的网格X和Y更密的Z数据),则在Grid的过程中,Surfer会自动进行插值计算,生成更密网格的数据。
如果你只是想绘原始数据的图,不想插值,则最好选择距离平方反比法(inverse distance to a power)方法(因为此法在插值点与取样点重合时,插值点值就是取样点值,而其它方法不能保证如此)。
Surfer使用教程

第3章Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 (以下简称Surfer)是一款画三维图(等值线,image map,3d surface)的软件,是美国Golden Software公司的系列绘图软件之一。
该软件简单易学,可以在几分钟内学会主要内容,且其自带的英文帮助文件(help菜单)是相当完美且容易阅读的,对如何使用Surfer,解释的很详细,只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图(contour map),是具有插值功能的绘图软件,因此,即使你的数据是不等间距的,依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map,等形式的图形,其功能是比较强大的。
Surfer的安装比较简单(目前,只有Windows操作系统下的版本,最为常用的是8.0版本),只要按其提示缺省安装即可。
其安装软件的大小不到30M,一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后,其环境界面如图3-1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面3.2 软件界面及命令菜单Surfer软件的界面非常友好,继承了Windows操作系统软件的特点。
从图3-1中可以看到,其最上方为命令菜单,在命令菜单的下方是命令菜单中的快捷工具栏(共两行),左侧的空白区域为目标管理窗口,用来更加方便的管理绘制的各个图形要素,右侧的空白区域为工作区,用来绘制图形,最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单(F)“文件菜单”如图3-2所示,主要是对文件进行操作,如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口,点击后即出现图3-1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
surfer插值方法

一、GIS中使用的一些插值方法(SURFER中也会用到如下的一些插值方法)Inverse Distance to a Power(反距离加权插值法)Kriging(克里金插值法)Minimum Curvature(最小曲率)Modified Shepard's Method(改进谢别德法)Natural Neighbor(自然邻点插值法)Nearest Neighbor(最近邻点插值法)Polynomial Regression(多元回归法)Radial Basis Function(径向基函数法)Triangulation with Linear Interpolation(线性插值三角网法)Moving Average(移动平均法)Local Polynomial(局部多项式法)1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
Surfer8_0等值线绘制中的十二种插值方法

第1期
陈欢欢等 : Surfer 8 1 0 等值 线绘制中的十二种插值方法
53
简单、 对系统要求低等优点得到广大用户的青睐, 成为普及度最高的绘 图软件之一。其最高版本 Surfer8 1 0 提供了十二种插值方法 , 用户可以根据 不同的需要选择不同方法来进行插值 , 来对其进 行分析, 以达到自己想要的效果。要科学地选择 插值方法和灵活地进行参数设置, 必须要熟悉各 种插值方法的 基本理论知识 , 下面 将介绍 Surf2 er8 1 0 中的十二种插值方法及其应用实例。
2 1 3 最小曲率法( Minimum Curvature) 最小曲率法广泛应用于地球科学, 是构造出具 有最小曲率的曲面, 使其穿过空间场的每一点, 并尽 可能使曲面变得光滑 。使用最小曲率法时要涉及 到两个参数: 最大偏差参数 ( Maximum Residuals) 和 最大循环次数( Maximum It eration paramet er) 参数来 控制最小曲率的收敛标准, 而且最小曲率法要求至 少有四个点。最小曲率法试图在尽可能严格地尊重 数据的同时, 生成尽可能圆滑的曲面。最小曲率法 主要考虑曲面的光滑性, 因此插值的成果容易失真, 往往超出了最大值和最小值的范畴, 由此绘出的等 值线与实际相差较大。实际应用中此法只能作为平 滑估值, 绘出的降水量等值线主要用于定性研究降 水的空间分布及走向。 2 1 4 改进谢别德法( Modified Shepard's Method) 使用反距离加权插值法, 当增加、 删除或改变一 个点时, 需要重新计算权函数 w i ( x, y) , 为了克服反 距离加权插值法的这一缺陷, 改进谢别德法同样使 用距离倒数加权的最小二乘方的方法, 主要有以下 两个方面的改进
3Dsurfer使用手册

3D Surfer用户使用手册3D Surfer用户使用手册目录简介三维数据成像软件3D Surfer主要用于地质,工程,科学计算等三维数据体的三维可视化成像显示.它支持两种成像方式:体成像和等值面成像.利用3D Surfer可以将数据在三维空间进行三维可视化显示,并且具有图形旋转,图形放缩,三维虚拟漫游,分层显示,图形切割,制作切片交互等功能.3D Surfer 2.0 支持Surfer切片图,高程模型图,曲折剖面,透明图层,叠加地形,贴图等功能.3D Surfer采用类似Surfer的操作方式,兼容Surfer定义的文本数据格式和GRD数据格式.支持规则数据和散乱数据的三维插值,与Surfer软件定义的色标等级文件兼容,支持*.lvl和*.clr的颜色等级文件,支持*.dat *.txt *.grd等数据格式.支持三维图像的输出转换,可以将三维图形转换为虚拟现实数据文件VRML数据格式,JPG,BMP等图形格式输出.1.原始数据读入1.1数据文件格式:3D Surfer支持Surfer定义的数据文件格式,可以载入txt,dat等格式的数据文件,数据文件格式要求:数据按行排列,每一列表示三维空间的坐标P(x,y,z)或者是坐标点处的值f(x,y,z),分隔符号可以是空格,TAB键,逗号,# | !等字符.在数据文件中还可以采用"//"进行注释.第一行还可以定义列的标题.一个典型的数据文件格式如下水平坐标(x) 垂直坐标(y) 水平坐标(z) 电阻率值5 5 2.5 55.010 5 2.5 58.015 5 2.5 70.0//备注:xxxxxxxxxxxxxxxxxxxxxxxxxx…1.2打开数据文件有三种方式可以读入数据文件(1)使用"数据"菜单,选择"读入原始数据"(2)从工具条上点按钮(3)使用菜单"文件",选择"打开文件",在打开文件对话框中选择三维数据文件(*.dat或者*.txt),3D Surfer格式文件的后缀名自动打开.1.3数据读入3D Surfer格式文件的格式和文件大小自动将三维点数据读入内存,读数据过程中将有一个进度提示,读数据时间将视数据大小不同,一般0.1秒到60秒.2.三维数据插值三维数据读入完成后,出现数据组织对话框,如下图.2.1成像列选择左上是数据选择,可以选择相应列的数据对应于3D Surfer的坐标系.3D Surfer默认坐标系统是x,z是平面方向,y为纵向坐标,坐标系遵守右手法则(见下图).2.2三维插值在数据插值中显示了原始数据的信息,最小值(Minimum),最大值(Maximum),插值间距(Spacing),插值点数(LineNo).缺省的插值点数是原始数据点中的节点数(如果原始数据中有重复点,前面的点将被后面的点取代).网格化(插值点)数:在LineNo里填入要插值(网格化)的点数,该参数将影响图形的精度,网格点数越多,成像精度越高,但内存分配就越大.插值一次性内存分配大小=XNum*YNum*ZNum*4 Bytes.根据成像的要求和计算机内存的大小合理选择该参数. 插值方法:3D Surfer提供了几种三维网格化插值方法,可以根据不同的数据体选择不同的方法.(1)近点线性插值该方法根据近点原理,在插值点附近三个方向上进行线性插值,该方法简单,计算速度快,适用于原始数据是规则网格数据.如果数据是散乱数据则不适用于该方法.(2)近点Cube插值该方法原理同近点线性插值,在插值点附近采用立体网格搜索方法,对插值点附近节点进行搜索,然后采用近点插值方式对网格点进行插值计算.该方法计算速度快,可以适应散乱数据.(3)局部距离加权插值该方法针对散乱数据,按距离加权的方式,采用在局部分块计算的方式,计算速度较快.(4)距离加权插值该方法是针对散乱数据的,采用全局方式,所有原始数据点都参与计算,计算速度较慢.(5)径向基函数插值该方法是针对散乱数据的,是一种全局插值方法,能够比较好地适应散乱数据,插值效果教好,计算速度比较慢,内存开销较大,内存耗费的大小与原始数据插值点的平方成正比.一般来说当原始数据点在10000以下,可以采用径向基函数插值.2.3数据的三维网格化设置好插值点数(LineNo),选定插值方法后,点输出"GRD文件"将进行插值计算,然后生成相应的GRD网格化数据文件.网格化数据文件格式基本同3D Surfer定义的格式,在Surfer格式的基础上增加了一列Z.3.三维数据体成像三维数据点在三维空间中表达成一个小长方体,长宽高的大小与数据体的三个方向的大小和比例有关.一幅三维图形被表达成一系列的小长方体,小方体的颜色就是该点的值.3D Surfer里有两种情况下可以生成体成像,一是原始数据体成像.二是GRD文件体成像.原始数据体成像直接利用原始数据点(可能是规则点或者是散乱数据点)和预定义色标值显示在三维空间中的原始数据点.该显示方法成像速度最快,可以对三维数据起到预览的作用.但是该成像不具有切割,分层显示,输出三维实体(VRML等格式),制作切片等功能.三维网格化数据的体成像.三维网格化数据是原始数据经过插值和网格化后生成的规则数据,利用它可以生成体成像图,具有图形切割,分层显示,切片制作,粘贴点位,输出为VRML实体图等功能.从"数据"菜单里选"读入网格化数据"或者从工具条中点按钮或者从文件对话框中打开*.GRD文件,将自动读入GRD网格化数据.在打开后的对话框中选择"体成像". 4.三维数据等值面成像三维等值面:是三维空间中的一个曲面,该面上的点具有相同的值,表示为相同的颜色.三维数据体是由三维空间中的一系列的实体点组成,三维等值面是由这些点组成的三维边界.三维等值面采用Marching Cubes方法,对整个三维网格进行搜索并构造等值面.该方法成像曲面较体成像平滑,分层明显,不构造实体内部点,显示速度较快,但是生成等值面时间较长.从"数据"菜单里选"读入网格化数据"或者从工具条中点按钮或者从文件对话框中打开*.GRD文件,将自动读入GRD网格化数据.在打开后的对话框中选择"等值面成像".5.色标制作读入网格化数据文件后,3D Surfer载入缺省的色标,在图形控制对话框中可以根据需要自定义色标.每一个数据值区间对应着一种颜色,颜色采用RGB色彩方式,在颜色区鼠标双击将出现颜色选择对话框,可以选择不同的颜色替换当前色.在表格中改变任一列的值将引起相应色标的改变.Add按钮:在当前位置(光标位置)插入一行,同时将该行的值设为前后两行的平均值. Delete按钮:删除该行的值值平均按钮:将所有的数据值按照行数进行平均分配.Load按钮:装载预先定义的色标文件,*.lvl *.clrSave按钮:保存当前的色标定义到文件*.clr中6.三维图形切割3D Surfer采用长方体切割,切割体由一个x,y,z方向的一定大小的长方体定义.图形切割后将重新计算,显示切割后的图形.切割体设置,在面版右上方切割体设置中,x1,x2,y1,y2,z1,z2,分别代表切割体三个方向的值.鼠标单击相应的选项,然后拖动下方的滚动条,可以将值设置到需要位置. 点击"显示切割模型"按钮将在绘图区以轮廓图的形式动态显示切割体的位置(如下图紫色部分).操作移动键可以移动该切割体并动态显示.切割体移动到合适位置后,点"切割"按钮将开始切割,切割完成后点"结束切割显示"将显示切割后的三维图形.7.切片制作在三维网格化图形后,点工具栏上的制作切片按钮在右下方将出现切片制作对话框,此时将关闭所有图层的显示而只显示切片.再次点此按钮将重新显示图层.7.1切片的方向切片根据垂直与x,y,z三个方向不同,将切片分为三类,分别代表垂直于三个坐标轴.7.2增加切片切片分三个方向(分别垂直于X,Y,Z轴),点击相应的标签页分别添加.用鼠标拖动滚动条,到指定位置(可以从0~到最大的切片数)按"添加"按钮,将增加一个切片到列表中,同时在屏幕绘图区中绘制出切片.重复以上步骤,可以设置多个切片.7.3删除切片在切片列表框中显示了切片所在的位置,用鼠标单击相应的切片,切片被选中(切片变成紫色),然后点右边的"删除"按钮,该切片将被删除.7.4旋转切片(1)参数旋转选中切片后,在旋转角度中填入要旋转的角度(旋转轴为切片的中心线,旋转方向顺时针为正,逆时针为负),然后点"旋转"按钮,切片将被旋转到指定位置.(2)鼠标旋转选中切片后,单击工具条上切片旋转按钮,按钮显示被压下,这时候按住鼠标左键盘往左右拖动,松开鼠标后,切片将被旋转,旋转的角度与鼠标拖动的距离成正比.最大不超过正负90度.再次单击上切片旋转按钮,按钮被弹起,结束切片旋转状态.7.5结束切片制作切片布置好后再次点工具栏上的制作切片按钮,该按钮被弹起,结束切片制作.屏幕刷新后将显示切片和图形.注意:如果看不到切片,说明切片被当前图形的图层所遮盖,关掉一部分图层后可以看到切片.8.三维标注标注是在图上加上一些点位符号和文字标注.标注是通过标注文件完成.8.1标注文件标注文件与原始数据文件一样,是文本文件,格式与原始数据文件相同,但是可以包含一列(或者几列)标注文字,格式如下水平坐标(x) 测线方向(z) 深度方向(y) 点位5 5 2.5 1号点#10 5 2.5 2号点#15 5 2.5 3号点#//备注:xxxxxxxxxxxxxxxxxxxxxxxxxx…其中x,y,z是点位坐标,表示符号要显示的位置,至少需要2列以上,如果缺少一列,则自动粘贴到数据体一恻的表面.点位是符号,可以是数字也可以是说明文字.8.2 打开标注文件点工具栏上标注按钮,打开标注文件,在x,y,z,text列表中选择对应的列,右边显示列信息,post x,y,z的范围要在x,y,z 范围之内,否则无法正确标注.如果列选择None,则自动标注到该面测面上.标注时至少需要两列数据.标注符号为十字符号,可以为符号指定大小和颜色.Text列缺省选择为None,表示不标注文字.如果选择了Text列,则将用该列数据值以文字方式显示在符号旁边.如果该列全为数字形式,则还可以指定该列数字显示的小数点位数.文字可以指定文字颜色和文字大小比例(相对比例).间隔数表示标注中可以不用连续标注,可以每隔多少个符号标注一次.标注参数设置好后,按"确定"按钮将在三维图形中输出标注.8.3 删除标注带标注的图形,如果点标注按钮,将显示当前标注信息,如果点"删除"按钮,将取消该图形的标注.9.图形输入/输出9.1图形输入支持*.G3D图形输入,*.g3d图形是3D Surfer保存的图形格式,图形中带有色标信息和图层信息.可以直接打开该类图形直接显示.JPG和BMP位图:3D Surfer可以打开JPG或者BMP位图直接显示.9.2图形输出3D Surfer支持*.g3d,*.jpg,*.bmp,*.wrl等格式的图形输出.(1)*.g3d格式输出:g3d是3D Surfer保存的图形格式,GRD文件成像可以输出为g3d 格式,该格式保留了图形信息和色标信息.可以直接被3D Surfer打开并显示.(2)JPG,BMP图形:3D Surfer可以直接将当前图形输出为图片格式.(3)VRML图形:VRML是虚拟现实语言,它定义的图形和虚拟场景可以用Internet Explorer浏览器打开并浏览显示.3D Surfer可以把体成像图和等值面图输出为VRML格式图形,方便其他的图形软件调用,做进一步处理.10.显示设置显示设置定义了3D Surfer的三维体的视见参数,包括:显示比例,刻度,字体,颜色,方向指示,透明设置等.10.1常规设置(1)字体比例和颜色:表示显示刻度字体颜色和相对比例.(2)x,y,z比例:三个方向的显示比例(3)显示矩形框:显示三维数据体的轮廓矩形框(4)显示色标值:显示图层的颜色值,当值字符比较长影响可视效果时可以去掉值的显示.(5)显示方向指针:当图形旋转过程中,在右下角显示一个方向指示针.显示刻度及参数设置(6)透明色:Alpha色彩融合开关,打开此开关将支持三维图层的透明显示,透明度设置从0(不透明)到100%(全透明,不可见).10.2 坐标及刻度设置坐标刻度是设置X轴,Y轴,Z轴三个方向上12条棱边上的刻度的显示方式,包括以下内容:刻度数目:每条棱边上总共刻度数目.标注间隔:刻度标注的间隔.首尾刻度:是否显示首刻度和尾刻度X轴坐标刻度对应如下图所示Y轴坐标刻度对应如下图所示Z轴坐标刻度对应如下图所示10.3 地层分层显示在三维网格化图形显示中,3D Surfer根据色标定义了一系列的图形分层(用颜色和数据值标志),在屏幕右下角的图层设置面板定义如下图所示.每个图层的复选框定义了三种状态,0不选择,1选择,2灰色,分别表示不显示,显示,透明显示.用鼠标点击复选框(或者借助"全部选择"和"取消全部"按钮)设置好图层的显示状态,然后点"更新显示",使图层显示设置生效.下图是全部显示和只显示指定图层的显示结果图.注意:如果选择显示全部图层,则当前显示的图形是经过处理后的三维图形表面,这样加快了显示速度.10.4 图层透明显示如果要显示覆盖图层下的图层,则可以将覆盖图层设置为透明显示.如果在图层设置面板中设置图层显示复选框按钮为灰色状态(如下图),则该图层支持透明显示.要使透明显示生效,需要打开Alpha色彩融合开关(透明显示开关)和设置透明度,参见常规设置,图层透明设置后的对比图如下图所示.11.数据处理3D Surfer支持异常提取(边缘检测),滤波,相干处理等功能.(1)异常提取:三维数据体异常检测:在三维图形显示中点异常检测按钮将开始计算三维数据体的边缘异常部分,计算完成后将重新生成三维图形.如果想恢复原始图形,点按钮将恢复到异常提取前的图形.下图是异常提取前和提取后的图形对比.原始图形异常检测后图形切片的异常提取:在制作和浏览切片状态时可以针对切片进行异常提取.首先在切片列表中选中切片,然后点工具栏上的异常检测按钮.异常检测后和检测前的对比图如下.原始切片异常检测后切片(2)滤波可以针对三维数据体选择两种方式的滤波,空间滤波和二维滤波.在显示三维体图形时点击工具栏上的滤波按钮,可以进行空间滤波.在切片显示状态,点击工具栏上的滤波按钮将针对切片进行二维滤波.空间滤波前图形空间滤波后图形二维切片滤波前图形二维切片滤波后图形(3)相干:相干处理只针对三维数据体.三维数据体技术主要是根据信号的相干性分析的原理,计算相邻测点不同频率下信号的相干性.在三维图形显示状态点击工具栏上的相干按钮即可进行相干计算,计算后显示相干结果图形.点恢复按钮将还原到相干前的状态.数据相干前图形数据相干后图形12.叠加地形3D Surfer可以再现有的三维图形上叠加地形剖面,地形高程数据被叠加到每个地层节点上过后,并可以显示地表的起伏变化和色彩.读入网格化地层数据文件后(体成像方式),选择叠加地形图标,载入地形数据文件.地形数据文件要求:(1)Surfer Grid网格化文件(2)数据值范围与地层表面数据值范围一致.地层缺省表面范围为minx~maxx minz~maxzSurfer GRID网格文件 minx~maxx miny~maxy(3)地层表面网格与Surfer Grid网格大小一致.载入地形数据后,自动将地形叠加到当前地层数据上,如图12所示.图12-1a是叠加地形后的地层起伏图,12-1b是加上贴图后的地层起伏图(参见导入图形-图元管理). 图12-1a叠加地形后地层起伏图图12-1b加上贴图后的地层起伏图注意:当右边的图层设置面板中所有图层处于选中状态时,为了加快图形显示速度,显示的地层经过特殊处理的表面图形(三维地层外表面).地形的调整使用图元调整功能.13.导入图形导入图形是在三维场景中要增加新的图元,图元包括:Surfer GRID切片Surfer GRID曲面地形曲面3D Surfer三维图形13.1导入Surfer GRID切片选择按钮,读入Surfer 三维网格化文件(*.grd,3D Surfer支持Surfer 6.0和Surfer 7.0网格化文件格式),3D Surfer将根据当前图形的比例和GRID文件切片大小自动缩放切片到合适大小,如果当前没有正在绘制的图形,则自动采用1的显示比例,初始添加的切片位置居中,以后添加的切片位置依次偏移1个单位,经过比例和位置调整后的图形如图所示(参见图元管理).13.2导入Surfer GRID曲面曲面与Surfer GRID切片类似,所不同的将第三列数据值作为高程绘制,缺省曲面起伏方向为Y方向.选择按钮,读入Surfer 三维网格化文件,3D Surfer自动设置比例和绘制曲面,经过比例和位置调整后的图形如图所示(参见图元管理).13.3 添加3D 图元选择按钮,读入3D Surfer三维网格化数据,3D Surfer自动设置比例和绘制3D实体图形,经过比例和位置调整后的图形如图所示(参见图元管理),图中两个小物体是添加的3D图元.13.4 载入测井数据选择按钮可以读入测井数据与地层数据进行对比.3D Surfer默认的测井数据格式如下:Position x(大地坐标x) z(大地坐标y) y(纵向坐标,井顶界面)纵向坐标1(深度) 电阻率值1纵向坐标2(深度) 电阻率值2纵向坐标3(深度) 电阻率值3….例Position 0.1 0.25 -10.0-10.00 2.35-10.50 4.20-11.00 3.30-11.50 3.25…注osition是关键字,表示后面的数据定位井顶界面位置.大地坐标x和大地坐标y 表示井平面位置,纵向坐标y表示井上顶面深度.如果缺少该字段,则默认井水平位置在图形中心,上顶面深度默认第一行数据表示的深度.3D Surfer将根据当前图形大小,自动设置测井柱状图的比例和大小.通过图元管理可以调整测井柱状图的位置和大小.经过比例和位置调整后的图形如图所示(参见图元管理).13.5 图元管理选择按钮,可以对导入的图形进行调整.图元调整界面如下.需要调整的图元包括四种类型的图形:直切片——从Surfer GRID 导入的切片二维曲面——Surfer GRID生成的二维曲面3D实体图——3D Surfer GRID生成的三维实体图3D 表面地形——叠加到地层表面的地形曲面图员调整主要具有以下功能.(1)删除图元首先在列表框中选中一个图形,点删除按钮将把该图形删除(不可恢复),删除3D表面地形的同时将自动调整当前地层的起伏,恢复到初始无地形起伏状态.(2)调整图元色标每类图元都具有自身的色标显示,图元的显示色彩由色标所定义.其中二维曲面的色彩由高程数据计算得出,3D 表面地形的色彩由地层表面数据计算得出.点"调整"按钮将打开色标调整对话框(色标调整参见5.色标制作).(3)叠加颜色剖面针对二维曲面,可以在曲面上叠加颜色剖面(其他图元不具有此特性),此操作要求:叠加剖面为Surfer GRID网格化文件,具有与二维曲面数据相同的网格大小. 点"叠加剖面"按钮读入网格化文件,调整色标,将显示出带色彩的二维曲面,此功能可以制作具有测线走向的实测剖面.(4)图元位置调整使用箭头移动可以将当前图元移动一个步长单位位置,其中左箭头表示沿X轴负向移动,右箭头X轴正向,上箭头Y轴正向,下箭头Y轴负向,"远"往Z轴负向,"近"往Z 轴正向.调节"▲","▼"按钮可以调整移动步长.在对应的三个坐标轴上填入实际位置,然后点"移动"按钮,当前图元的中心将移动到指定位置,点"中心"按钮,可以将所选图元移动到图形中心.(5)图元缩放从列表框中选中一个图元,在缩放框中填入需要缩放的比例(初始比例是根据图元实际大小与当前正在绘制的图形大小的比值),点设置按钮是缩放比例生效.注意:如果新添加的图元在图中不可见,可能的原因是由图元比例太小或者太大,超出当前图形可见区域,只要重新设置合适的比例,然后把图元居中显示即可. (6)图元旋转从列表框中选中一个图元,在图元旋转框中填入每个轴的旋转角度(以度为单位),然后点"旋转"按钮,当前图元将按照指定角度分别绕着坐标轴旋转.图元绕坐标轴旋转遵守右手法则,逆时针为正,顺时针为负.调节"▲","▼"按钮可以按一定角度和方向旋转.(7)图元透明处理所有图元都支持透明显示,勾选"透明"复选框,然后调节透明度滑动条(0%不透明,100%全透明),点更新按钮将把当前透明设置应用到该图元上.注:一个图元的透明设置,不影响其他图元和图层的透明特性.(8)表面贴图Surfer GRID曲面,表面地形图支持表面贴图功能.对于贴图文件的要求:图形文件为BMP格式,24 位位图(真彩色图形).图形分辨率大小(像素)必须是:2n×2n(n>=8),可以是64×64,128×128,256×256,1024×1024,2048×2048,…要应用贴图,首先勾选"贴图"复选框,然后"载入图形"载入用于贴图的BMP文件,点更新按钮,使贴图应用到当前图元上.注意:表面贴图将应用贴图图形的颜色与曲面颜色进行混合产生新的色彩,如果想完全使用贴图代替图元曲面色彩,可以调节图元色标,设置全部色标颜色为白色(R G B 分量均为255)即可.Nx(E)yz(S)SFRONT BOTTOM ddBOTTOMbzyxFRONT TOPBACK TOPBACK BOTTOMBACK RIGHTxyzFRONT LEFTBACK LEFTFRONT RIGHT ddBOTTOMbLEFT TOPRIGHT TOPxyzLEFT BOTTOMRIGHT BOTTOM。
Surfer使用教程

第3章 Surfer8.0绘图软件的使用3.1 软件运行环境及特点Golden Software Surfer 8.0 (以下简称Surfer)是一款画三维图(等值线,image map,3d surface)的软件,是美国Golden Software公司的系列绘图软件之一。
该软件简单易学,可以在几分钟内学会主要内容,且其自带的英文帮助文件(help菜单)是相当完美且容易阅读的,对如何使用Surfer,解释的很详细,只要学过英语的人都可以很快上手。
Surfer的主要功能是绘制等值线图(contour map),是具有插值功能的绘图软件,因此,即使你的数据是不等间距的,依然可以用它作图。
此外它还可以绘制张贴图、分类张贴图、矢量图、影像图、线框图、3d surface map,等形式的图形,其功能是比较强大的。
Surfer的安装比较简单(目前,只有Windows操作系统下的版本,最为常用的是8.0版本),只要按其提示缺省安装即可。
其安装软件的大小不到30M,一般的计算机硬件基本能够顺利使用该软件。
安装好Surfer以后,其环境界面如图3-1所示。
命令菜单绘图命令目标管理窗口工作区状态栏图3-1 Surfer8.0软件界面3.2 软件界面及命令菜单Surfer软件的界面非常友好,继承了Windows操作系统软件的特点。
从图3-1中可以看到,其最上方为命令菜单,在命令菜单的下方是命令菜单中的快捷工具栏(共两行),左侧的空白区域为目标管理窗口,用来更加方便的管理绘制的各个图形要素,右侧的空白区域为工作区,用来绘制图形,最右侧的一个竖条工具栏是绘图命令的快捷方式。
下面详细介绍各个命令菜单的主要内容。
3.2.1文件菜单(F)“文件菜单”如图3-2所示,主要是对文件进行操作,如文件的建立、加载、打印设置等。
图3-2 文件菜单新建—用来新建一个工作窗口,点击后即出现图 3-1界面。
打开—打开一个已经存在的Surfer可以识别的文件。
各种插值方法比较

各种插值方法比较空间插值可以有很多种分类方法,插值种类也难以举尽。
在网上看到这篇文章,觉得虽然作者没能进行分类,但算法本身介绍地还是不错的。
在科学计算领域中,空间插值是一类常用的重要算法,很多相关软件都内置该算法,其中GodenSoftware 公司的Surfer软件具有很强的代表性,内置有比较全面的空间插值算法,主要包括:Inverse Distance to a Power(反距离加权插值法)Kriging(克里金插值法)Minimum Curvature(最小曲率)Modified Shepard's Method(改进谢别德法)Natural Neighbor(自然邻点插值法)Nearest Neighbor(最近邻点插值法)Polynomial Regression(多元回归法)Radial Basis Function(径向基函数法)Triangulation with Linear Interpolation(线性插值三角网法)Moving Average(移动平均法)Local Polynomial(局部多项式法)下面简单说明不同算法的特点。
1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
surfer详细入门教程

2)Kriging(克里金插值法)
又称空间自协方差最佳插值法,考虑信息 样品的形状、大小及与待估计块段相互 间的空间位置等几何特征以及品位的空 间结构之后,为达到线性、无偏和最小估 计方差的估计,而对每一个样品赋与一定 的系数,最后进行加权平均来估计块段品 位的方法。
它的一大缺点是没有各种投影变化。
等值线图
线框图WIREFRAME图
Wireframe是对grd文件的三维表现形式,它
用绘制线条的方式来表现grd文件 。
图像图 IMAGE MAP
Shaded Relief Map
阴影地貌图
可以用来表现地 貌,其表现形式 立体感强,画面 细腻、柔和
Surface Map
1.基本数据文件
是指ASCII码(文本)格式的数据文 件,此数据文件最少包含三列,分别为 XYZ,其中X列和Y列表示x和y坐标,Z 列为在坐标(x,y)处的值(例如,高 程、矿层厚度、矿石品位、各种观测 量)。XYZ数据文件的文件名后缀一般 为(.dat)
数据文件可以在surfer 中的工作表中手工输入,也 可以是其它软件生成的文本 文件,例如Excel表格数据, 也可以转换成surfer所需要 的数据文件。一般的,任何 转换成(.txt)结尾的数据文 件,都可以被surfer成果读 取。Surfer支持字符,所以 字符也可以用在数据文件中, 除了第一行的字符可以看做 是文件头外,其它的字符一 般被认为是surfer的缺省值, 此值在做等高线等图形时将 不会显示。
流程:
用GRID NODE EDITOR命令打开 指定的文件。点击所要白化的点,出现 Z值,再键入CTRL+B或鼠标右键中的 白化节点。
surfer 三维教程

Golden software记录一些 Holz 自己写的或整理的 Golden Software 系列软件相关的文章。
Golden Software 系列软件包括 Surfer、Grapher、Didger、Mapviewer 和 Strater,几乎是地质工作者必备的工具软件,可用于各种数据分析、数据可视化和专题图制作。
转载请注明出处。
Didger 3 教程Holz 将以 Didger 3 英文版的依据写一些教程。
Didger 3 入门教程这个入门教程向大伙介绍 Didger 的部分功能,当然是最基本的那些。
我没有数字化仪、没有GPS之类,所以许多高级的 Didger 功能我都从来用不上。
所以这个教程是一个数字化的基础教程,您看完这个教程,应当能够使用 Didger 建立自己的工程了。
这个教程是很浅薄的,学好点E文准备看 Golden Software 给您提供的用户手册罢,据说您的问题通常都能在那上面找到。
当然您还有问题就去骚扰他们的技术支持罢,不用问我,我的水平差着呢~~~下面说说课程安排:第一课- 学习如何校准一个光栅图像,不要问我关于如何校准数字化仪、GPS 之类的,我没有,我不知道。
第二课 - 学习如何数字化一个点,如何设置点的属性和数字化线条。
第三课 - 学习如何保存您的 Didger 工程并且将数据输出以供其他程序使用。
第四课 - 学习如何建立多边形,如何从多段线建立多边形等。
(没啥重要的,完全可以忽略不看)第五课 - 学习光栅图像的处理、输出和再次利用等。
(也没啥重要的,也完全可以忽略不看)这个入门教程其实比 Didger 3 本身提供的要简陋,因此如果您的 E 文比较好,不用在此流连,直接看帮助罢。
第一课 - 校准(文字版)当你要数字化之前,首先要做的是什么呢?校准!无论你使用的是扫描的光栅图片还是放在数字化仪上的图纸,首先都要选 3-256 个点进行校准。
校准点不能都在一条直线上,应该是均匀分布在图纸上的。
Surfer8.0十二种空间插值方法

2. 等值线绘制基本原理和十二种空间插值方法介绍2.1 等值线绘制基本原理等值线绘制的基本原理是,根据空间上若干离散点的属性数据(如地面高程数据、水文观测站测得的降水量和蒸发量数据、气象站测得的气压、风力、风向值等),通过内插法生成一系列光滑曲线,即等值线(同一条等值线上任意一点的属性值相等)。
需要指出的是,有的软件又将上述空间数据内插的过程称为格网化,其实二者略有不同。
所谓格网化是指采用一定的格网化方法(即数学模型)对不规则分布的原始数据点进行插值,生成在原始数据分布范围内规则间距的数据点分布[2]。
格网化最终形成的是空间上离散的格网,而不是连续的线。
无论是绘制等值线或是格网化,构建或选用合适的数学模型均是其核心关键[3]。
2.2 S urfer 8.0十二种空间插值方法介绍2.2.1反距离加权插值法(Inverse Distance to a Power)反距离加权插值法,又称谢别德法(Shepard)[4],其插值原理是将待插值点邻域内已知散乱点属性值进行加权平均,权的大小与待插点的邻域内散乱点之间的距离有关,是距离k次方的倒数(0≤k≤2,k一般取值为2)。
反距离加权插值法综合了泰森多边形的邻近点法和多元回归法等渐变方法的长处,它假设A点的属性值是在局部邻域内中所有数据点的距离加权平均值,可以进行确切的或者圆滑的方式插值。
当计算一个格网结点时,给予一个特定数据点的权值,该权值与指定方次的结点到观测点的距离倒数成比例,给每个格网结点配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0的权重,所有其它观测点被给予一个几乎为0.0的权重[5][6],并且其必须指定一个大于0的平滑系数,平滑系数通过修匀已被插值的格网来降低某些“凸显”数据展现。
反距离加权插值法是一种精确性插值法,插值生成的表面的最大值和最小值只会出现在已知样本点的位置。
Surfer---九种插值方法

Surfer---九种插值方法Surfer---九种插值方法Inverse Distance to a Power--反距离加权插值法Kriging--克里金插值法)Minimum Curvature--最小曲率Modified Shepard's Method--改进谢别德法Natural Neighbor--自然邻点插值法Nearest Neighbor--最近邻点插值法Polynomial Regression--多元回归法Radial Basis Function--径向基函数法Triangulation with Linear Interpolation--线性插值三角网法Moving Average--移动平均法Local Polynomial--局部多项式法1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。
2、克里金法克里金法是一种在许多领域都很有用的地质统计格网化方法。
surfer软件使用手册

surfer软件使用手册Surfer软件使用手册1、简介本章节介绍Surfer软件的概述和主要功能。
1.1 软件概述Surfer是一款用于地质和地理数据可视化的专业软件。
它提供了各种强大的功能,使用户能够创建地图、插值数据、分析空间关系等等。
1.2 主要功能- 地图创建:Surfer允许用户创建二维和三维地图,包括等值线图、填充图、等高线图等。
- 数据插值:Surfer支持各种插值方法,包括克里金插值、样条插值等。
用户可以将散点数据插值成光滑的曲面。
- 空间分析:Surfer提供了丰富的空间分析工具,包括点匹配、区域统计、距离计算等。
- 3D可视化:Surfer具备强大的三维数据可视化功能,用户可以轻松创建三维地貌、地质模型等。
- 输出和共享:Surfer支持将结果输出为多种文件格式,包括图片、地图、图表等。
用户还可以将地图共享为交互式文件。
2、安装与配置本章节介绍Surfer软件的安装和配置过程。
2.1 安装Surfer- Surfer安装程序- 运行安装程序并按照提示进行安装- 完成安装并启动Surfer软件2.2 配置Surfer- 设置默认工作目录- 定义坐标系统- 配置插值方法- 其他配置项3、地图创建本章节介绍使用Surfer创建地图的方法。
3.1 导入数据- 导入点数据- 导入矢量数据- 导入栅格数据3.2 创建地图- 创建等值线图- 创建填充图- 创建等高线图- 其他类型地图的创建方法4、数据插值本章节介绍使用Surfer进行数据插值的方法。
4.1 插值方法- 克里金插值- 样条插值- 其他插值方法4.2 插值参数设置- 插值网格设置- 插值参数设置- 其他插值参数设置选项5、空间分析本章节介绍Surfer的空间分析功能。
5.1 点匹配- 点匹配方法- 点匹配结果分析5.2 区域统计- 区域统计方法- 区域统计结果分析5.3 距离计算- 距离计算方法- 距离计算结果分析6、3D可视化本章节介绍Surfer的三维可视化功能。
surfer插值法介绍

在科学计算领域中,空间插值是一类常用的重要算法,很多相关软件都内置该算法,其中GodenSoftware 公司的Surfer软件具有很强的代表性,内置有比较全面的空间插值算法,主要包括:Inverse Distance to a Power(反距离加权插值法)Kriging(克里金插值法)Minimum Curvature(最小曲率)Modified Shepard's Method(改进谢别德法)Natural Neighbor(自然邻点插值法)Nearest Neighbor(最近邻点插值法)Polynomial Regression(多元回归法)Radial Basis Function(径向基函数法)Triangulation with Linear Interpolation(线性插值三角网法)Moving Average(移动平均法)Local Polynomial(局部多项式法)下面简单说明不同算法的特点。
1、距离倒数乘方法距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。
方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。
对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。
换言之,该结点被赋给与观测点一致的值。
这就是一个准确插值。
距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。
用距离倒数格网化时可以指定一个圆滑参数。
大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。
SURFER常用版本中的各种插值法

Surfer常用插值方法1 反距离加权插值法反距离加权插值法(Inverse Distance to a Power)首先是由气象学家和地质工作者提出的,后来由于D.Shepard的工作被称为谢别德法(Shepard方法),它的基本原理是设平面上分布一系列离散点,己知其位置坐标(51- ,)和属性值a(i-1,2,),p(z,)为任一格网点,根据周围离散点的属性值,通过距离加权插值求P 点属性值。
距离加权插值法综合了泰森多边形的邻近点法和多元回归法的渐变方法的长处,它假设P点的属性值是在局部邻域内中所有数据点的距离加权平均值,可以进行确切的或者圆滑的方式插值。
周围点与P点因分布位置的差异,对P( )影响不同,我们把这种影响称为权函数m ,),方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降对于一个较大的方次,较近的数据点被给定一个较高的权重份额;对于一个较小的方次,权重比较均匀地分配给各数据点。
计算一个格网结点时,给予一个特定数据点的权值,与指定方次的结点到观测点的距离倒数成比例。
当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。
当一个观测点与一个格网结点重合时,该观测点被给予一个实际为1.0的权重.所有其它观测点被给予一个几乎为0.0的权重。
换言之,该结点被赋给与观测点一致的值.这就是一个准确插值。
权函数主要与距离有关,有时也与方向有关.若在P点周围四个方向上均匀取点.那么可不考虑方向因素,这时P(Z) \、五[ ,)]“\1 1式中( ,)一-4 t)。
+(y—) .表示由离散点( .)至P(x。
)点的距离)为要求的待插点的值。
权函数.w ( ,v)一1/Ed,(一v)] .“值一般取为2。
反距离加权插值法是GIS软件根据点数生成规则格网数据文件的最常见的方法,计算值易受数据点集群的影响,计算结果常出现一种孤立点数据明显高于周围数据点的“鸭蛋”分布模式,可在插值过程中通过滤波来处理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
is the interpolated value for grid node "j"; Zi are the neighboring points; dij is the distance between the grid node "j" and the neighboring point "i";
中等数据量(250到1000数据点),线性内插三角 形法网格化很快,并生成很好代表原始数据特点的 网格。Kriging法和径向基本函数法较慢,也可以产 生高质量的网格。 大的数据量(>1000数据点),最小曲率法最快,网格 足以代表原始数据特点。线性内插三角形法网格化 较慢,网格有足够的代表性。
以下的建议仅仅是一般的推荐
径向基本函数法类似Kriging法中的变异图。 在大多数情况下,多重二次曲面函数是最合 乎要求的。 R2参数是一个决定锐化或平滑的参数。 R2值愈大,山顶愈圆滑,等值线愈平滑。R2 合理的实验值是在一个平均样本间距和半个 平均样本间距之间。
最近临点法( 最近临点法(Nearest Neighbor) )
径向基本函数法 (Radial Basis Functions) )
径向基本函数法是一种准确插值的方法。其 中的多重二次曲面法被许多人认为是最好的 方法。在插值生成一个网格结点时,这些函 数确定了使用数据点的最优权重组。 径向基本函数法的函数类型包括:
反比多重二次曲面法; 多重对数; 多重二次曲面法; 自然三次样条和薄板样条。
平滑插值用于并不十分依赖原始数据,只试 图了解Z值的总体变化趋势的情况。 平滑插值不会给任何原始数据点以权重1,即 使某网格结点正好位于原始数据点。
距离反比法 (Inverse Distance to a Power)
一种加权平均插值的网格化方法。 在计算一个网格结点的Z值时,一定范围内,所有 数据点的权重的和为1,权重与某数据点到该结点 距离成反比,愈靠近该结点的原始数据点,其权重 愈大。 如果网格结点正好位于某原始数据点,该结点的Z 值就等于此原始数据点的Z值,即此原始数据点对 于该结点的权重为1,而其它数据点对于该结点的 权重为0。 距离反比法是一种准确插值方法。
一种相临点加权平均的内插算法,权重与 borrowed 区成正比。不能外推。
推荐的构造网格的数学模型
不同的网格化方法可以得到不同的网格文件,用 户应当选用最能代表自己数据特点的方法,选择网 格化方法时应当考虑原始数据点数量的多寡。 10 10个或10个以下的数据点,除了反映数据的一 10 般趋势外,没有多大意义。这样少的点,三角形法 无效,数据点<250个时,具线性变异图的Kriging法, 多重二次曲面法的径向基本函数法都可以产生较好 代表原始数据特点的网格。
权重系数(Power)的值反映随着数据点到网格结 点距离的增加,其权重降低的程度。
当权重系数为0时,所计算出的网格面是一个接近水平的 平面,其Z值为所有原始数据点的平均值。 随着权重系数的增加,形成最临近点插值,导致表面变 成多边形。
平滑参数(Smoothing)把不确定性与用户输入 的数据联系起来,平滑参数愈大,相邻网格的影响 愈小。平滑参数大于0,则没有任何一个数据点对 于某个结点的权重为1,即使该数据点正好位于网 格结点上。
多项式回归法(Polynomial on)
多项式回归法用来确定用户数据整体的趋势或构造一种模型。 多项式回归法实际上并不是一种插值,因为它并不试图预测 未知的Z值。用户可以在表面选定(Surface Difination)框 内选择以下4种曲面中的任一种。
①简单平面(Simple planer surface): z(x,y)=A+Bx+Cy ②双线性鞍形(Bi-linear saddle): z(x,y)=A+Bx+Cy+Dxy ③二次表面(Quadratic surface): z(x,y)=A+Bx+Cy+Dx2+Exy+Fy2 ④三次表面(Cubic surface): z(x,y)=A+Bx+Cy+Dx2+Exy+Fy2+Gx3+H x2y+Ix y2+Jy3 或由用用户自定义。 选定的曲面方程相应显示在下面;右面的 参数框内则显示X、Y和总的最高项次。 用户也可以利用Parameters框自定义多项 式方程。
Kriging法
Kriging法是用南美采矿工程师D. G. Krige的名字命名的一种 地学统计内插方法,原来是 试图比较准确地预测矿石储量。 已经发现在许多领域非常有用。Kriging法描述数据中隐含的 趋势。比如孤立的高值点“牛眼”,在使用Kriging法网格化 时可连成“山脊”。 变异图模型(Variogram Model):用来确定插值每一个 结点时所用数据点的邻域,以及在计算结点时给予数据点的 权重。 Surfer提供了多种最常用的变异图模型,它们是指数、高 斯模型、线性、对数、矿块效应、幂、二次模型、有理数二 次模型、球面模型和波(空洞效应)。如果拿不准用哪一种 变异图,可选用线性变异图,大多数情况下,效果较好。
距离反比法最快,但是围绕数据点,有产生“牛眼” 效应的趋势。 大部分情况下,具有线性变异图的Kriging法是十分 有效的,应首先予以推荐。其次是很接近的经向基 本函数法中的多重二次曲面法。这两种方法都能产 生较好地代表原始数据的网格。但对于大量数据的 网格化,Kriging法比较慢。
最小曲率法构成平滑的曲面,且多情况下, 网格化速度也快。 多项式回归是一种趋势面分析,反映整体趋 势。对于任何数量的数据点,网格化的速度 都非常快,但构成的网格缺少数据的局部细 节。 径向基本函数法十分灵活,与Kriging法产生 的网格十分类似。
插值方法分为两种:精确插值(Exact interpolators)和平滑插值(Smoothing interpolators)。 精确插值指当网格结点正好位于原始数据点 时,该结点的Z值等于此原始数据点的Z值。
对于加权平均内插算法,这就意味着此原始数据 点的权重为1,而其它数据点对于该结点的权重 为0。 增加网格密度,就增大了网格结点正好位于原始 数据点的可能性。
三角形线性插值法
(Triangulation with Linear Interpolation)
三角形线性插值法是一种准确插值,方法是在相邻 点之间连线构成三角形,并且保持任一三角形的边 都不与其它三角形的边相交。这样在网格范围内由 一系列三角形平面构成拼接图。 由于数据点平均分布,在通过地形变化显示断层 线时,三角形法非常有效。 因为每一个三角形都构成一个平面,所有的结点 都在三角形中,其坐标被三角形平面方程唯一地确 定。 对于有200至1000个数据点,且平均地分配在网 格区域里时,用三角形线性插值法最好。
最近临点法用最临近的数据点来计算每个 网格结点的值。这种方法通常用于已有规则 网格只需要转换为Surfer网格文件时,或数据 点几乎构成网格,只有个别点缺失,该方法 可以有效地填充“空洞”。 通过设置搜寻椭圆半径的值小于数据点之 间距离的方法,给缺少数据点的结点赋值为 空白。
普通临点法 Natural Neighbor
2.网格化方法 网格化方法
网格化基础知识
网格化是把以XYZ数据文件格式表示的、通 常是不规则分布的原始数据点,经过数学处 理,构筑一个规则的空间矩形网格的过程。 原始数据的不规则分布,造成缺失数据的 “空洞”。 网格化则用外推或内插的算法填充了这些 “空洞”。
大多数情况下,采用加权平均插值算法, 即所有其它参数相等的条件下,愈靠近结点 (计算出的规则点)的数据(原始数据点), 对计算该结点的Z值贡献愈大。
The equation used for Inverse Distance to a Power is:
where:
hij is the effective separation distance between grid node "j" and the neighboring point "i."
距离反比法的特点之一就是在网格区内围绕 着某些数据点可能产生牛眼状等值线 (Bull’s-eyes)。 距离反比法是一种快速网格化的方法,在 小于500数据点时,可以用全部数据点来生成 网格。
最小曲率法 (Minimum Curvature) )
这是一种在地学中广泛应用的网格化方法。 由最小曲率法构成的插值表面像一个线性弹 性薄板,是一个尽可能与原始数据点吻合的 最平滑的曲面。 最小曲率法不是准确插值,是典型的平滑插 值。
Shepard‘s法与距离反比法插值法相似,但没 有产生等值线“牛眼”效应的缺点。 线性内插三角形法对于中等数量的数据点, 网格化很快。一个优点是,当有足够的数据 点时,三角形法可以反映出数据文件所内含 的不连续性。例如断层线。
各向异性(Anisotropy):指在用原始数据点计算 网格点Z值时,对沿某一个坐标轴方向的数据点比 其它方向的数据点给予更多的权重。 多数情况下,在构筑网格时,不需要考虑方向性, 因为大多数等值线图或线网图的X、Y坐标是同一比 例尺。这时,1X单位=1Y单位。 当确实需要考虑各向异性时,Ratio对话框内为1个 Ratio 1 X单位相对与一个Y单位的比例。如选Ratio为2,则 意味1X单位=2Y单位.下面沿X轴方向伸长的椭圆 示意不同方向给予不同的权重。 选用不同的网格化方法,各向异性的参数略有不同。
最小曲率法的对话框包括以下内容: 最大残差(Max Reciduals):单位与数据的相同,比较 合适的值是数据精度的10%。缺省的最大残差为 0.001 (Zmax - Z min) 最大重复参数(Max lterations):通常设为网格结点数 的1到2倍。例如,对于50×50的网格,最大重复参数在 2500与5000之间。 内部和边缘张性系数(Internal and Boundary Tension): 设定弹性薄板内部和边缘弯曲度的参数。该值愈大,弯曲愈 小。缺省值均为0。 松弛系数(Relaxation Factor):算法参数,通常,该值 愈大,迭代算法会聚愈快。缺省值为1,一般不用另设定。
